Introduction

Local reactivity parameters are necessary to differentiate the reagent behavior of atoms forming a molecule. The Fukui function [1,2,3,4] [f(r)] and local softness [5, 6] [s(r)] are two of the most commonly used local reactivity parameters (Eq. 1).

$$ {\displaystyle \begin{array}{l}f\left(\mathbf{r}\right)={\left(\frac{\partial \rho \left(\mathbf{r}\right)}{\partial N}\right)}_{\nu}\\ {}s\left(\mathbf{r}\right)={\left(\frac{\partial \rho \left(\mathbf{r}\right)}{\partial \mu}\right)}_{\nu }={\left(\frac{\partial \rho \left(\mathbf{r}\right)}{\partial N}\right)}_{\nu}\cdot {\left(\frac{\partial N}{\partial \mu}\right)}_{\nu }=f\left(\mathbf{r}\right)\cdot S\end{array}} $$
(1)

The Fukui function is associated primarily with the response of the density function of a system to a change in the number of electrons (N) under the constraint of a constant external potential [v(r)]. The mathematical definitions of the Fukui function and local softness (Eq. 1) come from the so-called ensembles of the conceptual density functional theory (C-DFT) [7] where all global, local and non local reactivity descriptors are hierarchically organized. The Fukui function arises from the canonical ensemble where the number of electrons and the external potential are the essential variables. Meanwhile, the number of electrons and the electronic chemical potential are the essential variables for the local softness.

Due to the discontinuity of the electron density with regard to N, finite difference approximation leads to three types of Fukui function: f+(r), f−(r) and f0(r). They are defined as follows:

$$ {f}^{+}\left(\mathbf{r}\right)={\rho}_{N_0+1}\left(\mathbf{r}\right)-{\rho}_{N_0}\left(\mathbf{r}\right),\mathrm{fornucleophilic}\ \mathrm{attack}, $$
(2)
$$ {f}^{-}\left(\mathbf{r}\right)={\rho}_{N_0}\left(\mathbf{r}\right)-{\rho}_{N_0-1}\left(\mathbf{r}\right),\mathrm{forelectrophilic}\kern0.17em \mathrm{attack}, $$
(3)
$$ {f}^0\left(\mathbf{r}\right)=\frac{1}{2}\left({f}^{+}\left(\mathbf{r}\right)+{f}^{-}\left(\mathbf{r}\right)\right),\mathrm{for}\ \mathrm{neutral}\ \left(\mathrm{or}\ \mathrm{radical}\right)\ \mathrm{attack} $$
(4)

Theoretical development

The energy change [8] (ΔE) due to the electron transfer (ΔN) satisfies the parabolic approximation:

$$ \varDelta E\approx {\left(\frac{\partial E}{\partial N}\right)}_{\upsilon}\varDelta N+\frac{1}{2}{\left(\frac{\partial^2E}{\partial {N}^2}\right)}_{\upsilon}\kern0.24em \varDelta {N}^2\approx \mu \kern0.24em \varDelta N+\frac{1}{2}\eta \kern0.24em \varDelta {N}^2 $$
(5)

where μ and η are the electronic chemical potential and global hardness. Perdew et al. [9] show how the Hohenberg-Kohn theorem is extended to a fractional electron number (N), and the implications of derivative discontinuity for conceptual DFT are explored by Ayers and colleagues [10, 11]. Taking into account Eq. (5), and that the total energy is a functional of the density, it is reasonable to think that the second order expansion Eq. (6) can be an appropriate approximation.

$$ \varDelta {\rho}_N\left(\mathbf{r}\right)\approx {\left(\frac{\partial {\rho}_N\left(\mathbf{r}\right)}{\partial N}\right)}_{\upsilon}\varDelta N+\frac{1}{2}{\left(\frac{\partial^2{\rho}_N\left(\mathbf{r}\right)}{\partial {N}^2}\right)}_{\upsilon}\kern0.24em \varDelta {N}^2 $$
(6)

if we substitute the values ΔN= 1 and ΔN= −1 in Eq. (6), and also calculate \( \varDelta {\rho}_N^{-}\left(\mathbf{r}\right) \) (corresponding to ΔN= −1) and \( \varDelta {\rho}_N^{+}\left(\mathbf{r}\right) \) (corresponding to ΔN= 1). And finally, substituting in Eq. (6), we obtain:

$$ {\displaystyle \begin{array}{l}\varDelta {\rho}_N^{-}\left(\mathbf{r}\right)={\rho}_{N-1}\left(\mathbf{r}\right)-{\rho}_N\left(\mathbf{r}\right)\approx -{\left(\frac{\partial {\rho}_N\left(\mathbf{r}\right)}{\partial N}\right)}_{\upsilon }+\frac{1}{2}{\left(\frac{\partial^2{\rho}_N\left(\mathbf{r}\right)}{\partial {N}^2}\right)}_{\upsilon}\kern0.24em \\ {}\varDelta {\rho}_N^{+}\left(\mathbf{r}\right)={\rho}_{N+1}\left(\mathbf{r}\right)-{\rho}_N\left(\mathbf{r}\right)\approx {\left(\frac{\partial {\rho}_N\left(\mathbf{r}\right)}{\partial N}\right)}_{\upsilon }+\frac{1}{2}{\left(\frac{\partial^2{\rho}_N\left(\mathbf{r}\right)}{\partial {N}^2}\right)}_{\upsilon}\;\end{array}} $$
(7)

and we find a very simple system of equations with two unknowns; by solving them, we obtain Eq. (8). Expressions of this type (Eq. 6) have been used in previous works [12,13,14]. Also, implicit in the two articles the introduction of the concept of the dual descriptor [15, 16] because the expression used for the second derivative of the density with respect to the number of electrons corresponds to this kind of quadratic interpolation. Figure 1 graphically represents the physical meaning of the main parameters of Eqs. (6–8). It can be seen that the new formula of f(r) (see Eq. 8) is the same as that of f0(r) [see Eq. (4), neutral attack], this is logical since the quadratic expansion does not imply an electrophilic or nucleophilic attack.

$$ {\displaystyle \begin{array}{l}{\left(\frac{\partial {\rho}_N\left(\mathbf{r}\right)}{\partial N}\right)}_{\upsilon }=f\left(\mathbf{r}\right)\approx \frac{1}{2}\cdot \left({\rho}_{N+1}\left(\mathbf{r}\right)-{\rho}_{N-1}\left(\mathbf{r}\right)\right)\\ {}{\left(\frac{\partial^2{\rho}_N\left(\mathbf{r}\right)}{\partial {N}^2}\right)}_{\upsilon }={f}^{(2)}\left(\mathbf{r}\right)\approx {\rho}_{N+1}\left(\mathbf{r}\right)-2\cdot {\rho}_N\left(\mathbf{r}\right)+{\rho}_{N-1}\left(\mathbf{r}\right)\end{array}} $$
(8)
Fig. 1
figure 1

Graphic representation of the main parameters of Eqs. (6–8)

Full size image

On the other hand, the original operational formula proposed by Morell et al. [16] for the dual descriptor [15, 17, 18] is:

$$ {\left(\frac{\partial^2\rho \left(\mathbf{r}\right)}{\partial {N}^2}\right)}_{\nu \left(\mathbf{r}\right)}={f}^{(2)}\left(\mathbf{r}\right)=\rho {\left(\mathbf{r}\right)}_{N+1}-2\cdot \rho {\left(\mathbf{r}\right)}_N+\rho {\left(\mathbf{r}\right)}_{N-1} $$
(9)

As can be seen, the formula obtained by Morell et al. in Eq. (9) is the same as the formula of Eq. (8).

What changes when there is degeneracy of frontier molecular orbitals?

The use of these operational formulae, Eq. (9), can result in failure when applying them to molecular systems that present degeneracy in their frontier molecular orbitals [19]. The issue of degeneracy in conceptual DFT is not restricted to degenerate frontier orbitals because (in rare cases) you can have degenerate ground states in DFT without degenerate frontier orbitals [19,20,21,22].

To overcome this limitation of the dual descriptor (and Fukui functions), a more general operational formula was proposed by Martínez-Araya [23, 24]:

$$ {f}^{(2)}{\left(\mathbf{r}\right)}_{\mathrm{Mart}\acute{\text{\i}} \mathrm{nez}-\mathrm{Araya}}\approx \frac{q\cdot \rho {\left(\mathbf{r}\right)}_{N+p}-\left(p+q\right)\cdot \rho {\left(\mathbf{r}\right)}_N+p\cdot \rho {\left(\mathbf{r}\right)}_{N-q}}{p\cdot q} $$
(10)

where p and q stand for the degree of degeneracy of LUMO and HOMO, respectively.

When we apply these ideas proposed by Martínez-Araya to the system of Eq. (7), we obtain a new operative formula of f(2)(r) for degenerate cases:

$$ {f}^{(2)}{\left(\mathbf{r}\right)}_{\mathrm{Quadratic}\kern0.34em \mathrm{expansion}}\approx \frac{2\cdot \left[q\cdot \rho {\left(\mathbf{r}\right)}_{N+p}-\left(p+q\right)\cdot \rho {\left(\mathbf{r}\right)}_N+p\cdot \rho {\left(\mathbf{r}\right)}_{N-q}\right]}{p\cdot q\cdot \left(p+q\right)} $$
(11)

which is slightly different from the formula obtained by Martínez-Araya Eq. (10), but they are proportional. On the other hand, Eq. (12) is the operative formula for f0(r) in cases with degeneracy (applying the ideas of Martínez-Araya),

$$ {f}^0{\left(\mathbf{r}\right)}_{\mathrm{Mart}\acute{\text{\i}} \mathrm{nez}-\mathrm{Araya}}=\frac{q\cdot \rho {\left(\mathbf{r}\right)}_{N+p}+\left(p-q\right)\cdot \rho {\left(\mathbf{r}\right)}_N-p\cdot \rho {\left(\mathbf{r}\right)}_{N-q}}{2\cdot p\cdot q} $$
(12)

on the other hand, starting from the system of Eq. (7), we obtain:

$$ f{\left(\mathbf{r}\right)}_{\mathrm{Quadratic}\kern0.34em \mathrm{expansion}}=\frac{q^2\cdot \rho {\left(\mathbf{r}\right)}_{N+p}+\left({p}^2-{q}^2\right)\cdot \rho {\left(\mathbf{r}\right)}_N-{p}^2\cdot \rho {\left(\mathbf{r}\right)}_{N-q}}{\left({p}^2\cdot q+{q}^2\cdot p\right)} $$
(13)

In this case, it can be seen that f0(r)Martínez−Araya and f(r)Quadratic  expansion are not proportional. Appendix I in supplementary material includes a simple example that complements this conclusion and shows that the new operative formulas f (r) and f (2)(r) are different from the old ones. Finally, we propose a parabolic expansion as an alternative methodology to the finite difference approximation, and we rationalize this affirmation with the very simple example shown in Appendix II.

The new operational formulae for Fukui function and dual descriptor taking into account degrees of degeneracy in HOMO and LUMO are different to those ones based on finite difference. That makes sense in the case of a fractional value of ΔN. But when there is a degree of degeneracy greater than 1, meaning ΔN > 1, in such case there is no certainty that the Taylor expansion (Eq. 6) converges. The,n from the mathematical point of view, finite difference is a suitable approximation because it does not depend on the means of truncation of the Taylor expansion. That is why Eqs. (10) and (12) can be used as reference expressions, so that:

$$ {f}^{(2)}{\left(\mathbf{r}\right)}_{\mathrm{Mart}\acute{\text{\i}} \mathrm{nez}-\mathrm{Araya}}-{f}^{(2)}{\left(\mathbf{r}\right)}_{\mathrm{Quadratic}\kern0.34em \mathrm{expansion}}=\left(1-\frac{2}{p+q}\right)\;{f}^{(2)}{\left(\mathbf{r}\right)}_{\mathrm{Mart}\acute{\text{\i}} \mathrm{nez}-\mathrm{Araya}} $$
(14)

and for the Fukui function (the expression is not so simple):

$$ {\displaystyle \begin{array}{c}{f}^0{\left(\mathbf{r}\right)}_{\mathrm{Mart}\acute{\text{\i}} \mathrm{nez}-\mathrm{Araya}}-f{\left(\mathbf{r}\right)}_{\mathrm{Quadratic}\kern0.34em \mathrm{expansion}}=\\ {}=\frac{q\cdot \rho {\left(\mathbf{r}\right)}_{N+p}+\left(p-q\right)\cdot \rho {\left(\mathbf{r}\right)}_N-p\cdot \rho {\left(\mathbf{r}\right)}_{N-q}}{2\cdot p\cdot q}-\frac{q^2\cdot \rho {\left(\mathbf{r}\right)}_{N+p}+\left({p}^2-{q}^2\right)\cdot \rho {\left(\mathbf{r}\right)}_N-{p}^2\cdot \rho {\left(\mathbf{r}\right)}_{N-q}}{\left({p}^2\cdot q+{q}^2\cdot p\right)}\end{array}} $$
(15)

Computational details

All the structures included in this study were optimized at B3LYP/6-31G(d) [25, 26] theory level by using the Gaussian09 package. [27] The densities used in the new methodology were calculated at the same level of calculation for the neutral molecule, the cation and anion, through Gaussian09 software.

The new indices included in this study were calculated with a modified version of UCA-FUKUI v.2.1 software (http://www2.uca.es/dept/quimica_fisica/software/UCA-FUKUI_v2.exe) [28]. Figure 2 includes two screenshots of the main menu showing the calculation modules that have been added to obtain the new indexes. Figures S1–S3 in the supplementary material show some screenshots of the UCA-FUKUI software displaying the correspondence between the program interface and the equations of the text.

Fig. 2
figure 2

Upper panel UCA-FUKUI main menu: atomic Fukui indices based on a quadratic expansion. Lower panel UCA-FUKUI main menu: Fukui function based on a quadratic expansion

Full size image

Results and discussion

Obtaining atomic indices (condensed-to-atom)

Starting from Eq. (7) and by taking into account the response-of-molecular-fragment approach [29], (which is equivalent to the fragment-of-molecular-response approach for Hirshfeld partitioning [30,31,32]), the next condensed-to-atom system can be obtained:

$$ {\displaystyle \begin{array}{l}\varDelta {q}_k^{-}={q}_k^{N-r}-{q}_k^N\approx -{\left(\frac{\partial {q}_k^N}{\partial N}\right)}_{\upsilon}\cdot r+\frac{1}{2}{\left(\frac{\partial^2{q}_k^N}{\partial {N}^2}\right)}_{\upsilon}\cdot {r}^2\;\\ {}\varDelta {q}_k^{+}={q}_k^{N+p}-{q}_k^N\approx {\left(\frac{\partial {q}_k^N}{\partial N}\right)}_{\upsilon}\cdot p+\frac{1}{2}{\left(\frac{\partial^2{q}_k^N}{\partial {N}^2}\right)}_{\upsilon}\cdot {p}^2\end{array}} $$
(16)

where r and p are the global net charges of the ions. Solving the system:

$$ {\displaystyle \begin{array}{l}{\left(\frac{\partial {q}_k^N}{\partial N}\right)}_{\upsilon }=\frac{r^2\cdot {q}_k^{N+p}+\left({p}^2-{r}^2\right)\cdot {q}_k^N-{p}^2\cdot {q}_k^{N-r}}{\left({p}^2\cdot r+{r}^2\cdot p\right)}\\ {}{\left(\frac{\partial^2{q}_k^N}{\partial {N}^2}\right)}_{\upsilon }=\frac{2\cdot \left[r\cdot {q}_k^{N+p}-\left(p+r\right)\cdot {q}_k^N+p\cdot {q}_k^{N-r}\right]}{p\cdot r\cdot \left(p+r\right)}\end{array}} $$
(17)

where \( {q}_k^N \), \( {q}_k^{N+p} \) and \( {q}_k^{N-s} \) are the net atomic charges calculated with some population analysis (Hirshfeld, Mulliken, ...) for the neutral molecule and the corresponding ions. As an example, Table 1 shows the condensed \( {f}_k^{\mathrm{Quadratic}\kern0.34em \mathrm{expansion}} \) and \( {f}_k^0 \)(finite difference approximation [33]) indices obtained for SF6, which has triply degenerate HOMO, using the three different population analysis: Hirshfeld [34,35,36], Mulliken [37] and natural population analysis (NPA) [38,39,40]. As can be seen in Table 1, the \( {f}_k^{\mathrm{Quadratic}\kern0.34em \mathrm{expansion}} \) and \( {f}_k^0 \) indices are different.

Table 1 Comparison of the \( {f}_k^{\mathrm{Quadratic}\kern0.34em \mathrm{expansion}} \) indices with the corresponding \( {f}_k^0 \)
Full size table

Advantages of this method: Generalization of the finite difference approximation

The quadratic expansion Eq. (6) provides an important advantage, allowing interpolation Δρ(r) for fractional values of ΔN (−1 <ΔN<1). Thanks to this, we can use the finite difference approximation more generally. Suppose that ΔN is the fractional value ΔN∗, and, that, by substituting this value in Eq. (6), we are led to Δρ∗(r):

$$ \varDelta \rho {\left(\mathbf{r}\right)}^{\ast}\approx {\left(\frac{\partial \rho \left(\mathbf{r}\right)}{\partial N}\right)}_{\upsilon}\varDelta {N}^{\ast }+\frac{1}{2}{\left(\frac{\partial^2\rho \left(\mathbf{r}\right)}{\partial {N}^2}\right)}_{\upsilon}\kern0.24em {\left(\varDelta {N}^{\ast}\right)}^2 $$
(18)

Now, the function Δρ(r)∗ allows the finite difference approximation to be applied to calculate the Fukui indices in a more general way:

$$ f{\left(\mathbf{r}\right)}^{\ast }=\frac{\varDelta \rho {\left(\mathbf{r}\right)}^{\ast }}{\varDelta {N}^{\ast }} $$
(19)

Note that Fukui functions f(r)+ and f(r)− are particular cases of Eq. (19), where ΔN∗ takes the non-fractional values +1 and − 1. The recent work from the Gazquez group [41, 42] is the closest approach that we have been able to find in relation to this idea.

On the other hand, the amount of charge transfer ΔNA : B associated to the formation of A:B complex from acid A and base B, may be written as [43]:

$$ \varDelta {N}^{A:B}=\frac{\mu_B-{\mu}_A}{\eta_A+{\eta}_B} $$
(20)

then, combining Eqs. (18), (19), and (20), we obtain the formula:

$$ f{\left(\mathbf{r}\right)}^{A:B}=\frac{\varDelta \rho {\left(\mathbf{r}\right)}^{A:B}}{\varDelta {N}^{A:B}} $$
(21)

that allows to estimate an approximate Fukui function corresponding to a molecule (for example an acid A) when it is attacked by another concrete molecule (for example a base B). It is important to note that f(r)A : B (Eq. 21) is being calculated with a charge variation ΔNA : B with physical meaning, and the same can be said for variations Δρ(r)A : B. The idea of using a model based on chemical potentials μA and μB, instead of a finite-difference approximation, can be traced back to Parr and Bartolotti [44] (the value of such an approach and also its limitations was recently stressed by Heidar-Zadeh et al. [45, 46] and the Gazquez group recently showed that the parabolic model is especially relevant [47]).

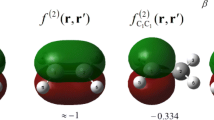
As an example, Fig. 3 (left) shows function f(r)A : B for the dienophile CH2CHCHO when it is attacked by a H2 molecule. In Fig. 3 (right) the function of Fukui f(r)− (Eq. 3) has been included to facilitate comparison. The images are similar because the two functions represent the nucleophile character of the CH2CHCHO molecule but they show some differences since function f(r)A : B takes into account the characteristics of the attacker (H2 molecule). All the images of Fig. 3 have been performed with Gaussview [48] and the “.cub” files used as a starting point were obtained from UCA-FUKUI software.

Fig. 3
figure 3

Left Function f(r)A : B of the CH2CHCHO when it is attacked by a H2 molecule. Right Fukui function f(r)− of the CH2CHCHO. The four images were obtained with isovalue: 0.0002

Full size image

Starting from the previous idea and Eq. (17) the condensed-to-atom value \( \varDelta {q}_k^{\ast } \) of Eq. (22) can be obtained:

$$ \varDelta {q}_k^{\ast}\approx {\left(\frac{\partial {q}_k^N}{\partial N}\right)}_{\upsilon}\varDelta {N}^{\ast }+\frac{1}{2}{\left(\frac{\partial^2{q}_k^N}{\partial {N}^2}\right)}_{\upsilon}\kern0.24em {\left(\varDelta {N}^{\ast}\right)}^2 $$
(22)

The values \( \varDelta {q}_k^{\ast } \) and ΔN∗ lead to the operative formula:

$$ {f}_k^{\ast }=\frac{\varDelta {q}_k^{\ast }}{\varDelta {N}^{\ast }} $$
(23)

Note that the Fukui indices \( {f}_k^{+} \) and \( {f}_k^{-} \) are particular cases of Eq. (21). Finally, combining Eqs. (22), (23), and (20) we obtain the formula:

$$ {f}_k^{A:B}=\frac{\varDelta {q}_k^{A:B}}{\varDelta {N}^{A:B}} $$
(24)

that is the condensed-to-atom version of Eq. (21).

Figure 4 shows the parameters \( {f}_k^{A:B} \) calculated for the dienophile CH2CHCl when it is attacked by different reagents (Hirshfeld population analysis was used to obtain atomic populations). The attackers A–C correspond to a set of dienes (see Fig. S4 in the Supplementary material), in addition the attackers H3O+ and OH− have been included. The condensed-to-atom indices \( {f}_k^{+} \), \( {f}_k^{-} \) and \( {f}_k^0 \) (Eqs. 2–4), nucleophilic, electrophilic and neutral attacks) have also been added for comparison. When the attacker is very electrophilic (for example see H3O+) the \( {f}_k^{A:B} \) values are close to the curve \( {f}_k^{-} \) (electrophilic attack); on the contrary, when the attacker is very nucleophilic (for example see OH−) the \( {f}_k^{A:B} \) values are close to the curve \( {f}_k^{+} \) (nucleophilic attack). Where the attacker possesses an electronic chemical potential similar to CH2CHCl (for example the dienes A-C) the \( {f}_k^{A:B} \) values tend to curve \( {f}_k^0 \) (neutral or radical attack). Figure S2 in the supplementary material shows an enlargement of Fig. 4 where D–H dienes, H2, HCl and Cl2 attackers have also been included (the data of Figs. 4 and S5 are shown in Table S1 in the supplementary material). Figures S6 to S10 of the Supplementary Material include some equivalent graphics for the CH2CHCHO, CH2CHNO2, CH2CHCN, CH2CHCH3 and CH2CHOCH3 molecules (see Fig. S11) and the results are equivalent to those shown in Fig. 4. In addition, Figure S12 in the Supplementary Material includes an additional graphic achieved from “atoms in molecules” (AIM) [49,50,51] theory through the AIMAll software (http://aim.tkgristmill.com/index.html), Figure S13 includes a graphic achieved from natural population analysis and Fig. S14 a graphic achieved from Mulliken approximation with a minimal basis set [52, 53] for the CH2CHCl reagent. The results, shown on these graphs, are qualitatively the same as those shown in Fig. 4. The comparison of all these methodologies led to the conclusion that the calculation method used to obtain the atomic populations does not change qualitatively the conclusions obtained.

Fig. 4
figure 4

Parameter \( {f}_k^{A:B} \) calculated with Eq. (21) and Hirshfeld population analysis for the CH2CHCl molecule taking into account different attackers. The parameters \( {f}_k^{+} \), \( {f}_k^{-} \) and \( {f}_k^0 \) have been added for comparison

Full size image

Future perspectives

Our intention is to modify the UCA-FUKUI [28] software, based on “conceptual DFT” and specialized in the calculation of local reactivity indices, to introduce the new definition of Fukui’s function in some methodologies (bond-reactivity-indices calculation and improved-frontier-molecular-orbital approximation) implemented in the program [54,55,56]. Once the software works properly with the new definitions, we will make representative calculations in order to compare the results with those obtained from previous definitions.

Conclusions

A new way of calculating f(r) and f(2)(r) has been developed, resulting in new operative formulas. The Fukui function has been obtained for those cases where one or both of the frontier orbitals are degenerate, and a more general operative formula was obtained. The new formulae are in agreement with the usual formulae but only in cases without degeneracy. The new f(2)(r) function is identical to the previous formula of dual descriptor in all cases where the frontier molecular orbitals are not degenerate, and in those cases with degeneracy it has been found that they are proportional functions. Finally, a new way of applying the finite difference approximation has been developed that leads to more realistic results (with more physical meaning) than the usual formulas.