Introduction

One of the essential tasks in chemistry is the analysis of chemical observations and their classification to ultimately be able to rationalize them in a model that even allows predicting the outcome of future experiments. This quite ambitious task has been met to admirable extent by introducing such classifications as acids and bases, hard and soft substances, and many more. Over time, a vast toolbox of concepts and quantities was introduced with many of these developed either before the advent of quantum mechanics or without relying on the latter theory. This has resulted in a sort of gap between much of chemical theory and quantum mechanics although clearly quantum mechanics can give rise to much more and deeper insight in the underlying mechanisms of chemical reactivity. Fortunately, some eminent scientists have, over the years, picked up the challenge of closing this gap. One of the leading persons in this, is Robert G. Parr who is among the founding fathers of what is now known as chemical density functional theory (often still referred to as conceptual density functional theory, cDFT) [1,2,3], and who was able to link many existing theories to the energy of a chemical system and its derivatives with respect to its basic variables, including the number of electrons and the external potential. This Taylor expansion of the energy has already given rise to numerous new reactivity descriptors or has allowed previously known key quantities like electronegativity to be identified with some of these derivatives.

In this work, we are interested in the dual-descriptor introduced by Morell et al. [4, 5] as the difference between the Fukui function for the addition of an electron minus that for the removal of an electron, or alternatively as the functional derivative of the hardness which in itself is the second derivative of the energy with respect to the number of electrons. As such, the dual-descriptor is a mixed third-order derivative of the energy [6]:

$$ f^{(2)}(\mathbf{r})\,=\,\left( \!\frac{\delta\left( \left( \frac{\partial^{2}{E}}{\partial{N}^{2}}\right)_{\!v(\mathbf{r})}\right)}{\delta v(\mathbf{r})}\!\right)_{\!N}\,=\,\left( \!\frac{\partial^{2}{}\left( \frac{\delta E}{\delta v\left( \mathbf{r}\right)}\right)_{\!N}}{\partial{}N^{2}}\!\right)_{\!v\left( \mathbf{r}\right)} $$
(1)

In Eq. 1, f (2)(r) is the dual-descriptor evaluated at a point r, E is the energy, N the number of electrons and v(r) the external potential. Provided that the system has no degenerate states, \(\left (\frac {\delta E}{\delta v\left (\mathbf {r}\right )}\right )_{N}\) corresponds to \(\rho \left (\mathbf {r}\right )\), the electron density function of the molecule. In case of degenerate states, the density to be used derives from degenerate perturbation theory [7,8,9]. Provided non-degenerate states, some trivial manipulations reveal that the dual-descriptor is actually the N-derivative of the Fukui function f(r) [10,11,12]:

$$ f(\mathbf{r})= \left( \frac {\partial{}\left( \frac{\delta E}{\delta v\left( \mathbf{r}\right)}\right)_{N}} {\partial{}N}\right)_{v\left( \mathbf{r}\right)} =\left( \frac{\partial\rho\left( \mathbf{r}\right)}{\partial{}N}\right)_{v\left( \mathbf{r}\right)} $$
(2)

The Fukui function indicates regions in a molecule that exhibit higher reactivity with respect to reactions that involve a change in the number of electrons in the molecule. The Fukui function is not only of interest by itself but is also an important function for generating many other chemical reactivity concepts in cDFT [1, 2]. Equation 2 shows that the Fukui function is an r-dependent function that describes the change in the electron density at the point r upon a change in the number of electrons in the molecule, under the constraint that the external potential remains unaltered. The electron density has slope discontinuities at the integer number of electrons and consequently, the left-side and right-side derivatives are different. Hence, one needs to consider two Fukui functions. The Fukui function for an increase in the number of electrons will be denoted f +(r) and for a decrease as f −(r). This way, one can express the dual-descriptor also as:

$$ f^{(2)}(\mathbf{r})=\left( \frac{\partial f\left( \mathbf{r}\right)}{\partial{}N}\right)_{v\left( \mathbf{r}\right)} $$
(3)

The main interest in the dual-descriptor stems from the fact that it allows one to predict the nature of molecular reactivity, i.e., electrophilic or nucleophilic with, provided a graphical representation, also the regioselectivity [4, 5]. In practice, the working equation for the dual-descriptor corresponds to:

$$ f^{(2)}(\mathbf{r})=f^{+}\left( \mathbf{r}\right)-f^{-}\left( \mathbf{r}\right) $$
(4)

This is often approximated in a frozen molecular orbital approximation as [4]:

$$ f^{(2)}(\mathbf{r})=\rho_{LUMO}\left( \mathbf{r}\right)-\rho_{HOMO}\left( \mathbf{r}\right) $$
(5)

where ρ L U M O (r) and ρ H O M O (r) are the densities of the frontier lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) of the molecule, respectively. This invokes a Koopmans-type approximation which may be quite an approximation. A different approach still relies on finite differences but considers the entire electron density and so includes electronic relaxation (but not geometric as we require constant external potential).

$$ f^{(2)}(\mathbf{r})=\rho_{N_{0}+1}\left( \mathbf{r}\right)-2\rho_{N_{0}}\left( \mathbf{r}\right)+\rho_{N_{0}-1}\left( \mathbf{r}\right) $$
(6)

where \(\rho _{N_{0}+1}(\mathbf {r})\), \(\rho _{N_{0}}(\mathbf {r})\), and \(\rho _{N_{0}-1}(\mathbf {r})\) are the densities in the molecule with N 0 + 1, N 0, and N 0 − 1 electrons, respectively.

In the present work, we examine in more detail the dual-descriptor by considering three main issues from a matrix formulation of this descriptor.

First, we consider the expression of the dual-descriptor in matrix form:

$$\begin{array}{@{}rcl@{}} f^{(2)}(\mathbf{r},\mathbf{r^{\prime}})\!\!&=&\!\!f^{+}(\mathbf{r},\mathbf{r^{\prime}})\,-\,f^{-}(\mathbf{r},\mathbf{r^{\prime}})\\ &=&\!\rho_{N_{0}+1}(\mathbf{r},\mathbf{r^{\prime}})\,-\,2\rho_{N_{0}}(\mathbf{r},\mathbf{r^{\prime}})\,+\,\rho_{N_{0}-1}(\mathbf{r},\mathbf{r^{\prime}}) \end{array} $$
(7)

where \(\rho _{N_{0}+1}(\mathbf {r},\mathbf {r^{\prime }})\), \(\rho _{N_{0}}(\mathbf {r},\mathbf {r^{\prime }})\), and \(\rho _{N_{0}-1}(\mathbf {r},\mathbf {r^{\prime }})\) are the first order reduced density matrices in the molecule with N 0 + 1, N 0, and N 0 − 1 electrons, respectively. We then express these in terms of an orthonormal basis, here the molecular orbitals of the system with N 0 electrons. Bultinck et al. [13, 14] and later on Alcoba et al. [15,16,17] extended the Fukui function to a Fukui matrix in the following way:

$$ f(\mathbf{r},\mathbf{r^{\prime}})=\left( \frac{\partial\rho\left( \mathbf{r}, \mathbf{r^{\prime}}\right)}{\partial{}N}\right)_{v(\mathbf{r})} $$
(8)

This Fukui matrix \(f(\mathbf {r},\mathbf {r^{\prime }})\) has previously been shown to lead to rich new insights into the properties of the Fukui function and allows rationalizing the quality of a frozen molecular orbital or Koopmans approximation to it [13, 14]. The Fukui function corresponds to the diagonal of the Fukui matrix in the same way as the density function corresponds to the diagonal of the first-order reduced density matrix. As in what follows, we will often refer to idempotent density matrices, we will mostly use spin-specific density matrices and Fukui matrices, defined as

$$ f^{\sigma}(\mathbf{r},\mathbf{r^{\prime}})=\left( \frac{\partial\rho^{\sigma}\left( \mathbf{r}, \mathbf{r^{\prime}}\right)}{\partial{}N}\right)_{v(\mathbf{r})} $$
(9)

where σ denotes the spin function σ ∈{α,β}. The matrix extension can straightforwardly also be introduced for the dual-descriptor as has been previously done by Alcoba et al. in both spin-free as well as spin-polarized versions [15,16,17]. However, the analysis presented here goes more into detail by application to a larger molecular set and analysis of the diagonal form of the dual-descriptor matrix. This will reveal in a way beyond graphical comparison whether the Koopmans approximation is a good approximation. Moreover, this analysis is performed over the entire molecule whereas the work of Zielinski et al. [18] concludes the lack of correlation between the Koopmans and finite difference based dual-descriptors on atom-condensed values. Although their work is clearly interesting, our work provides more insight by being able to perform the analysis prior to condensation. We also examine the spectrum of the matrix eigenvalues to see whether some interesting features may be found. In case of the Fukui matrix, we found that for idempotent density matrices (as is the case for spin-specific density matrices from single Slater determinant methods and Kohn–Sham DFT with the approximate density matrices) the Fukui matrix spectrum was especially interesting as it showed why the frontier molecular orbital theory (FMOT) works well at these levels but also why regions with negative Fukui functions are always possible and -indeed- likely [13, 14]. When idempotency is lost, these special matrix properties are lost to some extent. So, as the Fukui matrix is also not idempotent, we also expect the dual-descriptor matrix to have less special properties but it is of interest to see to what extent they still hold approximately.

The second goal is to atom condense the dual-descriptor matrix in both single-atom and diatomic (or where chemically applicable, bond) terms. This is reminiscent of recent work by the present authors for the Fukui matrix where an atom and bond condensation is carried out over both the r and \(\mathbf {r^{\prime }}\) coordinate [19]. Doing this for the dual-descriptor matrix makes it different from the work of Zielinski et al. [18] or e.g., Glossman-Mitnik [20] or Cao et al. [21] who all atom condense the dual-descriptor function and therefore cannot distinguish bond terms.

Third, we examine the effect of the actual position of the atom condensing operator \(\hat {w}_{A}(\mathbf {r})\). As has been described in detail by Bultinck et al. [22], for atoms in molecules (AIM) methods that yield such operators with an N dependence, the order of differentiation and condensation is important as for such methods one cannot assume \(\frac {\partial \hat {w}_{A}(\mathbf {r})}{\partial N}=0\). When introducing AIM-condensed Fukui functions for the first time, Yang and Mortier [23] used the commutability of parameter differentiation (finite-difference here) and integration over the AIM inherent in Mulliken’s use of Hilbert space, making the condensation operators N-independent. The present authors have examined the effect of using first differentiation and then condensation (the so-called fragment of the molecular response or FMR method) versus that of first condensation and then differentiation (the response of the molecular fragment or RMF method) for the Fukui matrix to find that the effect is significant. Zielinski et al. [18] mentioned the possible effect on dual-descriptor values but restricted themselves to one single-method RMF (note that they mention FMR but from the text one can derive this is an error), among others because of the lack of software required for the FMR method. The essential issue is therefore whether one uses:

$$ f^{(2)}_{RMF,AB}(\mathbf{r},\mathbf{r^{\prime}})=f^{+}_{RMF,AB}(\mathbf{r},\mathbf{r^{\prime}})-f^{-}_{RMF,AB}(\mathbf{r},\mathbf{r^{\prime}}) $$
(10)

or

$$ f^{(2)}_{FMR,AB}(\mathbf{r},\mathbf{r^{\prime}})=f^{+}_{FMR,AB}(\mathbf{r},\mathbf{r^{\prime}})-f^{-}_{FMR,AB}(\mathbf{r},\mathbf{r^{\prime}}) $$
(11)

However, mathematically, one could even derive more alternatives if one starts from the second derivative expression of the density and inserts the partitioning of the unity \({\sum }_{A} \hat {w}_{A}(\mathbf {r})=1\) in different places. The ones in Eqs. 10 and 11 are the most straightforward and if these already show significant differences, the use and reliability of atom condensation becomes questionable. Expressing the matrices again in an orthonormal basis allows diagonalization and therefore gives insight into the shape of the underlying functions (the AB dual-descriptor orbitals) along with their eigenvalues, shedding more light on the reactivity.

In what follows, the focus lies on the implementation and proof of the properties of the above matrices and atom and bond condensation. To that end, the relevant quantities are computed for a test set of ethylene derivatives and resulting (mathematical) properties discussed. As such, the chemical significance is not the main topic of the present work and is therefore not expanded upon to keep the focus of the work on the three goals described.

Computational methods

In order to illustrate the newly introduced dual-descriptor functions, matrices and their atom and bond counterparts, B3LYP/6-31G* calculations were performed on the set of ethylene derivatives shown in Fig. 1, recently used by Gonzalez-Suarez et al. [24] and Bultinck et al. [25] to derive atom- and bond-condensed Fukui functions and matrices using the Hirshfeld-I AIM method (i.e., molecules 1–18 from Gonzalez-Suarez et al. [24]). The original idea of this set of molecules was to examine the influence of the addition of certain electron-donating and electron-withdrawing groups on the 1-2 bond-condensed Fukui function. Geometry optimizations were carried out using the Cartesian 6-31G* basis set and all information required for the calculation of the Fukui matrices and hence dual-descriptor matrices was extracted from the formatted checkpoint file from Gaussian-03 [26]. Hirshfeld-I weight functions were computed using atomic densities obtained at the same level of theory. All required algebraic manipulations were described previously by Bultinck et al. [13] with straightforward extensions for the calculation of the dual-descriptor. For all molecules and molecular ions, it is assumed that the number of α spin electrons is always larger than or equal to the number of β spin electrons. In the following, we distinguish both α and β spin-blocks of the dual-descriptor matrices. The weight functions \({w_{A}\left (\mathbf {r}\right )}\) are expressed in the basis of the molecular orbitals. Visualizations are done using GaussView5 [27].

Fig. 1
figure 1

Ethylene derivatives considered in this work with explicit indication of atoms 1, 2, and 3

Full size image

Results and discussion

For all molecules, first both the electron-addition and electron-removal Fukui matrices have been computed using the expressions presented previously and yielding the data reported by Oña et al. [19]. These matrices are then used to compute the dual-descriptor matrices according to Eq. 7. Before proceeding to the properties of the dual-descriptor matrix, it is worth reiterating some properties [13, 14] of the Fukui matrices as these will impact on the former. First of all, the present level of theory, which corresponds to Kohn-Sham DFT, results in idempotent spin-specific density matrices, meaning that the occupation numbers of the spin orbitals are exactly zero or one. Admittedly, DFT does not produce a density matrix so we use the common approximation of using a density matrix based on the Kohn-Sham orbitals in the same way as the (legitimate) calculation of density matrices at the Hartree-Fock level of theory. The special properties of differences of idempotent matrices include the fact that eigenvalues can only be zero or one or must appear in pairs + x and − x. It has previously been shown that at both the Hartree-Fock and Kohn-Sham DFT level, the Fukui matrix has one eigenvalue exactly equal to one with all other eigenvectors being paired with an eigenvalue of + x and − x. The (necessary) presence of negative eigenvalues immediately explains why negative Fukui functions may exist and probably may be found in virtually any molecule. One simply needs to identify a region where the eigenvectors with negative eigenvalues outweigh the ones with positive eigenvalues and there a negative Fukui function will be found. The second important remark is that with the eigenvalue equal to 1, an eigenvector appears that has a coefficient very close to 1 for the relevant frontier molecular orbital. Hence, for \(f^{+}(\mathbf {r},\mathbf {r^{\prime }})\) expressed in the molecular orbital basis, one has a coefficient equal to 1 for the LUMO in the eigenvector with eigenvalue 1. This explains why FMOT works so well but the Fukui matrix revealed why negative Fukui functions are nothing exceptional or peculiar and why FMOT is not the complete story. At correlated level, the unity eigenvalue disappears but there remains one chief large eigenvalue compared to a large set of smaller (positive and negative) eigenvalues.

These special properties of the Fukui matrices have an impact on the dual-descriptor matrix. First of all, by the presence of eigenvalues + x and − x (x ≠ 0,1), the Fukui matrices are not idempotent. This immediately entails that we should expect a more complicated structure of the eigensystem. Obviously, the trace of the matrix in an orthonormal basis equals zero throughout but the presence of many non-zero eigenvalues indicates that using a Koopmans type approximation might be a rather poor choice. To shed more light on this, we first discern two spin-specific different dual-descriptors and the total dual-descriptor as:

$$\begin{array}{@{}rcl@{}} f^{(2,\alpha)}(\mathbf{r},\mathbf{r^{\prime}})=f^{(+,\alpha)}(\mathbf{r},\mathbf{r^{\prime}})-f^{(-,\alpha)}(\mathbf{r},\mathbf{r^{\prime}}) \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} f^{(2,\beta)}(\mathbf{r},\mathbf{r^{\prime}})=f^{(+,\beta)}(\mathbf{r},\mathbf{r^{\prime}})-f^{(-,\beta)}(\mathbf{r},\mathbf{r^{\prime}}) \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} f^{(2)}(\mathbf{r},\mathbf{r^{\prime}})=f^{(2,\alpha)}(\mathbf{r},\mathbf{r^{\prime}})+f^{(2,\beta)}(\mathbf{r},\mathbf{r^{\prime}}) \end{array} $$
(14)

The trace of \(f^{(2,\alpha )}(\mathbf {r},\mathbf {r^{\prime }})\) obviously equals 1 and of \(f^{(2,\beta )}(\mathbf {r},\mathbf {r^{\prime }})\) equals -1 as we always consider molecules and ions where the α electrons are in the majority. The total dual-descriptor matrix \(f^{(2)}(\mathbf {r},\mathbf {r^{\prime }})\) therefore has trace zero, as expected. Taking as an example ethyene and \(f^{(2,\alpha )}(\mathbf {r},\mathbf {r^{\prime }})\), we find that the most positive eigenvalue equals one to within 10−4. This is, however, not a universal feature as it is rather exceptional among the molecular set considered. In most molecules, the largest eigenvalue is slightly larger than 1. The most negative eigenvalue for ethylene has a value equal to −0.03879. In total there are 14 positive eigenvalues and 8 negative eigenvalues (eigenvalues between 10−4 and − 10−4 excluded), leading to the fact that the dual-descriptor can have any sign. For \(f^{(2,\beta )}(\mathbf {r},\mathbf {r^{\prime }})\) we find a trace of exactly minus 1 with the most negative eigenvalue equal to −1.00479 as one of the 8 negative eigenvalues. For the total dual-descriptor matrix, so the sum of the α and β parts, we find that -as expected- the trace equals zero but the sign of the largest eigenvalue in magnitude changes depending on the molecule. In only some of the cases we find something that suggests approximate validity of a Koopmans approximation, i.e. we find eigenvectors that contain sufficiently large coefficients for specifically the HOMO and the LUMO. Given the ease by which the dual-descriptor matrix can be computed according to Eq. 7 and subsequently diagonalized, we see little reason to still use a FMOT approximation. Moreover, Eq. 7 remains valid at correlated levels of theory where no orbital energy diagram can be obtained as easily as at the Hartree-Fock and formally the Kohn-Sham DFT level. Once the eigenvectors of the dual-descriptor matrix have been computed, another advantage is that the most important eigenvector(s) (those with the largest eigenvalues in magnitude) can be transformed to a basis that allows them to be visualized using common programs thereby allowing a very simple graphical and chemically interesting representation. Such visualizations will be shown below for the atom and bond dual-descriptor matrices.

The second goal of the present paper is to demonstrate the possibility to obtain atomic and diatomic (or where applicable, bond) dual-descriptor matrices by introducing a weight function in both the r and \(\mathbf {r^{\prime }}\) coordinate. We first use the FMR approach using the weight functions from the Hirshfeld-I method for the molecule with N 0 electrons. This entails that, based on earlier matrix partitioning studies for electron density [28] and the Fukui function [19], we use the following working expression:

$$\begin{array}{@{}rcl@{}} f^{(2)}_{FMR,AB}(\mathbf{r},\mathbf{r^{\prime}})\!&\,=\,&\!\frac{1}{2}(w_{A}(\mathbf{r};N_{0})w_{B}(\mathbf{r^{\prime}};N_{0})\\ &&\! + w_{A}(\mathbf{r^{\prime}};N_{0})w_{B}(\mathbf{r};N_{0}))f^{(2)}(\mathbf{r},\mathbf{r^{\prime}}) \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} f^{(2)}_{FMR,AB}(\mathbf{r},\mathbf{r^{\prime}})&\,=\,&\frac{1}{2}(w_{A}(\mathbf{r};N_{0})w_{B}(\mathbf{r^{\prime}};N_{0})\\ && +w_{A}(\mathbf{r^{\prime}};N_{0})w_{B}(\mathbf{r};N_{0}))[\rho_{N_{0}+1}(\mathbf{r},\mathbf{r^{\prime}})\\ && -2\rho_{N_{0}}(\mathbf{r},\mathbf{r^{\prime}})+\rho_{N_{0}-1}(\mathbf{r},\mathbf{r^{\prime}})] \end{array} $$
(16)

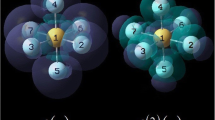
where we explicitly indicated the N dependence of the weight function as it occurs in the Hirshfeld-I AIM method [29] (the same applies to Bader’s QTAIM method [30, 31]). Note that the weight functions can also be expressed in the same orthonormal basis as the density matrices, such that \(f^{(2)}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\) can be expressed in the same orthonormal basis of, in this case, the molecular orbitals. Equation 16 gives the result for the total dual-descriptor but the different spin parts are obtained in analogous way. Note, however, that the weights are always derived using Hirshfeld-I and reflect the total density and hence are the same for computing \(f^{(2)}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\) or \(f^{(2,\alpha )}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\) and \(f^{(2,\beta )}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\). The matrices may be diagonalized to investigate their spectrum. Taking ethylene as an example (see Fig. 2 for atom numbering), Tables 1 and 2 present the data obtained for ethylene. Results for the other 17 compounds gathered in Fig. 1 are reported as Supporting Information.

Fig. 2
figure 2

Labels of the C2H4 molecule

Full size image
Table 1 Eigenvalues and traces of \(f^{(2,\alpha )}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\) dual matrices within the FMR framework for C2H4, calculated in the 6-31G* basis set on the B3LYP level of theory using weights from the neutral molecule
Full size table
Table 2 Eigenvalues and traces of the \(f^{(2,\beta )}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\) dual matrices for C2H4, calculated in the 6-31G* basis set on the B3LYP level of theory using weights from the neutral molecule
Full size table

These tables clearly show that for every combination of two atoms, one has both negative and positive eigenvalues. Note that many of them are not shown as they are quasi zero and hence of little interest. From these data AB condensed dual-descriptor values may be computed by simply taking the trace:

$$ \mathrm{F}^{(2)}_{FMR,AB}={\int}_{\mathbf{r}=\mathbf{r^{\prime}}}{f^{(2)}_{FMR,AB}(\mathbf{r},\mathbf{r^{\prime}})d\mathbf{r}} $$
(17)

and analogously for spin-specific parts. As required, the sum of the traces \(\mathrm {F}^{(2,\alpha )}_{FMR,AB}\) of the α spin dual-descriptor matrices corresponds to 1 or to −1 for the sum of the traces \(\mathrm {F}^{(2,\beta )}_{FMR,AB}\) of the β spin dual-descriptor matrices. Do note that obviously for each combination AB the eigenvectors differ from other combinations as they stem from different matrices so it is of no use to make a sum over the individual eigenvalues in these tables. For the trace, this is of no importance as this is independent of the orthonormal basis used. As the tables also show, the traces can have both signs. The total dual matrix, the sum of the α and β parts, has trace zero and may

well attach larger values in magnitude to certain combinations AB compared to its constituent parts. When reporting data in tabular form we take into account that for both the condensed dual function and dual-descriptor matrices values we have \(\mathrm {F}^{(2)}_{FMR,AB}=\mathrm {F}^{(2)}_{FMR,BA}\). The numerical data in the tables consistently report the data for \((2-\delta _{AB})\mathrm {F}^{(2)}_{FMR,AB}\) where the symbol δ A B means the Kronecker delta. A single atom condensed dual-descriptor value is also available by simple addition:

$$ \mathrm{F}^{(2)}_{FMR,A}=\sum\limits_{B} \mathrm{F}^{(2)}_{FMR,AB} $$
(18)

resulting in the data in Table 3 for ethylene for the total dual-descriptor.

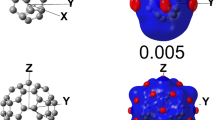
Table 3 Atom condensed dual functions \(\mathrm {F}^{(2)}_{FMR,A}\) using w A (r) from the neutral molecule
Full size table

The single-atom condensed values in Table 3 are computed using the FMR approach and hence are not directly comparable to the data based on differences of atomic charges. As the dual-descriptor matrices are expressed in an orthonormal basis that is directly linked to basis functions, the eigenvectors can be easily visualized using any common orbital plotting tool. This can be done for either the total dual-descriptor matrices or atom and bond condensed ones. For instance, Fig. 3 shows the eigenvectors for the lowest and highest eigenvalues for the α and β spin dual-descriptor matrices for molecules 1 and 2 of the test set.

Fig. 3
figure 3

The lowest and highest eigenvalues with their eigenvectors for the α and β AB condensed dual-descriptor matrices for A B = C 1 C 2 in molecules 1 (top row) and 15 (bottom row) of the set of ethylene derivatives within the FMR framework using w A (r) from the neutral molecule, all plotted for a 0.04 isovalue

Full size image

The individual eigenvectors can be compared to the frontier molecular orbitals, as has been done in Figs. 4 and 5. Such figures may, however, be deceptive, as they seem to indicate that FMOT is quite good. Still, one lacks all other eigenvalues and eigenvectors, entailing the risk that one may be led to make wrong assumptions about the nature of the dual-descriptor. This is reminiscent of the long-lasting discussion on the possibility of negative Fukui functions, closed ultimately with the proof that the Fukui matrix has negative eigenvalues. Again, given the ease with which one can compute the dual-descriptor matrix, we opt to always proceed that way, especially since exactly the same manipulations can be done at the correlated level of theory. Still, the plots may be informative when one is interested in where specifically a reaction will occur.

Fig. 4
figure 4

a The HOMO of C2H4 at the B3LYP/6-31G* level of theory, b the eigenvector with eigenvalue close to –1 of the total dual matrix and c and d the eigenvectors of the \(f^{(2, \beta )}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\) dual matrix with the highest absolute eigenvalues of respectively the A B = C 1 C 1 and C 1 C 2 atomic pairs, all plotted for a 0.04 isovalue. The eigenvalues corresponding to the dual orbitals are −0.334 and −0.206 within the FMR framework

Full size image
Fig. 5
figure 5

a The LUMO of C2H4 at the B3LYP/6-31G* level of theory, b eigenvector with the highest eigenvalue close to 1 of the total dual matrix and c and d the eigenvectors of the \(f^{(2,\alpha )}_{FMR,AB}(\mathbf {r},\mathbf {r^{\prime }})\) dual matrix with the highest eigenvalues of respectively the A B = C 1 C 1 and C 1 C 2 atomic pairs, all plotted for a 0.04 isovalue. The eigenvalues corresponding to the dual orbitals are 0.312 and 0.174 within the FMR framework

Full size image

A third issue discussed in the present paper concerns the impact of going from the FMR to the RMF scenario. In case of the RMF scenario, one needs to also deal with the dependence of the weight w A (r) on the number of electrons: \(\frac {\partial w_{A}(\mathbf {r})}{\partial N}\ne 0\). This makes the expressions slightly more complicated but, at least for Fukui functions, it is a more commonly used approach, as then the Fukui function corresponds to a simple difference in atomic charges. In Tables 4 and 5, we compare bond condensed (between atoms 1 and 2 plus between atoms 2 and 3) and the atom condensed dual-descriptor on atom 1 for the entire set of molecules. As the tables show, the difference between the FMR and RMF results is not so large that it would likely reverse conclusions on the reactivity of the atoms and bonds in the molecules. A sign reversal only occurs for the bond between atoms 1 and 2 in molecule 9.

Table 4 B3LYP/6-31G* Bond dual functions \(\mathrm {F}^{(2)}_{FMR,AB}\) between the indicated atoms and the atom condensed dual function on atom 1 within the FMR framework for each molecule using w A (r) from the neutral molecule
Full size table
Table 5 B3LYP/6-31G* Bond dual functions \(\mathrm {F}^{(2)}_{RMF,AB}\) between the indicated atoms and the atom condensed dual function on atom 1 within the RMF framework for each molecule
Full size table

Conclusions

In this work, a new partitioning of the dual-descriptor matrix has been proposed within the Hirshfeld-I framework. Starting from the molecular Fukui matrices and using a symmetrized product of weight functions for the atoms in a molecule, one- and two-atom dual-descriptor matrices have been obtained, giving rise to atom and bond condensed matrices, respectively. The resulting matrices in terms of the molecular orbitals are diagonalized, allowing much more insight in the nature of the dual-descriptor while still allowing the calculation of the usual position space and atom condensed dual-descriptors. As part of this extra insight, the eigenvectors can be easily plotted and inspected to evaluate the reactivity of a molecule. Moreover, once the Fukui matrices are available, the dual-descriptor matrix can be computed very easily without having to rely on a frontier molecular orbital approach. This eliminates the risk of undesirable (and undetected) approximations and allows the straightforward calculation of dual-descriptors at the correlated level of theory.