Efficient set containment join

Abstract

In this paper, we study the problem of set containment join. Given two collections $\mathcal {R}$ and $\mathcal {S}$ of records, the set containment join $\mathcal {R} \bowtie _\subseteq \mathcal {S}$ retrieves all record pairs $\{(r,s)\} \in \mathcal {R}\times \mathcal {S}$ such that $r \subseteq s$. This problem has been extensively studied in the literature and has many important applications in commercial and scientific fields. Recent research focuses on the in-memory set containment join algorithms, and several techniques have been developed following intersection-oriented or union-oriented computing paradigms. Nevertheless, we observe that two computing paradigms have their limits due to the nature of the intersection and union operators. Particularly, intersection-oriented method relies on the intersection of the relevant inverted lists built on the elements of $\mathcal {S}$. A nice property of the intersection-oriented method is that the join computation is verification free. However, the number of records explored during the join process may be large because there are multiple replicas for each record in $\mathcal {S}$. On the other hand, the union-oriented method generates a signature for each record in $\mathcal {R}$ and the candidate pairs are obtained by the union of the inverted lists of the relevant signatures. The candidate size of the union-oriented method is usually small because each record contributes only one replica in the index. Unfortunately, union-oriented method needs to verify the candidate pairs, which may be cost expensive especially when the join result size is large. As a matter of fact, the state-of-the-art union-oriented solution is not competitive compared to the intersection-oriented ones. In this paper, we propose a new union-oriented method, namely TT-Join, which not only enhances the advantage of the previous union-oriented methods but also integrates the goodness of intersection-oriented methods by imposing a variant of prefix tree structure. We conduct extensive experiments on 20 real-life datasets and synthetic datasets by comparing our method with 7 existing methods. The experiment results demonstrate that TT-Join significantly outperforms the existing algorithms on most of the datasets and can achieve up to two orders of magnitude speedup. Furthermore, to support large scale of datasets, we extend our techniques to distributed systems on top of MapReduce framework. With the help of careful designed load-aware distribution mechanisms, our distributed join algorithm can achieve up to an order of magnitude speedup than the baselines methods.

1 Introduction

Set-valued attributes play an important role in modeling database systems ranging from commercial applications to scientific studies. For instance, a set-valued attribute may correspond to the profile of a person, the tags of a post, the links or domain information of a webpage, and the tokens or q-grams of a document. In the literature, there has been a variety of interest in the computation of set-valued attributes, including but not limited to set containment searches (e.g., [14, 24, 29, 38, 39, 46, 47]), set similarity joins (e.g., [15, 17, 19, 21, 32, 42,43,44,45]), and set containment joins (e.g., [18, 23, 26, 27, 30, 31, 33, 34, 36]).

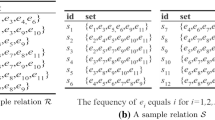
In this paper, we focus on the problem of set containment join. Given two collections $\mathcal {R}$ and $\mathcal {S}$ of records, each of which contains a set of elements, the set containment join, denoted by $\mathcal {R} \bowtie _\subseteq \mathcal {S}$, retrieves all pairs $\{(r,s)\}$ where $r \in \mathcal {R}$, $s \in \mathcal {S}$, and $r \subseteq s$. As a fundamental operation on massive collections of set values, the set containment join benefits many applications. For instance, companies may post a list of positions on an online job market Web site, each of which contains a set of required skills. Let $e_i$ denote a skill, Fig. 1a shows the skills required in four job advertisements in $\mathcal {R}$. A job-seeker, on the other hand, can submit his/her curriculum vitae to the Web site, which lists a set of his/her skills. Figure 1b illustrates the skill records of four job-seekers in $\mathcal {S}$. Naturally, a company would like to consider a job-seeker if his/her skill set covers all required skills for a position. We call such a pair of job-seeker and position a containment match. By executing a set containment join on the positions and job-seekers, the Web site is able to identify all possible matches, i.e., $\mathcal {R} \bowtie _\subseteq \mathcal {S}$, and make recommendations.

Fig. 1

A motivation example where $e_i$ denotes a skill, $\mathcal {R}$ consists of four job advertisements with required skills, and $\mathcal {S}$ represents four job-seekers with their skills

An algorithmic challenge is how to perform the set containment join in an efficient way. A naive algorithm is to compare every pair of records from $\mathcal {R}$ and $\mathcal {S}$, thus bearing a prohibitively $\mathcal {O}(n_rn_s)$ time complexity where $n_r$ and $n_s$ denote the number of records in $\mathcal {R}$ and $\mathcal {S}$, respectively. In view of such high cost, the prevalent approach in the past is to develop disk-based algorithms [26, 31, 33, 34, 36] for this problem. We call these algorithms union-oriented methods because, as shown in Sect. 3.2, the union is their core operator. In a high level, each record $r \in \mathcal {R}$ is assigned with a signature (e.g., bitmap), where an inverted index on $\mathcal {R}$ could also be built based on the signatures. For each $s \in S$, they generate all possible signatures by s or any of its subset. By computing the union of all the corresponding inverted lists, they obtain a set of candidate records within $\mathcal {R}$, each of which might be a subset of s. Then, set containment join results are available after verifying the candidate pairs.

With the development of hardware and distributed computing infrastructure, a recent trend is to design efficient in-memory set containment join algorithms (e.g., [18, 27, 30, 31]). It is interesting that the state-of-the-art techniques follow a very different computing paradigm, namely intersection-oriented method, where details are introduced in Sect. 3.1. In general, an inverted index is constructed based on every element of each record within $\mathcal {S}$. Then, for a record $r \in \mathcal {R}$, we can identify records $s \in \mathcal {S}$ with $r \subseteq s$ by the intersection of the inverted lists built on $\mathcal {S}$ for all elements within r. Following this computing paradigm, instead of processing each record r within $\mathcal {R}$ individually, three variants of prefix tree structures are designed in [18, 27, 30] to share computation costs among records within $\mathcal {R}$.

Compared to union-oriented methods, verification free is the most judicious property of the intersection-oriented method, especially when the join result size is large. Our empirical study shows that the state-of-the-art in-memory union-oriented method [30], which is an extension of previous disk-based methods, has been significantly outperformed by the state-of-the-art in-memory intersection-oriented techniques. Nevertheless, we show that this benefit is offset by the fact that every element in $s \in \mathcal {S}$ contributes to the inverted index due to the nature of intersection operator; that is, the ID of each record in $\mathcal {S}$ will be replicated in multiple inverted lists. This inevitably results in a large number of records visited in the join process, especially for the record $r \in \mathcal {R}$ with large size. With the same reason, we show that it is difficult for intersection-oriented method to exploit the skewness of the real-life data.

We are aware that there are several algorithms (e.g., [14, 29, 42]), which are devised for string similarity search, can also be utilized to handle set containment join with trivial modification. Algorithms in this category are called adapted methods, where the details are introduced in Sect. 3.3.

In this paper, we revisit and design a new union-oriented method, namely TT-Join, where an efficient set containment join algorithm is developed based on two different prefix trees built on $\mathcal {R}$ and $\mathcal {S}$, respectively. Through comprehensive cost analysis on simple intersection-oriented and union-oriented methods in Sect. 4.2, we show that the above two problems suffered by the intersection-oriented methods can be easily addressed by a new simple union-oriented method which uses the least frequent element as the signature. Not surprisingly, the new simple union-oriented method needs to verify candidates due to the inherent limit of union-oriented computing paradigm. Moreover, its pruning capability is limited by using only one element as the signature. To circumvent these limits, we propose a new prefix tree structure based on the k least frequent elements of the records within $\mathcal {R}$ such that we can (i) enhance the pruning power with a reasonable overhead and (ii) integrate the intersection semantics to directly validate a significant number of join results without invoking the verification. To share the computational cost among records within $\mathcal {S}$, we also build a regular prefix tree on $\mathcal {S}$. Then, we develop an efficient TT-Join algorithm to perform set containment join against two prefix trees.

Due to the limited computational resources (e.g., memory or CPU), it is often difficult to process large scale real-life datasets in a single machine. To alleviate this issue, we extend our techniques on top of MapReduce framework (e.g., Hadoop and Spark), which has attracted lots of interests in both academia and industry communities due to its high efficiency and scalability for batch processing tasks . The main challenge here is how to partition the two record collections such that good load balance on cluster nodes can be achieved at a small communication cost. To the best of our knowledge, there is no existing work on computing set containment join using MapReduce framework. It is worth mentioning that Kunkel et al. [27] recently propose a parallel algorithm PIEJoin to compute the set containment join. However, they achieve parallelization by creating a task thread for each recursive call of the crucial search function in their approach. Apparently, this method does not follow MapReduce framework which involves two crucial operations, map and reduce, on partitioning and dispatching the input data. We also notice that there are a few works in the literature on utilizing MapReduce to handle set similarity join (e.g., [13, 20, 25, 35, 37, 40]). Nevertheless, due to different nature of the two problems (i.e., set containment join and set similarity join), their techniques are not promising on processing our problem, which is verified by our empirical studies in Sect. 6.

In this paper, we propose a novel signature-based distribution scheme, which dispatch records based on the aforementioned record signature (i.e., the least frequent element). Specifically, we first partition the element domain into N disjoin intervals, each related to a reduce node. Then, for a record $r \in \mathcal {R}$, we find the interval where its signature falls and dispatch r to the corresponding reduce node. For a record $s \in \mathcal {S}$, it will be dispatched to all reduce nodes whose corresponding intervals cover at least one element of s. With the help of careful designed element domain partition approaches that are guided by the join cost estimation on reduce nodes, our signature-based distribution mechanism can achieve good load balance, low communication cost, and no duplicate in join results. Experimental results show that our method can achieve up to an order of magnitude speedup and much less communication cost compared to baseline distribution schemes.

Contributions Our principle contributions are summarized as follows.

• We classify the existing solutions into two categories, namely intersection-oriented and union-oriented methods, based on the nature of their computing paradigms. Through comprehensive analysis on two simple intersection-oriented and union-oriented methods, we show the advantages and limits of the methods in each category.

• We propose a new union-oriented method, namely TT-Join. Particularly, we design a k least frequent element-based prefix tree structure, namely kLFP-Tree, to organize the records within $\mathcal {R}$. Together with a regular prefix tree constructed on records from $\mathcal {S}$, we develop an efficient set containment join algorithm.

• We extend TT-Join on top of MapReduce framework. Particularly, we propose a signature-based distribution mechanism, which can achieve good load balance as well as low communication cost. As far as we know, this is the first work to extend set containment join system to a distributed environment.

• Our comprehensive experiments on 20 real-life set-valued data from various applications and synthetic datasets demonstrate the efficiency of our TT-Join algorithm. It is reported that TT-Join significantly outperforms the state-of-the-art algorithms on most of the datasets and can achieve up to two orders of magnitude speedup. On the other hand, our distributed set containment join algorithm can achieve much better scalability.

Road map The rest of the paper is organized as follows. Section 2 presents the preliminaries. Section 3 introduces the existing solutions. Our approach TT-Join is devised in Sect. 4. Section 5 presents distributed set containment join algorithm. Extensive experiments are reported in Sect. 6. Section 7 concludes the paper.

2 Preliminaries

In this section, we introduce basic concepts and definitions used in the paper. Table 1 summarizes the important mathematical notations used throughout this paper.

In this paper, each record x consists of a set of elements $\{e_1, e_2, \ldots , e_{|x|} \}$ from element domain $\mathcal {E}$. We use $\mathcal {X}$ to denote a relation with a set-valued attribute, i.e., a collection of records. By default, elements in a record are in decreasing order of their frequency in $\mathcal {X}$. Following the convention, we use $\mathcal {R}$ (resp. $\mathcal {S}$) to denote the left (resp. right) side relation (i.e., a collection of records) for the set containment join. Similar, we use r (resp. s) to denote a record within $\mathcal {R}$ (resp. $\mathcal {S}$).

Given two records r and s, we say r is contained by s, denoted by $r \subseteq s$, if all elements of r can be found in s. That is, for $\forall e \in r$, we have $e \in s$. In the paper, we also say r is a subset of s and s is a superset of r if $r \subseteq s$. For a record $r \in \mathcal {R}$, we use $\mathcal {S}(r)$ to denote all records $s \in \mathcal {S}$ with $r \subseteq s$. Similarly, $\mathcal {R}(s)$ denotes all records $r \in \mathcal {R}$ with $r \subseteq s$.

Definition 1

(Set Containment Join) Given two collections $\mathcal {R}$ and $\mathcal {S}$ of records, the set containment join between $\mathcal {R}$ and $\mathcal {S}$, denoted by $\mathcal {R} \bowtie _\subseteq \mathcal {S}$, is to find all pairs (r, s), such that $r \in \mathcal {R}$, $s \in \mathcal {S}$, and $r \subseteq s$. That is $\mathcal {R} \bowtie _\subseteq \mathcal {S} = \{(r,s)|r \in \mathcal {R}$, $s \in \mathcal {S}$, and $r \subseteq s\}$.

Example 1

Consider the example in Fig. 1. The result of set containment join is as follows: $\mathcal {R} \bowtie _\subseteq \mathcal {S} = \{(r_1, s_1), (r_2, s_2), (r_4, s_1), (r_4, s_4)\}$.

Table 1 The summary of notations

3 Existing solutions

A brute-force solution for set containment join is to enumerate and verify $|\mathcal {R}||\mathcal {S}|$ pairs of records, which is cost prohibitive. To improve the efficiency of computation, many advanced algorithms are proposed in the literature. We classify them into two categories based on their computing paradigms, namely intersection-oriented methods [18, 26, 27, 30, 31] and union-oriented methods [23, 30, 33, 34, 36]. We also review several methods proposed for set similarity search [14, 29, 42].

3.1 Intersection-oriented methods

Given two record collections $\mathcal {R}$ and $\mathcal {S}$, the key idea of intersection-oriented method is to build inverted index on $\mathcal {S}$ and then apply the intersection operator to calculate $\mathcal {R} \bowtie _\subseteq \mathcal {S}$. In this paper, we say these algorithms are $\mathcal {S}$-driven methods because their main index structures are built on $\mathcal {S}$.

Algorithm 1 illustrates a simple intersection-oriented method [31], namely RI-Join.¹ We use $I_{\mathcal {S}}(e)$ to denote the inverted list of an element e built on records in $\mathcal {S}$, which keeps IDs of the records containing the element e. Figure 2 depicts the inverted index of $\mathcal {S}$ in the example of Fig. 1. Lines 1–2 build the inverted index of $\mathcal {S}$. Then, for each record $r \in \mathcal {R}$, we can immediately identify $\mathcal {S}(r)$ (i.e., record $s \in \mathcal {S}$ with $r \subseteq s$) based on the intersection of the inverted lists for elements within r (Lines 4–6).

The dominant cost of Algorithm 1 is the intersection of the inverted lists (Line 5). We have

$$\begin{aligned} Cost(\mathcal {R} \bowtie _\subseteq \mathcal {S}) = \sum _{r \in \mathcal {R}} \sum _{ e \in r } |I_{\mathcal {S}}(e)|. \end{aligned}$$

(1)

Analysis A nice property of the intersection-oriented approach is verification free. On the downside, a significant drawback is that we need to consider every element of a record for inverted index construction (Line 2). This may lead to long inverted lists, and hence, a large number of records accessed during the join process (Line 5).

Below are details of advanced intersection-oriented set containment join algorithms.

Algorithm PRETTI Jampani et al. [26] propose a method called PRETTI to improve the performance of intersection-oriented method. Instead of processing each individual record in $\mathcal {R}$, a prefix tree $T_{\mathcal {R}}$ is built on $\mathcal {R}$ to share the computational cost. We define a (regular) prefix tree as follows.

Definition 2

(Prefix Tree) Each node v in the tree (except root) is associated with an element in $\mathcal {E}$, denoted by v.e. We use v.set to denote the set of elements associated with v and its ancestors. Similarly, we denote all elements in its ancestors by v.prefix (i.e., $v.prefix :=$ $v.set \setminus v.e$). We also use a list, denoted by v.list, to keep the IDs of all records $\{x|x=v.set\}$. Note that elements in each record follow a global order, and hence, each record is assigned to a unique tree node.

Figure 3 shows the prefix tree for the record set $\mathcal {R}$ in Fig. 1a. By utilizing the prefix tree, we can share computation among records with the same prefix. For instance, the intersection for inverted lists of $I_{\mathcal {S}}(e_1)$ and $I_{\mathcal {S}}(e_2)$ only needs to be performed once when we compute the superset of $r_1$ and $r_2$.

Algorithm 2 illustrates the details of PRETTI, which traverses the prefix tree on $\mathcal {R}$ in a depth-first manner. For each node v visited, we uses list to denote the intersection of the inverted lists of the elements in v.prefix, which is passed from its parent node. Based on the intersection of list and the inverted list of the element v.e $I_{\mathcal {S}}(v.e)$ (Line 6), we obtain the list of records in $\mathcal {S}$ each of which contains all elements in v.set. Lines 7–9 generate the join results regarding the node v. Then, the join will continue through its child nodes where the updated list will be passed (Lines 10–11).

Algorithm PRETTI+ To reduce the size of the prefix tree, Luo et al. [30] introduce an extension of PRETTI, namely PRETTI+. In particular, PRETTI+ employs a compact prefix tree, called Patricia trie, to replace the prefix tree in PRETTI. This new prefix tree is the same as the previous one except that the nodes along a single path are merged into one node. The Patricia trie on the records set $\mathcal {R}$ in Fig. 1a is shown in Fig. 4. We omit the details of PRETTI+, which are the same as PRETTI except that we may need to merge inverted lists of multiple elements associated with a node.

Fig. 2

Inverted index on $\mathcal {S}$

Fig. 3

Prefix tree on $\mathcal {R}$

Fig. 4

Patrica trie on $\mathcal {R}$

Fig. 5

Limited tree on $\mathcal {R}$

Algorithm LIMIT+(OPJ) To avoid exploring many inverted lists for the large size records within $\mathcal {R}$, Bouros et al. [18] propose a new algorithm, called LIMIT. Instead of building a complete prefix tree for $\mathcal {R}$, LIMIT only builds a prefix tree with limited height k; that is, it only considers the prefix of record with a fixed length. Figure 5 shows a limited prefix tree with $k=2$ for records set $\mathcal {R}$ in Fig. 1a.

Based on the limited prefix tree, LIMIT performs the join process following a two-phase procedure which involves candidates generation and candidates verification. In terms of algorithm implementation, LIMIT is basically the same as Algorithm 2 except the generation of join results (Lines 9 in Algorithm 2). Particularly, LIMIT handles this by considering two scenarios. If $|r| \le k$, we output the record pair (r, s) directly since the inverted lists of all elements in r participate in the intersection. Otherwise, we have to verify the record pair (r, s). Although we need to verify some candidate pairs in LIMIT due to the limited tree height, this cost is well paid off by significantly reducing the number of inverted lists involved in the intersection. To enhance the computation performance, the authors propose two optimization techniques as follows. (i) They dynamically determine the local height for each path of the prefix tree; (ii) the authors further propose a new paradigm, termed Order and Partition Join (OPJ), which partitions the records in each collection based on their first contained item, and then process these partitions progressively. Based on these optimization techniques, the advanced algorithms LIMIT(OPJ) and LIMIT+(OPJ) are devised. As a matter of fact, our empirical studies in Sect. 6.1 show that the two algorithms might achieve different performances under different data structures and programming languages.

Fig. 6

Augmented prefix tree on $\mathcal {S}$

Algorithm PIEJoin Recently, Kunkel et al. [27] propose a two-tree-based method, called PIEJoin, which aims to improve the performance of intersection-oriented method by exploiting advanced index technique on $\mathcal {S}$. PIEJoin builds two prefix trees $T_{\mathcal {R}}$ and $T_{\mathcal {S}}$ on relations $\mathcal {R}$ and $\mathcal {S}$, respectively, together with auxiliary structures on each tree node. In particular, for $T_{\mathcal {R}}$, each node is labeled with a preorder ID (e.g., $v_0, \ldots , v_9$ in Fig. 3), while for $T_{\mathcal {S}}$, there is a preorder interval on each node, which can be utilized to quickly decide whether a subtree contains a particular element. Figure 6 shows the augmented prefix tree $T_{\mathcal {S}}$ for $\mathcal {S}$ in Fig. 1b.

The details of PIEJoin are illustrated in Algorithm 3, which traverses two prefix trees simultaneously. The search starts from the root of $T_{\mathcal {R}}$ and $T_{\mathcal {S}}$ (Line 2). On each tree node pair v and w, we check whether there are some join pairs found (Line 5). In particular, if v.list is not empty (Line 11), then we find all records in the subtree rooted at w and enumerate join pairs (Lines 13–15). After collecting results in current tree node pair, we go further by traversing the children of v. For each child $v_i$, we find the descendants of w such that the element contained in these nodes is $v_i.e$ (Line 7). We then recursively conduct the search process for each node pair $v_i$ and $w_j$ (Line 9).

Compared to the previous solutions, PIEJoin employs a tree structure on records in $\mathcal {S}$, instead of the inverted index. This alleviates the problem of the large size inverted lists for $\mathcal {S}$. However, some auxiliary structures have to be engaged to facilitate the node match at Line 7. Note that we need to find the matches within the whole subtree, which may be cost expensive. As reported in [27], the performance of PIEJoin is not competitive compared with LIMIT(OPJ) [18], which builds inverted index on $\mathcal {S}$, under most of the datasets evaluated.

3.2 Union-oriented methods

In general, all methods in this category use signature-based techniques. Let $\mathcal {L}$ denote the domain of the signature values, we use a hash function h to map a record x into a set of signature values, denoted by h(x), with $h(x) \subseteq \mathcal {L}$. For instance, in the partition-based containment join algorithm [36], a record x will be mapped into a number between 0 and $k-1$. These algorithms are also named $\mathcal {R}$-driven methods because the main index is built on records in $\mathcal {R}$.

An important property of these signature-based techniques is as below. For any given records $r \in \mathcal {R}$ and $s \in \mathcal {S}$, we have $h(r) \subseteq h(s)$ if $r \subseteq s$. This implies that, for a given record $s \in \mathcal {S}$, we can safely exclude a record $r \in \mathcal {R}$ from set containment join result if $h(r) \not \subseteq h(s)$. That is, the signature-based techniques will not introduce any false negative.

Given two record collections $\mathcal {R}$ and $\mathcal {S}$, the key idea of union-oriented method is to generate candidate records within $\mathcal {R}$ for each record $s \in \mathcal {S}$ by the union of the inverted lists for the relevant signatures. Algorithm 4 illustrates a framework of simple union-oriented method. Lines 1–2 build inverted lists for possible signatures on $\mathcal {R}$. For each record $r \in \mathcal {R}$, Line 2 attaches its ID to the inverted list of the corresponding signature $\sigma$, denoted by $I_{\mathcal {R}}(\sigma )$. Then, Lines 4-7 generate containment join result candidates based on the union of the inverted lists of the signatures. For a record $s \in \mathcal {S}$, we consider the inverted lists of the signatures generated by s or any of its subsets. Line 8 verifies the candidate pairs within J to remove the false positives. Note that in the implementation, we usually do not need to explicitly enumerate all subsets of s to generate $M_s$ as shown at Line 5. Instead, $M_s$ can be generated efficiently by exploiting the characteristics of the specific signatures used.

The dominant cost of Algorithm 4 is the union of the inverted lists (Line 5) , denoted by $C_{filter}$, and the verification cost (Line 8), denoted by $C_{vef}$. We have

$$\begin{aligned} Cost(\mathcal {R} \bowtie _\subseteq \mathcal {S})&= C_{filter} + C_{vef} \nonumber \\&= \sum _{s \in \mathcal {S}} \sum _{ \sigma \in M_s } |I_{\mathcal {R}}(\sigma )| + C_{vef}. \end{aligned}$$

(2)

Analysis Compared with the intersection-oriented method in Algorithm 1, we need to verify the candidate pairs due to the nature of signature techniques, which usually brings false positives. Nevertheless, the advantage is that there is only one signature for each record. This leads to a smaller inverted index, and hence, a smaller number of records explored during the join process (Line 6).

Below are details of the existing union-oriented algorithms classified based on their signature techniques.

Partition-based techniques In [36], a partition-based method is proposed, where the signature of a record x is a number between 0 and $k-1$. For a given record $r \in \mathcal {R}$, the hash function h randomly selects an element e from r and maps e to an integer value between 0 and $k-1$ (Line 2 of Algorithm 4). We use this value as the signature of r. For a given record $s \in \mathcal {S}$, the signature subset $M_s$ (Line 5 of Algorithm 4) consists of different signatures generated by all elements of s. Obviously, for two given collections $\mathcal {R}$ and $\mathcal {S}$, we can divide the candidate join pairs into k partitions. Figure 7 shows the partitions for datasets in Fig. 1 where we assume that $k=4$ and an element $e_i$ is mapped into the value $(i\mod k)$. Several follow-up studies [33, 34] propose more sophisticated partitioning strategies (i.e., hash function h) to reduce the number of candidates in the partition pairs.

Bitmap-based techniques Helmer et al. [23] use a bitmap as the signature of a record x, and a bitmap consists of fixed b bits. Given two bitmaps $b_1$ and $b_2$, we say $b_1 \subseteq b_2$ if every 1 bit in $b_1$ is also set to 1 in $b_2$. Although comparing two bitmaps can be efficiently accomplished by basic bit operators, the task of enumerating all possible signatures by a record s or any of its subset (Line 5 of Algorithm 4) would be a bottleneck for the bitmap-based union-oriented method, since the number of subsets of a signature is exponential to the number of ’1’s in the bitmap, which is the bitmap length b in the worst case. To avoid such a straightforward way of enumerating the subsets of a signature, Luo et. al [30] recently propose a new algorithm, named PTSJ, based on a trie-based subsets enumeration method. In this method, the signatures of records in $\mathcal {R}$ are stored in a trie, where the leaf nodes store the record id in $\mathcal {R}$. Then, given a record $s \in \mathcal {S}$, it employs a breath-first search on the trie. For each tree node v, it stores the bit values 0 and 1 in the left child and right child, respectively. If the corresponding bit value of h(s) is 0, it only explores the left child. Otherwise, it will visit both children. Once finishing this traversal, the records in leaf nodes it accessed are the candidates.

Fig. 7

Partition-based method

Discussion PTSJ algorithm proposed in [30] is the state-of-the-art in-memory union-oriented method which significantly enhances the previous solutions in this category by advanced signature enumeration method and careful bitmap length selection. Nevertheless, our empirical study shows that PTSJ is not competitive compared with other state-of-the-art intersection-oriented solutions. According to our analysis in Sect. 4.2.2, PTSJ has two significant drawbacks: (i) does not utilize the data distribution and (ii) needs to verify all candidate pairs obtained.

3.3 Apply set similarity-based methods

We are aware that existing set similarity search/join algorithms can be applied to support set containment join by setting specific thresholds. In this paper, we consider three representative works that support set similarity search with different thresholds. It is worth mentioning that they are $\mathcal {S}$-driven methods in the sense that their main index structures are built on records from $\mathcal {S}$.

Li et al. [29] propose an efficient list merging algorithm, named DivideSkip, to solve the generalized T-occurrence query problem. Given a query record Q, T-occurrence problem is to find the set of record IDs that appear at least T times on the inverted lists of the elements in Q, where the inverted lists are built on $\mathcal {S}$. By setting T to the size of Q, DivideSkip can be immediately employed to process set containment search. Using a nested loop, DivideSkip can also be extended to compute set containment join.

Wang et al. [42] propose an adaptive framework for set similarity search, which adaptively selects the length of record prefix to build the inverted index. Since they apply the overlap similarity to handle different set similarity functions, by setting the overlap threshold T to the size of query Q, this framework can also be utilized to compute set containment join.

Agrawal et al. [14] study the problem of error-tolerant set containment search. To boost the query performance, they propose an frequent element set-based index structure that builds inverted index on careful chosen element set. By setting the error-tolerate threshold as 1, this index structure can also be applied to answer exact set containment query and therefore is also applicable to set containment join.

4 Our approach

In this section, we introduce a new in-memory set containment join algorithm, namely TT-Join, based on two tree structures constructed on $\mathcal {R}$ and $\mathcal {S}$, respectively.

4.1 Motivation

Our empirical study suggests that the existing competitive in-memory set containment join algorithms follow the intersection-oriented computing paradigm. However, to enjoy the nice property of verification free, we need to keep the ID of a record for each of its elements in the inverted index. This is an inherent limit of the intersection-oriented method which may lead to a large number of records explored during the join processing, especially when the number of inverted lists involved is large. Although an augmented prefix tree has been proposed in PIEJoin [27] to alleviate this issue, our empirical study suggests that the result is unsatisfactory due to the complicated data structure and expensive search cost incurred. Moreover, our analysis in Sect. 4.2.2 also suggests that it is difficult for intersection-oriented methods to exploit the data distribution.

This motivates us to revisit and design a new union-oriented approach. The drawbacks of existing union-oriented methods are twofold: (i) the signature techniques used are data independent, which cannot better exploit the distribution of the elements; (ii) they need to verify all candidate pairs. In this paper, we aim to design a new union-oriented method which not only enhances the nice property of union-oriented methods (i.e., small inverted list size) but also effectively addresses the above two issues.

In Sect. 4.2, we apply the ranked key [46] technique to use the least significant element as the signature of the record in the simple union-oriented algorithm (Algorithm 4). Through comprehensive cost analysis, we show that the performance of the new simple union-oriented method can significantly outperform that of simple intersection-oriented method (Algorithm 1) when data become skewed. It is rather intuitive to further enhance the filtering capacity by using k least frequent elements. We extend the inverted indexing of the new simple union-oriented method to accommodate the k least frequent element- based signature. Nevertheless, we show that a simple extension of inverted index is not promising due to the large overhead incurred.

This motivates us to impose a tree structure to accommodate the k least frequent element-based signatures. In Sect. 4.3, we build a prefix tree based on the k least frequent elements of the records in $\mathcal {R}$. By doing so, we can (i) further reduce the candidate size with a small overhead and (ii) naturally apply the intersection operator to validate a large number of candidates and hence reduce the verification cost. Together with a regular prefix tree constructed on $\mathcal {S}$, we develop an efficient set containment join algorithm, namely TT-Join.

4.2 Inverted index-based method

In this section, we introduce a simple union-oriented algorithm in Sect. 4.2.1 which uses the least frequent element as the signature. Section 4.2.2 conducts cost comparison between two simple intersection-oriented and union-oriented algorithms to reveal their inherent advantages and limits. Then, Sect. 4.2.3 investigates an extension of the inverted index to use k least frequent elements as the signature of a record such that the number of candidate pairs can be further reduced.

4.2.1 Using the least frequent element (IS-Join)

As shown in Sect. 3.2, different signature techniques are employed by the existing solutions to improve the performance of simple union-oriented method. However, none of them consider the distribution of the elements. To take advantage of the skewness of the real-life data, we apply the ranked key [46] technique to use the least significant element (i.e., least frequent element) as the signature of the record in the simple union-oriented algorithm (Algorithm 4). Our new simple union-oriented method, namely IS-Join,² is immediate, based on two minor changes of Algorithm 4: (1) at Line 2, the hash function h simply returns the least frequent element as the signature; (2) at Line 5, $M_s$ is the set of elements in s, i.e., considering |s| signatures.

Algorithm correctness For any result pair (r, s) (i.e., $r \subseteq s$), let $\sigma$ be the signature of r (i.e., the least frequent element), we have $r \in I(\sigma )$. Since $r \subseteq s$, we have $\sigma \in s$ and hence $\sigma \in M_s$ at Line 5. It is immediate that $r \in C$ (Line 6). After verification at Line 8, IS-Join algorithm can identify the pair (r, s).

Next, we use the running example in Fig. 1 to show the advantage of our least frequent element-based simple union-oriented method by comparing with the RI-Join (Algorithm 1).

Example 2

The inverted index on $\mathcal {S}$ and the least frequent inverted index on $\mathcal {R}$ are shown in Figs. 2 and 8, respectively. According to Eq. 1, we know that the cost for simple intersection-oriented method is 28, which is obtained by summing up the size of all inverted list in $I_{\mathcal {S}}$ for each record. Similarly, we have that the candidate size of union-oriented method is 8 according to Eq. 2, which means that the total cost is $8\times \mathcal {T}_{vef}$, where $\mathcal {T}_{vef}$ is the cost to verify a candidate.

The above example shows the candidate set of our union-oriented IS-Join algorithm is much smaller compared to that of intersection-oriented RI-Join algorithm. When the verification cost of IS-Join algorithm is not expensive, it has a good chance to outperform RI-Join algorithm.

Fig. 8

Inverted index on $\mathcal {R}$

4.2.2 Cost comparison

We now theoretically compare the expected costs of RI-Join (i.e., a simple intersection-oriented method in Algorithm 1) and the IS-Join algorithm (i.e., a simple union-oriented method in Algorithm 4 where the least significant element is used as the signature), denoted by $C_{RI}$ and $C_{IS}$, respectively. We use P(e) to denote the frequency distribution of an element $e \in \mathcal {X}$. Let $\theta (l)$ denote the probability that a record has l elements with $l \in [1, |x|_{max}]$ where $|x|_{max}$ is the maximum cardinality of a record in $\mathcal {X}$. In the cost analysis of this paper, we assume that $\mathcal {R}$ and $\mathcal {S}$ have the same distributions in terms of element frequency and record size. Moreover, we assume $|\mathcal {R}|$= $|\mathcal {S}|$ = n, $|r|_{avg}$ = $|s|_{avg}$ $= m$, and the distributions are independent.

Estimating ${{\varvec{C}}}_{{\varvec{RI}}}$ Since each element of any record in $\mathcal {S}$ leads to one entry in the inverted lists $I_{\mathcal {S}}$, we know that the expected number of entries in the inverted index is $|\mathcal {S}| \times |s|_{avg}$ where $|s|_{avg} = \sum _{l=1}^{|s|_{max}}\theta (l) \times l$ is the average size of a record in $\mathcal {S}$. Therefore, the size of the inverted list $I_{\mathcal {S}}(e)$ can be estimated as follows:

$$\begin{aligned} |I_{\mathcal {S}}(e)| = P(e) \times |\mathcal {S}| \times |s|_{avg}. \end{aligned}$$

(3)

According to Eq. 1, we have

$$\begin{aligned} C_{RI}&=\sum _{r \in \mathcal {R}} \sum _{ e \in r } |I_{\mathcal {S}}(e)| \nonumber \\&= |\mathcal {R}| \times |r|_{avg} \times \sum \limits _{e \in \mathcal {E}} P(e)|I_{\mathcal {S}}(e)| \nonumber \\&= |\mathcal {R}| \times |r|_{avg} \times |S| \times |s|_{avg} \times \sum \limits _{e \in \mathcal {E}} P(e)^2 \nonumber \\&= (nm)^2 \times \sum \limits _{e \in \mathcal {E}} P(e)^2. \end{aligned}$$

(4)

Equation 4 shows that, when the number of records (n) and the average size of the records (m) are fixed, RI-Join will achieve its best performance when all elements have the same frequency because $\sum _{e \in \mathcal {E}}P(e)= 1$. This implies that the skewness of the frequency distribution will deteriorate the performance of this simple intersection-oriented method, while it is well known that many real-life data are skewed.

Estimating ${\varvec{C}}_{{\varvec{IS}}}$ We first estimate the size of inverted list $I_{\mathcal {R}}(e)$ for an element e. Given a record $r \in \mathcal {R}$, r is in $I_{\mathcal {R}}(e)$ if and only if $e \in r$ and there is no element $e' \in r$ with lower frequency than e. Thus, the probability that r within $I_{\mathcal {R}}(e)$, denoted by $P(r \in I_{\mathcal {R}}(e))$, is

$$\begin{aligned} P(r \in I_{\mathcal {R}}(e))&= P(e) \times F(e)^{|r|-1} \nonumber \\&= \sum \limits _{l=1}^{|r|_{max}} \theta (l) \times l \times P(e) \times F(e)^{l-1} , \end{aligned}$$

(5)

where $F(e) = \sum _{e' \prec e} P(e')$ is the cumulative probability before e where elements are ranked by frequency decreasing order; that is, F(e) is the probability that a random chosen element has a higher frequency than e. Note that once an element e appears within the record r, it will serve as the signature with probability $F(e)^{|r|-1}$ due to the independent assumption. Thus, the expected size of list $I_{\mathcal {R}}(e)$ is as follows:

$$\begin{aligned} |I_{\mathcal {R}}(e)|&= \sum \limits _{r \in \mathcal {R}} P(r \in I_{\mathcal {R}}(e)) \nonumber \\&= |\mathcal {R}| \times \sum \limits _{l=1}^{|r|_{max}} \theta (l) \times l \times P(e) \times F(e)^{l-1}. \end{aligned}$$

(6)

According to Eq. 2, we have

$$\begin{aligned} C_{IS}&= \sum _{s \in \mathcal {S}} \sum _{ \sigma \in M_s } |I_{\mathcal {R}}(\sigma )| + C_{vef} \nonumber \\&= \sum _{s \in \mathcal {S}} \sum _{ e \in s } |I_{\mathcal {R}}(e)| + C_{vef} \nonumber \\&= |\mathcal {S}| \times |s|_{avg} \times \sum \limits _{e \in \mathcal {E}} P(e) \times |I_{\mathcal {R}}(e)| + C_{vef} \nonumber \\&{\mathop {=}\limits ^{(6)}} (nm)^2 \times \sum \limits _{e \in \mathcal {E}} P(e)^2 \times F(e)^{m-1} + C_{vef}. \end{aligned}$$

(7)

Compared with Eq. 4, it is immediate that the number of records explored by our union-oriented IS-Join algorithm is smaller than that of intersection-oriented RI-Join algorithm since $F(e)<1$. Our empirical study below clearly shows that this gain will eventually pay off the verification cost ($C_{vef}$) when the skewness of the data increases.

Empirical evaluation To evaluate the impact of the skewness toward the performance of two algorithms, we conduct a simple experiment on synthetic datasets. In particular, we generate datasets where the frequency of the elements follow the well-known Zipfian distribution with exponent z value varying from 0.2 to 1. Note that the data skewness increases when z grows. The number of records and the average record size are set to 100,000 and 10, respectively.

It is observed in Fig. 9 that intersection-oriented RI-Join algorithm outperforms our simple union-oriented IS-Join algorithm when z is small due to the extra verification cost of IS-Join. However, as z increases, the processing time of RI-Join continuously grows, while IS-Join can take great advantage of the skewness.

Fig. 9

Effect of data skewness

Fig. 10

2 least frequent element-based inverted index on $\mathcal {R}$

4.2.3 Extending to k least frequent elements (kIS-Join)

According to the above cost analysis, the least frequent element is a promising signature for union-oriented methods. To enhance the pruning capacity, it is natural to consider k least frequent elements. Following the existing inverted index technique, now each record is mapped to k elements (signatures). Figure 10 shows an example of the inverted index on $\mathcal {R}$ in Fig. 1a when $k=2$.

Then, for a given record $s \in \mathcal {S}$, we count the number of appearances for the records in C (Line 6 in Algorithm 4). If a record $r \in C$ appears k times (i.e., all k least frequent elements of r are contained in s), r is a candidate. Otherwise, we can prune r directly. We use kIS-Join to denote this algorithm which corresponds to IS-Join algorithm when $k=1$.

Estimating ${\varvec{C}}_{{\varvec{kIS}}}$ Similar to the cost analysis for IS-Join algorithm, we first estimate the size of inverted list $I_{\mathcal {R}}(e)$ for an element e. Note that $I_{\mathcal {R}}$ is the inverted index based on the k least frequent elements of records in $\mathcal {R}$. Given a record $r \in \mathcal {R}$, r is in $I_{\mathcal {R}}(e)$ iff e is one of r’s k least frequent elements. Thus, the probability that r is in $I_{\mathcal {R}}(e)$, denoted by $P(r \in I_{\mathcal {R}}(e))$, is:

$$\begin{aligned} P(r \in I_{\mathcal {R}}(e))&\approx P(e) \times \sum \limits _{i=1}^k F(e)^{l-i} \nonumber \\&= \sum \limits _{l=1}^{|r|_{max}} \theta (l) \times l \times P(e) \times \sum \limits _{i=1}^k F(e)^{l-i}. \end{aligned}$$

(8)

Now, the size of list $I_{\mathcal {R}}(e)$ is as follows:

$$\begin{aligned} |I_{\mathcal {R}}(e)|&= \sum \limits _{r \in \mathcal {R}} P(r \in I_{\mathcal {R}}(e)) \nonumber \\&{\mathop {=}\limits ^{(8)}} |\mathcal {R}| \times \sum \limits _{l=1}^{|r|_{max}} \theta (l) \times l \times P(e) \times \sum \limits _{i=1}^k F(e)^{l-i}. \end{aligned}$$

(9)

According to Eq. 2, we have

$$\begin{aligned} C_{kIS}&= \sum _{s \in \mathcal {S}} \sum _{ \sigma \in M_s } |I_{\mathcal {R}}(\sigma )| + C_{vef} \nonumber \\&= \sum _{s \in \mathcal {S}} \sum _{ e \in s } |I_{\mathcal {R}}(e)| + C_{vef} \nonumber \\&= |\mathcal {S}| \times |s|_{avg} \times \sum \limits _{e \in \mathcal {E}} P(e) \times |I_{\mathcal {R}}(e)| + C_{vef} \nonumber \\&{\mathop {=}\limits ^{(9)}} (nm)^2 \times \sum \limits _{e \in \mathcal {E}} P(e)^2 \times \sum \limits _{i=1}^k F(e)^{m-i} + C_{vef}. \end{aligned}$$

(10)

By comparing Eqs. 10 and 7, we know that the later is a special case of the former when $k=1$. Clearly, on one hand, the pruning cost of $C_{kIS}$ increases with k because kIS-Join touches more records due to the large inverted index size. On the other hand, the verification cost $C_{vef}$ decreases with k since a larger k can prune more non-promising records. Therefore, there is a trade-off between these two costs. Our experimental results in Sect. 6.1.2 show that the performance gain for $C_{vef}$ brought by a larger k value usually cannot pay off the increased pruning costs.

4.3 Tree-based method (TT-Join)

It is rather intuitive that the pruning power of our simple least frequent element-based union-oriented method can be enhanced by increasing k. However, as shown in the above analysis and empirical study, the overhead cost brought by a straightforward extension of the inverted index is expensive and the gain of the enhanced pruning capacity may not be well paid off. In this subsection, we aim to develop a new union-oriented algorithm which enables us to: (i) enhance the pruning capacity with small overhead and (ii) output some join result pairs during the tree traversal without going to the verification phase. Section 4.3.1 introduces the k-length least frequent prefix tree structure, namely kLFP-Tree, which is built on records in $\mathcal {R}$. Together with a prefix tree constructed on records in $\mathcal {S}$, Sect. 4.3.2 presents our TT-Join algorithm by traversing two prefix trees simultaneously. Section 4.3.3 conducts performance analysis on the TT-Join algorithm.

4.3.1 k-Length least frequent prefix tree (kLFP-Tree)

The kLFP-Tree is constructed based on the k-length least frequent prefix of each record, which is defined as follows.

Definition 3

(k-length least frequent prefix) Given a record $x=\{e_1,\ldots , e_n\}$ where elements are in decreasing order of their frequency in $\mathcal {X}$, we define $\{e_{n}, \ldots , e_{n-k+1}\}$ as its k-length least frequent prefix, denoted by $LFP_{k}(x)$. Note that $LFP_{k}(x)$ is the reverse of x if $|x| \le k$.

Given a set of k-length least frequent prefixes of the records in $\mathcal {R}$, the prefix tree (kLFP-Tree) is built up following Definition 2. Specifically, for each record x, we insert the last k elements (i.e., k least frequent elements in x) into the prefix tree following the reverse order, and it takes O(1) time to insert each element as a hash table is used to maintain child entries for each node in kLFP-Tree. Thus, the time complexity to construct kLFP-Tree is $O(|\mathcal {R}|k)$. With the same time complexity, we may remove a record x in kLFP-Tree by deleting its k least frequent elements in order. Note that there is only one replica of a record x, whose ID is kept on the corresponding node of kLFP-Tree based on $LFP_{k}(x)$.

Example 3

Take the relation $\mathcal {R}$ in Fig. 1a as an example. When $k=2$, we have $LFP_{k}(r_1) = \{e_3, e_2\}$, $LFP_{k}(r_2) = \{e_4, e_2\}$, $LFP_{k}(r_3) = \{e_4, e_3\}$, and $LFP_{k}(r_4) = \{e_5, e_2\}$. Then, the corresponding kLFP-Tree is illustrated in Fig. 11a.

4.3.2 TT-Join algorithm

We use $T_{\mathcal {R}}$ to denote the kLFP-Tree built on relation $\mathcal {R}$. To share computational cost, we also build a regular prefix tree for records in $\mathcal {S}$ following Definition 2, which is denoted by $T_\mathcal {S}$. Figure 11 illustrates the example of $T_{\mathcal {R}}$ and $T_\mathcal {S}$ based on the records in Fig. 1. Note that we use a circle (resp. rectangle) to represent the node of the tree built on $\mathcal {R}$ (resp. $\mathcal {S}$), and each tree node is denoted by $v_i$ (resp. $w_i$).

Algorithm 5 illustrates the details of TT-Join algorithm. In general, we traverse $T_{\mathcal {S}}$ following a depth-first strategy (Lines 5–13). Lines 5–11 compute the relevant join result for each visited node w. Specifically, for the record s associated with w (i.e., $s = w.set$), we find all records in $\mathcal {R}(s)$. Recall that $\mathcal {R}(s)$ denotes the records within $\mathcal {R}$ which are a subset of s. We use $R_1$ to denote those records within $\mathcal {R}(s)$ without element w.e, and $R_2$ to denote the remaining records. In the procedure processNode (Lines 5–13), the list passed from the parent node corresponds to $R_1$ because we have $w.prefix \subset s$ and $w.prefix = s \setminus w.e$. Then, Lines 6–8 identify the records in $R_2$. Particularly, Line 6 finds the node associated with element w.e in $T_{\mathcal {R}}$. Then, we only need to continue the search in its subtree because w.e is the least frequent element in r. As shown in the procedure traverse (Lines 14–24), for each node v in $T_\mathcal {R}$ accessed, Line 18 can immediately validate a record r in v.list if $|r|\le k$ (i.e., r is reported without verification). Otherwise, we need to verify whether $r \subseteq s$ at Line 20. Specifically, we employ a merge-sort manner to verify whether the rest of elements of r are contained in s. This procedure can be stopped early whenever possible and is linear in the record size in the worst case [32]. At Lines 21–23, we continue to find potential records within $R_2$ if any of the child nodes matches an element in w.prefix. After all records within $R_2$ are identified, we use the updated list to keep all records within $R_1 \cup R_2$. Lines 9–11 output the join results associated with the node w accessed.

Fig. 11

Tree structures for tree-based method

Algorithm correctness For any record $s \in \mathcal {S}$, s must appear in one of the tree nodes, say w, in $T_{\mathcal {S}}$. Because we traverse $T_{\mathcal {S}}$ in a depth-first manner, w must be considered during the traversal. For each record s in w.list, we can find all records $r \in \mathcal {R}$ with $r \subseteq s$. Particularly, every record r from $R_1$, which does not contain element w.e, will be passed from w’s parent node because we have $r \subseteq w.set$ if $r \subseteq w.prefix$ and $w.set =$ $w.prefix~\cup ~w.e$. For any record $r \in R_2$, it must appear within the subtree rooted at node v with $v.e = w.e$ (Line 6) because w.e is the least frequent element in r. Meanwhile, none of the record in $R_1$ may appear in this subtree since $w.e \not \in r$ for every $r \in R_1$. For a record $r \in R_2$, we use v to denote the corresponding node of r in $T_{\mathcal {R}}$ with $r \in v.list$. Since we explore all child nodes $v_i$ with $v_i.e \in w.prefix$ in the procedure traverse, we will eventually reach v and identify r. On the other hand, because we only explore child nodes $v_i$ with $v_i.e \in w.prefix$, this implies that $v.set \subseteq w.set$ for every node v accessed in the procedure traverse. Consequently, all results validated at Lines 17–18 are correct. Thus, the join results on each node are complete and correct.

Example 4

Consider the example in Fig. 1. The index trees on $\mathcal {R}$ and $\mathcal {S}$ are shown in Fig. 11a, b, respectively. We traverse $T_{\mathcal {S}}$ in a depth-first manner starting from $w_1$. We immediately turn to $T_{\mathcal {R}}$ to see whether there is a child node of the root of $T_{\mathcal {R}}$ matching the element of $w_1$ (i.e., $e_1$). The answer is no. We then continue the traversal processing until at $w_3$ where we find a child node $v_1$ in $T_{\mathcal {R}}$ with $w_3.e=v_1.e$. Next, we switch to traverse $T_{\mathcal {R}}$ starting from $v_1$ in a depth-first manner and find that $v_2$ matches $w_2$. At this point, we get a nonempty list (i.e., $r_1$) in $v_2$, which means that we get a candidate. We then conduct the verification and find that the remaining element $e_1$ of $r_1$ is in $w_3.set$. Therefore, $r_1$ is a subset of $w_3$. After that, we continue traversing $T_{\mathcal {S}}$ and reach $w_4$ where we would get two subsets $r_1$ and $r_4$. In particular, $r_1$ is passed from $w_3$ and $r_4$ is collected at $w_4$. Since the list of $w_4$ is not empty, we then generate join pairs, namely $(r_1, s_1)$ and $(r_4, s_1)$. We find the full join results after finishing traversing $T_{\mathcal {S}}$.

4.3.3 Cost analysis

Next, we analyze the cost of TT-Join, followed by a cost comparison with IS-Join and kIS-Join introduced in Sect. 4.2.

Estimating ${\varvec{C}}_{{\varvec{TT}}}$ In TT-Join, we build the inverted index for the least frequent prefix of each record in $\mathcal {R}$, which means that the size of the inverted index is fixed at $|\mathcal {R}|$. Besides, because the inverted index is determined by the least frequent element of each record in $\mathcal {R}$, we have that the inverted index size is exactly the same as shown in Eq. 6. On the other hand, for each least frequent prefix, we have to sequentially check whether a given record $s \in \mathcal {S}$ contains the remaining $k-1$ least frequent elements in the worst case. Therefore, the overall cost of TT-Join is as follows:

$$\begin{aligned} C_{TT}&= \sum _{s \in \mathcal {S}} \sum _{ \sigma \in M_s } |I_{\mathcal {R}}(\sigma )| + C_{check} + C_{vef} \nonumber \\&= (nm)^2 \times \sum \limits _{e \in \mathcal {E}} P(e)^2 \times F(e)^{m-1} \nonumber \\&\quad + C_{check} + C_{vef}, \end{aligned}$$

(11)

where $C_{check}$ is the overhead to check the least frequent elements.

Comparison with IS-Join Equations 11 and 7 indicate that TT-Join and IS-Join have the same pruning cost. However, in terms of the verification cost, $C_{vef}$ in Eq. 11 is smaller than that in Eq. 7, because TT-Join uses k least frequent elements as the signature of a record to enhance the pruning capacity. Therefore, with a reasonable checking cost $C_{check}$, TT-Join may benefit from increasing k.

Comparison with kIS-Join Because both kIS-Join and TT-Join use the k least frequent elements as signature, $C_{vef}$ in Eqs. 10 and 11 are exactly the same. The experimental results in Sect. 6.1.2 show that the $C_{check}$ is insignificant compared with the growth of the number of explored records when k increases. Therefore, compared with kIS-Join, TT-Join can achieve better trade-off by increasing k within a reasonable range (e.g., $1 \le k \le 5$ in our empirical study).

4.4 Discussion

In this section, we first discuss the difference between proposed method and the techniques in the existing solutions. Then, we discuss the difference between proposed method and a trie-based string similarity algorithm. Last we introduce how to extend proposed method to the context of selection predicates.

Comparison of TT-Join and other methods As shown in Sects. 3.1 and 3.3, both intersection-oriented methods and three modified similarity-based methods are $\mathcal {S}$-driven where their main index is built on $\mathcal {S}$. The key of their technique is, for each record $r \in \mathcal {R}$, how to utilize the index structure on $\mathcal {S}$ to find all records in $\mathcal {S}$, each of which contains r. On the contrary, TT-Join is $\mathcal {R}$-driven since the main index structure is built on $\mathcal {R}$. Moreover, although all algorithms use the variants of the inverted index as the main index, we show in the paper that TT-Join keeps one copy of the ID for each record in $\mathcal {R}$, while $\mathcal {S}$-driven methods need to maintain multiple copies of the ID for each record in $\mathcal {S}$. Consequently, the corresponding join algorithm of TT-Join is different to that of existing solutions.

Comparison of TT-Join and Trie-Join [41] The proposed method TT-Join is different from Trie-Join due to the following reasons. (i) Trie-Join uses one trie to index strings in both $\mathcal {R}$ and $\mathcal {S}$, where trie nodes are marked by belonging to which set, such as $\mathcal {R}$, $\mathcal {S}$, or $\mathcal {R} \cup \mathcal {S}$. (ii) Trie-Join works only for edit-distance similarity function. That is because the main technique in Trie-Join is dual subtrie pruning. In order to efficiently apply this pruning technique, the authors introduce the key concept of active-node set, where the computation is edit-distance dependent.

Handling the selection predicates In practice, it is useful to consider selection predicates for set containment join. As our index structure proposed is built on-the-fly, we can easily push down the selection predicates by using existing indexing techniques (e.g., B+tree). That is, we can select the corresponding records based on the given predicates, then apply our indexing and query processing techniques.

5 Distributed processing

In this section, we aim to support better scalability by deploying TT-Join on the top of MapReduce framework. We first review related work on utilizing MapReduce to process set similarity join problem in Sect. 5.1, followed by the detailed introduction of MapReduce framework in Sect. 5.2. Efficient load-aware distribution mechanism is introduced in Sect. 5.3.

5.1 Related work

To the best of our knowledge, there is no existing work that extends set containment join to MapReduce framework. Recently, Kunkel et al. [27] propose a parallel algorithm PIEJoin to compute the set containment join. Nevertheless, they achieve parallelization by creating a task thread for each recursive call of the crucial search function in their approach. This method does not follow the MapReduce framework which involves two important operations, namely map and reduce.

In the past decade, MapReduce has attracted tremendous interests in both academia and industry communities. Its high efficiency and scalability for batch processing tasks provides elegant solutions for many join problems. Here, we focus on the set similarity join problem in MapReduce, which is closely related to our set containment join problem. Vernica et al. [40] propose a prefix-based partition strategy for set similarity join based on prefix filter, which states that two records must share at least one common element in their prefixes if they are similar. After constructing the inverted index on elements of record prefix, records in the same inverted list are then dispatched to the same task node. Metwally et al. [35] present V-SMART-JOIN, which similarly builds inverted index on elements and compute the similarity of record pairs by sharing the computation in the element level using MapReduce. Deng et al. [20] propose a partition-based framework to solve set similarity join in MapReduce. The element set of a record is partitioned into $U+1$ disjoint segments, where U is a dissimilarity upper bound. Similar record pairs would be distributed to at least one common task nodes where they share the same segment. Afrati et al. [13] conduct theoretical analysis against multiple MapReduce-based similarity join algorithms, where they analyze the map, reduce, and communication cost.

5.2 Framework

Algorithm 6 illustrates the framework of computing set containment join on MapReduce. In MapReduce framework, each iteration consists of three phases, namely map phase, shuffle phase, and reduce phase. In the map phase as shown in Lines 1–2, each map node (i.e., mapper) sequentially reads record x (i.e., record in $\mathcal {R}$ or $\mathcal {S}$) from the file splits on this node and emits intermediate $\langle nid, x\rangle$ pairs, where nid is the ID of a task. These intermediate $\langle nid, x\rangle$ pairs are then shuffled based on the keys (i.e., nid) and transferred to the reduce nodes (i.e., reducers), where intermediate $\langle nid, x\rangle$ pairs with the same keys are shuffled to the same reduce node. Each reduce node then receives a key-value pair in the form of $\langle nid, list(x) \rangle$, where list(x) contains a list of records sharing the same nid (Line 3). After dividing the list(x) into two record sets R and S, local set containment join algorithm is then applied on the reduce node to compute the join result (Lines 4–6). Note that there might be an extra job to summarize the join results from all reduce nodes.

Challenges Following the theoretical analysis in [13], we consider three costs in a MapReduce iteration, which are map, reduce, and communication cost. The distribution strategy (i.e., Line 2 in Algorithm 6) should be able to handle load balance between the reduce nodes, since parallel computing is most important property of a MapReduce system. In the meanwhile, the communication cost should be as less as possible because the network band would become the bottleneck for a large cluster with many reduce nodes.

5.3 Distribution scheme

In this section, we present our distribution scheme which is employed by the mappers to dispatch records in $\mathcal {R}$ and $\mathcal {S}$ to relevant reducers for parallel processing. We first discuss random distribution method which is most straightforward, followed by a prefix-based method which is extended from the approach for processing set similarity join. We then propose a novel and efficient signature-based distribution method, which is computation load-aware and communication cost saving. For ease of explanation, we assume that there are N reduce tasks available for parallel processing. Our goal is to devise a good distribution scheme for the mappers to dispatch records in $\mathcal {R}$ and $\mathcal {S}$ to the N reduce tasks, each of which is identified by an ID in the range of [1, N]. To measure the communication cost, we count the number of copies emitted to the reduce nodes for each record x, which is denoted by C(x).

5.3.1 Baseline methods

Random-based distribution A straightforward way to implement random distribution is as follows. For each $r \in \mathcal {R}$, we randomly dispatch r to one of the N reduce nodes, and for each $s \in \mathcal {S}$, we dispatch s to all N reduce nodes. It is evident this distribution method generates no duplication in the join results, and the communication costs are $C_{rand}(r) = 1$ and $C_{rand}(s) = N$, respectively. In the following, we present an advanced random distribution scheme, which can decrease the communication cost to $\sqrt{N}$ and, at the same time, preserve the property of introducing no duplication in the join results.

We randomly divide records in $\mathcal {R}$ into $\sqrt{N}$ disjoint subsets. That is $\mathcal {R} = \cup _{1\le i \le \sqrt{N}}\mathcal {R}_i$, where for $1\le i \ne j \le \sqrt{N}$, $\mathcal {R}_i\cap \mathcal {R}_j=\emptyset$. Similarly, records in $\mathcal {S}$ are also randomly divided into $\sqrt{N}$ disjoint subsets where $\mathcal {S} = \cup _{1\le i \le \sqrt{N}}\mathcal {S}_i$. Then, records in each pair $(\mathcal {R}_i, \mathcal {S}_j)$ with $1\le i,j \le \sqrt{N}$ will be dispatched to uniquely one of the N reducers since there are N pairs in total. Apparently, the communication cost of random distribution is $\sqrt{N}$ for records in both $\mathcal {R}$ and $\mathcal {S}$; that is $C_{rand}(x) = \sqrt{N}$. Besides, there is no duplication in the reduce nodes. That is because, for any given record pair (r, s), it will only be dispatched to one reducer.

Fig. 12

Example of different distribution schemes

Prefix-based distribution In [40], efficient prefix-based distribution method is proposed for set similarity join. Given a record x and overlap similarity threshold T, we can compute the prefix of x, denoted by Prefix(x), which consists of the first $|x| - T + 1$ elements of x. Then, two records must share at least one common element in their prefixes if they are similar. Given a hash function h, record x is then dispatched to reduce node with ID $h(e_i)$ for each $e_i \in Prefix(x)$, where $h(e_i) = i \mod N + 1$ is widely used. This method is very efficient to process set similarity join because the prefix length is very limited. However, in our set containment join, the overlap similarity threshold T would be any value between 1 and |x| since any subset of x forms a set containment relation with x. Therefore, to make the prefix-based distribution strategy applicable for set containment join, we have to consider x itself as its prefix. Thus, we dispatch x to the reduce nodes corresponding to each element. Now, we estimate the communication cost as follows. For any reduce node, the probability that at least one element in x is dispatched to that node is $1-(1-\dfrac{1}{N})^{|x|}$. Therefore, the communication cost on N reduce nodes is

$$\begin{aligned} C_{pre}=N\left( 1-(1-\dfrac{1}{N})^{|x|}\right) . \end{aligned}$$

(12)

Note that this method might introduce duplicates in the join results because a record pair might be dispatched to different reduce nodes.

5.3.2 Our signature-based approach

Motivation Even though the random distribution enjoys the nice property of load balance on all reduce nodes, the corresponding communication cost is high, which renders this method impractical for large-scale datasets where we inevitably have to increase the value of N. Prefix-based method, on the other hand, is not able to handle dataset with large average record size, which is also verified by our experimental studies. According to Eq. 12, the communication cost is approaching N when the record size (i.e., |x|) increases. The above limits of baseline methods motivate us to devise a new approach such that (i) the communication cost is small and (ii) the workload on each reduce node is similar. By extending the idea of least significant element that used by TT-Join, we propose a signature-based distribution scheme in this section. Under the framework of this scheme, we devise efficient element domain partitioning algorithms in next section, which enable our signature-based approach to achieve the two goals (i) and (ii).

Our signature-based distribution scheme works as follows. We partition the ordered element domain $\mathcal {E} = \{e_1, e_2, \ldots , e_{|\mathcal {E}|}\}$ into N disjoint intervals, i.e., $[e_{l_1}, e_{h_1}]$, $[e_{l_2}, e_{h_2}]$, ..., $[e_{l_N}, e_{h_N}]$, where $l_1 = 1$, $h_N = |\mathcal {E}|$, and $l_{i+1}=h_i + 1$ for $1 \le i \le N-1$. We assume that there is a one-to-one relationship between element intervals and reduce nodes. Now, given a record $r \in \mathcal {R}$, let $\sigma$ be the signature (i.e., the least frequent element) of r. We find the interval where $\sigma$ falls and dispatch r to the corresponding reduce node. For each record $s \in \mathcal {S}$, we dispatch s to all reduce nodes whose corresponding intervals cover at least one element of s.

Theorem 1

Our signature-based distribution scheme is complete, i.e., it will not miss any join results.

Proof

Given any result pair (r, s) (i.e., $r \subset s$), let $\sigma$ be the signature of r (i.e., the least frequent element). Suppose $\sigma$ falls into the ith signature interval, which means that r will be dispatched to ith reduce node. Since $r \subset s$, we have $\sigma \in s$. Therefore, a copy of s will be dispatched to ith reduce node as well. After the execution of local join algorithm in ith reduce node, we get the pair (r, s). $\square$

Compared to the baseline methods, a key advantage of signature-based method is that its communication cost is much lower. Specifically, $C_{sig}(r) = 1$ for $r \in \mathcal {R}$ since r is only transferred to exactly one reduce node. $C_{sig}(s) \in [1, \min (|s|, N)]$ for $s \in \mathcal {S}$ because s is only emitted to the reduce nodes that cover at least one element of s. Note that the expected value of $C_{sig}(s)$ depends on how we partition the element domain, which we will discuss in the following section. Besides, it is evident that signature-based approach does not generate duplicates in the join results because each record $r \in \mathcal {R}$ is emitted to exactly one reduce node. Also, signature-based scheme can prefilter many unpromising candidate pairs by the signature during the distribution phase and thus reduce the local join cost substantially.

Example 5

Figure 12 shows an example of all the distribution schemes. Suppose $N=4$, $\mathcal {E} = \{e_1, e_2, \ldots , e_{16}\}$, and two records $r=\{e_1, e_4, e_6\}$ and $s=\{e_1, e_4, e_6, e_7\}$. For random scheme, r is dispatched to nodes 1 and 2, while s is distributed to nodes 2 and 4. Note that we apply a round-robin strategy to ensure that, for any record pair r and s, each of which will be dispatched to $\sqrt{N}$ reduce nodes, and they meet in exactly one reduce node. For prefix-based scheme, assuming $h(e_i) = i \mod N + 1$, and therefore $h(e_1) = 2$, $h(e_4) = 1$, $h(e_6) = 3$, and $h(e_7) = 4$. Thus, r is emitted to nodes 1, 2, 3, and s is emitted to all 4 nodes. For signature-based method, we assume that the element domain is evenly partitioned for ease of explanation. Therefore, r is dispatched to node 2, and s is dispatched to nodes 1 and 2. Clearly, our signature-based method introduces no replications and has the lowest communication cost in this example.

5.3.3 Load-aware partitioning

Our signature-based method makes use of a partition of the element domain. To find a good partition, a straightforward way is to partition $\mathcal {E}$ into N intervals evenly. However, as suggested by our experimental results, this method yields very poor performance. This is because many real-life data are skewed, and therefore, the records will be dispatched to the reduce nodes unevenly. In this section, we propose a judiciously designed cost model which takes local join computation cost into consideration to guide the partition of element domain, such that the reduce nodes can take similar workload. We first devise a dynamic programming-based optimal partition method, which bears a time and space complexity of $O(N|\mathcal {E}|^2)$. The high time and space complexity of this method is not suitable to dataset with large element domain size (i.e., $|\mathcal {E}|$). Consequently, we then resort to a heuristic partition algorithm, which is linear to the element domain size (i.e., $O(|\mathcal {E}|)$) for both time and space complexity.

Optimal partition In Sect. 4, given two collections $\mathcal {R}$ and $\mathcal {S}$, we conduct cost analysis for different join algorithms based on the element frequency distribution P(e) and record length distribution $\theta (l)$. Now, we are interested in analyzing the cost on each interval given a specific local join algorithm. First, we define an element partition instance as follows:

Definition 4

An element partition instance, denoted by $\mathcal {P}(e_l, e_h, n)$, defines a partition which splits the element range $[e_l, e_h]$ into n disjoint intervals, where each interval is represented by $[e_{l_i}, e_{h_i}]$ for $i \in [1, n]$, assuming $l_1 = l$ and $h_n = h$.

Note that a single interval $[e_l, e_h]$ is a partition instance with $n=1$, i.e., $\mathcal {P}(e_l, e_h, 1)$.

Estimating ${\varvec{Cost}}{} \mathbf ( \mathcal {P}{} \mathbf ( {\varvec{e}}_{{\varvec{l}}}, {\varvec{e}}_{{\varvec{h}}}{} \mathbf , \; \mathbf 1))$ Given a single interval $[e_l, e_h]$, we now aim to estimate the join cost on the corresponding reduce node against a given join algorithm. For ease of explanation, we use RI-Join algorithm to conduct the analysis because it has the simplest cost model as shown in Eq. 4. Clearly, in order to estimate $Cost(\mathcal {P}(e_l, e_h, 1))$, we need to know the record collections received by the corresponding reduce node. By $\mathcal {R}(e_l, e_h)$ and $\mathcal {S}(e_l, e_h)$, we denote the record sets from $\mathcal {R}$ and $\mathcal {S}$, respectively. First, we consider the unit intervals; that is $e_l=e_h=e_i$. Based on the distribution scheme of our signature-based approach, $\mathcal {R}(e_i,e_i)$ contains all records with $e_i$ as their least frequent element, where the size is shown in Eq. 6. On the other hand, $\mathcal {S}(e_i,e_i)$ consists of the records which contain $e_i$, where the size is shown in Eq. 3. According to Eq. 4, we have:

$$\begin{aligned}&Cost(\mathcal {P}(e_i,e_i,1)) = \sum _{r \in \mathcal {R}(e_i,e_i)}\sum _{e_j \in r}|I_{\mathcal {S}(e_i,e_i)}(e_j)| \nonumber \\&\quad = |\mathcal {R}(e_i,e_i)| \times |r|_{avg} \times \sum _{j \le i}P(e_j)|I_{\mathcal {S}(e_i,e_i)}(e_j)| \nonumber \\&\quad {\mathop {=}\limits ^{(6)}} |\mathcal {R}| \times \sum \limits _{l=1}^{|r|_{max}} \theta (l) \times l \times P(e_i) \times F(e_i)^{l-1} \nonumber \\&\quad \quad \times |r|_{avg} \times \sum _{j \le i}P(e_j)|I_{\mathcal {S}(e_i,e_i)}(e_j)| \nonumber \\&\quad {\mathop {=}\limits ^{(3)}} |\mathcal {R}| \times \sum \limits _{l=1}^{|r|_{max}} \theta (l) \times l \times P(e_i) \times F(e_i)^{l-1} \nonumber \\&\quad \times |r|_{avg} \times \sum _{j \le i}P(e_j)^2 \times |\mathcal {S}| \times P(e_i) \times |s|_{avg}^2 \nonumber \\&\quad = |\mathcal {R}|\times |\mathcal {S}| \times |r|_{avg}^2 \times |s|_{avg}^2 \times P(e_i)^2 \nonumber \\&\quad \quad \times F(e_i)^{l-1} \times \sum _{j \le i}P(e_j)^2. \end{aligned}$$

(13)

Since the inverted index size is linear to the data size received by the corresponding reduce node, it is implied that the join cost over an interval $[e_l, e_h]$ can be decomposed into the summation of the join cost over each unit interval $[e_i,e_i]$, where $e_i \in [e_l, e_h]$. That is:

$$\begin{aligned} Cost(\mathcal {P}(e_l, e_h, 1))=\sum _{l \le i \le h}Cost(\mathcal {P}(e_i,e_i,1)). \end{aligned}$$

(14)

Before presenting our partition algorithm, we first define a function f over $\mathcal {P}(e_l, e_h, n)$ to compute the maximal interval cost among n intervals as follows:

$$\begin{aligned} f(\mathcal {P}(e_l, e_h, n)) = \max _{\forall [e_{l_i}, e_{h_i}] \in \mathcal {P}(e_l, e_h, n)}Cost(\mathcal {P}(e_{l_i}, e_{h_i}, 1)). \end{aligned}$$

(15)

Since the overall performance of the system is affected by the slowest reduce node, our goal is to find an instance $\mathcal {P}(e_1, e_{|\mathcal {E}|}, N)$ such that $f(\mathcal {P}(e_1, e_{|\mathcal {E}|}, N))$ is minimized. We denote the optimal solution that minimizes $f(\mathcal {P}(e_l, e_h, n))$ by $\mathcal {P}^*(e_l, e_h, n)$. Then, our goal is equivalent to finding $\mathcal {P}^*(e_1, e_{|\mathcal {E}|}, N)$. To solve this problem, we propose a dynamic programming algorithm based on the following key observation:

$$\begin{aligned}&f(\mathcal {P}^*(e_l, e_h, n)) = \min _{l+n-2 \le i < h} \nonumber \\&\{\max \{f(\mathcal {P}^*(e_l, e_i, n-1)), f(\mathcal {P}^*(e_{i+1}, e_h, 1))\}\}. \end{aligned}$$

(16)

This observation indicates that the optimal partition of size n can be computed by enumerating the rightmost boundary of the optimal partition of size $n-1$.

Algorithm 7 illustrates our dynamic programming- based optimal partition method. Lines 1–2 compute the cost of single intervals based on Eq. 14. Lines 3–5 iteratively compute the optimal partition for a range with n intervals based on Eq. 16.

Time and space complexity Based on Eq. 14, it is easy to show that $Cost(\mathcal {P}(e_i, e_j, 1))$ can be computed in O(1) time if we compute and store the value of $Cost(\mathcal {P}(e_1, e_j, 1))$ for $1 \le j \le |\mathcal {E}|$ in advance. Note that this can be done in $O(|\mathcal {E}|)$ time. Thus, Lines 1–2 can be finished in $O(|\mathcal {E}|^2)$ time. The cost of Lines 3–5 is $O(N|\mathcal {E}|^2)$. Therefore, the time complexity of our optimal partition is $O(N|\mathcal {E}|^2)$. Evidently, the space complexity is $O(N|\mathcal {E}|^2)$ as well because we have to maintain a three- dimensional array for the cost of each instance $\mathcal {P}(e_l, e_h, n)$.

Heuristic partition The dynamic programming- based method can find the optimal partition. Nevertheless, its high time and space complexities make it unsatisfactory for datasets with considerably large element domain size (e.g., $|\mathcal {E}|$ is in millions). This motivates us to devise heuristic method to partition the element domain with linear time and space complexities regarding the element domain size.

Based on the cost function shown in Eq. 15 and the definition of optimal partition $\mathcal {P}^*(e_1, e_{|\mathcal {E}|}, N)$, it is evident that our goal is to find a partition such that the cost on each interval is as even as possible. Formally,

Theorem 2

If there exists an element partition instance $\mathcal {P}(e_1, e_{|\mathcal {E}|}, N)$, such that each interval is with the same cost; that is, $\forall i,j \in [1, N], Cost(\mathcal {P}(e_{l_i}, e_{h_i}, 1)) = Cost(\mathcal {P}(e_{l_j}, e_{h_j}, 1))$, then $\mathcal {P}(e_1, e_{|\mathcal {E}|}, N)$ is an optimal partition.

Proof

It is easy to show that $Cost(\mathcal {P}(e_{l}, e_{h}, 1))$ is monotonic with respect to [l, h]; that is, if $l' \le l$ and $h' \ge h$, then $Cost(\mathcal {P}(e_{l'}, e_{h'}, 1)) \ge Cost(\mathcal {P}(e_{l}, e_{h}, 1))$. For simplicity, assume we only have two intervals, which are $[e_{l_1}, e_{h_1}]$ and $[e_{l_2}, e_{h_2}]$, respectively. Suppose $Cost(\mathcal {P}(e_{l_1}, e_{h_1}, 1)) > Cost(\mathcal {P}(e_{l_2}, e_{h_2}, 1))$. Then, we can keep decreasing the value of $h_1$ and hence decreasing that of $l_2$ to reduce the value of $Cost(\mathcal {P}(e_{l_1}, e_{h_1}, 1))$ and increase that of $Cost(\mathcal {P}(e_{l_2}, e_{h_2}, 1))$, until we reach $Cost(\mathcal {P}(e_{l_1}, e_{h_1}, 1)) = Cost(\mathcal {P}(e_{l_2}, e_{h_2}, 1))$. At this point, we obtain the optimal partition since $Cost(\mathcal {P}(e_1, e_{|\mathcal {E}|}, N)) = \max \{Cost(\mathcal {P}(e_{l_1}, e_{h_1}, 1)), Cost(\mathcal {P}(e_{l_2}, e_{h_2}, 1))\}$. This proof generalizes to arbitrary N. $\square$

The main idea of our heuristic method is that we sequentially generate the intervals one by one from $e_1$ to $e_{|\mathcal {E}|}$. In particular, to generate the ith interval $P_i$, we fix the starting value $l_i$ and keep increasing the ending value $h_i$ until the cost of $P_i$ is no less than the value $Cost(\mathcal {P}(e_{l_i}, e_{|\mathcal {E}|}, 1)) / n$, where n is the number of intervals to partition for the rest of element range $\{e_{l_i},\ldots ,e_{|\mathcal {E}|}\}$. The intuition behind this method is that we use the cost of single interval on remaining element range as an estimation for each of the n intervals. Every time after splitting an interval off from it, we then re-estimate the cost for rest $n-1$ intervals.

Algorithm 8 depicts the details of our heuristic method. Lines 4–11 iteratively generate the N intervals. Note that, before generating a new interval, we first compute the mean cost for the rest partitions, as shown in Line 2 and Line 10.

Time and space complexity It is evident that the number of iterations (Lines 4–11) in Algorithm 8 is bounded by $|\mathcal {E}|$ since h is increased by 1 in each iteration. Meanwhile, the time complexity to compute $Cost(P(e_l, e_{|\mathcal {E}|}, 1))$ is O(1) as shown before. Therefore, the time complexity of our heuristic partition method is $O(|\mathcal {E}|)$. On the other hand, the space complexity is $O(|\mathcal {E}|)$ as well because we have to store $|\mathcal {E}|$ values of $Cost(\mathcal {P}(e_1, e_j, 1))$ for $1 \le j \le |\mathcal {E}|$.

6 Experimental studies

6.1 Centralized evaluations

In this section, we empirically evaluate the performance of TT-Join in a single machine. All experiments are conducted on PCs with Intel Xeon 2x2.3 GHz CPU and 128 GB RAM running Debian Linux.

Table 2 Characteristics of real-life datasets for evaluating main-memory algorithms

6.1.1 Experimental setup

Algorithms In the experiment, we evaluate the following algorithms.

• TT-Join Our approach proposed in Algorithm 5 in Sect. 4.3, where kLFP-Tree and a regular prefix tree are built on $\mathcal {R}$ and $\mathcal {S}$, respectively. By default, we set $k=3$ under all settings.

• LIMIT(OPJ) Intersection-oriented algorithm with optimization proposed in [18] (Sect. 3.1).

• PIEJoin Intersection-oriented algorithm proposed in [27] (Sect. 3.1).

• PRETTI+ Intersection-oriented algorithm proposed in [30] (Sect. 3.1).

• PTSJ Union-oriented algorithm proposed in [30] (Sect. 3.2).

• DivideSkip Adapted algorithm proposed in [29] (Sect. 3.3).

• Adapt Adapted algorithm proposed in [42] (Sect. 3.3).

• FreqSet Adapted algorithm proposed in [14] (Sect. 3.3).

Among the 8 algorithms, DivideSkip and Adapt are implemented in C++, where the source codes are obtained from the authors of [29] and [42], respectively. The rest 6 algorithms are all implemented in Java, and the JVM maximum heap size is set to 32 GB. For LIMIT(OPJ) and PIEJoin, we obtain the source codes from the authors of [27] since the source code of LIMIT(OPJ) is implemented in C++ and the authors of [27] re-implement LIMIT(OPJ) in Java. For completeness, we also re-implement LIMIT+(OPJ) in Java which uses the adaptive model trained in C++ in [18]. Nevertheless, the experiment results show that LIMIT(OPJ) outperforms LIMIT+(OPJ) on most cases which justifies the failure for LIMIT+(OPJ) to outperform LIMIT(OPJ) under different data structures and programming language. This issue has also been confirmed by the authors. Therefore, we choose LIMIT(OPJ) to evaluate for experimental comparison since its main competitors are implemented in Java. For PRETTI+ and PTSJ, we obtain the source code from the authors of [30]. We implement FreqSet in Java, where FP growth [22] method is employed to compute the frequent sets. Among the 4 state-of-the-art algorithms, PIEJoin and PRETTI+ are parameter free. For LIMIT(OPJ), we follow the same strategy adopted by authors of [27], where parameter tuning is carried out manually and individually for each dataset. Particularly, for datasets used in [27], we use the parameters tuned in [27], and for the rest datasets, we tune the best values individually. For PTSJ, we follow the strategy proposed by the authors, which show that a suitable signature length is between 16 and 32 times of the average length of records. In the experiments, we apply the middle value 24 for PTSJ. It is demonstrated in [27] that the frequency order of elements in records had a huge impact for LIMIT(OPJ), PIEJoin, and PRETTI+. Therefore, we follow their empirical conclusion to apply infrequent sort order for LIMIT and PIEJoin, and frequent sort order for PRETTI+, which are stated optimal for the corresponding algorithms. It is also worth mentioning that the Intersection-oriented methods, including LIMIT(OPJ) and PRETTI+, involve the procedure of computing the intersection of inverted lists. The source code of LIMIT(OPJ) is well implemented by using a hybrid method which switches between a merge-sort approach and a binary-search-based approach [16]. We re-implement the list intersection of PRETTI+ by following this approach. Among the three adapted algorithms, DivideSkip and Adapt are parameter free. For FreqSet, the frequency threshold a is set to 1000.

Datasets We employ both real-life and synthetic datasets to evaluate our algorithms. Note that a collection of records can be regarded as a relation with one attribute. Same as the previous studies, we evaluate the self set containment join on each dataset.

Real-life datasets We deploy 20 real-life datasets selected from different domains with various data properties. The detailed characteristics of the 20 datasets are shown in Table 2. For each dataset, we show the type of the dataset, what the record and element represent, the number of records in the dataset, the average record size, and the number of unique elements in the dataset. We also report the z-value (skewness) of the top 500 most frequent elements on each dataset by assuming that data follow Zipfian distribution. The datasets cover all datasets deployed in the state-of-the-art algorithms. In specific, Flickr-set, Orkut, Twitter, and Webbase are used in [30] to evaluate PRETTI+ and PTSJ algorithms, while BMS, Flickr-london, Kosarak, and Netflix are used in [18] to evaluate LIMIT(OPJ) algorithm. All of the eight datasets (with bold font in Table 2) are employed in [27] to evaluate PIEJoin.

Table 3 Statistics of synthetic datasets for evaluating main-memory algorithms

Synthetic datasets We generate synthetic datasets with respect to 4 aspects, including (i) the number of records, (ii) the average record size, (iii) the number of distinct elements, and (iv) the z-value (skewness) of elements. Table 3 summarizes the experimental parameters together with default values (in bold). Note that, when generating one set of datasets, we fix the rest parameters by using the corresponding default values.

Fig. 13

Effect of k on running time

Fig. 14

Processing time

6.1.2 Performance tuning

To better evaluate the impact of k value as well as the advantage of kLFP-Tree compared with the inverted index, we also implement an algorithm, namely IT-Join, which is an extension of kIS-Join algorithm where records in $\mathcal {S}$ are organized by a regular prefix tree. The traversal of the prefix tree is exactly the same as TT-Join (Algorithm 5) and the process of each visited node is based on kIS-Join algorithm in Sect. 4.2.3.

We choose four representative datasets from Table 2, including DISCO, KOSRK, NETFLIX, and TWITTER, which cover different types of dataset, various values of the average record size, as well as different z values. Note that, besides TT-Join and IT-Join, we also report the performance of IT-Join with $k=1$ to see whether the increase in k value in TT-Join and IT-Join algorithms got paid off.

Figure 13 reports the running time of three algorithms on the above four datasets with k increasing from 1 to 100. It is observed that IT-Join can only benefit from very small k values, such as 1 and 2, which implies that the performance gain from large k value cannot pay off the growth of filtering costs, i.e., the increase in the number of records explored on the inverted index. On the contrary, TT-Join performs much better than IT-Join when k increases in the range from 1 to 5. In particular, it can continuously benefit from the growth of k on KOSRK, while achieves the best performance when $k=4$, $k=2$, and $k=3$ on DISCO, NETFLIX, and TWITTER, respectively. This behavior verifies our cost analysis in Sects. 4.2 and 4.3 that the overhead of a straightforward extension of inverted index is expensive and the gain may not be well paid off, while TT-Join can achieve a much better trade-off. Since the performance of IT-Join is fully dominated by TT-Join under all datasets, it is excluded from the following experiments. By default, we set $k=3$ for TT-Join algorithm for all datasets.

Fig. 15

Memory usage

6.1.3 Comparison with existing algorithms

In this section, we compare our TT-Join algorithm with four state-of-the-art algorithms LIMIT(OPJ), PIEJoin, PRETTI+, and PSTJ as well as three modified algorithms DivideSkip, Adapt, and FreqSet on both real-life and synthetic datasets.

Processing Time on real-life datasets The experiment results in terms of processing time are reported in Fig. 14. Besides the set containment join time, the processing time also includes the index construction time because the indexes of all algorithms are generated on the fly. It is reported that our TT-Join algorithm outperforms all state-of-the-art algorithms on all datasets, except that it is slightly outperformed by LIMIT(OPJ) on NETFLIX. Among the existing algorithms, LIMIT(OPJ) achieves the best performance except on LINUX and SUALZ. The performance of PIEJoin is quite stable on all datasets, but it is always suppressed by LIMIT(OPJ) except on LINUX and SUALZ. The processing time of PRETTI+ and PTSJ is quite sensitive to the record length [30]. It is observed that PRETTI+ favors datasets with small record size, such as AMAZ, DISCO, LINUX, SUALZ, and TEAMS. However, PRETTI+ is extremely slow on datasets with relatively large record size, such as DELIC, ENRON, LIVEJ, NETFLIX, and TWITTER. It takes more than 10 h on NETFLIX in which the average record size is 209. As reported in [30], PTSJ, on the other hand, cannot efficiently handle datasets with small record size. For example, it takes hours for PTSJ to process AOL, while TT-Join spends less than 2 min. Generally, PTSJ has the worst overall performance. The reasons are twofold. First, PTSJ is a bitmap-signature-based method, which is data independent and does not make use of the distribution of the elements. Second, it considers records in $\mathcal {S}$ individually, which means there is no computation share between records, even for identical records. The results show that DivideSkip significantly outperforms other two adapted algorithms. Interestingly, DivideSkip even beats two state-of-the-art algorithms PRETTI+ and PTSJ on several datasets, such as AOL, DELIC, ENRON, FLICKR-L, LIVEJ, and ORKUT. The reason is that DivideSkip uses the same index strategy as PRETTI+, but DivideSkip can take advantage of the careful processing of long and short inverted lists in different ways. It is reported that Adapt and FreqSet are not competitive under all datasets. In particular, FreqSet fails to return results on half of the 20 datasets (we set allowed running time to be 10 h).

Fig. 16

Test on synthetic datasets

As reported in Fig. 14, TT-Join has the best overall performance on 20 real-life datasets and significantly outperforms other competitors on the majority of the datasets. This is because TT-Join not only enhanced the nice properties of the union-oriented approach, e.g., exploited the skewness of the data and had less number of records explored, but also can directly validate a significant number of pairs, which are verification free. In particular, TT-Join beats other algorithms by at least around one order of magnitude on datasets with large z-values, such as DISCO, KOSRK, LINUX, SUALZ, and TWITTER. This is because union-oriented TT-Join can effectively exploit the skewness of the data distribution. It is very interesting that TT-Join can also significantly outperform other competitors on ORKUT and WEBBS although they are not skewed, with z values 0.13 and 0.04, respectively. For instance, TT-Join outperforms other algorithms on WEBBS by one order of magnitude. We observe that there are a large number of distinct elements in ORKUT and WEBBS, and the average size of the records is large, which favor the least frequent element-based signature technique. For some datasets with moderate or small z-value, such as AMAZ, LAST, and TEAMS, TT-Join can also achieve a superior performance, at least 2 times faster than the second ranked algorithm. The reason is that the kLFP-Tree enables us to increase the filtering capacity with small overhead and validate a significant number of join results without explicitly invoking the verification during the join processing. NETFLIX is the only dataset in which TT-Join is slightly outperformed by other competitors. We observe that it is not skewed ($z=0.33$) and the number of distinct element ($|\mathcal {E}|=17{,}770$) is small compared to the dataset size ($n=480{,}189$ and $m=209$), both of which are not in favor of TT-Join.

Memory usage Figure 15 reports the memory usage of 8 algorithms. Same as [30], the used memory is measured by the difference between the total memory and free memory of JVM after indexes are constructed for algorithms implemented in Java. For algorithms implemented in C++, we measure the maximum amount of used memory. It is observed that DivideSkip consumes the smallest amount of memory under all datasets. Under most of the datasets, PTSJ and Adapt consume the second smallest amount of memory because PTSJ only builds Patricia trie index on $\mathcal {R}$, while Adapt only builds inverted list on $\mathcal {S}$. They are followed by TT-Join and PRETTI+. The memory usage of LIMIT(OPJ) and PIEJoin are similar and relatively larger than that of the other algorithms. This is because both of them use complicated index structures. Particularly, besides the prefix trees on both $\mathcal {R}$ and $\mathcal {S}$, PIEJoin also needs some auxiliary data structures to speed up the join processing.

Evaluation on synthetic datasets We finally evaluate TT-Join on the synthetic datasets. FreqSet is excluded from the evaluation because it fails to give response within allowed time on most of experimental settings. Figure 16a shows the effect of number of records. It is reported that the running time of the algorithms grow steadily as the number of records, and the performance rank of algorithms remains the same under most settings. Figure 16b reports the running time of algorithms by varying the average size of record. Interestingly, the running time increases quite slowly with respect to the average size of record for all algorithms except PRETTI+, which implies that PRETTI+ is more suitable for datasets with small record size. Figure 16c shows that the running time of all algorithms decreases as the number of distinct elements grows, which implies that the matching pairs are easier to recognize when the records contain more different elements. The experimental results of varying the z-value of elements are reported in Fig. 16d, which shows that TT-Join performs much better than its competitors when z-value increases. It is interesting that PTSJ is very insensitive to the z-value, which verifies our claim in Sect. 3.2 that the traditional union-oriented method (e.g., PTSJ) does not utilize the data distribution.

6.2 Distributed evaluations

In this section, we evaluate the performance of our distributed set containment join algorithm.

6.2.1 Experimental setup

We implement algorithms with both Hadoop 2.7.2 and Spark 2.0.0. By default, we run our experiments on Spark. All experiments are conducted on a 10-node (one namenode/master and nine datanodes/slavers) cluster. Each node in the cluster is a Debian 6.0.10 server that has 3.4 GHz Intel Xeon 8 cores CPU, 16 GB RAM, and gigabit Ethernet interconnect. For Hadoop, we allocate a JVM heap space of 4 MB for each mapper and reducer, and we allow at most 3 reducers running concurrently in each machine. We use the default block size 64 MB in HDFS and set the data replication factor of HDFS to 1. For Spark, we use standalone model and allocate 14 GB memory for each executor. On each executor, we allocate at most 3 cores. In the experiments, we evaluate two metrics, namely running time and communication/shuffle cost.

Algorithms We compare the following three distribution schemes.

• SIGNATURE Our signature-based distribution approach proposed in Sect. 5.3.2, where, by default, we apply the heuristic partition strategy proposed in Sect. 5.3.3.

• RANDOM Advanced random distribution approach proposed in Sect. 5.3.1.

• PREFIX Prefix-based distribution approach proposed in Sect. 5.3.1.

In the following experiments, we employ TT-Join as the local join algorithm, since it achieves the best overall performance as demonstrated in our centralized evaluation (Sect. 6.1).

Datasets We employ both real-life and synthetic datasets to evaluate our algorithms.

Real-life datasets Two real-life datasets are deployed to evaluate the algorithms. TWEETS is collected from Twitter, containing 74.6M tweets with an average number of terms being 6.3. MEMES is obtained from Memetracker [28], which tracks the quotes and phrases that appear most frequently over time across the entire online news spectrum. The quotes and phrases used in this paper are collected in April 2009, where we consider each meme as a record. The statistics of two datasets are summarized in Table 4.

Synthetic datasets Similar to the way that we generate synthetic datasets for evaluating main-memory algorithms, synthetic datasets here are generated by considering the 4 aspects as well; that is, (i) the number of records, (ii) the average record size, (iii) the number of distinct elements, and (iv) the z-value (skewness) of elements. Table 5 summarizes the details.

Table 4 Statistics of real-life datasets for evaluating distributed methods

Table 5 Statistics of synthetic datasets for evaluating distributed methods

6.2.2 Performance tuning

We start the experiments by tuning the performance of our approach SIGNATURE.

Compare partition strategies In Sect. 5.3.3, we propose two element domain partition methods. Recall that the optimal partition has a time complexity of $O(N|\mathcal {E}|^2)$ which is impractical on datasets with large element domain size. We therefore choose NETFLIX in Table 2, where the element domain size is 17,770, to conduct the experiments. Note that we also implement the even partition strategy, where the element domain is evenly partitioned into N intervals. As reported in Fig. 17a, our heuristic partition method, denoted by HEURISTIC, can achieve comparable performance as optimal partition method, denoted by OPTIMAL, in terms of running time, while even partition method, denoted by EVEN, is always beaten by other methods. That is because both OPTIMAL and HEURISTIC take the computation cost into consideration such that reduce nodes can take similar workload. It is interesting that all three methods have the similar communication cost under all settings as shown in Fig. 17b. The reason is that the communication cost is mainly determined by the distribution scheme and the number of intervals N. By default, we use HEURISTIC as the element domain partition method.

Effect of number of partitions In this experiment, we evaluate the effect of number of intervals N to our approach SIGNATURE against the two datasets in Table 4, namely TWEETS and MEMES, where the number of intervals is varied from 200 to 1800. Figure 18a reports that SIGNATURE can continuously benefit from growth of N on TWEETS regarding the running time, while it runs the fastest when $N=1000$ on MEMES. On the other hand, it is shown in Fig. 18b that the communication cost increases gradually when N increases. The reason is obvious because as N grows, we need to distribute records to more reduce nodes after map phase. Taking both running time and communication cost into consideration, we set $N=1000$ for SIGNATURE for all datasets in the following experiments.

Fig. 17

Compare partition strategies

Fig. 18

Vary number of intervals (N)

Fig. 19

Vary number of records on Spark

6.2.3 Performance evaluation

Scalability test In this set of experiments, we evaluate the scalability of 3 approaches. For each datasets, we randomly sample 20, 40, 60, 80, $100\%$ of records from the original dataset and conduct experiment on each sampled dataset. It is worth mentioning that we also tune the best number of partitions for RANDOM and PREFIX. In particular, for RANDOM, the numbers of partitions are set to 12, 14, 16, 18, 20 on both $\mathcal {R}$ and $\mathcal {S}$ under the 5 settings, while the number of intervals for SIGNATURE and PREFIX is set to 200, 400, 600, 800, 1000, correspondingly.

Fig. 20

Vary number of slave nodes on Spark

Fig. 21

Vary number of records on Hadoop

It is reported in Fig. 19 that our approach SIGNATURE performs the best under all settings with respect to both running time and communication cost. We also observe that SIGNATURE can scale much better than RANDOM does on TWEETS, and both RANDOM and PREFIX do on MEMES. Taking TWEETS for instance (Fig. 19a), when dataset size is $20\%$, SIGNATURE and RANDOM have comparable performance and finish in 200 and 244 s, respectively. However, when dataset size grows to $100\%$, these numbers become 357 and 4493, which means that SIGNATURE is more than one order of magnitude faster than RANDOM. We have similar conclusion in terms of communication cost. Interestingly, it is also observed from Fig. 19 that PREFIX has very difference performance on the two datasets. In particular, PREFIX achieves much better performance on TWEETS (Fig. 19a, b) than it does on MEMES (Fig. 19c, d). Taking the running time for example, it is only slightly beaten by SIGNATURE on TWEETS, while significantly outperformed by SIGNATURE on MEMES, where it is even marginally beaten by RANDOM when dataset size is less than $80\%$. The reason is that PREFIX is not suitable for dataset with large record size because it uses the entire record as prefix to build inverted index. Since the average record sizes of TWEETS and MEMES are 6.3 and 14, respectively, this explains why PREFIX performs better on TWEETS.

Fig. 22

Vary number of slave nodes on Hadoop

Fig. 23

Test on synthetic datasets

Effect of number of slave nodes In this experiment, we evaluate the effect of number of slave nodes by varying it from 5 to 9. Note that we only show the running time for this experiment since the shuffle cost is the same for an algorithm under different numbers of slave nodes. The experiment results are shown in Fig. 20. When the number of slave nodes increases, the running time of all algorithms decreases steadily. Figure 20a, b shows that SIGNATURE is more than one order of magnitude faster than RANDOM on TWEETS, and 5 times faster than both RANDOM and PREFIX on MEMES under all settings, respectively.

Evaluations on Hadoop Figures 21 and 22 report the performance of the algorithms running on Hadoop, which show similar behaviors as they do on Spark shown in Figs. 19 and 20. That is, the processing time increases when the number of records increases, while decreases with the growth number of slave nodes.

Interestingly, it is observed that the performance gap between SIGNATURE and other algorithms narrows on Hadoop. Take Figs. 19a and 21a for example. At the setting where the number of records is $100\%$, it takes 357 and 4493 s for SIGNATURE and RANDOM to finish on Spark. However, the numbers become 779 and 4058 on Hadoop. The reason is that SIGNATURE applies a two-stage strategy to compute the set containment join. In the first stage, we compute the element distribution, and based on that, we can find a good element domain partition. In the second stage, we distribute the records to reduce nodes according to the well-partitioned element intervals and compute set containment join locally on each reduce node. On the other hand, both RANDOM and PREFIX only consist of one stage. Since Spark stores data in memory, it is more efficient for processing multiple-stage jobs. Therefore, SIGNATURE performs better on Spark than it does on Hadoop.

Test on synthetic datasets Figure 23 reports the performance of the algorithms running against the synthetic datasets. The result is empty for PREFIX at some settings because it takes too long time. Figure 23a shows that SIGNATURE beats other methods under most experiment settings. In particular, the performance margin is getting larger as the number of records increases, which implies that SIGNATURE achieves better scalability. Figure 23b depicts the result in terms of average record size. It is reported that SIGNATURE can steadily outperform other methods, while PREFIX cannot efficiently handle datasets with large record size, which verifies our claim in Motivation of Sect. 5.3.2. Figure 23c reports the running time of the methods under different element domain size. It is interesting that both SIGNATURE and RANDOM consume less time on media element domain size (i.e., 100,000), while PREFIX prefers large element domain size. Figure 23d shows the experiment results when varying the data skewness. From the result, we see that SIGNATURE achieves much better performance than other methods when the data become skewer. For example, when $z=1.5$, SIGNATURE only spends 211 s to give the answer, while RANDOM needs 847 s and PREFIX fails to respond in allowed time.

7 Conclusion

In this paper, we study the problem of set containment join. Several in-memory set containment join algorithms have been developed in the literature. Based on the computing paradigms, we classify them into two categories, namely intersection-oriented and union-oriented methods. Through a comprehensive analysis, we show the advantages and limits of the algorithms in each category. Then, we propose a new union-oriented method, namely TT-Join, which can take advantage of both union-oriented and intersection-oriented approaches. Extensive experiments on 20 real-life set-valued datasets from a variety of applications and synthetic datasets demonstrate the superior performance of TT-Join compared with the state-of-the-art techniques. Furthermore, to support large scale of datasets, we extend our techniques to distributed systems on top of MapReduce framework. With the help of careful designed load-aware distribution mechanisms, our distributed join algorithm can scale out well.