Set containment join revisited

Abstract

Given two collections of set objects R and S, the $R\bowtie _{\subseteq }S$ set containment join returns all object pairs $(r,s) \in R\times S$ such that $r\subseteq s$. Besides being a basic operator in all modern data management systems with a wide range of applications, the join can be used to evaluate complex SQL queries based on relational division and as a module of data mining algorithms. The state-of-the-art algorithm for set containment joins ($\mathtt {PRETTI}$) builds an inverted index on the right-hand collection S and a prefix tree on the left-hand collection R that groups set objects with common prefixes and thus, avoids redundant processing. In this paper, we present a framework which improves $\mathtt {PRETTI}$ in two directions. First, we limit the prefix tree construction by proposing an adaptive methodology based on a cost model; this way, we can greatly reduce the space and time cost of the join. Second, we partition the objects of each collection based on their first contained item, assuming that the set objects are internally sorted. We show that we can process the partitions and evaluate the join while building the prefix tree and the inverted index progressively. This allows us to significantly reduce not only the join cost, but also the maximum memory requirements during the join. An experimental evaluation using both real and synthetic datasets shows that our framework outperforms $\mathtt {PRETTI}$ by a wide margin.

1 Introduction

Sets are ubiquitous in computer science and most importantly in the field of data management; they model among others transactions and scientific data, click streams and Web search data, text. Contemporary data management systems allow the definition of set-valued (or multi-valued) data attributes and support operations such as containment queries [1, 23, 37, 38, 42]. Joins are also extended to include predicates on sets (containment, similarity, equality, etc.) [21]. In this paper, we focus on the efficient evaluation of an important join operator: the set containment join. Formally, let R, S be two collections of set objects, the $R\bowtie _{\subseteq }S$ set containment join returns all pairs of objects $(r,s) \in R\times S$ such that $r\subseteq s$.

Application examples/scenarios Set containment joins find application in a wide range of domains for knowledge and data management. In decision support scenarios, the join is employed to identify resources that match a set of preferences or qualifications, e.g., on real estate or job agencies. Consider a recruitment agency which besides publishing job-offers also performs a first level filtering of the candidates. The agency retains a collection of job-offers R where an object r contains the set of required skills for each job, and a collection of job-seekers S with s capturing the skills of each candidate. The $R \bowtie _{\subseteq } S$ join returns all pairs of jobs and qualifying candidates for them which the agency then forwards to job-offerers for making the final decision. Containment joins can also support critical operations in data warehousing. For instance, the join can be used to compare different versions of set-valued records for entities that evolve over time (e.g., sets of products in the inventories of all departments in a company). By identifying records that subsume each other (i.e., a set containment join between two versions), the evolution of the data is monitored and possibly hidden correlations and anomalies are discovered.

In the core of traditional database systems and data engineering, set containment joins can be employed to evaluate complex SQL queries based on division [13, 32]. Consider for example Table 1 which shows two relations. The first relation shows students and the courses they have passed, while the second relation shows the required courses to be taken and passed in order for a student to acquire a skill. For example, Maria has passed Operating systems and Programming. As the courses required for a Systems Programming skill are Operating systems and Programming, it can be said that Maria has acquired this skill. Consider the query “for each student find the skills s/he has acquired” expressed in SQL below:

It is not hard to see that this query is in fact a set containment join between relations Requires and Passes, considering each skill and student as the set of courses they require or have passed, respectively. This example demonstrates the usefulness of set containment joins even in classic databases with relations in 1NF.

Table 1 Example of relational division based on set containment join: “for each student find the skills s/he has acquired”

In the context of data mining, containment join can act as a module during frequent itemset mining [31]. Consider the classic Apriori algorithm [2] which is well known for its generality and adaptiveness to mining problems in most data domains; besides, studies like [43] report that Apriori can be faster than FP-growth-like algorithms for certain support threshold ranges and datasets. At each level, the Apriori algorithm (i) generates a set of candidate frequent itemsets (having specific cardinality) and (ii) counts their support in the database. Candidates verification (i.e., step (ii)), which is typically more expensive than candidates generation (i.e., step (i)), can be enhanced by applying a set containment join between the collection of candidates and the collection of database transactions. The difference is that we do not output the qualifying pairs, but instead count the number of pairs where each candidate participates (i.e., a join followed by aggregation).

Motivation The above examples highlight not only the range of applications for set containment join but also the importance of optimizing its evaluation. Even though this operation received significant attention in the past with a number of algorithms proposed being either signature [21, 28–30] or inverted index based [24, 27], to our knowledge, since then, there have not been any new techniques that improve the state-of-the-art algorithm $\mathtt {PRETTI}$ [24]. $\mathtt {PRETTI}$ evaluates the join by employing an inverted index $I_S$ on the right-hand collection S and a prefix tree $T_R$ on the left-hand collection R that groups set objects with common prefixes in order to avoid redundant processing. The experiment analysis in [24] showed that $\mathtt {PRETTI}$ outperforms previous inverted index-based [27] and signature-based methods [29, 30], but as we discuss in this paper, there is still a lot of room for improvement primarily due to the following two shortcomings of $\mathtt {PRETTI}$. First, the prefix tree can be too expensive to build and store, especially if R contains sets of high cardinality or very long. Second, $\mathtt {PRETTI}$ completely traverses the prefix tree during join evaluation, which may be unnecessary, especially if the set of remaining candidates is small.

Contributions Initially, we tackle the aforementioned shortcomings of $\mathtt {PRETTI}$ by proposing an adaptive evaluation methodology. In brief, we avoid building the entire prefix tree $T_R$ on left-hand collection R which significantly reduces the requirements in both space and indexing time. Under this limited prefix tree denoted by $\ell T_R$, the evaluation of set containment join becomes a two-phase procedure that involves (i) candidates generation by traversing the prefix tree and (ii) candidates verification. Then, we propose a cost model to switch on-the-fly to candidates verification if the cost of verifying the remaining join candidates in current subtree is expected to be lower than prefix tree-based evaluation, i.e., candidates generation.

Next, we propose the Order and Partition Join ($\mathtt {OPJ}$) paradigm which considers the items of each set object in a particular order (e.g., in decreasing order of their frequency in the objects of $R\cup S$). Collection R and S are divided into partitions such that $R_i$ ($S_i$) contains all objects in R (S) for which the first item is i. Then, for each item i in order, $\mathtt {OPJ}$ processes partitions $R_i$ and $S_i$ by (i) updating inverted index $I_S$ to include all objects in $S_i$ and (ii) creating prefix tree $T_{R_i}$ for partition $R_i$ and joining it with $I_S$. As the inverted index is incrementally built, its lists are initially shorter and the join is faster. Further, the overall memory requirements are reduced since each $T_{R_i}$ is constructed and processed separately, but most importantly, it can be discarded right after joining it with $I_S$.

As an additional contribution of our study, we reveal that ordering the set items in increasing order of their frequency (in contrast with decreasing frequency proposed in [24]) in fact improves query performance. Although such an ordering may lead to a larger prefix tree (compared to $\mathtt {PRETTI}$), it dramatically reduces the number of candidates during query processing and enables our adaptive technique to achieve high performance gains.

We focus on main-memory evaluation of set containment joins (i.e., we optimize the main module of $\mathtt {PRETTI}$, which joins two in-memory partitions); note that our solution is easily integrated in the block-based approaches of [24, 27]. The fact that we limit the size of the prefix tree and that we use the $\mathtt {OPJ}$ paradigm, allows our method to operate with larger partitions compared to $\mathtt {PRETTI}$ in an external-memory problem, thus making our overall improvements even higher. Our thorough experimental evaluation using real datasets of different characteristics shows that our framework always outperforms $\mathtt {PRETTI}$, being up to more than one order of magnitude times faster and saving at least 50 % of memory.

Outline The rest of the paper is organized as follows. Section 2 describes in detail the state-of-the-art set containment join algorithm $\mathtt {PRETTI}$. Our adaptive evaluation methodology and the $\mathtt {OPJ}$ novel join paradigm are presented in Sects. 3 and 4, respectively. Section 5 presents our experimental evaluation. Finally, Sect. 6 reviews related work, and Sect. 7 concludes the paper.

2 Background on set containment join: the $\mathtt {PRETTI}$ algorithm

In this section, we describe in detail the state-of-the-art method $\mathtt {PRETTI}$ [24] for computing the $R \bowtie _{\subseteq } S$ set containment join of two collections R and S. The method has the following key features:

• (i) The left-hand collection R is indexed by a prefix tree $T_R$ and the right-hand collection S by an inverted index $I_S$. Both index structures are built on-the-fly, which enables the generality of the algorithm (for example, it can be applied for arbitrary data partitions instead of entire collections, and/or on data produced by underlying operators without interesting orders).

• (ii) $\mathtt {PRETTI}$ traverses the prefix tree $T_R$ in a depth-first manner. While following a path on the tree, the algorithm intersects the corresponding lists of inverted index $I_S$. The join algorithm is identical to the one proposed in [27] (see Sect. 6); however, due to grouping the objects under $T_R$, $\mathtt {PRETTI}$ performs the intersections for all sets in R with a common prefix only once.

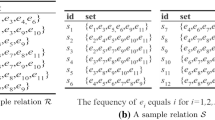
Algorithm 1 illustrates the pseudocode of $\mathtt {PRETTI}$. During the initialization phase (Lines 1–2), $\mathtt {PRETTI}$ builds prefix tree $T_R$ and inverted index $I_S$ for input collections R and S, respectively. To construct $T_R$, every object r in R is internally sorted, so that its items appear in decreasing order of their frequency in R (this ordering is expected to achieve the highest path compression for $T_R$).¹ Each node n of prefix tree $T_R$ is a triple (item, path, RL) where n.item is an item, n.path is the sequence of the items in the nodes from the root of $T_R$ to n (including n.item), and finally, n.RL is the set of objects in R whose content is equal to n.path. For example, Fig. 1a depicts prefix tree $T_R$ for collection R in Table 2a. Set n.RL is shown next to every node n unless it is empty. The inverted index $I_S$ on collection S associates each item i in the domain of S to a postings list denoted by $I_S[i]$. The $I_S[i]$ postings list has an entry for every object $s \in S$ that contains item i. Figure 1b pictures inverted index $I_S$ for collection S in Table 2b.

Table 2 Example of two collections R and S

The second phase of the algorithm involves the computation of the join result set J (lines 3–5). $\mathtt {PRETTI}$ traverses the subtree rooted at every child node c of $T_R$’s root by recursively calling the $\mathtt{ProcessNode}$ function. For a node n, $\mathtt{ProcessNode}$ receives as input from its parent node p in $T_R$, a candidates list CL. List CL includes all objects $s\in S$ that contain every item in p.path, i.e., $p.path \subseteq s$. Note that for every child of the root in $T_R$, $CL=S$. Next, $\mathtt{ProcessNode}$ intersects CL with inverted list $I_S[n.item]$ to find the objects in S that contain n.path and stores them in $CL'$ (Line 8). At this point, every pair of objects in $n.RL\times CL'$ is guaranteed to be a join result (lines 9–11). Finally, the algorithm calls $\mathtt{ProcessNode}$ for every child node of n (lines 12–13).

Fig. 1

Indices of $\mathtt {PRETTI}$ for the collections in Table 2. a Prefix tree $T_R$, b inverted index $I_S$

Example 1

We demonstrate $\mathtt {PRETTI}$ for the set containment join of collections R and S in Table 2. The algorithm constructs prefix tree $T_R$ and inverted index $I_S$ shown in Fig. 1a and b, respectively. To construct $T_R$ note that the items inside every object $r \in R$ are internally sorted in decreasing order of global item frequency in R (this is not necessary for the objects in S). First, $\mathtt {PRETTI}$ traverses the leftmost subtree of $T_R$ under the node labeled by item G. Considering paths $\langle /,G\rangle$ and $\langle /,G,F\rangle$, the algorithm intersects candidates list CL (initially containing every object in S, i.e., $\{s_1,\ldots ,s_{12}\}$) first with $I_S[G]$ and then with $I_S[F]$, and produces candidates list ${\{s_2,s_4,s_5,s_9,s_{10},s_{11},s_{12}\}}$, i.e., the objects in S that contain both G and F. The RL lists of the nodes examined so far are empty and thus, no result pair is reported. Next, path $\langle /,G,F,E\rangle$ is considered where CL is intersected with $I_S[E]$ producing ${CL' = \{s_2,s_5,s_9,s_{10},s_{12}\}}$. At current node, ${RL=\{r_5,r_7\}}$, and thus, $\mathtt {PRETTI}$ reports result pairs $(r_5,s_2)$, $(r_5,s_5)$, $(r_5,s_9)$, $(r_5,s_{10})$, $(r_5,s_{12})$, $(r_7,s_2)$, $(r_7,s_5)$, $(r_7,s_9)$, $(r_7,s_{10})$, $(r_7,s_{12})$. The algorithm proceeds in this manner to examine the rest of the prefix tree nodes performing in total 15 list intersections. The result of the join contains 16 pairs of objects.

Finally, to deal with the case where the available main memory is not sufficient for computing the entire set containment join of the input collections, a partition-based join strategy was also proposed in [24]. Particularly, the input collections R and S are horizontally partitioned so that the prefix tree and the inverted index for each pair of partitions $(R_i,S_j)$ from R and S, respectively, fit in memory. Then, in a nested-loop fashion, each partition $R_i$ is joined in memory with every partition $S_j$ in S invoking $\mathtt {PRETTI} (R_i,S_j)$.

3 An adaptive methodology

By employing a prefix tree on the left-hand collection R, $\mathtt {PRETTI}$ avoids redundant intersections and thus outperforms previous methods that used only inverted indices, e.g., [27]. However, we observe two important shortcomings of the $\mathtt {PRETTI}$ algorithm. First, the cost of building and storing the prefix tree on R can be high especially if R contains sets of high cardinality. This raises a challenge when the available memory is limited which is only partially addressed by the partition-based join strategy in [24]. Second, after a candidates list CL becomes short, continuing the traversal of the prefix tree to obtain the join results for CL may incur many unnecessary in practice inverted list intersections. This section presents an adaptive methodology which builds upon and improves $\mathtt {PRETTI}$. In Sect. 3.1 we primarily target the first shortcoming of $\mathtt {PRETTI}$ proposing the $\mathtt {LIMIT}$ algorithm, while in Sect. 3.2 we propose an extension to $\mathtt {LIMIT}$, termed $\mathtt {LIMIT{\small +}}$, that additionally deals with the second shortcoming.

3.1 The $\mathtt {LIMIT}$ algorithm

To deal with the high building and storage cost of the prefix tree $T_R$, [24] suggests to partition R, as discussed in the previous section. Instead, we propose to build $T_R$ only up to a predefined maximum depth $\ell$, called limit. Hence, computing set containment join becomes a two-phase process that involves a candidate generation and a verification stage; for every candidate pair (r, s) with $|r| > \ell$, we need to compare the suffixes of objects r and s beyond $\ell$ in order to determine whether $r \subseteq s$. This approach is adopted by the $\mathtt {LIMIT}$ algorithm.

Algorithm 2 illustrates the pseudocode of $\mathtt {LIMIT}$ . Compared to $\mathtt {PRETTI}$ (Algorithm 1), $\mathtt {LIMIT}$ differs in two ways. First in Line 1, $\mathtt {LIMIT}$ constructs limited prefix tree $\ell T_R$ on the left-hand collection R w.r.t. limit $\ell$. The $\ell T_R$ prefix tree has almost identical structure to unlimited $T_R$ built by $\mathtt {PRETTI}$ except that the n.RL list of a leaf node n contains every object $r \in R$ with $r \supseteq n.path$ instead of $r = n.path$. Figure 2a, b illustrates the limited versions of the prefix tree in Fig. 1b for $\ell = 2$ and $\ell = 3$, respectively. Second, the $\mathtt{ProcessNode}$ function distinguishes between two cases of objects in n.RL (lines 11–14). If, for a object $r\in n.RL$, $|r| \le \ell$ holds, then $r = n.path$ and, similar to $\mathtt {PRETTI}$, pair (r, s) is guaranteed to be part of the join result J (Line 12). Otherwise, $r \supset n.path$ holds and $\mathtt{ProcessNode}$ invokes the $\mathtt{Verify}$ function which compares the suffixes of objects r and s beyond $\ell$ (Line 14). Intuitively, the latter case arises only for leaf nodes according to the definition of the limited prefix tree. To achieve a low verification cost, the objects of both R and S collections are internally sorted, i.e., the items appear in decreasing order of their frequency in $R \cup S$, which enables Verify to operate in a merge-sort manner.

Fig. 2

Limited prefix tree $\ell T_R$ for collection R in Table 2. a $\ell = 2$. b $\ell = 3$

Example 2

We demonstrate $\mathtt {LIMIT}$ using collections R and S in Table 2; in contrast to $\mathtt {PRETTI}$ and Example 1, the objects of both collections are internally sorted. Consider first the case of $\ell = 2$. $\mathtt {LIMIT}$ constructs limited prefix tree $\ell T_R$ shown in Fig. 2a for collection R in Table 2a, and inverted index $I_S$ in Fig. 1b. Then, similar to $\mathtt {PRETTI}$, it traverses $\ell T_R$. When considering path $\langle /,G,F\rangle$, candidates list ${CL'=\{s_2,s_4,s_5,s_9,s_{10}, s_{11},s_{12}\}}$ is produced. The ${RL=\{r_1,r_2,r_5,r_7\}}$ set of current node (F) is non-empty, and thus, the algorithm examines every pair of objects from $RL \times CL'$ to report join results. As all objects in RL are of length larger than limit $\ell = 2$, $\mathtt {LIMIT}$ compares the suffixes beyond length $\ell = 2$ of all candidates by calling Verify, and finally, reports results $(r_5,s_2)$, $(r_5,s_5)$, $(r_5,s_9)$, $(r_5,s_{10})$, $(r_5,s_{12})$, $(r_7,s_2)$, $(r_7,s_5)$, $(r_7,s_9)$, $(r_7,s_{10})$, $(r_7,s_{12})$. At the next steps, the algorithm proceeds in a similar way to examine the rest of the prefix tree nodes performing 4 list intersections and verifying 37 candidate pairs by comparing their suffixes. Finally, if $\ell = 3$ $\mathtt {LIMIT}$ traverses similarly prefix tree $\ell T_R$ in Fig. 2b performing 8 this time list intersections but verifying only 10 candidate object pairs by comparing their suffixes.

The advantage of $\mathtt {LIMIT}$ over $\mathtt {PRETTI}$ and the partition-based join strategy of [24] is twofold. First, building the prefix tree up to $\ell$ is faster than building the entire tree, but most importantly, with $\ell$, the space needed to store the tree in main memory is reduced. If the unlimited $T_R$ does not fit in memory, $\mathtt {PRETTI}$ would partition R and construct a separate (memory-based) $T_{R_i}$ for each partition $R_i$; therefore, two objects $r_i$, $r_j$ of R that have the same $\ell$-prefix but belong to different partitions $R_i$ and $R_j$, would be considered separately, which increases the evaluation cost of the join. In other words, reducing the size of $T_R$ to fit in memory can have high impact on performance. In contrast, $\mathtt {LIMIT}$ guarantees that, for every path of length up to $\ell$ on limited $\ell T_R$, all redundant intersections are avoided similar to utilizing the unlimited prefix tree. Finally, an interesting aftermath of employing $\ell$ for set containment joins is related to the second shortcoming of $\mathtt {PRETTI}$. For instance, with $\ell = 3$ and prefix tree $\ell T_R$ in Fig. 1b, $\mathtt {LIMIT}$ will verify object $r_1$ against ${CL=\{s_2,s_5,s_9,s_{10},s_{12}\}}$ and quickly determine that it is not part of the join result without performing two additional inverted list intersections.

An issue still open involves how limit $\ell$ is defined and most importantly, whether there is an optimal value of $\ell$ that balances the benefits of using the limited prefix tree over the cost of including a verification stage. Determining the optimal value for $\ell$ is a time-consuming task which involves more than an extra pass over the input collections. In specific, it requires computing expensive statistics with a process reminiscent to frequent itemsets mining; note that this process must take place online before building $\ell T_R$. Instead, in Sect. 5.4, we discuss and evaluate four strategies for estimating a good $\ell$ value based on simple and cheap-to-compute statistics. Our analysis shows that typically these strategies tend to overestimate the optimal $\ell$. Besides, we also observe that the optimal $\ell$ value may in fact vary between different subtrees of $\ell T_R$ depending on the number of objects stored inside the nodes. In view of this, we next propose an adaptive extension to $\mathtt {LIMIT}$ which employs an ad hoc limit $\ell$ for each path of $\ell T_R$ by dynamically choosing between list intersection and verification of the objects under the current subtree.

3.2 The $\mathtt {LIMIT{\small +}}$ algorithm

As Example 2 shows, using limit $\ell$ for set containment joins introduces an interesting trade-off between list intersection and candidates verification which is directly related to the second shortcoming of the $\mathtt {PRETTI}$ algorithm. Specifically, as $\ell$ increases and $\mathtt {LIMIT}$ traverses longer paths of $\ell T_R$, candidates lists CL shorten due to the additional list intersections performed. Consequently, the number of object pairs to be verified by accessing their suffixes also reduces. However, from some point on, the number of candidates in CL no longer significantly reduces or, even worst, it remains unchanged; therefore, performing additional list intersections becomes a bottleneck. Similarly, if for a node n, CL is already too short, verifying the candidate pairs between the contents of CL and the objects contained under the subtree rooted at n can be faster than performing additional list intersections.

The $\mathtt {LIMIT}$ algorithm addresses only a few of the cases when candidates verification is preferred over list intersection, for instance the case of object $r_1$ in Table 2a with limit $\ell = 3$. Due to global limit $\ell$, the “blind” approach of $\mathtt {LIMIT}$ processes every path of the prefix tree in the same manner. To tackle this problem, we devise an adaptive strategy of processing $\ell T_R$ adopted by the $\mathtt {LIMIT{\small +}}$ algorithm. Apart from global limit $\ell$, $\mathtt {LIMIT{\small +}}$ also employs a dynamically determined local limit $\ell _p$ for each path p of the prefix tree. The basic idea behind this process is to decide on-the-fly for every node n of the prefix tree between:

• (A) performing the $CL' = CL \cap I_S[n.item]$ intersection, reporting the pairs in $n.RL \times CL'$, and then, processing the descendant nodes of n in a similar way, or

• (B) stopping the traversal of the current path and verifying the candidates between the objects of R contained in the subtree rooted at n denoted by $\ell T_R^n$ and those in CL, i.e., all candidate pairs in $\ell T_R^n \times CL$.

In the first case, $\mathtt {LIMIT{\small +}}$ would operate exactly as $\mathtt {LIMIT}$ does for the internal nodes of $\ell T_R$, while in the second case, it would treat node n as a leaf node but without performing the corresponding list intersection. Therefore, in practice, a local limit for current path n.path is employed by $\mathtt {LIMIT{\small +}}$.

Algorithm 3 illustrates the pseudocode of $\mathtt {LIMIT{\small +}}$. Compared to $\mathtt {LIMIT}$ (Algorithm 2), $\mathtt {LIMIT{\small +}}$ only differs on how a node of $\ell T_R$ is processed. Specifically, given a node n, $\mathtt{ProcessNode}$ calls the $\mathtt{ContinueAsLIMIT}$ function (Line 8) to determine whether the algorithm will continue processing n similar to $\mathtt {LIMIT}$ (lines 10–17), or it will stop traversing current path n.path and start verifying all candidates in $\ell T_R^n\times CL$ invoking the Verify function (lines 18–21). In the latter case, notice that for every verifying pair (r, s) with $r \in \ell T_R^n\times CL$ and $s \in CL$, the algorithm accesses the suffixes of r and s beyond length $\ell -1$ and not $\ell$ as the $CL \cap I_S[n.item]$ intersection has not taken place for current node n (Line 21).

Next, we elaborate on $\mathtt{ContinueAsLIMIT}$. Intuitively, in order to determine how $\mathtt {LIMIT{\small +}}$ will process current node n the function has to first estimate and then compare the computational costs $\mathcal {C}_\mathrm{A}$ and $\mathcal {C}_\mathrm{B}$ of the two alternative strategies: (A) processing current node and its descendants in the subtree $\ell T_R^n$ similar to $\mathtt {LIMIT}$, or (B) verifying candidates in $\ell T_R^n \times CL$. In practice, it is not possible to estimate the cost of processing current node n and its descendants in $\ell T_R^n$ similar to $\mathtt {LIMIT}$ since the involved intersections are not known in advance with the exception of $CL \cap I_S[n.item]$. Therefore, we estimate $\mathcal {C}_\mathrm{A}$ as the cost of computing the list intersection at current node n and, verifying, for each child node $c_i$ of n, the candidate pairs between all objects under subtree $\ell T_R^{c_i}$ and the objects in $CL'$. Figure 3 illustrates the two alternative strategies, the costs of which are compared by ContinueAsLIMIT.

Fig. 3

The two strategies considered by $\mathtt {LIMIT{\small +}}$. a Strategy for $\mathcal {C}_{\mathrm{A}}$, b strategy for $\mathcal {C}_{\mathrm{B}}$

We now discuss how costs $\mathcal {C}_\mathrm{A}$ and $\mathcal {C}_\mathrm{B}$ can be estimated. For this purpose, we first break n.RL set into two parts: $n.RL = n.RL^= \cup n.RL^{\supset }$, where $n.RL^=$ denotes the objects r in n.RL with $r = n.path$, while $n.RL^{\supset }$ the objects with $r \supset n.path$. Note that according to the definition of limited prefix tree $\ell T_R$, $n.RL = n.RL^=$ holds for every internal node n, as $n.RL^{\supset } = \emptyset$. Second, we introduce the following cost functions to capture the computational cost of the three tasks involved in strategies (A) and (B):

• (i) List intersection The cost of computing $CL' = CL \cap I_S[n.item]$ in current node n, denoted by $\mathcal {C}_{\cap }$, depends on the lengths of the involved lists and it is also related to the way list intersection is actually implemented. For instance, if list intersection is performed in a merge-sort manner, then $\mathcal {C}_{\cap }$ is linear to the sum of the lists’ length, i.e., $\mathcal {C}_{\cap } = \alpha _1\cdot |CL| + \beta _1\cdot |I_S[n.item]| + \gamma _1$. On the other hand, if the intersection is based on a binary search over the $I_S[n.item]$ list then $\mathcal {C}_{\cap } = \alpha _2\cdot |CL| \cdot \log _2(|I_S[n.item]|) + \beta _2$. Note that constants $\alpha _1$, $\alpha _2$, $\beta _1$, $\beta _2$ and $\gamma _1$ can be approximated by executing list intersection for several inputs and then employing regression analysis over the collected measurements.

• (ii) Direct output of results Similar to $\mathtt {PRETTI}$ and $\mathtt {LIMIT}$, after list intersection $CL' = CL \cap I_S[n.item]$, every pair (r, s) with $r \in n.RL$ and $s \in CL'$ such that $r = n.path$, i.e., $r \in n.RL^=$, is guaranteed to be among the join results and it would be directly reported. The cost of this task, denoted by $\mathcal {C}_\mathrm{d}$, is linear to the number of object pairs to be reported, and thus, $\mathcal {C}_\mathrm{d} = \alpha _3\cdot |CL'|\cdot |n.RL^=| + \beta _3$. Constants $\alpha _3$ and $\beta _3$ can be approximated by regression analysis.

• (iii) Verification To determine whether an (r, s) pair is part of the join result Verify would compare their suffixes in a merge-sort manner. Under this, the verification cost for each candidate pair is linear to the sum of their suffixes’ length. Both alternative strategies considered by ContinueAsLIMIT involve verifying all candidate pairs between a subset of objects in R and a subset in S (candidates list CL or $CL'$). Without loss of generality, consider the case of strategy (A). In total, $|\ell T_R^n \backslash n.RL^=|\cdot |CL'|$ candidates would be verified. Considering the length sum of the objects in $\ell T_R^n$ and of the objects in $CL'$, the total verification cost for (A) is

  $$\begin{aligned} \mathcal {C}_\mathrm{v}&= \alpha _4\cdot |CL'| \cdot \sum _{r \in \{\ell T_R^n \backslash n.RL^=\}}{(|r|-\ell )}\\&\quad + \beta _4 \cdot |\ell T_R^n \backslash n.RL^=| \cdot \sum _{s \in CL'}{(|s|-\ell )} + \gamma _4 \end{aligned}$$

  where $|r|-\ell$ ($|s|-\ell$) equals the length of the suffix for a object r (s) with respect to limit $\ell$. Similar to the previous tasks, constants $\alpha _4$, $\beta _4$ and $\gamma _4$ can be approximated by regression analysis. On the other hand, to approximate $|CL'| = |CL \cap I_S[n.item]|$ and $\sum _{s \in CL'}{(|s|-\ell )}$, we adopt an independent assumption approach based on the frequency of the item contained in current node n. Under this, $|CL'| \approx |CL|\cdot \frac{|I_S[n.item]|}{|S|}$ while the length sum of the objects in $CL'$ can be estimated with respect to the $\frac{|CL'|}{|CL|} \approx \frac{|I_S[n.item]|}{|S|}$ decrease ratio, hence, we have $\sum _{s \in CL'}{(|s|-\ell )} \approx \frac{|I_S[n.item]|}{|S|}\cdot \sum _{s \in CL}{(|s|-\ell )}$. Finally, note that $\sum _{r \in \{\ell T_R^n \backslash n.RL^=\}}{(|r|-\ell )}$ can be computed using statistics gathered while building prefix tree $\ell T_R$ and that $\sum _{s \in CL}{(|s|-\ell )}$ can be computed while performing the list intersection at the parent of current node n.

With $\mathcal {C}_{\cap }$, $\mathcal {C}_\mathrm{d}$, and $\mathcal {C}_\mathrm{v}$, the computational costs of the (A) and (B) strategies considered by ContinueAsLIMIT are estimated by:

$$\begin{aligned}&\mathcal {C}_\mathrm{A} = \mathcal {C}_{\cap }(CL,I_S[n.item]) + \mathcal {C}_\mathrm{d}(n.RL^=,CL') +\mathcal {C}_\mathrm{v}(\{\ell T_R^n \backslash n.RL^=\},CL',\ell )\\&\mathcal {C}_\mathrm{B} = \mathcal {C}_\mathrm{v}(\ell T_R^n,CL,\ell -1) \end{aligned}$$

As intersection $CL' = CL \cap I_S[n.item]$ is not computed in (B), candidates list CL and object suffixes beyond $\ell -1$ are considered by $\mathcal {C}_\mathrm{B}$ in place of $CL'$ and suffixes beyond $\ell$ considered by $\mathcal {C}_\mathrm{A}$.

Example 3

We illustrate the functionality of $\mathtt {LIMIT{\small +}}$ using Example 2. Assuming $\ell = 3$, $\mathtt {LIMIT{\small +}}$ constructs prefix tree $\ell T_R$ of Fig. 2b and inverted index $I_S$ of Fig. 1b. First, the algorithm traverses the subtree of $\ell T_R$ under the node labeled by item G. The computational cost of the alternative strategies for this node are as follows. $\mathcal {C}_\mathrm{A}$ involves the cost of computing $CL' = \{s_1,\ldots ,s_{12}\} \cap I_S[G] = \{s_2,s_4,s_5,s_7,s_8,$ $s_9,s_{10},s_{11},s_{12}\}$ and based on the two child nodes, the cost of verifying all candidates in $\{r_1,r_2,r_5,r_7\} \times CL'$ and $\{r_3\} \times CL'$; note that no direct join results exist as RL for current node is empty. On the other hand, $\mathcal {C}_\mathrm{B}$ captures the cost of verifying all candidates in $\{r_1,r_2,r_3,r_5,r_7\} \times CL$. Without loss of generality, assume $\mathcal {C}_\mathrm{A} < \mathcal {C}_\mathrm{B}$. Hence, $\mathtt {LIMIT{\small +}}$ processes current node (G) similar to $\mathtt {LIMIT}$: path $\langle /,G,F\rangle$ and the node labeled by F are next considered. Assuming $\mathcal {C}_\mathrm{A} > \mathcal {C}_\mathrm{B}$ for this node, $\mathtt {LIMIT{\small +}}$ imposes a local limit equal to 2 and verifies all candidates in $\{r_1,r_2,r_5,r_7\} \times CL$ with $CL= \{s_2,s_4,s_5,s_7,s_8,s_9,s_{10},s_{11},s_{12}\}$ (objects in S containing item G). Notice the resemblance to Example 2 for $\ell = 2$ with the exception that $\{s_2,s_4,s_5,s_7,s_8,s_9,s_{10},s_{11},$ $s_{12}\} \cap I_S[F]$ is not computed.

4 A novel join paradigm

As discussed in Sect. 2, the join paradigm of $\mathtt {PRETTI}$ [24], which is also followed by $\mathtt {LIMIT}$ and $\mathtt {LIMIT{\small +}}$, constructs the entire prefix tree $T_R$ (or $\ell T_R$) and the entire inverted index $I_S$ before joining them. However, we observe that the construction of $T_R$ and $I_S$ can be interleaved with the join process since for joining a set of objects from R that lie in a subtree of $T_R$ it is not necessary to have constructed the entire $I_S$. For example, consider again the $T_R$ and $I_S$ indices of Fig. 1. When performing the join for the nodes in the subtree rooted at node G, obviously, we need not have constructed the subtrees rooted at nodes F and E already. At the same time, only the objects from S that contain item G can be joined with each object in that subtree. Therefore, we only need a partially built $I_S$ which includes just these objects. In this section, we propose a new paradigm, termed Order and Partition Join ($\mathtt {OPJ}$), which is based on this observation. $\mathtt {OPJ}$ operates as follows:

• (i) Assume that for each object (in either R or S), the items are considered in a certain order (i.e., in decreasing order of their frequency in $R\cup S$). $\mathtt {OPJ}$ partitions the objects of each collection into groups based on their first item.² Thus, for each item i, there is a partition $R_i$ ($S_i$) of R (S) that includes all objects $r\in R$ ($s\in S$), for which the first item is i. For example, partition $R_G$ of collection R in Table 2a includes $\{r_1,r_2,r_3,r_5,r_7\}$, while partition $R_E$ includes just $r_6$. Due to the internal sorting of the objects, an object in $R_i$ or $S_i$ includes i but does not include any item j, which comes before i in the order (e.g., $r_6\in R_E$ cannot contain G or F). Then, $\mathtt {OPJ}$ initializes an empty inverted index $I_S$ for S.

• (ii) For each item i in order, $\mathtt {OPJ}$ creates a prefix tree $T_{R_i}$ for partition $R_i$ and updates $I_S$ to include all objects from partition $S_i$. Then, $T_{R_i}$ is joined with $I_S$ using $\mathtt {PRETTI}$ (or our algorithms $\mathtt {LIMIT}$ and $\mathtt {LIMIT{\small +}}$). After the join, $T_{R_i}$ is dumped from the memory and $\mathtt {OPJ}$ proceeds with the next item $i+1$ in order to construct $T_{R_{i+1}}$ using $R_{i+1}$, update $I_S$ using $S_{i+1}$ and join $T_{R_{i+1}}$ with $I_S$.

$\mathtt {OPJ}$ has several advantages over the $\mathtt {PRETTI}$ join paradigm. First, the entire $T_R$ needs not be constructed and held in memory. For each item i, the subtree of $T_R$ rooted at i (i.e., $T_{R_i}$) is built, joined, and then removed from memory. Second, the inverted index $I_S$ is incrementally constructed; therefore, $T_{R_i}$ for each item i in order is joined with a smaller $I_S$ which (correctly) excludes objects of S having only items that come after i. Thus, the inverted lists of the partially constructed $I_S$ are shorter, and the join is faster.³ Finally, the overall memory requirements of $\mathtt {OPJ}$ are much lower compared to $\mathtt {PRETTI}$ join paradigm as $\mathtt {OPJ}$ only keeps one $T_{R_i}$ in memory at a time (instead of the entire $T_R$).

Algorithm 4 illustrates a high-level sketch of the $\mathtt {OPJ}$ paradigm. $\mathtt {OPJ}$ receives as input collections R and S, and limit $\ell$; for $\mathtt {PRETTI}$ $\ell = \infty$ (i.e., $\ell T_{R_i}$ becomes $T_{R_i}$). Initially, collections R and S are partitioned to put all objects having i as their first item inside partitions $R_i$ and $S_i$, respectively (Line 1). Also, $I_S$ (the inverted index of S) is initialized (Line 2). Then, for each item i, $\mathtt {OPJ}$ computes the join results between objects from R having i as their first item and objects from S having i or a previous item in order as their first item (lines 3–9). Specifically, for each item i in order, $\mathtt {OPJ}$ builds a (limited) prefix tree $\ell T_{R_i}$ using partition $R_i$, adds all objects of partition $S_i$ into $I_S$, and finally joins $\ell T_{R_i}$ with $I_S$ using the methodology of $\mathtt {PRETTI}$, $\mathtt {LIMIT}$, or $\mathtt {LIMIT{\small +}}$. Note that for each $\ell T_{R_i}$ the root has a single child c with $c.item =i$, because all objects in $R_i$ have i as their first item. Thus, $\mathtt {OPJ}$ has to invoke the ProcessNode function (of either $\mathtt {PRETTI}$, $\mathtt {LIMIT}$ or $\mathtt {LIMIT{\small +}}$) only for c. In addition, note that candidates list CL is initialized with only the objects in S accessed so far instead of all objects in S according to the $\mathtt {PRETTI}$ join paradigm; the examination order guarantees that the rest of the objects in S cannot be joined with the objects in R under node c.

Table 3 Employing the $\mathtt {OPJ}$ join paradigm

Example 4

We demonstrate $\mathtt {OPJ}$ on collections R and S in Table 2. The items in decreasing frequency order over $R\cup S$ are G(14), F(13), E(12), D(11), C(9),  B(9),  A(3), resulting in the internally sorted objects shown in the figure. Without loss of generality, assume that the $\mathtt {PRETTI}$ algorithm is used to perform the join between each $\ell T_{R_i}$ and $I_S$ (i.e., $\ell = \infty$ and $\ell T_{R_i}=T_{R_i}$). Initially, the objects are partitioned according to their first item. The partitions for R are $R_G=\{r_1,r_2,r_3,r_5,r_7\}$, $R_F=\{r_4\}$, and $R_E=\{r_6\}$; the partitions for S are shown in Table 3a. $\mathtt {OPJ}$ first accesses partition $R_G$ and builds $T_{R_{G}}$, which is identical to the leftmost subtree of the unlimited $T_{R}$ in Fig. 1a. Then, $\mathtt {OPJ}$ updates the (initially empty) inverted index $I_S$ to include the objects of $S_G$; the resulting $I_S$ is shown on the right of $S_G$, at the top of Table 3b. After joining $T_{R_{G}}$ with $I_S$, $T_{R_{G}}$ is deleted from memory, and the next item F in order is processed. $\mathtt {OPJ}$ builds $T_{R_{F}}$ (which is identical to the second subtree of $T_R$ in Fig. 1a) and updates $I_S$ to include the objects in $S_F$; these updates are shown on the right of $S_F$ in Table 3b. Then, $T_{R_{F}}$ is joined with $I_S$, and $\mathtt {OPJ}$ proceeds to the next item E. In this case, $T_{R_{E}}$ is built (the rightmost subtree of $T_R$ in Fig. 1a), but $I_S$ is not updated as $S_E$ is empty. Still, $T_{R_{E}}$ is joined with current $I_S$. In the next round (item D), there is no join to be performed, because $R_D$ is empty. If there were additional partitions $R_i$ to be processed, $I_S$ would have to be updated to include the objects in $S_D$, as shown on the right of $S_D$ in Table 3b. However, since all objects from R have been processed, $\mathtt {OPJ}$ can terminate without processing $S_D$.

5 Experimental evaluation

In this section, we present an experimental evaluation of our methodology for set containment joins. Section 5.1 details the setup of our analysis. Section 5.2 investigates the preferred global ordering of the items, while Sect. 5.3 demonstrates the advantage of the $\mathtt {OPJ}$ join paradigm. Sect. 5.4 shows how limit $\ell$ affects the efficiency of our methodology and presents four strategies for estimating its optimal value. Finally, Sect. 5.5 conducts a performance analysis of our methods against the state-of-the-art $\mathtt {PRETTI}$ [24].

Table 4 Characteristics of real datasets

5.1 Setup

Our experimental analysis involves both real and synthetic collections. Particularly, we use the following real datasets:

• BMS is a collection of click-stream data from Blue Martini Software and KDD 2000 cup [43].

• FLICKR is a collection of photographs from Flickr Web site for the city of London [10]. Each object contains the union of “tags” and “title” elements.

• KOSARAK is a collection of click-stream data from a Hungarian online news portal available at http://fimi.ua.ac.be/data/.

• NETFLIX is a collection of user ratings on movie titles over a period of 7 years from the Netflix Prize and KDD 2007 cup.

Table 4 summarizes the characteristics of the real datasets. BMS covers the case of small domain collections, while FLICKR the case of datasets with very large domains. NETFLIX is a collection of extremely long objects. In addition, to study the scalability of the methods, we generated synthetic datasets with respect to (i) the collection cardinality, (ii) the domain size, (iii) the weighted average object length and (iv) the order of the Zipfian distribution for the item frequency. Table 5 summarizes the characteristics of the synthetic collections. On each test, we vary one of the above parameters while the rest are set to their default values.

Table 5 Characteristics of synthetic datasets

Similar to [24] for set containment joins (and other works on set similarity joins [9, 41]), our experiments involve only self-joins, i.e., $R = S$ (note, however, that our methods operate exactly as in case of non-self-joins, i.e., they take as input two copies of the same dataset). The collections and the indexing structures used by all join methods are stored entirely in main memory; as discussed in the introduction, we focus on the main module of the evaluation methods which joins two in-memory partitions, but our proposed methodology is easily integrated in the block-based approaches of [24, 27]. Further, we do not consider any compression techniques, as they are orthogonal to our methodology.

To assess the performance of each method, we measure its response time, the total number of intersections performed and the total number of candidates; note that the response time includes both the indexing and joining cost of the method, and in case of the $\mathtt {OPJ}$ paradigm, also the cost of sorting and partitioning the inputs. Finally, all tested methods are written in C++ and the evaluation is carried out on an 3.6 GHz Intel Core i7 CPU with 64 GB RAM running Debian Linux.

5.2 Items global ordering

The goal of the first experiment is to determine the most appropriate ordering for the items inside an object. In practice, only the characteristics of prefix tree $T_R$ and how it is utilized are affected by how we order the items inside each object (neither the size of inverted index $I_S$ nor the number of objects accessed from S depend on this ordering). Therefore, in this experiment, we only focus on the $\mathtt {PRETTI}$ join paradigm. In [24], to construct a compact prefix tree $T_R$, the items inside an object are arranged in decreasing order of their frequency. On the other hand, arranging the items in increasing frequency order allows for faster candidate pruning as the candidates list CL rapidly shrinks after a small number of list intersections. In other words, the ordering of the items affects not only the building cost and the storage requirements of $T_R$, but most importantly, the response time of the join method. In practice, we observe that the best ordering is also related to how the $CL \cap I_S[n.item]$ list intersection is implemented. Although the problem of list intersection is out of scope of this paper per se, we implemented: (i) a merge-sort based approach, and (ii) a hybrid approach based on [4] that either adopts the merge-sort approach or binary searches every object of CL inside the $I_S[n.item]$ postings list. Table 6 confirms our claim regarding the correlation between the global ordering of the items and the response time of the $\mathtt {PRETTI}$ join algorithm (note that the reported time involves both the indexing and the join phase of the method). Arranging the items in decreasing order of their frequency is generally better only if the merge-sort based approach is adopted for the list intersections, while in case of the hybrid approach, the objects should be arranged in increasing order; an exception arises for NETFLIX where adopting the increasing ordering is always more beneficial because of its extremely long objects. In summary, the combination of the hybrid approach and the increasing frequency global ordering minimizes the response time of the $\mathtt {PRETTI}$ algorithm in all cases. Thus, for the rest of this analysis, we employ the hybrid approach for list intersection and arrange the items inside an object in the increasing order of their frequency. Note that for matters of reference and completion, we also include the original version of [24] denoted by $\mathtt {org}\mathtt {PRETTI}$ corresponding to the Decreasing-Hybrid combination of Table 6.

Table 6 Determining items global ordering, response time (s) of the $\mathtt {PRETTI}$ algorithm

Table 7 Employing the $\mathtt {OPJ}$ join paradigm, response time (s)

5.3 Employing the join paradigm

Next, we investigate the advantage of $\mathtt {OPJ}$ (Sect. 4) over the $\mathtt {PRETTI}$ join paradigm of [24]. For this purpose, we devise an extension to the $\mathtt {PRETTI}$ algorithm that follows $\mathtt {OPJ}$, denoted by $\mathtt {PRETTI} ^*$. Table 7 reports the response time of the algorithms. The results experimentally prove the superiority of the $\mathtt {OPJ}$ paradigm; $\mathtt {PRETTI} ^*$ is from 1.3 to 1.5 times faster than $\mathtt {PRETTI}$. Recall at this point that compared to the algorithm discussed in [24], our version of $\mathtt {PRETTI}$ arranges the items in increasing order of their frequency as discussed in Sect. 5.2; thus, the overall improvement of $\mathtt {PRETTI} ^*$ (which follows $\mathtt {OPJ}$) over the original method of [24] $\mathtt {org}\mathtt {PRETTI}$ is even greater: $2.5\times$ for BMS-POS, $5.4\times$ for FLICKR, $2.5\times$ for KOSARAK and $38.5\times$ for NETFLIX. For the rest of our analysis, we adopt the $\mathtt {OPJ}$ paradigm for all tested methods.

5.4 The effect of limit

As discussed in Sect. 3, employing limit $\ell$ for set containment joins introduces a trade-off between list intersection and candidates verification. To demonstrate this effect, we run the $\mathtt {LIMIT}$ algorithm (adopting $\mathtt {OPJ}$ ) while varying limit $\ell$ from 1 to the average object length in R, and then plot its response time (Fig. 4), the number of list intersections performed (Fig. 5) and the total number of candidates (Fig. 6). The total number of candidates includes both (r, s) pairs which are directly reported as results, i.e., with $|r| \le \ell$, and those that are verified by comparing their prefixes beyond $\ell$, i.e., with $|r| > \ell$. To have a better understanding of this experiment, we also include the measurements for $\mathtt {PRETTI} ^*$ which uses an unlimited $T_R$. The figures clearly show the trade-off introduced by limit $\ell$ and confirm the existence of an optimal value that balances the benefits of using the limited prefix tree over the cost of including a verification stage. According to Figs. 5 and 6, as $\ell$ increases, $\mathtt {LIMIT}$ naturally performs more list intersections, and thus, the number of candidate pairs decreases until it becomes equal to the join results, i.e., the number of candidates for $\mathtt {PRETTI} ^*$. However, regarding its performance shown in Fig. 4, although $\mathtt {LIMIT}$ initially benefits from having to verify fewer candidate pairs, when $\ell$ increases beyond a specific value, performing additional list intersections becomes a bottleneck and the algorithm slows down until its response time becomes almost equal to the time of $\mathtt {PRETTI} ^*$.

Fig. 4

Vary limit $\ell$, response time. a BMS, b FLICKR, c KOSARAK, d NETFLIX

Fig. 5

Vary limit $\ell$, number of intersections. a BMS, b FLICKR, c KOSARAK, d NETFLIX

Fig. 6

Vary limit $\ell$, number of candidates (for $\mathtt {PRETTI} ^*$ equals the number of results). a BMS, b FLICKR, c KOSARAK, d NETFLIX

Apart from the trade-off introduced by limit $\ell$, Figs. 4, 5 and 6 also show that the $\mathtt {LIMIT}$ algorithm can be faster than $\mathtt {PRETTI} ^*$ as long as $\ell$ is properly set, i.e., close to its optimal value. However, as discussed in Sect. 3, determining the optimal $\ell$ value is a time-consuming procedure, reminiscent to frequent itemsets mining which cannot be employed in practice; recall that $\ell$ must be determined online. For this purpose, we propose the following simple strategies to select a good $\ell$ value based on cheap-to-compute statistics that require no more than a pass over the input collection R. First, strategies $AVG$ and W–$AVG$ set $\ell$ equal to the average and the weighted average object length in R, respectively. Similarly, strategy MDN sets $\ell$ to the median value of the object length in R. Last, we also devise a frequency-based strategy termed $FRQ$. The idea behind $FRQ$ is to estimate when paths greater than $\ell$ would only be contained in very few objects. We start with a path p that contains the most frequent item in R and progressively add the next items in decreasing frequency order. We estimate the probability that this path appears in a object by considering only the support of the items. When this probability falls under a threshold, which makes the expected cost of list intersection greater than the cost of verification (according to our analysis in Sect. 3.2), we stop adding items in p and set $\ell =|p|$. Note that this probability serves as an upper bound for all paths of length $\ell$ (assuming item independence), since p includes the most frequent items. Table 8 summarizes the values of $\ell$ determined by each strategy for the experimental datasets. Overall, $FRQ$ provides the best estimation of optimal $\ell$; in fact, for NETFLIX it identifies the actual optimal value. Figures 4, 5 and 6 confirm this observation as the performance of $\mathtt {LIMIT}$ with a limit set by $FRQ$ is very close to its performance for the optimal $\ell$. Thus, for the rest of our analysis we adopt $FRQ$ to set limit $\ell$ value.

Table 8 Limit $\ell$ determined by each estimation strategy

Fig. 7

Comparison of the set containment join methods on real datasets (limit $\ell$ set by FRQ according to Table 8). a BMS, b FLICKR, c KOSARAK, d NETFLIX

5.5 Comparison of the join methods

In Sect. 5.4, we showed that by properly selecting limit $\ell$ ($FRQ$ strategy), $\mathtt {LIMIT}$ outperforms $\mathtt {PRETTI} ^*$ and, based on Sects. 5.3 and 5.2, also $\mathtt {PRETTI}$ and $\mathtt {org}\mathtt {PRETTI}$. Next, we experiment with $\mathtt {LIMIT{\small +}}$ which (like $\mathtt {LIMIT}$) employs $FRQ$. Figure 7 reports the response time of $\mathtt {org}\mathtt {PRETTI}$, $\mathtt {PRETTI}$, $\mathtt {PRETTI} ^*$, $\mathtt {LIMIT}$ and $\mathtt {LIMIT{\small +}}$ on all four real datasets. To further investigate the properties of $\mathtt {LIMIT{\small +}}$, we also include the response time of two oracle methods⁴: (i) $\mathtt {L-ORACLE\,}$corresponds to $\mathtt {LIMIT}$ with $\ell$ set to its optimal value (see Table 8), (ii) $\mathtt {T-ORACLE}\,$is a version of $\mathtt {LIMIT{\small +}}$ which compares the actual execution time of the two alternative strategies for current prefix tree node instead of utilizing the cost model of Sect. 3.2; note that for this purpose, we run offline both alternative strategies for every prefix tree node and store their execution time. With the exception of $\mathtt {org}\mathtt {PRETTI}$ and $\mathtt {PRETTI}$, the rest of the algorithms follow the $\mathtt {OPJ}$ join paradigm. We break the response time of all methods into three parts, (i) building prefix tree $T_R$, (ii) building inverted index $I_S$ and (iii) computing the join results. Note that for $\mathtt {PRETTI} +$, $\mathtt {LIMIT}$, $\mathtt {LIMIT{\small +}}$ and the oracles, the indexing time additionally includes the sorting and partitioning cost of the input objects. As expected, the total indexing time is negligible compared to the joining time; an exception arises for FLICKR due its large number of objects.

Figure 7 shows that $\mathtt {LIMIT{\small +}}$ is the most efficient method for set containment joins. It is at least two times faster than $\mathtt {PRETTI}$. $\mathtt {LIMIT{\small +}}$ also outperforms $\mathtt {LIMIT}$ for the BMS, FLICKR and KOSARAK datasets, while for NETFLIX, both algorithms perform similarly as (i) the $FRQ$ strategy sets limit $\ell$ to its optimal value and (ii) the $T_R$ prefix tree for NETFLIX is quite balanced. The adaptive approach of $\mathtt {LIMIT{\small +}}$ that dynamically chooses between list intersection and candidates verification, copes better with (i) overestimated $\ell$ values and (ii) cases where $T_R$ is unbalanced. Specifically, due to employing an ad hoc limit for each path of the prefix tree, $\mathtt {LIMIT{\small +}}$ can be faster than $\mathtt {LIMIT}$ even with optimal $\ell$, i.e., faster than $\mathtt {L-ORACLE\,}$(see Fig. 7b, c). For these datasets, $T_R$ is quite unbalanced, and thus, there is no fixed value of $\ell$ to outperform the adaptive strategy. Note that even if $\ell$ is overestimated, e.g., using strategy W–$AVG$, the performance of $\mathtt {LIMIT{\small +}}$ is almost the same as when an optimal (or close to optimal) $\ell$ is used. Note also that the response time of $\mathtt {LIMIT{\small +}}$ is very close to that of $\mathtt {T-ORACLE}\,$which proves the accuracy of our cost model proposed in Sect. 3.2. We would like to stress at this point that the overall performance improvement achieved by $\mathtt {LIMIT{\small +}}$ over the original method of [24] which arranges the items inside an object in decreasing frequency order is as expected even larger compared to our version of $\mathtt {PRETTI}$; $\mathtt {LIMIT{\small +}}$ is 5 times faster than $\mathtt {org}\mathtt {PRETTI}$ for BMS, 11 times for FLICKR, 3.5 times for KOSARAK and 70 times for NETFLIX.

Fig. 8

Memory requirements ($\mathtt {LIMIT{\small +}}$ using $FRQ$). a $\mathtt {LIMIT{\small +}}$ (not $\mathtt {OPJ}$) versus $\mathtt {org}\mathtt {PRETTI}$. b $\mathtt {LIMIT{\small +}}$ ($\mathtt {OPJ}$) versus $\mathtt {org}\mathtt {PRETTI}$

Next, we analyze the advantage of $\mathtt {LIMIT{\small +}}$ (using $FRQ$) over $\mathtt {org}\mathtt {PRETTI}$ of [24] that arranges the items in decreasing frequency order, with respect to their memory requirements. Figure 8a shows the space for indexing only the left-hand collection R when neither method follows the $\mathtt {OPJ}$ paradigm. We observe that by constructing limited prefix tree $\ell T_R$ instead of unlimited $T_R$, $\mathtt {LIMIT{\small +}}$ saves at least 50 % of space compared to $\mathtt {org}\mathtt {PRETTI}$; for NETFLIX, where $T_R$ has the highest storing cost due to its extremely long objects, the savings are over 90 %. Then, in Fig. 8b we consider $\mathtt {LIMIT{\small +}}$ adopting $\mathtt {OPJ}$ and report the space for indexing both input collections while evaluating the join, compared to $\mathtt {org}\mathtt {PRETTI}$ which does not follow the $\mathtt {OPJ}$ paradigm. We observe that by incrementally building $\ell T_R$ and $I_S$, $\mathtt {LIMIT{\small +}}$ uses at least $50\,\%$ less space than $\mathtt {org}\mathtt {PRETTI}$. Naturally, the amount of space used by $\mathtt {LIMIT{\small +}}$ increases while examining the collection partitions, but it is always lower than the space for $\mathtt {org}\mathtt {PRETTI}$ due to never actually building and storing the entire prefix tree; only one subtree of $\ell T_R$ is kept in memory at a time. Finally, notice the different trend for NETFLIX as its partitions have balanced sizes; in contrast for BMS, FLICKR and KOSARAK, the first partitions contain very few objects while the last ones are very large.

Fig. 9

Scalability tests on synthetic datasets (limit $\ell$ set by FRQ), default parameter values: cardinality 5 M objects, domain size 100 K items, weighted avg object length 50 items, order of Zipfian distribution 0.5. a Cardinality, b domain size, c weighted avg object length, d Zipfian distribution

Finally, we present the results of our scalability tests on the synthetic datasets of Table 5. Figure 9 reports the response time of our best method $\mathtt {LIMIT{\small +}}$ and the $\mathtt {org}\mathtt {PRETTI}$ and $\mathtt {PRETTI}$ competitors. The purpose of these tests is twofold: (i) to demonstrate how the characteristics of a dataset affect the performance of the methods, and (ii) to determine their “breaking point.” First, we notice that all methods are affected in a similar manner; their response time increases as the input contains more or longer objects and decreases while the domain size becomes larger. An exception arises in Fig. 9d. The performance of $\mathtt {org}\mathtt {PRETTI}$ is severely affected when increasing the order of the Zipfian distribution; recall that $\mathtt {org}\mathtt {PRETTI}$ arranges the items inside an object, in decreasing frequency order. As expected, $\mathtt {LIMIT{\small +}}$ outperforms $\mathtt {org}\mathtt {PRETTI}$ and $\mathtt {PRETTI}$ under all setups, similar to the case of real datasets. Second, we also observe that both $\mathtt {org}\mathtt {PRETTI}$ and $\mathtt {PRETTI}$ are unable to cope with the increase in the cardinality and weighted average object length of the datasets. These two factors directly affect the size of the $T_R$ prefix tree and the memory requirements. In practice, $\mathtt {org}\mathtt {PRETTI}$ and $\mathtt {PRETTI}$ failed to run for inputs with more than 5M objects and/or when their weighted average length is larger than 50, because the unlimited prefix tree cannot fit inside the available memory; in these cases, the methods would have to adopt a block-based evaluation approach similar [24, 27]. In contrast, $\mathtt {LIMIT{\small +}}$ is able to index left-hand relation R due to employing limit $\ell$ and following $\mathtt {OPJ}$, and hence, compute the join results.

6 Related work

Our work is related to query operators on sets. In this section, we summarize previous work done for set containment queries, set containment joins, and set similarity joins. In addition, we review previous work on efficient computation of list intersection, which is a core module of our algorithms.

6.1 Set containment queries

Signatures and inverted files are two alternative indexing structures for set-valued data. Signatures are bitmaps used to exactly or approximately represent sets. With |D| being the cardinality of the items domain, a set x is represented by a |D|-length signature sig(x). The ith bit of sig(x) is set to 1 iff the ith item of domain D is present in x. If the sets are very small compared to |D|, exact signatures are expensive to store, and therefore, approximations of fixed length $l < |D|$ are typically used. Experimental studies [22, 44] showed that inverted files outperform signature-based indices for set containment queries on datasets with low cardinality set objects, e.g., typical text databases.

In [37, 38], the authors proposed extensions of the classic inverted file data structure, which optimize the indexing set-valued data with skewed item distributions. In [14], the authors proposed an indexing scheme for text documents, which includes inverted lists for frequent word combinations. A main-memory method for addressing error-tolerant set containment queries was proposed in [1]. In [42], Zhang et al. addressed the problem of probabilistic set containment, where the contents of the sets are uncertain. The proposed solution relies on an inverted file where postings are populated with the item’s probability of belonging to a certain object. The study in [23] focused on containment queries on nested sets, and proposes an evaluation mechanism that relies on an inverted file which is populated with information for the placement of an element in the tree of nested sets. The above methods use classic inverted files or extend them either by trading update and creation costs for response time [1, 14, 37, 38] or by adding information that is needed for more complex queries [23, 42]. Employing these extended inverted files for set containment joins (i.e., in place of our $I_S$) is orthogonal to our work.

6.2 Set containment joins

In [21], the Signature Nested Loops ($\mathtt {SNL}$) Join and the Signature Hash Join ($\mathtt {SHJ}$) algorithm for set containment joins were proposed, with $\mathtt {SHJ}$ shown to be the fastest. For each set object r in the left-hand collection R, both algorithms compare signatures to identify every object s in the right-hand collection S with $sig(r)~ \& ~\lnot sig(s)=0$ and $|r| \le |s|$ (filter phase), and then, perform explicit set comparison to discard false drops (verification phase). Later, the hash-based algorithms Partitioned Set Join ($\mathtt {PSJ}$) in [30] and Divide-and-Conquer Set Join ($\mathtt {DCJ}$) in [28] aimed at reducing the quadratic cost of the algorithms in [21]. In these approaches, the input collections are partitioned based on hash functions such that object pairs of the join result fall in the same partition. Finally, Melnik and Molina [29] proposed adaptive extensions to $\mathtt {PSJ}$ and $\mathtt {DCJ}$, termed $\mathtt {APSJ}$ and $\mathtt {ADCJ}$, respectively, to overcome the problem of a potentially poor partitioning quality.

Inverted files were employed by [24, 27] for set containment joins. Specifically, in [27], Mamoulis proposed a Block Nested Loops ($\mathtt {BNL}$) Join algorithm that indexes the right-hand collection S by an inverted file $I_S$. The algorithm iterates through each object r in the left-hand collection R and intersects the corresponding postings lists of $I_S$ to identify the objects in S that contain r. The experimental analysis in [27] showed that $\mathtt {BNL}$ is significantly faster than previous signature-based methods [21, 30]. In [24], Jampani and Pudi targeted the major weakness of $\mathtt {BNL}$; the fact that the overlaps between set objects are not taken into account. The proposed algorithm $\mathtt {PRETTI}$ employs a prefix tree on the left-hand collection, allowing list intersections for multiple objects with a common prefix to be performed just once. Experiments in [24] showed that $\mathtt {PRETTI}$ outperforms $\mathtt {BNL}$ and previous signature-based methods of [29, 30]. Our work first identifies and tackles the shortcomings of the $\mathtt {PRETTI}$ algorithm and then proposes a new join paradigm.

6.3 Set similarity joins

The set similarity join finds object pairs (r, s) from input collections R and S, such that $sim(r, s) \ge \theta$, where $sim(\cdot ,\cdot )$ is a similarity function (e.g., Jaccard coefficient) and $\theta$ is a given threshold. Computing set similarity joins based on inverted files was first proposed in [34]: For each object in one input, e.g., $r \in R$, the inverted lists that correspond to r’s elements on the other collection are scanned to accumulate the overlap between r and all objects $s \in S$. Among the optimization techniques on top of this baseline, Chaudhuri et al. [15] proposed a filter-refinement framework based on prefix filtering; for two internally sorted set objects r and s to satisfy $sim(r, s) \ge \theta$, their prefixes should have at least some minimum overlap. Later, [3, 9, 33, 41] built upon prefix filtering to reduce the number of candidates generated. Recently, Bouros et al. [10] proposed a grouping optimization technique to boost the performance of the method in [41], and Wang et al. [40] devised a cost model to judiciously select the appropriate prefix for a set object. An experimental comparison of set similarity join methods can be found in [25]. In theory, the above methods can be employed for set containment joins, considering for instance the asymmetric containment Jaccard measure, $sim(r,s) = \frac{|r \cap s|}{|r|}$ and threshold $\theta = 1$. In practice, however, this approach is not efficient as it generates a large number of candidates. For each object $r \in R$, prefix filtering can only prune objects in S that do not contain r’s first item while the rest of the candidates need to be verified by comparing the actual set objects. Therefore, the ideas proposed in previous work on set similarity joins are not applicable to set containment joins.

6.4 List intersection

In [19, 20], Demaine et al. presented an adaptive algorithm for computing set intersections, unions and differences. Specifically, the algorithm in [19] (ameliorated in [20] and extended in [7]) polls each list in a round-robin fashion. Baeza-Yates [4] proposed an algorithm that adapts to the input values and performs quite well in average. It can be seen as a natural hybrid of the binary search and the merge-sort approach. Experimental comparison of the above, among others, methods of list intersection, with respect to their CPU cost, can be found in [5, 6, 8]. The trade-off between the way sets is stored, and the way they are accessed in the context of the intersection operator was studied in [18]. Finally, recent work [35, 36, 39] considered list intersection with respect to the characteristics of modern hardware and focused on balancing the load between multiple cores. In [35, 36], Tatikonda et al. proposed inter-query parallelism and intra-query parallelism. The former exploits parallelism between different queries, while the latter parallelizes the processing within a single query. On the other hand, the algorithm in [39] probes the lists in order to gather statistics that would allow efficient exploration of the multi-level cache hierarchy. Efficient list intersection is orthogonal to our set containment join problem. Yet, in Sect. 5.2, we employ a hybrid list intersection method based on [4] to determine the preferred ordering of the items inside the objects.

6.5 Estimating set intersection size

Estimating the intersection size of two sets has received a lot of attention in the area of information retrieval [11, 12, 16, 17, 26], to determine the similarity between two documents modeled as sets of terms. Given sets A and B, the basic idea is to compute via sampling small sketches $\mathcal {S}(A)$ and $\mathcal {S}(B)$, respectively. Then, $|\mathcal {S}(A) \cap \mathcal {S}(B)|$ is used as an estimation of $|A \cap B|$. Our adaptive methodology for set containment joins (Sect. 3.2) involves estimating the size of a list intersection. Yet, the methods discussed above are not applicable as they require an expensive preprocessing step, i.e., precomputing and indexing the sketches for every list of the inverted index at the right-hand collection. In addition, one of the two lists at each intersection (i.e., candidates list CL) is the result of previous intersections. Thus, computing the sketch of CL should be done on-the-fly, i.e., the overall cost of the sketch-based intersection would exceed the cost of performing the exact list intersection (especially since CL becomes shorter every time it is intersected with an inverted list of the right-hand collection).

7 Conclusion

In this paper, we revisited the set containment join $R \bowtie _{\subseteq } S$ between two collections R and S of set objects r and s, respectively. We presented a framework which improves the state-the-art method $\mathtt {PRETTI}$, greatly reducing the space requirements and time cost of the join. Particularly, we first proposed an adaptive methodology (algorithms $\mathtt {LIMIT}$ and $\mathtt {LIMIT{\small +}}$) that limits the prefix tree constructed for the left-hand collection R. Second, we proposed a novel join paradigm termed $\mathtt {OPJ}$ that partitions the objects of each collection based on their first contained item, and then examines these partitions to evaluate the join while progressively building the indices on R and S. Finally, we conducted extensive experiments on real datasets to demonstrate the advantage of our methodology.

Besides the fact that the $\mathtt {OPJ}$ paradigm significantly reduces both the join cost and the maximum memory requirements, it can be applied in a parallel processing environment. For instance, by assigning each partition $R_i$ of the left-hand collection to a single computer node $v_i$ while replicating the partitions of the right-hand collection such that node $v_i$ gets every object in S which starts either by item i or an item before i according to the global item ordering, our method runs at each node and there is no need for communication among the nodes, since join results are independent and there are no duplicates. In the future, we plan to investigate the potential of such an implementation.