Vibration and dynamic instability analyses of functionally graded porous doubly curved panels with piezoelectric layers in supersonic airflow

Abstract

The present study, for the first time, investigates the vibration and flutter analyses of a doubly curved panel composed of functionally graded porous material contained by piezoelectric layers in supersonic flow. In this regard, the first-order piston theory for aerodynamic loading and Reddy’s third-order shear deformation theory for doubly curved panel analysis is used. The governing equations of motion are obtained using Hamilton’s principle and Maxwell’s equation. The Galerkin method is used to discretize the equations of motion. Three types of piezoelectric layers are used, in both open-circuit and closed-circuit electrical boundary conditions. The FG porous material with three types of porosity structure is investigated, including uniform distribution, X-shaped distribution, and V-shaped distribution. Also, the effect of the power of the FG porous material and the porosity coefficient on the frequencies and the flutter boundaries of spherical, cylindrical, doubly curved shell with $R_{y} = - R_{x}$ and plate structures are investigated. The comparison of the spherical panel, doubly curved panel, cylindrical panel, and plate shows that the spherical panel has the highest and the plate has the lowest stability regions. Also, as the radius to length of the panel increases, the critical flutter aerodynamic pressure increases and the flutter frequency decreases. Furthermore, the effects of piezoelectricity, electrical and mechanical boundary conditions, geometric parameters, and the radii of curvatures on the flutter boundaries and flutter frequencies of FG porous doubly curved panels are investigated in detail.

1 Introduction

Aeroelastic instability can occur in both static and dynamic cases. One of the phenomena of dynamic instability discussed here is called flutter. Flutter is a type of dynamic instability of flying objects that results from the interaction of elastic, inertial, and aerodynamic forces. This phenomenon is a type of unstable vibrations of self-stimulation in which the structure receives its required energy from airflow and usually leads to accidental failure of the structure. The Flutter occurs when the aerodynamic forces of two vibration modes combine to give rise to this phenomenon. The vibration and instability characteristics of structures in supersonic flow have been analyzed in numerous studies. Krumhaar [1] studied the use of linear piston theory for cylindrical shells. The aeroelastic stability of the plates and shells was investigated by Dowell [2]. Pidaparti [3] performed the flutter analysis of the cantilevered curved composite panels. Cunningham et al. [4] studied the effects of various parameters such as ply orientation, geometric parameters, and boundary conditions on the dynamic behaviour of doubly curved composite panels. Kumar et al. [5] investigated the dynamic instability of the composite doubly curved panels. Zhang et al. [6] studied the flutter analysis of airfoils in supersonic flow using a local piston theory. Oh and Kim [7] investigated the dynamic instability of the cylindrical composite panels in supersonic flow. Hadadpour et al. [8] inspected the flutter characteristics for plates made of functionally graded material (FGM) in supersonic flow. Chorfi and Houmat [9] analyzed the nonlinear vibrations of the doubly curved shell. Hosseini and Fazelzadeh [10] investigated the aerothermoelastic and free vibration analysis of FGM panels. The vibration analysis of doubly curved panels was researched by Kiani et al. [11]. Aeroelastic characteristics of panels with different boundary conditions and neglecting and considering the shear deformation are investigated by Li and song [12]. Shen et al. [13] inspected the Nonlinear dynamic behaviour of a doubly curved panel. Wattanasakulpong and Chaikittiratana [14] investigated the vibration analysis of FGM doubly curved shell. Ganji and Dowell [15] predicted the flutter boundaries for two-dimensional flow. Graver et al. [16] studied the flutter behaviour of composite plates subjected to yawed supersonic flow. The flutter of composite doubly curved sandwich panels was investigated by Malekzadehfard et al. [17]. Sankar et al. [18] explored the flutter boundaries of doubly curved sandwich panels with carbon nanotube (CNT) reinforced face sheets.

Song et al. [19] researched the vibration characteristics of composite plates. Zare Jouneghani et al. [20] performed the vibration analysis of FG porous doubly curved panels. Rezaei et al. [21] investigated the vibration behaviour of plates composed of functionally graded porous materials. The vibration behaviour of doubly curved panels composed of functionally graded composite and carbon nanotube (CNT) was performed by Pouresmaeeli et al. [22]. Lie et al. [23] researched the dynamic stability of cylindrical panels reinforced with carbon nanotubes. Shahverdi et al. [24] investigated the aerothermoelastic analysis of functionally graded plates. Navazi and Haddadpour [25] performed the aeroelastic stability of panels composed of functionally graded materials. Kiani et al. [26] inspected the vibration analysis of composite conical panels reinforced with functionally graded carbon nanotubes. Mehar et al. [27] inspected the vibration characteristics of composite curved panels reinforced by carbon nanotubes. The aeroelastic analysis of curved composite panels was inspected by Zhou et al. [28]. Lin et al. [29] studied the nonlinear aeroelastic behaviour of the composite plate surrounded by a piezoelectric material layer. The aeroelastic behaviour of plates made of porous materials was inspected by Saidi et al. [30]. The flutter characteristics of thick porous plates were investigated by Bahaadini et al. [31]. Muc et al. [32] inspected the flutter of plate and shell structures. Arani et al. [33] studied the aeroelastic stability analysis of cylindrical panels reinforced with carbon nanotubes.

The flutter behavior of curved panels composed of porous material was investigated by Aditya et al. [34]. They studied the influences of parameters such as material properties, boundary conditions, and geometric properties on the stability of the system. Bahaadini et al. [35] inspected the dynamic stability of fluid-conveying thin-walled rotating pipes. Majidi et al. [36] studied the flutter analysis of trapezoidal plates reinforced by carbon nanotubes. Esmaeili et al. [37] performed the vibration analysis of composite laminated doubly curved shells reinforced by graphene platelets. An and Sun [38] researched the aeroelastic behaviours of cylindrical composite panels. Ye et al. [39] inspected the aeroelastic analysis of the viscoelastic panel. Rahmanian and Javadi [40] studied the dynamic instability of cylindrical shells made of FG porous material. Adamian et al. [41] investigated the vibration characteristics of a doubly curved panel reinforced by graphene nanoplatelets. The flutter behaviour of cylindrical panels reinforced by the graphene platelets was researched by Zhou et al. [42]. The parameter studies are carried out, revealing the influences of the pore, and graphene platelets on the flutter behaviour of the cylindrical panels. The dynamic instability of doubly curved shells reinforced with functionally graded carbon nanotubes was researched by Amin Yazdi [43]. He showed that the influence of panel imperfection on flutter aerodynamic pressure is more considerable than functionally graded carbon nanotube volume fractions and distributions. Subramani et al. [44] performed the dynamic characteristics of the spherical sandwich shell panel with carbon nanotubes reinforced. Majidi et al. [45] investigated the aeroelastic behaviour of spinning cylindrical shells composed of functionally graded material reinforced with graphene nanoplatelets using the first-order shear deformation theory. Abdollahi et al. [46] performed the aeroelastic analysis of trapezoidal sandwich plates with functionally graded porous face sheets and honeycomb cores in supersonic airflow. Merdaci et al. [47] studied the dynamic response of plates with various porosity distributions. Houshangi et al. [48] studied the flutter analysis of sandwich conical shells. Chen et al. [49] inspected the aeroelastic behaviour of composite plates surrounded by a piezoelectric layer. Arani et al. [50] researched the supersonic flutter behaviour of sandwich plates. Khorshidi et al. [51] investigated the vibration and stability of rectangular plates in contact with sloshing fluid on one side and under supersonic aeroelastic load on the other side.

Piezoelectric materials are the best choice for use in intelligent mechanical structures in the future due to their coupling mechanical and electrical properties. This is because there is a coupling between the mechanical and electrical properties of the piezoelectric material. In addition, lightweight and ductility are also special properties of these materials. Many researchers have studied the use of these materials in structures under fluid flow. Crawley and Luis [52] investigated the use of piezoelectric materials in intelligent structures. Zhou et al. [53] derived the flutter aerodynamics pressure for isotropic plates with piezoelectric layers. Song et al. [54] studied the flutter boundaries of the composite laminated plates with the piezoelectric layer. Li. [55] investigated the influences of piezoelectric materials to improve the flutter characteristics of the plates. Tsushima and Su [56] investigated the aeroelastic instability of highly flexible piezoelectric wings. Li et al. [57] showed that the use of piezoelectric materials increases the flutter velocities of the supersonic beams. Xue et al. [58] inspected the flutter characteristics of plates made of functionally graded piezoelectric material (FGPM) in supersonic airflow. Wang et al. [59] studied the vibration of a plate surrounded by two piezoelectric layers. The vibration behaviour of FGM plates with piezoelectric layers was performed by Farsangi et al. [60]. Almedia et al. [61] studied the aeroelastic stability boundary of composite panels caused by the piezoelectric actuator. Zhang et al. [62] investigated the aerothermoelastic characteristics of composite panels with piezoelectric layers. Tian et al. [63] performed the nonlinear aeroelastic characteristics of a functionally graded piezoelectric material (FGPM) plate. Tham et al. [64] studied the vibration analysis of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) doubly curved shallow shells surrounded by piezoelectric layers.

To the best of the author’s knowledge, the piezoelectricity effects on the flutter analysis of the doubly curved panels have not been studied, yet. In this study, for the first time, the flutter boundaries for a doubly curved panel made of FG porous materials surrounded by piezoelectric layers subjected to supersonic flow have been investigated. The doubly curved shell analysis has the feature that by changing the radius of curvature, analyses of cylindrical shell, spherical shell, and plate can be performed. In this regard, considering Reddy’s third-order shear deformation theory and first-order piston theory, the governing equations of motion are obtained using Hamilton’s principle and Maxwell’s equation. The Galerkin method is used to discretize the equations of motion. To study the effects of piezoelectricity, three types of piezoelectric layers are investigated in both open-circuit and closed-circuit electrical boundary conditions. Also, the FG porous material with three types of porosity structure including uniform distribution, X-shaped distribution, and V-shaped distribution is investigated. Moreover, the effect of the power of the FG porous material and the porosity coefficient on the frequencies and the flutter boundaries are investigated. Flutter frequencies and flutter boundaries are compared for spherical, cylindrical, doubly curved shell with $R_{y} = - R_{x}$ and plate. Finally, the effects of mechanical boundary conditions, geometric parameters, and radii of curvatures of the middle surface on the flutter boundaries and flutter frequencies of FG porous doubly curved panels are investigated in detail. The results show that increasing the porosity coefficient reduces the stable range. Furthermore, open circuit electrical conditions cover a larger stable range. Also, using PZ4 piezoelectric layers results in the highest flutter boundaries and frequencies.

2 Mathematical formulation

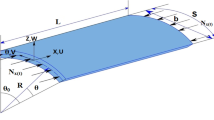
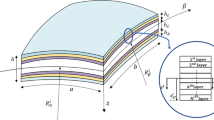
Figure 1, shows the FG porous doubly curved panel with length $a$, width $b$, and total thickness $H = 2\left( {h + h_{p} } \right)$ where $2h$ and $h_{p}$ are thickness of FG porous core and the thickness of each piezoelectric layers, respectively.

Fig. 1

Coordinate system and geometry of a doubly curved panel and schematic of three types of porosity distribution

The radii of principal curvatures of the middle surface are assumed to be $R_{x}$ and $R_{y}$. The Cartesian coordinate system is used. Based on Reddy’s third-order shear deformation theory assumptions for doubly curved panels, consistent the mid-surface displacements (u, v, w), mid-surface rotations $\left( {\psi_{x} ,\psi_{y} } \right)$, and displacements on a generic point of the panel $\left( {u_{x} , u_{y} , u_{z} } \right)$ are the association as (Reddy [65]):

$$\begin{aligned} u_{x} \left( {x,y,z,t} \right) & = \left( {1 + \frac{z}{{R_{x} }}} \right)u\left( {x,y,t} \right) + z\psi_{x} \left( {x,y,t} \right) - cz^{3} \left( {\psi_{x} \left( {x,y,t} \right) + \frac{{\partial w\left( {x,y,t} \right)}}{\partial x}} \right) \\ u_{y} \left( {x,y,z,t} \right) & = \left( {1 + \frac{z}{{R_{y} }}} \right)v\left( {x,y,t} \right) + z\psi_{y} \left( {x,y,t} \right) - cz^{3} \left( {\psi_{y} \left( {x,y,t} \right) + \frac{{\partial w\left( {x,y,t} \right)}}{\partial y}} \right) \\ u_{z} \left( {x,y,z,t} \right) & = w\left( {x,y,t} \right) \\ \end{aligned}$$

(1)

where $t$ stands for the time variable. The constant c is given by $c = \left( {\frac{4}{{3H^{2} }}} \right)$, which is obtained by satisfying the shear-free boundary conditions on the top and bottom surfaces of the shell as follows: (Reddy. [65], Murakami [70], Sciuva [71]).

$$\left. {\sigma_{xz} } \right|_{{z = \pm \frac{H}{2}}} = 0{ },{ }\left. {\sigma_{yz} } \right|_{{z = \pm \frac{H}{2}}} = 0{ }$$

(2)

The linear strain–displacement relations are obtained as follows:

$$\begin{aligned} \varepsilon_{xx} & = \left( {\frac{\partial u}{{\partial x}} + \frac{w}{{R_{x} }}} \right) + z\frac{{\partial \psi_{x} }}{\partial x} - cz^{3} \left( {\frac{{\partial \psi_{x} }}{\partial x} + \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{\partial u}{{R_{x} \partial x}}} \right) \\ \varepsilon_{yy} & = \left( {\frac{\partial v}{{\partial y}} + \frac{w}{{R_{y} }}} \right) + z\frac{{\partial \psi_{y} }}{\partial y} - cz^{3} \left( {\frac{{\partial \psi_{y} }}{\partial y} + \frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{\partial v}{{R_{y} \partial y}}} \right) \\ \varepsilon_{zz} & = 0 \\ \gamma_{xy} & = 2\varepsilon_{xy} = \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right) + z\left( {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \right) \\ & \;\;\;\; - cz^{3} \left( {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x} + 2\frac{{\partial^{2} w}}{\partial x\partial y} - \frac{\partial u}{{R_{x} \partial x}} - \frac{\partial v}{{R_{y} \partial y}}} \right) \\ \gamma_{xz} & = 2\varepsilon_{xz} = \left( {1 - \beta z^{2} } \right)\left( {\psi_{x} + \frac{\partial w}{{\partial x}} - \frac{u}{{R_{x} }}} \right) \\ \gamma_{yz} & = 2\varepsilon_{yz} = \left( {1 - \beta z^{2} } \right)\left( {\psi_{y} + \frac{\partial w}{{\partial y}} - \frac{v}{{R_{y} }}} \right) \\ \end{aligned}$$

(3)

Here, $\varepsilon_{xx}$ and $\varepsilon_{yy}$ are the normal strains; $\gamma_{xy}$, $\gamma_{xz}$ and $\gamma_{yz}$ are the shear strains and the constant $\beta$ is defined as:

$$\beta = 3c = \frac{4}{{H^{2} }}$$

(4)

The stress components are expressed as:

$$\left\{ {\begin{array}{*{20}l} {\sigma _{{xx}} } \\ {\sigma _{{yy}} } \\ {\begin{array}{*{20}l} {\sigma _{{xy}} } \\ {\sigma _{{xz}} } \\ {\sigma _{{yz}} } \\ \end{array} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {Q_{{11}} } \hfill &\quad {Q_{{12}} } \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ {Q_{{12}} } \hfill & \quad{Q_{{22}} } \hfill & \quad0 \hfill & \quad0 \hfill & \quad0 \hfill \\ 0 \hfill &\quad 0 \hfill & \quad{Q_{{66}} } \hfill & \quad0 \hfill & \quad0 \hfill \\ 0 \hfill & \quad0 \hfill & \quad0 \hfill & \quad{Q_{{55}} } \hfill & \quad0 \hfill \\ 0 \hfill & \quad0 \hfill & \quad0 \hfill & \quad0 \hfill & \quad{Q_{{44}} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\varepsilon _{{xx}} } \\ {\varepsilon _{{yy}} } \\ {\begin{array}{*{20}l} {2\varepsilon _{{xy}} } \\ {2\varepsilon _{{xz}} } \\ {2\varepsilon _{{yz}} } \\ \end{array} } \\ \end{array} } \right\}$$

(5)

These are defined as:

$$\begin{aligned} Q_{11} & = Q_{22} = \frac{E\left( z \right)}{{1 - \upsilon^{2} }} \\ Q_{12} & = Q_{21} = \frac{\upsilon E\left( z \right)}{{1 - \upsilon^{2} }} \\ Q_{44} & = Q_{55} = Q_{66} = \frac{1}{2}\left( {Q_{11} - Q_{12} } \right) = \frac{E\left( z \right)}{{2\left( {1 + \upsilon } \right)}} \\ \end{aligned}$$

(6)

The properties of FG porous layers can be written as:

$$P = P_{b} + \left( {P_{t} - P_{b} } \right)\left( {\frac{z + h}{{2h}}} \right)^{n} - \frac{e}{2}\left( {P_{t} + P_{b} } \right)\;\;\;\;\;{\text{homogeneous distribution}}$$

(7.a)

$$P = P_{b} + \left( {P_{t} - P_{b} } \right)\left( {\frac{z + h}{{2h}}} \right)^{n} - \frac{e}{2}\left( {P_{t} + P_{b} } \right)\left( {\left| {\frac{h - 2z}{{2h}}} \right|} \right)\;\;\;\;{\text{V}}\;{\text{distribution}}$$

(7.b)

$$P = P_{b} + \left( {P_{t} - P_{b} } \right)\left( {\frac{z + h}{{2h}}} \right)^{n} - \frac{e}{2}\left( {P_{t} + P_{b} } \right)\left( {\left| \frac{2z}{h} \right|} \right)\;\;\;\;{\text{X}}\;{\text{ distribution}}$$

(7.c)

The forms of porosity distribution for homogeneous, V and X distribution are given in Fig. 1. Equation (7.a) shows the homogeneous distribution of porosity, Eq. (7.b) shows that the porosity distribution is V type, and Eq. (7.c) shows that the porosity distribution is X type. In Eq. (7), $P$ represents the property of the material, $e,$ and $n$ represents the porosity and power law index.

Also, $P_{b}$ and $P_{t}$ represent the material properties on the bottom and top surfaces of the panel, respectively. (Ebrahimi and Jafari [66], Wattanasakulpong and Ungbhakorn [68]). In the present research, the materials on the bottom and top surfaces of the shell are ceramics and metal, respectively.

The constitutive equation for the piezoelectric materials is expressed as Eq. (8). (Wang et al. [59]).

$$\left\{ {\begin{array}{*{20}l} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\overline{c}_{11} } \\ {\overline{c}_{12} } \\ \end{array} } \\ {\begin{array}{*{20}l} 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\overline{c}_{12} } \\ {\overline{c}_{11} } \\ \end{array} } \\ {\begin{array}{*{20}l} 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}l} {c_{55} } \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}l} 0 \\ {c_{55} } \\ \end{array} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}l} 0 \\ 0 \\ \end{array} } \\ {\left( {\overline{c}_{11} - \overline{c}_{12} } \right)/2} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ \end{array} } \\ {\begin{array}{*{20}l} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \\ {\gamma_{xy} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}l} 0 & 0 & {\overline{e}_{31} } \\ 0 & 0 & {\overline{e}_{31} } \\ {\begin{array}{*{20}l} 0 \\ {e_{15} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} {e_{15} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\}$$

(8)

$$\left\{ {\begin{array}{*{20}l} {D_{x} } \\ {D_{y} } \\ {D_{z} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} 0 \\ 0 \\ {\overline{e}_{31} } \\ \end{array} } & {\begin{array}{*{20}l} 0 \\ 0 \\ {\overline{e}_{31} } \\ \end{array} } & {\begin{array}{*{20}l} 0 \\ {e_{15} } \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}l} {\begin{array}{*{20}l} {e_{15} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ \end{array} } \\ {\begin{array}{*{20}l} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \\ {\gamma_{xy} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {{\Xi }_{11} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} 0 \\ {{\Xi }_{11} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} 0 \\ 0 \\ {{\overline{\Xi }}_{33} } \\ \end{array} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\}$$

(9)

In which

$$\begin{aligned} \overline{c}_{11} & = c_{11} - \frac{{c_{13}^{2} }}{{c_{33} }},\;\;\;\; \overline{c}_{12} = c_{12} - \frac{{c_{13}^{2} }}{{c_{33} }} \\ \overline{e}_{31} & = e_{31} - \frac{{c_{13} }}{{c_{33} }}e_{33} ,\;\;\;\; {\overline{\Xi }}_{33} = {\Xi }_{33} + \frac{{e_{33}^{2} }}{{c_{33} }} \\ \end{aligned}$$

(10)

In Eq. (9), the electrical displacement and electric field in the piezoelectric layer are denoted by $D_{{i{ }}} { }$ and $E_{{i{ }}} \left( {i = x,{ }y,{ }z} \right)$ respectively. Besides, $c_{11} ,{ }c_{12} ,{ }c_{13} ,{ }c_{33} { }$ and $c_{55}$ are piezoelectric elastic moduli; ${ }e_{31} ,{ }e_{33} { }$ and $e_{15}$ are piezoelectric constant and ${\Xi }_{11} ,{ }$ and ${\Xi }_{33}$ are dielectric permittivity.

The electric field can be expressed as Eq. (11). So that ${\Phi }$ is the electric potential.

$$E_{x} = - \frac{{\partial {\Phi }}}{\partial x},\;\;\; E_{y} = - \frac{{\partial {\Phi }}}{\partial y}, \;\;\;E_{z} = - \frac{{\partial {\Phi }}}{\partial z}$$

(11)

In Eq. (12), ${\Phi }$ is defined for closed circuit conditions where $\phi \left( {x, y, t} \right)$ is the electric potential in the mid-surface of piezoelectric layers.

$${\Phi }\left( {x,y,z,t} \right) = \left\{ {\begin{array}{*{20}l} {\phi \left( {x,y,t} \right)\left[ {1 - \left( {\frac{{z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} } \right] \;\;\;\; \left( {h \le z \le h + h_{p} } \right)} \hfill \vspace*{3pt}\\ {\phi \left( {x,y,t} \right)\left[ {1 - \left( {\frac{{ - z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} } \right] \;\;\;\; \left( { - h - h_{p} \le z \le - h} \right)} \hfill \\ \end{array} } \right.$$

(12)

The electric potential function for open circuit condition is expressed as

$${\Phi }\left( {x,y,z,t} \right) = \left\{ {\begin{array}{*{20}l} \begin{gathered} \phi \left( {x,y,t} \right)\left[ {1 - \left( {\frac{{z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} + \frac{{4\left( {z - h} \right)}}{{h_{p} }}} \right] \hfill \\ + \frac{{\overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left\{ {\begin{array}{*{20}l} {\frac{\partial u}{{\partial x}} + \frac{w}{{R_{x} }} + \frac{\partial v}{{\partial y}} + \frac{w}{{R_{y} }} + \left[ {h + h_{p} - c\left( {h + h_{p} } \right)^{3} } \right]\left( {\frac{{\partial \psi_{x} }}{\partial x} - \frac{\partial u}{{R_{x} \partial x}} + \frac{{\partial \psi_{y} }}{\partial y} - \frac{\partial v}{{R_{y} \partial y}}} \right)} \\ { - c\left( {h + h_{p} } \right)^{3} \nabla^{2} w} \\ \end{array} } \right\}\left( {z - h} \right) \hfill \\ \end{gathered} & { \left( {h \le z \le h + h_{p} } \right)} \\ \begin{gathered} \phi \left( {x,y,t} \right)\left[ {1 - \left( {\frac{{ - z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} - \frac{{4\left( {z + h} \right)}}{{h_{p} }}} \right] \hfill \\ + \frac{{\overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left\{ {\begin{array}{*{20}l} {\frac{\partial u}{{\partial x}} + \frac{w}{{R_{x} }} + \frac{\partial v}{{\partial y}} + \frac{w}{{R_{y} }} - \left[ {h + h_{p} - c\left( {h + h_{p} } \right)^{3} } \right]\left( {\frac{{\partial \psi_{x} }}{\partial x} - \frac{\partial u}{{R_{x} \partial x}} + \frac{{\partial \psi_{y} }}{\partial y} - \frac{\partial v}{{R_{y} \partial y}}} \right)} \\ { + c\left( {h + h_{p} } \right)^{3} \nabla^{2} w} \\ \end{array} } \right\}\left( {z + h} \right) \hfill \\ \end{gathered} & { \left( { - h - h_{p} \le z \le - h} \right)} \\ \end{array} } \right.$$

(13)

According to the first-order piston theory, the aerodynamic pressure load is expressed as (Dowell. [67])

$$\Delta P = - \frac{{\rho_{\infty } U_{\infty }^{2} }}{{\sqrt {M_{\infty }^{2} - 1} }}\left( {\frac{{\partial w\left( {x,y,t} \right)}}{\partial x} + \frac{{M_{\infty }^{2} - 2}}{{M_{\infty }^{2} - 1}}\frac{1}{{U_{\infty } }}\frac{{\partial w\left( {x,y,t} \right)}}{\partial t}} \right)$$

(14)

where, $M_{\infty } , U_{\infty }$ and $\rho_{\infty }$ represent the Mach number, velocity, and density of airflow, respectively. The following simplification for high Mach numbers is utilized: (Dowell [67])

$$\frac{{M_{\infty }^{2} - 2}}{{M_{\infty }^{2} - 1}}\left( {\frac{\mu }{{\lambda \sqrt {M_{\infty }^{2} - 1} }}} \right)^{1/2} = \left( {\frac{\mu }{{\lambda M_{\infty } }}} \right)^{1/2}$$

(15.a)

$$\lambda = \frac{{\rho_{\infty } U_{\infty }^{2} a^{3} }}{{D_{m} \sqrt {M_{\infty }^{2} - 1} }}, \mu = \frac{{\rho_{\infty } a}}{{2\rho_{t} h}}$$

(15.b)

where, $\lambda$ is the non-dimension aerodynamic pressure.

Based on Hamilton’s principle, the governing equations are obtained as

$$\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \left( {\delta T - \delta U - \delta V} \right) dt = 0$$

(16)

In Eq. (16), the variational form of strain energy, kinetic energy, and virtual work of an aeroelastic force is demonstrated by $\delta U,$ $\delta T$ and $\delta V,$ respectively. So that, they can be expressed as

$$\delta U = \iint\limits_{A} {\int\limits_{{ - h - h_{p} }}^{{h + h_{p} }} {\left\{ {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{yy} \delta \varepsilon_{yy} + \sigma_{zz} \delta \varepsilon_{zz} + \sigma_{xy} \delta \gamma_{xy} + \sigma_{xz} \delta \gamma_{xz} + \sigma_{yz} \delta \gamma_{yz} } \right\}dAdz} }$$

(17)

$$\begin{aligned} {\int }_{{t}_{1}}^{{t}_{2}}\delta T dt &=-{\int }_{{t}_{1}}^{{t}_{2}}\underset{A}{\iint }\{\left[\left({I}_{0}+\frac{2}{{R}_{x}}{I}_{1}+\frac{1}{{{R}_{x}}^{2}}{I}_{2}\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+\left({I}_{1}+\frac{1}{{R}_{x}}{I}_{2}-c\left({I}_{3}+\frac{1}{{R}_{x}}{I}_{4}\right)\right)\frac{{\partial }^{2}{\psi }_{x}}{\partial {t}^{2}}-c\left({I}_{3}+\frac{1}{{R}_{x}}{I}_{4}\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}\right]\delta u\\&\quad +\left[\left({I}_{0}+\frac{2}{{R}_{y}}{I}_{1}+\frac{1}{{{R}_{y}}^{2}}{I}_{2}\right)\frac{{\partial }^{2}v}{\partial {t}^{2}}+\left({I}_{1}+\frac{1}{{R}_{y}}{I}_{2}-c\left({I}_{3}+\frac{1}{{R}_{y}}{I}_{4}\right)\right)\frac{{\partial }^{2}{\psi }_{y}}{\partial {t}^{2}}-c\left({I}_{3}+\frac{1}{{R}_{y}}{I}_{4}\right)\frac{{\partial }^{3}w}{\partial y\partial {t}^{2}}\right]\delta v\\&\quad +\left[\left({I}_{1}+\frac{1}{{R}_{x}}{I}_{2}-c{I}_{3}-\frac{c }{{R}_{x}}{I}_{4}\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+\left({I}_{2}-2c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{2}{\psi }_{x}}{\partial {t}^{2}}+\left(-c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}\right]\delta {\psi }_{x}\\&\quad +\left[\left({I}_{1}+\frac{{I}_{2}}{{R}_{y}}-c{I}_{3}-c\frac{{I}_{4}}{{R}_{y}}\right)\frac{{\partial }^{2}v}{\partial {t}^{2}}+\left({I}_{2}-2c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{2}{\psi }_{y}}{\partial {t}^{2}}+\left(-c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{3}w}{\partial y\partial {t}^{2}}\right]\delta {\psi }_{y}\\ &\quad +\left[{I}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}-c\left[\left({I}_{3}+\frac{{I}_{4}}{{R}_{x}}\right)\left(\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}\right)+\left({I}_{3}+\frac{{I}_{4}}{{R}_{y}}\right)\left(\frac{{\partial }^{3}v}{\partial y\partial {t}^{2}}\right)+\left({I}_{4}-c{I}_{6}\right)\left(\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {t}^{2}}\right)\right.\right.\\ &\quad\left.\left.+\left({I}_{4}-c{I}_{6}\right)\left(\frac{{\partial }^{3}{\psi }_{y}}{\partial y\partial {t}^{2}}\right)-c{I}_{6}\left(\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}w}{\partial {y}^{2}\partial {t}^{2}}\right)\right]\right]\delta w\} dA \end{aligned}$$

(18)

The virtual work of aeroelastic forces ($\delta V$) can be represented as:

$$\delta V = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \Delta P\delta w dz$$

(19)

Substituting Eqs. (17), (18) and (19) into Hamilton’s principle, the governing equations of motion are derived as:

$$\begin{aligned} \delta u: & \frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} + \frac{c}{{R_{x} }}\left( {\frac{{\partial S_{xx} }}{\partial x} + \frac{{\partial S_{xy} }}{\partial y}} \right) + \frac{\beta }{{R_{x} }}P_{x} - \frac{1}{{R_{x} }}Q_{x} \\ & = \left( {I_{0} + \frac{2}{{R_{x} }}I_{1} + \frac{1}{{R_{x}^{2} }}I_{2} } \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} + \left( {I_{1} + \frac{1}{{R_{x} }}I_{2} - c\left( {I_{3} + \frac{1}{{R_{x} }}I_{4} } \right)} \right)\frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} - c\left( {I_{3} + \frac{1}{{R_{x} }}I_{4} } \right)\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} \\ \end{aligned}$$

(20.a)

$$\begin{aligned} \delta v & : \frac{{\partial N_{yy} }}{\partial y} + \frac{{\partial N_{xy} }}{\partial x} + \frac{c}{{R_{y} }}\left( {\frac{{\partial S_{yy} }}{\partial y} + \frac{{\partial S_{xy} }}{\partial x}} \right) + \frac{\beta }{{R_{y} }}P_{y} - \frac{1}{{R_{y} }}Q_{y} \\ & = \left( {I_{0} + \frac{2}{{R_{y} }}I_{1} + \frac{1}{{R_{y}^{2} }}I_{2} } \right)\frac{{\partial^{2} v}}{{\partial t^{2} }} + \left( {I_{1} + \frac{1}{{R_{y} }}I_{2} - c\left( {I_{3} + \frac{1}{{R_{y} }}I_{4} } \right)} \right)\frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }} - c\left( {I_{3} + \frac{1}{{R_{y} }}I_{4} } \right)\frac{{\partial^{3} w}}{{\partial y\partial t^{2} }} \\ \end{aligned}$$

(20.b)

$$\begin{aligned} \delta \psi_{x} & : \frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - c\left( {\frac{{\partial S_{xx} }}{\partial x} + \frac{{\partial S_{xy} }}{\partial y}} \right) + Q_{x} - \beta P_{x} \\ & = \left( {I_{1} + \frac{1}{{R_{x} }}I_{2} - cI_{3} - \frac{c}{{R_{x} }}I_{4} } \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} + \left( {I_{2} - 2cI_{4} + c^{2} I_{6} } \right)\frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} + \left( { - cI_{4} + c^{2} I_{6} } \right)\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} \\ \end{aligned}$$

(20.c)

$$\begin{aligned} \delta \psi_{y} & : \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{yy} }}{\partial y} - c\left( {\frac{{\partial S_{xy} }}{\partial x} + \frac{{\partial S_{yy} }}{\partial y}} \right) + Q_{y} - \beta P_{y} \\ & = \left( {I_{1} + \frac{{I_{2} }}{{R_{y} }} - cI_{3} - c\frac{{I_{4} }}{{R_{y} }}} \right)\frac{{\partial^{2} v}}{{\partial t^{2} }} + \left( {I_{2} - 2cI_{4} + c^{2} I_{6} } \right)\frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }} + \left( { - cI_{4} + c^{2} I_{6} } \right)\frac{{\partial^{3} w}}{{\partial y\partial t^{2} }} \\ \end{aligned}$$

(20.d)

$$\begin{aligned} \delta w & :~\frac{{\partial Q_{x} }}{{\partial x}} + \frac{{\partial Q_{y} }}{{\partial y}} + \frac{{N_{{xx}} }}{{R_{x} }} + \frac{{N_{{yy}} }}{{R_{y} }} - c\left( {\frac{{\partial ^{2} S_{{xx}} }}{{\partial x^{2} }} + \frac{{\partial ^{2} S_{{yy}} }}{{\partial y^{2} }} + 2\frac{{\partial ^{2} S_{{xy}} }}{{\partial x\partial y}}} \right) - \beta \left( {\frac{{\partial P_{x} }}{{\partial x}} + \frac{{\partial P_{y} }}{{\partial y}}} \right) + \Delta P \\ & = I_{0} \frac{{\partial ^{2} w}}{{\partial t^{2} }} - c\left[ {\left( {I_{3} + \frac{{I_{4} }}{{R_{x} }}} \right)\left( {\frac{{\partial ^{3} u}}{{\partial x\partial t^{2} }}} \right) + \left( {I_{3} + \frac{{I_{4} }}{{R_{y} }}} \right)\left( {\frac{{\partial ^{3} v}}{{\partial y\partial t^{2} }}} \right)} \right. \\ & \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\, + \left( {I_{4} - cI_{6} } \right)\left( {\frac{{\partial ^{3} \psi _{x} }}{{\partial x\partial t^{2} }}} \right) + \left( {I_{4} - cI_{6} } \right)\left( {\frac{{\partial ^{3} \psi _{y} }}{{\partial y\partial t^{2} }}} \right) - cI_{6} \left( {\frac{{\partial ^{4} w}}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial ^{4} w}}{{\partial y^{2} \partial t^{2} }}} \right)} \right] \\ \end{aligned}$$

(20.e)

In Eq. (20), the forces and moments resultants can be defined as

$$\begin{aligned} N_{{xx}} & = A_{{11}} \left( {\frac{{\partial u}}{{\partial x}} + \frac{w}{{R_{x} }}} \right) + A_{{12}} \left( {\frac{{\partial v}}{{\partial y}} + \frac{w}{{R_{y} }}} \right) + B_{{11}} \frac{{\partial \psi _{x} }}{{\partial x}} + B_{{12}} \frac{{\partial \psi _{y} }}{{\partial y}} \\ & \;\;\;\; - cF_{{11}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial x^{2} }} - \frac{{\partial u}}{{R_{x} \partial x}}} \right) - cF_{{11}} \left( {\frac{{\partial \psi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial y^{2} }} - \frac{{\partial v}}{{R_{y} \partial y}}} \right) + T_{1} \varphi \\ N_{{yy}} & = A_{{21}} \left( {\frac{{\partial u}}{{\partial x}} + \frac{w}{{R_{x} }}} \right) + A_{{22}} \left( {\frac{{\partial v}}{{\partial y}} + \frac{w}{{R_{y} }}} \right) + B_{{21}} \frac{{\partial \psi _{x} }}{{\partial x}} + B_{{22}} \frac{{\partial \psi _{y} }}{{\partial y}} \\ & \;\;\;\;\; - cF_{{21}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial x^{2} }} - \frac{{\partial u}}{{R_{x} \partial x}}} \right) - cF_{{22}} \left( {\frac{{\partial \psi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial y^{2} }} - \frac{{\partial v}}{{R_{y} \partial y}}} \right) + T_{1} \varphi \\ N_{{xy}} & = A_{{66}} \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right) + B_{{66}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial \psi _{y} }}{{\partial x}}} \right) - cF_{{66}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial \psi _{y} }}{{\partial x}} + 2\frac{{\partial ^{2} w}}{{\partial x\partial y}} - \frac{{\partial u}}{{R_{x} \partial y}} - \frac{{\partial v}}{{R_{y} \partial x}}} \right) \\ M_{{xx}} & = B_{{11}} \left( {\frac{{\partial u}}{{\partial x}} + \frac{w}{{R_{x} }}} \right) + B_{{12}} \left( {\frac{{\partial v}}{{\partial y}} + \frac{w}{{R_{y} }}} \right) + D_{{11}} \frac{{\partial \psi _{x} }}{{\partial x}} + D_{{12}} \frac{{\partial \psi _{y} }}{{\partial y}} \\ & \;\;\;\; - cG_{{11}} \left( {\frac{{\partial \psi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w}}{{\partial x^{2} }} - \frac{{\partial u}}{{R_{x} \partial x}}} \right) - cG_{{12}} \left( {\frac{{\partial \psi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial y^{2} }} - \frac{{\partial v}}{{R_{y} \partial y}}} \right) + \bar{T}_{1} \varphi \\ M_{{yy}} & = B_{{11}} \left( {\frac{{\partial u}}{{\partial x}} + \frac{w}{{R_{x} }}} \right) + B_{{12}} \left( {\frac{{\partial v}}{{\partial y}} + \frac{w}{{R_{y} }}} \right) + D_{{11}} \frac{{\partial \psi _{x} }}{{\partial x}} + D_{{12}} \frac{{\partial \psi _{y} }}{{\partial y}} \\ & \;\;\;\; - cG_{{11}} \left( {\frac{{\partial \psi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w}}{{\partial x^{2} }} - \frac{{\partial u}}{{R_{x} \partial x}}} \right) - cG_{{12}} \left( {\frac{{\partial \psi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial y^{2} }} - \frac{{\partial v}}{{R_{y} \partial y}}} \right) + \bar{T}_{1} \varphi \\ M_{{xy}} & = B_{{66}} \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right) + D_{{66}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial \psi _{y} }}{{\partial x}}} \right) - cG_{{66}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial \psi _{y} }}{{\partial x}} + 2\frac{{\partial ^{2} w}}{{\partial x\partial y}} - \frac{{\partial u}}{{R_{x} \partial y}} - \frac{{\partial v}}{{R_{y} \partial x}}} \right) \\ Q_{x} & = A_{{55}} \left( {\psi _{x} + \frac{{\partial w}}{{\partial x}} - \frac{u}{{R_{x} }}} \right) + T_{5} \frac{{\partial \phi }}{{\partial x}} \\ Q_{y} & = A_{{44}} \left( {\psi _{y} + \frac{{\partial w}}{{\partial y}} - \frac{v}{{R_{y} }}} \right) + T_{5} \frac{{\partial \phi }}{{\partial y}} \\ S_{{xx}} & = F_{{11}} \left( {\frac{{\partial u}}{{\partial x}} + \frac{w}{{R_{x} }}} \right) + F_{{12}} \left( {\frac{{\partial v}}{{\partial y}} + \frac{w}{{R_{y} }}} \right) + G_{{11}} \frac{{\partial \psi _{x} }}{{\partial x}} + G_{{12}} \frac{{\partial \psi _{y} }}{{\partial y}} \\ & \;\;\;\; - cH_{{11}} \left( {\frac{{\partial \psi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w}}{{\partial x^{2} }} - \frac{{\partial u}}{{R_{x} \partial x}}} \right) - cH_{{12}} \left( {\frac{{\partial \psi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial y^{2} }} - \frac{{\partial v}}{{R_{y} \partial y}}} \right) - \bar{T}_{1} \phi \\ S_{{yy}} & = F_{{21}} \left( {\frac{{\partial u}}{{\partial x}} + \frac{w}{{R_{x} }}} \right) + F_{{22}} \left( {\frac{{\partial v}}{{\partial y}} + \frac{w}{{R_{y} }}} \right) + G_{{21}} \frac{{\partial \psi _{x} }}{{\partial x}} + G_{{22}} \frac{{\partial \psi _{y} }}{{\partial y}} \\ & \;\;\;\; - cH_{{21}} \left( {\frac{{\partial \psi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w}}{{\partial x^{2} }} - \frac{{\partial u}}{{R_{x} \partial x}}} \right) - cH_{{22}} \left( {\frac{{\partial \psi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w}}{{\partial y^{2} }} - \frac{{\partial v}}{{R_{y} \partial y}}} \right) - \bar{T}_{1} \phi \\ S_{{xy}} & = F_{{66}} \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right) + G_{{66}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial \psi _{y} }}{{\partial x}}} \right) - cH_{{66}} \left( {\frac{{\partial \psi _{x} }}{{\partial y}} + \frac{{\partial \psi _{y} }}{{\partial x}} + 2\frac{{\partial ^{2} w}}{{\partial x\partial y}} - \frac{{\partial u}}{{R_{x} \partial y}} - \frac{{\partial v}}{{R_{y} \partial x}}} \right) \\ P_{x} & = - \beta \left( {D_{{55}} \left( {\psi _{x} + \frac{{\partial w}}{{\partial x}} - \frac{u}{{R_{x} }}} \right) + \bar{T}_{5} \phi } \right) \\ P_{y} & = - \beta \left( {D_{{44}} \left( {\psi _{y} + \frac{{\partial w}}{{\partial y}} - \frac{v}{{R_{y} }}} \right) + \bar{T}_{5} \phi } \right) \\ \end{aligned}$$

(21)

Substituting Eq. (21) into Eq. (20), the governing equations can be presented as

$$\delta u: {ab}_{1}\frac{{\partial }^{2}u}{\partial {x}^{2}}+{ab}_{2}\frac{{\partial }^{2}u}{\partial {y}^{2}}+{ab}_{3}u+{ab}_{4}\frac{{\partial }^{2}v}{\partial x\partial y}+{ab}_{5}\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+{ab}_{6}\frac{{\partial }^{2}{\psi }_{x}}{\partial {y}^{2}}+{ab}_{7}{\psi }_{x}+{ab}_{8}\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+{ab}_{9}\frac{{\partial }^{3}w}{\partial {x}^{3}}+{ab}_{10}\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}+{ab}_{11}\frac{\partial w}{\partial x}+{T}_{2}\left(\left(\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{\partial w}{{R}_{x}\partial x}\right)+\left(\frac{{\partial }^{2}v}{\partial x\partial y}+\frac{\partial w}{{R}_{y}\partial x}\right)\right)+\frac{1}{{R}_{x}}\left({T}_{5}\frac{\partial \phi }{\partial x}+{T}_{7}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}\right)+{T}_{8}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{{\partial }^{2}u}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}-\frac{{\partial }^{2}v}{{R}_{y}\partial x\partial y}\right)-\beta \left({T}_{5z2}\frac{\partial \phi }{\partial x}+{T}_{7z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}\right)+{T}_{8z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{{\partial }^{2}u}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}-\frac{{\partial }^{2}v}{{R}_{y}\partial x\partial y}\right)\right)\right)+\frac{c}{{R}_{x}}\left({T}_{1z3}\frac{\partial \phi }{\partial x}+{T}_{3z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}\right)+{T}_{4z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{{\partial }^{2}u}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}-\frac{{\partial }^{2}v}{{R}_{y}\partial x\partial y}\right)\right)=\left({I}_{0}+\frac{2}{{R}_{x}}{I}_{1}+\frac{1}{{{R}_{x}}^{2}}{I}_{2}\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+\left({I}_{1}+\frac{1}{{R}_{x}}{I}_{2}-c\left({I}_{3}+\frac{1}{{R}_{x}}{I}_{4}\right)\right)\frac{{\partial }^{2}{\psi }_{x}}{\partial {t}^{2}}-c\left({I}_{3}+\frac{1}{{R}_{x}}{I}_{4}\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}$$

(22.a)

$$\delta v: {ac}_{1}\frac{{\partial }^{2}u}{\partial x\partial y}+{ac}_{2}\frac{{\partial }^{2}v}{\partial {x}^{2}}+{ac}_{3}\frac{{\partial }^{2}v}{\partial {y}^{2}}+{ac}_{4}v+{ac}_{5}\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+{ac}_{6}\frac{{\partial }^{2}{\psi }_{y}}{\partial {x}^{2}}+{ac}_{7}\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+{ac}_{8}{\psi }_{y}+{ac}_{9}\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}+{ac}_{10}\frac{{\partial }^{3}w}{\partial {y}^{3}}+{ac}_{11}\frac{\partial w}{\partial y}+{T}_{2}\left(\left(\frac{{\partial }^{2}u}{\partial x\partial y}+\frac{\partial w}{{R}_{x}\partial y}\right)+\left(\frac{{\partial }^{2}v}{\partial {y}^{2}}+\frac{\partial w}{{R}_{y}\partial y}\right)\right)+\frac{1}{{R}_{y}}\left({T}_{5}\frac{\partial \phi }{\partial y}+{T}_{7}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}\right)+{T}_{8}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}-\frac{{\partial }^{2}u}{{R}_{x}\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{3}w}{\partial {y}^{3}}-\frac{{\partial }^{2}v}{{R}_{y}\partial {y}^{2}}\right)-\beta \left({T}_{5z2}\frac{\partial \phi }{\partial y}+{T}_{7z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}\right)+{T}_{8z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}-\frac{{\partial }^{2}u}{{R}_{x}\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{3}w}{\partial {y}^{3}}-\frac{{\partial }^{2}v}{{R}_{y}\partial {y}^{2}}\right)\right)\right)+\frac{c}{{R}_{y}}\left({T}_{1z3}\frac{\partial \phi }{\partial y}+{T}_{3z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}\right)+{T}_{4z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}-\frac{{\partial }^{2}u}{{R}_{x}\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{3}w}{\partial {y}^{3}}-\frac{{\partial }^{2}v}{{R}_{y}\partial {y}^{2}}\right)\right)=\left({I}_{0}+\frac{2}{{R}_{y}}{I}_{1}+\frac{1}{{{R}_{y}}^{2}}{I}_{2}\right)\frac{{\partial }^{2}v}{\partial {t}^{2}}+\left({I}_{1}+\frac{1}{{R}_{y}}{I}_{2}-c\left({I}_{3}+\frac{1}{{R}_{y}}{I}_{4}\right)\right)\frac{{\partial }^{2}{\psi }_{y}}{\partial {t}^{2}}-c\left({I}_{3}+\frac{1}{{R}_{y}}{I}_{4}\right)\frac{{\partial }^{3}w}{\partial y\partial {t}^{2}}$$

(22.b)

$$\delta {\psi }_{x}: {ad}_{1}\frac{{\partial }^{2}u}{\partial {x}^{2}}+{ad}_{2}\frac{{\partial }^{2}u}{\partial {y}^{2}}+{ad}_{3}u+{ad}_{4}\frac{{\partial }^{2}v}{\partial x\partial y}+{ad}_{5}\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+{ad}_{6}{\psi }_{x}+{ad}_{7}\frac{{\partial }^{2}{\psi }_{x}}{\partial {y}^{2}}+{ad}_{8}\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+{ad}_{9}\frac{{\partial }^{3}w}{\partial {x}^{3}}+{ad}_{10}\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}+{ad}_{11}\frac{\partial w}{\partial x}+\left({T}_{1z}\frac{\partial \phi }{\partial x}+{T}_{3z}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}\right)+{T}_{4z}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{{\partial }^{2}u}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}-\frac{{\partial }^{2}v}{{R}_{y}\partial x\partial y}\right)-\left({T}_{5}\frac{\partial \phi }{\partial x}+{T}_{7}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}\right)+{T}_{8}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{{\partial }^{2}u}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}-\frac{{\partial }^{2}v}{{R}_{y}\partial x\partial y}\right)\right)\right)-\beta \left({T}_{5z2}\frac{\partial \phi }{\partial x}+{T}_{7z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}\right)+{T}_{8z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{{\partial }^{2}u}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}-\frac{{\partial }^{2}v}{{R}_{y}\partial x\partial y}\right)\right)-c\left({T}_{1z3}\frac{\partial \phi }{\partial x}+{T}_{3z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}\right)+{T}_{4z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{{\partial }^{2}u}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{y}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial x\partial {y}^{2}}-\frac{{\partial }^{2}v}{{R}_{y}\partial x\partial y}\right)\right)=\left({I}_{1}+\frac{1}{{R}_{x}}{I}_{2}-c{I}_{3}-\frac{c}{{R}_{x}}{I}_{4}\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+\left({I}_{2}-2c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{2}{\psi }_{x}}{\partial {t}^{2}}+\left(-c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}$$

(22.c)

$$\delta {\psi }_{y}: {af}_{1}\frac{{\partial }^{2}u}{\partial x\partial y}+{af}_{2}\frac{{\partial }^{2}v}{\partial {x}^{2}}+{af}_{3}\frac{{\partial }^{2}v}{\partial {y}^{2}}+{af}_{4}v+{af}_{5}\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+{af}_{6}\frac{{\partial }^{2}{\psi }_{y}}{\partial {x}^{2}}+{af}_{7}\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+{af}_{8}{\psi }_{y}+{af}_{9}\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}+{af}_{10}\frac{{\partial }^{3}w}{\partial {y}^{3}}+{af}_{11}\frac{\partial w}{\partial y}+\left({T}_{1z}\frac{\partial \phi }{\partial y}+{T}_{3z}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}\right)+{T}_{4z}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}-\frac{{\partial }^{2}u}{{R}_{x}\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{3}w}{\partial {y}^{3}}-\frac{{\partial }^{2}v}{{R}_{y}\partial {y}^{2}}\right)-c\left({T}_{1z3}\frac{\partial \phi }{\partial y}+{T}_{3z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}\right)+{T}_{4z3}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}-\frac{{\partial }^{2}u}{{R}_{x}\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{3}w}{\partial {y}^{3}}-\frac{{\partial }^{2}v}{{R}_{y}\partial {y}^{2}}\right)\right)\right)-\left({T}_{5}\frac{\partial \phi }{\partial y}+{T}_{7}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}\right)+{T}_{8}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}-\frac{{\partial }^{2}u}{{R}_{x}\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{3}w}{\partial {y}^{3}}-\frac{{\partial }^{2}v}{{R}_{y}\partial {y}^{2}}\right)\right)-\beta \left({T}_{5z2}\frac{\partial \phi }{\partial y}+{T}_{7z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}\right)+{T}_{8z2}\left(\frac{{\partial }^{2}{\psi }_{x}}{\partial x\partial y}+\frac{{\partial }^{3}w}{\partial {x}^{2}\partial y}-\frac{{\partial }^{2}u}{{R}_{x}\partial x\partial y}+\frac{{\partial }^{2}{\psi }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{3}w}{\partial {y}^{3}}-\frac{{\partial }^{2}v}{{R}_{y}\partial {y}^{2}}\right)\right)=\left({I}_{1}+\frac{{I}_{2}}{{R}_{y}}-c{I}_{3}-c\frac{{I}_{4}}{{R}_{y}}\right)\frac{{\partial }^{2}v}{\partial {t}^{2}}+\left({I}_{2}-2c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{2}{\psi }_{y}}{\partial {t}^{2}}+\left(-c{I}_{4}+{c}^{2}{I}_{6}\right)\frac{{\partial }^{3}w}{\partial y\partial {t}^{2}}$$

(22.d)

$$\begin{aligned}\delta w:& {ag}_{1}\frac{\partial u}{\partial x}+{ag}_{2}\frac{{\partial }^{3}u}{\partial {x}^{3}}+{ag}_{3}\frac{{\partial }^{3}u}{\partial x\partial {y}^{2}}+{ag}_{4}\frac{\partial v}{\partial y} +{ag}_{5}\frac{{\partial }^{3}v}{\partial {x}^{2}\partial y}+{ag}_{6}\frac{{\partial }^{3}v}{\partial {y}^{3}}+{ag}_{7}\frac{\partial {\psi }_{x}}{\partial x}+{ag}_{8}\frac{{{\partial }^{3}\psi }_{x}}{\partial {x}^{3}}\\ &\quad +{ag}_{9} \frac{{{\partial }^{3}\psi }_{x}}{\partial {x}^{2}\partial y}+{ag}_{10}\frac{\partial {\psi }_{y}}{\partial y} +{ag}_{11}\frac{{{\partial }^{3}\psi }_{y}}{\partial {y}^{3}}+{ag}_{12}\frac{{{\partial }^{3}\psi }_{y}}{\partial {x}^{2}\partial y}+{ag}_{13}\frac{{\partial }^{4}w}{\partial {x}^{4}}+{ag}_{14}\frac{{\partial }^{4}w}{\partial {y}^{4}}\\ &\quad +{ag}_{15}\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}+{ag}_{16}\frac{{\partial }^{2}w}{\partial {x}^{2}}+{ag}_{17}\frac{{\partial }^{2}w}{\partial {y}^{2}}+{ag}_{18}w+{T}_{5}\frac{{\partial }^{2}\phi }{\partial {x}^{2}}+{T}_{7}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}\bigg)\\ &\quad+{T}_{8}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{4}w}{\partial {x}^{4}}-\frac{{\partial }^{3}u}{{R}_{x}\partial {x}^{3}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {x}^{2}\partial y}\bigg)-\beta \bigg({{T}_{5z2}\frac{{\partial }^{2}\phi }{\partial {x}^{2}}+T}_{7z2}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}\bigg)\\ &\quad+{T}_{8z2}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{4}w}{\partial {x}^{4}}-\frac{{\partial }^{3}u}{{R}_{x}\partial {x}^{3}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {x}^{2}\partial y}\bigg)\bigg)+{T}_{5}\frac{{\partial }^{2}\phi }{\partial {y}^{2}}\\ &\quad+{T}_{7}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}\bigg)+{T}_{8}\bigg(\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {y}^{3}}+\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}u}{{R}_{x}\partial x\partial {y}^{2}}\bigg)-\beta \bigg({T}_{5z2}\frac{{\partial }^{2}\phi }{\partial {y}^{2}}\\ &\quad+{T}_{7z2}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}\bigg)+{T}_{8z2}\bigg(\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {y}^{3}}+\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}u}{{R}_{x}\partial x\partial {y}^{2}}\bigg)\bigg)\\ &\quad+c\bigg({T}_{1z3}\bigg(\frac{{\partial }^{2}\phi }{\partial {x}^{2}}+\frac{{\partial }^{2}\phi }{\partial {y}^{2}}\bigg)+{T}_{3z3}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}+\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}\bigg)+{T}_{4z3}\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{4}w}{\partial {x}^{4}}-\frac{{\partial }^{3}u}{{R}_{x}\partial {x}^{3}}\\ &\quad+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {x}^{2}\partial y}\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {y}^{3}}+\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}u}{{R}_{x}\partial x\partial {y}^{2}}\bigg)\bigg) \\ &\quad -\frac{{T}_{2}}{{R}_{x}}\bigg(\bigg(\frac{\partial u}{\partial x}+\frac{w}{{R}_{x}}\bigg)+\bigg(\frac{\partial v}{\partial y}+\frac{w}{{R}_{y}}\bigg)\bigg)-\frac{{T}_{2}}{{R}_{y}}\bigg(\bigg(\frac{\partial u}{\partial x}+\frac{w}{{R}_{x}}\bigg)+\bigg(\frac{\partial v}{\partial y}+\frac{w}{{R}_{y}}\bigg)\bigg)+\Delta P\\ &={I}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}-c\bigg[\bigg({I}_{3}+\frac{{I}_{4}}{{R}_{x}}\bigg)\bigg(\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}\bigg)+\bigg({I}_{3}+\frac{{I}_{4}}{{R}_{y}}\bigg)\bigg(\frac{{\partial }^{3}v}{\partial y\partial {t}^{2}}\bigg)+\bigg({I}_{4}-c{I}_{6}\bigg)\bigg(\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {t}^{2}}\bigg)\\ &\quad +\bigg({I}_{4}-c{I}_{6}\bigg)\bigg(\frac{{\partial }^{3}{\psi }_{y}}{\partial y\partial {t}^{2}}\bigg)-c{I}_{6}\bigg(\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}w}{\partial {y}^{2}\partial {t}^{2}}\bigg)\bigg]\end{aligned}$$

(22.e)

The constant quantities in Eq. (22), have been defined in “Appendix A”.

The mechanical boundary conditions can be expressed as

Simply supported boundary conditions (S)

$$\begin{aligned} {\text{at}}\;\;\;x & = 0, \,a \\ u & = 0 , v = 0 , \psi_{y} = 0 , M_{xx} - cP_{xx} = 0 , w = 0 , P_{xx} = 0 \\ \end{aligned}$$

(23.a)

$$\begin{aligned} {\text{at}}\;\;\;y & = 0, \,b \\ u & = 0 , v = 0 , \psi_{x} = 0 , M_{yy} - cP_{yy} = 0 , w = 0 , P_{yy} = 0 \\ \end{aligned}$$

(23.b)

Clamped boundary conditions (C)

$$\begin{aligned} {\text{at}}\;\;\;x & = 0, \,a \\ u & = 0 , v = 0 , \psi_{x} = 0, \psi_{y} = 0 , w = 0 , \frac{\partial w}{{\partial x}} = 0 \\ \end{aligned}$$

(24.a)

$$\begin{aligned} {\text{at}}\;\;\;y & = 0,\, b \\ u & = 0 , v = 0 , \psi_{x} = 0, \psi_{y} = 0 , w = 0 , \frac{\partial w}{{\partial x}} = 0 \\ \end{aligned}$$

(24.b)

The variables have to satisfy Maxwell’s equation (Farsangi et al. [69])

$$\mathop \int \limits_{{ - h - h_{p} }}^{ - h} \vec{\nabla } \cdot \vec{D} dz + \mathop \int \limits_{h}^{{h + h_{p} }} \vec{\nabla } \cdot \vec{D} dz = 0$$

(25)

Substituting Eq. (3) and (9), into Eq. (25) yields

$$\begin{aligned}\delta \phi :&{S}_{1}\left(\frac{\partial {\psi }_{x}}{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}}-\frac{\partial u}{{R}_{x}\partial x}+\frac{\partial {\psi }_{y}}{\partial y}+\frac{{\partial }^{2}w}{\partial {y}^{2}}-\frac{\partial v}{{R}_{y}\partial y}\right)-{S}_{2}\left(\frac{{\partial }^{2}\phi }{\partial {x}^{2}}+\frac{{\partial }^{2}\phi }{\partial {y}^{2}}\right)-{S}_{6}\left(\frac{u}{\partial {x}^{3}}+\frac{{\partial }^{2}w}{{R}_{x}\partial {x}^{2}}+\frac{{\partial }^{3}v}{\partial {x}^{2}\partial y}+\frac{{\partial }^{2}w}{{R}_{y}\partial {x}^{2}}+\frac{{\partial }^{3}u}{\partial x\partial {y}^{2}}+\frac{{\partial }^{2}w}{{R}_{x}\partial {y}^{2}}+\frac{{\partial }^{3}v}{\partial {y}^{3}}+\frac{{\partial }^{2}w}{{R}_{y}\partial {y}^{2}}\right)+{S}_{7}\left(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}+\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}\right)+{S}_{8}\left(\frac{{\partial }^{3}{\psi }_{x}}{\partial {x}^{3}}+\frac{{\partial }^{4}w}{\partial {x}^{4}}-\frac{{\partial }^{3}u}{{R}_{x}\partial {x}^{3}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {x}^{2}\partial y}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {x}^{2}\partial y}+\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}-\frac{{\partial }^{3}u}{{R}_{x}\partial x\partial {y}^{2}}+\frac{{\partial }^{3}{\psi }_{y}}{\partial {y}^{3}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}-\frac{{\partial }^{3}v}{{R}_{y}\partial {y}^{3}}\right)+{S}_{3}\left(\frac{\partial {\psi }_{x}}{\partial x}+\frac{\partial {\psi }_{y}}{\partial y}\right)-{S}_{4}\left(\frac{\partial {\psi }_{x}}{\partial x}+\frac{{\partial }^{2}w}{\partial {x}^{2}}-\frac{\partial u}{{R}_{x}\partial x}+\frac{\partial {\psi }_{y}}{\partial y}+\frac{{\partial }^{2}w}{\partial {y}^{2}}-\frac{\partial v}{{R}_{y}\partial y}\right)-{S}_{5}\phi =0\end{aligned}$$

(26)

The electrical boundary conditions at $x = 0, a , y = \pm \frac{b}{2}$ are:

$$\phi \left( {0, y, t} \right) = \phi \left( {a, y, t} \right) = 0$$

(27)

and

$$\mathop \int \limits_{{ - h - h_{p} }}^{ - h} D_{y} \left( {x,y,z,t} \right)dz + \mathop \int \limits_{{h + h_{p} }}^{h} D_{y} \left( {x,y,z,t} \right)dz = 0$$

(28)

In "Appendix B", the definitions of constant quantities in Eq. (26) have been presented.

3 Solution technique

The Galerkin method is used to discretize the partial differential equations into ordinary equations. The modal expansions are assumed to approximate the aeroelastic stability analysis of a doubly curved panel made of FG porous as follows. (Fung [75])

$$\begin{gathered} u\left( {x,y,t} \right) = {{\varvec{\Phi}}}_{u}^{T} {\varvec{q}}_{u} ,\;\;v\left( {x,y,t} \right) = {{\varvec{\Phi}}}_{v}^{T} {\varvec{q}}_{v} ,\;\; \psi_{x} \left( {x,y,t} \right) = {{\varvec{\Phi}}}_{{\psi_{x} }}^{T} {\varvec{q}}_{{\psi_{x} }} , \hfill \\ \psi_{y} \left( {x,y,t} \right) = {{\varvec{\Phi}}}_{{\psi_{y} }}^{T} {\varvec{q}}_{{\psi_{y} }} ,\;\; w\left( {x,y,t} \right) = {{\varvec{\Phi}}}_{w}^{T} {\varvec{q}}_{w} ,\;\; \phi \left( {x, y,t} \right) = {{\varvec{\Phi}}}_{\phi }^{T} {\varvec{q}}_{\phi } \hfill \\ \end{gathered}$$

(29)

where ${\varvec{q}}_{u}$, ${\varvec{q}}_{v}$, ${\varvec{q}}_{{\psi_{x} }}$, ${\varvec{q}}_{{\psi_{y} }} , {\varvec{q}}_{w}$ and ${\varvec{q}}_{\phi }$ denote the generalized coordinates; ${{\varvec{\Phi}}}_{u}$, ${{\varvec{\Phi}}}_{v}$, ${{\varvec{\Phi}}}_{{\psi_{x} }}$, ${{\varvec{\Phi}}}_{{\psi_{y} }} ,$ ${{\varvec{\Phi}}}_{w}$ and ${{\varvec{\Phi}}}_{\phi }$ expressed the unknown displacements that satisfy boundary conditions. The unknown displacements $\left( {u, v, \psi_{x} , \psi_{y} , w,\phi } \right)$ can be represented as

$$\begin{aligned} u\left( {x,y,t} \right) & ={\varvec{\varPhi}}_{u}^{T} {\varvec{q}}_{u} = \mathop \sum \limits_{n = 1}^{{n^{\prime} }} \mathop \sum \limits_{m = 1}^{{m^{\prime} }} q_{umn} \left( t \right)\varphi_{um} \left( x \right)\psi_{un} \left( y \right) \\ v\left( {x,y,t} \right) & ={\varvec{\varPhi}}_{v}^{T} {\varvec{q}}_{v} = \mathop \sum \limits_{n = 1}^{{n^{\prime} }} \mathop \sum \limits_{m = 1}^{{m^{\prime} }} q_{vmn} \left( t \right)\varphi_{vm} \left( x \right)\psi_{vn} \left( y \right) \\ \psi_{x} \left( {x,y,t} \right) & ={\varvec{\varPhi}}_{{\psi_{x} }}^{T} {\varvec{q}}_{{\psi_{x} }} = \mathop \sum \limits_{n = 1}^{{n^{\prime} }} \mathop \sum \limits_{m = 1}^{{m^{\prime} }} q_{xmn} \left( t \right)\varphi_{xm} \left( x \right)\psi_{xn} \left( y \right) \\ \psi_{y} \left( {x,y,t} \right) & ={\varvec{\varPhi}}_{{\psi_{y} }}^{T} {\varvec{q}}_{{\psi_{y} }} = \mathop \sum \limits_{n = 1}^{{n^{\prime} }} \mathop \sum \limits_{m = 1}^{{m^{\prime} }} q_{ymn} \left( t \right)\varphi_{ym} \left( x \right)\psi_{yn} \left( y \right) \\ w\left( {x,y,t} \right) & ={\varvec{\varPhi}}_{w}^{T} {\varvec{q}}_{w} = \mathop \sum \limits_{n = 1}^{{n^{\prime} }} \mathop \sum \limits_{m = 1}^{{m^{\prime} }} q_{wmn} \left( t \right)\varphi_{wm} \left( x \right)\psi_{wn} \left( y \right) \\ \phi \left( {x,y,t} \right) & ={\varvec{\varPhi}}_{\phi }^{T} {\varvec{q}}_{\phi } = \mathop \sum \limits_{n = 1}^{{n^{\prime} }} \mathop \sum \limits_{m = 1}^{{m^{\prime} }} q_{\phi mn} \left( t \right)\varphi_{\phi m} \left( x \right)\psi_{\phi n} \left( y \right) \\ \end{aligned}$$

(30)

where $m^{\prime}$ and $n^{\prime}$ are the truncation of the Galerkin expansion (or the number of modes). It is shown in Table. 2 that Eq. (30) converges in the sixth mode. So,

$$m^{\prime} = n^{\prime} = 6$$

(31)

The unknown displacements that satisfy appropriate simply supported (S) and clamped (C) boundary conditions can be written as

Simply supported (S):

$$\varphi_{rs} \left( {x,y} \right) = \sin \left( {r\frac{\pi x}{L}} \right)\sin \left( {s\frac{\pi y}{L}} \right)$$

(32)

Clamped (C):

$$\begin{aligned} \varphi_{rs} \left( {x,y} \right) & = \left( {\cosh \left( {k_{i} x} \right) - \cos \left( {k_{i} x} \right)} \right) \\ & \;\;\;\; - D_{i} \left( {\sinh \left( {k_{i} x} \right) - \sin \left( {k_{i} x} \right)} \right)\left( {\cosh \left( {k_{i} y} \right) - \cos \left( {k_{i} y} \right)} \right) \\ & \;\;\;\; - D_{i} \left( {\sinh \left( {k_{i} y} \right) - \sin \left( {k_{i} y} \right)} \right) \\ \end{aligned}$$

(33)

where

$$D_{i} = \frac{{\sinh \left( {k_{i} } \right) - \sin \left( {k_{i} } \right)}}{{\cosh \left( {k_{i} } \right) - \cos \left( {k_{i} } \right)}}$$

$$k_{1} = 4.7300, \;k_{2} = 7.8532, \;k_{3} = 10.9956, \;k_{4} = 14.1316,$$

$$k_{5} = 17.2887, \;\;i > 5 \Rightarrow k_{i} = \left( {2i + 1} \right)\frac{\pi }{2}$$

The Galerkin method is used to discretize form of governing equations which can be given as

$$\user2{M\ddot{q}}\left( t \right) + \user2{C\dot{q}}\left( t \right) + {\varvec{K}}_{{\varvec{e}}} {\varvec{q}}\left( t \right) = 0$$

(34)

In Eq. (34), the overall vector of generalized coordinates is expressed by ${\varvec{q}}$ =  $\left[ {{\varvec{q}}_{u}^{T} \quad {\varvec{q}}_{v}^{T} \quad{\varvec{q}}_{{\psi_{x} }}^{T} \quad{\varvec{q}}_{{\psi_{y} }}^{T}\quad {\varvec{q}}_{w}^{T}\quad {\varvec{q}}_{\phi }^{T} } \right]^{T}$. Furthermore, ${\varvec{K}}_{{\varvec{e}}}$$,{\varvec{M}}$ and ${\varvec{C}}$ represent the stiffness, mass and damping matrices, respectively. So, the stiffness matrix can be represented as

$$\left[\begin{array}{lll}{{\varvec{K}}}_{11}& {{\varvec{K}}}_{12}& \begin{array}{lll}{{\varvec{K}}}_{13}&\quad {{\varvec{K}}}_{14}&\quad \begin{array}{ll}{{\varvec{K}}}_{15}&\quad {{\varvec{K}}}_{16}\end{array}\end{array}\\ {{\varvec{K}}}_{21}& {{\varvec{K}}}_{22}& \begin{array}{lll}{{\varvec{K}}}_{23}&\quad {{\varvec{K}}}_{24}&\quad \begin{array}{ll}{{\varvec{K}}}_{25}&\quad {{\varvec{K}}}_{26}\end{array}\end{array}\\ \begin{array}{l}{{\varvec{K}}}_{31}\\ {{\varvec{K}}}_{41}\\ \begin{array}{l}{{\varvec{K}}}_{51}\\ {{\varvec{K}}}_{61}\end{array}\end{array}& \begin{array}{l}{{\varvec{K}}}_{32}\\ {{\varvec{K}}}_{42}\\ \begin{array}{l}{{\varvec{K}}}_{52}\\ {{\varvec{K}}}_{62}\end{array}\end{array}& \begin{array}{lll}\begin{array}{l}{{\varvec{K}}}_{33}\\ {{\varvec{K}}}_{43}\\ \begin{array}{l}{{\varvec{K}}}_{53}\\ {{\varvec{K}}}_{63}\end{array}\end{array}& \begin{array}{l}{{\varvec{K}}}_{34}\\ {{\varvec{K}}}_{44}\\ \begin{array}{l}{{\varvec{K}}}_{54}\\ {{\varvec{K}}}_{64}\end{array}\end{array}& \begin{array}{l}\begin{array}{ll}{{\varvec{K}}}_{35}&\quad {{\varvec{K}}}_{36}\end{array}\\ \begin{array}{ll}{{\varvec{K}}}_{45}&\quad {{\varvec{K}}}_{46}\end{array}\\ \begin{array}{ll}\begin{array}{l}{{\varvec{K}}}_{55}\\ {{\varvec{K}}}_{65}\end{array}& \begin{array}{l}{{\varvec{K}}}_{56}\\ {{\varvec{K}}}_{66}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left\{\begin{array}{l}\begin{array}{l}{{\varvec{q}}}_{u}\\ {{\varvec{q}}}_{v}\\ {{\varvec{q}}}_{{\psi }_{x}}\\ \begin{array}{l}{{\varvec{q}}}_{{\psi }_{x}}\\ {{\varvec{q}}}_{w}\end{array}\end{array}\\ {{\varvec{q}}}_{\phi }\end{array}\right\}=0$$

(35)

The above equation can be rewritten as

$$\begin{gathered} \overline{\user2{K}}_{11} {\varvec{q}} + \overline{\user2{K}}_{12} {\varvec{q}}_{\phi } = 0 \hfill \\ \overline{\user2{K}}_{21} {\varvec{q}} + \overline{\user2{K}}_{66} {\varvec{q}}_{\phi } = 0 \hfill \\ \end{gathered}$$

(36)

$$\overline{\user2{K}}_{11} = \left[ {\begin{array}{*{20}l} {{\varvec{K}}_{11} } & {{\varvec{K}}_{12} } & {\begin{array}{*{20}l} {{\varvec{K}}_{13} } &\quad {{\varvec{K}}_{14} } &\quad {{\varvec{K}}_{15} } \\ \end{array} } \\ {{\varvec{K}}_{21} } & {{\varvec{K}}_{22} } & {\begin{array}{*{20}l} {{\varvec{K}}_{23} } &\quad {{\varvec{K}}_{24} } &\quad {{\varvec{K}}_{25} } \\ \end{array} } \\ {{\varvec{K}}_{31} } & {{\varvec{K}}_{32} } & {\begin{array}{*{20}l} {{\varvec{K}}_{33} } &\quad {{\varvec{K}}_{34} } &\quad {{\varvec{K}}_{35} } \\ \end{array} } \\ {\begin{array}{*{20}l} {{\varvec{K}}_{41} } \\ {\begin{array}{*{20}l} {{\varvec{K}}_{51} } \\ {{\varvec{K}}_{61} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}l} {{\varvec{K}}_{42} } \\ {\begin{array}{*{20}l} {{\varvec{K}}_{52} } \\ {{\varvec{K}}_{62} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}l} {\begin{array}{*{20}l} {{\varvec{K}}_{43} } \\ {\begin{array}{*{20}l} {{\varvec{K}}_{53} } \\ {{\varvec{K}}_{63} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}l} {{\varvec{K}}_{44} } \\ {\begin{array}{*{20}l} {{\varvec{K}}_{54} } \\ {{\varvec{K}}_{64} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}l} {{\varvec{K}}_{45} } \\ {\begin{array}{*{20}l} {{\varvec{K}}_{55} } \\ {{\varvec{K}}_{65} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] ,\user2{ q} = \left\{ {{\varvec{q}}_{u}\,\,\,\, {\varvec{q}}_{v}\,\,\,\, {\varvec{q}}_{{\psi_{x} }}\,\,\,\, {\varvec{q}}_{{\psi_{y} }}\,\,\,\, {\varvec{q}}_{w} } \right\}^{T}$$

(37a)

$$\overline{\user2{K}}_{12} = \left[ {{\varvec{K}}_{16}\,\,\,\, {\varvec{K}}_{26} \,\,\,\,{\varvec{K}}_{36} \,\,\,\,{\varvec{K}}_{46}\,\,\,\, {\varvec{K}}_{56} } \right]^{T}$$

(37b)

$$\overline{\user2{K}}_{21} = \left[ {{\varvec{K}}_{61}\,\,\,\, {\varvec{K}}_{62} \,\,\,\,{\varvec{K}}_{63}\,\,\,\, {\varvec{K}}_{64}\,\,\,\, {\varvec{K}}_{65} } \right]^{{}}$$

(37c)

where

$${\varvec{K}}_{{\varvec{e}}} = \overline{\user2{K}}_{11} - \overline{\user2{K}}_{12} \overline{\user2{K}}_{66}^{ - 1} \overline{\user2{K}}_{21}$$

(38)

The state vector ${\varvec{Z}}\left( t \right) = \left\{ {{\varvec{q}}\left( t \right), \dot{\user2{q}}\left( t \right)} \right\}^{T}$ is defined and the Eq. (34) can be rewritten as

$$\dot{\user2{Z}}\left( t \right) = {\varvec{DZ}}\left( t \right),$$

(39)

where

$${\varvec{D}} = \left[ {\begin{array}{*{20}c} 0 & {\varvec{I}} \\ { - {\varvec{M}}^{ - 1} {\varvec{K}}_{{\varvec{e}}} } &\quad { - {\varvec{M}}^{ - 1} {\varvec{C}}} \\ \end{array} } \right],$$

(40)

${\varvec{I}}$ is the identity matrix.

Finally, substituting the state vector ${\varvec{Z}}\left( t \right) = \overline{\user2{Z}}e^{{\left( {\omega t} \right)}}$ into Eq. (39) yields

$$\left( {{\varvec{D}} - i\omega {\varvec{I}}} \right)\overline{\user2{Z}} = 0.$$

(41)

From Eq. (41), the eigenvalues $\omega$’s are obtained which are generally complex quantities and written as a form, $\omega = \omega_{R} + i\omega_{I}$. So $\omega_{I}$ represents the natural frequency of the system and $\omega_{R}$ is a real part. Dynamic instability occurs when the real part of the eigenvalue sign becomes positive. The aerodynamic pressure associated with this signal change is represented by the critical flutter aerodynamic pressure, $\lambda_{cr}$. This phenomenon is caused by the merging of two modes of torsion and bending, which is known as the flutter frequency, $\omega_{cr}$ (Saidi et al. [30]).

4 Numerical results

The dimensionless parameters can be defined as

$$\Omega = \omega \left( {\sqrt {\frac{{D_{m} }}{{2\rho_{t} ha^{4} }}} } \right), D_{m} = \frac{{2E_{t} h^{3} }}{{3\left( {1 - v_{t}^{2} } \right)}}$$

(42)

To evaluate the accuracy of the results obtained for vibration and dynamic instability analyses of FG Porous doubly curved Panels, a comparison has been made with some published results (e.g. [9, 21, 31, 72,73,74]). In Table 1, a comparison between the obtained results and those reported in the references (Matsunaga. [72], Chorfi and Houmat [9]) for FGM curved shells under simply supported boundary conditions has been made. For this validation, the material of the shell is considered according to the mentioned references, $\left( {{\text{Al}}/{\text{Al}}_{2} {\text{O}}_{3} } \right)$. The thickness of the piezoelectric layers and porosity coefficient is considered $\left( {h_{p} = 10^{ - 10} {\text{m }}} \right)$ and $\left( {e = 10^{ - 10} { }} \right)$ in order to obtain a curved shell similar to the mentioned references with a very good approximation. As it can be found from Table 1, good correlation between the results of the present analysis and the results obtained in the previous references can be seen. Also, the flutter aerodynamic pressure $\lambda_{cr}$ and flutter frequency ${ }\left( {\omega_{cr} } \right)$ for an isotropic square plate have been compared with the results presented by Prakash and Ganapathi [74] and Akbari et al. [73] in Table 2. It should be mentioned that Akbari et al. [73] used the generalized differential quadrature method (GDQM) and Prakash and Ganapathi [74] used the finite element method (FEM) for flutter analysis.

Table 1 The comparison of the natural frequency, for a FGM $\left( {{\text{Al}}/{\text{Al}}_{2} {\text{O}}_{3} } \right)$ shell $\left( {\omega^{*} = \omega h\sqrt {\frac{\rho }{E}} , , a/h = 10, a/b = 1} \right)$

Table 2 The comparison of the flutter aerodynamic pressure $\lambda_{cr}$ and flutter frequency $\left( {\omega_{cr} } \right)$ for an isotropic square plate

The non-dimensional frequencies $\overline{\omega } = \omega h\sqrt {\rho_{m} /E_{m} }$ of an SCSC and SSSS FG porous plate for power-law indices, porosity distributions, thickness-side ratios, various aspect ratios and porosity parameters have been compared with the results have been provided by Rezaei et al. [21], in Table 3. In Table 4, the flutter frequency $\omega_{cr}$ and flutter aerodynamic pressure $\lambda_{cr}$ of SSSS, CSCS and CCCC porous plate $\left( {b/a = 1,\; h_{p} /2h = 0.05 \;\;{\text{and}}\; \;2h/a = 0.1} \right)$ have been compared with the results have been presented by Bahaadini et al. [31]. As can be seen from these tables, there is a good agreement between the presented results and the results of previous research. The material properties of FG porous core and piezoelectric layers are prepared in Tables 5 and 6. Then the flutter boundaries for this system are studied using the Galerkin method. Table 7 shows the influence of different types of porosity coefficients and power-law index on the flutter aerodynamic pressure and flutter frequency.  The effects of various piezoelectric layers, radii of principal curvatures of the middle surface $\left( {R_{x} ,R_{y} } \right),$ FG porous distributions, power-law index, porosity coefficient, doubly curved panel thickness, electrical conditions (open condition and closed condition) and mechanical boundary conditions on the flutter boundaries of FG porous doubly curved panel are studied in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. In Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. The diagrams show the boundary between dynamic stability and instability. In a stable area, these vibrations are dumped, ie the air acts as a damper, while in an unstable region, the oscillations grow exponentially, leading to a flutter phenomenon.

Table 3 The comparison of the non-dimensional frequency, $\overline{\omega } = \omega h\sqrt {\rho_{m} /E_{m} }$,$\frac{h}{a} = 0.05,\frac{a}{b} = 1$

Table 4 The comparison of flutter aerodynamic pressure and flutter frequency of symmetric porous plate $\left( {e_{0} = 0.35, 2h/a = 0.15} \right)$

Fig. 2

Flutter boundary versus $R_{x} /a$ for different circuit conditions for ($PZT - 4,\;b/a = 1,\;h_{p} /2h = 0.05,\; n = 1,\;e = 0.1$) a critical aerodynamic pressure, b critical frequency

Fig. 3

Flutter boundary versus $R_{x} /a$ for different Piezoelectric layers for ($b/a = 1,h_{p} /2h = 0.05, n = 1,e = 0.1$) a critical aerodynamic pressure, b critical frequency

Fig. 4

Flutter boundary versus $R_{x} /a$ for different mechanical boundary conditions for ($b/a = 1,\;h_{p} /2h = 0.05, n = 1,\;e = 0.1$) a critical aerodynamic pressure, b critical frequency

Fig. 5

Flutter boundary versus $R_{x} /a$ for the different power-law index for ($b/a = 1,\;h_{p} /2h = 0.05,\;e = 0.1$) a critical aerodynamic pressure, b critical frequency

Fig. 6

Flutter boundary versus $R_{x} /a$ for different porosity for ($b/a = 1,h_{p} /2h = 0.05,e = 0.1$) a critical aerodynamic pressure, b critical frequency

Fig. 7

Flutter boundary versus $R_{x} /a$ for different FG porous panels for ($h_{p} /2h = 0.05,\;e = 0.1$) a critical aerodynamic pressure, b critical frequency

Fig. 8

Flutter boundary versus $R_{x} /a$ for different $\left( {b/a} \right)$ for ($h_{p} /2h = 0.05,\;e = 0.1$) a critical aerodynamic pressure, b critical frequency

Fig. 9

Flutter boundary versus $R_{x} /a$ for different piezoelectric layer thickness for ($b/a = 1, n = 1,\;e = 0.1$) a flutter aerodynamic pressure, b flutter frequency

Fig. 10

Flutter boundary versus $R_{x} /a$ for different piezoelectric layer thickness for ($b/a = 1, n = 1,\;e = 0.1$) a flutter aerodynamic pressure, b flutter frequency

Fig. 11

Flutter boundary versus $e$ for a different curved panel for ($b/a = 1,\;h_{p} /2h = 0.05, n = 1,\; R_{x} /a = 10$) a critical aerodynamic pressure, b critical frequency

Table 5 The material properties of the piezoelectric layer

Table 6 Material properties of FG material

Table 7 The influence of different types of porosity coefficient and power-law index on the flutter aerodynamic pressure and flutter frequency of SSSS FG porous doubly curved panels (b⁄a = 1, ℎp⁄2ℎ = 0.05 and 2ℎ⁄a = 0.1)

In these figures, the effects of various piezoelectric layers, radii of principal curvatures of the middle surface $\left( {R_{x} ,R_{y} } \right),$ FG porous distributions and power-law index on the flutter boundaries of FG porous doubly curved panels are investigated.

In Fig. 2 The influences of open circuit conditions and closed circuit conditions on the flutter boundaries of FG porous doubly curved panels in supersonic flow are performed. It can be seen from Fig. 2 that the open circuit condition predicts a higher stability boundary than the closed circuit condition. The effects of different piezoelectric layers on the flutter boundaries of FG porous doubly curved panels are studied in Fig. 3. From Fig. 3, can be observed that the PZT – 4 predicts the highest flutter boundaries for the FG porous doubly curved panel. In Fig. 4, the effects of mechanical boundary conditions on the flutter boundaries of the system are investigated. It can be seen from Fig. 4 that the clamped boundary conditions predict the highest stability boundaries. It also has the least stability with simply supported boundary conditions. Figure  5 shows the effects of the power-law index on the flutter boundaries. It can be seen from Fig. 5 that increasing the power-law index reduces the stability. Figure 6 shows the influences of porosity coefficient on the flutter boundaries. It can be observed from Fig. 6 that increasing the porosity coefficient reduces the stability. The effects of panel dimensions on the flutter boundaries of FG porous doubly curved panels have been investigated in Figs. 7, 8, 9. Figure 7 indicates the variation of flutter boundaries for different aspect ratios. The results show that increasing the aspect ratios reduces the stability boundary. In Fig. 8, the influences of the core panel’s thickness on the stability of the system are studied. It can be observed from Fig. 8 that increasing the thickness-length ratios decreases the stability. Figure 9, shows the effects of piezoelectric layer thickness on the flutter boundaries. Examination of the results shows that increasing the thickness of the piezoelectric layer increases the stability of the system. The effects of different FG porous materials on the flutter boundaries of FG porous doubly curved panels are studied in Fig. 10. It is clear from Fig. 10 that the use of V distribution raises the flutter boundaries. Figure 11, shows the influences of a different curved panel on the flutter boundaries. A comparison of the curves in Fig. 11 shows that the spherical panel has the highest stability. Figure 10 shows that the stability boundary of the spherical panel is higher than that of the doubly curved panel $\left( {R_{y} = 2R_{x} } \right)$, cylindrical panel, $\left( {R_{y} = - R_{x} } \right)$ and plate.

5 Conclusion

In this study, the flutter boundaries for a doubly curved panel made of FG porous materials surrounded by piezoelectric layers subjected to supersonic flow have been investigated. The governing equations of motion are obtained from Hamilton’s principle and Maxwell’s equation. In this regard, first-order piston theory and Reddy’s third-order shear deformation theory are used. The Galerkin method is used to discretize the equations of motion. Based on the present research, the following results have been obtained:

• 1. A comparison of the spherical panel, doubly curved panel with ${R}_{y}=2{R}_{x}$ and ${R_{y} = - R_{x} }$, cylindrical panel, and plate shows that the spherical panel has the highest and the plate has the lowest stability regions.

• 2. As the radius to length of the panel increases, the critical flutter aerodynamic pressure increases and the flutter frequency decreases.

• 3. The open-circuit electrical boundary condition predicts a higher flutter boundary as well as a higher flutter frequency than the closed-circuit electrical boundary condition. Also, the highest and lowest critical flutter aerodynamic pressure and flutter frequency are related to CCCC and SSSS mechanical boundary conditions, respectively.

• 4. By examining three piezoelectric materials, the PZT-4 type has the highest flutter boundary and flutter frequency, and the PZT-5A type has the lowest critical flutter aerodynamic pressure and flutter frequency. Also, increasing the ratio of piezoelectric layer thickness to panel thickness increases the critical flutter aerodynamic pressure and flutter frequency.

• 5. The stability of the system decreases by increasing the thickness to length, the width-length ratio, the power law index and the porosity coefficient.

• 6. Examination of different material distributions shows that V-distribution predicts the highest flutter boundary and flutter frequency.

Appendices

Appendix A

In Eq. (20), the terms expressing inertia and the resulting forces and moments are expressed as follows:

$$\left( {I_{0} ,I_{1} ,I_{2} ,I_{3} ,I_{4} ,I_{6} } \right) = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \rho \left( z \right)\left( {1,z,z^{2} ,z^{3} ,z^{4} ,z^{6} } \right) dz$$

(A.1)

$$\begin{aligned} \left( {N_{xx} , N_{xy} ,N_{yy} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xx} , \sigma_{xy} ,\sigma_{yy} } \right) dz \\ \left( {M_{xx} , M_{xy} ,M_{yy} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xx} , \sigma_{xy} ,\sigma_{yy} } \right) zdz \\ \left( {Q_{x} ,Q_{y} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xz} , \sigma_{yz} } \right) dz \\ \left( {S_{xx} , S_{xy} ,S_{yy} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xx} , \sigma_{xy} ,\sigma_{yy} } \right) z^{3} dz \\ \left( {P_{x} ,P_{y} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xz} , \sigma_{yz} } \right)z^{2} dz \\ \end{aligned}$$

(A.2)

The stiffness coefficients are presented in Eq. (21) as follows:

$$\begin{aligned} \left( {A_{11} ,A_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} )dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right) dz \\ A_{66} & = \mathop \int \limits_{ - h}^{ - h} Q_{66}^{{}} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right) dz \\ \left( {B_{11} ,B_{12} ,B_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) z dz \\ \left( {C_{11} ,C_{12} ,C_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) cz^{3} dz \\ \left( {D_{11} ,D_{12} ,D_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) z^{2} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} ,\left( {\overline{c}_{11} - \overline{c}_{12} } \right)} \right) z^{2} dz \\ \left( {E_{11} ,E_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) \left( {z^{2} - cz^{4} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right)\left( {z^{2} - cz^{4} } \right) dz \\ E_{66} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right) \left( {z^{2} - cz^{4} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right)\left( {z^{2} - cz^{4} } \right) dz \\ \left( {F_{11} ,F_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) cz^{4} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right) cz^{4} dz + \eta_{3} \\ F_{66} & = 2\mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right) cz^{4} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right) cz^{4} dz \\ A_{55} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right)\left( {1 - \beta z^{2} } \right) dz + + 2\mathop \int \limits_{h}^{{h + h_{p} }} \overline{c}_{55} \left( {1 - \beta z^{2} } \right) dz \\ \left( {G_{11}, G_{12}, G_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) z^{3} dz \\ \left( {H_{11}, H_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) \left( {z^{4} - cz^{6} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right)\left( {z^{4} - cz^{6} } \right) dz \\ H_{66} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right)\left( {z^{4} - cz^{6} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right)\left( {z^{4} - cz^{6} } \right) dz \\ \left( {L_{11} ,L_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) cz^{6} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right) cz^{6} dz \\ L_{66} & = 2\mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right)cz^{6} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right)cz^{6} dz \\ S_{55} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{b} } \right)\left( {z^{2} - \beta z^{4} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \overline{c}_{55} \left( {z^{2} - \beta z^{4} } \right) dz \\ \end{aligned}$$

(A.3)

The constant quantities in Eq. (22), can be expressed as follow:

$$\begin{aligned} ab_{1} & = A_{{11}} + 2c\frac{{F_{{11}} }}{{R_{x} }} + c^{2} \frac{{H_{{11}} }}{{R_{x}^{2} }} + T_{2} - \frac{{T_{8} }}{{R_{x}^{2} }} + \beta \frac{{T_{{8z2}} }}{{R_{x}^{2} }} - c\frac{{T_{{4z3}} }}{{R_{x}^{2} }} \\ ab_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{x} }} + c^{2} \frac{{H_{{66}} }}{{R_{x}^{2} }} \\ ab_{3} & = \frac{1}{{R_{x}^{2} }}\left( {\beta D_{{55}} - A_{{55}} } \right) \\ ab_{4} & = A_{{12}} + A_{{66}} + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) \\ &\quad + \frac{c}{{R_{x} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ab_{5} & = B_{{11}} - cF_{{11}} + c\frac{{G_{{11}} }}{{R_{x} }} - c^{2} \frac{{H_{{11}} }}{{R_{x} }} + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ab_{6} & = B_{{66}} - c\left( {F_{{66}} - \frac{{G_{{66}} }}{{R_{x} }}} \right) - c^{2} \frac{{H_{{66}} }}{{R_{x} }} \\ ab_{7} & = \frac{1}{{R_{x} }}\left( {A_{{55}} - \beta D_{{55}} } \right) \\ ab_{8} & = B_{{12}} + B_{{66}} - c\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {G_{{12}} + G_{{66}} } \right)\\ &\quad - \frac{{c^{2} }}{{R_{x} }}\left( {H_{{12}} + H_{{66}} } \right) + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ab_{9} & = - c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ab_{{10}} & = - c\left( {F_{{12}} + 2F_{{66}} + \frac{c}{{R_{x} }}\left( {H_{{12}} + 2H_{{66}} } \right)} \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ab_{{11}} & = \frac{1}{{R_{x} }}\left( {A_{{11}} + A_{{55}} - \beta D_{{55}} + \frac{{cF_{{11}} }}{{R_{x} }} + \frac{{A_{{12}} R_{x} }}{{R_{y} }} + \frac{{cF_{{12}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ac_{1} & = A_{{21}} + A_{{66}} + \frac{c}{{R_{x} }}\left( {F_{{21}} + F_{{66}} } \right) + \frac{c}{{R_{y} }}\left( {F_{{21}} + F_{{66}} } \right) \\ &\quad + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{21}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ac_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{y} }} + c^{2} \frac{{H_{{66}} }}{{R_{y}^{2} }} \\ ac_{3} & = A_{{22}} + 2c\frac{{F_{{22}} }}{{R_{y} }} + c^{2} \frac{{H_{{22}} }}{{R_{y}^{2} }} + T_{2} + \frac{1}{{R_{y}^{2} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ac_{4} & = \frac{1}{{R_{y}^{2} }}\left( {\beta D_{{44}} - A_{{44}} } \right) \\ ac_{5} & = B_{{21}} + B_{{66}} - c\left( {F_{{21}} + F_{{66}} } \right) + \frac{c}{{R_{y} }}\left( {G_{{21}} + G_{{66}} } \right) \\ &\quad + \frac{1}{{R_{y} }}\left( {T_{7} + T_{8} } \right) - \frac{{c^{2} }}{{R_{y} }}\left( {H_{{21}} + H_{{66}} } \right) + \frac{1}{{R_{y} }}\left( { - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{4z3}} + T_{{3z3}} } \right)} \right) \\ ac_{6} & = B_{{66}} - cF_{{66}} + c\frac{{G_{{66}} }}{{R_{y} }} - c^{2} \frac{{H_{{66}} }}{{R_{y} }} \\ ac_{7} & = B_{{22}} - cF_{{22}} + c\frac{{G_{{22}} }}{{R_{y} }} - c^{2} \frac{{H_{{22}} }}{{R_{y} }} + \frac{1}{{R_{y} }}\left( {T_{7} + T_{8} } \right) \\ &\quad + \frac{1}{{R_{y} }}\left( { - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{4z3}} + T_{{3z3}} } \right)} \right) \\ ac_{8} & = \frac{1}{{R_{y} }}\left( {A_{{44}} - \beta D_{{44}} } \right) \\ ac_{9} & = - c\left( {2F_{{66}} + F_{{21}} + 2\frac{c}{{R_{y} }}H_{{66}} + \frac{c}{{R_{y} }}H_{{21}} } \right) + \frac{1}{{R_{y} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ac_{{10}} & = - c\left( {F_{{22}} + \frac{c}{{R_{y} }}H_{{22}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ac_{{11}} & = \frac{1}{{R_{y} }}\left( {A_{{21}} \frac{{R_{y} }}{{R_{x} }} + A_{{22}} + A_{{44}} - \beta D_{{44}} + \frac{{cF_{{21}} }}{{R_{x} }} + \frac{{cF_{{22}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ad_{1} & = B_{{11}} + \frac{c}{{R_{x} }}G_{{11}} - cF_{{11}} - \frac{{c^{2} }}{{R_{x} }}H_{{11}} + \frac{1}{{R_{x} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right)A_{{66}} \\& \quad + 2c\frac{{F_{{11}} }}{{R_{x} }} + c^{2} \frac{{H_{{11}} }}{{R_{x}^{2} }} + T_{2} - \frac{{T_{8} }}{{R_{x}^{2} }} + \beta \frac{{T_{{8z2}} }}{{R_{x}^{2} }} - c\frac{{T_{{4z3}} }}{{R_{x}^{2} }} \\ ad_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{x} }} + c^{2} \frac{{H_{{66}} }}{{R_{x}^{2} }} \\ ad_{3} & = \frac{1}{{R_{x}^{2} }}\left( {\beta D_{{55}} - A_{{55}} } \right) \\ ad_{4} & = A_{{12}} + A_{{66}} + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {F_{{12}} + F_{{66}} } \right) \\ &\quad + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ad_{5} & = B_{{11}} - cF_{{11}} + c\frac{{G_{{11}} }}{{R_{x} }} - c^{2} \frac{{H_{{11}} }}{{R_{x} }} + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ad_{6} & = B_{{66}} - c\left( {F_{{66}} - \frac{{G_{{66}} }}{{R_{x} }}} \right) - c^{2} \frac{{H_{{66}} }}{{R_{x} }} \\ ad_{7} & = \frac{1}{{R_{x} }}\left( {A_{{55}} - \beta D_{{55}} } \right) \\ ad_{8} & = B_{{12}} + B_{{66}} - c\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {G_{{12}} + G_{{66}} } \right) - \frac{{c^{2} }}{{R_{x} }}\left( {H_{{12}} + H_{{66}} } \right) \\ &\quad + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ad_{9} & = - c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ad_{{10}} & = - c\left( {F_{{12}} + 2F_{{66}} + \frac{c}{{R_{x} }}\left( {H_{{12}} + 2H_{{66}} } \right)} \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ad_{{11}} & = \frac{1}{{R_{x} }}\left( {A_{{11}} + A_{{55}} - \beta D_{{55}} + \frac{{cF_{{11}} }}{{R_{x} }} + \frac{{A_{{12}} R_{x} }}{{R_{y} }} + \frac{{cF_{{12}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ af_{1} & = A_{{21}} + A_{{66}} + \frac{c}{{R_{x} }}\left( {F_{{21}} + F_{{66}} } \right) + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) \\ &\quad + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right)A_{{66}} + 2c\frac{{F_{{11}} }}{{R_{x} }} + c^{2} \frac{{H_{{11}} }}{{R_{x}^{2} }} + T_{2} - \frac{{T_{8} }}{{R_{x}^{2} }} + \beta \frac{{T_{{8z2}} }}{{R_{x}^{2} }} - c\frac{{T_{{4z3}} }}{{R_{x}^{2} }} \\ af_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{x} }} + c^{2} \frac{{H_{{66}} }}{{R_{x}^{2} }} \\ af_{3} & = \frac{1}{{R_{x}^{2} }}\left( {\beta D_{{55}} - A_{{55}} } \right) \\ af_{4} & = A_{{12}} + A_{{66}} + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ af_{5} & = B_{{11}} - cF_{{11}} + c\frac{{G_{{11}} }}{{R_{x} }} - c^{2} \frac{{H_{{11}} }}{{R_{x} }} + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ af_{6} & = B_{{66}} - c\left( {F_{{66}} - \frac{{G_{{66}} }}{{R_{x} }}} \right) - c^{2} \frac{{H_{{66}} }}{{R_{x} }} \\ af_{7} & = \frac{1}{{R_{x} }}\left( {A_{{55}} - \beta D_{{55}} } \right) \\ af_{8} & = B_{{12}} + B_{{66}} - c\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {G_{{12}} + G_{{66}} } \right) - \frac{{c^{2} }}{{R_{x} }}\left( {H_{{12}} + H_{{66}} } \right) \\ &\quad + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ af_{9} & = - c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ af_{{10}} & = - c\left( {F_{{12}} + 2F_{{66}} + \frac{c}{{R_{x} }}\left( {H_{{12}} + 2H_{{66}} } \right)} \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ af_{{11}} & = \frac{1}{{R_{x} }}\left( {A_{{11}} + A_{{55}} - \beta D_{{55}} + \frac{{cF_{{11}} }}{{R_{x} }} + \frac{{A_{{12}} R_{x} }}{{R_{y} }} + \frac{{cF_{{12}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ag_{1} & = \frac{1}{{R_{x} }}\left( { - A_{{55}} + \beta D_{{55}} - A_{{11}} - \frac{c}{{R_{x} }}F_{{11}} - \frac{{R_{x} }}{{R_{y} }}A_{{21}} - \frac{c}{{R_{y} }}F_{{21}} } \right) - T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ag_{2} & = c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{3} & = c\left( {2F_{{66}} + 2\frac{c}{{R_{x} }}H_{{66}} + F_{{21}} + \frac{c}{{R_{x} }}H_{{21}} } \right) + \frac{1}{{R_{x} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{4} & = \frac{1}{{R_{y} }}\left( { - A_{{44}} + \beta D_{{44}} - A_{{22}} - \frac{c}{{R_{x} }}F_{{12}} - \frac{{R_{y} }}{{R_{x} }}A_{{12}} - \frac{c}{{R_{y} }}F_{{22}} } \right) - T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ag_{5} & = c\left( {F_{{12}} + \frac{c}{{R_{y} }}H_{{12}} + 2F_{{66}} + 2\frac{c}{{R_{y} }}H_{{66}} } \right) + \frac{1}{{R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{6} & = c\left( {F_{{22}} + \frac{c}{{R_{y} }}H_{{22}} } \right) + \frac{1}{{R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{7} & = A_{{55}} - \beta D_{{55}} - \frac{{B_{{11}} }}{{R_{x} }} + \frac{c}{{R_{x} }}F_{{11}} - \frac{{B_{{21}} }}{{R_{y} }} + \frac{c}{{R_{y} }}F_{{21}} \\ ag_{8} & = c\left( {G_{{12}} - cH_{{11}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{9} & = c\left( {2G_{{66}} - 2cH_{{66}} + G_{{21}} - cH_{{21}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{{10}} & = A_{{44}} - \beta D_{{44}} - \frac{{B_{{12}} }}{{R_{x} }} + \frac{c}{{R_{x} }}F_{{12}} - \frac{{B_{{22}} }}{{R_{y} }} + \frac{c}{{R_{y} }}F_{{22}} \\ ag_{{11}} & = c\left( {G_{{22}} - cH_{{22}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{{12}} & = c\left( {2G_{{66}} - 2cH_{{66}} + G_{{12}} - cH_{{12}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{{13}} & = - c^{2} H_{{11}} + T_{8} - \beta T_{{8z2}} + cT_{{4z3}} \\ ag_{{14}} & = - c^{2} H_{{22}} + T_{8} - \beta T_{{8z2}} + cT_{{4z3}} \\ ag_{{15}} & = - c^{2} \left( {4H_{{66}} + H_{{21}} + H_{{12}} } \right) + 2T_{8} - 2\beta T_{{8z2}} + 2cT_{{4z3}} \\ ag_{{16}} & = A_{{55}} - \beta D_{{55}} + 2\frac{c}{{R_{x} }}F_{{11}} + \frac{c}{{R_{y} }}\left( {F_{{21}} + F_{{12}} } \right) \\ ag_{{17}} & = A_{{44}} - \beta D_{{44}} + 2\frac{c}{{R_{y} }}F_{{22}} + \frac{c}{{R_{x} }}\left( {F_{{21}} + F_{{12}} } \right) \\ ag_{{18}} & = - \left( {\frac{{A_{{11}} }}{{R_{x}^{2} }} + \frac{1}{{R_{x} R_{y} }}\left( {A_{{12}} + A_{{21}} } \right) + \frac{{A_{{22}} }}{{R_{y}^{2} }}} \right) - T_{2} \left( {\frac{1}{{R_{x}^{2} }} + \frac{1}{{R_{x} R_{y} }}} \right) - T_{2} \left( {\frac{1}{{R_{y}^{2} }} + \frac{1}{{R_{x} R_{y} }}} \right) \\ \end{aligned}$$

(A.4)

For open-circuit condition:

$$\begin{aligned} T_{1} & = \bar{e}_{{31}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi ^{t} }}{{\partial z}}~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\partial \varphi ^{b} }}{{\partial z}}~dz} \right) \\ T_{2} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}~dz \\ T_{3} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )~dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )~dz \\ T_{4} & = - \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}c(h + h_{p} )^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}c(h + h_{p} )^{3} ~dz \\ T_{5} & = e_{{15}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi ^{t} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \varphi ^{b} ~dz} \right) \\ T_{6} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)dz} \right) \\ T_{7} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)dz} \right) \\ T_{8} & = c\frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)^{3} \left( { - \mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)dz} \right) \\ T_{{1z}} & = \bar{e}_{{31}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi ^{t} }}{{\partial z}}z~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\partial \varphi ^{b} }}{{\partial z}}z~dz} \right) \\ T_{{2z}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z~dz \\ T_{{3z}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z~dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z~dz \\ T_{{4z}} & = - \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz(h + h_{p} )^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz(h + h_{p} )^{3} ~dz \\ T_{{1z3}} & = \bar{e}_{{31}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi ^{t} }}{{\partial z}}z^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\partial \varphi ^{b} }}{{\partial z}}z^{3} ~dz} \right) \\ T_{{2z3}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z^{3} ~dz \\ T_{{3z3}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z^{3} ~dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z^{3} ~dz \\ T_{{4z3}} & = - \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz^{3} (h + h_{p} )^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz^{3} (h + h_{p} )^{3} ~dz \\ T_{{5z2}} & = e_{{15}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} z^{2} \varphi ^{t} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} z^{2} \varphi ^{b} ~dz} \right) \\ T_{{6z2}} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)z^{2} dz} \right) \\ T_{{7z2}} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)z^{2} dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)z^{2} dz} \right) \\ T_{{8z2}} & = c\frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)^{3} \left( { - \mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)z^{2} dz} \right) \\ \end{aligned}$$

(A.5)

and for closed-circuit condition:

$$\begin{aligned} T_{1} & = \overline{e}_{31} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi^{t} }}{\partial z} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{\partial \varphi^{b} }}{\partial z} dz} \right), \\ T_{5} & = e_{15} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right), \\ T_{1z} & = \overline{e}_{31} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi^{t} }}{\partial z}z dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{\partial \varphi^{b} }}{\partial z}z dz} \right), \\ T_{1z3} & = \overline{e}_{31} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi^{t} }}{\partial z}z^{3} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{\partial \varphi^{b} }}{\partial z}z^{3} dz} \right), \\ T_{5z2} & = e_{15} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} z^{2} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} z^{2} \varphi^{b} dz} \right) \\ T_{2} & = T_{3} = T_{4} = T_{6} = T_{7} = T_{8} = T_{2z} = T_{3z} = T_{4z} = T_{2z3} = T_{3z3} = T_{4z3} = T_{6z2} = T_{7z2} = T_{8z2} = 0, \\ \end{aligned}$$

(A.6)

Appendix B

In Eq. (26), the definitions of constant quantities are expressed as follows:

For open-circuit condition:

$$\begin{aligned} \varphi^{t} & = 1 - \left( {\frac{{z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} , \varphi^{b} = 1 - \left( {\frac{{ - z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} \\ S_{1} & = \mathop \int \limits_{h}^{{h + h_{p} }} e_{15} \left( {1 - \beta z^{2} } \right) dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} e_{15} \left( {1 - \beta z^{2} } \right) dz \\ S_{2} & = {\Xi }_{11} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right) \\ S_{3} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} dz \\ S_{4} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} \beta z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} \beta z^{2} dz \\ S_{5} & = {\overline{\Xi }}_{33} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{d^{2} \varphi^{t} }}{{dz^{2} }} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{d^{2} \varphi^{b} }}{{dz^{2} }} dz} \right) \\ S_{6} & = S_{7} = S_{8} = 0 \\ \end{aligned}$$

(B.1)

and for closed-circuit condition:

$$\begin{aligned} \varphi^{t} & = 1 + \frac{{4\left( {z - h} \right)}}{{h_{p} }} - \left( {\frac{{z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} \\ \varphi^{b} & = 1 - \frac{{4\left( {z + h} \right)}}{{h_{p} }} - \left( {\frac{{ - z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} \\ S_{1} & = \mathop \int \limits_{h}^{{h + h_{p} }} e_{15} \left( {1 - \beta z^{2} } \right) dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} e_{15} \left( {1 - \beta z^{2} } \right) dz \\ S_{2} & = {\Xi }_{11} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right) \\ S_{3} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} dz \\ S_{4} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} \beta z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} \beta z^{2} dz \\ S_{5} & = {\overline{\Xi }}_{33} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right) \\ S_{6} & = \frac{{{\Xi }_{11} \overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \left( {z + h} \right)dz} \right) \\ S_{7} & = \frac{{{\Xi }_{11} \overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left( {h + h_{p} } \right)\left( { - \mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \left( {z + h} \right)dz} \right) \\ S_{8} & = \frac{{{\Xi }_{11} \overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left( {h + h_{p} } \right)^{3} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz - \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \left( {z + h} \right)dz} \right) \\ \end{aligned}$$

(B.2)