Dynamic response of open doubly curved sandwich shells with soft core subjected to a moving force

Abstract

This paper presents a forced vibration analysis of open doubly curved sandwich panels subjected to a moving constant force. In this paper, the effect of softness of the core is considered by implementing a semi-layerwise theory. To this aim, the first-order shear deformation theory is adopted for the face sheets and a higher-order theory which was obtained based on 3D elasticity theory is considered for the core. The presented formulation is general and as the deepness parameter is accounted in the strain–displacement relations, the formulation can be used for a wide range of deep as well as shallow doubly curved shells. To obtain the dynamic response of the system, the finite element method (FEM) along with the Newmark method is used. The proposed element is a higher-order one with nine nodes and each node has fifteen degrees of freedom. The effect of various parameters such as length-to-thickness ratio, in-plane aspect ratio, boundary conditions, lamination scheme, and fiber orientation angles on the dynamic response of the structure is examined. Additionally, the critical velocity of the force at which the structure experiences maximum dynamic deflection is obtained in each case. The results show that as the length-to-thickness ratio of the structure increases, the dynamic magnification factor curve increases with respect to non-dimensional velocity. This study provides insights into the dynamic behavior of doubly curved sandwich panels with soft cores and can aid in the design of such structures for specific applications. The results of this study can also serve as a benchmark for future studies on the forced vibration behavior of doubly curved sandwich panels.

1 Introduction

Sandwich panels are widely used in various engineering applications due to their high strength- and stiffness-to-weight ratios, and thermal and acoustic insulation properties. Sandwich panels with soft core are commonly used in various industries due to their desirable properties, where they are subjected to various types of dynamic loading conditions, including moving forces. Therefore, understanding the dynamic behavior of these structures is of great importance in the design and analysis. Dynamic analysis of sandwich panels is essential to ensure their safe and reliable operation subjected to various dynamic loads. The analysis typically involves predicting the structure's natural frequencies, mode shapes, and response amplitudes under different loading conditions. The dynamic response of sandwich panels can be affected by various factors such as the panel's geometry, boundary conditions, and the type of loading. The analysis can be performed using analytical or numerical methods, such as the finite element method (FEM), which can provide accurate and detailed predictions of the panel's behavior under dynamic loads. The results of dynamic analysis can be used to optimize the panel's design, identify potential failure modes, and develop guidelines and standards for the design and testing of sandwich panels. Additionally, the analysis can aid in the selection of appropriate materials and core structures to ensure the panel's safe and reliable operation under dynamic loads.

Free vibration analysis of sandwich panels with soft core has received significant attention in recent years due to their excellent mechanical properties and potential applications in various industries. In terms of free vibration analysis, Joseph and Mohanty [1] studied the free vibration of sandwich plates with viscoelastic core and functionally graded face sheets using FEM. Malekzadeh et al. [2] utilized an improved high-order sandwich plate theory and introduced a double Fourier series set of functions to investigate the vibration characteristics of composite sandwich panels with a viscoelastic core and arbitrary boundary conditions. Tian et al. [3] presented an analytical solution for the static and vibration analysis of sandwich plates with a soft core. They employed Navier-type solutions for both free vibration analysis and static bending under sinusoidal and uniformly distributed loads. Ghavidel et al. [4] studied the free vibration of cylindrical sandwich panels based on the first-order shear deformation theory of thick cylindrical shells referred to by Qatu (FSDTQ). They presented an analytical solution for simply supported boundary conditions, and the generalized differential quadrature method was used for other boundary conditions. Sahu et al. [5] examined the vibration and damping characteristics of doubly curved sandwich shells. They used a first-order shear deformation theory and assumed a viscoelastic core with functionally graded face sheets. Finite element analysis was employed to study the normal and shear deformations of the viscoelastic core. Chalak et al. [6] developed a ${C}_{0}$ two-dimensional finite element model to investigate the free vibration of laminated composite and sandwich plates based on the higher-order zigzag plate theory. Kant and Swaminathan [7, 8] conducted free vibration analysis of cross-ply laminated composite and sandwich plates based on higher-order shear and normal deformation theory. Belarbi et al. [9] created a higher-order layerwise finite element model utilizing a four-noded ${C}^{0}$ continuous isoparametric element to study the free vibration behavior of multilayer sandwich plates, assuming a first-order shear deformation theory for the face sheets and a higher-order shear deformation theory for the core. Bacciocchi et al. [10] used a nine-node quadratic rectangular element and the Reissner–Mindlin zigzag theory to investigate the natural frequencies of sandwich plates. Biswal and Mohanty [11] employed FEM to investigate the free vibration and damping characteristics of multilayer sandwich spherical shells with viscoelastic core and elastic face sheets based on the first-order shear deformation theory using an eight-noded element with fifteen degrees of freedom per node. Karakoti et al. [12] proposed a layerwise finite element formulation based on the first-order shear deformation theory for each layer to analyze the dynamic behavior of functionally graded material sandwich shell in thermal and non-thermal environments. Lastly, Hirane et al. [13] introduced an eight-noded quadrilateral ${C}^{0}$ element to analyze the static and free vibration analyses of FGM sandwich plates, assuming a higher-order displacement field for the core and first-order displacement field for the face sheets while maintaining continuity of displacement at layer interfaces.

When it comes to forced vibration analysis, Alambeigi et al. [14] analyzed the free and forced vibration of a sandwich beam considering porous core and SMA hybrid composite face layers. They employed first-order shear deformation theory in their analysis and the analytical solution was presented to solve the equations of motion using Navier’s solution. Chanda and Sahoo [15] conducted a study on the static and dynamic responses of simply supported sandwich plates. They employed the non-polynomial zigzag theory as their analytical framework. To find the solutions, they utilized Navier's solution technique along with Newmark's time integration scheme. Kapuria and Kulkarni [16] investigated the transient response of smart sandwich plates with electroded piezoelectric sensors and actuators based on a coupled improved zigzag theory. They employed quadrilateral elements with four physical nodes and one electrical node in their analysis. Wang et al. [17] investigated the dynamic response of asymmetric sandwich plates with metal foam core subjected to blast loading analytically and numerically. Higher-order dynamic response of composite sandwich panels with flexible core under simultaneous low-velocity impacts of multiple small masses was investigated by Malekzadeh et al. [18]. To model the compressibility of the core, they employed first-order Shear deformation theory for the face sheets while three-dimensional elasticity was used to model the soft core. Wang et al. [19] investigated the transient response of doubly curved composite shallow shells reinforced with graphene nanoplatelets under blast loads. The equations of motion were derived using Hamilton's principle and nonlinear strain–displacement relations of the von Karman type were employed. The influence of various parameters, such as the temperature difference between the upper and lower face sheets, length-to-thickness ratio, and shell depth, was analyzed. Yang and Qiao [20] presented a higher-order impact model to simulate the response of sandwich structures with flexible core. In this paper, the results were validated with a 3D finite element model obtained using commercial software such as ABAQUS and LS-DYNA. Fatt and Sirivolu [21] developed an analytical model to predict the response of a composite sandwich shell with PVC foam core under blast loading. They used Donnell's nonlinear shallow shell formulation and modeled the PVC foam core with isotropic and transversely isotropic elastic–plastic properties. Using higher-order sandwich panels theory, Khanjani et al. [22] investigated the effects of core thickness, radius of curvature, and sector angle on the static and dynamic response of composite cylindrical sandwich panels. In this paper, the Newmark method was implemented to obtain the dynamic response of the system. Katariya and Panda [23] computed static deflection, frequency and transient responses of the layered sandwich shell under various mechanical loading conditions. Mirfatah et al. [24] investigated the geometrical nonlinear dynamic behavior of shallow sandwich panels under various periodic and impulsive loadings. Sankar et al. [25] studied the vibration of doubly curved sandwich shells subjected to in-plane periodic load. In this paper, the problem of parametrically excited structure was investigated using QUAD-8 element which was developed using higher-order shear flexible theory. Using the finite element method, Biswal and Mohanty [26] investigated the static and dynamic stability of spherical sandwich shell panels with viscoelastic material core and laminated composite face sheets under uniaxial and biaxial harmonic excitations. Wattanasakulpong and Eiadtrong [27] investigated the transient responses of sandwich plates with a functionally graded porous core subjected to time-dependent loads. The study employed the first-order shear deformation theory (FSDT) to derive the equations of motion. The solution to these equations utilized the Ritz method with Jacobi polynomials for admissible displacements, coupled with the time integration of Newmark, providing insight into the dynamic response of the plates.

In the case of nonlinear dynamics, Songsuwan et al. [28] performed a nonlinear analysis of free and forced vibrations in FG-GPLRC beams subjected to time-dependent forces. The study was based on the third-order shear deformation theory, the equations were solved using the Ritz method while the Gram–Schmidt process was applied to derive admissible functions. Quan and Duc [29] provided analytical solutions for the nonlinear vibration of a porous functionally graded sandwich plate exposed to a blast load. The study employed Reddy's higher-order shear deformation theory with von Kármán type nonlinearity to formulate the governing equations for plate vibration. The obtained results were achieved through the application of the Galerkin method and the fourth-order Runge–Kutta method. Cong et al. [30] investigated nonlinear dynamic behavior of doubly curved shallow shells with negative Poisson’s ratios in auxetic honeycombs on elastic foundations subjected blast, mechanical and damping loads. employing Reddy’s third-order shear deformation theory with von Kármán type nonlinearity to formulate the governing equations for plate vibration. The obtained results were obtained using the Galerkin method and the fourth-order Runge–Kutta method. Nguyen et al. [31] presented an analytical solution to investigate nonlinear dynamic of imperfect functionally graded carbon nanotube reinforced composite (FG-CNTRC) double curved shallow shells subjected to blast load and temperature. In their paper, the higher-order shear deformation theory was used, and Galerkin method and fourth-order Runge–Kutta method were used to solve the problem.

In the case of moving loads, Song et al. [32] conducted research on the dynamic behavior of sandwich beams and plates, specifically focusing on those with isotropic face sheets and a viscoelastic core subjected to moving loads. They proposed the extended Rayleigh–Ritz solution along with the penalty method, and the differential quadrature method. Songsuwan et al. [33] explored the nonlinear transient response of sandwich beams featuring a functionally graded porous core under a moving load. The study employed Reddy's third-order shear deformation theory and incorporated the geometrical nonlinearity of the von Kármán assumption to formulate the governing equation system. Kiani [34, 35] examined the dynamic response of functionally graded composite cylindrical and conical panels under the influence of moving loads. The kinematics of the shell were formulated using the first-order shear deformation theory. The dynamic equations of the system were obtained using the Ritz method, wherein the shape functions were determined using the Gram–Schmidt process. The Newmark time marching scheme was employed to determine the system's response. Bahranifard et al. [36] investigated the dynamic responses of sandwich truncated conical shells with face sheets reinforced by graphene platelets composite (GPLRC), a porous core, and circumferential stiffeners when subjected to asymmetric internal ring-shaped moving loads. The equations of motion were derived based on the first-order shear deformation theory (FSDT) using the Chebyshev–Ritz method. The Newmark’s time integration scheme was used to solve the resulting ordinary differential equations of motion.

The review of the available literature shows that there has been no investigation into the dynamic analysis of doubly curved sandwich panels with a flexible core under the action of a moving load. This paper seeks to fill this gap by analyzing the influence of a constant amplitude moving force on the vibration characteristics of sandwich panels, taking into account the softness of the core material using finite element method (FEM). For this purpose, a new higher-order finite element with nine nodes which was presented by the authors [37] is used. The proposed element offers a significant advantage by considering the softness of the core, a critical parameter in sandwich structures. In this work, a semi-layerwise displacement field is introduced, employing the first-order shear deformation theory (FSDT) for the face sheets and a higher-order displacement field for the core. This innovative approach captures the softness term of the core in the analysis, providing a more accurate representation than previous equations. Indeed, using this element, it would be possible to model delaminated sandwich structures considering various delamination thickness-wise positions. In terms of disadvantages, the introduction of a semi-layerwise displacement field and consideration of the core's softness, while advantageous, may increase computational complexity. This could impact the computational resources required for analysis, particularly for larger and more intricate models. The obtained results based on the presented formulation are verified against the results obtained from the free vibration analysis of the structure, previously reported in the literature. The study examines the influence of various factors including side-to-thickness ratio, and boundary conditions, in-plane aspect ratio, the radius of curvature, lamination scheme, and fiber orientation angle. The critical velocity is reported in each case.

2 Kinematics

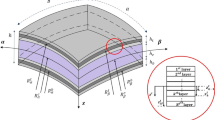
This study examines a doubly curved open shell, depicted in Fig. 1, consisting of three main layers. The core layer, with a thickness of ${h}_{c}$, is sandwiched between two thin laminated composite face sheets: the top and the bottom face sheets, with thicknesses of ${h}_{t}$ and ${h}_{b}$ and a total number of layers of ${N}_{t}$ and ${N}_{b}$, respectively. The panel has a length of $a$, a width of $b$, and a total thickness of $h={h}_{t}+{h}_{c}+{h}_{b}$. A global orthogonal curvilinear coordinate system, $O\alpha \beta z$, is chosen with its origin located at a vertex of the mid-surface ($z=0$). The $\alpha$- and $\beta$-axes align with the panel's length and width directions, respectively, while the $z$-axis is perpendicular to the mid-surface. Additionally, local coordinate systems with normal axes ${z}_{i}$ ($i=t, c, b$) are considered, with their origins at the mid-surfaces of the top face sheet, core, and bottom face sheet, respectively, parallel to the global $z$-axis. ${R}_{\alpha }^{i}$, and ${R}_{\beta }^{i}$ ($i=t, c, b$) represent the principal radii of curvature in the $\alpha$ and $\beta$ directions, respectively. For cylindrical panels, ${R}_{\alpha }=R$ and ${R}_{\beta }=\infty$, for spherical panels ${R}_{\alpha }={R}_{\beta }=R$, and for plates ${R}_{\alpha }={R}_{\beta }=\infty$, where $R$ is the radius of curvature. It is important to note that in all the notations that follow, the indices $t$, $c$, and $b$ refer to the top face sheet, the core, and the bottom face sheet, respectively.

Fig. 1

Schematic view of general doubly curved shell

To consider the boundary conditions, elastic restraints are assumed to be present on the panel's contour. The distributed elastic springs' constants are denoted by ${k}_{d}^{\alpha =0}$; ${k}_{d}^{\alpha =a}$; ${k}_{d}^{\beta =0}$; and ${k}_{d}^{\beta =b}$ for edge $\alpha =0$, $\alpha =a$, $\beta =0$ and $\beta =b$, respectively, in which $d$ denote the degrees of freedom of the system:

$$d \in \left\{ {u_{0}^{t} , \psi_{\alpha }^{t} , v_{0}^{t} , \psi_{\beta }^{t} , w_{0}^{t} , u_{0}^{b} , \psi_{\alpha }^{b} , v_{0}^{b} , \psi_{\beta }^{b} , w_{0}^{b} , u_{0} , u_{1} , v_{0} , v_{1} , w_{0} } \right\}$$

(1)

It should be noted that by simulating the boundary conditions using virtual springs, each degree of freedom can be fixed or free by letting ${k}_{d}=0$ or ${k}_{d}=\infty$, respectively. Consequently, cases of clamped, simply supported, free and elastically restrained edges can be considered using this method.

The face sheets are relatively thin and the first-order shear deformation theory is employed to represent the displacement field of them. This theory assumes that the displacement field at any arbitrary time $t$ can be estimated as follows:

$$\begin{aligned} & u_{i} \left( {\alpha ,\beta ,z_{i} } \right) = u_{0}^{i} \left( {\alpha ,\beta } \right) + z_{i} \psi_{\alpha }^{i} \left( {\alpha ,\beta } \right) \\ & v_{i} \left( {\alpha ,\beta ,z_{i} } \right) = v_{0}^{i} \left( {\alpha ,\beta } \right) + z_{i} \psi_{\beta }^{i} \left( {\alpha ,\beta } \right), \quad i = t,b \\ & w_{i} \left( {\alpha ,\beta ,z_{i} } \right) = w_{0}^{i} \left( {\alpha ,\beta } \right) \\ \end{aligned}$$

(2)

in which the displacement components ${u}_{i}$, ${v}_{i}$, and ${w}_{i}$ represent the displacements along the $\alpha$, $\beta$, and ${z}_{i}$ directions, respectively. The in-plane displacements of the middle surface of the top and bottom face sheets are represented by ${u}_{0}^{i}$ and ${v}_{0}^{i}$, respectively, while ${w}_{0}^{i}$ represents the transverse displacement. The rotation angles of the transverse normal about the $\beta$- and $\alpha$-directions are represented by ${\psi }_{\alpha }^{i}$ and ${\psi }_{\beta }^{i}$, respectively.

Based on EHSAPT, the displacement field of the core is formulated based on the 3D elasticity theory by considering the following displacement field [38]:

$$\begin{aligned} & u_{c} \left( {\alpha ,\beta ,z_{c} } \right) = u_{0} \left( {\alpha ,\beta } \right) + z_{c} u_{1} \left( {\alpha ,\beta } \right) + z_{c}^{2} u_{2} \left( {\alpha ,\beta } \right) + z_{c}^{3} u_{3} \left( {\alpha ,\beta } \right) \\ & v_{c} \left( {\alpha ,\beta ,z_{c} } \right) = v_{0} \left( {\alpha ,\beta } \right) + z_{c} v_{1} \left( {\alpha ,\beta } \right) + z_{c}^{2} v_{2} \left( {\alpha ,\beta } \right) + z_{c}^{3} v_{3} \left( {\alpha ,\beta } \right) \\ & w_{c} \left( {\alpha ,\beta ,z_{c} } \right) = w_{0} \left( {\alpha ,\beta } \right) + z_{c} w_{1} \left( {\alpha ,\beta } \right) + z_{c}^{2} w_{2} \left( {\alpha ,\beta } \right) \\ \end{aligned}$$

(3)

where ${u}_{c}$, ${v}_{c}$ and ${w}_{c}$ represent the displacement components of the core along $\alpha$, $\beta ,$ and ${z}_{c}$ directions, respectively. Additionally, ${u}_{i}$, ${v}_{i}$ and ${w}_{j}$ ($i=0, 1, 2, 3$ and $j=0, 1, 2$) represent the in-plane and transverse displacements of the core's mid-surface.

The strain–displacement relationships in orthogonal curvilinear coordinates can be expressed linearly as follows:

$$\begin{aligned} & \varepsilon_{\alpha } = \frac{1}{{A\left( {1 + z/R_{\alpha } } \right)}}\left( {\frac{\partial u}{{\partial \alpha }} + \frac{\partial A}{{\partial \beta }}\frac{v}{B} + \frac{Aw}{{R_{\alpha } }}} \right) \\ & \varepsilon_{\beta } = \frac{1}{{B\left( {1 + z/R_{\beta } } \right)}}\left( {\frac{\partial v}{{\partial \beta }} + \frac{\partial B}{{\partial \alpha }}\frac{u}{A} + \frac{Bw}{{R_{\beta } }}} \right) \\ & \varepsilon_{z} = \frac{\partial w}{{\partial z}} \\ & \gamma_{\alpha z} = \frac{1}{{A\left( {1 + z/R_{\alpha } } \right)}}\frac{\partial w}{{\partial \alpha }} + A\left( {1 + z/R_{\alpha } } \right)\frac{\partial }{\partial z}\left( {\frac{u}{{A\left( {1 + z/R_{\alpha } } \right)}}} \right) \\ & \gamma_{\beta z} = \frac{1}{{B\left( {1 + z/R_{\beta } } \right)}}\frac{\partial w}{{\partial \beta }} + B\left( {1 + z/R_{\beta } } \right)\frac{\partial }{\partial z}\left( {\frac{v}{{B\left( {1 + z/R_{\beta } } \right)}}} \right) \\ & \gamma_{\alpha \beta } = \frac{1}{{A\left( {1 + z/R_{\alpha } } \right)}}\left( {\frac{\partial v}{{\partial \alpha }} - \frac{\partial A}{{\partial \beta }}\frac{u}{B}} \right) + \frac{1}{{B\left( {1 + z/R_{\beta } } \right)}}\left( {\frac{\partial u}{{\partial \beta }} - \frac{\partial B}{{\partial \alpha }}\frac{v}{A}} \right) \\ \end{aligned}$$

(4)

where normal strains are represented by ${\varepsilon }_{\alpha }$, ${\varepsilon }_{\beta }$ and ${\varepsilon }_{z}$, and shear strains are represented by ${\gamma }_{\alpha z}$, ${\gamma }_{\beta z}$ and ${\gamma }_{\alpha \beta }$. The parameters $A$ and $B$ are Lamé parameters that allow for the consideration of various shell geometries. In the following sections, these parameters may be used with subscripts “$t$,” “$c$,” and “$b$” which refer to lamé parameters of the top, the core, and the bottom layers. By substituting the displacement fields into Eq. (4), the strain–displacement relations for each layer can be obtained. These relations can be written concisely in terms of mid-surface generalized strains as follows:

For the top and bottom layers ($i=t,b$),

$$\begin{aligned} & \varepsilon_{\alpha }^{i} = \frac{1}{{\left( {1 + z_{i} /R_{\alpha }^{i} } \right)}}\left( {\varepsilon_{0\alpha }^{i} + z_{i} \kappa_{\alpha }^{i} } \right) \\ & \varepsilon_{\beta }^{i} = \frac{1}{{\left( {1 + z_{i} /R_{\beta }^{i} } \right)}}\left( {\varepsilon_{0\beta }^{i} + z_{i} \kappa_{\beta }^{i} } \right) \\ & \varepsilon_{z}^{i} = \varepsilon_{0z}^{i} \\ & \gamma_{\alpha z}^{i} = \frac{{\gamma_{0\alpha z}^{i} }}{{\left( {1 + z_{i} /R_{\alpha }^{i} } \right)}} \\ & \gamma_{\beta z}^{i} = \frac{{\gamma_{0\beta z}^{i} }}{{\left( {1 + z_{i} /R_{\beta }^{i} } \right)}} \\ & \gamma_{\alpha \beta }^{i} = \frac{1}{{\left( {1 + z_{i} /R_{\alpha }^{i} } \right)}}\left( {\varepsilon_{0\alpha \beta }^{i} + z_{i} \kappa_{\alpha \beta }^{i} } \right) + \frac{1}{{\left( {1 + z_{i} /R_{\beta }^{i} } \right)}}\left( {\varepsilon_{0\beta \alpha }^{i} + z_{i} \kappa_{\beta \alpha }^{i} } \right) \\ \end{aligned}$$

(5)

For the core layer,

$$\begin{aligned} \varepsilon_{\alpha }^{c} &= \frac{1}{{A_{c} \left( {1 + z_{c} /R_{\alpha }^{c} } \right)}}\left( {\varepsilon_{0\alpha }^{c} + z_{c} \varepsilon_{1\alpha }^{c} + z_{c}^{2} \varepsilon_{2\alpha }^{c} + z_{c}^{3} \varepsilon_{3\alpha }^{c} } \right) \\ \varepsilon_{\beta }^{c} &= \frac{1}{{B_{c} \left( {1 + z_{c} /R_{\beta }^{c} } \right)}}\left( {\varepsilon_{0\beta }^{c} + z_{c} \varepsilon_{1\beta }^{c} + z_{c}^{2} \varepsilon_{2\beta }^{c} + z_{c}^{3} \varepsilon_{3\beta }^{c} } \right) \\ \varepsilon_{z}^{c} &= \varepsilon_{0z}^{c} + z_{c} \varepsilon_{1z}^{c} \\ \gamma_{\alpha z}^{c}& = \frac{1}{{A_{c} \left( {1 + z_{c} /R_{\alpha }^{c} } \right)}}\left( {\gamma_{0\alpha z}^{c} + z_{c} \gamma_{1\alpha z}^{c} + z_{c}^{2} \gamma_{2\alpha z}^{c} + z_{c}^{3} \gamma_{3\alpha z}^{c} } \right) \\ \gamma_{\beta z}^{c} &= \frac{1}{{B_{c} \left( {1 + z_{c} /R_{\beta }^{c} } \right)}}\left( {\gamma_{0\beta z}^{c} + z_{c} \gamma_{1\beta z}^{c} + z_{c}^{2} \gamma_{2\beta z}^{c} + z_{c}^{3} \gamma_{3\beta z}^{c} } \right) \\ \gamma_{\alpha \beta }^{c} &= \frac{1}{{A_{c} \left( {1 + z_{c} /R_{\alpha }^{c} } \right)}} \left( {\gamma_{0\alpha \beta }^{c} + z_{c} \gamma_{1\alpha \beta }^{c} + z_{c}^{2} \gamma_{2\alpha \beta }^{c} + z_{c}^{3} \gamma_{3\alpha \beta }^{c} } \right) \\ &\quad + \frac{1}{{B_{c} \left( {1 + z_{c} /R_{\beta }^{c} } \right)}}\left( {\gamma_{0\alpha z}^{c} + z_{c} \gamma_{1\alpha z}^{c} + z_{c}^{2} \gamma_{2\alpha z}^{c} + z_{c}^{3} \gamma_{3\alpha z}^{c} } \right) \\ \end{aligned}$$

(6)

In which the generalized strain terms used in Eqs. (5) and (6) are reported in [37, 39].

2.1 Constitutive equations and stress resultants

To model the behavior of each lamina in the top and bottom face sheets, the orthotropic properties are considered and the stress–strain relations for a typical $k{\text{th}}$ lamina are described as follows:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {\sigma_{\alpha }^{k} } \\ {\sigma_{\beta }^{k} } \\ {\tau_{\alpha \beta }^{k} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11}^{k} } &\quad {\overline{Q}_{12}^{k} } &\quad {\overline{Q}_{16}^{k} } \\ {\overline{Q}_{12}^{k} } &\quad {\overline{Q}_{22}^{k} } &\quad {\overline{Q}_{26}^{k} } \\ {\overline{Q}_{16}^{k} } &\quad {\overline{Q}_{26}^{k} } &\quad {\overline{Q}_{66}^{k} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{\alpha }^{k} } \\ {\varepsilon_{\beta }^{k} } \\ {\gamma_{\alpha \beta }^{k} } \\ \end{array} } \right\} \\ & \left\{ {\begin{array}{*{20}c} {\tau_{\beta z}^{k} } \\ {\tau_{\alpha z}^{k} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{44}^{k} } &\quad {\overline{Q}_{45}^{k} } \\ {\overline{Q}_{45}^{k} } &\quad {\overline{Q}_{55}^{k} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{\beta z}^{k} } \\ {\gamma_{\alpha z}^{k} } \\ \end{array} } \right\} \\ \end{aligned}$$

(7)

The transformed reduced stiffness coefficients ${\overline{Q} }_{ij}^{k}$, appearing in the equation above, can be expressed in terms of the stiffness coefficients [37].

The stress resultants $N$ and $Q$, as well as stress couples $M$, for the face sheets, are involved in the following relationships:

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {N_{\alpha }^{i} } \\ {N_{\alpha \beta }^{i} } \\ {Q_{\alpha }^{i} } \\ \end{array} } \right] = \mathop \sum \limits_{k = 1}^{{N^{i} }} \mathop \int \limits_{{z_{ik - 1} }}^{{z_{ik} }} \left[ {\begin{array}{*{20}c} {\sigma_{\alpha }^{i} } \\ {\sigma_{\alpha \beta }^{i} } \\ {\sigma_{\alpha z}^{i} } \\ \end{array} } \right]\left( {1 + \frac{{z_{i} }}{{R_{\beta }^{i} }}} \right){\text{d}}z_{i} \\ & \left[ {\begin{array}{*{20}c} {N_{\beta }^{i} } \\ {N_{\beta \alpha }^{i} } \\ {Q_{\beta }^{i} } \\ \end{array} } \right] = \mathop \sum \limits_{k = 1}^{{N^{i} }} \mathop \int \limits_{{z_{ik - 1} }}^{{z_{ik} }} \left[ {\begin{array}{*{20}c} {\sigma_{\beta }^{i} } \\ {\sigma_{\alpha \beta }^{i} } \\ {\sigma_{\beta z}^{i} } \\ \end{array} } \right]\left( {1 + \frac{{z_{i} }}{{R_{\alpha }^{i} }}} \right){\text{d}}z_{i} \\ & \left[ {\begin{array}{*{20}c} {M_{\alpha }^{i} } \\ {M_{\alpha \beta }^{i} } \\ \end{array} } \right] = \mathop \sum \limits_{k = 1}^{{N^{i} }} \mathop \int \limits_{{z_{ik - 1} }}^{{z_{ik} }} \left[ {\begin{array}{*{20}c} {\sigma_{\alpha }^{i} } \\ {\sigma_{\alpha \beta }^{i} } \\ \end{array} } \right]z_{i} \left( {1 + \frac{{z_{i} }}{{R_{\beta }^{i} }}} \right){\text{d}}z_{i} \\ & \left[ {\begin{array}{*{20}c} {M_{\beta }^{i} } \\ {M_{\beta \alpha }^{i} } \\ \end{array} } \right] = \mathop \sum \limits_{k = 1}^{{N^{i} }} \mathop \int \limits_{{z_{ik - 1} }}^{{z_{ik} }} \left[ {\begin{array}{*{20}c} {\sigma_{\beta }^{i} } \\ {\sigma_{\alpha \beta }^{i} } \\ \end{array} } \right]z_{i} \left( {1 + \frac{{z_{i} }}{{R_{\alpha }^{i} }}} \right){\text{d}}z_{i} \\ \end{aligned}$$

(8)

The following relationships for the stress resultants can be obtained by substituting Eq. (5) into Eq. (7), then substituting the resultant equations into Eq. (8), and carrying out the integration in the thickness direction for laminated composite top and bottom face sheets, which are composed of ${N}^{i}$ layers. The relationship between stress resultants and mid-surface strains for face sheets can be expressed as follows [37]:

$$\left[\begin{array}{c}{N}_{\alpha }^{i}\\ {N}_{\beta }^{i}\\ \begin{array}{c}{N}_{\alpha \beta }^{i}\\ {N}_{\beta \alpha }^{i}\\ \begin{array}{c}{M}_{\alpha }^{i}\\ {M}_{\beta }^{i}\\ \begin{array}{c}{M}_{\alpha \beta }^{i}\\ {M}_{\beta \alpha }^{i}\end{array}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}{\overline{A} }_{11}^{i}\\ {A}_{12}^{i}\\ {\overline{A} }_{16}^{i}\\ {A}_{16}^{i}\\ {\overline{B} }_{11}^{i}\\ {B}_{12}^{i}\\ {\overline{B} }_{16}^{i}\\ {B}_{16}^{i}\end{array}\begin{array}{c}{A}_{12}^{i}\\ {\widetilde{A}}_{22}^{i}\\ \begin{array}{c}{A}_{26}^{i}\\ {\widetilde{A}}_{26}^{i}\\ \begin{array}{c}{B}_{12}^{i}\\ \begin{array}{c}{\widetilde{B}}_{22}^{i}\\ \begin{array}{c}{B}_{26}^{i}\\ {\widetilde{B}}_{26}^{i}\end{array}\end{array}\end{array}\end{array}\end{array}\begin{array}{c}{\overline{A} }_{16}^{i}\\ {A}_{26}^{i}\\ {\overline{A} }_{66}^{i}\\ {A}_{66}^{i}\\ {\overline{B} }_{16}^{i}\\ {B}_{26}^{i}\\ {\overline{B} }_{66}^{i}\\ {B}_{66}^{i}\end{array}\begin{array}{c}{A}_{16}^{i}\\ {\widetilde{A}}_{26}^{i}\\ \begin{array}{c}{A}_{66}^{i}\\ {\widetilde{A}}_{66}^{i}\\ \begin{array}{c}{B}_{16}^{i}\\ \begin{array}{c}{\widetilde{B}}_{26}^{i}\\ \begin{array}{c}{B}_{66}^{i}\\ {\widetilde{B}}_{66}^{i}\end{array}\end{array}\end{array}\end{array}\end{array}\begin{array}{c}{\overline{B} }_{11}^{i}\\ {B}_{12}^{i}\\ {\overline{B} }_{16}^{i}\\ {B}_{16}^{i}\\ {\overline{C} }_{11}^{i}\\ {C}_{12}^{i}\\ {\overline{C} }_{16}^{i}\\ {C}_{16}^{i}\end{array}\begin{array}{c}{B}_{12}^{i}\\ {\widetilde{B}}_{22}^{i}\\ \begin{array}{c}{B}_{26}^{i}\\ {\widetilde{B}}_{26}^{i}\\ \begin{array}{c}{C}_{12}^{i}\\ \begin{array}{c}{\widetilde{C}}_{22}^{i}\\ \begin{array}{c}{C}_{26}^{i}\\ {\widetilde{C}}_{26}^{i}\end{array}\end{array}\end{array}\end{array}\end{array}\begin{array}{c}{\overline{B} }_{16}^{i}\\ {B}_{26}^{i}\\ {\overline{B} }_{66}^{i}\\ {B}_{66}^{i}\\ {\overline{C} }_{16}^{i}\\ {C}_{26}^{i}\\ {\overline{C} }_{66}^{i}\\ {C}_{66}^{i}\end{array}\begin{array}{c}{B}_{16}^{i}\\ {\widetilde{B}}_{26}^{i}\\ \begin{array}{c}{B}_{66}^{i}\\ {\widetilde{B}}_{66}^{i}\\ \begin{array}{c}{C}_{16}^{i}\\ \begin{array}{c}{\widetilde{C}}_{26}^{i}\\ \begin{array}{c}{C}_{66}^{i}\\ {\widetilde{C}}_{66}^{i}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{\varepsilon }_{0\alpha }^{i}\\ {\varepsilon }_{0\beta }^{i}\\ \begin{array}{c}{\varepsilon }_{0\alpha \beta }^{i}\\ {\varepsilon }_{0\beta \alpha }^{i}\\ \begin{array}{c}{\kappa }_{\alpha }^{i}\\ {\kappa }_{\beta }^{i}\\ \begin{array}{c}{\kappa }_{\alpha \beta }^{i}\\ {\kappa }_{\beta \alpha }^{i}\end{array}\end{array}\end{array}\end{array}\right], i=t,b$$

$$\left[ {\begin{array}{*{20}c} {Q_{\alpha }^{i} } \\ {Q_{\beta }^{i} } \\ \end{array} } \right] = k_{s} \left[ {\begin{array}{*{20}c} {\overline{A}_{55}^{i} } & {A_{45}^{i} } \\ {A_{45}^{i} } & {\tilde{A}_{44}^{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\gamma_{0\alpha z}^{i} } \\ {\gamma_{0\beta z}^{i} } \\ \end{array} } \right]$$

(9)

In which ${k}_{s}$ is the shear correction factor which is taken to be 5/6 [40, 41], and:

$$\begin{aligned} & \overline{A}_{mn}^{i} = A_{mn}^{i} - c_{0}^{i} B_{mn}^{i} \quad \tilde{A}_{mn}^{i} = A_{mn}^{i} + c_{0}^{i} B_{mn}^{i} \\ & \overline{B}_{mn}^{i} = B_{mn}^{i} - c_{0}^{i} C_{mn}^{i} \quad \tilde{B}_{mn}^{i} = B_{mn}^{x} + c_{0}^{i} C_{mn}^{i} \\ & \overline{C}_{mn}^{i} = C_{mn}^{i} - c_{0}^{i} D_{mn}^{i} \quad \tilde{C}_{mn}^{i} = C_{mn}^{i} + c_{0}^{i} D_{mn}^{i} \\ \end{aligned}$$

(10)

The stiffness coefficients ${A}_{mn}^{i}$, ${B}_{mn}^{i}$ and ${C}_{mn}^{i}$ are defined as follows, where $m,n=1, 2, 4, 5, 6$ and ${c}_{0}^{i}=(1/{R}_{\alpha }^{i}-1/{R}_{\beta }^{i})$, and the distance of the top and bottom surfaces of the kth layer from the face sheet mid-surface is indicated by ${{z}_{i}}_{k-1}$ and ${{z}_{i}}_{k}$, respectively.

$$\left( {A_{mn}^{i} , B_{mn}^{i} , C_{mn}^{i} ,D_{mn}^{i} } \right) = \mathop \sum \limits_{k = 1}^{{N^{i} }} \overline{Q}_{mn}^{\left( k \right)} \mathop \int \limits_{{z_{ik - 1} }}^{{z_{ik} }} \left( {1,z_{i} ,z_{i}^{2} ,z_{i}^{3} } \right){\text{dz}}_{i} ,\quad i = t,b$$

(11)

and the stress and couple resultants for the core can be described using the following expressions [37]:

$$\begin{aligned} \left[\begin{array}{c}{N}_{\alpha }\\ {N}_{\beta }\\ {N}_{\alpha \beta }\\ {N}_{\beta \alpha }\\ {M}_{1\alpha }\\ {M}_{1\beta }\\ {M}_{1\alpha \beta }\\ {M}_{1\beta \alpha }\\ {M}_{2\alpha }\\ {M}_{2\beta }\\ {M}_{2\alpha \beta }\\ {M}_{2\beta \alpha }\\ {M}_{3\alpha }\\ {M}_{3\beta }\\ {M}_{3\alpha \beta }\\ {M}_{3\beta \alpha }\end{array}\right] &=\left[\begin{array}{cccccccccccccccc}{\overline{A} }_{11}& {A}_{12}& {\overline{A} }_{16}& {A}_{16}& {\overline{B} }_{11}& {B}_{12}& {\overline{B} }_{16}& {B}_{16}& {\overline{C} }_{11}& {C}_{12}& {\overline{C} }_{16}& {C}_{16}& {\overline{D} }_{11}& {D}_{12}& {\overline{D} }_{16}& {D}_{16}\\ {A}_{12}& {\widetilde{A}}_{22}& {A}_{26}& {\widetilde{A}}_{26}& {B}_{12}& {\widetilde{B}}_{22}& {B}_{26}& {\widetilde{B}}_{26}& {C}_{12}& {\widetilde{C}}_{22}& {C}_{26}& {\widetilde{C}}_{26}& {D}_{12}& {\widetilde{D}}_{22}& {D}_{26}& {\widetilde{D}}_{26}\\ {\overline{A} }_{16}& {A}_{26}& {\overline{A} }_{66}& {A}_{66}& {\overline{B} }_{16}& {B}_{26}& {\overline{B} }_{66}& {B}_{66}& {\overline{C} }_{16}& {C}_{26}& {\overline{C} }_{66}& {C}_{66}& {\overline{D} }_{16}& {D}_{26}& {\overline{D} }_{66}& {D}_{66}\\ {A}_{16}& {\widetilde{A}}_{26}& {A}_{66}& {\widetilde{A}}_{66}& {B}_{16}& {\widetilde{B}}_{26}& {B}_{66}& {\widetilde{B}}_{66}& {C}_{16}& {\widetilde{C}}_{26}& {C}_{66}& {\widetilde{C}}_{66}& {D}_{16}& {\widetilde{D}}_{26}& {D}_{66}& {\widetilde{D}}_{66}\\ {\overline{B} }_{11}& {B}_{12}& {\overline{B} }_{16}& {B}_{16}& {\overline{C} }_{11}& {C}_{12}& {\overline{C} }_{16}& {C}_{16}& {\overline{D} }_{11}& {D}_{12}& {\overline{D} }_{16}& {D}_{16}& {\overline{E} }_{11}& {E}_{12}& {\overline{E} }_{16}& {E}_{16}\\ {B}_{12}& {\widetilde{B}}_{22}& {B}_{26}& {\widetilde{B}}_{26}& {C}_{12}& {\widetilde{C}}_{22}& {C}_{26}& {\widetilde{C}}_{26}& {D}_{12}& {\widetilde{D}}_{22}& {D}_{26}& {\widetilde{D}}_{26}& {E}_{12}& {\widetilde{E}}_{22}& {E}_{26}& {\widetilde{E}}_{26}\\ {\overline{B} }_{16}& {B}_{26}& {\overline{B} }_{66}& {B}_{66}& {\overline{C} }_{16}& {C}_{26}& {\overline{C} }_{66}& {C}_{66}& {\overline{D} }_{16}& {D}_{26}& {\overline{D} }_{66}& {D}_{66}& {\overline{E} }_{16}& {E}_{26}& {\overline{E} }_{66}& {E}_{66}\\ {B}_{16}& {\widetilde{B}}_{26}& {B}_{66}& {\widetilde{B}}_{66}& {C}_{16}& {\widetilde{C}}_{26}& {C}_{66}& {\widetilde{C}}_{66}& {D}_{16}& {\widetilde{D}}_{26}& {D}_{66}& {\widetilde{D}}_{66}& {E}_{16}& {\widetilde{E}}_{26}& {E}_{66}& {\widetilde{E}}_{66}\\ {\overline{C} }_{11}& {C}_{12}& {\overline{C} }_{16}& {C}_{16}& {\overline{D} }_{11}& {D}_{12}& {\overline{D} }_{16}& {D}_{16}& {\overline{E} }_{11}& {E}_{12}& {\overline{E} }_{16}& {E}_{16}& {\overline{F} }_{11}& {F}_{12}& {\overline{F} }_{16}& {F}_{16}\\ {C}_{12}& {\widetilde{C}}_{22}& {C}_{26}& {\widetilde{C}}_{26}& {D}_{12}& {\widetilde{D}}_{22}& {D}_{26}& {\widetilde{D}}_{26}& {E}_{12}& {\widetilde{E}}_{22}& {E}_{26}& {\widetilde{E}}_{26}& {F}_{12}& {\widetilde{F}}_{22}& {F}_{26}& {\widetilde{F}}_{26}\\ {\overline{C} }_{16}& {C}_{26}& {\overline{C} }_{66}& {C}_{66}& {\overline{D} }_{16}& {D}_{26}& {\overline{D} }_{66}& {D}_{66}& {\overline{E} }_{16}& {E}_{26}& {\overline{E} }_{66}& {E}_{66}& {\overline{F} }_{16}& {F}_{26}& {\overline{F} }_{66}& {F}_{66}\\ {C}_{16}& {\widetilde{C}}_{26}& {C}_{66}& {\widetilde{C}}_{66}& {D}_{16}& {\widetilde{D}}_{26}& {D}_{66}& {\widetilde{D}}_{66}& {E}_{16}& {\widetilde{E}}_{26}& {E}_{66}& {\widetilde{E}}_{66}& {F}_{16}& {\widetilde{F}}_{26}& {F}_{66}& {\widetilde{F}}_{66}\\ {\overline{D} }_{11}& {D}_{12}& {\overline{D} }_{16}& {D}_{16}& {\overline{E} }_{11}& {E}_{12}& {\overline{E} }_{16}& {E}_{16}& {\overline{F} }_{11}& {F}_{12}& {\overline{F} }_{16}& {F}_{16}& {\overline{G} }_{11}& {G}_{12}& {\overline{G} }_{16}& {G}_{16}\\ {D}_{12}& {\widetilde{D}}_{22}& {D}_{26}& {\widetilde{D}}_{26}& {E}_{12}& {\widetilde{E}}_{22}& {E}_{26}& {\widetilde{E}}_{26}& {F}_{12}& {\widetilde{F}}_{22}& {F}_{26}& {\widetilde{F}}_{26}& {G}_{12}& {\widetilde{G}}_{22}& {G}_{26}& {\widetilde{G}}_{26}\\ {\overline{D} }_{16}& {D}_{26}& {\overline{D} }_{66}& {D}_{66}& {\overline{E} }_{16}& {E}_{26}& {\overline{E} }_{66}& {E}_{66}& {\overline{F} }_{16}& {F}_{26}& {\overline{F} }_{66}& {F}_{66}& {\overline{G} }_{16}& {G}_{26}& {\overline{G} }_{66}& {G}_{66}\\ {D}_{16}& {\widetilde{D}}_{26}& {D}_{66}& {\widetilde{D}}_{66}& {E}_{16}& {\widetilde{E}}_{26}& {E}_{66}& {\widetilde{E}}_{66}& {F}_{16}& {\widetilde{F}}_{26}& {F}_{66}& {\widetilde{F}}_{66}& {G}_{16}& {\widetilde{G}}_{26}& {G}_{66}& {\widetilde{G}}_{66}\end{array}\right] \left[\begin{array}{c}{\varepsilon }_{0\alpha }\\ {\varepsilon }_{0\beta }\\ {\varepsilon }_{0\alpha \beta }\\ {\varepsilon }_{0\beta \alpha }\\ {\varepsilon }_{1\alpha }\\ {\varepsilon }_{1\beta }\\ {\varepsilon }_{1\alpha \beta }\\ {\varepsilon }_{1\beta \alpha }\\ {\varepsilon }_{2\alpha }\\ {\varepsilon }_{2\beta }\\ {\varepsilon }_{2\alpha \beta }\\ {\varepsilon }_{2\beta \alpha }\\ {\varepsilon }_{3\alpha }\\ {\varepsilon }_{3\beta }\\ {\varepsilon }_{3\alpha \beta }\\ {\varepsilon }_{3\beta \alpha }\end{array}\right] \end{aligned}$$

(12)

where:

$$\begin{aligned} & \overline{A}_{mn} = A_{mn} - c_{0} B_{mn} \quad \tilde{A}_{mn} = A_{mn} + c_{0} B_{mn} \\ & \overline{B}_{mn} = B_{mn} - c_{0} C_{mn} \quad \tilde{B}_{mn} = B_{mn} + c_{0} C_{mn} \\ & \overline{C}_{mn} = C_{mn} - c_{0} D_{mn} \quad \tilde{C}_{mn} = C_{mn} + c_{0} D_{mn} \\ & \overline{D}_{mn} = D_{mn} - c_{0} E_{mn} \quad \tilde{D}_{mn} = D_{mn} + c_{0} E_{mn} \\ & \overline{E}_{mn} = E_{mn} - c_{0} F_{mn} \quad \tilde{E}_{mn} = E_{mn} + c_{0} F_{mn} \\ & \overline{F}_{mn} = F_{mn} - c_{0} G_{mn} \quad \tilde{F}_{mn} = F_{mn} + c_{0} G_{mn} \\ & \overline{G}_{mn} = G_{mn} - c_{0} H_{mn} \quad \tilde{G}_{mn} = G_{mn} + c_{0} H_{mn} \\ \end{aligned}$$

(13)

and the coefficients ${A}_{mn}$, ${B}_{mn},$ …, ${G}_{mn}$ are:

$$\left( {A_{mn} , B_{mn} , C_{mn} , D_{mn} , E_{mn} , F_{mn} , G_{mn} , H_{mn} } \right) = \mathop \sum \limits_{i = 1}^{N} \overline{Q}_{mn}^{\left( k \right)} \mathop \int \limits_{{z_{ck - 1} }}^{{z_{ck - 1} }} \left( {1,z_{c} ,z_{c}^{2} ,z_{c}^{3} ,z_{c}^{4} ,z_{c}^{5} ,z_{c}^{6} ,z_{c}^{7} } \right){\text{d}}z_{c}$$

(14)

2.2 Energy equations

The equations of motion and relevant boundary conditions can be obtained by using Hamilton’s principle [42]:

$$\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \delta \left( {T - U + W_{F} } \right){\text{d}}t = 0$$

(15)

The expressions involve the variational operator $\delta$, as well as the initial and final times ${t}_{1}$ and ${t}_{2}$. ${U}$ and ${T}$ represent the total strain and kinetic energies of the structure, respectively, and ${W}_{F}$, on the other hand, represents the work done by external forces. ${U}$ and ${T}$ can be expressed using the following equations:

$$\begin{aligned} & U = U_{t} + U_{c} + U_{b} + U_{E} \\ & T = T_{t} + T_{c} + T_{b} \\ \end{aligned}$$

(16)

In which the terms ${T}_{t}$, ${T}_{c}$, and ${T}_{b}$ represent the kinetic energy of the top face sheet, core, and bottom face sheet, respectively. Similarly,${U}_{t}$, ${U}_{c}$, and ${U}_{b}$ denote the strain energy of the top face sheet, core, and bottom face sheet, respectively, while ${U}_{E}$ refers to the potential energy stored in the elastic edge supports. It is necessary to determine the energy terms for each main layer. The strain energy of the face sheets can be expressed using the following equation:

$$\begin{aligned} U_{i} &= \frac{1}{2}\mathop \int \limits_{\alpha }^{{}} \mathop \int \limits_{\beta }^{{}} \Bigg\{ N_{\alpha }^{i} \varepsilon _{{0\alpha }}^{i} + N_{\beta }^{i} \varepsilon _{{0\beta }}^{i} + N_{{\alpha \beta }}^{i} \varepsilon _{{0\alpha \beta }}^{i} \\ & \qquad + N_{{\beta \alpha }}^{i} \varepsilon _{{0\beta \alpha }}^{i} + M_{\alpha }^{i} \kappa _{\alpha }^{i} + M_{\beta }^{i} \kappa _{\beta }^{i} + M_{{\alpha \beta }}^{i} \kappa _{{\alpha \beta }}^{i} + M_{{\beta \alpha }}^{i} \kappa _{{\beta \alpha }}^{i} + Q_{\alpha }^{i} \gamma _{{0\alpha z}}^{i} + Q_{\beta }^{i} \gamma _{{0\beta z}}^{i} \Bigg\} \\ ~ & \quad A_{i} B_{{\text{i}}} {\text{d}}\alpha {\text{d}}\beta ,\quad i = t,b \\ \end{aligned}$$

(17)

where generalized strains and stress resultants are expressed in Eqs. (5) and (9), respectively. Similarly, the strain energy of the core can be expressed using the following equation:

$$\begin{aligned} U_{c} &= \frac{1}{2}\int\limits_{\alpha }^{{}} {\int\limits_{\beta }^{{}} {\left( {N_{\alpha } \varepsilon _{{0\alpha }} + M_{{1\alpha }} \varepsilon _{{1\alpha }} + M_{{2\alpha }} \varepsilon _{{2\alpha }} + M_{{3\alpha }} \varepsilon _{{3\alpha }} + N_{\beta } \varepsilon _{{0\beta }} + M_{{1\beta }} \varepsilon _{{1\beta }} } \right.} } \\ & \quad + M_{{2\beta }} \varepsilon _{{2\beta }} + M_{{3\beta }} \varepsilon _{{3\beta }} + R_{z} \varepsilon _{{0z}} + M_{z} \varepsilon _{{1z}} + Q_{{\alpha z}} \gamma _{{0\alpha z}} + M_{{Q1\alpha z}} \gamma _{{1\alpha z}} + M_{{Q2\alpha z}} \gamma _{{2\alpha z}} \\ & \quad +M_{{Q3\alpha z}} \gamma _{{3\alpha z}} + Q_{{\beta z}} \gamma _{{0\beta z}} + M_{{Q1\beta z}} \gamma _{{1\beta z}} + M_{{Q2\beta z}} \gamma _{{2\beta z}} + M_{{Q3\beta z}} \gamma _{{3\beta z}} + N_{{\alpha \beta }} \gamma _{{0\alpha \beta }} \\ & \quad +M_{{1\alpha \beta }} \gamma _{{1\alpha \beta }} + M_{{2\alpha \beta }} \gamma _{{2\alpha \beta }} + M_{{3\alpha \beta }} \gamma _{{3\alpha \beta }} + N_{{\beta \alpha }} \gamma _{{0\beta \alpha }} + M_{{1\beta \alpha }} \gamma _{{1\beta \alpha }} + M_{{2\beta \alpha }} \gamma _{{2\beta \alpha }} \\ & \quad +\left. {M_{{3\beta \alpha }} \gamma _{{3\beta \alpha }} } \right)A_{c} B_{c} d\alpha {\text{d}}\beta \end{aligned}$$

(18)

In which the strain and stress resultants of the core are expressed in Eqs. (6) and (12), respectively. Additionally, the strain energy stored in the elastic edge supports can be expressed using the following equation:

$${U}_{E}={U}_{E1}+{U}_{E2}+{U}_{E3}+{U}_{E4}$$

(19)

In which ${U}_{E1}$ is for the elastic restraints of edge $\alpha =0$ and can be defined as:

$${U}_{E1}=\frac{1}{2}\int_{\beta }\left[{K}_{{u}^{i}}^{\alpha =0}{{u}_{0}^{i}\left(0,\beta \right)}^{2}+{K}_{{{\psi }_{\alpha }}^{i}}^{\alpha =0}{{{\psi }_{\alpha }}^{i}\left(0,\beta \right)}^{2}+{K}_{{v}^{i}}^{\alpha =0}{{v}_{0}^{i}\left(0,\beta \right)}^{2}+{K}_{{{\psi }_{\beta }}^{i}}^{\alpha =0}{{{\psi }_{\beta }}^{i}\left(0,\beta \right)}^{2}+{K}_{{w}_{0}^{i}}^{\alpha =0}{{w}_{0}^{i}\left(0,\beta \right)}^{2}+{K}_{{u}_{0}}^{\alpha =0}{{u}_{0}\left(0,\beta \right)}^{2}+{K}_{{u}_{1}}^{\alpha =0}{{u}_{1}\left(0,\beta \right)}^{2}+{K}_{{v}_{0}}^{\alpha =0}{{v}_{0}\left(0,\beta \right)}^{2}+{K}_{{v}_{1}}^{\alpha =0}{{v}_{1}\left(0,\beta \right)}^{2}+{K}_{{w}_{0}}^{\alpha =0}{{w}_{0}\left(0,\beta \right)}^{2}\right]\left(1+\frac{z}{{R}_{\beta }^{i}}\right){\text{d}}\beta$$

(20)

${U}_{E2}$ is for elastic restraints of edge $\alpha =a$ and can be defined as:

$$\begin{aligned} {U}_{E2}&=\frac{1}{2}\int_{\beta}\Bigg[{K}_{{u}^{i}}^{\alpha =a}{{u}_{0}^{i}\left(a,\beta \right)}^{2}+{K}_{{{\psi }_{\alpha }}^{i}}^{\alpha =a}{{{\psi }_{\alpha }}^{i}\left(a,\beta \right)}^{2}+{K}_{{v}^{i}}^{\alpha =a}{{v}_{0}^{i}\left(a,\beta \right)}^{2}+{K}_{{{\psi }_{\beta }}^{i}}^{\alpha =a}{{{\psi }_{\beta }}^{i}\left(a,\beta \right)}^{2}\\ & \quad +{K}_{{w}_{0}^{i}}^{\alpha =a}{{w}_{0}^{i}\left(a,\beta \right)}^{2}+{K}_{{u}_{0}}^{\alpha =a}{{u}_{0}\left(a,\beta \right)}^{2}+{K}_{{u}_{1}}^{\alpha =a}{{u}_{1}\left(a,\beta \right)}^{2}+{K}_{{v}_{0}}^{\alpha =a}{{v}_{0}\left(a,\beta \right)}^{2}\\ & \quad +{K}_{{v}_{1}}^{\alpha =a}{{v}_{1}\left(a,\beta \right)}^{2}+{K}_{{w}_{0}}^{\alpha =a}{{w}_{0}\left(a,\beta \right)}^{2}\Bigg]\left(1+\frac{z}{{R}_{\beta }^{i}}\right){\text{d}}\beta \end{aligned}$$

(21)

Similarly, ${U}_{E3}$ is for the elastic restraints of edge $\beta =0$ and can be defined as:

$${U}_{E3}=\frac{1}{2}\int_{\alpha }\left[{K}_{{u}^{i}}^{\beta =0}{{u}_{0}^{i}\left(\alpha ,0\right)}^{2}+{K}_{{{\psi }_{\alpha }}^{i}}^{\beta =0}{{{\psi }_{\alpha }}^{i}\left(\alpha ,0\right)}^{2}+{K}_{{v}^{i}}^{\beta =0}{{v}_{0}^{i}\left(\alpha ,0\right)}^{2}+{K}_{{{\psi }_{\beta }}^{i}}^{\beta =0}{{{\psi }_{\beta }}^{i}\left(\alpha ,0\right)}^{2}+{K}_{{w}_{0}^{i}}^{\beta =0}{{w}_{0}^{i}\left(\alpha ,0\right)}^{2}+{K}_{{u}_{0}}^{\beta =0}{{u}_{0}\left(\alpha ,0\right)}^{2}+{K}_{{u}_{1}}^{\beta =0}{{u}_{1}\left(\alpha ,0\right)}^{2}+{K}_{{v}_{0}}^{\beta =0}{{v}_{0}\left(\alpha ,0\right)}^{2}+{K}_{{v}_{1}}^{\beta =0}{{v}_{1}\left(\alpha ,0\right)}^{2}+{K}_{{w}_{0}}^{\beta =0}{{w}_{0}\left(\alpha ,0\right)}^{2}\right]\left(1+\frac{z}{{R}_{\alpha }^{i}}\right){\text{d}}\alpha$$

(22)

and finally, ${U}_{E4}$ is for the elastic restraints of edge $\beta =b$ and can be defined as:

$${U}_{E4}=\frac{1}{2}\int_{\alpha }\left[{K}_{{u}^{i}}^{\beta =b}{{u}_{0}^{i}\left(\alpha ,b\right)}^{2}+{K}_{{{\psi }_{\alpha }}^{i}}^{\beta =b}{{{\psi }_{\alpha }}^{i}\left(\alpha ,b\right)}^{2}+{K}_{{v}^{i}}^{\beta =b}{{v}_{0}^{i}\left(\alpha ,b\right)}^{2}+{K}_{{{\psi }_{\beta }}^{i}}^{\beta =b}{{{\psi }_{\beta }}^{i}\left(\alpha ,b\right)}^{2}+{K}_{{w}_{0}^{i}}^{\beta =b}{{w}_{0}^{i}\left(\alpha ,b\right)}^{2}+{K}_{{u}_{0}}^{\beta =b}{{u}_{0}\left(\alpha ,b\right)}^{2}+{K}_{{u}_{1}}^{\beta =b}{{u}_{1}\left(\alpha ,b\right)}^{2}+{K}_{{v}_{0}}^{\beta =b}{{v}_{0}\left(\alpha ,b\right)}^{2}+{K}_{{v}_{1}}^{\beta =b}{{v}_{1}\left(\alpha ,b\right)}^{2}+{K}_{{w}_{0}}^{\beta =b}{{w}_{0}\left(\alpha ,b\right)}^{2}\right]\left(1+\frac{z}{{R}_{\alpha }^{i}}\right){\text{d}}\alpha$$

(23)

On the other hand, one can calculate the kinetic energy of the face sheets using the following equation:

$$T_{i} = \frac{1}{2}\int\limits_{\alpha } {\int\limits_{\beta } {\left\{ {\overline{I}_{0}^{i} \left( {\dot{u}_{0}^{i2} + \dot{v}_{0}^{i2} + \dot{w}_{0}^{i2} } \right) + \overline{I}_{1}^{i} \left( {\dot{\psi }_{\alpha }^{i2} + \dot{\psi }_{\beta }^{i} } \right) + \overline{I}_{2}^{i} \left( {\dot{u}_{0}^{i} \dot{\psi }_{\alpha }^{i} + \dot{v}_{0}^{i} \dot{\psi }_{\beta }^{i} } \right)} \right\}A_{i} B_{i} {\text{d}}\beta {\text{d}}\alpha ,\quad i = t,b} }$$

(24)

and for the core:

$$\begin{aligned}{T}_{c}&=\frac{1}{2}\int_{\alpha }\int_{\beta }\Bigg\{{\overline{I} }_{0}^{c}\left({{\dot{u}}_{0}}^{2}+{{\dot{v}}_{0}}^{2}+{{\dot{w}}_{0}}^{2}\right)+2{\overline{I} }_{1}^{c}\left({\dot{u}}_{0}{\dot{u}}_{1}+{\dot{v}}_{0}{\dot{v}}_{1}+{\dot{w}}_{0}{\dot{w}}_{1}\right)\\ & \quad +{\overline{I} }_{2}^{c}\left(2{\dot{u}}_{0}{\dot{u}}_{2} +{{\dot{u}}_{1}}^{2}+2{\dot{v}}_{0}{\dot{v}}_{2}+{{\dot{v}}_{1}}^{2}+2{\dot{w}}_{0}{\dot{w}}_{2}+{{\dot{w}}_{1}}^{2}\right)\\ & \quad +2{\overline{I} }_{3}^{c}\left({\dot{u}}_{0}{\dot{u}}_{3}+{\dot{u}}_{1}{\dot{u}}_{2}+{\dot{v}}_{0}{\dot{v}}_{3} +{\dot{v}}_{1}{\dot{v}}_{2}+{\dot{w}}_{1}{\dot{w}}_{2}\right)\\ & \quad +{\overline{I} }_{4}^{c}\left(2{\dot{u}}_{1}{\dot{u}}_{3}+{{\dot{u}}_{2}}^{2}+2{\dot{v}}_{1}{\dot{v}}_{3}+{{\dot{v}}_{2}}^{2}+{{\dot{w}}_{2}}^{2}\right)+2{\overline{I} }_{5}^{c}\left({\dot{u}}_{2}{\dot{u}}_{3}+{\dot{v}}_{2}{\dot{v}}_{3}\right)+{\overline{I} }_{6}^{c}({{\dot{u}}_{3}}^{2}+{{\dot{v}}_{3}}^{2})\Bigg\}{A}_{c}{B}_{c}{\text{d}}\beta {\text{d}}\alpha \end{aligned}$$

(25)

In which ${\overline{I} }_{j}^{i}$ ($j=0,...,6$) are inertia terms for the face sheets ($i=t,b$) and the core ($i=c$) which are defined as:

$$\begin{aligned} & \left[ {\overline{I}_{0}^{i} ,\overline{I}_{1}^{i} ,\overline{I}_{2}^{i} ,\overline{I}_{3}^{i} } \right] = \mathop \int \limits_{{ - \frac{{h_{i} }}{2}}}^{{\frac{{h_{i} }}{2}}} \rho_{i} \left[ {1,z_{i} ,z_{i}^{2} ,z_{i}^{3} } \right]\left( {1 + \frac{{z_{i} }}{{R_{\alpha }^{i} }}} \right)\left( {1 + \frac{{z_{i} }}{{R_{\beta }^{i} }}} \right){\text{d}}z_{i} \quad i = t,b \\ & \left[ {\overline{I}_{0}^{c} ,\overline{I}_{1}^{c} ,\overline{I}_{2}^{c} ,\overline{I}_{3}^{c} ,\overline{I}_{4}^{c} ,\overline{I}_{5}^{c} ,\overline{I}_{6}^{c} } \right] = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} \rho_{c} \left[ {1,z_{c}^{1} ,z_{c}^{2} ,z_{c}^{3} ,z_{c}^{4} ,z_{c}^{5} ,z_{c}^{6} } \right]\left( {1 + \frac{{z_{c} }}{{R_{\alpha }^{c} }}} \right)\left( {1 + \frac{{z_{c} }}{{R_{\beta }^{c} }}} \right){\text{d}}z_{c} \\ \end{aligned}$$

(26)

where ${\rho }_{i}$ ($i=t,b$) and ${\rho }_{c}$ are the mass density of the top, bottom, and core layers, respectively. On the other hand, ${W}_{F}$ can be presented as follows, since external force is applied perpendicular to the sandwich structure and on one of its top and bottom surfaces, it can be said:

$$W_{F} = \mathop \int \limits_{\beta }^{{}} \mathop \int \limits_{\alpha }^{{}} \left( {Fw^{i} } \right)\left( {1 + \frac{{z_{f} }}{{R_{\alpha }^{i} }}} \right)\left( {1 + \frac{{z_{f} }}{{R_{\beta }^{i} }}} \right)A_{i} B_{i}{\text{d}}\alpha {\text{d}}\beta ,\quad i = t,b$$

(27)

In which the components ${w}^{i}$ ($i=t,b$) and ${z}_{f}$ are determined depending on the location of the applied force. If the force is applied on the upper surface, ${w}^{i}={w}^{t}$ and ${z}_{f}=-{h}_{t}/2$, but if the force is applied on the lower surface, ${w}^{i}={w}^{b}$ and ${z}_{f}={h}_{b}/2$ are used. It is clear that the components $A$ and $B$ are also representative of the Lame parameters. Therefore, in order to simplify the equations, it can be said:

$$W_{F} = \mathop \int \limits_{\beta }^{{}} \mathop \int \limits_{\alpha }^{{}} \left( {F^{\prime}w^{i} } \right){\text{d}}\alpha {\text{d}}\beta ,\quad i = t,b$$

(28)

in which:

$$F^{\prime} = F\left( {1 + \frac{{z_{f} }}{{R_{\alpha }^{i} }}} \right)\left( {1 + \frac{{z_{f} }}{{R_{\beta }^{i} }}} \right)A_{i} B_{i} , i = t,b$$

(29)

2.3 Compatibility conditions

Assuming perfect bonding between the face sheets and the core, the compatibility relations at the interfaces are expressed in the following manner:

$$\begin{aligned} & u_{c} \left( {z_{c} = - \frac{{h_{c} }}{2}} \right) = u_{t} \left( {z_{t} = \frac{{h_{t} }}{2}} \right)\quad u_{c} \left( {z_{c} = \frac{{h_{c} }}{2}} \right) = u_{b} \left( {z_{b} = - \frac{{h_{b} }}{2}} \right) \\ & v_{c} \left( {z_{c} = - \frac{{h_{c} }}{2}} \right) = v_{t} \left( {z_{t} = \frac{{h_{t} }}{2}} \right)\quad v_{c} \left( {z_{c} = \frac{{h_{c} }}{2}} \right) = v_{b} \left( {z_{b} = - \frac{{h_{b} }}{2}} \right) \\ & w_{c} \left( {z_{c} = - \frac{{h_{c} }}{2}} \right) = w_{t} \left( {z_{t} = \frac{{h_{t} }}{2}} \right)\quad w_{c} \left( {z_{c} = \frac{{h_{c} }}{2}} \right) = w_{b} \left( {z_{b} = - \frac{{h_{b} }}{2}} \right) \\ \end{aligned}$$

(30)

By substituting Eqs. (2) and (3) in conditions (30), the compatibility conditions can be simplified as follows:

$$\begin{aligned} & u_{2} = \frac{{2\left( {u_{0}^{b} + u_{0}^{t} } \right) - h_{b} \psi_{\alpha }^{b} + h_{t} \psi_{\alpha }^{t} - 4u_{0} }}{{h_{c}^{2} }} \\ & u_{3} = \frac{{4\left( {u_{0}^{b} - u_{0}^{t} } \right) - 2\left( {h_{b} \psi_{\alpha }^{b} + h_{t} \psi_{\alpha }^{t} } \right) - 4h_{c} u_{1} }}{{h_{c}^{3} }} \\ & v_{2} = \frac{{2\left( {v_{0}^{b} + v_{0}^{t} } \right) - h_{b} \psi_{\beta }^{b} + h_{t} \psi_{\beta }^{t} - 4v_{0} }}{{h_{c}^{2} }} \\ & v_{3} = \frac{{4\left( {v_{0}^{b} - v_{0}^{t} } \right) - 2\left( {h_{b} \psi_{\beta }^{b} + h_{t} \psi_{\beta }^{t} } \right) - 4h_{c} v_{1} }}{{h_{c}^{3} }} \\ & w_{1} = \frac{{w_{0}^{b} - w_{0}^{t} }}{{h_{c} }} \\ & w_{2} = \frac{{2\left( {w_{0}^{b} + w_{0}^{t} - 2w_{0} } \right)}}{{h_{c}^{2} }} \\ \end{aligned}$$

(31)

Therefore, the number of problem unknowns can be reduced from twenty-one to fifteen.

2.4 Finite element solution

In this section, the finite element method is utilized to solve the problem at hand. To achieve this, a higher-order element with nine nodes is employed, and each node has fifteen degrees of freedom. Figure 2 visually presents this element for reference.

Fig. 2

Considered higher-order element

Therefore, the vector of element degrees of freedom can be defined as follows:

$$\left\{\delta \right\}={\left\{\left\{{\delta }_{1}\right\},\left\{{\delta }_{2}\right\},\left\{{\delta }_{3}\right\},\left\{{\delta }_{4}\right\},\left\{{\delta }_{5}\right\},\left\{{\delta }_{6}\right\},\left\{{\delta }_{7}\right\},\left\{{\delta }_{8}\right\},\left\{{\delta }_{9}\right\}\right\}}^{T}$$

(32)

where $\left\{{\delta }_{i}\right\}$ is the vector of degrees of freedom of each node and is defined as:

$$\left\{{\delta }_{i}\right\}={\left\{{u}_{0i}^{t}, {\psi }_{\alpha i}^{t}, {v}_{0i}^{t}, {\psi }_{\beta i}^{t}, {w}_{0i}^{t}, {u}_{0i}^{b}, {\psi }_{\alpha i}^{b}, {v}_{0i}^{b}, {\psi }_{\beta i}^{b}, {w}_{0i}^{b}, {u}_{0i}, {u}_{1i}, {v}_{0i}, {v}_{1i}, {w}_{0i}\right\}}^{T}$$

(33)

Using shape functions, it is possible to relate the assumed structural displacements and rotations to nodal displacements and rotations. Therefore:

$$\begin{aligned} & u_{0}^{t} = \left[ {N_{{u_{0}^{t} }} } \right]\left\{ \delta \right\},\quad \psi_{\alpha }^{t} = \left[ {N_{{\psi_{\alpha }^{t} }} } \right]\left\{ \delta \right\},\quad v_{0}^{t} = \left[ {N_{{v_{0}^{t} }} } \right]\left\{ \delta \right\},\quad \psi_{\beta }^{t} = \left[ {N_{{\psi_{\beta }^{t} }} } \right]\left\{ \delta \right\},\quad w_{0}^{t} = \left[ {N_{{w_{0}^{t} }} } \right]\left\{ \delta \right\} \\ & u_{0}^{b} = \left[ {N_{{u_{0}^{b} }} } \right]\left\{ \delta \right\},\quad \psi_{\alpha }^{b} = \left[ {N_{{\psi_{\alpha }^{b} }} } \right]\left\{ \delta \right\},\quad v_{0}^{b} = \left[ {N_{{v_{0}^{b} }} } \right]\left\{ \delta \right\},\quad \psi_{\beta }^{b} = \left[ {N_{{\psi_{\beta }^{b} }} } \right]\left\{ \delta \right\},\quad w_{0}^{t} = \left[ {N_{{w_{0}^{t} }} } \right]\left\{ \delta \right\} \\ & u_{0} = \left[ {N_{{u_{0} }} } \right]\left\{ \delta \right\},\quad u_{1} = \left[ {N_{{u_{1} }} } \right]\left\{ \delta \right\},\quad v_{0} = \left[ {N_{{v_{0} }} } \right]\left\{ \delta \right\},\quad v_{1} = \left[ {N_{{v_{1} }} } \right]\left\{ \delta \right\},\quad w_{0} = \left[ {N_{{w_{0} }} } \right]\left\{ \delta \right\} \\ \end{aligned}$$

(34)

In which:

$$\begin{gathered} \left[ {N_{{u_{0}^{t} }} } \right] = \left[ {N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{{14}} } \right] \hfill \\ \left[ {N_{{\psi _{\alpha }^{t} }} } \right] = \left[ {0,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{{13}} } \right] \hfill \\ \left[ {N_{{v_{0}^{t} }} } \right] = \left[ {\left\{ 0 \right\}_{2} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{5} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{{12}} } \right] \hfill \\ \left[ {N_{{\psi _{\beta }^{t} }} } \right] = \left[ {\left\{ 0 \right\}_{3} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{{11}} } \right] \hfill \\ \left[ {N_{{w_{0}^{t} }} } \right] = \left[ {\left\{ 0 \right\}_{4} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{{10}} } \right] \hfill \\ \left[ {N_{{u_{0}^{b} }} } \right] = \left[ {\left\{ 0 \right\}_{5} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{9} } \right] \hfill \\ \left[ {N_{{\psi _{\alpha }^{b} }} } \right] = \left[ {\left\{ 0 \right\}_{6} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{8} } \right] \hfill \\ \left[ {N_{{v_{0}^{b} }} } \right] = \left[ {\left\{ 0 \right\}_{7} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{7} } \right] \hfill \\ \left[ {N_{{\psi _{\beta }^{b} }} } \right] = \left[ {\left\{ 0 \right\}_{8} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{6} } \right] \hfill \\ \left[ {N_{{w_{0}^{b} }} } \right] = \left[ {\left\{ 0 \right\}_{9} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{5} } \right] \hfill \\ \left[ {N_{{u_{0} }} } \right] = \left[ {\left\{ 0 \right\}_{{10}} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{4} } \right] \hfill \\ \left[ {N_{{u_{1} }} } \right] = \left[ {\left\{ 0 \right\}_{{11}} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{3} } \right] \hfill \\ \left[ {N_{{v_{0} }} } \right] = \left[ {\left\{ 0 \right\}_{{12}} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,\left\{ 0 \right\}_{2} } \right] \hfill \\ \left[ {N_{{v_{1} }} } \right] = \left[ {\left\{ 0 \right\}_{{13}} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} ,0} \right] \hfill \\ \left[ {N_{{w_{0} }} } \right] = \left[ {\left\{ 0 \right\}_{{14}} ,N_{1} ,\left\{ 0 \right\}_{{14}} ,N_{2} ,\left\{ 0 \right\}_{{14}} ,N_{3} ,\left\{ 0 \right\}_{{14}} ,N_{4} ,\left\{ 0 \right\}_{{14}} ,N_{5} ,\left\{ 0 \right\}_{{14}} ,N_{6} ,\left\{ 0 \right\}_{{14}} ,N_{7} ,\left\{ 0 \right\}_{{14}} ,N_{8} ,\left\{ 0 \right\}_{{14}} ,N_{9} } \right] \hfill \\ \end{gathered}$$

(35)

and ${N}_{i}$ ($i=\mathrm{1,2},\dots ,9$) are Lagrange interpolation functions which are defined as follows:

$$\begin{aligned} & N_{1} \left( {\xi ,\eta } \right) = \frac{1}{4}\eta \xi \left( {\eta - 1} \right)\left( {\xi - 1} \right) \\ & N_{2} \left( {\xi ,\eta } \right) = - \frac{1}{2}\eta \left( {\xi^{2} - 1} \right)\left( {\eta - 1} \right) \\ & N_{3} \left( {\xi ,\eta } \right) = \frac{1}{4}\eta \xi \left( {\eta - 1} \right)\left( {\xi + 1} \right) \\ & N_{4} \left( {\xi ,\eta } \right) = - \frac{1}{2}\xi \left( {\eta^{2} - 1} \right)\left( {\xi - 1} \right) \\ & N_{5} \left( {\xi ,\eta } \right) = \left( {\eta^{2} - 1} \right)\left( {\xi^{2} - 1} \right) \\ & N_{6} \left( {\xi ,\eta } \right) = - \frac{1}{2}\xi \left( {\eta^{2} - 1} \right)\left( {\xi + 1} \right) \\ & N_{7} \left( {\xi ,\eta } \right) = \frac{1}{4}\eta \xi \left( {\eta + 1} \right)\left( {\xi - 1} \right) \\ & N_{8} \left( {\xi ,\eta } \right) = - \frac{1}{2}\eta \left( {\xi^{2} - 1} \right)\left( {\eta + 1} \right) \\ & N_{9} \left( {\xi ,\eta } \right) = \frac{1}{4}\eta \xi \left( {\eta + 1} \right)\left( {\xi + 1} \right) \\ \end{aligned}$$

(36)

where $\xi$ and $\eta$ are the natural coordinates of the system and defined as follows:

$$\xi =\frac{2\alpha }{{a}_{e}}-1, \eta =\frac{2\beta }{{b}_{e}}-1$$

(37)

It should be noted that ${a}_{e}$ and ${b}_{e}$ are the length and width of the assumed element. Now, in order to extract the vibration characteristics of the structure, the principle of energy is used. The use of the energy principle in the finite element method to calculate the dynamic and vibration characteristics of the structure is one of the most effective and efficient methods [43]. Therefore, by substituting Eqs. (34) in Eq. (16), the kinetic and potential energy terms are calculated as follows:

$$\begin{aligned} & T = \frac{1}{2}\left\{ {\dot{\delta }} \right\}^{T} \left[ {M_{e} } \right]\left\{ {\dot{\delta }} \right\} \\ & U = \frac{1}{2}\left\{ \delta \right\}^{T} \left[ {K_{e} } \right]\left\{ \delta \right\} \\ \end{aligned}$$

(38)

In which $\left[{M}_{e}\right]$ and $\left[{K}_{e}\right]$ are the mass and stiffness matrices of the element, respectively. On the other hand, using the defined element and substituting Eqs. (34) in Eq. (27), the work done by external forces can be expressed as follows:

$${W}_{F}={\left\{\delta \right\}}^{T}\left\{{F}_{e}\right\}$$

(39)

In which $\left\{{F}_{e}\right\}$ is the vector of elemental nodal forces. After assembling the mass and stiffness matrices and the force vector, the equation of motion for the system under external load can be expressed as follows:

$$\left[M\right]\left\{\ddot{\delta }\right\}+\left[K\right]\left\{\delta \right\}=\left\{F\right\}$$

(40)

In this equation, $\left[M\right]$ and $\left[K\right]$ represent the total mass and stiffness matrices, and $\left\{F\right\}$ represents the total external force vector. Additionally, $\left\{\delta \right\}$ and $\left\{\ddot{\delta }\right\}$ represent the displacements and accelerations of nodal points. By solving the differential Eq. (40), the response of the system under the applied load can be calculated. It should be mentioned that the static results of the system under the applied load can be obtained by setting the acceleration term in Eq. (40) equal to zero; the static deflection will be employed for nondimensionalizing the dynamic outcomes. For this purpose, the Newmark method is used. The Newmark method is an approximate method that is based on the finite difference method. According to this method, the response of the system under the applied load within the time interval $\overline{T }$ can be expressed as a sum of static responses of the system at each specified time ${t}_{n}$. Therefore, the time for solving the problem is divided into $n$ intervals, such that:

$$\Delta t = \frac{{\overline{T}}}{n}$$

(41)

Therefore:

$$t_{n} = n\Delta t,\;\;n = 1,2,3, \ldots ,n$$

(42)

It can be said that the solution of the system at each specific time ${t}_{n+1}$ can be calculated by solving the following equivalent equation:

$$\left[ {\overline{K}} \right]_{n + 1} \left\{ \delta \right\}_{n + 1} = \left\{ {\overline{F}} \right\}_{n + 1}$$

(43)

In which:

$$\begin{aligned} & \left[ {\overline{K}} \right]_{n + 1} = \left[ K \right]_{n + 1} + a_{0} \left[ M \right]_{n + 1} \\ & \left\{ {\overline{F}} \right\}_{n + 1} = \left\{ F \right\}_{n + 1} + \left[ M \right]_{n + 1} \left( {a_{0} \delta_{n + 1} + a_{2} \dot{\delta }_{n + 1} + a_{3} \ddot{\delta }_{n + 1} } \right) \\ \end{aligned}$$

(44)

By calculating ${\left\{\delta \right\}}_{n+1}$ from Eq. (43), the velocity and acceleration can also be calculated using the following equations:

$$\left\{ {\begin{array}{*{20}l} {\ddot{\delta }_{n + 1} = a_{0} \left( {\delta_{n + 1} - \delta_{n} } \right) - a_{2} \dot{\delta }_{n} - a_{3} \ddot{\delta }_{n} } \hfill \\ {\dot{\delta }_{n + 1} = \dot{\delta }_{n} + a_{6} \ddot{\delta }_{n} + a_{7} \ddot{\delta }_{n} } \hfill \\ \end{array} } \right.$$

(45)

In Eqs. (44) and (45), the constants ${a}_{0}$, ${a}_{2}$, ${a}_{3}$, ${a}_{6}$, and ${a}_{7}$ are defined as follows:

$$\begin{aligned} & a_{0} = \frac{1}{{\overline{\beta }\Delta t^{2} }},\;\; a_{2} = \frac{1}{{\overline{\beta }\Delta t}},\;\;a_{3} = \frac{1}{{2\overline{\beta }}} - 1 \\ & a_{6} = \left( {1 - \overline{\alpha }} \right)\Delta t,\;\;a_{7} = \overline{\alpha }\Delta t \\ \end{aligned}$$

(46)

and $\overline{\alpha }$ and $\overline{\beta }$ are constants that are determined using the selected method and the desired convergence rate. It should be noted that in this analysis, the linear acceleration method with $\overline{\alpha }=0.33$ and $\overline{\beta }=0.5$ has been used. The algorithm for using the Newmark method is summarized as follows:

• (a) Formation of overall mass and stiffness matrices

• (b) Determination of initial conditions, including initial displacement and velocity, and calculation of initial acceleration of the system

• (c) Determination of the time step and parameters $\overline{\alpha }$ and $\overline{\beta }$

• (d) Calculation of integration constants (Eq. (46))

• (e) Calculation of the effective stiffness matrix using Eq. (44)

Operations at each time step:

• (a) Calculation of the effective load at time $t+\Delta t$ using Eq. (44)

• (b) Calculation of displacement at time $t+\Delta t$ using Eq. (43)

• (c) Calculation of velocity and acceleration at time $t+\Delta t$ using Eq. (45)

3 Results and discussion

3.1 Material properties

Table 1 provides the mechanical characteristics of the face sheets and core, based on the assumption that M1 material is used for the core, and M2 material is used for the face sheets. In the following sections, a brief four-letter symbol is used to indicate the boundary conditions of the structure. For example, the abbreviation CFCS denotes a configuration in which the edges $\alpha =0$, $\beta =0$, $\alpha =a$, and $\beta =b$ are clamped, free, clamped, and simply supported, respectively.

Table 1 Mechanical properties for the core and the face sheets

3.2 Convergence and validation study

To evaluate the effectiveness and accuracy of both the mathematical modeling and the proposed finite element solution, the free vibration of the system is analyzed. This analysis assumes that there are no external loads acting upon the structure (i.e., ${W}_{F}=0$). First, an investigation is carried out to determine the optimum number of elements needed for achieving reasonable accuracy in a convergence study. Table 2 presents the first six dimensionless natural frequencies of the case study, where ${\rho }_{c}$, ${E}_{c}$, $\overline{\omega }$, $a$, and $h$ represent the density, Young's modulus of the core, the natural frequency, length, and height of the structure, respectively. The results are calculated for a simply supported sandwich cylindrical panel with a square plane form ($a/b=1$). The radius of curvature-to-length ratio (${R}_{\alpha }^{c}/a$) is set to $1$, the side-to-thickness ratio ($a/h$) is $10$, and the core thickness to total thickness ratio (${h}_{c}/h$) is $0.88$. The lamination scheme for both the top and bottom face sheets is $\left[0/90/0\right]$. Additionally, the core and face sheets are assigned material properties M1 and M2, respectively.

Table 2 Convergence study of the first six dimensionless natural frequencies, $\Omega =\overline{\omega }{a}^{2}\sqrt{{\rho }_{c}/{E}_{c}}/h$, of simply supported cylindrical sandwich panel

Considering the presented results in Table 1 and taking into account both accuracy and computation cost, a mesh density of $10\times 10$ is chosen and applied throughout all subsequent analyses. It should be mentioned that the reported runtime belongs to a Personal computer with processor properties: Intel (R) core (TM) i3-4170 CPU @ 3.70 GHz, and installed memory RAM: 8.00 GB.

To provide an example, a soft core sandwich plate with an unsymmetric lamination scheme $\left[0/90/{\text{Core}}/0/90\right]$ is considered, with material properties M1 and M2 designated for the core and the face sheets, respectively. To compare the results obtained using the proposed method with existing literature, Tables 3, 4 and 5 present the results for various $a/h$, ${h}_{c}/{h}_{f}$, and $a/b$ ratios. These results are compared against those based on exact theory [44], higher-order sandwich panel theory (HSAPT), and local–global and finite element method [45]. As can be seen, excellent agreements have been observed.

Table 3 Non-dimensional fundamental natural frequency ($\Omega =\overline{\omega }{a}^{2}\sqrt{{\left(\rho /{E}_{22}\right)}_{f}}/h$) of five-layered antisymmetric ($\left[0/90/{\text{Core}}/0/90\right]$) sandwich square plate (M3 and M4, ${h}_{c}/{h}_{f}=10$)

Table 4 Non-dimensional fundamental natural frequency ($\Omega =\overline{\omega }{a}^{2}\sqrt{{\left(\rho /{E}_{22}\right)}_{f}}/h$) of five-layered antisymmetric ${(\left[0/90/{\text{Core}}/0/90\right]}$) sandwich square plate (M3 and M4, $a/h=10$)

Table 5 Non-dimensional fundamental natural frequency ${(\Omega =\overline{\omega }{b}^{2}\sqrt{{\left(\rho /{E}_{22}\right)}_{f}}/h}$) of five-layered antisymmetric ${(\left[0/90/{\text{Core}}/0/90\right]}$) sandwich rectangular plate (M3 and M4, $a/h=10$, ${h}_{c}/{h}_{f}=10$)

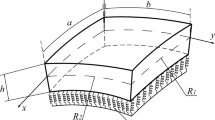
After evaluating the accuracy of the results, to investigate the dynamic response of the system, it is assumed that a load with a constant amplitude is moving along the central axis of the structure longitudinally with a constant speed $v$ (Fig. 3). Therefore, the force distribution is equal to:

$$f\left(\alpha ,\beta ,t\right)={f}_{0}\delta \left(\alpha -\zeta (t),\beta -\frac{b}{2}\right)$$

(47)

where $\zeta (t)$ represents the position of the moving load at time $t$. It should be noted that the time interval considered for investigating the vibrational system will be the period in which the force is present on the structure or $\left[0,a/v\right]$, where $a$ is the length of the structure.

Fig. 3

Sandwich shell subjected to a constant moving force

To investigate the dynamic response of the system, two types of diagrams are used. The first type of diagram shows the variation of the dynamic magnification factor (DMF) with respect to the non-dimensional velocity (${v}^{*}={T}_{f}/\tau$), where the DMF parameter represents the ratio of the maximum dynamic deflection at the midpoint of the structure to its static deflection. The parameter ${T}_{f}$ represents the fundamental vibration period of the structure and $\tau$ is the time required for the moving load to pass through the structure ($\tau =a/v$). By plotting the DMF diagram as a function of ${v}^{*}$, the critical velocity (${v}_{cr}$) of the system, where the maximum deflection occurs, can be determined. With the critical velocity, the ${\overline{w} }_{m}$ diagram as a function of the non-dimensional position ${\overline{x} }_{f}$ can be drawn. In this type of diagram, ${\overline{w} }_{m}$ represents the ratio of the dynamic deflection of the midpoint of the structure to its static deflection at critical velocity, and ${\overline{x} }_{f}$ represents the non-dimensional horizontal position ($vt/a$) of the moving force. It should be noted that in this section, to calculate the static response of the system, a force equal to ${f}_{0}$ is applied at the center of the structure ($\alpha =a/2$ and $\beta =b/2$).

3.3 Effect of length-to-thickness ratio

The first example in this section examines three different types of geometries: a sandwich plate, a cylindrical sandwich panel, and a spherical sandwich panel. The laminating scheme used in this example is a symmetric five-layer lamination $[0/90/{\text{Core}}/90/0]$. The structure has a square plane form with an aspect ratio of $a/b=1$. To investigate the effect of the length-to-thickness ratio, four different ratios of $a/h=10$, 20, 30, and 40 are examined. The ratio of core-to-face thickness is set to ${h}_{c}/{h}_{f}=10$. It is important to note that the results in this section are calculated using two different types of boundary conditions: simply supported (SSSS) and cantilever (CFFF). The results for the sandwich plate, cylindrical sandwich panel, and spherical sandwich panel are presented in Figs. 4, 5 and 6.

Fig. 4

DMF versus dimensionless velocity for a sandwich plate with a SSSS, and b CFFF boundary conditions and different thickness ratios

Fig. 5

DMF plot as a function of dimensionless velocity for a cylindrical sandwich panel with a SSSS, and b CFFF boundary conditions and various thickness ratios

Fig. 6

DMF plot as a function of dimensionless velocity for a spherical sandwich panel with a SSSS, and b CFFF boundary conditions and various thickness ratios

Based on the graphs presented above, it can be inferred that regardless of the type of geometry or boundary conditions, the DMF curve increases with non-dimensional velocity as the length-to-thickness ratio decreases (i.e., thickness increases). This indicates that thinner structures experience higher deflection in the same loading. Furthermore, the spherical geometry exhibits the highest deflection, while the flat geometry experiences the least deflection. Moreover, a comparison of the two boundary conditions indicates that the CFFF boundary condition results in more deflection than the SSSS boundary condition, which can be attributed to the overall stiffness of the structure due to different boundary conditions. Additionally, Table 6 provides the non-dimensional velocity (${v}^{*}$) at which the maximum DMF occurs for each structure.

Table 6 The critical dimensionless velocity for a sandwich plate, cylindrical sandwich panel, and spherical sandwich panel with SSSS and CFFF boundary conditions

It can be concluded that the maximum DMF occurs at ${t}^{*}\approx 1$ for all thickness ratios with SSSS boundary conditions. However, for the CFFF boundary conditions, the maximum DMF occurs at ${t}^{*}=1.4$. Based on this observation, it is possible to calculate the critical velocity for each structure. Therefore, the behavior of the midpoint of the three geometries (sandwich plate, cylindrical, and spherical sandwich panels) for both SSSS and CFFF boundary conditions is illustrated in Figs. 7, 8 and 9. It should be mentioned that for better comparison, dynamic deflection for all length-to-thickness ratios ($a/h=10, 20, 30$, and $40$) are divided to static deflection of the midpoint of the structure with $a/h=10$.

Fig. 7

Dynamic displacement of the structure's center as a function of dimensionless force location for a sandwich plate with a SSSS boundary conditions and b CFFF boundary conditions

Fig. 8

Dynamic displacement of the structure's center as a function of dimensionless force location for a cylindrical sandwich panel with a SSSS boundary conditions and b CFFF boundary conditions

Fig. 9

Dynamic displacement of the structure's center as a function of dimensionless force location for a spherical sandwich panel with a SSSS boundary conditions and b CFFF boundary conditions

To ensure a more accurate comparison, it is necessary to normalize the dynamic deflection of structures with varying length-to-thickness ratios ($a/h=10, 20, 30 \,\,{\text{and}} \,\,40$). This normalization is achieved by dividing the dynamic deflection by the static deflection of the midpoint of the structure, with a fixed aspect ratio of $a/h=10$. The analysis reveals that as the length-to-thickness ratio increases, the structure exhibits significantly higher deflections for both considered boundary conditions. This observation suggests a strong correlation between the length-to-thickness ratio and the magnitude of deflections.

3.4 Effect of in-plane aspect ratio

In this section, the focus is on investigating the effect of in-plane aspect ratio on the dynamic response of three types of geometries, namely sandwich plate, cylindrical, and spherical sandwich panels. These structures are considered with SSSS boundary conditions, $a/h=10$, core-to-face thickness ratio ${h}_{c}/{h}_{f}=10$, and $[0/90/{\text{core}}/90/0]$ layup. Four in-plane aspect ratios $a/b=1, 2, 3, 5$ are examined for each structure to study the impact of in-plane aspect ratio on their dynamic response. It is important to note that for cylindrical and spherical sandwich panels, the radius-to-length ratio is assumed to be ${R}_{\alpha }/a=5$. The DMF curve for each geometry is presented in Fig. 10 as a function of ${v}^{*}$.

Fig. 10

Variation of DMF with dimensionless velocity for various aspect ratios for a sandwich panel, b cylindrical sandwich panel, and c spherical sandwich panel

According to the above figure, it can be observed that in all three geometries, the DMF initially increases as the in-plane aspect ratio ($a/b$) increases at low velocities (${v}_{cr}<0.7$), where $a/b=1$ exhibits the lowest DMF, and $a/b=5$ shows the highest. However, as the velocity increases and after passing through a transition stage, the trend completely reverses, and DMF decreases with increase in $a/b$ ratio. Additionally, it is noteworthy that the critical velocity decreases with increase in $a/b$ ratio for all three geometries. Table 7 presents the critical velocity (${v}_{cr}$) for each geometry.

Table 7 Dimensionless critical velocity for sandwich plate, cylindrical, and spherical sandwich panels with SSSS boundary conditions

3.5 Effect of radius-to-length ratio

In this section, the effect of the radius-to-length ratio of the structure on its dynamic response is investigated by considering two geometries of cylindrical and spherical sandwich panels with square plane form ($a/b = 1$) and SSSS boundary conditions. The length-to-thickness ratio is set to $a/h = 10$, the core-to-face thickness ratio is $h_{c} /h_{f} = 10$, and the $\left[ {0 / 90 / {\text{core}} / 90 / 0} \right]$ lamination scheme is used for four different radius-to-length ratios $R_{\alpha } /a = 1, 2, 3, 5$. The DMF curves as a function of ${v}^{*}$ for each geometry are presented in Fig. 11. Additionally, Table 8 provides the critical velocity (${v}_{cr}$) for each geometry. As can be seen, low dimensionless velocities by increasing the radius of curvature-to-length ratio decrease; however, for high velocities the trend is completely reversed.

Fig. 11

Variation of DMF versus dimensionless velocity for various radius-to-length ratio for a cylindrical sandwich panel, and b spherical sandwich panel

Table 8 Dimensionless critical velocity for cylindrical, and spherical sandwich panels under SSSS boundary conditions

3.6 Effect of lamination scheme and fiber orientation angle

In this section, the effect of the lamination scheme and fiber orientation angle is investigated for three types of geometries, including sandwich plate, cylindrical, and spherical sandwich panels. Two types of symmetric five-layer lamination, $\left[ {0/\theta /{\text{core}}/\theta /0} \right]$ and unsymmetric five-layer lamination $\left[ {0/\theta /{\text{core}}/\theta /0} \right]$, are considered, along with fiber orientation angles of $\theta = 30, 45, 60$, and $90$. The length-to-thickness ratio of $a/h = 10$, square plane form $a/b = 1$, SSSS boundary conditions, core-to-face thickness ratio of $h_{c} /h_{f} = 10$, and radius-to-length ratio of $R_{\alpha } /a = 5$ for cylindrical and spherical sandwich panels are assumed. The results for the sandwich plate, cylindrical, and spherical sandwich panels are presented in Figs. 12, 13 and 14, respectively.

Fig. 12

The DMF plot versus non-dimensional velocity for the sandwich plate, a the non-symmetric lamination and b the symmetric lamination

Fig. 13

The DMF versus non-dimensional velocity for the cylindrical sandwich panel, a the non-symmetric lamination and b the symmetric lamination

Fig. 14

The DMF versus non-dimensional velocity for the spherical sandwich panel, a the non-symmetric lamination and b the symmetric lamination

It can be observed that in the case of the sandwich plate, as shown in Fig. 12, until reaching the critical velocity, DMF changes are very small for four different orientations. However, after the critical velocity until the non-dimensional velocity ${v}^{*}=2.1$, the maximum DMF is observed for $\theta =90$ among the considered fiber orientations, while the minimum DMF is observed for $\theta =30$. Then, the trend is reversed. In the case of the cylindrical sandwich panel, $\theta =30$ initially has the lowest DMF, but after ${v}^{*}=0.8$, it experiences the lowest DMF among the other fiber orientations in both types of arrangements. Similar results can be inferred for the spherical sandwich panel. The critical velocity for all three types of geometry and fiber orientation angles is given in Table 9. As can be seen, the sandwich plate has the highest values for the dimensionless critical velocity and the sandwich spherical panel has the lowest among considered geometries.

Table 9 Dimensionless critical velocity for sandwich plate, cylindrical and spherical sandwich panels in the case of various lamination scheme and different fiber orientation angle

3.7 Effect of boundary conditions

In this section, the effect of boundary conditions is investigated. Similar to previous sections, three types of geometry including, sandwich plate, cylindrical and spherical sandwich panels are considered. it is assumed that structures have square plane form, the length-to-thickness ratio is $a/h = 10$, and the lamination scheme is symmetric with five layers $\left[ {0/90/{\text{core}}/90/0} \right]$. The ratio of core-to-face thickness is $h_{c} /h_{f} = 10$, and for cylindrical and spherical sandwich panels, the radius-to-length ratio is $R_{\alpha } /a = 5$. The critical velocity is presented separately for each of the three structures and seven different boundary conditions in Table 10.

Table 10 Effect of boundary conditions on the dimensionless critical velocity of sandwich structures

4 Conclusions

This paper investigated the forced vibration characteristics of soft core sandwich panels when subjected to a moving force with constant amplitude. The compressibility of the core is effectively modeled using the extended higher-order sandwich panel theory (EHSAPT). The face sheets are represented using the first-order shear deformation theory (FSDT), while the core's displacement field employs a third-order polynomial function for in-plane components and a second-order function for the transverse displacement component. Numerical modeling of the structure is performed using a higher-order nine-node quadrilateral element, allowing for fifteen degrees of freedom per node. The dynamic response of the system is computed using the Newmark method. Validation is achieved by comparing these results with existing literature. The investigation delves into the impact of various parameters, such as the in-plane aspect ratio, side-to-thickness ratio, boundary conditions, lamination scheme, and fiber orientation angle, on the dynamic response of the structure. Additionally, the critical velocity is determined for each case study. The findings highlight crucial insights for the considered geometry and material properties:

• Regardless of the geometry or boundary conditions, the DMF curve increases when the length-to-thickness ratio decreases (i.e., thickness increases). This suggests that thinner structures experience higher deflections.

• Among the different geometries investigated, the spherical geometry exhibits the highest DMF, while the flat geometry experiences the least DMF.

• A comparison of two different boundary conditions reveals that the CFFF (Clamped-Free-Free-Free) boundary condition results in more DMF compared to the SSSS (Simply supported) boundary condition. This can be attributed to the overall stiffness of the structure, which is influenced by the boundary conditions.

• In all three geometries, the DMF initially increases as the in-plane aspect ratio ($a/b$) increases at low velocities (${v}_{cr}<0.7$). The geometry with a ratio of $a/b=1$ exhibits the lowest DMF, while a ratio of $a/b=5$ shows the highest. However, as the velocity increases and after passing through a transition stage, the trend completely reverses, and the DMF decreases with increase in $a/b$ ratio.

• Additionally, it is worth noting that the critical velocity (${v}_{cr}$) decreases with increase in in-plane aspect ratio ($a/b$) for all three geometries. This implies that as the $a/b$ ratio increases, the structure becomes more sensitive to higher velocities.

• The relationship between the radius of curvature-to-length ratio and the dimensionless velocities is observed to be inversely proportional. In other words, for low dimensionless velocities, an increase in the radius of curvature-to-length ratio leads to a decrease in uplift force. However, for high velocities, this trend is completely reversed.