1 Introduction

Thanks to the everlasting development of nanotechnology which is led to providing super-performance composite materials, great research interest is sparked in the field of composite materials reinforced with nanoscale fillers such as nanoparticle [1], nanofiber [2, 3], CNT [4,5,6,7,8,9,10] and various combinations of nanofillers [11]. Revealing the remarkable superiority of graphene platelets in terms of toughness, Young’s modulus, strength, etc., compared to other carbon reinforcements since its initial introduction, that is, since Novoselov et al. [12] exfoliated it from a bulk graphite in 2004, it has caused the attention of the research and industrial community. Owing to its superior mechanical properties, namely Young modulus-1TPa, ultimate strength-130 GPa and significant thermal and electrical characteristics, a very low amount of added GPLs to polymer matrix can result in significant enhancement of properties of polymer-GPL composites, as highlighted by Rafiee et al. [13], Biswas et al. [14], Parashar and Mertiny [15]. Due to the high strength-to-weight ratio of composites reinforced with graphene platelets, it is predicted that such types of composites will be one of the most promising materials in future advent industries, especially in the aerospace industry. The mentioned items, in addition to its lower relative cost of the manufacturing process, have been the sake of the tendency of research and industrial centers to use these materials and the inspiring for conducting extensive numerical and analytical research in this realm. Due to the prevention of agglomeration and other problems in the manufacturing process, graphene platelets are generally added in a low volume percentage to polymer matrices; therefore, to increase the reinforcing efficiency, the layer-wise functionally graded distribution pattern along one or two directions may be assumed [16]. In recent years, the dynamic and static behavior of composites reinforced with functionally grade graphene platelets has been well modeled and discussed. Yang et al. assuming that the randomly oriented GPLs are used to reinforce the polymer matrix, studied bending behavior [17], buckling and post-buckling characteristics [18, 19], dynamic instability [20] and large-deflection vibrations responses [21] of functionally graded GPL-reinforced composite (FG-GPLRC) beam [20, 21], FG-GPLRC plate [18], FG-GPLRC trapezoidal plate [17] and FG-GPLRC cylindrical shell [19].

Ganapathi et al. [20] within the framework of trigonometric shear flexible model used finite element method to study the nonlinear flutter phenomenon for the functionally graded GPL-reinforced porous curved panel. Niu and his colleagues dealt with dynamic behavior of rotating pre-twisted functionally graded composite cylindrical panel. They utilized Chebyshev-Ritz method to obtain the vibration responses of the FG-GPLRC cylindrical panel. They analyzed bending response [23], thermal buckling and post-buckling [24], dynamic instability [25] and nonlinear transient response [26] of the FG-GPLRC plates [23, 25, 26], FG-GPLRC cylindrical panel and FG-GPLRC cylindrical shell [24] in thermal environments. On the basis of a variational approach, Gholami and Ansari [27] explored the primary resonant dynamics of functionally graded GPL-reinforced composites. Also, Gholami and Ansari [28] formulated the nonlinear vibrations of plates made of functionally graded graphene platelet composites using a unified higher-order shear deformable theory. Zhou et al. [29] based on a higher-order model excavated the nonlinear buckling responses of laminated composite porous cylindrical shells considering various patterns of GPLs and porosity distribution. With the aid of a Navier solution method, the effects of distribution pattern, weight fraction, geometry and size of GPLs and the effect of total number of layers on free vibration frequency of FG-GPLRC plates were analytically studied by Song et al. [30]. Baghbadorani et al. [31] exploited the first-order shear deformation theory of shells in accompany with Donnell kinematic relations to perform a free vibration frequency analysis for FG-GPLRC cylindrical shells. Esmaeili and his co-researchers through a Ritz solution method explored the free vibration characteristics of functionally graded GPLRC doubly curved panels [32]. Besides, they analyzed thermal-induced vibrations of FG-GPLRC flat plates [33] and curved panels [34].

Piezoelectric materials have played an important role in coupling the mechanical and electrical fields. To utilize in various electromechanical applications as sensors and actuators, efficient structures with superior properties can be provided by combining composite materials with piezoelectric materials. On the basis of piezoelectricity, the direct and reverse effects of piezoelectric materials is described which system controllability is oriented from. So far, to perform dynamic analysis of piezoelectric-surrounded structures, researchers have developed different mathematical approaches. To numerically predict static and dynamic behaviors of smart FG-GPLRC microplates subjected to concurrently electrical and mechanical loads, Nguyen and Lee [35] developed a numerical model on the basis of a refined plate theory, modified couple stress theory and NURBS-based isogeometric analysis. Using 3D theory of elasticity, Jalali et al. [36] investigated free vibrations of functionally graded GPL-reinforced imperfect panel surrounded with piezoelectric layers. Dong et al. [37] perused the active vibration control of sandwich thin cylindrical shells made of FG-GPLRC core and piezoelectric face sheets. They also obtained free vibration frequencies of the structure by regarding effects of the thermo-electro-elastic field. Considering a high-order shear deformation model and von Kármán terms, Lin et al. [38] obtained vibration characteristics of multilayer plates made of GPL-reinforced composite material. They also reported aeroelastic response of the plates under the action of electrical and mechanical loads. Alibeigloo and Nouri [39] obtained three-dimensional static solution of functionally graded (FG) cylindrical shell with piezoelectric layers by adopting state-space approach and implementing differential quadrature method (DQM). With the accordance of first-order shear deformation theory (FSDT), and nonlinear von Kármán assumptions, Bayat et al. [40] formulated the large-amplitude vibration control of functionally graded piezoelectric cylindrical shells subjected to concurrently axial and radial external excitations.

Jinhua et al. [41] checked bifurcation and chaos of functionally graded multilayer composite cylindrical shells with GPL reinforcements and piezoelectric layers as a result of action of a combination of electrical, mechanical and thermal loads. Ebrahimi [42] exploited the 3D elasticity theory to present a general formula for frequency analysis of a fluid conveying composite multilayer cylindrical shell made of functionally graded material bounded with piezoelectric layers. With the accordance of a quasi-three-dimensional (3D) refined shear and normal deformation theory and through an electromechanical model, Alghanmi et al. [43] obtained bending response of functionally graded porous plates attached to a layer made of piezoelectric fiber-reinforced composite (PFRC). Such plates were under the action of sinusoidal electromechanical loads. Behavior of piezoelectric laminated composite plate exposed to various electromechanical loads was surveyed by Markad et al. [44] using the first-order shear deformation model.

The static and dynamic behaviors of panels with rectangular planform have assigned an important position in research topics in both scholar and industrial community; this importance comes from their various practical applications of these structures in various realms, including civil, mechanical, architectural, marine and aeronautical engineering. A number of theoretical analysis on such panels which performed to attain an efficient design are listed as follows:

Lore et al. [45] probed nonlinear free vibration characteristics of functionally graded plates and shell panels. Li et al. [46] investigated free vibrations of composite/sandwich shell panels. Shen and Wang [47] studied free vibrations of shear deformable FGM cylindrical panels considering the effects of thermal environment and effects of interaction between panel and elastic foundation. Viola et al. [48] used a 2D higher-order shear deformation theory to provide a general framework for dynamic investigation of doubly curved composite panels. Chen et al. [49] evaluated a novel formulation to study free vibration frequency of rotating pre-twisted laminated composite shell panels. Karimi et al. [50] in an orthogonal curvilinear coordinate system implemented higher-order model to probe forced vibration of anisotropic curved panels. Karimiasl and Alibeigloo [51] carried out free vibration analysis of composite sandwich cylindrical panels composed of double-V auxetic core and GPL-reinforced composite face sheets. In the above research, the effect of the aerohygrothermal environment was investigated. Free vibration frequencies of moderately thick cylindrical composite sandwich panels were obtained by Pourmoayed et al. [52] through an improved higher-order theory. Mohammadimehr et al. [53] discussed the parameters affecting the free vibration frequency of functionally graded CNT-reinforced magneto-electro-elastic cylindrical composite panel according to first-order shear deformation theory. Keleshteri and Jelovica [54] investigated free vibration characteristics and buckling behavior of sandwich panels made of functionally graded metal foam core surrounded with two thin face sheets.

The poor literature around free vibration analysis of FG-GPLRC cylindrical panel with piezoelectric layers is revealed with the aid of the above-presented literature review. Present study attempts to provide a numerical model with the ability of handling an arbitrary vast set of mechanical and electrical boundary conditions. Mechanical properties of the panel are approximated via Halpin–Tsai micromechanical model in accompany with the rule of mixtures. Electromechanically coupled governing equations are provided by applying Hamilton principle. Legendre-Ritz formulation is implemented to obtain discretized governing equations; accordingly, natural frequencies are calculated. The rest of article deals with validating present model and subsequently performing parametric studies. As shown for different combinations of edge supports, various GPL weight fractions and patterns, open circuit type of edge support results in higher frequencies.

2 Problem description

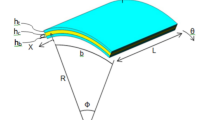
The functionally graded GPL-reinforced cylindrical panel surrounded with two identical piezoelectric layers is under free vibration analysis with details as follows. Its geometrical properties are symbolized as follows: length of straight edge: \(a\), length of curved edge: \(b\), radius of curvature: \(R\) and total thickness of panel: \(h+2{h}^{p} \mathrm{where} {h}^{p}\) is the thickness of piezoelectric layer and \(h\) is the thickness of the core. Figure 1 also provides a schematic of the structure.

Fig. 1
figure 1

Schematic of the structure composed of GPLRC core and piezoelectric faces

Full size image

It is assumed that an even number of GPL-reinforced layers (\({N}_{L}\)) of the same size, arranged according to a mathematical function are composed the panel. Besides, uniform dispersion and random orientation for GPLs in each layer is considered. To describe deformations and displacements, a curvilinear coordinate system mounted on mid-plane of the panel in such a way that it describes the panel domain as: \({-0.5a\le x}_{1}\le 0.5a, {-0.5b\le x}_{2}\le 0.5b\) and \({-0.5h-{h}^{p}\le x}_{3}\le 0.5h+{h}^{p}\) is considered.

Several types of GPL distribution profiles through the thickness may be assumed. Herein, the following distribution patterns with linear variations of GPL weight fraction from layer to layer are taken to account. Such patterns are demonstrated in Fig. 2 and are listed as:

  1. (a)

    FG-U

    Here, monotonic dispersion of GPLs through the panel thickness is assumed. Accordingly, we will deal with an isotropic and homogeneous cylindrical panel, i.e.,

    $${V}_{GPL}^{(k)}={V}_{GPL }^{*}\quad (k= 1, 2, \ldots ,{N}_{L})$$
    (1)
  2. (b)

    FG-X

    Based on this pattern, the layers with the highest GPL volume fraction are located in the top and bottom surfaces, while GPL-poor layers can be found in mid-surfaces. This pattern is symmetrical with respect to the mid-plane, i.e.,

    $${V}_{GPL}^{(k)}=2{V}_{GPL}^{*}\frac{|2k-{N}_{L}-1|}{{N}_{L}}\quad (k= 1, 2, \ldots ,{N}_{L})$$
    (2)
  3. (c)

    FG-O

    In this pattern, the positions of the GPL-rich and GPL-poor layers are completely in contrary to what was outlined about the FG-X pattern. For instance, GPL volume fraction is the lowest at top and bottom, i.e.,

    $${V}_{GPL}^{\left(k\right)}=2{V}_{GPL}^{*}\left(1-\frac{\left|2k-{N}_{L}-1\right|}{{N}_{L}}\right)\quad (k= 1, 2, \ldots ,{N}_{L})$$
    (3)
  4. (d)

    FG-V

    Next pattern which is an asymmetric pattern with respect to the middle plane provides the maximum amount of GPLs at top and its minimum at bottom, i.e.,

    $${V}_{GPL}^{\left(k\right)}={V}_{GPL}^{*}\frac{2k-1}{{N}_{L}}\quad (k= 1, 2, \dots ,{N}_{L})$$
    (4)
  5. (e)

    FG-A

    The last pattern, which is again an asymmetric pattern, is defined as linearly increasing variation of GPL volume fraction from top to bottom surface, i.e.,

    $${V}_{GPL}^{\left(k\right)}={V}_{GPL}^{*}\frac{-2k+1+2{N}_{L}}{{N}_{L}}\quad (k= 1, 2, \dots ,{N}_{L})$$
    (5)

The above relationships provide the GPL volume fraction of the \(k\)-th layer (\({V}_{GPL}^{\left(k\right)}\)) in terms of the total GPL volume fraction of the FG-GPLRC panel (\({V}_{GPL}^{*}\)).

The relationship between the GPL volume fraction (\({V}_{GPL}^{*}\)) and the GPL weight fraction (\({W}_{GPL}^{*}\)) having the density ratio (\({\rho }_{GPL}/{\rho }_{m}\)) is expressed as follows [31]

$${V}_{GPL}^{*}=\frac{{W}_{GPL}}{{W}_{GPL}+\frac{{\rho }_{GPL}}{{\rho }_{m}}(1-{W}_{GPL})}$$
(6)

By having the GPL volume fraction in each layer, the mechanical properties can be calculated.

Fig. 2
figure 2

Layer-wise functionally graded GPL distribution patterns

Full size image

First, Young’s modulus is estimated exploiting the Voigt–Reuss model as:

$${E}^{(k)}=\frac{3}{8}{E}_{1}^{(k)} +\frac{5}{8}{E}_{2}^{(k)}$$
(7)

Longitudinal modulus \({E}_{1}^{(k)}\) and transverse modulus \({E}_{2}^{(k)}\) are approximated via the Halpin–Tsai micromechanical model which is modified to include the effects of size and geometry of nanoscale fillers [31].

$$\begin{aligned} E_{1}^{\left( k \right)} & = \frac{{1 + \xi_{L} \eta_{L} V_{GPL}^{\left( k \right)} }}{{1 - \eta_{L} V_{GPL}^{\left( k \right)} }}E_{m} \\ E_{2}^{\left( k \right)} & = \frac{{1 + \xi_{T} \eta_{T} V_{GPL}^{\left( k \right)} }}{{1 - \eta_{T} V_{GPL}^{\left( k \right)} }}{ }E_{m} \\ \end{aligned}$$
(8)

where

$${\eta }_{L}=\frac{{E}_{GPL}-{E}_{m}}{{E}_{GPL}+{\xi }_{L}{E}_{m}}{\eta }_{T}=\frac{{E}_{GPL}-{E}_{m}}{{E}_{GPL}+{\xi }_{T}{E}_{m}}$$
(9)

Here, the elastic moduli are represented by \({E}_{m}\) and \({E}_{GPL}\), corresponding to the matrix and GPL, respectively. Also, \({\xi }_{L}\) and \({\xi }_{T}\) are two parameters that include both GPL size and geometry effects [31].

$${\xi }_{L}=2\frac{{l}_{GPL}}{{h}_{GPL}}{\xi }_{T}=2\frac{{w}_{GPL}}{{h}_{GPL}}$$
(10)

\({w}_{GPL}\), \({l}_{GPL}\) and \({h}_{GPL}\) in above are used for average width, length, and thickness of GPLs, respectively.

Next, the law of mixtures is utilized to calculate density and Poisson's ratio of the composite media as [31]

$$\begin{aligned} \nu^{\left( k \right)} & = \nu_{m} \left( {1 - V_{GPL}^{\left( k \right)} } \right) + \nu_{GPL} V_{GPL}^{\left( k \right)} \\ \rho^{\left( k \right)} & = \rho_{m} \left( {1 - V_{GPL}^{\left( k \right)} } \right) + \rho_{GPL} V_{GPL}^{\left( k \right)} \\ \end{aligned}$$
(11)

3 Mathematic model derivation

Different theories may be used to estimate and model the displacement in beams, plates and shell, see, e.g., [55,56,57,58,59,60,61,62,63]. Considering the piezoelectric layers leads to dealing with a moderately thick panel, hence, the first-order shear deformation model (FSDT) is the most optimal choice to describe the displacement field, accordingly [32,33,34],

$$\mathbf{U}=\left\{\begin{array}{c}{U}_{1}\left({x}_{1},{x}_{2},{x}_{3},t\right)\\ {U}_{2}\left({x}_{1},{x}_{2},{x}_{3},t\right)\\ {U}_{3}\left({x}_{1},{x}_{2},{x}_{3},t\right)\end{array}\right\}=\left\{\begin{array}{c}u\left({x}_{1},{x}_{2},t\right)+{x}_{3} {\theta }_{1}\left({x}_{1},{x}_{2},t\right)\\ v\left({x}_{1},{x}_{2},t\right)+{x}_{3} {\theta }_{2}\left({x}_{1},{x}_{2},t\right)\\ w\left({x}_{1},{x}_{2},t\right)\end{array}\right\}$$
(12)

The projections of displacement on the mid-plane along with \({x}_{1}\)-, \({x}_{1}\)- and \({x}_{3}\)-axes are represented by \(u\), \(v\) and \(w\), respectively. Besides, \({\theta }_{1}\) and \({\theta }_{2}\) signify to rotations of transverse normal about \({x}_{2}\)- and \({x}_{1}\)-axes, respectively.

On the basis of given displacement field, one can present linear strain–displacement relations as follows for the in-plane strains

$$\begin{aligned} \varepsilon _{{11}} & = U_{{1,x_{1} }} = \varepsilon _{{11}}^{0} + x_{3} \kappa _{1} = u_{{,x_{1} }} + x_{3} \theta _{{1,x_{1} }} \\ \varepsilon _{{22}} & = U_{{2,x_{2} }} = \varepsilon _{{22}}^{0} + x_{3} \kappa _{1} = v_{{,x_{1} }} + \frac{w}{R} + x_{3} \theta _{{2,x_{2} }} \\ \varepsilon _{{12}} & = U_{{1,x_{2} }} + U_{{2,x_{1} }} = \varepsilon _{{12}}^{0} + x_{3} \kappa _{{12}} = u_{{,x_{2} }} + v_{{,x_{1} }} + x_{3} \left( {\theta _{{1,x_{2} }} + \theta _{{2,x_{1} }} } \right) \\ \varepsilon _{{23}} & = \varepsilon _{{23}}^{0} = \theta _{2} + w_{{,x_{2} }} \\ \varepsilon _{{13}} & = \varepsilon _{{13}}^{0} = \theta _{1} + w_{{,x_{1} }} \\ \end{aligned}$$
(13)

In above relations and hereafter, (,) stands for differential operator.

4 Constitutive relations

4.1 Constitutive relations of GPLRC layers

For GPLRC layers, Hooke law compatible with the conditions of zero value for \({\sigma }_{33}^{(k)}\) states that stress vector, \({{\varvec{\upsigma}}}^{\left({\varvec{k}}\right)}={[{\sigma }_{11}^{(k)}, {\sigma }_{22}^{(k)}, {\sigma }_{12}^{(k)}, {\sigma }_{13}^{(k)},{\sigma }_{23}^{(k)}]}^{{\varvec{T}}}\) and strain vector, \({\varvec{\upvarepsilon}}={\left[{\varepsilon }_{11}. {\varepsilon }_{22}, { 2\varepsilon }_{12}, { 2\varepsilon }_{13},{ 2\varepsilon }_{23}\right]}^{T}\) are related by the following relation:

$${{\varvec{\upsigma}}}^{\left({\varvec{k}}\right)}={\mathbf{C}}^{\left({\varvec{k}}\right)}{\varvec{\upvarepsilon}}$$
(14)

\({\mathbf{C}}^{\left({\varvec{k}}\right)}\) is the elastic constant matrix for the \(k\)-th GPLRC layer.

$$\begin{aligned} {\mathbf{C}}^{{\left( \user2{k} \right)}} & = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{1}^{{\left( {\text{k}} \right)}} } &\quad 0 \\ 0 &\quad {{\mathbf{C}}_{2}^{{\left( {\text{k}} \right)}} } \\ \end{array} } \right] \\ {\mathbf{C}}_{1}^{{\left( {\text{k}} \right)}} & = \frac{{E^{{\left( k \right)}} }}{{1 - \upsilon ^{{\left( k \right)2}} }}\left[ {\begin{array}{*{20}l} 1 \hfill &\quad {\upsilon ^{{\left( k \right)}} } \hfill &\quad 0 \hfill \\ {\upsilon ^{{\left( k \right)}} } \hfill &\quad 1 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad {\frac{{1 - \upsilon ^{{\left( k \right)}} }}{2}} \hfill \\ \end{array} } \right]{\text{,~}} \\ {\mathbf{C}}_{2}^{{\left( {\text{k}} \right)}} & = \frac{{E^{{\left( k \right)}} }}{{2\left( {1 + \upsilon ^{{\left( k \right)}} } \right)}}\left[ {\begin{array}{*{20}c} 1 &\quad 0 \\ 0 &\quad 1 \\ \end{array} } \right] \\ \end{aligned}$$
(15)

4.2 Constitutive relations of top and bottom piezoelectric layers

In view of the piezoelasticity theory, the constitutive relation of piezoelectric layers may be written as:

$$\left\{\begin{array}{c}{{\varvec{\upsigma}}}^{\mathbf{p}}\\ \mathbf{D}\end{array}\right\}=\left[\begin{array}{cc}{\mathbf{C}}^{\mathbf{p}}&\quad -{\mathbf{e}}^{T}\\ \mathbf{e}&\quad{\varvec{\Xi}}\end{array}\right]\left\{\begin{array}{c}{\varvec{\upvarepsilon}}\\ \mathbf{E}\end{array}\right\}$$
(16)

In Eq. (16), \({\mathbf{C}}^{\mathbf{p}}\) signifies the elastic constant matrix for the piezoelectric layers, \({\varvec{\Xi}}\) is the dielectric permittivity constant matrix and \(\mathbf{e}\) represents the electromechanical coupling matrix; accordingly, they have following definition:

$$\begin{aligned} {\mathbf{C}}^{{\mathbf{p}}} & = \left( {\begin{array}{*{20}c} {\overline{Q}_{11}^{p} } &\quad {\overline{Q}_{12}^{p} } &\quad 0 &\quad 0 &\quad 0 \\ {\overline{Q}_{12}^{p} } &\quad {\overline{Q}_{22}^{p} } &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {\overline{Q}_{66}^{p} } &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad {Q_{44}^{p} } &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {Q_{55}^{p} } \\ \end{array} } \right) \\ {\mathbf{e}} & = \left[ {\begin{array}{*{20}c} 0 &\quad 0 &\quad {\begin{array}{*{20}c} 0 &\quad {e_{15} } &\quad 0 \\ \end{array} } \\ 0 &\quad 0 &\quad {\begin{array}{*{20}c} {e_{15} } &\quad 0 &\quad 0 \\ \end{array} } \\ {\overline{e}_{31} } &\quad {\overline{e}_{31} } &\quad {\begin{array}{*{20}c} 0 &\quad 0 &\quad 0 \\ \end{array} } \\ \end{array} } \right] \\ {{\varvec{\Xi}}} & = \left[ {\begin{array}{*{20}c} {\Xi_{11} } &\quad 0 &\quad 0 \\ 0 &\quad {\Xi_{22} } &\quad 0 \\ 0 &\quad 0 &\quad {\overline{\Xi }_{33} } \\ \end{array} } \right] \\ \end{aligned}$$
(17)

Elastic matrix components related to piezoelectric material are presented as

$$\begin{aligned} \overline{Q}_{11}^{p} & = \overline{Q}_{22}^{p} = Q_{11}^{p} - \frac{{Q_{13}^{p} Q_{13}^{p} }}{{Q_{33}^{p} }},{ }\quad \overline{Q}_{12}^{p} = Q_{12}^{p} - \frac{{Q_{13}^{p} Q_{13}^{p} }}{{Q_{33}^{p} }},{ }\quad \overline{Q}_{66}^{p} = \frac{1}{2}\left( {\overline{Q}_{11}^{p} - \overline{Q}_{12}^{p} } \right){ } \\ \overline{e}_{31} & = e_{31} - \frac{{Q_{13}^{p} }}{{Q_{33}^{p} }}e_{33} ,{ }\quad { }\overline{\Xi }_{33} = \Xi_{33} + \frac{{e_{33}^{2} }}{{Q_{33}^{p} }}{ } \\ \end{aligned}$$
(18)

Also, \({{\varvec{\upsigma}}}^{\mathbf{p}}\), \(\mathbf{E}\) and \(\mathbf{D}\) represent the stress field in piezoelectric layers compatible with the condition of absence of \({\sigma }_{33}^{p}\), the electrical field and the electrical displacement field, respectively, and may be written as:

$$\begin{aligned} {{\varvec{\upsigma}}}^{{\text{p}}} & = \left[ {\sigma_{11}^{p} ,{ }\sigma_{22}^{p} ,{ }\sigma_{12}^{p} ,\sigma_{23}^{p} ,{ }\sigma_{13}^{p} } \right]^{{\varvec{T}}} \\ {\mathbf{D}} & = \left[ {D_{1} ,{ }D_{2} ,{ }D_{3} } \right]^{{\varvec{T}}} \\ {\mathbf{E}} & = \left[ {E_{1} ,{ }E_{2} ,{ }E_{3} } \right]^{{\varvec{T}}} = - \left[ {\Phi_{{,x_{1} }} ,{ }\Phi_{{,x_{2} }} ,{ }\Phi_{{,x_{3} }} } \right]^{{\varvec{T}}} \\ \end{aligned}$$
(19)

where \(\Phi\) is electrical potential function which in accordance with the electrical boundary conditions will be specified in follow.

The relatively thin piezoelectric layers make it reasonable to assume the linearity of the electric potential changes along the thickness of the piezoelectric layers. Hereupon, the electrical potential function in top and bottom piezoelectric layers can be read as:

$$\Phi \left({x}_{1},{x}_{2},{x}_{3}\right)= \left\{\begin{array}{*{20}l}\frac{{x}_{3}-0.5h}{{h}^{p}}{\varphi }^{t}\left({x}_{1},{x}_{2}\right) 0.5h<z<0.5h+{h}^{p}\\ -\frac{{x}_{3}+0.5h}{{h}^{p}}{\varphi }^{b}\left({x}_{1},{x}_{2}\right) -0.5h-{h}^{p}<z<-0.5h\end{array}\right.$$
(20)

As applied in the above relation, it is assumed that the surface of piezoelectric layers bordering GPLRC layers is grounded; accordingly, the electrical potential at this surface is equal to zero.

The governing equations are obtained by exploiting the Hamilton’s principle that for the under consideration problem is extended in the following form [41]:

$${\int }_{0}^{t}\left(\delta U-\delta T\right)\mathrm{d}t=0$$
(21)

where \(t\) is an arbitrary time. Also the variations of strain energy, \(\delta U\) and kinetic energy, \(\delta T\) for the cylindrical shell panel are calculated as:

$$\begin{aligned} \delta U & = \mathop \int \limits_{ - 0.5b}^{0.5b} \mathop \int \limits_{ - 0.5a}^{0.5a} \mathop \sum \limits_{k = 1}^{{N_{L} }} \mathop \int \limits_{{h_{k - 1} }}^{{h_{k} }} \left( {\sigma_{11}^{\left( k \right)} \delta \varepsilon_{11} + \sigma_{22}^{\left( k \right)} \delta \varepsilon_{22} + 2\sigma_{12}^{\left( k \right)} \delta \varepsilon_{12} + 2\kappa_{s}^{\left( k \right)} \sigma_{23}^{\left( k \right)} \delta \varepsilon_{23} + 2\kappa_{s}^{\left( k \right)} \sigma_{13}^{\left( k \right)} \delta \varepsilon_{13} } \right){\text{d}}x_{3} {\text{d}}x_{1} {\text{d}}x_{2} \\ & \quad + \mathop \int \limits_{ - 0.5b}^{0.5b} \mathop \int \limits_{ - 0.5a}^{0.5a} \mathop \int \limits_{0.5h}^{{0.5h + 0.5h^{p} }} (\sigma_{11}^{p} \delta \varepsilon_{11} + \sigma_{22}^{p} \delta \varepsilon_{22} + 2\sigma_{12}^{p} \delta \varepsilon_{12} + 2\kappa_{s}^{p} \sigma_{23}^{p} \delta \varepsilon_{23} + 2\kappa_{s}^{p} \sigma_{13}^{p} \delta \varepsilon_{13} - D_{1} \delta E_{1} - D_{2} \delta E_{2}\\& - D_{3} \delta E_{3} ){\text{d}}x_{3} {\text{d}}x_{1} {\text{d}}x_{2} \\ & \quad + \mathop \int \limits_{ - 0.5b}^{0.5b} \mathop \int \limits_{ - 0.5a}^{0.5a} \mathop \int \limits_{{ - 0.5h - 0.5h^{p} }}^{ - 0.5h} (\sigma_{11}^{p} \delta \varepsilon_{11} + \sigma_{22}^{p} \delta \varepsilon_{22} + 2\sigma_{12}^{p} \delta \varepsilon_{12} + 2\kappa_{s}^{p} \sigma_{23}^{p} \delta \varepsilon_{23} + 2\kappa_{s}^{p} \sigma_{13}^{p} \delta \varepsilon_{13} \\&\quad- D_{1} \delta E_{1} - D_{2} \delta E_{2} - D_{3} \delta E_{3} ){\text{d}}x_{3} {\text{d}}x_{1} {\text{d}}x_{2} \\ & \quad \delta T = \mathop \int \limits_{ - 0.5b}^{0.5b} \mathop \int \limits_{ - 0.5a}^{0.5a} \mathop \sum \limits_{k = 1}^{{N_{L} }} \mathop \int \limits_{{h_{k - 1} }}^{{h_{k} }} \left( {\rho^{\left( k \right)} \left\{ {\dot{U}_{1} \left[ {\delta \dot{u} + x_{3} \delta \mathop {\theta_{1} }\limits } \right] + \dot{U}_{2} \left[ {\delta \dot{v} + x_{3} \delta \mathop {\theta_{2} }\limits } \right] + \dot{U}_{3} \delta \dot{w}} \right\}} \right){\text{d}}x_{3} {\text{d}}x_{1} {\text{d}}x_{2} { } \\ & \quad + \mathop \int \limits_{ - 0.5b}^{0.5b} \mathop \int \limits_{ - 0.5a}^{0.5a} \mathop \int \limits_{0.5h}^{{0.5h + 0.5h^{p} }} \left( {\rho^{p} \left\{ {\dot{U}_{1} \left[ {\delta \dot{u} + x_{3} \delta \mathop {\theta_{1} }\limits } \right] + \dot{U}_{2} \left[ {\delta \dot{v} + x_{3} \delta \mathop {\theta_{2} }\limits } \right] + \dot{U}_{3} \delta \dot{w}} \right\}} \right){\text{d}}x_{3} {\text{d}}x_{1} {\text{d}}x_{2} { } \\ & \quad + \mathop \int \limits_{ - 0.5b}^{0.5b} \mathop \int \limits_{ - 0.5a}^{0.5a} \mathop \int \limits_{{ - 0.5h - 0.5h^{p} }}^{ - 0.5h} \left( {\rho^{p} \left\{ {\dot{U}_{1} \left[ {\delta \dot{u} + x_{3} \delta \mathop {\theta_{1} }\limits } \right] + \dot{U}_{2} \left[ {\delta \dot{v} + x_{3} \delta \mathop {\theta_{2} }\limits } \right] + \dot{U}_{3} \delta \dot{w}} \right\}} \right){\text{d}}x_{3} {\text{d}}x_{1} {\text{d}}x_{2} { } \\ \end{aligned}$$
(22)

In above, \({\kappa }_{s}^{(k)}\) and \({\kappa }_{s}^{p}\) are the shear correction factor of \(k\)-th GPLRC layer and piezoelectric layers, respectively. They are considered as:

$$\begin{aligned} \kappa_{s}^{p} & = \frac{5}{6} \\ \kappa_{s}^{\left( k \right)} & = \frac{5}{{\left( {6 - \upsilon_{m}^{\left( k \right)} V_{m}^{\left( k \right)} - \upsilon_{GPL}^{\left( k \right)} V_{GPL}^{\left( k \right)} } \right)}} \\ \end{aligned}$$
(23)

5 Solution method

The strong form of the equations of motion along with Maxwell's equations can be derived by applying the Green theorem to Eq. (21). But in current work, energy-based methods are employed to present a comprehensive formulation for a wide set of boundary conditions. The Ritz method, as one of the energy-based methods, has demonstrated its competence in solving solid mechanics problems due to its high accuracy, fast convergence, and uncomplicated formulation that can be easily implemented. Hence, Ritz method on the basis of Legendre-type polynomials is implemented to attain the matrix representation of governing motion equations and Maxwell equations. Accordingly, each of the independent variables is expanded by means of a double series of a combination of two one-dimensional admissible functions [32,33,34]

$$\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {u\left( {x_{1} x_{2} ,t} \right)} \\ {v\left( {x_{1} x_{2} ,t} \right)} \\ {w\left( {x_{1} x_{2} ,t} \right)} \\ \end{array} } \\ {\theta_{1} \left( {x_{1} x_{2} ,t} \right)} \\ {\begin{array}{*{20}l} {\theta_{2} \left( {x_{1} x_{2} ,t} \right)} \\ {\begin{array}{*{20}c} {\varphi^{t} \left( {x_{1} x_{2} ,t} \right)} \\ {\varphi^{b} \left( {x_{1} x_{2} ,t} \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\} = \mathop \sum \limits_{n = 0}^{{N_{{x_{1} }} }} \mathop \sum \limits_{m = 0}^{{N_{{x_{2} }} }} \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {U_{nm} \left( t \right)} \\ {V_{nm} \left( t \right)} \\ {W_{nm} \left( t \right)} \\ \end{array} } \\ {X_{nm} \left( t \right)} \\ {\begin{array}{*{20}l} {Y_{nm} \left( t \right)} \\ {\begin{array}{*{20}c} {T_{nm} \left( t \right)} \\ {B_{nm} \left( t \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}\Gamma_{n} \left( {x_{1} } \right)\Gamma_{m} \left( {x_{2} } \right)$$
(24)

\({N}_{{x}_{1}}\) and \({N}_{{x}_{2}}\) specify the number of trial terms; besides, the one-dimensional admissible functions \({\Gamma }_{n}({x}_{1})\) and \({\Gamma }_{m}({x}_{2})\) are defined as the product of the n-th and m-th-order Legendre polynomials (\({L}_{n}\left({x}_{1}\right), {L}_{m}\left({x}_{2}\right))\) to boundary functions (\({\xi }^{\alpha }\left({x}_{1}\right),{ \varsigma }^{\alpha }({x}_{2}))\) which are made in compatible with the essential boundary conditions

$$\begin{aligned} & \Gamma_{n} \left( {x_{1} } \right) = L_{n} \left( {x_{1} } \right)\xi^{\alpha } \left( {x_{1} } \right) \\ & \Gamma_{m} \left( {x_{2} } \right) = L_{m} \left( {x_{2} } \right)\varsigma^{\alpha } \left( {x_{1} } \right) \\ & \left( {\alpha = u, v, w, \theta_{1}, \theta_{2} , \varphi^{t} , \varphi^{b} } \right) \\ \end{aligned}$$
(25)

where Legendre polynomials read as:

$$\begin{aligned} L_{0} \left( {x_{1} } \right) & = L_{0} \left( {x_{2} } \right) = 1 \\ L_{1} \left( {x_{1} } \right) & = \frac{{2x_{1} }}{a},\;L_{1} \left( {x_{2} } \right) = \frac{{2x_{2} }}{\grave{} b} \\ L_{n + 1} \left( {x_{1} } \right) & = \frac{{\left( {2n + 1} \right)\frac{{2x_{1} }}{a}L_{n} \left( {x_{1} } \right) - nL_{n - 1} \left( {x_{1} } \right)}}{n + 1} \\ L_{m + 1} \left( {x_{2} } \right) & = \frac{{\left( {2m + 1} \right)\frac{{2x_{2} }}{b}L_{m} \left( {x_{2} } \right) - mL_{m - 1} \left( {x_{2} } \right)}}{m + 1} \\ \end{aligned}$$
(26)

Boundary functions are proposed as the following general form to have the ability to easily update for the desired combination of boundary conditions:

$$\begin{aligned} \xi^{\alpha } \left( {x_{1} } \right) & = \left( {1 + \frac{{2x_{1} }}{a}} \right)^{{\chi_{1}^{\alpha } }} \left( {1 - \frac{{2x_{1} }}{a}} \right)^{{\chi_{2}^{\alpha } }} \\ \varsigma^{\alpha } \left( {x_{2} } \right) & = \left( {1 + \frac{{2x_{2} }}{b}} \right)^{{\chi_{3}^{\alpha } }} \left( {1 - \frac{{2x_{2} }}{b}} \right)^{{\chi_{4}^{\alpha } }} \\ \end{aligned}$$
(27)

\({\chi }_{i}^{\alpha }\) are the auxiliary parameters that must be assigned a value of zero or one in such a way as to enable the boundary function to satisfy the essential boundary conditions. In present work, sets of clamped (C), simply supported (S) and free (F) edges are considered. It should to be noted a conventional notation convention for citing boundary conditions is established upon which for an instance, a panel with simply supported edge at \(x = -a/2\), clamped edge at \(y = -b/2\), simply supported edge at \(x=a/2\) and free edge at \(y = b/2\) is cited as “SCSF panel”. The cells of Table 1 are filled with values of \({\chi }_{s}^{\alpha }\) \((\alpha =u, v, w, {\theta }_{1}, {\theta }_{2}\,\mathrm{and}\,s=1, 2, \mathrm{3,4})\) as an example for SCSF panel.

Table 1 Value of \({\upchi }_{\mathrm{s}}^{{\alpha }}({\alpha }=\mathrm{u},\mathrm{ v},\mathrm{ w}, {\uptheta }_{1}, {\uptheta }_{2}\,\mathrm{and\,s}=1, 2,{ 3,4})\) for SCSF panel
Full size table

The electrical displacement and the electrical field in all four edges of each of the two piezoelectric layers are considered equal to zero. (It is assumed that piezoelectric layers are grounded on all four edges.) Therefore, the electrical boundary conditions for the piezoelectric layers may be expressed as:

$$\begin{aligned} \varphi^{t} \left( {x_{1} ,{ }x_{2} } \right) & = 0{\text{ at }}\left( {0.5a,x_{2} } \right),{ }\left( { - 0.5a,x_{2} } \right),{ }\left( {x_{1} ,0.5b} \right){\text{ and }}\left( {x_{1} , - 0.5b} \right) \\ \varphi^{b} \left( {x_{1} ,{ }x_{2} } \right) & = 0{\text{ at }}\left( {0.5a,x_{2} } \right),{ }\left( { - 0.5a,x_{2} } \right),{ }\left( {x_{1} ,0.5b} \right){\text{ and }}\left( {x_{1} , - 0.5b} \right) \\ \end{aligned}$$
(28)

In view of the electrical boundary conditions and considering that the Legendre polynomials are not zero at the boundaries, the boundary functions should be selected in such a way that they satisfy the electrical boundary conditions, accordingly:

$$\begin{aligned} \xi^{\alpha } \left( {x_{1} } \right) & = \left( {1 + \frac{{2x_{1} }}{a}} \right)\left( {1 - \frac{{2x_{1} }}{a}} \right) \\ \varsigma^{\alpha } \left( {x_{2} } \right) & = \left( {1 + \frac{{2x_{2} }}{b}} \right)\left( {1 - \frac{{2x_{2} }}{b}} \right) \quad \alpha = \varphi^{t} , \varphi^{b} \\ \end{aligned}$$
(29)

By introducing the series expansion (24) into Eq. (21) and performing integration over the domain, the variations of essential variables are relived. Subsequently, a total of 7 \({N}_{{x}_{1}}{N}_{{x}_{2}}\) equations which contain unknown time-dependent functions are attained which can be recast in matrix form as:

$$\mathbf{M}\ddot{{\varvec{\Delta}}}+\mathbf{K} {\varvec{\Delta}}=0$$
(30)

where M and K are inertia and stiffness matrices, respectively. Besides, \({\varvec{\Delta}}\) represents unknown vector which contains \({U}_{nm}(t), {V}_{nm}(t), {W}_{nm}(t), {X}_{nm}(t), {Y}_{nm}(t), {T}_{nm}(t)\) and \({B}_{nm}(t)\). These set also may be presented as:

$$\mathbf{M}=\left[\begin{array}{c@{\quad}c}{\mathbf{M}}^{\mathbf{X}\mathbf{X}}& {\mathbf{M}}^{\mathbf{X}\mathbf{E}}\\ {\mathbf{M}}^{\mathbf{E}\mathbf{X}}& {\mathbf{M}}^{\mathbf{E}\mathbf{E}}\end{array}\right], \mathbf{K}=\left[\begin{array}{c@{\quad}c}{\mathbf{K}}^{\mathbf{X}\mathbf{X}}& {\mathbf{K}}^{\mathbf{X}\mathbf{E}}\\ {\mathbf{K}}^{\mathbf{E}\mathbf{X}}& {\mathbf{K}}^{\mathbf{E}\mathbf{E}}\end{array}\right], {\varvec{\Delta}}=\left\{\begin{array}{c}{{\varvec{\Delta}}}^{\mathbf{X}}\\ {{\varvec{\Delta}}}^{\mathbf{E}}\end{array}\right\}$$
(31)

The other above-mentioned matrices read as:

$$\begin{aligned} {\mathbf{M}}^{{{\mathbf{EX}}}} & = {\mathbf{M}}^{{{\mathbf{XE}}}} = {\mathbf{M}}^{{{\mathbf{EE}}}} = 0 \\ {\mathbf{M}}^{{XX}} & = \left[ {\begin{array}{*{20}l} {{\mathbf{M}}^{{uu}} } \hfill & {{\mathbf{M}}^{{uv}} } \hfill & {{\mathbf{M}}^{{u\theta _{1} }} } \hfill & {{\mathbf{M}}^{{u\theta _{2} }} } \hfill & {{\mathbf{M}}^{{uw}} } \hfill \\ {{\mathbf{M}}^{{vu}} } \hfill & {{\mathbf{M}}^{{vv}} } \hfill & {{\mathbf{M}}^{{v\theta _{1} }} } \hfill & {{\mathbf{M}}^{{v\theta _{2} }} } \hfill & {{\mathbf{M}}^{{vw}} } \hfill \\ {{\mathbf{M}}^{{\theta _{1} u}} } \hfill & {{\mathbf{M}}^{{\theta _{1} v}} } \hfill & {{\mathbf{M}}^{{\theta _{2} \theta _{1} }} } \hfill & {{\mathbf{M}}^{{\theta _{1} \theta _{2} }} } \hfill & {{\mathbf{M}}^{{\theta _{2} w}} } \hfill \\ {{\mathbf{M}}^{{\theta _{2} u}} } \hfill & {{\mathbf{M}}^{{\theta _{2} v}} } \hfill & {{\mathbf{M}}^{{\theta _{2} \theta _{1} }} } \hfill & {{\mathbf{M}}^{{\theta _{2} \theta _{2} }} } \hfill & {{\mathbf{M}}^{{\theta _{2} w}} } \hfill \\ {{\mathbf{M}}^{{wu}} } \hfill & {{\mathbf{M}}^{{wv}} } \hfill & {{\mathbf{M}}^{{w\theta _{1} }} } \hfill & {{\mathbf{M}}^{{w\theta _{2} }} } \hfill & {{\mathbf{M}}^{{ww}} } \hfill \\ \end{array} } \right] \\ {\mathbf{K}}^{{XX}} & = \left[ {\begin{array}{*{20}l} {{\mathbf{K}}^{{uu}} } \hfill & {{\mathbf{K}}^{{uv}} } \hfill & {{\mathbf{K}}^{{u\theta _{1} }} } \hfill & {{\mathbf{K}}^{{u\theta _{2} }} } \hfill & {{\mathbf{K}}^{{uw}} } \hfill \\ {{\mathbf{K}}^{{vu}} } \hfill & {{\mathbf{K}}^{{vv}} } \hfill & {{\mathbf{K}}^{{v\theta _{1} }} } \hfill & {{\mathbf{K}}^{{v\theta _{2} }} } \hfill & {{\mathbf{K}}^{{vw}} } \hfill \\ {{\mathbf{K}}^{{\theta _{1} u}} } \hfill & {{\mathbf{K}}^{{\theta _{1} v}} } \hfill & {{\mathbf{K}}^{{\theta _{2} \theta _{1} }} } \hfill & {{\mathbf{K}}^{{\theta _{1} \theta _{2} }} } \hfill & {{\mathbf{K}}^{{\theta _{2} w}} } \hfill \\ {{\mathbf{K}}^{{\theta _{2} u}} } \hfill & {{\mathbf{K}}^{{\theta _{2} v}} } \hfill & {{\mathbf{K}}^{{\theta _{2} \theta _{1} }} } \hfill & {{\mathbf{K}}^{{\theta _{2} \theta _{2} }} } \hfill & {{\mathbf{K}}^{{\theta _{2} w}} } \hfill \\ {{\mathbf{K}}^{{wu}} } \hfill & {{\mathbf{K}}^{{wv}} } \hfill & {{\mathbf{K}}^{{w\theta _{1} }} } \hfill & {{\mathbf{K}}^{{w\theta _{2} }} } \hfill & {{\mathbf{K}}^{{ww}} } \hfill \\ \end{array} } \right] \\ {\mathbf{K}}^{{X{\text{E}}}} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\mathbf{u}}{\varvec{\varphi }}^{\user2{t}} }} } \\ {{\mathbf{K}}^{{{\mathbf{u}}{\varvec{\varphi }}^{\user2{b}} }} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\mathbf{v}}{\varvec{\varphi }}^{\user2{t}} }} } & {{\mathbf{K}}^{{{\mathbf{w}}{\varvec{\varphi }}^{\user2{t}} }} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\mathbf{v}}{\varvec{\varphi }}^{\user2{b}} }} } & {{\mathbf{K}}^{{{\mathbf{w}}{\varvec{\varphi }}^{\user2{b}} }} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\theta }}_{1} {\varvec{\varphi }}^{\user2{t}} }} } & {{\mathbf{K}}^{{{\varvec{\theta }}_{2} {\varvec{\varphi }}^{\user2{t}} }} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\theta }}_{1} {\varvec{\varphi }}^{\user2{b}} }} } & {{\mathbf{K}}^{{{\varvec{\theta }}_{2} {\varvec{\varphi }}^{\user2{b}} }} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{{\text{T}}} \\ {\mathbf{K}}^{{{\text{EX}}}} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{t}} \user2{u}}} } \\ {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{b}} \user2{u}}} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{t}} \user2{v}}} } & {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{t}} \user2{w}}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{b}} \user2{v}}} } & {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{b}} \user2{w}}} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{t}} {\varvec{\theta }}_{1} }} } & {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{t}} {\varvec{\theta }}_{2} }} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{b}} {\varvec{\theta }}_{1} }} } & {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{b}} {\varvec{\theta }}_{2} }} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{{}} \\ {\mathbf{K}}^{{{\text{EE}}}} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{t}} {\varvec{\varphi }}^{\user2{t}} }} } \\ {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{t}} {\varvec{\varphi }}^{\user2{b}} }} } \\ \end{array} } & {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{b}} {\varvec{\varphi }}^{\user2{t}} }} } \\ {{\mathbf{K}}^{{{\varvec{\varphi }}^{\user2{b}} {\varvec{\varphi }}^{\user2{b}} }} } \\ \end{array} } \\ \end{array} } \right] \\ \end{aligned}$$
(32)

By merging two above matrix equations, one can obtain a single equation to predict vibration behavior of FG-GPLRC panel surrounded with piezoelectric layers

$${\mathbf{M}}^{{\varvec{X}}{\varvec{X}}}{\ddot{\boldsymbol{\Delta }}}^{{\varvec{X}}}+{\mathbf{K}}^{\mathbf{e}}{\boldsymbol{\Delta }}^{{\varvec{X}}}=0$$
(33)

Here, recast stiffness matrix has the following definition:

$${\mathbf{K}}^{\mathbf{e}}={\mathbf{K}}^{\mathbf{X}\mathbf{X}}-{\mathbf{K}}^{\mathbf{X}\mathbf{E}}{{\mathbf{K}}^{\mathbf{E}\mathbf{E}}}^{-1}{\mathbf{K}}^{\mathbf{E}\mathbf{X}}$$
(34)

Since we are dealing with a free vibration problem, the solution to the problem will be in the form of \({\boldsymbol{\Delta }}^{{\varvec{X}}}={\varvec{\updelta}}\mathrm{cos}(\omega t+\beta )\), where \(\omega\) is the natural frequency. By substituting the solution in Eq. (33), we attain an eigenvalue problem as:

$${(\mathbf{K}}^{\mathbf{e}}-{\upomega }^{2}{\mathbf{M}}^{{\varvec{X}}{\varvec{X}}}){\boldsymbol\delta } =0$$
(35)

It is worth noting, in current research, two types of electrical boundary conditions, namely closed circuit and open circuit, are taken into account. Based upon the open circuit electrical boundary conditions, electrical potentials at free surface of piezoelectric layers are non-zero unknowns. In closed circuit case, it’s assumed that top and bottom surfaces of the both piezoelectric layers are grounded so \({\mathbf{K}}^{\mathbf{e}}={\mathbf{K}}^{\mathbf{E}\mathbf{E}}.\)

Non-trivial solutions of Eq. (35) are the natural frequencies of FG-GPLRC panel bounded with piezoelectric layers.

6 Results and discussion

To perform numerical studies on free vibration of functionally graded GPL-reinforced cylindrical panel integrated with piezoelectric layers, the following mechanical properties for Epoxy matrix and GPL reinforcement (with \({l}_{GPL}=2.5\upmu \hbox{m} , {w}_{GPL}=1.5\upmu \hbox{m}\) and \({h}_{GPL}=1.5\upmu \hbox{m})\upmu \hbox{m}\) are considered

$$\begin{aligned} E_{GPL} & = 1010\,{\text{GPa}} , \quad \rho_{GPL} = 1062.5\frac{{{\text{kg}}}}{{{\text{m}}^{3} }} ,\quad \nu_{GPL} = 0.186 \\ E_{m} & = 3\,{\text{GPa}} ,\quad \rho_{m} = 1200\frac{{{\text{kg}}}}{{{\text{m}}^{3} }} ,\quad \nu_{m} = 0.34 \\ \end{aligned}$$
(36)

It is assumed that PZT-4 is used as top and bottom piezoelectric layers; accordingly, the following electromechanical properties for piezoelectric layers are taken into account:

$$\begin{aligned} Q_{{11}}^{p} & = 132\,{\text{GPa}},\,Q_{{12}}^{p} = 71\,{\text{GPa}},\,Q_{{33}}^{p} = 115\,{\text{GPa}},\,Q_{{13}}^{p} = 73\,{\text{GPa}},\,Q_{{55}}^{p} = 26\,{\text{GPa}}\,\rho ^{p} = 7500\frac{{{\text{kg}}}}{{{\text{m}}^{3} }}, \\ e_{{31}} & = e_{{32}} = - 4.1\frac{C}{{m^{2} }},e_{{15}} = e_{{24}} = 10.5\frac{C}{{m^{2} }},e_{{33}} = 14.1\frac{C}{{m^{2} }},\Xi _{{11}} = \Xi _{{22}} = 7.124\frac{{nF}}{m}\,{\text{and}} \\ \Xi _{{33}} & = 5.841\,nF/m \\ \end{aligned}$$
(37)

Besides, if no other value is mentioned, the following geometrical specifications are used:

$$\frac{a}{b}=1,\frac{a}{h}=20,\frac{R}{a}=5,\frac{{h}^{p}}{h}=0.05$$
(38)

One of the main factors which affects the numerical results in Ritz method is the number of shape functions. In the open literature this factor is analyzed as a convergence study. Previous research from the third author of this study [5] reveals that when the number of shape functions is set equal to 14 in each direction, accurate results are achieved for free vibrations of cylindrical panels. As a result, the number of shape functions is set equal to 14 in each direction of the panel for all of the results.

Herein, the first subsection aims to show the validity and accuracy of the present formulation and the numerical results subsequently.

First comparison of this study is devoted to experimental results. The case of an isotropic homogeneous cylindrical panel is considered with all edges clamped where the geometrical characteristics are \(b=0.0762\,\mathrm{m}, a=0.1016\,\mathrm{m}, h=0.03302\,\mathrm{cm}, R=0.762\,\mathrm{m}, E=68.947\,\mathrm{GPa}, \rho =2657.27\,\mathrm{kg}/{m}^{3}, \nu =0.33\). Comparison is performed in Table 2. First ten frequencies in Hertz are obtained and compared with those of Olson and Lindberg [64]. It is seen that results are in close agreement.

Table 2 Comparison of frequencies in Hertz (\({\upomega }^{*}=\upomega /2\uppi\)) between our results and those of Olson and Lindberg [64] for the case of fully clamped isotropic homogeneous panel
Full size table

The second comparison case is established in such a way that fundamental frequency parameters (\(\Omega =\omega {a}^{2}/h\sqrt{{\rho }_{m}/{E}_{m}}\)) of completely clamped (CCCC) FG-GPLRC cylindrical shell panel for various values of geometrical parameters are obtained and their accuracy are evaluated in comparison with those of reported by Van do and lee [65] which are tabulated in Table 3. Rectangular planform and 1 percent by weight fraction of GPL reinforcement are considered for development of results of this section.

Table 3 Validation of the first frequency parameter \(\Omega\) of CCCC FG-GPLRC cylindrical panel
Full size table

Based on what can be seen from Table 3, it can be claimed that implementing the present theory and formulations for an FG-GPLRC cylindrical panel leads to excellent accuracy for results.

Next comparative study is carried out with the research performed by Majidi‑Mozafari et al. [66] in which through an analytical approach, the free vibrations of sandwich plates reinforced with graphene nanoplatelets were investigated. To do so, the first three natural frequencies of FG-GPLRC plate with PZT-4 piezoelectric layer for various types of electrical and mechanical boundary conditions are computed and compared with those reported by Majidi–Mozafari et al. [66]. Table 4 shows the results of this comparison study. PZT-4 is considered as the piezoelectric material, and following data are considered to perform such comparison study: \({W}_{GPL}=0.5\%,a/b=1, a/h=20, h/{h}^{p}=20.\)

Table 4 Validation of the first three natural frequencies (in Hz) of FG-GPLRC plate integrated with PZT-4 layers
Full size table

As Table 4 also confirms, again for free vibration analysis of the structures surrounded by piezoelectric layers, the current model provides remarkable accuracy.

Now that through performing a number of comparison studies, the required confidence in the accuracy and correctness of the results has been attained; by providing novel numerical data, parametric studies are planned with the aim of evaluating the effects of the number of GPLRC layers, GPL weight fraction, structure curvature, mechanical boundary conditions and piezoelectric layer thickness on the characteristics of free vibrations of the FG-GPLRC cylindrical panel surrounded with piezoelectric layers. It should to be noted that hereafter a frequency parameter with definition of \(\Omega =\omega {a}^{2}/h\sqrt{{\rho }_{m}/{E}_{m}}\) is used to present results.

The effects of the number of GPLRC layers on the first five frequency parameters of completely clamped FG-GPLRC cylindrical panel with symmetric (FG-U, FG-X, FG-O) and asymmetric (FG-V, FG-A) GPL distributions are illustrated in Tables 5 and 6. For better grasp, the first frequency parameters are also depicted in Fig. 3 for open circuit electrical boundary conditions. In this case study, the reinforcing parameter is fixed as \({W}_{GPL}=0.5\%\).

Table 5 Variation of the first four frequency parameters in CCCC panels versus changing the number of layers with symmetric distribution of GPLs
Full size table
Table 6 Variation of the first four frequency parameters \(\Omega\) in CCCC panels versus changing the number of layers with asymmetric distribution of GPLs
Full size table
Fig. 3
figure 3

Variations of fundamental frequency parameter \({\Omega }_{1}\) by adding the number of layers

Full size image

It is evident that the first natural frequency of FG-U panel, which is a homogeneous model, is not affected by the number of layers; whereas by increasing the number of layers ascending trend is observed in variation of frequencies of FG-X model, descending trend can be seen for FG-O, FG-V and FG-A model. The same behavior is seen for higher frequencies.

This behavior, which is same to that observed for higher frequencies, is caused by the fact that the greater the distribution of GPLs in the outer layers, the greater the bending stiffness of the structure and subsequently the natural frequency of the structure. Besides, as Fig. 3 shows, frequencies hardly change when the number of layers is greater than 14. Thus, an FG-GPLRC panel with 10 layers may serve as a panel with continuous change of properties. Subsequently, the next results are obtained for a panel with 10 GPLRC layers.

The effects of the mechanical and electrical boundary conditions on the first five frequency parameters for FG-GPLRC cylindrical panel integrated with piezoelectric layers are investigated in Tables 7 and 8. 0.5 percent by weight of GPL reinforcement is considered. As demonstrated in these tables, panels with more edge constraints shows more natural frequencies. The observation that the frequencies are maximum for CCCC panel and are minimum for the CFFF panel supports this claim. As the second observation from Tables 7 and 8, the FG-GPLRC cylindrical panel with piezoelectric layers under open circuit condition has greater natural frequencies than the case with closed circuit condition. That is because during panel vibration, piezoelectric layers with open circuit boundary condition convert the electric potential into mechanical energy, while piezoelectric layers with closed circuit boundary conditions don’t have this capability so evacuate the electrical energy.

Table 7 The effect of electrical and mechanical boundary conditions on first four frequency parameters of FG-GPLRC cylindrical panel with piezoelectric layers in symmetric distribution of GPLS
Full size table
Table 8 The effect of electrical and mechanical boundary conditions on first four frequency parameters of FG-GPLRC cylindrical panel with piezoelectric layers in asymmetric distribution of GPLS
Full size table

Tables 9 and 10 show the variation of first four frequency parameters of the SCSC FG-GPLRC panel versus the weight fraction of augmented GPLs to epoxy matrix for different GPL distribution pattern. Needless to more discuss, adding more GPL to the epoxy matrix leads to more increase in natural frequencies. The feature has been verified in many of the studies on GPLRC structures; see, e.g., [67,68,69,70,71,72,73]. This is due to the fact the elasticity modulus of GPL is much higher than that of Epoxy. The increasing rate is higher for the FG-X pattern and lower for the FG-O pattern as depicted in Fig. 4. The reason for this observation can be found in the greater bending stiffness of FG-X model and the less bending stiffness of the FG-O model.

Table 9 The effect of GPL weigh fractions on first four frequency parameters of SCSC FG-GPLRC cylindrical panel surrounded with PZT layers with symmetric pattern
Full size table
Table 10 The effect of GPL weigh fractions on first four frequency parameters of SCSC FG-GPLRC cylindrical panel surrounded with PZT layers with asymmetric pattern
Full size table
Fig. 4
figure 4

Variation of the first frequency parameter with respect to adding more GPL to epoxy matrix in SCSC panels

Full size image

The effect of piezoelectric layer thickness-to-panel thickness ratio on the natural frequency of the SCSC FG-GPLRC cylindrical panel surrounded with piezoelectric layers with open/closed electrical boundary condition is studied in Table 11 and for first frequency parameter of X-GPLRC panel is displayed in Fig. 5. It can be seen that panels with thicker piezoelectric layers experience higher natural frequencies. Also, Fig. 5 reveals that natural frequencies of the panels with open circuit electrical boundary conditions are more sensitive to the thickness of piezoelectric layer than those with closed circuit electrical boundary conditions.

Table 11 Variations of the first four frequency parameters of FG-GPLRC cylindrical panel versus the ratio of hp/h
Full size table
Fig. 5
figure 5

How the first frequency parameter is affected by piezoelectric layer thickness changes

Full size image

Table 12 represents variation of frequency parameters versus \(R/a\) ratio of the SCSC FG-GPLRC panel with \({W}_{GPL}=0.5\%\) for different GPL distribution patterns. It is observed that increasing panel curvature leads to growing the frequencies as a consequence of increasing configuration stiffness.

Table 12 The effect of \(R/a\) on first four frequency parameters of the FG-GPLRC panel with top and bottom piezoelectric layers
Full size table

7 Conclusions

The present work deals with free vibrations of functionally graded graphene platelet-reinforced cylindrical panels completely surrounded with top and bottom piezoelectric layers. Mechanical properties of GPLRC layers were estimated in accordance with modified Halpin–Tsai micromechanical model, rule of mixtures and the concept of layer-wise functionally graded distribution of GPLs. Hamilton principle was utilized to obtain coupled PDEs of motions on the basis of FSDT and Maxwell equation. With the aid of Legendre-Ritz technique, spatial domain was discretized and inertia and equivalent stiffness matrix were calculated. Through a number of comparison studies, the accuracy of present solution procedure was validated and subsequently novel numerical data were generated to establish the parameter studies. Some conclusions are outlined as:

  • Increasing the number of layers leads to an increase in frequency for the FG-X pattern and a decrease in frequency for FG-O and asymmetric patterns. However, the change in frequencies is negligible when the number of layers is greater than 10. As a result, a panel with only 10 layers may serve as a panel with continuous change of GPL weight fraction.

  • As the piezoelectric layer becomes thicker frequencies show more dependency on electric boundary conditions, for thinner piezoelectric layer, frequency parameters grow rapidly with thickening piezoelectric layer.

  • Deeper panel has higher natural frequencies.

  • In general, increasing the GPL weight fraction or exploiting models with more dispersion of GPLs in the outer layers leads to an enrichment of the panel stiffness and, as a result, a growth in natural frequencies.

  • FG-X panel has the maximum frequencies, and FG-O panel has the minimum frequencies

  • Open circuit condition results in higher frequencies.