A Vibration Analysis of a Thick Micro Sandwich Panel with Metamaterial or Porous Core and Carbon Nanotubes/Graphene Platelets Reinforced Composite Based on HSDT and NSGT

Abstract

In the present study, vibration analysis of thick walled sandwich panel reinforced by nanocomposite facesheets based on higher-order shear deformation (HSDT) and nonlocal strain gradient theories (NSGT) is investigated. In this work, there are all components of normal and shear strain/stress. On the other hands, the novelty of this work is to investigate general strain/stress because the sandwich structure is assumed as a thick-walled panel. Also, the current work's significance and necessity is the investigation of two-types reinforcements including carbon nanotubes (CNTs) or graphene’s platelets (GPL) with two-types cores such as porous or metamaterials [graphene origami (GOri) with negative Poisson’s ratio] to analyze vibration response of a thick-walled sandwich panel using higher order shear deformation theory (HSDT) and considering size effect based on nonlocal strain gradient theory (NSGT), thus the above highlights were not done simultaneously until now and becomes the novelty of the present work. The governing motion’s equations for the sandwich panel are obtained using the Hamilton's principle and the extended mixture rule. The effects of different parameters such as Eringen’s non-local parameter, material length scale parameter, various distributions of porosity, porosity coefficient and various distributions of CNT, volume fraction of CNT, volume fraction of GPL, weight fraction of GOri, the folding degree $\left( {H_{Gr} } \right)$ and geometric dimensions of GPL on natural frequency is studied. The results of this study show that with an increase in non-local parameter and the length of structure, the natural frequency reduces and by enhancing the material length scale parameter and CNT volume fraction, the natural frequency increases because of increasing the stiffness of the structure. The functionally graded FG-X with respect to FG-O and uniform distribution (UD) has the highest natural frequency because it increases the most stiffness of sandwich panel and finally, the FG-O has the lowest natural frequency. With increasing the length and width of the GPL, the natural frequency increases and vice versa for the thickness of GPL.

Introduction

In the last decades, some researchers worked about sandwich structures because increasing the strength to weight ratio in these structures. Thus, in this study, the sandwich structures with soft core and carbon nanotubes or graphene platelets as reinforcements in matrix are used. Because high strength to weight, these structures are considered in various industries including aerospace, airplane, the body of automobile and ship.

Rahmani et al. [1] considered the effect of external loads on vibration and buckling of the cylindrical shell using sandwich panel theory. They solved these equations using three dimensional elastic theory and assumed that environmental and axial stiffness was negligible. Natarajan et al. [2] considered the influences of the different values of CNT volume fraction, core-to-face sheet thicknesses ratio on frequency and deflection for a sandwich plate. Loghman and Cheraghbake [3] analyzed the stress and distribution of the electric potential of the reinforced cylinder with electrical, thermal, magnetic loads, they have been employed the Mori–Tanaka model for the mechanical properties. The results indicated that stresses are increased by enhancing the volume fraction of the carbon tube. In the other work, they [4] presented the creep analysis of a rotating cylinder made of nano composite under thermo-magneto-mechanical loadings. Their results showed that in the presence of magnetic field, deformations and radial displacement are lower. Mohammadimehr and Mostafavifar [5] considered the vibration for a sandwich plate by considering a flexible core with carbon nanotubes and composite laminates. They assumed the mechanical properties such as shear and elasticity moduli as a function of temperature. Ghorbanpour Arani et al. [6] investigated vibration for a sandwich structures under electro-magneto-mechanical loading, the core consists of a piezo-magnetic micro plate with two layers, as well as the layers. Kant and Punera [7] presented static and dynamic for a curved shell. In the other work, they [8] studied an elasto-statics for a laminated and FG sandwich cylindrical shells based on principle of minimum potential energy. Ghorbanpour Arani and Zamani [9] demonstrated bending analysis for a sandwich structures with FG porous core and piezoelectric actuators. Bahaadini and Saidi [10] investigated the instability of thin-walled structures reinforced with single layer carbon nanotubes containing fluid flow. They considered the properties of composite materials as uniform distribution and two types of FG distributions. Safaei et al. [11] illustrated the effect of temperature gradient on the natural frequencies for a sandwich plate reinforced with carbon nanotubes using FSDT. They considered the volume fraction and density of carbon nanotubes in the thickness of each nanocomposite with temperature-dependent properties. (Kiani et al. [12], Zghal et al. [13]) investigated vibration for a cylindrical panel and shell of FG cylinders reinforced with CNT along the thickness of the panel, respectively. They found that FG-X and FG-O is related to the maximum and minimum natural frequency, respectively. Arefi et al. [14] used the different distribution of graphene’s platelets on a Pasternak foundation. They also found the Young's modulus and Poisson's ratio increased by using volume fraction of graphene’s platelets. Naderi Beni [15] analyzed the free vibration of circular circular sandwich panels and different boundary conditions. Selim et al. [16] investigated the active control of FG composite sheets with piezo-electric layers. Civalek et al. [17] studied bending, buckling and vibration of carbon nanotubes using Euler–Bernoulli nanobeam. Kolahdouzan et al. [18] considered vibration and buckling for an elastically restrained FG-CNTRC sandwich annular nano-plates. Amir et al. [19] demonstrated the vibration for a magneto-rheological fluid plate with magneto-strictive layers. They investigated that the natural frequencies increases by enhancing of the magnetic field intensity. Alambeigi et al. [20] considered free and forced vibration analysis of sandwich beam considering porous core and SMA hybrid composite face layers on Vlaosv’s foundation. Singh and Azam [21] analyzed vibration of embedded FG-NP using nonlocal classical plate theory. Hadji and Avcar [22] studied the HSDBT for vibration of porous FG nanobeams. Quyen et al. [23] considered nonlinear forced vibration for a sandwich panel with auxetic honeycombs core and CNTRC facesheets. Miao et al. [24] investigated a dual-functional gradient CNTRC in which both the matrix and the CNTs that they assumed to be FG along the thickness direction, also, the matrix is considered as the metal–ceramic FGM. Monajemi et al. [25] considered the stability for a spinning visco-elastic sandwich beam with soft-core and CNTs reinforced metal matrix nanocomposites skin under residual stress. Li et al. [26] considered the magneto-elastic superharmonic-principal parametric joint resonance of an axially variable-speed moving beam. Lukešević et al. [27] presented moving point load on a beam with viscoelastic foundation containing fractional derivatives of complex order. Charekhli-Inanllo et al. [28] illustrated the effect of various shape core materials by FDM on low velocity impact behavior of a sandwich composite plate. Farazin et al. [29] considered flexible self-healing nanocomposite based gelatin/tannic acid/acrylic acid reinforced with zinc oxide nanoparticles and hollow silver nanoparticles based on porous silica for rapid wound healing. Safari et al. [30] considered free and forced vibration of a sandwich Timoshenko beam made of GPLRC and porous core.

Bang and Yang [31] illustrated application of machine learning to predict the engineering characteristics of construction material. Chang et al. [32] considered to predict the mechanical properties of unidirectional composites using machine learning. Jin et al. [33] considered hydromechanical geotechnical large deformation problems based on two-phase two-layer SNS-PFEM. Dalklint et al. [34] presented computational design of metamaterials with self-contact. Farazin et al. [35] considered design, fabrication, and evaluation of green mesoporous hollow magnetic spheres with antibacterial activity. Chang et al. [36] predicted the mechanical properties of unidirectional composites using machine learning. Ho et al. [37] considered the effect of single vacancy defects on graphene nanoresonators. Khalid and Kim [38] depicted recent studies on stress function-based approaches for the free edge stress analysis of smart composite laminates. Emdadi et al. [39] presented vibration of a nanocomposite annular sandwich microplate based on higher-order shear deformation theory using differential quadrature method. They obtained various boundary conditions on the natural frequency of annular sandwich microplate. Murari et al. [40] investigated on nonlinear free vibration and postbuckling behaviours of functionally graded graphene origami-enabled auxetic metamaterial tapered beams immersed in fluid. Bamdad et al. [41] analyzed the vibrations and buckling of Timo Shinko magneto-electro-elastic sandwich beam with porous core and polyvinylidene fluoride matrix reinforced by carbon nanotube facesheet. Khalid et al. [42] presented the combined thermo-electromechanical coupling effect in a series solution-based approach to analyze the free-edge interlaminar stresses in smart composite laminates. They obtained the interlaminar stresses produced by the echanical load are substantially decreased at the free edge and the layer interfaces by applying the appropriate thermal and electric loading. Ramesh et al. [43] presented porous metal–organic frameworks derived carbon and nickel sulfides composite electrode for energy storage materials. They showed that the composite materials show improved specific capacitances on the 6 M KOH electrolyte and also the composite electrode has an excellent retention in the 5000 cycles.

The previous works have analyzed cylindrical shells with the assumption of plane strain or plane stress, and the general strain/stress is expressed as a challenge, which in the present work, this challenge is solved by considering the general displacement field, moreover, in the present work, all components of displacement fields are as third order, thus there are all components of normal and shear strain/stress. On the other hands, the novelty of this work is to investigate general strain/stress because the sandwich structure is assumed as a thick-walled panel. Also, the current work's significance and necessity is the investigation of two-types reinforcements including carbon nanotubes (CNTs) or graphene’s platelets (GPL) with two-types cores such as porous or metamaterials to analyze vibration response of a thick-walled sandwich panel using higher order shear deformation theory (HSDT) and considering size effect based on nonlocal strain gradient theory (NSGT), thus the above highlights were not done simultaneously until now and becomes the novelty of the present work. The results of this work can be used in energy industries including power generation and transmission, industries of oil, gas, petrochemical, transportation industries, and aerospace industries. The governing equations of motion for the sandwich panel are obtained using Hamilton's principle and the extended mixture rule. The effects of different parameters such as non-local parameter, material length scale parameter, various distributions of porosity, porosity coefficient and various distributions of CNT, volume fraction of CNT, volume fraction of GPL, weight fraction of GOri, the folding degree $\left( {H_{Gr} } \right)$ and geometric dimensions of GPL on natural frequency is studied.

Geometry and Material Properties

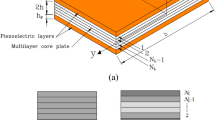
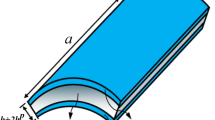
Figure 1 shows a schematic view of sandwich panel with carbon nanotube or graphene platelets with length $L$, total thickness $h$, core thickness $h_c$, top facesheet thickness $h_t$, bottom facesheet thickness $h_b$, the coordinate axes $z\,,\,\theta \,,\,x$, panel angle $\phi$, the arc length of the panel $b$, radius of panel $R$ from the center to the middle of the core.

Fig. 1

A schematic view of sandwich panel with carbon nanotube or graphene platelets

Thus, the Young's modulus for graphene origami metamaterials is considered as follows (Murari [40]):

$$\begin{aligned} E & = \frac{{1 + \xi \eta V_{GR} }}{{1 - \eta V_{GR} }}E_{cu} f_E \left( {H_{GR} ,V_{GR} } \right) \\ \upsilon & = \left( {\upsilon_{GR} V_{GR} + \upsilon_{cu} V_{cu} } \right)f_\upsilon \left( {H_{GR} ,V_{GR} } \right) \\ \rho & = \left( {\rho_{GR} V_{GR} + \rho_{cu} V_{cu} } \right)f_\rho \left( {V_{GR} } \right) \\ f_E \left( {H_{GR} ,V_{GR} } \right) & = 1.11 - 1.22V_{GR} - 0.134 + 0.559V_{GR} - 5.5V_{GR} H_{GR} + 38V_{GR}^2 H_{GR} - 20.6V_{GR}^2 H_{GR}^2 \\ f_\rho \left( {V_{GR} } \right) & = 1.01 - 2.01V_{GR}^2 - 0.0131 \\ f_\upsilon \left( {H_{GR} ,V_{GR} } \right) & = 1.01 - 1.43V_{GR} + 0.165 - 16.8V_{GR} H_{GR} - 1.1V_{GR} H_{GR} + 16V_{GR}^2 H_{GR}^2 \\ \end{aligned}$$

(1)

where

$$\begin{aligned} \eta_L & = \frac{{\left( {E_{GR} /E_{cu} } \right) - 1}}{{\left( {E_{GR} /E_{cu} } \right) + \xi }} \\ \xi & = 2\frac{{l_{GR} }}{{t_{GR} }} \\ V_{GR} & = V_{GR}^* \\ V_{GR}^* & = \frac{{W_{GR} }}{{W_{GR} + \left( {\rho_{GR} /\rho_{cu} } \right)\left( {1 - W_{GR} } \right)}} \\ \end{aligned}$$

(2)

The relationships of different porous cores such as uniform porosity, symmetric (type 1) and asymmetric (type 2) porosity are written as follows (Bamdad [41]):

$$\begin{aligned} E_c (z) & = E_1^c (1 - e_0 \lambda ) \\ G_c (z) & = \frac{E_c (z)}{{2(1 + \upsilon_c (z))}} \\ \rho_c (z) & = \rho_1^c (1 - e_m \lambda ) \\ \upsilon_c (z) & = 0.221\rho^{\prime} + \upsilon_1 (0.342\rho^{{\prime} 2} - 1.21\rho^{\prime} + 1) \\ \rho^{\prime} & = 1 - \left( {\frac{\rho_c (z)}{{\rho_1^c }}} \right) \\ \lambda & = \cos ({{\pi z} / {h_c ) \to }}\,{\text{Porosity Distribution 1 or nonuniform symmetric}} \\ \lambda & = \cos ({{\pi z} / {h_c + {\pi / 4}) \to }}\,{\text{Porosity Distribution 2 or nonuniform asymmetric}} \\ \lambda & = \frac{1}{e_0 } - \frac{1}{e_0 }\left( {\frac{2}{\pi }\sqrt {1 - e_0 } - \frac{2}{\pi } + 1} \right)^2 \to {\text{Porosity Distribution 3 or uniform}} \\ \end{aligned}$$

(3)

The porosity coefficient is derived from the following equation:

$$\begin{aligned} e_0 & = 1 - \frac{E_2 }{{E_1 }} \\ e_m & = 1 - \sqrt {1 - e_0 } \\ \end{aligned}$$

(4)

Different distribution types of carbon nanotube in top and bottom facesheet layers are considered as (Bamdad [41]):

$$\begin{aligned} V_{CNT} & = \left\{ \begin{gathered} V_{CNT}^t = V^* \hfill \\ V_{CNT}^b = 2\left( {1 - \frac{(z + h_b /2 + h_c /2)}{{h_b }}} \right)V^* \hfill \\ \end{gathered} \right. \to {\text{Pattern:}}\,\,{\text{UD,}}\,\,\,{\text{FG-O}} \\ V_{CNT} & = \left\{ \begin{gathered} V_{CNT}^t = V^* \hfill \\ V_{CNT}^b = V^* \hfill \\ \end{gathered} \right. \to {\text{Pattern:}}\,\,{\text{Uniform}} \\ V_{CNT} & = \left\{ \begin{gathered} V_{CNT}^t = \frac{4}{h_t }(z - h_t /2 - h_c /2)V^* \hfill \\ V_{CNT}^b = \frac{4}{h_b }(z + h_b /2 + h_c /2)V^* \hfill \\ \end{gathered} \right. \to {\text{Pattern:}}\,\,{\text{FG-XX}} \\ \end{aligned}$$

(5)

that $V^*$ the volume fraction of the carbon nanotubes based on the generalized mixture rule is written as follows (Bahaadini and Saidi [10]):

$$\begin{aligned} E_{11} & = \eta_1 V_{CNT} E_{11}^{CNT} + V_m E^m ,\,\,\frac{\eta_2 }{{E_{22} }} = \frac{{V_{CNT} }}{{E_{22}^{CNT} }} + \frac{V_m }{{E^m }},\,\frac{\eta_3 }{{G_{12} }} = \frac{{V_{CNT} }}{{G_{12}^{CNT} }} + \frac{V_m }{{G^m }} \\ \upsilon_{12} & = V_{CNT}^* \upsilon_{12}^{CNT} + V_m \upsilon^m ,\,\rho = V_{CNT} \rho^{CNT} + V_m \rho^m ,\,\alpha_{11} = V_{CNT} \alpha_{11}^{CNT} + V_m \alpha^m \\ \alpha_{22} & = (1 + \upsilon_{12}^{CNT} )V_{CNT} \alpha_{22}^{CNT} + (1 + \upsilon^m )V_m \alpha^m - \upsilon_{12} \alpha_{11} \\ \end{aligned}$$

(6)

where $E^m$ and $E_{11}^{CNT}$, $E_{22}^{CNT}$ are the elastic modulus for the matrix and the carbon nanotube, respectively, and also, $G^m$ and $G_{12}^{CNT}$ denote shear moduli for matrix and CNT, respectively.

The Young's modulus using Halpin–Tsai approach is defined as follows (Bahaadini and Saidi [10]):

$$\begin{aligned} E & = \frac{3}{8}\frac{{1 + \xi_L \eta_L V_{GPL} }}{{1 - \eta_L V_{GPL} }}E_m + \frac{5}{8}\frac{{1 + \xi_L \eta_T V_{GPL} }}{{1 - \eta_T V_{GPL} }}E_m \\ \eta_L & = \frac{{\left( {{{E_{GPL} } / {E_m }}} \right) - 1}}{{\left( {{{E_{GPL} } / {E_m }}} \right) + \xi_L }},\quad \eta_T = \frac{{\left( {{{E_{GPL} } / {E_m }}} \right) - 1}}{{\left( {{{E_{GPL} } / {E_m }}} \right) + \xi_T }} \\ \xi_L & = 2\frac{{a_{GPL} }}{{t_{GPL} }},\quad \xi_T = 2\frac{{b_{GPL} }}{{t_{GPL} }} \\ \upsilon & = V_{GPL} \upsilon^{GPL} + V_m \upsilon^m ,\quad \rho = V_{GPL} \rho^{GPL} + V_m \rho^m \\ \end{aligned}$$

(7)

where $E_m$ and $E_{GPL}$ are the Young's modulus of matrix and the graphene platelets, respectively. $\rho^m$ and $\rho^{GPL}$ the density of matrix and graphene’s plate, respectively.

The displacement fields of the sandwich panel based on HSDT are presented as follows (Punera and Kant [8]):

$$\begin{aligned} u(x,\theta ,z,t) & \approx u_0 (x,\theta ,t) + z\varphi_1 (x,\theta ,t) + z^2 \varphi_2 (x,\theta ,t) + z^3 \varphi_3 (x,\theta ,t) \\ v(x,\theta ,z,t) & \approx v_0 (x,\theta ,t) + z\varphi_4 (x,\theta ,t) + z^2 \varphi_5 (x,\theta ,t) + z^3 \varphi_6 (x,\theta ,t) \\ w(x,\theta ,z,t) & \approx w_0 (x,\theta ,t) + z\varphi_7 (x,\theta ,t) + z^2 \varphi_8 (x,\theta ,t) + z^3 \varphi_9 (x,\theta ,t) \\ \end{aligned}$$

(8)

where $u_0$, $v_0$ and $w_0$ denote displacement fields at middle plane (z = 0) along $x,\theta$ coordinates, respectively.

The strain–displacement relations (kinematic equations) for sandwich panel are written as follows (Kant and Punera [7]):

$$\begin{aligned} \varepsilon_x & = \frac{\partial u}{{\partial x}},\quad \varepsilon_\theta = \frac{1}{R\beta }\left[ {\frac{\partial v}{{\partial \theta }} + w} \right],\quad \varepsilon_z = \frac{\partial w}{{\partial z}} \\ \gamma_{x\theta } & = \frac{\partial v}{{\partial x}} + \frac{1}{R\beta }\frac{\partial u}{{\partial \theta }},\quad \gamma_{xz} = \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}},\quad \gamma_{\theta z} = \frac{1}{R\beta }\left[ {\frac{\partial w}{{\partial \theta }} + \frac{\partial v}{{\partial z}}\left( {R + z} \right) - v} \right] \\ \end{aligned}$$

(9)

where $\varepsilon_x$, $\varepsilon_\theta$, and $\varepsilon_z$ are the normal strains and $\gamma_{x\theta }$, $\gamma_{xz}$, and $\gamma_{\theta z}$ denote the shear strain for sandwich panel that $\beta$ is defined as follows:

$$\beta = 1 + {z / R}$$

(10)

Substituting Eq. (8) into Eq. (9) yields the kinematic equations for sandwich panel based on HSDT as follows:

$$\begin{aligned} \varepsilon_x & = \left\{ {\varepsilon_x^0 + z\varepsilon_x^1 + z^2 \varepsilon_x^2 + z^3 \varepsilon_x^3 } \right\} \\ \varepsilon_\theta & = \frac{1}{R\beta }\left\{ {\varepsilon_\theta^0 + z\varepsilon_\theta^1 + z^2 \varepsilon_\theta^2 + z^3 \varepsilon_\theta^3 } \right\} \\ \varepsilon_z & = \left\{ {\varepsilon_z^0 + z\varepsilon_z^1 + z^2 \varepsilon_z^2 + z^3 \varepsilon_z^3 } \right\} \\ \gamma_{x\theta } & = \left\{ {\gamma_{x\theta }^0 + z\gamma_{x\theta }^1 + z{\,}^2\gamma_{x\theta }^2 + z^3 \gamma_{x\theta }^3 } \right\} + \frac{1}{R\beta }\left\{ {\lambda_{x\theta }^0 + z\lambda_{x\theta }^1 + z^2 \lambda_{x\theta }^2 + z^3 \lambda_{x\theta }^3 } \right\} \\ \gamma_{xz} & = \left\{ {\gamma_{xz}^0 + z\gamma_{xz}^1 + z{\,}^2\gamma_{xz}^2 + z^3 \gamma_{xz}^3 } \right\} \\ \gamma_{\theta z} & = \frac{1}{R\beta }\left\{ {\gamma_{\theta z}^0 + z\gamma_{\theta z}^1 + z^2 \gamma_{\theta z}^2 + z^3 \gamma_{\theta z}^3 } \right\} \\ \end{aligned}$$

(11)

The parameters $\varepsilon_x^0$, $\varepsilon_x^1$, $\varepsilon_x^2$, $\varepsilon_x^3$, $\varepsilon_\theta^0$, $\varepsilon_\theta^1$, $\varepsilon_\theta^2$, $\varepsilon_\theta^3$, $\varepsilon_z^0$, $\varepsilon_z^1$, $\varepsilon_z^2$, $\varepsilon_z^3$, $\gamma_{x\theta }^0$, $\gamma_{x\theta }^1$, $\gamma_{x\theta }^2$, $\gamma_{x\theta }^3$, $\lambda_{x\theta }^0$, $\lambda_{x\theta }^1$, $\lambda_{x\theta }^2$, $\lambda_{x\theta }^3$, $\gamma_{xz}^0$, $\gamma_{xz}^1$, $\gamma_{xz}^2$, $\gamma_{xz}^3$, $\gamma_{\theta z}^0$, $\gamma_{\theta z}^1$, $\gamma_{\theta z}^2$ and $\gamma_{\theta z}^3$ in Eq. (11) are defined in appendix (22).

The strain–stress relations (constitutive equations) are as follows (Punera and Kant [8]):

$$\begin{aligned} \varepsilon_1 & = \frac{\sigma_1 }{{E_{11} (z)}} - \upsilon_{21} \frac{\sigma_2 }{{E_{22} (z)}} - \upsilon_{31} \frac{\sigma_3 }{{E_{33} (z)}} \\ \varepsilon_2 & = \frac{\sigma_2 }{{E_{22} (z)}} - \upsilon_{12} \frac{\sigma_1 }{{E_{11} (z)}} - \upsilon_{32} \frac{\sigma_3 }{{E_{33} (z)}} \\ \varepsilon_3 & = \frac{\sigma_3 }{{E_{33} (z)}} - \upsilon_{13} \frac{\sigma_1 }{{E_{11} (z)}} - \upsilon_{23} \frac{\sigma_2 }{{E_{22} (z)}} \\ \gamma_{12} & = \frac{{\tau_{12} }}{{G_{12} (z)}},\quad \gamma_{13} = \frac{{\tau_{13} }}{{G_{13} (z)}},\quad \gamma_{23} = \frac{{\tau_{23} }}{{G_{23} (z)}} \\ \end{aligned}$$

(12)

where $\varepsilon_1$, $\varepsilon_2$ and $\varepsilon_3$ are the normal strains along on-axis coordinates, and $\sigma_1$, $\sigma_2$ and $\sigma_3$ denote the normal stress along on-axis coordinates.$\gamma_{12}$, $\gamma_{13}$ and $\gamma_{23}$ are shear strains, and $\tau_{12}$, $\tau_{13}$ and $\tau_{23}$ denote shear stresses. The stress–strain equations along on-axis coordinate are obtained as follows (Punera and Kant [8]):

$$\left\{ \begin{gathered} \sigma_1 \hfill \\ \sigma_2 \hfill \\ \sigma_3 \hfill \\ \tau_{12} \hfill \\ \tau_{13} \hfill \\ \tau_{23} \hfill \\ \end{gathered} \right\}_n^z = \left[ \begin{gathered} Q_{11} \,\,\,\,\,Q_{12} \,\,\,\,\,Q_{13} \,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0 \hfill \\ Q_{21} \,\,\,\,\,Q_{22} \,\,\,\,\,Q_{23} \,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0 \hfill \\ Q_{31} \,\,\,\,\,Q_{32} \,\,\,\,\,Q_{33} \,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0 \hfill \\ \,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,Q_{44} \,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0 \hfill \\ \,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,Q_{55} \,\,\,\,\,\,\,0 \hfill \\ \,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,Q_{66} \hfill \\ \end{gathered} \right]\left\{ \begin{gathered} \varepsilon_1 \hfill \\ \varepsilon_2 \hfill \\ \varepsilon_3 \hfill \\ \gamma_{12} \hfill \\ \gamma_{13} \hfill \\ \gamma_{23} \hfill \\ \end{gathered} \right\}_n^z$$

(13)

where the stiffness matrix [Q] are written in appendix (23).

The constitutive equations along off-axis coordinate are presented as follows (Punera and Kant [8]):

$$\left\{ \begin{gathered} \sigma_x \hfill \\ \sigma_\theta \hfill \\ \sigma_z \hfill \\ \tau_{x\theta } \hfill \\ \tau_{xz} \hfill \\ \tau_{\theta z} \hfill \\ \end{gathered} \right\}_n^z = \left[ \begin{gathered} C_{11} \,\,\,\,\,C_{12} \,\,\,\,\,C_{13} \,\,\,\,\,\,C_{14} \,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0 \hfill \\ C_{21} \,\,\,\,\,C_{22} \,\,\,\,\,C_{23} \,\,\,\,\,C_{24} \,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0 \hfill \\ C_{31} \,\,\,\,\,C_{32} \,\,\,\,\,C_{33} \,\,\,\,\,C_{34} \,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0 \hfill \\ C_{41} \,\,\,\,\,C_{42} \,\,\,\,\,C_{43} \,\,\,\,\,C_{44} \,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0 \hfill \\ \,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,C_{55} \,\,\,\,\,C_{56} \hfill \\ \,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,C_{65} \,\,\,\,\,C_{66} \hfill \\ \end{gathered} \right]\left\{ \begin{gathered} \varepsilon_x \hfill \\ \varepsilon_\theta \hfill \\ \varepsilon_z \hfill \\ \gamma_{x\theta } \hfill \\ \gamma_{xz} \hfill \\ \gamma_{\theta z} \hfill \\ \end{gathered} \right\}_n^z$$

(14)

where the stiffness matrix [C] are defined in appendix (25).

Hamilton's Principle for a Sandwich Panel

The kinematic energy for sandwich panel based on HSDT is written as follows (Kant and Punera [7]):

$$\delta T = \delta \int_V {\left( {\frac{1}{2}\rho \dot{u}^2 + \frac{1}{2}\rho \dot{v}^2 + \frac{1}{2}\rho \dot{w}^2 } \right)} R\beta \,dx\,d\theta \,dz = \int_V {\left( {\rho \dot{u}\delta \dot{u} + \rho \dot{v}\delta \dot{v} + \rho \dot{w}\delta \dot{w}} \right)} R\beta \,dx\,d\theta \,dz$$

(15)

The strain energy for sandwich panel based on HSDT is considered as follows (Kant and Punera [7]):

$$\delta U = \int_V {\left( {\sigma_x \delta \varepsilon_x + \sigma_\theta \delta \varepsilon_\theta + \sigma_z \delta \varepsilon_z + \tau_{x\theta } \delta \gamma_{x\theta } + \tau_{\theta z} \delta \gamma_{\theta z} + \tau_{xz} \delta \gamma_{xz} } \right)} R\beta \,dx\,d\theta \,dz$$

(16)

The resultant forces and moments of a sandwich panel using HSDT are presented as follows:

$$\left[ \begin{gathered} N_x^0 \,\,\,\,\,N_\theta^0 \hfill \\ N_x^1 \,\,\,\,\,N_\theta^1 \hfill \\ N_x^2 \,\,\,\,\,N_\theta^2 \hfill \\ N_x^3 \,\,\,\,\,N_\theta^3 \hfill \\ \end{gathered} \right] = \sum_{k = 1}^{k = N_l } {\int_{h_{k - 1} }^{h_k } {\left[ \begin{gathered} 1 \hfill \\ z \hfill \\ z^2 \hfill \\ z^3 \hfill \\ \end{gathered} \right]} } \left[ {\beta \sigma_x \,\,\,\,\,\sigma_\theta } \right]dz$$

(17a)

$$\left[ \begin{gathered} N_{x\theta }^0 \,\,\,\,\,N_{\theta x}^0 \hfill \\ N_{x\theta }^1 \,\,\,\,\,N_{\theta x}^1 \hfill \\ N_{x\theta }^2 \,\,\,\,\,N_{\theta x}^2 \hfill \\ N_{x\theta }^3 \,\,\,\,\,N_{\theta x}^3 \hfill \\ \end{gathered} \right] = \sum_{k = 1}^{k = N_l } {\int_{h_{k - 1} }^{h_k } {\left[ \begin{gathered} 1 \hfill \\ z \hfill \\ z^2 \hfill \\ z^3 \hfill \\ \end{gathered} \right]} } \left[ {\beta \tau_{x\theta } \,\,\,\,\,\tau_{\theta x} } \right]dz$$

(17b)

$$\left[ \begin{gathered} S_x^0 \,\,\,\,\,S_\theta^0 \hfill \\ S_x^1 \,\,\,\,\,S_\theta^1 \hfill \\ S_x^2 \,\,\,\,S_\theta^2 \hfill \\ S_x^3 \,\,\,\,\,S_\theta^3 \hfill \\ \end{gathered} \right] = \sum_{k = 1}^{k = N_l } {\int_{h_{k - 1} }^{h_k } {\left[ \begin{gathered} 1 \hfill \\ z \hfill \\ z^2 \hfill \\ z^3 \hfill \\ \end{gathered} \right]} } \left[ {\beta \tau_{xz} \,\,\,\,\,\tau_{\theta z} } \right]dz,\quad \left[ \begin{gathered} A \hfill \\ B \hfill \\ D\, \hfill \\ \end{gathered} \right] = \sum_{k = 1}^{k = N_l } {\int_{h_{k - 1} }^{h_k } {\beta \sigma_z \left[ \begin{gathered} 1 \hfill \\ z \hfill \\ z^2 \hfill \\ \end{gathered} \right]} } \,dz$$

(17c)

The elements of stiffness matrix for a sandwich panel with porous core and nano composite facesheet layers are considered as follows:

$$\begin{aligned} C_{12}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{12}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{12}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{12}^{(t)} (z)z^i dz} \\ C_{21}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{21}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{21}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{21}^{(t)} (z)z^i dz} \\ C_{14}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{12}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{14}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{14}^{(t)} (z)z^i dz} \\ C_{41}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{41}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{41}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{41}^{(t)} (z)z^i dz} \\ C_{23}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{23}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{23}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{23}^{(t)} (z)z^i dz} \\ C_{32}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{32}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{32}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{32}^{(t)} (z)z^i dz} \\ C_{24}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{24}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{24}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{24}^{(t)} (z)z^i dz} \\ C_{42}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{42}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{42}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{42}^{(t)} (z)z^i dz} \\ C_{34}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{34}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{34}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{34}^{(t)} (z)z^i dz} \\ C_{43}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{43}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{43}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{43}^{(t)} (z)z^i dz} \\ C_{44}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{44}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{44}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{44}^{(t)} (z)z^i dz} \\ C_{56}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{56}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{56}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{56}^{(t)} (z)z^i dz} \\ C_{65}^{(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{65}^{(b)} (z)z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{65}^{(c)} (z)z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{65}^{(t)} (z)z^i dz} \\ \end{aligned}$$

(18a)

$$\begin{aligned} C_{11}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{11}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{11}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{11}^{(t)} (z)\beta z^i dz} \\ C_{13}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{13}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{13}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{13}^{(t)} (z)\beta z^i dz} \\ C_{31}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{31}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{31}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{31}^{(t)} (z)\beta z^i dz} \\ C_{14}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{14}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{14}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{14}^{(t)} (z)\beta z^i dz} \\ C_{41}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{41}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{41}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{41}^{(t)} (z)\beta z^i dz} \\ C_{33}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{33}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{33}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{33}^{(t)} (z)\beta z^i dz} \\ C_{34}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{34}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{34}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{34}^{(t)} (z)\beta z^i dz} \\ C_{43}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{43}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{43}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{43}^{(t)} (z)\beta z^i dz} \\ C_{44}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{44}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{44}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{44}^{(t)} (z)\beta z^i dz} \\ C_{55}^{*(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{55}^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{55}^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{55}^{(t)} (z)\beta z^i dz} \\ C_{22}^{**(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{22}^{(b)} (z)\frac{z^i }{\beta }dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{22}^{(c)} (z)\frac{z^i }{\beta }dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{22}^{(t)} (z)\frac{z^i }{\beta }dz} \\ C_{24}^{**(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{24}^{(b)} (z)\frac{z^i }{\beta }dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{24}^{(c)} (z)\frac{z^i }{\beta }dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{24}^{(t)} (z)\frac{z^i }{\beta }dz} \\ C_{42}^{**(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{42}^{(b)} (z)\frac{z^i }{\beta }dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{42}^{(c)} (z)\frac{z^i }{\beta }dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{42}^{(t)} (z)\frac{z^i }{\beta }dz} \\ C_{44}^{**(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{44}^{(b)} (z)\frac{z^i }{\beta }dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{44}^{(c)} (z)\frac{z^i }{\beta }dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{44}^{(t)} (z)\frac{z^i }{\beta }dz} \\ C_{66}^{**(i)} & = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {C_{66}^{(b)} (z)\frac{z^i }{\beta }dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {C_{66}^{(c)} (z)\frac{z^i }{\beta }dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {C_{66}^{(t)} (z)\frac{z^i }{\beta }dz} \\ \end{aligned}$$

(18b)

The coefficients of mass matrix for the sandwich panel are calculated as follows:

$$I^{*(i)} = \int_{ - h_b - {{h_c } / 2}}^{ - {{h_c } / 2}} {\rho^{(b)} (z)\beta z^i dz} + \int_{ - {{h_c } / 2}}^{{{h_c } / 2}} {\rho^{(c)} (z)\beta z^i dz} + \int_{{{h_c } / 2}}^{{{h_c } / 2} + h_t } {\rho^{(t)} (z)\beta z^i dz}$$

(19)

Nonlocal strain gradient theory (NSGT) is defined as follows:

$$[1 - (e_0 a)^2 \nabla^2 ]\sigma_{ij} = (1 - l_m^2 \nabla^2 )C_{ijkl} \varepsilon_{kl}$$

(20)

The details of Eq. (20) for sandwich panel based on HSDT and NSGT is stated in “Appendix 2”.

The Equations of Motion for a Sandwich Panel

Substituting (9) and (22) into Eq. (24) and applying Hamilton's principle and the resultant forces and moments, the equations of motion for sandwich panel with porous core and nanocomposite facesheet layers reinforced by carbon nanotube or graphene’s platelets based on HSDT and NSGT are obtained as follows:

$$\begin{aligned} & \delta u_0 {:}\quad (1 - l_m ^2 \nabla ^2 )\frac{{\partial N_x^0 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_{\theta x}^0 }}{{\partial \theta }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(0)} \frac{{\partial ^2 u_0 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(1)} \frac{{\partial ^2 \varphi _1 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 \varphi _2 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _3 }}{{\partial t^2 }} = 0 \\ & \delta v_0 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial N_{x\theta }^0 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_\theta ^0 }}{{\partial \theta }} + (1 - l_m ^2 \nabla ^2 )\frac{{S_\theta ^0 }}{R} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(0)} \frac{{\partial ^2 v_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(1)} \frac{{\partial ^2 \varphi _4 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 \varphi _5 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _6 }}{{\partial t^2 }} = 0 \\ & \delta w_0 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial S_x^0 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial S_\theta ^0 }}{{\partial \theta }} - (1 - l_m ^2 \nabla ^2 )\frac{{N_\theta ^0 }}{R} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(0)} \frac{{\partial ^2 w_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(1)} \frac{{\partial ^2 \varphi _7 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 \varphi _8 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _9 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _1 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial N_x^1 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_{\theta x}^1 }}{{\partial \theta }} - (1 - l_m ^2 \nabla ^2 )S_x^0 + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(1)} \frac{{\partial ^2 u_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 \varphi _1 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _2 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _3 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _4 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial N_{x\theta }^1 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_\theta ^1 }}{{\partial \theta }} - (1 - l_m ^2 \nabla ^2 )S_\theta ^0 + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(1)} \frac{{\partial ^2 v_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 \varphi _4 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _5 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _6 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _7 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial S_x^1 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial S_\theta ^1 }}{{\partial \theta }} - (1 - l_m ^2 \nabla ^2 )\frac{{N_\theta ^1 }}{R} - A + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(1)} \frac{{\partial ^2 w_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 \varphi _7 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _8 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _9 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _2 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial N_x^2 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_{\theta x}^2 }}{{\partial \theta }} - 2(1 - l_m ^2 \nabla ^2 )S_x^1 + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 u_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _1 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _2 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(5)} \frac{{\partial ^2 \varphi _3 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _5 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial N_{x\theta }^2 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_\theta ^2 }}{{\partial \theta }} - 2(1 - l_m ^2 \nabla ^2 )S_\theta ^1 - (1 - l_m ^2 \nabla ^2 )\frac{{S_\theta ^2 }}{R} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 v_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _4 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _5 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(5)} \frac{{\partial ^2 \varphi _6 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _8 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial S_x^2 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial S_\theta ^2 }}{{\partial \theta }} - (1 - l_m ^2 \nabla ^2 )\frac{{N_\theta ^2 }}{R} - 2B + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 w_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _7 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _8 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(5)} \frac{{\partial ^2 \varphi _9 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _3 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial N_x^3 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_{\theta x}^3 }}{{\partial \theta }} - 3(1 - l_m ^2 \nabla ^2 )S_x^2 + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 u_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _1 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(5)} \frac{{\partial ^2 \varphi _2 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(6)} \frac{{\partial ^2 \varphi _3 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _6 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial N_{x\theta }^3 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial N_\theta ^3 }}{{\partial \theta }} - 3(1 - l_m ^2 \nabla ^2 )S_\theta ^2 - 2(1 - l_m ^2 \nabla ^2 )\frac{{S_\theta ^3 }}{R} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 v_0 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _4 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(5)} \frac{{\partial ^2 \varphi _5 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(6)} \frac{{\partial ^2 \varphi _6 }}{{\partial t^2 }} = 0 \\ & \delta \varphi _9 {:}\quad(1 - l_m ^2 \nabla ^2 )\frac{{\partial S_x^3 }}{{\partial x}} + (1 - l_m ^2 \nabla ^2 )\frac{1}{R}\frac{{\partial S_\theta ^3 }}{{\partial \theta }} - (1 - l_m ^2 \nabla ^2 )\frac{{N_\theta ^3 }}{R} - 3D + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(2)} \frac{{\partial ^2 w_0 }}{{\partial t^2 }} \\ & \quad + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(3)} \frac{{\partial ^2 \varphi _7 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(4)} \frac{{\partial ^2 \varphi _8 }}{{\partial t^2 }} + [1 - (e_0 a)^2 \nabla ^2 ]I^{*(5)} \frac{{\partial ^2 \varphi _9 }}{{\partial t^2 }} = 0 \\ \end{aligned}$$

(21)

The governing equations of motion for sandwich panel with porous core and nanocomposite facesheet layers reinforced by carbon nanotube or graphene’s platelets based on HSDT and NSGT are considered.

Figure 2 shows a flowchart representing the overall proposed methodology of a thick micro sandwich panel with metamaterial (graphene origami (GOri) with negative Poisson’s ratio) or porous core and carbon nanotubes (CNTs)/graphene platelets (GPLs) reinforced composite for the reader's ease of understanding.

Fig. 2

A flowchart representing the overall proposed methodology of a thick micro sandwich panel with metamaterial or porous core and carbon nanotubes/graphene platelets reinforced composite

Numerical Results and Discussion

In this section, the vibration analysis of a thick-walled sandwich panel with porous core and and nanocomposite facesheets reinforced by carbon nanotubes or graphene’s platelets based on HSDT and NSGT is investigated. Also, the effect of small scale parameter, strain gradient parameter,, types of porosity, porosity coefficient, different distribution of carbon nanotube, and volume of carbon nanotubes, volume fraction of graphene’s platelets, geometric of graphene’s platelets on the natural frequency are studied.

The geometry of a sandwich panel for carbon nanotubes and graphen platelet is considered in Table 1.

Table 1 The geometry of carbon nanotubes and graphen platelet

The mechanical properties of core and facesheets (carbon nanotubes and graphen platelet) for a sandwich panel are considered in Table 2. Also, the values of efficiency parameters are reported in Table 3.

Table 2 The mechanical properties of core and facesheets for sandwich panel (Rahmani et al. [1]) and the mechanical properties of graphen platelet (GPL) for sandwich panel (Arefi et al. [14])

Table 3 The values of efficiency parameters (Bahaadini and Saidi [10])

The results of this research has been validated by the other literature Rahmani et al. [1] and Garg et al. [44] that this validate is shown in Table 4. It is seen that there are a good agreement between them.

Table 4 The natural frequency for the present work and the obtained results by Rahmani et al. [1] in ${h / L} = 0.01$, $\Omega = {{\omega L^2 ({\rho / {E_2 }})_f^{1 / 2} } / h}$

Figures 3 and 4 show the effect of small scale (nonlocal) and strain gradient parameters on the natural frequency for a sandwich panel, respectively. In Fig. 3, by increasing the nonlocal parameter, frequency reduces due to decreasing the stiffness of sandwich structure. Also, with an increase in the facesheet to core thickness ratio, due to increasing the stiffness of sandwich structure, frequency for sandwich panel increases. As seen in Fig. 4, the frequency increases with a enhance in the strain gradient parameter due to the increasing stiffness of structure.

Fig. 3

The effect of nonlocal parameter on the natural frequency of sandwich panel

Fig. 4

The effect of strain gradient parameter on the natural frequency of sandwich panel

The effect of porosity on the natural frequency of sandwich panel with uniform, type 1 (symmetric porosity) and 2 (asymmetric porosity) distributions of porosity is shown in Fig. 5a–c, respectively. As shown in Fig. 5, as the porosity coefficient increases, both the stiffness matrix and the mass matrix reduces; while the decrease for the mass matrix is greater than stiffness matrix in this structure, thus increasing the natural frequency.

Fig. 5

The effect of porosity on the natural frequency with a uniform distribution, b type 1 distribution, c type 2 distribution of porosity by considering V^*_CNT = 0.12

The effect of various porosity distributions with the porosity coefficient of 0.4 including uniform distribution, symmetric (type 1) and asymmetric (type 2) on the natural frequency are observed in Fig. 6. It can be seen that the natural frequency for asymmetric distribution of porosity is more than two other cases.

Fig. 6

The effect of various porosity distributions including uniform distribution, symmetric (type 1) and asymmetric (type 2) on the natural frequency with $e_0 = 0.4$, and V^*_CNT = 0.12

Figure 7 shows the effect of volume fraction for CNT on the natural frequency. As it is observed in this Fig. 7, enhancing the volume fraction of the carbon nanotubes leads to enhance frequency, because the stiffness matrix enhances.

Fig. 7

The effect of different volume fraction of carbon nanotubes on the natural frequency with $e_0 = 0.4$

Figure 8 shows the effects of CNTs distribution including uniform, FG-O and UD, and FG X-X on the natural frequency. It can be realized that the distribution of FG X-X for the carbon nanotube gives the most natural frequency because it increases more the stiffness matrix of sandwich panel.

Fig. 8

The effect of different distribution of carbon nanotubes including uniform, FG-O and UD, and FG X-X ith $e_0 = 0.4$, and V^*_CNT = 0.12

Figure 9a–c indicate the effect of he length, width and thickness of the graphene’s platelets on the natural frequency, respectively. As it can be seen, by increasing the length and width of the graphene’s platelets, the natural frequencies increases; while, increasing the thickness of the graphene’s platelets leads to decrease the natural frequencies.

Fig. 9

The effect of the a length, b width and c thickness of the graphene’s platelets on the natural frequency for sandwich panel

In Fig. 10, the effects of folding degree (H^*_GR) and weight fraction (w^*_GR) for graphene origami metamaterials (GOM) on Poisson’s ratio are shown. It is seen that with an enhance in the H^*_GR and w^*_GR, the Poisson’s ratio has a negative value, this means that as the length of the beam for graphene origami metamaterials enhances, while the width and height also increase.

Fig. 10

The effects of folding degree (H^*_GR) and weight fraction (w^*_GR) for GOM on Poisson’s ratio

In Figs. 11 and 12, the weight fraction of GOM (w^*_GR) and the graphene origami metamaterials (GOM) folding degree (H^*_GR) on the natural frequency of a thick sandwich panel, it is shown that with an increase the weight fraction and folding degree (H^*_GR) of GOM, due to increasing stiffness of structures, the natural frequency enhances. It is shown that the negative Poisson’s ratio has a large effect on the natural frequency.

Fig. 11

The effect of weight fraction (W^*_GR) and H^*_GR = 0.1 for GOM on the natural frequency of sandwich panel

Fig. 12

The effect of folding degree (H^*_GR) and W^*_GR = 0.15 for GOM on the natural frequency of sandwich panel

Conclusion

In previous studies, cylindrical shells have been mostly discussed, but each other considers only plane strain or plane stress, while in this work, there are all components of normal and shear strain/stress. On the other hands, the novelty of this work is to investigate general strain/stress because the sandwich structure is assumed as a thick-walled panel. Also, the current work's significance and necessity is the investigation of a thick sandwich panel by considering two-types reinforcements including CNTs or GPL with two-types cores such as porous or metamaterials with negative Poisson’s ratio to analyze vibration response of a this structure based on HSDT and NSGT, thus the above highlights were not considered simultaneously until now in any work and becomes the novelty of the present work. So that it is widely used in aerospace, marine, military and energy industries. The governing equations of motion for the sandwich panel are obtained using the Hamilton's principle, the extended mixture rule, and the Halpin Tsai approach. The results of this research have been validated by the other literature Rahmani et al. [1] and Garg et al. [44] that it is shown in Table 4 and there are a good agreement between them. The effects of different parameters such as Eringen’s non-local parameter, material length scale parameter, various distributions of porosity, porosity coefficient and various distributions of CNT, volume fraction of CNT, volume fraction of GPL, geometric dimensions of GPL, weight fraction of GOri, and the folding degree $\left( {H_{Gr} } \right)$ on natural frequency is studied. In this work, the stiffness and mass matrices are 12 × 12 by considering general strain for displacement fields from third order because this displacement field has twelve unknown function.

The obtained results from this research are presented as follows:

• 1. It is shown that by increasing the nonlocal parameter, the natural frequency reduces due to decreasing the stiffness of sandwich structure. Also, with an increase in the facesheet to core thickness ratio, due to increasing the stiffness of sandwich structure, the natural frequency of sandwich panel increases.

• 2. As shown in the Fig. 5, as the porosity coefficient increases, both the stiffness matrix and the mass matrix reduces; while the reduction of the mass matrix is greater than the stiffness matrix for the sandwich panel, thus increasing the natural frequency.

• 3. As it is observed in this Fig. 7, increasing the volume fraction of the carbon nanotubes leads to increase the natural frequency, because the stiffness matrix enhances.

• 4. It can be realized that the distribution of FG X–X for the carbon nanotube gives the most natural frequency because it increases more the stiffness matrix of sandwich panel.

• 5. As it can be seen, by enhancing length and width of graphene’s platelets, frequencies increases; while, increasing the thickness of the graphene’s platelets leads to decrease the natural frequencies.

• 6. It is shown that with an enhance in weight fraction of GOri (w^*_GR) and the folding degree (H^*_GR) and, because in metamaterials, the Poisson’s ratio has a negative value, this means that as the length of the beam for graphene origami metamaterials enhances, while the width and height also increase.

• 7. It is shown that with an increase the weight fraction and folding degree of GOM, due to increasing stiffness of structures, the natural frequency enhances. It is illustrated that the negative Poisson’s ratio has a large effect on the natural frequency.

• 8. It is concluded that with increasing of the material length scale parameter because the enhancement of stiffness for the structures, the natural frequency increases.

• 9. It can be seen that the natural frequency for asymmetric distribution of porosity is more than two other cases.

In the future work, the authors will suggest the vibration of various reinforcements and cores to select the best reinforcement and core to increase the strength to weight ratio.

Appendices

Appendix 1

The parameters $\varepsilon_x^0$, $\varepsilon_x^1$, $\varepsilon_x^2$, $\varepsilon_x^3$, $\varepsilon_\theta^0$, $\varepsilon_\theta^1$, $\varepsilon_\theta^2$, $\varepsilon_\theta^3$, $\varepsilon_z^0$, $\varepsilon_z^1$, $\varepsilon_z^2$, $\varepsilon_z^3$, $\gamma_{x\theta }^0$, $\gamma_{x\theta }^1$, $\gamma_{x\theta }^2$, $\gamma_{x\theta }^3$, $\lambda_{x\theta }^0$, $\lambda_{x\theta }^1$, $\lambda_{x\theta }^2$, $\lambda_{x\theta }^3$, $\gamma_{xz}^0$, $\gamma_{xz}^1$, $\gamma_{xz}^2$, $\gamma_{xz}^3$, $\gamma_{\theta z}^0$, $\gamma_{\theta z}^1$, $\gamma_{\theta z}^2$ and $\gamma_{\theta z}^3$ in Eq. (11) are defined as follows:

$$\begin{aligned} \left\{ {\varepsilon_x^0 \,\,\,\,\,\varepsilon_x^1 \,\,\,\,\,\varepsilon_x^2 \,\,\,\,\,\varepsilon_x^3 } \right\} & = \left\{ {\frac{\partial u_0 }{{\partial x}}\,\,\,\,\,\frac{\partial \varphi_1 }{{\partial x}}\,\,\,\,\,\frac{\partial \varphi_2 }{{\partial x}}\,\,\,\,\,\frac{\partial \varphi_3 }{{\partial x}}} \right\} \\ \left\{ {\varepsilon_\theta^0 \,\,\,\,\,\varepsilon_\theta^1 \,\,\,\,\,\varepsilon_\theta^2 \,\,\,\,\,\varepsilon_\theta^3 } \right\} & = \left\{ {\frac{\partial v_0 }{{\partial \theta }} + w_0 \,\,\,\,\,\frac{\partial \varphi_4 }{{\partial \theta }} + \varphi_7 \,\,\,\,\,\frac{\partial \varphi_5 }{{\partial \theta }} + \varphi_8 \,\,\,\,\,\frac{\partial \varphi_6 }{{\partial \theta }} + \varphi_9 } \right\} \\ \left\{ {\varepsilon_z^0 \,\,\,\,\,\varepsilon_z^1 \,\,\,\,\,\varepsilon_z^2 \,\,\,\,\,\varepsilon_z^3 } \right\} & = \left\{ {\varphi_7 \,\,\,\,\,2\varphi_8 \,\,\,\,\,3\varphi_9 \,\,\,\,\,0} \right\} \\ \left\{ {\gamma_{x\theta }^0 \,\,\,\,\,\gamma_{x\theta }^1 \,\,\,\,\,\gamma_{x\theta }^2 \,\,\,\,\,\gamma_{x\theta }^3 } \right\} & = \left\{ {\frac{\partial v_0 }{{\partial x}}\,\,\,\,\,\frac{\partial \varphi_4 }{{\partial x}}\,\,\,\,\,\frac{\partial \varphi_5 }{{\partial x}}\,\,\,\,\,\frac{\partial \varphi_6 }{{\partial x}}} \right\} \\ \left\{ {\lambda_{x\theta }^0 \,\,\,\,\,\lambda_{x\theta }^1 \,\,\,\,\,\lambda_{x\theta }^2 \,\,\,\,\,\lambda_{x\theta }^3 } \right\} & = \left\{ {\frac{\partial u_0 }{{\partial \theta }}\,\,\,\,\,\frac{\partial \varphi_1 }{{\partial \theta }}\,\,\,\,\,\frac{\partial \varphi_2 }{{\partial \theta }}\,\,\,\,\,\frac{\partial \varphi_3 }{{\partial \theta }}} \right\} \\ \left\{ {\gamma_{xz}^0 \,\,\,\,\,\gamma_{xz}^1 \,\,\,\,\,\gamma_{xz}^2 \,\,\,\,\,\gamma_{xz}^3 } \right\} & = \left\{ {\frac{\partial w_0 }{{\partial x}} + \varphi_1 \,\,\,\,\,\frac{\partial \varphi_7 }{{\partial x}} + 2\varphi_2 \,\,\,\,\,\frac{\partial \varphi_8 }{{\partial x}} + 3\varphi_3 \,\,\,\,\,\frac{\partial \varphi_9 }{{\partial x}}} \right\} \\ \left\{ {\gamma_{\theta z}^0 \,\,\,\,\,\gamma_{\theta z}^1 \,\,\,\,\,\gamma_{\theta z}^2 \,\,\,\,\,\gamma_{\theta z}^3 } \right\} & = \left\{ {\frac{\partial w_0 }{{\partial \theta }} + R\varphi_4 - v_0 \,\,\,\,\,\frac{\partial \varphi_7 }{{\partial \theta }} + 2R\varphi \,\,\,\,\,\frac{\partial \varphi_8 }{{\partial \theta }} + 3R\varphi_6 + \varphi_5 \frac{\partial \varphi_9 }{{\partial \theta }} + 2\varphi_6 } \right\} \\ \end{aligned}$$

(22)

The elements of stiffness matrix [Q] for Eq. (13) are written as follows:

$$\begin{aligned} Q_{11} & = \frac{{(1 - \upsilon_{23} \upsilon_{32} )}}{\Delta }E_{11} ,\quad Q_{12} = \frac{{(\upsilon_{21} + \upsilon_{31} \upsilon_{23} )}}{\Delta }E_{11} \\ Q_{13} & = \frac{{(\upsilon_{31} + \upsilon_{21} \upsilon_{32} )}}{\Delta }E_{11} ,\quad Q_{21} = \frac{{(\upsilon_{12} + \upsilon_{13} \upsilon_{32} )}}{\Delta }E_{22} \\ Q_{22} & = \frac{{(1 - \upsilon_{31} \upsilon_{13} )}}{\Delta }E_{22} ,\quad Q_{23} = \frac{{(\upsilon_{32} + \upsilon_{31} \upsilon_{12} )}}{\Delta }E_{22} \\ Q_{31} & = \frac{{(\upsilon_{13} + \upsilon_{12} \upsilon_{23} )}}{\Delta }E_{33} ,\quad Q_{32} = \frac{{(\upsilon_{23} + \upsilon_{13} \upsilon_{21} )}}{\Delta }E_{33} \\ Q_{33} & = \frac{{(1 - \upsilon_{12} \upsilon_{21} )}}{\Delta }E_{33} \\ Q_{44} & = G_{12\,} ,\quad Q_{55} = G_{13\,} ,\quad Q_{66} = G_{23} \\ \Delta & = 1 - \upsilon_{12} \upsilon_{21} - \upsilon_{23} \upsilon_{32} - \upsilon_{31} \upsilon_{13} - 2\upsilon_{12} \upsilon_{23} \upsilon_{31} \\ \end{aligned}$$

(23)

The elements of the stiffness matrix [C] for Eq. (14) are defined as follows:

$$\begin{array}{*{20}l} {C_{11} = Q_{11} c^4 + 2(Q_{12} + 2Q_{44} )s^2 c^2 + Q_{22} s^4 } \hfill & {C_{24} = (Q_{11} - Q_{12} - 2Q_{44} )cs^3 + (Q_{12} - Q_{22} + 2Q_{44} )sc^3 \,} \hfill \\ {C_{12} = Q_{12} (c^4 + s^4 ) + (Q_{11} + Q_{22} - 4Q_{44} )s^2 c^2 } \hfill & {C_{33} = Q_{33} ,\quad C_{34} = (Q_{31} - Q_{32} )sc} \hfill \\ {C_{13} = Q_{13} c^2 + Q_{23} s^2 } \hfill & {C_{44} = (Q_{11} - 2Q_{12} + Q_{22} - 2Q_{44} )s^2 c^2 + Q_{44} (c^4 + s^4 )\,} \hfill \\ {C_{14} = (Q_{11} - Q_{12} - 2Q_{44} )sc^3 + (Q_{12} - Q_{22} + 2Q_{44} )cs^3 } \hfill & {C_{55} = Q_{55} c^2 + Q_{66} s^2 ,\quad C_{56} = (Q_{66} - Q_{55} )cs} \hfill \\ {C_{22} = Q_{11} s^4 + Q_{22} c^4 + 2(Q_{12} + 2Q_{44} )s^2 c^2 } \hfill & {C_{66} = Q_{55} s^2 + Q_{66} c^2 } \hfill \\ {C_{23} = Q_{13} s^2 + Q_{23} c^2 } \hfill & {\,} \hfill \\ \end{array}$$

(24)

so that $C_{ij} = C_{ji}$ in return $i,j = 1 - 6\,c = \cos \alpha \,\,,\,\,s = \sin \alpha$ and $\alpha$ is fiber angle.

Appendix 2

The details of Eqs. (20) for sandwich panel based on higher order shear deformation and nonlocal strain gradient theories is considered as follows:

$$\begin{aligned} [1 - (e_0 a)^2 \nabla^2 ]\sigma_x & = (1 - l_m^2 \nabla^2 )C_{11} \varepsilon_x + (1 - l_m^2 \nabla^2 )C_{12} \varepsilon_\theta + (1 - l_m^2 \nabla^2 )C_{13} \varepsilon_z + (1 - l_m^2 \nabla^2 )C_{14} \gamma_{x\theta } \, \\ [1 - (e_0 a)^2 \nabla^2 ]\sigma_\theta & = (1 - l_m^2 \nabla^2 )C_{21} \varepsilon_x + (1 - l_m^2 \nabla^2 )C_{22} \varepsilon_\theta + (1 - l_m^2 \nabla^2 )C_{23} \varepsilon_z + (1 - l_m^2 \nabla^2 )C_{24} \gamma_{x\theta } \\ [1 - (e_0 a)^2 \nabla^2 ]\sigma_z & = (1 - l_m^2 \nabla^2 )C_{31} \varepsilon_x + (1 - l_m^2 \nabla^2 )C_{32} \varepsilon_\theta + (1 - l_m^2 \nabla^2 )C_{33} \varepsilon_z + (1 - l_m^2 \nabla^2 )C_{34} \gamma_{x\theta } \\ [1 - (e_0 a)^2 \nabla^2 ]\tau_{x\theta } & = (1 - l_m^2 \nabla^2 )C_{41} \varepsilon_x + (1 - l_m^2 \nabla^2 )C_{42} \varepsilon_\theta + (1 - l_m^2 \nabla^2 )C_{43} \varepsilon_z + (1 - l_m^2 \nabla^2 )C_{44} \gamma_{x\theta } \\ [1 - (e_0 a)^2 \nabla^2 ]\tau_{xz} & = (1 - l_m^2 \nabla^2 )C_{55} \gamma_{xz} + (1 - l_m^2 \nabla^2 )C_{56} \gamma_{\theta z} \\ [1 - (e_0 a)^2 \nabla^2 ]\tau_{\theta z} & = (1 - l_m^2 \nabla^2 )C_{65} \gamma_{xz} + (1 - l_m^2 \nabla^2 )C_{66} \gamma_{\theta z} . \\ \end{aligned}$$

(25)