Dynamic stability analysis of Mindlin viscoelastic plates subjected to constant and harmonic in-plane compressions based on free vibration analysis of elastic plates

Abstract

In this paper, a dynamic stability analysis of moderately thick viscoelastic plates is performed employing the Boltzmann integral law with constant bulk modulus. The remarkable and new point of the proposed method is that the frequency of a Mindlin viscoelastic plate subjected to simultaneous constant and harmonic in-plane compressive loads is explicitly predictable based on free vibration analysis of an elastic plate. Moreover, the damped part of frequency is easily calculated. Also, the critical excitation for which the system becomes unstable is determined. This method is completely new and significantly reduces the computational cost. The obtained results are compared with other existing results to show the efficiency and accuracy of the proposed method. This method is used to investigate the effects of viscoelastic properties and in-plane compressions on the steady-state responses of Mindlin viscoelastic plates under time-dependent compressive loads.

1 Introduction

Composite structures have been widely used in various engineering applications. Since composite structures exhibit time-dependent properties, it is necessary to model them by viscoelastic theories. The vibration responses of plates have many applications in mechanical and structural engineering. The dynamic stability of plates subjected to in-plane compressive load is one of the most interesting problems in the field of structural vibration, because the instability may occur below the critical load of the plate even by a small excitation.

The dynamic stability of viscoelastic perfect columns made of Kelvin materials subjected to constant axial compression was studied by Dost and Glocknwe [1], and Szyszkowski and Glocknwe [2]. Li et al. [3] investigated the dynamic stability of a simply supported viscoelastic column subjected to a periodic axial force using the averaging method based on the Kelvin–Voigt fractional derivative stress–strain relation. Leung et al. [4] considered the steady-state response of a simply supported viscoelastic column based on the fractional Kelvin constitutive model subjected to axial harmonic excitation with delayed feedback.

The classical Kirchhoff plate theory is effective in solving some plate problems, but its accuracy decreases as the thickness of the plate increases. Aboudi and Cederbaum [5] considered the dynamic stability of linear viscoelastic Kirchhoff plates subjected to periodic in-plane loads based on the Boltzmann superposition principle. They solved the problem numerically, using Lyapunov exponents. Teifouet [6] presented the nonlinear vibration analysis of viscoelastic rectangular plates under tangential follower forces based on classical plate theory. Amabili [7] considered the nonlinear vibration analysis of viscoelastic thin rectangular plates using the von Kármán assumptions and the Kelvin–Voigt solids. Balasubramanian et al. [8] studied the viscoelastic response and nonlinear damping of rubber plates in nonlinear vibration of rectangular plates. Amabili [9] considered the nonlinear damping in nonlinear vibrations of rectangular plates based on the theory of viscoelasticity and experimental validation. Zhou and Wang [10] studied the transverse vibration and dynamic stability of the axially moving thin viscoelastic plates with two opposite edges simply supported based on the Kelvin–Voigt model. Amabili et al. [11] investigated the nonlinear vibrations and damping of fractional linear viscoelastic rectangular plates.

Shear-deformable plates are investigated in some papers. Singha and Daripa [12] considered the nonlinear vibration and dynamic stability analysis of elastic composite shear-deformable rectangular plates under transverse harmonic pressures. Zamani et al. [13] investigated the free vibration of thick laminated viscoelastic composite plates on a Pasternak viscoelastic medium with simply supported boundary conditions using the third-order shear deformation theory. Jafari et al. [14] presented the approximation method for geometrically nonlinear analysis of moderately thick time-dependent composite plates based on elasticity responses at asymptotic times. Arshid et al. [15] considered the bending, buckling, and free vibration analyses of FG-GNP-reinforced porous nanocomposite annular micro-plates based on the modified strain gradient theory. Saeed et al. [16] studied the free vibration of smart annular three-layered plates subjected to a magnetic field in a viscoelastic medium. Saeed et al. [17] employed the quasi-3D tangential shear deformation theory for size-dependent free vibration analysis of three-layered FG porous micro-rectangular plates integrated by nanocomposite faces in hygrothermal environment. Jafari and Azhari [18] considered the free vibration analysis of Mindlin viscoelastic plates employing the Boltzmann integral law with constant bulk modulus based on the free vibration analysis of elastic plates. Khorasani et al. [19] investigated the vibration of graphene nanoplatelets’ reinforced composite plates integrated by piezo-electromagnetic patches on the piezo-electromagnetic media using sinusoidal shear deformation plate theory.

To solve the dynamic stability of viscoelastic problems, the averaging method that belongs to Ilyushin approximation was used in some papers, although this method loses some information. Ilyasov and Akoz [20] examined the static and dynamic behavior of viscoelastic triangular plates with simply supported boundary conditions under static and dynamic loads employing the Boltzmann–Volterra principle based on classical plate theory. Dynamic stability of viscoelastic plates under linearly increasing compressing loads was numerically studied by Eshmatov [21] using the Bubnov–Galerkin procedure and quadrature formulas. Eshmatov [22] investigated the nonlinear vibrations and dynamic stability of viscoelastic orthotropic rectangular plates subjected to increasing compressing forces based on weakly singular Koltunov–Rzhanitsyn kernel. Sofiyev et al. [23] studied the free vibration and dynamic stability of functionally graded viscoelastic plates under compressive loads and resting on elastic foundations.

An overview of previous studies shows that the literature on the dynamic stability analysis of viscoelastic plates subjected to constant in-plane compressive loads is abundant. But, due to the difficulty and complexity of the equations, the dynamic stability analysis of viscoelastic plates under time-dependent in-plane compressive loads is rarely explored, especially for moderately thick plates. Thus, the present paper investigates the dynamic stability of viscoelastic columns, Kirchhoff viscoelastic plates, and moderately thick viscoelastic plates subjected to constant and harmonic in-plane compressive loads, simultaneously. Also, an approximated closed-form solution is proved and introduced, which calculates the frequency of viscoelastic structures explicitly, based on the frequency of elastic structures. Moreover, the critical harmonic excitation for which the system becomes unstable is calculated. The stress–strain relation is written based on the Boltzmann integral law with constant bulk modulus. The shear effect is described by the first-order shear deformation theory. The displacement field is approximated using the separation of variables technique. The Laplace transform is employed to convert equations from the time domain to the Laplace domain. Constant and decreasing frequencies of simply supported viscoelastic columns and viscoelastic plates with different properties are easily analyzed with low computational cost. Many numerical results are presented, demonstrating that the present method is in high agreement with the corresponding analytical solutions.

The organization of this paper is as follows: the extraction of equations of Kirchhoff and Mindlin viscoelastic plates is described in Sect. 2. The numerical results are presented in Sect. 3. Section 4 presents conclusions. The extraction of equations of viscoelastic columns is described in the “Appendix”.

2 Governing equations

2.1 Dynamic stability analysis of square Kirchhoff viscoelastic plates with simply supported boundary conditions

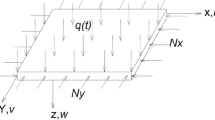
The equilibrium equation of a Kirchhoff viscoelastic plate subjected to time-dependent compression, as illustrated in Fig. 1, is defined as [5]:

$$\frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }} - N_{x} \left( t \right)\frac{{\partial^{2} w\left( {x,y,t} \right)}}{{\partial x^{2} }} - N_{y} \left( t \right)\frac{{\partial^{2} w\left( {x,y,t} \right)}}{{\partial y^{2} }} - \rho h\frac{{\partial^{2} w\left( {x,y,t} \right)}}{{\partial t^{2} }} = 0$$

(1)

in which $t$ is time, $h$ is the plate thickness, $\rho$ is the mass of a unit volume of the plate, $w$ is an out-of-plane displacement, $M_{x}$, $M_{y}$, and $M_{xy}$ are the bending moments, and $N_{x} \left( t \right)$ and $N_{y} \left( t \right)$ are the in-plane compressive forces.

Fig. 1

A viscoelastic plate subjected to time-dependent in-plane compressive forces

The bending moment $M_{ij}$ can be expressed as:

$$M_{ij} = \mathop \int \limits_{ - h/2}^{h/2} z\sigma_{ij} \left( {x,y,t} \right){\text{d}}z$$

(2)

The constitutive equations of a linear viscoelastic material based on the Boltzmann integral can be given as [24]:

$${{\varvec{\upsigma}}}\left( t \right) = {\mathbf{C}}\left( t \right){{\varvec{\upvarepsilon}}}\left( 0 \right) + \mathop \int \limits_{0}^{t} {\mathbf{C}}\left( {t - \tau } \right){\dot{\varvec{\upvarepsilon }}}\left( \tau \right){\text{d}}\tau ,\quad {\dot{\varvec{\upvarepsilon }}} = \frac{{\partial {{\varvec{\upvarepsilon}}}}}{\partial t}$$

(3)

where ${\mathbf{C}}\left( t \right)$ is the relaxed modulus tensor and ${{\varvec{\upsigma}}}$ is the stress vector associated with the strain vector, ${{\varvec{\upvarepsilon}}}$. The relaxed modulus tensor of a Kirchhoff plate can be defined as follows:

$${\mathbf{C}}\left( t \right) = \left[ {\begin{array}{*{20}c} {c_{1} \left( t \right)} & {c_{2} \left( t \right)} & 0 \\ {c_{2} \left( t \right)} & {c_{1} \left( t \right)} & 0 \\ 0 & 0 & {c_{3} \left( t \right)} \\ \end{array} } \right],$$

$$c_{1} \left( t \right) = \frac{E\left( t \right)}{{1 - \upsilon \left( t \right)^{2} }},\; c_{2} \left( t \right) = \frac{\upsilon \left( t \right)E\left( t \right)}{{1 - \upsilon \left( t \right)^{2} }}, \;c_{3} \left( t \right) = \frac{E\left( t \right)}{{2\left( {1 + \upsilon \left( t \right)} \right)}}.$$

(4)

Assuming the bulk modulus to be constant, $K$, the elastic modulus, $E\left( t \right)$, and Poisson’s ratio, $\nu \left( t \right)$, can be stated in the time domain as follows [25]:

$$E\left( t \right) = \frac{{9K\eta \left( t \right)}}{{2 + \eta \left( t \right)}},\,\nu \left( t \right) = \frac{{1 - \eta \left( t \right)}}{{2 + \eta \left( t \right)}}$$

(5)

where the dimensionless relaxation function, $\eta \left( t \right)$, can be defined by the exponential function as follows, [14, 18, 25]:

$$\eta \left( t \right) = c_{1} + c_{2} {\text{e}}^{ - \lambda t} , c_{1} + c_{2} = 1, \lambda = 1/t_{s}$$

(6)

$c_{1}$, $c_{2}$ are constant parameters, and $t_{s}$ is the relaxation time of a viscoelastic material.

The strain vector of a Kirchhoff viscoelastic plate can be expressed as follows:

$${{\varvec{\upvarepsilon}}}\left( {x{,}y{,}z{,}t} \right) = - z\left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} w\left( {x{,}y{,}t} \right)}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w\left( {x{,}y{,}t} \right)}}{{\partial x^{2} }}} \\ {2\frac{{\partial^{2} w\left( {x{,}y{,}t} \right)}}{\partial x\partial y}} \\ \end{array} } \right\}.$$

(7)

For the dynamic stability analysis, the displacement vector of a viscoelastic plate can be approximated using the separation of variables method as follows [5, 10, 26]:

$$w\left( {x{,}y{,}t} \right) = w\left( {x{,}y} \right)F\left( t \right)$$

(8)

Substituting Eq. (8) into Eq. (7), the strain vector of a viscoelastic plate can be expressed as follows:

$${{\varvec{\upvarepsilon}}}\left( {x{,}y{,}z{,}t} \right) = - z\left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {2\frac{{\partial^{2} w}}{\partial x\partial y}} \\ \end{array} } \right\}F\left( t \right) = - z{{\varvec{\upkappa}}}F\left( t \right), \,{{\varvec{\upkappa}}} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {2\frac{{\partial^{2} w}}{\partial x\partial y}} \\ \end{array} } \right\}.$$

(9)

Substituting Eq. (9) into Eq. (3), the stress vector associated with the strain vector is defined as follows:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{{x}} } \\ {\sigma_{y} } \\ {\sigma_{{xy}} } \\ \end{array} } \right\} = {\mathbf{C}}\left( t \right)\left( { - z} \right){{\varvec{\upkappa}}}F\left( 0 \right) + \mathop \int \limits_{0}^{t} {\mathbf{C}}\left( {t - \tau } \right)\left( { - z} \right){{\varvec{\upkappa}}}\dot{F}\left( \tau \right){\text{d}}\tau.$$

(10)

Substituting Eq. (10) into Eq. (2), the bending moment vector is defined as follows:

$$\left\{ {\begin{array}{*{20}c} {M_{x} } \\ {M_{y} } \\ {M_{{xy}} } \\ \end{array} } \right\} = - \frac{{h^{3} }}{12}{\mathbf{C}}\left( t \right){{\varvec{\upkappa}}}F\left( 0 \right) - \frac{{h^{3} }}{12}\mathop \int \limits_{0}^{t} {\mathbf{C}}\left( {t - \tau } \right){{\varvec{\upkappa}}}\dot{F}\left( \tau \right){\text{d}}\tau.$$

(11)

Replacing Eq. (11) in Eqs. (1), (12) is obtained:

$$\frac{{ - h^{3} }}{12}\frac{E\left( t \right)}{{1 - \upsilon \left( t \right)^{2} }}F\left( 0 \right)\left[ {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }} + 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right] - \left[ {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }} + 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right]\mathop \int \limits_{0}^{t} \frac{{h^{3} }}{12}\frac{{E\left( {t - \tau } \right)}}{{1 - \upsilon \left( {t - \tau } \right)^{2} }}\dot{F}\left( \tau \right){\text{d}}\tau - N_{x} \left( t \right)F\left( t \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} - N_{y} \left( t \right)F\left( t \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} - \rho hw\ddot{F}\left( t \right) = 0.$$

(12)

Considering simply supported boundary conditions, the displacement may be represented by:

$$w\left( {x{,}y} \right) = \sin \frac{\pi x}{a}\sin \frac{\pi y}{b}, a = b = l.$$

(13)

$a$ and $b$ are the lengths of the rectangular plate in the $x$ and $y$ directions, respectively.

Substituting Eq. (13) into Eqs. (12), (14) is derived:

$$\frac{{4\pi^{4} }}{{l^{4} }}\frac{{h^{3} }}{12}c_{1} \left( t \right)F\left( 0 \right) + \frac{{4\pi^{4} }}{{l^{4} }}\frac{{h^{3} }}{12}\mathop \int \limits_{0}^{t} c_{1} \left( {t - \tau } \right)\dot{F}\left( \tau \right){\text{d}}\tau - N_{x} \left( t \right)F\left( t \right)\frac{{\pi^{2} }}{{l^{2} }} - N_{y} \left( t \right)F\left( t \right)\frac{{\pi^{2} }}{{l^{2} }} + \rho h\ddot{F}\left( t \right) = 0.$$

(14)

Investigating the time-dependent compression in the $x$ direction, $N_{y} \left( t \right) = 0$, Eq. (15) is obtained:

$$N_{x} \left( t \right) = N_{\rm cr} \left( {\alpha_{1} + \beta_{1} \cos \varphi t} \right){, 0 } \le \alpha_{1} < 1, \beta_{1} \ge 0, 0 < \varphi < \pi /2$$

(15)

in which $\alpha_{1}$ and $\beta_{1}$ are arbitrary constant coefficients, and $\varphi$ is the excitation frequency. The critical stability load of a square Kirchhoff viscoelastic plate with simply supported boundary conditions subjected to uniaxial compression at time zero, $N_{\rm cr}$, is defined as [26]:

$$N_{\rm cr} = 4\frac{{\pi^{2} }}{{l^{2} }}\frac{{h^{3} }}{12}c_{1} \left( 0 \right) = \frac{{\pi^{2} h^{3} K}}{{l^{2} }}, c_{1} \left( 0 \right) = \frac{E\left( 0 \right)}{{1 - \upsilon \left( 0 \right)^{2} }} = 3K.$$

(16)

The time function of a Kirchhoff viscoelastic plate, $F\left( t \right)$, can be defined as follows:

$$F\left( t \right) = {\text{e}}^{{s_{0} t}} , \dot{F}\left( t \right) = s_{0} {\text{e}}^{{s_{0} t}} , \ddot{F}\left( t \right) = s_{0}^{2} {\text{e}}^{{s_{0} t}},$$

(17)

Replacing Eq. (5) in Eq. (4), Eq. (18) is obtained:

$$c_{1} \left( t \right) = \frac{E\left( t \right)}{{1 - \upsilon \left( t \right)^{2} }} = \frac{{3K\eta \left( t \right)\left( {2 + \eta \left( t \right)} \right)}}{{\left( {1 + 2\eta \left( t \right)} \right)}}.$$

(18)

Substituting Eqs. (15–18) into Eqs. (14), (19) is derived:

$$\frac{{h^{3} }}{12}\frac{{4\pi^{4} }}{{l^{4} }}\frac{{3K\eta \left( t \right)\left( {2 + \eta \left( t \right)} \right)}}{{\left( {1 + 2\eta \left( t \right)} \right)}} + \frac{{4\pi^{4} }}{{l^{4} }}\frac{{h^{3} }}{12}3K\mathop \int \limits_{0}^{t} \frac{{\eta \left( {t - \tau } \right)\left( {2 + \eta \left( {t - \tau } \right)} \right)}}{{\left( {1 + 2\eta \left( {t - \tau } \right)} \right)}}s_{0} {\text{e}}^{{s_{0} \tau }} {\text{d}}\tau - \left( {\alpha_{1} + \beta_{1} \cos \varphi t} \right)\frac{{\pi^{2} h^{3} K}}{{l^{2} }}F\left( t \right)\frac{{\pi^{2} }}{{l^{2} }} + \rho hs_{0}^{2} F\left( t \right) = 0.$$

(19)

Defining:

$${\Omega }^{2} = \frac{{\pi^{4} h^{3} K}}{{l^{4} \rho h}}, D\left( t \right) = \frac{{\eta \left( t \right)\left( {2 + \eta \left( t \right)} \right)}}{{\left( {1 + 2\eta \left( t \right)} \right)}}$$

(20)

in which ${\Omega }$ is the fundamental natural frequency of free vibration analysis of a thin viscoelastic square plate with simply supported boundary conditions at time zero [26], Eq. (19) can be rewritten as follows:

$$\Omega^{2} D\left( t \right) + \Omega^{2} s_{0} \mathop \int \limits_{0}^{t} D\left( {t - \tau } \right){\text{e}}^{{s_{0} \tau }} {\text{d}}\tau - \alpha_{1} \Omega^{2} F\left( t \right) - \beta_{1} \Omega^{2} \cos \varphi tF\left( t \right) + s_{0}^{2} F\left( t \right) = 0.$$

(21)

Using the Laplace transform and according to the proof presented in the “Appendix”, the convolution integral of Eq. (21) can be simplified as follows:

$$\Omega^{2} D^{*} + \left( {\Omega^{2} s_{0} D_{{s_{0} }}^{*} - \alpha_{1} \Omega^{2} + s_{0}^{2} } \right)F^{*} - \beta_{1} \Omega^{2} \left( {\cos \varphi tF\left( t \right)} \right)^{*} = 0.$$

(22)

One can write Eq. (22) as follows:

$${\Omega }^{2} D^{*} + \left( {{\Omega }^{2} s_{0} D_{{s_{0} }}^{*} - \alpha_{1} {\Omega }^{2} + s_{0}^{2} } \right)\frac{1}{{s - s_{0} }} - \frac{{\beta_{1} {\Omega }^{2} }}{2}\left( {\frac{1}{{s - s_{0} + i\varphi }} + \frac{1}{{s - s_{0} - i\varphi }}} \right) = 0$$

(23)

in which:

$$s_{0} D_{{s_{0} }}^{*} = \frac{{s_{0} \eta_{{s_{0} }}^{*} \left( {2 + s_{0} \eta_{{s_{0} }}^{*} } \right)}}{{1 + 2s_{0} \eta_{{s_{0} }}^{*} }} , \,\eta_{{s_{0} }}^{*} = \left( {\frac{{c_{1} }}{{s_{0} }} + \frac{{c_{2} }}{{s_{0} + \lambda }}} \right).$$

(24)

Considering harmonic responses for viscoelastic materials, $s_{0}$ cab be replaced by $i\omega_{0} - \alpha_{0}$ so that $\omega_{0}$ and $\alpha_{0}$ are real numbers and $\alpha_{0} \ge 0$. So, Eq. (25) is obtained:

$$s_{0} \eta_{{s_{0} }}^{*} = c_{1} + c_{2} \frac{{i\omega_{0} - \alpha_{0} }}{{i\omega_{0} - \alpha_{0} + \lambda }} \approx c_{1} + c_{2} + i\frac{{c_{2} \lambda }}{{\omega_{0} }}, s_{0} D_{{s_{0} }}^{*} \approx 1 + i\frac{2}{3}\frac{{c_{2} \lambda }}{{\omega_{0} }}.$$

(25)

According to the proof presented in the “Appendix”, if the Laplace parameter, $s$, is replaced by $i\left( {\omega_{0} + \varphi } \right)$, by neglecting $D^{*} = \left( {\frac{{c_{1} }}{{i\left( {\omega_{0} + \varphi } \right)}} + \frac{{c_{2} }}{{i\left( {\omega_{0} + \varphi } \right) + \lambda }}} \right)\frac{{\left( {2 + s\eta^{*} } \right)}}{{\left( {1 + 2s\eta^{*} } \right)}}$, Eq. (23) may be rewritten as:

$${\Omega }^{2} \left( {1 + i\frac{2}{3}\frac{{c_{2} \lambda }}{{\omega_{0} }}} \right) - \alpha_{1} {\Omega }^{2} + \left( {i\omega_{0} - \alpha_{0} } \right)^{2} - \beta_{1} {\Omega }^{2} \frac{{\left( {i\varphi + \alpha_{0} } \right)^{2} }}{{2i\varphi \alpha_{0} + \alpha_{0}^{2} }} = 0.$$

(26)

Separating the real and imaginary parts:

$${\Omega }^{2} - \omega_{0}^{2} + \alpha_{0}^{2} - \alpha_{1} {\Omega }^{2} - \beta_{1} {\Omega }^{2} \frac{{3\varphi^{2} \alpha_{0}^{2} + \alpha_{0}^{4} }}{{4\varphi^{2} \alpha_{0}^{2} + \alpha_{0}^{4} }} = 0,$$

(27)

$${\Omega }^{2} \frac{2}{3}\frac{{c_{2} \lambda }}{{\omega_{0} }} - 2\omega_{0} \alpha_{0} - \beta_{1} {\Omega }^{2} \frac{{2\varphi^{3} \alpha_{0} }}{{4\varphi^{2} \alpha_{0}^{2} + \alpha_{0}^{4} }} = 0,$$

(28)

Since $\alpha_{0} \ll {\Omega },{ }\lambda \ll {\Omega }$, by ignoring $\left( {\frac{{\alpha_{0} }}{{\Omega }}} \right)^{2}$, $\left( {\frac{\lambda }{{\Omega }}} \right)^{2},$ and $\frac{\lambda }{{\Omega }}\frac{{\alpha_{0} }}{{\Omega }}$, Eqs. (29–30) are derived:

$$\omega_{0} \approx {\Omega }\sqrt {1 - \alpha_{1} - \frac{3}{4}\beta_{1} } ,\, {\Omega }^{2} = \frac{{\pi^{4} h^{3} K}}{{l^{4} \rho h}},$$

(29)

$$\frac{{\alpha_{0} }}{{\Omega }} \approx \frac{{\frac{2}{3}\frac{{c_{2} \lambda }}{{\Omega }} + \sqrt {\left( {\frac{2}{3}\frac{{c_{2} \lambda }}{{\Omega }}} \right)^{2} - 4\beta_{1} \frac{\varphi }{{\Omega }}\left( {1 - \alpha_{1} - \frac{3}{4}\beta_{1} } \right)^{3/2} } }}{{4 \times \left( {1 - \alpha_{1} - \frac{3}{4}\beta_{1} } \right)}}.$$

(30)

Employing Eqs. (29–30), the natural frequency, $\omega_{0}$, and viscous damping frequency, $\alpha_{0}$, of thin square viscoelastic plates with simply supported boundary conditions are calculated easily, explicitly, and exactly.

Considering Eq. (30) shows that the Kirchhoff viscoelastic plate is always stable if the conditions below are satisfied:

$$\begin{aligned} & 1 - \alpha_{1} - \frac{3}{4}\beta_{1} > 0,\, \left( {\frac{2}{3}\frac{{c_{2} \lambda }}{{\Omega }}} \right)^{2} \ge 4\beta_{1} \frac{\varphi }{{\Omega }}\left( {1 - \alpha_{1} - \frac{3}{4}\beta_{1} } \right)^{\frac{3}{2}} , \\ & {0 } \le \alpha_{1} < 1, \,\beta_{1} \ge 0, \,0 < \varphi < \frac{\pi }{2}. \\ \end{aligned}$$

(31)

2.2 Dynamic stability analysis of moderately thick viscoelastic plates

According to the first-order shear theory, the displacement vector of a time-dependent viscoelastic plate can be expressed as:

$$\left\{ {\begin{array}{*{20}c} {u\left( {x{,}y{,}z{,}t} \right)} \\ {v\left( {x{,}y{,}z{,}t} \right)} \\ {w\left( {x{,}y{,}z{,}t} \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - z\theta_{x} \left( {x{,}y{,}t} \right)} \\ { - z\theta_{y} \left( {x{,}y{,}t} \right)} \\ {w\left( {x{,}y{,}t} \right)} \\ \end{array} } \right\}$$

(32)

in which $t$ is time, $\theta_{x}$ and $\theta_{y}$ are the rotations concerning $y$ and $x$ axes, respectively, and $w\left( {x{,}y{,}t} \right)$ is an out-of-plane displacement of the mid surface.

The strain vector of a Mindlin viscoelastic plate can be given as follows:

$${{\varvec{\upvarepsilon}}}\left( {x{,}y{,}z{,}t} \right) = \left\{ {\begin{array}{*{20}c} { - z\theta_{{x{,}x}} } \\ { - z\theta_{{y{,}y}} } \\ { - z\left( {\theta_{{x{,}y}} + \theta_{{y{,}x}} } \right)} \\ {w_{{{,}x}} - \theta_{x} } \\ {w_{{{,}y}} - \theta_{y} } \\ \end{array} } \right\}.$$

(33)

2.2.1 Constitutive relations of viscoelastic plates

Employing the constitutive relations introduced in Eq. (3), the stress vector, ${{\varvec{\upsigma}}}$, associated with the strain vector can be defined as:

$${{\varvec{\upsigma}}} = \begin{array}{*{20}c} {\begin{array}{*{20}c} {{\upsigma }_{x} } & {{\upsigma }_{y} } & {\tau_{xy} } \\ \end{array} } & {\begin{array}{*{20}c} {\tau_{xz} } & {\tau_{yz} } \\ \end{array} } \\ \end{array}^{T}.$$

(34)

2.2.2 Energy definition

At time $t$, the strain, $U\left( t \right)$, kinetic, $T\left( t \right)$, and potential, $V\left( t \right)$, energies are defined as follows:

$$U\left( t \right) = \frac{1}{2}\mathop \int \limits_{V}^{{}} {{\varvec{\upsigma}}}^{T} {{\varvec{\upvarepsilon}}}{\text{d}}V = \frac{1}{2}\mathop \int \limits_{V}^{{}} {{\varvec{\upvarepsilon}}}\left( 0 \right)^{T} {\mathbf{C}}\left( t \right){{\varvec{\upvarepsilon}}}{\text{d}}V + \frac{1}{2}\mathop \int \limits_{V}^{{}} \mathop \int \limits_{0}^{t} {\dot{\varvec{\upvarepsilon }}}\left( \tau \right)^{T} {\mathbf{C}}\left( {t - \tau } \right){\text{d}}\tau {{\varvec{\upvarepsilon}}}{\text{d}}V,$$

(35)

$$T\left( t \right) = \frac{1}{2}\mathop \int \limits_{V}^{{}} \rho \left[ {\left( {\frac{\partial u}{{\partial t}}} \right)^{2} + \left( {\frac{\partial v}{{\partial t}}} \right)^{2} + \left( {\frac{\partial w}{{\partial t}}} \right)^{2} } \right]{\text{d}}V,$$

(36)

$$V\left( t \right) = \frac{1}{2}\mathop \int \limits_{A}^{{}} \left[ {N_{x} \left( t \right)\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + 2N_{xy} \left( t \right)\left( {\frac{\partial w}{{\partial x}}} \right)\left( {\frac{\partial w}{{\partial y}}} \right) + N_{y} \left( t \right)\left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right]{\text{d}}A$$

(37)

where $\rho$ is the mass of a unit volume of the plate and $N_{x} \left( t \right)$, $N_{y} \left( t \right)$, $N_{xy} \left( t \right)$ are the in-plane compressive forces.

2.2.3 Equilibrium equation

At time $t$, the equation of motion can be expressed as follows:

$$\delta U - \delta T - \delta V = 0,$$

(38)

The variations of strain, kinetic, and potential energies are written as:

$$\delta U = \mathop \int \limits_{V}^{{}} {{\varvec{\upsigma}}}^{T} \delta {{\varvec{\upvarepsilon}}}{\text{d}}V = \mathop \int \limits_{V}^{{}} {{\varvec{\upvarepsilon}}}\left( 0 \right)^{T} {\mathbf{C}}\left( t \right)\delta {{\varvec{\upvarepsilon}}}{\text{d}}V + \mathop \int \limits_{V}^{{}} \mathop \int \limits_{0}^{t} {\dot{\varvec{\upvarepsilon }}}\left( \tau \right)^{T} {\mathbf{C}}\left( {t - \tau } \right){\text{d}}\tau \delta {{\varvec{\upvarepsilon}}}{\text{d}}V,$$

(39)

$$\delta T = \mathop \int \limits_{V}^{{}} \rho \left[ {\frac{\partial u}{{\partial t}}\frac{\partial \delta u}{{\partial t}} + \frac{\partial v}{{\partial t}}\frac{\partial \delta v}{{\partial t}} + \frac{\partial w}{{\partial t}}\frac{\partial \delta w}{{\partial t}}} \right]{\text{d}}V = - \mathop \int \limits_{V}^{{}} \rho \left[ {\frac{{\partial^{2} u}}{{\partial t^{2} }}\delta u + \frac{{\partial^{2} v}}{{\partial t^{2} }}\delta v + \frac{{\partial^{2} w}}{{\partial t^{2} }}\delta w} \right]{\text{d}}V,$$

(40)

$$\delta V = \mathop \int \limits_{A}^{{}} \left[ {N_{x} \left( t \right)\frac{\partial w}{{\partial x}}\frac{\partial \delta w}{{\partial x}} + N_{xy} \left( t \right)\frac{\partial w}{{\partial x}}\frac{\partial \delta w}{{\partial y}} + N_{xy} \left( t \right)\frac{\partial w}{{\partial y}}\frac{\partial \delta w}{{\partial x}} + N_{y} \left( t \right)\frac{\partial w}{{\partial y}}\frac{\partial \delta w}{{\partial y}}} \right]{\text{d}}A.$$

(41)

2.2.4 Approximation of the displacement using separation of variables

The displacement vector of a moderately thick viscoelastic plate can be approximated employing the separation of variables method as follows:

$${\mathbf{u}}\left( {x{,}y{,}t} \right) = \left\{ {\begin{array}{*{20}c} {w\left( {x{,}y{,}t} \right)} \\ {\theta_{x} \left( {x{,}y{,}t} \right)} \\ {\theta_{y} \left( {x{,}y{,}t} \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {w\left( {x{,}y} \right)} \\ {\theta_{x} \left( {x{,}y} \right)} \\ {\theta_{y} \left( {x{,}y} \right)} \\ \end{array} } \right\}F\left( t \right) = {\mathbf{u}}^{xy} F\left( t \right).$$

(42)

The variation of the displacement vector and the rate of displacement vector can be stated as:

$$\delta {\mathbf{u}}\left( {x{,}y{,}t} \right) = \delta {\mathbf{u}}^{xy} F,$$

(43)

$${\dot{\mathbf{u}}}\left( {x{,}y{,}t} \right) = {\mathbf{u}}^{xy} \dot{F}\left( t \right).$$

(44)

Utilizing Eqs. (42)–(44), the strain vector, the rate of strain vector, and the variation of strain vector may be written as:

$${{\varvec{\upvarepsilon}}} = \left\{ {\begin{array}{*{20}c} { - z\theta_{{x{,}x}} \left( {x{,}y} \right)} \\ { - z\theta_{{y{,}y}} \left( {x{,}y} \right)} \\ { - z\left( {\theta_{{x{,}y}} \left( {x{,}y} \right) + \theta_{{y{,}x}} \left( {x{,}y} \right)} \right)} \\ {w_{{{,}x}} \left( {x{,}y} \right) - \theta_{x} \left( {x{,}y} \right)} \\ {w_{{{,}y\left( {x{,}y} \right)}} - \theta_{y} \left( {x{,}y} \right)} \\ \end{array} } \right\}F\left( t \right) = {{\varvec{\upvarepsilon}}}^{xyz} F\left( t \right),$$

(45)

$${\dot{\varvec{\upvarepsilon }}} = {{\varvec{\upvarepsilon}}}^{xyz} \dot{F}\left( t \right),$$

(46)

$$\delta {{\varvec{\upvarepsilon}}} = \delta {{\varvec{\upvarepsilon}}}^{xyz} F\left( t \right).$$

(47)

2.2.5 Discretization

According to discretization based on the simple hp cloud mesh-free method, [25, 27], the displacement vector can be expressed as:

$${\mathbf{u}}^{xy} = \left\{ {\begin{array}{*{20}c} {w\left( {x{,}y} \right)} \\ {\theta_{x} \left( {x{,}y} \right)} \\ {\theta_{y} \left( {x{,}y} \right)} \\ \end{array} } \right\} = {\mathbf{NU}}^{xy}$$

(48)

in which ${\mathbf{N}}$ is the vector of the basis functions, and ${\mathbf{U}}^{xy}$ can be defined as:

$${\mathbf{U}}^{xy} = \left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1}^{T} } & {{\mathbf{U}}_{2}^{T} } & {..} \\ \end{array} \begin{array}{*{20}c} {..} & {{\mathbf{U}}_{N}^{T} } \\ \end{array} } \right]{,} {\mathbf{U}}_{i} = \begin{array}{*{20}c} {w_{i} } & {\theta_{{x_{i} }} } & {\theta_{{y_{i} }} } \\ \end{array}^{T} {, }i = 1:N.$$

(49)

$N$ is the number of selected nodes in the domain of the plate.

Substituting Eqs. (42)–(49) into Eqs. (39), (50) is derived:

$$\delta U = \int\limits_{V}^{{}} {{\mathbf{U}}^{{xy^{{\text{T}}} }} } {\mathbf{B}}^{{\text{T}}} {\text{F}}\left( 0 \right){\mathbf{C}}\left( t \right){\mathbf{B}}\delta {\mathbf{U}}^{{xy}} F\left( t \right){\text{d}}V + \int\limits_{V}^{{}} {\int\limits_{0}^{t} {{\mathbf{U}}^{{xy^{{\text{T}}} }} } } {\mathbf{B}}^{{\text{T}}} \dot{F}\left( \tau \right){\mathbf{C}}\left( {t - \tau } \right){\text{d}}\tau {\mathbf{B}}\delta {\mathbf{U}}^{{xy}} F\left( t \right){\text{d}}V.$$

(50)

Inserting Eqs. (42–49) into Eq. (40), Eq. (51) is obtained:

$$\delta T = - \int\limits_{V}^{{}} {{\mathbf{U}}^{{xy^{{\text{T}}} }} } {\mathbf{N}}^{{\text{T}}} {\mathbf{C}}_{{\text{m}}} \ddot{F}\left( t \right){\mathbf{N}}\delta {\mathbf{U}}^{{xy}} F\left( t \right){\text{d}}V.$$

(51)

Substituting Eqs. (42–49) into Eqs. (41), (52) is derived:

$$\delta V = \mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} F\left( t \right){\mathbf{N}}_{p} \left( t \right){\mathbf{B}}_{{\text{G}}} \delta {\mathbf{U}}^{xy} F\left( t \right){\text{d}}A$$

(52)

where ${\mathbf{N}}_{p} \left( t \right)$ is the matrix of in-plane forces as follows:

$${\mathbf{N}}_{p} \left( t \right) = \left[ {\begin{array}{*{20}c} {N_{x} \left( t \right)} & {N_{xy} \left( t \right)} \\ {N_{xy} \left( t \right)} & {N_{y} \left( t \right)} \\ \end{array} } \right].$$

(53)

In the above equations, ${\mathbf{B}}$ and ${\mathbf{B}}_{{\text{G}}}$ are the strain–displacement transformation matrices introduced in Sect. 2.2.8.

2.2.6 Integrating over the thickness

Carrying out integrating over the thickness of the plate, Eqs. (50, 51) can be rewritten as:

$$\delta U = \mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{B}}^{{\text{T}}} F\left( 0 \right){\mathbf{D}}\left( t \right)F\left( t \right){\mathbf{B}}\delta {\mathbf{U}}^{xy} {\text{d}}A + \mathop \int \limits_{A}^{{}} \mathop \int \limits_{0}^{t} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{B}}^{{\text{T}}} \dot{F}\left( \tau \right){\mathbf{D}}\left( {t - \tau } \right){\text{d}}\tau F\left( t \right){\mathbf{B}}\delta {\mathbf{U}}^{xy} {\text{d}}A,$$

(54)

$$\delta T = - \mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{N}}^{{\text{T}}} \ddot{F}\left( t \right){\mathbf{D}}_{{\text{m}}} F\left( t \right){\mathbf{N}}\delta {\mathbf{U}}^{xy} {\text{d}}A$$

(55)

in which the effective modulus tensor of a moderately thick viscoelastic plate can be expressed as:

$${\mathbf{D}}\left( t \right) = \left[ {\begin{array}{*{20}c} {\frac{{E\left( t \right)h^{3} }}{{12\left( {1 - \nu \left( t \right)^{2} } \right)}}\left[ { \begin{array}{*{20}c} 1 & {\nu \left( t \right)} & 0 \\ {\nu \left( t \right)} & 1 & 0 \\ 0 & 0 & { \frac{1 - \nu \left( t \right)}{2}} \\ \end{array} } \right]} & \mathbf{0} \\ \mathbf{0} & {\frac{Ehk}{{2\left( {1 + \nu \left( t \right)} \right)}}\left[ {\begin{array}{*{20}c} { 1} & 0 \\ 0 & { 1} \\ \end{array} } \right]} \\ \end{array} } \right].$$

(56)

In the above equation, $k$ is the shear correction factor of the first-order shear deformation theory, and $h$ is the plate thickness. Also, the mass density matrix, ${\mathbf{D}}_{{\text{m}}}$, is defined as:

$${\mathbf{D}}_{{\text{m}}} = \rho \left[ {\begin{array}{*{20}c} h & 0 & 0 \\ 0 & {\frac{{h^{3} }}{12}} & 0 \\ 0 & 0 & {\frac{{h^{3} }}{12}} \\ \end{array} } \right].$$

(57)

Substituting Eqs. (52), (54), and (55) into Eqs. (38), (58) is derived:

$$\mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{B}}^{{\text{T}}} \left( {F\left( 0 \right){\mathbf{D}}\left( t \right)F\left( t \right) + \left( {\mathop \int \limits_{0}^{t} \dot{F}\left( \tau \right){\mathbf{D}}\left( {t - \tau } \right){\text{d}}\tau } \right)F\left( t \right)} \right){\mathbf{B}}\delta {\mathbf{U}}^{xy} {\text{d}}A + \mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{N}}^{{\text{T}}} \ddot{F}\left( t \right){\mathbf{D}}_{{\text{m}}} F\left( t \right){\mathbf{N}}\delta {\mathbf{U}}^{xy} {\text{d}}A - \mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} F\left( t \right){\mathbf{N}}_{p} \left( t \right) F\left( t \right){\mathbf{B}}_{G} \delta {\mathbf{U}}^{xy} {\text{d}}A = 0.$$

(58)

Removing $\delta {\mathbf{U}}^{xy}$ and $F\left( t \right)$ from Eq. (58), $\delta {\mathbf{U}}^{xy} \ne 0,F\left( t \right) \ne 0$, Eq. (59) is obtained:

$$\mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{B}}^{{\text{T}}} \left( {F\left( 0 \right){\mathbf{D}}\left( t \right) + \mathop \int \limits_{0}^{t} \dot{F}\left( \tau \right){\mathbf{D}}\left( {t - \tau } \right){\text{d}}\tau } \right){\mathbf{B}}{\text{d}}A + \mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{N}}^{{\text{T}}} \ddot{F}\left( t \right){\mathbf{D}}_{m} {\mathbf{N}}{\text{d}}A - \mathop \int \limits_{A}^{{}} {\mathbf{U}}^{{xy^{{\text{T}}} }} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} F\left( t \right){\mathbf{N}}_{p} \left( t \right){ }{\mathbf{B}}_{G} {\text{d}}A = 0.$$

(59)

2.2.7 Weighted residual statement

Employing the weighted residual method, Eq. (59) can be written as follows:

$$\mathop \int \limits_{0}^{\infty } W\left( t \right)\left\{ {\mathop \int \limits_{A}^{{}} {\mathbf{B}}^{{\text{T}}} \left( {F\left( 0 \right){\mathbf{D}}\left( t \right) + \mathop \int \limits_{0}^{t} \dot{F}\left( \tau \right){\mathbf{D}}\left( {t - \tau } \right){\text{d}}\tau } \right){\mathbf{B}}{\text{d}}A + \mathop \int \limits_{A}^{{}} {\mathbf{N}}^{{\text{T}}} \ddot{F}\left( t \right){\mathbf{D}}_{{\text{m}}} {\mathbf{N}}{\text{d}}A - \mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} F\left( t \right){\mathbf{N}}_{p} \left( t \right){ }{\mathbf{B}}_{{\text{G}}} {\text{d}}A} \right\}{\text{d}}t{\mathbf{U}}^{xy} = 0$$

(60)

where $W\left( t \right)$ is the desired weight function. The weight function can be defined as follows:

$$W\left( t \right) = {\text{e}}^{{ - {\text{st}}}} { }.$$

(61)

Substituting Eq. (61) into Eqs. (60), (62) is derived:

$$\mathop \int \limits_{0}^{\infty } \left\{ {\mathop \int \limits_{A}^{{}} {\mathbf{B}}^{{\text{T}}} \left( {F\left( 0 \right){\mathbf{D}}\left( t \right) + \mathop \int \limits_{0}^{t} \dot{F}\left( \tau \right){\mathbf{D}}\left( {t - \tau } \right){\text{d}}\tau } \right){\mathbf{B}}{\text{d}}A + \mathop \int \limits_{A}^{{}} {\mathbf{N}}^{{\text{T}}} \ddot{F}\left( t \right){\mathbf{D}}_{{\text{m}}} {\mathbf{N}}{\text{d}}A - \mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} F\left( t \right){\mathbf{N}}_{p} \left( t \right){ }{\mathbf{B}}_{G} {\text{d}}A} \right\}{\text{e}}^{{ - {\text{st}}}} {\text{d}}t{\mathbf{U}}^{xy} = 0.$$

(62)

Separating the time parts of Eqs. (62), (63) is obtained:

$$\mathop \int \limits_{A}^{{}} {\mathbf{B}}^{{\text{T}}} \left\{ {\mathop \int \limits_{0}^{\infty } \left( {F\left( 0 \right){\mathbf{D}}\left( t \right) + \mathop \int \limits_{0}^{t} \dot{F}\left( \tau \right){\mathbf{D}}\left( {t - \tau } \right){\text{d}}\tau } \right){\text{e}}^{{ - {\text{st}}}} {\text{d}}t} \right\}{\mathbf{B}}{\text{d}}A{\mathbf{U}}^{xy} + \mathop \int \limits_{A}^{{}} {\mathbf{N}}^{{\text{T}}} {\mathbf{D}}_{{\text{m}}} \left\{ {\mathop \int \limits_{0}^{\infty } \ddot{F}\left( t \right){\text{e}}^{{ - {\text{st}}}} {\text{d}}\left( t \right)} \right\}{\mathbf{N}}{\text{d}}A{\mathbf{U}}^{xy} - \mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} \left\{ {\mathop \int \limits_{0}^{\infty } F\left( t \right){\mathbf{N}}_{p} \left( t \right){\text{e}}^{{ - {\text{st}}}} {\text{d}}\left( t \right)} \right\}{\mathbf{B}}_{{\text{G}}} {\text{d}}A{\mathbf{U}}^{xy} = 0.$$

(63)

The time function of Mindlin viscoelastic plates, $F\left( t \right)$, can be defined as follows:

$$F\left( t \right) = {\text{e}}^{{s_{0} t}} ,\dot{F}\left( t \right) = s_{0} F\left( t \right),\ddot{F}\left( t \right) = s_{0}^{2} F\left( t \right).$$

(64)

Also, the matrix ${\mathbf{N}}_{p} \left( t \right)$ may be defined as follows:

$${\mathbf{N}}_{p} \left( t \right) = N_{\rm cr} \left( {\alpha_{1} + \beta_{1} \cos \varphi t} \right)\left[ {\begin{array}{*{20}c} 1 & {k_{2} } \\ {k_{2} } & {k_{1} } \\ \end{array} } \right]{,}$$

$${ }k_{1} = \frac{{N_{y} }}{{N_{\rm cr} }}{,} k_{2} = \frac{{N_{xy} }}{{N_{\rm cr} }}, 0 \le \alpha_{1} < 1, \beta_{1} \ge 0, 0 < \varphi < \pi /2$$

(65)

in which $N_{{{\text{cr}}}}$ is the critical stability load of a viscoelastic plate at time zero, $\alpha_{1}$ and $\beta_{1}$ are arbitrary constant coefficients, and $\varphi$ is the excitation frequency.

2.2.8 Transformation to Laplace domain

Using the Laplace transform, the convolution integral of Eq. (63) can be simplified as follows:

$$\left( {\mathop \int \limits_{A}^{{}} {\mathbf{B}}^{{\text{T}}} s_{0} {\mathbf{D}}_{{s_{0} }}^{*} F^{*} {\mathbf{B}}{\text{d}}A + \mathop \int \limits_{A}^{{}} {\mathbf{N}}^{{\text{T}}} {\mathbf{D}}_{{\text{m}}} s_{0}^{2} F^{*} {\mathbf{N}}{\text{d}}A - \mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} \left( {F\left( t \right){\mathbf{N}}_{p} \left( t \right)} \right)^{*} {\mathbf{B}}_{{\text{G}}} {\text{d}}A} \right){\mathbf{U}}^{xy} = 0$$

(66)

in which $F^{*}$, ${\mathbf{D}}^{*}$, and $\left( {F\left( t \right){\mathbf{N}}_{p} \left( t \right)} \right)^{*}$ are the Laplace transformation of $F\left( t \right)$, ${\mathbf{D}}\left( t \right)$, and $F\left( t \right){\mathbf{N}}_{p} \left( t \right)$, respectively, and ${\mathbf{D}}_{{s_{0} }}^{*}$ is defined in Eq. (69).

Inserting Eqs. (64) and (65) into Eqs. (66), (67) is obtained:

$$\left( {s_{0} F^{*} \mathop \int \limits_{A}^{{}} {\mathbf{B}}^{{\text{T}}} {\mathbf{D}}_{{s_{0} }}^{*} {\mathbf{B}}{\text{d}}A + s_{0}^{2} F^{*} \mathop \int \limits_{A}^{{}} {\mathbf{N}}^{{\text{T}}} {\mathbf{D}}_{{\text{m}}} {\mathbf{N}}{\text{d}}A - N_{{{\text{cr}}}} F^{*} \left( {\alpha_{1} + \beta_{1} \frac{{\left( {\cos \varphi tF\left( t \right)} \right)^{*} }}{{F^{*} }}} \right)\mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} \left[ {\begin{array}{*{20}c} 1 & {k_{2} } \\ {k_{2} } & {k_{1} } \\ \end{array} } \right]{\mathbf{B}}_{{\text{G}}} {\text{d}}A} \right){\mathbf{U}}^{xy} = 0.$$

(67)

According to the proof presented in the “Appendix”, if the Laplace parameter, $s$, is replaced by $i\left( {\omega_{0} + \varphi } \right)$ and by removing $F^{*}$, Eq. (68) is derived:

$$\left( {s_{0} \mathop \int \limits_{A}^{{}} {\mathbf{B}}^{{\text{T}}} {\mathbf{D}}_{{s_{0} }}^{*} {\mathbf{B}}{\text{d}}A + s_{0}^{2} \mathop \int \limits_{A}^{{}} {\mathbf{N}}^{{\text{T}}} {\mathbf{D}}_{{\text{m}}} {\mathbf{N}}{\text{d}}A - N_{{{\text{cr}}}} \left( {\alpha_{1} + \beta_{1} \frac{{\left( {i\varphi + \alpha_{0} } \right)^{2} }}{{2i\varphi \alpha_{0} + \alpha_{0}^{2} }}} \right)\mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} \left[ {\begin{array}{*{20}c} 1 & {k_{2} } \\ {k_{2} } & {k_{1} } \\ \end{array} } \right]{\mathbf{B}}_{{\text{G}}} {\text{d}}A} \right){\mathbf{U}}^{xy} = 0.$$

(68)

The Laplace transform of the stiffness matrix can be divided into the bending and the shear parts as follows:

$${\mathbf{K}}_{{s_{0} }}^{*} = \mathop \int \limits_{A}^{{}} {\mathbf{B}}^{{\text{T}}} {\mathbf{D}}_{{s_{0} }}^{*} {\mathbf{B}}{\text{d}}A = \mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{b}}}^{{\text{T}}} {\mathbf{D}}_{{\text{b}}}^{\user2{*}} {\mathbf{B}}_{{\text{b}}} {\text{d}}A + \mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{s}}}^{{\text{T}}} {\mathbf{D}}_{{\text{s}}}^{\user2{*}} {\mathbf{B}}_{{\text{s}}} {\text{d}}A, {\mathbf{D}}_{{s_{0} }}^{*} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{{\text{b}}}^{\user2{*}} } & 0 \\ 0 & {{\mathbf{D}}_{{\text{s}}}^{\user2{*}} } \\ \end{array} } \right]$$

(69)

in which:

$${\mathbf{B}}_{{\text{b}}}^{i} = \left[ {\begin{array}{*{20}c} 0 & { - {\mathbf{N}}_{{{,}x}}^{i} } & 0 \\ 0 & 0 & { - {\mathbf{N}}_{{{,}y}}^{i} } \\ 0 & { - {\mathbf{N}}_{{{,}y}}^{i} } & { - {\mathbf{N}}_{{{,}x}}^{i} } \\ \end{array} } \right]{, }\,{\mathbf{B}}_{{\text{s}}}^{i} = \left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{{{,}x}}^{i} } & { - {\mathbf{N}}^{i} } & 0 \\ {{\mathbf{N}}_{{{,}y}}^{i} } & 0 & { - {\mathbf{N}}^{i} } \\ \end{array} } \right].$$

(70)

The shear ${\mathbf{D}}_{{\text{s}}}^{*}$ and the bending ${\mathbf{D}}_{{\text{b}}}^{*}$ effective modulus tensors can be written as [18]:

$${\mathbf{D}}_{{\text{b}}}^{\user2{*}} = h^{3} /12\left[ { \begin{array}{*{20}c} {3K\eta_{{s_{0} }}^{*} \frac{{\left( {2 + s_{0} \eta_{{s_{0} }}^{*} } \right)}}{{\left( {1 + 2s_{0} \eta_{{s_{0} }}^{*} } \right)}}} & {3K\eta_{{s_{0} }}^{*} \frac{{\left( {1 - s_{0} \eta_{{s_{0} }}^{*} } \right)}}{{\left( {1 + 2s_{0} \eta_{{s_{0} }}^{*} } \right)}}} & 0 \\ {3K\eta_{{s_{0} }}^{*} \frac{{\left( {1 - s_{0} \eta_{{s_{0} }}^{*} } \right)}}{{\left( {1 + 2s_{0} \eta_{{s_{0} }}^{*} } \right)}}} & {3K\eta_{{s_{0} }}^{*} \frac{{\left( {2 + s_{0} \eta_{{s_{0} }}^{*} } \right)}}{{\left( {1 + 2s_{0} \eta_{{s_{0} }}^{*} } \right)}}} & 0 \\ 0 & 0 & { 3/2K\eta_{{s_{0} }}^{*} } \\ \end{array} } \right],$$

(71)

$${\mathbf{D}}_{{\text{s}}}^{\user2{*}} = hk\left[ {\begin{array}{*{20}c} { 3/2K\eta_{{s_{0} }}^{*} } & 0 \\ 0 & { 3/2K\eta_{{s_{0} }}^{*} } \\ \end{array} } \right], \,\eta_{{s_{0} }}^{*} = \mathop \int \limits_{0}^{\infty } \eta \left( t \right){\text{e}}^{{ - s_{0} t}} {\text{d}}t = \frac{{c_{1} }}{{s_{0} }} + \frac{{c_{2} }}{{s_{0} + \lambda }},$$

(72)

The mass and geometry matrices are defined as follows:

$${\mathbf{K}}_{{\text{m}}} = \mathop \int \limits_{A}^{{}} {\mathbf{N}}^{{\text{T}}} {\mathbf{D}}_{{\text{m}}} {\mathbf{N}}{\text{d}}A,$$

(73)

$${\mathbf{K}}_{{\text{G}}} = \mathop \int \limits_{A}^{{}} {\mathbf{B}}_{{\text{G}}}^{{\text{T}}} \left[ {\begin{array}{*{20}c} 1 & {k_{2} } \\ {k_{2} } & {k_{1} } \\ \end{array} } \right]{\mathbf{B}}_{{\text{G}}} {\text{d}}A$$

(74)

where ${\mathbf{B}}_{{\text{G}}}^{i}$ can be defined as follows:

$${\mathbf{B}}_{{\text{G}}}^{i} = \left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{{{,}x}}^{i} } & 0 & 0 \\ {{\mathbf{N}}_{{{,}y}}^{i} } & 0 & 0 \\ \end{array} } \right].$$

(75)

Using Eqs. (70–75), Eq. (76) is derived:

$$\left( {s_{0} {\mathbf{K}}_{{s_{0} }}^{*} + s_{0}^{2} {\mathbf{K}}_{{\text{m}}} - N_{{{\text{cr}}}} \alpha_{1} {\mathbf{K}}_{{\text{G}}} - \beta_{1} \frac{{\left( {i\varphi + \alpha_{0} } \right)^{2} }}{{2i\varphi \alpha_{0} + \alpha_{0}^{2} }}{\mathbf{K}}_{{\text{G}}} } \right){\mathbf{U}}^{xy} = \mathbf{0}.$$

(76)

2.2.9 Dynamic stability analysis

To solve Eq. (76), the determinant of its coefficients must be zero. Therefore, Eq. (77) must hold:

$$\det \left( {s_{0} {\mathbf{K}}^{\user2{*}} + s_{0}^{2} {\mathbf{K}}_{{\text{m}}} - N_{{{\text{cr}}}} \alpha_{1} {\mathbf{K}}_{{\text{G}}} - \beta_{1} \frac{{\left( {i\varphi + \alpha_{0} } \right)^{2} }}{{2i\varphi \alpha_{0} + \alpha_{0}^{2} }}{\mathbf{K}}_{{\text{G}}} } \right) = 0,\quad s_{0} = i\omega_{0} - \alpha_{0}.$$

(77)

Thus, the problem of dynamic stability of a moderately thick viscoelastic plate is reduced to finding $\omega_{0}$ and $\alpha_{0}$, which may be calculated by iteration.

3 Numerical results

MATLAB programming is used to model the dynamic stability analysis of moderately thick viscoelastic plates. The mechanical properties of the assumed viscoelastic plates are: $K$ = $3 \times 10^{7} \;{\text{N/m}}^{3}$,${ }\rho$ = 7800${\text{kg/m}}^{3}$, and the shear correction factor is supposed to be 5/6. In the calculations, simply supported viscoelastic square plates having a width-to-thickness ratio of 10 are investigated. In the following, ${\Omega }$ is defined as the fundamental natural frequency calculated by the free vibration analysis of moderately thick viscoelastic square plates with simply supported boundary conditions at time zero. Various numerical examples are presented in this Section.

3.1 Verification

To verify the accuracy of the numerical results, the buckling coefficients of viscoelastic plates at time zero can be compared with the results obtained for elastic materials. Table 1 shows the buckling coefficients of simply supported moderately thick square plates under uniaxial compressions.

Table 1 Buckling coefficients, $k = l^{2} \sigma_{{{\text{cr}}}} /\pi^{2} D,\;D = Eh^{3} /12\left( {1 - \upsilon^{2} } \right)$, of simply supported elastic square plates under uniaxial compressions

Also, Table 2 shows the dimensionless natural frequency of simply supported elastic square plates with two width-to-thickness ratios.

Table 2 Fundamental natural frequency,$1000\Omega h\sqrt {\rho /E}$, of simply supported elastic square plates with two width-to-thickness ratios

Besides, the results of free vibration analysis ($\alpha_{1} = 0,\beta_{1} = 0$) of viscoelastic plates are investigated. Table 3 compares the viscous damping, $\alpha_{0}$, of moderately thick simply supported viscoelastic square plates obtained by the proposed method and Ref. [18]. Both studies calculate the natural frequency as $\omega_{0} = 18.18$.

Table 3 Viscous damping frequency of simply supported Mindlin viscoelastic square plates with different materials ($t_{{\text{s}}} = 100{\text{s}},\; \alpha_{1} = 0,\;\beta_{1} = 0$)

As the results show, the values of viscous damping frequencies are different in two cases: (i) solving ${\text{det}}\left( {{\mathbf{K}}^{*} + s_{0} {\mathbf{K}}_{{\text{m}}} } \right) = 0,$ and (ii) solving ${\text{det}}\left( {s_{0} {\mathbf{K}}^{*} + s_{0}^{2} {\mathbf{K}}_{{\text{m}}} } \right) = 0$. But, due to the existence of complex numbers in the equations, the correct answers belong to ${\text{det}}\left( {s_{0} {\mathbf{K}}^{*} + s_{0}^{2} {\mathbf{K}}_{{\text{m}}} } \right) = 0$.

The results of Tables 1, 2, and 3 indicate a good agreement between the method proposed and the results in other available references.

3.2 Effect of time-dependent compression

Table 4 shows the natural frequency, $\omega_{0}$, and viscous damping frequency, $\alpha_{0}$, of moderately thick simply supported viscoelastic square plates with different $\lambda /{\Omega }$ subjected to different axial compressions, $N_{x} \left( t \right) = N_{\rm cr} \left( {\alpha_{1} + \beta_{1} \cos \varphi t} \right)$.

Table 4 Natural frequency and viscous damping frequency of simply supported Mindlin viscoelastic square plates with different materials subjected to different compressions ($\beta_{1} = 0.0001$, $\varphi /{\Omega } = 1$)

The results of Table 4 indicate that the natural frequency of a moderately thick viscoelastic plate subjected to constant and harmonic compression is approximately equal to $\omega_{0} \cong {\Omega }\sqrt {1 - \alpha_{1} - 0.75\beta_{1} }$. In addition, by decreasing $\lambda /{\Omega }$, the viscous damping frequency is decreased.

Using Eqs. (42), (78) is obtained:

$$w\left( {x{,}y{,}t} \right) = w\left( {x{,}y} \right)F\left( t \right), \quad F\left( t \right) = {\text{e}}^{{i\omega_{0} t - \alpha_{0} t}} = {\text{e}}^{{ - \alpha_{0} t}} \cos \omega_{0} t + i{\text{e}}^{{ - \alpha_{0} t}} {\text{sin}}\omega_{0} t.$$

(78)

Equation (78) can be normalized as follows:

$$\frac{{w\left( {x{,}y{,}t} \right)}}{{w\left( {x{,}y} \right)}} = F\left( t \right), \quad {\text{Real}} \left( {F\left( t \right)} \right) = {\text{e}}^{{ - \alpha_{0} t}} \cos \omega_{0} t, {\text{ Imag}} \left( {F\left( t \right)} \right) = {\text{e}}^{{ - \alpha_{0} t}} {\text{sin}}\omega_{0} t.$$

(79)

Figures 2, 3, 4, and 5 show the variations of the imaginary part of the time functions, ${\text{e}}^{{ - \alpha_{0} t}} {\text{sin}}\left( {\omega_{0} t} \right)$, for a moderately thick viscoelastic square plate with simply supported boundary conditions subjected to different harmonic compressive loads versus time.

Fig. 2

Variations of the imaginary part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $c_{1} = 0.1$, $\lambda /\Omega = 0.01$, $\alpha_{1} = 0$, $\beta_{1} = 0.00001$, $\varphi /\Omega = 1$)

Fig. 3

Variations of the imaginary part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $c_{1} = 0.1$, $\lambda /\Omega = 0.01$, $\alpha_{1} = 0.25$, $\beta_{1} = 0.00001$, $\varphi /\Omega = 1$)

Fig. 4

Variations of the imaginary part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $c_{1} = 0.1$, $\lambda /\Omega = 0.01$, $\alpha_{1} = 0.5$, $\beta_{1} = 0.00001$, $\varphi /\Omega = 1$)

Fig. 5

Variations of the imaginary part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $c_{1} = 0.1$, $\lambda /\Omega = 0.01$, $\alpha_{1} = 0.75$, $\beta_{1} = 0.00001$, $\varphi /\Omega = 1$)

The results of Figs. 2, 3, 4, and 5 indicate that by increasing the constant compressive force, $\alpha_{1}$, the viscous damping frequency is increased, while the natural frequency, $\omega_{0}$, is decreased. In other words, for the constant $\beta_{1}$, by increasing $\alpha_{1}$ the transversal displacement converges to zero faster.

Tables 5 and 6 show the natural frequency and viscous damping frequency of moderately thick simply supported viscoelastic square plates subjected to different axial compressions and different frequencies of harmonic compression.

Table 5 Natural frequency and viscous damping frequency of simply supported Mindlin viscoelastic square plates subjected to different compressions ($\beta_{1} = 0.0005,\lambda /{\Omega } = 0.1$)

Table 6 Natural frequency and viscous damping frequency of simply supported Mindlin viscoelastic square plates subjected to different compressions ($\beta_{1} = 0.001,\lambda /{\Omega } = 0.1$)

As the results show, the frequency of a Mindlin viscoelastic plate subjected to different harmonic compressions is approximately equal to $\omega_{0} \cong {\Omega }\sqrt {1 - \alpha_{1} - 0.75\beta_{1} }$. Moreover, the viscous damping frequency is increased by increasing $\alpha_{1}$. Also, by increasing $\varphi$ the viscous damping frequency is decreased, but the variation of the natural frequency is negligible.

Figure 6 shows the variations of the real part of the time function, ${\text{e}}^{{ - \alpha_{0} t}} \cos \omega_{0} t$, for a moderately thick viscoelastic square plate with simply supported boundary conditions subjected to different constant compressive loads versus time. The results of Fig. 6 show that by increasing constant in-plane compression, the viscous damping frequency is increasing, too.

Fig. 6

Variations of the real part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $c_{1} = 0.1$, $\lambda /{\Omega } = 0.1$, $\beta_{1} = 0.0005$, $\varphi /\Omega = 1$)

Figure 7 shows the variations of the real part of the time function, ${\text{e}}^{{ - \alpha_{0} t}} \cos \omega_{0} t$, for a moderately thick viscoelastic square plate with simply supported boundary conditions subjected to different excitations versus time. As the results of Fig. 7 illustrate, by increasing the excitation frequency, $\varphi /\Omega$, the viscous damping frequency is decreasing.

Fig. 7

Variations of the real part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $c_{1} = 0.1$, $\lambda /\Omega = 0.01$, $\alpha_{1} = 0.5$, $\beta_{1} = 0.001$)

The natural frequency and viscous damping frequency of moderately thick simply supported viscoelastic square plates subjected to different harmonic compressions with different excitations are given in Table 7. The results of Table 7 indicate that the natural frequency and viscous damping frequency, $\alpha_{0}$, are decreasing by increasing $\beta_{1}$. In addition, by increasing $\varphi$, the viscous damping frequency is decreased, but the variation of the natural frequency, $\omega_{0}$, is negligible.

Table 7 Natural frequency and viscous damping frequency of simply supported Mindlin viscoelastic square plates subjected to different compressions ($\alpha_{1} = 0.5,\lambda /{\Omega } = 0.1$)

Figure 8 shows the variations of the real part of the time function, ${\text{e}}^{{ - \alpha_{0} t}} \cos \omega_{0} t$, for a moderately thick viscoelastic square plate with simply supported boundary conditions subjected to different excitations versus time. The results of Fig. 8 show that by increasing the value of harmonic in-plane compression, $\beta_{1}$, the viscous damping frequency is decreasing.

Fig. 8

Variations of the real part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $c_{1} = 0.1$, $\lambda /\Omega = 0.01$, $\alpha_{1} = 0.5$, $\varphi /\Omega = 1$)

3.3 Effect of materials

The natural frequency and viscous damping frequency of moderately thick simply supported viscoelastic square plates with different materials subjected to the same harmonic compression are illustrated in Table 8.

Table 8 Natural frequency and viscous damping frequency of simply supported Mindlin viscoelastic square plates with different materials ($\alpha_{1} = 0,\;\varphi /{\Omega } = 1,\;\beta_{1} = 0.0001,\;\lambda /{\Omega } = 0.1,\;{\Omega }\sqrt {1 - \alpha_{1} - 0.75\beta_{1} } = 18.17$)

As the results show, the natural frequencies do not change by changing $c_{1}$. Also, $\omega_{0}$ is approximately equal to ${\Omega }\sqrt {1 - \alpha_{1} - 0.75\beta_{1} }$. Moreover, as the $c_{1}$ increases and the material tends to be elastic, the viscous damping frequencies are decreasing, as expected.

Figure 9 shows the variations of the real part of the time function, ${\text{e}}^{{ - \alpha_{0} t}} \cos \omega_{0} t$, for a simply supported moderately thick viscoelastic square plate with different materials versus time. As the results of Fig. 9 indicate, when the material tends to be elastic, the viscous damping frequency is decreasing.

Fig. 9

Variations of the real part of the time function versus time for a simply supported moderately thick viscoelastic square plate ($h/L = 0.1$, $\lambda /\Omega = 0.1$, $\alpha_{1} = 0$,$\beta_{1} = 0.0001$, $\varphi /\Omega = 1$)

3.4 Calculation of critical ${\varvec{\beta}}_{{1{\text{cr}}}}$

Tables 9, 10, and 11 show the critical harmonic compressions of simply supported Mindlin viscoelastic square plates with different materials. The results of Tables 9, 10, and 11 indicate that by increasing $\varphi$, the critical harmonic compression, $\beta_{{1{\text{cr}}}}$, is decreasing with the inverse ratio. Also, by increasing $\alpha_{1}$, the critical harmonic loads are increasing.

Table 9 Critical harmonic compressions of simply supported Mindlin viscoelastic square plates ($c_{1} = 0.1, \lambda /{\Omega } = 0.1)$

Table 10 Critical harmonic compressions of simply supported Mindlin viscoelastic square plates ($c_{1} = 0.1, \lambda /{\Omega } = 0.01)$

Table 11 Critical harmonic compressions of simply supported Mindlin viscoelastic square plates ($c_{1} = 0.2, \lambda /{\Omega } = 0.1)$

4 Conclusions

The present paper focuses on the dynamic stability analysis of moderately thick viscoelastic plates subjected to constant and harmonic compressions, simultaneously, and a new solution technique is proposed. The stress–strain relation is written based on the Boltzmann integral law with constant bulk modulus. The shear effect is described by the first-order shear deformation theory. The displacement field is approximated using the separation of variables technique.

The obtained numerical results demonstrated the efficiency of the proposed method. The results were compared to other available references, and the proposed method showed good agreement.

The results show that the time response of a viscoelastic plate, subjected to time-dependent compression $N_{x} \left( t \right) = N_{{{\text{cr}}}} \left( {\alpha_{1} + \beta_{1} \cos \varphi t} \right)$, can be written as $F\left( t \right) = {\text{e}}^{{i\omega_{0} t - \alpha_{0} t}}$ so that:

• (i) The natural frequency of the viscoelastic plate is approximately equal to $\omega_{0} \cong {\Omega }\sqrt {1 - \alpha_{1} - 0.75\beta_{1} }$ in which $\Omega$ is the fundamental natural frequency of the free vibration analysis of a moderately thick viscoelastic square plate with simply supported boundary conditions at time zero.

• (ii) The viscous damping frequency, $\alpha_{0}$, is increasing by increasing $\alpha_{1}$. Also, by increasing $\varphi$, the viscous damping frequency is decreasing. Moreover, the viscous damping frequency is decreasing by increasing $\beta_{1}$.

• (iii) The critical excitation for which the system becomes unstable is calculated.

Appendix: Dynamic stability analysis of a simply supported viscoelastic column

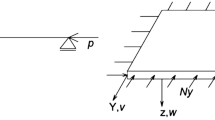
The equation of a viscoelastic column subjected to a time-dependent compressive load $p\left( t \right)$, as illustrated in Fig. 10, is defined as [2]:

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} - p\left( t \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} = m\frac{{\partial^{2} w}}{{\partial t^{2} }}$$

(80)

in which $x$ is the longitudinal axis, $w$ is the transverse displacement, and $m$ denotes the mass per unit length.

The bending moment $M$ can be expressed as:

$$M = \mathop \int \limits_{A}^{{}} \sigma \left( {x,y,t} \right)y{\text{d}}A$$

(81)

where $y$ is the transverse axis.

Fig. 10

A viscoelastic column subjected to time-dependent axial compressive load

The constitutive equation of a linear viscoelastic material based on the Boltzmann integral can be given as [24]:

$$\sigma \left( {x,y,t} \right) = E\left( t \right)\varepsilon \left( 0 \right) + \mathop \int \limits_{0}^{t} E\left( {t - \tau } \right)\dot{\varepsilon }\left( \tau \right){\text{d}}\tau$$

(82)

where $E\left( t \right)$ is the relaxation function. It is noted that in case of steady harmonic vibrations employing Eq. (82) is not necessary, and the problem reduces to the study of the storage and loss modulus [30]. But, since the goal of this paper is to study the dynamic stability of columns subjected to axial compression, using Eq. (83) is necessary.

For a Bernoulli beam, the relation between the strain $\varepsilon$ and the deflection $w$ can be written as [2]:

$$\varepsilon \left( {x,y,t} \right) = - y\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}.$$

(83)

Considering simply supported boundary conditions and by supposing that all points of the column move in phase, the deflection may be represented by [1, 4]:

$$w\left( {x,t} \right) = F\left( t \right){\text{ sin}}\frac{\pi x}{l}.$$

(84)

The relaxation function can be defined as follows:

$$E\left( t \right) = E_{0} \eta \left( t \right), \eta \left( t \right) = c_{1} + c_{2} {\text{e}}^{ - \lambda t}$$

(85)

where $E_{0}$ is the elasticity modulus at time zero.

Substituting Eqs. (82–85) into Eq. (80), Eq. (86) is obtained:

$$E\left( t \right)\frac{{I\pi^{4} }}{{l^{4} }}F\left( 0 \right) + E_{0} \frac{{I\pi^{4} }}{{l^{4} }}\mathop \int \limits_{0}^{t} \eta \left( {t - \tau } \right)\dot{F}\left( \tau \right){\text{d}}\tau - \frac{{\pi^{2} }}{{l^{2} }}p\left( t \right)F\left( t \right) + m\ddot{F}\left( t \right) = 0$$

(86)

in which $I$ is the column moment of inertia.

The time-dependent compressive load, $p\left( t \right)$, may be given as:

$$p\left( t \right) = \left( {\alpha_{1} + \beta_{1} \cos \varphi t} \right)P_{{\text{e}}} , P_{{\text{e}}} = \frac{{\pi^{2} E_{0} I }}{{l^{2} }}, 0 \le \alpha_{1} < 1, \beta_{1} \ge 0, 0 < \varphi < \pi /2$$

(87)

in which $\alpha_{1}$ and $\beta_{1}$ are constant, and $\varphi$ is the excitation frequency. Replacing Eq. (87) in Eq. (85), Eq. (88) is obtained:

$$\eta \left( t \right)F\left( 0 \right) + \mathop \int \limits_{0}^{t} \eta \left( {t - \tau } \right)\dot{F}\left( \tau \right){\text{d}}\tau - \alpha_{1} F\left( t \right) - \beta_{1} \cos \varphi tF\left( t \right) + \frac{{\ddot{F}\left( t \right)}}{{\Omega^{2} }} = 0$$

(88)

where the fundamental natural frequency at time zero is defined as follows:

$${\Omega }^{2} = \frac{{E_{0} I\pi^{4} }}{{ml^{4} }}.$$

(89)

For a viscoelastic column, the time function can be defined as:

$$F\left( t \right) = {\text{e}}^{{s_{0} t}}.$$

(90)

So, one can write Eq. (91) as follows:

$$\dot{F}\left( t \right) = s_{0} F\left( t \right), \ddot{F}\left( t \right) = s_{0}^{2} F\left( t \right).$$

(91)

Replacing Eq. (91) in Eq. (88), Eq. (92) is obtained:

$$\eta \left( t \right) + s_{0} \mathop \int \limits_{0}^{t} \eta \left( {t - \tau } \right)F\left( \tau \right){\text{d}}\tau - \alpha_{1} F\left( t \right) - \beta_{1} \cos \varphi tF\left( t \right) + \left( {\frac{{s_{0} }}{\Omega }} \right)^{2} F\left( t \right) = 0.$$

(92)

If Laplace transform is taken from Eq. (92), Eq. (93) is obtained:

$$\eta^{*} + s_{0} \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{t} \eta \left( {t - \tau } \right)F\left( \tau \right){\text{d}}\tau {\text{e}}^{{ - {\text{st}}}} {\text{d}}t - \alpha_{1} F^{*} - \beta_{1} \left( {\cos \varphi tF\left( t \right)} \right)^{*} + \frac{{\ddot{F}^{*} }}{{\Omega^{2} }} = 0$$

(93)

in which $\eta^{*}$, $F^{*}$, $\ddot{F}^{*},$ and $\left( {\cos \varphi tF\left( t \right)} \right)^{*}$ are the Laplace transformations of $\eta \left( t \right)$, $F\left( t \right)$, $\ddot{F}\left( t \right)$, and $\cos \varphi tF\left( t \right)$, respectively.

According to Laplace transform properties, the second term of Eq. (93) can be calculated as:

$$s_{0} \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{t} \eta \left( {t - \tau } \right)F\left( \tau \right){\text{d}}\tau {\text{e}}^{{ - {\text{st}}}} {\text{d}}t = s_{0} \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{t} \eta \left( \tau \right)F\left( {t - \tau } \right){\text{d}}\tau {\text{e}}^{{ - {\text{st}}}} {\text{d}}t = s_{0} \mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{t} \eta \left( \tau \right){\text{e}}^{{s_{0} \left( {t - \tau } \right)}} {\text{d}}\tau {\text{e}}^{{ - {\text{st}}}} {\text{d}}t = s_{0} \mathop \int \limits_{0}^{\infty } \left( {\mathop \int \limits_{0}^{t} \eta \left( \tau \right){\text{e}}^{{ - s_{0} \tau }} {\text{d}}\tau } \right){\text{e}}^{{ - {\text{st}} + s_{0} t}} {\text{d}}t.$$

(94)

On the other hand, the convolution integral of Eq. (94) can be calculated as:

$$s_{0} \mathop \int \limits_{0}^{\infty } \left( {\mathop \int \limits_{0}^{t} \eta \left( \tau \right){\text{e}}^{{ - s_{0} \tau }} {\text{d}}\tau } \right){\text{e}}^{{ - {\text{st}} + s_{0} t}} {\text{d}}t = s_{0} \mathop \int \limits_{0}^{\infty } \eta \left( \tau \right){\text{e}}^{{ - s_{0} \tau }} {\text{d}}\tau \mathop \int \limits_{0}^{\infty } e^{{s_{0} t}} {\text{e}}^{{ - {\text{st}}}} {\text{d}}t = s_{0} \eta_{{s_{0} }}^{*} F^{*} ,$$

$$\eta_{{s_{0} }}^{*} = \left( {\frac{{c_{1} }}{{s_{0} }} + \frac{{c_{2} }}{{s_{0} + \lambda }}} \right), F^{*} = \mathop \int \limits_{0}^{\infty } {\text{e}}^{{s_{0} t}} {\text{e}}^{{ - {\text{st}}}} {\text{d}}t = \frac{1}{{s - s_{0} }}.$$

(95)

Using Eqs. (90) and (95), Eq. (93) can be simplified as:

$$\eta^{*} + s_{0} \eta_{{s_{0} }}^{*} F^{*} - \alpha_{1} F^{*} + \left( {\frac{{s_{0} }}{\Omega }} \right)^{2} F^{*} - \beta_{1} \left( {\cos \varphi tF\left( t \right)} \right)^{*} = 0.$$

(96)

Alternatively:

$$\eta^{*} + \left( {s_{0} \eta_{{s_{0} }}^{*} - \alpha_{1} + \left( {\frac{{s_{0} }}{\Omega }} \right)^{2} } \right)\frac{1}{{s - s_{0} }} - \frac{{\beta_{1} }}{2}\left( {\frac{1}{{s - s_{0} + i\varphi }} + \frac{1}{{s - s_{0} - i\varphi }}} \right) = 0.$$

(97)

If Eq. (92) is solved in the time domain too, Eq. (98) is derived:

$$\left( {s_{0} \left( {\frac{{c_{1} }}{{s_{0} }} + \frac{{c_{2} }}{{s_{0} + \lambda }}} \right) - \alpha_{1} + \left( {\frac{{s_{0} }}{{\Omega }}} \right)^{2} } \right)\frac{1}{{i\varphi + \alpha_{0} }} - \beta_{1} \frac{{i\varphi + \alpha_{0} }}{{2i\varphi \alpha_{0} + \alpha_{0}^{2} }} = 0.$$

(98)

Comparing Eq. (97) and Eq. (98), the Laplace parameter in Eq. (97) can be replaced by $i\left( {\omega_{0} + \varphi } \right){ },$ that is, $s = i\left( {\omega_{0} + \varphi } \right)$.

Replacing $s = i\left( {\omega_{0} + \varphi } \right)$ and ignoring $\eta^{*} = \frac{{c_{1} }}{{i\left( {\omega_{0} + \varphi } \right)}} + \frac{{c_{2} }}{{i\left( {\omega_{0} + \varphi } \right) + \lambda }}$, Eq. (97) can be rewritten as follows:

$$s_{0} \eta_{{s_{0} }}^{*} - \alpha_{1} + \left( {\frac{{s_{0} }}{{\Omega }}} \right)^{2} - \beta_{1} \frac{{\left( {i\varphi + \alpha_{0} } \right)^{2} }}{{2i\varphi \alpha_{0} + \alpha_{0}^{2} }} = 0, s_{0} \eta_{{s_{0} }}^{*} = c_{1} + \frac{{c_{2} s_{0} }}{{s_{0} + \lambda }} , s_{0} = i\omega_{0} - \alpha_{0}$$

(99)

Replacing $s_{0} = i\omega_{0} - \alpha_{0}$ in Eq. (99) and separating the real and imaginary parts, Eqs. (100) and (101) are obtained:

$$c_{1} + c_{2} \frac{{\omega_{0}^{2} + \alpha_{0}^{2} - \alpha_{0} \lambda }}{{\omega_{0}^{2} + \left( { - \alpha_{0} + \lambda } \right)^{2} }} - \alpha_{1} - \left( {\frac{{\omega_{0} }}{{\Omega }}} \right)^{2} + \left( {\frac{{\alpha_{0} }}{{\Omega }}} \right)^{2} - \beta_{1} \frac{{3\varphi^{2} \alpha_{0}^{2} + \alpha_{0}^{4} }}{{4\varphi^{2} \alpha_{0}^{2} + \alpha_{0}^{4} }} = 0,$$

(100)

$$c_{2} \frac{{\lambda \omega_{0} }}{{\omega_{0}^{2} + \left( { - \alpha_{0} + \lambda } \right)^{2} }} - 2\frac{{\omega_{0} }}{{\Omega }}\frac{{\alpha_{0} }}{{\Omega }} - \beta_{1} \frac{{2\varphi^{3} \alpha_{0} }}{{4\varphi^{2} \alpha_{0}^{2} + \alpha_{0}^{4} }} = 0.$$

(101)

Since $\alpha_{0} \ll {\Omega },{ }\lambda \ll {\Omega }$, by ignoring $\left( {\alpha_{0/} {\Omega }} \right)^{2}$, $\left( {\lambda /{\Omega }} \right)^{2}$, and $\left( {\lambda /{\Omega }} \right)\left( {\alpha_{0/} {\Omega }} \right)$, Eqs. (102–103) are derived:

$$c_{1} + c_{2} - \alpha_{1} - \left( {\frac{{\omega_{0} }}{{\Omega }}} \right)^{2} - \frac{3}{4}\beta_{1} \approx 0 or \frac{{\omega_{0} }}{{\Omega }} \approx \sqrt {1 - \alpha_{1} - \frac{3}{4}\beta_{1} }.$$

(102)

Inserting $\omega_{0}$ in Eq. (103), $\alpha_{0}$ is obtained:

$$c_{2} \frac{\lambda }{{\omega_{0} }} - 2\frac{{\omega_{0} }}{{\Omega }}\frac{{\alpha_{0} }}{{\Omega }} - \beta_{1} \frac{\varphi }{{2\alpha_{0} }} \approx 0{ }.$$

(103)

Alternatively:

$$\frac{{\alpha_{0} }}{{\Omega }} \approx \frac{{\frac{{c_{2} \lambda }}{{\Omega }} + \sqrt {\left( {\frac{{c_{2} \lambda }}{{\Omega }}} \right)^{2} - 4\beta_{1} \frac{\varphi }{{\Omega }}\left( {1 - \alpha_{1} - \frac{3}{4}\beta_{1} } \right)^{3/2} } }}{{4 \times \left( {1 - \alpha_{1} - \frac{3}{4}\beta_{1} } \right)}}.$$

(104)

If the free vibration is studied ($\alpha_{1} = 0,\beta_{1} = 0$), then $\omega_{0} \approx {\Omega }$ and $\alpha_{0} \approx \frac{{c_{2} \lambda }}{2}$, which is consistent with the results of Ref. [2].

Substituting Eqs. (102) and (103) into Eq. (84), Eq. (105) is derived

$$w\left( {x,t} \right) = {\text{e}}^{{\left( {i\omega_{0} - \alpha_{0} } \right)t}} {\text{sin}}\frac{\pi x}{l} = {\text{e}}^{{ - \alpha_{0} t}} \left( {\cos \omega_{0} t + i\sin \omega_{0} t} \right){\text{sin}}\frac{\pi x}{l}.$$

(105)

Considering Eq. (104), the viscoelastic column is always stable if the conditions below are satisfied:

$$1 - \alpha_{1} - \frac{3}{4}\beta_{1} > 0, \left( {\frac{{c_{2} \lambda }}{{\Omega }}} \right)^{2} \ge 4\beta_{1} \frac{\varphi }{{\Omega }}\left( {1 - \alpha_{1} - \frac{3}{4}\beta_{1} } \right)^{\frac{3}{2}} ,$$

$$0 \le \alpha_{1} < 1, \beta_{1} \ge 0, 0 < \varphi < \pi /2.$$

(106)

Finally, one can solve Eq. (107) for calculating $\beta_{{{\text{cr}}}}$ as follows:

$$\left( {\frac{{c_{2} \lambda }}{{\Omega }}} \right)^{2} = 4\beta_{{{\text{cr}}}} \frac{\varphi }{{\Omega }}\left( {1 - \alpha_{1} - \frac{3}{4}\beta_{{{\text{cr}}}} } \right)^{3/2}.$$

(107)