Dynamic behaviour of bidirectional functionally graded sandwich beams under a moving mass with partial foundation supporting effect

Abstract

Dynamic analysis of bidirectional functionally graded sandwich beams under a moving mass with the effect of partial support by a Pasternak foundation is presented on the basis of a quasi-3D theory. The face layers of the sandwich beams are made of bidirectional functionally graded material (FGM), while the core is axially FGM. The material properties of the skin layers are varied smoothly in both the axial and transverse directions by power gradation laws, and they are evaluated by both Voigt and Mori–Tanaka micromechanical models. A finite element formulation is derived and employed to construct the equation of motion of the beams. Dynamic characteristics, including the dynamic deflections, dynamic magnification factors and stress distribution, are computed with the aid of the Newmark method. The numerical results reveal that the ratio of the foundation supporting part to the total beam length plays an important role in the dynamic response of the beams. The influence of the micromechanical model on the dynamic response of the beams is found to be dependent on the foundation stiffness and the power-law indexes. The effects of the material gradation, the foundation and loading parameters on the dynamic behaviour of the beams are examined in detail and highlighted.

1 Introduction

Sandwich structures are extensively used in different engineering applications, such as in the automotive, aerospace and defense industries, because of their light weight and high stiffness-to-weight ratio. However, these structures tend to delaminate under excessive inter-laminar stresses. Thanks to advanced manufacturing methods [1, 2], functionally graded materials (FGMs), a new type of composite materials initiated by Japanese researchers in the mid-1980s [3], can be incorporated into sandwich construction to improve the performance of structures. Functionally graded sandwich (FGSW) structures can be designed to have a smooth variation of the effective properties between layers, and this feature helps to eliminate the above drawback of conventional sandwich structures. Many investigations on the behaviour of FGSW beams are summarized in a review paper by Sayyad and Ghugal [4]; the contributions that are most relevant to the present work are briefly discussed below.

Fig. 1

A BFGSW beam partially resting on elastic foundation under a moving mass

Fig. 2

Variation of $V_c$ and $V_m$ of BFGSW beam for $n_x=n_z=0.5$ and $n_x=n_z=3$

Fig. 3

Comparison of time histories for mid-span deflection of FGM sandwich beam under a moving force ($L/h=10$, $n_x=0$, $n_z=0.5$, $v=50$ m/s)

Fig. 4

Time histories for mid-span deflection of (2-1-1) beam for various values of moving mass speed and foundation stiffness parameter ($L/h=20, n_x=n_z=0.5, r_m=0.5, \alpha _F=0.5$)

Fig. 5

Time histories for mid-span deflection of (2-1-1) beam for different mass ratios and foundation supporting parameters ($L/h=20,\; n_x=n_z=0.5,\; \; k_1=100, \; k_2=10$, $v=50$ m/s)

Fig. 6

Variation of dynamic magnification factor of (2-1-1) beam with power-law indexes for $L/h=20$, $r_m=0.5$, $k_1=100, \; k_2=10$ and $v=50$ m/s

Fig. 7

Variation of dynamic magnification factor with moving mass speed for $L/h=20$, $k_1=100, \; k_2=10$, $r_m=0.5$ and different foundation supporting parameters

Fig. 8

Variation of dynamic magnification factor with moving mass speed of (2-1-1) beam with moving mass speed for $L/h=20$, $k_1=100, \; k_2=10$, $\alpha _F=0.5$ and different mass ratios

Fig. 9

Variation of dynamic magnification factor of (2-1-1) beam with foundation stiffness parameters ($L/h=20,\; n_x=n_z=0.5,\; r_m=0.5,\; \alpha _F=0.5$)

Fig. 10

Relation between dynamic magnification factor with power-law indexes for different micromechanical models ($L/h=20, \; k_1=100, \; k_2=10, \; r_m=0.5, \; v=50$ m/s)

Fig. 11

Thickness distribution of axial stress for $L/h=10, \; n_x=0.5, \; k_1=100, \; k_2=10, r_m=0.5$ and $v=50$ m/s

Chakraborty et al. [5] presented a finite element formulation for thermoelastic analysis of sandwich Timoshenko beams with an FGM core. The efficiency of the formulation is improved by using the solution of equilibrium equations of a beam segment to interpolate the displacement field. The effect of temperature on buckling and vibration of sandwich beams with a viscoelastic core was examined by Bhangale and Ganesan [6] via a finite element procedure. The modified differential quadrature method was employed by Pradhan and Murmu [7] to investigate the influence of temperature rise on natural frequencies of FGSW beams on an elastic foundation. On the basis of various beam models, Apetre et al. [8] studied the bending response of FGSW beams subjected to distributed loads. The effect of the beam model on the behaviour of the beams was examined. Rahmani et al. [9] presented a high-order sandwich panel theory for free vibration analysis of sandwich beams with a flexible functionally graded syntactic core. The radial point interpolation method was used in combination with the Newmark method by Bui et al. [10] to study the dynamic behaviour of a sandwich beam with FGM core under a tip load. The effect of elastic foundation on bending and vibration of FGSW beams was investigated by Zenkour et al. [11] and Su et al. [12]. Both Voigt model and Mori–Tanaka scheme were used in [12] to evaluate the effective material properties. Various higher-order shear deformation theories were proposed in [13,14,15,16,17,18,19] for analysis of FGSW beams. In these theories, the transverse displacement is split into bending and shear parts, or in-plane displacement is modified using hyperbolic functions. Yang et al. [20] carried out free vibration analysis of FGSW beams using the meshfree boundary-domain integral equation method. Free vibration and buckling of sandwich beams with FGM face sheets were examined in [21] via a quasi-3D theory. An analytical method was used in the work to obtain the natural frequencies and buckling loads of the beams. Based on a quasi-3D theory, Yarasca et al. [22] derived a finite element formulation for bending analysis of FGSW beams. The distribution of the normal and shear stresses was examined in detail. Vibration and buckling of FGSW beams were studied by Kahya and Turan [23] using a first-order shear deformable finite element.

Fig. 12

Thickness distribution of normal stress for $L/h=10, \; n_x=0.5, \; k_1=100, \; k_2=10, r_m=0.5$ and $v=50$ m/s

Fig. 13

Thickness distribution of shear stress for $L/h=10, \; n_x=0.5, \; k_1=100, \; k_2=10, \; r_m=0.5$ and $v=50$ m/s

Fig. 14

Effect of micromechanical model on thickness distribution of axial stress for $L/h=10, \; n_x=0.5, \; k_1=100, \; k_2=10, \; r_m=0.5, \; \alpha _F=0.4$ and $v=50$ m/s

Fig. 15

Effect of micromechanical model on thickness distribution of shear stress for $L/h=10, \; n_x=0.5, \; k_1=100, \; k_2=10, \; r_m=0.5, \; \alpha _F=0.4$ and $v=50$ m/s

The influence of material gradation on the dynamic behaviour of beams under moving loads has been investigated by several authors recently. Şimşek and Kocatürk [24] and Şimşek [25] approximated the displacement field by polynomials to compute the dynamic response of FGM beams to a moving force. The effect of the material gradation in the thickness direction on the dynamic deflection and stress distribution was examined by the authors. Using the above method, the dynamic behaviour of axially FGM beams under a moving harmonic load [26] and an FGSW beam under two moving loads [27] was investigated. Khalili et al. [28] employed the differential quadrature method to examine the effect of material gradation in the thickness direction on the dynamic behaviour of an Euler–Bernoulli beam traversed by a moving mass. The exponential and power gradation laws were considered for the material properties. The Runge–Kutta method was used by Rajabi et al. [29] to compute the dynamic response of an FGM beam to a moving oscillator. In [30, 31], the finite element method was used in combination with the Newmark method to compute dynamic response of FGM Timoshenko beams under moving loads. Chen et al. [32] employed the Ritz method to study the effects of porosities on dynamic deflection of FGM Timoshenko beams. The nonlinear variation of elastic moduli and mass density due to the graded non-uniform porosity was considered by the authors. The Ritz method was also used by Songsuwan et al. [33] to study the effect of the thickness gradation of material properties on the vibration of sandwich Timoshenko beams under a moving harmonic load. The influence of an elastic foundation on the dynamic behaviour of the sandwich beams was taken into account by the authors. The effect of axial gradation of the material properties and the temperature on the dynamic behaviour of a Timoshenko beam was studied by Wang and Wu [34] using the Lagrange method.

The material properties of the beams discussed in the above references are graded in only one direction, the axial or the transverse direction. Many applications in practice are demanding FGM structures with material properties varying in two or more directions to meet the multifunctional requirements [35]. Analysis of beams with material properties varying in both the axial and transverse directions has been carried out in recent years. Lü et al. [36] presented a semi-analytical method for studying bending and thermal deformation of two-directional FGM beams. The material properties are supposed to vary exponentially along both the longitudinal and the transverse directions. The NURBS isogeometric finite element method was used in [37, 38] to study thermo-mechanical behaviour and free vibration of bidirectional FGM beams, respectively. Free vibration of FGM beams with exponential variation of properties in axial and transverse direction was investigated in [39, 40]. Şimşek [41] studied the vibration of an exponential gradation FGM beam under a moving point load. The effect of material gradation in the axial and transverse directions on the vibration characteristics was examined by the author with the aid of the Newmark method. Pydah and Sabale [42] studied the bending of circular FGM Euler–Bernoulli beams with material properties varying in both the tangential and the thickness direction. The analytical solution was obtained for a cantilever beam under various tip loads. Pydah and Batra [43] employed a logarithmic function to develop a shear deformation theory for the analysis of thick circular FGM beams with material properties varying in the tangential and the thickness direction by exponential and power gradation laws. The numerical investigation by the authors showed that the maximum stresses can be reduced significantly for a sandwich beam with bidirectional material gradation. Nguyen et al. [44] used a Timoshenko finite element formulation to compute the dynamic response of a bidirectional FGM beam to a moving load. The beam is made from four distinct materials with effective properties being graded in the length and thickness directions by power gradation laws. Free vibration of tapered power-law bidirectional FGM beams was studied by Nguyen and Tran [45] using a hierarchical finite element formulation. Static bending of sandwich beams with power-law variation of properties was investigated by Karamanli [46] via a quasi-3D theory. The dependence of the deflections and stresses on the material gradation of the beams under uniform and sinusoidal distributed loads was examined using the symmetric smoothed particle hydrodynamics (SPH) method. The SPH method was also used in [47] in the bending analysis of bidirectional FGM beams. Nguyen and Lee [48] developed a finite element model for flexural-torsion vibration and buckling analysis of thin-walled bidirectional FGM beams. The influence of the material gradation on the frequencies and buckling loads of the beams has been examined in detail. The effect of porosities on buckling behaviour of power-law bidirectional FGM beams was investigated by Lei et al. [49] using the generalized differential quadrature method. Tang et al. [50] employed the general differential quadrature method to study nonlinear vibration in the asymmetric mode of FGM Euler–Bernoulli beams with exponential variation of material properties in axial and transverse direction. The differential quadrature method was also used in [51] to study nonlinear vibration of bidirectional FGM beams in hygro-thermal environment. The finite element method was used by Rajasekaran and Khaniki [52] in studying the forced vibration of non-uniform bidirectional FGM microbeams on an elastic foundation due to a moving harmonic load/mass. Various material grading models, including the exponential, linear, parabolic and sigmoidal models, were considered by the authors. Very recently, Nguyen et al. [53] investigated the dynamic response of bidirectional sandwich Timoshenko beams with bidirectional power-law gradation FGM face layers under a moving point load.

As seen from the above literature review, the analysis of bidirectional functionally graded sandwich (BFGSW) beams has not been considered sufficiently. Keeping this in view, the present paper is an attempt to fill this gap by studying the dynamic behaviour of BFGSW beams under a moving mass. The study is carried out on the basis of a quasi-3D shear deformation theory. The beams consist of three layers, an axially FGM core and two skin layers of bidirectional power-law FGM. Both the Voigt and Mori–Tanaka micromechanical models are used to evaluate the effective material properties of the beams. In addition, as shown in [54,55,56], the vibration of a beam partially resting on an elastic foundation is much different from that of the beam fully resting on the foundation. Motivated by these works, the effect of partial support by a Pasternak foundation on the dynamic behaviour of the BFGSW beams is also taken into consideration herein. In order to handle the longitudinal variation of the beam rigidities, a finite element formulation is derived and employed to construct the equation of motion for the beams. The dynamic response of the beam is computed with the aid of an implicit Newmark method. Numerical investigation is carried out to highlight the effects of the material distribution, the foundation and moving mass parameters on the dynamic behaviour of the beams.

2 BFGSW beam

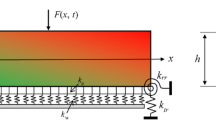
A simply supported beam with length L, rectangular cross section ($b \times h$), partially supported by an elastic foundation as depicted in Fig. 1 is considered. The core of the sandwich beam is made of axially FGM, while the face layers are made of bidirectional FGM. The Pasternak foundation model represented by Winkler springs with stiffness $k_w$ and a shear layer with stiffness $k_s$ is adopted herein. In the figure, $\alpha _F$ is the ratio of the foundation supporting part $L_F$ to the total beam length L, $\alpha _F=L_F/L$. The beam is under action of a mass m, moving with a constant speed $v$ from the left end to the right end of the beam. It is assumed that the mass m is always in contact with the beam. The Cartesian coordinate system (x, y, z) in Fig. 1 is chosen such that the (x, y) plane is coincident with the beam's mid-plane, and the z-axis is perpendicular to the mid-plane and it directs upward. Denoted by $z_0$, $z_1$, $z_2$ and $z_3$ ($z_0=-h/2$, $z_3=h/2$) are, respectively, the vertical coordinates of the bottom surface, the interfaces between the layers and the top surface.

The beam is assumed to be made from a mixture of ceramic and metal. The volume fraction of ceramic $(V_c)$ and metal $(V_m)$ is considered to vary in both the thickness and the longitudinal direction by the following power gradation laws:

$$\begin{aligned} \begin{aligned}&V_c = {\left\{ \begin{array}{ll} \Big (\dfrac{z-z_0}{z_1-z_0}\Big )^{n_z}\Big (1-\dfrac{x}{2L}\Big )^{n_x} \quad \text {for} \;\; z\in [z_0, z_1] \qquad \\ \Big (1-\frac{x}{2L}\Big )^{n_x} \quad \text {for} \;\; z\in [z_1, z_2] \qquad \\ \Big (\dfrac{z-z_3}{z_2-z_3}\Big )^{n_z}\Big (1-\dfrac{x}{2L}\Big )^{n_x} \quad \text {for} \;\; z\in [z_2, z_3] \qquad \\ \end{array}\right. } \\&\text {and} \quad V_m =1-V_c, \end{aligned} \end{aligned}$$

(1)

where $n_x$ and $n_z$ are, respectively, the axial and transverse power-law indexes, defining the variation of the constituent materials in the x and z directions, respectively. The subscripts ‘c’ and ‘m’ in Eq. (1) and hereafter stand for ceramic and metal, respectively. The volume fraction in Eq. (1) was modified slightly from that of Ref. [46], so that the conventional unidirectional FGM sandwich beam, e.g. the sandwich beams in Refs. [12, 15], can be obtained from (1) by simply setting $n_x$ to zero. The thickness ratio of the beam layers from the bottom layer to the top layer is denoted herein by three numbers in parentheses, e.g. (2-1-2). Figure 2 shows the variation of $V_c$ and $V_m$ in the thickness and length directions of the (2-2-1) beam for two pairs of the power-law indexes, $n_x=n_z=0.5$ and $n_x=n_z=3$.

Two micromechanical models, namely the Voigt model and the Mori–Tanaka scheme, are employed in this paper to evaluate the effective material properties of the beam. The effective property $({\mathscr {P}}_f)$ such as the Young’s modulus and mass density evaluated by the Voigt model is of the form

$$\begin{aligned} {\mathscr {P}}_f={\mathscr {P}}_c V_c + {\mathscr {P}}_m V_m, \end{aligned}$$

(2)

where ${\mathscr {P}}_c$ and ${\mathscr {P}}_m$ are the properties of the ceramic and metal, respectively. Substituting Eq. (1) into Eq. (2), one gets

$$\begin{aligned} \begin{aligned} {\mathscr {P}}_f(x,z)= {\left\{ \begin{array}{ll} {\mathscr {P}}_m+({\mathscr {P}}_c-{\mathscr {P}}_m)\Big (\dfrac{z-z_0}{z_1-z_0}\Big )^{n_z}\Big (1-\dfrac{x}{2L}\Big )^{n_x} \quad \text {for} \;\; z\in [z_0, z_1] \\ {\mathscr {P}}_m+({\mathscr {P}}_c-{\mathscr {P}}_m)\Big (1-\dfrac{x}{2L}\Big )^{n_x} \quad \text {for} \;\; z\in [z_1, z_2] \\ {\mathscr {P}}_m+({\mathscr {P}}_c-{\mathscr {P}}_m)\Big (\dfrac{z-z_3}{z_2-z_3}\Big )^{n_z}\Big (1-\dfrac{x}{2L}\Big )^{n_x} \quad \text {for} \;\; z\in [z_2, z_3] \\ \end{array}\right. } \end{aligned} \end{aligned}$$

(3)

According to the Mori–Tanaka scheme [57], the effective Young’s modulus $(E_f)$ and Poisson’s ratio $(\nu _f)$ can be expressed as

$$\begin{aligned} E_f = \dfrac{{9K_f}{G_f}}{3K_f+G_f}\; , \quad \nu _f = \dfrac{3K_f-2G_f}{6K_f+2G_f}, \end{aligned}$$

(4)

where $K_f$ and $G_f$ are, respectively, the effective local bulk modulus and shear modulus, which can be calculated from the moduli and volume fraction of the constituent materials as follows:

$$\begin{aligned} \begin{array}{ll} \dfrac{K_f-K_m}{K_c-K_m} &{} = \dfrac{V_c}{1+V_m(K_c-K_m)/(K_m+4G_m/3)},\\ \dfrac{G_f-G_m}{G_c-G_m} &{} = \dfrac{V_c}{1+V_m(G_c-G_m)/[G_m+G_m(9K_m+8G_m)/(6K_m+12G_m)]}, \end{array} \end{aligned}$$

(5)

where $K_c, \; K_m, \; G_c, \; G_m$ are the bulk modulus and shear modulus of the ceramic and metal. Note that the effective mass density $(\rho _f)$ is still calculated by the Voigt model according to Eq. (3).

3 Mathematical formulation

Based on the quasi-3D shear deformation theory [15], the displacements of a point in the x and z direction are, respectively, given by

$$\begin{aligned} \begin{aligned} u(x,z,t)=&u_0(x,t)-zw_{b,x}(x,t)-f(z)w_{s,x}(x,t),\\ w(x,z,t)=&w_b(x,t)+w_s(x,t)+g(z)w_z(x,t), \end{aligned} \end{aligned}$$

(6)

where $u_0(x,t)$ is the axial displacement of the point on the x-axis; $w_b(x,t), w_s(x,t)$ and $w_z(x,t)$ are, respectively, the bending, shear and thickness stretching components of the transverse displacement; t is the time variable, and

$$\begin{aligned} f(z)=\dfrac{4z^3}{3h^2}, \;\;\; g(z)=1-\dfrac{4z^2}{h^2}. \end{aligned}$$

(7)

In Eq. (6) and hereafter, a subscript comma is used to denote the partial derivative with respect to the variable which follows.

The axial strain $(\epsilon _{xx})$, normal strain $(\epsilon _{zz})$ and shear strain $(\gamma _{xz})$ resulting from Eq. (6) are

$$\begin{aligned} \epsilon _{xx}=&u_{,x}=u_{0,x}-zw_{b,xx}-f(z)w_{s,xx},\\ \epsilon _{zz}=&w_{,z}=g(z)_{,z}\, w_z, \\ \gamma _{xz}=&u_{,z}+w_{,x}=g(z)(w_{s,x}+w_{z,x}). \end{aligned}$$

(8)

The constitutive equation based on the linear behaviour of the beam material is given by

$$\begin{aligned} \left\{ \begin{matrix} \sigma _{xx} \\ \sigma _{zz} \\ \tau _{xz} \end{matrix} \right\} = \begin{bmatrix} C_{11} &{} C_{13} &{} 0 \\ C_{13} &{} C_{11} &{} 0 \\ 0 &{} 0 &{} C_{55} \end{bmatrix} \left\{ \begin{matrix} \epsilon _{xx} \\ \epsilon _{zz} \\ \gamma _{xz} \end{matrix} \right\}, \end{aligned}$$

(9)

where $\sigma _{xx}$, $\sigma _{zz}$ and $\tau _{xz}$ are, respectively, the axial, normal and shear stresses associated with the train components in Eq. (8), and

$$\begin{aligned} C_{11}=\frac{E_f}{1-\nu _f^2} , \;\; C_{13}=\frac{E_f\nu _f}{1-\nu _f^2}, \;\; C_{55}=G_f. \end{aligned}$$

(10)

Noting that the effective Young’s modulus and Poisson’s ratio in the above equation are dependent on both the x and z coordinates. In addition, $C_{11}=E_f$ and $C_{13}=0$ if the thickness stretching effect is omitted ($\epsilon _{zz}=0$).

The elastic strain energy of the beam ($U_{\text {B}}$) is given by

$$\begin{aligned} \begin{aligned} U_{\text {B}}=\frac{1}{2}\int _{0}^{L}\int _{A}(\sigma _{xx}\epsilon _{xx}+\sigma _{zz}\epsilon _{zz}+\tau _{xz}\gamma _{xz}){\mathrm{d}}A{\mathrm{d}}x, \end{aligned} \end{aligned}$$

(11)

where A is the cross-sectional area of the beam.

Substituting Eqs. (8) and (9) into Eq. (11), one gets

$$\begin{aligned} \begin{aligned} U_{\text {B}}=&\frac{1}{2}\int _{0}^{L}\Big [ A_{11}u_{0,x}^2-2A_{12}u_{0,x}w_{b,xx}+A_{22}\Big (w_{b,xx}^2+\frac{64}{h^4}w_z^2\Big )\\&-\frac{8}{3h^2}A_{34}u_{0,x}w_{s,xx} +\frac{8}{3h^2}A_{44}w_{b,xx}w_{s,xx}+\frac{16}{9h^4}A_{66}w_{s,xx}^2\\&+\frac{16}{h^2}\Big (B_{12}u_{0,x}-B_{22}w_{b,xx}-\frac{4}{3h^2}B_{44}w_{s,xx}\Big )w_z\\&+\Big (D_{11}-\frac{8}{h^2}D_{22}+\frac{16}{h^4}D_{44}\Big )(w_{s,x}+w_{z,x})^2\Big ]{\mathrm{d}}x, \end{aligned} \end{aligned}$$

(12)

where $A_{11}, \; A_{12}, \; A_{22}, \; A_{34}, \; A_{44}, \; A_{66}, \; B_{12}, \; B_{22}, \; B_{44}$ and $D_{11}, \; D_{22}, \; D_{44}$ are the beam rigidities, defined as

$$\begin{aligned} \begin{aligned} (A_{11}, A_{12}, A_{22}, A_{34}, A_{44}, A_{66})=\,&b\int _{-h/2}^{h/2} \frac{E_f}{1-\nu _f^2}\left( 1,z,z^2,z^3, z^4,z^6\right) {\mathrm{d}}z,\\ (B_{12}, B_{22}, B_{44})=\,&b\int _{-h/2}^{h/2} \frac{E_f\nu _f}{1-\nu _f^2} \left( z,z^2,z^4\right) {\mathrm{d}}z, \\ (D_{11}, D_{22}, D_{44})=\,&b\int _{-h/2}^{h/2} G_f\left( 1,z^2,z^4\right) {\mathrm{d}}z. \end{aligned} \end{aligned}$$

(13)

It is necessary to note that since $E_f$, $G_f$ and $\nu _f$ are dependent upon the x and z coordinates, the rigidities in the above equation are function of x.

The strain energy stored in the elastic foundation $(U_{\text {F}})$ based on the mid-plane transverse displacement is of the form

$$\begin{aligned} \begin{aligned} U_{\text {F}}=\,&\frac{1}{2}\int _{0}^{L_F}\Big [k_w w^2(x,0,t) + k_s w^2_{,x}(x,0,t) \Big ]{\mathrm{d}}x\\ =\,&\frac{1}{2}\int _{0}^{L_F}\Big [k_w (w_b+w_s+w_z)^2 + k_s (w_{b,x}+w_{s,x}+w_{z,x})^2 \Big ]{\mathrm{d}}x, \end{aligned} \end{aligned}$$

(14)

where $L_F$, as above mentioned, is the length of the foundation supporting part.

The kinetic energy (T) of the beam is given by

$$\begin{aligned} \begin{aligned} T=\frac{1}{2}\int _{0}^{L}\int _{A}\rho _f(\dot{u}^2 + \dot{w}^2){\mathrm{d}}A{\mathrm{d}}x, \end{aligned} \end{aligned}$$

(15)

where the effective mass density $\rho _f$ is defined by Eq. (3), and an over dot is used to denote the derivative with respect to the time variable. From Eqs. (6) and (7), one can write the above kinetic energy in the form

$$\begin{aligned} \begin{aligned} T=&\frac{1}{2}\int _{0}^{L}\Big \{I_{11}\left[ \dot{u}_0^2 + (\dot{w}_b+\dot{w}_s+\dot{w}_z)^2\right] -2I_{12}\dot{u}_0\dot{w}_{b,x}\\&+I_{22}\Big [\dot{w}_{b,x}^2 -\frac{8}{h^2}(\dot{w}_{b}+\dot{w}_{s}+\dot{w}_{z})\dot{w}_{z}\Big ]-\frac{8}{3h^2}I_{34}\dot{u}_0\dot{w}_{s,x}\\&+\frac{8}{h^2}I_{44}\Big (\frac{1}{3}\dot{w}_{b,x}\dot{w}_{s,x}+\frac{2}{h^2}\dot{w}_z^2\Big ) +\frac{16}{9h^4}I_{66}\dot{w}_{s,x}^2 \Big \}{\mathrm{d}}x, \end{aligned} \end{aligned}$$

(16)

where $I_{11}, \; I_{12}, \; I_{22}, \; I_{34}, \; I_{44}, \; I_{66}$ are the mass moments, defined as

$$\begin{aligned} (I_{11}, I_{12}, I_{22}, I_{34}, I_{44}, I_{66})=b\int _{-h/2}^{h/2} \rho _f\left( 1,z,z^2,z^3,z^4,z^6\right) {\mathrm{d}}z. \end{aligned}$$

(17)

Noting that since $\rho _f$ is dependent on the x and z coordinates, the above mass moments are functions of x.

Finally, the potential energy due to the moving mass is given by [58, 59]

$$\begin{aligned} V=-\int _{0}^{L}\left[ (mg - m\ddot{w}-2mv\dot{w}_{,x}-mv^2w_{,xx})w-m \ddot{u}_0 u_0(x,t) \right] \delta (x-vt){\mathrm{d}}x, \end{aligned}$$

(18)

where g is the gravity acceleration; $m\ddot{u}_0$ and $m\ddot{w}$ are, respectively, the axial and transverse inertial forces; $2mv\dot{w}_{,x}$ and $mv^2w_{,xx}$ are the Coriolis and centrifugal forces, respectively; $\delta (.)$ is the Dirac delta function; x is the abscissa of the moving mass, measured from the left end of the beam. Noting that the transverse displacement w in Eq. (18) is evaluated at $z=0$.

Differential equations of motion for the beam can be obtained by applying Hamilton’s principle to Eqs. (12), (14), (16) and (18). However, since the beam rigidities and mass moments are functions of the coordinate x, a closed-form solution for such equations is hardly obtained. A finite element formulation is derived in the next section for computing the dynamic response of the beam.

4 Finite element formulation

A two-node $C^1$ beam element with length of l is considered herewith. The vector of nodal displacements $(\mathbf {d})$ for the element is given by

$$\begin{aligned} \underset{12\times 1}{{\mathbf {d}}}=\left\{ {\mathbf {d}}_{u_0} \;\;\; {\mathbf {d}}_{w_b} \;\;\; {\mathbf {d}}_{w_s} \;\;\; {\mathbf {d}}_{w_z} \right\} ^T, \end{aligned}$$

(19)

where

$$\begin{aligned} {{\mathbf {d}}}_{u{_0}}=\,&\{u_{01} \;\;\; u_{02}\}^T , \quad \; {{\mathbf {d}}}_{w{_b}}=\{w_{b1} \;\;\; w_{b,x1} \;\;\; w_{b2} \;\;\; w_{b,x2} \}^T,\\ {{\mathbf {d}}}_{w{_s}}=\,&\{w_{s1} \;\;\; w_{s,x1} \;\;\; w_{s2} \;\;\; w_{s,x2} \}^T , \quad {{\mathbf {d}}}_{w{_z}}=\{w_{z1} \;\;\; w_{z2}\}^T \end{aligned}$$

(20)

are, respectively, the vectors of the nodal axial, bending, shear transverse displacements and thickness stretching components. The superscript ‘T’ in Eq. (20) and hereafter is used to denote the transpose of a vector or a matrix.

The displacements are interpolated from their nodal values according to

$$\begin{aligned} u_0=\mathbf {N}{\mathbf {d}}_{u_0}, \quad w_z=\mathbf {N}{\mathbf {d}}_{w_z}, \quad w_b=\mathbf {H}{\mathbf {d}}_{w_b}, \quad w_s=\mathbf {H}{\mathbf {d}}_{w_s}, \end{aligned}$$

(21)

where $\mathbf {N}$ and $\mathbf {H}$ are the matrices of interpolating functions with the following forms

$$\begin{aligned} \mathbf {N}= [N_1\, N_2], \quad \mathbf {H}=[H_1\, H_2\,H_3\,H_4 ]. \end{aligned}$$

(22)

In the present work, linear interpolation functions are used for $N_i$, and cubic Hermite polynomials are adopted for $H_i$.

With the interpolation, one can write the strain energy of the beam in the form

$$\begin{aligned} U_{\text {B}}=\frac{1}{2}\sum ^{ne_\mathrm{B}}{\mathbf {d}}^T\mathbf {k}_{\text {B}} {\mathbf {d}}, \end{aligned}$$

(23)

where the summation is taken over the total number of elements, $ne_\mathrm{B}$, and $\mathbf {k}_\mathrm{B}$ is the element stiffness matrix, which can be written in sub-matrices as

$$\begin{aligned} \underset{12 \times 12}{\mathbf {k}_{\text {B}}} = \begin{bmatrix} \mathbf {k}_{u_0u_0}^\text {B}&{}\mathbf {k}_{u_0w_b}^\text {B}&{}\mathbf {k}_{u_0w_s}^\text {B}&{}\mathbf {k}_{u_0w_ z}^\text {B}\\ \left( \mathbf {k}_{u_0w_b}^\text {B}\right) ^T&{}\mathbf {k}_{w_bw_b}^\text {B}&{}\mathbf {k}_{w_bw_s}^\text {B}&{}\mathbf {k}_{w_bw_z}^\text {B}\\ \left( \mathbf {k}_{u_0w_s}^\text {B}\right) ^T&{}\left( \mathbf {k}_{w_bw_s}^\text {B}\right) ^T &{} \mathbf {k}_{w_sw_s}^\text {B}&{}\mathbf {k}_{w_sw_z}^\text {B}\\ \left( \mathbf {k}_{u_0w_z}^\text {B}\right) ^T&{}\left( \mathbf {k}_{w_bw_z}^\text {B}\right) ^T &{} \left( \mathbf {k}_{w_sw_z}^\text {B}\right) ^T&{}\mathbf {k}_{w_zw_z}^\text {B}\\ \end{bmatrix}. \end{aligned}$$

(24)

In the above equation, the sub-matrices $\mathbf {k}_{u_0u_0}^\text {B}, \; \mathbf {k}_{w_bw_b}^\text {B}, \; \mathbf {k}_{w_sw_s}^\text {B}, \; \mathbf {k}_{w_zw_z}^\text {B}$ are, respectively, the element stiffness matrices stemming from the axial stretching, bending, shear, thickness stretching deformation, and they have the following forms:

$$\begin{aligned} \begin{aligned} \mathbf {k}_{u_0u_0}^\text {B}&=\int _{0}^{l} \mathbf {N}_{,x}^TA_{11}\mathbf {N}_{,x}{\mathrm{d}}x , \quad \mathbf {k}_{w_bw_b}^\text {B}=\int _{0}^{l} \mathbf {H}_{,xx}^TA_{22}\mathbf {H}_{,xx}{\mathrm{d}}x, \\ \mathbf {k}_{w_sw_s}^\text {B}&=\int _{0}^{l} \left[ \frac{16}{9h^4}\mathbf {H}_{,xx}^TA_{66}\mathbf {H}_{,xx} + \left( D_{11}-\frac{8}{h^2}D_{22}+\frac{16}{h^4}D_{44}\right) \mathbf {H}_{,x}^T\mathbf {H}_{,x}\right] {\mathrm{d}}x,\\ \mathbf {k}_{w_zw_z}^\text {B}&=\int _{0}^{l} \left[ \frac{64}{h^4}\mathbf {H}^TA_{22}\mathbf {N} + \left( D_{11}-\frac{8}{h^2}D_{22}+\frac{16}{h^4}D_{44}\right) \mathbf {N}_{,x}^T\mathbf {N}_{,x}\right] {\mathrm{d}}x, \end{aligned} \end{aligned}$$

(25)

and $\mathbf {k}_{u_0w_b}^\text {B}$, $\mathbf {k}_{u_0w_s}^\text {B}$, $\mathbf {k}_{u_0w_z}^\text {B}$, $\mathbf {k}_{w_bw_s}^\text {B}$, $\mathbf {k}_{w_bw_z}^\text {B}$, $\mathbf {k}_{w_sw_z}^\text {B}$ are, respectively, the axial-bending, axial-shear, axial-thickness stretching, bending shear, bending-thickness stretching, bending-shear and shear-thickness stretching coupling matrices with the following forms:

$$\begin{aligned} \begin{aligned} \mathbf {k}_{u_0w_b}^\text {B}&=-\int _{0}^{l} \mathbf {N}_{,x}^TA_{12}\mathbf {H}_{,xx}{\mathrm{d}}x , \quad \mathbf {k}_{u_0w_s}^\text {B}=- \frac{4}{3h^2}\int _{0}^{l}\mathbf {N}_{,x}^TA_{34}\mathbf {H}_{,xx}{\mathrm{d}}x, \\ \mathbf {k}_{u_0w_z}^\text {B}&= \frac{8}{h^2}\int _{0}^{l}\mathbf {N}_{,x}^TB_{12}\mathbf {N}{\mathrm{d}}x , \quad \mathbf {k}_{w_bw_s}^\text {B}= \frac{4}{3h^2}\int _{0}^{l} \mathbf {H}_{,xx}^TA_{44}\mathbf {H}_{,xx}{\mathrm{d}}x, \\ \mathbf {k}_{w_bw_z}^\text {B}&=- \frac{8}{h^2}\int _{0}^{l}\mathbf {H}_{,xx}^TB_{22}\mathbf {N}{\mathrm{d}}x, \\ \mathbf {k}_{w_sw_z}^\text {B}&=\int _{0}^{l} \left[ -\frac{32}{3h^4}\mathbf {H}_{,xx}^TB_{44}\mathbf {N} + \left( D_{11}-\frac{8}{h^2}D_{22}+\frac{16}{h^4}D_{44}\right) \mathbf {H}_{,x}^T\mathbf {N}_{,x}\right] {\mathrm{d}}x. \end{aligned} \end{aligned}$$

(26)

The strain energy $U_{\text {F}}$ in Eq. (14) can also be written as

$$\begin{aligned} U_{\text {F}}=\frac{1}{2}\sum ^{ne_\mathrm{F}}{\mathbf {d}}^T\mathbf {k}_{\text {F}}{\mathbf {d}}, \end{aligned}$$

(27)

where $ne_\mathrm{F}$ is number of the elements used for the foundation, and

$$\begin{aligned} \underset{12 \times 12}{\mathbf {k}_{\text {F}}} = \begin{bmatrix} 0&{}0&{}0&{}0\\ 0&{}\mathbf {k}_{w_bw_b}^\text {F}&{}\mathbf {k}_{w_bw_s}^\text {F}&{}\mathbf {k}_{w_bw_z}^\text {F}\\ 0&{}\left( \mathbf {k}_{w_bw_s}^\text {F}\right) ^T&{}\mathbf {k}_{w_sw_s}^\text {F}&{}\mathbf {k}_{w_sw_z}^\text {F}\\ 0&{}\left( \mathbf {k}_{w_bw_z}^\text {F}\right) ^T&{}\left( \mathbf {k}_{w_sw_z}^\text {F}\right) ^T&{}\mathbf {k}_{w_zw_z}^\text {F} \end{bmatrix} \end{aligned}$$

(28)

is the element foundation stiffness matrix with the following sub-matrices

$$\begin{aligned} \begin{aligned} \mathbf {k}_{w_bw_b}^\text {F}&=\mathbf {k}_{w_sw_s}^\text {F}=\mathbf {k}_{w_bw_s}^\text {F}=\int _{0}^{l} \left( \mathbf {H}^Tk_w \mathbf {H} + \mathbf {H}_{,x}^T k_s\mathbf {H}_{,x} \right) {\mathrm{d}}x,\\ \mathbf {k}_{w_bw_z}^\text {F}&=\mathbf {k}_{w_sw_z}^\text {F}=\int _{0}^{l} \left( \mathbf {H}^Tk_w \mathbf {N} + \mathbf {H}_{,x}^T k_s\mathbf {N}_{,x} \right) {\mathrm{d}}x,\\ \mathbf {k}_{w_zw_z}^\text {F}&=\int _{0}^{l} \left( \mathbf {N}^Tk_w \mathbf {N} + \mathbf {N}_{,x}^T k_s\mathbf {N}_{,x} \right) {\mathrm{d}}x. \end{aligned} \end{aligned}$$

(29)

The total element stiffness is

$$\begin{aligned} \mathbf{k}=\mathbf{k}_\mathrm{B}+\mathbf{k}_\mathrm{F} \end{aligned}$$

(30)

for the element resting on the foundation, and $\mathbf{k}=\mathbf{k}_\mathrm{B}$ for the element without the foundation support.

Similarly, we can write the kinetic energy in the form

$$\begin{aligned} T=\frac{1}{2}\sum ^{ne_\mathrm{B}}\dot{{\mathbf {d}}}^T\mathbf {m} \dot{{\mathbf {d}}} \end{aligned}$$

(31)

with the element mass matrix $\mathbf{m}$ having the form

$$\begin{aligned} \underset{12 \times 12}{\mathbf {m}} = \begin{bmatrix} \mathbf {m}_{u_0u_0}&{}\mathbf {m}_{u_0w_b}&{}\mathbf {m}_{u_0w_s}&{}0\\ \mathbf {m}_{u_0w_b}^T &{} \mathbf {m}_{w_bw_b}&{}\mathbf {m}_{w_bw_s}&{}\mathbf {m}_{w_bw_z}\\ \mathbf {m}_{u_0w_s}^T &{} \mathbf {m}_{w_bw_s}^T &{} \mathbf {m}_{w_sw_s}&{}\mathbf {m}_{w_sw_z}\\ 0 &{} \mathbf {m}_{w_bw_z}^T &{} \mathbf {m}_{w_sw_z}^T &{} \mathbf {m}_{w_zw_z}\\ \end{bmatrix} \end{aligned}$$

(32)

in which

$$\begin{aligned} \begin{aligned} \mathbf {m}_{u_0u_0}&=\int _{0}^{l} \mathbf {N}^T I_{11}\mathbf {N} {\mathrm{d}}x , \quad \mathbf {m}_{u_0w_b}=-\int _{0}^{l} \mathbf {N}^T I_{12}\mathbf {H}_{,x} {\mathrm{d}}x,\\ \mathbf {m}_{u_0w_s}&=-\frac{4}{3h^2}\int _{0}^{l} \mathbf {N}^T I_{34}\mathbf {H}_{,x} {\mathrm{d}}x , \quad \mathbf {m}_{w_bw_b}=\int _{0}^{l} \left( \mathbf {H}^T I_{11}\mathbf {H} + \mathbf {H}_{,x}^T I_{22}\mathbf {H}_{,x} \right) {\mathrm{d}}x,\\ \mathbf {m}_{w_bw_s}&=\int _{0}^{l} \left( \mathbf {H}^T I_{11}\mathbf {H} + \frac{4}{3h^2}\mathbf {H}_{,x}^T I_{44}\mathbf {H}_{,x} \right) {\mathrm{d}}x , \;\; \mathbf {m}_{w_bw_z}=\mathbf {m}_{w_sw_z}=\int _{0}^{l} \left( I_{11} - \frac{4}{h^2} I_{22} \right) \mathbf {H}^T \mathbf {N} {\mathrm{d}}x,\\ \mathbf {m}_{w_sw_s}&=\int _{0}^{l} \left( \mathbf {H}^T I_{11}\mathbf {H} + \frac{8}{9h^4}\mathbf {H}_{,x}^T I_{66}\mathbf {H}_{,x} \right) {\mathrm{d}}x , \;\; \mathbf {m}_{w_zw_z} =\int _{0}^{l} \left( I_{11} - \frac{8}{h^2} I_{22} + \frac{16}{h^4} I_{44} \right) \mathbf {N}^T \mathbf {N} {\mathrm{d}}x. \end{aligned} \end{aligned}$$

(33)

The potential energy in Eq. (18) is now of the form

$$\begin{aligned} V=\sum ^{ne_\mathrm{B}}\left( \ddot{\mathbf{d}}^T\mathbf{m}_m\ddot{\mathbf{d}}+\dot{\mathbf{d}}^T\mathbf{c}_m\dot{\mathbf{d}}+\mathbf{d}^T\mathbf{k}_m\mathbf{d}-\mathbf{d}^T\mathbf{f}_m\right), \end{aligned}$$

(34)

where $\mathbf {m}_m, \; \mathbf {c}_m$ and $\mathbf {k}_m$ are, respectively, the element mass, damping and stiffness matrices due to the effects of the inertia, Coriolis and the centrifugal forces of the moving mass; $\mathbf {f}_m$ is the time-dependent element nodal load vector generated by the moving mass. The expressions for these matrices and vector are as follows:

$$\begin{aligned} \begin{aligned} \underset{12 \times 12}{\mathbf {m}_m}&=m \begin{bmatrix} \mathbf {N}^T\mathbf {N} \;\; &{} \;\; \mathbf {0} \;\; &{} \;\; \mathbf {0} \;\;&{} \;\; \mathbf {0} \\ \mathbf {0} \;\; &{} \;\; \mathbf {H}^T\mathbf {H} \;\; &{} \;\; \mathbf {H}^T\mathbf {H} \;\; &{} \;\; \mathbf {H}^T\mathbf {N} \\ \mathbf {0} \;\; &{} \;\; \mathbf {H}^T\mathbf {H} \;\; &{} \;\; \mathbf {H}^T\mathbf {H} \;\; &{} \;\; \mathbf {H}^T\mathbf {N} \\ \mathbf {0} \;\; &{} \;\; \mathbf {N}^T\mathbf {H} \;\; &{} \;\; \mathbf {N}^T\mathbf {H} \;\; &{} \;\; \mathbf {N}^T\mathbf {N} \end{bmatrix} _{x_e}{,} \\ \underset{12 \times 12}{\mathbf {c}_m}&=2mv \begin{bmatrix} \mathbf {0} \;\; &{} \;\; \mathbf {0} \;\; &{} \;\; \mathbf {0} \;\; &{} \;\; \mathbf {0} \\ \mathbf {0} \;\; &{} \mathbf {H}^T\mathbf {H}_{,x} \;\; &{} \;\; \mathbf {H}^T\mathbf {H}_{,x} \;\; &{} \;\; \mathbf {H}^T\mathbf {N}_{,x}\\ \mathbf {0} \;\; &{} \;\; \mathbf {H}^T\mathbf {H}_{,x} \;\; &{} \;\; \mathbf {H}^T\mathbf {H}_{,x} \;\; &{} \;\; \mathbf {H}^T\mathbf {N}_{,x}\\ \mathbf {0} \;\; &{} \;\; \mathbf {N}^T\mathbf {H}_{,x} \;\; &{} \;\; \mathbf {N}^T\mathbf {H}_{,x} \;\; &{} \;\; \mathbf {N}^T\mathbf {N}_{,x} \end{bmatrix} _{x_e}{,} \\ \underset{12 \times 12}{\mathbf {k}_m}&=mv^2 \begin{bmatrix} \mathbf {0} \;\; &{} \;\; \mathbf {0} \;\; &{} \;\; \mathbf {0} \;\; &{} \;\; \mathbf {0} \\ \mathbf {0} \;\; &{} \;\; \mathbf {H}^T\mathbf {H}_{,xx} \;\; &{} \;\; \mathbf {H}^T\mathbf {H}_{,xx} \;\; &{} \;\; \mathbf {0}\\ \mathbf {0} \;\; &{} \;\; \mathbf {H}^T\mathbf {H}_{,xx} \;\; &{} \;\; \mathbf {H}^T\mathbf {H}_{,xx} \;\; &{} \;\; \mathbf {0}\\ \mathbf {0} \;\; &{} \;\; \mathbf {N}^T\mathbf {H}_{,xx} \;\; &{} \;\; \mathbf {N}^T\mathbf {H}_{,xx} \;\; &{} \;\; \mathbf {0} \end{bmatrix} _{x_e} \end{aligned} \end{aligned}$$

(35)

and

$$\begin{aligned} \underset{12 \times 1}{\mathbf {f}_m} =mg \begin{bmatrix} \mathbf {0} \;&\; \mathbf {H}^T \;&\; \mathbf {H}^T \;&\; \mathbf {N}^T \end{bmatrix}_{x_e}^T. \end{aligned}$$

(36)

The notation $[.]_{x_e}$ in Eqs. (35) and (36) means that [.] is evaluated at $x_e$—the current abscissa of the moving mass with respect to the left node of the element. Except for the element under the moving mass, the element matrices $\mathbf {m}_m$, $\mathbf {c}_m$, $\mathbf {k}_m$ and the force vector $\mathbf {f}_m$ are zeros for all other elements. Since the beam rigidities and mass moments are functions of the longitudinal coordinate x, explicit expressions for the integrals in the element stiffness and mass matrices in Eqs. (25), (26) and (33) are hardly obtained. Gauss quadrature with 6 points along the element length and thickness is used herein to evaluated the integrals. More points have been used, but no improvement in the numerical result is seen.

Having the element stiffness and mass matrices derived, one can write the equation of motion for the beam in the following form [60]:

$$\begin{aligned} (\mathbf {M} + \mathbf {M}_m)\,\ddot{{\mathbf {d}}} + \mathbf {C}_m\,\dot{{\mathbf {d}}} + (\mathbf {K} + \mathbf {K}_m)\,{\mathbf {d}}=\mathbf {F}, \end{aligned}$$

(37)

where ${\mathbf {d}},\; \dot{{\mathbf {d}}}$ and $\ddot{{\mathbf {d}}}$ are, respectively, the vectors of nodal displacements, velocities and accelerations; $\mathbf{M}$, $\mathbf{M}_m$, $\mathbf{C}_m$, $\mathbf{K}$, $\mathbf{K}_m$ and $\mathbf{F}$ are, respectively, the global matrices and vector, obtained by, respectively, assembling the matrices $\mathbf {m}$, $\mathbf {m}_m$, $\mathbf {c}_m$, $\mathbf {k}$, $\mathbf {k}_m$ and $\mathbf {f}_m$ over the elements. Equation (37) can be solved by the direct integration Newmark method. The average acceleration method that ensures the numerical instability [61] is adopted herein.

5 Results and discussion

Dynamic behaviour of the BFGSW beam partially resting on the elastic foundation under the moving mass is numerically investigated in this section. To this end, a simply supported beam with $b=1$m, $h=1$m and various values of span-to-height ratio is considered. The geometric boundary conditions for the simply supported beam are as follows:

• At $x=0$ : $u_0(0,t)=w_b(0,t)=w_s(0,t)=w_z(0,t)=0$,

• At $x=L$ : $w_b(L,t)=w_s(L,t)=w_z(L,t)=0$.

The beam is made from alumina (Al$_2$O$_3$) and aluminium (Al) with the material data are as follows [12]:

• $E_c=380$ GPa, $\rho _c=3960$ kg/m$^3$, $\nu _c=0.3$ for alumina,

• $E_m=70$ GPa, $\rho _m=2702$ kg/m$^3$, $\nu _m=0.3$ for aluminium.

Following the works in [12, 33], the following non-dimensional parameters for the dynamic magnification factor $(D_d)$, mass ratio ($r_m$), foundation stiffness parameters $(k_1)$ and $(k_2)$ are introduced as

$$\begin{aligned} {D_d}=\text {max}\Big ( \frac{w(L/2,t)}{w_{st}}\Big ), \;\; r_m=\frac{m}{\rho _cAL}, \;\; k_1= \frac{k_wL^4}{E_cI}, \;\; k_2=\frac{k_sL^2}{E_cI}, \end{aligned}$$

(38)

where $w_{st}=mgL^3/48E_cI$ is the static deflection of an alumina beam under a load mg acting at the mid-span, and $A=bh$ is the cross-sectional area. A uniform time step $\varDelta t=\varDelta T/500$, with $\varDelta T$ is the total time necessary for the mass to cross the beam, is used for the Newmark procedure.

5.1 Formulation verification

Before computing the dynamic response of the BFGSW beam, the accuracy of the derived formulation is necessary to verify. Since there are no data on the BFGSW beam partially supported by the elastic foundation under a moving mass, the verification is carried out by comparing the frequencies and dynamic response for some special cases.

Table 1 Comparison of fundamental frequency parameters of (1-1-1) beam fully resting on foundation for $n_x=0$, $L/h=10$

Table 2 Comparison of the fundamental frequency parameters of a bidirectional FGM beam

Table 3 Comparison of dynamic magnification factors of FGM beam under a moving mass

Table 1 compares the frequency parameter, $\mu =\omega L^2/h\,\sqrt{\rho _m/E_m}$, of a unidirectional FGSW beam fully supported by a Pasternak foundation obtained in the present work with the result of Su et al. [12]. The sandwich beam in [12] is a special case of the present beam model when $n_x=0$. As can be observed from the table, the results obtained in the present work are in excellent agreement with that of Ref. [12], regardless of the transverse power-law index $n_z$, the foundation stiffness and the micromechanical model. Noting that the result of Ref. [12] was obtained by using Timoshenko beam theory and the general Fourier formulation. In Table 2, the fundamental frequency parameters of an exponentially bidirectional FGM beam obtained by the dived formulation are compared with the result based on Timoshenko beam theory and a semi-analytical method of Ref. [41]. The frequency parameter in Table 2 is defined in accordance with Ref. [41], and it is obtained for a simply supported beam with the geometric and material data given in the reference. A good agreement is noted from Table 2, regardless of the span-to-height ratio and the material grading indexes.

In Table 3, the dynamic magnification factors of a FGM beam with the material properties varying in the thickness direction under a moving mass of the present paper are compared with the result of Khalili et al. [28] and Song et al. [62]. The result of Ref. [28] is based on Euler–Bernoulli beam theory and the differential quadrature method, while the Kirchhoff plate theory and the differential quadrature method are used in Ref. [62]. A good agreement between the dynamic magnification factors of the present work with that of Refs. [28, 62] is noted from Table 3. It is necessary to note that the result in Table 3 has been obtained for a FGM beam made from alumina and steel with the geometrical and material data given in [28]. In order to verify the formulation in some more further, Fig. 3 compares the time histories for mid-span deflection of the unidirectional FGSW beam ($n_x=0$) obtained herein with the result of Songsuwan et al. [33] using the Timoshenko beam theory and the Ritz method. Very good agreement between the present result with that of Ref. [33] is seen from Fig. 3.

Table 4 Convergence of the formulation in evaluating dynamic magnification factors of BFGSW beam ($L/h=20$, $r_m=0.5$, $k_1=50$, $k_2=5$ and $v=50$ m/s)

The convergence of the derived formulation in evaluating dynamic response of the BFGSW beam is shown in Table 4, where the dynamic magnification factors of symmetric (2-1-2) and non-symmetric (2-1-1) beams obtained by different number of the elements are given for $L/h=20$, $r_m=0.5$, $k_1=50$, $k_2=5$, $v=50$ m/s and various values of the foundation supporting parameter $\alpha _F$. The result in the table is based on the Voigt model and a uniform mesh for both the beam and the foundation. Thus, the number of elements used for the foundation is $ne_{\text {F}}=0, ne_{\text {B}}/2$ and $ne_{\text {B}}$ for $\alpha =0, 0.5$ and 1, respectively. The convergence of the derived formulation, as seen from the table, is fast, and it is achieved by using sixteen elements, regardless of the layer thickness ratio and the power-law indexes. Because of this convergence result, a uniform mesh of sixteen elements is used in all computations reported below.

5.2 Parametric study

The effects of various parameters, including the power-law indexes, the moving mass and foundation parameters, on the dynamic behaviour of the BFGSW beam are investigated in this subsection.

In Figs. 4 and 5, the time histories for mid-span deflection of a (2-1-1) beam are depicted for various values of the moving mass speed v, foundation stiffness parameters $k_1, \; k_2$, foundation supporting parameter $\alpha _F$ and the mass ratio $r_m$. Both the Voigt model and the Mori–Tanaka scheme are employed to obtain the deflections of the beam. It can be seen from Fig. 4 that the mid-span deflection is remarkably influenced by the moving mass speed, and the maximum mid-span deflection is larger for a higher moving mass speed. The beam tends to execute less vibration cycles when it is subjected to the mass with a higher moving speed. The effect of the foundation supporting parameter $\alpha _F$ on the time histories of the beam, as seen from Fig. 5, is more significant than that of the mass ratio $r_m$. Furthermore, the mass ratio can slightly change the amplitude of the mid-span deflection, but it hardly changes the way the beam vibrates. For most of the travelling time, the deflections obtained from the Mori–Tanaka scheme are higher than that obtained by the Voigt model.

Table 5 Dynamic magnification factors for $L/h=5,\; k_1=100, \; k_2=10, \; r_m=0.5$ and $v=50$ (m/s)

Table 6 Dynamic magnification factors for $L/h=20,\; k_1=100, \;k_2=10,\; r_m=0.5$, and $v=50$ (m/s)

In order to study the effect of the power-law indexes and the foundation supporting parameter on the dynamic response of the BFGSW beam, the dynamic magnification factors of symmetric and non-symmetric beams are evaluated. The numerical results are presented in Tables 5 and 6, where the dynamic factors of the beams with two values of the span-to-height ratio, $L/h=5$ and $L/h=20$, are given for $k_1=100$, $k_2=10$, $r_m=0.5$, $v=50$ m/s and various values of the foundation supporting parameter $\alpha _F$. The tables show a significant influence of both the foundation supporting parameter and the power-law indexes on the factor $D_d$ of the beams. The factor $D_d$ increases with the increase in the power-law indexes, and it decreases by increasing the foundation supporting parameter, regardless of the layer thickness ratio. The effect of the power-law indexes can be seen more clearly from Fig. 6, where the variation of the Mori–Tanaka scheme-based factor $D_d$ with the power-law indexes is depicted for $L/h=20$, $r_m=0.5$, $k_1=100, \; k_2=10$, $v=50$ m/s and various values of the supporting parameter $\alpha _F$. The influence of the indexes $n_x$ and $n_z$ on the dynamic magnification factor is more significant for the indexes smaller than 2.5, regardless of the foundation supporting parameter. By comparing the result in Tables 5 and 6, one can see that the span-to-height ratio also plays an important role on the dynamic response of the beam, and the dynamic magnification factor $D_d$ is higher for the beam with a smaller span-to-height ratio. This tendency is correct for all the power-law indexes and the foundation supporting parameters.

Figures 7 and 8 show the variation of the dynamic magnification factor $D_d$ with the moving mass speed $v$ for different foundation supporting parameters and the mass ratios, respectively. The results in the figures are shown for the $D_d$ obtained by both the Voigt model and the Mori–Tanaka (MT) scheme. As in case of the moving load on a FGM beam [25], the dynamic factor $D_d$ in Figs. 7 and 8 repeatedly increases and decreases when increasing the moving mass speed v, and it then approaches a maximum value. Figure 7 shows that for most of the moving mass speed, the dynamic factor $D_d$ of both the symmetric and non-symmetric beams is smaller for a larger supporting parameter $\alpha _F$. As expected, the dynamic magnification factor $D_d$, as seen from Fig. 8, is higher when the beam is under a larger moving mass. The moving mass speed at which the dynamic magnification factor attains a maximum value is very much dependent on the foundation supporting parameter and the mass ratio.

In order to show the influence of the foundation stiffness on the dynamic response of the beam, the variation of the dynamic magnification factor $D_d$ with the foundation stiffness parameters $k_1$ and $k_2$ is depicted in Fig. 9 for $L/h=20$, $n_x=n_z=0.5$, $r_m=0.5$, $\alpha _F=0.5$ and two values of the moving mass speeds, $v=30$ and 80 m/s. As expected, the dynamic magnification factor decreases with the increase in the foundation parameters, irrespective of the moving mass speed. The figure also shows a clear difference between the dynamic factor obtained by the Voigt model and the Mori–Tanaka scheme. It is worthy to note that the influence of the micromechanical model is more significant for $0\le k_1\le 60$ and $0\le k_2 \le 6$. In other words, the influence of the micromechanical model on the dynamic magnification factor is dependent on the foundation stiffness, and this influence is less significant for the high stiffness foundation.

To explore the influence of the micromechanical model on the dynamic response of the BFGSW beam in some more further, Fig. 10 shows the relation between the dynamic magnification factor obtained by the two micromechanical models with the power-law indexes of symmetric (2-1-2) and non-symmetric (2-1-2) beams for $L/h=20$, $k_1=100, \; k_2=10$, $r_m=0.5$ and $v=50$ m/s. As seen from the figure, the difference on the dynamic magnification factor is the more significant for the power-law indexes smaller than 4. This difference is, however, dependent on the foundation supporting parameter $\alpha _F$, and it becomes less significant for the smaller parameter $\alpha _F$.

For completeness, the thickness distribution of the axial, normal and shear stresses of the symmetric (2-1-2) and non-symmetric (2-1-1) beams is depicted in Figs. 11, 12 and 13 for $L/h = 10, \; n_x = 0.5, \; k_1 = 100, \; k_2 = 10, \; r_m = 0.5$, $v = 50$ m/s and various values of the transverse index $n_z$. The stresses in the figures are obtained by using the Voigt model, and they are computed at the time when the moving mass arrives at the mid-span. All the stresses are normalized by $\sigma _0=mg/bh$, that is $\sigma _{xx}^*=\sigma _{xx}(L/2,z)/\sigma _0$, $\sigma _{zz}^*=\sigma _{zz}(L/2,z)/\sigma _0$ and $\tau _{xz}^*=\tau _{xz}(0,z)/\sigma _0$. Some difference between the stresses of the symmetric and non-symmetric beams can be seen from the figures. At the given value of the axial index $n_x$, the increase in the transverse index $n_z$ leads to the decrease in the maximum tensile and compressive stresses $\sigma _{xx}^*$ and $\sigma _{zz}^*$ of the symmetric beam (Figs. 11a,b, 12a,b), while the corresponding stresses of the non-symmetric beam are variable (Figs. 11c,d, 12c,d). The shear stress of both the symmetric and non-symmetric beams increases by the increase in the transverse index (Fig. 13). All the stresses of the symmetric beam are seen to be symmetric with respect to the mid-plane, while that is not true for the non-symmetric beam. The effect of the micromechanical model on the thickness distribution of the stresses is, respectively, shown in Figs. 14 and 15 for the normal stress and shear stress of the symmetric (2-1-2) and non-symmetric (2-1-1) beams. Figure 15 shows that the shear stress obtained by the Mori–Tanaka scheme is always larger than that using the Voigt model, while the effect of the micromechanical model on the normal stress, as seen from Fig. 14, is dependent on the transverse index.

6 Conclusion

The dynamic behaviour of BFGSW beams partially resting on a Pasternak foundation under a moving mass has been studied on the basis of the quasi-3D shear deformation beam theory. The beams consist of three layers, an axially FGM core and two bidirectional FGM face layers. The material properties of the beams are considered to follow the power gradation laws, and they are estimated by both the Voigt and the Mori–Tanaka micromechanical models. The equation of motion in terms of the finite element analysis has been derived and solved by the Newmark method. The accuracy of the formulation has been confirmed through a comparison study. Results obtained from the numerical investigation reveal that the foundation supporting parameter $\alpha _F$, defined as the ratio of the supporting part to the total beam length, plays an important role regarding the dynamic behaviour of the beams. The effects of various parameters, including the material power-law indexes, the layer thickness ratio, the moving mass speed and the mass ratio, on the dynamic characteristics have been examined in detail and highlighted. The most important findings from the numerical results can be summarized as follows:

• The dynamic response is significantly influenced by the material gradation, and the dynamic magnification factor is increased by an increase in the power-law indexes, regardless of the foundation and moving mass parameters.

• The micromechanical model plays an important role on the dynamic response of the beam, and for most of the moving mass speeds, the dynamic magnification factor based on the Voigt model is smaller than that using the Mori–Tanaka scheme. The influence of the micromechanical model on the dynamic response is dependent on the power-law indexes.

• The foundation supporting parameter $\alpha _F$ has a significant effect on the dynamic response, and the influence of the micromechanical model on the behaviour of the beam is dependent on the parameter $\alpha _F$.

• The layer thickness ratio has a significant influence on the dynamic behaviour of the beam, and the stress distribution of the non-symmetric beam is greatly different from that of the symmetric beam.

It is necessary to note that although the numerical investigation was carried out for the simply supported beam, the formulation derived in the present work can be used to evaluate the dynamic response of BFGSW beams with other boundary conditions as well.