Vibration of a three-phase bidirectional functionally graded sandwich beam carrying a moving mass using an enriched beam element

Abstract

Three-phase bidirectional functionally graded sandwich (BFGSW) beams are particular type of composite beams whose properties are tailored to vary continuously in both the longitudinal and transverse directions, depending on the constituent composition distribution. These beams are known to provide superior mechanical performance and to overcome the drawbacks of the traditional sandwich beams. In this paper, a beam element is formulated for modelling free and forced vibration of a three-phase BFGSW beam carrying a moving mass. The core of the sandwich beam is homogeneous, while the two face sheets are made from power-law bidirectional functionally graded material. In addition to the Voigt micromechanical model, the Maxwell formula is used for the first time to evaluate the effective elastic moduli of the three-phase functionally graded material. The beam element based on the sinusoidal shear deformation theory is derived using hierarchical functions to enrich the conventional Lagrange and Hermite shape functions. Using the derived element, differential equations of motion for the beams are solved to obtain natural frequencies and dynamic response of the beam. The numerical result shows that the derived element is efficient, and it can yield accurate vibration characteristics with small number of elements. An extensive parametric study is carried out to highlight the effects of the material gradation, the beam geometry and velocity of the moving mass on the vibration behaviour of the beam. The influence of the micromechanical model on the vibration of the beam is also examined and discussed.

1 Introduction

Sandwich structures with high specific stiffness and strength-to-weight ratios have wide applications in practice, especially in aerospace and automobile industries. Recently, sandwich construction becomes even more attractive due to the introduction of functionally graded materials for the faces and the core. Understanding vibration behaviour of functionally graded (FG) sandwich structures under dynamic loads is crucial for appropriately using these structures. Many investigations on vibration of FG structures, by both analytical and numerical methods, have been reported in the last two decades.

Table 1 Convergence of enriched beam element in evaluating frequency parameter $\mu _1$ of three-phase BFGSW beam (L/h = 20)

Table 2 Convergence of enriched beam element in evaluating dynamic magnification factor of three-phase BFGSW beam (L/h = 20, $r_\mathrm{m}$ = 0.5, v = 50 m/s, Voigt model)

Table 3 Comparison of fundamental frequency parameters of FG sandwich beam for $n_x$ = 0 and L/h = 10

Table 4 Comparison of dynamic magnification factor of a unidirectional FG beam under a moving mass (L/h =20, Voigt model)

Fig. 1

A simply supported beam made from three-phase BFGSW, two ceramics (M1 and M2) and a metal (M3), with a moving mass

Fig. 2

Distribution of $V_1$, $V_2$ and $V_3$ for $n_x=n_z=0.3$ and $z_1=-z_2=-h/4$

Fig. 3

Comparison of time histories for mid-span deflection of beams under a moving force with $v=50$ m/s: a unidirectional two-phase FG sandwich beam; b three-phase BFGSW beam

Fig. 4

Variation of the fundamental frequency parameters with power-law indices of BFGSW beam with $L/h=10$

Fig. 5

Relation between frequency parameter $\mu _1$ and span-to-height ratio L/h of BFGSW beam

Fig. 6

Variation of the first four natural frequency parameters with power-law indices of (1-1-1) beam with $L/h=10$ (Maxwell formula)

Fig. 7

Time histories for mid-span deflection for $L/h=20$, $n_x=n_z=0.5$, $r_\mathrm{m}=0.5$ and various moving mass velocities

Fig. 8

Time histories for mid-span deflection for $L/h=20$, $n_x=n_z=0.5$, $v=50$ m/s and various mass ratios

Regarding to the numerical analysis of FG and FG sandwich beams, the topic discussed in the present work, Chakraborty et al. [1] derived a first-order shear deformable beam element for thermoelastic analysis of a sandwich beam with a FG core. The convergence of the element was improved using the solution of the equilibrium equations of a beam segment to interpolate the displacement field. Bhangale and Ganesan [2] investigated the thermal effects on bucking and vibration of FG sandwich beams with a viscoelastic core using a two-node FG sandwich beam element. Shahba et al. [3] considered exact variations of the beam cross-sectional profile in derivation of a finite element formulation for vibration and stability analyses of axially FG tapered Timoshenko beams. Finite element method was also used by Alshorbagy et al. [4], Eltaher et al. [5, 6] in free vibration study of FG beams and FG nanobeams, respectively. Taeprasartsit [7] solved the nonlinear equilibrium equations of Timoshenko beam element and used the solution to interpolate the displacement field in derivation of stiffness matrix for buckling analysis of FG Timoshenko beams. Nguyen [8, 9], Nguyen and Gan [10] derived the co-rotational beam elements for large displacement analysis of FG tapered beams with material properties varying in the thickness or longitudinal direction. It was shown by the authors that the large displacement behaviour of the beams is significantly influenced by the material gradation. Using the differential quadrature rule, Jin and Wang [11] derived a beam element for vibration analysis of FG Euler-Bernoulli beams. Numerical investigation by the authors showed that the element is accurate, and it can yield accurate frequencies with small number of nodal points. Based on the first-order shear deformation theory and Lagrange interpolations, Kahya and Turan [12] derived a five-node beam element for vibration and buckling analysis of FG beams. The element with ten degrees of freedom can accurately predict frequencies of buckling loads of the beams.

Table 5 Fundamental frequency parameters for L/h = 5 and different power-law indices and layer thickness ratios

Table 6 Fundamental frequency parameters for L/h=20 and different power-law indices and layer thickness ratios

Table 7 Dynamic magnification factors for different power-law indices and layer thickness ratios (L/h=10, $r_\mathrm{m}$=0.5, v=50 m/s)

Fig. 9

Variation of dynamic magnification factor with power-law indices of BFGSW beam for L/h = 10, $r_\mathrm{m} = 0.5$ and $v=50$ m/s

Fig. 10

Relation between dynamic magnification factor with moving mass velocity for $L/h=20$ and $r_\mathrm{m} = 0.5$

Fig. 11

Effect of mass ratio on the relation between magnification factor and moving mass velocity of BFGSW beam with $L/h=20$ and $n_x=n_z=0.5$

Fig. 12

Effect of span-to-height ratio on relation between dynamic magnification factor and moving mass velocity of BFGSW beam ($r_\mathrm{m}=0.5$)

Fig. 13

Thickness distribution of axial stress of three-phase BFGSW beam for $L/h=10$, $n_x=0.5$, $r_\mathrm{m}=0.5$ and $v=50$ m/s

Fig. 14

Thickness distribution of shear stress of three-phase BFGSW beam for $L/h=10$, $n_x=0.5$, $r_\mathrm{m}=0.5$ and $v=50$ m/s

To avoid the use of a shear correction factor which requires by the first-order shear deformation theory, higher-order beam theories were employed in formulating beam elements for analyzing the FG beams. Kadoli et al. [13] studied bending behaviour of FG beams using a third-order shear deformable finite element formulation. The formulation is derived using the cross-sectional rotation or the shear rotation as an independent variable. The numerical tests by the authors show that convergence of the shear rotation element is faster than that of the cross-sectional rotation element. Frikha et al. [14] used a mixed formulation to formulate a third-order C$^0$ beam element for bending study of FG beams. The element with 4 degrees of freedom per node gives the exact solution at the nodal points. The refined third-order shear deformation theories, in which the transverse displacement is split into bending and shear parts, were adopted by Vo et al. [15, 16] in formulating finite element formulations for free vibration and buckling analyses of FG sandwich beams. Lagrange and Hermite functions were employed by the authors to interpolate the displacements field. A C$^1$ beam element for bending analysis of FG and FG sandwich beams was derived by Yarasca et al. [17] in the basic of a quasi-3D hybrid higher-order shear deformation theory. The two-dimensional plane stress problem was adopted by Akbaş et al. [18] in formulating a finite element formulation for computing dynamic response of FG sandwich beams under a pulse load, taking into account the influence of porosities and viscous damping. The refined trigonometric shear deformation theory was employed by Ebrahimi and Dabbagh [19], Dabbagha et al. [20] to derive the finite element formulations for analyzing FG composite nanobeams. The free transverse shear stress conditions on the bottom and top surfaces of the beams in the theory are satisfied by appropriate choice of the shape functions for the transverse displacement.

Dynamic analysis of beams under moving loads is an important topic in structural mechanics, and it has drawn much attention from researchers for a long time. This problem, originated in civil engineering for the design of bridges and highways, also arises in many modern machining operations. A large number of solutions for homogenous beams under moving loads are given in the excellent monograph by Frýba [21]. The influence of spatial gradation of material properties on dynamic behaviour of beams carrying moving loads has been investigated in recent years. Şimşek and Kocatürk [22], Şimşek [23,24,25] employed polynomials to approximate the displacement fields to study vibration of FG beams excited by a moving load, taking into account the effect of thickness gradation of material properties. The method is simple, and it is then extended by Şimşek et al. [26] in dynamic analysis of beams under a moving load with material properties varying in the longitudinal direction. Khalili et al. [27] computed dynamic response of FG Euler-Bernoulli beams under a moving mass using the differential quadrature (DQ) method. Numerical investigation by the authors showed that compared to the Newmark and Wilson methods, the proposed DQ method gives better accuracy using larger time step sizes. Vibration analysis of a FG Euler-Bernoulli beam under a moving oscillator was carried out by Rajabi et al. [28] using the Runge-Kutta method. The Ritz method was used by Chen et al. [29] to study vibration of FG Timoshenko beams with a moving load, taking the effect of porosities into account. Lagrange method was used in conjunction with Newmark method by Wang and Wu [30], Wang et al. [31] to investigate the effect of temperature and porosities on dynamic behaviour of FG Timoshenko beams and FG sandwich beams traversed by moving loads, respectively. Songsuwan et al. [32] examined dynamic behaviour of FG sandwich beams on Pasternak foundation under a moving harmonic load using the Ritz method. The authors showed that the frequencies and dynamic deflections are significantly influenced by the thickness variation of the material properties and the layer thickness ratio of the beams. The effect of longitudinal variation of material properties and cross section on dynamic behaviour of FG Timoshenko beams was studied by Gan et al. [33] using a finite element formulation. The finite element method was also used by Esen [34, 35] to compute dynamic response of FG beams carrying a variable speed moving mass. The element formulations in the works are simple, but require a shear correction factor to amend the incorrect distribution of the transverse shear stress.

The beams in the above discussed references have material properties varying in only one direction, the thickness or longitudinal direction. Development of FG structures with material properties being graded in two or more directions to meet the multi-functional requirements is of great demand [36]. Analysis of bidirectional FG beams has been carried out by several authors recently. Lezgy-Nazargah [37] employed the NURBS isogeometric finite element method to investigate bending behaviour of FG beams with material properties varying in both longitudinal and transverse directions. Şimşek [38] studied vibration of Timoshenko beams carrying a moving load with material properties exponentially varying in both the length and thickness directions under a moving point load. The author revealed that the material properties of the beams can be tailored to meet the desired goals of optimizing the response by choosing suitable material indices. Nguyen et al. [39] derived a two-node Timoshenko beam element for computing dynamic response of bidirectional power-law FG and FG sandwich beams under a moving load. The element used the third-order polynomials to interpolate the transverse displacement is fast convergent. The element was then extended to study vibration of a bidirectional functionally graded sandwich (BFGSW) beam due to a moving load [40]. A Timoshenko beam element was formulated by Nguyen and Tran [41] for computing frequencies of bidirectional FG tapered beams. The element was derived using the hierarchical interpolation to avoid the shear locking and to improve the convergence of the element. The modified couple stress theory was employed by Rajasekaran and Khaniki [42] to derive a finite element formulation for vibration analysis of non-uniform bidirectional FG micro-beams on elastic foundation under a harmonic mass. It has been shown by the authors that the material scale factor plays an important role on the dynamic response of the beams. The third-order Reddy beam theory has been used in conjunction with the modified couple stress theory by Attia and Mohamed [43] to study nonlinear vibration of pre- and post-buckled tapered microbeams with material properties being graded in both the thickness and longitudinal directions by the power gradation law. The differential quadrature method was employed by the authors to obtain the vibration characteristics of the beams. Based on a quasi-3D shear deformation theory, Vu et al. [44] derived a finite element formulation for dynamic analysis of a two-phase BFGSW beam traversed by a moving mass. The effect of partial support by a Pasternak foundation on the dynamic behaviour of the beam has been investigated by the authors.

Improvement of accuracy and efficiency of finite element formulations is of great demand in finite element analysis of structures. This topic grows in importance due to the increasing use of material gradation to optimize structures. There are various methods to improve the efficiency of a finite element formulation, amongst which the use of trigonometric or hierarchical functions to enrich the conventional interpolations is an effective way. In this line of work, Arndt et al. [45] employed trigonometric functions to enrich the linear interpolations in driving a bar element for longitudinal free vibration analysis of trusses. The convergence of the resulted element is significantly improved. Hsu [46] enriched the conventional linear interpolation by hierarchic functions in formulating a Timoshenko beam element for free vibration analysis of beams. The enriched beam element is efficient, and it is free of shear-locking. Hsu and Deitos [47] showed that the efficiency of an Euler-Bernoulli beam element in computing dynamic response of 2D frames under wind loading is significantly improved by using trigonometric functions to enrich the conventional Lagrange and Hermite shape functions. Recently, Le et al. [48] formulated an enriched third-order shear deformation beam element for free vibration and buckling analysis of BFGSW beams. The element is capable to give accurate frequencies and buckling loads by small number of elements. Motivated by these works, the present paper formulates an enriched beam element for vibration analysis of a three-phase BFGSW beam carrying a moving mass. The element employed hierarchical functions for enrichment of the conventional interpolation as in Ref. [48], but it is derived in the basis of the sinusoidal shear deformation theory [49, 50]. The theory, which does not require a shear correction factor as the first-order theory, satisfies the free transverse shear stress conditions on the top and bottom beam surfaces using a sinusoidal shape function for the transverse displacement. The core of the sandwich beam is homogeneous while its two skin layers are made from a three-phase FG material with effective properties varying in both the thickness and longitudinal directions by power gradation laws. In addition to the Voigt micromechanical model [51], the Maxwell formula [52, 53] is also employed herein for the first time to evaluate effective elastic moduli of the three-phase FG material. Thus, in addition to the use of the Maxwell formula, the vibration analysis of the three-phase BFGSW beam carrying a moving mass by the enriched beam element presented herein for the first time are the main novel points of this paper. Numerical investigations are carried out to show the efficiency of the derived beam element and to highlight the effects of the material distribution and loading parameters on vibration behaviour of the beams.

Following the above introduction, the rest of this paper is organized as follows. The mathematical formulation for the BFGSW beam with a moving mass is presented in Sect. 2. Section 3 describes the beam element with hierarchical interpolation enrichment and equation of motion in the discretized form. Section 4 is devoted to numerical investigation, demonstrating the effects of various parameters on vibration of the beam. Finally, conclusions based on the numerical investigation are given in the last section.

2 Mathematical formulation

The mathematical formulation is provided in this section, including the beam geometry, the gradual material properties, the displacement field based on the sinusoidal shear deformation theory and the resultant expressions of strain, as well as the energies associated with the dynamical loading and the system of equations to be solved.

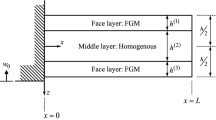
Figure 1 shows a simply supported sandwich beam with rectangular cross section ($b \times h$) under a mass m, moving from the left to right with a constant velocity v. The beam consists of three layers, a homogeneous core and two FG skin layers with material properties varying in both the length and thickness directions. It is assumed that the mass m is always in contact with the beam. The Cartesian coordinate system (x, y, z) in the figure with the origin at the left end of the beam is chosen such that the (x, y) plane is on the beam mid-plane, and the x-axis directs to the beam axis while the z-axis directs upward. Denoting $z_0$, $z_1$, $z_2$ and $z_3$ with $z_0=-h/2$ and $z_3=h/2$ are, respective, the coordinates along the z-axis of the bottom layer, the interfaces between the layers and the top layer.

The beam is assumed to be made from three materials, two ceramics M1 and M2, and a metal M3, whose volume fractions varying in both the longitudinal and transverse directions according to the power-law distributions as [40, 54]

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} \; V_1 &{} = \left( \frac{z-z_0}{z_1-z_0}\right) ^{n_z} \\ \; V_2 &{} = \left[ 1-\left( \dfrac{z-z_0}{z_1-z_0}\right) ^{n_z}\right] \left[ 1-\left( \dfrac{x}{L}\right) ^{n_x}\right] \qquad \; \text {for} \;\; z\in [z_0, z_1]\\ \ V_3 &{} = \left[ 1-\left( \dfrac{z-z_0}{z_1-z_0}\right) ^{n_z}\right] \left( \dfrac{x}{L}\right) ^{n_x} \end{array}\right. } \\&\quad \; V_1=1 , V_2=V_3=0 \quad \;\; \text {for} \;\; z\in [z_1, z_2] \\&{\left\{ \begin{array}{ll} \; V_1 &{} = \left( \frac{z-z_3}{z_2-z_3}\right) ^{n_z} \\ \; V_2 &{} = \left[ 1-\left( \dfrac{z-z_3}{z_2-z_3}\right) ^{n_z}\right] \left[ 1-\left( \dfrac{x}{L}\right) ^{n_x}\right] \qquad \; \text {for} \;\; z\in [z_2, z_3] \\ \ V_3 &{} = \left[ 1-\left( \dfrac{z-z_3}{z_2-z_3}\right) ^{n_z}\right] \left( \dfrac{x}{L}\right) ^{n_x} \end{array}\right. } \end{aligned} \end{aligned}$$

(1)

where L is the beam length; $V_1$, $V_2$ and $V_3$ are, respectively, the volume fraction of M1, M2 and M3; $n_x$ and $n_z$ are the axial and transverse grading indices. Figure 2 shows the distribution of the $V_1$, $V_2$ and $V_3$ for $n_x=n_z=0.3$ and $z_1=z_2=-h/4$.

Two micromechanical models, namely, the Voigt model and Maxwell formula, are used herein to evaluate the effective elastic moduli of the beam. An effective property ${{\mathcal {P}}}_f$, such as the Young’s modulus $E_f$ and mass density $\rho _f$, evaluated by the Voigt model is of the form

$$\begin{aligned} {\mathcal {P}}_f(x,z)={\mathcal {P}}_1 V_1 + {\mathcal {P}}_2 V_2 + {\mathcal {P}}_3 V_3 \end{aligned}$$

(2)

with ${\mathcal {P}}_1$, ${\mathcal {P}}_2$ and ${\mathcal {P}}_3$ are the properties of the M1, M2 and M3, respectively. Substituting Eq. (1) into Eq. (2), one gets

$$\begin{aligned} \begin{aligned} {\mathcal {P}}_f(x,z)= {\left\{ \begin{array}{ll} \left[ {\mathcal {P}}_1-{\mathcal {P}}_{23}(x)\right] \left( \dfrac{z-z_0}{z_1-z_0}\right) ^{n_z} + {\mathcal {P}}_{23}(x) &{} \text{ for } \qquad z\in [z_0, z_1]\\ {\mathcal {P}}_1&{} \text{ for } \quad z \in [z_1, z_2] \\ \left[ {\mathcal {P}}_1-{\mathcal {P}}_{23}(x) \right] \left( \dfrac{z-z_3}{z_2-z_3}\right) ^{n_z} + {\mathcal {P}}_{23}(x) &{} \text{ for } \quad z\in [z_0, z_1]\\ \end{array}\right. } \end{aligned} \end{aligned}$$

(3)

with

$$\begin{aligned} {\mathcal {P}}_{23} (x)={\mathcal {P}}_2-\big ({\mathcal {P}}_2-{\mathcal {P}}_3 \big )\Big (\frac{x}{L}\Big )^{n_x} \end{aligned}$$

(4)

One can easily verify that if $n_x$=0 or M2 is identical to M3, Eq. (3) returns to the effective properties of the unidirectional transverse FG sandwich beam in [15].

According to the Maxwell formula (or extended Mori-Tanaka scheme) the effective bulk modulus $(K_\mathrm{f})$ and shear modulus $(G_\mathrm{f})$ of a three-phase composite with matrix M3 are given by [52, 53]

$$\begin{aligned} \begin{aligned} K_\mathrm{f}&=\left( \sum _{i=1}^3\dfrac{V_i}{K_i+\frac{4}{3}G_3}\right) ^{-1}-\dfrac{4}{3}G_3 , \\ G_\mathrm{f}&=\left( \sum _{i=1}^3\dfrac{V_i}{G_i+G_3^*}\right) ^{-1} -G_3^* ,\\&\quad \text {with} \;\; G_3^*=G_3\dfrac{9K_3+8G_3}{6K_3+12G_3} \end{aligned} \end{aligned}$$

(5)

where $K_i$ and $G_i$ $(i=1\ldots 3)$ are, respectively, the bulk and shear moduli of the inclusion ceramic phases M1, M2 and the matrix phase M3. The effective Young’s modulus $(E_\mathrm{f})$ and Poisson ratio $(\nu _\mathrm{f})$ are calculated from the above effective bulk and shear moduli according to

$$\begin{aligned} E_\mathrm{f}=\dfrac{9K_\mathrm{f}G_\mathrm{f}}{3K_\mathrm{f}+G_\mathrm{f}} , \quad \nu _f=\dfrac{3K_f-2G_f}{6K_f+2G_f} \end{aligned}$$

(6)

Noting that Eq. (3) is still used in calculate the effective mass density $(\rho _f)$ of the beam.

The sinusoidal shear deformation theory [49, 50] is adopted herein to describe the displacements of the beam. The theory satisfies the free transverse shear stress conditions on the top and bottom surfaces of the beam without using a shear correction factor. According to the theory, the displacements in the x and z directions, u(x, z, t) and w(x, z, t), of a point in the beam are respectively given by

$$\begin{aligned} \begin{aligned} u(x,z,t)=&u_0(x,t)-zw_{b,x}(x,t)+f(z)w_{s,x}(x,t)\\ w(x,z,t)=&w_b(x,t)+w_s(x,t) \end{aligned} \end{aligned}$$

(7)

where $u_0(x,t)$ is the axial displacement of the point on the mid-plane; $w_b(x,t)$ and $w_s(x,t)$ are, respectively, the bending and shear components of the transverse displacement; t is the time variable, and the shape function f(z) is of the form

$$\begin{aligned} f(z)=-z+\frac{h}{\pi }\,\sin {\dfrac{\pi z}{h}} \end{aligned}$$

(8)

In Eq. (7) and hereafter, a subscript comma denotes the derivative with respect to the variable that follows. e.g. $w_{b,x}=\partial w_b/\partial x$.

Equation (7) gives the axial strain ($\epsilon _{xx}$) and shear strain ($\gamma _{xz}$) in the forms

$$\begin{aligned} \begin{aligned} \epsilon _{xx}=&u_{0,x}-zw_{b,xx}+f(z)w_{s,xx}\\ \gamma _{xz}=&g(z)w_{s,x} \end{aligned} \end{aligned}$$

(9)

where $g(z)=\cos {\frac{\pi z}{h}}$.

The constitutive equation based on linear behaviour of the beam material is of the form

$$\begin{aligned} \left\{ \begin{matrix} \sigma _{xx} \\ \tau _{xz} \end{matrix} \right\} =\begin{bmatrix} E_\mathrm{f}(x,z) &{} 0 \\ 0 &{} G_\mathrm{f}(x,z) \end{bmatrix} = \left\{ \begin{matrix} \epsilon _{xx} \\ \gamma _{xz} \end{matrix} \right\} \end{aligned}$$

(10)

where $\sigma _{xx}$ and $\tau _{xz}$ are, respectively, the axial and shear stresses; $E_\mathrm{f}(x,z)$ and $G_\mathrm{f}(x,z)$ respectively are the effective Young’s modulus and shear modulus, defined by Eq. (3) or by Eqs. (5) and (6).

The elastic strain energy of the beam (${\mathcal {U}}$) is given by

$$\begin{aligned} {\mathcal {U}}=\frac{1}{2}\int _{0}^{L}\int _{A}(\sigma _{xx}\epsilon _{xx}+\tau _{xz}\gamma _{xz})\mathrm{d}A\mathrm{d}x \end{aligned}$$

(11)

where $A=bh$ is the beam cross-sectional area.

From Eqs. (9) and (10), one can write the strain energy in Eq. (11) in the form

$$\begin{aligned} \begin{aligned} {\mathcal {U}}=&\frac{1}{2}\int _{0}^{L}\Big [ A_{11}u_{0,x}^2-2A_{12}u_{0,x}(w_{b,xx}+w_{s,xx})\\&+A_{22}\Big (w_{b,xx}+w_{s,xx}\Big )^2\\&+2B_{11}u_{0,x}w_{s,xx}-2B_{12}\Big (w_{s,xx}^2+w_{s,xx}w_{b,xx}\Big )\\&+B_{22}w_{s,xx}^2 +D_{11}w_{s,x}^2 \Big ]\mathrm{d}x \end{aligned} \end{aligned}$$

(12)

where $A_{11}, A_{12}, A_{22}, \, B_{11}, B_{12}, B_{22}$ and $D_{11}$ are the beam rigidities, defined as

$$\begin{aligned} \begin{aligned} (A_{11}, A_{12}, A_{22})=&b\int _{-h/2}^{h/2} E_f(x,z)\Big ( 1,z,z^2\Big )\mathrm{d}z\\ (B_{11}, B_{12}, B_{22})=&\frac{bh}{\pi }\int _{-h/2}^{h/2}E_f(x,z)\Big ( 1,z,\frac{h}{\pi }\sin \frac{\pi z}{h}\Big )\sin \frac{\pi z}{h} \, \mathrm{d}z \\ D_{11}=&b\int _{-h/2}^{h/2} G_f(x,z) \cos ^2\frac{\pi z}{h} \, \mathrm{d}z \end{aligned} \end{aligned}$$

(13)

The kinetic energy ${\mathcal {T}}$ of the beam is given by

$$\begin{aligned} \begin{aligned} {\mathcal {T}}=\frac{1}{2}\int _{0}^{L}\int _{A}\rho _f(x,z)({\dot{u}}^2 + {\dot{w}}^2)\mathrm{d}A\mathrm{d}x \end{aligned} \end{aligned}$$

(14)

where $\rho _f(x,z)$ is the effective mass density defined by Eq. (3); an over dot is used to denote the derivative with respect to the time variable. From Eqs. (7) and (8), one can write the above kinetic energy in the form

$$\begin{aligned} \begin{aligned} {\mathcal {T}}=&\frac{1}{2}\int _{0}^{L}\Big \{I_{11}\big [{\dot{u}}_0^2 + ({\dot{w}}_b+{\dot{w}}_s)^2]-2I_{12}{\dot{u}}_0({\dot{w}}_{b,x}+{\dot{w}}_{s,x})\\&+I_{22}({\dot{w}}_{b,x}+{\dot{w}}_{s,x})^2 +2J_{11}{\dot{u}}_0{\dot{w}}_{s,x}-2J_{12}({\dot{w}}_{s,x}^2\\&+{\dot{w}}_{b,x}{\dot{w}}_{s,x}) +J_{22}{\dot{w}}_{s,x}^2 \Big \}\mathrm{d}x \end{aligned} \end{aligned}$$

(15)

where the mass moments $I_{11}, I_{12}, I_{22}, J_{11}, J_{12}, J_{22}$ are defined as

$$\begin{aligned} \begin{aligned} (I_{11}, I_{12}, I_{22})&=b\int _{-h/2}^{h/2} \rho _f(x,z)\Big ( 1,z,z^2\Big )\mathrm{d}z \\ (J_{11}, J_{12}, J_{22})&=b\frac{h}{\pi }\int _{-h/2}^{h/2}\rho _f(x,z)\\&\Big ( 1,z,\frac{h}{\pi }\sin \frac{\pi z}{h}\Big )\sin \frac{\pi z}{h} \, \mathrm{d}z \end{aligned} \end{aligned}$$

(16)

The potential energy due to the moving mass is given by [34, 44]

$$\begin{aligned} {\mathcal {V}}= & {} -\int _{0}^{L}\Big [(mg - m\ddot{w} -2mv{\dot{w}}_{,x}-mv^2w_{,xx})w\nonumber \\&-m \ddot{u}_0 u_0 \Big ]\delta (x_m-vt)dx \end{aligned}$$

(17)

where $g=9.81$ m/s$^2$ is the gravity acceleration; $m\ddot{u}_0$ and $m\ddot{w}$ are, respectively, the axial and transversal inertia forces; $2mv{\dot{w}}_{,x}$ and $mv^2w_{,xx}$ are the Coriolis and centrifugal forces, respectively; $\delta (.)$ is the Dirac delta function; $x_m$ is the abscissa of the moving mass, measured from the left end of the beam (see Fig. 1).

Applying Hamilton’s principle to Eqs. (12), (15) and (17), one can obtain the following differential equations of motion for the beam as

$$\begin{aligned} \begin{aligned} \updelta u_o: \;&\left[ A_{11}u_{0,x}-A_{12}(w_{b,xx}+w_{s,xx})+B_{11}w_{s,xx}\right] _{,x} \\&\quad -I_{11}\ddot{u}_0+I_{12}(\ddot{w}_{b,x}+\ddot{w}_{s,x}) -J_{11}\ddot{w}_{s,x}-\left( m\ddot{u}_{0}\right) _{x=x_m}=0\\ \updelta w_b: \;&\left[ -A_{12}u_{0,x}+A_{22}w_{b,xx}-(B_{12}-A_{22})w_{s,xx}\right] _{,xx}\\&+\left[ I_{12}\ddot{u}_0-I_{22}\ddot{w}_{b,x}+(J_{12}-I_{22})\ddot{w}_{s,x}\right] _{,x} + I_{11}(\ddot{w}_b+\ddot{w}_s) \\&+ \left[ m(\ddot{w}_b+\ddot{w}_s)+2mv({\dot{w}}_{b,x}+{\dot{w}}_{s,x})\right. \\&\left. + mv^2(w_{b,xx}+w_{s,xx})\right] _{x=x_m}=mg \\ \updelta w_s: \;&\left[ (B_{11}-A_{12})u_{0,x}+(A_{22}-B_{12})w_{b,xx}\right. \\&\left. +(A_{22}-2B_{12}+B_{22})w_{s,xx}\right] _{,xx}\\&+\left[ (I_{12}-J_{11})\ddot{u}_0-(I_{22}-J_{12})\ddot{w}_{b,x}-(I_{22}-2J_{12}\right. \\&\left. +J_{22})\ddot{w}_{s,x}\right] _{,x}\\&+I_{11}(\ddot{w}_b+\ddot{w}_s)-(D_{11}w_{s,x})_{,x} +\big [m(\ddot{w}_{b}+\ddot{w}_{s})\\&+2mv({\dot{w}}_{b,x}+{\dot{w}}_{s,x})\\&+mv^2(w_{b,xx}+w_{s,xx})\big ]_{x=x_m}=mg \end{aligned} \end{aligned}$$

(18)

and the natural boundary conditions at $x=0$ and $x=L$ are of the forms

$$\begin{aligned} \begin{aligned}&A_{11}u_{0,x}-A_{12}(w_{b,xx}+w_{s,xx})+B_{11}w_{s,xx}={\overline{N}}\\&\qquad \left[ -A_{12}u_{0,x}+A_{22}(w_{b,xx}+w_{s,xx})-B_{12}w_{s,xx}\right] _{,x}\\&\qquad -I_{12}\ddot{u}_0+I_{22}(\ddot{w}_{b,x}+\ddot{w}_{s,x})-J_{12}\ddot{w}_{s,x}={\overline{Q}}_b \\&\qquad \left[ (A_{12}-B_{11})u_{0,x}+(B_{12}-A_{22})w_{b,xx}\right. \\&\qquad \left. +(2B_{12}-A_{22}-B_{22})w_{s,xx}\right] _{,x}\\&\qquad +D_{11}w_{s,x}+(J_{11}-I_{12})\ddot{u}_0+(I_{22}-J_{12})\ddot{w}_{b,x}\\&\qquad +(I_{22}-2J_{12}+J_{22})\ddot{w}_{s,x}={\overline{Q}}_s\\&\qquad -A_{12}u_{0,x}+A_{22}(w_{b,xx}+w_{s,xx})-B_{12}w_{s,xx}={\overline{M}}_b \\&\qquad (A_{12}-B_{11})u_{0,x}+(B_{12}-A_{22})w_{b.xx}\\&\qquad +(2B_{12}-A_{22}-B_{22})w_{s,xx}={\overline{M}}_s \end{aligned} \end{aligned}$$

(19)

where ${\overline{N}}$, ${\overline{Q}}_b$, ${\overline{Q}}_s$, ${\overline{M}}_b$, ${\overline{M}}_s$ are, respectively, the axial forces, bending and shear components of the shear forces and moments at the beam ends. The geometric boundary conditions for the simply supported beam in Fig. 1 are as follows

$$\begin{aligned} \begin{aligned} \bullet \;\;\;&\text {At} \;\; x=0: \;\; \quad u_0(0,t)=w_b(0,t)=w_s(0,t)=0 \qquad \\ \bullet \;\;\;&\text {At} \;\; x=L: \;\; \quad w_b(0,t)=w_s(0,t)=0 \end{aligned} \end{aligned}$$

(20)

Since the beam rigidities and the mass moments, as seen from Eqs. (13) and (16), are functions of the longitudinal coordinate x, a closed-form solution for the system of variable coefficient equations (18) is hardly to obtain. A finite beam element is derived in the next section for solving Eq. (18).

3 Beam element formulation

This section presents the hierarchical enriched beam element, including the beam mass and stiffness matrices as well as the mass, damping and stiffness matrices resulted from the effects of the inertia, Coriolis and the centrifugal forces of the moving mass. The discrete equation of motion for the beam is also provided.

3.1 Enriched interpolation

A two-node beam element with length l is considered herewith. A conventional $C^1$ beam element can be derived from the energy expressions in the previous section using the linear Lagrange and cubic Hermite polynomials to interpolate the axial displacement and transverse displacements, namely

$$\begin{aligned} u_0=\mathbf{N }\mathbf{d }_{u_0}, \quad w_b=\mathbf{H }\mathbf{d }_{w_b}, \quad w_s=\mathbf{H }\mathbf{d }_{w_s} \end{aligned}$$

(21)

where

$$\begin{aligned} \begin{aligned} \mathbf{d }_{u_0}=&\{u_{01} \;\;\;\; u_{02}\}^T, \\ \mathbf{d }_{w_b}=&\{w_{b1} \;\;\;\; w_{b,x1} \;\;\;\; w_{b2} \;\;\;\; w_{b,x2} \}^T,\\ \mathbf{d }_{w_s}=&\{w_{s1} \;\;\;\; w_{s,x1} \;\;\;\; w_{s2} \;\;\;\; w_{s,x2} \}^T \end{aligned} \end{aligned}$$

(22)

are, respectively, the vectors of nodal displacement for $u_0, \; w_b$ and $w_s$ at node 1 and node 2; $\mathbf{N }=[N_0 \, N_1]$ and $\mathbf{H }=[H_0\, H_1 \, H_2 \, H_3 ]$ are matrices of the following Lagrange and Hermite shape functions

$$\begin{aligned} N_0=\frac{l-x}{l},\quad N_1=\frac{x}{l} \end{aligned}$$

(23)

and

$$\begin{aligned} \begin{aligned} H_0=&1-3\frac{x^2}{l^2}+2\frac{x^3}{l^3},\quad H_1=x-2\frac{x^2}{l}+\frac{x^3}{l^2}\\ H_2=&3\frac{x^2}{l^2}-2\frac{x^3}{l^3},\quad H_3=-\frac{x^2}{l}+\frac{x^3}{l^2} \end{aligned} \end{aligned}$$

(24)

Substituting Eqs. (21)–(24) into Eqs. (12), (15) and (17), one can obtain stiffness, mass, damping matrices and the vector of nodal load forces of a conventional two-node beam element for vibration analysis of the FGSW beam with a moving mass.

To improve the efficiency of the beam element, the above Lagrange and Hermite interpolations are enriched herein by hierarchical functions. To this end, the above interpolation functions $N_i \; (i=0,1)$ and $H_j \; (j=1\ldots 3)$ are supplemented by the following higher-order functions

$$\begin{aligned} \widehat{\mathbf{N }}_p=\{N_2 \quad N_3 ... \quad N_p\}, \quad \widehat{\mathbf{H }}_k=\{H_4 \quad H_5 ... \quad H_k\} \end{aligned}$$

(25)

with $p\ge 2, k\ge 4$; $N_p$ and $H_k$ are the enrichment functions of degrees p and k, respectively. Four higher-order hierarchic polynomials are used herewith to enrich the original functions, and the interpolation (21) is now replaced by

$$\begin{aligned} u_0= & {} \mathbf{N }\mathbf{d }_{u_0} + \widehat{\mathbf{N }}_5\hat{\mathbf{d }}_{u_0}, \qquad w_b=\mathbf{H }\mathbf{d }_{w_b} + \widehat{\mathbf{H }}_7\hat{\mathbf{d }}_{w_b},\nonumber \\ w_s= & {} \mathbf{H }\mathbf{d }_{w_s} + \widehat{\mathbf{H }}_7\hat{\mathbf{d }}_{w_s} \end{aligned}$$

(26)

where $\hat{\mathbf{N }}_5=\{N_2 \, N_3 \, N_4 \, N_5\}$ and $\hat{\mathbf{H }}_7=\{H_4 \, H_5 \, H_6 \, H_7\}$ are matrices of the enriched shape functions; $\hat{\mathbf{d }}_{u_0}, \, \hat{\mathbf{d }}_{w_b}$ and $\hat{\mathbf{d }}_{w_s}$ are the supplemented vectors of unknowns with the following forms

$$\begin{aligned} \begin{aligned} \hat{\mathbf{d }}_{u_0}&=\{{\hat{u}}_{01} \quad {\hat{u}}_{02} \quad {\hat{u}}_{03} \quad {\hat{u}}_{04} \}^T\\ \hat{\mathbf{d }}_{w_b}&=\{{\hat{w}}_{b1} \quad {\hat{w}}_{b2} \quad {\hat{w}}_{b3} \quad {\hat{w}}_{b4} \}^T\\ \hat{\mathbf{d }}_{w_s}&=\{{\hat{w}}_{s1} \quad {\hat{w}}_{s2} \quad {\hat{w}}_{s3} \quad {\hat{w}}_{s4} \}^T \end{aligned} \end{aligned}$$

(27)

The enrichment functions $N_i \; (i=2 \ldots 5)$ and $H_j \; (j=4 \ldots 7)$, derived in Ref. [55] and previously employed in [46, 48], are given below

$$\begin{aligned} \begin{aligned} N_2&=\sqrt{6} \, \frac{x}{l}\Big (\frac{x}{l}-1\Big ), \\ N_3&=\sqrt{10} \,\frac{x}{l}\Big (\frac{x}{l}-1 \Big )\Big (\frac{2x}{l}-1 \Big ),\\ N_4&=\sqrt{14} \,\frac{x}{l}\Big (\frac{x}{l}-1\Big ) \Big (\frac{5x^2}{l^2}-\frac{5x}{l}+1 \Big ),\\ N_5&=\sqrt{18} \, \frac{x}{l}\Big (\frac{x}{l}-1\Big ) \Big (\frac{7x^2}{l^2}-\frac{7x}{l} +1\Big )\Big (\frac{2x}{l}-1 \Big ) \end{aligned} \end{aligned}$$

(28)

and

$$\begin{aligned} \begin{aligned} H_4&=\sqrt{10} \,\frac{x^2}{l^2}\Big (1-\frac{x}{l}\Big )^2, \\ H_5&=\sqrt{14} \, \frac{x^2}{l^2}\Big (1-\frac{x}{l}\Big )^2\Big (\frac{2x}{l}-1\Big ),\\ H_6&=\sqrt{2} \, \frac{x^2}{l^2}\Big (1-\frac{x}{l}\Big )^2 \Big (-\frac{14x^2}{l^2}+\frac{14x}{l}-3\Big ),\\ H_7&=\sqrt{22} \, \frac{x^2}{l^2}\Big (1-\frac{x}{l}\Big )^2 \Big (\frac{6x^2}{l^2}-\frac{6x}{l}+1\Big )\Big (\frac{2x}{l}-1\Big ) \end{aligned} \end{aligned}$$

(29)

With the enriched interpolations, the vector of degrees of freedom for the element $(\mathbf{d})$ contains 22 components, and it can be written as

$$\begin{aligned} \underset{22 \times 1}{\mathbf{d }}=\{\mathbf{d }_{u_0} \quad \hat{\mathbf{d }}_{u_0} \quad \mathbf{d }_{w_b} \quad \hat{\mathbf{d }}_{w_b} \quad \mathbf{d }_{w_s} \quad \hat{\mathbf{d }}_{w_s}\}^T \end{aligned}$$

(30)

where $\mathbf{d }_{u_0}, \; \mathbf{d }_{w_b}, \; \mathbf{d }_{w_s}$ are given by Eq. (22), and $\hat{\mathbf{d }}_{u_0}, \; \hat{\mathbf{d }}_{w_b}, \; \hat{\mathbf{d }}_{w_s}$ are defined by (27).

3.2 Beam element stiffness and mass matrices

Using Eqs. (26) and (30), one can write the strain energy in Eq. (12) in the following matrix form

$$\begin{aligned} {\mathcal {U}}=\frac{1}{2}\sum _{i=1}^{nele}\mathbf{d }^T_i\,\mathbf{k }_i\, \mathbf{d }_i \end{aligned}$$

(31)

where nele is the total number of elements used to discrete the beam, and $\mathbf{k }$ is the element stiffness matrix, which can be split into sub-matrices as

$$\begin{aligned} \underset{22 \times 22}{\mathbf{k }} = \begin{bmatrix} \mathbf{k }_{u_0u_0}&{}\mathbf{k }_{u_0{\hat{u}}_0}&{}\mathbf{k }_{u_0w_b}&{}\mathbf{k }_{u_0{\hat{w}}_b}&{}\mathbf{k }_{u_0w_s}&{}\mathbf{k }_{u_0{\hat{w}}_s}\\ \mathbf{k }_{u_0{\hat{u}}_0}^T&{}\mathbf{k }_{{\hat{u}}_0{\hat{u}}_0}&{}\mathbf{k }_{{\hat{u}}_0w_b}&{}\mathbf{k }_{{\hat{u}}_0{\hat{w}}_b}&{}\mathbf{k }_{{\hat{u}}_0w_s}&{}\mathbf{k }_{{\hat{u}}_0{\hat{w}}_s}\\ \mathbf{k }_{u_0w_b}^T&{}\mathbf{k }_{{\hat{u}}_0w_b}^T&{}\mathbf{k }_{w_bw_b}&{}\mathbf{k }_{w_b{\hat{w}}_b}&{}\mathbf{k }_{w_bw_s}&{}\mathbf{k }_{w_b{\hat{w}}_s}\\ \mathbf{k }_{u_0{\hat{w}}_b}^T&{}\mathbf{k }_{{\hat{u}}_0{\hat{w}}_b}^T&{}\mathbf{k }_{w_b{\hat{w}}_b}^T&{}\mathbf{k }_{{\hat{w}}_b{\hat{w}}_b}&{}\mathbf{k }_{{\hat{w}}_bw_s}&{}\mathbf{k }_{{\hat{w}}_b{\hat{w}}_s}\\ \mathbf{k }_{u_0w_s}^T&{}\mathbf{k }_{{\hat{u}}_0w_s}^T&{}\mathbf{k }_{w_bw_s}^T&{}\mathbf{k }_{{\hat{w}}_bw_s}^T&{}\mathbf{k }_{w_sw_s}&{}\mathbf{k }_{w_s{\hat{w}}_s}\\ \mathbf{k }_{u_0{\hat{w}}_s}^T&{}\mathbf{k }_{{\hat{u}}_0{\hat{w}}_s}^T&{}\mathbf{k }_{w_b{\hat{w}}_s}^T&{}\mathbf{k }_{{\hat{w}}_b{\hat{w}}_s}^T&{}\mathbf{k }_{w_s{\hat{w}}_s}^T&{}\mathbf{k }_{{\hat{w}}_s{\hat{w}}_s}\\ \end{bmatrix} \end{aligned}$$

(32)

The sub-matrices in the diagonal of the above element stiffness matrix have the following forms

$$\begin{aligned} \begin{aligned} \underset{2 \times 2}{\mathbf{k }_{u_0u_0}}&=\int _{0}^{l} \mathbf{N }_{,x}^TA_{11}\mathbf{N }_{,x}\mathrm{d}x , \\ \underset{4 \times 4}{\mathbf{k }_{{\hat{u}}_0{\hat{u}}_0}}&=\int _{0}^{l} \widehat{\mathbf{N }}_{5,x}^TA_{11}\widehat{\mathbf{N }}_{5,x}\mathrm{d}x \\ \underset{4 \times 4}{\mathbf{k }_{w_bw_b}}&=\int _{0}^{l} \mathbf{H }_{,xx}^TA_{22}\mathbf{H }_{,xx}\mathrm{d}x , \\ \underset{4 \times 4}{\mathbf{k }_{{\hat{w}}_b{\hat{w}}_b}}&=\int _{0}^{l} \widehat{\mathbf{H }}_{7,xx}^TA_{22}\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x \\ \underset{4 \times 4}{\mathbf{k }_{w_sw_s}}&=\int _{0}^{l} \Big [\mathbf{H }_{,xx}^T(A_{22}-2B_{12}+ B_{22}) \mathbf{H }_{,xx} +\mathbf{H }_{,x}^TD_{11}\mathbf{H }_{,x}\Big ] \mathrm{d}x\\ \underset{4 \times 4}{\mathbf{k }_{{\hat{w}}_s{\hat{w}}_s}}&=\int _{0}^{l} \Big [\widehat{\mathbf{H }}_{7,xx}^T(A_{22}-2B_{12}+ B_{22}) \widehat{\mathbf{H }}_{7,xx} +\widehat{\mathbf{H }}_{7,x}^TD_{11}\widehat{\mathbf{H }}_{7,x}\Big ] \mathrm{d}x \end{aligned} \end{aligned}$$

(33)

and the off-diagonal sub-matrices are

$$\begin{aligned} \begin{aligned} \underset{2 \times 4}{\mathbf{k }_{u_0{\hat{u}}_0}}&=\int _{0}^{l} \mathbf{N }_{,x}^TA_{11}\widehat{\mathbf{N }}_{5,x}\mathrm{d}x, \\ \underset{2 \times 4}{\mathbf{k }_{u_0w_b}}&=-\int _{0}^{l}\mathbf{N }_{,x}^TA_{12}\mathbf{H }_{,xx}\mathrm{d}x,\\ \underset{2 \times 4}{\mathbf{k }_{u_0{\hat{w}}_b}}&=-\int _{0}^{l}\mathbf{N }_{,x}^TA_{12}\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x, \\ \underset{2 \times 4}{\mathbf{k }_{u_0w_s}}&=\int _{0}^{l}\mathbf{N }_{,x}^T(-A_{12}+B_{11})\mathbf{H }_{,xx}\mathrm{d}x,\\ \underset{2 \times 4}{\mathbf{k }_{u_0{\hat{w}}_s}}&=\int _{0}^{l}\mathbf{N }_{,x}^T(-A_{12}+B_{11})\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{k }_{{\hat{u}}_0w_b}}&=-\int _{0}^{l}\widehat{\mathbf{N }}_{5,x}^TA_{12}\mathbf{H }_{,xx}\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{k }_{{\hat{u}}_0{\hat{w}}_b}}&=-\int _{0}^{l}\widehat{\mathbf{N }}_{5,x}^TA_{12}\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{k }_{{\hat{u}}_0w_s}}&=\int _{0}^{l}\widehat{\mathbf{N }}_{5,x}^T(-A_{12}+B_{11})\mathbf{H }_{,xx}\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{k }_{{\hat{u}}_0{\hat{w}}_s}}&=\int _{0}^{l}\widehat{\mathbf{N }}_{5,x}^T(-A_{12}+B_{11})\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{k }_{w_b{\hat{w}}_b}}&=\frac{1}{2}\int _{0}^{l}\mathbf{H }_{,xx}^TA_{22}\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{k }_{w_bw_s}}&=\int _{0}^{l}\mathbf{H }_{,xx}^T(A_{22}-A_{12})\mathbf{H }_{,xx}\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{k }_{w_b{\hat{w}}_s}}&=\int _{0}^{l}\mathbf{H }_{,xx}^T(A_{22}-A_{12})\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{k }_{{\hat{w}}_bw_s}}&=\int _{0}^{l}\widehat{\mathbf{H }}_{7,xx}^T(A_{22}-A_{12})\mathbf{H }_{,xx}\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{k }_{{\hat{w}}_b{\hat{w}}_s}}&=\int _{0}^{l}\widehat{\mathbf{H }}_{7,xx}^T(A_{22}-A_{12})\widehat{\mathbf{H }}_{7,xx}\mathrm{d}x,\\ \mathbf{k }_{w_s{\hat{w}}_s}&=\frac{1}{2}\int _{0}^{l}\Big [\mathbf{H }_{,xx}^T(A_{22}-2B_{12}+B_{22})\widehat{\mathbf{H }}_{7,xx}+\mathbf{H }_{,x}^TD_{11}\widehat{\mathbf{H }}_{7,x}\Big ]\mathrm{d}x\\ \end{aligned} \end{aligned}$$

(34)

Similarly, the kinetic energy ${\mathcal {T}}$ in Eq (15) can also be written in the following matrix form as

$$\begin{aligned} {\mathcal {T}}=\frac{1}{2}\sum _{i=1}^{nele}\dot{\mathbf{d }}_i^T\,\mathbf{m }_i\, \dot{\mathbf{d }}_i \end{aligned}$$

(35)

with the element mass matrix of the beam $\mathbf{m }$ can be written in sub-matrices as

$$\begin{aligned} \underset{22\times 22}{\mathbf{m }} = \begin{bmatrix} \mathbf{m }_{u_0u_0}&{}\mathbf{m }_{u_0{\hat{u}}_0}&{}\mathbf{m }_{u_0w_b}&{}\mathbf{m }_{u_0{\hat{w}}_b}&{}\mathbf{m }_{u_0w_s}&{}\mathbf{m }_{u_0{\hat{w}}_s}\\ \mathbf{m }_{u_0{\hat{u}}_0}^T&{}\mathbf{m }_{{\hat{u}}_0{\hat{u}}_0}&{}\mathbf{m }_{{\hat{u}}_0w_b}&{}\mathbf{m }_{{\hat{u}}_0{\hat{w}}_b}&{}\mathbf{m }_{{\hat{u}}_0w_s}&{}\mathbf{m }_{{\hat{u}}_0{\hat{w}}_s}\\ \mathbf{m }_{u_0w_b}^T&{}\mathbf{m }_{{\hat{u}}_0w_b}^T&{}\mathbf{m }_{w_bw_b}&{}\mathbf{m }_{w_b{\hat{w}}_b}&{}\mathbf{m }_{w_bw_s}&{}\mathbf{m }_{w_b{\hat{w}}_s}\\ \mathbf{m }_{u_0{\hat{w}}_b}^T&{}\mathbf{m }_{{\hat{u}}_0{\hat{w}}_b}^T&{}\mathbf{m }_{w_b{\hat{w}}_b}^T&{}\mathbf{m }_{{\hat{w}}_b{\hat{w}}_b}&{}\mathbf{m }_{{\hat{w}}_bw_s}&{}\mathbf{m }_{{\hat{w}}_b{\hat{w}}_s}\\ \mathbf{k }_{u_0w_s}^T&{}\mathbf{m }_{{\hat{u}}_0w_s}^T&{}\mathbf{m }_{w_bw_s}^T&{}\mathbf{m }_{{\hat{w}}_bw_s}^T&{}\mathbf{m }_{w_sw_s}&{}\mathbf{m }_{w_s{\hat{w}}_s}\\ \mathbf{m }_{u_0{\hat{w}}_s}^T&{}\mathbf{m }_{{\hat{u}}_0{\hat{w}}_s}^T&{}\mathbf{m }_{w_b{\hat{w}}_s}^T&{}\mathbf{m }_{{\hat{w}}_b{\hat{w}}_s}^T&{}\mathbf{m }_{w_s{\hat{w}}_s}^T&{}\mathbf{m }_{{\hat{w}}_s{\hat{w}}_s}\\ \end{bmatrix} \end{aligned}$$

(36)

in which

$$\begin{aligned} \begin{aligned} \underset{2 \times 2}{\mathbf{m }_{u_0u_0}}&=\int _{0}^{l} \mathbf{N }^TI_{11}\mathbf{N }\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{m }_{w_bw_b}}&=\int _{0}^{l}\Big (\mathbf{H }^TI_{11}\mathbf{H } + \mathbf{H }_{,x}^TI_{22}\mathbf{H }_{,x}\Big )\mathrm{d}x\\ \underset{4 \times 4}{\mathbf{m }_{{\hat{u}}_0{\hat{u}}_0}}&=\int _{0}^{l}\widehat{\mathbf{N }}_5^TI_{11}\widehat{\mathbf{N }}_5\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{m }_{{\hat{w}}_b{\hat{w}}_b}}&=\int _{0}^{l}\Big (\widehat{\mathbf{H }}_7^TI_{11}\widehat{\mathbf{H }}_7+ \widehat{\mathbf{H }}_{7,x}^TI_{22}\widehat{\mathbf{H }}_{7,x} \Big )\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{w_sw_s}}&=\int _{0}^{l}\Big [\mathbf{H }^TI_{11}\mathbf{H } + \mathbf{H }_{,x}^T(I_{22}-2J_{12}+J_{22})\mathbf{H }_{,x}\Big ]\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{m }_{{\hat{w}}_s{\hat{w}}_s}}&=\int _{0}^{l}\Big [\widehat{\mathbf{H }}_7^TI_{11}\widehat{\mathbf{H }}_7+ \widehat{\mathbf{H }}_{7,x}^T(I_{22}-2J_{12}+J_{22})\widehat{\mathbf{H }}_{7,x} \Big ]\mathrm{d}x,\\ \end{aligned} \end{aligned}$$

(37)

and

$$\begin{aligned} \begin{aligned} \underset{2 \times 4}{\mathbf{m }_{u_0{\hat{u}}_0}}&=\int _{0}^{l} \mathbf{N }^TI_{11}\widehat{\mathbf{N }}_5\mathrm{d}, \\ \underset{2 \times 4}{\mathbf{m }_{u_0w_b}}&=-\int _{0}^{l}\mathbf{N }^TI_{12}\mathbf{H }_{,x}\mathrm{d}x,\\ \underset{2 \times 4}{\mathbf{m }_{u_0{\hat{w}}_b}}&=-\int _{0}^{l}\mathbf{N }^TI_{12}\widehat{\mathbf{H }}_{7,x}dx, \\ \underset{2 \times 4}{\mathbf{m }_{u_0w_s}}&=\int _{0}^{l}\mathbf{N }^T(-I_{12}+J_{11})\mathbf{H }_{,x}\mathrm{d}x,\\ \underset{2 \times 4}{\mathbf{m }_{u_0{\hat{w}}_s}}&=\int _{0}^{l}\mathbf{N }^T(-I_{12}+J_{11})\widehat{\mathbf{H }}_{7,x}\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{m }_{{\hat{u}}_0w_b}}&=-\int _{0}^{l}\widehat{\mathbf{N }}_5^TI_{12}\mathbf{H }_{,x}\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{{\hat{u}}_0{\hat{w}}_b}}&=-\int _{0}^{l}\widehat{\mathbf{N }}_5^TI_{12}\widehat{\mathbf{H }}_{7,x}\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{m }_{{\hat{u}}_0w_s}}&=\int _{0}^{l}\widehat{\mathbf{N }}_5^T(-I_{12}+J_{11})\mathbf{H }_{,x}\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{{\hat{u}}_0{\hat{w}}_s}}&=\int _{0}^{l}\widehat{\mathbf{N }}_5^T(-I_{12}+J_{11})\widehat{\mathbf{H }}_{7,x}\mathrm{d}x, \\ \underset{4 \times 4}{\mathbf{m }_{w_b{\hat{w}}_b}}&=\int _{0}^{l}\Big (\mathbf{H }^TI_{11}\widehat{\mathbf{H }}_7 + \mathbf{H }_{,x}^TI_{22}\widehat{\mathbf{H }}_{7,x} \Big )\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{w_bw_s}}&=\int _{0}^{l}\Big [\mathbf{H }^TI_{11}\mathbf{H } + \mathbf{H }_{,x}^T(I_{22}-J_{12})\mathbf{H }_{,x} \Big ]\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{w_b{\hat{w}}_s}}&=\int _{0}^{l}\Big [\mathbf{H }^TI_{11}\widehat{\mathbf{H }}_7 + \mathbf{H }_{,x}^T(I_{22}-J_{12})\widehat{\mathbf{H }}_{7,x} \Big ]\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{{\hat{w}}_bw_s}}&=\int _{0}^{l}\Big [\widehat{\mathbf{H }}_7^TI_{11}\mathbf{H } + \widehat{\mathbf{H }}_{7,x}^T(I_{22}-J_{12})\mathbf{H }_{,x}\Big ]\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{{\hat{w}}_b{\hat{w}}_s}}&=\int _{0}^{l}\Big [\widehat{\mathbf{H }}_7^TI_{11}\widehat{\mathbf{H }}_7 + \widehat{\mathbf{H }}_{7,x}^T(I_{22}-J_{12})\widehat{\mathbf{H }}_{7,x}\Big ]\mathrm{d}x,\\ \underset{4 \times 4}{\mathbf{m }_{w_s{\hat{w}}_s}}&=\int _{0}^{l}\Big [\mathbf{H }^TI_{11}\widehat{\mathbf{H }}_7 + \mathbf{H }_{,x}^T(I_{22}-2J_{12}+J_{22})\widehat{\mathbf{H }}_{7,x} \Big ]\mathrm{d}x,\\ \end{aligned} \end{aligned}$$

(38)

Gauss quadrature with eight points in both the element length and thickness is used herein to evaluate the integrals in Eqs. (33), (34), (37) and (38). More points have been used, but no improvement in the numerical results was observed.

3.3 Moving mass matrices and load vector

The element mass, damping, stiffness matrices and the load vector resulted from the moving mass are given in this subsection. By substituting Eq. (26) into Eq. (17), one can write the potential energy of the moving mass in the form

$$\begin{aligned} {\mathcal {V}}=\sum _{i=1}^{nele}\Big (\ddot{\mathbf{d}}^T_i\, \mathbf{m }_{m_i}\ddot{\mathbf{d }}_i + \dot{\mathbf{d}}^T_i \mathbf{c }_{m_i}\dot{\mathbf{d }}_i + \mathbf{d }^T_i\mathbf{k }_{m_i}\mathbf{d }_i-\mathbf{d }^T_i\mathbf{f }_{m_i}\Big ) \end{aligned}$$

(39)

where $\mathbf{m }_m$, $\mathbf{c }_m$ and $\mathbf{k }_m$ are, respectively, the element mass, damping and stiffness matrices due to the effects of the inertia, Coriolis and the centrifugal forces of the moving mass; $\mathbf{f }_m$ is the time-dependent element nodal load vector generated by the moving mass. The expressions for $\mathbf{m }_m$, $\mathbf{c }_m$, $\mathbf{k }_m$ and $\mathbf{f }_m$ are, respectively, given by Eqs. (40), (41), (42) and (43) in the below.

$$\begin{aligned} \underset{22 \times 22}{\mathbf{m }_m} =m \begin{bmatrix} \mathbf{N }^T\mathbf{N } &{}\mathbf{N }^T\widehat{\mathbf{N }}_5 &{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 } \\ \widehat{\mathbf{N }}_5^T\mathbf{N } &{}\widehat{\mathbf{N }}_5^T\widehat{\mathbf{N }}_5 &{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 } \\ \mathbf{0 }&{}\mathbf{0 } &{}\mathbf{H }^T\mathbf{H } &{}\mathbf{H }^T\widehat{\mathbf{H }}_7&{}\mathbf{H }^T\mathbf{H } &{}\mathbf{H }^T\widehat{\mathbf{H }}_7 \\ \mathbf{0 }&{}\mathbf{0 } &{}\widehat{\mathbf{H }}_7^T\mathbf{H } &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_7&{}\widehat{\mathbf{H }}_7^T\mathbf{H } &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_7 \\ \mathbf{0 }&{}\mathbf{0 } &{}\mathbf{H }^T\mathbf{H } &{}\mathbf{H }^T\widehat{\mathbf{H }}_7&{}\mathbf{H }^T\mathbf{H } &{}\mathbf{H }^T\widehat{\mathbf{H }}_7 \\ \mathbf{0 }&{}\mathbf{0 } &{}\widehat{\mathbf{H }}_7^T\mathbf{H } &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_7&{}\widehat{\mathbf{H }}_7^T\mathbf{H } &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_7 \\ \end{bmatrix} _{x_e} , \end{aligned}$$

(40)

$$\begin{aligned} \underset{22 \times 22}{\mathbf{c }_m} =2mv \begin{bmatrix} \mathbf{0 } &{}\mathbf{0 } &{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 } \\ \mathbf{0 } &{}\mathbf{0 } &{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 } \\ \mathbf{0 }&{}\mathbf{0 } &{}\mathbf{H }^T\mathbf{H }_{,x} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,x}&{}\mathbf{H }^T\mathbf{H }_{,x} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,x} \\ \mathbf{0 }&{}\mathbf{0 } &{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,x} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,x}&{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,x} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,x} \\ \mathbf{0 }&{}\mathbf{0 } &{}\mathbf{H }^T\mathbf{H }_{,x} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,x}&{}\mathbf{H }^T\mathbf{H }_{,x} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,x} \\ \mathbf{0 }&{}\mathbf{0 } &{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,x} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,x}&{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,x} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,x} \\ \end{bmatrix} _{x_e} , \end{aligned}$$

(41)

$$\begin{aligned} \underset{22 \times 22}{\mathbf{k }_m} =mv^2 \begin{bmatrix} \mathbf{0 } &{}\mathbf{0 } &{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 } \\ \mathbf{0 } &{}\mathbf{0 } &{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 }&{}\mathbf{0 } \\ \mathbf{0 }&{}\mathbf{0 } &{}\mathbf{H }^T\mathbf{H }_{,xx} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,xx}&{}\mathbf{H }^T\mathbf{H }_{,xx} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,xx} \\ \mathbf{0 }&{}\mathbf{0 } &{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,xx} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,xx}&{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,xx} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,xx} \\ \mathbf{0 }&{}\mathbf{0 } &{}\mathbf{H }^T\mathbf{H }_{,xx} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,xx}&{}\mathbf{H }^T\mathbf{H }_{,xx} &{}\mathbf{H }^T\widehat{\mathbf{H }}_{7,xx} \\ \mathbf{0 }&{}\mathbf{0 } &{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,xx} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,xx}&{}\widehat{\mathbf{H }}_7^T\mathbf{H }_{,xx} &{}\widehat{\mathbf{H }}_7^T\widehat{\mathbf{H }}_{7,xx} \\ \end{bmatrix} _{x_e} , \end{aligned}$$

(42)

and

$$\begin{aligned} \underset{22 \times 1}{\mathbf{f }_m} =mg \begin{bmatrix} \mathbf{0 }&{}\mathbf{0 }&{}\mathbf{H }^T&{}\widehat{\mathbf{H }}_7^T&{}\mathbf{H }^T&{}\widehat{\mathbf{H }}_7^T \\ \end{bmatrix}^T_{x_e} \end{aligned}$$

(43)

The notation $[.]_{x_e}$ in the above equations means that the expression [.] is evaluated at $x_e$ - the current abscissa of the moving mass with respect to the left node of the element. Noting that except for the element under the moving mass, the element matrices $\mathbf{m }_m$, $\mathbf{c }_m$, $\mathbf{k }_m$ and the force vector $\mathbf{f }_m$ are zeros for all other elements.

3.4 Discrete equation of motion

The stiffness and mass matrices, as well as the nodal force vector for entire beam are constructed by assembling the derived element matrices and vector to form the equation of motion for the vibration analysis of the beam as

$$\begin{aligned} (\mathbf{M } + \mathbf{M }_m)\ddot{\mathbf{D }} + (\mathbf{C }+\mathbf{C }_m)\dot{\mathbf{D }} + (\mathbf{K } + \mathbf{K }_m)\mathbf{D }=\mathbf{F } \end{aligned}$$

(44)

where $\mathbf{D }$, $\dot{\mathbf{D }}$ and $\ddot{\mathbf{D }}$ are, respectively, the global vectors of nodal displacement, velocity and acceleration; $\mathbf{M }$, $\mathbf{M }_m$, $\mathbf{C }_m$, $\mathbf{K }$, $\mathbf{K }_m$ and $\mathbf{F }$ are, respectively, the global matrices and vector, constructed by assembling the matrices $\mathbf{m }$, $\mathbf{m }_m$, $\mathbf{c }_m$, $\mathbf{k }$, $\mathbf{k }_m$ and $\mathbf{f }$ over the elements, respectively; the global damping matrix $\mathbf{C}$ of a FG beam can be determined by the theory of Rayleigh damping as [35]

$$\begin{aligned} \mathbf{C }=\alpha \mathbf{M } + \beta \mathbf{K } \end{aligned}$$

(45)

where

$$\begin{aligned} \alpha = \dfrac{2\omega _i\omega _j(\xi _i\omega _j-\xi _j\omega _i)}{\omega _j^2-\omega _i^2}, \;\; \beta = \dfrac{2(\xi _j\omega _j-\xi _i\omega _i)}{\omega _j^2-\omega _i^2} \end{aligned}$$

(46)

with $\xi _i$ and $\xi _j$ are the damping ratios corresponding to two natural frequencies of the beam, $\omega _i$ and $\omega _j$. A value of 0.5%, previously used in [42], is adopted for both $\xi _i$ and $\xi _j$ herein.

Equation (44) can be solved by the direct integration Newmark method. The average acceleration method which ensures the unconditional convergence [56] is adopted herein. The detail of the average acceleration method and its implementation are described in Ref. [56].

4 Numerical investigation

Numerical investigation is carried out in this section to validate the formulated beam element and to illustrate the effects of the material gradation and loading parameters on the vibration behaviour of the BFGSW beam. To this end, a simply supported beam with $b=0.5$ m, $h=1$ m and geometric boundary conditions stated in Eq. (20) is employed in the analysis. Various values of the length-to-height ratio L/h are considered. The beam is made from alumina (Al$_2$O$_3$) as M1, zirconia (ZrO$_2$) as M2 and aluminum (Al) as M3. The material data for the constituents are as follows [15, 57]

• $E_1=380$ MGPa, $\rho _1=3960$ kg/m$^3$, $\nu _1=0.3$ for alumina

• $E_2=151$ GPa, $\rho _2=3000$ kg/m$^3$, $\nu _2=0.3$ for zirconia

• $E_3= \; 70$ GPa,  $\rho _3=2702$ kg/m$^3$, $\nu _3=0.3$ for aluminum

The dimensionless parameters, $\mu _i$, $D_\mathrm{d}$ and $r_\mathrm{m}$, are respectively introduced for the natural frequencies, dynamic magnification factor and mass ratio as follows [32, 39]

$$\begin{aligned} \mu _i=\dfrac{\omega _i L^2}{h}\sqrt{\dfrac{\rho _3}{E_3}} , \;\; D_\mathrm{d}=\text {max}\left( \dfrac{w(L/2),t}{w_\text {st}}\right) , \;\; r_\mathrm{m}=\dfrac{m}{\rho _1 AL} \end{aligned}$$

(47)

where $\omega _i$ is the $i\text {th}$ natural frequency, and $w_\text {st}=mgL^3/48E_1I$ is the maximum static deflection of the fully alumina beam under the load mg. A uniform time step $\Delta t=\Delta T/300$ with $\Delta T$ is the total time necessary for the mass crossing the beam is used for the Newmark procedure. Three numbers in parentheses, e.g. (2-1-1), are used below to denote the thickness ratio of the beam layers, from the bottom layer to the top layer.

4.1 Accuracy and convergence studies

The accuracy and convergence of the derived beam element are investigated in this sub-section. To this end, Table 1 lists the fundamental frequency parameters of symmetric (2-1-2) and non-symmetric (2-2-1) beams with $L/h=20$ obtained by the Voigt model and different number of the present enriched beam elements. For comparison purpose, the frequency parameters obtained by 26 Timoshenko beam elements of Ref. [40] are also given in the table. As seen from the table, the convergence of the present enriched element is very fast, and it is capable to give the accurate frequencies by using just one elements, regardless of the layer thickness ratio and the power-law indices. The convergence of the present element in evaluating the frequencies is the same as that of Ref. [48], where the frequencies of the two-phase BFGSW beam can also be obtained by using one enriched third-order shear deformation beam element. The convergence of the derived element in evaluating the dynamic magnification factor $D_\mathrm{d}$ is shown in Table 2, where the dynamic factors of symmetric (2-1-2) and non-symmetric (2-2-1) beams obtained by different number of the elements are given for various power-law indices. The table shows that the dynamic magnification factor $D_\mathrm{d}$ needs eight elements to converges, which is also very fast. It is worthy to mention that the frequency parameter and the dynamic magnification factor respectively require sixteen and twenty non-enriched elements to converge (not shown herein). Regarding the processing time, a desktop with processor Intel quartet core i5-8250U 1.8 GHz and 4GB RAM needs 1.0621 s for the uniform mesh of 8 enriched beam elements to get the factor $D_\mathrm{d}$ of (2-1-2) beam with $n_x=0.5$ and $n_z=1$ in Table 2, while the corresponding time for the mesh of 20 non-enriched elements is 1.2988 s. The processing time of the enriched and non-enriched elements required for the frequency is much more different, namely 0.0961 s for the mesh of one enriched element, and 0.5502 s for the mesh of 18 non-enriched elements. Thus, compared to the non-enriched element, the enriched element is efficient in term of both the element requirement and processing time.

To show the accuracy of the derived beam element in some more further, Table 3 compares the fundamental frequency parameters of a two-phase unidirectional FG sandwich beam obtained by the present element with that of Su et al. [58] using the general Fourier formulation. The two-phase beam in [58] is a special case of the present beam when $n_x=0$ or M2 is identical M3, and in this case the Maxwell formula returns to the original Mori-Tanaka scheme [52, 53]. Very good agreement between the result of the present work with that of Ref. [58] is noted from Table 3, regardless of the micromechanical model and the layer thickness ratio. Table 4 compares the dynamic magnification factors of a two-phase unidirectional FG beam with $L/h=20$, obtained by four elements of the present work with the results using the Ritz-DQ method of Khalili et al. [27], and Song et al. [59]. The table shows good agreement between the dynamic magnification factors of the present work with that of the references, especially Ref. [27], regardless of the moving mass velocity and the power-law index. The result of Ref. [27] is based on the Euler-Bernoulli beam theory, while the Kirchhoff plate theory is employed in Ref. [59], and the differential quadrature method is adopted in both the references in computing the dynamic response of the beam. The small difference between the result of the present work with that of Refs. [27, 59] in Table 4 is resulted from the different theories and methods used in the works. The comparison of the time-histories for mid-span deflection of a two-phase unidirectional FG sandwich beam and a three-phase BFGSW beam under a moving point force obtained herein with the result of Ref. [32] and Ref. [40], as shown in Fig. 3a and b, respectively, also confirms the accuracy of the derived element in evaluating the dynamic response of the sandwich beam. Noting that Figs. 3a and b have been obtained with the beam geometric and material data of Refs. [32] and [40], respectively, and the damping effect was ignored.

4.2 Natural frequencies

The fundamental frequency parameters of the three-phase BFGSW beam with various power-law indices and layer thickness ratios are listed in Tables 5 and 6 for two values of the span-to-height ratio, $L/h=5$ and $L/h=20$, respectively. The frequency parameters are given for both the Voigt model and Maxwell formula. An opposite influence of the axial and transverse indices on the frequency of the beam is seen from the tables. The frequency parameter $\mu _1$ increases with the increase of the axial index $n_x$ and it decreases with increasing the transverse index $n_z$, irrespective of the micromechanical model and the span-to-height ratio. The effect of the layer thickness ratio and the micromechanical model on the frequency parameter can also be observed from the tables. The frequency parameter is higher for the beam associated with a large core thickness, regardless of the span-to-height ratio and the power-law indices. The influence of the power-law indices and the layer thickness ratio on the fundamental frequency can be explained by the change in the percentage of the constituent materials, as stated in Ref. [40]. The micromechanical model also plays an important role on the fundamental frequency, and the frequencies obtained by the Maxwell formula are always lower than that using the Voigt model, regardless of the power-law indices. A careful examination of the table shows that the sensitivity to the change of the power-law indices is different for the frequencies obtained by the Voigt model and the Maxwell formula. For example, the frequency parameter based on the Voigt model of the (2-1-2) beam with $n_x=0.5$ in Table 5 decreases 27.07% by increasing $n_z$ from 0.5 to 5, while the corresponding value of the parameter using the Maxwell formula is just 20.92%. Furthermore, when increase $n_x$ from 0.5 to 5, the frequency parameter using the Voigt model of the (2-1-2) beam with $n_z=1$ in Table 5 increases only 6.92%, while the corresponding value using the Maxwell formula is 13.39%. Thus, the dependence of the frequencies upon the power-law indices is influenced by the micromechanical model. The influence of the material distribution and micromechanical model on the fundamental frequencies of the beam can be seen in some more further from Fig. 4, where the variation of the fundamental frequency parameter of symmetric (1-1-1) and non-symmetric (2-2-1) beams obtained by both the Voigt model and Maxwell formula is depicted for $L/h=10$. The frequency parameter based on the Voigt model, as seen from the figure, is always higher than that obtained by the Maxwell formula, irrespective of the power-law indices and the beam type.

Figure 5 shows the relation between the frequency parameter $\mu _1$ and the span-to-height ratio L/h of symmetric (1-1-1) and non-symmetric (2-2-1) beams. Both the Voigt model and Maxwell formula are used to obtained the curves in the figure. As expected, an increase of the span-to-height ratio results in an increase of the frequency parameter, regardless of the micromechanical model and the beam type. The result in the figure shows the ability of the derived beam element in modelling the shear deformation effect on the frequencies of the BFGSW beam, and this effect is more significant for the beam with $L/h<15$.

The influence of the material distribution on the higher frequencies of the BFGSW beam is illustrated in Fig. 6, where the variation of the first four natural frequency parameters with the power-law indices is depicted for symmetric (1-1-1) and non-symmetric (2-2-1) beams with $L/h=10$. The Maxwell formula was employed to obtain the frequencies in the figure. Similar to the fundamental frequency, the higher frequencies also increase with the increase of the index $n_x$, and they decrease with increasing the index $n_z$. Based on the variation of the natural frequencies upon the power-law indices in Fig. 6, a BFGSW beam with desired frequencies can be designed by choosing appropriate values of the power-law indices $n_x$ and $n_z$.

4.3 Dynamic response

The time histories for mid-span deflection of symmetric (1-1-1) and non-symmetric (2-2-1) beams with $L/h=20$ are given in Fig. 7 for $r_\mathrm{m}=0.5$, $n_x=n_z=0.5$ and various values of the moving mass velocity. The velocity, as seen from the figure, has a significant influence on the way the beam vibrates, and the beam tends to executive more vibration cycles when it is under a moving mass with a lower velocity. For most of the travelling time, the mid-span deflection of the beam obtained by the Voigt model is lower than that using the Maxwell formula. In Fig. 8, the time histories for mid-span deflection of the symmetric (1-1-1) and non-symmetric (2-2-1) beams with $L/h=20$ obtained by both the Voigt model and Maxwell formula are depicted for $n_x=n_z=0.5$, $v=50$ m/s and various values of the moving mass ratio. The mass ratio, as expected, changes the dynamic deflection significantly, and the maximum mid-span deflection of the beams is larger for a higher moving mass ratio. Figures 7 and 8 show an important role of the micromechanical model on the dynamic response of beams. Not only the deflection amplitude but also the time at which the deflection attains the maximum value are significantly influenced by the micromechanical model.

In Table 7, the dynamic magnification factors of the BFGSW beam with $L/h=10$ are given for $r_\mathrm{m}$=0.5, v=50 m/s and various values of the power-law indices and the layer thickness ratio. The dynamic magnification factor in the table increases with the increase of the transverse index $n_z$ and it decreases with increasing the axial index $n_x$, regardless of the layer thickness ratio and the micromechanical model. The influence of the material distribution and the micromechanical model on the dynamic magnification factor can be seen more clearly from Fig. 9, where the variation of the factor $D_\mathrm{d}$ with the indices $n_x$ and $n_z$ of symmetric (1-1-1) and non-symmetric (2-2-1) beams is depicted for $L/h=10$, $r_\mathrm{m}=0.5$ and $v=50$ m/s. The factor $D_\mathrm{d}$ obtained by the Voigt model is always lower than that using the Maxwell formula, regardless of the power-law indices and the beam type. Based on the result in Fig. 9, the beam can be tailored to achieve a desired dynamic magnification factor by appropriately selecting the indices $n_x$ and $n_z$.

The relation between the factor $D_\mathrm{d}$ with the moving velocity v of the BFGSW beam obtained by the two micromechanical models is illustrated in Fig. 10 for two pairs of the power-law indices, $n_x=n_z=0.5$ and $n_x=n_z=5$, of symmetric (1-1-1) and non-symmetric (2-2-1) beams with $L/h=20$. The non-symmetric beam with a larger core thickness contains higher percentage of alumina, and thus it is stiffer than the symmetric beam. This is the reason for the lower dynamic magnification factor of the non-symmetric (2-2-1) beam compared to the symmetric (1-1-1) beam. The factor $D_\mathrm{d}$ obtained by the Voigt model attains the maximum value at a higher velocity than the one does using the Maxwell formula. From the frequencies and the dynamic magnification factors obtained by the two micromechanical models, one can conclude that the Voigt model is more conservative compared to the Maxwell formula. It is worthy to note that while Voigt model is just an arithmetic average, the Maxwell formula treats the matrix and inclusions differently, and thus it describes better the material microstructures of the beam [52, 53]. This leads to the difference between the vibration characteristics obtained by the two homogenization models. The influence of the mass ratio on the dynamic behaviour of the sandwich beam is shown in Fig. 11, where the relation between the factor $D_\mathrm{d}$ with the velocity v of the (1-1-1) and (2-2-1) beams is shown for $L/h=20$, $n_x=n_z=0.5$ and various values of the mass ratio. As expected, for most of the moving mass velocity, dynamic magnification factor is higher when the beam under a larger ratio moving mass.

The effect of the span-to-height ratio on the dynamic response of the BFGSW beam is shown in Fig. 12, where the relation between the dynamic factor $D_\mathrm{d}$ and the moving mass velocity v of symmetric (1-1-1) and non-symmetric (2-2-1) beams is depicted for various values of the ratio L/h and two pairs of the power-law indices, $n_x=n_z=0.3$ and $n_x=n_z=3$. The figure shows an important role of the span-to-height ratio on the relation between the factor $D_\mathrm{d}$ and the velocity v. The velocity at which the factor $D_\mathrm{d}$ attained the maximum value is considerably higher for the beam having a lower ratio L/h, regardless of the power-law-indices and the beam type. In addition, the range of the velocity in which the dynamic magnification factors repeatedly increases and decreases is also wider for the beam with a lower span-to-height ratio.

Finally, the influence of the material distribution and the micromechanical model on the stress distribution of the three-phase BFGSW beam is investigated. To this end, Figs. 13 and 14 respectively show the thickness distribution of the axial and shear stresses of symmetric (1-1-1) and non-symmetric (2-2-1) beams for $L/h=10$, $n_x=0.5$, $r_\mathrm{m}=0.5$, $v=50$ m/s and two values of the transverse index $n_z$, $n_z=0.5$ and $n_z=5$. The stresses in the figures are computed at the time when the moving mass arrives at the mid-span of the beam, and they are normalized as $\sigma _{xx}^*= \sigma _{xx}(L/2,z)/\sigma _0$ and $\tau _{xz}^*= \tau _{xz}(L/2,z)/\sigma _0$, with $\sigma _0=mg/bh$. The influence of the transverse index $n_z$ on the axial stress distribution of both the symmetric and non-symmetric beams is clearly seen from Fig. 13a and b, especially in the two skin layers. It can be seen from Fig. 14 that the computed shear stress vanishes at the bottom and top surfaces of the beam, and this is in agreement with the free transverse shear stress conditions on the surfaces of the sinusoidal theory. The transverse index $n_z$, as seen from Fig. 14, significantly changes the shear stress amplitude, and the maximum shear stress of both the symmetric and non-symmetric beams increases by increasing the index $n_z$. The difference between the stress distribution of the symmetric beam and the non-symmetric beam can be observed from Figs. 13 and 14. The change in the thickness direction of the axial stress in the upper layer of the non-symmetric beam (Fig. 13b) is much more significant compared to that of the symmetric beam (Fig. 13b). The shear stress of the non-symmetric beam (Fig. 14b) is no longer symmetric with respect to the mid-plane as in case of the symmetric beam (Fig. 14a). In addition, the maximum axial and shear stresses obtained by the Maxwell formula are considerably higher than that obtained by the Voigt model.

5 Conclusions

The vibration analysis of a three-phase BFGSW beam with a moving mass using the sinusoidal shear deformation enriched beam element has been presented in this paper for the first time. The beam consists of a homogeneous core and two FG layers with material properties varying in both the longitudinal and transverse directions by the power gradation laws. In addition to the Voigt model, the Maxwell formula were firstly used herein to evaluate effective elastic moduli of the beam. The conventional Lagrange and Hermite interpolations were enriched by the hierarchical functions in derivation of the element stiffness and mass matrices. An extensive numerical investigations have been carried out, and the effects of the beam and loading parameters on vibration behaviour of the beam have been investigated. The difference in the frequencies and dynamic response of the three-phase FGSW beam obtained by the Voigt model and the Maxwell formula is studied this paper for an initial time. The main findings from the numerical results can be summarized as follows:

• The beam element with enrichment interpolation derived in the present work is accurate and efficient in modelling vibration of the BFGSW beam carrying a moving mass. The element can yield accurate frequencies and dynamic response of the beam with a small number of elements.

• The material distribution plays an important role on the vibration behaviour of the beam, and the beam can be tailored to achieve desired vibration characteristics by choosing appropriate power-law indices.

• The micromechanical model has an important role on both the free and forced vibration of the BFGSW beam. The natural frequencies obtained by the Voigt model are always higher than that using the Maxwell formula, while the dynamic magnification factors using the Voigt model are smaller than the corresponding values using the Maxwell formula.

It is worthy to mention that though the numerical investigations are presented in this paper for the simply supported beam only, the beam element derived herein can be used in vibration analysis of BFGSW beams with other boundary conditions as well. In addition, more efforts should be made to take into account influence of some practical factors such as porosities in the beam microstructure and environmental temperature on the vibration of the sandwich beam.