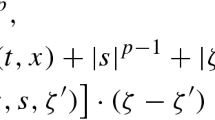Existence and uniqueness of a renormalized solution of parabolic problems in Orlicz spaces

Abstract

In this work, we shall be concerned with the existence and uniqueness result to the nonlinear parabolic equations whose prototype is

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial b( u)}{\partial t} -\varDelta _{M}u - \text{ div } \left( \overline{c}(x,t)\overline{M}^{-1}M\left( \frac{\alpha _{0}}{\lambda }|b(u)|\right) \right) =f &{} \text {in}&{} Q_{T},\\ \displaystyle u(x,t)=0 &{} \text {on} &{} \partial \varOmega \times (0,T),\\ b(u)(t=0)=b(u_{0}) &{} \text {in} &{} \varOmega , \end{array} \right. \end{aligned}$$

where $-\,\varDelta _{M}u{=}-\,\text{ div } ((1+|u|)^{2}Du\frac{\log (e+Du)}{|Du|})$, $\overline{c}\in (L^{\infty }(Q_{T}))^{N}$ and $M(t)= t\log (e+t)$ is an N-function. The data f and $b(u_{0})$ in $L^{1}(Q_T)$ and $L^{1}(\varOmega )$.

1 Introduction

Let $\varOmega$ be a bounded open set of $\mathbb {R}^N$$(N\ge 2)$, T is a positive real number, and $Q_T=\varOmega \times (0,T)$. Consider the following nonlinear Dirichlet equation:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial b(u)}{\partial t} -\hbox {div}(a(x,t,u,\nabla u))+ \hbox {div}(\varPhi (x,t,u)) = f &{} \text {in} &{} Q_{T},\\ u(x,t)=0 &{} \text {on} &{} \partial \varOmega \times (0,T),\\ b(u)(t=0)=b(u_{0}) &{} \text {in} &{} \varOmega , \end{array}\right. \end{aligned}$$

(1)

where $A(u)=-\hbox {div}(a(x,t,u,\nabla u))$ is a Leary-Lions operator defined on the inhomogeneous Orlicz–Sobolev space $W_{0}^{1,x}L_{M}(Q_{T})$, M is an N-function related to the growth of A(u) (see Assumptions (9)–(11)), and to the growth of the lower order Carathéodory function $\varPhi (x,t,u)$ (see Assumption (12)). $b:\mathbb {R}\longrightarrow \mathbb {R}$ is a strictly increasing $C^1$-function, the second term f in $L^{1}(Q_{T})$.

In the classical Lebesgue spaces $L^{p}(0,T,W^{1,p}_{0}(\varOmega ))$, the notion of renormalized solution of (1) was early introduced by Di-Perna and Lions [14] for the study of Boltzmann equation and Blanchard, Murat and Redwane were adapted it to parabolic equations with $L^{1}$-data in [9, 11] where they treated the existence and uniqueness with b(u) a linear function ($b(u)=u)$ and $a(x,t,u,\nabla u)+ \varPhi (u)$ with $\varPhi \in \mathcal {C}^{\infty }(\mathbb {R})$, $u\in L^{\infty }(0,T,L^{1}(\varOmega ))$ and the source data is a measure $\mu =f-\text{ div }(G)$.

Recently Blanchard et al. [12] have studied Stefan problem the function in the evolution term b is maximal graph on $\mathbb {R}$ and Aberqi et al. [1] where b is a general strictly increasing $\mathcal {C}^{1}(\mathbb {R})$-function.

Another approach to define a suitable generalized solution is that of entropy solution which was introduced in [8] in the elliptic case and by Prignet [26] in the parabolic case.

Aharouch and Bennouna [3] have proved the existence and uniqueness of entropy solutions in the framework of Orlicz-Sobolev spaces $W^{1}_{0}L_{M}(\varOmega )$ assuming the $\triangle _{2}$-condition on the N-function M. Recently, Mukminov [24, 25] proved the uniqueness of renormalized solutions to the Cauchy problem for parabolic equation using Kruzhkovis method of doubling the variable.

In the generalized-Orlicz spaces, the work [5] is a continuation of [3] where Al-Hawmi, Benkirane, Hjiaj and Touzani proved the existence and uniqueness of entropy solution for

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle -\hbox {div}(a(x,u,\nabla u)) = f &{} \text {in} &{} \varOmega ,\\ u(x)=0 &{} \text {on} &{} \partial \varOmega , \end{array}\right. \end{aligned}$$

(2)

where $\varPhi =0$ and $\overline{M}$ satisfy the $\triangle _{2}$-condition. Antontsev and Shmarev [6] proved theorems of existence and uniqueness of weak solutions of Dirichlet problem for a class of nonlinear parabolic equations with nonstandard anisotropic growth conditions in the variable exponent Lebesgue spaces. Equations of this class generalize the evolution p(x, t)-Laplacian of the type

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t} - \sum _{i}\frac{\partial }{\partial x_{i}}[a_{i}(x,t,u)|D_{i}u|^{p_{i}(x,t)-2}D_{i}u+ b_{i}(x,t,u)] = 0 &{} \quad \text {in} \ Q_{T},\\ u(x,t)=0 &{} \quad \text {on} \ \partial \varOmega \times (0,T),\\ u(x,0)=u_{0}(x) &{} \quad \text {in} \ \varOmega . \end{array}\right. \end{aligned}$$

(3)

The study of the problem in the framework of renormalized solutions is motivated by the lack of regularity of the distributional formulation (it’s not enough to assure the uniqueness, for more detail see [26] and the counterexample in [29]).

Our novelty in the present paper is to give an existence and uniqueness result of renormalized solution of (1) in the general framework of inohomogeneous Orlicz spaces with a lower order term $\varPhi$ which depends on x, t and u, that is with $a(x,t,u,\nabla u)$ replaced by $a(x,t,u,\nabla u)+\varPhi (x,t,u)$. The difficulty encountered during the proof of the existence of the solution is that the term $\varPhi$ does not satisfy the coercivity condition. Nonlinearities are characterized by N-functions M, for which $\triangle _{2}$-conditions are not imposed, losing the reflexivity of the spaces $L_{M}(Q_{T})$ and $W_{0}^{1}L_{M}(Q_{T})$.

In the literature up to our knowledge there is no result on the uniqueness of the operator $a(x,t,u,\nabla u)+\varPhi (x,t,u)$ in the framework of Orlicz spaces. So the crucial question that we will focus in this paper is to impose appropriate conditions on each term of problem (1) in order to obtain a uniqueness result (see Theorem 3).

This paper is organized as follows. In the Sect. 2, we recall some well-known preliminaries properties and results of Orlicz-Sobolev spaces. Section 3 is devoted to specify the essential assumptions on b, a, $\varPhi$ and f and we introduce the Definition 1 of a renormalized solution of (1) and the existence result given in Theorem 2. In Sect. 4 we prove Theorem 2 and in Sect. 5 we establish the uniqueness result. The proof of Lemma 8 is given in the “Appendix”.

2 N-function and Orlicz spaces

Let $\displaystyle M :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}$  be an N-function, that is, M is continuous, convex, with $M(t) > 0$ for $t > 0$, $\displaystyle M(t)/t \rightarrow 0$ as $t\rightarrow 0$, and $\displaystyle M(t)/t\rightarrow +\infty$ as $t\rightarrow +\infty$. Equivalently, M admits the representation $\displaystyle M(t) =\int _{0}^{t} a(s)ds$, where $a:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}$  is nondecreasing, right continuous, with $a(0) = 0$, $a(t) > 0$ for $t > 0$, and $a(t)\rightarrow +\infty$ as $t\rightarrow +\infty$. The N-function $\overline{M}$ conjugate to M is defined by $\displaystyle \overline{M}(t) =\int _{0}^{t} \overline{a}(s)ds$, where $\displaystyle \overline{a} : {\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}$, is given by $\displaystyle \overline{a}(t) = \sup \{s : a(s) \le t\}$.

We extend these N-functions to even functions on all ${\mathbb {R}}$.

Example 1

For $\displaystyle M(t)=\frac{|t|^{p}}{p}$, $\displaystyle \overline{M}(t)=\frac{|t|^{q}}{q}$ where $\displaystyle \frac{1}{p}+\frac{1}{q}=1$ and $\displaystyle p,q\in (1;+\infty )$.

For $\displaystyle M(t)=\exp (t^{2})-1-|t|$, $\displaystyle \overline{M}(t)=(1+|t|)\ln (1+|t|)-|t|$.

The N-function M is said to satisfy the $\triangle _2$-condition if, for some k,

$$\begin{aligned} M(2t)\le k M(t)\quad \text{ for } \text{ all }\quad t\in \mathbb {R}. \end{aligned}$$

Let P and Q be two N-functions.  $P \ll Q$ means that P grows essentially less rapidly than Q, that is, for each $\displaystyle \epsilon > 0$, $\displaystyle \lim \nolimits _{t\rightarrow +\infty }\frac{P(t)}{Q(\epsilon t)}=0$.

Proposition 1

$P \ll M$ if and only if, for all $\epsilon > 0$ there exists a constant $c_{\epsilon }$ such that,

$$\begin{aligned} P(t) \le M(\epsilon t) +c_{\epsilon },\quad \forall t\ge 0. \end{aligned}$$

(4)

Proof

Let $\epsilon >0$, then by the definition of $P \ll M$, there exists $t_{\epsilon }>0$ such that $\forall t>t_{\epsilon }$,

$$\begin{aligned} P(t)\le M(\epsilon t). \end{aligned}$$

(5)

On the other hand, for $t\in [0,t_{\epsilon }]$, we use the continuity of P and then there exists a constant $C_{\epsilon }$ such that

$$\begin{aligned} P(t)\le C_{\epsilon }, \end{aligned}$$

(6)

where $C_{\epsilon }=\sup _{t\in [0,t_{\epsilon }]}P(t)$. We combine (5) and (6) we conclude (4).

The Orlicz class $K_{M}(\varOmega )$ (resp. the Orlicz space $L_{M}(\varOmega )$)  is defined as the set of (equivalence classes of) real valued measurable functions u on $\varOmega$  such that

$$\begin{aligned} \int _{\varOmega } M(u(x)) dx< +\infty \quad \left( \text{ resp. }\ \int _{\varOmega } M\left( \frac{u(x)}{\lambda }\right) dx < +\infty \quad \text{ for } \text{ some }\quad \lambda > 0\right) . \end{aligned}$$

The set $L_{M}(\varOmega )$  is Banach space under the norm

$$\begin{aligned} \Vert u\Vert _{M,\varOmega }= \inf \{\lambda > 0:\int _{\varOmega } M\left( \frac{u(x)}{\lambda }\right) dx \le 1\}, \end{aligned}$$

and $K_{M}(\varOmega )$ is a convex subset of $L_{M}(\varOmega )$ . The closure in $L_{M}(\varOmega )$  of the set of bounded measurable functions with compact support in $\overline{\varOmega }$  is denoted by $E_{M}(\varOmega )$ . The dual $E_{M}(\varOmega )$  can be identified with $L_{\overline{M}}(\varOmega )$  by means of the duality pairing $\displaystyle \int _{\varOmega }uvdx$ and the dual norm of $L_{\overline{M}}(\varOmega )$  is equivalent to $\Vert u\Vert _{\overline{M},\varOmega }$. We now turn to the Orlicz-Sobolev space, $W^{1}L_{M}(\varOmega )$  [resp. $W^{1}E_{M}(\varOmega )$ ] is the space of all functions u such that u and its distributional derivatives up to order 1 lie in $L_{M}(\varOmega )$  [resp. $E_{M}(\varOmega )$ ]. It is a Banach space under the norm

$$\begin{aligned} \Vert u\Vert _{1,M}=\sum _{|\alpha |\le 1}\Vert D^{\alpha }u\Vert _{M,\varOmega }. \end{aligned}$$

Thus, $W^{1}L_{M}(\varOmega )$  and $W^{1}E_{M}(\varOmega )$  can be identified with subspaces of product of $N + 1$ copies of $L_{M}(\varOmega )$ . Denoting this product by $\varPi L_{M}$  we will use the weak topologies $\sigma (\varPi L_{M},\varPi E_{\overline{M}})$ and $\sigma (\varPi L_{M},\varPi L_{\overline{M}})$. The space $W^{1}_{0}E_{M}(\varOmega )$  is defined as the (norm) closure of the Schwartz space $\mathcal {D}(\varOmega )$ in $W^{1}E_{M}(\varOmega )$  and the space $W^{1}_{0}L_{M}(\varOmega )$  as the $\sigma (\varPi L_{M},\varPi E_{\overline{M}})$ closure of $\mathcal {D}(\varOmega )$ in $W^{1}L_{M}(\varOmega )$ .

Let $W^{-1}L_{\overline{M}}(\varOmega )$  [resp. $W^{-1}E_{\overline{M}}(\varOmega )$ ] denote the space of distributions on $\varOmega$ which can be written as sums of derivatives of order $\le 1$ of functions in $L_{\overline{M}}(\varOmega )$ [resp. $E_{\overline{M}}(\varOmega )$]. It is a Banach space under the usual quotient norm (for more details see [2]). $\square$

We recall the following lemmas:

Theorem 1

(Banach–Alaoglu–Bourbaki [13]) Let E be a Banach space and $E'$ be the dual space.

The closed unit ball $B_{E'}=\{f\in E';\Vert f\Vert \le 1\}$ is compact in the weak-* topology $\sigma (E',E)$.

Lemma 1

(Dominated convergence) Let $f_{k}, f$ in $L_{M}(\varOmega )$.

If $f_{k}\rightarrow f$ a.e. and $|f_{k}|\le |g|$ a.e. and $\displaystyle \int _{\varOmega }M(\lambda |g|)dx<\infty$ for every $\lambda >0$, then $f_{k}\rightarrow f$ in $L_{M}(\varOmega )$.

Lemma 2

(See [19, 22, p. 132]) If a sequence $g_{n}\in L_{M}(\varOmega )$ converges a.e. to g and $g_{n}$ remains bounded in $L_{M}(\varOmega )$, then $g\in L_{M}(\varOmega )$ and $g_{n}\rightarrow g$ in $\sigma (L_{M}, E_{\overline{M}})$.

Lemma 3

Let $F:\mathbb {R}\rightarrow \mathbb {R}$ be uniformly Lipschitzian, with $F(0)=0$. Let $u\in W^{1}L_{M}(\varOmega )$. Then $F(u)\in W^{1}L_{M}(\varOmega )$.

Moreover if the set D of discontinuity points of $F'$ is finite, then

$$\begin{aligned} \frac{\partial }{\partial x_{i}}F(u)=\left\{ \begin{array}{cc} F'(u)\frac{\partial u}{\partial x_{i}} &{} \text{ a.e. } \text{ in }\quad \{x\in \varOmega ; u(x)\not \in D\}\\ 0 &{} \text{ a.e. } \text{ in }\quad \{x\in \varOmega ; u(x)\in D\}. \end{array} \right. \end{aligned}$$

Proof

It is easily adapted from that given in [21] in the case $W^{1}L_{M}(\varOmega )$, by Theorem 1 of [20] instead of Theorem 4 of [20] (see also Remark 5 of [21]). $\square$

Lemma 4

(See [17]) Let $F:\mathbb {R}\rightarrow \mathbb {R}$ be uniformly Lipschitzian, with $F(0)=0$. We suppose that the set of discontinuity points of $F'$ is finite. Let M be an N-function. Then the mapping $F : W^{1}L_{M}(\varOmega )\rightarrow W^{1}L_{M}(\varOmega )$ is sequentially continuous with respect to the weak-* topology $\sigma (\varPi L_{M}, \varPi E_{\overline{M}})$.

Inhomogeneous Orlicz-Sobolev spaces :

Let M be an N-function, for each $\alpha \in \mathbb {N}^{N}$,  denote by $\nabla _{x}^{\alpha }$  the distributional derivative on $Q_{T}$  of order $\alpha$ with respect to the variable $x \in \mathbb {R}^{N}$. The inhomogeneous Orlicz-Sobolev spaces are defined as follows

$$\begin{aligned}&W^{1,x}L_{M}(Q_{T}) =\{u \in L_{M}(Q_{T}):\nabla _{x}^{\alpha }u \in L_{M}(Q_{T}), \ \forall \alpha \in \mathbb {N}^{N} ,\ |\alpha | \le 1 \},\\&W^{1,x}E_{M}(Q_{T}) =\{u \in E_{M}(Q_{T}):\nabla _{x}^{\alpha }u \in E_{M}(Q_{T}), \ \forall \alpha \in \mathbb {N}^{N} , \ |\alpha | \le 1 \}. \end{aligned}$$

The last space is a subspace of the first one, and both are Banach spaces under the norm

$$\begin{aligned} \Vert u\Vert =\sum _{|\alpha |\le 1}\Vert \nabla _{x}^{\alpha }u\Vert _{M,Q_{T}}. \end{aligned}$$

The space $W^{1,x}_{0}E_{M}(Q_{T})$  is defined as the (norm) closure $W^{1,x}E_{M}(Q_{T})$  of $\mathcal {D}(Q_{T})$. We can easily show that when $\varOmega$  has the segment property, then each element u  of the closure of $\mathcal {D}(Q_{T})$  with respect of the weak* topology $\sigma (\varPi L_{M},\varPi E_{\overline{M}})$  is a limit in $W^{1,x}_{0}E_{M}(Q_{T})$,  of some subsequence in $\mathcal {D}(Q_{T})$  for the modular convergence.

This implies that $\displaystyle \overline{ \mathcal {D}(Q_{T}) } ^{\sigma (\varPi L_{M},\varPi E_{\overline{M}})}=\overline{ \mathcal {D}(Q_{T}) } ^{\sigma (\varPi L_{M},\varPi L_{\overline{M}})}.$ This space will be denoted by $\displaystyle W^{1,x}_{0}L_{M}(Q_{T})$ . Furthermore,  $\displaystyle W^{1,x}_{0}E_{M}(Q_{T})=W^{1,x}_{0}L_{M}(Q_{T})\cap \varPi E_{M}$, and the dual space of $W^{1,x}_{0}E_{M}(Q_{T})$ will be denoted by

$$\begin{aligned} W^{-1,x} L_{\overline{M}}(Q_{T})=\bigg \{ f=\sum _{|\alpha |\le 1}\nabla _{x}^{\alpha }f_{\alpha } : \quad f_{\alpha } \in L_{\overline{M}}(Q_{T})\bigg \}. \end{aligned}$$

This space will be equipped with the usual quotient norm $\Vert f\Vert =\inf \sum _{|\alpha |\le 1}\Vert f_{\alpha }\Vert _{\overline{M},Q_{T}}.$

Remark 1

We can easily check, using Lemma 3, that each uniformly Lipschitzian mapping F, with $F(0)=0$, acts in inhomogeneous Orlicz-Sobolev spaces of order 1: $W^{1,x}L_{M}(Q_{T})$ and $W_{0}^{1,x}L_{M}(Q_{T})$.

Lemma 5

(See [15]) For all $u \in W_{0}^{1}L_{M}(Q_{T})$  with $meas(Q_T)<+\infty$ one has

$$\begin{aligned} \int _{Q_{T}}M\left( \frac{|u|}{\lambda }\right) dx dt \le \int _{Q_{T}}M(|\nabla u|)dx dt \end{aligned}$$

(7)

where $\lambda =\text{ diam }(Q_{T})$, is the diameter of $Q_{T}$.

3 Essential assumptions and the existence result

Throughout this paper, we assume that the following assumptions hold true.

Let M  and P be two N-functions  such that $P\ll M$.

$b: \mathbb {R}\rightarrow \mathbb {R}$ is a strictly increasing $\mathcal {C}^{1}(\mathbb {R})$-function, $b(0) = 0$,

$$\begin{aligned} b_{0}<b'(s)<b_{1}, \quad \forall s\in \mathbb {R}\quad \text{ such } \text{ that }\quad b_{1}<\frac{1}{\alpha _{0}}. \end{aligned}$$

(8)

where $\alpha _{0}$ is the constant appearing in (12).

$a:Q_{T}\times \mathbb {R}\times \mathbb {R}^{N} \rightarrow \mathbb {R}^{N}$ is Carathéodory function and there exists a constant $\nu >0$ such that for a.e. $x\in \varOmega$ and for all $s\in \mathbb {R}$, $\xi ,\xi ^{*}\in \mathbb {R}^{N}$, $\xi \ne \xi ^{*}$:

$$\begin{aligned} |a(x,t,s,\xi )|\le \nu (a_0(x,t)+\overline{ M}^{-1}P(|s|)+\overline{ M}^{-1}M(|\xi |)) \end{aligned}$$

(9)

$\quad \text{ with } \quad a_0(.,.)\in E_{\overline{M}}(Q_{T}),$

$$\begin{aligned}&(a(x,t,s,\xi )-a(x,t,s,\xi ^{*}))(\xi -\xi ^{*})>0, \end{aligned}$$

(10)

$$\begin{aligned}&a(x,t,s,\xi ).\xi \ge \alpha M(|\xi |). \end{aligned}$$

(11)

$\varPhi :Q_{T}\times \mathbb {R}\rightarrow \mathbb {R}^{N}$ is a Carathéodory function such that

$$\begin{aligned} |\varPhi (x,t,s)|\le c(x,t)\overline{M}^{-1}M\left( \frac{\alpha _{0}}{\lambda }|b(s)|\right) , \end{aligned}$$

(12)

where $\lambda =\text{ diam }(Q_{T})$, $\Vert c(.,.)\Vert _{L^{\infty }(Q_T)}\le \min (\frac{\alpha }{\alpha _{0}+1};\frac{\alpha }{2(\alpha _{0}b_{1}+1)})$ and $0<\alpha _{0}<1.$

$$\begin{aligned}&\displaystyle f\in L^{1}(Q_{T}), \end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle u_{0}\in L^{1}(\varOmega )\ \text{ such } \text{ that }\ b(u_{0})\in L^{1}(\varOmega ). \end{aligned}$$

(14)

Note that $\langle ,\rangle$ means for either the pairing between $W^{1,x}_{0}L_{M}(Q_{T})\cap L^{\infty }(Q_T)$ and $W^{-1,x}L_{\overline{M}}(Q_{T})+ L^{1}(Q_T)$ or between $W^{1,x}_{0}L_{M}(Q_{T})$ and $W^{-1,x}L_{\overline{M}}(Q_{T})$.

Let $T_{k}$, $k > 0$ denotes the truncation function at level k defined on $\mathbb {R}$ by $T_{k}(r) = \max (-k; \min (k; r))$.

The definition of a renormalized solution of problem (1) can be stated as follows.

Definition 1

A measurable function u defined on $Q_{T}$ is a renormalized solution of problem (1), if it satisfies the following conditions:

$$\begin{aligned}&\displaystyle b(u)\in L^{\infty }(0, T; L^{1}(\varOmega )), \end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle T_{k}(b(u)) \in W_{0}^{1,x}L_{M}(Q_{T}),\quad \forall k>0, \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle \lim _{m\rightarrow +\infty }\int _{\{(x,t)\in Q_{T}:m\le |u|\le m+1\}}a(x,t,u,\nabla u)\nabla udxdt=0, \end{aligned}$$

(17)

and if, for every function $S\in W^{2,\infty }(\mathbb {R})$ which is piecewise $C^{1}$ and such that $S'$ has a compact support, we have in the sense of distributions

$$\begin{aligned}&\frac{\partial S( b(u))}{\partial t}-\text{ div }\Big (S'(b(u))(a(x,t,u,\nabla u)-\varPhi (x,t,u))\Big )\nonumber \\&\quad +S''(b(u))\Big (a(x,t,u,\nabla u)+\varPhi (x,t,u)\Big )= f S'(b(u))\quad \text{ in }\quad \mathcal {D}(Q_{T}), \end{aligned}$$

(18)

$$\begin{aligned}&S(b(u))(t = 0) = S(b(u_{0})) \quad \qquad \text{ in } \quad \varOmega . \end{aligned}$$

(19)

Theorem 2

Assume that (8)–(14) hold true. Then there exists at least one renormalized solution u of the problem (1) in the sense of the definition 1.

4 The stages of the Proof of Theorem 2

Truncated problem.

For each $n>0$, we define the following approximations:

$$\begin{aligned}&\displaystyle b_{n}(s)=b(T_{n}(s)), \ \forall \ s\in \mathbb {R}, \end{aligned}$$

(20)

$$\begin{aligned}&\displaystyle a_{n}(x,t,s,\xi )=a(x,t,T_{n}(s),\xi )\quad \text{ a.e. }\ (x,t)\in Q_T,\ \forall \ s\in \mathbb {R},\ \forall \ \xi \in {\mathbb {R}^{N}}, \end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle \varPhi _{n}(x,t,s) = \varPhi (x,t,T_{n}(s))\quad \text{ a.e. }\ (x,t)\in Q_T,\ \forall \ s\in \mathbb {R}, \end{aligned}$$

(22)

$$\begin{aligned}&\displaystyle \text{ Let }\ f_{n} \ \text{ be } \text{ a } \text{ smooth } \text{ function } \text{ such } \text{ that } \ f_{n} \rightarrow f\ \text{ strongly } \text{ in } \ L^{1}(Q_{T}) \end{aligned}$$

(23)

and

$$\begin{aligned} u_{0 n}\in \mathcal {C}^{\infty }_{0}(\varOmega ) \,\text{ such } \text{ that }\ b_{n}(u_{0 n})\rightarrow b(u_{0})\ \text{ strongly } \text{ in } \ L^{1}(\varOmega ). \end{aligned}$$

(24)

Consider the approximate problem:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial b_{n}(u_{n})}{\partial t} -div(a_{n}(x,t,u_{n},\nabla u_{n}) +\varPhi _{n}(x,t,u_{n})) =f_{n}&{} \text{ in } &{} Q_{T},\\ \displaystyle u_{n}(x,t)=0 &{} \text{ on } &{} \partial \varOmega \times (0,T),\\ \displaystyle b_{n}(u_{n})(t=0)=b_{n}(x,u_{0 n})&{} \text{ in } &{} \varOmega . \end{array} \right. \end{aligned}$$

(25)

Let $u_{n}\in W^{1,x}_{0}L_{M}(Q_{T})$, then for any fixed $n > 0$, there exists at least one solution $u_{n}\in W^{1,x}_{0}L_{M}(Q_{T})$ of (25), (see [23]).

Note that by Lemma 3 and Remark 1, we have $T_{k}(u_{n})\in W^{1,x}_{0}L_{M}(Q_{T})$, and by (8), (11), (12) and Young inequality, the quantity $\displaystyle \int _{Q_{T}} M(|\nabla T_{k}(u_{n})|)dxdt$ is finite for all $k>0$.

Remark 2

The explicit dependence in x and t of the functions a and $\varPhi$ will be omitted so that $a(x, t, u,\nabla u) = a(u,\nabla u)$ and $\varPhi (x, t, u) = \varPhi (u)$.

Step 1: A priori estimates.

Lemma 6

Let $u_{n}$ be a solution of the approximate problem (25), then for all $k>0$, there exists a constant C and for a subsequence, still indexed by n we have

$$\begin{aligned}&\int _{Q_{T}} M(|\nabla T_{k}(u_{n})|)dxdt \le kC, \end{aligned}$$

(26)

$$\begin{aligned}&u_{n}\rightarrow u \ \text{ a.e } \text{ in } \ Q_{T},\ \text{ where } \ u \ \text{ is } \text{ a } \text{ measurable } \text{ function } \text{ on }\ Q_{T}, \end{aligned}$$

(27)

$$\begin{aligned}&b_n(u_{n})\rightarrow b(u) \quad \text{ a.e } \text{ in }\quad Q_{T}, \quad b(u)\in L^{\infty }(0,T,L^{1}(\varOmega )), \end{aligned}$$

(28)

$$\begin{aligned}&a_{n}(T_{k}(u_{n}),\nabla T_{k}(u_{n})) \quad \text{ is } \text{ bounded } \text{ in }\quad (L_{\overline{M}}(Q_{T}))^{N}, \end{aligned}$$

(29)

Proof

Fix $k>0$ and $\tau \in (0,T)$. Let $T_{k}(u_{n})\chi _{(0,\tau )}$ a test function in problem (25). Using the Young inequality we get

$$\begin{aligned}&\displaystyle \int _{\varOmega } B_{n}(u_{n}(\tau ))dx+\int _{Q_{\tau }} a_{n}(u_n,\nabla u_n)\nabla T_{k}(u_{n})dxdt +\int _{Q_{\tau }}\varPhi _{n}(u_{n})\nabla T_{k}(u_{n})dxdt\nonumber \\&\quad \le k[\Vert f_{n}\Vert _{L^{1}(Q_{T})}+\Vert b(u_{0})\Vert _{L^{1}(Q_{T})}], \end{aligned}$$

(30)

where $\displaystyle B_{n}(r)=\int _{0}^{r}\frac{\partial b_{n}(s)}{\partial s} T_{k}(s)ds$.

By definition, we have $\displaystyle \int _{\varOmega } B_{n}(u_{n}(\tau ))dx\ge 0$ and $\displaystyle \int _{\varOmega } B_{n}(u_{n}(0))dx\le kb_{1}\Vert b(u_{0})\Vert _{L^{1}(Q_{T})}$.

By (12), (8) and Young inequality we have

$$\begin{aligned}&\displaystyle \int _{Q_{\tau }} \varPhi _{n}(u_{n})\nabla T_{k}(u_{n})dxdt\le \Vert c(.,.)\Vert _{L^{\infty }(Q_{T})}[\alpha _{0}b_{1}\int _{Q_{\tau }}M(\frac{|T_{k}(u_{n})|}{\lambda })dxdt\\&\quad +\int _{Q_{\tau }}M(|\nabla T_{k}(u_{n})|) dxdt], \end{aligned}$$

thanks to Lemma 5, we obtain

$$\begin{aligned} \displaystyle \int _{Q_{\tau }} \varPhi _{n}(u_{n})\nabla T_{k}(u_{n})dxdt\le \Vert c(.,.)\Vert _{L^{\infty }(Q_{T})}(\alpha _{0}b_{1}+1)\int _{Q_{\tau }}M(|\nabla T_{k}(u_{n})|) dxdt, \end{aligned}$$

return to (30) and using (11) we get

$$\begin{aligned} \int _{Q_{\tau }} a_{n}(u_n,\nabla u_n)\nabla T_{k}(u_{n})dxdt\le & {} \frac{(\alpha _{0}b_{1}+1)}{\alpha }\int _{Q_{\tau }} a_{n}(u_n,\nabla u_n)\nabla T_{k}(u_{n})dxdt\\&+\, k[\Vert f_{n}\Vert _{L^{1}(Q_{T})}+\Vert b(u_{0})\Vert _{L^{1}(Q_{T})}], \end{aligned}$$

thus

$$\begin{aligned} \left[ 1-\frac{(\alpha _{0}b_{1}+1)}{\alpha }\Vert c(.,.)\Vert _{L^{\infty }(Q_{T})}\right] \int _{Q_{T}} a_{n}(u_n,\nabla u_n)\nabla T_{k}(u_{n})dxdt \le kc_{1}. \end{aligned}$$

We take $\displaystyle \frac{1}{c_{2}}=[1-\frac{(\alpha _{0}b_{1}+1)}{\alpha }\Vert c(.,.)\Vert _{L^{\infty }(Q_{T})}]$.

By (12) we have $c_{2}>0$ and we obtain

$$\begin{aligned} \displaystyle \int _{Q_{\tau }}a(u_n,\nabla u_n)\nabla T_{k}(u_{n})dxdt \le kC, \end{aligned}$$

where $C=c_{1}c_{2}.$ And by (11) we have (26).

We conclude that $(T_{k}(u_{n}))$ is bounded in $W^{1,x}_{0}L_{M}(Q_{T})$ independently of n. Since $(E_{\overline{M}}(Q_{T}))'=L_{M}(Q_{T})$ then by Theorem 1, the set $\{(T_{k}(u_{n}))\}$ is compact for the weak topology $\sigma (\varPi L_{M},\varPi E_{\overline{M}})$ so there exists a subsequence still denoted by $u_{n}$ and there exists a measurable function $\xi _{k}$ such that $T_{k}(u_{n})\rightharpoonup \xi _{k}$ for the weak topology $\sigma (\varPi L_{M},\varPi E_{\overline{M}})$.

On the other hand, using Lemma 5, we have

$$\begin{aligned} M\left( \frac{k}{\lambda }\right) \text{ meas }\{|u_{n}|>k\}= & {} \int _{\{|u_{n}|>k\}}M\left( \frac{| T_{k}(u_{n})|}{\lambda }\right) dxdt\\\le & {} \int _{Q_{T}}M(|\nabla T_{k}(u_{n})|)dxdt \le kC, \end{aligned}$$

then $\displaystyle \text{ meas }\{|u_{n}|>k\}\le \frac{ kC}{M(\frac{k}{\lambda })}$ for all n and for all k.

Thus, we get $\displaystyle \lim _{k\rightarrow \infty }\text{ meas }\{|u_{n}|>k\}=0.$$\square$

Proof of (27) and (28): For $k<n$, let $g_{k}\in W^{2,\infty }(\mathbb {R})$, such that $g_{k}'$, has a compact support $\text{ supp } (g_{k}' )\subset [-k,k]$. We multiply the Eq. (25) by $g_{k}'(u_{n})$, to obtain in $\mathcal {D}'(Q_{T})$,

$$\begin{aligned} \frac{\partial B_{g_{k}}^{n}(u_{n})}{\partial t}= & {} div(g_{k}'(u_{n})(a_{n}(u_{n},\nabla u_{n})+\varPhi _{n}(u_{n}))\nonumber \\&- g_{k}''(u_{n})(a_{n}(u_{n},\nabla u_{n})+\varPhi _{n}(u_{n}))\nabla u_{n}+f_{n} g_{k}'(u_{n}) \end{aligned}$$

(31)

where $\displaystyle B_{g_{k}}^{n}(r)=\int ^{r}_{0}g_{k}'(s)\frac{\partial b_{n}(s)}{\partial s}ds$.

Then, we show that

$$\begin{aligned} \Big ( B_{g_{k}}^{n}(u_{n})\Big )\quad \hbox {is bounded in}\quad W^{1,x}_{0}L_{M}(Q_{T}), \end{aligned}$$

(32)

and

$$\begin{aligned} \Big ( \frac{\partial B_{g_{k}}^{n}(u_{n})}{\partial t}\Big )\quad \hbox {is bounded in} \quad L^{1}(Q_{T})+W^{-1,x}L_{\overline{M}}(Q_{T}) \end{aligned}$$

(33)

independently of n.

Indeed, first we have $|\nabla B_{g_{k}}^{n}(u_{n})|\le b_{1}|\nabla T_{k}(u_{n})|\Vert g_{k}'\Vert _{L^{\infty }(\mathbb {R})}$ a.e. in $Q_{T}$, and using (26) we obtain (32). To show that (33) holds true, since $\text{ supp }( g_{k}')$ and $\text{ supp }( g_{k}'')$ are both included in $[-k,k]$, $u_{n}$ may be replaced by $T_{k}(u_{n})$ in each of these terms. As a consequence, each term in the right hand side of (31) is bounded either in $W^{-1,x}L_{\overline{M}}(Q_{T})$ or in $L^{1}(Q_{T})$ which shows that (33) holds true.

Arguing again as in [10] estimates (32), (33) and the following remark, imply that, for a subsequence, still indexed by n,

$$\begin{aligned} u_{n}\rightarrow u \ \text{ a.e } \text{ in } \ Q_{T} \ \text{ and } \ b(u)\in L^{\infty }(0,T,L^{1}(\varOmega )), \end{aligned}$$

where u is a measurable function defined on $Q_{T}$.

Remark 3

For every $g\in W^{2,\infty }(\mathbb {R})$, nondecreasing function such that $\text{ supp }( g') \subset [-k,k]$ and (8), we have

$$\begin{aligned} b_{0}|g(r)-g(r')|\le |B_{g}(r)-B_{g}(r')|\le b_{1}|g(r)-g(r')|\quad \text{ for } \text{ every } \quad \text{ in }\quad \mathbb {R}. \end{aligned}$$

(34)

Proof of (29) : As in [4], we may deduce that $a_{n}(T_{k}(u_{n}),\nabla T_{k}(u_{n}))$ is a bounded sequence in $(L_{\overline{M}}(Q_{T}))^{N}$, and we obtain (29).

Step 2: Almost everywhere convergence of the gradients. In order to show that the gradient converges almost everywhere, we need to prove the next proposition.

Proposition 2

Let $u_{n}$ be a solution of the approximate problem (25), then

$$\begin{aligned}&\lim _{m\rightarrow \infty } \limsup _{n\rightarrow \infty }\int _{\{m\le |u_{n}|\le m+1\}}a(u_{n},\nabla u_{n})\nabla u_{n}dxdt=0, \end{aligned}$$

(35)

$$\begin{aligned}&\lim _{m\rightarrow \infty } \limsup _{n\rightarrow \infty }\int _{\{m\le |u_{n}|\le m+1\}}\varPhi (u_{n})\nabla u_{n}dxdt=0. \end{aligned}$$

(36)

For any $r>0$ and $0<\delta <1$, we have

$$\begin{aligned}&\lim _{n\rightarrow +\infty }\int _{Q_{T}}[(a(T_{k}(u_{n}),\nabla T_{k}(u_{n}))-a(T_{k}(u_{n}),\nabla T_{k}(u)\chi _{\{| \nabla T_{k}(u)|\le k\}})\nonumber \\&\quad \times (\nabla T_{k}(u_{n})-\nabla T_{k}(u)\chi _{\{|\nabla T_{k}(u)|\le k\}})]^{\delta }\,dxdt=0, \end{aligned}$$

(37)

$$\begin{aligned}&\nabla u_{n}\rightarrow \nabla u \quad \text{ a.e. } \text{ in } \quad Q_{T}. \end{aligned}$$

(38)

Proof

Taking $Z_{m}(u_{n})=T_{1}(u_{n}-T_{m}(u_{n}))$ as a test function in the approximate Eq. (25) we get

$$\begin{aligned}&\displaystyle \int _{\{m\le |u_{n}|\le m+1\}} a_{n}(u_{n}, \nabla u_{n})\nabla u_{n}dxdt\le C[\int _{Q_{T}}f_{n}Z_{m}(u_{n})\,dxdt\\&\quad +\int _{\{|u_{0n}|>m\}}|b_{n}(u_{0n})|dxdt, \end{aligned}$$

where $\displaystyle \frac{1}{C}=[1-\frac{(\alpha _{0}b_{1}+1)}{\alpha }\Vert c(.,.)\Vert _{L^{\infty }(Q_{T})}]>0.$

Passing to the limit as $n\rightarrow +\infty$, using the pointwise convergence of $u_{n}$  and strongly convergence in $L^{1}(Q_{T})$  of $f_{n}$  we get

$$\begin{aligned}&\lim _{n\rightarrow +\infty }\displaystyle \int _{\{m\le |u_{n}|\le m+1\}} a_{n}(u_{n}, \nabla u_{n})\nabla u_{n}dxdt\le C[\int _{Q_{T}}fZ_{m}(u)\,dxdt\\&\quad +\int _{\{|u_{0}|>m\}}|b(u_{0})|dxdt. \end{aligned}$$

Owning to Lebesgue’s theorem and passing to the limit as $m\rightarrow +\infty$, in the all terms of the right-hand side, we get (35).

From (11), we deduce also

$$\begin{aligned} \lim _{m\rightarrow +\infty }\lim _{n\rightarrow +\infty }\int _{\{m\le |u_{n}|\le m+1\}}M(|\nabla Z_{m}(u_{n})|)dxdt=0. \end{aligned}$$

(39)

On the other hand, we have

$$\begin{aligned}&\lim _{m\rightarrow +\infty }\lim _{n\rightarrow +\infty }\int _{Q_{T}} \varPhi _{n}(u_{n})\nabla Z_{m}(u_{n})dx dt\le \lim _{m\rightarrow +\infty }\lim _{n\rightarrow +\infty }\int _{Q_{T}}M(|\nabla Z_{m}(u_{n})|)dx dt,\\&\quad +\lim _{m\rightarrow +\infty }\lim _{n\rightarrow +\infty }\int _{\{m \le |u_{n}| \le m+1\}}\overline{M}(|\varPhi _{n}(u_{n})|)dx dt. \end{aligned}$$

Using the pointwise convergence of $u_{n}$  and by Lebegue’s theorem, in the second term of the right side of this last expression, we get

$$\begin{aligned} \lim _{n\rightarrow +\infty }\int _{\{m \le |u_{n}| \le m+1\}}\overline{M}(|\varPhi _{n}(u_{n})|)dx dt=\int _{\{m \le |u| \le m+1\}}\overline{M}(|\varPhi (u)|)dx dt, \end{aligned}$$

and also, by Lebesgue’s theorem

$$\begin{aligned} \lim _{m\rightarrow +\infty } \int _{\{m \le |u| \le m+1\}}\overline{M}(|\varPhi (u)|)dx dt=0. \end{aligned}$$

(40)

Thus with (39) and (40), we get the (36).

The proof of (37) is the same as the corresponding result in [18, 27].

Finally, for the almost everywhere convergence of the gradients we use the following lemma and same techniques as in [4] and [18].

Lemma 7

(See [7]) Under the Assumptions (8)–(14), let $(z_{n})$ be a sequence in $W^{1,x}_{0}L_{M}(Q_{T})$ such that:

$$\begin{aligned}&z_{n}\rightharpoonup z \quad \hbox {for} \quad \sigma (\varPi L_{M},\varPi E_{\overline{M}}), \end{aligned}$$

(41)

$$\begin{aligned}&(a(x, t, z_{n},\nabla z_{n})) \quad \hbox {is bounded in } (L_{\overline{M}}(Q_{T}))^{N}, \end{aligned}$$

(42)

$$\begin{aligned}&\int _{Q_{T}}[a(x,t,z_{n},\nabla z_{n})-a(x,t,z_{n},\nabla z\chi _{s})][\nabla z_{n}-\nabla z\chi _{s}]dxdt \rightarrow 0 \end{aligned}$$

(43)

as n and s tend to $+\infty$, and where $\chi _{s}$ is the characteristic function of

$Q^{s}=\{x\in Q_{T};|\nabla z|\le s\}.$

Then,

$$\begin{aligned}&\nabla z_{n} \rightarrow \nabla z \quad \hbox {a.e. in } Q_{T}, \end{aligned}$$

(44)

$$\begin{aligned}&\lim _{n \rightarrow +\infty }\int _{Q_{T}}a(x,t,z_{n},\nabla z_{n})\nabla z_{n} dxdt= \int _{Q_{T}}a(x,t,z,\nabla z)\nabla z dxdt, \end{aligned}$$

(45)

$$\begin{aligned}&M(|\nabla z_{n}|)\rightarrow M(|\nabla z|) \quad \hbox {in } L^{1}(Q_{T}). \end{aligned}$$

(46)

$\square$

Step 3: We show that u satisfies the conditions of Definition1 For this, let show that (17) holds.

We have for any $m>0,$

$$\begin{aligned} \displaystyle \int _{\{m\le |u_{n}|\le m+1\}}a(u_{n},\nabla u_{n})\nabla u_{n} dxdt= & {} \int _{Q_{T}}a(u_{n},\nabla u_{n})[\nabla T_{m+1}(u_{n})-\nabla T_{m}(u_{n})]dxdt\nonumber \\= & {} \int _{Q_{T}}a(T_{m+1}(u_{n}),\nabla T_{m+1}(u_{n}))\nabla T_{m+1}(u_{n})dxdt\nonumber \\&-\int _{Q_{T}}a(T_{m}(u_{n}),\nabla T_{m}(u_{n}))\nabla T_{m}(u_{n})dxdt. \end{aligned}$$

According to (45), we pass to the limit as n tends to $+\infty$ for fixed $m > 0$ and we obtain

$$\begin{aligned}&\displaystyle \lim _{n\rightarrow +\infty }\int _{\{m\le |u_{n}|\le m+1\}}a(u_{n},\nabla u_{n})\nabla u_{n} dxdt\\&\quad =\int _{Q_{T}}a(T_{m+1}(u),\nabla T_{m+1}(u))\nabla T_{m+1}(u)dxdt\\&\qquad -\int _{Q_{T}}a(T_{m}(u),\nabla T_{m}(u))\nabla T_{m}(u)dxdt\\&\quad =\int _{\{m\le |u|\le m+1\}}a(u,\nabla u)\nabla u dxdt, \end{aligned}$$

with (35), we easily obtain (17).

Similarly we deduce

$$\begin{aligned} \displaystyle \lim _{m\rightarrow +\infty }\int _{\{m\le |u|\le m+1\}}\varPhi (u)\nabla u dxdt=0. \end{aligned}$$

(47)

Let $S\in W^{2,\infty }(\mathbb {R})$ which is a piecewise $C^{1}$-function and such that $S'$ has a compact support, Let $K >0$ such that $\text{ supp } (S')\subset [-K,K]$. Pointwise multiplication of the approximate problem (25) by $S'(u_{n})$, we get

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial S( b(u_{n}))}{\partial t}+\text{ div }\Big (S'(b(u_{n}))(a(x,t,u_{n},\nabla u_{n})-\varPhi (x,t,u_{n}))\Big )\\ \displaystyle +S''(b(u_{n}))\Big (a(x,t,u_{n},\nabla u_{n})-\varPhi (x,t,u_{n})\Big )\nabla b(u_{n})\\ \displaystyle = fS'(b(u_{n})). \end{array} \right. \end{aligned}$$

(48)

Now we will pass to the limit as $n\rightarrow +\infty$ of each term of (48),

• Limit of $\frac{\partial S( b(u_{n}))}{\partial t}$

  since S is bounded, and $S( b(u_{n}))$ converges to S(b(u)) a.e. in $Q_{T}$ and weakly in $L^{\infty }(Q_{T})$, then $\frac{\partial S( b(u_{n}))}{\partial t}$ converges to $\frac{\partial S( b(u))}{\partial t}$ in $\mathcal {D}'(Q_{T})$.

• Limit of $S'(b(u_{n}))a(u_{n},\nabla u_{n})$

  since $\text{ supp } (S')\subset [-K,K]$ and (8) we have

  $$\begin{aligned} S'(b(u_{n}))a(u_{n},\nabla u_{n})=S'(b(u_{n}))a(T_{\frac{k}{b_{0}}}(u_{n}),\nabla T_{\frac{k}{b_{0}}}(u_{n})) \quad \text{ a.e. } \text{ in }\quad Q_{T}. \end{aligned}$$

  Owing to the pointwise convergence of $u_{n}$ to u, the bounded character of $S'$, and by Lemma 7 and Proposition 2, we conclude $a(T_{\frac{k}{b_{0}}}(u_{n}),\nabla T_{\frac{k}{b_{0}}}(u_{n}))$ converges to $a(T_{\frac{k}{b_{0}}}(u_{n}),\nabla T_{\frac{k}{b_{0}}}(u_{n}))$ weakly in $(L_{\overline{M}}(Q_{T}))^{N}$. This allows us to obtain $S'(b(u_{n}))a(T_{\frac{k}{b_{0}}}(u_{n}),\nabla T_{\frac{k}{b_{0}}}(u_{n}))$ converges to

  $S'(b(u))a(T_{\frac{k}{b_{0}}}(u),\nabla T_{\frac{k}{b_{0}}}(u))$ weakly for $\sigma (\varPi L_{\overline{M}} , \varPi E_{M})$, and $S'(b(u))a(T_{\frac{k}{b_{0}}}(u),\nabla T_{\frac{k}{b_{0}}}(u)=S'(b(u))a(u,\nabla u)\quad \text{ a.e. } \text{ in }\quad Q_{T}.$

• Limit of $S''(b(u_{n}))a(u_{n},\nabla u_{n})\nabla b(u_{n})$

  since $\text{ supp } (S')\subset [-K,K]$ and (8), we get

  $S''(b(u_{n}))a(u_{n},\nabla u_{n})\nabla b(u_{n})= S''(b(u_{n}))a(T_{\frac{k}{b_{0}}}(u_{n}),\nabla T_{\frac{k}{b_{0}}}(u_{n}))\nabla b(u_{n})$ a.e. in $Q_{T}$. Owing to the pointwise convergence of $S''(b(u_{n}))$ to $S''(b(u_{n}))$ as n tends to $+\infty$, the bounded character of $S''$ and by Lemma 7 and Proposition 2, we conclude $S''(b(u_{n}))a(T_{\frac{k}{b_{0}}}(u_{n}),\nabla T_{\frac{k}{b_{0}}}(u_{n}))\nabla b(u_{n})\rightharpoonup S''(b(u))a(T_{\frac{k}{b_{0}}}(u),\nabla T_{\frac{k}{b_{0}}}(u))\nabla b(u)$$\text{ weakly } \text{ in }\quad L^{1}(Q_{T})$ as $n\rightarrow +\infty$, and $S''(b(u))a(T_{\frac{k}{b_{0}}}(u),\nabla T_{\frac{k}{b_{0}}}(u))\nabla b(u)=S''(b(u))a(u,\nabla u)\nabla b(u) \quad \text{ a.e. } \text{ in }\quad Q_{T}.$

• Limit of $S'(b(u_{n}))\varPhi (u_{n})$

  since $\text{ supp } (S')\subset [-K,K]$ and (8) we have $S'(b(u_{n}))\varPhi (u_{n})=S'(b(u_{n}))\varPhi (T_{\frac{k}{b_{0}}}(u_{n}))$ a.e. in $Q_{T}.$

  In a similar way, we obtain $S'(b(u_{n}))\varPhi (u_{n})\rightarrow S'(b(u))\varPhi (u)$ weakly for $\sigma (\varPi L_{\overline{M}} , \varPi E_{M}).$

• Limit of $S''(b(u_{n}))\varPhi (x,t,u_{n})\nabla b(u_{n})$

  Also we have

  $$\begin{aligned} S''(b(u_{n}))\varPhi (u_{n})\nabla b(u_{n})=S''(b(u_{n}))\varPhi (T_{\frac{k}{b_{0}}}(u_{n}))\nabla T_{\frac{k}{b_{0}}}(u_{n}) b'(u_{n}) \end{aligned}$$

  using the weakly convergence of truncation, it is possible to prove that,

  $$\begin{aligned} S''(b(u_{n}))\varPhi (u_{n})\nabla b(u_{n})\rightarrow S''(b(u))\varPhi (u)\nabla b(u)\hbox { strongly in }L^{1}(Q_{T}). \end{aligned}$$

• Limit of $f_{n}S'(b(u_{n}))$

  we have $u_{n}\rightarrow u$ a.e. in $Q_{T}$, $S'$ and b are piecewise $C^{1}$. It is enough to use (23) to get that $f_{n}S'(b(u_{n}))\rightarrow fS'(b(u))$ strongly in $L^{1}(Q_{T})$.

Finally, to show (19), remark that S being bounded, $S(b(u_{n}))$ is bounded in $L^{\infty }(Q_{T})$. The Eq. (48) allows to show that $\frac{\partial S( b(u_{n}))}{\partial t}$ is bounded in $W^{-1,x}L_{\overline{M}}(Q_{T})+L^{1}(Q_{T})$. By Lemma 5 in [16] this implies that $S(b(u_{n}))$ lies in a compact set of $C^{0}([0,T];L^{\infty }(\varOmega ))$. It follows that, on one hand, $S(b(u_{n})(t=0))$ converges to $S(b(u)(t=0))$ strongly in $L^{1}(Q_{T})$. On the other hand, the smoothness of S imply that $S(b(u)(t=0))=S(b(u_{0}))$ in $\varOmega$. This complete the proof of the existence result.

Example 2

As an example of equations to which the present result on the existence of renormalized solutions can be applied, we give:

• 1. For $\displaystyle M(t)=\frac{1}{p}|u|^{p}$, $\displaystyle b(u)=|u|^{p-2}u$, $a(x, t, u, \nabla u)=|\nabla u|^{p-2}\nabla u$

  and $\displaystyle \varPhi (x,t,u)=\exp \Big (\frac{\eta }{\Vert x\Vert +t+2}\Big )\beta (\frac{\alpha _{0}}{\lambda })^{\frac{p}{q}} |u|^{\frac{p}{q}}$.

  $$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial b(u)}{\partial t}-\triangle _{M} - \text{ div } \Big (\exp \Big (\frac{\eta }{\Vert x\Vert +t+2}\Big )\beta \Big (\frac{\alpha _{0}}{\lambda }\Big )^{\frac{p}{q}} |u|^{\frac{p}{q}}\Big )=f &{} \text {in} &{} \quad Q_{T},\\ \displaystyle u(x,t)=0 &{} \text {on} &{} \partial \varOmega \times (0,T),\\ \displaystyle b(u(x,0))=b(u_{0})(x) &{} \text {in} &{} \varOmega . \end{array}\right. \end{aligned}$$

• 2. For $\displaystyle -\triangle _{M}=-\text{ div }(\frac{m(|\nabla u|)}{|\nabla u|}.\nabla u)$ where m is the derivative of M, $\displaystyle b(u)=u$ and $\overline{c}\in (L^{\infty }(Q_{T}))^{N}$.

  $$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u}{\partial t}-\triangle _{M} - div (\overline{c}(x,t)\overline{M}^{-1}M(\frac{\alpha _{0}}{\lambda }|b(u)|))=f &{} \text {in} &{} Q_{T},\\ \displaystyle u(x,t)=0 &{} \text {on} &{} \partial \varOmega \times (0,T),\\ \displaystyle u(x,0)=u_{0}(x) &{} \text {in} &{} \varOmega . \end{array}\right. \end{aligned}$$

• 3. For $\displaystyle M(t) = t \log (1 + t)$, $\displaystyle a(x, t, u, \nabla u) =(1 + |u|)^{2}\nabla u \frac{\log (1 + |\nabla u|)}{|\nabla u|}$ and $\overline{c}\in (L^{\infty }(Q_{T}))^{N}$.

  $$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial b(u)}{\partial t}-div(1 + |u|)^{2}\nabla u \frac{log(1 + |\nabla u|)}{|\nabla u|} - \text{ div } (\overline{c}(x,t)\overline{M}^{-1}M(\frac{\alpha _{0}}{\lambda }b(u)))=f \quad \text {in} \quad Q_{T},\\ \displaystyle u(x,t)=0 \qquad \qquad \qquad \quad \text {on} \qquad \partial \varOmega \times (0,T),\\ \displaystyle b(u(x,0))=b(u_{0})(x) \qquad \quad \text {in} \qquad \varOmega . \end{array}\right. \end{aligned}$$

5 Uniqueness result

Before showing the uniqueness of the solution of the problem (1), we will give the following technical lemma.

Let u and v be two renormalized solutions of the problem (1) and let us define for any $0<k<s,$

$$\begin{aligned}&\displaystyle \varGamma (u,v,s,k)=\int _{\begin{array}{l} \{b(s)-k<b(u)<b(s)+k\} \\ \cup \{b(-s)-k<b(u)<b(-s)+k\} \end{array} }\nonumber \\&\quad b'(u)\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt\nonumber \\&\quad +\int _{\begin{array}{ll} \{b(s)-k<b(v)<b(s)+k\} \\ \cup \{b(-s)-k<b(v)<b(-s)+k\} \end{array} }b'(v)\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt.\nonumber \\ \end{aligned}$$

(49)

Lemma 8

Assume that (8)–(14) hold. Then for any $r>0$ we have

$$\begin{aligned} \liminf _{s\rightarrow +\infty }\limsup _{k\rightarrow 0}\frac{1}{k}\varGamma (u,v,s,k)=0. \end{aligned}$$

(50)

Proof

See “Appendix”. $\square$

Theorem 3

Assume that Assumptions (8)–(14) hold true and moreover that for any compact set $D \subset \mathbb {R}$, there exists $L_{D}\in E_{\overline{M}}(Q_{T})$ and $\rho _{D} > 0$ such that $\forall s,\overline{s}\in D,$

$$\begin{aligned}&|a(x,t,s,\xi )-a(x,t,\overline{s},\xi )|\le \Big (L_{D}(x,t)+ \rho _{D}\overline{P}^{-1}P(|\xi |)\Big )|s-\overline{s}|, \end{aligned}$$

(51)

$$\begin{aligned}&|\varPhi (x,t,s)-\varPhi (x,t,\overline{s})|\le L_{D}(x,t)|s-\overline{s}|, \end{aligned}$$

(52)

$$\begin{aligned}&|b'(s)-b'(\overline{s})|\le \beta _{D}|s-\overline{s}|, \end{aligned}$$

(53)

for almost every $(x, t)\in Q_{T}$ and for every $\xi \in \mathbb {R}^{N}$. Then the problem (1) has a unique renormalized solution.

Proof

We define a smooth approximation of $\widetilde{T}_{n}(r)=\min (b(n), \max (r,b(-n)))$ by $\widetilde{T}_{n}^{\sigma }$ where $\widetilde{T}_{n}^{\sigma }(0)=0$ and

$$\begin{aligned} (\widetilde{T}_{n}^{\sigma })'(r)= \left\{ \begin{array}{cc} 0 \qquad \qquad \text{ for } \quad r\ge b(n)+\sigma ,\\ \\ \frac{b(n)+\sigma -r}{\sigma } \qquad \text{ for } \quad b(n)\le r\le b(n)+\sigma ,\\ \\ 1 \quad \qquad \text{ for } \quad b(-n)\le r\le b(n),\\ \\ \frac{r+\sigma -b(-n)}{\sigma } \qquad \text{ for } \quad b(-n)-\sigma \le r\le b(-n),\\ \\ 0 \quad \qquad \text{ for } \quad r\le b(-n)-\sigma . \end{array} \right. \end{aligned}$$

(54)

For a fixed $n>0$, we have for any $z\in L^{1}(Q_{T})$,

$$\begin{aligned} \lim _{\sigma \rightarrow 0} (\widetilde{T}_{n}^{\sigma })'(b(z))=\chi _{\{|z|\le n\}} \quad \text{ a.e. } \text{ in } \quad Q_{T}, \end{aligned}$$

(55)

and

$$\begin{aligned} \lim _{\sigma \rightarrow 0}\widetilde{T}_{n}^{\sigma }(b(z))=\widetilde{T}_{n}(b(z)) \quad \text{ a.e. } \text{ in } \quad Q_{T}. \end{aligned}$$

(56)

Consider now two renormalized solutions u and v of (15)–(18) for the data f and $b(u_{0})$. Since $\widetilde{T}_{n}^{\sigma }\in W^{2,\infty }(\mathbb {R})$ and $supp((\widetilde{T}_{n}^{\sigma })')\subset [b(-n)-\sigma , b(n)+\sigma ]$ , then we take $S=\widetilde{T}_{n}^{\sigma }$ and we use $\frac{1}{k}T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v)))$ as a test function in the difference of equations (18) for u and v, we get

$$\begin{aligned}&\frac{1}{k}\int _{0}^{T}\int _{0}^{t} \left\langle \frac{\partial \left( \widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v)))\right) }{\partial t}; T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v))\right\rangle dsdt\nonumber \\&\quad +I_{1,n}^{\sigma }+I_{2,n}^{\sigma }+I_{3,n}^{\sigma }+I_{4,n}^{\sigma }=I_{5,n}^{\sigma }, \end{aligned}$$

(57)

where

$$\begin{aligned}&I_{1,n}^{\sigma }=\frac{1}{k}\int _{0}^{T}\int _{0}^{t}\int _{\varOmega }\Big [(\widetilde{T}_{n}^{\sigma })'(b(u))a(u,\nabla u)\\&\quad \quad \quad -(\widetilde{T}_{n}^{\sigma })'(b(v))a(v,\nabla v)\Big ]\nabla T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v)))dxdsdt,\\&I_{2,n}^{\sigma }=\frac{1}{k}\int _{0}^{T}\int _{0}^{t}\int _{\varOmega }\Big [(\widetilde{T}_{n}^{\sigma })''(b(u))a(u,\nabla u)\nabla b(u)\\&\quad \quad \quad -(\widetilde{T}_{n}^{\sigma })''(b(v))a(v,\nabla v)\nabla b(v)\Big ] T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v)))dxdsdt,\\&I_{3,n}^{\sigma }=\frac{1}{k}\int _{0}^{T}\int _{0}^{t}\int _{\varOmega }\Big [(\widetilde{T}_{n}^{\sigma })'(b(u))\varPhi (u)-(\widetilde{T}_{n}^{\sigma })'(b(v))\varPhi (v)\Big ]\nabla T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))\\&\quad \quad \quad -\widetilde{T}_{n}^{\sigma }(b(v)))dxdsdt,\\&I_{4,n}^{\sigma }=\frac{1}{k}\int _{0}^{T}\int _{0}^{t}\int _{\varOmega } \Big [(\widetilde{T}_{n}^{\sigma })''(b(u))\varPhi (u)\nabla b(u)\\&\quad \quad \quad -(\widetilde{T}_{n}^{\sigma })''(b(v))\varPhi (v)\nabla b(v)\Big ] T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v)))dxdsdt,\\&I_{5,n}^{\sigma }=\frac{1}{k}\int _{0}^{T}\int _{0}^{t}\int _{\varOmega }f \Big [(\widetilde{T}_{n}^{\sigma })'(b(u))-(\widetilde{T}_{n}^{\sigma })'(b(v)) \Big ] T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))\\&\quad \quad \quad -\widetilde{T}_{n}^{\sigma }(b(v)))dxdsdt, \end{aligned}$$

for any $k>0$, $n>0$, $\sigma >0$.

The following lemma will be useful in the sequel,

Lemma 9

$$\begin{aligned}&\lim _{n\rightarrow +\infty }\lim _{k\rightarrow 0}\lim _{\sigma \rightarrow 0}\frac{1}{k}\int _{0}^{T}\int _{0}^{t}\left\langle \frac{\partial \Big (\widetilde{T}_{n}^{\sigma }(b(u)) -\widetilde{T}_{n}^{\sigma }(b(v))\Big )}{\partial t}; T_{k}(\widetilde{T}_{n}^{\sigma }(b(u)) -\widetilde{T}_{n}^{\sigma }(b(v)))\right\rangle dsdt\nonumber \\&\quad =\int _{Q_{T}}|b(u)-b(v)|dxdt. \end{aligned}$$

(58)

Proof

Notice that

$$\begin{aligned} \widetilde{T}_{n}^{\sigma }(b(u))(t=0)=\widetilde{T}_{n}^{\sigma }(b(v))(t=0)=\widetilde{T}_{n}^{\sigma }(b(u_{0}))\quad \text{ a.e. } \text{ in }\quad \varOmega , \end{aligned}$$

and

$$\begin{aligned}&\frac{1}{k}\int _{0}^{T}\int _{0}^{t}\left\langle \frac{\partial \Big (\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v))\Big )}{\partial t}; T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v))\Big )\right\rangle dsdt\\&\quad =\frac{1}{k}\int _{Q_{T}}\overline{T}_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v)))dxdt, \end{aligned}$$

where $\displaystyle \overline{T}_{k}(r)=\int _{0}^{r}T_{k}(z)dz$.

Passing to the limit we obtain

$$\begin{aligned}&\lim _{k\rightarrow 0}\lim _{\sigma \rightarrow 0}\frac{1}{k}\int _{Q_{T}}\overline{T}_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v)))dxdt\\&\quad =\int _{Q_{T}}|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|dxdt, \end{aligned}$$

and letting $n\rightarrow +\infty$ in this last equality, we deduce (58). $\square$

Now, we analyze the limit of $I_{1,n}^{\sigma }, I_{2,n}^{\sigma }, I_{3,n}^{\sigma }, I_{4,n}^{\sigma }$ and $I_{5,n}^{\sigma }$ one by one.

The limit of$I_{1,n}^{\sigma }$: Notice that

$$\begin{aligned} I_{1,n}^{\sigma }= \frac{1}{k}\int _{0}^{T}\int _{0}^{t}\int _{\varOmega }Q_{n}^{\sigma }dxdsdt=\frac{1}{k}\int _{Q_{T}}(T-t)Q_{n}^{\sigma }dxdt, \end{aligned}$$

where $Q_{n}^{\sigma }=(\widetilde{T}_{n}^{\sigma })'(b(u))a(u,\nabla u)-(\widetilde{T}_{n}^{\sigma })'(b(v))a(v,\nabla v)]\nabla T_{k}(\widetilde{T}_{n}^{\sigma }(b(u))-\widetilde{T}_{n}^{\sigma }(b(v))).$

Since $\displaystyle \text{ supp }( (\widetilde{T}_{n}^{\sigma })')\subset [b(-n)-\sigma , b(n)+\sigma ]$,

then

$$\begin{aligned} \displaystyle (\widetilde{T}_{n}^{\sigma })'(b(u))a(u,\nabla u)=(\widetilde{T}_{n}^{\sigma })'(b(u)) a(T_{n+1}(u),\nabla T_{n+1}(u)) \end{aligned}$$

and

$$\begin{aligned} (\widetilde{T}_{n}^{\sigma })'(b(v))a(v,\nabla v)=(\widetilde{T}_{n}^{\sigma })'(b(u)) a(T_{n+1}(v),\nabla T_{n+1}(v)). \end{aligned}$$

Then by (55), (56) and (54) one has

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle Q_{n}^{\sigma } \quad \text{ converges } \text{ to } \quad [\chi _{\{|u|\le n\}}a(u,\nabla u)-\chi _{\{|v|\le n\}}a(v,\nabla v)]\nabla T_{k}(\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))),\\ \displaystyle |Q_{n}^{\sigma }|\le C_{n}^{2}b_{1}[|a(T_{n+1}(u),\nabla T_{n+1}(u))|+|a(T_{n+1}(v),\nabla T_{n+1}(v))|]\\ \displaystyle \times (|\nabla T_{n+1}(u)| + |\nabla T_{n+1}(v)|)\chi _{\{|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|\le k\}}=R_{n}. \end{array} \right. \end{aligned}$$

where $C_{n}=\max (|b(-n)-\sigma |, b(n)+\sigma ).$

Since $R_{n}\in L^{1}(Q_{T})$ we use the Lebesgue dominated convergence theorem to have

$$\begin{aligned} \displaystyle \lim _{\sigma \rightarrow 0} I_{1,n}^{\sigma }= & {} \lim _{\sigma \rightarrow 0}\frac{1}{k}\int _{Q_{T}}(T-t)Q_{n}^{\sigma }dxdt\nonumber \\ \displaystyle= & {} \frac{1}{k}\int _{Q_{T}}(T-t)[\chi _{\{|u|\le n\}}a(u,\nabla u)\nonumber \\&\quad -\chi _{\{|v|\le n\}}a(v,\nabla v)]\nabla T_{k}(T_{n}(b(u))-T_{n}(b(v)))dxdt\nonumber \\= & {} J_{1}+J_{2}+J_{3}+J_{4}+J_{5}, \end{aligned}$$

(59)

where

$$\begin{aligned} J_{1}= & {} \frac{1}{k}\int _{\{|b(u)-b(v)|\le k, |u|\le n, |v|\le n\}}(T-t)\Big (a(u,\nabla u)-a(u,\nabla v)\Big )(\nabla u- \nabla v)b'(u)dxdt,\\ J_{2}= & {} \frac{1}{k}\int _{\{|b(u)-b(v)|\le k, |u|\le n, |v|\le n\}}(T-t)\Big (a(u,\nabla v)-a(v,\nabla v)\Big )(\nabla u- \nabla v)b'(u)dxdt,\\ J_{3}= & {} \frac{1}{k}\int _{\{|b(u)-b(v)|\le k, |u|\le n, |v|\le n\}}(T-t)\Big (a(u,\nabla u)-a(v,\nabla v)\Big )\nabla v(b'(u)- b'(v))dxdt,\\ \displaystyle J_{4}= & {} \frac{1}{k}\int _{\{|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|\le k, |u|> n, |v|\le n\}}(T-t)a(v,\nabla v)\nabla b(v)dxdt,\\ J_{5}= & {} \frac{1}{k}\int _{\{{|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|\le k, |u|\le n, |v|> n}\}}(T-t)a(u,\nabla u)\nabla b(u)dxdt. \end{aligned}$$

Since $a(u,\nabla u)$ satisfies the condition (11), one has

$$\begin{aligned} J_{1}\ge 0. \end{aligned}$$

(60)

On the other hand by (51) we have

$$\begin{aligned}&|J_{2}|\le \frac{b_{1}}{k}T\int _{Q_{T}}\chi _{\{|b(u)-b(v)|\le k\}, |u|\le n, |v|\le n\}}|u-v|\Big (L_{D}(x,t)+ \rho _{D}\overline{P}^{-1}P(|v|)\Big )\\&\quad \times (|\nabla u|+ |\nabla v|)dxdt. \end{aligned}$$

Using (8), one has $|u-v|\le \frac{1}{b_{0}}|b(u)-b(v)|\le \frac{1}{b_{0}}$, then

$$\begin{aligned} |J_{2}|\le \frac{b_{1}}{b_{0}}T\int _{\{|b(u)-b(v)|\le k\}}\Big (L_{D}(x,t)+ \rho _{D}\overline{P}^{-1}P(|v|)\Big )(|\nabla u|+ |\nabla v|)dxdt. \end{aligned}$$

Since $L_{D}(x,t)\in E_{\overline{M}}(Q_{T})$, u and v in $W^{1,x}L_{M}(Q_{T})$ and using (4), one has $(L_{D}(x,t)+ \rho _{D}\overline{P}^{-1}P(|v|))(|\nabla u|+ |\nabla v|)\in L^{1}(Q_{T})$ and the Lebesgue dominated convergence theorem allows us to conclude that for all $n\ge 1$

$$\begin{aligned} \limsup _{k\rightarrow 0}J_{2}=0. \end{aligned}$$

(61)

We denote by $C_{n}$ the compact subset $[-n-1, n+1]$. Due to (53), there exists a positive number $\beta _{n}$ such that $|b'(r_{1})-b'(r_{2})|\le \beta _{n} |r_{1}-r_{2}|$ for all $r_{1}$ and $r_{2}$ lying in $C_{n}$. Using (8) and Rolle’s theorem, we get

$$\begin{aligned} |b'(r_{1})-b'(r_{2})|\le \frac{\beta _{n}}{b_{0}} |b(r_{1})-b(r_{2})|. \end{aligned}$$

Then $|b'(r_{1})-b'(r_{2})|\le k\frac{\beta _{n}}{b_{0}}$ on $\{|b(u)-b(v)|\le k, |u|\le n, |v|\le n\}$ and we get

$$\begin{aligned}&|J_{3}|\le \frac{\beta _{n}}{b_{0}}T\int _{Q_{T}}\Big (a(T_{n}(u),\nabla T_{n}(u))- a(T_{n}(v),\nabla T_{n}(v))\Big )|\nabla v|\chi _{\{|b(u)-b(v)|\le k, |u|\le n, |v|\le n, u\ne v\}}dxdt. \end{aligned}$$

$$\begin{aligned}&\hbox {Since }\left\{ \begin{array}{ll} \displaystyle \lim _{k\rightarrow 0}\chi _{\{|b(u)-b(v)|\le k, |u|\le n, |v|\le n, u\ne v\}}=0 \quad \text{ a.e. } \text{ in } \quad Q_{T},\\ \displaystyle |a(T_{n}(u),\nabla T_{n}(u))- a(T_{n}(v),\nabla T_{n}(v))||\nabla T_{n}(v)|\in L^{1}(Q_{T}),\qquad \qquad \qquad \qquad \qquad \end{array} \right. \end{aligned}$$

we use the Lebesgue dominated convergence theorem to conclude that, for all $n\ge 1,$

$$\begin{aligned} \lim _{k\rightarrow 0}J_{3}=0. \end{aligned}$$

(62)

In view of the definition of $\widetilde{T}_{n}$, we have

$$\begin{aligned} J_{4}=\frac{1}{k}\int _{\begin{array}{l} \{b(n)-k\le b(v)\le b(n)\} \\ \cup \{b(-n)\le b(v)\le b(-n)+k\} \end{array} }(T-t)a(v,\nabla v)\nabla b(v)dxdt, \end{aligned}$$

and using (11) we deduce

$$\begin{aligned} \liminf _{n\rightarrow +\infty }\limsup _{k\rightarrow 0}J_{4}\ge 0. \end{aligned}$$

(63)

Similarly we have

$$\begin{aligned} J_{5}=\frac{1}{k}\int _{\begin{array}{l} \{b(n)-k\le b(u)\le b(n) \}\\ \cup \{b(-n)\le b(u)\le b(-n)+k\} \end{array} }(T-t)a(u,\nabla u)\nabla b(u)dxdt, \end{aligned}$$

and

$$\begin{aligned} \liminf _{n\rightarrow +\infty }\limsup _{k\rightarrow 0}J_{5}\ge 0. \end{aligned}$$

(64)

Now from (59)–(64) we obtain

$$\begin{aligned} \liminf _{n\rightarrow +\infty }\limsup _{k\rightarrow 0}\lim _{\sigma \rightarrow 0}I_{1,n}^{\sigma }\ge 0. \end{aligned}$$

(65)

The limit of$I_{2,n}^{\sigma }$and$I_{4,n}^{\sigma }$ : Now we claim that

$$\begin{aligned} |I_{2,n}^{\sigma }|+|I_{4,n}^{\sigma }|\le \frac{T}{\sigma }\varGamma (u,v,n,\sigma ). \end{aligned}$$

(66)

From a simple derivation of the function $(\widetilde{T}_{n}^{\sigma })'$ it yields that for any $\sigma >0$ and $k>0$

$$\begin{aligned} |I_{2,n}^{\sigma }|\le & {} \frac{T}{\sigma }\int _{\begin{array}{l} \{b(n)-\sigma \le b(u)\le b(n)\} \\ \cup \{b(-n)\le b(u)\le b(-n)+\sigma \} \end{array}}a(u,\nabla u))\nabla b(u)dxdt\nonumber \\&+\frac{T}{\sigma }\int _{\begin{array}{l} \{b(n)-\sigma \le b(v)\le b(n)\} \\ \cup \{b(-n)\le b(v)\le b(-n)+\sigma \} \end{array}}a(v,\nabla v))\nabla b(v)dxdt. \end{aligned}$$

(67)

Similarly we have

$$\begin{aligned} |I_{4,n}^{\sigma }|\le & {} \frac{T}{\sigma }\int _{\begin{array}{l} \{b(n)-\sigma \le b(u)\le b(n)\} \\ \cup \{b(-n)\le b(u)\le b(-n)+\sigma \} \end{array}}\varPhi (u)\nabla b(u)dxdt\nonumber \\&+\frac{T}{\sigma }\int _{\begin{array}{l} \{b(n)-\sigma \le b(v)\le b(n)\} \\ \cup \{b(-n)\le b(v)\le b(-n)+\sigma \} \end{array}}\varPhi ( v)\nabla b(v)dxdt. \end{aligned}$$

(68)

By combining (67) and (68) we readily deduce (66).

The limit of$I_{3,n}^{\sigma }$: There we prove that

$$\begin{aligned} \limsup _{\sigma \rightarrow 0}|I_{3,n}^{\sigma }|\le \frac{T}{k}\varGamma (u,v,n,k)+\epsilon (k), \end{aligned}$$

(69)

where $\epsilon (k)$ is a positive function such that $\lim _{k\rightarrow 0}\epsilon (k)=0.$

For $n\ge 0$ we have

$$\begin{aligned} \limsup _{\sigma \rightarrow 0}|I_{3,n}^{\sigma }|= & {} \left| \frac{1}{k}\int _{Q_{T}}(T-t)(\chi _{\{|u|\le n\}}\varPhi (u)\right. \\&\left. -\chi _{\{|v|\le n\}}\varPhi (v))\nabla T_{k}(\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v)))dxdt\right| .\\\le & {} K_{1}+K_{2}+K_{3}, \end{aligned}$$

where

$$\begin{aligned} K_{1}= & {} \frac{T}{k}\int _{Q_{T}}\chi _{\{|u|\le n, |v|> n \}}|\varPhi (u)||\nabla T_{k}(\widetilde{T}_{n}(b(u))-b(n. \text{ sgn }(v))|dxdt,\\ K_{2}= & {} \frac{T}{k}\int _{Q_{T}}\chi _{\{|u|> n, |v|\le n\}}|\varPhi (v)||\nabla T_{k}(\widetilde{T}_{n}(b(v))-b(n. \text{ sgn }(u))|dxdt,\\ K_{3}= & {} \frac{T}{k}\int _{Q_{T}}\chi _{\{|u|\le n, |v|\le n \}}|\varPhi (u)-\varPhi (v)||\nabla T_{k}(\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v)))|dxdt. \end{aligned}$$

We estimate $K_{1}$ and $K_{2}$ by (12) we have

$$\begin{aligned} K_{1}\le & {} \frac{T}{k}\int _{Q_{T}}\chi _{\{|u|\le n, |v|> n \}}\chi _{\{|b(u)-b(n. \text{ sgn }(v))|\le k\}}|\varPhi (u)||\nabla b(u)|dxdt\nonumber \\\le & {} \frac{T}{k}\int _{\begin{array}{l} \{b(n)-k\le b(u)\le b(n)\} \\ \cup \{b(-n)\le b(u)\le b(-n)+k\} \end{array}}|\varPhi (u)||\nabla b(u)|dxdt, \end{aligned}$$

(70)

and similarly

$$\begin{aligned} K_{2}\le \frac{T}{k}\int _{\begin{array}{l} \{b(n)-k\le b(v)\le b(n)\} \\ \cup \{b(-n)\le b(v)\le b(-n)+k\} \end{array}}|\varPhi (v)||\nabla b(v)|dxdt. \end{aligned}$$

(71)

On the other hand, by (53) one have since $L_{D}\in L_{\overline{M}}(Q_{T}),$

$$\begin{aligned} K_{3}\le \frac{T}{k}\int _{\{|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|\le k \}\cap \{|u|\le n, |v|\le n \}}L_{D}(x,t)|u-v||\nabla T_{k}(\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v)))|dxdt \end{aligned}$$

by (8) we obtain

$$\begin{aligned} K_{3}\le & {} \frac{T}{k}\int _{\{|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|\le k \}\cap \{|u|\le n, |v|\le n \}}\\&\frac{1}{b_{0}}L_{D}(x,t)|b(u)-b(v)||\nabla T_{k}(\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v)))|dxdt\\= & {} \frac{T}{k}\int _{\{|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|\le k \}\cap \{|u|\le n, |v|\le n \}}\\&\frac{T}{b_{0}}L_{D}(x,t)|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))||\nabla T_{k}(\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v)))|dxdt\\\le & {} \frac{T}{b_{0}}\int _{\{|\widetilde{T}_{n}(b(u))-\widetilde{T}_{n}(b(v))|\le k \}\cap \{|u|\le n, |v|\le n \}}\\&L_{D}(x,t)(|\nabla \widetilde{T}_{n}(b(u))|+|\nabla \widetilde{T}_{n}(b(v))|)dxdt=\epsilon (k). \end{aligned}$$

Since $L_{D}$ in $L_{\overline{M}}(Q_{T})$ and due to (16), the function $L_{D}(x,t)(|\nabla T_{n}(b(u))|+|\nabla T_{n}(b(v))|)\in L^{1}(Q_{T})$. Using the Lebesgue dominated convergence theorem we obtain $\lim _{k\rightarrow 0}\epsilon (k)=0$ and

$$\begin{aligned} \displaystyle \lim _{k\rightarrow 0}|K_{3}|=0. \end{aligned}$$

(72)

Estimates (70)–(72) imply (69).

The limit of$I_{5,n}^{\sigma }$:

Using the Lebesgue theorem and (55) and (56), we obtain

$$\begin{aligned} \lim _{\sigma \rightarrow 0}|I_{5,n}^{\sigma }|\le \frac{T}{k}\int _{Q_{T}}|T_{k}(\widetilde{T}_{n}(b(u)-\widetilde{T}_{n}(b(v))|\times |f||\chi _{\{|u|\le n\}}-\chi _{\{|v|\le n\}}|dxdt. \end{aligned}$$

Since $\lim _{k\rightarrow 0}\frac{T_{k}(z)}{k}= \text{ sgn }(z)$ in $\mathbb {R}$ and weakly-* in $L^{\infty }$ then

$$\begin{aligned} \lim _{k\rightarrow 0}\lim _{n\rightarrow +\infty }\lim _{\sigma \rightarrow 0}|I_{5,n}^{\sigma }|\le T\lim _{n\rightarrow +\infty }\left( \int _{\{|u|\ge n\}}|f|dxdt+\int _{\{|v|\ge n\}}|f|dxdt\right) =0. \end{aligned}$$

Then

$$\begin{aligned} \lim _{k\rightarrow 0}\liminf _{n\rightarrow +\infty }\lim _{\sigma \rightarrow 0}I_{5,n}^{\sigma }=0. \end{aligned}$$

(73)

Finally, going back to (57) and using Lemma 8, one may deduce that $u=v$ a.e. in $Q_{T}.$

Appendix

Proof of Lemma 8

Define the functions

$$\begin{aligned} L_{1}(s)= & {} \int _{\{0<b(u)<s\}}\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt\nonumber \\&+\int _{\{0<b(v)<s\}}\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt, \end{aligned}$$

(74)

and

$$\begin{aligned} L_{2}(s)= & {} \int _{\{-s<b(u)<0\}}\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt\nonumber \\&+\int _{\{-s<b(v)<0\}}\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt. \end{aligned}$$

(75)

Due to (10) the functions $L_{1}$ and $L_{2}$ are monotone increasing. $L_{1}$ and $L_{2}$ are differentiable almost everywhere (see [28]), with $L'_{1}$ and $L'_{2}$ measurable and so we have for any $s>\eta >0$

$$\begin{aligned} L_{1}(s)-L_{1}(\eta )\ge \int _{\eta }^{s}L_{1}'(\xi )d\xi \quad \text{ and } \quad L_{2}(s)-L_{2}(\eta )\ge \int _{\eta }^{s}L_{2}'(\xi )d\xi , \end{aligned}$$

(76)

and for almost any $s>0$

$$\begin{aligned} L'_{1}(s)= & {} \frac{1}{2}\limsup _{k\rightarrow 0}\frac{1}{k}\left[ \int _{\{s-k<b(u)<s+k\}}\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt\right. \nonumber \\&\left. +\int _{\{s-k<b(v)<s+k\}}\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt\right] , \end{aligned}$$

(77)

and

$$\begin{aligned} L'_{2}(s)= & {} \frac{1}{2}\limsup _{k\rightarrow 0}\frac{1}{k}\left[ \int _{\{-s-k<b(u)<-s+k\}}\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt \right. \nonumber \\&\left. +\int _{\{-s-k<b(v)<-s+k\}}\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt\right] . \end{aligned}$$

(78)

If the thesis of the lemma is not true, let $\epsilon _{0}>0$ and let $n_{0}>0$ be a real number such that for every real number $s\ge n_{0}$ we have

$$\begin{aligned} \limsup _{k\rightarrow 0}\frac{1}{k}\varGamma (u,v,s,k)\ge \epsilon _{0}. \end{aligned}$$

(79)

Since $b'$ is a continuous and positive function, we have for almost $\xi \ge n_{0}$,

$$\begin{aligned}&\displaystyle \limsup _{k\rightarrow 0}\frac{1}{k}\varGamma (u,v,s,k)\nonumber \\&\quad \le b'(s)\limsup _{k\rightarrow 0}\frac{1}{k}\left[ \int _{\{b(s)-k<b(u)<b(s)+k\}}\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt\right. \nonumber \\&\qquad \left. +\int _{\{b(s)-k<b(v)<b(s)+k\}}\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt\right] \nonumber \\&\qquad +\, b'(-s)\limsup _{k\rightarrow 0}\frac{1}{k}\left[ \int _{\{b(-s)-k<b(u)<b(-s)+k\}}\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt \right. \nonumber \\&\qquad \left. +\int _{\{b(-s)-k<b(v)<b(-s)+k\}}\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt\right] . \end{aligned}$$

(80)

From (77), (79) and (78) it follows that

$$\begin{aligned} b'(\xi )L_{1}'(b(\xi ))+b'(-\xi )L_{2}'(-b(-\xi ))\ge \frac{\epsilon _{0}}{2}. \end{aligned}$$

In view of (76), we deduce that for any $s>\eta >n_{0}$ we have

$$\begin{aligned} L_{1}(b(s))-L_{1}(b(\eta ))+L_{2}(-b(-s))-L_{2}(-b(-\eta ))\ge \frac{\epsilon _{0}}{2}(s-\eta ). \end{aligned}$$

(81)

Taking $s=n+1$ and $\eta =n$ with $n>n_{0}$ we have

$$\begin{aligned}&\int _{\{n\le |u|\le n+1\}}\Big (a(u,\nabla u)\nabla u +|\varPhi (u)||\nabla u|\Big )dxdt\\&\quad +\int _{\{n\le |v|\le n+1\}}\Big (a(v,\nabla v)\nabla v +|\varPhi (v)||\nabla v|\Big )dxdt\ge \frac{\epsilon _{0}}{2}. \end{aligned}$$

The last inequality contradicts (17) and (47). $\square$