1 Introduction

For any \(x\in [0,1)\), it can be uniquely expanded into its terminating dyadic expansion:

$$\begin{aligned} x=\frac{x_1}{2}+\frac{x_2}{2^2}+\frac{x_3}{2^3}+\cdots , \end{aligned}$$

where \(x_n\in \{0,1\}\) is called the digit of x. The run-length function \(l_n(x)\) is the longest run of 1’s in the first n digits of the dyadic expansion of x. A classic result due to Erdös and Rényi [5] asserts that

$$\begin{aligned} \lim _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}}=1 \end{aligned}$$

for Lebesgue almost all \(x\in [0,1)\). Ma, Wen and Wen [13] proved that the set of all points in [0, 1) for which the above Erdös-Rényi’s theorem does not hold has Hausdorff dimension one. For an increasing integer sequence \((\delta _n)_{n\ge 1}\), Zou [16] considered the set of points whose run-length function behaves asymptotically as \(\delta _n\), that is

$$\begin{aligned} E\left( \{\delta _n\}\right) =\left\{ x\in [0,1):\lim _{n\rightarrow +\infty }\frac{l_n(x)}{\delta _{n}}=1\right\} . \end{aligned}$$

He showed that the set \(E\left( \{\delta _n\}\right) \) has Hausdorff dimension one under the condition \(\lim _{n\rightarrow +\infty } \frac{\delta _{n+\delta _n}}{\delta _n}=1\). A similar result holds in an infinite symbolic system: continued fraction dynamical system, see [15].

Remark 1

Applying Zou’s result to \(\delta _n=\left[ \alpha \log _2 n\right] \) with \(\alpha \in (0,+\infty )\), \(\delta _n=\left[ \log _2\log _2 n\right] \) and \(\delta _n=[\sqrt{n}]\) respectively, we get for any \(\alpha \in [0,+\infty ]\),

$$\begin{aligned} \dim _{\mathrm H}\left\{ x\in [0,1) :\lim _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}}=\alpha \right\} =1, \end{aligned}$$

in view of the inclusions

$$\begin{aligned} \left\{ x\in [0,1) :\lim _{n\rightarrow +\infty }\frac{l_n(x)}{\left[ \log _2\log _2 n\right] }=1\right\} \subset \left\{ x\in [0,1) :\lim _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}}=0\right\} \end{aligned}$$

and

$$\begin{aligned} \left\{ x\in [0,1) :\lim _{n\rightarrow +\infty }\frac{l_n(x)}{[\sqrt{n}]}=1\right\} \subset \left\{ x\in [0,1) :\lim _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}}=+\infty \right\} , \end{aligned}$$

where \([\cdot ]\) denotes the integer part function and \(\dim _{\mathrm H}\) denotes the Hausdorff dimension.

Recently, Li and Wu [11, 12] studied the extreme situation for general asymptotic behaviour of run-length function. More precisely, they proved that the set

$$\begin{aligned} \left\{ x\in [0,1):\liminf _{n\rightarrow +\infty }\frac{l_n(x)}{\varphi (n)}=0,\ \limsup _{n\rightarrow +\infty }\frac{l_n(x)}{\varphi (n)}=+\infty \right\} \end{aligned}$$

has Hausdorff dimension 0 or 1 according as \(\limsup _{n\rightarrow +\infty }\frac{n}{\varphi (n)}<+\infty \) or \(\limsup _{n\rightarrow +\infty }\frac{n}{\varphi (n)}=+\infty \), where \(\varphi :\ \mathbb N\rightarrow \mathbb R^+\) is a monotonically positive increasing function with \(\lim _{n\rightarrow +\infty }\varphi (n)=+\infty \).

Remark 2

If we take \(\varphi (n)=\log _2 n\), it follows that

$$\begin{aligned} \dim _{\mathrm H}\left\{ x\in [0,1):\liminf _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2 n}=0,\ \limsup _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2 n}=+\infty \right\} =1 \end{aligned}$$

In this note, we would like to consider a subtle question: what is the Hausdorff dimension of the set

$$\begin{aligned} E_{\alpha ,\beta }=\left\{ x\in [0,1):\liminf _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}}=\alpha ,\ \limsup _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}}=\beta \right\} \end{aligned}$$

with \(0\le \alpha \le \beta \le +\infty \). We show

Theorem 1.1

$$\begin{aligned} \dim _{\mathrm H}E_{\alpha ,\beta }=1. \end{aligned}$$

The first analogous investigation on the fractal sets of this type goes back to Besicovitch [3], where he considered the Hausdorff dimension of the level sets determined by the frequency of digits in dyadic system. Eggleston [4] generalised Besicovitch’s result to base \(m\ge 2\). Their results were recovered and generalized by Barreira, Saussol and Schmeling [2] using a multidimensional version of multifractal analysis. Similar questions had also been extensively studied for the recurrent sets in various dynamical system, see [1, 7–10, 14] and reference therein. For more details about Hausdorff dimension, we refer to the book of Falconer [6].

2 Proof of the main result

In this section, we will prove the main result of this note. The proof of Theorem 1.1 rests on the following proposition applied successfully in [11] and [13].

Proposition 2.1

[13] Given a set of positive integers \(\mathcal {J}=\left\{ j_1<j_2<j_3<\cdots \right\} \) and an infinite sequence \(\left\{ a_i\right\} _{i\ge 1}\) of 0’s and 1’s, let

$$\begin{aligned} E\left( \mathcal {J},\left\{ a_i\right\} \right) =\left\{ x\in [0,1) :x=\sum _{i=1}^{+\infty }\frac{x_i}{2^i},\ x_i=a_i, \forall i\in \mathcal {J}\right\} . \end{aligned}$$

If the density of \(\mathcal {J}\) is zero, that is,

$$\begin{aligned} \lim _{n\rightarrow +\infty } \frac{\#\{i\le n:i\in \mathcal {J}\}}{n}=0, \end{aligned}$$

then \(\dim _{\mathrm H}E\left( \mathcal {J},\left\{ a_i\right\} \right) =1\), where \(\#\) denotes the number of elements in a set.

Proof of Theorem 1.1

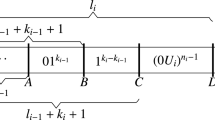
By Remarks 1 and 2, we need only to prove the theorem for the cases \(0<\alpha<\beta <+\infty \), \(0=\alpha<\beta <+\infty \) and \(0<\alpha <\beta =+\infty \). The whole proof is divided into two parts: a detailed proof for the case \(0<\alpha<\beta <+\infty \) and sketches of proof for the remaining cases. We now first restrict ourselves to the case \(0<\alpha<\beta <+\infty \). Our strategy is to construct a subset of real numbers for which the maximal lengths of blocks of digits 1 among the dyadic expansions reach at suitable scattered positions, which guarantee that the points are in \(E_{\alpha ,\beta }\) and also the subset with full Hausdorff dimension. Choose two subsequences \(\{m_k\}_{k\ge 1}\) and \(\{n_k\}_{k\ge 1}\) satisfying, for each \(k\ge 1\),

$$\begin{aligned} n_1=\left[ 2^{\frac{\beta }{\alpha }}\right] ,\ n_{k+1}=\left[ n_k^{\frac{\beta }{\alpha }}\right] ,\ m_k=n_k+\left[ \beta \log _2 n_k\right] . \end{aligned}$$

Clearly, \(\{n_k\}_{k\ge 1}\) increases super-exponentially, and there exists \(K\ge 1\) such that for any \(k\ge K\), we have \(n_k<m_k<n_{k+1}\). For \(k\ge K\), let \(t_k\) be the largest integer such that \(m_k+t_k(m_k-n_k)<n_{k+1}\). Take

$$\begin{aligned} \mathcal {D}:=\mathcal {D}\left( \{m_k\},\{n_k\}\right) =\{1,2,\ldots ,n_K-1, \text {and}\ n_k, n_k+1, \ldots , m_k-1, m_k,\\ m_k+(m_k-n_k),\ldots , m_k+t_k(m_k-n_k),\ \text {for}\ k\ge K\}. \end{aligned}$$

Define an infinite sequence \(\left\{ a_i\right\} _{i\ge 1}\) as follows. For \(1\le i< n_K\), set

$$\begin{aligned} a_i=0. \end{aligned}$$

For \(k\ge K\), set

$$\begin{aligned} a_{n_k}=0,\ a_{n_k+1}=\cdots =a_{m_k-1}=1,\ a_{m_k}=0 \end{aligned}$$

and

$$\begin{aligned} a_{m_k+(m_k-n_k)}=a_{m_k+2(m_k-n_k)}=\cdots =a_{m_k+t_k(m_k-n_k)}=0. \end{aligned}$$

We consider the set E of real numbers \(x\in [0,1)\) whose dyadic expansion \(x=\sum _{i=1}^{+\infty }\frac{x_i}{2^i}\) satisfies \(x_i=a_i\) for all \(i\in \mathcal {D}\), that is

$$\begin{aligned} E:=E\left( \mathcal {D},\left\{ a_i\right\} \right) =\left\{ x\in [0,1) :x=\sum _{i=1}^{+\infty }\frac{x_i}{2^i},\ x_i=a_i, \forall i\in \mathcal {D}\right\} . \end{aligned}$$

Now we prove \(E\subset E_{\alpha ,\beta }\). Fix \(x\in E\), for any \(n\ge n_{K+1}\), let k be the integer such that \(n_k\le n<n_{k+1}\). From the construction of the set E, we see that

$$\begin{aligned}&l_n(x)\\&\quad =\left\{ \begin{array}{ll} m_{k-1}-n_{k-1}-1=\left[ \beta \log _2 n_{k-1}\right] -1,&{} \quad \text { if }\ n_k\le n\le n_k+m_{k-1}-n_{k-1}-1,\\ n-n_k,&{} \quad \text { if }\ n_k+m_{k-1}-n_{k-1}\le n\le m_k-1,\\ m_k-n_k-1=\left[ \beta \log _2 n_{k}\right] -1,&{} \quad \text { if }\ m_k\le n< n_{k+1}. \end{array} \right. \end{aligned}$$

Thus

$$\begin{aligned} \begin{array}{ll} \liminf _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}} &{}=\liminf _{k\rightarrow +\infty }\min \left\{ \frac{l_{n_k+m_{k-1}-n_{k-1}-1}(x)}{\log _2{(n_k+m_{k-1}-n_{k-1}-1)}},\frac{l_{n_{k+1}-1}(x)}{\log _2{(n_{k+1}-1)}}\right\} \\ &{}=\liminf _{k\rightarrow +\infty }\min \left\{ \frac{\left[ \beta \log _2 n_{k-1}\right] -1}{\log _2{(n_k+\left[ \beta \log _2 n_{k-1}\right] -1)}},\frac{\left[ \beta \log _2 n_{k}\right] -1}{\log _2{(n_{k+1}-1)}}\right\} \\ &{}=\alpha , \end{array} \end{aligned}$$

and

$$\begin{aligned}\begin{array}{ll} \limsup _{n\rightarrow +\infty }\frac{l_n(x)}{\log _2{n}} &{}=\limsup _{k\rightarrow +\infty }\max \left\{ \frac{l_{n_k}(x)}{\log _2{n_k}},\frac{l_{m_k-1}(x)}{\log _2{(m_k-1)}}\right\} \\ &{}=\limsup _{k\rightarrow +\infty }\max \left\{ \frac{\left[ \beta \log _2 n_{k-1}\right] -1}{\log _2{n_k}},\frac{\left[ \beta \log _2 n_{k}\right] -1}{\log _2{(n_k+\left[ \beta \log _2 n_k\right] -1)}}\right\} \\ &{}=\beta . \end{array} \end{aligned}$$

Hence \(x\in E_{\alpha ,\beta }\).

In the following, we show that the density of \(\mathcal {D}\subset \mathbb N\) is zero. Clearly, for any \(n\ge n_{K+1}\), there exists \(k\ge {K+1}\) such that \(n_k\le n<n_{k+1}\),

  • if \(n_k\le n\le m_k\), then

    $$\begin{aligned} \#\left\{ i\le n,\ i\in \mathcal {D}\right\} =n_K+\sum _{j=K}^{k-1}\left[ (m_j-n_j+1)+t_j\right] +n-n_k; \end{aligned}$$

  • if \(m_k+t(m_k-n_k)\le n<m_k+(t+1)(m_k-n_k)\) for some \(0\le t\le t_k-1\), then

    $$\begin{aligned} \#\left\{ i\le n,\ i\in \mathcal {D}\right\} = n_K+\sum _{j=K}^{k-1}\left[ (m_j-n_j+1)+t_j\right] +m_k-n_k+t; \end{aligned}$$

  • if \(m_k+t_k(m_k-n_k)\le n< n_{k+1}\), then

    $$\begin{aligned} \#\left\{ i\le n,\ i\in \mathcal {D}\right\} =n_K+\sum _{j=K}^{k-1}\left[ (m_j-n_j+1)+t_j\right] +m_k-n_k+t_k. \end{aligned}$$

It follows that

$$\begin{aligned}&\limsup _{n\rightarrow +\infty }\frac{1}{n} \#\left\{ i\le n,\ i\in \mathcal {D}\right\} \\&\quad \le \limsup _{k\rightarrow +\infty }\max _{0\le t\le t_k}\left\{ \frac{n_K+\sum _{j=K}^{k-1}\left[ (m_j-n_j+1)+t_j\right] +m_k-n_k+t}{m_k+t(m_k-n_k)}\right\} \\&\quad \le \limsup _{k\rightarrow +\infty }\left\{ \frac{n_K+\sum _{j=K}^{k-1}\left[ (m_j-n_j+1)+t_j\right] +m_k-n_k}{m_k}+\frac{1}{m_k-n_k}\right\} \\&\quad =0. \end{aligned}$$

Therefore, by Proposition 2.1, we have \(\dim _{\mathrm H}E=1\).

Since the proof for the remaining cases is similar to the proof of the case \(0<\alpha<\beta <+\infty \). We will only give the constructions for the proper sequences \(\{m_k\}_{k\ge 1}\) and \(\{n_k\}_{k\ge 1}\). One can verify the corresponding \(\mathcal {D}\left( \{m_k\},\{n_k\}\right) \) is of density zero and \(E\left( \mathcal {D},\left\{ a_i\right\} \right) \) with full Hausdorff dimension is a subset of \(E_{\alpha ,\beta }\) for different cases.

Case 1: \(\alpha =0\) and \(\beta <+\infty \), take \(n_k=2^{2^{2^k}}\) and \(m_k=n_k+\left[ \beta \log _2 n_k\right] \) for \(k\ge 1\).

Case 2: \(\alpha >0\) and \(\beta =+\infty \), take \(n_1=2\), \(n_{k+1}=n_k^k\) and \(m_k=n_k+\left[ \alpha k \log _2 n_k\right] \) for \(k\ge 1\).