1 Introduction

The aim of the present paper is to solve a problem on exceptional sets in Erdős–Rényi limit theorem which was posed in [20]. Let us recall the background and some notation in [20]. The run-length function \(r_n(x),\) which was introduced to measure the length of consecutive terms of “heads” in n Bernoulli trials, is defined as follows. It is well known that every \(x\in [0,1]\) admits a dyadic expansion:

$$\begin{aligned} x=\sum _{k=1}^\infty \frac{x_k}{2^k}, \end{aligned}$$

where \(x_k\in \{0,1\}\) for any \(k\ge 1\). Write

$$\begin{aligned} \Sigma ^{\infty }=\{0,1\}^\mathbb {N}=\{(x_1,x_2, x_3,\ldots ):x_i\in \{0,1\},\; i=1,2,\ldots \}. \end{aligned}$$

The infinite sequence \((x_1,x_2, x_3,\ldots )\in \Sigma ^{\infty }\) is called the digit sequence of x. Let \(\pi :\Sigma ^{\infty }\rightarrow [0,1]\) be the code map, that is, \(\pi ((x_1,x_2, x_3,\ldots ))=x.\) For each \(n\ge 1\) and \(x\in [0,1]\), the run-length function \(r_n(x)\) is defined as the length of the longest run of 1’s in \((x_1,x_2,\ldots ,x_n)\), that is,

$$\begin{aligned} r_n(x)=\max \{\ell : x_{i+1}=\cdots =x_{i+\ell }=1 \text { for some } 0\le i\le n-\ell \}. \end{aligned}$$

The run-length function has been extensively studied in probability theory and used in reliability theory, biology, quality control. Erdős and Rényi [9] (see also [28]) proved the following asymptotic behavior of \(r_n\): for Lebesgue almost all \(x\in [0,1]\),

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{r_n(x)}{\log _2n}=1. \end{aligned}$$
(1)

Roughly speaking, the rate of growth of \(r_n(x)\) is \(\log _2n\) for almost all \(x\in [0,1].\) Recently, some special sets consisting of points whose run-length function obey other asymptotic behavior instead of \(\log _2n\) was considered by Zou [29]. Chen and Wen [8] studied some level sets on the frequency involved in dyadic expansion and run-length function. For more details about the run-length function, we refer the reader to the book [28].

The limit in (1) may not exist. Therefore, it is natural to study the exceptional set in the above Erdős–Rényi limit theorem. Let

$$\begin{aligned} E=\left\{ x\in [0,1]:\liminf \limits _{n\rightarrow \infty }\frac{r_n(x)}{\log _2n}<\limsup \limits _{n\rightarrow \infty }\frac{r_n(x)}{\log _2n}\right\} . \end{aligned}$$

It follows from the Erdős–Rényi limit theorem that the set E is negligible from the measure-theoretical point of view. On the other hand, we also often employ some fractal dimensions to characterize the size of a set. Hausdorff dimension perhaps is the most popular one. Ma et al. [21] proved that the set of points that violate the above Erdős and Rényi law has full Hausdorff dimension, that is, has Hausdorff dimension 1. It is worth pointing out that E is smaller than the set considered in [21] because we consider the asymptotic behavior of \(r_n(x)\) with respect to the fixed speed \(\log _2 n.\) There is a natural question: what is the Hausdorff dimension of the set E? In fact, questions related to the exceptional sets from dynamics and fractals have recently attracted huge interest in the literature. Generally speaking, exceptional sets are big from the dimensional point of view, and they have the same fractal dimensions as the underlying phase spaces, see [1–3, 11, 12, 14, 15, 19, 23, 25–27] and references therein.

Define

$$\begin{aligned} E_{\max }=\left\{ x\in [0,1]:\liminf \limits _{n\rightarrow \infty }\frac{r_n(x)}{\log _2n}=0, \limsup \limits _{n\rightarrow \infty }\frac{r_n(x)}{\log _2n}=+\infty \right\} . \end{aligned}$$

That is, \(E_{\max }\) is the set consisting of those “worst” divergence points. Clearly, \(E_{\max }\subset E.\)

Intuitively, we feel that the set \(E_{\max }\) shall be “small”. However, the authors showed in [20] that \({{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_{\max }=1.\) Here and in the sequel, \({{\mathrm{\mathrm{dim}_\mathrm{H}}}}E\) denotes the Hausdorff dimension of the set E. For more details about Hausdorff dimension and the theory of fractal dimensions, we refer the reader to the famous book [10].

Moreover, it is also natural to study the asymptotic behavior of run-length function with respect to other speeds instead of \(\log _2n.\) In fact, In [20] the authors proved that the exceptional sets with respect to a more general class of speeds still have full dimensions. To state the result, we need to introduce some notation. Let H denote the set of monotonically increasing function \(\varphi :\mathbb {N}\rightarrow (0,+\infty )\) with \(\lim _{n\rightarrow +\infty }f(n)=+\infty \). For \(\varphi \in H\), define

$$\begin{aligned} E_{\max }^\varphi =\left\{ x\in [0,1]:\liminf \limits _{n\rightarrow \infty }\frac{r_n(x)}{\varphi (n)}=0, \limsup \limits _{n\rightarrow \infty }\frac{r_n(x)}{\varphi (n)}=+\infty \right\} . \end{aligned}$$
(2)

Consider the following subset of H:

$$\begin{aligned} A=\left\{ \varphi \in H: \text {there exists} ~0<\alpha \le 1\,\, \mathrm{such~ that} \limsup \limits _{n\rightarrow \infty }\frac{n}{\varphi (n^{1+\alpha })}=+\infty \right\} . \end{aligned}$$

In [20], the authors obtained the following result.

Theorem 1

[20] Let \(\varphi \in A\) and \(E_{\max }^\varphi \) be defined as in (2). Then

$$\begin{aligned} {{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_{\max }^\varphi =1. \end{aligned}$$

It is easy to check that \(\log _2 n\in A\) and \(n^\beta \in A\), where \(0<\beta <1\). Unfortunately, many other speeds are not in the set A. In [20], the authors conjectured that for \(\varphi \in H\), the Hausdorff dimension of \(E_{\max }^\varphi \) is either one or zero. In this paper, we solve this conjecture affirmatively. More precisely, we have the following result.

Theorem 2

Let \(\varphi \in H\) and \(E_{\max }^\varphi \) be defined as in (2).

  1. (1)

    If \(\limsup _{n\rightarrow \infty }\frac{n}{\varphi (n)}=+\infty \) then \({{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_{\max }^\varphi =1;\)

  2. (2)

    If \(\limsup _{n\rightarrow \infty }\frac{n}{\varphi (n)}<+\infty \) then \({{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_{\max }^\varphi =0.\)

Remark 1

In fact, under the condition \(\limsup _{n\rightarrow \infty }\frac{n}{\varphi (n)}<+\infty \) the set \(E_{\max }^\varphi =\emptyset \) since \(r_n(x)\le n\) for any \(n\ge 1\) and \(x\in [0,1].\)

We would like to emphasize that the method in [20] cannot be applied to the generalized functions \(\varphi \in H\). To prove Theorem 2, we will use another method which is inspired by the idea in [12].

Clearly, if \(\varphi \in A\) then \(\varphi \) satisfies the condition in the first part of Theorem 2. Therefore, Theorem 2 generalizes Theorem 1.

We can also discuss the size of \(E_{\max }^\varphi \) from the topological point of view, which is another way to describe the size of a set. Recall that in a metric space X, a set R is called residual if its complement is of the first category, that is, if its complement is a countable union of nowhere dense sets. Moreover, in a complete metric space a set is residual if it contains a dense \(G_\delta \) set (i.e. a countable intersection of open sets), see [24]. Recent results show that certain exceptional sets can also be large from the topological point of view, see, for example, [4–6, 13, 16–19, 22] and references therein. In [20] the authors also showed that the set \(E_{\max }^\varphi \) is residual if \(\varphi \in A\). The following result is a generalization of it.

Theorem 3

Let \(\varphi \in H\) with \(\limsup _{n\rightarrow \infty }\frac{n}{\varphi (n)}=+\infty \) and \(E_{\max }^\varphi \) be defined as in (2). Then the set \(E_{\max }^\varphi \) is residual in [0, 1].

Noting Remark 1, Theorem 3 tells us that for any \(\varphi \in H\) the set \(E_{\max }^\varphi \) is either residual or empty.

2 Proofs

This section is devoted to the proofs of Theorems 2 and 3. First we need to introduce some notation. For \(n\in \mathbb {N}\), let

$$\begin{aligned} \Sigma ^{n}=\{({\omega _{1}},\ldots ,{\omega _{n}}):x_i\in \{0,1\},\; i=1,\ldots ,n\} \end{aligned}$$

and

$$\begin{aligned} \Sigma ^{*}=\bigcup _{n \in \mathbb {N}}{\Sigma ^{n}}. \end{aligned}$$

For each \(\omega =(\omega _1,\ldots ,\omega _n)\in \Sigma ^{n}\), let \(|\omega |=n\) denote the length of the word \(\omega .\) For \(\omega =({\omega _{1}}\ldots {\omega _{n}})\in {\Sigma ^{n}}\) and a positive integer m with \(m\le n\), or for \(\omega =(\omega _{1},\omega _{2},\ldots )\in \Sigma ^{\infty }\) and a positive integer m, let \(\omega |_m=(\omega _{1}\ldots \omega _{m})\) denote the truncation of \(\omega \) to the mth place. For two words \(\omega =(\omega _1,\omega _2,\ldots , \omega _n)\in \Sigma ^{n}\) and \(\tau =(\tau _1,\tau _2,\ldots ,\tau _m)\in \Sigma ^{m}\), we denote their concatenation by \(\omega \tau =(\omega _1,\ldots ,\omega _n,\tau _1,\ldots ,\tau _m),\) which is a word of length \(n+m.\) Similarly, the notation \(a^m \) means \(\underbrace{a\cdots a}_{m\,\, \text {times}}\), where \(a=0\) or 1.

It is well known that the space \(\Sigma ^{\infty }\) is compact if it is equipped with the usual metric defined by

$$\begin{aligned} d(x,y)=2^{-\min \{k:x_{k+1}\not =y_{k+1}\}}, \quad x,y\in \Sigma ^{\infty }. \end{aligned}$$

Finally, in this paper the notation [x] denotes the integer part of x.

Before giving the proof of Theorem 2, we would like to show our strategy. For sufficient large integer p, we take a subset \(E_p\subset {\Sigma ^{\infty }}\) with Hausdorff dimension \(\frac{p-2}{p}\). Then, we construct a subset of \(E_{\max }^\varphi \) such that every point of the subset is obtained by inserting some words to some point from \(E_p\) at suitable places. Finally, it follows from the fact that p is large enough and the relationship between \(E_p\) and the constructed subset of \(E_{\max }^{\varphi }\) that \(E_{\max }^{\varphi }\) has Hausdorff dimension 1.

Proof of Theorem 2

Noting Remark 1, we only need to prove the first part. Let \(\varphi \in H\) and \(\limsup _{n\rightarrow \infty }\frac{n}{\varphi (n)}=+\infty \). It is sufficient to show that \({{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_{\max }^\varphi \ge 1-\gamma \) for any \(\gamma >0\).

Fix \(0<\gamma <1\). Choose \(p\in \mathbb {N}\) such that \(\frac{p-2}{p}>1-\gamma .\) Let

$$\begin{aligned} E_p=\{x\in \Sigma ^{\infty }: x_{kp+1}=x_{kp+p}=0\,\,\text {for any}~ k\ge 1\}. \end{aligned}$$

Since the set \(E_p\) can be viewed as set defined by digit restrictions, its Hausdorff dimension is equal to the lower density of the set \(S=\cup _{k=1}^\infty \{kp+2, \ldots , kp+p-1\}\cup \{1, 2, \ldots , p\}\), see Example 3.3 in [7]. More precisely,

$$\begin{aligned} {{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_p=\liminf \limits _{n\rightarrow \infty }\frac{\#(S\cap \{1,\ldots , n\})}{n}=\frac{p-2}{p}, \end{aligned}$$

where \(\# (A)\) denotes the number of elements in A.

By means of \(E_p\) we will construct a set \(E^*_p\) such that \(\pi (E^*_p)\subset E_{\max }^\varphi \) and define a one-to-one map f from \(E_p\) onto \(E^*_p\). Moreover, the map \(f^{-1}\) is nearly Lipschitz on \(f(E_p)\), namely, for any \(\varepsilon >0\), there exists some \(N_0\) such that \(d(f(x),f(y))<2^{-n}\) implies that \(d(x,y)<2^{-n(1-\varepsilon )}\) for any \(n>N_0.\) This implies that \({{\mathrm{\mathrm{dim}_\mathrm{H}}}}E^*_p={{\mathrm{\mathrm{dim}_\mathrm{H}}}}f(E_p)\ge {{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_p\) (see Proposition 2.3 of [10]) . Therefore,

$$\begin{aligned} {{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_{\max }^\varphi \ge {{\mathrm{\mathrm{dim}_\mathrm{H}}}}\pi (E^*_p)={{\mathrm{\mathrm{dim}_\mathrm{H}}}}f(E_p)\ge {{\mathrm{\mathrm{dim}_\mathrm{H}}}}E_p=\frac{p-2}{p}>1-\gamma , \end{aligned}$$

as desired. Here the first equality follows from that facts that \(\pi :\Sigma ^{\infty }\rightarrow [0,1]\) is a bi-Lipschitz map except a countable set (the set of binary endpoints) and the Hausdorff dimension of a countable set is zero.

Next we will construct the desired set \(E^*_p.\) Let \(n_0=\inf \{n:\log \varphi (n)\ge p\}\). Since \(\limsup _{n\rightarrow \infty }\frac{n}{\varphi (n)}=+\infty \), there exists a subsequence \(\{n_k\}_{k\ge 1}\) such that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\frac{n_k}{\varphi (n_k)}=+\infty \end{aligned}$$
(3)

and

$$\begin{aligned} n_{2k+1}-[\log \varphi (n_{2k+1})]>n_{2k}+2;\quad n_{2k+2}-\left[ \frac{1}{2}n_{2k+2}\right] >n_{2k+1}+2 \end{aligned}$$
(4)

for \(k\ge 0\).

For each \(x=\{x_i\}_{i\ge 1}\in E_p,\) we will construct a sequence \(\{x^{(n)}\}_{n\ge 0}\) of points in \(\Sigma ^{\infty }\) by induction. Let \(x^{(0)}=x.\) Suppose we have defined \(x^{(j)}=x_1^{(j)}x_2^{(j)}\cdots x_n^{(j)}\cdots \) for \(0\le j\le 2k\). We define \(x^{(2k+1)}\) and \(x^{(2k+2)}\) as follows. Let

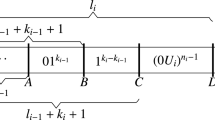
$$\begin{aligned} x^{(2k+1)}=x_{1}^{(2k)}\cdots x^{(2k)}_{n_{2k+1}-1-[\log \varphi (n_{2k+1})]}01^{[\log \varphi (n_{2k+1})]}0 x_{n_{2k+1}-[\log \varphi (n_{2k+1})]}^{(2k)}\cdots . \end{aligned}$$

Namely, \(x^{(2k+1)}\) is obtained by inserting word \(01^{[\log \varphi (n_{2k+1})]}0\) in \(x^{(2k)}\) at the place \(n_{2k+1}-[\log \varphi (n_{2k+1})]\). Then, let

$$\begin{aligned} x^{(2k+2)}=x^{(2k+1)}_1\cdots x^{(2k+1)}_{n_{2k+2}-1-[\frac{1}{2}n_{2k+2}]}01^{[\frac{1}{2}n_{2k+2}]}0 x_{n_{2k+2}-[\frac{1}{2}n_{2k+2}]}^{(2k+1)}\cdots . \end{aligned}$$

Similarly, \(x^{(2k+2)}\) is obtained by inserting word \(01^{[\frac{1}{2}n_{2k+2}]}0\) in \(x^{(2k+1)}\) at the place \(n_{2k+2}-[\frac{1}{2}n_{2k+2}]\).

By (4), we have \(n_{2k+2}-1-[\frac{1}{2}n_{2k+2}]>n_{2k+1}+1\). Therefore, it is not difficult to check that

$$\begin{aligned} x^{(2k+2)}|_{n_{2k+2}-1-[\frac{1}{2}n_{2k+2}]}=x^{(2k+1)}|_{n_{2k+2}-1-[\frac{1}{2}n_{2k+2}]}. \end{aligned}$$

In other words, for \(k\ge 1\) we have

$$\begin{aligned} d(x^{(2k+1)},x^{(2k+2)})\le \left( \frac{1}{2}\right) ^{(n_{2k+2}-1-[\frac{1}{2}n_{2k+2}])}. \end{aligned}$$

Similarly, we can check that for \(k\ge 1\)

$$\begin{aligned} d(x^{(2k)},x^{(2k+1)})\le \left( \frac{1}{2}\right) ^{\left( n_{2k+1}-1-[\log \varphi (n_{2k+1})]\right) }. \end{aligned}$$

The above two inequalities imply that the limit of \(\{x^{(n)}\}_{n\ge 0}\) exists. Let \(x^*=\lim _{n\rightarrow \infty }x^{(n)}.\)

We claim that \(\pi (x^*)\in E_{\max }^\varphi \). In fact, it follows from the construction of \(x^*\) that \(r_{n_{2k-1}}(\pi (x^*))=[\log \varphi (n_{2k-1})]\) and \(r_{n_{2k}}(\pi (x^*))=[\frac{1}{2}n_{2k}]\) for \(k\ge 1.\) Therefore, by (3) and (4) we have

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\frac{r_{n}(\pi (x^*))}{\varphi (n)}\le \lim \limits _{k\rightarrow \infty }\frac{r_{n_{2k-1}}(\pi (x^*))}{\varphi (n_{2k-1})}=\lim \limits _{k\rightarrow \infty }\frac{[\log \varphi (n_{2k-1})]}{\varphi (n_{2k-1})}=0 \end{aligned}$$

and

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }\frac{r_{n}(\pi (x^*))}{\varphi (n)}\ge \lim \limits _{k\rightarrow \infty }\frac{r_{n_{2k}}(\pi (x^*))}{\varphi (n_{2k})}=\lim \limits _{k\rightarrow \infty }\frac{[\frac{1}{2}n_{2k}]}{\varphi (n_{2k})}=+\infty . \end{aligned}$$

Define map \(f:E_p\rightarrow \Sigma ^{\infty }\) by \(f(x)=x^*\) and let

$$\begin{aligned} E^*_p=f(E_p). \end{aligned}$$

Clearly, f is injective. We now show that the map \(f^{-1}\) is nearly Lipschitz on \(E^*_p\). For any \(n\ge n_0\), there exists some \(k\ge 1\) such that \(n_{2k-1}\le n< n_{2k}\) or \(n_{2k}\le n< n_{2k+1}\). We only discuss the case \(n_{2k-1}\le n< n_{2k}\) because the other case can be treated similarly. Suppose \(d(f(x),f(y))=d(x^*,y^*)<2^{-n}\), then \(x^*_1x^*_2\cdots x^*_n=y^*_1y^*_2\cdots y^*_n\). Since \(x=f^{-1}(x^*), y=f^{-1}(y^*)\) is obtained by removing the inserted words we have \(x_1x_2\cdots x_{n'}=y_1y_2\cdots y_{n'}\), where

$$\begin{aligned} n'=n-\left( (2+[\log \varphi (n_1)])+\left( 2+\left[ \frac{1}{2}n_2\right] \right) \ldots +(2+[\log \varphi (n_{2k-1})])\right) . \end{aligned}$$

By (4) and the fact that \(\lim _{n\rightarrow \infty }\varphi (n)=+\infty \), we have

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\frac{\left( 2+[\log \varphi (n_1)])+(2+[\frac{1}{2}n_2])\ldots +(2+[\log \varphi (n_{2k-1})]\right) }{n_{2k-1}}=0. \end{aligned}$$

Therefore, for any \(\varepsilon >0\) there exists an integer \(N_1>n_0\) such that \(n'> n-\varepsilon n_{2k-1}\ge (1-\varepsilon )n\) for any \(n>N_1\) Therefore, \(d(x,y)<2^{-n(1-\varepsilon )}\). Similarly, in the other case there exists some integer \(N_2>n_0\) such that \(d(x,y)<2^{-n(1-\varepsilon )}\) for any \(n>N_2\). Finally, let \(N_0=\max \{N_1,N_2\}\). The proof of Theorem 2 is completed. \(\square \)

Proof of Theorem 3

To prove Theorem 3, it is sufficient to construct a dense \(G_\delta \) subset \(F\subset [0,1]\) such that \(F\subset E_{\max }^\varphi .\)

We first introduce a notation. For \(\omega =(\omega _1,\ldots ,\omega _{m})\in \Sigma ^{*}\) or \(\omega =(\omega _1,\ldots ,\omega _{m}\ldots ) \in \Sigma ^{\infty }\) and \(n\in \mathbb {N}\) with \(n\le m\), let \(r_n(\omega )\) denote the length of the longest run of 1’s in \(\omega |_n=(\omega _1,\omega _2,\ldots ,\omega _{n})\), that is,

$$\begin{aligned} r_n(\omega )=\max \{\ell : \omega _{i+1}=\cdots =\omega _{i+\ell }=1\,\,\text {for some}~ 0\le i\le n-\ell \}. \end{aligned}$$

Since \(\limsup _{n\rightarrow \infty }\frac{n}{\varphi (n)}=+\infty \) and \(\lim _{n\rightarrow \infty }\varphi (n)=+\infty \), there exists a strictly monotonically increasing subsequence \(\{m_k\}_{k\ge 1}\subset \mathbb {N}\) such that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\frac{m_k}{\varphi (m_k)}=+\infty . \end{aligned}$$
(5)

Before presenting the construction, we introduce a notation. For each \(\omega \in \Sigma ^{*}\), define the cylinder set

$$\begin{aligned} I(\omega )=\{\rho \in \Sigma ^{\infty }: \rho |_n=\omega \}. \end{aligned}$$

Let \(\Omega _{0} =\Sigma ^{*}\). For each \(\omega \in \Omega _{0},\) choose positive integer \(n_1=n_1(\omega )\in \{m_k\}_{k\ge 1}\) such that \(n_1-[\log \varphi (n_1)]- |\omega |>0\) and \([\log \varphi (n_1)]\ge |\omega |\). These conditions can always be satisfied by choosing \(n_1\) large enough.

Define

$$\begin{aligned} \Omega _1=\bigcup _{\omega \in \Omega _{0}}I\left( \omega 0^{n_1-[\log \varphi (n_1)]-|\omega |}1^{[\log \varphi (n_1)]}\right) . \end{aligned}$$

For any \(\tau \in \Omega _1,\) there exists some \(\omega \in \Omega _{0}\) with \(|\omega |=n_1(\omega )\) such that \(\tau =\omega 0^{n_1-[\log \varphi (n_1)]-|\omega |}1^{[\log \varphi (n_1)]}.\) It is easy to check that \(|\tau |=n_1(\omega )\) and \(r_{n_1}(\tau )=[\log \varphi (n_1(\omega ))]\) since \(n_1-[\log \varphi (n_1)]- |\omega |>0\) and \([\log \varphi (n_1)]\ge |\omega |\).

Then, for \(\tau \in \Omega _1,\) choose a positive integer \(n_2=n_2(\tau )\in \{m_k\}_{k\ge 1}\) such that \(n_2>2n_1\). Define

$$\begin{aligned} \Omega _2=\bigcup _{\tau \in \Omega _{1}}I\left( \tau 0^{n_2-[\frac{1}{2}n_2]-n_1}1^{[\frac{1}{2}n_2]}\right) . \end{aligned}$$

Analogously, for any \(\xi \in \Omega _2\) there exists some word \(\tau \in \Omega _{1}\) with \(|\tau |=n_1\) such that \(\xi =\tau 0^{n_2-[\frac{1}{2}n_2]-n_1}1^{[\frac{1}{2}n_2]}\) and \(|\xi |=n_2(\tau )\). It follows from \(n_2> 2n_1\) that \(n_2-[\frac{1}{2}n_2]-n_1>0\) and therefore \(r_{n_2}(\xi )=[\frac{1}{2}n_2]\).

Suppose we have chosen the positive integers \(n_1,n_2,\ldots , n_{2m-1}, n_{2m}, \) and have defined the sets \(\Omega _1, \Omega _2,\ldots , \Omega _{2m-1}, \Omega _{2m},\) we next show how to define the sets \(\Omega _{2m+1}\) and \(\Omega _{2m+2}\). For \(\eta \in \Omega _{2m}\) with \(|\eta |=n_{2m}\), choose integer \(n_{2m+1}=n_{2m+1}(\eta )\in \{m_k\}_{k\ge 1}\) such that \(n_{2m+1}-[\log \varphi (n_{2m+1})]-n_{2m}>0\) and \([\log \varphi (n_{2m+1})]\ge |\eta |\). Again, these conditions can always be satisfied by choosing \(n_{2m+1}\) large enough.

Define

$$\begin{aligned} \Omega _{2m+1}=\bigcup _{\eta \in \Omega _{2m}}I\left( \eta 0^{n_{2m+1}-[\log \varphi (n_{2m+1})]-n_{2m}}1^{[\log \varphi (n_{2m+1})]}\right) . \end{aligned}$$

For any \(\mu \in \Omega _{2m+1},\) there exists some word \(\eta \in \Omega _{2m}\) with \(|\eta |=n_{2m}\) such that \(\mu =\eta 0^{n_{2m+1}-[\log \varphi (n_{2m+1})]-n_{2m}}1^{[\log \varphi (n_{2m+1})]}\). It is easy to check that \(|\mu |=n_{2m+1}\). Moreover, \(r_{n_{2m+1}}(\mu )=[\log \varphi (n_{2m+1})]\) since \(n_{2m+1}-[\log \varphi (n_{2m+1})]-n_{2m}>0\) and \([\log n_{2m+1}]\ge |\eta |\).

Then, for \(\sigma \in \Omega _{2m+1}\) with \(|\sigma |=n_{2m+1}\), choose a integer \(n_{2m+2}=n_{2m+2}(\sigma )\in \{m_k\}_{k\ge 1}\) such that \(n_{2m+2}>2n_{2m+1}\), and define

$$\begin{aligned} \Omega _{2m+2}=\bigcup _{\sigma \in \Omega _{2m+1}}I\left( \sigma 0^{n_{2m+2}-[\frac{1}{2}n_{2m+2}]-n_{2m+1}}1^{[\frac{1}{2}n_{2m+2}]}\right) . \end{aligned}$$

Analogously, for any \(\nu \in \Omega _{2m+2},\) we have \(|\nu |=n_{2m+2}\) and \(r_{n_{2m+2}}(\nu )=[\frac{1}{2} n_{2m+2}]\) since \(n_{2m+2}>2n_{2m+1}\).

Next, define

$$\begin{aligned} \Omega =\bigcap _{k=0}^\infty \Omega _k. \end{aligned}$$

Then, we claim that \(\Omega \) is residual in \(\Sigma ^{\infty }.\) In fact, \(\Omega \) is a \(G_\delta \) set in \(\Sigma ^{\infty }\) since it is not difficult to check that each cylinder set \(\Omega _k\) is open. Moreover, by construction, each set \(\Omega _k\) is dense, and so it follows from Baire’s theorem that \(\Omega \) is also dense in \(\Sigma ^{\infty }\).

Write \(\Sigma _{\max }^\varphi =\pi ^{-1}(E_{\max }^\varphi ).\) we will show that

$$\begin{aligned} \Omega \subset \Sigma _{\max }^\varphi . \end{aligned}$$
(6)

For \(\omega \in \Omega \), it follows from the construction of the set \(\Omega \) that

$$\begin{aligned} r_{n_{2m-1}}(\omega )=[\log \varphi (n_{2m-1})], \quad r_{n_{2m}}(\omega )=\left[ \frac{1}{2}n_{2m}\right] ,\; m\ge 1. \end{aligned}$$

Therefore, by (5) we have

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\frac{r_n(\omega )}{\varphi (n)}\le \lim \limits _{m\rightarrow \infty }\frac{r_{n_{2m-1}}(\omega )}{\varphi (n_{2m-1})}=\lim \limits _{m\rightarrow \infty }\frac{[\log \varphi (n_{2m-1})]}{\varphi (n_{2m-1})}=0 \end{aligned}$$

and

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }\frac{r_n(\omega )}{\varphi (n)}\ge \lim \limits _{m\rightarrow \infty }\frac{r_{n_{2m}}(\omega )}{\varphi ( n_{2m})}=\lim \limits _{m\rightarrow \infty }\frac{[\frac{1}{2}n_{2m}]}{\varphi ( n_{2m})}=+\infty , \end{aligned}$$

which imply \(\Omega \subset \Sigma _{\max }^\varphi \).

Finally, we use the set \(\Omega \) to define the desired set F.

Let

$$\begin{aligned} B=\left\{ x\in [0,1]:x=\frac{k}{2^n}, k, n\in \mathbb {N}\right\} , \end{aligned}$$

and write

$$\begin{aligned} \widetilde{\Sigma }=\Sigma ^{\infty }{\setminus } \pi ^{-1}(B), \quad \widetilde{E}=[0,1]{\setminus } B. \end{aligned}$$

The map \(\pi :\widetilde{\Sigma }\rightarrow \widetilde{E}\) is bijective. Note that \(\pi ^{-1}(B)\) is a \(F_\sigma \) set, the set \(\widetilde{\Sigma }\) is a \(G_\delta \) set. Moreover, it is easy to check that \(\widetilde{\Sigma }\) is dense in \(\Sigma ^{\infty }.\)

Now, let

$$\begin{aligned} F=\pi (\Omega \cap \widetilde{\Sigma }). \end{aligned}$$

Following the argument in [20], we can check that F is the desired set. \(\square \)