1 Introduction

In geotechnical and geological engineering, one of the most crucial parameters that can evaluate a rock's mechanical behavior is the strength of the intact rock with the discontinuities’ presence (Grima and Babuška 1999; Gokceoglu 2002). Even though it is clear that the strength envelopes of an intact rock are a nonlinear function of the level of stress, because of its simplicity, still the linear model of Mohr–Coulomb for the shear strength of rocks is used in the actual engineering applications (Shen and Jimenez 2018).

The criterion of Mohr–Coulomb includes two parameters of cohesion (c) and friction angle (\(\varphi\)). Parameter c is related to the bond between crystals or particles of rock, and parameter \(\varphi\) is related to the friction internally created along the shear surface (Singh et al. 2020). Before the employment of the Mohr–Coulomb criterion in practice, parameters c and \(\varphi\) should be estimated (Adrien et al. 2020).

The popularity of triaxial tests conducted on rocks at different confining pressures to evaluate the Mohr–Coulomb parameters of c and \(\varphi\) is quite obvious. However, because of the high time and cost associated with the triaxial tests, the need for alternative methods to achieve the Mohr–Coulomb parameters is fully felt (Ulusay et al. 1994; Kahraman et al. 2009; Cai 2010; Beiki et al. 2013; Shen and Jimenez 2018). To this end, many attempts have been made to develop faster and cheaper indirect tests to estimate the uniaxial compressive strength (UCS) of rocks, such as Schmidt hammer (Mohammed et al. 2020; Howarth and Rowlands 1986), point load index (Şahin et al. 2020), impact strength (Jing et al. 2020), sound velocity (Kurtulus et al. 2018), and Los Angeles abrasion (Teymen 2019). Other researchers have conducted studies on the achievement of rock shear strength parameters with the help of UCS and uniaxial tensile strength (UTS) when the triaxial test data are not available (Beyhan 2008; Farah 2011; Karaman et al. 2015; Shen and Jimenez 2018).

Recently, non-traditional regression-based methods, and soft-computing artificial intelligence (AI) based techniques such as group method of data handling (GMDH)-type neural networks (NN) have been successfully used in a wide range of geotechnical fields (Zendehboudi et al. 2018; Cevik et al. 2011; Mahmoodzadeh and Zare 2016; Yin et al. 2017; Liu et al. 2018; Mahmoodzadeh et al. 2019; Elbaz et al. 2019; Miah et al. 2020). However, AI techniques have not yet been widely used to predict the shear strength parameters of rocks. Recently, in their study, Shen and Jimenez (2018) applied genetic programming (GP) to predict the Mohr–Coulomb parameters of c and \(\varphi\) for Sandstone rocks. Their proposed model provided good forecasting performance in the absence of triaxial data. It was concluded that their model could be employed to estimate the practical strength of intact Sandstones at the pre-construction phase of geotechnical projects or data unavailability for the triaxial test.

Since there are many different AI algorithms, evaluating other algorithms' prediction performance can be imperative. For this purpose, this work aims to estimate the shear strength parameters (c and \(\varphi\)) of intact rocks using three parameters of UCS, UTS, and confining stress σ3 by three AI methods of Gaussian process regression (GPR), support vector regression (SVR), decision trees (DT), and long-short term memory (LSTM). Parameters UCS and UTS are direct indicators of strength under uniaxial stress conditions. These parameters can be obtained in the laboratory using relatively normalized and straightforward procedures without requiring more specialized techniques. The UCS can be measured using the uniaxial compression test. The UTS can be estimated using the Brazilian test; the International Society has recommended procedures for both tests for Rock Mechanics (ISRM). In addition, to consider the non-linearity of failure envelopes and increase the reliability of predictions, we account for the influence of the stress range under which the shear failure will occur, as indicated by σ3.

A database including 244 datasets previously employed by Shen and Jimenez (2018) in their research is employed in the AI models. The K-fold cross-validation (CV) method is considered to evaluate the prediction performance of the models. Finally, through analyzing the results of several statistical indices, the most accurate forecasting model is specified.

In the next step, to improve the predictions made by the proposed ML model between the four applied models, six hybrid models that are a combination of the proposed model and six metaheuristic optimization algorithms of grey wolf optimization (GWO), particle swarm optimization (PSO), social spider optimization (SSO), sine cosine algorithm (SCA), multiverse optimization (MVO), and moth flame optimization (MFO), are developed to fine-tuning of the LSTM hyper-parameters. Then, the prediction performance of the developed models for predicting parameters C and \(\varphi\) is investigated. Finally, the most robust model between the developed hybrid models is suggested.

This application demonstrates that LSTM-based metaheuristic optimization algorithms have advantages in solving the following problems: many complex parameters will affect the process and results, and the understanding of the process and results is not enough, and where there are historical or experimental data. The prediction of parameters C and \(\varphi\) is also of this type.

To determine the most influential factors between the three inputs of σ3, UCS, and UTS on the parameters C and \(\varphi\), the mutual information test method is applied.

With the above explanations, the following are the main novelties of this work to predict parameters C and \(\varphi\).

  1. 1.

    Investigating four ML-based models of GPR, SVR, DT, and LSTM to predict C and \(\varphi\). These models have not been studied for this purpose before.

  2. 2.

    Six metaheuristic algorithms of GWO, PSO, SSO, SCA, MVO, and MFO are developed to fine-tune the hyper-parameters of the proposed model in the prediction of parameters C and \(\varphi\).

  3. 3.

    The dropout technique is used to overcome the issue of overfitting, which has not been considered in the previous ML methods for predicting C and \(\varphi\).

  4. 4.

    The mutual information test is used for sensitivity analysis of the input parameters on the parameters C and \(\varphi\).

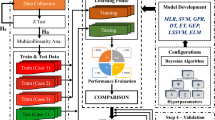
The overall flowchart of the study is presented in Fig. 1.

Fig. 1
figure 1

Overall procedure of shear strength parameters prediction using AI techniques

Full size image

2 Database

To predict the shear strength parameters (c and \(\varphi\)) of intact rocks in this article, according to the literature and data availability, three effective input parameters of UCS, UTS, and σ3 are considered. Parameters UCS and UTS are direct indicators of strength under uniaxial stress conditions. To apply σ3, a cylindrical rock specimen is placed in a specifically designed cell and the lateral pressure is applied through a liquid (usually oil) which is pumped into the cell.

A database including 244 datasets previously employed by Shen and Jimenez (2018) in their research is employed in this study. They investigated the use of linear correlations for Sandstone. To that end, they gathered extensive datasets from RocData software, presented by the company Rocscience (2012), which contains various rock properties of different rocks collected from published references. The UCS and UTS values were provided in the RocData database. They calculated the values of c and \(\varphi\) using Eqs. 1–4 with the triaxial tests available for datasets.

$$\mathrm{sin} \theta =\frac{k-1}{k+1}$$
(1)
$$c=\frac{{\sigma }_{{{\mathrm{c}}_{i}}_{\mathrm{fitted}}}}{2\sqrt{k}}$$
(2)
$$k=\frac{\sum ({\sigma }_{3}{\sigma }_{1})-\frac{\sum {\sigma }_{3}\sum {\sigma }_{1}}{N}}{\sum {\sigma }_{3}^{2}-\frac{{(\sum {\sigma }_{3})}^{2}}{N}}$$
(3)
$${\sigma }_{{\mathrm{c}}_{i}\_\mathrm{fitted}}=\frac{\sum {\sigma }_{1}}{N}-k\frac{\sum {\sigma }_{3}}{N}$$
(4)

where \({\sigma }_{1}\) and \({\sigma }_{3}\) are the maximum and minimum principal stresses, \(k\) is an intermediate auxiliary parameter, \({\sigma }_{{\mathrm{c}}_{i}\_\mathrm{fitted}}\) is the fitted UCS value from regression analysis, and \(N\) is the number of tests.

An overview of the database is presented in Table 1.

Table 1 An overview on the database
Full size table

3 Statistical Evaluation Indices

To evaluate the accuracy of the forecasting models, some statistical evaluation indices, including coefficient of determination (R2), mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) are taken into account. The following formulas for calculating these indices are presented (Eqs. 5–9).

$${R}^{2}=1-\frac{\mathrm{sum \;squared \;regression} \;\left(\mathrm{SSR}\right)}{\mathrm{sum \;of \;squares\; total} \;\left(\mathrm{SST}\right)}$$
(5)
$$\mathrm{MAE}=\left(\frac{1}{n}\right)\sum_{i=1}^{n}\left|{y}_{i}-{y}_{i}^{^{\prime}}\right|$$
(6)
$$\mathrm{MAPE}=\frac{1}{n}\sum_{i=1}^{n}\left|\frac{{y}_{i}-{y}_{i}^{^{\prime}}}{{y}_{i}}\right|\times 100\%$$
(7)
$$\mathrm{MSE}=\frac{1}{n}\sum_{1}^{n}{\left({y}_{i}-{y}_{i}^{^{\prime}}\right)}^{2}$$
(8)
$$\mathrm{RMSE}=\sqrt{\left(\frac{1}{n}\right)\sum_{i=1}^{n}{\left({y}_{i}-{y}_{i}^{^{\prime}}\right)}^{2}}$$
(9)

where \({y}_{i}\) is the actual value, \({y}_{i}^{^{\prime}}\) is the predicted value, \({\overline{y} }_{i}\) and \({\overline{y} }_{i}^{^{\prime}}\) are the means of actual and predicted values, and \(n\) is the number of samples.

4 Prediction Models of Shear Strength Parameters (c and \(\boldsymbol{\varphi }\))

4.1 GPR

A Gaussian procedure (GP) is a gathering \(F\) of arbitrary factors \({F}_{{x}_{1}}, {F}_{{x}_{2}}, \dots\) for which any finite subset of the factors has a joint multivariate Gaussian conveyance. The factors are listed by components x of a set \(X\). For any finite length vector of lists \(x={[{x}_{1}, {x}_{2}, \dots , {x}_{n}]}^{T}\), we have a comparing vector \({F}_{x}={[{F}_{{x}_{1}}, {F}_{{x}_{2}}, \dots , {F}_{{x}_{n}}]}^{T}\) of factors that have a multivariate Gaussian (or ordinary) distribution (Eq. 10) (Mahmoodzadeh et al. 2021a):

$${F}_{x}\sim N\left\{\mu \left(x\right), k(x,x)\right\}$$
(10)

where the components of \(\mu \left(x\right)\) are given by an earlier mean capacity \(\mu \left({x}_{i}\right)\), and \(k\) is the portion work. The portion uses two files \({x}_{i}\) and \({x}_{j}\) that provides the covariance between their comparing factors \({F}_{{x}_{i}}\) and \({F}_{{x}_{j}}\). Given vectors of lists \({x}_{i}\) and \({x}_{j}\), \(k\) returns the framework of covariances between all sets of factors where the first in the pair originates from \({F}_{{x}_{i}}\) and the second from \({F}_{{x}_{j}}\). Each \({F}_{{x}_{i}}\) is barely Gaussian, with a mean of \(\mu \left({x}_{i}\right)\) and difference of \(k({x}_{i},{x}_{i})\) (Mahmoodzadeh et al. 2021b).

Assume there has a capacity \(f(x)\) that would want to upgrade. In addition to that, suppose that \(f\) could not be watched legitimately, yet that an arbitrary variable \({F}_{x}\) can be seen that is listed by the same space as \(f\) and whose normal esteem is \(f\), i.e., \(\forall x\in X, E\left[Fx\right]=f(x)\). Notably, it is accepted that the earlier conviction about the capacity \(f\) complies with a Gaussian procedure with earlier mean \(\mu\) and part \(k\). Furthermore, assume that \({F}_{x}\) is a perception of \(f(x)\) that has been tainted by zero-mean, i.i.d. Gaussian clamor, i.e., \({F}_{x}=f(x)+\epsilon\), where \(\epsilon \sim N(0,{\sigma }_{\epsilon }^{2})\). Consequently, \(f(x)\) is a shrouded variable whose back appropriation and could be able to derive in the wake of watching tests of \({F}_{x}\) at different areas in the space. The following subtraction is called Gaussian procedure relapse (Mahmoodzadeh et al. 2021c, d).

Give x a chance to be the arrangement of perceptions focuses and \({F}_{x}\) be the subsequent genuine esteemed perceptions. This required to process the back appropriation of some new point \(\widehat{x}\in X\). The appropriation will be Gaussian with mean and difference (Eqs. 11 and 12).

$$\mu \left(\widehat{x}\left|x)=\mu (\right.\widehat{x}\right)+k\left(\widehat{x},x\right)k(x,x{)}^{-1} ({F}_{x}-\mu (x))$$
(11)
$${\sigma }^{2}\left(\widehat{x}\left|x\right.\right)=k\left(\widehat{x},\widehat{x}\right)-k\left(\widehat{x},x\right)k(x,x{)}^{-1} k(x,\widehat{x})$$
(12)

The key features of the GPR model, which motivate us to use it, are as follows:

  • GPR directly captures the model uncertainty. For example, in regression, GPR directly distributes the prediction value rather than just one value as the prediction. This uncertainty is not directly captured in neural networks.

  • We can add prior knowledge and specifications about the model's shape by selecting different kernel functions when using GPR. For example, based on the answers to the following questions, we may choose different priors. Is the model smooth? Is it sparse? Should it be able to change drastically? Should it be differentiable? This capability gives researchers flexible models, which can be fitted to various kinds of datasets.

In the regression learner app embedded in MATLAB software 2018, four different GPR models are provided: squared exponential, rational quadratic, exponential, and Matern 5/2. After modeling by this program, the model type with the most accurate results is taken into account. Also, the optimization mode is considered in the app, so that the app itself optimizes the amount and type of hyper-parameters of the GPR model. The optimized type and value of the GPR hyper-parameters produced by the regression learner app are presented in Table 2.

Table 2 The optimized parameters of the GPR model
Full size table

The fivefold CV results of cohesion and friction angle predicted by the GPR model are shown in Figs. 2 and 3, respectively. For both actual and predicted values of parameters C and \(\varphi\) in Figs. 2 and 3, the smoothing spline method is used to fit a curve on the data. As in Figs. 2 and 3, both actual and predicted curves change together and agree well. Similar changes in these graphs and their proximity to each other indicate the proper training of the GPR model. Therefore, it can be said that the GPR model has acted correctly and accurately in predicting parameters C and \(\varphi\). With the help of Figs. 2 and 3, it can be seen that in the high values of parameters C and \(\varphi\), the accuracy of the predictions has decreased compared to the low values of these parameters. This may be due to the lack of data in the ranges with high values of C and \(\varphi\). Therefore, the number of data and their range are very effective in predicting the accuracy of a ML model. The R2 results produced by the GPR model for both output parameters of c and \(\varphi\) are shown in Fig. 4. According to Fig. 4, in the GPR model, the R2 values are 0.9615 and 0.7206 for both c and \(\varphi\), respectively. Clearly, the GPR model has shown a higher ability to predict parameter c than parameter \(\varphi\). The other statistical indices results presented in Table 3, also confirm this assessment. The reason can be due to the type of input parameters considered in the forecast model. This means that parameters UCS, UTS, and σ3 have a higher effect on parameter c. However, to achieve higher accuracy in predicting the parameter \(\varphi\), it may be necessary to consider other effective parameters on the parameter \(\varphi\).

Fig. 2
figure 2

Comparison of the cohesion results predicted by the GPR model with the actual ones

Full size image
Fig. 3
figure 3

Comparison of the friction angle results predicted by the GPR model with the actual ones

Full size image
Fig. 4
figure 4

Shear strength parameters results produced by the GPR model vs. the actual results (Left: Cohesion, Right: Friction angle)

Full size image
Table 3 Statistical evaluation indices results for the GPR model
Full size table

4.2 SVR

Vapnik (1995) modified his first version model (ε-support vector regression, SVR) by changing the ε-insensitive loss function. This modification permits the SVR model to use the margin idea in the regression process. Margin in the modified model can be described as the summation of the hyperplane's distances from the two classes' closest points. Minimizing errors between the actual training data and the hyperplane are the main target of the SVR. The kernel function idea has introduced by Vapnik (1995) for nonlinear SVR. Readers are directed to Vapnik (1995) to understand more about SVR (Mahmoodzadeh et al. 2021e).

The key features of the SVR model, which motivate us to use it, is as follows:

SVR is characterized by kernels such as linear, polynomial and Radial basis function (RBF), sparse solution, and Vapnik–Chervonenkis (VC) control of the margin and the number of support vectors. One of the main advantages of SVR is that its computational complexity does not depend on the dimensionality of the input space. It performs lower computation compared to other regression techniques. Additionally, it has excellent generalization capability, high prediction accuracy, and is robust to outliers (Awad and Khanna 2015).

The regression learner app embedded in the Matlab 2018 software was applied to get the SVR model predictions. Six model types, including cubic, linear, medium Gaussian, quadratic, fine Gaussian, and coarse Gaussian, are provided for the SVR method in MATLAB 2018. ThSVR hyper-parameters' type and values were obtained type and values of the SVR hyper-parameters were obtained through the optimization mode in the regression learner app in Table 4.

Table 4 The optimized parameters of the SVR model
Full size table

The fivefold CV results of Mohr–Coulomb parameters of cohesion and friction angle predicted by the SVR model are shown in Figs. 5 and 6, respectively. As in Figs. 5 and 6, the actual values of parameters c and \(\varphi\) are very close to the ones predicted by the SVR model. As the GPR model, the SVR model has also presented good and acceptable predictions. As discussed for the first model, the number of data in certain ranges of the input and output parameters has shown its effect on the prediction curves. However, looking at these figures, it can be seen that the training of the SVR model is also done correctly. The R2 results produced by the SVR model for both output parameters of c and \(\varphi\) are shown in Fig. 7. According to Fig. 7, the SVR model has produced R2 values of 0.9510 and 0.6981 for both c and \(\varphi\), respectively. Clearly, as in the GPR model, the accuracy produced by the SVR model for the prediction of parameter c is higher than the prediction of parameter \(\varphi\). This achievement can also be concluded from other statistical indices results presented in Table 5. Therefore, for the SVR model, it can be said that parameter c is more sensitive to changes in input parameters than parameter \(\varphi\). The correlation between parameter c and inputs is greater than the correlation between parameter \(\varphi\) and model inputs.

Fig. 5
figure 5

Comparison of the cohesion results predicted by the SVR model with the actual ones

Full size image
Fig. 6
figure 6

Comparison of the friction angle results predicted by the SVR model with the actual ones

Full size image
Fig. 7
figure 7

Shear strength parameters results produced by the SVR model vs. the actual results (Left: Cohesion, Right: Friction angle)

Full size image
Table 5 Statistical evaluation indices results for the SVR model
Full size table

4.3 DT

  1. 1.

    The DT is one of the classifications and regression methods based on the non-parametric survived learning technique. Furthermore, it consists of a set of if–then-else decision rules. The best perdition of the model occurs when the DT goes deeper and deeper to make the best fit with the actual data. There are several advantages of the DT. First, the distribution of explanatory variables does not require assumption. Second, strong relations among independent variables do not affect the DT outcomes. Third, various dependent variables such as survived data, categorical and numerical can be covered by DT. Fourth, this technique comprises the influential variables and eliminates the least powerful variables which describe the dependent variable. For the DT, it is possible to predict small and large datasets well, even though this technique was initially developed to only well predict extensive data (Mahmoodzadeh et al. 2020a, b, c).

The algorithm of DT can be explained as follow:

  1. 1.

    First, the calculation of the targeted variance is performed.

  2. 2.

    Based on the various attributes, the database is divided into distinct parts, and the variance of each sectioned part is deducted from the variance before the division. This can be defined as variance reduction.

    The decided node of the attribute is based on the highest VR.

    Node \(N\) can be defined by the variance reduction as Eq. 13:

    $${I}_{\mathrm{V}}\left(N\right)=\frac{1}{{\left|S\right|}^{2}}\sum_{i\in S} \sum_{j\in S}\frac{1}{2}{({x}_{i}-{x}_{j})}^{2}-\left(\frac{1}{{\left|{S}_{\mathrm{t}}\right|}^{2}}\sum_{i\in {S}_{\mathrm{t}}} \sum_{j\in {S}_{\mathrm{t}}}\frac{1}{2}{\left({x}_{i}-{x}_{j}\right)}^{2}+\frac{1}{{\left|{S}_{\mathrm{f}}\right|}^{2}}\sum_{i\in {S}_{\mathrm{f}}} \sum_{j\in {S}_{\mathrm{f}}}\frac{1}{2}{\left({x}_{i}-{x}_{j}\right)}^{2}\right)$$
    (13)

    \(S\) is a group of samples that is not separated yet, \({S}_{\mathrm{t}}\) is a group of separated samples with true result and \({S}_{\mathrm{f}}\) is a group of separated samples with a false result. Without referring to the mean, each of the summands presented above is variance estimates written in a form. Variance estimation is required in each summation term in Eq. 10 so the mean is not referred to directly.

  3. 3.

    Depending on the values of selected attributes, the datasets are separated. If the variance of a part is more than zero, it is separated once more.

  4. 4.

    Keep another trial going until all the data is evaluated.

The key features of the DT model, which motivate us to use it, are as follows:

Decision trees (DTs) are supervision learning algorithms that repeatedly split the sample based on certain sample questions. These are very useful for prediction problems. They are relatively easy to understand and very effective. DTs represent several decisions followed by different chances of occurrence. This technique helps us to define the most significant variables and the relation between two or more variables. In our problem, the variables are related to each other, so we select DT to compare models. In other words, a e decision tree's significant advantage is that it forces the consideration of all possible outcomes of a decision and traces each path to a conclusion. It creates a comprehensive analysis of the consequences along each branch and identifies decision nodes that need.

Key advantages:

  • No preprocessing is needed on data.

  • No assumptions on the distribution of data.

  • Handles collinearity efficiently.

  • DT can provide an understandable explanation for the prediction.

In the DT approach, three models, medium, coarse, and fine, are embedded in the MATLAB 2018. The Mohr–Coulomb parameters predictions were performed through these three models and eventually considered the model that provided more precise results. The information about the optimized DT's hyper-parameters considered in this analysis is provided in Table 6.

Table 6 The optimized model type and hyper-parameters of the DT method
Full size table

The fivefold CV results of Mohr–Coulomb parameters of cohesion and friction angle predicted by the DT model are shown in Figs. 8 and 9, respectively. As in Figs. 8 and 9, the actual values of parameters c and \(\varphi\) are in good agreement with the ones predicted by the DT model. The R2 results of the DT model for both output parameters of c and \(\varphi\) are shown in Fig. 10. According to Fig. 10, the DT model has produced R2 values of 0.9459 and 0.5950 for both parameters c and \(\varphi\), respectively. Clearly, as in the GPR and SVR models, the accuracy produced by the DT model for the prediction of parameter c is higher than the prediction of parameter \(\varphi\). This achievement can also be concluded from other statistical indices results presented in Table 7. Therefore, as the GPR and SVR models, for the DT model, it can be said that parameter c is more sensitive to changes in input parameters than parameter \(\varphi\). The correlation between parameter c and inputs is greater than the correlation between parameter \(\varphi\) and model inputs.

Fig. 8
figure 8

Comparison of the cohesion results predicted by the DT model with the actual ones

Full size image
Fig. 9
figure 9

Comparison of the friction angle results predicted by the DT model with the actual ones

Full size image
Fig. 10
figure 10

Shear strength parameters results produced by the DT model vs. the actual results (Left: Cohesion, Right: Friction angle)

Full size image
Table 7 Statistical evaluation indices result for the DT model
Full size table

4.4 LSTM

The LSTM method is a form of repeat-neural network (RNN), and the final step output data is used in this step. It is utilized for the storing, prediction and classification of time series results. A standard LSTM system comprises an input gate, a cell, a forgotten gate, plus an output gate. Data are recalled by the cell through unspecified times, then the information flows into and out of the cell through the three gates. The problem of long-term RNN dependencies has been solved by LSTM, where the RNN does not expect the word kept in the long term, but it can more precisely expect the latest data. With increasing the duration gap, the RNN can not achieve good outcomes, and LSTM can retain details for a long time by default.

The type and value of the LSTM hyper-parameters considered in this research are presented in Table 8.

Table 8 Type of parameters considered in the LSTM model
Full size table

The fivefold CV results of cohesion and friction angle predicted by the LSTM model are shown in Figs. 11 and 12, respectively. As in Figs. 11 and 12, the actual values of parameters c and \(\varphi\) are very close to the ones predicted by the LSTM model. The R2 results of the LSTM model for both output parameters of c and \(\varphi\) are shown in Fig. 13. According to Fig. 13, the LSTM model has produced R2 values of 0.9842 and 0.8543 for parameters c and \(\varphi\), respectively. Clearly, as in the GPR, SVR, and DT models, the accuracy produced by the LSTM model for the prediction of parameter c is higher than the prediction of parameter \(\varphi\). This achievement can also be concluded from other statistical indices results presented in Table 9. Therefore, as the GPR, SVR, and DT models, for the LSTM model, it can be said that parameter c is more sensitive to changes in input parameters than parameter \(\varphi\). The correlation between parameter c and inputs is more significant than the correlation between parameter \(\varphi\) and model inputs.

Fig. 11
figure 11

Comparison of the cohesion results predicted by the LSTM model with the actual ones

Full size image
Fig. 12
figure 12

Comparison of the friction angle results predicted by the LSTM model with the actual ones

Full size image
Fig. 13
figure 13

Shear strength parameters results produced by the LSTM model vs. the actual results (Left: Cohesion, Right: Friction angle)

Full size image
Table 9 Statistical evaluation indices result for the LSTM model
Full size table

5 Results Comparison

To determine the best prediction model among four ML models used in this paper to predict the shear strength parameters, in Fig. 14 and Table 10, a comparison between the results predicted by them has been made. By analyzing and comparing the values of the obtained statistical evaluation indices for each model, it can be concluded that the prediction performance of the four models for prediction of both cohesion and friction angle parameters from high to low is LSTM, GPR, SVR, and DT (see Fig. 14 and Table 10).

Fig. 14
figure 14

Comparison between the R2 of the prediction models (Left: Cohesion, Right: Friction angle)

Full size image
Table 10 Comparison among the results produced by the ML models
Full size table

Table 10 illustrates the performance index results and system of ranking for ML models of LSTM, GPR, SVR, and DT in predicting rock shear strength parameters. Figure 15 shows the results of the overall ranking graphically. Figure 16 shows five evaluation indices results of the ML models. Lastly, the comprehensive ranking indicates that the LSTM model is the most robust and accurate model compared to the other three models.

Fig. 15
figure 15

Comprehensive ranking comparison of the prediction models

Full size image
Fig. 16
figure 16

Evaluation indices results of the ML models

Full size image

6 Discussion

The problem of overfitting in deep learning methods such as LSTM, when the size of datasets is small, can affect the correct performance of the model. Only 244 data were applied in this study, an order of magnitude less than the data used in language and picture recognition. In ANNs, overfitting is a liable problem because of the availability of many parameters with limited training data. To obtain a reliable prediction, it is essential to avoid overfitting. The use of ANNs to predict parameters C and \(\varphi\) is more challenging due to overfitting potential. The dropout approach is a useful regularization tool considered in this study for the LSTM model to alleviate the overfitting problem. The primary objective of dropout is to prevent networks from becoming overly reliant on individual neurons and minimize co-adaptability among neurons. The neurons are multiplied by a random variable that follows the Bernoulli distribution with a probability of \(p\) at each iteration throughout the training phase. The dropout rate is consistent with (\(1-p\)). The difference in structure between models with and without dropout is shown in Fig. 17. The corresponding formulas are as follows.

Fig. 17
figure 17

Dropout technique for overfitting: (left) without dropout; (right) with dropout

Full size image

Without dropout:

$${\tilde{p }}_{t}={w}_{^\circ }{h}_{t}+{b}_{^\circ }$$
(14)

With dropout:

$$\tilde{p}_{t} = w \circ \tilde{h}_{t} + b \circ = w \circ \left( {r_{t} \odot h_{t} } \right) + b^\circ \,$$
(15)

where \({\tilde{p }}_{t}\) denotes the model output before it is processed by the active function at time \(t\); \({h}_{t}\) denotes the hidden layer's output vector as described in; The weight matrix and bias that connect the hidden and output layers are represented by \({w}_{^\circ }\) and \({b}_{^\circ }\), respectively. The output vector of the hidden layer following dropout is represented by \({\tilde{h }}_{t}\); \({r}_{t}\) denotes a Bernoulli distribution-based random vector. The final model output is:

$${{p}_{t}=f(\tilde{p }}_{t})$$
(16)

where \({p}_{t}\) is the model output; \(f()\) represents the output layer's activation function.

It should be noted that each model predicted the cohesion parameter more accurately than the friction angle parameter. One of the reasons for this is the more significant impact of input parameters on cohesion. Other parameters may be needed to achieve higher accuracy in predicting the friction angle parameter. For example, in this paper, in addition to the three input parameters considered, the cohesion parameter was also considered the fourth input in predicting the friction angle. The values of statistical indices in predicting the friction angle using four input parameters are presented in Table 11. As in Table 11, the friction angle parameter is predicted with higher accuracy by influencing the cohesion parameter as the fourth input in the prediction models. This shows the significant impact of the type of input parameters in predicting the output parameter.

Table 11 Statistical evaluation indices results in the prediction of friction angle parameter considering the cohesion parameter as the fourth input parameter
Full size table

To accurately predict the shear strength parameters of C and \(\varphi\), the impact of factors should be comprehensively studied and evaluated. In this study, three input parameters, including \({\sigma }_{3}\), UCS, and UTS taking into account as the effective parameters on C and \(\varphi\). However, the sensitivity of these parameters individually is unclear on parameters C and \(\varphi\) and needs more study to reveal it. In this study, the mutual information test (MIT) proposed by Verron et al. (2008) is used to investigate the impact of the input parameters on the model output. The MIT is a filtering technique applied to capture the desired relationship between each parameter and the label. This measure is the interdependence between parameters and shows the strength of the relationship between them. The information gain can calculate the mutual information size between the parameters:

$$\mathrm{Gain}\left(Y,X\right)=\mathrm{Ent}\left(Y\right)-\sum_{v=1}^{V}\frac{\left|{Y}^{v}\right|}{\left|Y\right|}\mathrm{Ent}({Y}^{v})$$
(17)

where, \(v\) indicates the number of all possible values for \(X\), \({Y}^{v}\) is the set \(Y\) related to when \(x\) takes \({x}_{v}\), and Ent(Y) is the entropy of the information. As \(\mathrm{Gain}(Y,X)\) increases, the correlation between \(X\) and \(Y\) is increased.

Lastly, according to the score of the parameters in the MIT method, the importance degree of the input parameters on C and \(\varphi\) was calculated. The results obtained by the MIT method are illustrated in Fig. 18 for each input parameter. Looking at Fig. 18, it is revealed that all the three parameters of \({\sigma }_{3}\), UCS, and UTS with important scores of 1. 48, 1.35, and 1.02 in the prediction of parameter C, and with important scores of 1.31, 1.17, and 0.85 in the prediction of parameter \(\varphi\), respectively, have a great impact on the parameters C and \(\varphi\). Therefore, these parameters are influential parameters that need to be considered in predicting C and \(\varphi\). It also should be noted that, among the three input parameters, \({\sigma }_{3}\) and UCS have the most and least impact on predicting parameters C and \(\varphi\), respectively.

Fig. 18
figure 18

Score importance of input parameters on the prediction of parameters C and \(\varphi\)

Full size image

Some scholars such as Shen and Jimenez (2018), Tariq et al. (2017), and Rezaee et al. (2020) have conducted related research on rock shear strength parameters estimation and prediction through machine learning techniques in the past few years. However, achieving high accuracy in using machine learning methods is complex, and it is crucial to select the hyperparameters of the relevant model reasonably at this time.

In order to select the best model hyperparameters, this paper develops a set of hybrid prediction models to prediction of the shear strength parameters, combining LSTM and six metaheuristic optimization algorithms, including grey wolf optimization (GWO), particle swarm optimization (PSO), social spider optimization (SSO), sine cosine algorithm (SCA), multiverse optimization (MVO), and moth flame optimization (MFO). For more information about these algorithms and to get acquainted with them, readers can refer to Zhou et al. (2021), Qiu et al. (2021), and Zendehboudi et al. (2014).

The overall analysis and hybrid modeling process is shown in Fig. 19. According to this figure, the hybrid modeling is mainly divided into four steps: (1) data set preparation; (2) model establishment; (3) model verification and evaluation; (4) result analysis. The six hybrid LSTM-based models i.e., PSO-LSTM, SCA- LSTM, SSO- LSTM, MVO- LSTM, MFO- LSTM, and GWO- LSTM are constructed to predict C and \(\varphi\). The evaluation indices results obtained by these six hybrid models are presented in Table 12. Looking at Table 12, it can be seen that the hybrid models have increased the accuracy of the predictions compared to the non-optimized LSTM model. Also, the use of optimization algorithms to properly select the hyper-parameters has caused the predicted results related to parameter \(\varphi\) to be as accurate as the parameter C. Here, it can be said that one of the most important reasons for the low accuracy of the predictions for the parameter \(\varphi\) with the help of non-optimized previous models was that the type and amount of their hyper-parameters were not optimized. Therefore, optimizing the hyper-parameters of the ML models can be very important and increase the accuracy of forecasting models to a considerable extent.

Fig. 19
figure 19

The overall analysis process of hybrid intelligence models based on LSTM

Full size image
Table 12 Comparison among the results produced by the LSTM model and six hybrid models
Full size table

Table 12 also illustrates the ranking system for the LSTM and six hybrid models of PSO-LSTM, SCA- LSTM, SSO- LSTM, MVO- LSTM, MFO- LSTM, and GWO- LSTM in the prediction of rock shear strength parameters. Figure 20 shows the results of the overall ranking graphically. Figure 21 shows five evaluation indices results of the LSTM model and six hybrid models. The results indicate that, all the hybrid models have produced more acceptable and accurate results than the previous non-optimized techniques. According to Fig. 20, the six hybrid models' prediction performance for predicting cohesion parameters from high to low is PSO-LSTM, GWO-LSTM, MVO-LSTM, MFO-LSTM SCA-LSTM, and SSO-LSTM with ranking scores of 34, 29, 24, 21, 14, and 12, respectively. Also, the six hybrid models' prediction performance for predicting friction angle parameters from high to low is PSO-LSTM, GWO-LSTM, MVO-LSTM, MFO-LSTM, SCA-LSTM, and SSO-LSTM with ranking scores of 34, 31, 23, 18, 15, and 14, respectively. However, the most robust results are produced by the PSO-LSTM model.

Fig. 20
figure 20

Comprehensive ranking comparison of the LSTM model and six hybrid prediction models

Full size image
Fig. 21
figure 21

Evaluation indices results of the LSTM model and six hybrid models

Full size image

Achieving high-precision rock strength parameters in constructing tunnels, dams, buildings, and many other geotechnical engineering problems in the early stages and their construction is fundamental. The proposed PSO-LSTM model in this study is of particular importance in geotechnical engineering. Since laboratory tests require a high time and cost to achieve rock strength parameters, and it is challenging to prepare standard samples for laboratory tests in many cases, the proposed method can be critical. With very little time and cost compared to laboratory tests, this method can produce outstanding results in terms of rock strength parameters.

7 Conclusions

This study first proposed four ML models of GPR, SVR, DT, and LSTM to predict shear strength parameters of C and \(\varphi\). 244 extensive datasets available in the RockData software, including three input parameters of UCS, UTS, σ3, and two targets of c and \(\varphi\) were employed in the models. The fivefold CV method was used to evaluate the prediction performance of the models. The prediction performance of the four models for prediction of cohesion parameter from high to low was LSTM (R2: 0.9842; MAE: 0.846; MSE: 1.677; RMSE: 1.295; MAPE: 0.0009), GPR (R2: 0.9615; MAE: 1.191; MSE: 4.023; RMSE: 2.005; MAPE: 0.0012), SVR(R2: 0.9510; MAE: 1.599; MSE: 5.182; RMSE: 2.276; MAPE: 0.0032), and DT (R2: 0.9459; MAE: 1.7001; MSE: 5.6528; RMSE: 2.3775; MAPE: 0.0043).

Also, it was concluded that the prediction performance of the four models for prediction of friction angle parameter from high to low is LSTM (R2: 0.8543; MAE: 1.336; MSE: 3.448; RMSE: 1.857; MAPE: 1.4301), GPR(R2: 0.7206; MAE: 1.692; MSE: 6.596; RMSE: 2.568; MAPE: 1.827), SVR (R2: 0.6981; MAE: 1.316; MSE: 8.281; RMSE: 2.877; MAPE: 2.9980), and DT (R2: 0.5950; MAE: 2.243; MSE: 9.880; RMSE: 3.143; MAPE: 5.138).

Lastly, compared to the other three models, the comprehensive ranking indicated that the LSTM model is the most robust and accurate model to predict the shear strength parameters of C and \(\varphi\).

In the next step, to fine-tune the hyper-parameters of the proposed LSTM model, six hybrid models combining LSTM model and six metaheuristic optimization algorithms of PSO, GWO, MVO, MFO, SCA, and SSO were developed. The dropout technique was used to overcome the overfitting problem in the LSTM model and six hybrid models. The six hybrid models' prediction performance for predicting cohesion parameters from high to low was PSO-LSTM, GWO-LSTM, MVO-LSTM, MFO-LSTM, SCA-LSTM, and SSO-LSTM with ranking scores of 34, 29, 24, 21, 14, and 12, respectively. Also, the six hybrid models' prediction performance for predicting friction angle parameters from high to low was PSO-LSTM, GWO-LSTM, MVO-LSTM, MFO-LSTM, SCA-LSTM, and SSO-LSTM with ranking scores of 34, 31, 23, 18, 15, and 14, respectively. However, the most robust results were produced by the PSO-LSTM model.

Finally, the results indicated that using the metaheuristic optimization algorithm to tune the hyper-parameters of the LSTM model can significantly improve the prediction results.

The MIT method was applied in order to sensitivity analysis of the input parameters considered in this study on the prediction of parameters C and \(\varphi\). Finally, it was revealed that all the three parameters of \({\sigma }_{3}\) UCS, and UTS with important scores of 1. 48, 1.35, and 1.02 in predicting parameter C, and essential scores of 1.31, 1.17, and 0.85 in predicting parameter \(\varphi\), respectively, significantly impact the prediction the parameters C and \(\varphi\).

It should be noted that the PSO-LSTM hybrid model proposed in this study as the most robust model for predicting the parameters C and \(\varphi\) just is recommended in similar conditions because it is designed based on the model inputs considered in this study. Furthermore, the procedure to predict the parameters C and \(\varphi\) introduced by this research can be implemented by other deep learning hybrid models and different optimization algorithms. The focus of this research was on the parameters C and \(\varphi\), although LSTM-based hybrid techniques could be used to predict a wide range of geotechnical engineering problems.

Lastly, the hybrid PSO-LSTM model proposed in this study is practicable in estimating the parameters C and \(\varphi\) under similar conditions in terms of characteristics of rock mass and material conditions. The proposed models in this study can be used as practical techniques to estimate the parameters C and \(\varphi\) for similar rock mass and material properties in the site investigation step.

It is recommended that other deep learning-based hybrid techniques to predict the parameters C and \(\varphi\) and other rock strength parameters. In addition, in the next plan, more laboratory tests may be helpful to enrich more datasets to train and construct the deep learning hybrid models for predicting the parameters C and \(\varphi\).