1 Introduction

In tunnelling, construction of roads and dams in hilly areas, and foundations for buildings and other infrastructure, uniaxial compressive strength (UCS) has significantly and profoundly influenced the behaviour of intact rock. As the rock is heterogeneous and anisotropic, the value of UCS changes from place to place. Along with the heterogeneity, impurities are also present in the rock, which may be introduced during its formation and affect its strength as shown in Fig. 1. The primary method for assessing UCS is laboratory testing of the specimens according to the guidelines established by the Bureau of International Society for Rock Mechanics (ISRM), the American Society for Testing Materials (ASTM), and the Indian Standard (IS) [1, 2]. Often, laboratory trials do not offer a time or money-efficient way to estimate the strength of a rock directly [3]. Additionally, exposure to a sufficient number of high-quality core specimens is a condition that is difficult to meet in delicate or severely worn rocks. Therefore, the researchers have tried to estimate UCS by indirect methods; i.e., statistical techniques like simple and multivariate regression methods are often used to develop empirical equations [4,5,6,7,8].

Fig. 1
figure 1

Images showing heterogeneous structure as well as impurities in the specimens after UCS test

Full size image

Mishra and Basu [9], Lashkaripour [10], and Aydin and Basu [11] used rock geomechanical properties and index tests to estimate UCS. Tugrul and Zarif [8] used porosity to predict UCS, while Mishra and Basu [9] predicted UCS with index tests such as the block punch index test (BPI) and the PLI. In recent years, several equations for the prediction of UCS have been developed; some of these are presented in Table 1. With the development of artificial intelligence (AI), Mishra et al. [20], Madhubabu et al. [14], and Yilmaz and Yuksek [15] applied soft computing methods for solving geotechnical and rock engineering problems, which have shown considerable and promising results [15, 21,22,23,24,25]. Soft computing approaches function like the human mind and can learn in uncertain and imprecise situations. Examples of modern UCS prediction approaches that emphasise probabilistic and soft computation strategies include multiple linear regression (MLR), particle swarm optimisation (PSO), generalised feed-forward neural network (GFFN), radial basis function (RBF), adaptive neuro-fuzzy inference systems (ANFIS), multi-layer perceptron (MLP), support vector regression (SVR), genetic programming (GP), and Sugeno fuzzy logic. Some of the techniques are mentioned in Table 2.

Table 1 Examples of simple and multiple regression equations for predicting UCS
Full size table
Table 2 Some soft computing models for predicting UCS
Full size table

In this paper, input parameters (PLI, porosity (n), bulk density (ρ), water content (%), and P-wave velocity (Vp)) were selected in such a manner that they were either index test (PLI) or non-destructive test (P-wave velocity), and some of them had their physical properties. Then correlation was generated amongst UCS and other parameters with the simple and multiple regression techniques. Then, soft-computing methods were applied to generate a predictive model of UCS from the input parameters as discussed above. Soft computing models are KNN, LSTM, ANN-PSO, and ANFIS-PSO. A check was done, and an error matrix was drawn to validate the model’s adequacy. Then, the model with the least error is finalised as the best predictive model for UCS.

2 Material and Methods

2.1 Study Area

The study area is Jharia of Dhanbad district in Jharkhand state, India, at a latitude of 23.74° N and longitude of 86.41° E, as shown in Fig. 2. The economy of Jharia mainly depends on local coal mines to produce coke. Sandstone (a sedimentary rock) and coal (a metamorphosed sedimentary rock) are also available in this area. The sedimentary rock in this region belongs to the Gondwana, around 200 million years old.

Fig. 2
figure 2

Location map of sandstone at Jharia in Jharkhand, India

Full size image

2.2 Specimen Preparation

Cores were brought from the site, and the specimens were prepared for different tests, i.e., UCS, PLI, P-wave velocity, density, water content, and porosity. For specimen preparation, the precision of the Indian Standard (IS) code is considered [1, 28]. Due to the challenges and time constraints associated with preparing rock specimens for laboratory testing, it is necessary to carefully measure and cut the specimens. This approach ensures that the remaining portions of the rock cores can be utilised for the measurement of additional physical properties such as density, porosity, and water content.

The diameter of the specimens was 47.5 mm. The specimens were prepared with a ratio of length to diameter between 2.5 and 2.7, and the length of each specimen was measured in the range of 119 to 127 mm. Then, the edges of the specimen were ground and polished so that the ends were flat to ±0.02 mm [29]. The P-wave velocity is a non-destructive test, so the P-wave test and UCS are performed on the same sample. The specimens for PLI are cut in such a way that their L/D ratio is greater than 1.5 so that a diametrical point load index test can be performed. The specimen density is measured by the water displacement method, in which the part of the specimen is weighed, and its volume is measured by the water displacement method [30]. For water content measurement, the specimen’s bulk weight is measured and then kept in the oven for 24 h at 100 ± 5 °C, and then its dry weight is measured. An empirical formula is used to find water content, as given in Table 3. An empirical equation is used for porosity measurements, as suggested by IS code [34]. All the results of the tests are shown in Table 4.

Table 3 Standards for determination of different parameters of rocks
Full size table
Table 4 Descriptive statistics of the laboratory work
Full size table

2.3 Simple Regression

Regression is a statistical method for exploring the nature and strength of the relationship between a single dependent variable (often represented by the letter Y) and a single independent variable (often represented by the letter X). The straight line represents linear regression, and its slope demonstrates how changes in the independent variable impact changes in the dependent variable. The y-intercept of the linear regression line is the value of the dependent variable value when all other values are zero. The other nonlinear regression methods are substantially more complex. Nonlinear regression is a type of regression analysis that can be used to draw conclusions about the underlying relationships between the independent variables and the observed data by using a nonlinear function combination of the independent model parameters and one or more independent variables. Consecutive approximations are used to fit the data. A statistical model of this sort is used in nonlinear regression to establish relationships between a set of independent variables (x) and a set of observed dependent variables (y). Nonlinear functions include the exponential, logarithmic, trigonometric, power, and Gaussian functions, as well as the Lorentz and Gaussian distributions.

2.4 ANFIS

When something is unclear or cannot be defined in a specific manner, we refer it as having “fuzzy” qualities. In the actual world, there are situations with no clear “right” answer to an issue or a statement. At this juncture, the most optimal answer between the true and the false is the idea of outcome flexibility.

Conventional methods for tackling diverse civil engineering problems are inadequate for dealing with uncertainty and are not well-defined [35]. Machine learning is quite useful in the examination of these types of systems. Fuzzy logic, network-based, and genetic algorithms are a few examples of machine-learning techniques. Fuzzy logic provides the advantage of accounting for numerous real-world uncertainties. The if-then fuzzy rule creates systems, although neural networks have several advantages. The combination takes advantage of both technologies and creates a hybrid system known as the ANFIS, which stands for adaptive network-based fuzzy inference system [36] (Fig. 3).

Fig. 3
figure 3

An ANFIS model structure

Full size image

2.5 ANN

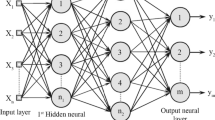
Artificial neural networks are built up of “units,” which are essential artificial neurons. These components of the system of artificial neural networks collectively are organised in a series of layers. A layer’s density of units may range from a few to millions, depending on the complexity of the underlying system. Input, output, and hidden layers are the usual constituents of ANN. Information outside the neural network processing unit is sent into the input layer. The data are routed via a succession of hidden layers before being changed into a format readable by the final layer. The output layer produces an artificial neural network’s reaction to the incoming data.

Most neural networks link units from one layer to the next. Each of these links has associated weights that define the impact of one unit on another unit. As input is sent from one unit to another unit, the neural network acquires ever-increasing knowledge of the data, resulting in an output from the output layer (Fig. 4).

Fig. 4
figure 4

The structure of an ANN model

Full size image

The weights and biases of the neurons in an ANN model are obtained using the sets of output data after training the model using the known input datasets. The network is trained to get the most appropriate values for the different weights and biases. There are many methods for determining the ideal weights and biases. In this paper, particle swarm optimisation (PSO) using MATLAB optimise the network’s training. After the network has been adequately trained using a training dataset, it is tested using a testing dataset.

2.6 Particle Swarm Optimisation (PSO)

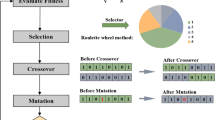
In this paper, we focused only on particle swarm optimisation (PSO), which was used to improve the results of the ANN and ANFIS models. A potent meta-heuristic optim technique, particle swarm optimisation (PSO), is motivated by the swarm behaviour seen in nature, such as fish and bird schools, and was proposed by Kennedy and Eberhart in 1995 [37]. PSO simulates a streamlined social structure. The PSO algorithm’s initial goal was to visually imitate a flock of birds doing an elegant yet unexpected ballet. Any bird’s viewable range is limited in nature to a certain area. However, having several birds in a swarm enables all of the birds to be aware of the greater surface of a fitness function. A population of potential solutions, or “swarm,” is how a fundamental variation of the PSO algorithm operates (called particles). These particles are shifted in the search space using a few simple formulae. Each particle’s best-known location in the search area and the best-known position of the whole swarm serve as a guide for its motions. When more advantageous spots are found, the swarm motion will then be directed by these. Repetition of the procedure increases the likelihood that a workable solution will be found at the end as a result.

During the first search phase, the basic PSO technique often converges quickly and subsequently slows down. It is prone to being caught in local minima exhibiting sluggish convergence. Furthermore, inertia weights w, c1, and c2 significantly influence the PSO convergence. The main difference between PSO and the basic PSO approach is how each particle is updated. The following equations are used to update the location and velocity of the particles in this algorithm:

$${Vi}^{k+1}=\left(2{r}_1-0.5\right){v_i}^k+\left(2{r}_2-0.5\right)\ \left({{\textrm{Pbest}}_i}^k\hbox{--} {x_i}^k\right)+\left(2{r}_3-0.5\right)\ \left({\textrm{Gbest}}^k\hbox{--} {x_i}^k\right)$$
(1)
$${W}^{k+1}=\left(2{r}_4-0.5\right)\ \left({\textrm{Gbest}}^{\textrm{k}}\hbox{--} {{\textrm{Pbest}}_{\textrm{i}}}^{\textrm{k}}\right)+\left(2{r}_5-0.5\right)\ \left({\textrm{Gbest}}^{\textrm{k}}\hbox{--} {x_i}^k\right)$$
(2)
$${X_i}^{k+1}={{\textrm{Pbest}}_{\textrm{i}}}^{\textrm{k}}+\left(2{r}_6-0.5\right){v_i}^{k+1}+\left(2{r}_7-0.5\right)\ {w}^{\textrm{k}+1}$$
(3)

where r1, r2, r3… are random numbers between 0 and 1, Pbest is the position that gives the best f(X) value explored by the particle i, and Gbest is the best value of f(x) that is explored by all the particles in the swarm. Similarly, Xi is the particle’s position, W is inertia weight, and Vi is the particle’s velocity.

ANN has ten hidden layers, whereas ANFIS has five hidden layers. Based on this, the ANN-PSO and ANFIS-PS0 models run. The maximum number of iterations is limited to 500, with an inertia weight of 1 and a damping rate of 0.99, and with the values of C1 and C2 equal to 1.0 and 2.0, respectively. The flow chart for the working of ANN and ANFIS with PSO is shown in Fig. 5.

Fig. 5
figure 5

The structure of ANN and ANFIS along with PSO

Full size image

2.7 K-NN

The K-nearest neighbours algorithm (k-NN) is a non-parametric supervised learning approach pioneered in 1951 by two statisticians, namely, Evelyn Fix and Joseph Hodges [38]. For a continuous outcome, K-NN regression is a non-parametric approach that averages the data in the same neighbourhood to approximate the relationship between the independent variables. While it may be used for regression and classification problems, it is often used as a classification approach base on the assumption that equivalent points can be found nearby. Regression problems are similar to classification problems in that the average of the k-nearest neighbours is used to construct a classification prediction. The main distinction is that classification is use for discrete data, while regression is use for continuous values. However, before creating a category, the distance must be calculated. The Euclidean distance d (x, y), provided in Eq. 4, is the most commonly used distance, and the nearest neighbour for the model is five with leaf size set at 30.

$$d\left(x,y\right)=\sqrt{{\left(\sum \nolimits_{i-1}^n\Big({y}_i-{x}_i\right)}^2}$$
(4)

2.8 LSTM

One artificial neural network used in deep learning and AI is long short-term memory (LSTM). Unlike traditional feed-forward neural networks, LSTM contains feedback connections. In addition to analysing single data points (like photographs), a recurrent neural network (RNN) can examine whole data sequences (such as speech or video). Due to this quality, LSTM networks are ideal for data processing and prediction.

The LSTM cell is made up of three gates. A forget gate, an input gate, and an output gate are all included. The gates determine which information is significant and which may be ignored. The cell state and hidden state are the two states of the cell, which are constantly updated and include information from prior to the current time steps. The cell state represents “long-term” memory, while the concealed state represents “short-term” memory.

Each LSTM cell goes through a series of cyclical phases. First, the forget gate has been calculated. Then, the value of the input gate is calculated. The two outputs mentioned above are used to update the cell state, and lastly, the output gate is used to calculate the output (hidden state). Every LSTM cell goes through this process. The LSTM notion is that the cell and hidden states carry past knowledge and pass it on to subsequent time steps. The cell state aggregates all the previous data information and serves as the long-term information retainer. The hidden state stores the output of the previous cell, or short-term memory. Because of the mix of long-term and short-term memory approaches, LSTMs function well with time series and subsequent data. Figure 6 shows the structure of LSTM, in which Ct-1 is the cell state vector, ht is the hidden state vector of the LSTM unit, Xt-1 is the input vector of the LSTM unit, and w is the weight matrix, which needs to be learnt during the process of training. Similarly, σ and tanh are the activation functions. Five input parameters (i.e., PLI, porosity, density, water content, and P-wave velocity) and one output parameter (UCS) have been used in the present model. The sigmoid (σ) has been used as the activation function, and the number of epochs used in the model is 500.

Fig. 6
figure 6

The structure of LSTM

Full size image

2.9 Model Validation and Performance Assessment

The ten important statistical measures are the coefficient of determination (R2), the mean biased error (MBE), the median absolute deviation (MAD), the weighted mean absolute percentage error (WMAPE), the root mean square error (RMSE), the mean absolute error (MAE), the expanded uncertainty (U95), the global performance indicator (GPI), the mean absolute percentage error (MAPE), and the value account for (VAF) [39]. For the optimal model, the ideal value of R2 is 1, VAF is 100%, and the values of the parameters; i.e., RMSE, MAE, MBE, WMAPE, U95, and MAPE are 0. Mathematical expressions for these parameters are given below.

$${R}^2=\frac{\sum_{i=1}^n{\left({a}_{\textrm{i}}-{a}_{\textrm{mean}}\right)}^2-{\sum}_{i=1}^n{\left({a}_{\textrm{i}}-{y}_{\textrm{i}}\right)}^2}{\sum_{i=1}^n{\left({a}_{\textrm{i}}-{a}_{\textrm{mean}}\right)}^2}$$
(5)
$$\textrm{RMSE}=\sqrt{\frac{\sum_{i=1}^n{\left({a}_{\textrm{i}}-{y}_{\textrm{i}}\right)}^2}{\textrm{N}}}$$
(6)
$$\textrm{MAE}=\frac{\sum_{i=1}^n\left|\left({y}_{\textrm{i}}-{a}_{\textrm{i}}\right)\right|}{N}$$
(7)
$$\textrm{MBE}=\frac{\sum_{i=1}^n\left({y}_{\textrm{i}}-{a}_{\textrm{i}}\right)}{N}$$
(8)
$$\textrm{MAD}=\textrm{median}\left(\left|{y}_1-{a}_1\right|,\left|{y}_2-{a}_2\right|,\cdots \cdots, \left|{y}_{\textrm{n}}-{a}_{\textrm{n}}\right|,\right)$$
(9)
$$\textrm{WMAPE}=\frac{\sum_{\textrm{i}=1}^{\textrm{n}}\left|\frac{{\textrm{a}}_{\textrm{i}}-{\textrm{y}}_{\textrm{i}}}{{\textrm{d}}_{\textrm{i}}}\right|\times {\textrm{a}}_{\textrm{i}}}{\sum_{\textrm{i}=1}^{\textrm{n}}{\textrm{a}}_{\textrm{i}}}$$
(10)
$${\textrm{U}}_{95}=1.96{\left(\textrm{RMS}{\textrm{E}}^2+\textrm{S}{\textrm{D}}^2\right)}^{1/2}$$
(11)
$$\textrm{GPI}=\textrm{RMSE}\times \textrm{MBE}\times {\textrm{U}}_{95}\times {\textrm{t}}_{\textrm{stat}}\times \left(1-{\textrm{R}}^2\right)$$
(12)
$$\textrm{MAPE}={\sum}_{\textrm{i}=1}^{\textrm{n}}\left|\frac{{\textrm{y}}_{\textrm{i}}-{\textrm{a}}_{\textrm{i}}}{{\textrm{a}}_{\textrm{i}}}\right|\times 100\%$$
(13)
$$\textrm{VAF}=\left(1-\frac{\operatorname{var}\left({\textrm{y}}_{\textrm{i}}-{\textrm{a}}_{\textrm{i}}\right)}{\operatorname{var}\ {\textrm{a}}_{\textrm{i}}}\right)\times 100$$
(14)

where ai is the observed value at the ith data point, yi is the predicted value at the ith data point, amean is the mean of the observed value, and N is the total number of data points. The short-term effectiveness of the formula is assessed by comparing the expected value to the actual value and then calculating U95. The U95 displays uncertainty up to a 95% confidence level, the coverage factor is 1.96, and the standard deviation of the difference between the projected and actual data is the standard deviation (SD). Through Eq 12, we can see the mathematical connection between the GPI’s five constituent parts. Therefore, a higher GPI number implies a more accurate model, whereas a lower GPI value indicates an erroneous model.

2.10 Data Pre-processing

The dataset is separated into training and testing sets for creating a soft computing model. The model is trained on one set of data and then tested on another set to determine its accuracy. Seventy percent of the data is used when training the model, while 30% is reserved for testing. The data used for training and testing were chosen at random. After the available data is partitioned into distinct subgroups, the variables are pre-processed by rescaling them to an appropriate form. As a result of removing the dimension of the variables, scaling makes it such that all inputs roughly have the same range of values. All research variables, input and output alike, are scaled from 0 to 1 by normalising against their maximum and minimum values using Eq. 15.

$$y=\frac{x-{x}_{min}}{x_{max}-{x}_{min}}$$
(15)

where y represents normalised input and output variables, x represents the actual input and, output variables, and xmax and xmin represent the maximum and the minimum values.

3 Results and Discussion

3.1 Simple Regression

The tested results for porosity, PLI, density, water content, P-wave, and UCS values of the laboratory test on sandstone rocks are given in Table 4. The simple regression technique has been used to develop the relation between UCS with porosity, PLI, density, water content, and P-wave velocity. The graph obtained is linear, logarithmic, and exponential, as depicted in Fig. 7. After analysing all the plots, it can be said that all the regressions are giving good results with the correlation between UCS and PLI being the best, with R2 equal to 0.86. All these results are incorporated in Table 5 with correlation equations and their corresponding R2 values (Table 5).

Fig. 7
figure 7

Simple regression plot between UCS and other properties of sandstones

Full size image
Table 5 Results of correlation studies between UCS and different physical properties of sandstone using the simple regression technique
Full size table

3.2 Multilinear Regression

The simple regression results show that a single parameter cannot adequately predict UCS values. Therefore, multiple parameters are used for the prediction of UCS values. The results of the multilinear regression analysis between UCS and other physical and mechanical properties of the rocks, i.e., PLI, porosity, density, water content, and P-wave velocity, are given in Table 6 and Fig. 8a, b, c, and d. From this, it is evident that the coefficient of determination (R2) has increased from 0.86 to 0.93 as the number of independent variables increases. It is also observed that PLI and P-wave velocity are the more influential parameters for the UCS values.

Table 6 Results of correlation studies between UCS and different physical and mechanical properties of sandstone rocks using multivariate techniques
Full size table
Fig. 8
figure 8

Graphs between predicted and actual values of UCS obtained from multivariate regression analysis

Full size image

3.3 Soft Computing Technique

The dependency of all five independent parameters mentioned above is measured with AI models, and the best of all these models is finalised as the predicted model. Four AI models have been developed to predict the value of UCS, i.e., ANN-PSO, ANFIS-PSO, K-NN, and LSTM models. First, the data is normalised and then divided into two parts training (TR) and testing (TS) purposes in a ratio of 70% and 30% on a random basis. Then, ANN-PSO and ANFIS-PSO models are run in MATLAB-22, while KNN and LSTM models are run in Python. Graphs are plotted between the predicted and actual UCS values of ANN-PSO, ANFIS-PSO, K-NN, and LSTM to analyse the results, as shown in Figs. 9, 10, 11, and 12, respectively.

Fig. 9
figure 9

Correlation between predicted and actual UCS values generated with ANN-PSO for training (TR) and testing (TS) dataset

Full size image
Fig. 10
figure 10

Correlation between predicted and actual UCS values generated with ANFIS-PSO for training (TR) and testing (TS) dataset

Full size image
Fig. 11
figure 11

Correlation between predicted and actual UCS values generated with KNN for training (TR) and testing (TS) dataset

Full size image
Fig. 12
figure 12

Correlation between predicted and actual UCS values generated with LSTM for training (TR) and testing (TS) dataset

Full size image

3.4 Error Plot

For better analysis of the models developed from ANN-PSO, ANFIS-PSO, LSTM, and KNN, graphs are plotted to show the combination of error between actual and predicted UCS for each specimen. After analysing all four models, it is seen that the error per specimen is the least in the KNN model, with a minimum error close to 0 and a maximum error of 14.88%, and a maximum in the LSTM model, with a maximum error of 18.37% and the minimum value close to 0. This analysis can be seen in Figs. 13, 14, 15, and 16. The histogram graph is plotted to visualise the error difference among all the models, as shown in Fig. 17.

Fig. 13
figure 13

UCS predicted values along with the error by ANN-PSO model

Full size image
Fig. 14
figure 14

UCS predicted values along with the error by ANFIS-PSO model

Full size image
Fig. 15
figure 15

UCS predicted values along with the error by KNN model

Full size image
Fig. 16
figure 16

UCS predicted values along with the error by LSTM model

Full size image
Fig. 17
figure 17

Error diagram of all the models (ANN-PSO, ANFIS-PSO, K-NN, LSTM)

Full size image

3.5 Error Matrix

The error matrix has been drawn for the detailed analysis of the four models with their training and testing data, as shown in Fig. 18. It is a comparison matrix for the performance parameters to find the best model. The matrix including R2, MAPE, and RMSE is used to assess the level of accuracy associated with the model’s performance. R2, RMSE, and WMAPE values should all be set to one, zero, and zero, respectively, for optimal performance. Depending on the study, the proficiency of all models for both the training and testing datasets R2, RMSE, MAE, MBE, MAD, WMAPE, U95, GPI, VAF, and MAPE values were found to be between 81 and 99.62%, 2 and 14%, 0 and 11%, close to 0%, 0 and 10%, 0 and 28%, 6 and 38%, close to 0, 1 and 16%, and 0 and 15%, respectively. The error matrix is a comparison heat map showing the best performance settings. Further compression tests are performed to compare the models, and their overall accuracy is rated from 0 to 38%. All the training and testing data for proficiency are given in Table 7 and Table 8, respectively.

Fig. 18
figure 18

The error matrix for ANN-PSO, ANFIS-PSO, KNN, and LSTM models

Full size image
Table 7 Proficiency parameters for the training dataset
Full size table
Table 8 Proficiency parameters for the testing dataset
Full size table

4 Conclusions

In the present study, five parameters, namely, the point load strength (PLI), porosity, water content, density, and P-wave velocity, were considered to predict the UCS of the sandstone rocks. The performance of multilinear regression was found to be better than that of simple regression. Simple regression has the best value of R2 of 0.86, while multilinear regression has the best value of R2 of 0.93. However, it was found that the performance of soft computing models was better than multiregression analysis with ANFIS-PSO (TR) having the best value of R2 of 0.99.

The performance of the KNN model is the best among all the four soft computing models used in the present study, with R2 equal to 0.95 for training and 0.94 for testing, RMSE equal to 0.03 for training and 0.04 for testing, and GPI close to 0 for both training and testing. The error matrix (Fig. 18) shows that the training result for the KNN model is almost green. Hence, it can be concluded that the KNN model can best predict UCS values from PLI, porosity, water content, density, and P-wave velocity for sandstone rocks from Jharia, Dhanbad district of Jharkhand in India.

Since the present study is for sandstone rocks from Jharia, Dhanbad district of Jharkhand in India, it is therefore recommended to develop similar correlation equations for other types of rocks in the study area.