1 Introduction

Most types of rocks exhibit time-dependent behavior. During the excavation of a tunnel, the surrounding rock deforms gradually due to the natural rock rheology. After the excavation is complete, supports typically in the form of concrete or shotcrete liners are put in place to seal the rock and to reduce radial deformations. Displacements of the surrounding rock and pressure between liner and rock are critical parameters to be determined for tunnel design. Therefore, proper simulation of the sequence of actions involved in tunneling, including the whole process of excavation and support construction, is of great importance to obtain a reliable tool for the determination of optimal values of tunneling parameters to achieve optimal design.

This problem can be tackled either numerically or analytically. Numerical methods are widely used in many complex underground projects (Chehade and Shahrour 2008; Prazeres et al. 2012). Although numerical methods such as finite element, finite difference, discrete element, and boundary element can provide useful answers, the insight into the nature of the problem that can be gained from analytical solutions is an important aspect that cannot be overlooked (Carranza-Tores and Fairhurst 1999). In fact, analytical solutions in closed form can be used to obtain a first estimation of the design parameters, providing guidance in the conceptual stage of the design process. They make it possible to run parametric analyses for a wide range of values of the problem parameters so that a better understanding of the physics of the problem can be gained by investigating the sensitivity of the solution to the input parameters. In addition, closed-form solutions provide a benchmark against which the overall correctness of numerical analyses can be assessed.

Tunnel excavation is a long-term process which takes place over a significant time, during which the tunnel face advances at variable speed. If a cross-section of the tunnel is considered, its radius grows over time according to the excavation process employed. However, in the closed-form analytical solutions presented in the literature to date, the excavation process is assumed to be instantaneous. In this paper, instead, the excavation time is accounted for so that the influence of the excavation process on the final tunnel convergence and pressure acting on the liners can be investigated by a parametric analysis. This allows optimization of the excavation time, which thus becomes a design parameter.

Analytical solutions for stresses within a wedge-shaped body subject to gravity were presented by Rashba (1953), who carried out the earliest analytical studies on problems with time-dependent geometry. The first analytical research in civil engineering considering construction processes considered stress analysis of filled culverts (Brown et al. 1968; Christiaon and Chuntranuluk 1974). Analytical solutions for some problems with changing geometry were also provided by Namov (1994). More recently, research has been carried out to seek analytical solutions for viscoelastic problems involving time-dependent boundary regions using the principle of correspondence (Cao 2000; Wang and Nie 2010; Wang and Cao 2006). In tunnel construction, unlike the aforementioned research, the domain of the problem decreases during the excavation stage, and increases subsequently during the construction of the liners. Furthermore, the surrounding ground material is rheological; i.e., its mechanical properties are time dependent. These factors add to the complexity of the problem, making it difficult to achieve analytical solutions in closed form.

Unlike the case of linear elastic materials with constitutive equations in the form of algebraic equations, linear viscoelastic materials have their constitutive relations expressed by a set of operator equations. In general, it is very difficult to obtain analytical solutions for most viscoelastic problems, especially in case of time-dependent boundaries, although some closed-form or theoretical solutions have been developed for excavations in rheological rock (Gnirk and Johnson 1964; Ladanyi and Gill 1984; Brady and Brown 1985). However, in all these works, excavation is assumed to take place instantaneously. Concerning the geomaterial–liner interaction, several studies (Savin 1961; Peck et al. 1972; Einstein and Schwartz 1979) have been carried out for excavations in elastic or viscoelastic rock. Sulem et al. (1987) presented an analytical solution to determine the radial displacements and the pressure applied on tunnel linings having assumed a Kelvin–Voigt model to describe the time-dependent behavior of the surrounding rock. Using the complex variable method and assuming the rock to be elastic, Wang and Li (2009) achieved analytical solutions for the fields of stress and displacement around a lined circular tunnel, accounting for both misfit and the interaction between liner and the surrounding geomaterial. In previous research (Sulem et al. 1987; Ahmad et al. 2010), the effect of the progressive advancement of the tunnel face along the longitudinal direction was accounted for. Assuming an isotropic stress state and a viscoelastic Burgers model for the rock, Nomikos et al. (2011) derived analytical solutions in closed form and performed a parametric study on the effect of the liner parameters. Different supports such as sprayed liners, two-liner systems, and anchor-grouting support were analyzed by Mason and Stacey (2008) and Mason and Abelman (2009). Liners were assumed to be instantaneously applied at the end of the excavation. In tunnel practice, however, liners may be installed at any time after excavation, which is the case considered in this paper.

In summary, in the current literature on the construction of lined tunnels in viscoelastic rock, the process of excavation is ignored and only the longitudinal advancement of the tunnel face is considered by introducing a fictitious lining pressure so that the problem can be mathematically cast as a fixed boundary problem. Many problems of linear viscoelasticity can be solved using the principle of correspondence (Lee 1955; Christensen 1982; Gurtin and Sternberg 1962). However, the cross-section of a tunnel is excavated in stages, which implies a time-dependent geometrical domain, so the principle of correspondence cannot be employed.

In this paper, an axisymmetric tunnel excavated in rheological rock supported first by a primary liner, then by a secondary one is analyzed. The rheological properties of the rock mass are accounted for within a unified viscoelastic model. Also a time-dependent excavation process is considered in the development of the solutions, assuming that the radius of the tunnel grows from zero until its final value according to a time-dependent function to be specified by designers. Although the obtained analytical solutions are rigorously applicable only to the axisymmetric case, i.e., a single deeply buried tunnel, Schuerch and Anagnostou (2012) demonstrated that solutions achieved for axisymmetric conditions are still valid for a wide range of different ground conditions and for several cases of noncircular tunnels with small error. In case of twin tunnels, the solution is applicable only if the distance between the tunnels is such that the influence of the presence of one tunnel on the stress state of the rock around the other is negligible.

In this paper, first the proposed analytical solutions are derived, then two examples are considered to illustrate the influence of the excavation process and the installation times of the liners on the obtained time-dependent stresses and displacements.

2 Definition of the Problem

Excavation of an axisymmetric circular tunnel in a rheological rock mass is considered. The following assumptions are made:

  1. 1.

    The rock mass is homogeneous, isotropic, and linearly viscoelastic.

  2. 2.

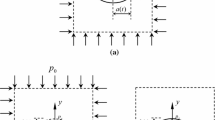
    The tunnel is first excavated and then supported by the construction of two liners at different times. First the radius of the tunnel grows from zero to R 1, at the end of the excavation; secondly support is provided by a temporary concrete liner; third, after some time, a second, permanent liner is installed. The problem is cast as a two-dimensional (2D) infinite viscoelastic plane subject to a hydrostatic uniform stress with a circular opening whose radius varies with time.

  3. 3.

    The rate of excavation is small, so that it can be assumed that it does not induce any dynamic stress.

In the analysis, the effect of the advancement of the tunnel along the longitudinal direction is not accounted for. This means that the cross-section considered in this analysis is at a sufficient distance from the tunnel face that stresses and strains are unaffected by three-dimensional effects. The tunneling process can be divided into three stages. During the first stage (excavation stage) spanning from time \( t = 0 \) to \( t = t_{1} \), with t 1 being the installation time of the first liner, the radius of the tunnel varies as follows:

$$ R(t) = \left\{ {\begin{array}{*{20}l} {R_{0} + a(t)} & {0 \le t \le t_{0} } \\ {R_{1} } & {t > t_{0} } \\ \end{array} } \right.$$
(1)

with \( R(t) \) being the time-dependent radius of the tunnel, R 1 the final tunnel radius at the end of the excavation process, R 0 the initial radius \( ({0 \le R_{0} \le R_{1} }) \), and \( a = a(t) \) being a function accounting for the actual excavation process as prescribed by the designers. t 0 is the end time of the excavation. From t 0 to t 1, the rock is free to expand since no liners are present. In this stage, no supporting pressure is present. In order to release part of the pressure, the first liner is often put in place after some time elapses from the end of excavation. Hence, in this derivation, the first liner is built at time \( t = t_{1} \), with \( p_{1} (t) \) being the contact pressure between rock and the first liner. The second stage (first liner stage) spans from the installation of the first liner at \( t = t_{1} \) to the installation of the second liner at \( t = t_{2} \). The third stage (second liner stage) spans from the installation of the second liner, at time \( t = t_{2} \), onwards. For \( t > t_{2} \), the contact pressure between rock and the first liner is \( p_{2} (t) \) with \( q_{1} (t) \) being the pressure between the first and the second liner.

3 Mechanical Analysis During the Construction Process

3.1 Analysis of the Rock Mass

Cylindrical coordinates (r, \( \theta \), z) are employed in the derivation of the analytical solution. As shown in Fig. 1, \( p_{0} \) is the hydrostatic in situ stress. The boundary condition for the rock mass is

Fig. 1
figure 1

Boundary conditions for rock and liners

Full size image
$$ \sigma_{r} (R(t),t) = -p(t), \quad \sigma_{r} (\infty ,t) = -p_{0} (t), $$
(2)

where \( p(t) = \left\{ {\begin{array}{*{20}c} 0 & {0 \le t < t_{1} } \\ {p_{1} (t)} & {t_{1} \le t < t_{2} } \\ {p_{2} (t)} & {t \ge t_{2} } \\ \end{array} } \right. \) is an undetermined function.

In rock mechanics, Hookean elastic springs and Newtonian viscous dashpots are used to model a variety of rheological characteristics of the rock mass. Figure 2 provides a one-dimensional (1D) illustration of the general Kelvin and Maxwell viscoelastic models with parameters \( E_{i} \) and \( \eta_{i} \), to be experimentally determined (Flügge 1975). To simulate more complex rock rheologies, additional elastic springs or dashpots can be connected in parallel or in series in the general Kelvin and Maxwell models. The constitutive equations of a general viscoelastic model can be expressed in the form of convolution integrals as

Fig. 2
figure 2

General viscoelastic physical models

Full size image
$$ s_{ij} (r,t) = 2G(t) * \text{d}e_{ij} (r,t), $$
(3a)
$$ \sigma_{\mathrm{mm}} (r,t) = 3K(t) * \text{d}\varepsilon_{\mathrm{mm}} (r,t) $$
(3b)

with \( s_{ij} \) and \( e_{ij} \) the deviator tensors of the stress and strain tensors, \( \sigma_{ij} \) and \( \varepsilon_{ij} \), respectively. By definition,

$$ s_{ij} = \sigma_{ij} - \frac{1}{3}\delta_{ij} \sigma_{\mathrm{mm}}, $$
(4a)
$$ e_{ij} = \varepsilon_{ij} - \frac{1}{3}\delta_{ij} \varepsilon_{\mathrm{mm}}. $$
(4b)

G(t) and K(t) are the so-called relaxation moduli, which can be expressed by \( E_{i} \) (or \( G_{i} \)) and \( \eta_{i} \) in the viscoelastic model. The asterisk (*) in Eq. (3) indicates the convolution integral, the definition of which is

$$ f_{1} (t) * \hbox{d}f_{2} (t) = f_{1} (t) \cdot f_{2} (0) + \int\limits_{0}^{t} {f_{1} (t - \tau )} \frac{{\hbox{d}f_{2} (\tau )}}{\hbox{d}\tau }\hbox{d}\tau . $$
(5)

For the case of axisymmetric deformations under plane-strain conditions, the general solution for the radial displacement and the three stress components of a rock mass in the Laplace space can be written as (Wang and Nie 2010)

$$ \overline{{u_{r} }} = \frac{A(s)}{r} + rB(s), $$
(6)

and

$$ \begin{aligned} \overline{{\sigma_{r} }} &= \overline{2G(t)} \cdot s\left[ - \frac{1}{{r^{2} }}A(s) + \frac{1}{3}B(s)\right] + 2\overline{K(t)} \cdot sB(s), \\ \overline{{\sigma_{\theta }}} &= \overline{2G(t)} \cdot s\left[\frac{1}{{r^{2} }}A(s) + \frac{1}{3}B(s)\right] + 2\overline{K(t)} \cdot sB(s), \\ \overline{{\sigma_{z} }} &= 2\left[\overline{K(t)} - \frac{2}{3}\overline{G(t)} \right]sB(s). \\\end{aligned}$$
(7)

\( A(s) \) and \( B(s) \) are two undetermined functions of the transform parameter s defined in the Laplace transform of a time function, \( f(t) \), as

$$ \overline{f} (s) = \int\limits_{0}^{\infty } {\hbox{e}^{ - st} f(t)\hbox{d}t} , $$

the inverse transform of which is

$$ L^{ - 1} [\overline{f} (s)] = f(t) = \frac{1}{2\pi \text{i}} \int\limits_{\beta - \text{i}\infty }^{\beta + \text{i}\infty } {\overline{f} (s)\hbox{e}^{st} \hbox{d}t} . $$

The inverse transform of Eq. (7) is

$$ \begin{aligned} \sigma_{r}&= - \frac{2}{{r^{2} }}L^{-1} [ {\overline{G(t)} \cdot sA(s)}] + 2L^{ - 1} \left[ {\left( {\frac{1}{3}\overline{G(t)} + \overline{K(t)} } \right)B(s)s} \right] \\ \sigma_{\theta} &= \frac{2}{{r^{2} }}L^{ - 1} [ {\overline{G(t)} \cdot sA(s)} ] + 2L^{ - 1} \left[ {\left( {\frac{1}{3}\overline{G(t)} + \overline{K(t)} } \right)B(s)s} \right] \\ \sigma_{z}&= 2L^{ - 1} \left[ {\overline{K(t)} \cdot sB(s)} \right] - \frac{4}{3}L^{ - 1} \left[ {\overline{G(t)} \cdot sB(s)} \right]. \hfill \\ \end{aligned} $$
(8)

According to the boundary condition of Eq. (2), the functions A(s) and B(s) can be determined as

$$ A(s) = - \frac{1}{{2s\overline{G(t)} }}\left[ {\overline{{p_{0} R^{2} (t)}} - \overline{{p(t)R^{2} (t)}} } \right], $$
(9)
$$ B(s) = - \frac{{3\overline{{p_{0} }} }}{{2s\left[ {\overline{G(t)} + 3\overline{K(t)} } \right]}}. $$
(10)

Substituting Eqs. (9) and (10) into Eq. (8) provides the explicit form for the radial and hoop stresses in the rock as

$$ \begin{aligned} \sigma_{r} &= - p_{0} (t)\left[1 - \frac{{R^{2} (t)}}{{r^{2} }}\right] - \frac{{p(t)R^{2} (t)}}{{r^{2} }}, \\ \sigma_{\theta } &= - p_{0} (t)\left[1 + \frac{{R^{2} (t)}}{{r^{2} }}\right] + \frac{{p(t)R^{2} (t)}}{{r^{2} }}. \\ \end{aligned} $$
(11)

The radial displacement in the time domain is

$$ u_{r} = \frac{1}{r}L^{ - 1} [A(s)] + rL^{ - 1} [B(s)]. $$
(12)

Assuming

$$ H(t) \equiv L^{ - 1} \left[ {\frac{1}{{s\overline{G(t)} }}} \right]\quad I(t) \equiv L^{ - 1} \left[ {\frac{1}{s}\frac{1}{{\overline{G(t)} + 3\overline{K(t)} }}} \right], $$
(13)

then according to the properties of the convolution integral of the Laplace transform, Eqs. (9) and (10) can be simplified to

$$ \begin{aligned} L^{-1} [{A(s)}] &= - \frac{1}{2}H(t)*[p_{0} R^{2} (t) - p(t) R^{2} (t)] = - \frac{1}{2} \int\limits_{0}^{t} {p_{0} R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + \frac{1}{2} \int\limits_{0}^{t} {p(\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau \\ L^{ - 1} [{B(s)}] &= - \frac{3}{2}I(t)*p_{0} (t) = - \frac{3}{2} \int\limits_{0}^{t} {p_{0} (\tau )} I(t - \tau )\hbox{d}\tau.\\ \end{aligned} $$
(14)

Substituting Eq. (14) into Eq. (12) yields

$$ u_{r} = \frac{1}{2r}\left\{ { - \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + \int\limits_{0}^{t} {p(\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau } \right\} - \frac{3}{2}r \int\limits_{0}^{t} {p_{0} (\tau )} I(t - \tau )\hbox{d}\tau. $$
(15)

Equation (15) provides the general expression for the radial displacements. If the rock mass is incompressible, that is, \( K(t) = \infty \), no displacements occur before excavation. Considering now the installation of the first liner at time t 1 and the second liner at time t 2, the expression becomes

$$ u_{r}^{0} ({r,t}) = - \frac{1}{2r} \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau \quad{\text{for}}\;0 \le t \le t_{1}, $$
(16a)

and

$$ u_{r}^{1} ({r,t}) = \frac{1}{2r}\left\{ { - \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{1} }}^{t} {p_{1} (\tau )} H(t - \tau )\hbox{d}\tau } \right\}\quad{\text{for}}\ t_{1} < t \le t_{2} , $$
(16b)

and

$$ u_{r}^{2} ({r,t}) = \frac{1}{2r}\left\{ { -\int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{1} }}^{{t_{2} }} {p_{1} (\tau )} H(t - \tau )\,\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{2} }}^{t} {p_{2} (\tau )} H(t - \tau )\hbox{d}\tau } \right\} \quad{\text{for}}\ t > t_{2}. $$
(16c)

Displacements in the rock mass at a generic time \( t > t_{1} \) can be calculated as long as the supporting pressures \( p_{1} (t) \) and \( p_{2} (t) \) are known.

3.2 Mechanical Analysis of the Liners

Liners are made of concrete. Here, the Young’s moduli \( E_{\mathrm{L}1} \) and \( E_{\mathrm{L}2} \), and the Poisson’s ratios \( \nu_{\mathrm{L}1} \) and \( \nu_{\mathrm{L}2} \) are considered for the first and second liner, respectively. According to elasticity theory, the radial displacement of the first liner subject to the stress boundary conditions outlined in Fig. 1 is

$$ u_{r\mathrm{L}1} (r,t) = - \frac{1}{{2G_{\mathrm{L}1} r}} \cdot \frac{{R_{1}^{2} R_{2}^{2} }}{{R_{1}^{2} - R_{2}^{2} }}[p(t) - q(t)] - \frac{{1 + \nu_{\mathrm{L}1} }}{{K_{\mathrm{L}1} }} \cdot \frac{{R_{1}^{2} p(t) - R_{2}^{2} q(t)}}{{R_{1}^{2} - R_{2}^{2} }} \cdot r\quad {\text{with}}\quad t \ge t_{1} , $$
(17)

where \( R_{2} \) is the inner radius of the first liner, \( q(t) = \left\{ \begin{array}{*{20}l} 0& t_{1} \le t < t_{2} \\ q_{1} (t)& t \ge t_{2} \\ \end{array} \right. \) is the pressure between the liners, and \( G_{\mathrm{L}1} = \frac{{E_{\mathrm{L}1} }}{{2(1 + \nu_{\mathrm{L}1} )}} \) and \( K_{\mathrm{L}1} = \frac{{E_{\mathrm{L}1} }}{{1 - 2\nu_{\mathrm{L}1} }} \) are the shear and bulk elastic moduli of the first liner, respectively. The expression for the radial displacement undergone by the second liner is

$$ u_{r\mathrm{L}2} (r,t) = - \frac{1}{{2G_{\mathrm{L}2} r}} \cdot \frac{{R_{2}^{2} R_{3}^{2} }}{{R_{2}^{2} - R_{3}^{2} }}q_{1} (t) - \frac{{1 + \nu_{\mathrm{L}2} }}{{K_{\mathrm{L}2} }} \cdot \frac{{R_{2}^{2} q_{1} (t)}}{{R_{2}^{2} - R_{3}^{2} }} \cdot r\quad {\text{with}}\quad t \ge t_{2}, $$
(18)

where \( R_{3} \) is the inner radius of the second liner, and \( G_{\mathrm{L}2} \) and \( K_{\mathrm{L}2} \) are the shear and bulk elastic moduli of the second liner, respectively. The stresses acting on the first liner are

$$ \begin{aligned} \sigma_{r\mathrm{L}1} &= \left(1 - \frac{{R_{1}^{2} }}{{r^{2} }}\right)\frac{{R_{2}^{2} }}{{R_{1}^{2} - R_{2}^{2} }}q(t) - \left(1 - \frac{{R_{2}^{2} }}{{r^{2} }}\right)\frac{{R_{1}^{2} }}{{R_{1}^{2} - R_{2}^{2} }}p(t), \\ \sigma_{\theta \mathrm{L}1} &= \left(1 + \frac{{R_{1}^{2} }}{{r^{2} }}\right)\frac{{R_{2}^{2} }}{{R_{1}^{2} - R_{2}^{2} }}q(t) - \left(1 + \frac{{R_{2}^{2} }}{{r^{2} }}\right)\frac{{R_{1}^{2} }}{{R_{1}^{2} - R_{2}^{2} }}p(t), \\ \end{aligned} $$
(19)

whilst the stresses on the second liner are

$$ \sigma_{r\mathrm{L}2} = - \left(1 - \frac{{R_{3}^{2} }}{{r^{2} }}\right)\frac{{R_{2}^{2} }}{{R_{2}^{2} - R_{3}^{2} }}q_{1} (t),\quad \sigma_{\theta \mathrm{L}2} = - \left(1 + \frac{{R_{3}^{2} }}{{r^{2} }}\right)\frac{{R_{2}^{2} }}{{R_{2}^{2} - R_{3}^{2} }}q_{1} (t). $$
(20)

3.3 Determination of the Supporting Pressure After Construction of the First Liner

Having already imposed the boundary condition on the stresses at the interface between the first liner and the rock, the only boundary condition left concerns the displacements:

$$ u_{r} (R_{1} ,t) - u_{r} (R_{1} ,t_{1} ) = u_{r\mathrm{L}1} (R_{1} ,t)\quad {\text{with}}\ t \ge t_{1}. $$
(21)

According to Eq. (16), the increment of radial displacement in the rock from time \( t_{1} \) until a generic time t with \( t < t_{2} \) is

$$ \begin{aligned} &u_{r} (r,t) - u_{r} (r,t_{1} ) \\ &\quad =\frac{1}{2r}\left\{ { \int\limits_{0}^{{t_{1} }} {p_{0} (\tau )R^{2} (\tau )} H(t_{1} - \tau )\hbox{d}\tau - \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{1} }}^{t} {p_{1} (\tau )} H(t - \tau )\hbox{d}\tau } \right\}. \end{aligned} $$
(22)

Substituting into Eq. (21) yields the following second-type Volterra integral equation:

$$ \begin{gathered} \frac{1}{{2R_{1} }}\left\{ { \int\limits_{0}^{{t_{1} }} {p_{0} (\tau )R^{2} (\tau )} H(t_{1} - \tau )\hbox{d}\tau - \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{1} }}^{t} {p_{1} (\tau )} H(t - \tau )\hbox{d}\tau } \right\} \hfill \\ = - \frac{1}{{2G_{\mathrm{L}1} }} \cdot \frac{{R_{1} R_{2}^{2} }}{{R_{1}^{2} - R_{2}^{2} }}p_{1} (t) - \frac{{1 + \nu_{\mathrm{L}1} }}{{K_{\mathrm{L}1} }} \cdot \frac{{R_{1}^{3} }}{{R_{1}^{2} - R_{2}^{2} }}p_{1} (t). \end{gathered} $$
(23)

Defining the parameters \( D_{1} = \frac{1}{{2G_{\mathrm{L}1} }} \cdot \frac{{R_{1}^{2} R_{2}^{2} }}{{R_{1}^{2} - R_{2}^{2} }} \) and \( D_{2} = \frac{{1 + \nu_{\mathrm{L}1} }}{{K_{\mathrm{L}1} }} \cdot \frac{{R_{1}^{2} }}{{R_{1}^{2} - R_{2}^{2} }} \), and rearranging Eq. (23) for \( p_{1} (t) \), the following is obtained:

$$ \begin{aligned} p_{1} (t) &= - \frac{R_{1}^{2}}{{2D_{1} + 2D_{2} R_{1}^{2} }} \int\limits_{{t_{1} }}^{t} {p_{1} (\tau )} H(t - \tau )\hbox{d}\tau \\&\quad+ \frac{1}{{2D_{1} + 2D_{2} R_{1}^{2} }}\left\{ { - \int\limits_{0}^{{t_{1} }} {p_{0} (\tau )R^{2} (\tau )} H(t_{1} - \tau )\hbox{d}\tau +\int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau } \right\} . \end{aligned} $$
(24)

Specifying the function H = H(t) according to the viscoelastic model of interest, the analytical expression for the supporting pressure acting after the construction of the first liner can be obtained from Eq. (24).

3.4 Determination of the Supporting Pressure After Construction of the Second Liner

In the derivation of the solution, two boundary compatibility conditions will be imposed; the first one is at the boundary between rock and the first liner:

$$ u_{r} (R_{1} ,t) - u_{r} (R_{1} ,t_{1} ) = u_{r\mathrm{L}1} (R_{1} ,t) \;{\text{with}}\quad t \ge t_{2}, $$
(25)

whilst the second one is at the boundary between the two liners:

$$ u_{r\mathrm{L}1} (R_{2} ,t) - u_{r\mathrm{L}1} (R_{2} ,t_{2} ) = u_{r\mathrm{L}2} (R_{2} ,t)\;{\text{with}}\quad t \ge t_{2}. $$
(26)

The increment of radial displacement in the rock from time \( t_{1} \) until a generic time t, with \( t > t_{2} \), is

$$ \begin{aligned} &u_{r} (r,t) - u_{r} (r,t_{1} )\\&\quad = \frac{1}{2r}\left\{ { \int\limits_{0}^{{t_{1} }} {p_{0} (\tau )R^{2} (\tau )} H(t_{1} - \tau )\hbox{d}\tau - \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{1} }}^{{t_{2} }} {p_{1} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{2} }}^{t} {p_{2} (\tau )} H(t - \tau )\hbox{d}\tau } \right\}. \end{aligned} $$
(27)

Substituting Eq. (27) into Eq. (25), the following is obtained:

$$ \begin{aligned} &\frac{1}{{2R_{1} }}\left\{ { \int\limits_{0}^{{t_{1} }} {p_{0} (\tau )R^{2} (\tau )} H(t_{1} - \tau )\hbox{d}\tau - \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{1} }}^{{t_{2} }} {p_{1} (\tau )} H(t - \tau )\hbox{d}\tau + R_{1}^{2} \int\limits_{{t_{2} }}^{t} {p_{2} (\tau )} H(t - \tau )\hbox{d}\tau } \right\}\\ &\quad = \frac{{D_{1} }}{{R_{1} }}[p_{2} (t) - q_{1} (t)] - [D_{2} p_{2} (t) - D_{3} q_{1} (t)] \cdot R_{1},\end{aligned} $$
(28)

where \( D_{3} = \frac{{1 + \nu_{\mathrm{L}1} }}{{K_{\mathrm{L}1} }} \cdot \frac{{R_{2}^{2} }}{{R_{1}^{2} - R_{2}^{2} }} \), \( q_{1} (t) \) and \( p_{2} (t) \) being as yet unknown functions. Defining \( D_{4} = \frac{{1 + \nu_{\mathrm{L}2} }}{{K_{\mathrm{L}2} }} \cdot \frac{{R_{2}^{2} }}{{R_{2}^{2} - R_{3}^{2} }} ,\;D_{5} = \frac{1}{{2G_{\mathrm{L}2} }} \cdot \frac{{R_{2}^{2} R_{3}^{2} }}{{R_{2}^{2} - R_{3}^{2} }}\), and substituting Eqs. (17) and (18) into Eq. (26) yields

$$ - \frac{{D_{1} }}{{R_{2} }}[p_{2} (t) - q_{1} (t)] - [D_{2} p_{2} (t) - D_{3} q_{1} (t)] \cdot R_{2} + \frac{{D_{1} }}{{R_{2} }}p_{1} (t_{2} ) + D_{2} p_{1} (t_{2} ) \cdot R_{2} = - \frac{{D_{5} }}{{R_{2} }}q_{1} (t) - D_{4} q_{1} (t) \cdot R_{2}. $$
(29)

Defining \( D_{6} = \frac{{D_{1} + D_{2} R_{2}^{2} }}{{D_{5} + D_{1} + D_{4} R_{2}^{2} + D_{3} R_{2}^{2} }} \), then rearranging, one obtains

$$ q_{1} (t) = D_{6} [p_{2} (t) - p_{1} (t_{2} )]. $$
(30)

Substituting Eq. (30) into Eq. (28), the equation for \( p_{2} (t) \) is obtained as

$$ \begin{aligned} p_{2} (t) &= \frac{{R_{1}^{2} }}{{2(D_{1} - D_{1} D_{6} - D_{2} R_{1}^{2} + D_{3} D_{6} R_{1}^{2} )}} \int\limits_{{t_{2} }}^{t} {p_{2} (\tau )} H(t - \tau )\hbox{d}\tau \\ &\quad+\frac{1}{{2(D_{1} - D_{1} D_{6} - D_{2} R_{1}^{2} + D_{3} D_{6} R_{1}^{2} )}}\left\{ \int\limits_{0}^{{t_{1} }} {p_{0} (\tau )R^{2} (\tau )} H(t_{1} - \tau )\hbox{d}\tau - \int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} H(t - \tau )\hbox{d}\tau\right.\\&\quad+ \left.R_{1}^{2} \int\limits_{{t_{1} }}^{{t_{2} }} {p_{1} (\tau )} H(t - \tau )\hbox{d}\tau - 2D_{1} D_{6} p_{1} (t_{2} ) - 2D_{3} D_{6} R_{1}^{2} p_{1} (t_{2} )\right\}.\end{aligned} $$
(31)

Hence, the equations for the supporting pressures \( p_{2} (t) \) and \( q_{1} (t) \) after construction of the second liner are given in Eqs. (30) and (31) by specifying the function H = H(t) according to the viscoelastic model of interest.

4 Analytical Solution for the Maxwell Model

Let us consider weak, soft or highly jointed rock masses, and/or rock masses subject to high stresses, which are prone to excavation-induced continuous viscous flows. The Maxwell viscoelastic model (Fig. 3) is suitable to simulate their rheology, since it accounts for both primary and secondary rock creep. Now, assuming the validity of the Maxwell model and incompressible behavior, the constitutive parameters for the rock (see Eq. 3) become

Fig. 3
figure 3

Maxwell viscoelastic physical model

Full size image
$$ G(t) = G_{\mathrm{M}} \cdot \hbox{e}^{{ - \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}t}} ,\quad K(t) = \infty . $$
(32)

Substituting Eq. (32) into Eq. (13) yields

$$ H(t) = \frac{1}{{G_{\mathrm{M}} }}\delta (t) + \frac{1}{{\eta_{\mathrm{M}} }},\quad I(t) = 0. $$
(33)

The radial displacement in the absence of liners is

$$ u_{r}^{0} ({r,t}) = - \frac{1}{2r}\left[ {\frac{{p_{0} (t)R^{2} (t)}}{{G_{\mathrm{M}} }} + \frac{1}{{\eta_{\mathrm{M}} }}\int\limits_{0}^{t} {p_{0} (\tau )R^{2} (\tau )} \hbox{d}\tau } \right]\;{\text{for any }} t. $$
(34)

4.1 Supporting Pressure and Displacements After Construction of the First Liner

Substituting Eq. (33) into Eq. (24) and defining \( \lambda_{1} = - \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }} \cdot \frac{1}{{D_{7} }} \) and \( D_{7} = 1 + 2G_{\mathrm{M}} \frac{{D_{1} }}{{R_{1}^{2} }} + 2G_{\mathrm{M}} D_{2} \), the standard integral equation becomes

$$ p_{1} (t) = \lambda_{1} \int\limits_{{t_{1} }}^{t} {k_{\mathrm{M}} (t,\tau ) \cdot p_{1} (\tau )\hbox{d}\tau } + f_{\mathrm{M}1} (t). $$
(35)

The kernel of this integral equation is \( k_{\mathrm{M}} (t,\tau ) \equiv 1 \), and the free term is \( f_{\mathrm{M}1} (t) \equiv - \lambda_{1} \cdot p_{0} (t - t_{1} ) \). According to the theory of integral equations (Chambers 1976), the iterated kernel can be determined by iteration as

$$ \begin{aligned} k_{\mathrm{M}1} (t,\tau ) &= k_{\mathrm{M}} (t,\tau ) = 1,\quad k_{\mathrm{M}2} (t,\tau ) =\int\limits_{\tau }^{t} {k_{\mathrm{M}} (t,u) \cdot k_{\mathrm{M}1} (u,\tau )} \text{d}u = t - \tau ,\quad \hfill \\ k_{\mathrm{M}3} (t,\tau ) &=\int\limits_{\tau }^{t} {k_{\mathrm{M}} (t,u) \cdot k_{\mathrm{M}2} (u,\tau )} \text{d}u = (t - \tau )^{2} /2, \ldots ,k_{\mathrm{M}n} (t,\tau ) = (t - \tau )^{n - 1} /(n - 1)! \end{aligned} $$
(36)

Then, the kernel function of Eq. (35) can be written as

$$ W_{\mathrm{M}} (t,\tau ,\lambda_{1} ) = \sum\limits_{n = 1}^{\infty } {\lambda_{1}^{n - 1} k_{\mathrm{M}n} (t,\tau )} = \sum\limits_{n = 1}^{\infty } {\lambda_{1}^{n - 1} \frac{{(t - \tau )^{n - 1} }}{(n - 1)!}} = \hbox{e}^{{\lambda_{1} (t - \tau )}}. $$
(37)

Finally, the solution of Eq. (35) can be expressed as

$$ p_{1} (t) = f_{\mathrm{M}1} (t) + \lambda_{1}\int\limits_{{t_{1} }}^{t} {W_{\mathrm{M}} (t,\tau ,\lambda_{1} )f_{\mathrm{M}1} (\tau )\hbox{d}\tau } = - \lambda_{1} \cdot p_{0} \cdot (t - t_{1} ) - \lambda_{1}^{2} \cdot p_{0}\int\limits_{{t_{1} }}^{t} {\hbox{e}^{{\lambda_{1} (t - \tau )}} (\tau - t_{1} )\hbox{d}\tau }. $$
(38)

Then, after integration and simplifying, the following solution is obtained:

$$ p_{1} (t) = p_{0} - p_{0} \hbox{e}^{{\lambda_{1} (t - t_{1} )}}. $$
(39)

Substituting Eq. (39) into Eq. (16), the radial displacement of the rock mass at a time t with \( t_{1} \le t < t_{2} \) can be expressed as

$$ u_{r}^{1} (r,t) = - \frac{{p_{0}}}{{2G_{\mathrm{M}} r}}\left\{ {R_{1}^{2} \hbox{e}^{{\lambda_{1} (t - t_{1} )}} \left(1 + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }}\right) - R_{1}^{2} \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }} + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}\int\limits_{0}^{{t_{0} }} {R^{2} (\tau )\hbox{d}\tau } + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}R_{1}^{2} \cdot (t_{1} - t_{0} )} \right\}. $$
(40)

Hence, the obtained displacement varies with time according to an exponential function. Substituting Eq. (39) into Eq. (11) yields the following expressions for the stress

$$ \sigma _{r} = \left\{ {\begin{array}{*{20}l} { - p_{0} \left( {1 - \frac{{R^{2} (t)}}{{r^{2} }}} \right)} & {{\text{with}}\quad 0 \le t \le t_{1} } \\ { - p_{0} + p_{0} \hbox{e}^{{\lambda _{1} (t - t_{1} )}} \cdot \frac{{R_{1} ^{2} }}{{r^{2} }}} & {{\text{with}}\quad t > t_{1} } \\ \end{array} } \right., \sigma _{\theta } = \left\{ {\begin{array}{*{20}l} { - p_{0} \left( {1 + \frac{{R^{2} (t)}}{{r^{2} }}} \right)} & {{\text{with}}\quad 0 \le t \le t_{1} } \\ { - p_{0} - p_{0} \hbox{e}^{{\lambda _{1} (t - t_{1} )}} \cdot \frac{{R_{1} ^{2} }}{{r^{2} }}} & {{\text{with}}\quad t > t_{1} } \\ \end{array} } \right. $$
(41)

Now considering the case of an instantaneous excavation, that is, R(t) = R 1 (with t > 0) and t 0 = 0, the expressions for the displacements and stresses reduce to

$$ u_{r} (r,t) = - \frac{{p_{0} R_{1}^{2} }}{{2G_{\mathrm{M}} r}}\left\{ {\hbox{e}^{{\lambda_{1} (t - t_{1} )}} \left(1 + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }}\right) - \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }} + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}t_{1} } \right\}\quad \quad {\text{with}}\quad t \ge 0, $$
(42)
$$ \sigma_{r} = - p_{0} + p_{0} \hbox{e}^{{\lambda_{1} \,(t - t_{1} )}} \cdot \frac{{R_{1}^{2} }}{{r^{2} }},\;\sigma_{\theta } = - p_{0} - p_{0} \hbox{e}^{{\lambda_{1} (t - t_{1} )}} \cdot \frac{{R_{1}^{2} }}{{r^{2} }}\quad {\text{with}}\quad t \ge 0. $$
(43)

The solution appearing in Eq. (42), which is valid only for the particular case of an instantaneous excavation, coincides with the solution provided by Nomikos et al. (2011), who considered a Burgers viscoelastic model for the rock mass, in case the spring of the Kelvin element is infinitely stiff, \( G_{\mathrm{K}} \to \infty \).

4.2 Supporting Pressure and Displacements After Construction of the Second Liner

Substituting the constitutive parameters into Eq. (31), the integral equation for \( p_{2} (t) \) can be obtained as

$$ p_{2} (t) = \lambda_{2}\int\limits_{{t_{2} }}^{t} {k_{\mathrm{M}}^{*} (t,\tau ) \cdot p_{2} (\tau )\hbox{d}\tau } + f_{\mathrm{M}2} (t), $$
(44)

where \( k_{\mathrm{M}}^{*} (t,\tau ) \equiv 1 \), \( f_{\mathrm{M}2} (t) \equiv - \lambda_{2} \cdot p_{0} (t - t_{2} ) + \frac{{\lambda_{2} }}{{\lambda_{1} }} \cdot p_{0} [1 - \hbox{e}^{{\lambda_{1} (t_{2} - t_{1} )}} ] + \frac{{D_{8} }}{{D_{9} }}p_{1} (t_{2} ) \), \( \lambda_{2} = - \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }} \cdot \frac{1}{{D_{9} }}, \)

\( D_{8} = - 2G_{\mathrm{M}} \frac{{D_{1} D_{6} }}{{R_{1}^{2} }} - 2G_{\mathrm{M}} D_{3} D_{6}, \) and \( D_{9} = D_{7} + D_{8}. \) By using the same method outlined in Sect. 4.1, the following is obtained:

$$ p_{2} (t) = p_{0} - p_{0} \hbox{e}^{{\lambda_{1} (t_{2} - t_{1} ) + \lambda_{2} (t - t_{2} )}} . $$
(45)

According to Eq. (30),

$$ q_{1} (t) = D_{6} \cdot p_{0} \hbox{e}^{{\lambda_{1} (t_{2} - t_{1} )}} [ - \hbox{e}^{{\lambda_{2} (t - t_{2} )}} + 1], $$
(46)

so that the displacement of the rock at a generic time t with \( t \ge t_{2} \) can be obtained as

$$ \begin{aligned} u_{r}^{2} (r,t) &= - \frac{{p_{0} }}{{2G_{\mathrm{M}} r}}\left\{ {R_{1}^{2} \hbox{e}^{{\lambda_{1} (t_{2} - t_{1} ) + \lambda_{2} (t - t_{2} )}} \left(1 + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{2} }}\right) + \frac{{G_{\mathrm{M}} R_{1}^{2} }}{{\eta_{\mathrm{M}} }}\hbox{e}^{{\lambda_{1} (t_{2} - t_{1} )}} \left(\frac{1}{{\lambda_{1} }} - \frac{1}{{\lambda_{2} }}\right)} \right.\\ &\quad \left. { - R_{1}^{2} \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }} + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}\int\limits_{0}^{{t_{0} }} {R^{2} (\tau )\hbox{d}\tau } + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}R_{1}^{2} (t_{1} - t_{0} )} \right\}. \end{aligned} $$
(47)

Now, for tunnel engineers it is of interest to know the total additional displacement occurring after the construction of the second liner, i.e.,

$$ \Updelta u_{\mathrm{tot}}^{2} = u_{r} (r,\infty ) - u_{r} (r,t_{2} ) = \frac{{R_{1}^{2} p_{0} }}{{2G_{\mathrm{M}} r}}\left( {\frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{2} }} + 1} \right)\hbox{e}^{{\lambda_{1} (t_{2} - t_{1} )}},$$
(48)

and the total additional displacement occurring between the installation of the two liners, i.e.,

$$ \Updelta u_{\mathrm{tot}}^{1} = u_{r} (r,t_{2} ) - u_{r} (r,t_{1} ) = - \frac{{R_{1}^{2} p_{0} }}{{2G_{\mathrm{M}} r}}\left( {\frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }} + 1} \right)\left[ {\hbox{e}^{{\lambda_{1} (t_{2} - t_{1} )}} - 1} \right]. $$
(49)

Substituting Eq. (46) into Eq. (11), the stresses arising after the construction of the second liner can be determined as

$$ \sigma_{r} = - p_{0} + p_{0} \cdot \frac{{R_{1}^{2} }}{{r^{2} }}\hbox{e}^{{\lambda_{1} (t_{2} - t_{1} ) + \lambda_{2} (t - t_{2} )}} ,\;\sigma_{\theta } = - p_{0} - p_{0} \cdot \frac{{R_{1}^{2} }}{{r^{2} }}\hbox{e}^{{\lambda_{1} (t_{2} - t_{1} ) + \lambda_{2} (t - t_{2} )}} \;{\text{with}}\quad t \ge t_{2} . $$
(50)

4.3 Results and Discussion

To illustrate the influence of the excavation process and the installation times of the liners on the resulting stresses and displacements, an example is presented herein. Back-analysis is often used to identify the most suitable rheological model for the rock and its related parameters. Yang et al. (2001) derived rheological models and their constitutive parameters from in situ measurements during the excavation of a long tunnel, whereas Feng et al. (2006) derived them using genetic algorithms applied to the results of rock creep tests. Considering these experimental results, we have adopted the following values for the two parameters of the Maxwell model: \( G_{\mathrm{M}} = 2,000\,\hbox{MPa} \) and \( \eta_{\mathrm{M}} = 4,000\,\hbox{MPa}\,\text{day}, \) which lie in the ranges of values identified by Feng et al. (2006). Now, with regard to the elastic parameters for the concrete liners, \( G_{\mathrm{L}1} = G_{\mathrm{L}2} = 10,000\,\hbox{MPa} \) and \( \nu_{\text{L}1} = \nu_{\text{L}2} = 0.2 \) have been assumed; hence, the elastic bulk moduli result to be \( K_{\mathrm{L}1} \) = \( K_{\mathrm{L}2} \) = \( 40,000\hbox{MPa}.\) An excavation process with a linear increase of radius is considered here, i.e.,

$$ R(t) = \left\{ \begin{array}{*{20}l} R_{0} + \text{v}t& 0 \le t \le t_{0} \\ R_{1} & t > t_{0} \end{array} \right. $$
(51)

An in situ stress at infinity of \( p_{0} = 15\;\hbox{MPa} \) is assumed. In the example excavation process considered here, the radius of the tunnel grows from \( R_{0} = 1\,\hbox{m} \) until \( R_{1} = 6\,\hbox{m} \) at the end of the excavation process. The thicknesses of the first and second liner are 100 and 200 mm, respectively, so that \( R_{2} = 5.9\,\hbox{m} \) and \( R_{3} = 5.7\,\hbox{m} .\) For convenience of notation, the absolute value of the radial displacement will be presented in all the following figures, since radial displacements are always opposite to the radial coordinate r (i.e., the tunnel exhibits convergence).

4.3.1 Influence of the Excavation Rate

First, the displacement progression over time is investigated for three values of excavation rate: \( 0.625\,\hbox{m/day} \), \( 1\,\hbox{m/day}\), and \( 5\,\hbox{m/day} \), corresponding to total excavation periods of 8, 5, and 1 day, respectively. In this example, the first liner is installed immediately after completion of the excavation process to reduce displacements as much as possible. The second liner instead is installed after a time interval of 7 days from the installation of the first liner.

In Fig. 4, the radial displacements calculated at \( r = R_{1} \) are plotted for the aforementioned values of excavation rate. The asterisk and filled-triangle symbols indicate the installation of the first and second liner, respectively. The general trend is that the radial displacement increases over time and reaches a constant value after around 30 days. The results show that a lower excavation rate implies a longer excavation time, which leads to a larger value of displacement at the end of the excavation process at time t 1 = t 0, since the tunnel is immediately supported by the first liner after completion of the excavation. In the following two stages (\( t_{1} \le t < t_{2} \) and \( t > t_{2} \)), there is no significant difference among the three curves in terms of additional displacement. Overall, faster excavation rates imply lower total displacements at the end of every stage, and also in the long term.

Fig. 4
figure 4

Radial displacement versus time for various excavation rates; asterisks indicate the installation times of the first liner, whilst filled triangles indicate the installation times of the second liner. In all cases, the first liner is installed at t = t 0 = t 1

Full size image

In Fig. 4 it can be observed that the three curves intersect at around the 17th day: at the beginning (before the 17th day), high excavation rates imply larger displacements, whereas later on (after the 17th day), the opposite is true. So, it emerges that a fast excavation leads to high rates of displacement early on. However, the final stable state is reached earlier, with the final total displacement being lower than the case of slow excavation, as can be expected.

In Fig. 5, the stress responses of the rock calculated at the interface between rock and the first liner, r = 6 m, where the highest hoop stress is expected to develop, are displayed for the analyzed excavation rates. In all three cases considered, the stresses are the same at the end of excavation and at the time of installation of the second liner. However, for lower excavation rates, the change in stress is more gradual. Absolute values of radial and circumferential stresses reach their minimum and maximum at the end of the excavation phase, and would remain unchanged if no liners were installed. After installation of the first liner, the radial stress increases whereas the circumferential one decreases, so that the rock mass becomes subject to a more isotropic state of stress, which is beneficial for the stability of the tunnel.

Fig. 5
figure 5

Stresses calculated at the interface between rock and the first liner (r = 6 m) versus time for various excavation rates. Asterisks indicate the installation times of the first liner, whilst filled triangles indicate the installation times of the second liner

Full size image

4.3.2 Influence of the First Liner Installation Time

The analytical expression for the reduction of the radial displacements in the rock due to the presence of the first liner results as

$$ \Updelta u_{ - }^{1} ({r,t}) \equiv u_{r}^{0} ({r,t}) - u_{r}^{1} ({r,t}) = - \frac{{p_{0} R_{1}^{2} }}{{2G_{\mathrm{M}} r}}\left\{ {1 - \hbox{e}^{{\lambda_{1} (t - t_{1} )}} \left(1 + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }}\right) + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }} + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}(t - t_{1} )} \right\} ,\quad {\text{with}}\ t_{1} \le t < t_{2}. $$
(52)

\( \Updelta u_{ - }^{1} \) depends on the installation time of the first liner. The earlier the first liner is put in place, the larger the reduction of displacement will be. The analytical expression for the incremental displacement occurring since the installation of the first liner results as

$$ \Updelta u_{ + }^{1} (r,t) \equiv u_{r}^{1} (r,t) - u_{r}^{1} (r,t_{1} ) = - \frac{{p_{0} R_{1}^{2} }}{{2G_{\mathrm{M}} r}}\left(1 + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{1} }}\right)\left[ {\hbox{e}^{{\lambda_{1} (t - t_{1} )}} - 1} \right]\;\;\;{\text{with}}\quad t_{1} \le t < t_{2}. $$
(53)

Here, the influence of the installation time of the first liner was analyzed for an excavation rate of \( 0.625\,\hbox{m/day} ,\) which implies an excavation period of 8 days \( (t_{0} = 8). \) Four options were considered, with the first liner installed on the 8th, 10th, 12th, and 15th day. In all the cases, the second liner is installed on the 15th day. In Fig. 6, the resulting radial displacements, calculated at the interface between rock and the first liner, are displayed. It can be noted that earlier installation of the liner reduces the rate of displacement, and also leads to a shorter time to reach the stable state.

Fig. 6
figure 6

Radial displacement versus time for various installation times of the first liner \( (\text{v} =0.625\,\hbox{m/day} ).\) Asterisks indicate the installation times of the first liner

Full size image

4.3.3 Influence of the Second Liner Installation Time

The analytical expression for the reduction of the radial displacements in the rock due to the presence of the second liner results as

$$ \begin{aligned} \Updelta u_{ - }^{2} ({r,t}) & \equiv u_{r}^{1} ({r,t}) - u_{r}^{2} ({r,t}) \\ &= \frac{{p_{0} R_{1}^{2} \hbox{e}^{{\lambda_{1} (t_{2} - t_{1} )}} }}{{2G_{\mathrm{M}} r}}\left\{ \vphantom{\left[ {\frac{{\hbox{e}^{{\lambda_{1} (t - t_{2} )}} }}{{\lambda_{1} }} - \frac{{\hbox{e}^{{\lambda_{2} (t - t_{2} )}} }}{{\lambda_{2} }}} \right]}{\left[ {\hbox{e}^{{\lambda_{2} (t - t_{2} )}} - \hbox{e}^{{\lambda_{1} (t - t_{2} )}} } \right] - \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}\left[ {\frac{{\hbox{e}^{{\lambda_{1} (t - t_{2} )}} }}{{\lambda_{1} }} - \frac{{\hbox{e}^{{\lambda_{2} (t - t_{2} )}} }}{{\lambda_{2} }}} \right] + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} }}\left(\frac{1}{{\lambda_{1} }} - \frac{1}{{\lambda_{2} }}\right)} \right\} , {\text{ with}}\quad t \geq t_{2}. \end{aligned} $$
(54)

According to Eq. (54), it emerges that \( \Updelta u_{ - }^{2} \) depends on the time interval between the installation of the first and the second liner, i.e., \( t_{2} - t_{1} \). Earlier installation of the first liner leads to smaller reduction of displacements due to the installation of the second liner. In Fig. 7, curves representing the reduction of displacement versus the installation time of the second liner, t 2, are plotted for three values of t 1. From the figure, it emerges that, in order to minimize deformations, the second liner has to be put in place as soon as possible. Conversely, postponing the installation of the second liner leads to more pressure acting on the rock and the first liner, so that a more economical design of the second liner can be achieved.

Fig. 7
figure 7

Reduction of the radial displacement in the rock induced by the second liner calculated at the interface between rock and the first liner (r = 6 m) for various installation times of the first liner versus the installation time of the second liner (t 2)

Full size image

Now we consider the case of the first liner being built immediately after completion of the excavation process on the 8th day, with the second liner being installed at different dates, namely the 8th, 15th, and 20th day. In Fig. 8, the displacements calculated at the interface between rock and the first liner (\( r = 6\,\hbox{m} \)) are displayed. Early installation of the second liner leads to smaller displacements, with the stable state reached earlier.

Fig. 8
figure 8

Radial displacement versus time for various installation times of the second liner \(\text{v} = 0.625\,\hbox{m/day} \)). The asterisk indicates the installation time of the first liner, whilst filled triangles indicate the installation times of the second liner

Full size image

In Fig. 9, the stresses in the rock at the interface between rock and the first liner are plotted for the following time intervals between the construction of the two liners: 2, 6, and 10 days, with v = 0.625 m/day and t 0 = 8 days. It is worth noting that early installation of the second liner leads to a smaller radial stress and a larger circumferential one.

Fig. 9
figure 9

Stresses calculated at the interface between rock and the first liner (r = 6 m) versus time for various installation times of the second liner. The asterisk indicates the installation time of the first liner, whilst filled triangles indicate the installation times of the second liner

Full size image

The incremental displacement occurring since the installation of the second liner is

$$ \Updelta u_{ + }^{2} (r,t) \equiv u_{r}^{2} (r,t) - u_{r}^{2} (r,t_{2} ) = - \frac{{p_{0} R_{1}^{2} \hbox{e}^{{\lambda_{1} (t_{2} - t_{1} )}} }}{{2G_{\mathrm{M}} r}}\left(1 + \frac{{G_{\mathrm{M}} }}{{\eta_{\mathrm{M}} \lambda_{2} }}\right)\left[ {\hbox{e}^{{\lambda_{2} (t - t_{2} )}} - 1} \right]\quad {\text{with}}\quad t \geq t_{2}. $$
(55)

This incremental displacement depends on the time period \( t_{2} - t_{1} \) and on the installation time of the second liner. The larger \( t_{2} \) is, the larger the value of \( \Updelta u_{ + }^{2} \) will be.

5 Analytical Solution for the Boltzmann Model

For rock masses with good mechanical properties or subject to low stresses, the exhibited mechanical behavior shows limited viscosity. For this type of behavior, the Boltzmann viscoelastic model (Fig. 10) is commonly employed. The material parameters adopted in the model are the two elastic shear moduli \( G_{\mathrm{B}1} \) and \( G_{\mathrm{B}} \) and the viscosity coefficient \( \eta_{\mathrm{B}} \). Assuming that the rock is incompressible, the two relaxation moduli appearing in the constitutive equations (see Eq. 3) are as follows:

Fig. 10
figure 10

Boltzmann viscoelastic physical model

Full size image
$$ G(t) = \frac{{G_{\mathrm{B}1}^{2} }}{{G_{\mathrm{B}1} + G_{\mathrm{B}} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}1} + G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} + \frac{{G_{\mathrm{B}} \cdot G_{\mathrm{B}1} }}{{G_{\mathrm{B}1} + G_{\mathrm{B}} }},\quad K(t) = \infty . $$
(56)

Substituting Eq. (56) into Eq. (13) yields

$$ H(t) = \frac{1}{{G_{\mathrm{B}1} }}\delta (t) + \frac{1}{{\eta_{\mathrm{B}} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} ,\;I(t) = 0. $$
(57)

Substituting Eq. (57) into Eq. (15), and according to the properties of the Laplace transform, the analytical expression for the radial displacement can be derived as

$$ u_{r} (r,t) = \frac{1}{{2G_{\mathrm{B}1} r}}R^{2} (t)[p(t) - p_{0} (t)] + \frac{1}{{2\eta_{\mathrm{B}} r}}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}}\int\limits_{0}^{t} {R^{2} (\tau )[p} (\tau ) - p_{0} (\tau )]\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau . $$
(58)

5.1 Supporting Pressure and Displacement After Construction of the First Liner

Substituting Eq. (58) into (21), and defining \( \varphi_{1} (t) \equiv p_{1} (t)\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} \),\( \lambda_{3} = - \frac{{R_{1} }}{{2D_{10} \eta_{\mathrm{B}} }}, \) and \( D_{10} = \frac{{R_{1} }}{{2G_{\mathrm{B}1} }} + \frac{1}{{2G_{\mathrm{L}1} }} \cdot \frac{{R_{1} R_{2}^{2} }}{{R_{1}^{2} - R_{2}^{2} }} + \frac{{1 + \nu_{\mathrm{L}1} }}{{K_{\mathrm{L}1} }} \cdot \frac{{R_{1}^{3} }}{{R_{1}^{2} - R_{2}^{2} }} \), the integral equation becomes

$$ \varphi_{1} (t) = \lambda_{3}\int\limits_{{t_{1} }}^{t} {k_{\mathrm{B}} (t,\tau ) \cdot \varphi_{1} (\tau )\hbox{d}\tau } + f_{\mathrm{B}1} (t) $$
(59)

with

\( k_{\mathrm{B}} (t,\tau ) \equiv 1 \), \( f_{\mathrm{B}1} (t) \equiv \frac{{p_{0} }}{{2\eta_{\mathrm{B}} R_{1} D_{10} }} \cdot \hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right] \cdot (\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} - \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} ) \). Following the methodology shown in Sect. 4.1, solving the integral equations yields

$$ \varphi_{1} (t) = \frac{{p_{0} }}{{2D_{10} \eta_{\mathrm{B}} R_{1} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right] \cdot \left[ {\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} - \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} + \lambda_{3}\int\limits_{{t_{1} }}^{t} {\hbox{e}^{{\lambda_{3} (t - \tau )}} (} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} - \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} )\hbox{d}\tau } \right]. $$
(60)

Integrating and rearranging, the final solution is obtained as

$$ \varphi_{1} (t) = \frac{{D_{11} p_{0} }}{{2D_{10} \eta_{\mathrm{B}} R_{1} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right]\left(\hbox{e}^{{\lambda_{3} t + \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} - \lambda_{3} t_{1} }} - \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}}\right ), $$
(61)

with \( D_{11} = \frac{{G_{\mathrm{B}} }}{{G_{\mathrm{B}} - \eta_{\mathrm{B}} \lambda_{3} }} \). Thus, the pressure acting on the first liner before the second liner is installed is obtained as

$$ p_{1} (t) = \frac{{D_{11} p_{0} }}{{2D_{10} \eta_{\mathrm{B}} R_{1} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right]\left[\hbox{e}^{{(\lambda_{3} - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }})(t - t_{1} )}} - 1\right]\;{\text{with}}\quad t_{1} \le t < t_{2}. $$
(62)

Substituting Eq. (62) into Eq. (58), the analytical expression for the radial displacement of the rock mass for \( t_{1} \le t < t_{2} \) is achieved as

$$ \begin{aligned} u_{r}^{1} (r,t) &= \frac{{p_{0} R_{1}^{2} }}{{2G_{\mathrm{B}1} r}}\left\{ {\frac{{D_{11} }}{{2D_{10} \eta_{\mathrm{B}} R_{1} }} \cdot \hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right] \left[ {\hbox{e}^{{(\lambda_{3} - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }})(t - t_{1} )}} - 1} \right] - 1} \right\} \hfill \\ &\quad - \frac{{p_{0} }}{{2\eta_{\mathrm{B}} r}}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} \left\{ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau + } \right.\frac{{\eta_{\mathrm{B}} R_{1}^{2} }}{{G_{\mathrm{B}} }}\left(\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} - \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} \right). \hfill \\& \left. {\quad - \frac{{D_{11} R_{1} }}{{2D_{10} \eta_{\mathrm{B}} }} \cdot \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right] \left[ {\frac{1}{{\lambda_{3} }}\hbox{e}^{{\lambda_{3} (t - t_{1} )}} - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}(t - t_{1} )}} + \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }} - \frac{1}{{\lambda_{3} }}} \right]} \right\}. \hfill \\ \end{aligned} $$
(63)

When \( t_{1} \le t < t_{2} \), the incremental displacement occurring after the installation of the first liner is

$$ \begin{aligned} \Updelta u_{ + }^{1} (r,t) \equiv u_{r}^{1} (r,t) - u_{r} (r,t_{1} ) &= \frac{{p_{0} R_{1} }}{{4D_{10} \eta_{\mathrm{B}} G_{\mathrm{B}1} r}}\hbox{e}^{{ - \frac{G}{\eta }t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right] \left[ {\hbox{e}^{{(\lambda_{3} - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }})(t - t_{1} )}} - 1} \right] \hfill \\ &\quad - \frac{{p_{0} }}{{2\eta_{\mathrm{B}} r}}\left(\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} - \hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }}\right)\left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right] \hfill \\ &\quad + \frac{{D_{11} p_{0} R_{1} }}{{4D_{10} \eta_{\mathrm{B}}^{2} r}}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right] \left[ {\frac{1}{{\lambda_{3} }}\hbox{e}^{{\lambda_{3} (t - t_{1} )}} - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}(t - t_{1} )}} + \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }} - \frac{1}{{\lambda_{3} }}} \right] \hfill \\ \end{aligned} . $$
(64)

According to Eqs. (62) and (63), the supporting pressure and displacements are related to the supporting time and the excavation process, which was not the case for the solution obtained for the Maxwell model. Substituting Eq. (62) into Eq. (11) leads to the following expressions for the stresses:

$$ \begin{aligned} \sigma_{r} &= \left\{ {\begin{array}{*{20}l} { - p_{0} \left[ {1 - \frac{{R^{2} (t)}}{{r^{2} }}} \right]\quad \quad {\text{with}}\quad \quad 0 \le t < t_{1} } \\ { - p_{0} - \frac{{D_{11} p_{0} R_{1} }}{{2D_{10} \eta_{\mathrm{B}} \cdot r^{2} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} R_{1}^{2} }}{{G_{\mathrm{B}} }}\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right]\left[ {\hbox{e}^{{(\lambda_{3} - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }})(t - t_{1} )}} - 1} \right] + \frac{{p_{0} R_{1}^{2} }}{{r^{2} }}\quad{\text{with}}\;t_{1} \le t < t_{2} ,} \\ \end{array} } \right. \hfill \\ \sigma_{\theta } &= \left\{ {\begin{array}{*{20}c} { - p_{0} \left[ {1 + \frac{{R^{2} (t)}}{{r^{2} }}} \right]\quad {\text{with}}\quad \quad \;0 \le t < t_{1} } \\ { - p_{0} + \frac{{D_{11} p_{0} R_{1} }}{{2D_{10} \eta_{\mathrm{B}} \cdot r^{2} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} R_{1}^{2} }}{{G_{\mathrm{B}} }}\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right]\left[ {\hbox{e}^{{(\lambda_{3} - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }})(t - t_{1} )}} - 1} \right] - \frac{{p_{0} R_{1}^{2} }}{{r^{2} }}\quad{\text{with}}\;t_{1} \le t < t_{2} }. \\ \end{array} } \right. \end{aligned} $$
(65)

Hence, also the stresses turn out to depend on the excavation procedure.

5.2 Supporting Pressure and Displacement After Construction of the Second Liner

According to the analysis in Sect. 3.4, the integral equation for the supporting pressure p 2 = p 2(t) is obtained by substituting Eq. (57) into (31) as

$$ \begin{aligned} &\left\{ \frac{{D_{1} }}{{R_{1} }} - \frac{{D_{1} D_{6} }}{{R_{1} }} + D_{2} R_{1} - D_{3} D_{6} R_{1} + \frac{{R_{1} }}{{2G_{\mathrm{B}1} }}\right\} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} p_{2} (t) = - \frac{{R_{1} }}{{2\eta_{\mathrm{B}} }}\int\limits_{{t_{2} }}^{t} {\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} p_{2} (\tau )} \hbox{d}\tau - \left(\frac{{D_{1} D_{6} }}{{R_{1} }} + D_{3} D_{6} R_{1}\right )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} p_{1} (t_{2} ) \\&\quad + \frac{{p_{0} }}{{2\eta_{\mathrm{B}} R_{1} }}[1 - \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}(t - t_{1} )}} ]\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{1}{{2\eta_{\mathrm{B}} }}R_{1}\int\limits_{{t_{1} }}^{{t_{2} }} {p_{1} (\tau )} \cdot \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau + \frac{{p_{0} R_{1} }}{{2\eta_{\mathrm{B}} }}\int\limits_{{t_{0} }}^{t} {\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau } - \frac{{p_{0} R_{1} }}{{2\eta_{\mathrm{B}} }}\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}(t - t_{1} )}}\int\limits_{{t_{0} }}^{{t_{1} }} {\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau }, \\ \end{aligned} $$
(66)

where \( p_{1} (t_{2} ) \) can be calculated by Eq. (62) as

$$ p_{1} (t_{2} ) = \frac{{D_{11} p_{0} }}{{2D_{10} \eta_{\mathrm{B}} R_{1} }}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right]\left[\hbox{e}^{{(\lambda_{3} - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }})(t_{2} - t_{1} )}} - 1\right]. $$
(67)

Assuming that

$$ \varphi_{2} (t) \equiv p_{2} (t)\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} $$
(68)

and \( D_{12} = \frac{{D_{1} }}{{R_{1} }} - \frac{{D_{1} D_{6} }}{{R_{1} }} + D_{2} R_{1} - D_{3} D_{6} R_{1} + \frac{{R_{1} }}{{2G_{1} }} \), the integral equation for \( \varphi_{2} (t) \) can be obtained from Eq. (66) after some rearrangements as

$$ \varphi_{2} (t) = \lambda_{4}\int\limits_{{t_{2} }}^{t} {k_{\mathrm{B}}^{*} (t,\tau ) \cdot \varphi_{2} (\tau )\hbox{d}\tau } + f_{\mathrm{B}2} (t), $$
(69)

where \( k_{\mathrm{B}}^{*} (t,\tau ) \equiv 1 \), \( \lambda_{4} = - \frac{{R_{1} }}{{2\eta_{\mathrm{B}} }} \cdot \frac{1}{{D_{12} }} \), and

\( \begin{gathered} f_{\mathrm{B}2} (t) \equiv - \left(\frac{{D_{1} D_{6} }}{{R_{1} }} + D_{1} D_{6} R_{1}\right)\frac{1}{{D_{12} }}\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} p_{1} (t_{2} ) + \frac{{p_{0} }}{{2\eta_{\mathrm{B}} R_{1} D_{12} }}[1 - \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}(t - t_{1} )}} ]\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau \hfill \\ - \frac{{R_{1} }}{{2\eta_{\mathrm{B}} D_{12} }}\int\limits_{{t_{1} }}^{{t_{2} }} {p_{1} (\tau )} \cdot \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau + \frac{{p_{0} R_{1} }}{{2\eta_{\mathrm{B}} D_{12} }}\int\limits_{{t_{0} }}^{t} {\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau } - \frac{{p_{0} R_{1} }}{{2\eta_{\mathrm{B}} D_{12} }}\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}(t - t_{1} )}}\int\limits_{{t_{0} }}^{{t_{1} }} {\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau }. \end{gathered} \)

The kernel function of Eq. (69) is written as \( W_{\mathrm{B}} (t,\tau ) = \hbox{e}^{{\lambda_{4} (t - \tau )}} \). Thus, the solution for the integral equation can be expressed analytically as

$$ \varphi_{2} (t) = f_{\mathrm{B}2} (t) + \lambda_{4}\int\limits_{{t_{2} }}^{t} {W_{\mathrm{B}} (t,\tau )f_{\mathrm{B}2} (\tau )\hbox{d}\tau }. $$
(70)

So, the expression for \( p_{2} (t) \) can be obtained from Eq. (68). Since the integral expression in Eq. (70) is very long, the explicit expression is here omitted. Substituting Eqs. (67) and (70) into Eq. (30), we obtain

$$ q_{1} (t) = D_{6} \left\{ {p_{2} (t) - \frac{{D_{11} p_{0} }}{{2D_{10} \eta_{\mathrm{B}} R_{1} }} \cdot \hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{1} }} \left[ {\int\limits_{0}^{{t_{0} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{\eta_{\mathrm{B}} }}{{G_{\mathrm{B}} }}R_{1}^{2} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{0} }} } \right][\hbox{e}^{{(\lambda_{3} - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }})(t_{2} - t_{1} )}} - 1]} \right\}. $$
(71)

The analytical expression for the radial displacement of the rock mass for \( t \ge t_{2} \) can be obtained by substituting \( p_{1} (t) \) (Eq. 62) and \( p_{2} (t) \) into Eq. (58) and rearranging:

$$ \begin{aligned} u_{r}^{2} (r,t) &= \frac{{R_{1}^{2} }}{{2G_{\mathrm{B}1} r}}\left[ {p_{2} (t) - p_{0} } \right] + \frac{{\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} }}{{2\eta_{\mathrm{B}} r}}\left\{ { - p_{0}\int\limits_{0}^{{t_{1} }} {R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau } \right. \\ &\quad +\left. {R_{1}^{2}\int\limits_{{t_{1} }}^{{t_{2} }} {\left[ {p_{1} (\tau ) - p_{0} } \right]} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau + R_{1}^{2}\int\limits_{{t_{2} }}^{t} {\left[ {p_{2} (\tau ) - p_{0} } \right]} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau } \right\}. \end{aligned} $$
(72)

The incremental displacement occurring in the second liner stage is

$$ \begin{aligned} \Updelta u_{ + }^{2} &\equiv u_{r}^{2} (r,t) - u_{r} (r,t_{2} ) = \frac{{R_{1}^{2} }}{{2G_{\mathrm{B}1} r}}[p_{2} (t) - p_{2} (t_{2} )] - \frac{1}{{2\eta_{\mathrm{B}} r}}\left(\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}} - \hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{2} }}\right) \\ &\quad\times \left[ {\int\limits_{0}^{{t_{0} }} {p_{0} (\tau )R^{2} } (\tau )\hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - R_{1}^{2}\int\limits_{{t_{1} }}^{{t_{2} }} {p_{1} (\tau )} \cdot \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau } \right] - \frac{{R_{1}^{2} }}{{2\eta_{\mathrm{B}} r}}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}}\int\limits_{{t_{2} }}^{t} {p_{2} (\tau )} \cdot \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau \\ &\quad +\frac{{R_{1}^{2} }}{{2\eta_{\mathrm{B}} r}}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t}}\int\limits_{{t_{0} }}^{t} {p_{0} (\tau )} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau - \frac{{R_{1}^{2} }}{{2\eta_{\mathrm{B}} r}}\hbox{e}^{{ - \frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}t_{2} }}\int\limits_{{t_{0} }}^{{t_{2} }} {p_{0} (\tau )} \hbox{e}^{{\frac{{G_{\mathrm{B}} }}{{\eta_{\mathrm{B}} }}\tau }} \hbox{d}\tau. \end{aligned} $$
(73)

5.3 Results and Discussion

According to the experimental data available (Feng et al. 2006), reasonable values for the constitutive parameters of the viscoelastic rock are: \( G_{\mathrm{B}} = 1,000\,\hbox{MPa} \), \( G_{\mathrm{B}1} = 2,000\,\hbox{MPa} \), and \( \eta_{\mathrm{B}} = 10,000\,\hbox{MPa} \, \hbox{day} \). With regard to the concrete employed for the liners, its properties are outlined in Sect. 4.3. The same geometry (tunnel geometry and thicknesses of the liners), in situ stress state, excavation process, and excavation rates as in Sect. 4 were assumed. The only difference from Sect. 4 is the rock model applied.

The displacement response calculated at the interface between rock and the first liner (\( r = 6\,\hbox{m} \)) for various values of excavation rate is illustrated in Fig. 11. Trends similar to the response obtained for the Maxwell model, but with faster convergence, are shown.

Fig. 11
figure 11

Radial displacement versus time for various excavation rates; asterisks indicate the installation times of the first liner, whilst filled triangles indicate the installation times of the second liner

Full size image

To assess the influence of the installation times of the first and second liners, an excavation rate of 0.625 m/day as in Sect. 4.3.2 was assumed. Four options were considered, with the first liner installed on the 8th, 10th, 12th, and 15th day. In all the cases, the second liner was installed on the 15th day. In Fig. 12, the resulting radial displacements, calculated at the interface between rock and the first liner (\( r = 6\,\hbox{m} \)), are displayed. Again, it can be noted that early installation of the liner reduces the rate of displacement, and also leads to a shorter time to reach the stable state. Considering now different times for the installation of the second liner, assuming that the first liner was installed immediately after completion of the excavation process, the radial displacements calculated at the interface between rock and the first liner are shown in Fig. 13. Comparing Figs. 12 and 13 with Figs. 6 and 8, respectively, it emerges that the trends are similar for both models; however, from a quantitative point of view, the influence of the time of installation of the liners on the radial displacements is more significant in the Maxwell model.

Fig. 12
figure 12

Radial displacement versus time for various installation times of the first liner (v = 0.625 m/day). Asterisks indicate the installation times of the first liner

Full size image
Fig. 13
figure 13

Radial displacement versus time for various installation times of the second liner (v = 0.625 m/day). Filled triangles indicate the installation time of the second liner

Full size image

With regard to the influence of the excavation rate on the state of stress within the rock mass, in Fig. 14 the hoop and radial stresses developed within the rock mass at the interface with the first liner are plotted. As in Sect. 4, it was assumed that the first liner was installed immediately after excavation. In comparison with the Maxwell model (Sect. 4.3.4), the trends shown are similar, although the quantitative variation of the stress level over time is remarkably less significant.

Fig. 14
figure 14

Stresses calculated at the interface between rock and the first liner (r = 6 m) versus time for various excavation rates. Asterisks indicate the installation times of the first liner, whilst filled triangles indicate the installation times of the second liner

Full size image

Finally, looking at the analytical expression derived for the pressure acting on the first liner for the Maxwell model (Eqs. 39, 45, 46), it can be observed that the supporting pressure is independent of the excavation process. However, when applying the Boltzmann model instead, the supporting pressures \( p(t) \) and \( q(t) \) depend on the excavation rate, as shown in Figs. 15 and 16. In Fig. 15, the supporting pressure acting on the first liner is plotted against the time difference \( \Updelta t = t - t_{1}, \) with t 1 being the installation time of the first liner, whilst in Fig. 16, the supporting pressure acting on the second liner is plotted against the time difference \( \Updelta t' = t - t_{2}, \) with t 2 being the installation time of the second liner. From these figures it emerges that the supporting pressure is larger for higher excavation rates.

Fig. 15
figure 15

Pressure on the first liner versus time for various excavation rates. Filled triangles indicate the installation times of the second liner

Full size image
Fig. 16
figure 16

Pressure on the second liner versus time for various excavation rates

Full size image

6 Conclusions

Closed-form analytical expressions for stresses and displacements of deeply buried circular tunnels excavated in a viscoelastic medium supported by two liners were derived for any installation time of the liners. An initial hydrostatic stress field was assumed, with the rock mass modeled as linearly viscoelastic and the liners as purely elastic. To simulate realistically the process of tunnel excavation, solutions were developed for a time-dependent excavation process with the radius of the tunnel growing from zero until a final value according to a time-dependent function to be specified by the designers. The integral equations for the supporting pressures were established according to the given boundary conditions. Solutions of the equations were obtained assuming either the Maxwell or the Boltzmann viscoelastic model for the rock mass so that explicit closed-form analytical expressions for the time-dependent supporting pressures, stresses, and displacements in the rock and the liners could be derived.

The Maxwell viscoelastic model accounts for primary and secondary creep commonly observed in rock masses with weak mechanical properties or subject to high compressive stresses. In this case, radial displacements after liner installation increase exponentially over time, and reach a stable value asymptotically. Radial displacements are a function of the excavation process and of the installation time of the liners. Assuming that the first liner is installed immediately after excavation, a parametric analysis for various excavation rates showed that slow rates lead to smaller displacements in the short term but to larger ones in the long term, so that longer times are required for the stresses to stabilize to a constant value. Then, a parametric analysis for various times of liner installation was carried out, showing that early construction results in smaller displacements in the long term.

The Boltzmann viscoelastic model is commonly employed for rock masses exhibiting limited viscosity. Unlike the Maxwell model, the closed-form solutions obtained for the Boltzmann model showed that the development of pressure on the liners depends on the excavation process and the times of liner installation.

Although the obtained analytical solutions are rigorously applicable only for axisymmetric plane-strain conditions, according to the recent work of Schuerch and Anagnostou (2012), these solutions can be applied to a much wider range of ground conditions and to several cases of noncircular tunnels.