1 Introduction

Many types of rock exhibit time-dependent behaviors [23] which may, in some cases, contribute up to 70% of their total deformations [33]. In addition, tunnel excavations are long-term processes, during which the tunnel faces advance, and the cross-sections change over time. In particular, sequential excavations are technique which are becoming increasingly popular in several countries for the excavation of non-circular tunnels with large cross-sections [7, 24, 34]. Since the displacements and stresses of the surrounding rock are important aspects for tunnel designs, fast and detailed analyses which consider the rheology of the rock, as well as the sequential excavations, are important for the construction of deep tunnels [31, 34] to achieve the optimal tunneling parameters.

In the past several decades, many numerical studies have been carried out which were related to the determination of the time-dependent ground responses around underground openings [27, 29, 30]. However, the full three-dimensional (3D) analyses of the extended longitudinal sections of tunnels are found to be generally very computationally expensive. As a consequence, analytical solutions, by which a wide range of values of the input parameters can be effectively performed [4], are employed as first estimations of design parameters to provide guidance for the preliminary designs. In addition, these solutions have been generally used to validate the results of various numerical methods [18].

In this study, the rheology of the rock is accounted for using the linear viscoelastic relationship. Although there have been several closed-form or theoretical solutions developed for the excavations of rheological rock [6, 12, 19], all of these previous studies merely focused on circular tunnels under hydrostatic stress states, or cases where the cross-section excavations take place instantaneously. Recently, several analytical solutions were provided for deeply buried lined circular tunnels, or twin tunnels in viscoelastic rock, which considered the enlargements of the sequential excavations [35,36,37, 39]. However, for the purpose of minimizing excavation volumes, while still meeting the geometrical constraints, tunnels with non-circular cross-sections (for example, elliptical, horse-shoe, square cross-sections, and so on) have actually became rather common for railway tunnels [1, 2, 32], and rock caverns [40], as well as subway tunnels [13]. The analytical or semi-analytical solutions [8, 9, 18] for non-circular tunnels were mainly derived for elastic two-dimensional problems by introducing complex potential functions, along with conformal mapping functions. In the current related literature [38], the time-dependent rheological behavior of rock, as well as sequential excavations, was accounted for in the excavations of elliptical tunnels. However, the in situ initial shear stresses and pressures along the tunnel boundaries have yet to be considered. Due to tectonic activities, or the presence of fracture sets and discontinuities near tunnels, the principal directions of the initial stress states will possibly no longer be in horizontal or vertical directions [3], namely, the initial shear stresses are generated, which have been proven to be key parameters which significantly influence the stresses and displacements around non-circular tunnels [8, 20]. Moreover, the internal pressures induced by supports and water may also be crucial for tunnel stability, and these factors should not be neglected [21, 22].

The analytical solutions presented in this study will be potentially applicable for non-circular tunnels (e.g., elliptical and square tunnels), where the initial shear stresses and internal pressures are taken into consideration, which were not regarded in the aforementioned related literatures. The enlargement sequential excavations of the tunnel cross-sections, as well as various viscoelastic rock models, are also accounted for. These solutions potentially provide alternative approaches for the accurate predictions of the stress concentrations and time-dependent displacements around non-circular tunnels in the future preliminary designs of deep buried tunnels.

2 Descriptions and assumptions

The sequential enlargement excavations of tunnels with non-circular cross-sections in rheological rock are considered in this study. Throughout the analysis process, the following assumptions are made:

  1. 1.

    The surrounding rock is homogeneous and isotropic. Also, its rheological behavior can be described as linear viscoelasticity;

  2. 2.

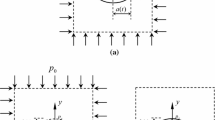
    The tunnel is deeply buried and subjected to relatively high initial stresses. Therefore, the variations in gravity across the height of the excavations can be neglected. The ground is subjected to in situ (or far-field) uniform non-hydrostatic initial stresses, which are idealized as vertical compressive stresses σ ∞ y , horizontal compressive stresses σ ∞ x , and shear stresses σ ∞ xy , as shown in Fig. 1a;

    Fig. 1
    figure 1

    Boundary conditions, coordinate system and sign conventions: a boundary conditions and coordinate system; b sign conventions for polar coordinate

    Full size image
  3. 3.

    The tunnel cross-section is sequentially excavated. For example, for elliptical tunnels, the half major a(t) and minor b(t) axes of the section are time-dependent, in which the variations against time are likely to be discontinuous. The analytical solutions which are provided in this study will be potentially applicable to the types of sequential enlargement excavations which increase either stepwise or continuously over time, as long as the mapping functions of the tunnel shapes during the excavation times are known;

  4. 4.

    No dynamic stresses are induced at any time, i.e., a quasi-static analysis is performed in this study.

For lined non-circular tunnels, it is very difficult to determine the stresses at the interfaces by the compatibility conditions of the stresses and displacements between the ground and liner for time-dependent problems. However, convergence-confinement methods [14] provide efficient ways to determine the rock–support interactions and have been widely used in engineering practices. By employing this method, the support pressures can be determined by the intersections between the convergence and confinement curves, where the convergence curves quantify the tunnel wall convergences as functions of the internal pressures, while the confinement curves quantify the pressures taken by the supports when the tunnel walls converge. In this study, the aim is to find the time-dependent convergence of rock as a function of the uniform internal pressures, which approximately accounts for the effects of the supports. For the cases with approximate anisotropic tunnel closures and installed liners with full slip, the supporting forces can be approximately treated as uniform pressures. In addition, the water pressure in the hydraulic tunnels can also be regarded as uniform internal pressures [21, 22].

Then, by employing the same assumption as in Ref. [38], the cross-section considered in the current analyses is determined to be located at a sufficiently far distance away from the longitudinal tunnel boundary, which results in the stresses and strains being unaffected by the three-dimensional effects. According to these assumptions, the equivalent plane strain analysis can be reduced in the direction perpendicular to the cross-section, as shown in Fig. 1a. The Cartesian coordinates (x, y), as well as the polar coordinates (r, α) and local coordinates (en, et), are employed in the derivation of the analytical solutions. The sign conventions are defined as positive for tension, and negative for compression, as shown in Fig. 1b.

With regard to the sequential excavation, the construction process can be divided into two stages. The first stage (for example, the excavation stage) spans from t = 0 to \(t = t_{ \sup }^{{}}\), with \(t_{ \sup }^{{}}\) being the time the internal pressure is applied. The second stage spanned from t = tsup to the end. It is noted that, from t = 0 to \(t = t_{\text{exc}}^{{}}\) in the first stage, where \(t_{\text{exc}}^{{}}\) represents the ending time of the cross-section excavation, the shape or size of the hole vary with time. For example, the values of the half major and minor axes of the elliptical tunnel are found to vary as follows:

$$\left\{ \begin{array}{l} a(t) = a_{0} + a_{m} (t) \hfill \\ b(t) = b_{0} + b_{m} (t), \hfill \\ \end{array} \right.$$
(1)

where a0 and b0 represent the initial values of the axes at t = 0; am(t) and bm(t) are function variations over time, which account for the real excavation process as prescribed by the designers. Following the cross-section excavations, from \(t = t_{\text{exc}}^{{}}\) to \(t = t_{ \sup }^{{}}\) represents a period of stabilization, with the half major and minor axes represented by a1 and b1 (constants), respectively.

3 Solutions to the viscoelastic problem involving time-dependent boundaries

3.1 Analysis of the general viscoelastic problem

The stress–strain behavior of the linear viscoelastic rock’s constitutive equations can be expressed in an integral form as follows:

$$\left\{ \begin{array}{l} s_{ij}^{v} ({\mathbf{X}},t) = 2\left[ {G(t)e_{ij}^{v} ({\mathbf{X}},0) + \int_{0}^{t} {G(t - \tau )\frac{{{\text{d}}e_{ij}^{v} ({\mathbf{X}},\tau )}}{{{\text{d}}\tau }}{\text{d}}\tau } } \right], \hfill \\ \sigma_{kk}^{v} ({\mathbf{X}},t) = 3\left[ {K(t)\varepsilon_{kk}^{v} ({\mathbf{X}},0) + \int_{0}^{t} {K(t - \tau )\frac{{{\text{d}}\varepsilon_{kk}^{v} ({\mathbf{X}},\tau )}}{{{\text{d}}\tau }}{\text{d}}\tau } } \right], \hfill \\ \end{array} \right.$$
(2)

where \({\mathbf{X}}\) is the position vector; s v ij and e v ij represent the tensors of the stress and strain deviators (the superscript ‘v’ denotes the quantities applied in the viscoelastic cases), respectively, which are defined as follows:

$$s_{ij}^{v} = \sigma_{ij}^{v} - \frac{1}{3}\delta_{ij} \sigma_{kk}^{v} \;,\quad e_{ij}^{v} = \varepsilon_{ij}^{v} - \frac{1}{3}\delta_{ij} \varepsilon_{kk}^{v} ,$$
(3)

where δij denotes the unit tensor; and G(t) and K(t) represent the shear and bulk relaxation moduli of viscoelastic models, respectively. In geo-material, a usual assumption is that the rock exhibits a purely elastic volumetric response [26]. Therefore, K(t) can be treated as equal to the elastic bulk modulus Ke. Figure 2 presents five physical viscoelastic models commonly employed in geo-engineering to simulate the rheological characteristics of different rock. The expressions of the shear relaxation moduli G(t) of these models are detailed in Table 1.

Fig. 2
figure 2

Viscoelastic models and the degeneration relationship between the models, a Maxwell model, b Kelvin model, c generalized Kelvin model, d Burgers model, e Poynting–Thomson model

Full size image
Table 1 Shear relaxation modulus for the five viscoelastic models
Full size table

The methodology for solving general viscoelastic problems involving time-dependent boundaries is expounded in reference section [38]. With respect to time, the Laplace transformation can be applied to the constitutive equations in Eq. (2), in order to obtain the linear relationships between the Laplace transformed stress and strain. By applying the Laplace transformation to all of the governing equations, with the exception of the boundary conditions, the relationship between the general viscoelastic and elastic solutions can be obtained as follows:

$$u_{i}^{v} ({\mathbf{X}},t) = \mathscr{L}^{ - 1} \left[ {\left. {u_{i}^{e} ({\mathbf{X}},s)} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } } \right]\quad \quad {\text{and}}\quad \sigma_{ij}^{v} ({\mathbf{X}},t) = \mathscr{L}^{ - 1} \left[ {\left. {\sigma_{ij}^{e} ({\mathbf{X}},s)} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } } \right]\;,$$
(4)

where u e i and σ e ij denote the elastic solutions of displacement and stresses, respectively; \(\mathscr{L}^{ - 1} \left[ \cdot \right]\) denotes the inverse Laplace transformation; Ge and Ke are the elastic shear and bulk moduli, respectively; and \(\widehat{f}(s)\) denotes a function with respect to the variable s defined in the Laplace transformation of the function f(t) as follows:

$$\widehat{f}(s) = \int_{\,0}^{\,\infty } {\exp^{ - st} f(t){\text{d}}t} .$$
(5)

In the following, the symbol \(\mathscr{L}\left[ \cdot \right]\) also denotes the Laplace transformation of [·]. Therefore, by substituting Eq. (4) into the boundary conditions, the set of equations can be addressed as satisfied by the particular solution of the viscoelastic case.

3.2 Complex potential representation for the viscoelastic problem

In regard to the mechanical analyses of the non-circular tunnel excavations in this study, a Muskhelishvili complex potential representation [25] is combined with the conformal mapping, which is found to be effective in determining the elastic solutions. All of the physical quantities can be expressed in terms of two complex potential functions, i.e., φ1 = φ1(z) and ψ1 = ψ1(z) with z = x + iy and \(i = \sqrt { - 1}\) [25]. If the boundaries are determined to be time-dependent, the two complex potentials become time-dependent as well.

In this study, according to Eq. (4) and the complex variable theory, the general solutions for the viscoelastic problem can be performed as follows:

$$\begin{aligned} u_{x}^{v} + iu_{y}^{v} & = \mathscr{L}^{ - 1} \left\{ {\frac{1}{{2s\widehat{G}(s)}}\left[ {\mu (s)\left. {\widehat{\varphi }_{1} (z,s)} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } - z\left. {\overline{{\frac{{\partial \widehat{\varphi }_{1} (z,s)}}{\partial z}}} } \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } - \left. {\overline{{\widehat{\psi }_{1} (z,s)}} } \right|{}_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} }} \right]} \right\} \\ \begin{array}{*{20}c} {\sigma_{x}^{v} } \\ {\sigma_{y}^{v} } \\ \end{array} & =\, Re\left\langle { 2\mathscr{L}^{ - 1} \left[ {\left. {\frac{{\partial \widehat{\varphi }_{1} (z,s)}}{\partial z}} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } } \right] \mp \mathscr{L}^{ - 1} \left[ {\overline{z} \left. {\frac{{\partial^{2} \widehat{\varphi }_{1} (z,s)}}{{\partial z^{2} }}} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } + \left. {\frac{{\partial \widehat{\psi }_{1} (z,s)}}{\partial z}} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } } \right]} \right\rangle \\ \sigma_{xy}^{v} & = Im\left\langle {\mathscr{L}^{ - 1} \left[ {\overline{z} \left. {\frac{{\partial^{2} \widehat{\varphi }_{1} (z,s)}}{{\partial z^{2} }}} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } + \left. {\frac{{\partial \widehat{\psi }_{1} (z,s)}}{\partial z}} \right|_{\begin{subarray}{l} G_{e} \to s\widehat{G} \\ K_{e} \to s\widehat{K} \end{subarray} } } \right]} \right\rangle \\ \end{aligned}$$
(6)

where \(\mu (s) = \frac{{3\widehat{K}(s) + 7\widehat{G}(s)}}{{3\widehat{K}(s) + \widehat{G}(s)}}\) for the plane strain analysis; \(\overline{g(z,t)}\) denotes the conjugate of the complex function g = g(z, t); and \(\text{Re} [ \cdot ]\) and \(\text{Im} [ \cdot ]\) denote the real and imaginary components of the complex variable [·], respectively. Then, by imposing the boundary conditions, the equations for the unknown time-dependent coefficients in φ1 and ψ1 are established.

According to the analyses detailed by Muskhelishvili [25], in case of the finite multiplied connected regions bounded by several simple closed contours (L1, L2, …, Lm), the two potentials can be determined via equilibrium equations, strain displacement relationships and constitutive equations. The two potentials can be expressed as follows:

$$\begin{aligned} \varphi_{1} (z,t) & = - \frac{1}{2\pi (1 + \kappa )}\sum\limits_{k = 1}^{N} {(X_{k} + iY_{k} )\text{l} \text{n} (z - z_{k} )} + \varphi_{1*} (z,t) \\ \psi_{1} (z,t) & = \frac{\kappa }{2\pi (1 + \kappa )}\sum\limits_{k = 1}^{N} {(X_{k} - iY_{k} )\text{l} \text{n} (z - z_{k} )} + \psi_{1*} (z,t) \\ \end{aligned}$$
(7)

where (Xk, Yk) represents the resultant vector of all of the external forces acting on the contours Lk; zk denotes the fixed point chosen inside the contours Lk; N denotes the number of the holes; and φ1* and ψ1* represent the undetermined analytic functions with respect to variables z and t. For the cases which are analyzed in this study, a single hole is contained in an infinite plane (simply connected region, N = 1), and the resultant vector of the external forces acting on the internal boundary is zero. Therefore, the two potentials in these cases can be expressed as follows:

$$\begin{aligned} \varphi_{1} (z,t) & = \varphi_{1*} (z,t) = \sum\limits_{k = 0}^{ + \infty } {a_{k} z^{ - k} } \\ \psi_{1} (z,t) & = \psi_{1*} (z,t) = \sum\limits_{k = 0}^{ + \infty } {b_{k} z^{ - k} } \\ \end{aligned}$$
(8)

It is worth noting that in Eq. (8), no material parameters are shown in φ1 and ψ1. Therefore, the stress expressions in Eq. (6) can be rewritten as follows:

$$\begin{aligned} \begin{array}{*{20}c} {\sigma_{x}^{v} } \\ {\sigma_{y}^{v} } \\ \end{array} & = Re\left\langle { 2\left[ {\frac{{\partial \varphi_{1} (z,t)}}{\partial z}} \right] \mp \left[ {\overline{z} \frac{{\partial^{2} \varphi_{1} (z,t)}}{{\partial z^{2} }} + \frac{{\partial \psi_{1} (z,t)}}{\partial z}} \right]} \right\rangle \\ \sigma_{xy}^{v} & = Im\left\langle {\overline{z} \frac{{\partial^{2} \varphi_{1} (z,t)}}{{\partial z^{2} }} + \frac{{\partial \psi_{1} (z,t)}}{\partial z}} \right\rangle \\ \end{aligned}$$
(9)

By comparing Eq. (9) with the stress expressions of the elastic problems, it is observed that the stresses are the same in both the elastic and viscoelastic cases. According to Eq. (6), the displacements in the viscoelastic cases are addressed as follows:

$$u_{x}^{v} + iu_{y}^{v} = \mathscr{L}^{ - 1} \left\{ {\frac{1}{{2s\widehat{G}(s)}}\left[ {\mu (s)\widehat{\varphi }_{1} (z,s) - z\overline{{\frac{{\partial \widehat{\varphi }_{1} (z,s)}}{\partial z}}} - \overline{{\widehat{\psi }_{1} (z,s)}} } \right]} \right\}$$
(10)

Assuming that:

$$H(t) = \mathscr{L}^{ - 1} \left[ {\frac{1}{{s\widehat{G}(s)}}} \right],\quad I(t) = \mathscr{L}^{ - 1} \left[ {\frac{\mu (s)}{{s\widehat{G}(s)}}} \right],$$
(11)

and together with the properties of the convolution integral, the displacements in Eq. (10) are rewritten as follows:

$$u_{x}^{v} + iu_{y}^{v} = \frac{1}{2}\int_{0}^{t} {I(t - \tau )\varphi_{1}^{{}} (z,\tau ){\text{d}}\tau } - \frac{1}{2}\int_{0}^{t} {H(t - \tau )\left[ {z\overline{{\frac{{\partial \varphi_{1}^{{}} (z,\tau )}}{\partial z}}} + \overline{{\psi_{1}^{{}} (z,\tau )}} } \right]{\text{d}}\tau } .$$
(12)

The expressions of H(t) and I(t) of the five viscoelastic models are detailed in Table 2.

Table 2 Two functions defined in Eq. (11) for the five viscoelastic models
Full size table

For the cases which are analyzed in this study, the initial stresses and internal pressures are successively applied at different stages. Therefore, if the rock rheology is considered, the displacements at specific times are dependent on the entire stress history. This is different from what occurs in the elastic cases, where the displacements are solely dependent on the stresses applied at that time. In this study, it is assumed that the external forces (Loads 1, 2, …, l) are exerted successively on the structures at the times tb1, tb2, …, tbl, and then removed at the times tm1, tm2, …, tml, respectively. If φ ( k)1 and ψ ( k)1 are the two potentials for the elastic problem only with the application of Load k, then based on the superposition principle for viscoelastic problems [11] and Eq. (12), the total displacements at time t (t ≥ tbl) can be achieved as follows:

$$u_{x}^{v} + iu_{y}^{v} = \frac{1}{2}\sum\limits_{k = 1}^{l} {\int_{{t_{bk}^{{}} }}^{{T_{k}^{{}} }} {I(t - \tau )\varphi_{1}^{(k)} (z,\tau ){\text{d}}\tau } } - \frac{1}{2}\sum\limits_{k = 1}^{l} {\int_{{t_{bk}^{'} }}^{{T_{k}^{{}} }} {H(t - \tau )\left[ {z\overline{{\frac{{\partial \varphi_{1}^{(k)} (z,\tau )}}{\partial z}}} + \overline{{\psi_{1}^{(k)} (z,\tau )}} } \right]{\text{d}}\tau } }$$
(13)

where Tk = min {tmk, t}. Then, according to Eq. (9), the stress expressions can be obtained as follows:

$$\begin{aligned} \begin{array}{*{20}c} {\sigma_{x}^{v} } \\ {\sigma_{y}^{v} } \\ \end{array} & = Re\left\langle { 2\left[ {\sum\limits_{k = 1}^{l} {\frac{{\partial \varphi_{1}^{(k)} (z,t)}}{\partial z}} } \right] \mp \left[ {\overline{z} \sum\limits_{k = 1}^{l} {\left( {\frac{{\partial^{2} \varphi_{1}^{(k)} (z,t)}}{{\partial z^{2} }} + \frac{{\partial \psi_{1}^{(k)} (z,t)}}{\partial z}} \right)} } \right]} \right\rangle \\ \sigma_{xy}^{v} & = Im\left\langle {\overline{z} \sum\limits_{k = 1}^{l} {\left[ {\frac{{\partial^{2} \varphi_{1}^{(k)} (z,t)}}{{\partial z^{2} }} + \frac{{\partial \psi_{1}^{(k)} (z,t)}}{\partial z}} \right]} } \right\rangle . \\ \end{aligned}$$
(14)

4 Displacements and stresses around non-circular tunnels

In this study, the stresses along the anticipated tunnel boundary prior to the excavation (for example, the horizontal and vertical components σ 0 x and σ 0 y shown in Fig. 3a) are induced by the initial far-field stresses. However, these boundary stresses become zero following the tunnel excavation. Therefore, the excavation-induced incremental displacements can be achieved by exerting the tractions − σ 0 x and − σ 0 y on the tunnel boundary from t = 0, as shown in Fig. 3b [38]. Following the excavation, the additional boundary stresses σ a ij (for example, the uniform internal pressures) are subsequently applied. In the following derivation, the tractions − σ 0 x and − σ 0 y are represented as Load 1, which is applied from tb1 = 0 to tm1 = ∞. The other additional loads (σ a ij ) are represented as Load 2, up to l. First of all, the two elastic potentials for case only subjected to Load j (j = 1, 2, …, l) will be obtained, and then the viscoelastic solutions will be addressed in the following subsections according to the derivation in Sect. 3.

Fig. 3
figure 3

Boundary conditions, a prior to excavation; b for calculations of excavation-induced incremental components. σ a ij is the additional load applied after excavation

Full size image

4.1 Conformal mapping process and its inverse

In regard to the elastic problems involving a single non-circular hole in an infinite medium, conformal mapping z = ω(ζ) is introduced so that the tunnel boundary and its exterior in the z-plane are mapped into the exterior or interior of the circle boundary, with a unit radius in the ζ-plane (ζ = ξ + iη = ρeiθ). If the region involving a time-dependent inner boundary in the z-plane, is mapped into the exterior of the circle in the ζ-plane, the conformal mapping can be expressed in the following series form, with respect to time [25]:

$$z = \omega \left( {\zeta ,t} \right) = R(t)\left[ {\zeta + \sum\limits_{i = 1}^{\infty } {\alpha_{i} (t)\zeta^{ - i} } + \alpha_{0} (t)} \right],\quad \left| \zeta \right| \ge 1$$
(15)

where R(t) is a positive real function which reflects the size of the hole in the z-plane; αi (i = 1, 2, …, ∞) are complex functions which reflect the shape of the hole; and α0 is correlated with the position of the coordinate origin in the z-plane. For example, the conformal mapping of the elliptical tunnels can be expressed as follows:

$$z = \omega \left( {\zeta ,t} \right) = c\left( t \right)\left[ {\zeta + \frac{m(t)}{\zeta }} \right]$$
(16)

where

$$c(t) = \frac{a(t) + b(t)}{2}\quad {\text{and}}\quad m(t) = \frac{a(t) - b(t)}{a(t) + b(t)}$$
(17)

and a(t), b(t) represent the half major and minor axes of the ellipse, respectively. In regard to squared tunnels, the conformal mapping is an infinite series, which is detailed in Eq. (39) in “Appendix” section.

In this research study, by employing mapping functions, the potentials of φ1 and ψ1 are expressed with respect to the variables ζ and t. However, for the viscoelastic cases which involve time-dependent boundaries, the displacements in Eq. (10) are expressed by φ1(z, t) and ψ1(z, t), in which the variable ‘z’ should be treated as a constant for the Laplace transform. In order to replace ζ with z and t in the final solutions, an inverse function of the conformal mapping ζ = χ(z, t) is required to be formulated. The determination of the inverse mapping function, and the investigation of its reliability and accuracy, are presented in Appendixes 7.1 and 7.2, respectively.

4.2 Determination of the potentials

In accordance with the complex variable theory and conformal representation, the potentials (represented by ‘PA’) for the elliptical and square holes in an infinite plane, which is subjected to tension at infinity in a direction with an angle β0 with respect to the Ox axis, have been provided in References [25] and [28], respectively. The potentials (represented by ‘P0’) of an infinite plane without holes subjected to the same far-field stresses are as follows:

$$\varphi_{1}^{(0)} \left( z \right) = - \frac{{(\sigma_{x}^{\infty } + \sigma_{y}^{\infty } )z}}{4},\quad \psi_{1}^{(0)} \left( z \right) = - \frac{{(\sigma_{y}^{\infty } - \sigma_{x}^{\infty } )z}}{2} + \sigma_{xy}^{\infty } zi$$
(18)

Therefore, by subtracting the P0 potentials from the PA potentials (shown in References [25] and [28]), the potentials of an infinite plane with holes which is subjected to tractions (Load 1) along the boundary can be obtained.

In the following, the solutions are given by superposition principle for the cases subjected to far-field stresses which are shown in Fig. 1a. Due to the fact that the signs of the initial far-field stresses in Fig. 1a have been considered in the derivation, σ ∞ x , σ ∞ y , and σ ∞ xy are all positive values in the following equations.

The potentials for Load 1 (traction on the boundary) of the elliptical and square tunnels under complex initial stress states can be obtained by a summation of the potentials under the following four simple initial stress states as follows:

  • Case (1): Only with compressive stress σ ∞ x at infinity with \(\beta_{0} = 0^{^\circ }\), as shown in Fig. 4;

    Fig. 4
    figure 4

    Far-field stress conditions of various cases in derivation of solutions for problem under complex initial stress state

    Full size image

  • Case (2): Only with compressive stress σ ∞ y at infinity with \(\beta_{0} = 90^{^\circ }\), as shown in Fig. 4;

  • Case (3): Only with tensile stress σ ∞ xy at infinity with \(\beta_{0} = 45^{^\circ }\), as shown in Fig. 4;

  • Case (4): Only with compressive stress σ ∞ xy at infinity with \(\beta_{0} = 135^{^\circ }\), as shown in Fig. 4.

It is also worth noting that the combination of Cases (3) and (4) is equivalent to the case with only far-field shear stress σ ∞ xy . Therefore, by utilizing the summation of the aforementioned four potentials, the potentials under the complex initial stress state are achieved as follows:

For the elliptical tunnels:

$$\begin{aligned} \varphi_{1}^{(1)} \left( {\zeta ,t} \right) & = \frac{{\left[ {\sigma_{y}^{\infty } - \sigma_{x}^{\infty } + 2i\sigma_{xy}^{\infty } + (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(t)} \right]c(t)}}{2\zeta } \\ \psi_{1}^{(1)} \left( {\zeta ,t} \right) & = \frac{c(t)}{2\zeta }\left[ {(\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )\left( {1 + m^{2} (t)} \right) + 2(\sigma_{y}^{\infty } - \sigma_{x}^{\infty } )m(t)} \right] \\ & \quad +\, \frac{{\left[ {\sigma_{y}^{\infty } - \sigma_{x}^{\infty } + 2i\sigma_{xy}^{\infty } + (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(t)} \right]\left[ {1 + m^{2} (t)} \right]c(t)}}{{2\zeta \left[ {\zeta^{2} - m(t)} \right]}} \\ \end{aligned}$$
(19)

For the square tunnels:

$$\begin{aligned} \varphi_{1}^{(1)} \left( {\zeta ,t} \right) & = \frac{{\left[ {\left( {\sigma_{y}^{\infty } - \sigma_{x}^{\infty } } \right)\frac{3}{7} + \frac{6}{5}i\sigma_{xy}^{\infty } } \right]R(t)}}{\zeta } - \frac{{\left( {\sigma_{x}^{\infty } + \sigma_{y}^{\infty } } \right)R(t)}}{{12\zeta^{3} }} \\ \psi_{1}^{(1)} \left( {\zeta ,t} \right) & = \frac{13}{6}\frac{{\left[ {\left( {\sigma_{y}^{\infty } - \sigma_{x}^{\infty } } \right)\frac{3}{7} + \frac{6}{5}i\sigma_{xy}^{\infty } } \right]R(t)\zeta }}{{2\zeta^{4} + 1}} + \frac{13}{12}\frac{{\left( {\sigma_{x}^{\infty } + \sigma_{y}^{\infty } } \right)R(t)\zeta^{3} }}{{2\zeta^{4} + 1}} + \frac{{\left( {\sigma_{x}^{\infty } - \sigma_{y}^{\infty } + 2i\sigma_{xy}^{\infty } } \right)R(t)}}{{12\zeta^{3} }} \\ \end{aligned}$$
(20)

If assuming σ ∞ x  = σ ∞ y  = − σ sup n and σ ∞ xy  = 0, with σ sup n being the value of the uniform internal pressure along the tunnel boundary (Load 2), the tractions acting on the tunnel boundary are reduced to the uniform normal tensile stress, with the value being σ sup n . Therefore, the potentials for the tunnel subjected to Load 2 can be obtained by replacing σ ∞ x and σ ∞ y with − σ sup n , and σ ∞ xy with zero in Eqs. (19) and (20) as follows:

$${\text{For the elliptical tunnels:}}\quad \varphi_{1}^{(2)} \left( {\zeta ,t} \right) = - \frac{{\sigma_{n}^{\sup } (t)m_{1} c_{1} }}{\zeta },\quad \psi_{1}^{(2)} \left( {\zeta ,t} \right) = - \frac{{\sigma_{n}^{\sup } (t)c_{1} \left( {1 + m_{1}^{2} } \right)\zeta }}{{\zeta^{2} - m_{1} }},\quad t \ge t_{\sup }$$
(21)
$${\text{For the square tunnels:}}\quad \varphi_{1}^{(2)} \left( {\zeta ,t} \right) = \frac{{\sigma_{n}^{\sup } (t)R_{1} }}{{6\zeta^{3} }},\, \psi_{1}^{(2)} \left( {\zeta ,t} \right) = - \frac{{13\sigma_{n}^{\sup } (t)R_{1} \zeta^{3} }}{{6(2\zeta^{4} + 1)}},\quad t \ge t_{\sup }$$
(22)

where m1, c1, and R1 are the final values of m(t), c(t), and R(t), respectively.

4.3 Solutions for the displacements and stresses

By substituting the potentials [Eqs. (19) and (21), or Eqs. (20) and (22)] into Eq. (13), and then replacing the variable ζ with the inverse mapping χ(z1, t) [see Eq. (34)], the excavation-induced displacements \(\Delta u_{{d_{1} }}^{v} (t)\) and \(\Delta u_{{d_{2} }}^{v} (t)\) along the d1 and d2 directions, respectively, are obtained, where d1 and d2 denote the two orthogonal directions of the coordinates system. The expressions of the induced displacements for the elliptical tunnels are as follows:

$$\Delta u_{{d_{1} }}^{v} (t) + i\Delta u_{{d_{2} }}^{v} (t) = \left\{ \begin{array}{ll} e^{ - i\gamma } B_{1} (z,t)&\quad 0 \le t < t_{\sup } \hfill \\ e^{ - i\gamma } \left[ {B_{1} (z,t) + B_{2} (z,t)} \right]&\quad t \ge t_{\sup } \hfill \\ \end{array} \right.$$
(23)

where γ denotes the angle between the horizontal axis x and d1, and

$$\begin{aligned} B_{1} (z,t) & = \frac{1}{2}\int_{0}^{t} {I(t - \tau )\varphi_{1}^{(1)} (z,\tau ){\text{d}}\tau } - \frac{1}{2}\int_{0}^{t} {H(t - \tau )\left\{ {z\overline{{\frac{{\partial \varphi_{1}^{(1)} (z,\tau )}}{\partial z}}} + \overline{{\psi_{1}^{(1)} (z,\tau )}} } \right\}{\text{d}}\tau } \\ & = \frac{1}{4}\int_{0}^{t} {I(t - \tau )\left[ {\frac{{\left[ {\sigma_{y}^{\infty } - \sigma_{x}^{\infty } + 2i\sigma_{xy}^{\infty } + (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(\tau )} \right]c(\tau )}}{{\chi (z_{1} ,\tau )}}} \right]{\text{d}}\tau } \\ & \quad + \frac{z}{4}\int_{0}^{t} {H(t - \tau )\left[ {\frac{{\sigma_{y}^{\infty } - \sigma_{x}^{\infty } - 2i\sigma_{xy}^{\infty } + (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(\tau )}}{{\chi^{2} (\overline{{z_{1} }} ,\tau ) - m(\tau )}}} \right]{\text{d}}\tau } \\ & \quad - \frac{1}{4}\int_{0}^{t} {H(t - \tau )\left[ {\frac{{\left[ {\left( {1 + m^{2} (\tau )} \right)(\sigma_{y}^{\infty } + \sigma_{x}^{\infty } ) + 2m(\tau )(\sigma_{y}^{\infty } - \sigma_{x}^{\infty } )} \right]c\left( \tau \right)}}{{\chi \left( {\overline{{z_{1} }} ,\tau } \right)}}} \right]{\text{d}}\tau } \\ & \quad + \frac{1}{4}\int_{0}^{t} {H(t - \tau )\left[ {\frac{{\left[ {\sigma_{x}^{\infty } - \sigma_{y}^{\infty } + 2i\sigma_{xy}^{\infty } - (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(\tau )} \right]\left[ {1 + m^{2} (\tau )} \right]c\left( \tau \right)}}{{\chi (\overline{{z_{1} }} ,\tau )\left[ {\chi^{2} (\overline{{z_{1} }} ,\tau ) - m(\tau )} \right]}}} \right]{\text{d}}\tau } \\ \end{aligned}$$
(24)
$$\begin{aligned} B_{2} (z,t) & = \frac{1}{2}\int_{{t_{ \sup }^{{}} }}^{t} {I(t - \tau )\varphi_{1}^{(2)} (z,\tau ){\text{d}}\tau } - \frac{1}{2}\int_{{t_{ \sup }^{{}} }}^{t} {H(t - \tau )\left[ {z\overline{{\left( {\frac{{\partial \varphi_{1}^{(2)} (z,\tau )}}{\partial z}} \right)}} + \overline{{\psi_{1}^{(2)} (z,\tau )}} } \right]{\text{d}}\tau } \\ & = - \frac{{m_{1} c_{1} }}{{2\chi (z_{1} )}}\int_{{t_{ \sup }^{{}} }}^{t} {I(t - \tau )\sigma_{n}^{\sup } (\tau ){\text{d}}\tau } - \frac{{zm_{1} - c_{1} \left( {1 + m_{1}^{2} } \right)\overline{{\chi (z_{1} )}} }}{{2\left[ {\overline{{\chi^{2} (z_{1} )}} - m_{1} } \right]}}\int_{{t_{ \sup }^{{}} }}^{t} {H(t - \tau )\sigma_{n}^{\sup } (\tau ){\text{d}}\tau } \\ \end{aligned}$$
(25)

In Eq. (25), B1 represents the displacements induced by the tractions, and B2 represents the displacements induced by the internal pressure.

Therefore, for the elliptical tunnels, according to Eq. (14), the excavation-induced stresses \(\Delta \sigma_{{d_{1} }}^{v}\) and \(\Delta \sigma_{{d_{2} }}^{v}\), and shear stress \(\Delta \sigma_{{d_{1} d_{2} }}^{v}\), can be obtained as follows:

$$\Delta \sigma_{{d_{1} }}^{v} = \left\{ \begin{array}{ll} \Delta \sigma_{{d_{1} - 1}}^{v} &\quad t < t_{\sup } \hfill \\ \Delta \sigma_{{d_{1} - 1}}^{v} + \sigma_{{d_{1} - 2}}^{v} &\quad t \ge t_{\sup } \hfill \\ \end{array} \right.,\quad \Delta \sigma_{{d_{2} }}^{v} = \left\{ \begin{array}{ll} \Delta \sigma_{{d_{2} - 1}}^{v} &\quad t < t_{\sup } \hfill \\ \Delta \sigma_{{d_{2} - 1}}^{v} + \sigma_{{d_{2} - 2}}^{v} &\quad t \ge t_{\sup } \hfill \\ \end{array} \right.,\quad \Delta \sigma_{{d_{1} d_{2} }}^{v} = \left\{ \begin{array}{ll} \Delta \sigma_{{d_{1} d_{2} - 1}}^{v} &\quad t < t_{\sup } \hfill \\ \Delta \sigma_{{d_{1} d_{2} - 1}}^{v} + \sigma_{{d_{1} d_{2} - 2}}^{v} &\quad t \ge t_{\sup } \hfill \\ \end{array} \right.$$
(26)

where

$$\begin{array}{*{20}c} {\Delta \sigma_{{d_{1} - 1}}^{v} } \\ {\Delta \sigma_{{d_{2} - 1}}^{v} } \\ \end{array} = Re\left\{ {D_{1} (z,t)} \right\} \mp Re\left\{ {e^{2i\gamma } \left[ {D_{2} (z,t) + D_{3} (z,t) + D_{4} (z,t)} \right]} \right\}$$
(27)
$$\Delta \sigma_{{d_{1} d_{2} - 1}}^{v} = Im\left\{ {e^{2i\gamma } \left[ {D_{2} (z,t) + D_{3} (z,t) + D_{4} (z,t)} \right]} \right\}$$
(28)
$$\begin{array}{*{20}c} {\sigma_{{d_{1} - 2}}^{v} } \\ {\sigma_{{d_{2} - 2}}^{v} } \\ \end{array} = \sigma_{n}^{\sup } (t)Re\left\{ {E_{1} (z,t)} \right\} \mp \sigma_{n}^{\sup } (t) \cdot Re\left\{ {\left. {e^{2i\gamma } E_{2} (z,t)} \right\}} \right.$$
(29)
$$\sigma_{{d_{1} d_{2} - 2}}^{v} = \sigma_{n}^{\sup } (t) \cdot Im\left\{ {\left. {e^{2i\gamma } E_{2} (z,t)} \right\}} \right.$$
(30)

with

$$\begin{aligned} D_{1} (z,t) & = \frac{{\sigma_{x}^{\infty } - \sigma_{y}^{\infty } - 2i\sigma_{xy}^{\infty } - (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(t)}}{{\chi^{2} (z_{1} ,t) - m(t)}}, \\ D_{2} (z,t) & = - \frac{{\overline{z} \left[ {\sigma_{x}^{\infty } - \sigma_{y}^{\infty } - 2i\sigma_{xy}^{\infty } - (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(t)} \right]\chi^{3} (z_{1} ,t)}}{{c(t)[\chi^{2} (z_{1} ,t) - m(t)]^{3} }}, \\ D_{3} (z,t) & = - \frac{{(\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )\left( {1 + m^{2} (t)} \right) + 2(\sigma_{y}^{\infty } - \sigma_{x}^{\infty } )m(t)}}{{2[\chi^{2} (z_{1} ,t) - m(t)]}}, \\ D_{4} (z,t) & = \frac{{\left[ {1 + m^{2} (t)} \right]\left[ {\sigma_{x}^{\infty } - \sigma_{y}^{\infty } - 2i\sigma_{xy}^{\infty } - (\sigma_{y}^{\infty } + \sigma_{x}^{\infty } )m(t)} \right][3\chi^{2} (z_{1} ,t) - m(t)]}}{{2\left[ {\chi^{2} (z_{1} ,t) - m(t)} \right]^{3} }}, \\ E_{1} (z,t) & = \frac{{2m_{1} }}{{\chi^{2} (z_{1} ) - m_{1} }},\quad E_{2} (z,t) = - \frac{{2\overline{z} m_{1} \chi^{3} (z_{1} ) - c_{1} \chi^{2} (z_{1} )\left( {1 + m_{1}^{2} } \right)\left[ {\chi^{2} (z_{1} ) + m_{1} } \right]}}{{c_{1} \left[ {\chi^{2} (z_{1} ) - m_{1} } \right]^{3} }} \\ \end{aligned}$$

Therefore, the total stresses in the rock mass can be obtained by superimposing the initial stresses in Eq. (26).

The expressions for the stresses [Eq. (26)] are determined to be suitable to all of the linear viscoelastic models, due to the fact that the stress state is independent of the viscoelastic constitutive parameters. However, the displacement expressions are dependent on the considered viscoelastic model. Therefore, by substituting the functions H(t) and I(t) defined in Eq. (11) (which are detailed in Table 2 for the five viscoelastic models) into Eqs. (23)–(25), the exact expressions of the displacements are obtained for the specific models. When the notations d1, d2, and γ in Eqs. (23) and (26) are replaced with those listed in Table 3, then the solutions for the displacements and stresses in the corresponding coordinate systems (for example, the Cartesian, polar, or local coordinates) are obtained.

Table 3 Notations of directions d1 and d2, angel γ in the Cartesian, polar and local coordinates
Full size table

In regard to the square tunnels, by substituting the potentials in Eqs. (20) and (22) into Eq. (13), and then replacing the variable ζ with the inverse mapping χ(z, t) in Eq. (34), the excavation-induced displacements are obtained. Furthermore, substituting the potentials into Eq. (9) yields the induced stresses. It is found that the use of this method can be extended for tunnels with any cross-section shape, if the potentials for the tunnels subjected to far-field stresses and internal uniform pressures have been available.

4.4 Comparison with the numerical results

In order to validate the proposed analytical solutions which were derived in the previous sections, a number of examples are performed in this subsection to compare the results obtained from the analytical solutions with those predicted using the finite element method (FEM) software ANSYS.

The problems encountered in tunnel excavations in infinite viscoelastic rock masses are examined for the initial conditions of vertical stresses \(\sigma_{y}^{\infty } = 10\,{\text{MPa}}\), horizontal stresses \(\sigma_{x}^{\infty } = 5\,{\text{MPa}}\), and shear stresses \(\sigma_{xy}^{\infty } = 1\,{\text{MPa}}\). Then, two tunnel excavation cases with different tunnel shapes and excavation processes are adopted for the following analyses, and the time variations of the tunnel boundaries are presented in Table 4. It should be noted that the cross-section excavations finishes at texc = 3rd day for the elliptical tunnel, while the square tunnel is assumed to be excavated instantaneously. Following the excavations, time-dependent uniform internal pressures are applied from t = 6th day, with the value being given as follows:

$$\begin{aligned} & {\text{For elliptical tunnel:}}\quad \sigma_{n}^{\sup } (t) = \left\{ \begin{aligned} {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 7}}\right.\kern-0pt} \!\lower0.7ex\hbox{$7$}} \cdot (t - 6)\quad \quad \quad \quad 6 \le t &< 20 \hfill \\ 2.0\quad \quad \quad \quad \quad t \ge 20 \hfill \\ \end{aligned} \right.\quad \left({\text{Units: }}\hbox{``MPa'' for stress};\text{``Day'' for time} \right). \\ & {\text{For square tunnel:}}\quad \sigma_{n}^{\sup } (t) = 1\quad t \ge 6 \\ \end{aligned}$$
(31)
Table 4 Variation of tunnel boundary (excavation steps) in FEM simulations
Full size table

The rock is simulated as a Poynting–Thomson model in the elliptical tunnel case, whereas generalized as a Kelvin model in the square tunnel case. The constitutive parameters are listed in Table 5. The stresses discussed in the following figures of this section are defined as positive for the compression, and negative for the tension. All of the FEM analyses are carried out with a small displacement formulation in order to be consistent within the derivation of the analytical solutions.

Table 5 Parameters of viscoelastic models in the FEM and analytical calculations
Full size table

In the FEM simulations, plane strain conditions are employed with far boundaries located at a distance further than 16–40 times that of the tunnel size. Figure 5 presents the calculation domain and mesh of the vicinity of the rock mass. In the numerical simulations, the initial stresses are first applied on the finite planes in order to obtain the displacements and stresses prior to the excavations. For the two viscoelastic models with parameters listed in Table 5, these displacements are found to be almost stable after 30 days. Therefore, the 31st day is chosen to be the time when the excavations begins. Parts I–III (Fig. 5a) of the elliptical tunnel are sequentially excavated on the 31st day (t = 0 day), 32nd day (t = 1 day), and 34th day (t = 3 day), respectively. Meanwhile, the square tunnel was excavated instantaneously on t = 31st day. Consequently, the induced displacements and stresses by the FEM can be obtained by subtracting the quantities occurred before the excavation from the total. In the FEM analyses, the elements were removed at the respective excavation times, in a way that the stiffness of these elements was set to zero (the stiffness matrix was multiplied with coefficient \(10^{{{ - }6}}\)), and then recalculated. During the calculation process, the time step was set to 0.1 day.

Fig. 5
figure 5

Mesh of the domain of the tunnel in FEM simulation, a Mesh of the domain for the elliptical tunnel, A, B, C and D are the points where displacements and stresses were compared. Parts I–III are sequentially excavated. b Mesh of the domain for the square tunnel, E is the point where displacements and stresses were compared

Full size image

Figure 6 details this study’s comparison of the displacements at points A, B, C, and D (Fig. 5a) on the final internal boundary of the elliptical tunnel, between the analytical solution and the FEM results. Figure 7 presents the comparison of induced stresses. In this example, the numerical results are found to be almost the same as the analytical ones. In regard to the square tunnel, the same quantities are also compared between the analytical and numerical results for point E (Fig. 5b), as shown in Fig. 8. These figures show that all of the analytical quantities for the square tunnel can matched well with the results obtained from the FEM analyses.

Fig. 6
figure 6

Comparison on the displacements versus time for elliptical tunnel between analytical and FEM results at the points A, B, C and D (see Fig. 5a) at the final tunnel boundary: a horizontal displacements; b vertical displacements

Full size image
Fig. 7
figure 7

Comparison on the stresses versus time for elliptical tunnel between analytical and FEM results of the points A, B, C and D at the final tunnel boundary (see Fig. 5a): a normal stresses along x direction; b normal stresses along y direction; c shear stress

Full size image
Fig. 8
figure 8

Comparison on the displacements and stresses versus time for square tunnel between analytical and FEM results at point E (see Fig. 5b): a displacements; b stresses

Full size image

5 Examples and discussion

In this section, the proposed analytical solutions are employed to study the influences of the initial shear stresses and internal pressures on the displacements and stresses of the elliptical and square tunnels. For the elliptical tunnel, a0 and b0 represent the values of the half major and minor axes at time t = 0, respectively. Meanwhile, a1 and b1 represent the final values of the axes. The functions of the half major and minor axes representing the time-dependent excavations are as follows:

$$ a(t) = \left\{ \begin{aligned} 1.5\quad 0 \le t < 2\;\;\;{\text{Step 1}} \hfill \\ 3.0\quad 2 \le t < 5\;\;\;{\text{Step 2}} \hfill \\ 5.0\quad \quad \;\,t \ge 5\;\;\;{\text{Step 3}} \hfill \\ \end{aligned} \right.,\quad b(t) = \left\{ \begin{aligned} 1.5\quad 0 \le t < 2\;\;\;{\text{Step 1}} \hfill \\ 3.0\quad 2 \le t < 5\;\;\;{\text{Step 2}} \hfill \\ 3.0\quad \quad \,\;t \ge 5\;\;\;{\text{Step 3}} \hfill \\ \end{aligned} \right.\quad \left( \begin{array}{l} {\text{Unit:}}\quad \hbox{``}m\hbox{''}\quad {\text{for}}\quad a(t)\quad {\text{and}}\quad b(t); \hfill \\ \hbox{``Day''}\quad {\text{for}}\quad {\text{time }}t. \hfill \\ \end{array} \right) $$
(32)

For the square tunnel, a circular cross-section with a radius of 3 m is first excavated at t = 0 (Step 1), and a final square cross-section with a side length of 6 m is achieved at \(t = 5^{\text{th}} \,{\text{day}}\) by the enlargement excavation (Step 2). The variations of the tunnel boundaries are displayed in Fig. 9.

Fig. 9
figure 9

Boundary shape variations due to sequential excavation for a elliptical tunnel; b square tunnel

Full size image

In the following analyses, the rock is simulated using a Burgers viscoelastic model in the case of the elliptical tunnel excavation, and simulated by a generalized Kelvin model for the square tunnel excavation. Table 6 presents the values of the parameters of the viscoelastic models [10, 41], as well as the initial stresses employed in the calculations. Also, the internal pressures, which are applied at the t = 10th day, are a constant (0.1 MPa) in the following examples in Sect. 5.1.

Table 6 Parameters of viscoelastic models and initial stress conditions in parametric investigation
Full size table

5.1 Influences of the initial shear stresses

Figure 10 presents the variations in the excavation-induced displacements (displacement in short) over time along the final tunnel boundary, at the points where α = 0°, 45°, 90° and 135°, for the elliptical tunnels subjected to various values of initial shear stress. It is observed that the displacements instantaneously increase or decrease at each excavation time, gradually increase over time following the completion of the tunnel excavation, and reach constant values after a certain period of time. Figure 10a and e illustrates that the normal displacements at the points with α = 0° and 90° are independent of the initial shear stresses, whereas, at the point where α = 45°, the final normal displacement is observed to decrease with the increase of initial shear stress (Fig. 10c). Also, at the point where α = 135°, it is found to increase against the initial shear stress (Fig. 10g). As can be seen in Fig. 10b, d, f, and h, the tangential displacements are significantly influenced by the initial shear stresses. For example, the final tangential displacements increase with the increase of the initial shear stresses at the points where α = 0°, 45°, and 90°; rather than at the point where α = 135°, the final tangential displacements are observed to first decrease from negative values to zero, and then increase to positive values with the increases in the initial shear stresses. Generally speaking, the presence of initial shear stress (positive) will lead to additional significantly positive tangential displacements along the upper half of a tunnel boundary, as well as additional negative/positive normal displacements along the upper right/left sections of a tunnel boundary.

Fig. 10
figure 10figure 10

Excavation induced displacements versus time under different condition of initial shear stress: a, c, e, g normal displacements versus time at the boundary points with α = 0°, α = 45°, α = 90°, α = 135°, respectively; b, d, f, h tangential displacements versus time at the boundary points with α = 0°, α = 45°, α = 90°, α = 135°, respectively

Full size image

In this study, for the square tunnels subjected to various values of initial shear stresses, the displacements versus θ (the angle of the radial direction in the ζ-plane with respect to the horizontal direction, as shown in Fig. 17d) are plotted in Fig. 11 at three specific times (t = 3rd, 8th, and 50th day). It is observed that the variation patterns of the displacements against θ are similar. However, the magnitudes are found to be quite different at the three specific times. The horizontal displacements (Δu v x ) are observed to first decrease, and then increase over θ. They are observed to be almost the same value on the right side of the tunnel boundary (θ = 0°–30°, the right side of square tunnel) under the different conditions of the initial shear stresses. However, in the other region, they are quite different. The horizontal displacements are observed to increase, and finally remain at peak values against θ (θ ∊ [30°, 180°]) when the initial shear stress is 7 MPa. Meanwhile, they continuously increases against θ (θ ∊ [90°, 180°]) when the initial shear stresses are zero or 3 MPa. If the initial shear stress is zero, the vertical displacement (Δu v y ) first increases with θ to a peak value (at the tunnel crown), and then decreases. However, it is found to first decreases to zero, and then increases to a peak value (at approximately θ = 100°, left side of the tunnel near the crown), and finally decreases, if the initial shear stress is not zero (positive value). At the tunnel crown (at approximately θ = 90°), the Δu v y is found to be less influenced by the initial shear stresses. However, at the sides of the tunnel, especially in the region with θ = 0°–45° and 135°–180°, the vertical displacements are found to be quite different under the various conditions of the initial shear stresses. It is observed that, with the increase in positive initial shear stresses, the upward vertical displacement at θ = 0° significantly increases.

Fig. 11
figure 11

Excavation induced displacements versus θ at different times: a, b horizontal and vertical displacements for initial shear stress being zero, respectively; c, d horizontal and vertical displacements for initial shear stress being 3 MPa, respectively; e, f horizontal and vertical displacements for initial shear stress being 7 MPa, respectively

Full size image

The contour maps of the final state of the principal stress under the various conditions of the initial shear stresses are presented in Fig. 12 (for the elliptical tunnel) and Fig. 13 (for the square tunnel). It can be observed from figures that the presence of the initial shear stresses leads to a lack of symmetry in the stress contours, along with larger stress concentrations around the tunnels. For elliptical tunnel (Fig. 12), when the initial shear stress is zero, the major and minor principal stresses are found to all be compressive. The maximum major principal stress with a value of 3.3 σ ∞ y occurred at the points along tunnel boundary with α = 0° and 180°. However, when the initial shear stress is not zero (3–7 MPa), the minor principal stress becomes tensile at the left of the tunnel, at approximately the point with α = 120°–135°, and the maximum major principal stress along the tunnel boundary, whose value is between 3.5σ ∞ y and 4.1σ ∞ y , occurs at the point where α = 5°–10°. Therefore, if the initial shear stress is positive, the major principal stress around the left side of the tunnel is observed to be much less than that around the right side of the tunnel.

Fig. 12
figure 12

Contour maps of principal stresses for elliptical tunnel excavation under various conditions of initial shear stress, a contour maps of the final major and minor principal stresses for initial shear stress being zero, b contour maps of the final major and minor principal stresses for initial shear stress being 3 MPa, c contour maps of the final major and minor principal stresses for initial shear stress being 7 MPa

Full size image
Fig. 13
figure 13

Contour maps of principal stresses for square tunnel excavation under various condition of initial shear stress, a contour maps of the final major and minor principal stresses for initial shear stress being zero, b contour maps of the final major and minor principal stresses for initial shear stress being 3 MPa, c contour maps of the final major and minor principal stresses for initial shear stress at infinity being 7 MPa

Full size image

In regard to the square tunnel (Fig. 13), the stress concentration is observed to occur at the corners in all of the cases. The maximum major principal stresses are determined to be 4.5 σ ∞ y , 6.3 σ ∞ y , and 8.2 σ ∞ y , respectively, in the cases with initial shear stresses of 0, 3, and 7 MPa. The larger positive initial shear stresses lead to the higher stress concentration occurring at the right corner. Furthermore, when the initial shear stress is zero or 3 MPa, all of the principal stresses are observed to be compressive; however, the minor principal stress becomes tensile at the left corner of the square tunnel when the initial shear stress increases to 7 MPa, which indicates that a tensile failure tends to occur.

5.2 Influences of the time-dependent internal pressures

In this subsection, three variation forms against the times of the internal pressure σ sup n are assumed in the elliptical tunnel excavation in order to simulate the time-dependent water pressures as follows:

$$\begin{aligned} & {\text{Exponential form:}}\quad \sigma_{n}^{\sup } (t) = p_{\infty } - p_{\infty } \cdot \exp [ - 0.1 \cdot (t - t_{\sup } )] \\ & {\text{Linear form:}}\quad \sigma_{n}^{\sup } (t) = \left\{ \begin{aligned} p_{\infty } \cdot (t - t_{\sup } )/(t_{\text{e}} - t_{\sup } )\quad \quad \quad \quad t_{\sup } \le t < t_{\text{e}} \hfill \\ p_{\infty } \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;t \ge t_{\text{e}} \hfill \\ \end{aligned} \right. \\ & {\text{Constant:}}\quad \sigma_{n}^{\sup } (t) = p_{\infty } , \\ \end{aligned}$$
(33)

where p∞ represents the final value of σ sup n (t); tsup is the time that the internal pressure is initially applied; and te represents the ending time of the pressure variation. As an example, this study assumes that the final pressure is approximately 20% of the initial horizontal stress. The other parameters are adopted as: \(t_{\sup } = 10.0\;{\text{day}}\), and \(t_{\text{e}} = 25\;{\text{day}}\). Then, the three forms of pressure in Eq. (33) of the internal pressures over time are plotted, as detailed in Fig. 14.

Fig. 14
figure 14

Internal pressure versus time

Full size image

At this point, the displacements and principal stresses versus time at two points (α = 0° and 135°) along the final elliptical tunnel boundary are plotted for the various internal pressures, as shown in Figs. 15 and 16. It should be noted that the tangential displacements are independent of the internal pressure, as shown in Fig. 15b and d. However, the normal displacements are found to be significantly influenced by the variation forms of the internal pressures (Fig. 15a, c). When the pressures display exponential forms, the normal displacements are observed to be increased functions of time following the applications of the pressures. Furthermore, it first increases with time, then decreases, and finally increases to stable values when the internal pressures are in linear forms. It is found that the normal displacements instantaneously drop at t = tsup, and then quickly increase with time to stable values if the internal pressures are constants.

Fig. 15
figure 15

Excavation induced displacements along tunnel boundary versus time for different time-dependent internal pressures: a, b normal and tangential displacements at point with α = 0°, respectively; c, d normal and tangential displacements at point with α = 135°, respectively

Full size image
Fig. 16
figure 16

Principal stresses versus time for different time-dependent inner pressures: a, b major and minor principal stresses at point with α = 0°, respectively; c, d major and minor principal stresses at point with α = 135°, respectively

Full size image

As can be seen in Fig. 16, the presence of internal pressures leads to smaller final major principal stresses, and larger final minor principal stresses at the point where α = 0°, which indicates that safer conditions existed in the rock around this point, according to the Mohr–Coulomb failure criteria. However, at point α = 135°, the final minor principal stress is observed to be tensile, and the major principal stress is compressive. It is observed that these both increase with the increase in internal pressures, probably resulting in the tensile failures of the rock in this region. It should also be noted that the variations in the stresses against time after 10th day display forms similar to the internal pressures.

6 Conclusions

It was found in this study that the derived analytical solutions of the non-circular tunnels subjected to far-field stresses and uniform pressures at the internal boundaries accounted for the sequence of the excavations, and the rheological properties of the host rock. The initial vertical and horizontal stresses, as well as shear stresses, were applied for the purpose of accounting for more general geological conditions. In addition, uniform pressures were applied at the internal boundaries of the tunnels in order to simulate the water and supporting pressures. Then, solutions were derived for the excavations of the tunnel cross-sections, with the sizes and/or shapes of the tunnels varying with time, in accordance with the time-dependent function specified by the designers.

In this study, particular viscoelastic solutions for both elliptical and squared tunnels were derived by employing Laplace transform techniques, and a Muskhelishvili complex variable method. The obtained solutions were confirmed to be suitable for any viscoelastic models by substituting the corresponding relaxation moduli into the general solutions. Then, in order to validate the methodology, FEM analyses were performed for both elliptical and square tunnel excavations using Burgers or Poynting–Thomson viscoelastic models. It was observed that there was a good agreement between the analytical and FEM solutions. Finally, a parametric analysis was performed to investigate the influences of the initial shear stresses and internal pressures on the displacements and stresses. The methodology described in this study may in principle be applied to obtain analytical solutions for arbitrary tunnel shapes which have been sequentially excavated in viscoelastic rock masses.

Furthermore, coupling analyses with presented analytical solutions, and a discrete element method (DEM) [5, 15,16,17], will be proposed in future research endeavors, in order to consider other potential failures in the zones near deep tunnel excavations.