Magnetohydrodynamic peristaltic flow of Williamson nanofluid with heat and mass transfer through a non-Darcy porous medium

Abstract

In this work, the peristaltic motion of a Williamson nanofluid through a non-Darcy porous medium inside an asymmetric channel is investigated. The Hall current, viscous dissipation and Joule heating are considered. The problem is modulated mathematically by a set of nonlinear partial differential equations which describe the conservation of mass, momentum, energy and concentration of nanoparticles. The non-dimensional form of these equations is simplified under the assumption of long wavelength and low Reynolds number. Then, resulting equations of coupled nonlinear differential equations are then tackled numerically with appropriate boundary conditions by using NDSolve technique. Graphical results are presented for dimensionless velocity, temperature and concentration in order to illustrate the variations of various parameters of this problem on these obtained solutions.

1 Introduction

Nanofluid is a new dynamic subclass of nanotechnology-based heat transfer fluids obtained by dispersing and stably suspended nanoparticles with typical dimensions of shape and size 1–100 nm (Das et al. 2007). In the last few decades, most of the researchers and scientists around the world continuously tried to work on novel features of nanotechnology. Choi (1995) of Argonne National Laboratory named the mixture of these particulate matters of particle sized in the order of nanometer as “nanofluid”. Nanotechnology is starting to permit researcher, scientific expert, chemist and biologist work at the sub-atomic and cell levels create essential advances in the life sciences and medical services. Due to the board utilizations of metallic nanoparticles in biotechnology, biomedical, material sciences much consideration has been paid to the blend of diverse sorts of metal nanoparticles (Lomascolo et al. 2015). Nano-metallic particulate suspension in a base fluid makes it superior ad finer in terms of heat transfer compared to conventional fluids. The abrasion related properties of nanofluid are found to be excellent over the traditional fluid–solid mixture. From the family of all metallic nanoparticles, the gold is noblest. Gold nanoparticles have different and distinctive shapes including spherical, cylindrical, octahedral nanotriangles and nanorods are significant. Gold nanoparticles are finest and efficient drug-carrying vehicles molecules (Hatami et al. 2014; Khan et al. 2014). Natural convection in a flexible sided triangular cavity with internal heat generation under the effect of inclined magnetic field has been studied by Selimefendigil and Öztop in (2016). Selimefendigil et al. (2017) have discussed the mixed convection in superposed nanofluid and porous layers in square enclosure with inner rotating cylinder.

A phenomenon in which reduction and expansion of an extensible tube generate dynamic waves which propagate along the length of the tube infusing and transposing the fluid in the direction of the wave propagation is known as peristaltic flow. Usually one encounters such motion in digestive tract such as the human gastrointestinal tract where smooth muscle tissue contracts and relaxes in sequence to produce a peristaltic wave, which propels the bolus (a ball of food) while in the esophagus and upper gastrointestinal tract, along the tract. The peristaltic movements not only avoid retrograde motion of the bolus but always keep pushing it in the forward direction, that is the important aspect of peristalsis is that it can propel the bolus against gravity effectively. Peristaltic movements are effectively used by animals like earthworms and larvae of certain insects for their locomotion. Motivated by such biomechanisms, there are machineries that limitate peristalsis to cater for specific day-to-day requirements. Other important applications of peristalsis involve movements of chyme in intestine, movement of eggs in fallopian tube, transport of the spermatozoa in cervical canal, transport of bile in the bile duct, circulation of blood in small blood vessels and transport of urine from kidney to urinary bladder and so on. Over past few decades, peristalsis has attracted much attention of a large class of researchers due to its important engineering and biomedical applications. Following the pioneering works of Latham (1996), there have been several reports in literature on the theoretical and experimental studies concerning peristaltic flow of Newtonian/non-Newtonian fluids. Elshahawy et al. (2000) studied the peristaltic motion of a generalized Newtonian fluid through a porous medium. Ebaid (2008) discussed the effects of magnetic field and wall slip conditions on the peristaltic transport of a Newtonian fluid in asymmetric channel. Mekheimer and Abd Elmaboud (2008) analyzed the peristaltic flow of a couple stress fluid in an annulus. Hayat et al. (2011) investigated the steady flow of Maxwell fluid with convective boundary conditions. Eldabe et al. (2016) investigated the Hall effects on the peristaltic transport of Williamson fluid through a porous medium with heat and mass transfer. Hayat et al. (2017) studied the influence of radial magnetic field on the peristaltic flow of Williamson fluid in a curved complaint walls channel.

Current advances in the subject of Hall current involve Hall accelerators, nuclear power reactors, flight MHD and MHD generators, the Hall current IC switch or sensors are extremely useful to detect the presence or absence of a magnetic field and gives a digital signal for on and off. Large values of Hall current parameter in the presence of heavy-duty magnetic field corresponds to Hall current, which is how it shakes the current density and allows one to understand the impact of Hall current on the flow (Nowar 2014). Hall effect on peristaltic flow of third order fluid in a porous medium with heat and mass transfer has been studied by Eldabe et al. (2015). Hayat et al. (2016) discussed Hall and ion slip effects on peristaltic flow of Jeffrey nanofluid with Joule heating.

Many applications in geophysical and industrial engineering involve conjugate phenomenon of the heat and mass transfer which occurs as a consequence of buoyancy effects. The simultaneous effects of heat and mass transfer are found handy in the improvement of energy transport technologies, metallurgy, power generation, production of polymers and ceramics, food drying, oil recovery, food processing, fog dispersion, the distribution of temperature and moisture in the field of agriculture and so far. Some relevant studies can be consulted via references (Abd-Alla et al. 2014; Selimefendigil and Öztop 2016; Nabil 2017).

Recent past, peristaltic flow through porous medium has gained a lot of interest in researchers due to its biological, physical and chemical applications. In mechanical procedures, the porous medium is used for enhancing the convention heat and mass transfer properties (Nield and Bejan 2006).

Convection fluid flow, heat and mass transfer with a porous medium happen in power station of numerous design characteristics where cooling or heating is required, for example, cooling turbine sharp blades, cooling electronic hardware, filtration, warm protection, ground water, oil stream and a wide range of heat exchangers. As per some fundamental focal points of utilizing of a porous medium, first its dissipation region is larger than the usual fins that increase the heat convection. Another point is the irregular movement of the fluid flow around the individual globules which blends the fluid all the more viably. That’s why; it would be the best combination; porous medium and nanofluid, for effective convective heat transfer (Mahdi 2015). Eldabe et al. (2001) studied the magnetohydrodynamic peristaltic flow of Jeffery nanofluid with heat transfer through a porous medium in a vertical tube.

There has been an interest in Darcy and non-Darcy flow in Newtonian and non-Newonian fluid flow saturating porous medium. This continuing interest due to its application such as chemical reactors, building insulation, packed bed, enhanced oil recovery, food technology and filtration processes. A square velocity term is added to Darcian velocity in momentum equation by Forchheimer (1901). Shehazed et al. (2016) discussed the properties of Darcy-Forchheimer flow of an Oldroyd-B liquid. They considered Cattaneo-Christov heat flux theory in energy equation. The Darcy-Forchheimer flow of Maxwell fluid in the presence of temperature-dependent thermal conductivity is studied by Haya et al. (2016).

The main aim of this paper is to investigate the peristaltic flow of an electrically conducting non-Newtonian nanofluid in an asymmetric channel embedded with a non-Darcy porous medium. Williamson non-Newtonian constitutive model is employed for the transport fluid. The porous medium is modeled by Darcy-Brinkman-Forchheimer law. The effects of Hall current, viscous dissipation and Joule heating are taken into consideration. The governing equations of motion, energy and concentration have been reduced under the well-established long wavelength and low Reynolds number approximations. A detailed mathematical formulation is presented and numerical solution graphically for velocity, temperature and nanofluid phenolmena have been presented.

2 Mathematical formulation of the problem

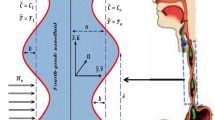
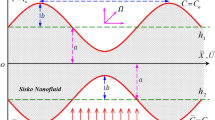
In this section, the mathematical formulation of the problem under investigation is presented, A two dimensional peristaltic transport of an incompressible, electrically conducting Williamson Nanofluid in an asymmetric channel with flexible walls, generated by propagation of waves on the channel walls travelling with different amplitudes and phases but with the same constant speed c has been considered. The region between the walls is assumed to be filled with a sparsely packed porous medium of permeability $K^{*}$. We select coordinate system in such a manner that X-axis lies along the length of the channel and Y-axis is taken normal to X-axis (see Fig. 1).

The wall shapes are given by as follows:

$$H_{1} \left( {X,t} \right) = d_{1} + a_{1} \cos \left[ {\frac{2\pi }{\lambda }\left( {X - ct} \right)} \right] \;\;\;(upper\,\,wall),$$

(1)

$$H_{2} \left( {X,t} \right) = - d_{2} - a_{2} \cos \left[ {\frac{2\pi }{\lambda }\left( {X - ct} \right) + \phi } \right] \;\;\;(lower\,\,wall),$$

(2)

where $a_{1}$ and $a_{2}$ are the wave amplitudes of the waves for the upper and the lower walls respectively, $\lambda$ is the wavelength, $d_{1} + d_{2}$ is the width of the channel, $c$ is the speed of wave propagation, $t$ is the time and $\phi$ is the phase difference which varies in the range $0 \le \phi \le \pi$. It should be noted that $\phi = 0$ corresponds to a symmetric channel with waves out of phase and for $\phi = \pi$, the waves are in phase. Moreover, $a_{1} , a_{2} , d_{1} , d_{2}\,\, {\text{and}}\,\,\phi$ satisfy the following condition:

$$a_{1}^{2} + a_{2}^{2} + 2a_{1} a_{2} \cos \left( \phi \right) \le \left( {d_{1} + d_{2} } \right)^{2} ,$$

(3)

in order for the channel not to colloide.

At the lower wall of the channel the temperature is $T_{1}$ and the concentration is $C_{1}$, while at the upper wall the temperature is $T_{0}$ and the concentration is $C_{0}$.

A strong uniform magnetic field with magnetic flux density $\varvec{B} = \left( {0,0,B_{0} } \right)$ is applied and the Hall effects are taken into account. The induced magnetic field is neglected by assuming a very small magnetic Reynolds number $\left( {Re_{m} < < < 1} \right)$, also it is assumed that there is no applied polarization voltage so that the total electric field $\varvec{E} = 0$. The generalized ohm’s law can be written as:

$$\varvec{J} = \sigma \left[ {\varvec{E} + \varvec{V} \times \varvec{B} - \frac{1}{{e n_{e} }}\left( {\varvec{J} \times \varvec{B}} \right)} \right],$$

(4)

where $\sigma$ is the electrical conductivity of the fluid, $\varvec{V}$ is the velocity vector, $e$ is the electric charge of electrons, $n_{e}$ is the number density of electrons. Equation (4) can be solved in $\varvec{J}$ to yield the Lorentz force vector in the form:

$$\varvec{J} \times \varvec{B} = \frac{{ - \sigma B_{0}^{2} }}{{1 + m^{2} }}\left[ {\left( {U - m V} \right)\hat{i} + \left( {m U + V} \right)\hat{j}} \right],$$

(5)

where $\left( {U, V} \right)$ are velocities along the coordinate axes in the fixed frame $\left( {X, Y} \right)$, $m = \frac{{\sigma B_{0} }}{{e n_{e} }}$ is the hall parameter.

The constitutive equation for a Williamson fluid is:

$$\tau = \left[ {\mu_{\infty } + \left( {\mu_{0} + \mu_{\infty } } \right)\left( {1 - \varGamma \dot{\gamma }} \right)^{ - 1} } \right]\dot{\gamma },$$

(6)

where $\tau$ is the extra stress tensor, $\mu_{\infty }$ is the infinite shear rate viscosity, $\mu_{0}$ is the zero shear rate viscosity, $\varGamma$ is the time constant and generalized shear rate $\dot{\gamma }$ is expressed in terms of the second invariant strain tensor as:

$$\dot{\gamma } = \sqrt {\frac{1}{2} \mathop \sum \limits_{i} \mathop \sum \limits_{j} \dot{\gamma }_{ij } \dot{\gamma }_{ji} } = \sqrt {\frac{1}{2}{\varvec{\Pi}}} ,$$

(7)

in which ${\varvec{\Pi}} = trac \left( {grad \varvec{V} + \left( {grad \varvec{V}} \right)^{T} } \right)^{2}$.

By considering $\mu_{\infty } = 0$ and $\varGamma \dot{\gamma } < 1$ in the constitutive Eq. (6), the extra stress tensor can be written as:

$$\begin{aligned} \tau =\,\, & \mu_{0} \left( {1 - \varGamma \dot{\gamma }} \right)^{ - 1} \dot{\gamma }, \\ \tau =\,\, & \mu_{0} \left( {1 + \varGamma \dot{\gamma }} \right) \dot{\gamma }. \\ \end{aligned}$$

(8)

The above model reduces to a Newtonian fluid in case $\varGamma = 0.$

The basic equations that govern the flow in presence of heat and mass transfer with the effects of viscous dissipation and Joule heating are of the form:

$$\nabla \cdot \varvec{V} = 0 ,$$

(9)

$$\rho_{f} \left[ {\frac{{\partial \varvec{V}}}{\partial t} + \varvec{V} \cdot \nabla \varvec{V}} \right] = - \nabla P + \nabla \cdot\varvec{\tau}+ \varvec{J} \times \varvec{B} + \frac{{\mu_{0} }}{{K^{*} }} \varvec{V} - \frac{{\rho_{f} c_{b} }}{{\sqrt {K^{*} } }} \varvec{V} \left| \varvec{V} \right|,$$

(10)

$$\left( {\rho c} \right)_{f} \left[ {\frac{\partial T}{\partial t} + \varvec{V} \cdot \nabla T} \right] = K \nabla^{2} T + \tau \cdot \nabla \varvec{V} + \frac{{\varvec{J} \cdot \varvec{J}}}{\sigma } + \left( {\rho c} \right)_{p} \left[ {\begin{array}{*{20}c} {D_{B} \left( {\nabla {\text{C}} \nabla T} \right) + } \\ {\frac{{D_{T} }}{{T_{0} }}\left( {\nabla T \nabla T} \right)} \\ \end{array} } \right],$$

(11)

$$\left[ {\frac{{\partial {\text{C}}}}{\partial t} + \varvec{V} \cdot \nabla {\text{C}}} \right] = D_{B} \nabla^{2} {\text{C}} + \frac{{D_{T} }}{{T_{0} }}\left( {\nabla^{2} T} \right),$$

(12)

where $\rho_{f}$ is the density of the fluid, $P$ is the pressure, $c_{b}$ is the volume dimensionless quadratic drag coefficient, $\left( {\rho c} \right)_{f}$ is the heat capacity of the fluid, $T$ is the temperature of the fluid, $K$ is the thermal conductivity, $\left( {\rho c} \right)_{p}$ is the effective heat capacity of the nanoparticle material, $D_{B}$ is the Brownian diffusion coefficient, $C$ is the nanoparticle concentration and $D_{T}$ is the thermophoretic diffusion.

Introducing a wave frame $\left( {x,y} \right)$ moving with velocity $c$ away from the fixed frame $\left( {X,Y} \right)$ by the transformation:

$$x = X - ct,\;\; y = Y,\;\; u = U - c,\;\; v = V,\;\; p\left( x \right) = P\left( {X,t} \right),$$

(13)

in which $\left( {x,y} \right),\left( {u,v} \right)\,\,{\text{and}}\,\, p$ are the coordinates, velocity components and pressure in the wave frame.

Introducing the stream function $\psi$ (such that $u = \frac{\partial \psi }{\partial y}\,\,{\text{and}}\,\, v = - \frac{\partial \psi }{\partial x}$) and defining the following non-dimensional quantities

$$\begin{aligned} \bar{x} = & \frac{x}{\lambda } , \bar{y} = \frac{y}{{d_{1} }} , \bar{u} = \frac{u}{c} , \bar{v} = \frac{v}{c} , \bar{t} = \frac{c}{\lambda } t, d = \frac{{d_{2} }}{{d_{1} }}, a = \frac{{a_{1} }}{{d_{1} }} , b = \frac{{b_{1} }}{{d_{1} }}, \\ h_{1} = & \frac{{H_{1} }}{{d_{1} }} , h_{2} = \frac{{H_{2} }}{{d_{2} }} , \bar{\psi } = \frac{\psi }{{c d_{1} }} , Re = \frac{{\rho_{f} c d_{1} }}{{\mu_{0} }} , \delta = \frac{{d_{1} }}{\lambda } , \bar{p} = \frac{{d_{1}^{2} p}}{{\mu_{0} c \lambda }} , \\ \bar{\tau }_{{\bar{x}\bar{x}}} = & \frac{\lambda }{{\mu_{0} c}}\tau_{xx} , \bar{\tau }_{{\bar{x}\bar{y}}} = \frac{{d_{1} }}{{\mu_{0} c}}\tau_{xy} , \bar{\tau }_{{\bar{y}\bar{y}}} = \frac{{d_{1} }}{{\mu_{0} c}}\tau_{yy} , We = \frac{\varGamma c}{{d_{1} }} , \bar{\dot{\gamma }} = \frac{{d_{1} \dot{\gamma }}}{c} , \\ M = & \sqrt[ ]{{\frac{\sigma }{{\mu_{0} }}}} B_{0} d_{1} , d_{a} = \frac{{K^{*} }}{{d_{1}^{2} }} , F_{S} = \frac{{c_{b} d_{1}^{2} c}}{{\nu_{f} \sqrt {K^{*} } }} , \bar{\theta } = \frac{{T - T_{0} }}{{T_{1} - T_{0} }} , \bar{\varOmega } = \frac{{C - C_{0} }}{{C_{1} - C_{0} }}, \\ Pr = & \frac{{\nu_{f} }}{ \alpha } , E_{c} = \frac{{c^{2} }}{{c_{f} \left( {T_{1} - T_{0} } \right)}} , N_{b} = \frac{{\left( {\rho c} \right)_{p} D_{B} \left( {C_{1} - C_{0} } \right)}}{K} , N_{t} = \frac{{\left( {\rho c} \right)_{p} D_{B} \left( {T_{1} - T_{0} } \right)}}{{T_{0 } K}}, \\ S_{c} = & \frac{{\nu_{f} }}{{D_{B} }}. \\ \end{aligned}$$

(14)

where $Re$ is the Reynolds number, $\delta$ is the dimensionless wave number, $We$ is the Weissenberg number, $M$ is the Hartman number, $D_{a}$ is the Darcy number, $F_{S}$ is the Forchheimer number, $Br$ is the local nanoparticle Grashof number, $Pr$ is the Prandtl number, $E_{c}$ is the Eckert number, $S_{c}$ is the Schmidt number, $N_{b}$ is the Brownain motion parameter and $N_{t}$ is the thermophoresis parameter.

Using Eqs. (13) and the above set of non-dimensional variable and parameters (14) into Eqs. 10–12. In the wave frame, the resulting equations in terms of the stream function $\bar{\psi }$ $\left( {u = \frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} \;{\text{and }}\;v = - \delta \frac{{\partial \bar{\psi }}}{{\partial \bar{x}}}} \right)$ are:

$$\begin{aligned} Re~\delta \left[ {\left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}}~\frac{\partial }{{\partial \bar{x}}} - \frac{{\partial \bar{\psi }}}{{\partial \bar{x}}}~\frac{\partial }{{\partial \bar{y}}}} \right)\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}}} \right] = & - \frac{{\partial \bar{p}}}{{\partial \bar{x}}} + \delta ^{2} \frac{\partial }{{\partial \bar{x}}}\left( {\bar{\tau }_{{\bar{x}\bar{x}}} } \right) + \frac{\partial }{{\partial \bar{y}}}\left( {\bar{\tau }_{{\bar{x}\bar{y}}} } \right) - \delta \frac{{m~M^{2} }}{{1 + m^{2} }}\left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{x}}}} \right) \\ & \;\; - ~\left( {\frac{{M^{2} }}{{1 + m^{2} }} + ~\frac{1}{{D_{a} }}} \right)\left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} + 1} \right) - F_{s} \left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} + 1} \right)^{2} , \\ \end{aligned}$$

(15)

$$\begin{aligned} Re \delta^{3} \left[ {\left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{x}}} \frac{\partial }{{\partial \bar{y}}} - \frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} \frac{\partial }{{\partial \bar{x}}}} \right)\frac{{\partial \bar{\psi }}}{{\partial \bar{x}}}} \right] = & - \frac{{\partial \bar{p}}}{{\partial \bar{y}}} + \delta^{2} \frac{\partial }{{\partial \bar{x}}}\left( {\bar{\tau }_{{\bar{y}\bar{x}}} } \right) + \delta \frac{\partial }{{\partial \bar{y}}}\left( {\bar{\tau }_{{\bar{y}\bar{y}}} } \right) - \delta \frac{{m M^{2} }}{{1 + m^{2} }}\left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} + 1} \right) \\ & \;\; + \delta^{2} \left( {\frac{{M^{2} }}{{1 + m^{2} }} + \frac{1}{{D_{a} }}} \right)\left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{x}}}} \right) - \delta^{3} F_{s} \left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{x}}}} \right)^{2} , \\ \end{aligned}$$

(16)

$$\begin{aligned} Re \delta \left[ {\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} \frac{{\partial \bar{\theta }}}{{\partial \bar{x}}} - \frac{{\partial \bar{\psi }}}{{\partial \bar{x}}} \frac{{\partial \bar{\theta }}}{{\partial \bar{y}}}} \right] = & \frac{1}{Pr}\left( {\frac{{\partial^{2} \bar{\theta }}}{{\partial \bar{y}^{2} }} + \delta^{2} \frac{{\partial^{2} \bar{\theta }}}{{\partial \bar{x}^{2} }}} \right) + E_{c} \left[ {\left( {\begin{array}{*{20}c} {\delta^{2} \bar{\tau }_{{\bar{x}\bar{x}}} \frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{x} \partial \bar{y}}} + \bar{\tau }_{{\bar{x}\bar{y}}} \frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{y}^{2} }}} \\ { - \delta^{2} \bar{\tau }_{{\bar{y}\bar{x} }} \frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{x}^{2} }} - \delta \bar{\tau }_{{\bar{y}\bar{y} }} \frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{y} \partial \bar{x}}}} \\ \end{array} } \right)} \right] \\ & \;\; + \; E_{c } \frac{{M^{2} }}{{1 + m^{2} }}\left[ {\begin{array}{*{20}c} {\delta^{2} \left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{x}}}} \right)^{2} + } \\ {\left( {\frac{\partial \psi }{\partial y} + 1} \right)^{2} } \\ \end{array} } \right] + \frac{{N_{b} }}{Pr}\left( {\delta^{2} \frac{{\partial \bar{\varOmega }}}{{\partial \bar{x}}} \frac{{\partial \bar{\theta }}}{{\partial \bar{x}}} + \frac{{\partial \bar{\varOmega }}}{{\partial \bar{y}}} \frac{{\partial \bar{\theta }}}{{\partial \bar{y}}}} \right) \\ & \;\; + \; \frac{{N_{t} }}{Pr}\left[ {\delta^{2} \left( {\frac{{\partial \bar{\theta }}}{{\partial \bar{x}}}} \right)^{2} + \left( {\frac{{\partial \bar{\theta }}}{{\partial \bar{y}}}} \right)^{2} } \right], \\ \end{aligned}$$

(17)

$$Re \delta S_{c} \left[ {\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} \frac{{\partial \bar{\varOmega }}}{{\partial \bar{x}}} - \frac{{\partial \bar{\psi }}}{{\partial \bar{x}}} \frac{{\partial \bar{\varOmega }}}{{\partial \bar{y}}}} \right] = \left( {\frac{{\partial^{2} \bar{\varOmega }}}{{\partial \bar{y}^{2} }} + \delta^{2} \frac{{\partial^{2} \bar{\varOmega }}}{{\partial \bar{x}^{2} }}} \right) + \frac{{N_{t} }}{Nb}\left( {\frac{{\partial^{2} \bar{\theta }}}{{\partial \bar{y}^{2} }} + \delta^{2} \frac{{\partial^{2} \bar{\theta }}}{{\partial \bar{x}^{2} }}} \right) ,$$

(18)

where

$$\bar{\dot{\gamma }} = \left[ {2 \delta^{2} \left( {\frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{x} \partial \bar{y}}}} \right)^{2} + \left( {\frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{y}^{2} }} - \delta^{2} \frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{x}^{2} }}} \right)^{2} + 2 \delta^{2} \left( {\frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{y} \partial \bar{x}}}} \right)^{2} } \right]^{{\frac{1}{2}}} .$$

(19)

Under the assumption of long wavelength $\delta < < 1$ and low Reynolds number, we finally obtain (after dropping the bars):

$$0 = - \frac{\partial p}{\partial x} + \frac{\partial }{\partial y}\left[ {\left( {1 + We \frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right] - \left( {\frac{{M^{2} }}{{1 + m^{2} }} + \frac{1}{{D_{a} }}} \right)\left( {\frac{\partial \psi }{\partial y} + 1} \right) - F_{s} \left( {\frac{\partial \psi }{\partial y} + 1} \right)^{2} ,$$

(20)

$$0 = \frac{\partial p}{\partial y},$$

(21)

$$0 = \frac{1}{Pr}\left( {\frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) + E_{c} \left[ {\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + We \left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{3} } \right] + E_{c } \frac{{M^{2} }}{{1 + m^{2} }}\left[ {\left( {\frac{\partial \psi }{\partial y} + 1} \right)^{2} } \right] + \frac{{N_{b} }}{Pr}\left( {\frac{\partial \varOmega }{\partial y} \frac{\partial \theta }{\partial y}} \right) + \frac{{N_{t} }}{Pr}\left( {\frac{\partial \theta }{\partial y}} \right)^{2} ,$$

(22)

$$0 = \frac{{\partial^{2} \varOmega }}{{\partial y^{2} }} + \frac{{N_{t} }}{Nb}\left( {\frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right).$$

(23)

Equation (21) implies that $p \ne p\left( y \right)$, so we can write Eq. (20) in the form:

$$0 = \frac{{\partial^{2} }}{{\partial y^{2} }}\left[ {\left( {1 + We \frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} - \left( {\frac{{M^{2} }}{{1 + m^{2} }} + \frac{1}{{D_{a} }}} \right)\psi } \right] - 2 F_{s} \left( {\frac{\partial \psi }{\partial y}} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right).$$

(24)

The non-dimensional boundaries will take the form

$$h_{1} = 1 + a \cos \left( {2\pi x} \right),$$

(25)

$$h_{2} = - d - b\cos \left( {2\pi x + \phi } \right),$$

(26)

where $a, b, \phi , d$ satisfy the relation

$$a^{2} + b^{2} + 2 a b \cos \phi \le \left( {1 + d} \right)^{2} .$$

(27)

The non dimensional boundary conditions in the wave frame are given by:

$$\begin{aligned} \psi = \frac{F}{2} , \frac{\partial \psi }{\partial y} = - 1 , \theta = 0 , \varOmega = 0, \; at\; y = h_{1} \hfill \\ \psi = - \frac{F}{2} , \frac{\partial \psi }{\partial y} = - 1 , \theta = 1 , \varOmega = 1,\; at\; y = h_{2} , \hfill \\ \end{aligned}$$

(28)

where $F$ is the dimensionless average flux in the wave frame defined by

$$F = \mathop \int \limits_{{h_{2} \left( x \right)}}^{{h_{1} \left( x \right)}} \frac{\partial \psi }{\partial y} dy.$$

(29)

The time mean $Q$ in the wave frame is defined by

$$Q = F + 1 + d .$$

(30)

3 Results and discussion

In order to investigate the physical significance of the problem, a program was designed by Mathematica 10 software including using of parametric ND solve package to simulate the numerical solutions of the system of the differential equations which describe our problem. The purpose of these numerical computations is to illustrate the influence of various governing physical parameters on the velocity $u$, the temperature $\theta$ and the nanoparticle concentration $\varOmega$ at several sections of the fluid motion.

Fig. 1

Physical sketch of the problem

3.1 Velocity profile

Figures 2, 3, 4, 5 are prepared to study the effects of increasing the Hartman number $M$, the Weissenberg number $We$, the Darcy number $D_{a}$ and the Forchheimer number $F_{S}$ on the velociy profile. Figure 2 shows that the behaviour of of the velocity near the channel walls and at the central region of the channel is not similar in view of the Hartman number $M$. The velocity field increases with the increase in $M$ near the channel walls and decreases at the central region of the channel. Figures 3, 4 show that the effects of the Weissenberg number $We$, the Darcy number $D_{a}$ on the velocity profile are the same and opposite to that of the Hartman number $M$. It is seen from these figures that the behaviour of the velocity near the channel walls and at the centeral region of the channel is not similar in view of $We$ and $D_{a}$. The velocity field decreases with the increase in $We$ and $D_{a}$ near the channel walls and increases at the central region of the channel. It is noticed that the effects of increasing $We$ and $D_{a}$ are slight at some sections of the fluid motion (see Figs. 3b–e, 4b–e).

Fig. 2

The velocity profile $u$ is plotted against y for several values of $M$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2, m = 1,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$ ${\mathbf{a}}\;x = - 1 , {\mathbf{b}}\;x = - 0.6 , {\mathbf{c}} \, x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e }}\;x = 0.6,$$\, {\mathbf{f}}\; x = 1.$

Fig. 3

The velocity profile $u$ is plotted against y for several values of $We$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , D_{a} = 0.2 , M = 1.5 , m = 1,$ $F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$ ${\mathbf{a}}\;x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}} \, x = - 0.4 , {\mathbf{d}} \, x = 0.4 , {\mathbf{e}}\;{\mathbf{ }}x = 0.6,$$\, {\mathbf{f}}\; x = 1 .$

Fig. 4

The velocity profile $u$ is plotted against y for several values of $D_{a}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , M = 1.5 , m = 1 ,$ $F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$ ${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\;x = 0.6 ,$$\; {\mathbf{f}}\; x = 1 .$

Fig. 5

The velocity profile $u$ is plotted against y for several values of $F_{S}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2 , M = 1.5 ,$$m = 1 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\;x = 1.$

Figure 5 illustrate the change of the velocity profile with several values of the Forchheimer number $F_{s}$. It is clear that the velocity decreases near the channel walls with the increase of $F_{s}$, whereas it increase at the center of the channel. It is observed that a reduction in the distribution occurs and the variation becomes narrow at some sections of the fluid motion (see Fig. 5b–e).

3.2 Temperature profile

The effects of the Weissenberg number $We$, the Darcy number $D_{a}$, the Hartman number $M$, the prandtl number $Pr$, the Eckert number $E_{c}$, the Forchheime number $F_{S}$, the Hall parameter $m$, the Brownain motion parameter $N_{b}$ and the thermophoresis parameter $N_{t}$ on the temperature profile are shown in Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14. It is clear that the temperature is always positive. It is seen from Fig. 6 that with an increase in $We$, the temperature field increases up to a certain point (which may be called as the point of inflection), after which the trend is reversed and the temperature decreases. Figures 7, 8, 9, 10, 11, 12 illustrate that the effects of $D_{a}$, $M$, $Pr$ and $E_{c}$ on the temperature profile are the same and opposite to these of $F_{S}$, and $m$. The temperature profile increases by increasing $D_{a}$, $M$, $Pr$ and $E_{c}$, while it decreases with the increase of $F_{S}$, and $m$. In view of $m$, it is noticed that a reduction in the distribution occurs and the variation becomes narrow (see Fig. 12b, c and e). Figures 13, 14 illustrate that the effects of increasing $N_{b}$ and $N_{t}$ on the temperature profile are the same. It is clear that the temperature profile decreases up to an inflection point and increases after crossing that point.

Fig. 6

The temperature profile $\theta$ is plotted against y for several values of $We$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , D_{a} = 0.2 , M = 1.5 , m = 1 ,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\;x = - \;0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$ $\, {\mathbf{f}}\;x = 1 .$

Fig. 7

The temperature profile $\theta$ is plotted against y for several values of $D_{a}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , M = 1.5 , m = 1 ,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\;x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\;x = 1$

Fig. 8

The temperature profile $\theta$ is plotted against y for several values of $M$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2 , m = 1 ,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\;x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 9

The temperature profile $\theta$ is plotted against y for several values of $Pr$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2 , M = 1.5 ,$ $m = 1 , F_{S} = 0.2 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 10

The temperature profile $\theta$ is plotted against y for several values of $E_{c}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2 , M = 1.5,$ $m = 1 , F_{S} = 0.2 , Pr = 1 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$$\; {\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 11

The temperature profile $\theta$ is plotted against y for several values of $F_{S}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.5 , M = 1.5 ,$$m = 1 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$$\; {\mathbf{a}}\; x = - \;1 , {\mathbf{b}} x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\,{\mathbf{f}}\;x = 1$

Fig. 12

The temperature profile $\theta$ is plotted against y for several values of $m$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 2 , D_{a} = 0.2 , M = 1.5 ,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - \;1 , {\mathbf{b}}\; x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 13

The temperature profile $\theta$ is plotted against y for several values of $N_{b}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 2 , M = 1.5 ,$$m = 1 , F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\;x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\,{\mathbf{f}}\; x = 1$

Fig. 14

The temperature profile $\theta$ is plotted against y for several values of $N_{t}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 2 , M = 1.5 ,$$m = 1 , F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , F = 1 , {\text{when }}$${\mathbf{a}}\; x = - \;1 , {\mathbf{b}}\; x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

3.3 Concentration profile

Influence of the Weissenberg number $We$ on the concentration is shown in Fig. 15. From this Figure it is noticed that with an increase in $We$, the concentration field decreases up to a certain point (which may be called as the point of inflection), after which the trend is reversed and the concentration increases. The effects of the Darcy number $D_{a}$, the Forchheime number $F_{S}$ and the Hall parameter $m$ on the concentration are the same as shown in Figs. 16, 17, 18. The increase in $D_{a}$, $F_{S}$ and $m$ lead to an increase in the concentration. In view of $m$, it is observed that a reduction in the distribution occurs and the variation becomes narrow (see Fig. 18b, d). The effects of increasing the Hartman number $M$, the prandtl number $Pr$ and the Eckert number $E_{c}$ on the concentration profile are the same. It is clear from Figs. 19, 20, 21 that the concentration profile decreases with the increase in $M$, $Pr$ and $E_{c}$. The effects of the Brownain motion parameter $N_{b}$ and the thermophoresis parameter $N_{t}$ on the concentration profile are displayed in Figs. 22, 23. It is clear that increasing $N_{b}$ and $N_{t}$ have opposite effects on the concentration. The concentration profile increases as $N_{b}$ increases, while it decreases as $N_{t}$ increases.

Fig. 15

The concentration profile $\varOmega$ is plotted against y for several values of $We$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , D_{a} = 0.2 , M = 1.5 , m = 1 ,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - \;1 , {\mathbf{b}}\; x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 16

The concentration profile $\varOmega$ is plotted against y for several values of $D_{a}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , M = 1.5 , m = 1,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when }}$${\mathbf{a}}\; x = - \;1 , {\mathbf{b}}\; x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 17

The concentration profile $\varOmega$ is plotted against y for several values of $F_{S}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.5 , M = 1.5 ,$$m = 1 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 18

The concentration profile $\varOmega$ is plotted against y for several values of $m$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 2 , D_{a} = 0.2 , M = 1.5,$$F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$ ${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$ $\, {\mathbf{f}}\; x = 1$

Fig. 19

The concentration profile $\varOmega$ is plotted against y for several values of $M$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2 , m = 1,$ $F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\; x = 1$

Fig. 20

The concentration profile $\varOmega$ is plotted against y for several values of $Pr$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2 , M = 1.5,$$m = 1 , F_{S} = 0.2 , E_{c} = 0.5 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - 1 , {\mathbf{b}}\; x = - 0.6 , {\mathbf{c}}\;x = - 0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6,$ $\, {\mathbf{f}}\;x = 1$

Fig. 21

The concentration profile $\varOmega$ is plotted against y for several values of $E_{c}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 0.2 , M = 1.5,$$m = 1 , F_{S} = 0.2 , Pr = 1 , N_{b} = 0.7 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - \;1 , {\mathbf{b}}\; x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6 ,$$\, {\mathbf{f}}\;x = 1$

Fig. 22

The concentration profile $\varOmega$ is plotted against y for several values of $N_{b}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 2 , M = 1.5,$$m = 1 , F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{t} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - \;1 , {\mathbf{b}}\; x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6,$$\, {\mathbf{f}}\; x = 1$

Fig. 23

The concentration profile $\varOmega$ is plotted against y for several values of $N_{t}$ at $a = 0.5 , b = 0.5 , d = 1 , \phi = \frac{\pi }{4} , We = 0.2 , D_{a} = 2 , M = 1.5,$$m = 1 , F_{S} = 0.2 , Pr = 1 , E_{c} = 0.5 , N_{b} = 0.7 , F = 1 , {\text{when}}$${\mathbf{a}}\; x = - \;1 , {\mathbf{b}}\; x = - \;0.6 , {\mathbf{c}}\;x = - \;0.4 , {\mathbf{d}}\;x = 0.4 , {\mathbf{e}}\; x = 0.6,$$\, {\mathbf{f}}\; x = 1$

4 Conclusion

The peristaltic flow of a Williamson nanofluid with heat and mass transfer in an asymmetric channel through a non-Darcy porous medium under the effects of Hall current, viscous dissipation and Joule heating is studied under assumption of long wavelength and low Reynolds number. The main results are summarized as follow:

• Increasing the Hartman number $M$ and the Forcheimer number $F_{S}$ have the same effects on the velocity. The velocity field increases near the channel walls and decreases at the central region of the channel.

• The effect of increasing the Weissenberg number $We$ on the velocity is similar to that of increasing the Darcy number $D_{a} .$ The velocity field decreases near the channel walls and increases at the central region of the channel.

• The temperature decreases with an increase in the Darcy number $D_{a}$, while it increases when the Forchheimernumber $F_{S}$ increases.

• The increase in the Hartman number $M$, the prandtl number $P_{r}$ and the Eckert number $E_{c}$ lead to the increase of the temperature.

• The concentration profile increases by increasing the Darcy number $D_{a}$ and the Forrcheimer number $F_{S}$.

• The effect of the Brownain motion parameter $N_{b}$ on the concentration is opposite to that of the thermophoresis parameter $N_{t} .$

• The small increase in the thermophoresis parameter $N_{t}$ effects the large differences in the concentration profile.