1 Introduction

In 1991, Sumio Iijima discovered the fullerene-based carbon nanotube (CNT) [1]. CNTs [2] are known for their excellent mechanical, electrical and chemical properties. DWCNTs are comprised of two concentric carbon nanotubes (CNTs), one tube nested within the other. Applications of DWCNTs may be seen in the areas of lasers [3,4,5], sensors [6,7,8,9,10] and transistors and switches [11, 12]. Electrostatic actuation is used in applications of DWCNTs as resonator sensors for mass sensing. Pull-in instability is a phenomenon that occurs in systems under electrostatic actuation [13]. Free vibration response of DWCNTs has been previously reported [14]. For this case, coaxial vibration has been considered.

Yan et al. [15] employed the concept of nonlinear normal modes (NNMs) to model the nonlinear dynamical behavior of DWCNTs. They used a continuum elastic beam model devoid of damping and external forces with an intent to focus on free vibration. They investigated the case of internal resonance and the case of no internal resonance using the method of multiple scales (MMS) to approximate the solutions of the NNMs. They concluded that, in the coaxial mode of vibration, the inner and outer carbon nanotubes vibrate with an amplitude ratio that is “very close to unity.” Natsuki et al. [16] also used a continuum Euler–Bernoulli beam model to characterize DWCNTs of varying lengths of inner and outer carbon nanotubes, and under free vibration. They investigated the natural frequencies of a DWCNT up to the seventh mode of vibration and concluded that vibrational frequencies decrease when the length of either the inner or outer carbon nanotube is increased, while the other is kept constant. The utility of controlling the lengths of the inner and outer carbon nanotubes of DWCNTs is that they may operate at different frequencies as desired.

Murmu et al. [17] used nonlocal Euler–Bernoulli beam theory to model a DWCNT subjected to an axial magnetic field. Their analytical solutions were for natural frequencies of the DWCNTs under a magnetic field. They concluded that for both coaxial and noncoaxial modes of vibrations, the presence of the longitudinal magnetic field increases the natural frequencies. Hajnayeb and Khadem [18] modeled DWCNTs using Euler–Bernoulli beam theory to include linear damping, stretching terms, nonlinear intertube van der Waals and nonlinear electrostatic forces. They applied a perturbation method and long-time integration method to approximate for solutions for the amplitude–frequency response under primary and secondary resonance conditions. They concluded that, like single-walled carbon nanotubes (SWCNTs), DWCNTs experienced softening and hardening behavior depending on the value of DC voltage. Additionally, they remarked that when the AC frequency is at either the coaxial or noncoaxial frequency, the other mode is “damped out in the steady-state response because of system damping.” Hudson and Sinha [19] applied order reduction methods, i.e., modal domain analysis (MDA) and modified modal domain analysis (MMDA), in atomistic simulations to investigate the effects of defects on the vibrational behavior of carbon nanotubes. They concluded that, compared to MDA, MMDA results in a “valid and useful approximation of the perturbed system” and both are suitable tools for investigation of high-degree-of-freedom systems.

In this paper, the amplitude–frequency response of parametric resonance of cantilevered DWCNTs under soft alternating current (AC) electrostatic actuation is investigated. The AC frequency is near first coaxial natural frequency. The electrostatic and intertube van der Waals forces are nonlinear. Reduced-order models (ROMs) [20, 21] of up to five modes of vibration (terms) are used to transform the partial differential equation of motion into a system of ordinary differential equations. The ROM using one mode of vibration is solved using the method of multiple scales (MMS) [22]. In the analytical solution of MMS, the equations are coupled by the intertube van der Waals force. A Taylor polynomial is used to approximate the nonlinear electrostatic force per unit length. The equations of motion are decoupled in their linear part by using modal coordinates. These coordinates are then used for the nonlinear problem, and the amplitude–frequency response of the DWCNT coaxial vibrations is reported. Also, numerical integrations of ROMs using two, three, four and five modes of vibration are utilized to investigate the parametric resonance of coaxial vibrations of DWCNTs. The effects of voltage and damping parameters on the DWCNT amplitude–frequency response are reported.

2 Differential equations of motion

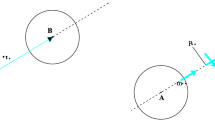
Euler–Bernoulli elastic beam model, valid for structures with high length-to-diameter ratio [23], is used in this work. The model of DWCNTs (Fig. 1) accounts for electrostatic, damping and intertube van der Waals forces. The governing partial differential equations of motion are given by

$$\begin{aligned}&\rho A_1 \frac{\partial ^{2}y_1 }{\partial t^{2}}+EI_1 \frac{\partial ^{4}y_1 }{\partial x^{4}}=f_{\mathrm{vdWT}-T} \end{aligned}$$
(1)
$$\begin{aligned}&\rho A_2 \frac{\partial ^{2}y_2 }{\partial t^{2}}+EI_2 \frac{\partial ^{4}y_2 }{\partial x^{4}}=-b\frac{\partial y_2 }{\partial t}-f_{\mathrm{vdWT}-T} +f_{\mathrm{elec}}\nonumber \\ \end{aligned}$$
(2)

where \(y_1 \left( {x,t} \right) \) and \(y_2 \left( {x,t} \right) \) are the deflections, \(A_1 \) and \(A_2 \) the cross-sectional areas, \(I_1 \) and \(I_2 \) cross-sectional moments of inertia of inner and outer CNTs, respectively, x the axial longitudinal coordinate, t time, \(\rho \) density and b the damping per unit length coefficient. The forces acting on the DWCNT are given at the right side of Eqs. (1) and (2). The forces are: damping due to viscosity, intertube van der Waals \(f_{\mathrm{vdWT}-T} \) and electrostatic force \(f_{\mathrm{elec}} \). The subscripts 1 and 2 in Eqs. (1) and (2) represent the inner and outer tubes, respectively.

Fig. 1
figure 1

DWCNT cantilever under electrostatic, damping and van der Waals forces

Full size image
Table 1 Physical constants [25]
Full size table
Table 2 Fluid damping conditions (dry air)
Full size table

Due to the presence of a viscous (air) environment, the damping force must be taken into account when modeling the DWCNT. Since the viscous fluid comes into direct contact with the outer tube, the damping is assumed to be acting only on the outer tube. Damping is considered to be proportional to the velocity of the tube as follows \(f_\mathrm{damp} =b\cdot \partial y_2 /\partial t\). Bhiladvala and Wang [24] provide a linear, fluid damping model that relates pressure and temperature to the fluid damping coefficient. A dry air medium under a pressure of 110 Pa (medium vacuum) and temperature of 300 K (room temperature) is considered. The values for the physical constants and dry air conditions for fluid damping afterward numerical simulations are given in Tables 1 and 2.

The intertube force \(f_{\mathrm{vdWT}-T} \)provides the coupling that introduces the two modes of vibration of a DWCNT: coaxial (in-phase CNTs) and noncoaxial (\(180^{\circ }\) out-of-phase CNTs). A Taylor polynomial describes the intertube van der Waals force as follows [25]:

$$\begin{aligned} f_{\mathrm{vdWT}-T} =C_1 (y_2 -y_1 )+C_3 (y_2 -y_1 )^{3} \end{aligned}$$
(3)

where \(C_{1}\) is the van der Waals interlayer interaction coefficient of the linear term and \(C_{3}\) is the van der Waals interlayer interaction coefficient of the cubic term.

Using a standard capacitance model of a multiwalled carbon nanotube [13, 26] and assuming that all charges dominate and are applied only on the outer carbon nanotube due to the Faraday Cage Effect [27], the electrostatic force per unit length is given by [2, 13]:

$$\begin{aligned} f_{\mathrm{elec}} =\frac{\pi \varepsilon _0 V^{2}}{R_2 \sqrt{\frac{\hat{{r}}_2 (\hat{{r}}_2 +2R_2 )}{R_2 ^{2}}}\ln ^{2}\left[ {1+\frac{\hat{{r}}_2 }{R_2 }+\sqrt{\frac{\hat{{r}}_2 (\hat{{r}}_2 +2R_2 )}{R_2 ^{2}}}} \right] } \end{aligned}$$
(4)

where \(\varepsilon _{0}\) is the permittivity of vacuum, \(R_{2}\) is the radius of the conducting outer tube and \(\hat{r}_{2}\) is the distance from the ground plate (graphite sheet) to the bottom of the outer carbon nanotube (Fig. 1). The AC voltage is given by

$$\begin{aligned} V=V_0 \cos \varOmega t \end{aligned}$$
(5)

where \(V_0 \) and \(\varOmega \) are the amplitude and circular frequency of the AC voltage, respectively. The gap g is the distance from the graphite sheet to the center of the DWCNT (Fig. 1), and it is given by:

$$\begin{aligned} g=y_2 +R_2 +\hat{{r}}_2 \end{aligned}$$
(6)

Consider the following dimensionless variables:

$$\begin{aligned} w_n =\frac{y_n }{g}; \quad z=\frac{x}{\ell }; \quad \tau =\frac{t}{\ell ^{2}}\sqrt{\frac{EI_2 }{\rho A_2 }} \end{aligned}$$
(7)

where \(n = 1,2, \ell \) is the length of the DWCNT; w, z and \(\tau \) are dimensionless deflection, dimensionless longitudinal coordinate and dimensionless time, respectively; and y, x and t are their corresponding dimensional variables. Substituting Eqs. (5) and (7) into Eqs. (1) and (2), the following system of dimensionless partial differential equations of motion result:

$$\begin{aligned} \left\{ {\begin{array}{l} A^{*}\frac{\partial ^{2}w_1 }{\partial \tau ^{2}}+I^{*}\frac{\partial ^{4}w_1 }{\partial z^{4}}=\bar{{f}}_{\mathrm{vdWT}-T} \\ \frac{\partial ^{2}w_2 }{\partial \tau ^{2}}+\frac{\partial ^{4}w_2 }{\partial z^{4}}=-b^{*}\frac{\partial w_2 }{\partial \tau }-\bar{{f}}_{\mathrm{vdWT}-T}\\ \quad +\,\delta \bar{{f}}_{\mathrm{elec}} \cos ^{2}\varOmega ^{*}\tau \\ \end{array}} \right. \end{aligned}$$
(8)

where the dimensionless intertube van der Waals force \(\bar{{f}}_{\mathrm{vdWT}-T}\) and electrostatic force \(\bar{{f}}_{\mathrm{elec}}\) are given by

$$\begin{aligned} \bar{{f}}_{\mathrm{vdWT}-T}= & {} C_1 ^{*}(w_2 -w_1 )+C_3 ^{*}(w_2 -w_1 )^{3} \end{aligned}$$
(9)
$$\begin{aligned} \bar{{f}}_{\mathrm{elec}}= & {} \left[ {(1-w_2 )^{2}-s_2 ^{2}} \right] ^{-\frac{1}{2}}\nonumber \\&\quad \times \ln ^{-2}\left( {\frac{1-w_2 }{s_2 }+\sqrt{\frac{(1-w_2 )^{2}}{s_2^2 }-1}} \right) \nonumber \\ \end{aligned}$$
(10)

and \(s_2 =R_2 /g\). The dimensionless electrostatic force Eq. (10) is approximated using a third degree Taylor polynomial as follows:

$$\begin{aligned} \bar{{f}}_{\mathrm{elec}} (w_2 )=\sum _{k=0}^3 {\alpha _k w_2 ^{k}} \end{aligned}$$
(11)

Dimensionless area \(A^{*}\), dimensionless moment of inertia \(I^{*}\), dimensionless coefficients \(C_{1}^{*}\) and \(C_{3}^{*}\) of linear and cubic terms of intertube van der Waals force, dimensionless damping \(b^{*}\), dimensionless voltage parameter \(\delta \) and dimensionless AC frequency \(\varOmega ^{*}\) of Eq. (8) are given by:

$$\begin{aligned} A^{*}= & {} \frac{A_1 }{A_2 },\quad I^{*}=\frac{I_1 }{I_2 } ,\quad C_1 ^{*}=\frac{C_1 \ell ^{4}}{EI_2 } ,\quad \nonumber \\ C_3 ^{*}= & {} \frac{C_3 g^{2}\ell ^{4}}{EI_2 } \delta =\frac{\pi \varepsilon _0 \ell ^{4}V_0 ^{2}}{EI_2 g^{2}} ,\quad \nonumber \\ \varOmega ^{*}= & {} \varOmega \ell ^{2}\sqrt{\frac{\rho A_2 }{EI_2 }} ,b^{*}=\frac{b\ell ^{2}}{\sqrt{\rho A_2 EI_2 }} \end{aligned}$$
(12)
Table 3 Dimensional parameters of the system [13]
Full size table
Fig. 2
figure 2

DWCNT cross section

Full size image

Tables 1 and 3 give the values of the physical constants and dimensional parameters of the DWCNT used for the afterward numerical simulations. The areas and moments of inertia are calculated as follows (Fig. 2):

$$\begin{aligned} A_n= & {} \pi \left[ {(R_i +h/2)^{2}-(R_i -h/2)^{2}} \right] \end{aligned}$$
(13)
$$\begin{aligned} I_n= & {} \frac{\pi }{4}\left[ {(R_i +h/2)^{4}-(R_i -h/2)^{4}} \right] \end{aligned}$$
(14)

where \(n = 1,2\) and h is the effective thickness of each tube in the DWCNT.

3 Modal coordinate transformation

The two concentric CNTs are coupled through the intertube van der Waals force. Modal coordinates are used to decouple the linearized system of partial differential equations of motion, not to include damping, resulting from Eq. (8). Then the modal coordinates are substituted into the partial differential equations of motion (Eqs. (8)). This way, the differential equations of motion are written in terms of modal coordinates, denoted by r. Consider the linearized system of partial differential equations resulting from Eq. (8), i.e., DWCNT system under free vibration to include the linear van der Waals force being applied:

$$\begin{aligned} \left\{ {\begin{array}{l} A^{*}\frac{\partial ^{2}w_1 }{\partial \tau ^{2}}+I^{*}\frac{\partial ^{4}w_1 }{\partial z^{4}}=-C_1 ^{*}(w_1 -w_2 ) \\ \frac{\partial ^{2}w_2 }{\partial \tau ^{2}}+\frac{\partial ^{4}w_2 }{\partial z^{4}}=C_1 ^{*}(w_1 -w_2 ) \\ \end{array}} \right. \end{aligned}$$
(15)

Assume the deflections of the inner and outer tubes as follows:

$$\begin{aligned} w_1 =u_1 (\tau )\phi _1 (z); \quad w_2 =v_1 (\tau )\phi _1 (z) \end{aligned}$$
(16)

where \(\phi _1 (z)\) is the first cantilever mode shape and \(u_1 \) and \(v_1 \) are functions of time of the inner and outer tubes, respectively. Assume

$$\begin{aligned} u_1 \left( \tau \right) =A\cos \omega _{1I} \tau ; \quad v_1 \left( \tau \right) =B\cos \omega _{1O} \tau \end{aligned}$$
(17)

where A and \(\omega _{1I} \), and B and \(\omega _{1O} \) are the amplitudes and natural frequencies of the inner and outer tubes, respectively. To find the natural frequencies of the CNTs, the right sides of Eq. (15) are equated to zero, i.e., free vibrations not to include van der Waals forces. Substituting Eqs. (16) and (17) into Eq. (15) yields the following:

$$\begin{aligned} \left\{ {\begin{array}{l} I^{*}\phi ^{(4)}(z)=A^{*}\omega _{1I} ^{2}\phi (z) \\ \phi ^{(4)}(z)=\omega _{1O} ^{2}\phi (z) \\ \end{array}} \right. \end{aligned}$$
(18)

From Eq. (18), the following relationship can be established:

$$\begin{aligned} \omega _{1O} ^{2}=\frac{A^{*}}{I^{*}}\omega _{1I} ^{2} \end{aligned}$$
(19)

Substituting Eqs. (16–19) into Eq. (15) yields the following system of second-order ordinary differential equations:

$$\begin{aligned} \left\{ {\begin{array}{l} A^{*}{\ddot{u}}_1 +A^{*}\omega _{1I} ^{2}u_1 =C_1 ^{*}(v_1 -u_1 ) \\ {\ddot{v}}_1 +\omega _{1O} ^{2}v_1 =C_1 ^{*}(u_1 -v_1 ) \\ \end{array}} \right. \end{aligned}$$
(20)

Equation (20) is rewritten as follows:

$$\begin{aligned} M\left[ {{\begin{array}{l} {{\ddot{u}}_1 } \\ {{\ddot{v}}_1 } \\ \end{array} }} \right] +K\left[ {{\begin{array}{l} {u_1 } \\ {v_1 } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} 0 \\ 0 \\ \end{array} }} \right] \end{aligned}$$
(21)

where M is the mass matrix and K is the stiffness matrix. M and K are as follows:

$$\begin{aligned} M=\left[ {{\begin{array}{ll} {A^{*}}&{}\quad 0 \\ 0&{}\quad 1 \\ \end{array} }} \right] , \quad K=\left[ {{\begin{array}{ll} {C_1 ^{*}+A^{*}\omega _{1I} ^{2}}&{}\quad {-C_1 ^{*}} \\ {-C_1 ^{*}}&{}\quad {C_1 ^{*}+\omega _{1O} ^{2}} \\ \end{array} }} \right] \end{aligned}$$
(22)

The mass-normalized stiffness matrix is given by:

$$\begin{aligned} {\tilde{K}}=M^{-\frac{1}{2}}KM^{-\frac{1}{2}} \end{aligned}$$
(23)

Solving the symmetric eigenvalue problem det(\(\tilde{K}-\lambda I\)) yields \(\lambda _{1,}\lambda _{2}\) and \({{\varvec{V}}}_{1,} {{\varvec{V}}}_{2}\), the eigenvalues and eigenvectors of the system, respectively. The P-matrix is constructed as follows:

$$\begin{aligned} P=\left[ {{\begin{array}{ll} {V_1 }&{}\quad {V_2 } \\ \end{array} }} \right] \end{aligned}$$
(24)

Matrix S that transforms the coordinate system from the u-coordinates to modal r-coordinates is given by

$$\begin{aligned} S=M^{-\frac{1}{2}}P \end{aligned}$$
(25)
Table 4 Coordinate transformation constants 1T ROM
Full size table

Therefore, the modal coordinate transformation for the DWCNT system is given by \({{\varvec{u}}} = {{\varvec{Sr,}}}\) and it can be written as follows:

$$\begin{aligned} \left[ {{\begin{array}{l} {u_1 } \\ {v_1 } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} c&{}\quad d \\ e&{}\quad f \\ \end{array} }} \right] \left[ {{\begin{array}{l} {r_1 } \\ {r_2 } \\ \end{array} }} \right] \end{aligned}$$
(26)

where c, d, e and f are components of the matrix S. They are given in Table 4. Using Eq. (26), Eq. (8) becomes:

$$\begin{aligned} {\ddot{r}}+\varLambda r=P^{T}M^{-\frac{1}{2}}F(r), \quad \varLambda =\left[ {{\begin{array}{ll} {\bar{{\omega }}_1^2 }&{}\quad 0 \\ 0&{}\quad {\bar{{\omega }}_2^2 } \\ \end{array} }} \right] \end{aligned}$$
(27)

where F(r) is the column matrix of applied forces found at the right-hand side of Eq. (8), \(\bar{{\omega }}_1\) and \(\bar{{\omega }}_2\) are the DWCNT’s coaxial and noncoaxial frequencies of resonance, 3.07309 and 29660.65309, respectively, and \(r=\left[ {r_1 r_2 } \right] ^{T}\). One should mention that \(r_1 , r_2 \) are coaxial and noncoaxial modal coordinates, respectively. Moreover, F(r) is the column matrix F of the applied forces after the substitution of modal coordinate transformation given by Eq. (26). To be able to use Eq. (27) with nonlinear terms, Eq. (16) is substituted into Eq. (8) which is then multiplied by the operator \(\int \nolimits _0^1 {\cdot \phi _1 (z)\mathrm{d}z} \). The following coefficients result:

$$\begin{aligned} g_k =\int \limits _0^1 {\phi _1^{k+1} (z)\mathrm{d}z} \end{aligned}$$
(28)

These coefficients have been previously calculated by Caruntu and Knecht [28] (Table 5).

Table 5 g-coefficients for first natural frequency [28]
Full size table
Table 6 Taylor expansion coefficients of Eq. (4)
Full size table

4 Method of multiple scales (MMS)

To investigate the parametric resonance of DWCNTs, MMS is used to solve the r-coordinate system of differential equations where solutions of zero- and first-order problems may be found more readily. Consider \(b^{*}\) and \(\delta \) to be small, i.e., the system is under soft excitation and small damping. The intertube coefficients may not be assumed to be small; in fact, they are large coefficients. Setting the small parameters to a slow timescale by multiplying them by \(\varepsilon \), a small dimensionless bookkeeping parameter (Eq. (27)) becomes:

$$\begin{aligned} \left\{ {\begin{array}{l} {\ddot{r}}_1 +\bar{{\omega }}_1 ^{2}r_1 =cC_3 ^{*}\left( {er_1 +fr_2 -cr_1 -dr_2 } \right) ^{3}g_3 \\ \quad + e\left[ {C_3 ^{*}\left( {cr_1 +dr_2 -er_1 -fr_2 } \right) ^{3}g_3 -\varepsilon b^{*}(e{\dot{r}}_1 } \right. \\ \quad \left. {+f{\dot{r}}_2 )+\varepsilon \delta \sum _{k=0}^3 {\alpha { }_kg_k (er_1 +fr_2 )^{k}\cos ^{2}\varOmega ^{*}\tau } } \right] \\ {\ddot{r}}_2 +\bar{{\omega }}_2 ^{2}r_2 =dC_3 ^{*}\left( {er_1 +fr_2 -cr_1 -dr_2 } \right) ^{3}g_3 \\ \quad + f\left[ {C_3 ^{*}\left( {cr_1 +dr_2 -er_1 -fr_2 } \right) ^{3}g_3 -\varepsilon b^{*}(e{\dot{r}}_1 } \right. \\ \quad \left. {+f{\dot{r}}_2 )+\varepsilon \delta \sum _{k=0}^3 {\alpha { }_kg_k (er_1 +fr_2 )^{k}\cos ^{2}\varOmega ^{*}\tau } } \right] \\ \end{array}} \right. \end{aligned}$$
(29)

where the values of coefficients \(\alpha _k\) are given in Table 6. Consider fast \(T_0 =\tau \) and slow \(T_1 =\varepsilon \tau \) timescales, and first-order expansions of \(r_{1}\) and \(r_{2}\) as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} r_1 =r_{10} +\varepsilon r_{11} \\ r_2 =r_{20} +\varepsilon r_{21} \\ \end{array}} \right. \end{aligned}$$
(30)

where \(r_{10} , r_{20} \), and \(r_{11}, r_{21} \) are the zero-order and first-order approximation solutions, respectively. The time derivative is then expressed in terms of derivatives with respect to the fast and slow scales:

$$\begin{aligned} \frac{\partial }{\partial \tau }=D_0 +\varepsilon D_1; \quad \frac{\partial ^{2}}{\partial \tau ^{2}}=D_0 ^{2}+2\varepsilon D_0 D_1; \quad D_i =\frac{\partial }{\partial T_i } \end{aligned}$$
(31)

Substituting Eqs. (30) and (31) into Eq. (29), it results:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\begin{array}{l} \left( {D_0 ^{2}+2\varepsilon D_0 D_1 } \right) \left( {r_{10} +\varepsilon r_{11} } \right) +\bar{{\omega }}_1 ^{2}\left( {r_{10} +\varepsilon r_{11} } \right) \\ \quad =cC_3 ^{*}\big [ e\left( {r_{10} +\varepsilon r_{11} } \right) +f\left( {r_{20} +\varepsilon r_{21} } \right) \\ \qquad -c\left( {r_{10} +\varepsilon r_{11} } \right) -d\left( {r_{20} +\varepsilon r_{21} } \right) \big ]^{3}g_3 \\ \qquad +e\big \{ C_3 ^{*}\big [ c\left( {r_{10} +\varepsilon r_{11} } \right) +d\left( {r_{20} +\varepsilon r_{21} } \right) \\ \qquad -e\left( {r_{10} +\varepsilon r_{11} } \right) -f\left( {r_{20} +\varepsilon r_{21} } \right) ) \big ]^{3}g_3 \\ \qquad -\varepsilon b^{*}\big [ e\left( {D_0 +\varepsilon D_1 } \right) \left( {r_{10} +\varepsilon r_{11} } \right) \\ \qquad +f\left( {D_0 +\varepsilon D_1 } \right) \left( {r_{20} +\varepsilon r_{21} } \right) \big ] \\ \qquad + \varepsilon \delta \sum _{k=0}^3 \alpha _k g_k \big [ e\left( {r_{10} +\varepsilon r_{11} } \right) \\ \qquad +f\left( {r_{20} +\varepsilon r_{21} } \right) \big ] ^{k}\cos ^{2}\varOmega ^{*}T_0 \big \} \\ \end{array}} \\ {\begin{array}{l}\\ \left( {D_0 ^{2}+2\varepsilon D_0 D_1 } \right) \left( {r_{20} +\varepsilon r_{21} } \right) +\bar{{\omega }}_2 ^{2}\left( {r_{20} +\varepsilon r_{21} } \right) \\ \quad =dC_3 ^{*}[e\left( {r_{10} +\varepsilon r_{11} } \right) +f\left( {r_{20} +\varepsilon r_{21} } \right) \\ \qquad -c\left( {r_{10} +\varepsilon r_{11} } \right) -d\left( {r_{20} +\varepsilon r_{21} } \right) ]^{3}g_3 \\ \qquad +f\big \{ C_3 ^{*}\big [ c\left( {r_{10} +\varepsilon r_{11} } \right) +d\left( {r_{20} +\varepsilon r_{21} } \right) \\ \qquad -e\left( {r_{10} +\varepsilon r_{11} } \right) -f\left( {r_{20} +\varepsilon r_{21} } \right) \big ]^{3}g_3 \\ \quad -\varepsilon b^{*}\big [ e\left( {D_0 +\varepsilon D_1 } \right) \left( {r_{10} +\varepsilon r_{11} } \right) \\ \qquad +f\left( {D_0 +\varepsilon D_1 } \right) \left( {r_{20} +\varepsilon r_{21} } \right) \big ] \\ \quad +\varepsilon \delta \sum _{k=0}^3 \alpha _k g_k \big [ e\left( {r_{10} +\varepsilon r_{11} } \right) \\ \qquad +f\left( {r_{20} +\varepsilon r_{21} } \right) \big ]^{k}\cos ^{2}\varOmega ^{*}T_0 \big \} \\ \end{array}} \\ \end{array} }} \right. \end{aligned}$$
(32)

From Eq. (32), the following two problems result, the zero-order problem

$$\begin{aligned} \varepsilon ^{0}:\left\{ {{\begin{array}{l} D_0 ^{2}r_{10} +\bar{{\omega }}_1 ^{2}r_{10} =\left( {c-e} \right) C_3 ^{*}g_3 \\ \quad \left( {er_{10} +fr_{20} -cr_{10} -dr_{20} } \right) ^{3} \\ D_0 ^{2}r_{20} +\bar{{\omega }}_2 ^{2}r_{20} =\left( {d-f} \right) C_3 ^{*}g_3 \\ \quad \left( {er_{10} +fr_{20} -cr_{10} -dr_{20} } \right) ^{3} \\ \end{array} }} \right. \end{aligned}$$
(33)

and first-order problem:

$$\begin{aligned} \varepsilon ^{1}:\left\{ {{\begin{array}{l} D_0 ^{2}r_{11} +\bar{{\omega }}_1 ^{2}r_{11} =-2D_0 D_1 r_{10} \\ \quad -eb^{*}\left( {eD_0 r_{10} +fD_0 r_{20} } \right) +e\delta \sum _{k=0}^3 \alpha _k g_k \\ \quad \left( {er_{10} +fr_{20} } \right) ^{k}\cos ^{2}\varOmega ^{*}T_0 \\ D_0 ^{2}r_{21} +\bar{{\omega }}_2 ^{2}r_{21} =-2D_0 D_1 r_{20} \\ \quad -fb^{*}\left( {eD_0 r_{10} +fD_0 r_{20} } \right) +f\delta \sum _{k=0}^3 \alpha _k g_k \\ \quad \left( {er_{10} +fr_{20} } \right) ^{k}\cos ^{2}\varOmega ^{*}T_0 \\ \end{array} }} \right. \end{aligned}$$
(34)
Fig. 3
figure 3

Free response of the coaxial vibrational mode of the free end \(z = 1\) of DWCNT

Full size image

In order to solve the zero-order problem (Eq. (33)), consider \(r_{10} \) and \(r_{20} \) to be as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} r_{10} =p(T_1 )\left[ {e^{i\omega T_0 }+e^{-i\omega T_0 }} \right] \\ r_{20} =q(T_1 )\left[ {e^{i\omega T_0 }+e^{-i\omega T_0 }} \right] \\ \end{array}} \right. \end{aligned}$$
(35)

and use the harmonic balance method (HBM). Substituting Eq. (35) into Eq. (33) and multiplying by \(\int \nolimits _0^{\cdot 2\pi /\omega } {\cos \left( {\omega t} \right) dT_0 } \), the following system of equations results:

$$\begin{aligned} \left\{ {\begin{array}{l} m[(e-c)p+(f-d)q]^{3}=\left( {\bar{{\omega }}_1 ^{2}-\omega ^{2}} \right) p\mu _1 \\ m[(e-c)p+(f-d)q]^{3}=\left( {\bar{{\omega }}_2 ^{2}-\omega ^{2}} \right) q\mu _2 \\ \end{array}} \right. \end{aligned}$$
(36)

where

$$\begin{aligned} \begin{array}{l} \mu _1 =\frac{2}{c-e}\int _0^{\frac{2\pi }{\omega }} {\cos ^{2}\left( {\omega T_0 } \right) \mathrm{d}T_0 } \\ \mu _2 =\frac{2}{d-f}\int _0^{\frac{2\pi }{\omega }} {\cos ^{2}\left( {\omega T_0 } \right) \mathrm{d}T_0 } \\ m=8C_3 ^{*}g_3 \int _0^{\frac{2\pi }{\omega }} {\cos ^{4}\left( {\omega T_0 } \right) \mathrm{d}T_0 } \\ \end{array} \end{aligned}$$
(37)

Solving Eq. (36) for amplitudes p and q yields the amplitude–frequency response for free vibration. Two cases result in coaxial vibrations [25], i.e., the inner and outer tubes move together synchronously with the same amplitude (Fig. 3), and noncoaxial vibrations, i.e., the inner and outer tubes move in opposite phase (Fig. 4). This work deals with coaxial vibrations. In this case, the following conclusion can be reached \(u_1 =u_2 \) [14] (Eq. (26)):

$$\begin{aligned} e\cdot r_{10} +f\cdot r_{20} -c\cdot r_{10} -d\cdot r_{20} =0 \end{aligned}$$
(38)
Fig. 4
figure 4

Free response of the noncoaxial vibrational mode of the free end \(z = 1\) of DWCNT

Full size image

4.1 Coaxial parametric resonance

For coaxial parametric resonance, the AC frequency \(\varOmega ^{*}\) is near coaxial frequency \(\bar{{\omega }}_1 \):

$$\begin{aligned} \varOmega ^{*}T_0 =\bar{{\omega }}_1 T_0 +\sigma T_1 \end{aligned}$$
(39)

where \(\sigma \) is the detuning parameter for the frequency of actuation. Substituting Eq. (35) with \(\omega =\bar{{\omega }}_1 \) into Eq. (34) and rewriting the amplitudes in polar form

$$\begin{aligned} p=\frac{1}{2}a_1 e^{i\beta }, \quad q=\frac{1}{2}a_2 e^{i\beta } \end{aligned}$$
(40)

yield the following secular terms expression equated to zero:

$$\begin{aligned}&-i\bar{{\omega }}_1 {a}^{\prime }_1 -i\bar{{\omega }}_1 a_1 (i{\beta }')-\frac{1}{2}i\bar{{\omega }}_1 e^{2}b^{*}a_1\nonumber \\&\quad +\frac{1}{8}\alpha _1 \delta e^{2}g_1 \left( {2+e^{2i(\sigma T_1 -\beta )}} \right) a_1 \nonumber \\&\quad + \frac{1}{16}\alpha _3 \delta e^{4}g_3 \left( {3+2e^{2i(\beta -\sigma T_1 )}} \right) a_1 ^{3}=0 \end{aligned}$$
(41)

Denote

$$\begin{aligned} \gamma =\sigma T_1 -\beta \end{aligned}$$
(42)

Applying steady-state assumptions \({\gamma }'={a}'_1 =0\), the imaginary and real components of Eq. (41) yield zero-amplitude steady-state solutions and nonzero-amplitude steady-state solutions given by the following amplitude–frequency \(a_1 ,\sigma \) equations:

$$\begin{aligned} a_1= & {} \sqrt{\frac{8e^{2}b^{*}\bar{{\omega }}_1 }{\alpha _3 \delta e^{4}g_3 }\cdot \frac{1}{\sin 2\gamma }-\frac{2\alpha _1 g_1 }{\alpha _3 e^{2}g_3 }} \end{aligned}$$
(43)
$$\begin{aligned} \sigma= & {} -\frac{\alpha _1 \delta e^{2}g_1 }{8\bar{{\omega }}_1 }\left( {2+\cos 2\gamma } \right) \nonumber \\&-\frac{\alpha _3 \delta e^{4}g_3 }{16\bar{{\omega }}_1 }\left[ {3+2\cos 2\gamma } \right] a_1 ^{2} \end{aligned}$$
(44)
Table 7 Coefficients of electrostatic denominator \(\sum _{k=0}^5 {a_k w_2^k }\)
Full size table
Table 8 Coordinate transformation constants for 5T ROM
Full size table

5 Reduced-order model (ROM)

Reduced-order models (ROMs) with up to six modes of vibration are used in this paper. Equation (8) can be written as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} A^{*}\frac{\partial ^{2}w_1 }{\partial \tau ^{2}}+I^{*}\frac{\partial ^{4}w_1 }{\partial z^{4}}=\bar{{f}}_{\mathrm{vdWT}-T} \\ \frac{\partial ^{2}w_2 }{\partial \tau ^{2}}+\frac{\partial ^{4}w_2 }{\partial z^{4}}=-b^{*}\frac{\partial w_2 }{\partial \tau }-\bar{{f}}_{\mathrm{vdWT}-T} +\frac{\delta \cos ^{2}\varOmega ^{*}\tau }{\sum \nolimits _{k=0}^5 {a_k w_2^k } } \\ \end{array}} \right. \end{aligned}$$
(45)

in which the electrostatic force \(f_{\mathrm{elec}} \) is approximated by a fifth-degree Taylor polynomial in the denominator. This way, the singularities of the electrostatic force \(f_{\mathrm{elec}} \) are approximated and not lost as in the case of Taylor polynomial in the numerator approximation [2]. 5T ROM is more accurate for both weak and strong nonlinearities, as well as for both small and large amplitudes. ROM accuracy increases with the number of modes of vibrations considered. The solutions of the dimensionless deflections are assumed as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} w_1 (z,\tau )=\sum \limits _{i=1}^N {u_i (\tau )\phi _i (z)} \\ w_2 (z,\tau )=\sum \limits _{i=1}^N {v_i (\tau )\phi _i (z)} \\ \end{array}} \right. \end{aligned}$$
(46)

where N is the number of ROM terms (modes of vibration), \(u_{i}\) and \(v_{i}\) are the time functions to be determined and \(\phi _i\) are cantilever mode shapes. Note that \(\phi _i (1)\) is the value of the mode shape at the tip (free end) of the DWCNT resonator. Substituting Eq. (46) into Eq. (45) and multiplying the second equation by \(\sum \nolimits _{k=0}^5 {a_k w_2^k } \), and then multiplying the entire system of equations by the operator \(\int \nolimits _0^1 {\cdot \phi _n (z)\mathrm{d}z} \) yield:

$$\begin{aligned}&A^{*}\sum _{i=1}^N {\frac{\partial ^{2}u_i }{\partial \tau ^{2}}} h_{ni} =-I^{*}\sum _{i=1}^N {\omega _i ^{2}u_i } h_{ni} \nonumber \\&\quad +\,c_1 ^{*}\left( {\sum _{i=1}^N {v_i } h_{ni} -\sum _{i=1}^N {u_i } h_{ni} } \right) \nonumber \\&\quad +\,c_3 ^{*}\left( {\sum _{i=1}^N {v_i } h_{ni} -\sum _{i=1}^N {u_i } h_{ni} } \right) ^{3} \end{aligned}$$
(47)
$$\begin{aligned}&\sum _{i=1}^N {\frac{\partial ^{2}v_i }{\partial \tau ^{2}}} \left( {a_0 h_{ni} +\sum _{k=1}^5 {a_k \sum _{j_1 \ldots j_{k=1} }^N {v_{j_1 \ldots } v_{j_k } h_{nij_1 \ldots j_k } } } } \right) \nonumber \\&\quad =-b^{*}\sum _{i=1}^N {\frac{\partial v_i }{\partial \tau }} \left( {a_0 h_{ni} +\sum _{k=1}^5 {a_k \sum _{j_1 \ldots j_{k=1} }^N {v_{j_1 \ldots } v_{j_k } h_{nij_1 \ldots j_k } } } } \right) \nonumber \\&\qquad - \sum _{i=1}^N {\omega _i ^{2}} v_i \left( {a_0 h_{ni} +\sum _{k=1}^5 {a_k \sum _{j_1 \ldots j_{k=1} }^N {v_{j_1 \ldots } v_{j_k } h_{nij_1 \ldots j_k } } } } \right) \nonumber \\&\qquad -\,c_1 ^{*}\left[ \sum _{i=1}^N \left( {v_i -u_i } \right) \left( a_0 h_{ni} \right. \right. \nonumber \\&\qquad \left. \left. +\sum _{k=1}^5 {a_k \sum _{j_1 \ldots j_{k=1} }^N {v_{j_1 \ldots } v_{j_k } h_{nij_1 \ldots j_k } } } \right) \right] \nonumber \\&\qquad -\, c_3 ^{*}\left[ \sum _{i=1}^N \left( {v_i -u_i } \right) ^{3}\left( {a_0 h_{ni}}\right. \right. \nonumber \\&\qquad \left. \left. {+\sum _{k=1}^5 {a_k \sum _{j_1 \ldots j_{k=1} }^N {v_{j_1 \ldots } v_{j_k } h_{nij_1 \ldots j_k } } } } \right) \right] \nonumber \\&\qquad \,\,+\,\delta h_n \cos ^{2}\varOmega ^{*}\tau \end{aligned}$$
(48)

where \(n = 1, 2,{\ldots }\), N and i, \(j_{1}\ldots j_{k }= 1, 2,{\ldots }, N\). The values of \(a_k\) coefficients are given in Table 7, and coefficients h are as follows:

$$\begin{aligned} h_n= & {} \int \limits _0^1 {\phi _n \mathrm{d}z} ,h_{ni} =\int \limits _0^1 {\phi _i \phi _n \mathrm{d}z} ,h_{nij_1 } \nonumber \\= & {} \int \limits _0^1 {\phi _i \phi _{j_1 } \phi _n \mathrm{d}z} \cdots h_{nij_1 \ldots j_k } \nonumber \\= & {} \int \limits _0^1 {\phi _i \phi _{j_1 } \ldots \phi _{j_k } \phi _n \mathrm{d}z} \end{aligned}$$
(49)

One should notice that \(h_{ni} =\delta _{ni} \) where \(\delta _{ni} \) is Kronecker’s delta. In the case of an N-term ROM, the linearized system of differential equations, similar to Eq. (20), is

$$\begin{aligned}&\left[ {{\begin{array}{llllll} {A^{*}}&{}\quad \cdots &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad {A^{*}}&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ 0&{}\quad \cdots &{}\quad 0&{}\quad 1&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 1 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {{\ddot{u}}_1 } \\ \vdots \\ {{\ddot{u}}_N } \\ {{\ddot{v}}_1 } \\ \vdots \\ {{\ddot{v}}_N } \end{array} }} \right] \nonumber \\&\quad +\left[ {{\begin{array}{llllll} {C_1^*+I^{*}\omega _{1I}^2 }&{}\quad \cdots &{}\quad 0&{}\quad {-c_1^*}&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad {C_1^*+I^{*}\omega _{NI}^2 }&{}\quad 0&{}\quad \cdots &{}\quad {-c_1^*} \\ {-c_1^*}&{}\quad \cdots &{}\quad 0&{}\quad {C_1^*+\omega _{1O}^2 }&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad {-c_1^*}&{}\quad 0&{}\quad \cdots &{}\quad {C_1^*+\omega _{NO}^2 } \\ \end{array} }} \right] \nonumber \\&\qquad \left[ {{\begin{array}{l} {u_1 } \\ \vdots \\ {v_N } \\ {u_1 } \\ \vdots \\ {v_N } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} 0 \\ \vdots \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array}}} \right] \end{aligned}$$
(50)

Following the same modal analysis procedure outlined in Eqs. (21–25), the modal coordinate transformation for an N-term ROM becomes:

$$\begin{aligned} \left[ {{\begin{array}{l} {u_1 } \\ \vdots \\ {u_N } \\ {v_1 } \\ \vdots \\ {v_N } \\ \end{array} }} \right] =\left[ {{\begin{array}{llllll} {c_1 }&{}\quad \cdots &{}\quad 0&{}\quad {d_1 }&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad {c_N }&{}\quad 0&{}\quad \cdots &{}\quad {d_N } \\ {e_1 }&{}\quad \cdots &{}\quad 0&{}\quad {f_1 }&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad {e_N }&{}\quad 0&{}\quad \cdots &{}\quad {f_N } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {r_{11} } \\ \vdots \\ {r_{1N} } \\ {r_{21} } \\ \vdots \\ {r_{2N} } \\ \end{array} }} \right] \end{aligned}$$
(51)

where the square matrix consists of four diagonal sub-matrices. Coefficients \(c_{i}, d_{i}, e_{i}\) and \(f_{i}\) are given in Table 8. Subsequently, substituting Eq. (51) into Eq. (46), a ROM is constructed in the modal r-coordinate system as:

$$\begin{aligned} \left\{ {\begin{array}{l} w_1 (z,\tau )=\sum \limits _{i=1}^N {(c_i r_{1i} +d_i r_{2i} )(\tau )\phi _i (z)} \\ w_2 (z,\tau )=\sum \limits _{i=1}^N {(e_i r_{1i} +f_i r_{2i} )(\tau )\phi _i (z)} \\ \end{array}} \right. \end{aligned}$$
(52)

From Eqs. (27) and (38), the modal ROM system of equations in modal r-coordinate is as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \sum _{i=1}^N {\ddot{r}}_{1i} \phi _i (z)+b^{*}\sum _{i=1}^N e_i ^{2}{\dot{r}}_{1i} \phi _i (z)\\ \qquad +b^{*}\sum _{i=1}^N {e_i f_i {\dot{r}}_{2i} \phi _i (z)} +\sum _{i=1}^N {\bar{{\omega }}_{1i} ^{2}r_{1i} \phi _i (z)} \\ \quad =\sum _{i=1}^N {\frac{e_i \delta V_t ^{2}}{\sum _{k=0}^5 {a_k \left[ {(e_i r_{1i} +f_i r_{2i} )\phi _i (z)} \right] ^{k}} }} \\ \sum \limits _{i=1}^N {\ddot{r}}_{2i} \phi _i (z)+b^{*}\sum _{i=1}^N e_i f_i {\dot{r}}_{1i} \phi _i (z) \\ \qquad +b^{*}\sum _{i=1}^N {f_i ^{2}{\dot{r}}_{2i} \phi _i (z)} +\sum _{i=1}^N {\bar{{\omega }}_{2i} ^{2}r_{2i} \phi _i (z)} \\ \quad =\sum \limits _{i=1}^N {\frac{e_i \delta V_t ^{2}}{\sum _{k=0}^5 {a_k \left[ {(e_i r_{1i} +f_i r_{2i} )\phi _i (z)} \right] ^{k}} }} \\ \end{array}} \right. \end{aligned}$$
(53)

This system of equations for \(N = 1,2,3,4\) is numerically integrated using MATLAB in order to predict time responses of the system and AUTO-07P in order to predict the amplitude–frequency response of the system. CNT deflections \(w_1 (z,\tau )\) and \(w_2 (z,\tau )\) (Eq. 52) can be written as the sum of coaxial modal deflection and noncoaxial modal deflection. The coaxial modal deflections \(w_{11N} (z,\tau )\) and \(w_{21N} (z,\tau )\) contain the coaxial modal coordinates \(r_{1i} (\tau )\), while the noncoaxial modal deflections \(w_{12N} (z,\tau )\) and \(w_{22N} (z,\tau )\) contain the noncoaxial modal coordinates \(r_{2i} (\tau )\). Therefore, the CNT deflections can be written (decomposed) as \(w_1 =w_{11N} +w_{12N} \) and \(w_2 =w_{21N} +w_{22N}\), for N terms ROM used, where

$$\begin{aligned} w_{11N} (z,\tau )= & {} \sum _{i=1}^N {c_i \cdot r_{1i} (\tau )\phi _i (z)} ,\nonumber \\ w_{12N} (z,\tau )= & {} \sum _{i=1}^N {d_i \cdot r_{2i} (\tau )\phi _i (z)} \nonumber \\ w_{21N} (z,\tau )= & {} \sum _{i=1}^N {e_i \cdot r_{1i} (\tau )\phi _i (z)} ,\nonumber \\ w_{22N} (z,\tau )= & {} \sum _{i=1}^N {f_i \cdot r_{2i} (\tau )\phi _i (z)} \end{aligned}$$
(54)

For instance, \(w_{12N} (z,\tau )\) is the noncoaxial modal deflection of \(w_1 \) of inner CNT containing the \(r_{2i} (\tau )\) noncoaxial modal coordinates, for N terms ROM. The reason for this decomposition is the later use of modal truncation method [29-31] for \(N = 5,6\), i.e., 5T ROM and 6T ROM. In this method, modes of frequency far from excitation frequency can be neglected. Truncated models reduce the size of the ROM and therefore allow for numerical simulations of ROMs with larger number N of modes, such as 5T ROM and 6T ROM. In this work, the terms \(w_{12N} \) and \(w_{22N} \) containing the noncoaxial modal coordinates \(r_{2i} (\tau )\) in the tested cases are shown to be negligible and therefore to not contradict the truncation method. Therefore, only coaxial modal coordinates \(r_{1i} (\tau )\), \(i = 1,2,{\ldots }N\), are significant. In modal truncation method, the noncoaxial modal coordinates \(r_{2i} (\tau )\) are neglected, as well as their differential equations. This way, the system of Eq. (53) is replaced by the truncated model

$$\begin{aligned}&\sum _{i=1}^N {{\ddot{r}}_{1i} \phi _i (z)+b^{*}\sum _{i=1}^N {e_i ^{2}{\dot{r}}_{1i} \phi _i (z)} } +\sum _{i=1}^N \bar{{\omega }}_{1i} ^{2}r_{1i} \phi _i (z)\nonumber \\&\quad =\sum _{i=1}^N {\frac{e_i \delta V_t ^{2}}{\sum \nolimits _{k=0}^5 {a_k \left[ {e_i r_{1i} \phi _i (z)} \right] ^{k}} }} \end{aligned}$$
(55)

Similar to Eqs. (47)–(48), Eq. (55) is multiplied by the denominators at the right-hand side. Then, the resulting equation is multiplied by \(\phi _n (z)\) and integrated from 0 to 1, \(n = 1,2,{\ldots },N\), resulting in a system of N second-order differential equations

$$\begin{aligned}&\sum _{i=1}^N {\frac{\partial ^{2}r_{1i} }{\partial \tau ^{2}}} \left( \sum _{j_1 =1}^N {a_0 h_{nj_1 } } \right. \nonumber \\&\qquad \left. +\sum _{k=1}^5 {a_k \sum _{j_2 \ldots j_{k=1} }^N {e_{j_2 \ldots } e_{j_k } r_{1j_2 \ldots } r_{1j_k} h_{nj_1 j_2 \ldots j_k } } } \right) \nonumber \\&\quad =-b^{*}\sum _{i=1}^N {e_i ^{2}\frac{\partial v_i }{\partial \tau }} \left( \sum _{j_1 =1}^N {a_0 h_{nj_1 } }\right. \nonumber \\&\qquad \left. +\sum _{k=1}^5 {a_k \sum _{j_2 \ldots j_{k=1} }^N {e_{j_2 \ldots } e_{j_k } r_{1j_2 \ldots } r_{1j_k } h_{nj_1 j_2 \ldots j_k } } } \right) \nonumber \\&\qquad -\sum _{i=1}^N {\bar{{\omega }}_{1i} ^{2}} v_i \left( \sum _{j_1 =1}^N {a_0 h_{nj_1 } }\right. \nonumber \\&\qquad \left. +\sum _{k=1}^5 {a_k \sum _{j_2 \ldots j_{k=1} }^N {e_{j_2 \ldots } e_{j_k } r_{1j_2 \ldots } r_{1j_k } h_{nj_1 j_2 \ldots j_k } } } \right) \nonumber \\&\qquad +\sum _{i=1}^N {e_i \delta h_n \cos ^{2}\varOmega ^{*}\tau } \end{aligned}$$
(56)

Besides \(n = 1, 2,{\ldots }, N,\) the subscripts \(j_{1}\), \(j_{2}\ldots j_{k }= 1, 2,{\ldots }, N.\) The values of \(a_k\) coefficients are given in Table 7, and coefficients h are as follows:

$$\begin{aligned} h_n= & {} \int \limits _0^1 {\phi _n \mathrm{d}z} ,h_{nj_1 } =\int \limits _0^1 {\phi _{j_1 } \phi _n \mathrm{d}z} ,h_{nj_1 j_2 } \nonumber \\= & {} \int \limits _0^1 {\phi _{j_1 } \phi _{j_2 } \phi _n \mathrm{d}z} \cdots h_{nj_1 j_2 \ldots j_k } \nonumber \\= & {} \int \limits _0^1 {\phi _{j_1 } \phi _{j_2 } \ldots \phi _{j_k } \phi _n \mathrm{d}z} \end{aligned}$$
(57)

6 Numerical simulations

AUTO-07P, a software package for continuation and bifurcation, is utilized to calculate ROMs’, \(N = 2,3,4,5,6\), solutions and predict the frequency–amplitude response. To investigate solutions of higher amplitudes, and validate those of small amplitudes, ROMs with a larger number of modes of vibration are used. While it is more accurate at higher amplitudes, these ROMs are computationally demanding.

MATLAB software is used to plot the amplitude–frequency response predicted by MMS which is a perturbation technique [32,33,34] utilized due to the ease of identifying amplitude–frequency responses for weak nonlinearities and small amplitudes. MMS provides an approximate analytical solution for ROM with one mode of vibration.

MATLAB is also used to numerically integrate ROMs and predict time responses of the structure. In this work, time responses for specified parameters are obtained using a MATLAB ODE solver, namely ode15s. One should mention that ode15s is a “multistep, variable-order solver based on numerical differentiation formulas” [35, 36].

Fig. 5
figure 5

Amplitude–frequency response, parametric resonance, using five terms (5T) ROM (present work) and MMS, \({b}^* = 0.0003\), \(\delta = 0.15\)

Full size image
Fig. 6
figure 6

Time response using 5T ROM for DWCNT resonator for AC frequency near natural frequency; \({b}^{*} = 0.0003\), \(\delta = 0.15\), a initial amplitude \(U_{0} = 0.25\), \(\sigma = -0.001\), b initial amplitude \(U_{0} = 0.9\), \(\sigma = -0.001\), c initial amplitude \(U_{0} = 0.1\), \(\sigma = -0.0004\), d initial amplitude \(U_{0} = 0.25\), \(\sigma = 0\)

Full size image
Fig. 7
figure 7

Time response using 1T ROM for DWCNT resonator for AC frequency near natural frequency. Initial amplitude \(U_{0} = 0.05\), \(b^* = 0.0003\), \(\delta = 0.15\), \(\sigma = 0\). a\(r_{1i}\) only, b\(r_{2i}\) only

Full size image

Figure 5 shows the amplitude–frequency response of the DWCNT under parametric resonance using 5T ROM and a direct comparison with MMS. Dash and solid lines represent the unstable and stable solutions, respectively. This response is characterized by two Hopf bifurcations: subcritical with the bifurcation point at A and supercritical with the bifurcation point at B. Both methods, 5T ROM solved using AUTO-07P and 1T ROM solved using MMS, are in agreement for amplitudes less than 0.5 of the gap. However, for amplitudes larger than 0.5 of the gap MMS overestimates both the stable and the unstable steady-state amplitudes. (MMS branches are above 5T ROM branches.) This is expected since MMS is valid only for weak nonlinearities to include small amplitudes (small geometric nonlinearities). For 5T ROM, the unstable branch (left) of the subcritical bifurcation divides the area into two distinct regions. For initial amplitudes below the dash line, the system settles to zero amplitudes, while for initial amplitudes above the dash line the resonator is “pulled in” to the ground plate or settles to large amplitudes. For frequencies below that of point C, the MEMS resonator settles to zero amplitude regardless of initial amplitude. For frequencies between those of point A and D, the resonator is pulled in regardless of initial amplitude. One can observe that for amplitudes less than 0.5 of the gap, the ROM and MMS are in excellent agreement. MMS underestimates the softening effect and does not predict the pull-in phenomenon from large amplitudes, points C and D.

Figure 6a–d shows time responses of the tip of the DWCNT resonator using 5T ROM for \(b^* = 0.0003\) and \(\delta = 0.15\) considering various initial amplitudes and values of detuning frequency, where \(u=w_1 (1,\tau )\) and \(v=w_2 (1,\tau )\). They are in excellent agreement with the frequency responses from 5T ROM AUTO and MMS, as shown in Fig. 5. Pull-in phenomena are evidenced in Fig. 6b, c, while attenuation to zero-amplitude results is shown in Fig. 6a, d. One should mention that pull-in is reached when the dimensionless amplitude of the tip of the DWCNT reaches 1, i.e., the dimensional amplitude reaches the value of the gap, so the DWCNT makes contact with the ground plate. The observed beating behavior is typical in the transient response nonlinear oscillators subjected to harmonic forcing [37, 38]. It is important to note that a large enough time span is chosen for each case in order for the responses to reach a steady-state solution.

7 Discussion and conclusions

This work predicted the effects of voltage and damping on amplitude–frequency of coaxial parametric resonance of cantilever DWCNTs. Five ROMs using one through five modes of vibration were developed and used. All ROMs were expressed in terms of modal coordinates of the DWCNT. Modal coordinates have been found using undamped DWCNT to include linear intertube van der Waals forces. Two modes of vibration resulted: coaxial and noncoaxial. The coaxial mode of vibration was investigated.

The ROM using one mode of vibration was solved using the method of multiple scales in order to obtain the amplitude–frequency response. All other ROMs using one through five modes of vibration were solved either through numerical integration in MATLAB in order to obtain time responses [20,21,22, 28, 39], or using AUTO-07P, a software package for continuation and bifurcation, in order to obtain the amplitude–frequency response. All methods are in agreement for amplitudes lower than 0.5 of the gap. For larger amplitudes, only ROM using five modes of vibration predicts accurately the behavior of the DWCNT. Increasing voltage and/or decreasing damping results in a larger range of frequencies for which pull-in occurs.

Fig. 8
figure 8

Time response using 2T ROM for DWCNT resonator for AC frequency near natural frequency. Initial amplitude \(U_{0} = 0.05\), \(b^* = 0.0003\), \(\delta = 0.15\), \(\sigma = 0\). a\(r_{1i}\) only, b\(r_{2i}\) only

Full size image
Fig. 9
figure 9

Time response using 3T ROM for DWCNT resonator for AC frequency near natural frequency. Initial amplitude \(U_{0} = 0.05\), \(b^* = 0.0003\), \(\delta = 0.15\), \(\sigma = 0\). a\(r_{1i}\) only, b\(r_{2i}\) only

Full size image
Fig. 10
figure 10

Time response using 4T ROM for DWCNT resonator for AC frequency near natural frequency. Initial amplitude \(U_{0} = 0.05\), \(b^* = 0.0003\), \(\delta = 0.15\), \(\sigma = 0\). a\(r_{1i}\) only, b\(r_{2i}\) only

Full size image

In Figs. 7, 8, 9 and 10, the modal truncation method is tested. Numerical investigation conducted using 1T, 2T, 3T and 4T ROMs of parametric resonance of coaxial vibrations in which the response of the resonator, investigation that includes both coaxial \(r_{1i} (\tau )\) and noncoaxial \(r_{2i} (\tau )\) modal coordinates, i.e., full-order modal system, is shown not to contradict the modal truncation method (includes only coaxial \(r_{1i} (\tau )\) modal coordinates) that was used for 5T and 6T ROMs. Time responses for \(b^* = 0.0003\), \(\delta = 0.15\), small initial amplitude \(U_{0} = 0.05\) and zero detuning frequency have been simulated for 1T–4T ROMs, respectively. Modal deflections, coaxial \(w_{11N} \) and \(w_{21N} \), and noncoaxial \(w_{12N} \) and \(w_{22N} \), represented in Figs. 7, 8, 9 and 10 are the decomposition of Eq. (52) as shown in Eq. (54) that relate the modal coordinates to the dimensionless deflections. One can notice that all noncoaxial modal deflections \(w_{12N} \) and \(w_{22N} \) of inner and outer CNTs, respectively, for all ROMs \(N = 1,2,3,4\), are in the \(10^{-12}\) order of magnitude, while the coaxial modal deflections \(w_{11N} \) and \(w_{21N} \) are in the \(10^{-2}\) order of magnitude. Then, Figs. 7, 8, 9 and 10 do not contradict the fact that noncoaxial modal coordinates \(r_{2i} (\tau )\) can be neglected, since they do not have any effect on the deflections of Eq. (52). So, this does not contradict the modal truncation method in which the noncoaxial modal coordinates \(r_{2i} (\tau )\), and their differential equations, can be neglected. Therefore, the tip deflection of the DWCNT resonator may be defined satisfactorily by considering only the coaxial modal coordinates \(r_{1i} (\tau )\). Since the AC actuation frequency is near the first natural frequency of the coaxial vibration, the coaxial resonant case investigated in this paper is far from the noncoaxial resonance and thus devoid of any internal resonance. From perturbation methods, such as MMS, the nonresonant mode, i.e., noncoaxial mode, is “damped out” after steady-state assumptions are made [18]. The concept of modal system reduction is also known as modal truncation, with the general basis that “certain modes occur at frequencies well outside the system’s domain of operating frequencies...these modes can be safely removed from the model with minimal approximation error since they [do] not contribute much to the relevant dynamics of the system” [29,30,31]. Moreover, the full-order modal responses were numerically compared with their modally truncated (no \(r_{2}\)) models for time responses and bifurcation diagrams for 1T–4T ROMs. There was no significant difference. The errors were observed in the \(10^{-12}\) range. Therefore, for higher-order ROM, the expansions are performed using only \(r_{1i} (\tau )\), which not only reduces the system of equations by half, but also reduces computational time in the MATLAB time responses.

Fig. 11
figure 11

ROM AUTO convergence of the amplitude–frequency response for DWCNT resonator using two terms (2T ROM), three terms (3T ROM), ... and six terms (6T ROM). AC frequency near natural frequency. \(b^* = 0.0001\), \(\delta = 0.15\)

Full size image

Figure 11 illustrates the convergence of the ROM method. Using numerical simulation with AUTO-07P, the number of terms considered is between two and six. One can see that the difference between 5T ROM AUTO and 6T ROM AUTO is in the \(10^{-3}\) order of magnitude, meaning that tip deflections can be achieved with adequate accuracy by 5T ROM with reduced computational time. Between the two bifurcation points, the zero-amplitude steady states are unstable, and the system either experiences pull-in or settles to nonzero steady-state amplitudes on the stable branch, regardless of the initial amplitude.

Figure 12 shows the solution convergence to increasing the degree of the Taylor polynomial in the denominator for ROM, Eq. (45). Similar to the term convergence shown in Fig. 11, a numerical solution convergence may be seen in the fifth degree Taylor polynomial approximation of the electrostatic force in the denominator.

Fig. 12
figure 12

ROM AUTO Taylor polynomial degree of the denominator convergence for the amplitude–frequency response of DWCNT resonator using five terms (5T ROM). AC frequency near natural frequency. \(b^*=0.0003\), \(\delta = 0.15\)

Full size image
Fig. 13
figure 13

Effect of applied voltage, \(\delta \), on frequency response, MMS and ROM AUTO

Full size image
Fig. 14
figure 14

Effect of dimensionless damping, \({b}^*\), on frequency response, MMS and ROM AUTO

Full size image

Figure 13 shows the effect of applied voltage on the amplitude–frequency response. The voltage parameter \(\delta \) has a significant effect on the response. Increasing the voltage parameter increases the distance between the Hopf bifurcations; therefore, the range of frequencies for which the system experiences pull-in is significantly larger. Also, both branches shift to lower frequencies, the unstable branch more than the stable branch. Furthermore, increasing the voltage parameter shows an increase in softening effect.

Figure 14 illustrates the effect of dimensionless damping on the amplitude–frequency response. As damping increases, the distance between the subcritical and supercritical Hopf bifurcations decreases, until the unstable and stable branches coalesce for high enough damping coefficients. Increasing damping reduces the range of frequencies for which the DWCNT undergoes large amplitudes or pull-in.

The applicability of Euler–Bernoulli beam modeling over molecular dynamics (MD) methodology and nonlocal continuum mechanics (small-scale effect) has been comprehensibly discussed in the study of electrostatically actuated single-walled carbon nanotubes [2]. It has been shown that the small-scale effect does not have a significant influence on the fundamental frequencies of long slender carbon nanotubes [2]. A model limitation is that this investigation does not account for thermal vibrations that arise from an axial load induced by thermal expansion [40]. Also, this work does not include the effects of various parameters on natural frequencies. Elishakoff [41] reported on fundamental natural frequencies of double-walled carbon nanotubes, and Ouakad and Younis [42] reported on the effects of slack and DC voltage on natural frequencies of initially curved carbon nanotube resonators.