1 Introduction

Vibration energy harvesters, which can transfer the vibration energy into the electrical energy by piezoelectric, electromagnetic and electrostatic mechanism, have been improved largely (Tiwari et al. 2014; Yang et al. 2014). However, for linear energy harvesters, the larger bandwidth and lower resonant frequency are the two main difficulties when they are used in the practical environment (Cammarano et al. 2014). In the literatures, researchers have proposed many methods to solve the above problems, among which the nonlinear energy harvesting technique is one of the feasible solutions (Liu et al. 2012; Karami and Inman 2011; Pellegrini et al. 2013; Sebald et al. 2011). Mann and Foisal designed nonlinear EM energy harvester based on magnet repulsion, and they obtained that the sizes of magnet and distance between magnets can improve harvesting bandwidth (Mann and Owens 2010; Foisal et al. 2012). Maryam put forward the vibration energy harvester model based on nonlinear damping, and obtained that output power and bandwidth were better than linear energy harvester (Maryam and Stephen 2014). Nonlinear PE energy harvester designed by Al-Ashtari can adjust resonant frequency by changing force between magnets, and the resonant frequency of energy harvester can increase 70% (Al-Ashtari et al. 2012). Energy harvesting bandwidth of MEMS PE energy harvester designed by Marzencki can increase 36% through adjusting the structure stiffness (Marzencki et al. 2009). Besides, Challa designed nonlinear PE energy harvester by utilizing attractive force between magnets, which can regulate the resonant frequency by changing equivalent stiffness (Challa et al. 2008). In the design, four magnets were applied, among two of them were fixed on two sides of mass block, and the others were placed on the framework opposite the mass block. Through experimental test, it can be obtained that natural frequency of linear energy harvester can be increased or decreased 20% by this technique. However, in the paper, the static method was applied to analyze performances under sinusoidal excitation, and output characteristics of energy harvester under random excitation were not mentioned.

Above references on nonlinear energy harvester were all based on ideal harmonic excitation, while the practical application environment of energy harvester is mainly random vibration (Cottone et al. 2012; Blystad et al. 2010). Therefore, research on output characteristics of energy harvester under random excitation has much more practical significance. For nonlinear energy harvester at random excitation, Ferrari analyzed the response output of nonlinear PE energy harvester, and derived that energy harvester can output much more mean power at bistability, which can be utilized in MEMS energy harvesting devices (Ferrari et al. 2010). Jiang established analysis model of nonlinear PE energy harvester by methods of statistical linearization method and FPK (Fokker–Planck–Kolmogorov) equation. under Gaussian white noise excitation, and obtained that the output voltage increases with the spectral density of the random excitation increasing; the output voltage decreases slightly with the coefficient of cubic nonlinearity for small excitation spectral density, while increases for large density (Jiang and Chen 2013, 2014). Others, Daqaq established working model of monostable duffing-type nonlinear EM energy harvester, and analyzed output characteristics of nonlinear energy harvester under white noise and colored noise excitation through FPK equation. It was concluded that that compared with linear energy harvester, nonlinear damping can improve output performances (Daqaq 2011, 2012). However, there is a most dominant function, which makes output power reach maximum. Besides, by FPK equation. and equivalent linearization method, Green deduced output characteristics of nonlinear EM energy harvester based magnetic spring, and got that natural frequency of energy harvester can be regulated with no change of structural mass and stiffness by means of Monte Carlo simulation and experimental test (Green et al. 2012; Green et al. 2013). In addition, Kumar establish state equation of coupled electromechanical characteristics by FPK equation, and analyzed output voltage of nonlinear energy harvester in different acceleration spectral density (Kumar et al. 2014). Meimukhin analyzed output power of nonlinear energy harvester based soft spring structure under white noise excitation, and derived that nonlinear structures with negative stiffness can be used to enhance the conversion, and bistable oscillators performance considerably better than their linear counterpart under band-limited excitation (Meimukhin et al. 2013).

Besides, to improve the energy conversion efficiency and application ranges, researchers proposed a kind of hybrid energy harvesting technology by coupling PE and EM mechanism together, which can benefit from the advantages of two techniques simultaneously (Torsten and Armaghan 2010; Wu et al. 2008). For linear hybrid PE and EM energy harvester, the authors have researched electromechanical coupling model and performances under random and harmonic excitation respectively (Li et al. 2015; Li et al. 2014). For nonlinear hybrid PE and EM energy harvester, the authors have established the working model under harmonic excitation and output performances were studied by simulation and experimental test (Li et al. 2016). In addition, Shan and Yang analyzed output characteristics of nonlinear energy harvester under harmonic excitation by theoretical modeling, numerical simulation and experimental test respectively, and obtained energy harvesting bandwidth of nonlinear hybrid energy harvester is three times as big as energy harvester with single energy harvesting mechanism, and its output power is much bigger (Yang et al. 2014; Shan et al. 2013). However, Shan and Yang did not consider the feedback effect of PE and EM electrical outputs to the vibration response of harvesting system in their analysis, and they did not involve performances of nonlinear hybrid energy harvester under random excitation.

Therefore, in this paper, the authors designed a nonlinear hybrid PE and EM energy harvester with adjustable stiffness, and then its governing equations considering the electromechanical coupling effect were established. By means of statistical linearization method, expressions of mean amplitude, output voltage, current and power of harvester under the random excitation were derived. Then, by numerical calculation, simulation and experimental test, the effects of nonlinear strength, power density of the excitation, load resistance on amplitude, power output and the natural frequency of nonlinear hybrid energy harvester were studied and the results were compared with output performances of linear hybrid energy harvester.

2 Nonlinear hybrid energy harvester model

2.1 Structural design

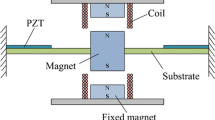
The designed nonlinear hybrid PE and EM energy harvester is shown in Fig. 1. The movable magnet as mass is supported by double-clamped compound beam, and two coils are placed above and below the movable magnet respectively. Besides, two magnets are fixed inside the coils respectively, and their magnetic pole are opposite to the mass magnet, which means the force between the movable magnet and fixed magnet is attractive, so the force can decrease the natural frequency of harvester. Therefore, the stiffness of hybrid energy harvester can be changed to adjust the vibration response because the attractive force varies with the distance between the magnets. In addition, piezoelectric layers polarized in the beam thickness direction are died on the top surface of beams, and based on piezoelectric effect and law of electromagnetic induction, PZT layers and coils will output voltage signal under the external excitation.

Fig. 1
figure 1

Nonlinear energy harvester structure model

Full size image

In the structure design, cylindrical magnets are used to apply the desired magnetic force, and the magnetic force between any two cylinder magnets is given as (Mann and Owens 2010; Owens and Mann 2012)

$$F_{m} \, \frac{{3\mu_{0} M_{1} V_{1} \cdot M_{0} V_{0} }}{{2\pi d^{4} }}$$
(1)

where µ0 = 4π × 10−7 H/m is magnetic permeability, V1 and V0 are volumes of two magnets, M1 and M0 are magnetization of two magnets respectively, and d is static distance between the magnets. For the designed nonlinear hybrid energy harvester, under the external excitation, when the displacement of mass magnet is z (suppose the direction near the below fixed magnet), the forces between the mass magnet and above, below fixed magnets are Fm1 and Fm2 respectively. By Eq. (1), the nonlinear magnetic force is

$$F_{m} \left( z \right) = F_{m1} - F_{m2} = 3\mu M_{m} V_{m} \left[ {\frac{{M_{t} V_{t} }}{{2\pi \left( {d + z} \right)^{4} }} - \frac{{M_{b} V_{b} }}{{2\pi \left( {d - z} \right)^{4} }}} \right]$$
(2)

where Mm and Vm are magnetization and volume of mass magnet respectively; Mt and Vt are magnetization and volume of above magnet respectively; Mb and Vb are magnetization and volume of the below magnet respectively. To avoid plastic deformation of the beam, the nonlinear force should be less than the elastic restoring force of the beam, which means

$$\left| F_{m} (z) < \left| {k_{b}} z \right|\right.$$
(3)

where kb is the stiffness of the beam.

For the designed nonlinear hybrid energy harvester, the above and below magnets are the same, and the static distances between them are equal to each other. By the method of Taylor expansion (Tongji 2007), when neglecting high-order terms and z < d, Eq. (2) can be expressed as

$$F_{m} (z) = k_{1} z + k_{3} z^{3}$$
(4)

where

$$k_{1} = 12\mu_{0} M_{m} V_{m} \frac{{M_{b} V_{b} }}{{\pi d^{5} }}$$
(5)
$$k_{3} = \frac{5}{{d^{2} }}k_{1}$$
(6)

By the results in the former study for hybrid energy harvester (Li et al. 2016), the governing equations of nonlinear hybrid PE and EM energy harvester can be illustrated as

$$m_{e} \ddot{z}(t) + c_{m} \dot{z}(t) + k_{b} z(t) + F_{m} (z(t)) + g_{e} I_{em} (t) + \theta V_{p} (t) = - m_{e} \ddot{y}(t)$$
(7)
$$L_{c} \dot{I}_{em} (t) + (R_{c} + R_{m} )I_{em} (t) - g_{e} \dot{z}(t) = 0$$
(8)
$$\frac{{V_{p} (t)}}{{R_{p} }} + C_{p} \dot{V}_{p} (t) - \theta \dot{z}(t) = 0$$
(9)

where \(\ddot{z}(t)\) is the excitation acceleration; Rp, Rm are load resistance of PE and EM element respectively; Cp is equivalent capacitance of PE layer; Vp is output voltage of PE energy harvesting element; Iem is output current of EM energy harvesting element; Rc and Lc refers to resistance and inductance of coils; θ and ge are PE and EM transfer factors respectively. These parameters are dependent on the material constants and the design of the energy harvester, which can be derived by standard model analysis (Spreemann and Manoli 2012; Erturk and Inman 2011).

2.2 White noise excitation

According to reference (Halvorsen 2008), random vibration can be assumed as white noise signal when the excitation frequency bandwidth is much bigger than 3 dB bandwidth of energy harvesting system and the excitation has a flat power spectral density in frequency domain,

In the analysis, supposing the stochastic acceleration excitation is Gaussian white noise, and it can be obtained that Eq. (7) is Duffing equation. After substituting Eq. (4) into Eq. (7). By the statistical linearization method, vibration response and output performances of nonlinear hybrid PE and EM energy harvester under the random excitation can be derived (Zhuang and Chen 1986).

Then, Eq. (7) is expressed as

$$\ddot{z} + 2\zeta \omega_{n} \dot{z} + \omega_{n}^{2} z + \frac{{k_{3} }}{{m_{e} }}z^{3} + \frac{\theta }{{m_{e} }}V_{p} + \frac{{g_{e} }}{{m_{e} }}I_{em} = - a(t)$$
(10)

In Eq. (10), \(\omega_{n}^{2} = \frac{K}{{m_{e} }}\left( {K = k_{b} + k_{1} } \right)\) and \(2\zeta \omega_{n} = \frac{{c_{m} }}{{m_{e} }}\). As \(\frac{{k_{3} }}{{m_{e} }}z^{3}\) is only nonlinear term in Eq. (10), device equivalence in the statistical linearization method is used in the analysis (Zhuang and Chen 1986). Supposed

$$\frac{{k_{3} }}{{m_{e} }}z^{3} = \lambda_{1} + \lambda_{2} z$$
(11)

Among them, λ1 and λ2 are constant. Let

$$F(z) = \frac{{k_{3} }}{{m_{e} }}z^{3}$$
(12)
$$F_{*} (z) = \lambda_{1} + \lambda_{2} z$$
(13)

In Eqs. (12) and (13), F(z) and \({\text{F}}_{*} \left( {\text{z}} \right)\) are random function. So

$$\Delta F(z) = F(z) - F_{*} (z)$$
(14)

In the paper, the designed nonlinear hybrid energy harvesting system is nonlinear time-invariant system. Therefore, under Gaussian white noise excitation, the response of energy harvesting system is also time-invariant, and ΔF(z) is stationary random function. Then, when the mean square value E[(ΔF)2] in Eq. (15) reaches the minimum, the parameters λ1 and λ2 can be derived.

$$E[\Delta F^{2} (z)] = \int_{ - \infty }^{ + \infty } {[F(z) - F_{*} (z)} ]^{2} p(z)dz$$
(15)

In Eq. (15), p(z) is probability density function. For the weak nonlinear harvesting system, when it is excited by a stationary Gaussian process, the response is the approximate normal distribution; furthermore, for zero mean excitation, the output of nonlinear system is also the zero mean. Supposing σ z is variance of response, then

$$p(z) = \frac{1}{{\sqrt {2\pi } \sigma_{z} }}\exp \left( { - \frac{{z^{2} }}{{2\sigma_{z}^{2} }}} \right)$$
(16)

Substituting Eq. (16) into Eq. (15), it can be derived that

$$E[\Delta F^{2} (z)] = \int_{ - \infty }^{ + \infty } {[F(z) - F_{*} (z)} ]^{2} \frac{1}{{\sqrt {2\pi } \sigma_{z} }}\exp \left( { - \frac{{z^{2} }}{{2\sigma_{z}^{2} }}} \right)dz$$
(17)

Through

$$\frac{{\partial E[\Delta F^{2} (z)]}}{{\partial \lambda_{1} }} = 0$$
(18)
$$\frac{{\partial E[\Delta F^{2} (z)]}}{{\partial \lambda_{2} }} = 0$$
(19)

λ1 and λ2 can be obtained that

$$\lambda_{1} = 0$$
(20)
$$\lambda_{2} = 3\frac{{k_{3} }}{{m_{e} }}\sigma_{z}^{2}$$
(21)

Substituting Eqs. (20) and (21) into Eq. (13), then

$$F_{*} (z) = 3\frac{{k_{3} }}{{m_{e} }}\sigma_{z}^{2} z$$
(22)

Thus, according to Eq. (9), Eq. (10) after equivalence linearization can be transformed as

$$\ddot{z} + 2\zeta \omega_{n} \dot{z} + \left( {\omega_{n}^{2} + 3\frac{{k_{3} }}{{m_{e} }}\sigma_{z}^{2} } \right)z + \frac{\theta }{{m_{e} }}V_{p} + \frac{{g_{e} }}{{m_{e} }}I_{em} = - a(t)$$
(23)

which means that Eq. (23) is the linear random response equation and can be analyzed using correlation function and frequency response function.

According to Wiener–Khinchin theorem (Liu 2008), for stationary random process, its spectral density \(S(\omega )\) and autocorrelation function \(R(\tau )\) is Fourier transform pair, as shown in Eq. (24). Moreover, when \(\tau = 0\), \(R(0)\) is mean square value of the random signal.

$$R(\tau ) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {S(\omega )} e^{i\omega \tau } d\omega$$
(24)

In addition, when nonlinear energy harvesting system is excited by random acceleration of \(S_{A} (\omega )\), spectral density of amplitude response of energy harvesting system is

$$S_{Z} (\omega ) = \left| {H(\omega )} \right|^{2} S_{A} (\omega )$$
(25)

According to reference (Serre et al. 2007), the inductance of coil can be neglected in the low vibrating frequency (lower than 1 kHz) because the impedance is mainly determined by the resistance of coil. Therefore, Fourier transform is carried on Eqs. (8)–(9), and it can obtained that

$$I_{e} (\omega ) = \frac{1}{{R_{c} + R_{m} }}g_{e} z(\omega )i\omega$$
(26)
$$V_{p} (\omega ) = \frac{{\theta R_{p} }}{{1 + i\omega C_{p} R_{p} }}z(\omega )i\omega$$
(27)

After Fourier transform is carried on Eq. (7), substituting Eqs. (26), (27) into it, the frequency response function of amplitude of energy harvester can be illustrated as

$$H(\omega ) = \frac{z(\omega )}{a(\omega )} = \frac{{ - m_{e} - i\omega C_{p} R_{p} m_{e} }}{{m_{e} C_{p} R_{p} (i\omega )^{3} + \left[ {m_{e} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }}} \right)C_{p} R_{p} } \right](i\omega )^{2} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }} + K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right)i\omega + K_{e} }}$$
(28)

In Eq. (28), \(K_{e}\) is defined as equivalent stiffness, and \(K_{e} = k + k_{1} + 3k_{3} \sigma_{z}^{2}\). When spectral density SA(w) of stationary random acceleration is a constant S0, mean square value of amplitude is

$$\sigma_{z}^{2} = R(0) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {S_{Z} (\omega )d\omega } = \frac{1}{2\pi }S_{0} (\omega )\int\limits_{ - \infty }^{ + \infty } {\left| {H(\omega )} \right|^{2} d\omega }$$
(29)

Substitute Eq. (28) into Eq. (29), and by James formula (Gradshtenyn and Ryzhik 1994), it can be obtained that

$$\sigma_{z}^{2} = \frac{1}{2}S_{0} \frac{{\left( {C_{p} R_{p} m_{e} } \right)^{2} \cdot K_{e} + m_{e}^{2} \cdot \left[ {m_{e} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }}} \right)C_{p} R_{p} } \right]}}{{K_{e} \left\{ {\left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }} + K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right) \cdot \left[ {m_{e} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }}} \right)C_{p} R_{p} } \right] - K_{e} m_{e} C_{p} R_{p} } \right\}}}$$
(30)

Then, mean square value of amplitude can be obtained through solving the Eq. (30). Furthermore, it can be concluded that when the system parameters are determined, frequency domain response of nonlinear PE–EM energy harvesting system will not be assured, while it is related to spectral density S0 of excitation, which is one of the biggest differences from linear energy harvester. Besides, vibration response and output characteristics of nonlinear hybrid PE and EM energy harvester under Gaussian white noise excitation is mainly related to the stiffness of harvesting structure, the equivalent mass, parameters of PE element and EM element, nonlinear parameters, load resistance and excitation spectral density.

2.3 Output power

From Eq. (28),

$$z(\omega ) = H(\omega )a(\omega )$$
(31)

So transfer functions of PE and EM energy harvesting element are

$$H_{{I_{e} }} (\omega ) = \frac{{I_{e} (\omega )}}{a(\omega )} = \frac{{g_{e} }}{{R_{c} + R_{m} }}i\omega H(\omega )$$
(32)
$$H_{{V_{P} }} (\omega ) = \frac{{V_{p} (\omega )}}{a(\omega )} = \frac{{i\omega \theta R_{p} }}{{1 + i\omega C_{p} R_{p} }} \cdot H(\omega )$$
(33)

Substitute Eq. (28) into Eqs. (32), (33), and it can be obtained that respectively

$$H_{{I_{e} }} (\omega ) = \frac{{ - \frac{{g_{e} m_{e} }}{{R_{c} + R_{m} }}i\omega - \frac{{g_{e} m_{e} }}{{R_{c} + R_{m} }}R_{p} C_{p} (i\omega )^{2} }}{{m_{e} C_{p} R_{p} (i\omega )^{3} + \left[ {m_{e} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }}} \right)C_{p} R_{p} } \right](i\omega )^{2} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }} + K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right)i\omega + K_{e} }}$$
(34)
$$H_{{V_{P} }} (\omega ) = \frac{{\left[ { - m_{e} \theta R_{p} (i\omega ) - \theta m_{e} R_{p}^{2} C_{p} (i\omega )^{2} } \right]}}{{\left\{ \begin{aligned} m_{e} (C_{p} R_{p} )^{2} (i\omega )^{4} + \left[ {2m_{e} C_{p} R_{p} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }}} \right)(C_{p} R_{p} )^{2} } \right](i\omega )^{3} + \left[ {m_{e} + \left( {2c_{m} + \frac{{2g_{e}^{2} }}{{R_{c} + R_{m} }} + K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right)C_{p} R_{p} } \right](i\omega )^{2} \hfill \\ + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }} + 2K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right)i\omega + K_{e} \hfill \\ \end{aligned} \right\}}}$$
(35)

Then, mean square values of output current of EM energy harvesting element and output voltage of PE energy harvesting element are respectively

$$\overline{{I_{e}^{2} }} = \frac{1}{2\pi }S_{0} \int\limits_{ - \infty }^{ + \infty } {\left| {H_{{I_{e} }} (\omega )} \right|^{2} d\omega }$$
(36)
$$\overline{{V_{P}^{2} }} = \frac{1}{2\pi }S_{0} \int\limits_{ - \infty }^{ + \infty } {\left| {H_{{V_{P} }} (\omega )} \right|^{2} d\omega }$$
(37)

According to James formula (Gradshtenyn and Ryzhik 1994), Eqs. (36) and (37) can be solved as

$$\overline{{I_{e}^{2} }} = \frac{{S_{0} }}{2}\frac{{\left( {\frac{{g_{e} m_{e} }}{{R_{c} + R_{m} }}R_{p} C_{p} } \right)^{2} \cdot \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }} + K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right) + \left( {\frac{{g_{e} m_{e} }}{{R_{c} + R_{m} }}} \right)^{2} \cdot m_{e} C_{p} R_{p} }}{{m_{e} C_{p} R_{p} \cdot \left\{ {\left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }} + K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right) \cdot \left[ {m_{e} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }}} \right)C_{p} R_{p} } \right] - K_{e} m_{e} C_{p} R_{p} } \right\}}}$$
(38)
$$\overline{{V_{P}^{2} }} = \frac{1}{2\pi }S_{0} \pi \frac{{A_{1} B_{2}^{2} + A_{3} B_{1}^{2} }}{{A_{1} A_{2} A_{3} - A_{0} A_{3}^{2} - A_{1}^{2} A_{4} }}$$
(39)

In Eq. (39), \(B_{2} = - \theta m_{e} R_{p}^{2} C_{p}\), \(B_{1} = - m_{e} \theta R_{p}\), \(A_{0} = K_{e}\), \(A_{1} = c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }} + 2K_{e} C_{p} R_{p} + \theta^{2} R_{p}\), \(A_{2} = m_{e} + \left( {2c_{m} + \frac{{2g_{e}^{2} }}{{R_{c} + R_{m} }} + K_{e} C_{p} R_{p} + \theta^{2} R_{p} } \right)C_{p} R_{p}\), \(A_{3} = 2m_{e} C_{p} R_{p} + \left( {c_{m} + \frac{{g_{e}^{2} }}{{R_{c} + R_{m} }}} \right)\left( {C_{p} R_{p} } \right)^{2}\), \(A_{4} = m_{e} \left( {C_{p} R_{p} } \right)^{2}\).

Based on \(E[P(t)] = E\left[ {\frac{V(t)}{{R_{load} }}} \right] = \frac{E[V(t)]}{{R_{load} }}\), mean power apply on EM load and PE load are respectively

$$P_{e} = R_{m} \overline{{I_{e}^{2} }}$$
(40)
$$P_{p} = \frac{{\overline{{V_{p}^{2} }} }}{{R_{p} }}$$
(41)

Therefore, total output power of hybrid PE and EM energy harvester is the sum of output power of PE energy harvesting element and EM energy harvesting element. That is

$$P = P_{p} + P_{e} = \frac{{\overline{{V_{p}^{2} }} }}{{R_{p} }} + R_{m} \overline{{I_{e}^{2} }}$$
(42)

Furthermore, by Eq. (42), optimal load of PE and EM element is respectively

$$\frac{\partial P}{{\partial R_{p} }} = 0 \to R_{p} = R_{{p{\text{-}}optimal}}$$
(43)
$$\frac{\partial P}{{\partial R_{m} }} = 0 \to R_{m} = R_{{m{\text{-}}optimal}}$$
(44)

3 Numerical calculation and simulation analysis

From above analysis results, it can be concluded that main factors determined output performances of nonlinear hybrid PE and EM energy harvester are structural parameters, nonlinear stiffness, characteristic parameters of PE and EM element, load resistance and spectral density of excitation. Therefore, in this part, effects of above factors on performances of nonlinear hybrid energy harvester by numerical calculation and simulation analysis.

Based on state equations of nonlinear hybrid energy harvester shown in Eqs. (7)–(9), output characteristics of harvester under the random vibration excitation is simulated by matlab software, and compared with the theory results. In the simulation, the fourth order Runge–Kutta method is used, and the electric output signal of harvester under random excitation is obtained from the simulation. Then, adopting matlab digital signal processing technology to process the signals obtained in the simulation, and mean square value and SD of output signals are obtained. Finally, we can have the root mean square (RMS) value of output voltage, current, and power, spectral density of harvester. The structural parameters and materials properties are shown in Table 1.

Table 1 Structural parameters and material properties
Full size table

3.1 Effect of load resistance on output performances

From results in Sect. 2, load resistance is one of main factors that influence the amplitude and output power of nonlinear energy harvester. When the acceleration spectral density S0 is 0.1(m/s2)2/rad/s, effects of load resistance of PE and EM harvesting element on mean amplitude and power of nonlinear hybrid energy harvester are analyzed, and optimal PE and EM loads corresponding to the maximal power can be obtained.

3.1.1 Amplitude

For the nonlinear energy harvester, the bigger amplitude, the larger bending deformation of beam and the bigger stress in PE layer are; moreover, amplitude can also change the distance between magnet and coil. When spectral density S0 of random excitation is 0.1 (m/s2)2/rad/s, the amplitude of nonlinear hybrid energy harvester varied with PE and EM loads is studied, and results compared with simulation result are shown in Fig. 2. In the analysis, EM load is 40 Ω and PE load is 390 kΩ.

Fig. 2
figure 2

Effect of load on amplitude: a PE load, b EM load

Full size image

Based on results shown in Fig. 2b, amplitude of nonlinear hybrid energy harvester decreased firstly and then increased with PE load increasing, and it reached the minimum at optimal PE load. It is because that the load is related to coupling effect of electric element on vibration system, and coupling effect of PE element reaches the maximum at PE optimal load. When PE load fixed and EM load increased only, coupling effect of EM element on energy harvester falls as EM load increasing, which indicates effect of equivalent electrical damping reduced. So amplitude of energy harvester increased with EM load increasing, and it reached the maximum at open circuit, as shown in Fig. 2a.

3.1.2 Mean power

Under the random excitation S0 = 0.1(m/s2)2/rad/s, effect of PE and EM loads on output power of nonlinear hybrid energy harvester were analyzed, and the results were compared with output power of linear hybrid energy harvester. When PE element of energy harvester is connected with optimal load, output power varied with EM load is shown in Fig. 3. In this case, the natural frequency of linear energy harvester was 77 Hz, while the resonant frequency of nonlinear energy harvester decreased to 34 Hz because of effect of nonlinear magnetic force. At this case, their corresponding internal resistance of PE element is 170 and 390 kΩ respectively.

Fig. 3
figure 3

Effect of EM load on output power

Full size image

In addition, because of the influence of magnetic force, the stiffness of nonlinear harvester is much smaller than that of linear harvester, and natural frequency decreases. Moreover, total output power is much bigger than that of linear hybrid energy harvester. However, compared with EM element, increasing degree of PE element output power is more obvious. When PE element connects with optimal load, total output power of nonlinear and linear hybrid energy harvester all increases firstly and then decreases with load of EM element increasing, but EM optimal load of nonlinear energy harvester is much bigger. From Fig. 3, the optimal EM loads of nonlinear and linear energy harvester are 30 and 47 Ω respectively.

On the other hand, effect of PE load on output power is analyzed when EM load is 40 and 30 Ω respectively, and results are shown in Fig. 4.

Fig. 4
figure 4

Effect of PE load on output power: a Linear energy harvester; b nonlinear energy harvester

Full size image

According to analysis results shown in Fig. 4, output power of hybrid energy harvester and PE element reached the maximal power at the same PE load. However, as the natural frequency is different, optimal PE load of linear energy harvester is smaller than that of nonlinear energy harvester, which are 177 and 398 kΩ respectively. On the other hand, output power of EM element reduced firstly and then increased with PE load increasing, and it reached the minimum at optimal PE load. Otherwise, output power of EM element of linear energy harvester is bigger than the power of its PE element, while for the nonlinear energy harvester, PE output power is bigger than EM power only for some PE loads.

Therefore, after adopting nonlinear method, the natural frequency of energy harvester decreases while output power enhances. Compared with EM element, increasing degree of PE element output power is much more obvious. Thus, nonlinear energy harvester is more benefit in the application of low frequency environment, and the natural frequency of energy harvester analyzed in this paper decreased by 56%, while output power increased by 72%.

3.2 Effect of acceleration spectral density on output performances

In this section, output power of nonlinear hybrid energy harvester was analyzed under different acceleration spectral density. When acceleration spectral density is 0.01, 0.05, 0.1 (m/s2)2/rad/s, and PE and EM load resistance is 390 kΩ, 40 Ω respectively, output power of harvester are shown in Fig. 5. It can be concluded that the bigger acceleration spectral density, the bigger output power, but EM and PE optimal loads do not change with excitation spectral density increasing.

Fig. 5
figure 5

Output power of energy harvester under different random acceleration excitation: a total output power at different EM load; b EM power at different EM load; c total output power at different PE load; d PE power at different PE load. [S1 = 0.1(m/s2)2/rad/s, S2 = 0.05(m/s2)2/rad/s, S3 = 0.01(m/s2)2/rad/s]

Full size image

Then, the simulation results of displacement, PE output voltage and EM output current are shown in Fig. 6 when S0 = 0.1(m/s2)2/rad/s, Rp = 390 kΩ and Rm = 40 Ω.

Fig. 6
figure 6

Simulation results

Full size image

In addition, output power of nonlinear energy harvester varied with acceleration spectral density is shown in Fig. 7, while load resistance of PE and EM element is 390 kΩ and 40 Ω respectively. In can be concluded that mean power of energy harvester linearly increases with acceleration spectral density increasing. Compared with linear harvester, increasing degree of output power of nonlinear energy harvester is much more obvious. In addition, variation law of amplitude, output voltage of PE element and output current of EM element is the same as acceleration spectral density increasing.

Fig. 7
figure 7

Effect of acceleration spectral density on characteristics of energy harvester: a total output power; b amplitude; c PE voltage; d EM current

Full size image

3.3 Effect of nonlinear strength on output performances

For the nonlinear energy harvester, nonlinear force between magnets represents the nonlinear strength, and the less dynamic magnet distance, the bigger nonlinear strength. Furthermore, only when magnets are closed to each other, energy harvester can have obvious nonlinear response. Otherwise, its output is similar to linear energy harvester.

When acceleration spectral density is 0.1(m/s2)2/rad/s and static distance between magnets are 13, 13.5 and 14 mm respectively, output power of energy harvester at different EM and PE loads are shown in Fig. 8. The less magnet distance, the stronger nonlinear magnetic force and the smaller equivalent stiffness of energy harvester are, which causes the smaller resonant frequency. When the static distance is 13, 13.5 and 14 mm, the resonant frequency is 33.5, 44.2 and 51.2 Hz respectively, and optimal load of PE energy harvesting element is 390, 297 and 256 kΩ respectively.

Fig. 8
figure 8

Output power of different magnet distance: a different EM load; b different PE load

Full size image

Meanwhile, when EM and PE element connected with optimal load, the output power of nonlinear hybrid energy harvester varied with static magnetic distance is shown in Fig. 9. It can be concluded that the bigger magnet distance, the smaller nonlinear magnetic force and output power of nonlinear energy harvester are. Therefore, effect of magnetic force can be neglected when the distance is increased to some given extent. At this time, output power is equal to output power of linear energy harvester.

Fig. 9
figure 9

Relationship between magnet distance and output power

Full size image

4 Experimental validation

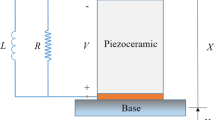
In order to test the output performances of hybrid PE–EM energy harvester at different acceleration spectral density, a meso hybrid energy harvester is designed and its experimental installation is shown in Fig. 10. In the test, the signal generator is used to provide the random excitation to the harvester, and dynamic signal analyzer records the acceleration, output voltage of PE and EM element.

Fig. 10
figure 10

Experimental setup

Full size image

The mean power of nonlinear hybrid energy harvester at the different spectral density of acceleration is shown in Fig. 11. It illustrates that output power is linearly proportional to the acceleration spectral density, which is consistent with theoretical analysis results. However, because of uncertainly of random excitation, there are errors between experimental test results and theoretical analysis results. For random signals process, the appearances of errors are in the expected range (Jackson et al. 2013)

Fig. 11
figure 11

Effect of acceleration SD on output power

Full size image

5 Conclusion

Aim at designed nonlinear hybrid energy harvester, the state equations considered electromechanical coupling are established, and expressions of amplitude, output power, voltage and current of harvester at stochastic excitation are derived through statistical linearization method. By theoretical analysis, simulation and experimental test, effects of load resistance, excitation spectral density and nonlinear strength on vibration response and electric output of nonlinear hybrid energy harvester are studied. We can conclude the following results.

  1. 1.

    For nonlinear hybrid energy harvester, when the system parameters are determined, its frequency domain response will not be assured, while it is related to spectral density of excitation. In addition, vibration response and performances of nonlinear hybrid PE and EM energy harvester under random excitation is mainly related to structural parameters, nonlinear stiffness, characteristic parameters of PE and EM element, load resistance and spectral density of excitation.

  2. 2.

    The nonlinear force between magnets can be used to lower the resonant frequency and improve the power output. Moreover, the bigger magnet distance, the smaller nonlinear magnetic force and output power of nonlinear energy harvester are. However, the effect of nonlinear force can be neglected when the distance is increased to some given extent.

  3. 3.

    Amplitude of nonlinear harvester that influenced by the loads increases firstly and then decreases with PE load increasing, and it reaches minimum at optimal PE load; moreover, the amplitude of energy harvester increased with EM load increasing, and it reached the maximum at open circuit.

  4. 4.

    Output mean power of nonlinear energy harvester linearly increases with acceleration spectral density increasing. Furthermore, output power of EM element is influenced by PE load, and it reaches the minimum at optimal PE load.

  5. 5.

    Compared to linear energy harvester, the designed nonlinear energy harvester is more benefit in the low frequency environment, and natural frequency of energy harvester analyzed in this paper decreased by 56%, while output power increased by 72%.