1 Introduction

Vibration energy harvester, which can be used as a renewable energy device to take the place of chemical battery, has been focused by many researchers in recent years, and its performances have been improved largely (Tiwari et al. 2014; Yang et al. 2014). For linear energy harvester, the power reaches the maximum at the resonant frequency, and 3 dB bandwidth is just about several Hz, which limits the application in the practical environment (Cammarano et al. 2014). Besides, the vibration frequency of the environment is usually less than 100 Hz (Dhakar et al. 2013). Due to the effect of harvester volume, how to effectively reduce the natural frequency is another difficulty for the harvester.

Recently, researchers proposed many methods to solve the above problems, among which the nonlinear technique was one of the feasible solutions (Liu et al. 2012; Karami and Inman 2011; Pellegrini et al. 2013; Sebald et al. 2011a). Therefore, Harne reviewed the bistable nonlinear vibration energy harvester from the aspects of the solutions of governing equation, device design, the challenges in the future and so on (Harne and Wang 2013). Moreover, Pellegrini summarized current development of nonlinear energy harvester from the bistable harvester design, theoretical model and methods of measure (Pellegrini et al. 2013). Besides, Mann analyzed the output performances of nonlinear EM energy harvester that adopted the magnetic spring, and obtained that nonlinear technology can enlarge the bandwidth (Mann and Owens 2010). Foisal studied nonlinear EM energy harvester through experimental test, and obtained the bandwidth of energy harvester could reach 7–10 Hz by optimization the turns, position and wire diameter of coil (Foisal et al. 2012). In addition, Challa designed a nonlinear PE energy harvester, whose stiffness can be varied by magnetic force to adjust the resonant frequency and bandwidth, and four magnets were used: two of which were fixed on two sides of mass, and the others were installed on the frame toward the mass. By experimental test, the natural frequency of harvester can be increased or decreased 20 % by this technique, but the dynamic response characteristics were not concerned in modeling (Challa et al. 2008). Furthermore, Marzencki designed a MEMS PE energy harvester, which was based on double-clamped beam, and adjusted the beam stiffness through nonlinear strain caused by internal stress of interlayer in harvester structure. By theoretical modeling and experimental test, it was illustrated that the bandwidth of harvester can increase 36 % under the excitation of 2 g (Marzencki et al. 2009). Ghandchi put forward the vibration energy harvester model based on nonlinear damping, and got that the power output and bandwidth of this model were all superior to those of linear energy harvester (Ghandchi Tehrani and Elliott 2014). Sebald designed a nonlinear energy harvester model, which can adjust the resonance frequency by changing the magnetic force, and by experimental test it can be got that the resonance frequency of nonlinear PE energy harvester can be increased by 70 % (Sebald et al. 2011b). Ferrari analyzed the random response of nonlinear PE energy harvester under the white noise excitation, and obtained the harvester can output the bigger mean power at the bistable state, and this technique can be applied in MEMS device (Ferrari et al. 2010). Moreover, Shan and Yang did not consider the feedback effect of PE and EM electrical outputs to the vibration response of harvesting system in their analysis (Yang et al. 2014; Shan et al. 2013). Therefore, according to the above references, it can be seen that compared with linear energy harvester, the nonlinear methods for harvester can not only improve the output power and bandwidth but also can adjust the natural frequency.

However, at present, researches mainly focused on nonlinear PE or EM energy harvester with single energy converting mechanism, and the nonlinear studies were seldom reported for hybrid PE and EM energy harvester. Therefore, in this paper, a novel nonlinear hybrid PE and EM energy harvester that can lower the natural frequency and improve the bandwidth and power was proposed, and then its governing equations considering the electromechanical coupling effect was established. By means of harmonic balance, expressions of amplitude, output voltage, current and power of harvester under the harmonic excitation were derived, and the normalized forms of performances were obtained by the defined dimensionless parameters. Then, by numerical calculation and experimental test, the effects of nonlinear factor, excitation frequency, load resistance and input excitation on amplitude, bandwidth, power output and the natural frequency of nonlinear hybrid energy harvester were studied and compared with performances of linear energy harvester.

2 Modeling of nonlinear hybrid energy harvester

2.1 Structure design

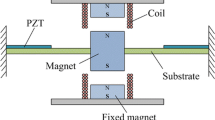
The designed nonlinear hybrid PE and EM energy harvester, which can be fabricated by MEMS technology, is shown in Fig. 1. The movable magnet as mass is supported by double-clamped compound beam, and two coils are placed above and below the mass magnet. Besides, two magnets are fixed inside the coils respectively, and their magnetic pole are opposite to the mass magnet, which means the force between the movable magnet and fixed magnet is attractive, which can decrease the natural frequency of harvester and avoid the effects on performances of EM element. Therefore, the stiffness of hybrid energy harvester can be changed to adjust the vibration response because the attractive force varies with the distance between the magnets. In addition, the piezoelectric layers are died on the top surface of beams, and based on piezoelectric effect and law of electromagnetic induction, PZT layers and coils can output voltage signal under the external excitation.

Fig. 1
figure 1

Structure model of nonlinear hybrid energy harvester

Full size image

For the designed hybrid PE and EM energy harvester, the equivalent vibration model of the nonlinear harvester can be modeled as a mass-spring-damper-PE element-EM element system, as shown in Fig. 2. When the acceleration is applied to the harvesting system, an effective mass me is bounded on a linear spring of effective stiffness k, a nonlinear spring of effective stiffness kn, a damper of coefficient cm, a PE element and an EM element.

Fig. 2
figure 2

An equivalent model for the nonlinear hybrid PE and EM energy harvester

Full size image

2.2 Theoretical modeling

In the structure, cylindrical magnets are used to apply the desired magnetic force, and the magnetic force between any two cylinder magnets is given as (Mann and Owens 2010; Owens and Mann 2012)

$$F_{m} = \frac{{3\mu_{0} M_{1} V_{1} \cdot M_{0} V_{0} }}{{2\pi d^{4} }}$$
(1)

where µ0 = 4π × 10−7 H/m is magnetic permeability, V1 and V0 are volumes of two magnets, M1 and M0 are magnetization of two magnets respectively, and d is the static distance between the magnets. For the designed hybrid energy harvester, under the external excitation, when the displacement of mass magnet is z (suppose the direction near the below fixed magnet), the forces between the mass magnet and above, below fixed magnets are Fm1 and Fm2 respectively. By Eq. (1), the nonlinear magnetic force is

$$F_{m} (z) = F_{m1} { - }F_{m2} = 3\mu_{0} M_{m} V_{m} \left[\frac{{M_{t} V_{t} }}{{2\pi (d + z)^{4} }} - \frac{{M_{b} V_{b} }}{{2\pi (d - z)^{4} }}\right]$$
(2)

where Mm and Vm are magnetization and volume of mass magnet respectively; Mt and Vt are magnetization and volume of above magnet respectively; Mb and Vb are magnetization and volume of the below magnet respectively. To avoid the plastic deformation of the beam, the nonlinear force should be less than the elastic restoring force of the beam, which means

$$\left| {F_{m} (z)} \right| < \left| {k_{b} z} \right|$$
(3)

where kb is the stiffness of the beam.

For the designed hybrid energy harvester, the above and below magnets are the same, and their static distances between mass magnet are equal to each other. By the method of Taylor expansion (Tongji University, Department of Mathematics 2007), when neglecting high-order terms and z < d, Eq. (2) can be expressed as

$$F_{m} (z) = k_{1} z + k_{3} z^{3}$$
(4)

where

$$k_{1} = - 12\mu_{0} M_{m} V_{m} \frac{{M_{b} V_{b} }}{{\pi d^{5} }}$$
(5)
$$k_{3} = \frac{5}{{d^{2} }}k_{1}$$
(6)

According to Fig. 2 and combining the former study for linear hybrid energy harvester (Li et al. 2015), the governing equations of nonlinear hybrid PE and EM energy harvester can be illustrated as

$$m_{e} \textit{\"{z}}(t) + c_{m} \dot{z}(t) + k_{b} z(t) + F_{m} (z(t)) + g_{e} I_{em} (t) + \theta V_{p} (t) = - m_{e} \textit{\"{y}}(t)$$
(7)
$$L_{c} \dot{I}_{em} (t) + (R_{c} + R_{m} )I_{em} (t) - g_{e} \dot{z}(t) = 0$$
(8)
$$\frac{{V_{p} (t)}}{{R_{p} }} + C_{p} \dot{V}_{p} (t) - \theta \dot{z}(t) = 0$$
(9)

where \(\textit{\"{y}}(t)\) is the excitation acceleration; Rp, Rm are load resistance of PE and EM element respectively; Cp is equivalent capacitance of PE layer; Vp is output voltage of PE energy harvesting element; Iem is output current of EM energy harvesting element; Rc and Lc refers to resistance and inductance of coils; θ and ge are PE and EM transfer factors respectively. These parameters are dependent on the material constants and the design of the energy harvester, which can be derived by standard model analysis (Spreemann and Manoli 2012; Erturk and Inman 2011a).

3 Modeling solve

In the analysis, supposing the excitation is harmonic acceleration, and it can be obtained that Eq. (7) is the typical Duffing Equation after substituting Eq. (4) into Eq. (7). By the method of harmonic balance, the vibration response and performances of nonlinear hybrid PE and EM energy harvester can be derived. According to references (Vinod et al. 2013; Erturk and Inman 2011b), the inductance of coil can be neglected in the low vibrating frequency (lower than 1 kHz) because the impedance is mainly determined by the resistance of coil.

Suppose

$$\omega_{n}^{2} = \frac{K}{{m_{e} }},\;K = k_{b} + k_{1} ,\;2\zeta \omega_{n} = \frac{{c_{m} }}{{m_{e} }},\;\beta = \frac{{g_{e} }}{{R_{c} + R_{m} }},\;\mu = \frac{1}{{R_{p} C_{p} }}$$
(10)

and for the weak nonlinear situation, the amplitude of mass, PE voltage and EM current are assumed in Eqs. (11), (12) respectively.

$$z(t) = A_{1} \cos \omega t$$
(11)
$$V_{p} (t) = A_{2} \cos (\omega t + \phi_{1} )$$
(12)
$$I_{em} (t) = A_{3} \cos (\omega t + \phi_{2} )$$
(13)

Substitute Eqs. (11)–(13) into Eq. (7) and ignore higher order harmonics, then

$$\begin{gathered} A_{1} (\omega_{n}^{2} - \omega^{2} )\cos \omega t - 2A_{1} \zeta \omega_{n} \omega \sin \omega t\\ \quad + \frac{{3k_{3} A_{1}^{3} }}{{4m_{e} }}\cos \omega t + \frac{{A_{2} \theta }}{{m_{e} }}\cos (\omega t + \phi_{1} ) \hfill \\ \quad + \frac{{A_{3} g_{e} }}{{m_{e} }}\cos (\omega t + \phi_{2} ) = Y\cos (\omega t + \varphi ) \hfill \\ \end{gathered}$$
(14)

Equating coefficients of \(\sin \omega t\) and \(\cos \omega t\) in two sides of Eq. (14) respectively, and the results are

$$A_{1} (\omega_{n}^{2} - \omega^{2} ) + A_{1}^{3} \frac{{3k_{3} }}{{4m_{e} }} + A_{2} \frac{\theta }{{m_{e} }}\cos \phi_{1} + A_{3} \frac{{g_{e} }}{{m_{e} }}\cos \phi_{2} = Y\cos \varphi$$
(15)
$$2A_{1} \zeta \omega_{n} \omega + A_{2} \frac{\theta }{{m_{e} }}\sin \phi_{1} + A_{3} \frac{{g_{e} }}{{m_{e} }}\sin \phi_{2} = Y\sin \varphi$$
(16)

where \(A_{2}\), \(A_{3}\), \(\cos \phi_{1}\), and \(\cos \phi_{2}\) are obtained by the following analysis.

Substitute Eqs. (11)–(13) into Eq. (9), then

$$- A_{2} \omega \sin (\omega t + \phi_{1} ) + \mu A_{2} \cos (\omega t + \phi_{1} ) + \frac{\theta }{{C_{p} }}A_{1} \omega \sin \omega t = 0$$
(17)

Similarly, the coefficients of \(\sin \omega t\) and \(\cos \omega t\) are equaled for the two sides of Eq. (17) respectively, so

$$- A_{2} \omega \cos \phi_{1} - \mu A_{2} \sin \phi_{1} + \frac{\theta }{{C_{p} }}A_{1} \omega = 0$$
(18)
$$- A_{2} \omega \sin \phi_{1} + \mu A_{2} \cos \phi_{1} = 0$$
(19)

and Eq. (19) can be rearranged as

$$\sin \phi_{1} = \frac{\mu }{\omega }\cos \phi_{1}$$
(20)

Then substitute Eq. (20) into Eq. (18), and

$$- A_{2} \omega \cos \phi_{1} - A_{2} \frac{{\mu^{2} }}{\omega }\cos \phi_{1} + \frac{\theta }{{C_{p} }}A_{1} \omega = 0$$
(21)

So

$$\cos \phi_{1} = \frac{{\theta \omega^{2} }}{{C_{p} (\omega^{2} + \mu^{2} )}}\frac{{A_{1} }}{{A_{2} }}$$
(22)
$$\sin \phi_{1} = \frac{\mu \theta \omega }{{C_{p} (\omega^{2} + \mu^{2} )}}\frac{{A_{1} }}{{A_{2} }}$$
(23)

by \(\sin^{2} \phi_{1} + \cos^{2} \phi_{1} = 1\), Eq. (24) can be got by Eqs. (22) and (23).

$$A_{2} = \frac{\theta \omega }{{C_{p} \sqrt {\omega^{2} + \mu^{2} } }}A_{1}$$
(24)

Then, Eqs. (11)–(13) are substituted into Eq. (8), and by the similar analysis above, the following Eqs. (25) and (26) can be obtained.

$$\cos \phi_{2} = 0$$
(25)
$$\sin \phi_{2} = \frac{{A_{1} }}{{A_{3} }}\beta \omega$$
(26)

and

$$A_{3} = A_{1} \beta \omega$$
(27)

Substituting Eqs. (22)–(24), (25)–(27) into Eqs. (15) and (16), the results are

$$A_{1} (\omega_{n}^{2} - \omega^{2} ) + A_{1}^{3} \frac{{3k_{3} }}{{4m_{e} }} + A_{1} \frac{\theta }{{m_{e} }}\frac{{\theta \omega^{2} }}{{C_{p} (\omega^{2} + \mu^{2} )}} = Y\cos \varphi$$
(28)
$$2A_{1} \zeta \omega_{n} \omega + A_{1} \frac{\theta }{{m_{e} }}\frac{\mu \theta \omega }{{C_{p} (\omega^{2} + \mu^{2} )}} + A_{1} \frac{{g_{e} }}{{m_{e} }}\beta \omega = Y\sin \varphi$$
(29)

By squaring and summing Eqs. (28) and (29), six-order nonlinear expression of amplitude \(z_{M}\) of harvester can be derived, such that

$$\begin{gathered} z_{M}^{2} = A_{1}^{2} \hfill \\ = \frac{{Y^{2} }}{{[(\omega_{n}^{2} - \omega^{2} ) + z_{M}^{2} \frac{{3k_{3} }}{{4m_{e} }} + \frac{\theta }{{m_{e} }}\frac{{\theta \omega^{2} }}{{C_{p} (\omega^{2} + \mu^{2} )}}]^{2} + [2\zeta \omega_{n} \omega + \frac{\theta }{{m_{e} }}\frac{\mu \theta \omega }{{C_{p} (\omega^{2} + \mu^{2} )}} + \frac{{g_{e} }}{{m_{e} }}\beta \omega ]^{2} }} \hfill \\ \end{gathered}$$
(30)

Based on the structural parameters of designed hybrid energy harvester, amplitude of mass \(z_{M}\) can be calculated by Eq. (30). At the same time, the phase of displacement also can be obtained from the Eqs. (28) and (29).

Furthermore, by Eq. (24), the output voltage of PE element is

$$V_{p} = \frac{\theta \omega }{{C_{p} \sqrt {\omega^{2} + (\frac{1}{{R_{p} C_{p} }})^{2} } }}z_{M}$$
(31)

and by Eq. (27), the output current of EM element can be expressed as

$$I_{em} = \frac{{g_{e} \omega }}{{R_{c} + R_{m} }}z_{M}$$
(32)

Therefore, mean power output of PE and EM energy harvesting element are illustrated in Eqs. (33) and (34) respectively.

$$P_{p} = \frac{1}{2}\frac{{V_{p}^{2} }}{{R_{p} }} = \frac{{\theta^{2} \omega^{2} }}{{2R_{p} C_{p}^{2} [\omega^{2} + (\frac{1}{{R_{p} C_{p} }})^{2} ]}}z_{M}^{2}$$
(33)
$$P_{em} = \frac{1}{2}R_{m} I_{em}^{2} = \frac{{R_{m} g_{e}^{2} \omega^{2} }}{{2(R_{c} + R_{m} )^{2} }}z_{M}^{2}$$
(34)

Finally, the total output power of designed nonlinear hybrid PE and EM energy harvester is

$$P = P_{p} + P_{em} = \left\{ \frac{{\theta^{2} \omega^{2} }}{{2R_{p} C_{p} [\omega^{2} + (\frac{1}{{R_{p} C_{p} }})^{2} ]}} + \frac{{g_{e}^{2} \omega^{2} }}{{2R_{m} (R_{c} + R_{m} )^{2} }}\right\} z_{M}^{2}$$
(35)

3.1 Normalized forms

In order to get more compact expressions of performances of nonlinear hybrid PE and EM energy harvester, the dimensionless parameters are assumed that

\(\eta_{p} = \frac{{\theta^{2} }}{{KC_{p} }}\) as piezoelectric coupling coefficient;

\(\eta_{e} = \frac{{\omega_{n} g_{e}^{2} }}{{KR_{c} }}\) as electromagnetic coupling coefficient;

\(\lambda = \frac{\omega }{{\omega_{n} }}\) as dimensionless vibration frequency;

\(\zeta_{m} = \frac{{c_{m} }}{{2m_{e} \omega_{n} }}\) as mechanical damping ratio;

\(r_{p} = R_{p} C_{p} \omega_{n}\) as dimensionless load resistance of PE element;

\(r_{m} = \frac{{R_{m} }}{{R_{c} }}\) as dimensionless load resistance of EM element;

\(\varGamma_{nl} = (\frac{{m_{e} Y}}{K})^{2} \frac{{k_{3} }}{K}\) as nonlinear factor

Then, the more compact forms of Eqs. (30)–(34) involving the dimensionless parameters can be derived, such that respectively

$$\begin{gathered} \overline{{z_{M}^{2} }} = \frac{{z_{M}^{2} }}{{(\frac{{m_{e} Y}}{K})^{2} }} \hfill \\ = \frac{1}{{[(1 - \lambda^{2} ) + \overline{{z_{M}^{2} }} \frac{{3\varGamma_{nl} }}{4} + \eta_{p} \frac{{(\lambda r_{p} )^{2} }}{{(\lambda r_{p} )^{2} + 1}}]^{2} + [2\lambda \zeta + \eta_{p} \frac{{\lambda r_{p} }}{{(\lambda r_{p} )^{2} + 1}} + \frac{\lambda }{{1 + r_{m} }}\eta_{e} ]^{2} }} \hfill \\ \end{gathered}$$
(36)
$$\overline{{V_{p} }} = \frac{{V_{p} }}{{\frac{{m_{e} Y}}{\theta }}} = \frac{{\lambda \eta_{p} r_{p} }}{{\sqrt {(\lambda r_{p} )^{2} + 1} }}\overline{{z_{M} }}$$
(37)
$$\overline{{I_{e} }} = \frac{{I_{e} }}{{\frac{{m_{e} Y}}{{g_{e} }}}} = \frac{{\lambda \eta_{e} }}{{1 + r_{m} }}\overline{{z_{M} }}$$
(38)
$$\overline{{P_{p} }} = \frac{{P_{p} }}{{\frac{{(m_{e} Y)^{2} }}{{m_{e} \omega_{n} }}}} = \frac{1}{2}\frac{{\lambda^{2} \eta_{p} r_{p} }}{{(\lambda r_{p} )^{2} + 1}}\overline{{z_{M}^{2} }}$$
(39)
$$\overline{{P_{e} }} = \frac{{P_{e} }}{{\frac{{(m_{e} Y)^{2} }}{{\omega_{n} m_{e} }}}} = \frac{{r_{m} \eta_{e} \lambda^{2} }}{{2(1 + r_{m} )^{2} }}\overline{{z_{M}^{2} }}$$
(40)

Therefore, the normalized total power of nonlinear hybrid PE and EM energy harvester is

$$\overline{P} = \overline{{P_{p} }} + \overline{{P_{e} }} = \frac{1}{2}\left[\frac{{\lambda^{2} \eta_{p} r_{p} }}{{(\lambda r_{p} )^{2} + 1}} + \frac{{r_{m} \eta_{e} \lambda^{2} }}{{(1 + r_{m} )^{2} }}\right]\overline{{z_{M}^{2} }}$$
(41)

3.2 Optimal frequency

According to reference (Al-Ashtari et al. 2012), the nonlinear vibration energy harvester outputs the maximal power at the optimal vibration frequency which is corresponding to the peak amplitude. Thus, the optimal excitation frequency of nonlinear energy harvester should be analyzed furthermore.

In the analysis, the Eq. (36) is rearranged as

$$G(\overline{{z_{M} }} ,\lambda ) = 0$$
(42)

Then,

$$\frac{{\partial \overline{{z_{M} }} }}{\partial \lambda } = - \frac{{\frac{\partial G}{\partial \lambda }}}{{\frac{\partial G}{{\partial \overline{{z_{M} }} }}}}$$
(43)

Thus, the maximal amplitude \(\overline{{z_{\hbox{max} } }}\) and its corresponding vibration frequency \(\lambda_{0}\) can be obtained by the solution of \(\frac{{\partial \overline{{z_{M} }} }}{\partial \lambda } = 0\), such that

$$\begin{gathered} \left[ {(1 - \lambda _{0}^{2} ) + \overline{{z_{{\max }}^{2} }} \frac{{3\Gamma _{{nl}} }}{4} + \eta _{p} \frac{{(\lambda _{0} r_{p} )^{2} }}{{(\lambda _{0} r_{p} )^{2} + 1}}} \right] \cdot \left[ { - 2\lambda _{0} + 2\eta _{p} \frac{{\lambda _{0} r_{p}^{2} [(\lambda _{0} r_{p} )^{2} + 1] - (\lambda _{0} r_{p} )^{2} \lambda _{0} r_{p}^{2} }}{{[(\lambda _{0} r_{p} )^{2} + 1]^{2} }}} \right] + \hfill \\ \left[ {2\lambda _{0} \zeta + \eta _{p} \frac{{\lambda _{0} r_{p} }}{{(\lambda _{0} r_{p} )^{2} + 1}} + \frac{{\lambda _{0} }}{{1 + r_{m} }}\eta _{e} } \right] \cdot \left[ {2\zeta + \eta _{p} \frac{{r_{p} [(\lambda _{0} r_{p} )^{2} + 1] - 2\lambda _{0}^{2} r_{p}^{3} }}{{[(\lambda _{0} r_{p} )^{2} + 1]^{2} }} + \frac{1}{{1 + r_{m} }}\eta _{e} } \right] = 0 \hfill \\ \end{gathered}$$
(44)

By Eq. (44), it can be concluded that except for the structural parameters, the optimal vibration frequency also varies with the excitation and load resistance.

3.3 Optimal load

In addition, based on the analysis method in reference (Cammarano et al. 2014), the optimal load resistance giving the maximum power can be derived. Equation (41) is rearranged as

$$\overline{{z_{M}^{2} }} = \frac{{2\overline{P} }}{{\frac{{\lambda^{2} \eta_{p} r_{p} }}{{(\lambda r_{p} )^{2} + 1}} + \frac{{r_{m} \eta_{e} \lambda^{2} }}{{(1 + r_{m} )^{2} }}}}$$
(45)

Substituting Eq. (45) into Eq. (36), the result is

$$\begin{aligned} \frac{{2\overline{P} }}{{\frac{{\lambda^{2} \eta_{p} r_{p} }}{{(\lambda r_{p} )^{2} + 1}} + \frac{{r_{m} \eta_{e} \lambda^{2} }}{{(1 + r_{m} )^{2} }}}} &= 1/\left\{ \left[(1 - \lambda^{2} ) + \frac{{2\overline{P} }}{{\frac{{\lambda^{2} \eta_{p} r_{p} }}{{(\lambda r_{p} )^{2} + 1}} + \frac{{r_{m} \eta_{e} \lambda^{2} }}{{(1 + r_{m} )^{2} }}}}\frac{{3\varGamma_{nl} }}{4}\right.\right. \\ &\quad \left.+ \eta_{p} \frac{{(\lambda r_{p} )^{2} }}{{(\lambda r_{p} )^{2} + 1}}\right]^{2} \hfill \\ & \left.\quad+ \left[2\lambda \zeta + \eta_{p} \frac{{\lambda r_{p} }}{{(\lambda r_{p} )^{2} + 1}} + \frac{\lambda }{{1 + r_{m} }}\eta_{e} \right]^{2} \right\} \hfill \\ \end{aligned}$$
(46)

and simplified to

$$G(P,r_{p} ,r_{m} ) = 0$$
(47)

Applying the implicit function theory, it can be got that

$$\frac{\partial P}{{\partial r_{p} }} = - \frac{{\frac{\partial G}{{\partial r_{p} }}}}{{\frac{\partial G}{\partial P}}}$$
(48)
$$\frac{\partial P}{{\partial r_{m} }} = - \frac{{\frac{\partial G}{{\partial r_{m} }}}}{{\frac{\partial G}{\partial P}}}$$
(49)

The optimal load of PE and EM element can be derived from the solutions of \(\frac{\partial P}{{\partial r_{p} }} = 0\) and \(\frac{\partial P}{{\partial r_{m} }} = 0\).

4 Numerical results

According to analysis results shown in Eqs. (36)–(41), the displacement and electric performances of nonlinear hybrid energy harvester mainly depend on the nonlinear factor Гnl, the mechanical damping ratio ζm, the coupling coefficient ηp and ηe, the normalized load rp and rm, and vibration frequency λ. Therefore, in order to output the maximum power, it should be taken by structure optimization to get the optimal PE and EM coupling coefficient and nonlinear factor, or selecting the optimal PE and EM load and exciting at the optimal vibration frequency. And we will discuss the effects of above factors on performances of nonlinear hybrid energy harvester in the following parts. Besides, in the study, the coupling coefficients of PE and EM elements are determined, and the parameters of harvester are shown in Table 1.

Table 1 The parameters of harvester in the analysis
Full size table

4.1 Effect of nonlinear factor on performances

Based on Eqs. (36)–(41), one of key factors that decide the nonlinear vibration response and electrical performances of harvester is the nonlinear factor \(\varGamma_{nl}\). From analysis results in Eq. (36), if \(\varGamma_{nl} = 0\), the nonlinear harvester becomes linear hybrid energy harvester; moreover, only if \(\varGamma_{nl} < 0 ,\)the response of harvester expresses the characteristics of the soft spring. Therefore, the effects of nonlinear factor on vibration response and performances of hybrid PE and EM energy harvester are analyzed in this part, and the results are shown in Fig. 3.

Fig. 3
figure 3

Effect of nonlinear factors on performances of harvester in frequency domain: a The normalized amplitude; b The normalized total power; c The normalized PE voltage; d The normalized EM current

Full size image

According to numerical results in Fig. 3, the larger nonlinear factor, the bigger amplitude of energy harvester, and the stronger nonlinear response, which means the response curve of harvester bends to the left obviously; while the maximum PE voltage and EM current show the slight variation of increase and decrease respectively with the nonlinear factor enhancing, but the maximum of total power output of hybrid energy harvester is hardly affected by nonlinear factor. In addition, at \(\varGamma_{nl} = - 0.0193\), the response curve appears the jumping phenomenon, and when the nonlinear factor increases from −0.0036 to −0.0193, the lower energy orbit of harvester response almost keeps stable, while the higher energy orbit is mainly affected by nonlinear factor. Therefore, with the nonlinear factor enhancing, the response curve of harvester bending to left is much more obvious, which means that the frequency corresponding to the maximal amplitude and power lowers, so it is more beneficial for harvester to work at the environment of low vibration frequency. At this case, the power variation of the harvester with the vibration frequency is relatively slow near the maximum power, which shows the harvester has the much bigger bandwidth.

Furthermore, when Гnl = −0.0036, the response of nonlinear harvester is similar to the linear energy harvester; moreover, if nonlinear factor is close to zero, response of nonlinear hybrid energy harvester is the linear characteristics completely. However, when Гnl = −0.0193, the nonlinear response of the harvester becomes more obvious, and the optimal frequency is far lower and 3 dB bandwidth is bigger than that of the harvester at Гnl = −0.0036. Besides, when the normalized frequency is about 0.8, the response of harvester has three periodic solutions, which includes two stable solutions and one unsteady state solution. For the two stable solutions, one is relatively small and the other is relatively big. Therefore, in order to output larger power and decrease the optimal frequency, the nonlinear harvester should work at stable response of high energy orbit.

In addition, under the single excitation frequency, variations of the normalized amplitude, output power, PE voltage and EM current with nonlinear factor are shown in Fig. 4. When the excitation frequency λ is 0.7, 0.75, 0.8, 0.85, 0.9 respectively, output performances of nonlinear hybrid energy harvester are also compared.

Fig. 4
figure 4

Effects of nonlinear factors on performances of nonlinear hybrid energy harvester for different excitation: a Amplitude; b The total power; c PE voltage; d EM current. (λ is 0.7, 0.75, 0.8, 0.85, 0.9 respectively)

Full size image

By the analysis results shown in Fig. 4, there is an optimal nonlinear factor for nonlinear hybrid PE and EM energy harvester, where the normalized amplitude, output power, PE voltage and EM current all reach the maximum. Moreover, the optimal nonlinear factor is different for different vibration frequency, and the lower excitation frequency, the bigger optimal nonlinear factor is. When λ decreases from 0.9 to 0.8, the optimal nonlinear factor Гnl varies from −0.0136 to −0.0191. For λ = −0.0191, the amplitude and performances of harvester varying with nonlinear factor appear the jumping phenomenon. However, on low energy orbit, the amplitude and performances rise with nonlinear factor increasing, but on high energy orbit, performances decrease with nonlinear factor increasing.

Besides, when the normalized frequency λ varies from 0.7 to 0.9, the maximum of normalized amplitude increases from 4.8 to 5.9, while the maximal values of normalized power, PE voltage and EM current hardly vary, which means the harvester can output the large power in the frequency range from 0.7 to 0.9, but their nonlinear response extent is changed. Moreover, the influence of excitation frequency on steady value on high energy orbit is relatively small, but there is larger effect on low energy orbit, and the lower excitation frequency, the smaller normalized power and PE voltage and EM current are.

Thus, the nonlinear factor can largely affect the vibration response and electrical performances of nonlinear hybrid PE and EM energy harvester. As the nonlinear factor increases, the resonant frequency of harvester lowers and the bandwidth widens; meanwhile, there is an optimal nonlinear factor for nonlinear hybrid energy harvester to output the maximum power.

4.2 Effect of load resistance on performances of harvester

By Eqs. (36)–(41), when the structure of harvester and nonlinear factor are determined, the normalized amplitude, output power, PE voltage and EM current are mainly affected by the normalized load resistance of PE and EM elements. Therefore, in this part, the effect of load resistance on harvester performances are studied in order to get the optimal PE and EM loads, where the harvester can output the maximum power. In the analysis, the nonlinear factor Гnl is equal to −0.0146. When the normalized load of EM element increases from 1 to 7 and that of PE element increases from 0.5 to 5, the amplitude and performances of nonlinear energy harvester at different vibration frequencies are shown in Figs. 5, 6, 7, and 8.

Fig. 5
figure 5

Effects of EM load on amplitude: a Amplitude at different frequency; b The maximum amplitude at different EM load

Full size image
Fig. 6
figure 6

Effects of PE load on amplitude: a Amplitude at different frequency; b The maximum amplitude at different PE load

Full size image
Fig. 7
figure 7

Effects of EM load on EM power: a EM power at different frequency; b The maximum EM current and power at different EM load

Full size image
Fig. 8
figure 8

Effects of PE load on PE power: a PE power at different frequency; b The maximum PE voltage and power at different PE load

Full size image

From analysis results in Fig. 5, as EM load resistance increases, the amplitude at the resonant frequency rises accordingly, and the vibration response curve bending to left is more obvious, so the jumping frequency decreases accordingly, which shows the resonant frequency lower. When rm varies from 1 to 6, the normalized maximum amplitude rises from 2.6 to 6.13, and the jumping frequency decreases from 0.96 to 0.78. From the Fig. 6, the maximal amplitude and nonlinear response degree of harvester all decrease firstly and then increase with PE load increasing, and the amplitude reaches the minimum at rp = 1.2, where the nonlinear response extent is the weakest. However, the inverse regularity happens to the resonant frequency giving the maximal amplitude.

Because the power, voltage and current of nonlinear harvester vary with the amplitude, the load variation would lead to the different electrical performances for energy harvesting elements. Based on the results in Figs. 8 and 9, with PE and EM loads hiking respectively, output power of PE and EM elements rise firstly and fall later, and reach the maximum at the optimal load of PE and EM elements respectively, which is consistent with the experimental results tested by Erturk and Inman (Erturk and Inman 2011a). In this case, the normalized optimal loads of PE and EM elements are equal to 1.2 and 4 respectively. Besides, PE voltage increases with PE load increasing and reaches the maximum at the open circuit; while EM current decreases with EM load increasing and reaches the maximum at the short circuit.

Fig. 9
figure 9

Effects of loads on optimal frequency: a EM load; b PE load

Full size image

Besides, when the load resistance rises up to a certain value, the vibration and electrical output response of harvester will appear the jumping phenomenon, and there are two steady values and one unsteady value. In this case, the response of energy harvester bends to left obviously, and the response of energy harvester can jump from high energy orbit to low energy orbit at jumping frequency. Thus, in order to output the maximum power, the designed nonlinear energy harvester should operate on high energy orbit as much as possible.

According to above analysis, the load resistance of nonlinear hybrid PE and EM energy harvester not only affects the maximum power and the resonant frequency but also changes the nonlinear response degree of energy harvester. So it needs to further study the effect of load resistance at the resonant frequency. From the results in Fig. 9, the resonant frequency corresponding to the maximum power increases firstly and then falls with PE load increasing, while it rises with EM load decreasing, which is due to that the effect of PE and EM loads would heighten the equivalent stiffness and damping of harvester.

5 Experimental study

5.1 Experimental setup

In order to test the performances of nonlinear hybrid PE and EM energy harvester, the nonlinear hybrid energy harvester is fabricated, and experimental installation is shown in Fig. 10. The whole setup of the device is mounted on the vibrating shaker which is connected to a signal generator through a power amplifier. The signal generator is used to provide the excitation signals. Lead wires from the piezoelectric cantilever beam and coil are connected across the variable resistor to maximize the power output. In addition, an accelerometer is used to record vibration acceleration, and the dynamic signal analyzer is used to record output voltages of piezoelectric and electromagnetic energy harvesting element. In the experiment, to alleviate magnetic field interference from the shaker, the harvester is distanced away from the shaker base. Besides, material properties and structural parameters of harvester are illustrated in Table 2.

Fig. 10
figure 10

Experimental setup

Full size image
Table 2 Structural parameters and material properties
Full size table

5.2 Experimental results and discussion

By experimental test, when the acceleration is 0.2 g, the optimal loads of PE and EM elements of linear energy harvester (without magnetic force) are 123 kΩ and 15.5 Ω respectively; while optimal PE and EM loads of nonlinear energy harvester are 140 kΩ and 17.3 Ω respectively, which are shown in the following test. Then, at the optimal load, output power of nonlinear hybrid energy harvester and its corresponding linear energy harvester are illustrated in Fig. 11. In the test, the above and below coils are connected with the same load.

Fig. 11
figure 11

Power output of linear and nonlinear hybrid energy harvester

Full size image

From the Fig. 11, experimental results are basically in agreement with the theoretical model. With the acceleration of 0.2 g, the output power of nonlinear energy harvester is 0.44 mW, while the power of linear energy harvester is 0.4 mW. Meanwhile, compared with the linear harvester, the resonant frequency of nonlinear energy harvester lower, and from the Fig. 11, the resonant frequency of linear and nonlinear energy harvester are 119 Hz and 113.5 Hz respectively. With the effect of nonlinear magnetic force, the equivalent stiffness of harvester is reduced, so the resonant frequency lowers and the amplitude of mass magnet rises, which causes the bigger stress in PZT layer and greater flux through the coils. Therefore, the power output of nonlinear energy harvester is bigger than that of linear energy harvester. Therefore, it can be concluded that the nonlinear hybrid PE and EM energy harvester not only can increase the power output, but also lower the resonant frequency to make the harvester be suitable for the practical vibration environment. In addition, the resonant frequency can be further decreased by optimization design of the structure.

In the paper, we take the figure of merit (FOM) in the reference (Sebald et al. 2011a, b) to compare the performances of nonlinear and linear energy harvester further, and the FOM is expressed in Eq. (50), which comprehensively considers the output power, 3 dB bandwidth, center frequency and excitation acceleration.

$$F_{OM} = \frac{{P_{\hbox{max} } }}{{A_{0}^{2} }}\frac{{\omega_{2} - \omega_{1} }}{{\omega_{0} }}$$
(50)

where Pmax is the maximum power; ω2 and ω1 are half-power cutoff frequencies, and ω0 is the frequency giving the maximum power Pmax; A0 refers to excitation acceleration. Furthermore, by the experimental results, 3 dB bandwidths of linear and nonlinear hybrid energy harvester are 2.6 and 3.8 Hz respectively. Based on Eq. (50), FOM ratio of nonlinear and linear energy harvester is 1.69, which means the performance of nonlinear energy harvester is 1.69 times that of the linear harvester. Therefore, compared with linear energy harvester, nonlinear energy harvester should be adopted to harvest more vibration energy within relatively bigger bandwidth.

Moreover, based on Eqs. (33)–(35) and (44), the excitation acceleration can affect the maximum power of nonlinear energy harvester and its corresponding frequency. Thus, by experiment, the effect of acceleration on harvester performances is studied. With the same load, when the acceleration is 0.3, 0.45 and 0.6 g respectively, variations of total output power of hybrid energy harvester with the frequency are illustrated in Fig. 12, among which PE load is 212 kΩ and EM load is 22.5 Ω.

Fig. 12
figure 12

Output power of nonlinear harvester in different accelerations

Full size image

As the magnetic force rises with the acceleration hiking, the equivalent stiffness of harvester is further reduced, which causes the lower resonant frequency and the larger amplitude. From the test results in Fig. 12, when the acceleration is 0.3, 0.45 and 0.6 g, the maximal output power is 0.52, 1.76 and 3.54 mW respectively; meanwhile, when the acceleration increases from 0.3 to 0.6 g, the resonant frequency decreases from 113.2 to 110.5 Hz. Therefore, it can be concluded that the maximum power and bandwidth of nonlinear harvester increase with the acceleration rising, and the nonlinear effect strengthens accordingly; moreover, the resonant frequency lowers, which is different with the linear harvester.

As the resonant frequency decreases with the acceleration increasing, the optimal load resistance would be varied. Thus, for different accelerations, variations of PE voltage and power with the PE loads are tested at the resonant frequency, and the results are shown in Fig. 13, where EM element is connected with the optimal load.

Fig. 13
figure 13

PE performances at different accelerations: a the voltage; b the power

Full size image

From the Fig. 13, when the acceleration are 0.2 and 0.45 g, the optimal PE load resistance giving the maximum power are 140, 190 kΩ respectively, and the corresponding power are 0.085, 0.5 mW. Therefore, PE optimal load rises with the acceleration increasing as the resonant frequency falls; meanwhile, the smaller acceleration is, the much easier of PE voltage reaches the maximum.

Similarly, EM voltage and power are tested at the different load resistances when the PE load is optimal. When the accelerations are 0.2 and 0.45 g respectively, the results are shown in Fig. 14. In the experiment, the voltages are tested at the resonant frequency of the harvester, and the loads of above and below coils are the same. From the results in Fig. 14, the conclusions of variation of EM voltage and power with the acceleration are similar with PE element, and EM optimal load rises with the acceleration rising. When the acceleration is 0.2 and 0.45 g, the optimal EM load is 17.5 and 21 Ω respectively, and the maximal EM power is 0.14 and 1.19 mW.

Fig. 14
figure 14

EM performances at different accelerations: a the voltage; b the power

Full size image

6 Conclusions

Aimed at designed nonlinear hybrid PE and EM energy harvester, the governing electromechanical equations are established, and by harmonic balance method, expressions of amplitude, output power, voltage and current of harvester at harmonic excitation are obtained. By the defined dimensionless parameters, the normalized forms of amplitude and electrical performances of hybrid PE and EM energy harvester are derived, from which it can be concluded that performances of harvester are mainly affected by nonlinear factor Гnl, excitation frequency λ, load resistance of energy harvesting elements (rp, rm) and coupling coefficients (ηe, ηp).

By numerical calculation and experimental test, effects of nonlinear factor, the normalized frequency, normalized PE and EM load and external acceleration on output performances of harvester are analyzed, and we obtain that with nonlinear factor enhancing, the resonant frequency and power lowers and the bandwidth widens, so it is more beneficial for harvester to work at the environment of low vibration frequency; meanwhile, there is an optimal nonlinear factor for nonlinear hybrid energy harvester to output the maximal power. Besides, the nonlinear hybrid energy harvester should connect with the optimal PE and EM load, where the harvester outputs the maximum power, and the effects of load resistance on resonant frequency should be considered in the harvester design. Meanwhile, compared with linear energy harvester without magnetic force, designed nonlinear hybrid energy harvester not only can decrease the resonant frequency and increase output power, but also widen the bandwidth. However, it should be noted that the optimal resistance varies with the acceleration largely, which is different from the linear harvester. Therefore, the nonlinear magnetic force used in structure design is effective for hybrid piezoelectric and electromagnetic energy harvester.