Large-amplitude vibrations of functionally graded shallow arches subjected to cooling shock

Abstract

In this paper, the nonlinear large-amplitude vibrations of shallow arch structures made of functionally graded materials (FGMs) under cooling shock have been investigated. It is considered that the FG shallow arch is made of low carbon steel $\left(\mathrm{AISI }1020\right)$ and stainless steel $(\mathrm{SUS }304)$, whose material properties change in the thickness direction. Using the kinematic assumptions that are modeled based on the first-order shear deformation theory (FSDT) and the von Kármán’s geometrical nonlinearity; along with the aid of Hamilton’s principle, the shallow arch motion equations are obtained. The material properties vary in the direction of arch’s thickness due to the temperature changes and material distribution. Based on the Voigt rule of mixture and power law distribution, the dependence of material properties on temperature and material distribution is defined. Assuming uncoupled theory of thermoelasticity, first, the one-dimensional heat conduction equation is solved along the thickness of the arch in order to obtain the temperature distribution. Afterward, the equations of motion are solved. For the numerical solution of the heat conduction equation and the nonlinear equations of motion, the iterative hybrid method of generalized differential quadrature and the Newmark time integration scheme has been used in an iterative Newton–Raphson loop. After validating the present formulation, a parametric scrutiny is conducted regarding the influence of various parameters, namely, thermal load rapidity time, FG-index, dimensional parameters on the mid-plane non-dimensional lateral deflection of the arch as well as the changes in stress and material properties.

1 Introduction

Functionally graded materials (FGMs) are a novel class of composites with several applications in various fields. Many studies have been done on the dynamic behavior of structures made of FGMs under rapid heating shock considering various types of geometries. Recently, the vibrational behavior of circular FGM plates under cooling shock has been investigated by Babaee and Jelovica [1]. They conducted experiments on the properties of materials at low temperature and presented a model regarding how the properties of material change when exposed to cooling shock. Many problems occur in reality where structures experience cooling shocks, and experiments show that significant thermal stresses are created in structures subjected to cooling load. Consequently, the vibrational behavior analysis of these materials requires further investigations.

Before Boley's study [2], the temperature profile obtained from the heat conduction equation was integrated into the governing equilibrium equations for a solid structure under thermal shock. The resulting displacements determined by this method are recognized as the quasi-static response of the structure. Nevertheless, Boley [2] demonstrated that, even though the quasi-static analysis may be suitable in numerous cases, it can lead to misleading conclusions, particularly for slender beams, plates, and shells. As highlighted, the introduction of the temperature profile into the equations of motion can give rise to the occurrence of thermally-induced vibrations. These vibrations manifest as oscillations around the quasi-static response, in accordance with earlier observations made by researchers.

In [3], the vibrations of multilayer piezoelectric plates with embedded or attached layers were investigated. Sheng and Wang [4], by applying thermal and mechanical loads on FGM cylindrical shell containing flowing fluid, studied structural vibrations in an elastic environment. Analysis of flexural vibrations of functionally inhomogeneous materials in the geometries of rectangular plates and beams under cyclic loads of external force and temperature change has been carried out in [5]. Ansari et al. [6] investigated the thermal buckling of single-walled carbon nanotubes in an elastic medium with the assumption of nonlocal Timoshenko beam. Also in [7], single-walled carbon nanotubes with the assumption of nano-scale Euler–Bernoulli beam under a time-varying temperature profile in a viscoelastic matrix have been investigated in terms of dynamic stability. Size-dependent vibrations of FGM curved micro-beams have been studied based on modified strain gradient elasticity theory in [8]. Employing nonlocal elasticity theory of Eringen and finite element method, the free vibration of carbon and silica carbide nanotubes resting on an Winkler-Pasternak elastic foundation is studied in [9]. Asadi et al. [10] investigated beams made with laminated hybrid composite reinforced with shape memory alloy fiber through an analytical approach in terms of vibration and thermal post-buckling. The study of nonlinear vibrations of a magneto-elastic beam under magnetic field and thermal load has been carried out by G. Wu in [11]. Also, the vibrations of FGM nanobeams have been investigated under sinusoidal pulse heating in [12]. Zarezadeh et al. [13] studied the instability of electrostatically excited functionally graded (FG) cantilever and clamped microswitches employing the Galerkin method. Based on the classical plate theory, the vibrations of axisymmetric FGM circular plates under uniform in-plane force have been investigated and the numerical results are presented in [14]. Vibrational investigation of rectangular FGM plates under rapid heating has been done by Alipour et al. [15]. In [16], by applying nonuniform heating on conical plates made of laminated composites and using the finite element method, static numerical response and normal stress pattern have been developed. In [17], considering a modified nonlocal continuum model to show the effects of surface energy, the vibration of double-layer graphene nanosheets under thermal and mechanical loads in elastic medium has been investigated. Chu et al. [18] have analyzed the thermally induced dynamic behavior of FGM flexoelectric nanobeams, using the simplified non-local strain gradient elasticity. In [19], nonlinear isogeometric transient analysis has been performed on porous FGM plates under hygro-thermo-mechanical loads. Babaei has investigated the large amplitude vibrations of functionally graded carbon nanotubes reinforced composite pipes under thermomechanical loading [20]. In [21], by presenting a new tubular beam model, the vibrations of FGM tubes containing fluid flow in elastic medium has been investigated. The examination of the vibrations of materials with bidirectional functionally graded distribution has also been done for porous beams under hygro-thermal loading in [22]. FGM porous shallow arches under hygro-thermal loading were investigated in terms of dynamic buckling in [23]. In addition, the nonlinear vibration of FGM porous circular plates under hygro-thermal loading is investigated in [24]. Investigation of superharmonic and subharmonic response of beams under moving mass loading with viscoelastic foundation according to theory based on finite strain has been done in [25]. In [26], nonlinear thermally induced vibrations and dynamic snap-through of FGM materials for deep spherical shell geometry is studied. In [27], the vibrational behavior of a cracked post-buckled FGM plate subjected to uniaxial compressive load is investigated. Ansari et al. [28] analyzed the nonlinear large amplitude vibrations by applying the cooling shock to the FGM higher-order beam. The dynamic response of FGM rectangular plates under thermal loading is investigated in [29]. In [30], the control and suppression of thermal vibrations using magnetostrictive layers for plates and homogeneous isotropic beams is studied. The effect of heat flux characteristics on thermally induced vibrations is investigated by experimental and laboratory results for a thin-walled beam in [31]. In [32], a research on free and forced vibrations of multi-layered curved beams reinforced with graphene platelets was conducted. FGM shallow spherical shells with temperature-dependent properties in [33] were investigated regarding its thermally induced vibrations. Zamanzadeh et al. [34] explored the thermal vibrations of a cantilever micro-beam composed of FG material when exposed to a laser beam in motion, utilizing simulating a dynamic system equivalent to the third-order to understand the system's response. In [35], the stability of a micro-beam made of FGM was analyzed utilizing the modified couple stress theory (MCST) exposed to nonlinear electrostatic pressure, and the effects of thermal variations, including convection and radiation were investigated. Another study has been focused on investigating the nonlinear vibration characteristics of a cantilever micro-beam made of FGM subjected to a bias DC voltage and influenced by a sinusoidal heat source [36].

Refrigerant liquid leakage on the structures is one of the reasons of cooling shock. Also, the transfer and storage of liquid natural gas (LNG), which is retained at small temperatures ($-163\mathrm{^\circ{\rm C} }$), and its proximity to pipes and tanks can be another issue where cooling shock occurs [26, 27]. In the present research, the large-amplitude thermally-induced vibrations of an FGM shallow arch under rapid cooling have been investigated. Thermo-mechanical properties of the material depend on the temperature and the coordinates in the thickness direction. By solving one-dimensional heat conduction equation in the direction of thickness using the GDQ and Newmark methods, the temperature profile and hence the force caused by thermal shock that affect the arch are obtained. Also, novel thermal boundary conditions which are closer to real-life engineering applications are defined. The thermal forces and moments are applied in the motion equations that are obtained based on a first-order shear deformable shallow arch model using Hamilton’s principle and assuming von Kármán’s geometrical nonlinear relations. The equations of motion are also discretized by the GDQ method and solved in the Newton–Raphson loop using the Newmark method. With a comprehensive parametric study conducted on the dimensionless lateral deflection of the middle plane of the shallow arch, the effects of parameters such as aspect ratio, power law index, thermal load rapidity time, and boundary conditions, on the vibrational behavior of the shallow arch have been analyzed. Also, the stress distribution in the structure is studied.

2 Governing equations

2.1 Functionally graded arch model

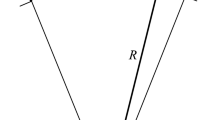
An FGM shallow arch with radius $R$, initial angle ${\theta }_{0}$, and with cross section $b\times h$ is considered. As illustrated in Fig. 1, a polar coordinate system is defined in which the $z$ axis is in the thickness direction and the $\theta$ axis is aligned with the circumferential direction.

Fig. 1

Schematic and geometry of shallow arch and coordinate system

The properties of materials depend on both the type of material and its temperature. In thermal shock problems of structures made of FG materials, there are both temperature and material distribution along the thickness. Accordingly, to define the thermomechanical properties of FGMs such as thermal expansion coefficient $(\alpha )$, specific heat capacity $({C}_{v})$, Young’s modulus $(E)$, density $(\rho )$, Poisson’s ratio $(\vartheta )$, and thermal conductivity $(k)$, the Voigt rule of mixture is employed. A non-homogeneous thermo-mechanical property of the functionally graded arch $q$ is given as [39]

$$q\left( {Z,T} \right) = P_{A} \left( T \right)V_{A} \left( Z \right) + P_{S} \left( T \right)V_{S} \left( Z \right)$$

(1)

where subscripts $A$ and $S$ defines ${\text{AISI 1020}}$ and ${\text{SUS 304}}$, respectively.

Temperature dependence of material properties in the temperature range 50–300 K is modeled using the results obtained from the experiments by Babaee and Jelovica [1]

$${\text{for d}}L/L, E, \vartheta , \rho : P\left( T \right) = a + bT + cT^{2} + dT^{3} + eT^{4}\,{\text{for}}\;K\;{\text{and}}\;C_{v} :\log _{{10}} P\left( T \right) = a + b\left( {\log _{{10}} T} \right) + c\left( {\log _{{10}} T} \right)^{2} + d\left( {\log _{{10}} T} \right)^{3} + e\left( {\log _{{10}} T} \right)^{4} + f\left( {\log _{{10}} T} \right)^{5} + g\left( {\log _{{10}} T} \right)^{6} + h\left( {\log _{{10}} T} \right)^{7} + i\left( {\log _{{10}} T} \right)^{8}$$

(2)

in which $T$ is the absolute temperature, and $a,{ }b, \ldots ,i$ are given in Tables 1 and 2, which depend on the temperature.

Table 1 Constituents temperature dependent factors for $k$ and $C_{v}$ between $50$ to $300 K$ [1]

Table 2 Constituents temperature-dependent factors for $E , v , \rho$ and $dL/L$ between 50 and 300 $K$ [1]

According to the power law, ${\text{AISI 1020}}$ volume fraction $V_{A}$ and ${\text{SUS 304}}$ volume fraction $V_{S}$ are given as follows [39]

$$V_{S} = \left( {\frac{1}{2} + \frac{Z}{h}} \right)^{\xi }$$

(3)

$$V_{A} = 1 - \left( {\frac{1}{2} + \frac{Z}{h}} \right)^{\xi }$$

where $\xi$ is the power-law index through the $Z$ axis.

2.2 Kinematic, kinetic, and constitutive relations

According to the first-order shear deformation theory, the displacement field for the shallow arch structure can be written as [40]

$$u_{\theta } \left( {\theta ,z,t} \right) = v\left( {\theta ,t} \right) + z\varphi \left( {\theta ,t} \right)u_{z} \left( {\theta ,z,t} \right) = w\left( {\theta ,t} \right)$$

(4)

where $v$ and $w$ denote the displacements of the middle plane points along the $\theta$ and $z$ axes, sequentially, and $\varphi$ represents the cross-sectional rotation.

By taking the von Kármán’s type of geometrical nonlinearity, the elements of the strain field for a shallow arch can be written as

$$\varepsilon_{\theta \theta } = \frac{1}{R}\left( {v_{,\theta } + z\varphi_{,\theta } - w} \right) + \frac{1}{{2R^{2} }}w_{,\theta }^{2}$$

(5)

$$\gamma_{\theta z} = \frac{1}{R} w_{,\theta } + \varphi$$

The constitutive equations based on the Hook’s law for a shallow arch, relate the stress components to the strain components as

$$\left\{ {\begin{array}{*{20}c} {\sigma_{\theta \theta } } \\ {\tau_{\theta z} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & 0 \\ 0 & {Q_{55} } \\ \end{array} } \right]\left( {\left\{ {\begin{array}{*{20}c} {\varepsilon_{\theta \theta } } \\ {\gamma_{\theta z} } \\ \end{array} } \right\} - \Delta T\left\{ {\begin{array}{*{20}c} \alpha \\ 0 \\ \end{array} } \right\}} \right)$$

(6)

where $Q_{11}$ and $Q_{55}$ are as follows

$$Q_{11} = E\left( {z,t} \right), Q_{55} = \frac{{E\left( {z,t} \right)}}{{2\left( {1 + \vartheta \left( {z,t} \right)} \right)}}$$

(7)

3 Temperature profile

In this section, the temporal evolution of temperature profile is achieved by the one-dimensional heat conduction equation in the thickness direction as [39]

$$\left( {k\left( {z,T} \right)T_{,z} } \right)_{,z} = \rho \left( {z,T} \right)C_{v} \left( {z,T} \right)\dot{T}$$

(8)

It is considered that the structure is rested at the reference temperature before applying the load, hence the initial condition for solving the above heat conduction differential equation is as follows

$$T\left( {z,0} \right) = T_{0}$$

(9)

In real problems, the application of thermal shock is accompanied by some delay. A new type of boundary condition has been used to consider the delay in the application of thermal shock and the temperature difference in this problem. This type of boundary condition introduces a parameter called thermal load rapidity time $({t}_{R})$, which shows the duration in which the thermal shock is applied until the desired temperature difference is reached.

In the following, two different loading cases regarding thermal boundary conditions are examined. In both cases, the temperature of the lower surface of the arch is constant and only the upper surface’s loading is different. In loading case 1, the temperature change in the upper surface is done in a time-dependent process to reach the desired temperature difference and stabilize afterward; but in loading case 2, first the loading is applied as in the case 1, and after some time the loading is withdrawn and the created temperature difference in the upper side diminishes and finally reaches the initial temperature. How the temperature changes in this type of new thermal boundary conditions and the effect of ${t}_{R}$ parameter on applying the thermal load can be seen in the diagram of Fig. 2.

Fig. 2

Temporal changes in temperature at the upper surface of the arch for two loading cases

The mathematical form of this type of thermal boundary conditions can be written as follows:

Case 1

$$T\left( { + 0.5h,t} \right) = ~\left\{ {\begin{array}{llll} {\left( {\frac{{T_{S} - T_{0} }}{{t_{R} }}} \right)t + T_{0} ~~} & \quad {t < t_{R} } \\ {T_{S} ~~~~} & \quad {t \ge t_{R} } \\ \end{array} } \right.\;,\;~T\left( { - 0.5h,t} \right) = T_{A}$$

(10)

Case 2

$$T\left(+0.5h,t\right)=\left\{\begin{array}{llll}\left(\frac{{T}_{S}-{T}_{0}}{{t}_{R}^{L}}\right)t+{T}_{0} , t<{t}_{R}^{L}\\ {T}_{S} , {t}_{R}^{L}\le t<\left(\frac{{t}_{f}}{2}\right)\\ \quad \left(\frac{{T}_{0}-{T}_{S}}{{t}_{R}^{unL}}\right)t+{T}_{S}+\left(\frac{{T}_{S}-{T}_{0}}{{t}_{R}^{unL}}\right)\left(\frac{{t}_{f}}{2}\right) , \left(\frac{{t}_{f}}{2}\right)\le t<\left(\frac{{t}_{f}}{2}\right)+{t}_{R}^{unL}\\ {T}_{0} , t\ge \left(\frac{{t}_{f}}{2}\right)+{t}_{R}^{unL}\end{array}\right.$$

$$T\left( { - 0.5h,t} \right) = T_{A}$$

where ${T}_{S}$ and ${T}_{0}$ are the $SUS 304$ rich surface and initial temperatures, respectively. ${t}_{R}^{L}$ and ${t}_{R}^{unL}$ are, respectively, the thermal load and unload rapidity times, and ${t}_{f}$ is the final time depicted in Fig. 2.

4 Motion equations

The equations of motion of the shallow arch under thermal loading considering the uncoupled thermo-elasticity theory can be derived by using Hamilton’s principle [40]

$$\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \delta {\Pi } {\text{d}}t = \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \left( {\delta T - \delta U^{{{\text{int}}}} + \delta w^{{{\text{ext}}}} } \right){\text{d}}t = 0$$

(11)

where the total virtual strain energy $\delta U^{{{\text{int}}}}$ can be written as

$$\delta U^{{{\text{int}}}} = \mathop \int \limits_{\forall }^{ } \left( {\sigma_{\theta \theta } \delta \varepsilon_{\theta \theta } + \tau_{\theta z} \delta \gamma_{\theta z} } \right){\text{d}}\forall$$

(12)

$$= \mathop \int \limits_{0}^{{\theta_{0} }} \left( {N_{\theta \theta } \left[ {\frac{1}{R}\delta v_{,\theta } - \delta w + \delta \left( {\frac{1}{{2R^{2} }}w_{,\theta }^{2} } \right)} \right] + M_{\theta \theta } \left[ {\delta \varphi_{,\theta } } \right] + Q_{\theta z} \left[ {\delta \left( {\frac{1}{R}w_{,\theta } + \varphi } \right)} \right]} \right){\text{d}}\theta$$

employing the FSDT, the stress resultants are related to the stress components considering the following equations

$$\left( {N_{\theta \theta } ,M_{\theta \theta } ,Q_{\theta z} } \right) = \mathop \int \limits_{ - 0.5h}^{ + 0.5h} \left( {\sigma_{\theta \theta } ,z\sigma_{\theta \theta } ,\tau_{\theta z} } \right){\text{d}}z$$

(13)

By substituting Eq. (4) in Eq. (6) and with the aid of Eq. (13) the stress resultants in terms of displacement components of the mid-plane are obtained as

$$\left\{ {\begin{array}{*{20}c} {N_{\theta \theta } } \\ {M_{\theta \theta } } \\ {Q_{\theta z} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {B_{11} } & 0 \\ {B_{11} } & {D_{11} } & 0 \\ 0 & 0 & {A_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\frac{1}{R}\left( {v_{,\theta } - w} \right) + \frac{1}{{2R^{2} }}w_{,\theta }^{2} } \\ {\frac{1}{R}\varphi_{,\theta } } \\ {\frac{1}{R}w_{,\theta } + \varphi } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {N^{T} } \\ {M^{T} } \\ 0 \\ \end{array} } \right\}$$

(14)

where

$$\left( {A_{11} ,B_{11} ,D_{11} } \right) = \mathop \int \limits_{ - 0.5h}^{ + 0.5h} \left( {1,z ,z^{2} } \right)Q_{11} {\text{d}}z$$

(15)

$$\left( {A_{55} } \right) = \mathop \int \limits_{ - 0.5h}^{ + 0.5h} Q_{55} {\text{d}}z$$

The virtual work of external applied loads $\delta w^{{{\text{ext}}}}$ is absent in this problem, and the virtual kinetic energy $\delta T$ is obtained as follows:

$$\delta T = R\mathop \int \limits_{0}^{{\theta_{0} }} \mathop \int \limits_{ - 0.5h}^{0.5h} \rho \left( z \right)\left( {\dot{u}_{\theta } \delta \dot{u}_{\theta } + \dot{u}_{z} \delta \dot{u}_{z} } \right) {\text{d}}z{\text{d}}\theta = - R\mathop \int \limits_{0}^{{\theta_{0} }} \left\{ {\left( {I_{0} \ddot{v} + I_{1} \ddot{\varphi }} \right)\delta v + \left( {I_{0} \ddot{w}} \right)\delta w + \left( {I_{1} \ddot{v} + I_{2} \ddot{\varphi }} \right)\delta \varphi } \right\}{\text{d}}\theta$$

(16)

where

$$\left( {I_{0} , I_{1} , I_{2} } \right) = \mathop \int \limits_{ - 0.5h}^{ + 0.5h} \rho \left( z \right)\left( {1, z, z^{2} } \right) {\text{d}}z$$

(17)

By substituting Eq. (12) and Eq. (16) in Eq. (11) the equations of motion for shallow arches are obtained as follows: [40]

$$\delta v : \frac{1}{R}\frac{{\partial N_{\theta \theta } }}{\partial \theta } = I_{0} \ddot{v} + I_{1} \ddot{\varphi }$$

(18)

$$\delta w : \frac{1}{{R^{2} }}\frac{\partial }{\partial \theta }\left( {N_{\theta \theta } w_{,\theta } } \right) + \frac{1}{R}N_{\theta \theta } + \frac{1}{R}\frac{{\partial Q_{\theta z} }}{\partial \theta } = I_{0} \ddot{W}$$

$$\delta \varphi : \frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } - Q_{\theta z} = I_{1} \ddot{v} + I_{2} \ddot{\varphi }$$

For the simply support at the edges of arch, the boundary conditions can be given as

$$v = w = M_{\theta \theta } = 0$$

(19)

5 Solution methodology

5.1 Generalized differential quadrature method

One of the numerical solution methodologies of differential equations is the GDQ method. This method, by approximating the derivatives using a higher-order polynomial, has the ability to be directly applied to differential equations without changing them. The GDQ method has a very high convergence speed using limited number of grid points. The derivative of order $m$ for an arbitrary function $f$ at ${x}_{i}$ which is a random nodal point is given as a weighted sum of functional values at all nodal points as [41]

$${f}_{,x}^{\left(m\right)}\left({x}_{i}\right)=\sum_{j=1}^{{N}_{x}}{w}_{ij}^{m} {f}_{j}$$

(20)

where ${w}_{ij}^{m}$ are the weighting coefficients for the $m$-th order derivation with respect to the $x$ direction, and

$$w_{{ij}}^{m} = \left\{ {\begin{array}{*{20}l} {if\;m = 1\left\{ {\begin{array}{*{20}l} {\frac{{M(x_{i} )}}{{\left( {x_{i} - x_{j} } \right)M(x_{j} )}}when\; \quad i \ne j} \hfill \\ { - \sum\limits_{{k = 1,k \ne i}}^{{N_{x} }} {w_{{ik}}^{{(1)}} } when\; \quad i = j} \hfill \\ \end{array} } \right.} \hfill \\ {if\;m = 2, \ldots ,N\left\{ {\begin{array}{*{20}l} {m\left( {w_{{ij}}^{{(1)}} w_{{ii}}^{{\left( {m - 1} \right)}} - \frac{{w_{{ij}}^{{\left( {m - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right)when\; \quad i \ne j} \hfill \\ { - \sum\limits_{{k = 1,k \ne i}}^{{N_{x} }} {w_{{ik}} } when\; \quad i = j} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(21)

also, $M\left( {x_{i} } \right)$ is calculated by

$$M\left( {x_{i} } \right) = \mathop \prod \limits_{k = 1,k \ne i}^{{N_{x} }} \left( {x_{i} - x_{k} } \right)$$

(22)

5.2 Discretization of heat transfer equation

By discretizing Eq. (8) using the GDQ methodology as discussed, the Fourier-type heat conduction differential equation may be written as

$${\mathbf{K}}_{,z} {\mathbf{T}}_{,z} + {\mathbf{KT}}_{,zz} = {\mathbf{\rho C}}_{{\mathbf{v}}} {\dot{\mathbf{T}}}$$

(23)

$${\mathbf{D}}_{z}^{\left( 1 \right)} {\mathbf{KD}}_{z}^{\left( 1 \right)} {\mathbf{T}} + {\mathbf{KD}}_{z}^{\left( 2 \right)} {\mathbf{T}} = {\mathbf{\rho C}}_{{\mathbf{v}}} {\dot{\mathbf{T}}}$$

$$\left( {diag\left( {{\mathbf{D}}_{z}^{\left( 1 \right)} {\mathbf{K}}} \right){\mathbf{D}}_{z}^{\left( 1 \right)} + {\mathbf{KD}}_{z}^{\left( 2 \right)} } \right){\mathbf{T}} - {\mathbf{\rho C}}_{{\mathbf{v}}} {\dot{\mathbf{T}}} = 0$$

which takes the following form

$${\mathbf{M}}_{{\mathbf{T}}} \ddot{{\rm T}} + {\mathbf{C}}_{{\mathbf{T}}} \dot{{\rm T}} + {\mathbf{K}}_{{\mathbf{T}}} {\mathbf{T}} = {\mathbf{F}}_{{\mathbf{T}}}$$

(24)

where

$${\mathbf{K}}_{{\mathbf{T}}} = \left( {{\text{diag}}\left( {{\mathbf{D}}_{z}^{\left( 1 \right)} {\mathbf{K}}} \right){\mathbf{D}}_{z}^{\left( 1 \right)} + {\mathbf{KD}}_{z}^{\left( 2 \right)} } \right)$$

(25)

$${\mathbf{C}}_{{\mathbf{T}}} = {\text{diag}}\left( {{{\varvec{\uprho}}}.{\mathbf{C}}_{{\mathbf{v}}} } \right)$$

(26)

$${\mathbf{M}}_{{\mathbf{T}}} = 0_{{N_{z} \times N_{z} }}$$

(27)

$${\mathbf{F}}_{{\mathbf{T}}} = 0_{{N_{z} \times 1}}$$

(28)

where $N_{z}$ is the number of sample points through the thickness. The force vector ${\mathbf{F}}_{{\mathbf{T}}}$ is updated after implement the thermal boundary conditions and have nonzero components.

In Eq. (24), after approximating spatial derivatives using the GDQ method, time derivatives have still remained in the equation. To solve Eq. (24), Newmark-beta time integration method is used to approximate time derivative in this work. After applying Newmark, Eq. (24) becomes

$${\mathbf{AT}}_{t + \Delta t} = {\mathbf{B}}$$

(29)

where ${\mathbf{T}}_{t + \Delta t}$ is the nodal unknown temperature vector in the subsequent time step, also, ${\mathbf{A}}$ and ${\mathbf{B}}$ are given as [42]

$${\mathbf{A}} = \frac{1}{{\alpha \left( {\Delta t} \right)^{2} }}{\mathbf{M}}_{{\mathbf{T}}} + \frac{\beta }{{\alpha \left( {\Delta t} \right)}}{\mathbf{C}}_{{\mathbf{T}}} + {\mathbf{K}}_{{\mathbf{T}}}$$

(30)

$${\mathbf{B}} = {\mathbf{F}}_{{\mathbf{T}}} \left( {t + \Delta t} \right) + \left[ {\frac{{{\mathbf{T}}_{t} }}{{\alpha \left( {\Delta t} \right)^{2} }} + \frac{{{\dot{\mathbf{T}}}_{t} }}{{\alpha \left( {\Delta t} \right)}} + \left( {\frac{1}{2\alpha } - 1} \right)\ddot{T}_{t} } \right] {\mathbf{M}} + \left[ {\frac{\beta }{{\alpha \left( {\Delta t} \right)}}{\mathbf{T}}_{t} + \left( {\frac{\beta }{\alpha } - 1} \right){\dot{\mathbf{T}}}_{t} + \Delta t\left( {\frac{\beta }{2\alpha } - 1} \right)\ddot{T}_{t} } \right]{\mathbf{C}}$$

(31)

First/second-order derivatives with respect to time for the next time step ${\dot{\mathbf{T}}}_{t + \Delta t}$ and $\ddot{T}_{t + \Delta t}$ will be calculated as

$$\ddot{{\bf T}}_{t + \Delta t} = \frac{{\left( {{\mathbf{T}}_{t + \Delta t} - {\mathbf{T}}_{t} } \right)}}{{\alpha \left( {\Delta t} \right)^{2} }} - \frac{{\dot{T}_{t} }}{{\alpha \left( {\Delta t} \right)}} - \left( {\frac{1}{2\alpha } - 1} \right)\ddot{T}_{t}$$

(32)

$${\dot{\mathbf{T}}}_{t + \Delta t} = \frac{\beta }{{\alpha \left( {\Delta t} \right)}}\left( {{\mathbf{T}}_{t + \Delta t} - {\mathbf{T}}_{t} } \right) - \left( {\frac{\beta }{\alpha } - 1} \right){\dot{\mathbf{T}}}_{t} - \Delta t\left( {\frac{\beta }{2\alpha } - 1} \right){\ddot{\mathbf{T}}}_{t}$$

(33)

where $\alpha$ and $\beta$ are Newmark parameters which are defined in three different types as follows

$${\text{Linear acceleration}}: \beta = \frac{1}{2}\;{\text{and}}\;\alpha = \frac{1}{6}$$

(34)

Average acceleration: $\beta = \frac{1}{2}$ and $\alpha = \frac{1}{4}$.

Central difference: $\beta = \frac{1}{2}$ and $\alpha = 0$.

In the present study, the average acceleration is employed.

5.3 Discretization of equations of motion

By replacing Eq. (14) into Eq. (18), the motion equations in terms of displacement field are obtained. After discretization of these equations with the aid of Eqs. (20–22), the equations of motion take the form

$${\mathbb{M}\ddot{\mathbb{U}}} + {\mathbb{C}\dot{\mathbb{U}}} + {\mathbb{K}\mathbb{U}} = {\mathbb{F}}$$

(35)

where

$${\mathbb{M}} = \left[ {\begin{array}{*{20}c} {{{\mathfrak{M}}}_{11} } & {{{\mathfrak{M}}}_{12} } & {{{\mathfrak{M}}}_{13} } \\ {{{\mathfrak{M}}}_{21} } & {{{\mathfrak{M}}}_{22} } & {{{\mathfrak{M}}}_{23} } \\ {{{\mathfrak{M}}}_{31} } & {{{\mathfrak{M}}}_{32} } & {{{\mathfrak{M}}}_{33} } \\ \end{array} } \right]$$

(36)

$${\mathbb{C}} = 0_{{3N_{\theta } \times 3N_{\theta } }}$$

(37)

$${\mathbb{K}} = \left[ {\begin{array}{*{20}c} {{\mathfrak{h}}_{{11}} } & {{\mathfrak{h}}_{{12}} } & {{\mathfrak{h}}_{{13}} } \\ {{\mathfrak{h}}_{{21}} } & {{\mathfrak{h}}_{{22}} } & {{\mathfrak{h}}_{{23}} } \\ {{\mathfrak{h}}_{{31}} } & {{\mathfrak{h}}_{{32}} } & {{\mathfrak{h}}_{{33}} } \\ \end{array} } \right]$$

(38)

$${\mathbb{F}} = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{1} } & {{\mathbf{F}}_{2} } & {{\mathbf{F}}_{3} } \\ \end{array} } \right]^{T}$$

(39)

$${\mathbb{U}} = \left[ {\begin{array}{*{20}c} {v_{1} v_{2} \ldots v_{{N_{\theta } }} } & {w_{1} w_{2} \ldots w_{{N_{\theta } }} } & {\varphi_{1} \varphi_{2} \ldots \varphi_{{N_{\theta } }} } \\ \end{array} } \right]^{T}$$

(40)

where $N_{\theta }$ denotes the number of grid points along the $\theta$, the components of the matrices ${\mathbb{K}}$ and ${\mathbb{M}}$ are given in Appendix 1.

After inserting the boundary conditions that are defined in Eq. (19), using the Newmark’s method for approximating time derivatives, Eq. (35) is represented as

$${{{\mathbf{\mathbb{A}}}}{\mathbb{U}}}_{t + \Delta t} = {\mathbb{B}}$$

(41)

where ${\mathbb{U}}_{t + \Delta t}$ is a vector containing unknown displacements of the grid points at the next time step, that ${{\mathbf{\mathbb{A}}}}$ and ${\mathbb{B}}$ may be obtained as [42]

$${{\mathbf{\mathbb{A}}}}_{t} = \frac{1}{{\alpha \left( {\Delta t} \right)^{2} }} {\mathbb{M}} + \frac{\lambda }{{\alpha \left( {\Delta t} \right)}}{\mathbb{C}} + {\mathbb{K}}$$

(42)

$${\mathbb{B}}_{t} = {\mathbb{F}}\left( {t + \Delta t} \right) + \left[ {\frac{{{\mathbb{U}}_{t} }}{{\alpha \left( {\Delta t} \right)^{2} }} + \frac{{\mathop {\mathbb{U}}\limits^{.}_{t} }}{{\alpha \left( {\Delta t} \right)}} + \left( {\frac{1}{2\alpha } - 1} \right)\mathop {\mathbb{U}}\limits^{..}_{t} } \right] {\mathbb{M}} + \left[ {\frac{\beta }{{\alpha \left( {\Delta t} \right)}}{\mathbb{U}}_{t} + \left( {\frac{\beta }{\alpha } - 1} \right)\mathop {\mathbb{U}}\limits^{.}_{t} + \Delta t\left( {\frac{\beta }{2\mu } - 1} \right)\mathop {\mathbb{U}}\limits^{..}_{t} } \right]\Delta$$

(43)

$$\mathop {\mathbb{U}}\limits^{..}_{t + \Delta t} = \frac{{\left( {{\mathbb{U}}_{t + \Delta t} - {\mathbb{U}}_{t} } \right)}}{{\mu \left( {\Delta t} \right)^{2} }} - \frac{{\mathop {\mathbb{U}}\limits^{.}_{t} }}{{\alpha \left( {\Delta t} \right)}} - \left( {\frac{1}{2\alpha } - 1} \right)\mathop {\mathbb{U}}\limits^{..}_{t}$$

(44)

$$\mathop {\mathbb{U}}\limits^{.}_{t + \Delta t} = \frac{\beta }{{\alpha \left( {\Delta t} \right)}}\left( {{\mathbb{U}}_{t + \Delta t} - {\mathbb{U}}_{t} } \right) - \left( {\frac{\beta }{\alpha } - 1} \right)\mathop {\mathbb{U}}\limits^{.}_{t} - \Delta t\left( {\frac{\beta }{2\alpha } - 1} \right)\mathop {\mathbb{U}}\limits^{..}_{t}$$

(45)

6 Results and discussion

In this section, an FGM shallow arch is considered and the large-amplitude vibration of its mid-plane under cooling shock loading are evaluated. The desired arch is made of low carbon steel and stainless steel, and the following two parameters are used to define the geometry of the arch

$$\mu = \sqrt {12} \frac{{R\theta_{0} }}{h}$$

(46)

$$\lambda = \sqrt {12} \frac{{R\theta_{0}^{2} }}{4h}$$

(47)

where $R$ and $\theta_{0}$ are the radius and initial angle of the arch, respectively.

In the representation of non-dimensional lateral deflection ($w/f)$, the deflection of the mid-plane is indicated by $w$ and the arch rise is indicated by $f$, which

$$f = R\left( {1 - \left( {\cos \left( {\frac{{\theta_{0} }}{2}} \right)} \right)} \right)$$

(48)

In addition, material properties $P$ and the temperature-dependent material coefficients $a, b, \ldots ,i$ are given in Tables 1 and 2.

6.1 Comparison study

In this section, to validate the results obtained from the present formulation, the results have been compared and validated from two aspects. In Fig. 3, in order to validate the temperature-dependent properties of material subjected to cooling shock at the temperature of 50 to 300 K, by applying the present formulation on the geometry of circular plate, a comparison is made with the results reported in the work of A. Babaee and J. Jelovica. [1]. The comparison of the present results with the work of Javani et al. to [40] validates the formulation of the shallow arch geometry by applying heating shock is done in Fig. 4.

Fig. 3

Large amplitude thermally induced vibrations of circular plate under cooling shock compared to the work of A. Babaee and J. Jelovica [1]

Fig. 4

Temporal evolution of maximum nondimensional lateral deflection of FGM shallow arch under heating shock compared to the work of Javani et al. [40]

6.2 Parametric study

In this section, the results obtained from this study are examined from different aspects, and the change in the vibrational behavior of a shallow arch under the cooling shock has been measured in relation to the changes in different parameters. Henceforth, in all subsections, an FGM shallow arch is considered, which has rested at the reference temperature $\left( {T_{0} = 293 K} \right)$ before applying the loading. The upper surface of the arch (${\text{SUS 304}}$ rich) is subjected to cooling shock and the lower side (${\text{AISI 1020}}$ rich) is conserved at an immutable temperature ($T_{A} = 293 K)$.

6.2.1 Effect of thermal load rapidity time $\left( {t_{R} } \right)$

Here, the effect of thermal load rapidity time $\left( {t_{R} } \right)$ on the thermally induced large amplitude vibrations of a functionally graded shallow arch with FG-index $\xi = 3$ and geometric characteristics $\mu = 200$, $\lambda = 2$, and thickness $h = 0.001{\text{ m}}$ under rapid cooling with ${\Delta }T = - 100{ }K$ is investigated. This analysis has been done for two types of loading mentioned in Sect. 3, and the results of loading cases 1 and 2 are shown in Figs. 5 and 6, respectively. The thermal load rapidity time parameter $\left( {t_{R} } \right)$ shows the duration of the thermal shock application, a smaller $t_{R}$ means a more sudden thermal shock and the amplitude of the vibrations are higher, and a larger $t_{R}$ means that the loading is applied gently and the vibrations amplitude lessens and the dynamic response tends to the quasi-static response.

Fig. 5

Effect of $t_{R}^{L}$ on the large amplitude vibrations of FGM shallow arch under first case of thermal loading

Fig. 6

Effect of $t_{R}^{L}$ and $t_{R}^{unL}$ on the large amplitude vibrations of FGM shallow arch under second case of thermal loading

Considering an FGM shallow arch with specifications $\xi = 3$, $\mu = 200$, $\lambda = 2$, $h = 0.01 {\text{m}}$, and ${\Delta }T = - 100 K$, the effect of $t_{R}$ on the variation of maximum circumferential normal stress $\left( {\sigma_{\theta \theta } } \right)$ in three upper, middle and bottom surfaces is demonstrated in Fig. 7. By increasing $t_{R}$, the delay in load application and stress generation can be clearly seen.

Fig. 7

The effect of $tR^{L}$ on the circumferential normal stress generated in the FGM shallow arch due to rapid cooling shock in a upper surface b mid-plane c lower surface

6.2.2 Effect of temperature variation

In examining the effect of the temperature difference on the large amplitude vibrations of an FGM shallow arch with $\xi = 3$, $\mu = 160$, $\lambda = 2$, $t_{R}^{L} = 5 \times 10^{ - 4} s$, and $h = 1 {\text{mm}}$, according to the observations in Fig. 8, the increase in the vibration amplitude has a direct relationship with the increase in the amount of the temperature variation.

Fig. 8

Influence of temperature rise on the large amplitude vibration of the FGM shallow arch under rapid cooling shock

In Fig. 9, an FGM shallow arch with specifications $\xi = 3$, $\mu = 180$, $t_{R}^{L} = 5 \times 10^{ - 4} {\text{s}},$ $\lambda = 1.2$ and $h = 0.01 {\text{m}}$ is considered. The change in specific heat capacity as one of the thermophysical properties of the material through the thickness of the arch at both the initial time and also 0.5 s after applying the loading in several distinct temperature differences has been investigated considering various FG-indices. It can be seen that with increasing the temperature difference, the specific heat capacity of the material decreases significantly along the thickness. By augment of the FG parameter $\xi$, the penetration percentage of ${\text{AISI 1020}}$ increases and causes a significant decrease in the specific heat capacity.

Fig. 9

Effect of thermal loading and FG-index on changes in the specific heat capacity along the thickness after 0.05 s

6.2.3 Effect of geometrical parameters

In Fig. 10, influence of two geometrical parameters, $\mu$ and $\lambda$, has been investigated. It can be seen that $\mu$ and $\lambda$ parameters have a direct and inverse relationship with the amplitude and range of FGM shallow arch vibrations, respectively. In this figure $\Delta T = - 100 K, t_{R}^{L} = 5 \times 10^{ - 4} s, \xi = 3,$ and $h = 1{\text{mm}}$.

Fig. 10

Influence of $\mu$ and $\lambda$ on the large amplitude vibration of the FGM shallow arch under rapid cooling shock

Another geometric parameter is the thickness of the shallow arch. In the vibrations of thin arches under sudden cooling shock, the non-dimensional lateral deflection is first negative and after some time enters the positive range. According to Fig. 11, by increase in the thickness of the arch, the lateral deflection with a higher vibration amplitude remains in the negative range. The loading specifications and desired arch geometry are shown in Fig. 11 are $\Delta T = - 100 K, t_{R}^{L} = 5 \times 10^{ - 4} s, \xi = 3, \mu = 150,$ and $\lambda = 2$.

Fig. 11

Influence of arch thickness on the large amplitude vibration of the FGM shallow arch under rapid cooling shock

6.2.4 Influence power-law index $\left( \xi \right)$

In Fig. 12, the influence of FG-index on large amplitude vibrations of a shallow arch considering $\Delta T = - 100 K, t_{R}^{L} = 5 \times 10^{ - 4} , h = 1{\text{ mm}}, \mu = 160$, and $\lambda = 2$ is investigated. Based on the presented results, by increasing the FG parameter, which means increasing the penetration percentage of ${\text{AISI 1020}}$ in the desired FGM structure, the dimensionless deflection of the mid-plane of the structure enters the positive range in a shorter period of time from the negative range and vibrates in a limited range.

Fig. 12

Effect of FG-index on the large amplitude vibration of the FGM shallow arch under rapid cooling shock

7 Conclusion

In this paper, the study of the thermally induced large-amplitude vibrations caused by the cooling shock of a functionally graded material shallow arch has been done. The study of thermally induced vibrations under sudden cooling shock has not been carried out on shallow arch geometry hitherto. The kinematic assumptions of a shear deformable shallow arch are modeled by von Kármán’s type of geometrical nonlinearity. According to the uncoupled thermoelasticity assumption, the temperature profile is achieved based on the one-dimensional heat transfer equation and inserted into the shallow arch motion equations. The equations are discretized by the GDQ method and afterward solved using the Newmark method in an iterative Newton–Raphson loop. During several examples, the effects of different parameters on the vibrational characteristics of the mid-plane of shallow arch under cooling shock are investigated. The effects of parameters including thermal load rapidity time, power law index, thermal boundary conditions, geometrical characteristics, and temperature change in the thermally induced vibrations of shallow arch have been analyzed and investigated, which yielded the following remarks:

• An escalation in the thermal load rapidity time $\left( {t_{R} } \right)$ leads to a reduction in the vibrational amplitude of the structure.

• Elevating the temperature difference between the top and bottom surfaces applied to the structure leads to an augment in the amplitude of vibrations.

• In connection with the geometry of the structure, an increase in $\lambda$ and a decrease in $\mu$ both result in a reduction in vibrations. Additionally, augmenting the thickness of the arch contributes to diminishing the vibrations.

• While investigating the FG index $\left( \xi \right)$, it is observed that considering the FG structure, as opposed to the pure ${\text{SUS 304}}$ state, the vibrations of the structure stabilize in a shorter period of time.

Appendix 1

$${\varvec{\mathfrak{M}}}_{11} = - I_{0} {\mathbf{I}}_{{N_{\theta } \times N_{\theta } }}$$

$${\varvec{\mathfrak{M}}}_{12} = 0_{{N_{\theta } \times N_{\theta } }}$$

$${\varvec{\mathfrak{M}}}_{13} = - I_{1} {\mathbf{I}}_{{N_{{N_{\theta } }} \times N_{{N_{\theta } }} }}$$

$${\varvec{\mathfrak{M}}}_{21} = 0_{{N_{\theta } \times N_{\theta } }}$$

$${\varvec{\mathfrak{M}}}_{22} = - I_{0} {\mathbf{I}}_{{N_{\theta } \times N_{\theta } }}$$

$${\varvec{\mathfrak{M}}}_{23} = 0_{{N_{\theta } \times N_{\theta } }}$$

$${\varvec{\mathfrak{M}}}_{31} = - I_{1} {\mathbf{I}}_{{N_{\theta } \times N_{\theta } }}$$

$${\varvec{\mathfrak{M}}}_{32} = 0_{{N_{\theta } \times N_{\theta } }}$$

$${\varvec{\mathfrak{M}}}_{33} = - I_{2} {\mathbf{I}}_{{N_{\theta } \times N_{\theta } }}$$

$$\hbar_{11} = \frac{{A_{11} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{2}$$

$$\hbar_{12} = \frac{{A_{11} }}{{R^{3} }}{\mathbf{D}}_{\theta }^{2} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{1} - \frac{{A_{11} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{1}$$

$$\hbar_{13} = \frac{{B_{11} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{2}$$

$$\hbar_{21} = \frac{{A_{11} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{1} + \frac{{A_{11} }}{{R^{3} }}\left[ {{\mathbf{D}}_{{{\varvec{\uptheta}}}}^{1} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{2} + {\mathbf{D}}_{\theta }^{2} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{1} } \right]$$

$$\hbar_{22} = 1.5 \times \frac{{A_{11} }}{{R^{4} }}{\mathbf{D}}_{\theta }^{2} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{1} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{1}$$

$$- \frac{{A_{11} }}{{R^{3} }}\left[ {0.5 \times {\mathbf{D}}_{\theta }^{1} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{1} + \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{2} } \right] + \frac{{A_{55} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{2} - \frac{{A_{11} }}{{R^{2} }}{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }}$$

$$\hbar_{23} = \frac{{B_{11} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{1} + \frac{{B_{11} }}{{R^{3} }}\left[ {{\mathbf{D}}_{{{\varvec{\uptheta}}}}^{1} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{2} + {\mathbf{D}}_{\theta }^{2} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{1} } \right] + \frac{{A_{55} }}{R}{\mathbf{D}}_{\theta }^{1}$$

$$\hbar_{31} = \frac{{B_{11} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{2}$$

$$\hbar_{32} = \frac{{B_{11} }}{{R^{3} }}{\mathbf{D}}_{\theta }^{2} \left( {{\mathbf{I}}_{{N_{\theta } \times N_{\theta } }} {\mathbf{w}}_{{N_{\theta } \times 1}} } \right){\mathbf{D}}_{\theta }^{1} - \frac{{B_{11} }}{{R^{2} }}{\mathbf{D}}_{\theta }^{1} - \frac{{A_{55} }}{R}{\mathbf{D}}_{\theta }^{1}$$

$$\hbar_{{33}} = \frac{{\varvec{D}_{{11}} }}{{R^{2} }}{\varvec{D}}_{\theta }^{2} - A_{{55}} {\varvec{I}}_{{N_{\theta } \times N_{\theta } }}$$

Herein, ${\mathbf{I}}$ is the $N_{\theta } \times N_{\theta }$ identity matrix, ${\mathbf{D}}_{\theta }^{{\mathbf{m}}}$ represents the derivative matrix of order $m$, and ${\mathbf{w}}$ is the vector of nodal lateral deflections.