1 Introduction

Micro-/nanopositioning stages have been widely utilized in modern precision engineering applications demanding the merits of high accuracy and fast response. Such applications involve atomic force microscopy (Park et al. 2010), micro/nano-assembly (Gozen and Ozdoganlar 2012), micro/nano-manipulation (Tian et al. 2010), lithography machining of semiconductors (Shinno et al. 2007), X-ray lithography and micro scanning (Indermuehle et al. 1994; Chen et al. 1992), etc. In recent years, more attention has been paid towards the performance improvement of the nanopositioning stages (Colinjivadi et al. 2008).

In view of the kinematic scheme, the mechanical designs of flexure-based nanopositioning mechanisms generally lie in two categories in terms of serial-kinematic and parallel-kinematic mechanisms. Concerning a serial-kinematic stage, the motion in each axis can be independently measured and easily controlled (Kenton and Leang 2012). However, the assembly error and accumulated error caused by parasitic motion in different axes are the main weakness of serial-kinematic mechanisms. By contrast, the parallel-kinematic mechanisms exhibit many advantages including structural compactness, high stiffness, and high accuracy. Yet, the coupling of the cross-axis motion, complex kinematic equation, and small workspace block a wide application of the parallel-kinematic mechanism in nanopositioning field (Liu et al. 2014).

To mitigate the cross-axis error of the parallel-kinematic stage, flexure joints have been widely applied. In addition, the flexure joints also have the advantages of negligible backlash, stick-slip friction and wear free, smooth and continuous displacement, an almost linear displacement relationship between input and output, and an inherently infinite resolution (Kang and Gweon 2013; Wang et al. 2011; Smith et al. 1997; Lobontiu et al. 2001). Generally, a monolithic structure is designed to achieve an XY stage. The monolithic design is easy to fabricate in practice. However, the maintenance work is not easy once one part of the stage is damaged. To overcome this limitation, a modular design concept is proposed to devise a nanopositioning stage in this work. Specifically, the comprehensive design of a novel parallel XY nanopositioning stage is proposed. By employing two modules, an XY nanopositioning stage is easily generated and maintained.

Usually, the piezoelectric actuators are employed to drive the flexure stages to achieve the merits of rapid response and ultra-high resolution of the displacement. Due to the stroke limit of piezoelectric actuators, the mechanical amplifier is widely applied in nanopositioning stages. Among various research efforts in this area, popular magnification approaches for flexure mechanism include level-principle amplifier (Qin et al. 2014) and bridge-principle amplifier (Zhang and Xu 2015a). For instance, it has been shown that the flexure mechanism can obtain the output of 480 μm by integrating the bridge-principle amplifier into the flexure mechanism design (Zhang and Xu 2015b).

To achieve a precision positioning, the implementation of a control methodology is demanded to overcome the hysteresis and creep nonlinearities introduced by the piezoelectric actuators. In the literature, sliding mode control (SMC) is widely used as a nonlinear control approach to deal with external disturbances. The discrete-time sliding mode control (DSMC) has been presented for the implementation on sampled-data systems (Bartoszewicz 1998; Xu 2015). In addition, the adaptive control of nonlinear systems has being developed rapidly in the past two decades (Yao and Tomizuka 1997). Numerous works combining SMC and adaptive control have been conducted in recent years (Chen and Hisayama 2008; Goodwin et al. 1980). However, most of these works only utilize continuous-time sliding mode control, or not all of unknown parameters are estimated. In this work, a new adaptive discrete sliding mode control (ADSMC) is developed, where the adaptive law is devised to estimate the mass, damping coefficient, and stiffness parameters. The effectiveness of the reported control scheme has been validated by carrying out experimental studies.

The major contribution of this work is the new mechanism and control design of an XY nanopositioning stage. The overall size of stage is only \(68.5\times 68.5\times 68.5\) mm3. To yield a large displacement, dual-stacked bridge-type amplifiers are employed. Actuated by two piezoelectric actuators, the stage can obtain the decoupled motion by combining the amplifier with the flexure prismatic (P) joints. The developed ADSMC scheme enables a positioning precision better than 20 nm for the nanopositioning stage.

The following parts of this paper are organized as follows. The mechanical design of the XY parallel stage is presented in Sect. 2. Then, FEA simulation is conducted in Sect. 3. Section 4 presents the open-loop testing results of prototype nanostage. Afterwards, the control design is outlined in Sect. 5 along with experimental studies. Finally, Sect. 6 concludes this paper.

2 Mechanical design and kinematics analysis

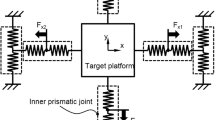
The use of the piezoelectric actuator (PZT) enables the stage an ultrahigh-resolution displacement. Due to the limited output stroke of the PZT actuator, two stacked amplifiers are employed to magnify the actuator’s stroke. In order to achieve decoupled output motion in X and Y axes, a two-prismatic-prismatic (2-PP) parallel mechanism is constructed. The components of the XY stage are denoted in the CAD model, as shown in Fig. 1.

Fig. 1
figure 1

CAD model of the designed XY nanopositioning stage

Full size image

2.1 Bridge-principle amplifier

Due to the double symmetry property, elastic deformation of one quarter model of bridge-type mechanism is picked out as shown in Fig. 2. This part can be considered as a beam which is simply supported in X and Y axes. The basic trigonometric amplification model for the bridge-principle amplifier can be generated by the following equation (Pokines and Garcis 1998)

$$\begin{aligned} R_{0}=\Big |\frac{\sin \alpha -\sin (\alpha -\varDelta \alpha )}{\cos \alpha -\cos (\alpha -\varDelta \alpha )} \Big | \end{aligned}$$
(1)

Based on this model, the following theoretical derivations are deduced.

Fig. 2
figure 2

a The parameters of the bridge amplifier (unit: mm), b comparison of results obtained by different methods

Full size image

2.1.1 Kinematic relation analysis

First, the displacement amplification ratio of bridge-type mechanism can be derived by analyzing kinematic relations and the instantaneous velocity of bridge-type mechanism (Ma et al. 2006). That is,

$$\begin{aligned} R_{1}=\tan \alpha \end{aligned}$$
(2)

2.1.2 Analysis based on elastic beam theory

Based on the elastic beam theory, another simple model is given by (Qi et al. 2015):

$$\begin{aligned} R_{2}=\frac{{3(h-t)}(L_1+2L_2)}{{3(h-t)}(h-t)+t^2} \end{aligned}$$
(3)

2.1.3 Combination of elastic beam theory and kinematic relation analysis

The kinematic analysis for bridge-type amplifier is derived in combination with the elastic beam theory. The ideal displacement amplification ratio of bridge-type mechanism was derived in Xu and Li (2011) using geometric relations of the input displacement and output displacement. An elastic analysis in consideration of the torsional stiffness \(K_r\) and translational stiffness \(K_t\) is given to verify the value of amplification ratio for bridge amplifier.

$$\begin{aligned} R_{3}= \frac{k_t(h-t)(L_1+2L_2)^3}{2k_r[(L_1+2L_2)^2+(h-t)^2]+k_t(h-t)^2(L_1+2L_2)^2} \end{aligned}$$
(4)

where the torsional stiffness \(K_r\) of the flexure hinges of the part can be computed as:

$$\begin{aligned} K_r=\frac{Ebt^3}{12(\delta ^3 L_1+2L_2)} \end{aligned}$$
(5)

By considering the beam to be a serially connected flexure of three parts, \(\delta =\frac{t}{h}\), the translational stiffness \(K_t\) of the flexure is derived as:

$$\begin{aligned} K_t=\frac{Ebt}{(\delta ^3L_1+2L_2)} \end{aligned}$$
(6)

After substituting Eqs. (5) and (6) into Eq. (4), the amplification ratio can be derived as

$$\begin{aligned} R_{3}=\frac{6(h-t)(L_1+2L_2)^3}{t^2[(L_1+2L_2)^2+(h-t)^2]+6(h-t)^2(L_1+2L_2)^2} \end{aligned}$$
(7)

2.1.4 FEA simulation result

Preliminary work of the nanopostioning stage design is presented in our previous work Zhang and Xu (2015a). FEA result of the amplification ratio is denoted by \(R_{4}\). By assigning an input displacement of 14.5 μm which is the stroke limit of the piezo actuator, the bridge amplifier obtains the output of 110.4 μm as shown in the FEA result in Fig. 2b. The comparison of the amplification ratios is tabulated in Table 1. It is obvious that \(R_3\) is closer to the FEA result \(R_4\). But the deviation is still over 0.25. So, the amplifier ratio \(R_4\) is employed in the following equations.

Table 1 Calculation results of the amplification ratio
Full size table

It is notable that the analysis models can be employed to perform an optimum design of the stage parameters in a computationally effective manner.

2.2 Dual-stacked bridge amplifier

The dual-stacked bridge amplifier can not only obtain a lager enlarged ratio but also change the direction of the output. The principle of the dual-stacked amplifier is a little different from the single one due to the serial connection of the first and second amplifiers. The amplification ratio of the stacked amplifiers cannot be calculated as \(R_{amp}^2\) directly, because the existence of the serial connection decreases the factor \(\upsilon\). An empirical factor \(\upsilon\) can be obtained from the FEA simulation as analyzed in the previous work Wang et al. (2011). As shown in Fig. 2a, if the shaded part A is not taken into consideration, the amplification ratio \(R_{t}\) of the dual-stacked amplifier can be simplified as the following equation by balancing the damping coefficient of the serial connection and the push force.

$$\begin{aligned} R_{t}=\upsilon {R_{3}}^2 \end{aligned}$$
(8)

where \(\upsilon\) = 0.154 as generated by FEA simulation.

2.3 Parasitic motion analysis

When the stage is only actuated by the PZT along X-axis with an input displacement \(\delta _p\) as shown in Fig. 3, the output \(\delta _a\) is enlarged by the amplifier. The output motion of the mobile platform along the X-axis will cause a small parasitic motion \(\delta _y\) in the Y-aixs direction and hence a cross-talk error between the two working axes.

With reference to Fig. 3, the relationship between \(\delta _p\) and \(\delta _a\) can be obtained:

$$\begin{aligned} \delta _a=R_t\delta _p=\delta _s \end{aligned}$$
(9)

where \(\delta _s\) is the displacement of the point A. \(\delta _x\) and \(\delta _y\) can be derived from the following equations based on geometric relationships:

$$\begin{aligned} \delta _x \;= \; L_4\sin \beta \end{aligned}$$
(10)
$$\begin{aligned} \delta _y\;=\; L_4(1-\cos \beta ) \end{aligned}$$
(11)

where \(\beta =\frac{\delta _s}{L_4}\).

The percentage value of the cross-axis error \(\epsilon\) can be expressed by:

$$\begin{aligned} \epsilon =\frac{\delta _y}{\delta _x}=\tan {\beta \over 2}=\tan {{R_t\delta _P}\over 2L_4} \end{aligned}$$
(12)

The parameter \(L_4\) = 20 mm. And \(\delta _p\) = 14.5 μm is the maximum output of the PZT. Thus, the percentage value of the cross axis error \(\epsilon\) is only 0.011 %, which is calculated by combining Eqs. (8) and (12). It is obvious that the motion of this XY parallel stage is decoupled around point A.

Fig. 3
figure 3

Parasitic motion representation

Full size image

2.4 Dynamics modeling

Owing to the decoupled property of the 2-PP parallel mechanism, the XY parallel stage is capable of producing decoupled motion in X and Y ases. For the convenience of analytical modeling, it is assumed that the XY stage is totally decoupled. Based on this assumption, if two PZT actuators produce the input displacements of \(q_1\) and \(q_2\), the platform yields the output motion \(d_x\) and \(d_y\).

The kinetic energy function can be calculated as:

$$\begin{aligned} T & = \left[ {m_{1} \left( {\frac{1}{2}R_{t}^{2} + \frac{1}{4}R_{4}^{2} + \frac{1}{4}} \right) + m_{2} \left( {\frac{{17}}{{48}}R_{t}^{2} + \frac{{41}}{{48}}R_{4}^{2} + \frac{1}{8}} \right)} \right. \\ & \quad \left. { +\;m_{3} \left( {\frac{3}{4}R_{t}^{2} + \frac{1}{4}R_{4}^{2} } \right) + (m_{4} + m_{5} )\left( {\frac{1}{2}R_{t}^{2} } \right)(\dot{q}_{1}^{2} + \dot{q}_{2}^{2} )} \right] \\ \end{aligned}$$
(13)

where each mass part is illustrated in Fig. 2a. In addition, \(m_4\) is the mass of the P joint and \(m_5\) represents the mass of the platform.

Referring to Fig. 4, taking into account the analysis of the compound parallelogram flexure, yields the stiffness of one leaf flexure for the P joint can be derived as:

$$\begin{aligned} K_{p}=\frac{Ebt^3}{L_4} \end{aligned}$$
(14)

where \(L_4\) = 20 mm presents the length of the P joint as shown in Fig. 3.

Fig. 4
figure 4

Stiffness model of the XY stage

Full size image

In addition, the potential energy is derived as follows.

$$\begin{aligned} V=16\times \frac{1}{2}K_r(\theta ^2_1+\theta ^2_2)+\frac{1}{2}K_p[(R_t{q_1})^2+(R_t{q_2})^2] \end{aligned}$$
(15)

where

$$\begin{aligned} {\theta _1=\frac{({q_1}+{q_2})R_4}{2(L_1+2L_2)}, \theta _2=\frac{({q_1}+{q_2})R_t}{2(L_1+2L_2)}.} \end{aligned}$$

In view of the Lagrange’s equations, the dynamics model can be developed based on:

$$\begin{aligned} \frac{d}{dt}\left(\frac{\partial T}{\partial \dot{q}}\right)-\frac{\partial T}{\partial q}+\frac{\partial V}{\partial q}=F_o \end{aligned}$$
(16)

To solve the natural frequency of the stage, the external force \(F_o\) is assigned as zero. Then, by combining Eqs. (13), (15), and (16), the dynamic model can be derived as

$$\begin{aligned} \mathbf {M}\ddot{q}+\mathbf {K}q=0 \end{aligned}$$
(17)

So, the natural frequency of the stage in one working direction is computed in unit of Hertz as follows.

$$\begin{aligned} f =\frac{1}{2\pi }\sqrt{\frac{K}{M}} \end{aligned}$$
(18)

3 Finite element analysis simulation

Simulation study is conducted by using finite element analysis (FEA) method to verify the output of the XY parallel stage. Figure 5a shows that the average output of the stage in Y-axis is 127 μm. As there is no distinct difference between the X and Y direction of the XY parallel stage, the output along X-axis is similar to the Y-axis motion when the X-axis PZT actuator is driven.

Fig. 5
figure 5

FEA simulation results of static structural analysis. a Output along the Y axis, b cross-axis error in the X axis

Full size image

3.1 Cross-axis error analysis

Figure 5b shows that the cross-axis errors of the stage in the X-axis distribute from 0.0078 to 7.01 μm, which are varied from 0.006 to 5.4 % of the output range of 129 μm. The average error is calculated as 2.7 %. The FEA simulation result reveals that the displacement in Y-axis is partly decoupled from X-axis. The deviation between the analytical result and FEA simulation result is caused by the ignorance of the dual-staked amplifier and platform in the analytical analysis.

3.2 Stress analysis of the stage

When the Y-axis actuator is driven to produce an Y-axis motion, the stress distribution of the XY stage is shown in Fig. 6. It is observed from the FEA simulation results that the largest stress appears on the thinnest part of the amplifier. The largest stress value is 67.2 MPa as shown on the top of the color bar, which is much less than the yield stress of 275 MPa of the Al-6061 material. The safety factor is 4.1, which means that the flexure hinges can work stably in normal operation.

Fig. 6
figure 6

The stress distribution of the stage

Full size image

3.3 Dynamics analysis of the stage

Moreover, the modal analysis is performed by FEA to verify the dynamic performance. In the simulation, the material parameters are assigned and the mesh model is created using the element size of 1 mm. The surface planes of the base are fixed.

From the modal analysis results as shown in Fig. 7, the first natural frequency of 222.2 Hz can be extracted. The derived dynamics model (18) predicts a natural frequency of 243.5 Hz. It is observed that the analytical model underestimates the resonance frequency of the mechanism with a derivation around 9.7 % relative to the FEA result.

In addition, the first-six resonant frequencies as predicted by the modal analysis with ANSYS are shown in Table 2, and the corresponding mode shapes are illustrated in Fig. 7. The FEA results reveal that the second and third mode shapes are contributed by the translations along the two working axes, respectively. This result is consistent with the analytical result.

Table 2 The first-six resonant frequencies
Full size table
Fig. 7
figure 7

FEA simulation results of resonant modes for the XY stage. a First mode, b second mode, c third mode, d fourth mode, e fifth mode, f sixth mode

Full size image

4 Prototype development and testing

4.1 Prototype fabrication

The developed prototype of the XY stage is shown in Fig. 8. The stage is manufactured by the wire-EDM process using the material of Al-6061 alloy. Two modules of PP link are employed to constructed the XY stage. As shown in Fig. 8, two low-voltage PZT actuators (TS18-H5-202 from PIEZO SYSTEMS, Inc.) are adopted to drive the amplification mechanism. Each PZT actuator is inserted into the mechanical amplifier and preloaded through a screw mounted at the tip of the actuator. This produces interference fits between the PZT and the amplifier. Thus, no clearances exist during the operation thanks to elastic deformations of the flexure hinges.

Fig. 8
figure 8

Experimental setup of the XY nanopositioning stage

Full size image

In addition, each piezoelectric actuator is actuated by a linear voltage amplifier (model: EPA-104 from Piezo Systems, Inc). The voltage will be enlarged by ten times using the amplifier. For the measurement of output position of the stage, two capacitive displacement sensors (model: D-510.050, from Physik Instrumente Co., Ltd.) are equipped. The resolution of the capacitive sensor is 10 nm within a measuring range –62.5 to 62.5 μm. The control hardware is based on National Instruments (NIs) cRIO-9022 real-time (RT) controller integrated with cRIO-9118 reconfigurable chassis that contains a field-programmable gate array core. Furthermore, the chassis also contains NI-9263 analog output module and NI-9215 analog input module. NI LabVIEW software is employed to seamlessly integrate the control algorithm, sensor, and the communication with the XY parallel stage.

4.2 Decoupling experimental performance testing results

In order to confirm the decoupling performance of the parallel stage, an open-loop testing experiment is conducted. A 10-V input triangle voltage with 0.5-Hz frequency is given to X-axis of the stage and enlarged to 100 V by the voltage amplifier, and the Y-axis is left free. The average displacement of X-axis is almost 127 μm as shown in Fig. 9. The cross-axis error in extreme position along Y direction can be calculated. It is found that the maximum X-axis displacement induces an Y-axis displacement of 6 μm, which indicates a cross-axis error of 4.7 %.

The output displacement obtained by three approaches of analytical modeling, FEA simulation, and experiment are shown in Table 3. As compared with the experimental result, the analytical model underestimates the displacement by 7.9 %. The reason lies in that a preloading is applied in the experimental setup to fix the PZT actuators, which causes a larger amplification of the bridge-type amplifier than calculated one. In addition, the deviation between the simulation and experimental results is only 1.6 %.

Table 3 Comparison of the maximum output displacement
Full size table
Fig. 9
figure 9

Open-loop experimental testing results. Output along the X axis and cross-axis error in the Y axis

Full size image

Open-loop experimental testing shows that the stage exhibits a motion range of 127 μm in each working axis. However, the output-input relation reveals a clear hysteresis curve which is introduced by the piezoelectric actuators. To overcome the cross-axis error and the piezoelectric nonlinearity and to achieve a precision positioning, a control scheme is devised in the subsequent section.

5 Control design and experimental studies

In this section, an adaptive digital sliding mode positioning control scheme is proposed and the performance of the developed nanopositioning stage is verified by conducting several experimental studies. The block diagram of the control frame is shown in Fig. 10.

Fig. 10
figure 10

Control block diagram of designed controller

Full size image

5.1 Design of adaptive reference model

In this paper, an adaptive reference model is adopted to compensate for the uncertain parameters in dynamical model such as mass, damping coefficient and stiffness. Definitely, these coefficients can be identified through system identification. However, the exact model is hard to identified due to the existence of disturbance and measuring error. In order to avoid this kind of negative influence, an adaptive reference model is designed as follows.

The dynamic model of stage in one working direction accompanied with unknown disturbance can be conducted below:

$$\begin{aligned} m\ddot{q}+b\dot{q}+kq=du+P \end{aligned}$$
(19)

where m, b, k and q represent the mass, damping coefficient, stiffness, and displacement along X-axis, respectively; d is the piezoelectric coefficient, and u denotes the input voltage. In addition, P stands for the overall perturbation of the system arising from model parameter uncertainties, unmodeled dynamics, cross coupling effect, and other unknown terms.

The first step is to transform the second order equation to state-space equation. Rewriting Eq. (19), we have

$$\begin{aligned} \ddot{q}=-\frac{k}{m}q-\frac{b}{m}\dot{q}+\frac{kd}{m}u+\frac{P}{m} \end{aligned}$$
(20)

Then, the state-space equation can be expressed as:

$$\begin{aligned}&\dot{X}=AX+BU+G\nonumber \\&Y=CX \end{aligned}$$
(21)

where A = \(\begin{bmatrix} 0&1\\ -\frac{k}{m}&-\frac{b}{m}\\ \end{bmatrix}\), B = \(\begin{bmatrix} 0,&\frac{d}{m} \end{bmatrix}^T\), U = u, G = \(\begin{bmatrix} 0,&\frac{P}{m} \end{bmatrix}^T\), C = \(\begin{bmatrix} 1,&0 \end{bmatrix}\), and X = \(\begin{bmatrix} q,&\dot{q} \end{bmatrix}^T\).

Because A and B are unknown, it is practical to apply the following parallel model, which ignores the disturbance.

$$\begin{aligned} \dot{\hat{X}}=\hat{A}\hat{X}+\hat{B}U \end{aligned}$$
(22)

where \(\hat{A}\), \(\hat{B}\) are the estimations of A, B at time t to be generated by an adaptive law, and \(\hat{X}\) is the estimate of the vector X.

The estimation error vector \(\epsilon _1\) is defined as

$$\begin{aligned} \epsilon _1=X-\hat{X} \end{aligned}$$
(23)

which satisfies

$$\begin{aligned} \dot{\epsilon }_1=A\epsilon _1-\tilde{A}\hat{X}-\tilde{B}U \end{aligned}$$
(24)

where \(\tilde{A}=\hat{A}-A,\;\tilde{B}=\hat{B}-B\).

In order to estimate the value of A and B, the general format of the adaptive law is assumed:

$$\begin{aligned} \dot{\hat{A}}=f_1(\epsilon _1,X,\hat{X},U), \;\dot{\hat{B}}=f_2(\epsilon _1,X,\hat{X},U) \end{aligned}$$

where \(f_1\) and \(f_2\) are functions of known terms that need to be chosen to make the equilibrium point to be

$$\begin{aligned} \hat{A}_e=A,\hat{B}_e=B, \epsilon _{1e}=0 \end{aligned}$$

To satisfy the above requirements, first, the Lyapunov candidate function is considered:

$$\begin{aligned} V(\epsilon _1,\tilde{A},\tilde{B})=\epsilon _1^T\Lambda \epsilon _1+tr\left(\frac{\tilde{A}^T\Lambda \tilde{A}}{\gamma _1}\right)+tr\left(\frac{\tilde{B}^T\Lambda \tilde{B}}{\gamma _2}\right) \end{aligned}$$
(25)

where tr(A) denotes the trace of matrix A, \(\gamma _1,\gamma _2>0\) are constant scalars, and \(\Lambda =\Lambda ^T>0\) is selected according to the solution of the Lyapunov equation

$$\begin{aligned} \Lambda A+A^T\Lambda =-I \end{aligned}$$
(26)

whose existence is guaranteed by the stability of A.

The time derivative of V is given by

$$\begin{aligned}\dot{V} & =\dot{\epsilon }_1^T\Lambda \epsilon +\epsilon _1^T\Lambda \dot{\epsilon }_1+tr\left(\frac{\dot{\tilde{A}}^T\Lambda \tilde{A}}{\gamma _1}+\frac{\tilde{A}^T\Lambda \dot{\tilde{A}}}{\gamma _1}\right)\nonumber \\ & \quad +tr\left(\frac{\dot{\tilde{B}}^T\Lambda \tilde{B}}{\gamma _2}+\frac{\tilde{B}^T\Lambda \dot{\tilde{B}}}{\gamma _2}\right) \end{aligned}$$
(27)

Substituting \(\dot{\epsilon }_1,\dot{\tilde{A}},\dot{\tilde{B}}\) into Eq. (28), yields

$$\begin{aligned}\dot{V} & = \epsilon _1^T(\Lambda A+A^T\Lambda )\epsilon _1-2\epsilon _1^T\Lambda \tilde{A}\hat{X}-2\epsilon _1^T\Lambda \tilde{B}U\nonumber \\ & \quad +tr\left(2\frac{\dot{\tilde{A}}^T\Lambda F_1}{\gamma _1}+2\frac{\tilde{B}^T\Lambda F_2}{\gamma _2}\right) \end{aligned}$$
(28)

Due to the properties of trace, one has

$$\begin{aligned}&\epsilon _1^T\lambda \tilde{A}\hat{X}=\hat{X}^T\tilde{A}^T\lambda \epsilon _1=tr(\tilde{A}^T\lambda \epsilon _1\hat{X}^T)\\&\epsilon _1^T\lambda \tilde{B}U=tr(\tilde{B}^T\lambda \epsilon _1U^T) \end{aligned}$$

Consequently, the time derivative of V can be rewritten as

$$\begin{aligned}\dot{V} & = -\epsilon _1^T\epsilon _1+2tr \big (\frac{\tilde{A}^T\Lambda F_1}{\gamma _1}-\tilde{A}^T\Lambda \epsilon _1\hat{X}^T\nonumber \\ & \quad +\frac{\tilde{B}^T\Lambda F_2}{\gamma _2}-\tilde{B}^T\Lambda \epsilon _1U^T\big) \end{aligned}$$
(29)

Obviously, in order to cancel the indefinite terms, the choices for \(f_1, f_2\) are

$$\begin{aligned} \dot{\hat{A}}=F_1=\gamma _1\epsilon _1\hat{X}^T, \; \dot{\hat{B}}=F_2=\gamma _2\epsilon _1U^T \end{aligned}$$
(30)

Then, the time derivative \(\dot{V}\) satisfies

$$\begin{aligned} \dot{V}=-\epsilon _1^T\epsilon _1\le 0 \end{aligned}$$
(31)

which implies that the equilibrium \(\hat{A}_e=A,\hat{B}_e=B,\epsilon _{1e}=0\) of the respective equations is uniform stable. Furthermore, the trajectory \(\epsilon _1(t),\hat{A}(t),\hat{B}(t)\) is bounded for all \(t\ge 0\). Since \(\epsilon _1=X-\hat{X}\) and \(X\in \pounds _{\infty }\), then, \(\hat{q}\in \pounds _{\infty }\). Besides, it can be deduced that

$$\begin{aligned} \lim _{t\rightarrow \infty }V(\epsilon _1,\tilde{A},\tilde{B})=V_{\infty }< \infty \end{aligned}$$

Therefore,

$$\begin{aligned} \int _{0}^{\infty }\epsilon _1^2(\tau )d\tau =-\int _{0}^{\infty }\dot{V}=V_0-V_\infty \end{aligned}$$

Hence, it can be concluded that \(\epsilon _1\in \pounds _2,\dot{\epsilon _1}\in \pounds _{\infty }\) and

$$\begin{aligned} |\epsilon _1(t)|\rightarrow 0, ||\dot{\hat{A}}(t)||\rightarrow 0, ||\dot{\hat{B}}(t)||\rightarrow 0 \quad as \quad t\rightarrow \infty \end{aligned}$$

The convergence properties of \(\hat{A},\hat{B}\) to their true values A, B, respectively, depend on the properties of the input u. Therefore, the estimations of A, B are given by

$$\begin{aligned} \hat{A}= & {} \int _{0}^{t}\gamma _1\epsilon _1X^Td\tau \end{aligned}$$
(32)
$$\begin{aligned} \hat{B}= & {} \int _{0}^{t}\gamma _2\epsilon _1U^Td\tau \end{aligned}$$
(33)

However, A, B still cannot be estimated, because the input u is till unknown. In the following discussion, a sliding mode controller is designed in detail.

5.2 Discrete-time sliding mode control design

Using sampling time T, the continuous-time system model (25) can be discretized as

$$\begin{aligned} &X_{k+1} = G_kX_{k}+H_ku_k+P_k \nonumber \\ &Y_k = CX_k \end{aligned}$$
(34)

where \(X_k=X(kT)\), \(\hat{A}_k=A(kT)\), and \(\hat{B}_k=B(kT)\) are time series. In addition,

$$\begin{aligned}G_k & =e^{\hat{A}_kT}=e^{\int _{0}^{kT}\gamma _1\epsilon _1X^TT}\nonumber \\ H_k & =\int _{0}^{T}e^{\hat{A}_k\tau }d\tau \hat{B}_k\nonumber \\ & =\int _{0}^{T}e^{\int _{0}^{k\tau }\gamma _1\epsilon _1X^T\tau }d\tau \int _{0}^{kT}\gamma _2\epsilon _1U^Td\tau \end{aligned}$$
(35)

It is notable that Eq. (35) gives better approximation only when \(\hat{A}_k\) is slowly varying.

In this paper, the lumped perturbation term \(P_k\) is estimated by its one-step delay by employing the perturbation estimation technique (Xu 2015; Elmali and Olgac 1996).

$$\begin{aligned} \hat{P}=P_{k-1}=X_{k-1}-G_{k-1}X_{k-1}-H_{k-1}u_{k-1} \end{aligned}$$
(36)

Consequently, the dynamical model (34) can be rewritten into

$$\begin{aligned} X_{K+1}=G_kX_k+H_ku_k+\hat{P}_k-\tilde{P}_k \end{aligned}$$
(37)

where \(\tilde{P}_k=\hat{P}_k-P_k\) is the perturbation estimation error, and it is assumed that the first derivative of the perturbation term is bounded, i.e., \(|\dot{P}(t)| \le \Delta\). Then, the following deduction holds:

$$\begin{aligned} |\tilde{P}_k| \le \Delta T \end{aligned}$$
(38)

which indicates that the perturbation error is also bounded.

Substituting Eq. (36) into Eq. (37), the discrete state can be calculated as

$$\begin{aligned}X_{k+1} & =G_kX_k+H_ku_k+X_{k-1}\nonumber \\& \quad -G_{k-1}X_{k-1}-H_{k-1}u_{k-1}-\tilde{P}_k \end{aligned}$$
(39)

According to the position error \(e_k=Y_k-Y_{d,k}\), where \(Y_{d,k}\) is the desired position at time KT, a proportional integral (PI)-type sliding surface function can be defined as follows:

$$\begin{aligned} s_k=K_pe_k+K_I\varepsilon _k \end{aligned}$$
(40)

where \(K_p\) and \(K_I\) are the proportional and integral gains, respectively. Besides, the integral error \(\varepsilon _k\) is

$$\begin{aligned} \varepsilon _k=\sum _{i=1}^{k}e_i=e_k+\varepsilon _{k-1} \end{aligned}$$
(41)

Assuming that the equivalent control \(u^{eq}\) is the solution to \(\Delta s_k=s_k-s_{k-1}=0\) (Furuta 1990), which can also be regarded as one-step delay of \(s_k\):

$$\begin{aligned} s_k&=K_pe_{k+1}+K_I\varepsilon _{k+1}\nonumber \\&=(K_p+K_I)e_{k+1}+K_I\varepsilon _{k}\nonumber \\&=(K_p+K_I)(Y_{k+1}-Y_{d,k+1})+K_I\varepsilon _{k}\nonumber \\&=(K_p+K_I)(CX_{k+1}-Y_{d,k+1})+K_I\varepsilon _{k} \end{aligned}$$
(42)

Then, substituting Eq. (39) into Eq. (42) and ignoring the estimation error \(\tilde{P}_k\) leads to the equivalent control

$$\begin{aligned} u_{k}^{{eq}} & = H_{k}^{{ - 1}} H_{{k - 1}} u_{{k - 1}} + (CH_{k} )^{{ - 1}} \left( {\frac{{s_{k} }}{{K_{p} + K_{I} }} - \frac{{K_{I} \varepsilon _{k} }}{{K_{p} + K_{I} }}+ Y_{{d,k + 1}} } \right) \\ & \quad + H_{k}^{{ - 1}} (G_{{k - 1}} X_{{k - 1}} - G_{k} X_{k} ) \\ \end{aligned}$$
(43)

This equivalent controller is effective when the position trajectory is kept on the sliding surface. Nevertheless, the standalone equivalent control is difficult to regulate the position trajectory towards the sliding surface when the initialization of the system is relatively far from sliding surface or there are large uncertainties and disturbances occurring during the sliding phase. Therefore, an extra control action \(u^{sw}\) is indispensable to keep the system stable.

$$\begin{aligned} u_k=u_k^{eq}+u^{sw} \end{aligned}$$
(44)

In the paper, the control \(u_k\) is selected as

$$\begin{aligned} u_{k} & = H_{k}^{{ - 1}} H_{{k - 1}} u_{{k - 1}} + (CH_{k} )^{{ - 1}} \left( {\frac{{s_{k} }}{{K_{p} + K_{I} }} - \frac{{K_{I} \varepsilon _{k} }}{{K_{p} + K_{I} }} + Y_{{d,k + 1}} } \right) \\ & \quad + H_{k}^{{ - 1}} (G_{{k - 1}} X_{{k - 1}} - G_{k} X_{k} ) - H_{k}^{{ - 1}} K_{s} sgn(s_{k} ) \\ \end{aligned}$$
(45)

where sgn(.) denotes the signum function and \(K_s\) is an arbitrary positive control gain.

5.3 Stability analysis

Theorem 1

For the system (34) with sliding function (40) and assumption (38), if the controller (45) is implemented, then the discrete sliding mode will occur after a finite number of steps.

Proof

The sliding function (38) can be rewritten into the form according to \(\Delta s_k=s_k-s_{k-1}=0\)

$$\begin{aligned}s_{k+1}&=K_pe_{k+1}+K_I(e_{k+1}+\varepsilon _k)\nonumber \\&=(K_p+K_I)(Y_{k+1}-Y_{d,k+1})+K_I\varepsilon _k\nonumber \\&=(K_p+K_I)(CX_{k+1}-Y_{d,k+1})+K_I\varepsilon _k \end{aligned}$$
(46)

Then, inserting Eq. (45) into Eq. (46), a relationship operation gives

$$\begin{aligned} s_{k+1}=s_k-(K_p+K_I)[K_ssgn(s_k)+\tilde{P}_k] \end{aligned}$$
(47)

Note that \(K_p\), \(K_I\), and \(K_s\) are all positive scalars. In the case of \(s_{k_1} \ge 0\), it can be derived that

$$\begin{aligned} s_{k+1} \le s_{k} \quad if \; K_s\ge |\tilde{P}_k| \end{aligned}$$
(48)

Otherwise, if \(s_{k} \le 0\), then

$$\begin{aligned} s_{k+1} \ge s_{k} \quad if \; K_s\ge |\tilde{P}_k| \end{aligned}$$
(49)

Therefore, in view of (48) and (49), the following conclusion can be drawn:

$$\begin{aligned} |s_{k+1}| \le |s_k| \quad if \; K_s \ge |\tilde{P}_k| \end{aligned}$$
(50)

According to the assumption (38), the relationship (50) is verified, which indicates that \(s_k\) decreases mono-tonously, and the discrete sliding mode is reached after a finite number of steps. \(\square\)

Remark 1

Even though Eq. (50) is sufficient for the existence of discrete sliding mode, because of the discontinuity of the signum function sgn(.), chattering may occur in the control process. In order to alleviate the chattering phenomenon, the saturation function is adopted to replace the signum function.

$$sat(s_{k} ) = \left\{ {\begin{array}{*{20}l} {sgn(s_{k} ),} \hfill & {if\;{\kern 1pt} |s_{k} |\; > \;\delta } \hfill \\ {\frac{{s_{k} }}{\delta },} \hfill & {if\; |\frac{{s_{k} }}{\delta }|\; \le \;\delta } \hfill \\ \end{array} } \right.$$

where the parameter \(\delta\) of the boundary layer thickness.

5.4 Experimental results

The closed-loop experimental study is conducted using the implemented ADSMC controller. In order to make a comparison study, a DSMC controller with fixed value of A and B is implemented. The corresponding parameters in the dynamics model are obtained as:

$$\begin{aligned} {\mathbf {A}}= \left[ \begin{array}{ll} 0.7881 &{} 0.0025 \\ -151.654 &{} -0.2236 \end{array}\right] , {\mathbf {B}}= \left[ \begin{array}{l} 0 \\ 977.36 \end{array}\right] , {\mathbf {C}}= \left[ \begin{array}{ll} 1 &{} 0\\ \end{array}\right] \end{aligned}$$
(51)

Furthermore, a PID controller is also realized owing to its popularity. The PID control gains \(K_P\), \(K_I\), and \(K_D\) are optimally tuned through intensive tests with the values \(K_P=0.123\), \(K_I=0.45\), and \(K_D=0.0012\) in this work.

5.4.1 Resolution testing results

The first step of this experiment is to test the minimum resolution of the stage using a consecutive-step signal. It is carried out with a step size of 20 nm, and the results are shown in Fig. 11. Obviously, the step could be clearly identified, and the error is less than 20 nm, which is almost the resolution level of capacitive sensor. Consequently, the experimental result indicates that the proposed ADSMC controller enables a positioning resolution better than 20 nm for the system.

Fig. 11
figure 11

a Resolution testing results using the 20-nm consecutive step input, b tracking error

Full size image

5.4.2 Set-point positioning performance testing results

Second, the set-point positioning capability of the nano-positioning system is examined using the three controllers. The step size of the input is 1 μm. As shown in Fig. 12, the overshoot of all the tree controllers is near 20 % larger than the input reference and the response time is about 0.03 s. It is observed that the PID control produces the maximum error (MAXE) and root-mean-square error (RMSE) of 0.048 and 0.0387 μm, that is, 4.8 and 3.87 % of the motion range, respectively. Compared with PID control, the DSMC controller reduces the MAXE and RMSE by 25 and 22.2 %, respectively. In addition, the ADSMC scheme mitigates the MAXE and RMSE to 0.023 and 0.0135 μm, i.e., 2.3 and 1.35 % of the positioning range, respectively. The experimental result indicates that ADSMC can effectively reduce the positioning error though it cannot boost the response speed.

Fig. 12
figure 12

a Experimental results of set-point positioning testing with 1-μm step input, b tracking error

Full size image

5.4.3 Sinusoid tracking performance testing results

Afterwards, the path tracking performance of the proposed nanopositioning stage is carried out using 2, and 10-Hz sinusoid reference inputs. The results are shown in Figs. 13, and 14, respectively. When the reference is 2 Hz with 0.2 μm amplitude, the largest MAXE and RMSE are still produced by PID control, which are 0.044 and 0.0355 μm, respectively. Similarly, in comparison with PID and DSMC control, ADSMC control can effectively reduce the MAXE and RMSE to 0.024 and 0.0112 μm, that is, 12 and 5.6 % of the motion range, respectively.

Fig. 13
figure 13

a The tracking result of 2-Hz sinusoid reference position input, b tracking error

Full size image
Fig. 14
figure 14

a The tracking result of 10-Hz sinusoid reference position input, b tracking error

Full size image

Increasing the frequency and amplitude to 10 Hz and 10 μm simultaneously, the superiority of ADSMC control becomes more obvious as compared with PID and DSMC results. Obviously, the performance of PID control decreases dramatically, whose MAXE is 0.1383 μm and RMSE is 0.0992 μm. In contrast, the DSMC scheme reduces the MAXE and RMSE by 47.8 and 52.2 %, respectively. In addition, the ADSMC mitigates the MAXE to 0.063 μm and RMSE to 0.035 μm, respectively. The experimental results show that the ADSMC control has much better performance in high-speed operation and can augment the bandwidth effectively. The details of the experimental results are shown in Table 4.

Table 4 The results of positioning control experiments
Full size table

Furthermore, when estimating the adaptive reference, another limitation is that the estimation gains \(\gamma _1\) and \(\gamma _2\) can also influence the speed of system. In this work, \(\gamma _1\) = 0.386 and \(\gamma _2\) = 0.754 are assigned in the experimental study. The optimal values will be generated in the future work.

5.4.4 Discussion

The obtained experimental results indicate that the nano-positioning stage has satisfactory performance and the adaptive discrete-time sliding mode controller successfully eliminates the external disturbance and drives the stage to pre-designed reference position. A precise positioning with a resolution of 20 nm is achieved, and the motion tracking results also show its advantages.

As aforementioned, the controller parameters are not optimally designed. The adaptive gain \(\gamma _1\) and \(\gamma _2\) are the constant values in these experiments. Further testing shows that a slight variance of the value would affect the steady-state error finally. Therefore, it is recommended to adopt small adaptive gains which are less than one. Some optimal algorithm (such as, least squares) will be tried in the future work. In addition, parameter \(\delta\) in the saturation function also influences the final steady-state error and the output value of u. A small value of \(\delta\) is able to reduce the steady-state error, but the chattering phenomenon will become obvious. To make a comprise, \(\delta =0.0004\) is selected to obtain better results in this work.

6 Conclusion

This paper presents the design and control of a new XY parallel-kinematic flexure stage. It is found that a displacement amplification ratio of 8.9 can be obtained for the stage. FEA simulation results show that the cross-axis error is suppressed to be lower than 1 %. A prototype is developed for experimental testing, which reveals a motion range of 127 μm in each working axis with the natural frequency over 200 Hz. To suppress the cross-axis error and piezoelectric nonlinearity, an adaptive discrete-time sliding mode controller is proposed for position tracking control of the nanopositioning stage. Experimental results show that the chattering-free control enables a rapid response and low-level of positioning error of the XY stage with a resolution of 20 nm with appreciated motion tracking results. In the future, displacement sensors with better resolution will be employed to further improve the positioning accuracy of the developed stage. Moreover, the proposed modular conceptual design can be easily extended to devise nanopositioning stages with multiple-axis motion.