1 Introduction

Stack-type piezo actuators are typically used as actuating sources for ultra-precision positioning. A stack-type piezo actuator formed by multi-layered thin piezo films has the advantages of high force generation and rapid response, whereas it has the disadvantages of small displacement, hysteresis, and the requirement of high power for the rapid response [1,2,3,4]. In addition, stack-type piezo actuators conduct non-bipolar operations, such as unipolar or semi-bipolar operations [3]. As the input voltage of the stack-type piezo actuator is asymmetric due to the non-bipolar operation, the displacement is also asymmetric in a full range. For example, a stack-type piezo actuator can be supplied by a voltage from − 30 V to 150 V. Much higher negative voltage causes de-poling of the stack-type piezo actuator.

Ultra-precision mechanisms consisting of flexure hinges are called compliant mechanisms or a flexure mechanisms [6,7,8,9,10,11]. An XY stage with two translational motions can be implemented by a motion guide mechanism with 2-PP or 4-PP compliant parallel mechanisms [2, 12,13,14,15,16,17,18,19,20], where P denotes a prismatic joint. Given that the structure of the 4-PP compliant mechanism is symmetric, the rotation error can be reduced compared to that of the 2-PP compliant mechanism.

A piezo-driven XY stage with a 4-PP compliant mechanism has also been studied for ultra-precision positioning applications [15]. Piezo-driven stages require force transmission mechanisms consisting of flexure hinges in addition to linear guide mechanisms. The force transmission mechanism can be implemented with a lever mechanism or a bridge-type amplification mechanism [21,22,23,24,25,26,27,28,29,30,31,32] driven by a piezo actuator. When only two piezo actuators are integrated into the 4-PP compliant mechanism with force transmission mechanisms, the symmetric structure is no longer valid due to the piezo actuators. Therefore, the 4-PP compliant mechanism with two piezo actuators causes rotation error.

Because the characteristics of a piezo-driven stage are determined according to those of a stack-type piezo actuator, it is important that the compliant mechanism of the piezo-driven stage is designed to overcome the disadvantages of the stack-type piezo actuator. Among these disadvantages, the non-bipolar operation of the stack-type piezo actuator causes non-bidirectional motion on the piezo-driven stage. For example, the alignment process requires that the home position is at the center of the full operation range for fully bidirectional motion. When the home position is at one end of the operating rage, the target platform may not be able to move to the desired position along the positive or negative direction. There are two home positioning strategies at the center of the full operation range. One is to apply offset voltage to the piezo actuator and the other is to employ a bi-directional mechanism. In the former, because the home position is changed from the one end of a full operating range to the center, the target platform of the stage can be operated along a positive direction and a negative direction. However, when the input voltage is removed, the target platform returns to its original position. On the other hand, in the latter case, the home position does not change even when the input voltage is removed. Therefore, a piezo-driven stage with a compliant mechanism for bi-directional motion is necessary. The concept of the bidirectional compliant mechanism [33] for one degree-of-freedom (DOF) translational motion was previously proposed by the authors. However, a parallel-type bi-directional mechanism for multi-DOF requires a modification of the one-DOF bi-directional mechanism, whereas a serial-type bi-directional mechanism for multi-DOF can be simply implemented by adding one-DOF bi-directional mechanisms.

This paper proposes a piezo-driven XY stage with a monolithic compliant parallel mechanism for fully bi-directional operation. The proposed mechanism employs two piezo actuators for each axis, whereas conventional piezo-driven XY mechanisms employ only one piezo actuator for each axis. In addition, the structure of a previously introduced one-DOF bidirectional mechanism [33] is modified for application to an XY parallel mechanism. The proposed mechanism consists of four bridge-type actuating mechanisms and four linear guide mechanisms based on flexure hinges. The actuating mechanisms and the linear guide mechanisms are arranged antagonistically. Therefore, the target platform can be driven by the differential force of the two actuating mechanisms. Owing to this mechanism, the proposed mechanism has bi-directional motion, whereas the conventional mechanism has only uni-directional motion. Because the proposed mechanism has four actuating mechanisms instead of two, it has the disadvantages of increased control complexity and a higher cost. However, in addition to bi-directional motion, it has the advantages of larger displacement, higher stiffness and less rotation error than the same mechanism equipped with two piezo actuators.

This paper proceeds as follows. The concrete structure of the proposed mechanism is described in Sect. 2. The mathematical modelling, analysis and design of the mechanism are presented in Sect. 3. The designed mechanism is verified using a Finite Element Analysis tool in Sect. 4. In Sect. 5, experiments are conducted to demonstrate the performance of the mechanism. Finally, conclusions are given in Sect. 6.

2 Mechanical Structure of a Compliant XY Stage

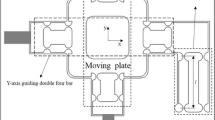
The concept of the proposed mechanism is shown in Fig. 1. Here, it is assumed that the springs are flexure-based prismatic joints. In a PP chain, the motion of the inner prismatic joint is perpendicular to that of the outer prismatic joint. Flexure-based 4-PP chains are arranged at the four sides of the target platform to realize a parallel mechanism for two translational motions. The inner prismatic joint expresses a linear actuator generating only pull force so that the target platform can be operated according to the difference between the two forces along the same axis. The outer prismatic joint guides the motion generated by the other directional forces.

Fig. 1
figure 1

A conceptual mechanism for two translations driven by differential forces

Full size image

The prismatic joints can be implemented by flexure-based mechanisms for linear motion, as shown in Fig. 2. In Fig. 2a, the inner prismatic joint is replaced by an actuating mechanism and the outer prismatic joint is switched to a linear guide mechanism. Because the displacement of the stack-type actuator is 0.1–0.2% [15] of the length of the actuator, the displacement must be amplified for some applications. The actuating mechanism is a bridge type flex-tensional amplification mechanism [27,28,29,30,31,32] for mechanical displacement amplification driven by a stack-type piezo actuator. The amplification ratio depends on the length of the flexure and the offset distance between two flexures which are serially connected. The linear guide mechanism guides the linear motion generated by two actuating mechanisms arranged in the perpendicular direction. This proposed mechanism is equipped with four piezo actuators instead of two for bi-directional operation on both the x- and y-axes, leading to the disadvantages of greater control complexity and a higher cost. However, in addition to bi-directional motion, it has the advantages of larger displacement, higher stiffness and less rotation error than the same mechanism equipped with two piezo actuators, as noted above.

Fig. 2
figure 2

The structure of the proposed mechanism; a Implementation based on flexure mechanism, b Operating principle

Full size image

The operation of the proposed mechanism is described in Fig. 2b. The actuating mechanism generates pull force while the piezo actuator generates push force, and the target platform is driven by the differential force of the two actuating mechanisms. Initially, the piezo actuators generate initial force F0. The target platform is stationary, as it is pulled by the same force generated from the actuating mechanisms from all sides. Therefore, the home position is at the center of the full operating range due to the antagonistic arrangement of the joint chains. In this state, the target platform is movable along the positive and negative directions from the home position when the two piezo actuators generate different forces. For example, when the force of one piezo actuator for the x-axis increases the force by ΔFx while that of the other piezo actuator for the same direction decreases the force by ΔFx, the target platform is moved along the x-axis by differential piezo force. At the same time, the actuating mechanisms for the y-axis tilts and moves as the target platform moves along the x-axis. In addition, due to the x-directional motion of the actuating mechanisms, the outer linear guide mechanisms for the y-axis moves along the x-axis. The tilt motion of the actuating mechanism is caused by the deformation of the flexure hinges. Although the tilt motion violates the assumption of a prismatic joint, it does not affect the linear motion with respect to the x- and y-axes.

3 Analysis and Design of the Proposed Mechanism Based on Mathematical Model

3.1 Mathematical Modeling

A flexure-based mechanism can be modeled using beam theory and the geometric relationships between the flexure hinges and rigid bodies. In a simple structured mechanism, the equation of motion can be derived in an explicit form. A mechanism with bridge-type amplification mechanisms is too complex when attempting to obtain an explicit equation of motion. Although many researchers have proposed mathematical models of bridge-type mechanisms with flexure hinges, their interests focused mainly on the amplification ratio and not on equations of motion. Therefore, matrix-based modeling [29, 34] is the best choice to obtain the equation of motion here.

The proposed mechanism consists of rigid bodies and flexure hinges. Assuming that the flexure hinges are massless springs, the equation of motion can be expressed using the equivalent mass matrix \({\tilde{\mathbf{M}}}\), equivalent stiffness matrix \({\tilde{\mathbf{K}}}\), coordinated vector q, and force vector F, as follows:

$$ {\mathbf{\tilde{M}\ddot{q}}} + {\tilde{\mathbf{K}}\mathbf{q}} = {\mathbf{F}}.{ } $$
(1)

The origin of each coordinate vector is on the mass center of each rigid body. Considering only planar motion of the rigid body, the coordinate vector q is expressed by

$$ {\mathbf{q}} = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{1} } & \cdots & {{\mathbf{q}}_{n} } \\ \end{array} } \right]^{T} , $$
(2)

and

$$ {\mathbf{q}}_{i} = \left[ {\begin{array}{*{20}c} {x_{i} } & {y_{i} } & {\theta_{i} } \\ \end{array} } \right]^{T} ,\quad i = 1\;{\text{to}}\;n $$
(3)

where xi, yi and θi are correspondingly the translations and rotation at the origin oi, and n denotes the number of rigid bodies.

The equivalent mass matrix has only diagonal terms as follows:

$$ {\tilde{\mathbf{M}}} = {\text{diag}}\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1} } & \cdots & {{\mathbf{M}}_{n} } \\ \end{array} } \right], $$
(4)

and

$$ {\mathbf{M}}_{i} = {\text{diag}}\left[ {\begin{array}{*{20}c} {m_{i} } & {m_{i} } & {J_{i} } \\ \end{array} } \right], $$
(5)

where mi and Ji are the mass and mass inertia moment of the i-th rigid body, respectively.

The stiffness matrix of multiple flexure hinges connected between two rigid bodies as shown in Fig. 3 is defined by

$$ {\mathbf{K}}_{ijk} = {\mathbf{R}}_{ijk} {\mathbf{K}}_{ijk}^{h} {\mathbf{R}}_{ijk }^{T} , $$
(6)

where Khijk is the stiffness matrix of the flexure hinge defined at the coordinated Oijk-xijkyijk and the third subscript k represents the k-th flexure hinge between the rigid body i and the rigid body j. Rijk is the rotation matrix of the corresponding flexure hinge defined by

$$ {\mathbf{R}}_{ijk} = \left[ {\begin{array}{*{20}c} {\cos \theta_{ijk} } & { - \sin \theta_{ijk} } & 0 \\ {\sin \theta_{ijk} } & {\cos \theta_{ijk} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]. $$
(7)
Fig. 3
figure 3

Flexure hinges connected between two rigid bodies; a Coordinates, b Displacement vectors

Full size image

The equivalent stiffness matrix is then defined by

$$ {\tilde{\mathbf{K}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\tilde{\mathbf{K}}}_{11} } & { - {\tilde{\mathbf{K}}}_{12} } \\ { - {\tilde{\mathbf{K}}}_{21} } & {{\tilde{\mathbf{K}}}_{22} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & { - {\tilde{\mathbf{K}}}_{1n} } \\ \cdots & { - {\tilde{\mathbf{K}}}_{2n} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ { - {\tilde{\mathbf{K}}}_{n1} } & { - {\tilde{\mathbf{K}}}_{22} } \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \vdots \\ \cdots & {{\tilde{\mathbf{K}}}_{nn} } \\ \end{array} } \\ \end{array} } \right]. $$
(8)

When m flexure hinges are connected between rigid bodies i and j in this equation, the element stiffness term is defined by [34]

$$ {\tilde{\mathbf{K}}}_{ii} = \mathop \sum \limits_{j = 0,j \ne i}^{n} \mathop \sum \limits_{k = 1}^{m} {\mathbf{D}}_{ijk} {\mathbf{K}}_{jik} {\mathbf{D}}_{ijk}^{T} ,{ } $$
(9)
$$ {\tilde{\mathbf{K}}}_{ij} = \mathop \sum \limits_{k = 1}^{m} {\mathbf{D}}_{ijk} {\mathbf{H}}_{ijk} {\mathbf{K}}_{ijk} {\mathbf{D}}_{jik}^{T} ,{ } $$
(10)

where the distance matrices Dijk and Lijk are also defined using the distance vectors shown in Fig. 3; they are correspondingly expressed as

$$ {\mathbf{D}}_{ijk} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ { - d_{yijk} } & {d_{xijk} } & 1 \\ \end{array} } \right], $$
(11)
$$ {\mathbf{L}}_{ijk} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ { - l_{yijk} } & {l_{xijk} } & 1 \\ \end{array} } \right], $$
(12)

where dxijk, dyijk and lxijk, lyijk are the elements of vector dijk and lijk along the x and y axes.

Kijk is the stiffness matrix of the flexure hinge between Oijk and Ojik. The stiffness matrix is the inverse of the compliance matrix Cijk. When a rectangular beam type flexure hinge with dimensions of Lf× tf× hf with respect to the x-, y- and z-axes is employed in the proposed mechanism, the compliance of the flexure hinge is expressed by

$$ {\mathbf{C}}^{h} = \left[ {\begin{array}{*{20}c} {\frac{{L_{f} }}{{Et_{f} h_{f} }}} & 0 & 0 \\ 0 & {\frac{{4L_{f}^{3} }}{{Et_{f}^{3} h_{f} }}} & {\frac{{6L_{f}^{2} }}{{Et_{f}^{3} h_{f} }}} \\ 0 & {\frac{{6L_{f}^{2} }}{{Et_{f}^{3} h_{f} }}} & {\frac{{6L_{f} }}{{Et_{f}^{3} h_{f} }}} \\ \end{array} } \right] . $$
(13)

3.2 Analysis of the Proposed Mechanism

The proposed mechanism without piezo actuators has 33 rigid bodies; therefore, n = 33. The proposed mechanism was analyzed using Eqs. (1) to (13). Simplifying the analysis, the overall size of the proposed mechanism and the dimensions of the rigid bodies are fixed. The proposed mechanism is designed on a duralumin (AL-7075) plate 160 × 160 × 10 mm3 in size. In addition, the thickness of the rigid bodies and flexures were both set to 10 mm. In the actuating mechanism, the selected type of piezo actuator was a stack-type piezoelectric element 10 × 10 × 36 mm3 in size.

As shown in Fig. 4, only four parameters were considered. In the actuating mechanism, the length and thickness of the flexure hinges and the offset distance between two flexures were chosen. In addition, in the linear guide mechanism, only the thickness of the flexure was chosen because the length of the flexure was fixed at 15 mm due to the overall size of the proposed mechanism. The nominal values and limits of the parameters are listed in Table 1.

Fig. 4
figure 4

Parameters

Full size image
Table 1 Parameters for analyzing the proposed mechanism
Full size table

Only one parameter was changed from the minimum limit to the maximum limit when the others were set to nominal values. Figure 5 shows the simulation results. Figure 5a presents the results of an analysis of the stiffness of the mechanism. The stiffness increases with the thickness ti of the flexure hinge in the actuating mechanism and the thickness to of the flexure hinge in the linear guide mechanism, whereas the stiffness decreases with the length Li of the flexure in the actuating mechanism. While the effect of the parameter ti is most sensitive, those of the parameters ti and Li are less sensitive. In addition, the effect of the offset ei between two flexures in the actuating mechanism is trivial. Higher stiffness can be attained with thicker and shorter flexure hinges. The amplification ratio was also analyzed, as shown in Fig. 5b. The amplification ratio decreases with the parameters Li, ti and to. The amplification ratio increases steeply and then decreases slowly with the parameter ei. The parameter ei is most sensitive, whereas the others are less sensitive. A higher amplification ratio can be attained with thinner and shorter flexure hinges, and a shorter offset. Specifically, the maximum amplification ratio is generated when the normalized value of the parameter ei is around 0.1.

Fig. 5
figure 5

Simulation results of the proposed mechanism without piezo actuators; a Stiffness, b Amplification ratio

Full size image

The stack-type piezo actuator can be modeled as a point mass and two flexures as shown in Fig. 6. One end of one flexure is connected to the point mass and the other end of the flexure is connected to the rigid body of the actuating mechanism. The point mass encompasses both the mass mpzt and the mass moment of inertia moment Jpzt of the piezo actuator. The stiffness Kpzt of the piezo actuator can be calculated by Eq. (13). In this case, the number of rigid bodies is increased by the number of the piezo actuators. Therefore the sizes of the equivalent mass matrix and the equivalent stiffness matrix are augmented.

Fig. 6
figure 6

Model of the stack-type piezo actuator

Full size image

Due to the piezo actuators, the rigid bodies of the proposed mechanism are augmented from 33 to 37. The piezo-driven proposed mechanism was analyzed using Eqs. (1) to (13). The displacement of the proposed mechanism was analyzed by applying the piezo forces. Because two piezo actuators produce forces to move along one axis, each piezo actuator produces force F as follows:

$$ F_{ij} = \frac{1}{2}F_{max} \pm \Delta F_{i} , $$
(14)

where i = x, y, and j = 1, 2. In addition, Fmax is the maximum piezo force. When \(\Delta F_{i} = \frac{1}{2}F_{max}\), maximum displacement can be obtained.

The maximum displacement was analyzed as shown in Fig. 7a. The amplification ratio decreases with the parameters Li, ti and to. The amplification ratio increases steeply and then decreases with the parameter ei. Higher displacement can be attained with thinner and shorter flexure hinges, and a shorter offset. Specifically, the maximum displacement has a peak value when the normalized value of the parameter ei is approximately 0.2.

Fig. 7
figure 7

Simulation results of the proposed mechanism with piezo actuators; a Maximum displacement, b Resonance frequency

Full size image

The characteristic equation of Eq. (1) is expressed by

$$ \left| {{\mathbf{I}} - {\tilde{\mathbf{M}}}^{ - 1} {\tilde{\mathbf{K}}}} \right| = 0 , $$
(15)

where λ and I are correspondingly the characteristic roots and the identity matrix. Equation (15) causes resonance frequencies as follows:

$$ f_{i} = \frac{1}{2\pi }\sqrt {_{i} } ,{ } $$
(16)

where λi is the i-th characteristic root and fi is the i-th resonance frequency.

Using Eq. (16), the lowest translational resonance frequency was obtained as shown in Fig. 7b. The resonance frequency increases with the parameters ti, ei, and to, and it decreases with the parameter Li. A higher resonance frequency can be attained with thicker and shorter flexure hinges and a larger offset.

3.3 Design of the Proposed Mechanism

The proposed mechanism was designed to optimize the maximum displacement dmax due to the maximum piezo force, as follows:

Minimize

$$ \frac{1}{{d_{max} }} . $$
(17)

Subject to

$$ v_{i, min} \le v_{i} \le v_{i, max} , $$
(18)

and

$$ \sigma_{max} - \frac{{\sigma_{Y} }}{{S_{f} }} \le 0 , $$
(19)
$$ f_{d} - \Delta f \le f_{tr} \le f_{d} + \Delta f, $$
(20)

where vi denotes design parameter ti, Li, ei or to. The subscripts min and max represent the limits of the parameters. The variables σmax, σY, Sf, fd, Δf and ftr are the maximum stress of the mechanism, the yield stress of the material of the mechanism, a safety factor, the desired frequency, the frequency deviation and the lowest translational resonance frequency of the mechanism, respectively. AL-7075 with yield stress of 505 MPa was chosen as the material of the proposed mechanism, and a safety factor of 3 was selected. In addition, the desired frequency was 200 Hz and the frequency deviation is 20 Hz.

The stress on the surfaces of the ends of the flexure hinge can be calculated by

$$ {\sigma } = K_{a} \frac{{F_{a} }}{A} + K_{b} \frac{{M_{b} }}{I}\frac{{t_{f} }}{2}{ },{ } $$
(21)

where σ is the stress, Ka and Kb are correspondingly the stress concentration factors under axial force and bending moment, A is the section area of the flexure hinge, I is the area moment of inertia, and tf is the thickness of the flexure hinge. In a static state, the relative displacement of the two rigid bodies can be obtained by Eq. (1) when forces are applied to the rigid bodies. After the relative displacement of the flexure hinge between two rigid bodies is calculated from the displacements of the two rigid bodies, the force and moment at the ends of the flexure hinge can be derived by

$$ F_{a} = \frac{AE}{{L_{f} }}\delta_{a} , $$
(22)
$$ M_{b} = - 6\frac{EI}{{L_{f}^{2} }}\delta_{b} + 4\frac{EI}{{L_{f} }}\theta_{b} , $$
(23)

where δa, δb, θb and Lf are the axial elongation, lateral deflection, deflection angle, and the length of the flexure hinge, respectively. The ends of the flexure hinges were corner filleted to prevent stress concentration. The radius of the corner fillet is 0.2 mm.

The designed parameters were calculated, as listed in Table 2. The stiffness of the proposed mechanism without piezo actuators was calculated using the designed parameters. When force is applied to the target platform, the calculated stiffness was 0.075 N/μm. The amplification ratio was also calculated. After push and pull forces of 1 N were applied to the four input platforms in the actuating mechanisms for the x-axis, the displacement of each input platform was 0.084 μm and the displacement of the output platform was 2.227 μm. Therefore, the calculated amplification ratio was 6.63.

Table 2 Designed parameters for the proposed mechanism
Full size table

When the piezo actuators were mounted in the mechanism, the maximum displacement, the resonance frequency and the maximum stress were calculated. The maximum displacement was ± 123 μm, and the lowest translational resonance frequency was 204 Hz. In addition, the maximum stress generated on the ends of the flexure hinge of the actuating mechanism was 131 MPa.

Instead of differential actuation, the effect of a single actuation was investigated. Only one piezo actuator per axis was employed. The maximum displacement then reached 201 μm, which is 82% to that with differential actuation. Therefore, differential actuation can increase the displacement by 22% compared to single actuation. In addition, maximum stress of 154 MPa was generated on the ends of the flexure hinge, which is greater than that with differential actuation.

The rotation error distributions were investigated in both the differential actuation and the single actuation cases. Although single actuation operates with the same flexure mechanism used with differential actuation, the entire mechanism becomes an asymmetric structure with addition of a single actuator per axis. Subsequently, this causes parasitic rotation error.

Figure 8 shows the rotation error distribution. The rotation error was calculated using Eq. (1). The rotation error at a desired position (x, y) can be calculated by the Newton-Rapson algorithm. The position (x, y) of the proposed mechanism is repeatedly updated to reach the desired position by controlling the piezo forces using this algorithm. If the calculated position is close to the desired position within an acceptable level of error, the rotation error can then be obtained. Figure 8a shows the rotation error distribution in the single actuation case, whereas Fig. 8b shows that in the differential actuation case. In Fig. 8a, the rotation error increases positively along the x-axis and negatively along the y-axis. The maximum rotation error reaches 0.58 × 10–3 rad. However, in Fig. 8b, the rotation error reaches 0.56 × 10–14 rad, which is negligible. This demonstrates that differential actuation can reduce the rotation error significantly compared to single actuation.

Fig. 8
figure 8

Comparison of rotation errors calculated from the mathematical model; a Single actuation case, b Differential actuation case

Full size image

4 Verification Using Finite Element Analysis (FEA)

The optimally designed mechanism was analyzed using COMSOL Multiphysics Version 5.3a. The 3D geometric modeling was carried out by Solidworks, and the geometric model was then imported into COMSOL Multiphysics. In COMSOL Multiphysics, the designed mechanism was considered as a linear elastic material, in this case AL-7075. The piezo actuators were considered to be as a linear elastic material with an elastic modulus of 45 GPa, Poisson’ ratio of 0.29, and density of 8000 kg/m3. The external faces of the mechanism were fixed as constraints. Free tetrahedral meshes were generated automatically. Finer meshes were generated in the flexure hinges, while coarser meshes were generated in the other parts.

Initially, a static analysis of the mechanism without the piezo actuators was conducted, as shown in Fig. 9. When force of 1 N was applied to the target platform, the displacement of the target platform was 13.1 μm, as shown in Fig. 9a. Thus, the stiffness of the mechanism is 0.076 N/μm, which nearly coincides with the calculated value. Displacement of 1 μm was applied to the input platforms in the actuating mechanisms for the x-axis as shown in Fig. 9b. One actuating mechanism was pushed while the other actuating mechanism was pulled by the input displacement. Differential displacement applied as the input was 4 μm. The displacement of the target platform was then 26.6 μm. Thus, the amplification ratio of this mechanism is 6.65, which nearly coincides with the calculated value. Because this mechanism has a symmetric structure, the analysis of the y-axis is identical to that of the x-axis.

Fig. 9
figure 9

Static analysis results of the proposed mechanism without piezo actuators; a Applying to the target platform, b Applying displacement to the input platforms

Full size image

After integrating the piezo actuators in the mechanism, forces were applied both ends of the piezo actuators as shown in Fig. 10. Figure 10a is the single actuation case, whereas Fig. 10b is the differential actuation case. In the single actuation case, the displacement reached 199 μm, and maximum stress of 140 MPa was generated at the ends of the flexure hinges. The FEA results show values which are 1% lower in terms of the maximum displacement and 10% lower in terms of the maximum stress as compared to the calculated results. In addition, it was observed that the target platform of the mechanism rotates as the piezo force is increased, which causes rotation error.

Fig. 10
figure 10

Static analysis results of the proposed mechanism equipped with piezo actuators; a Single actuation case, b Differential actuation case

Full size image

In the differential actuation case, the maximum displacement can be reached when one piezo actuator generates a maximum force and the other side piezo actuator does not generate force. In the analysis, displacement of 120 μm was generated in the target platform, as shown in Fig. 10b. Therefore, this mechanism can reach 240 μm in the bipolar operation mode. Maximum stress of 110 MPa was generated at the flexures in the actuating mechanisms, satisfying Eq. (19). The FEA results were 2.5% lower in terms of the maximum displacement and 10% lower in terms of the maximum stress as compared to the calculated results. In addition, the displacement in the differential actuation mode is about 17% greater than that of single actuation.

The rotation error was simulated as shown in Fig. 11. In the single actuation case, the rotation error increases positively along the x-axis and negatively along the y-axis. In the differential actuation case, the distribution of the rotation error is similar to that of the single actuation case. The maximum rotation error with single actuation reached 0.6 × 10–3, while that of differential actuation reached 0.7 × 10–5 rad. In the single actuation case, the rotation angle analyzed by the FEM is nearly identical to the calculated value. However, in the differential actuation case, the rotation error analyzed by the FEM shows a large difference relative to the calculated value. Although the difference is large, the magnitude of the analyzed rotation error remains small because the calculated rotation error is practically negligible. It is considered that this difference stems from the minute deformation of the target platform, which is assumed to be a rigid body. In addition, the rotation error in the differential actuation case is only 1/117 times at most compared to that in the single actuation case. This indicates that differential actuation can reduce rotation error significantly compared to single actuation.

Fig. 11
figure 11

Comparison of rotation errors using Finite Element Analysis; a Single actuation case, b Differential actuation case

Full size image

The resonance frequency was analyzed by means of a frequency analysis, and the first translational mode was obtained as shown in Fig. 12. The translational resonance frequency was generated at 202 Hz, which is in fairly good agreement with the calculated value. The resonance frequency satisfies Eq. (20).

Fig. 12
figure 12

Mode shape at translational resonance frequency

Full size image

5 Experimentation with the Proposed Compliant Stage

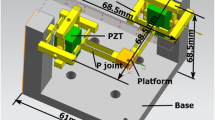
A compliant stage was assembled by integrating piezo actuators and displacement sensors into the proposed mechanism, as shown in Fig. 13. The mechanism was machined monolithically by means of wire electro-discharge machining for flexure hinges. Four stack-type piezo actuators (PSt 150/10 × 10/40) manufactured by Piezomechanik GmbH [5] were inserted into the bridge-type amplification mechanisms as shown in Fig. 13a. Two capacitive sensors (D-100) with two-electrode plates manufactured by Physik Instrumente [3] were embedded to measure the displacement of the target platform as shown in Fig. 13b. In addition, a PCI board as a control system (E-761) manufactured by Physik Instrumente [3] was used for the high voltage outputs, sensor inputs, and proportional-integral controllers.

Fig. 13
figure 13

Flexure-based XY stage driven by differential piezo forces; a Top view, b Bottom view

Full size image

The frequency response of the compliant stage was assessed in an open-loop state by impacting the target platform. Figure 14 shows the frequency responses of the x- and y-axes as depicted using NanoCapture™ software provided by Physik Instrumente. The first resonance frequencies were generated at 190 Hz in the x-axis, as shown in Fig. 14a and at 195 Hz in the y-axis as shown in Fig. 14b. A difference between the two resonance frequencies of less than 2.6% was observed in the x- and y-axes. This difference is considered to be due to machining and assembling errors. The experimental frequencies have errors within 7% of the FEA result.

Fig. 14
figure 14

Frequency responses; a x-axis, b y-axis

Full size image

Experiments were conducted to assess the operating range of the stage. Here, the input voltage of one piezo actuator for one axis is V1 and that of the other piezo actuator is V2. When V0 is the initial voltage and ΔV is the control voltage, the input voltage is

$$ V_{i} = V_{0} \pm \Delta {\text{V}}, $$
(24)

where i = 1 and 2. The input voltage V0 is 50 V, and the control input ΔV can then be changed from − 50 to 50 V.

Figure 15 shows the operating ranges along the x- and y-axes in the open-loop state. While the input voltage V1 was changed from 0 to 100 V and then back to 0 V, the other input voltage V2 was changed from 100 to 0 V and then back to 100 V. The displacement of the target platform increased and then decreased. In this figure, the motion of the target platform showed typical hysteresis behavior caused by the piezo actuator. In addition, bi-directional operation was demonstrated by tracing the motion of the target platform along the positive and negative directions from the zero position. The operating range attained was ± 110 μm, with error of 9% compared to the simulation result shown in Fig. 10b.

Fig. 15
figure 15

Operating ranges

Full size image

The hysteresis behavior of the target platform was compensated by a proportional-integral controller using the control system (E-761). The proportional gain and integral gain were empirically determined. Using the control system, the step responses of the control system were measured, as shown in Fig. 16. In Fig. 16a and b, step responses with overshoot of 4% were generated and then converged to the position of 10 μm in the x- and y-axes. The rising and settling times of the step responses were 10 ms and 40 ms, respectively.

Fig. 16
figure 16

Step responses; a x-axis, b y-axis

Full size image

Using the control system, a series of step inputs with a step of 4 nm was increased and then decreased. Then the responses for the x- and y-axes were measured as shown in Fig. 17. The responses shown in Fig. 17a, b attained a resolution of 4 nm.

Fig. 17
figure 17

Stepwise responses; a x-axis, b y-axis

Full size image

The response of the target platform was measured as a sine wave swept from 1 to 1000 Hz was applied to the input of the control system. The frequency responses of the control system were then obtained, as shown in Fig. 18. The bandwidth of the system was approximately 20 Hz.

Fig. 18
figure 18

Frequency responses using a proportional-integral control system

Full size image

Using the proportional-integral control system, the rotation of the target platform was measured while the target platform was positioned along the x- and y-axes, as shown in Fig. 19. In the range of ± 100 μm, the rotation error reached 3 × 10–5 rad. Although the experimental rotation error is approximately four times greater than analytical rotational error in the differential actuation case according to the FEA, it is 1/20 times compared to that in the single actuation case according to the FEA.

Fig. 19
figure 19

Distribution of rotation error

Full size image

6 Conclusion

In this paper, we proposed a piezo-driven XY stage with a monolithic compliant parallel mechanism for fully bidirectional operation. Flexure-based 4-PP chains were arranged antagonistically at the four sides of a target platform of an XY stage. The motion of each axis was conducted by differential force between piezo actuators in two actuating mechanisms arranged at both sides of a target platform along the same axis. The actuating mechanism is a piezo-driven bridge-type amplification mechanism. Due to this antagonistic arrangement, the home position of the target platform was at the center position of the full operating range, and the target platform was movable along the positive and negative directions from the home position.

The proposed mechanism was analyzed using the matrix-based mathematical model. Four parameters were selected with which to analyze the mechanism, after which these parameters were determined by the optimal design. In addition, FEA was carried out to verify the performance of the designed mechanism. Finally, we demonstrated the proposed bidirectional operation of the piezo-driven XY stage through an experiment with an operating range of ± 110 μm in the x- and y-axes. The experiments revealed that the piezo-driven XY stage had a rising time of 10 ms, a settling time of 40 ms, a bandwidth of 20 Hz, and a resolution of 4 nm in the x- and y-axes. In addition, it was verified that the proposed mechanism using differential actuation dramatically reduces the parasitic rotation error compared to the mechanism using single actuation.