1 Introduction

In recent years, due to the description is more in line with real life, singular systems, that is, descriptor systems or generalised systems, have been widely conducted in various aspects of control field, such as electromagnetic systems, biological systems, flexible structures [1,2,3]. Generalized systems, which are more superior to complex phenomena than the normal system, so it has attracted the attention of many scholars [4,5,6]. Nevertheless, with the deepening of research, generalized system is far from meeting the needs of normal applications, so the fractional order system has slowly entered our sight. The industrial process has been refined under the fractional derivatives and calculus, which makes the research of fractional order systems(FOSs) very meaningful [7,8,9]. For an operating system, maintaining stable performance is the most valued actual issue. Lots of efficient stability conditions of FOSs have been established in [10,11,12,13]. According to LMIs, the stability analysis of fractional commensurate order systems with the cases of \(0<\alpha <2\) was presented in [10]. As stated in [13], a novel conceptual unified framework for fractional neural networks was proposed because of fractional calculus has been classified as artificial neural networks. Since these two systems both play a vital role in control theory, the two systems are combined into a complex system, singular fractional order system, which is a new area worthy researching and have achieved abundant research results in recent years [14,15,16]. Guo et al. [14] focused on the stabilization problem for SFOSs by LMIs and a static output feedback controller was designed. In [15], a superior criteria have been put forward by strict LMI approach without equality constraints to obtain the stability of SFOS.

As we all know, in practice, most physical models are nonlinear. The control approach based on Takagi-Sugeno fuzzy systems is an efficient way to discuss complex nonlinear systems. Up to now, fuzzy systems have gained widespread attention and significant results have been published for T-S fuzzy systems [17,18,19,20]. With a novel fuzzy observer and membership functions, Wang et al. [17] designed an algorithm and a novel controller to guarantee the asymptotically stable of the fuzzy \(H_{\infty }\) systems. Han et al. [18] addressed the application of multi-dimensional T-S fuzzy systems to eliminate the impact of failures. In [19], the novel descriptor observer and controller were designed to estimate faults, external noise and promoted the transformed closed-loop system to be asymptotically stable. Afterwards, an adaptive sliding mode controller strategy, whose sliding surface has already been constructed to process T-S fuzzy SFOSs with unknown constants in [21]. In order to be more realistic and achieve better performance, Asemani et al. [22] proposed sufficient conditions for stabilizing and designed a robust \(H_{\infty }\) observed-based controller for T-S fuzzy systems with uncertainty by LMI.

In fact, due to engineering and practical applications, it is inevitable that faults always exist, which requires many experts to spend a lot of energy to eliminate [23,24,25,26]. Compared with traditional feedback control, adaptive control design can better deal with the uncertainties in system dynamics and failures that may occur during system operation. In [26], a novel way is proposed to rape with the unknown singular systems by transforming it into the non-singular form with faults. Furthermore, an adaptive neural network approximation model for a nonlinear function is given. The key to the design task is to find a suitable adaptive law and a matched controller, so that under the condition of model matching, the adaptive controller still automatically adjust the remaining controller even though other actuators in the control system have unknown failures, which eventually achieve the desired control objective [27,28,29]. For the in-depth study, it is necessary to research the specific system, whose development is not completed, and there are still some aspects worth complementing.

Motivated by the above discussions, as a result of the increase in engineering accuracy requirements, it is inevitable to study the issue of adaptive observer for T-S fuzzy singular FOSs, which have not been studied completely. The contributions of the paper can be summarized as follows:

  1. 1.

    A new adaptive observer based on fault-tolerant control for SFOSs is proposed by designing sliding mode reaching law, which ensure that the stability of T-S fuzzy SFOSs and the regular condition towards the sliding surface has been improved.

  2. 2.

    A convex combination technique is developed, such that the proposed fault-tolerant control way is valid for the fuzzy systems with faults.

  3. 3.

    Due to the information obtained by the above observer and the designed adaptive parameters, according to the adaptive control law, an adaptive observer-based controller is proposed, which is more practical to estimate actuator faults of the SFOSs. The stability conditions in this paper reduce the conservatism and computational burden.

  4. 4.

    Further, novel sufficient conditions are obtained to ensure the stability ofthe proposed T-S fuzzy SFOSs with \(H_{\infty }\) performance in terms of LMI. Compared with the existed references, the \(H_{\infty }\) control method is more concise and more convenient for calculation with faults. Finally, to illustrate the proposed method is available, numerical examples are presented.

The rest of the paper is divided into the following sections. Section 2 presents some basic formula expressions. Section 3 gives an account of main results of the paper. In Sect. 4, numerical examples are given to display the validity of the theorem we proposed and Sect. 5 is the conclusion of the paper.

Notation: Here, it gives the definition of the symbols used in this paper. \(X^T\) expresses the transposition of the matrix X. \(\mathrm {sym}\{X\}\) means the form of \(X+X^T. \) \(*\) notes a corresponding symmetric matrix. If there is no special description, for the dimensions of the matrix, which should be compatible.

2 Problem formulation and preliminaries

In this part, some preliminary for T-S fuzzy singular fractional order systems are given.

Definition 1

[11] The Caputo derivative of f(t) is expressed as follows , where \(\alpha \) belongs (0, 1) : 

$$\begin{aligned} _{c}D^{\alpha }_{t}x(t)=\frac{d^{\alpha }f(t)}{dt^{\alpha }}=\frac{1}{\varGamma (\varsigma -\alpha )}\int ^{t}_{0}\frac{f^{(\varsigma )}(\tau )}{(t-\tau )^{\alpha +1-\varsigma }}d\tau , \end{aligned}$$
(1)

where \(\varsigma -1<\alpha \le \varsigma , \varsigma \in Z^+,\) and \(\varGamma (x)=\int ^{\infty }_{0}e^{-t}t^{x-1}dt\) is gamma function. For convenience, we simplify \(_{c}D^{\alpha }_{t}x(t)\) to  \(D^{\alpha }x(t).\)

Immediately afterwards, the continuous-time fuzzy T-S singular fractional order systems is given as follows:

\(R_{i}(t):\) IF \(\mu _{1}(t)\) is \(D_{1i}\), \(\mu _{2}(t)\) is \(D_{12},\)..., \(\mu _{j}(t)\) is \(D_{1j},\) THEN

$$\begin{aligned} \left\{ \begin{array}{l} ED^{\alpha }x(t)=A_{i}x(t)+B_{i}(u(t)+f_a(t)),\\ y(t)=C_{i}x(t).~~~~~~~~~~~~~~~~~ \end{array} \right. \end{aligned}$$
(2)

where i is the number of IF-THEN rules, \(i=1,2,...,r.\) \(D_{i j}\) are the fuzzy sets, \(x(t)\in \mathbb {R}^{n}\) stands state vector, \(u(t)\in \mathbb {R}^{m}\) represents control input, \(f_a(t)\) means actuator faults. \(A_{i}, B_{i}, C_{i}\) are constant matrices. \(E\in \mathbb {R}^{n}\) and \(\mathrm {rank}(E)=r<n,\) which is singular. Afterwards, the overall T-S fuzzy SFOSs are expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} ED^{\alpha }x(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))\{A_{i}x(t)+B_{i}(u(t)+f_a(t))\},\\ y(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))C_{i}x(t).~~~~~~~~~~~~~~~~~~~~ \end{array} \right. \end{aligned}$$
(3)

where \(h_i(\mu (t))=\frac{\varpi _{i}(\mu (t))}{\sum \nolimits _{i=1}^{r}\varpi _{i}(\mu (t))},\) \(\varpi _{i}(\mu (t))=\prod \nolimits _{j=1}^{p}D_{ij}(\mu _{j}(t)),\) in which \(D_{ij}(\mu _{j}(t))\) are the grade of membership of \(\mu _{j}(t)\) in \(D_{ij}.\) If \(\varpi _{i}(\mu (t))>0,\) then, \(\sum \nolimits _{i=1}^{r}\varpi _{i}(\mu (t))\ge 0.\) Therefore, \(h_i(\mu (t))\ge 0,\) \(\sum \nolimits _{i=1}^{r}h_i(\mu (t))=1.\)

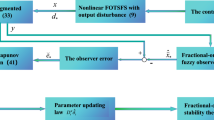
In addition, the fault-tolerant control problem is investigated. The next step is to devise an adaptive control law that forces the system state to reach the sliding surface under possible actuator fault. The detailed flow diagram of the proposed approach is shown in Fig. 1 to clarify the design procedure and structure.

Fig. 1
figure 1

Flow diagram in SFOS (3)

Full size image

Next, in order to achieve our objective, some Lemmas are needed in the sequel.

Definition 2

[30] For a generalized fractional order system \(ED^{\alpha }(t)=Ax(t),\) which is said to be regular if \(\mathrm {det}(s^{\alpha }E-A)\) is not identially zero. When \(\mathrm {deg}(\mathrm {det}(sE-A))=\mathrm {rank}(E),\) unforced SFOSs are impulse free, which is also stable as the generalized eigenvalues of \(\mathrm {det}(\lambda E-A)=0\) lying in \(D_{\alpha }=\{\lambda : |arg(\lambda )| > \frac{\alpha \pi }{2}\}.\) SFOSs are admissibile if the above three conditions are fulfilled.

Lemma 1

[15] The singular FOS in Definition 2 with \(0<\alpha <1\) is admissible iff there exist matrices X and Y, P satisfying

$$\begin{aligned} \left[ \begin{array}{cc} EX &{} EY\\ -EY&{}EX \end{array} \right] =\left[ \begin{array}{cc} X^TE^T &{} -Y^TE^T\\ Y^TE^T&{}X^TE^T \end{array} \right] \ge 0, \end{aligned}$$
(4)

and

$$\begin{aligned} \mathrm {sym}\{rA^TP\}<0. \end{aligned}$$

where \(r=e^{j(1-\alpha )\frac{\pi }{2}}.\)

Lemma 2

[14] Suppose SFOS in Definition 2 is regular, and M and N are invertible matrices such that

$$\begin{aligned} MEN=\left[ \begin{array}{cc} I_m &{} 0\\ 0&{} N_{n-m} \end{array} \right] ,~MAN=\left[ \begin{array}{cc} \bar{A_1} &{} 0\\ 0&{} I_{n-m} \end{array} \right] , \end{aligned}$$
(5)

where \(\lambda _{max}(\bar{A_1})>0,\,N_{n-m}\) is nilpotent matrix.

When the regularity of SFOS in definition 2 is unknown, and M and N are invertible matrices such that

$$\begin{aligned} MEN=\left[ \begin{array}{cc} I_m &{} 0\\ 0&{} 0 \end{array} \right] ,MAN=\left[ \begin{array}{cc} A_{11} &{} A_{12}\\ A_{21}&{} A_{22} \end{array} \right] \end{aligned}$$
(6)

Lemma 3

[31] A, B are known matrices and \(\varTheta \in \mathrm {H}_{n},\varPhi \in \mathrm {H}_{2},\varOmega \in \mathrm {H}_{2}\). Define \(\varLambda \) as follows,

$$\begin{aligned} \varLambda (\varPhi ,\varOmega )=\left\{\lambda \in C|\left[ \begin{array}{cc} \lambda \\ 1 \end{array} \right] ^*\varPhi \left[ \begin{array}{cc} \lambda \\ 1 \end{array} \right] =0,\left[ \begin{array}{cc} \lambda \\ 1 \end{array} \right] ^*\varPsi \left[ \begin{array}{cc} \lambda \\ 1 \end{array} \right] \ge 0 \right\}. \end{aligned}$$

Then, there exist \(P,Q>0\) such that

$$\begin{aligned} \left[ \begin{array}{ccc} A&{}B\\ E&{}0 \end{array} \right] ^*(\varPhi \otimes P +\varPsi \otimes Q) \left[ \begin{array}{ccc} A&{}B\\ E&{}0 \end{array} \right] +\varTheta <0 \end{aligned}$$

Lemma 4

[30] Suppose \(S_1\) and \(S_3\) are symmetric matrices and \(S_2\) is constants matrix, then \(S_1+S_2S^{-1}_3S_2^T<0\) iff

$$\begin{aligned} \left[ \begin{array}{cc} S_1 &{} S_2\\ S_2^T &{} S_3 \end{array} \right] <0. \end{aligned}$$

Lemma 5

[9] Suppose D and E are constant matrices and S is a symmetric matrix, which satisfy the following inequality \(S+DFE+(DFE)^T<0\) with F satisfying \(F^TF\le I,\) if and only if for some \(\varepsilon >0,\)

$$\begin{aligned} S+\left[ \begin{array}{cc} E^T &{} D\\ \end{array}\right] \left[ \begin{array}{cc} \varepsilon ^{-1}I &{} 0\\ 0&{}\varepsilon I\end{array}\right] \left[ \begin{array}{cc} E\\ D^T \end{array} \right] <0 \end{aligned}$$

3 Main results

3.1 Adaptive observer design

First, based on the adaptive control strategy, an observer is designed.

$$\begin{aligned} \left\{ \begin{array}{lll} ED^{\alpha }{\hat{x}}(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))\{A_{i}{\hat{x}}(t)+L_{i}(y(t)-{\hat{y}}(t))\},\\ {\hat{y}}(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))C_{i}{\hat{x}}(t).~~~~~~~~~~~~~~~~~~ \end{array} \right. \end{aligned}$$
(7)

Subsequently, \(e(t)=x(t)-{\hat{x}}(t)\) means the error of state variable and \(e_{y}(t)=y(t)-{\hat{y}}(t)\) represents the error of output variable. Therefore, the above-mentioned equivalent adaptive fuzzy controller can be rephrased into the following form:

$$\begin{aligned} \begin{array}{l} u_a(t)=\sum \limits _{j=1}^{r}h_j(\mu (t))\{\mathcal {K}_{i}{\hat{x}}(t)-(H_{j}B_{j})^{-1}H_{j}A_{j}e(t)-f_a(t)\},\\ \end{array} \end{aligned}$$
(8)

where \(H_{i}, \mathcal {K}_{i}\) are constant matrices under the constraint condition \(\mathrm {det}(H_{i}B_{i})\ne 0.\) Next, the error system is given as follows:

$$\begin{aligned} \left\{ \begin{array}{l} ED^{\alpha }e(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))\{(A_{i}-L_{i}C_{i})e(t)+B_{i}\mathcal {K}_{i}{\hat{x}}-B_{i}(H_{i}B_{i})^{-1}H_{i}A_{i})e(t)\},\\ e_{y}(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))C_{i}e(t).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{array} \right. \end{aligned}$$
(9)

Substituting the equivalent control law (8) into (3) and defining \(\xi (t)=\left[ \begin{array}{ccc} x^{T}(t)&e^{T}(t) \end{array} \right] ^T,\) the error dynamic can be acquired as:

$$\begin{aligned} ED^{\alpha }\xi (t)=\sum \limits _{i=1}^{r}h_i(\mu (t)){\bar{A}}_{i}\xi (t) \end{aligned}$$
(10)

where \({\bar{A}}_{i}=\left[ \begin{array}{ccc} A_{i}+B_{i}\mathcal {K}_{i}&{}-B_{i}\mathcal {K}_{i}-G_{i}A_{i}\\ A_{i}-L_{i}C_{i}-B_{i}\mathcal {K}_{i}-G_{i}A_{i}&{}B_{i}\mathcal {K}_{i}, \end{array} \right] ,\) \(G_i=B_{i}(H_{i}B_{i})^{-1}H_{i}.\)

3.2 Admissibility analysis

In this section, we consider the issue of the admissibility of closed-loop error dynamic system (10). In order to simplify, we make the following equivalent transformation of the symbol. \(h_{\mu }=\sum \limits _{i=1}^{r}h_i(\mu (t)),{\bar{A}}_{h}=h_{\mu }{\bar{A}}_{i}, C_{h}=h_{\mu }C_{i}, G_{h}=h_{\mu }G_{i}, L_{h}=h_{\mu }L_{i}, \mathcal {K}_{h}=h_{\mu }\mathcal {K}_{i}.\)

Theorem 1

T-S singular FOS (3) is asymptotically stable with adaptive controller (8) and the fractional order belongs to \( 0<\alpha <1 \) if X is symmetric matrix and \(P_{1i}>0,P_{2i}>0,Y\) are constant matrices and a scalar \(\beta >0\) satisfying the following LMIs:

$$\begin{aligned}&\left[ \begin{array}{cc} EX &{} EY\\ -EY&{}EX \end{array} \right] =\left[ \begin{array}{cc} {X^{T}} {E^{T}} &{} -{Y^{T}} {E^{T}}\\ {Y^{T}} {E^{T}}&{} {X^{T}} {E^{T}} \end{array} \right] \ge 0, \end{aligned}$$
(11)
$$ \mathrm {sym}(r({\bar{A}}_{h}^{T}P)<0. $$
(12)

where

$$ P=\left[ \begin{array}{cc} P_{1i} & 0\\ 0& \beta P_{2i}\\ \end{array} \right] , r=e^{j\frac{\pi }{2}\alpha }\omega ^{\alpha }. $$

Proof

Substituting \({\bar{A}}_{h},\) and P into (12), we can obtain the inequality (13), then, the following results are given:

$$ \mathrm {sym}\left[ \begin{array}{lll} r(A_i+B_{i}\mathcal {K}_{i})^{T}P_{1i}&{}r(A_{i}-L_{i}C_{i}-B_{i}{\mathcal {K}_{i}}-{\bar{G}}_{i}A_{i})^{T}P_{2i}\\ -r(B_{i}{\mathcal {K}_{i}}+{\bar{G}}_i{\bar{A}}_{i})^TP_{1i}-r\beta (B_{i}{\mathcal {K}_{i}})^{T}P_{2i}&{}r(B_{i}{\mathcal {K}_{i}})^TP_{2i} \end{array} \right]<0, $$
(13)
$$ r(A_{h}+B_{h}\mathcal {K}_{h})^{T}P_{1i}+r^{*}P^{T}_{1i}(A_{h}+B_{h}\mathcal {K}_{h})<0.$$
(14)

As a result of lemma 1, T-S singular FOS (10) is asymptotically stable.

Remark 1

It is obvious that the inequality (11) in Theorem 1, is not strict LMIs, which contains constraints condition and make calculation difficult. To solve the problem, matrix S is given, satisfying \(ES=0\) and we give the following Theorem.

Theorem 2

T-S singular FOS (3) is asymptotically stable with adaptive controller (8) and the fractional order belongs to \( 0<\alpha <1 \) if there exists real symmetric matrices X, Y,  \(P,Q_{i}\) satisfying the following LMIs:

$$\left[ \begin{array}{cc} X&{}Y\\ -Y&{}X \end{array} \right]> 0,$$
(15)
$$ \mathrm {sym} \{r{\bar{A}}^T_{h}(PE^T+SQ_{h})+r^{*}{\bar{A}}_{h}YE^{T}\}<0.$$
(16)

After that, since the proof method is similar to Theorem 1, it will not be explained in detail herein.

3.3 Adaptive laws design

In this part, an adaptive law is designed to guarantee the error system reach stability state in a limited time. In order to be necessary, we pull in the following assumption.

Assumption 1

The subsystem of the error dynamic system (9) is bounded and satisfying

$$ \underset{0\le t<\infty }{\mathrm {sup}}\Vert e(t)\Vert \le \delta _{i},i=1,2,...,r $$

where \(\delta _{i}\) are known positive constant.

Subsequently, we give the adaptive control laws, whose parameters are given below. The adaptive parameters \(\hat{\delta }_{i}, \hat{\gamma }_{i1}, \hat{\gamma }_{i2}\) to estimate \(\delta _{i}, \gamma _{i1}, \gamma _{i2}\), respectively. The estimation errors are expressed as follows:

$$\begin{aligned} \begin{array}{lll} \tilde{\delta }_{i}=\hat{\delta }_{i}-\delta _{i}, \tilde{\gamma }_{i1}=\hat{\gamma }_{i1}-\gamma _{i1}, \tilde{\gamma }_{i2}=\hat{\gamma }_{i2}-\gamma _{i2}. \end{array} \end{aligned}$$

Then, we propose the adaptive controller laws such that the reachability condition is obtained.

$$\begin{aligned} u_{i_{c}}(t)=\mathcal {K}_{i}x(t)-(H_{i}B_{i})^{-1} \left \{-H_{i}T_{i}C_{i}e(t)+\frac{\nu _{i}(t)}{\Vert \nu _{i}(t)\Vert }~ (\Vert H_{i}A_{i}+T_{i}C_{i}\Vert \hat{\delta }_{i} +\Vert H_{i}B_{i}\Vert \hat{\gamma }_{i1}+\Vert H_{i}B_{i}\Vert \Vert y(t)\Vert \hat{\gamma }_{i2}+\varepsilon _{0}) \right \}\end{aligned}$$
(17)
$$\begin{aligned} \left\{ \begin{array}{lll} E_1D^{\alpha }\hat{\delta }_{i}=\sigma _{1i}\Vert \nu _{i}(t)\Vert \Vert H_{i}A_{i}+T_{i}C_{i}\Vert ,\\ E_1D^{\alpha }\hat{\gamma }_{i1}=\sigma _{2i}\Vert \nu _{i}(t)\Vert \Vert H_{i}B_{i}\Vert ,\\ E_1D^{\alpha }\hat{\gamma }_{i2}=\sigma _{3i}\Vert \nu _{i}(t)\Vert \Vert H_{i}B_{i}\Vert \Vert y(t)\Vert . \end{array} \right. \end{aligned}$$
(18)

where \(\sigma _{1i}, \sigma _{2i},\sigma _{3i},\varepsilon _{0}\) are positive scalar, \(E_1=MEN=\left[ \begin{array}{cc} I_m &{} 0\\ 0&{} N_{n-m} \end{array} \right] \) is defined in lemma 2, \(\nu _{i}(t)\) is continuous differentiable function, whose expression is given in (19) below and \( T_{i}\) is constant known matrix.

Afterwards, in order to prove that the designed controller make the system stable in a finite time, we propose a Lyapunov functional candidate.

$$\begin{aligned} V_{i}(t)=\frac{1}{2}\nu ^{T}_{i}(t)\nu _{i}(t)+\frac{1}{2\sigma _{1i}}\tilde{\delta }^2_{i}+\frac{1}{2\sigma _{2i}}\tilde{\gamma }^2_{i1}+\frac{1}{2\sigma _{3i}}\tilde{\gamma }^2_{i2} \end{aligned}$$
(19)

Calculating the fractional derivative of \(T_{i}(t)\), then

$$\begin{aligned} \left\{ \begin{array}{lll} E_1D^{\alpha }V_{i}(t)=E_1D^{\alpha } \left\{\nu ^{T}_{i}(t)\nu _{i}(t)+\frac{1}{\sigma _{1i}}\tilde{\delta }_{i}\hat{\delta }_{i}+\frac{1}{\sigma _{2i}}\tilde{\gamma }_{i1}\hat{\gamma }_{i1} +\frac{1}{\sigma _{3i}}\tilde{\gamma }_{i2}\hat{\gamma }_{i2} \right \},\\ \nu _{i}(t)=h_\mu \left \{H_{i}E_1D^{\alpha -1}e(t)-H_{i}\int ^{t}_{0}L_{i}C_{i}e(s)ds \right \}. \end{array} \right. \end{aligned}$$
(20)

Substituting (17) into (19), the following inequality is given.

$$\begin{aligned} \left\{ \begin{array}{lll} E_1D^{\alpha }V_{i}(t)\le \parallel \nu _{i}(t)\parallel ^T E_1D^{\alpha }\parallel \nu _{i}(t)\parallel +E_1D^{\alpha } \left \{\frac{1}{\sigma _{1i}}\tilde{\delta }_{i}\hat{\delta }_{i} +\frac{1}{\sigma _{2i}}\tilde{\gamma }_{i1}\hat{\gamma }_{i1} +\frac{1}{\sigma _{3i}}\tilde{\gamma }_{i2}\hat{\gamma }_{i2}\right \}\\ =\parallel \nu _{i}(t)\parallel \left\{\Vert H_{i}A_{i}+{T_{i}C_{i}}\Vert \tilde{\delta }_{i}~~~\right.\\ ~\left. ~~~+\Vert H_{i}B_{i}\Vert \tilde{\gamma }_{i1}+\Vert H_{i}B_{i}\Vert \Vert y(t)\Vert \tilde{\gamma }_{i2}+\varepsilon _{0} \right \}\\ ~~~+\frac{1}{\sigma _{1i}}\dot{\tilde{\delta }}_{i}\dot{\hat{\delta }}_{i}+\frac{1}{\sigma _{2i}}\dot{\tilde{\gamma }}_{i1}\dot{\hat{\gamma }}_{i1}+\frac{1}{\sigma _{3i}}\dot{\tilde{\gamma }}_{i2}\dot{\hat{\gamma }}_{i2}~~ \end{array} \right. \end{aligned}$$
(21)

Then, to exchange (18) into (21), it obtains,

$$\begin{aligned} E_1D^{\alpha }V_{i}(t)\le -\varepsilon _{0}\parallel \nu _{i}(t)\parallel <0. \end{aligned}$$
(22)

After that, it prove that the designed controller make the error system stable in a finite time.

Remark 2

In practical applications, Under normal circumstances, e(t) is unknown or difficult to obtain directly, so we usually find \(e_y(t)\) to obtain e(t) according to the equation \(e_y(t)=Ce(t).\)

3.4 \(H_{\infty }\) performance control of T-S singular FOS

The control problem of continuous time T-S fuzzy SFOSs with \(H_{\infty }\) performance is considered in this section.

Definition 3

[31] The \(T_{wz}\) is defined as the transfer function of the system (3) in the following form:

$$\begin{aligned} T_{wz}=C_{i}(s^{\alpha }E-A_{i})^{-1}B_{i}+D_{i}, \end{aligned}$$
(23)

   Then, in frequency domain, the \(H_{\infty }\) norm is defined as follows:

$$\begin{aligned} \Vert T_{wz}\Vert _{\infty }=\sup \limits _{\omega }\bar{\sigma }(T_{wz}(j\omega )), \omega \ge 0. \end{aligned}$$
(24)

Theorem 3

Continuous time T-S singular FOS (10) is asymptotically stable with fractional order belonging \(0<\alpha <1 \) and \(\Vert T_{wz}\Vert _{\infty }<\gamma ,\) if there exists matrices \(P_{1i}>0,P_{2i}>0,Z_{1i}>0, Z_{2i}>0\) and a scalar \(\beta >0\) such that (15) and the follow LMIs satisfied:

$$\begin{aligned} \left[ \begin{array}{ccc} \mathrm {sym}\{r{\bar{A}}_{h}^{T}P\}+\varLambda &{} r^{*}(Z^{T}-P^{T})&{} {\bar{C}}^{T}\\ * &{} -\gamma I &{} {\bar{D}}^T \\ * &{} * &{} -\gamma I\\ \end{array} \right] <0, \end{aligned}$$
(25)

where \({\bar{A}}_{h}\) is consistent with Theorem 1, and

$$\begin{aligned}&Z=\left[ \begin{array}{ccc} Z_{1i} &{}Z_{2i} \\ -\beta P_{2i} &{} \beta P_{2i} \end{array} \right] , P=\left[ \begin{array}{cc} P_{1i} &{} 0\\ 0&{} \beta P_{2i}\\ \end{array} \right] , \nonumber \\&\quad {\bar{C}}_{h}=\left[ \begin{array}{cc} C_i &{} 0 \\ 0&{}C_{i} \end{array} \right] ,{\bar{D}}=\left[ \begin{array}{cc} D_{i} &{} 0 \\ 0&{}D_{i} \end{array} \right] , \varLambda =\left[ \begin{array}{cccc} 0 &{} 0 \\ 0 &{} -\gamma I \end{array} \right] . \end{aligned}$$
(26)

Proof

Substituting \({\bar{A}}_{h},{\bar{C}}_{h}, Z, {\bar{D}}, P, \varLambda \) into (25), it obtains that:

$$\begin{aligned} \left[ \begin{array}{ccccc} \bigvee &{}r^*(Z^T-P^T)\\ *&{} -\gamma I \\ \end{array} \right] <0. \end{aligned}$$
(27)

where

$$\begin{aligned} \bigvee =\mathrm {sym}\{r{\bar{A}}_{i}^TP\}+\varLambda +\gamma ^{-1}{\bar{D}}^T{\bar{D}}+\gamma ^{-1}{\bar{C}}^T{\bar{C}}. \end{aligned}$$
(28)

due to the inequality (27), it obtains that: \(\bigvee <0,\) which is expressed in (29), \(\bigvee =\)

$$\begin{aligned}&\mathrm {sym} \Bigg \{r\left[ \begin{array}{ccccccccccccccccc} (A_i+B_i\mathcal {K}_i)^TP_{1i}&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~\\ -(B_i\mathcal {K}_i+{\bar{G}}_i{\bar{A}}_{i})^TP_{1i}-\beta (B_i\mathcal {K}_i)^TP_{2i}&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~\\ *&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~&{}~ \end{array} \right. \nonumber \\&\quad \left. \begin{array}{ccc} ~&{}(A_{i}-L_{i}C_{i}-B_{i}\mathcal {K}_{i}-{\bar{G}}_{i}A_{i})^TP_{2i}&{}Z_{1i}-P_{1i}\\ ~&{}(B_i\mathcal {K}_i)^TP_{2i}&{}-\beta P_{2i}\\ ~&{}*&{}-\gamma I \end{array} \right] \Big\}<0, \end{aligned}$$
(29)
$$\begin{aligned}&\quad \varTheta =\mathrm {sym}\{r\gamma ({\bar{A}}_{i}+B_{i}\mathcal {K}_{i})^TP_{1i}\}+{\bar{D}}^T{\bar{D}}, \end{aligned}$$
(30)

then,

$$\begin{aligned} -\varTheta -{\bar{C}}^T{\bar{C}}>0. \end{aligned}$$
(31)

   Since the continuous time system (10) is admissibile, pre- and post-multiplying (31) by \(B^T_{i}(s^{\alpha }E-{\bar{A}}_{i})^{-T}\) and its transform, respectively, we have that,

$$\begin{aligned} \varUpsilon =\gamma ^2 I-B^T_{i}(s^{\alpha }E-{\bar{A}}_{i})^{-T}{\bar{C}}^T{\bar{C}}(s^{\alpha }E-{\bar{A}}_{i})B^T_{i}, \end{aligned}$$
(32)

where \(\gamma ^2 I>0.\) Then, the above inequality can be converted into

$$\begin{aligned} \varUpsilon -B^T_{i}(s^{\alpha }E-{\bar{A}}_{i})^{-T}\varTheta (s^{\alpha }E-{\bar{A}}_{i})B^T_{i}>0, \end{aligned}$$

    From lemma 3 and substitute \(\varPsi ,\varOmega ,\) we have that:

$$\begin{aligned} \left[ \begin{array}{cccc} {\bar{A}}_{i}&{}B_i\\ E&{}0 \end{array} \right] ^T(\varPhi \otimes Z+\varPsi \otimes P) \left[ \begin{array}{cccc} {\bar{A}}_{i}&{}B_i\\ E&{}0 \end{array} \right] +\left[ \begin{array}{cccc} \varTheta &{}0\\ 0&{}-\varUpsilon \end{array} \right] <0, \end{aligned}$$
(33)

where

$$\begin{aligned} \varPhi =\left[ \begin{array}{ccc} 0&{}e^{j\theta }\\ e^{-j\theta }&{}0 \end{array} \right] ,\varPsi =\left[ \begin{array}{ccc} 0&{}e^{-j\theta }\\ e^{j\theta }&{}0 \end{array} \right] . \end{aligned}$$

    Further, \(\varUpsilon >0,\) it means that \(\Vert T_{wz}\Vert _{\infty }<\gamma .\) The proof of the theorem has been completed.

Theorem 4

Continuous time T-S singular fractional order system (10) is output-feedback stabilizable if there exists matrices \( P_{1i}>0, P_{2i}>0,\) and \(Z_{ji}(j=1,2,...,6), Q_{ji}(j=1,2,...,8), J, M, N, \mathcal {K }\) are constant matrices and a scalar \( \beta >0 \) such that (15) and the LMI (34), which is at the top of next page, satisfied:

$$\left[ \begin{array}{ccccccccc} \varOmega _{11} &{} * &{} * &{} * &{} * &{} * &{} ~* &{} ~*&{} \\ \varOmega _{21} &{} \varOmega _{22} &{} * &{} * &{} * &{} * &{} ~ *&{} ~*&{}\\ \varOmega _{31} &{} \varOmega _{32} &{} \varOmega _{33} &{} * &{} * &{} * &{} ~* &{} ~*&{}\\ \varOmega _{41} &{} \varOmega _{42} &{} \varOmega _{43} &{} \varOmega _{44} &{} * &{} * &{} ~* &{} ~*&{} \\ r^{*}Q_{2i}^{T}{\bar{A}}_{h}+rL &{} r^{*}Q_{2i}^{T}{\bar{B}}_{h}-rP_{2i} &{} r^{*}Q_{2i}^{T}{\bar{B}}_{h}&{} -r^{*}Q_{2i}^{T} &{} -rP_{2i}-r^{*}P_{2i} &{} * &{} ~ *&{} ~*&{}\\ \varOmega _{61} &{}\varOmega _{62} &{} \varOmega _{63} &{} \varOmega _{64} &{} -rQ_{6i} &{} -rQ_{7i}-r^{*}Q_{7i}^{T} &{} ~ *&{} ~*&{}\\ r^{*}Q_{4i}^{T}{\bar{A}}_{h} &{} r^{*}Q_{4i}^{T}{\bar{B}}_{h} &{} r^{*}Q_{4i}^{T}{\bar{B}}_{h} &{} - r^{*}Q_{4i}^{T} &{} 0 &{} -r^{*}Q_{8i}^{T} &{}~ -rP_{2i}-r^{*}P_{2i}&{} ~*&{}\\ r{\bar{C}}_{h} &{} r{\bar{D}} &{} r{\bar{D}} &{}0 &{} 0 &{} 0 &{} 0&{} -\gamma I \end{array} \right] <0,$$
(34)

where

$$\begin{aligned} \begin{array}{llllllllllllllllll} \varOmega _{11}= \mathrm {sym}\{r({\bar{A}}^{T}_{h}Z_{1i}-\mathcal {K}^TZ_{1i}+\beta M^{T}P_{2i}M-\beta M^{T}J-\beta J^{T}M)\},\\ \varOmega _{21}=r^{*}Z_{2i}^{T}{\bar{A}}_{h}+r{\bar{B}}^{T}_{h}Z_{1i}^{T}+r^{*}\beta J+r\beta J,~~~\\ \varOmega _{22}=r{\bar{B}}^{T}_{h}Z_{2i}+r^{*}Z_{2i}^{T}{\bar{B}}_{h}-r\beta P_{2i}-r^{*}\beta P_{2i} ,\\ \varOmega _{31}=r{\bar{A}}^{T}_{h}Z_{3i}+r^{*}Z_{1i}^{T}{\bar{B}}_{h}-r\beta N^{T}J-r^{*}\beta N^{T}J+r\beta N^{T}P_{2i}M+r^{*}\beta N^{T}P_{2i}M,\\ \varOmega _{32}=r{\bar{B}}^{T}_{h}Z_{3i}+r^{*}Z_{2i}^{T}{\bar{B}}_{h},~\varOmega _{42}=-rZ_{2i}+r^{*}Q_{1i}^{T}{\bar{B}}_{h}\\ \varOmega _{33}=r{\bar{B}}^{T}_{h}Z_{3i}+r^{*}Z_{3i}^{T}{\bar{B}}_{h}+r\beta N^{T}P_{2i}N+r^{*}\beta N^{T} P_{2i}N-\gamma I,\\ \varOmega _{41}=rP_{1i}-rZ_{1i}+r^{*}Q_{1i}^{T}A,~\varOmega _{43}=-rZ_{3i}+r^{*}Q_{1i}^{T}{\bar{B}}_{h},~~~~~~\\ \varOmega _{44}=-rQ_{1i}-r^{*}Q_{1i}^{T},~\varOmega _{61}=rP_{1i}-rQ_{4i}+r^{*}Q_{3i}^{T}{\bar{A}}_{h},~~~~~~~~\\ \varOmega _{62}=-rZ_{5i}+r^{*}Q_{3i}^{T}{\bar{B}}_{h},~\varOmega _{63}=-rZ_{6i}+r^{*}Q_{3i}^{T}{\bar{B}}_{h}, \varOmega _{64}=-rQ_{5i}-r^{*}Q_{3i}^{T}.\\ \end{array} \end{aligned}$$

Theorem 4 can be regarded as the extension of Theorem 3, so the proof is not expressed in detail.

figure a

4 Simulation results

Numerical examples are given to show the validity of the above approach in this section.

Example 1

The following fuzzy singular fractional order systems are considered with two fuzzy rules and the parameter matrices are described as follows.

$$\begin{aligned} \left\{ \begin{array}{ccc} ED^{\alpha }x(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))\{A_{i}x(t)+B_{i}(u(t)+f_a(t))\},\\ y(t)=\sum \limits _{i=1}^{r}h_i(\mu (t))C_{i}x(t).~~~~~~~~~~~~~~~~~~~~ \end{array} \right. \end{aligned}$$
(35)

where

$$\begin{aligned}&\alpha =\frac{3}{4},~E=\left[ \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right] , A_1=\left[ \begin{array}{ccc} -1 &{} 3 &{} 0\\ 1 &{} 0 &{} -1\\ -1 &{} -6 &{} 0 \end{array} \right] , A_2=\left[ \begin{array}{ccc} 2 &{} 3 &{} 0\\ 1 &{} -1&{}0\\ -1 &{} 0 &{} -6 \end{array} \right] ,B_1=\left[ \begin{array}{ccc} 0\\ 1\\ 0 \end{array} \right] , \\&\quad B_2=\left[ \begin{array}{ccc} 1\\ 0\\ 0 \end{array} \right] ,C_{1}=\left[ \begin{array}{ccc} 1\\ 1\\ 0\\ \end{array} \right] ^T,C_{2}=\left[ \begin{array}{ccc} 0\\ 1\\ 0\\ \end{array} \right] ^T,h_1(\mu (t))=\frac{1+sin^{2}(x_1(t))}{3}, \\&\quad h_2(\mu (t))=\frac{1+cos^{2}(x_1(t))}{3},~f_{a}(t)= {\left\{ \begin{array}{ll} 0,&{} {t<2}\\ \frac{1}{1+2^{-t}},&{} {t\ge 2} \end{array}\right. }. \end{aligned}$$

As a result of Theorem 3, to solve the inequalities (15) and (25), it obtains that the following solution:

$$\begin{aligned}&P_1=10^8 *\left[ \begin{array}{cccc} 0.8072 &{} -0.4548 &{} 0\\ -0.4548 &{} 1.5022 &{} 1.7059\\ -1.7059 &{} -1.7059 &{} 1.7059 \end{array} \right] , P_2=10^8 *\left[ \begin{array}{cccc} -0.8187 &{} -0.9555 &{} 0\\ -0.9555 &{} 3.6438 &{} 1.5675\\ -1.5675 &{} -1.5675 &{} 1.5675 \end{array} \right] , \\&\quad Z_1=10^8 *\left[ \begin{array}{cccc} 3.1138 &{} -1.6482 &{} 1.8387\\ -1.6482 &{} 3.7259 &{} 3.2577\\ 1.8387 &{} 3.2577 &{} 3.9148 \end{array} \right] , Z_2=10^8 *\left[ \begin{array}{cccc} -1.1041 &{} -3.6205 &{} 3.1062\\ -3.6205 &{} 4.2988 &{} 0.0936\\ 3.1062 &{} 0.0936 &{} 3.0042 \end{array} \right] , \\&\quad \mathcal {K}_1=\left[ \begin{array}{cccc} 0.0305 &{} 0 &{} 0\\ 0 &{} 0.0305 &{} 0\\ 0 &{} 0 &{} 0.0305 \end{array} \right] , \mathcal {K}_2=\left[ \begin{array}{cccc} 0.4100 &{} 0 &{} 0\\ 0 &{} 0.4100 &{} 0\\ 0 &{} 0 &{} 0.4100 \end{array} \right] , \\&\quad L_1=\left[ \begin{array}{cccc} 0.0152&0.0152&0 \end{array} \right] ^T, L_2=\left[ \begin{array}{cccc} -1.4322&0.1895&0.4176 \end{array} \right] ^T. \\&\quad \begin{array}{ccc} \Vert T_{wz}\Vert _{\infty }\le \gamma _{1}=1.1991*10^8, \beta _{1}=3.2300*10^8,\\ \Vert T_{wz}\Vert _{\infty }\le \gamma _{2}=3.6749*10^{8}, \beta _{2}=3.6427*10^{7}.\\ \end{array} \end{aligned}$$
Fig. 2
figure 2

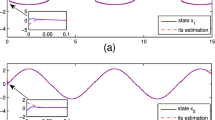
(a) \(x_1(t)\) and the error estimation of \(x_1(t)\)(b) \(x_2(t)\) and the error estimation of \(x_2(t)\)(c) \(x_3(t)\) and the error estimation of \(x_3(t)\)(d) State trajectories of error dynamic system (8)

Full size image
Fig. 3
figure 3

The controllers \(\nu _1(t)\) and \(\nu _2(t)\) in Example 1

Full size image
Fig. 4
figure 4

The adaptive parameters in Example 1

Full size image

Figures 1a–c shows \(x_{i}(t)(i=1,2,3)\) can be estimated and tracked accurately under observer-based adaptive fault-tolerant controller, whose curves are depicted in Fig. 2. After that, under the effect of the adaptive parameters, which is shown in Fig. 3, we get that the error system in Fig. 1d converges to zero, so that dynamic system (35) is asymptotically stable and Theorem 3 is valid.

Example 2

Considering electrical circuit shown in Fig. 5, which are widely used, including the following circuit element, a load resistance R,  source voltage \(e_1, e_2,\) and capacitances \(C_1, C_2, C_3.\) Then, the circuit symbols are given , \(u_{1}(t), u_{2}(t), u_{3}(t)\) represent the voltage of capacitances, respectively. Afterwards, the state equation is given as follows,

$$\begin{aligned} \left[ \begin{array}{ccc} RC_{1} &{} 0 &{} 0\\ C_{1} &{} C_{2} &{} -C_{3}\\ 0 &{} 0 &{} 0 \end{array} \right] \left[ \begin{array}{ccc} D^{\alpha }u_{1}(t)\\ D^{\alpha }u_{2}(t)\\ D^{\alpha }u_{3}(t) \end{array} \right] =\left[ \begin{array}{ccc} 0 &{} -1 &{} 2\\ 1 &{} -2 &{} 2\\ 0 &{} 1 &{} 0 \end{array} \right] \left[ \begin{array}{ccc} u_{1}(t)\\ u_{2}(t)\\ u_{3}(t) \end{array} \right] +\left[ \begin{array}{ccc} 1&{}0\\ 0&{}0\\ 0&{}1 \end{array} \right] \left[ \begin{array}{ccc} e_1\\ e_2\\ \end{array} \right] \end{aligned}$$

where \(\alpha =0.25,\) \(C_1=C_2=C_3=1,\) \(R=1,\) \( f_{a}(t)= {\left\{ \begin{array}{ll} 0,&{} {t<2}\\ \frac{1}{sin(0.5t-5)},&{} {t\ge 2}, \end{array}\right. }\ \)

$$\begin{aligned} \begin{array}{cccc} h_1(\mu (t))=\frac{1+sin(x_1(t))}{6},h_2(\mu (t))=1-h_1(\mu (t)). \end{array} \end{aligned}$$

Due to Theorem 2 and solving inequalities (15) and (16), it obtains a series of feasible solutions as follows:

$$\begin{aligned}&X=\left[ \begin{array}{cccc} 2.6613 &{} -0.8871 &{} 0.0534\\ -0.8871 &{} 0.2957 &{} -0.0178\\ 0.0534 &{} -0.0178 &{} 3.1853 \end{array} \right] , Y=\left[ \begin{array}{cccc} 1.1978 &{} 0.4285 &{} 0.5039\\ -0.4285 &{} -0.3406 &{} 1.2105\\ -0.5039 &{} -1.2105 &{} -3.0381 \end{array} \right] , \\&\quad P =\left[ \begin{array}{cccc} 2.7778 &{} 3.9200 &{} -0.8296\\ 3.9200 &{} 1.1422 &{} 0.5348\\ -0.8296 &{} 0.5348 &{} -2.7944 \end{array} \right] , Q=\left[ \begin{array}{cccc} -0.3038&0.3467&-1.2055 \end{array} \right] , \\&\quad L=\left[ \begin{array}{cccc} 0.4854&-0.6179&-0.1441 \end{array} \right] ^T. \end{aligned}$$
Fig. 5
figure 5

Electrical circuit illustration in Example 2

Full size image
Fig. 6
figure 6

The error estimation of the system (10) in Example 2

Full size image
Fig. 7
figure 7

The adaptive parameters in Example 2

Full size image

Further, Fig. 6 shows that the error dynamic system (10) is asymptotically stable and the designed adaptive controller (8) with the adaptive parameters shown in Fig. 7, which means that the state variables of T-S fuzzy SFOSs are tracked precisely with actuator faults.

Table 1 Application range comparison of existing methods and ours
Full size table

Remark 3

Through the above table, We extend the stability of the SFOS to fuzzy T-S systems. Compared with [15], our approach is easy to solve. We reduce the conservative for stabilization and own practical applications. [9] constructed a sliding surface with reduced dimension by the method of state transformation but increases the computational burden. In general, our result is better and stronger than the existing results.

5 Conclusion

This paper deals with the issue of adaptive control of T-S singular FOSs with faults and \(H_{\infty }\) performance, where the fractional order belongs to (0, 1). Firstly, according to adaptive laws and fuzzy approximation technology, an adaptive observer has been given to dedicate to guarantee the preset tracking performance, which keep the estimation of the unmeasurable or partially measurable state and faults, simultaneously. Secondly, a controller has been designed through constructing the sliding mode surface of fuzzy singular fractional order systems with adaptive sliding mode control strategy. Moreover, a convex combination technique has been developed, such that it is shown that the proposed approach is valid for the systems with faults and unknown disturbances. Further, in order to ensure the stability of the proposed system with \(H_{\infty }\) performance, novel sufficient conditions have been obtained by LMIs, Finally, to illustrate the availability of the presented method, numerical simulation and practical examples have been presented.