1 Introduction

Over the past two decades, the data-driven watershed runoff models have played a key role in flood forecasting studies. Extensive efforts have been conducted to enhance the capabilities of artificial intelligence-based methods in the development of flood forecasting and warning systems [1, 2]. However, due to the complex, nonlinear and dynamic nature of the rainfall–runoff process, accurate modeling of this process has always been challenging [3,4,5]. The models presented to simulate the hydrologic behavior of the watershed can be classified into three general categories, including physical, conceptual and data-driven models [6]. Where the calibration of conceptual models is challenging and time-consuming due to the multiple parameters and insufficient available datasets, data-driven models can be appropriate alternatives. The popularity of data-driven models is due to their ability to discover complex relationships and create a nonlinear mapping between input and output spaces in the presence of limited and noisy data sets [7,8,9]. Nowadays, artificial intelligence including machine learning approaches, fuzzy inference systems, evolutionary computations and complementary wavelet models has been found wide applications in hydrology [10,11,12,13,14,15,16,17,18,19,20,21]. In this regard, artificial neural networks (ANNs) as one of the most promising machine learning approaches have been widely used in rainfall–runoff modeling [22,23,24,25,26]. An artificial neural network is a parallel data processing system that is capable of storing information obtained through the learning process as well as generalizing the acquired knowledge to different events [27, 28].

So far, many studies have been conducted to compare different ANN models in river flow forecasting. Anctil et al. [29], using the multilayer perceptron (MLP) neural network in the single-step-ahead flow forecasting, showed that this model is affected by the length of the training dataset. Cigizoglu [30] used the generalized regression neural network (GRNN) to estimate daily mean flows and showed that this algorithm has fewer problems such as trapping at the local minima and has higher accuracy compared to the feed-forward neural network, regression and stochastic methods. Studying different ANN models in some cases has shown the superiority of the radial basis function neural network (RBFNN) model to other supervised methods, due to features such as smaller extrapolation errors, faster convergence and higher reliability [31,32,33,34,35,36]. However, RBFNN performance is deteriorated by inadequate training data [37]. Furthermore, to enhance the forecasting accuracy of a neural network, the model can be combined with other methods of artificial intelligence; including evolutionary algorithms and wavelet-based methods, which have shown good performance in hydrology science [38,39,40,41]. Nourani [42] employed the emotional backpropagation (EmBP)-based neural network for the rainfall–runoff modeling and obtained better results than the feed-forward neural network in multi-step-ahead forecasting. Yaseen et al. [43] used the extreme learning machine (ELM) neural network to the river flow forecasting and showed that the method has a simpler architecture and more learning speed than the MLP. Yaseen et al. [44] combined the ELM model with wavelet-based methods and achieved higher accuracy in river flow forecasting. Araghinejad et al. [45] used a modified neural network that is different in terms of activation function compared to the MLP. Moreover, to increase the forecasting accuracy of low and high flow values, initially, they performed the classification of these flows using a probabilistic neural network. Darbandi and Pourhosseini [46] used the MLP neural network based on the firefly optimization algorithm to river flow forecasting. The firefly optimization algorithm is based on moving the population toward the brightest firefly. Ni et al. [47] predicted the monthly river flow, by developing two hybrid models based on the long short-term memory network (LSTM). A comparison of models performance showed that the LSTM-based hybrid models, LSTM and MLP models illustrated the highest accuracy, respectively.

Some other data-driven methods such as support vector machines (SVMs) have also shown good performance in various prediction problems. YU et al. [48] proposed an algorithm to train SVMs on a bound vectors set that was extracted based on Fisher projection. They used linear and nonlinear problems to verify the proposed algorithm. For each case, they selected a certain ratio samples whose projections were adjacent to those of the other class as bound vectors. For the first time, a two-side cross-domain collaborate filtering model was proposed by YU et al. [49]. They assumed that there existed two auxiliary domains, i.e., user-side domain and item-side domain, where this two-side domain shared the same aligned users and items, respectively. YU et al. [50] proposed a cross-domain collaborative filtering algorithm to overcome some drawbacks including that most recommender systems only take advantage of information from a two-side cross-domain, i.e., user-side domain and item-side domain.

Despite the abilities of artificial neural networks for rainfall–runoff modeling, these methods also shown some challenges and problems in the previous studies. Overtraining, the challenge of predicting extreme values, local minima, adjusting the architecture and tuning the training parameters are some of these problems [22, 43, 51,52,53]. Also, inadequate and limited training data sets reduce the accuracy of ANN prediction [54, 55]. On the other hand, in a low number of training epochs, the accuracy of the ANN will also be reduced. So far, various methods have been proposed to solve these problems, such as wavelet-based artificial neural networks [56,57,58]. Therefore, providing a model with the least complexity in terms of the number of parameters, simple structure and fast learning at the same accuracy is very important. Recently, the study of human psychological features, as an intelligent emotional entity, has led to the appearance of a new class of ANNs based on emotions [59]. Emotional ANNs can be classified into two general categories, including ANNs based on emotional backpropagation (EmBP) and ANNs based on brain emotional learning (BEL) [60, 61]. BEL network is based on the mammalian emotional brain, which is more like human emotional processes than EmBP [62]. In this paper, as the first application in hydrology, the supervised BEL (SBEL) neural network has been used in rainfall–runoff modeling. Biologically, when faced with a danger in which the logical mind does not have enough time to process, the emotional stimulus can react more quickly using short paths in the emotional brain [63, 64]. The operation of BEL is similar to the response of the brain to emotional stimuli. Rapid response to stimuli due to the existence of short paths in the emotional brain and the presence of a part that inhibits inappropriate responses in critical situations are some characteristics of this kind of neural network, which will increase the accuracy of the model [65]. Therefore, the model is based on the interaction of emotion and cognition. On the other hand, it has a simple architecture and, due to the lack of hidden layers in its structure, does not encounter the usual challenge in designing the architecture of a MLP neural network. The special features of this class of ANNs motivate this study. The SBEL has been successful in different applications such as chaotic time series prediction [66,67,68,69], prediction of geological science events [59, 70, 71] and prediction of wind power [62]. Besides, it has been applied to controlling the heat and air conditions [72] and smart machines [73, 74].

This paper aims to develop a rainfall–runoff model using SBEL on a daily time scale and compare its performance with the MLP as the universal approximator. The biological basis of the emotional brain, structure and mathematical model of SBEL will be described. Then, the ability of SBEL to predict peak flows and also discharge at non-rainy days as well as rainy days (with at least one recorded rainfall event in all precipitation stations) will be investigated. Also, the network performance will be examined in conditions of limited training data by reducing the length of the training dataset in three different scenarios, including dry, normal and wet training periods. The learning speed and accuracy of the network will also be measured by reducing the number of training epochs. In all aforementioned analysis, the SBEL performance has been compared to the MLP as the most common ANN in hydrologic modeling.

2 Methodology

2.1 Multilayer perceptron artificial neural network

The MLP neural network with backpropagation training algorithm is a widely used type of ANNs, applied in various fields of hydrology to predict nonlinear systems [22, 75]. The MLP model, called the universal approximator, can create nonlinear mappings between input and output spaces, which can estimate any nonlinear function desirably [76]. The MLP structure includes one input layer, one or more hidden layers and one output layer [27]. The schematic diagram of an MLP neural network with one hidden layer is presented in Fig. 1. Due to the effect of topology and learning algorithm on the performance of the MLP, it is essential to precisely determine some factors such as the number of neurons in each hidden layer, the activation functions and, finally, the network weights [77]. The number of neurons in the input and output layers is determined based on the problem statement [78]. The number of hidden layers, as well as the number of neurons in each layer, depends on the complexity of the problem and are usually determined by trial and error [79]. The small number of neurons in hidden layer can lead to reduced network learning ability, while a large number may cause problems such as overtraining [78]. The activation functions in the neurons are responsible for the non-linearization of the input signals [80], and the most commonly used functions are sigmoid and hyperbolic tangent. Adjusting network weights is also performed in the training phase based on the back propagation (BP) algorithm by propagating the error to the back layers to minimize the difference between the observed and calculated values [81].

Fig. 1
figure 1

Multilayer perceptron artificial neural network

Full size image

2.2 Brain emotional learning-based artificial neural network

Emotional learning is caused by emotional stimuli such as rewards and punishments received from various real-life situations and associated with emotional states such as happiness, fear, etc. [82]. All of these processes, such as receiving rewards and punishments, processing emotional stimuli and creating emotional states, take place in the central area of the brain called the limbic system (LS), which plays an important role in the emotional process [83, 84]. Figure 2 shows the limbic system and its main components, including the thalamus, sensory cortex, amygdala, orbitofrontal cortex, hypothalamus and hippocampus [83,84,85]. There are two ways to get external stimuli by the amygdala. One path is short and fast, including a naïve content that comes directly from the thalamus, and the other is a long and slower path, including more veritable information coming from the sensory cortex [86]. Given the pathways mentioned above, the amygdala will give an imprecise but quick response to stimuli. Then, based on the interactive mechanism that exists in the emotional brain between the amygdala and the orbitofrontal cortex, imprecise responses of the amygdala to the stimuli will be inhibited by the orbitofrontal cortex [87, 88].

Fig. 2
figure 2

Limbic system in the brain [82]

Full size image

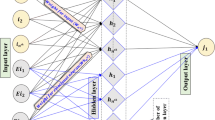
The existence of short paths and rapid responses to the learning process of the emotional brain, as well as the correction of inaccurate responses, has led to mathematical modeling of this type of learning process and the emergence of a new class of artificial neural networks based on emotional intelligence. Several models of BEL have been presented so far, all of which are based on the amygdala–orbitofrontal model [61, 87]. In this study, we used the supervised BEL (SBEL) as a universal approximator that was first proposed by Lotfi and Akbarzadeh-T [89] by modifying the amygdala–orbitofrontal model. In Fig. 3, SBEL is presented with \(n\) inputs, single output and one sensory cortex area.

Fig. 3
figure 3

Brain emotional learning-based artificial neural network [82]

Full size image

The model consists of four neural components in the emotional brain, including the thalamus, sensory cortex, amygdala and orbitofrontal cortex that interact with each other. Figure 3 shows the data flow as solid lines and the learning flow in the form of dashed lines. The number of nodes in each area equals the number of inputs except in the amygdala, which has an additional node.

First, inputs enter the thalamus, and the added imprecise input will be generated using a feature expansion function according to Eq. (1). The feature expansion function makes the new features by the input characteristics and can be a sinusoidal, Gaussian or max function.

If \(p=[{p}_{1}.{p}_{2}.\dots .{p}_{n}]\) be the input vector, then the expanded feature will be computed as:

$$ p_{{n + 1}} = \max _{{j = 1,n,n}} \left( {p_{j} } \right) $$
(1)

where \({p}_{n+1}\) is the expanded input to the amygdala. The sensory cortex receives the input signal \(p\) from the thalamus and releases it to the amygdala and orbitofrontal cortex. The orbitofrontal cortex receives \(n\) inputs from the sensory cortex. It does not receive any input from the thalamus, while the amygdala, in addition to receiving inputs from the sensory cortex, also directly receives the expanded feature of the thalamus as input. Finally, the SBEL output will be calculated according to Eq. (2).

$${{E}} \, ={ \, {{E}}}_{{a}} \, -{ \, {{E}}}_{\text{o}}$$
(2)

where \({E}_{a}\) and \({E}_{o}\) are the outputs of the amygdala and orbitofrontal cortex, respectively, and are calculated as follows:

$$ E_{a} {\mkern 1mu} = \sum _{{j = 1}}^{{n + 1}} \left( {v_{j} t \times p_{j} } \right) $$
(3)
$$ E_{o} = \mathop \sum \limits_{j = 1}^{n} \left( {w_{j} \times p_{j} } \right) + b $$
(4)

In Eqs. (3) and (4), \({v}_{j}\) is the learning weight of the amygdala, and \({w}_{j}\) and \(b\) are the learning weight and the bias of orbitofrontal, respectively.

After calculating the final output, it is necessary to correct the weights \(w\), \(v\) and the bias so that the network output leads to the least error as follows:

$$ v_{j}^{k + 1} = \left( {1 - \gamma } \right) \times v_{j}^{k} + \alpha \times \max \left( {T - E_{a} , 0} \right) \times p_{j}^{k} \quad j = 1, \ldots ,n + 1 . $$
(5)
$$ w_{j}^{k + 1} = w_{j}^{k} + \beta \times \left( {E - T} \right) \times p_{j}^{k} \quad j = 1, \ldots ,n $$
(6)
$$ B^{k + 1} = B^{k} + \beta \times \left( {E - T} \right) $$
(7)

where \(\alpha \) and \(\beta \) are learning rates, \(\gamma \) is the proposed decay rate, \(T\) is the target value, and \(k\) is the learning step. The max operator in Eq. (5) will also result in monotonic learning [82]. In the learning process of the amygdala, \(\gamma \) controls the effects of target values as well as monotonic learning in the model and simulates the forgetting role of the amygdala [90]. In this way, controlling the monotonic learning will lead to model performance improvement and consistent decision making [89].

3 Case study and dataset

The Dez River, with upstream catchment area of 17,000 sq. km and an average annual discharge of 245 cms released to the Dez Dam reservoir, is one of the major rivers of Iran in terms of runoff volume. The presence of the 203 meters height Dez Dam and hydroelectric power plant upstream of Dezful city with the aim of flood control, power generation and supplying water to the Dezful Plain has increased its importance.

With many destructive flood events generated annually in this catchment, it is necessary to develop flood management strategies, especially early flood forecasting and warning systems on the Dez River to optimal maneuvering of the dam gated spillways and reservoir operation to protect the downstream plane.

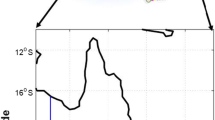
The Taleh-Zang hydrometric station has been constructed on the Dez River, upstream of the Dez Dam, that measures the inflow to the dam reservoir. The mean daily discharge data at this station besides precipitation data at twelve rain gauges for the period September 1982 to September 2014 (7304 events) were used in this study (Fig. 4).

Fig. 4
figure 4

The location map of the study area

Full size image

To predict mean discharge of Taleh-Zang hydrometric station through rainfall–runoff modeling at a given day, fifteen independent variables have been used, including discharges of one and 2 days ago, daily rainfall of twelve rain-gauge stations and a weighted antecedent precipitation index (WAPI). The WAPI is a weighted sum of previous rainfall values used as a modified antecedent soil moisture content of the watershed.

In this paper, WAPI is calculated by Eq. (8) based on the weighted summation of daily precipitation values of 12 precipitation stations in the past 5 days.

$$ API = \frac{{1\left( {\overline{p}_{t - 1} } \right) + 0.9\left( {\overline{p}_{t - 2} } \right) + 0.8\left( {\overline{p}_{t - 3} } \right) + 0.7\left( {\overline{p}_{t - 4} } \right) + 0.6(\overline{p}_{t - 5} )}}{1 + 0.9 + 0.8 + 0.7 + 0.6} $$
(8)

In Eq. (8), WAPI is the weighted antecedent precipitation index in millimeters and \({\overline{P} }_{t-1}\), \({\overline{P} }_{t-2}\), \({\overline{P} }_{t-3}\), \({\overline{P} }_{t-4}\) and \({\overline{P} }_{t-5}\) are the antecedent mean daily precipitation of whole 12 precipitation stations during one to five previous days. The weight given to each rainfall average is such that the recent days will receive greater weights, linearly.

4 Results and discussion

4.1 Experimental design

In this paper, the data set was scaled in order to balance the data range, prevent early saturation of the neurons and avoid variables with large numerical ranges dominating the role of the smaller numerical ranges.

The following equation is used for data normalization:

$$ x_{n} = {0}{\text{.05}} + { 0}{\text{.9}} \times \frac{{\left( {x - x_{min} } \right)}}{{\left( {x_{max} - x_{min} } \right)}} $$
(9)

where \(x\), \({x}_{n}\), \({x}_{min}\) and \({x}_{max}\) are raw, normalized, minimum and maximum values of observations, respectively. Accordingly, the data are converted to the range [0.05, 0.95]. Using this domain instead of the range [0, 1] is due to add more flexibility to the model in simulating possible future events. This option allows values less than the minimum as well as larger than maximum of the available data to be better processed in probable future circumstances.

In this paper, statistical indicators such as coefficient of determination (\({R}^{2}\)), root mean square error (\(RMSE\)), mean relative error (\(MRE\)), Taylor diagram and Violin plot have been used to evaluate the performance of MLP and SBEL models in rainfall–runoff simulation.

$$ R^{2} = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {Q_{oi} - \overline{{Q_{o} }} } \right)\left( {Q_{ci} - \overline{{ Q_{c} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {Q_{oi } - \overline{{ Q_{o} }} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {Q_{ci } - \overline{{ Q_{c} }} } \right)^{2} } }}} \right]^{2} $$
(10)
$$ RMSE = { }\sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {Q_{oi} - Q_{ci} } \right)^{2} }}{n}} $$
(11)
$$ MRE\,\left( \% \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\left| {Q_{oi } - Q_{ci} } \right|}}{{Q_{oi} }} \times 100 $$
(12)

where \({R}^{2}\), \(RMSE\) and \(MRE\) are the coefficient of determination, root mean square error and mean relative error percentage, respectively. Also \({Q}_{oi}\), \({Q}_{ci}\), \(\overline{{Q }_{o}}\), \(\overline{{Q }_{c}}\) and \(n\) are the observed discharge, computed discharge, mean observed discharge, mean computed discharge and number of observations, respectively.

The Taylor diagram is a graph that simplifies the comparison and evaluation of different models. It has recently been frequently used in weather studies [91,92,93,94]. This diagram was first proposed by Taylor [95], which is based on the geometric relationship between correlation coefficient (\(R\)), the standard deviation of time series and root mean square difference (\(RMSD\)). The latter is calculated as follows [91, 95]:

$$ RMSD^{2} = \sigma_{c}^{2} + \sigma_{o}^{2} - 2\sigma_{c} \sigma_{o} R . $$
(13)
$$ \sigma_{c}^{2} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} (Q_{ci} - \overline{{Q_{c} }} )^{2} $$
(14)

where \({\sigma }_{c}^{2}\) and \({\sigma }_{o}^{2}\) are the variance of computed and observed data, respectively.

The Taylor diagram is presented in the form of a half-circle (to show positive and negative correlations) or a quarter circle (to show positive correlations). In either case, values of the correlation coefficient in the form of the radius of the circle, the standard deviation values in the form of co-centric circles around the origin of coordinates and the values of RMSD as co-centric circles around the reference point are plotted. The reference point represents the location of the observed data. To evaluate and compare the performance of models, the location of the models based on the three above-mentioned indices will be plotted on the graph, and any model whose position on the chart is closer to the reference point will have more precision in the forecasting.

The Violin graph is a combination of box and density graphs representing the distribution of data and their probability density. The superiority of this plot than the box diagrams is the form of the data distribution that is drawn as prominence on the left and right of the box plot. It will also be able to identify data clusters, as well as minimum and maximum values [96]. A wider section of the graph in a given value indicates the greater the density of data at that value, and the smaller width, the less likely the sample will take that value.

4.2 Overall performance of the models

In this section, the ability of the MLP and SBEL models in simulating the daily rainfall–runoff process of Dez Dam watershed is compared. The proposed SBEL and MLP models have been written and evaluated on MATLAB R2014b. In the MLP model, determining the number of hidden layers and the number of neurons in each layer, as well as the number of training epochs, is considered to be an important issue. In this paper, through trial and error, the MLP neural network with one hidden layer containing eight neurons and 176 training epochs has been used. In the hidden and output layers, tangent sigmoid and linear activation functions have been used, respectively. Also, by trial and error, the momentum coefficient and the learning rate of MLP are set as 0.0011 and 0.0017, respectively. On the other hand, due to the absence of the hidden layer in SBEL structure, the challenge of determining the number of hidden neurons does not exist in this model. The performance of SBEL was evaluated using the sinusoidal, Gaussian and max operators as feature expansion functions. No significant difference in the SBEL performance was observed using these functions. Therefore, since the previous studies used the max operator to feature expansion, in this study the max function was selected as well [55, 69, 82, 89]. All three parameters of the SBEL model can also take values in the range [0, 1], which are adjusted to 0.01, 0.01 and 0 by trial and error for \(\alpha \), \(\beta \) and \(\gamma \), respectively. These values are consistent with the results reported by Lotfi and Akbarzadeh [90]. The linear activation function in SBEL is adopted for both the amygdala output and the final output. In order to evaluate the performance of the MLP and SBEL models, the watershed data have been divided into 70, 15 and 15 percentages for training, cross-validation and validation, respectively.

The distribution of the observed and forecasted river flow by MLP and SBEL models is presented in the Violin plot, as shown in Fig. 5. This figure shows that the most river discharges are in the range from 0 to 200 cms, and the river flow distribution predicted by SBEL is closer to the observed flow distribution. Considering the higher correlation between the observed and predicted data by SBEL, as shown in the scatter plots of Fig. 6, it can be concluded that the overall performance and accuracy of the SBEL in the river flow prediction is higher than the MLP. Also, SBEL can estimate the peak discharges closer to their observations and has higher accuracy than MLP. In table 1, the lower values of RMSE and MRE and higher correlation between observed and predicted discharge values in all three training, cross-validation and validation phases denote more accuracy in SBEL compared to MLP. Also, SBEL has been able to improve the MRE percentage of MLP up to 59.9%, 56.2%, 57.5% and 69.8% for predicting total data, training, cross-validation and validation data, respectively.

Fig. 5
figure 5

Violin plot of the observed and predicted runoff time series using MLP and SBEL models (all datasets)

Full size image
Fig. 6
figure 6

The scatter plots of the predicted versus the observed runoff time series using a MLP and b SBEL models (all datasets)

Full size image
Table 1 Overall performance indicators of MLP and SBEL models
Full size table

4.3 Predicting peak discharges

The accurate prediction of peak values is usually a challenge in data-driven modeling, including rainfall–runoff simulation. Therefore, due to the importance of peak flows in flood management, the peak discharge in each water year has been extracted and the prediction accuracy of peak flow values is investigated using MLP and SBEL models. According to the results shown in Table 2, SBEL has a lower RMSE than MLP and has improved the MRE percentage than the MLP model up to 21%. On the other hand, considering the scatter plots presented in Fig. 7 and the hydrograph illustrated in Fig. 8, SBEL is more capable of predicting peak flows. If peak discharges can be interpreted as emotional stimuli, it can be deduced that the brain’s emotional learning features mentioned in Sect. 2.2, including the existence of the emotional processor and also imprecise response modifier, have improved the SBEL performance. Therefore, SBEL can be useful in developing flood warning systems with an emphasis on forecasting peak discharges.

Table 2 Performance of MLP and SBEL models in peak discharges prediction of each water year
Full size table
Fig. 7
figure 7

The scatter plots of the predicted versus the observed peak discharges using a MLP and b SBEL models

Full size image
Fig. 8
figure 8

Observed and predicted peak discharge time series

Full size image

4.4 Limiting the training data

In hydrological time series, high flows usually have much less abundance than low flows. Therefore, most data-driven methods require a large and varied set of training data to predict high flow values accurately. As training data are not always available sufficiently in many cases, this is a serious limitation for data-driven models. In ANNs, inadequate training data also lead to a decrease in generalization capability and an increase in forecasting error. In this section of the study, the performance of the MLP and SBEL models has been evaluated by limiting the number of training samples from 70% to 10% of all samples (equivalent to two water years). The observed and predicted runoff hydrographs are presented in Fig. 9. Results show that the SBEL has been more effectively trained and also has forecasted the peak discharge values with more accuracy even under the condition of a limited training dataset. On the other hand, considering Fig. 10, the RMSE and MRE of the SBEL are significantly lower than the MLP for the total data, training, cross-validation and validation data, e.g., the SBEL has been able to improve the MRE by 74.5%. According to Table 3, the predicted runoff volume by the SBEL is closer to the observed runoff volume. Considering the satisfactory agreement between the observed and predicted runoff resulted by SBEL in the cross-validation and validation phases, it can be concluded that the SBEL model has a higher generalization ability even under conditions of limited data availability.

Fig. 9
figure 9

Observed and predicted hydrographs (trained models by a limited dataset)

Full size image
Fig. 10
figure 10

Performance of MLP and SBEL models in case of the limited training data

Full size image
Table 3 The observed and predicted runoff volume using the MLP and SBEL models with limited training data
Full size table

Moreover, to further compare the performance of both ANNs trained with 10% of the total data, where the training data are not sufficiently varied, three different training scenarios, including training data located in dry, normal and wet periods, separately, are considered. The results presented in Table 4 show that by reducing training data from 70% to 10% and restricting them to a specific scenario, the MLP network could not adequately be trained, and its generalization capability in cross-validation and validation is reduced compared to SBEL. In contrast, SBEL has been better trained and is able to generalize its knowledge with acceptable performance under different conditions.

Table 4 Performance indicators of the MLP and SBEL models, trained with limited training data in dry, normal and wet scenarios
Full size table

The less RMSE and MRE in the SBEL indicate the superiority of this model in the condition of limiting the training data. Also, SBEL has been able to improve the MRE percentage of MLP in predicting total data, training, cross-validation and validation data, respectively, up to 68.2%, 54.2%, 70.8% and 67.7% for the scenario of dry water years, 68.7%, 64.7%, 66.5% and 70.8% for the scenario of normal water years and 76.6%, 65.1%, 72.9% and 75.2% for the scenario of wet water years.

According to the Taylor diagram in Fig. 11, it can be seen that the performance of both models decreases during the training phase in the normal period than the wet period, as well as the training in the dry period compared to the normal period. However, SBEL is more accurate than MLP in all three scenarios. The results show a higher performance of SBEL versus MLP in the case of limited training data.

Fig. 11
figure 11

The Taylor diagram of the MLP and SBEL models trained with limited training data, in dry, normal and wet scenarios

Full size image

4.5 Discharge forecasting in non-rainy events

To evaluate the performance of the models at daily events in which no rainfall has been observed, the days with zero precipitation records have been extracted. Then, the accuracy of the models has been evaluated in terms of forecasting discharge on these events. According to Fig. 12 and Table 5, the correlation between observed and predicted flows in the SBEL is somewhat more than the MLP. Also, the RMSE in the SBEL model is amended, and the MRE is improved by 78.3% compared to the MLP.

Fig. 12
figure 12

Scatter plots of predicted versus observed runoff using a MLP and b SBEL models (non-rainy events)

Full size image
Table 5 Performance criteria of MLP and SBEL (non-rainy events)
Full size table

4.6 Discharge forecasting in rainy events

River flow forecasting when the basin response is due to rainfall excitation is more complex and challenging than when no precipitation enters the hydrological system. Hence, the performance of models has been evaluated in discharge forecasting of days which include recorded rainfall events in at least one meteorological station. The results in Fig. 13 and Table 6 indicate that the SBEL improved the coefficient of determination and MRE percentage and was more accurate in discharge forecasting of rainy events.

Fig. 13
figure 13

Scatter plots of the predicted versus the observed runoff using a MLP and b SBEL models (rainy events)

Full size image
Table 6 Performance indicators of the MLP and SBEL models in the discharge prediction (rainy days)
Full size table

4.7 Training speed

In most early flood forecasting and warning systems, the training (or calibration) speed of the forecasting model is of paramount importance in system reliability. Through this perspective, a model that is capable of achieving appropriate learning in fewer training epochs is more efficient. Figure 14 illustrates the trend of training error reduction in MLP and SBEL models versus the number of iterations. Considering the vertical dashed lines drawn in the diagram, the error will reach an acceptable value (3% of the previous step error value) after 26 epochs in SBEL and after 49 epochs in MLP models. Therefore, the SBEL model has achieved faster training with fewer iterations.

Fig. 14
figure 14

Training error versus the number of training epochs

Full size image

According to the indices presented in Table 7, it is clear that by reducing the number of training epochs, the performance of both models deteriorates. However, the SBEL is more robust than MLP, confronting the reduction of training epochs. At the same time, the SBEL was able to perform lower RMSE and MRE values than the MLP model in different numbers of iterations. Also, the SBEL was appropriately trained, even with a very low number of iterations, i.e., 10 epochs, and due to its performance in cross-validation and validation periods, it has shown acceptable generalization ability. In the MLP and SBEL models, after 176 and 107 training epochs, respectively, the error reached its minimum value and then remained constant. Therefore, in Table 7, the number of iterations of 176, which is related to the lowest error rate in MLP, is considered to start comparing the performance of the models while reducing the training epochs.

Table 7 Results of the MLP and SBEL models in different training epochs
Full size table

Figure 15 demonstrates the RMSE value of both models in four different training epochs. According to this figure, the SBEL performance is nearly constant with decreasing the number of training epochs from 75 to 35, while in the MLP, the error is continuously increasing. It can be concluded that SBEL can learn faster with less number of iterations, while capable of generalizing its knowledge achieved in the training phase to different conditions with acceptable accuracy. Therefore, the application of SBEL in flood forecasting and warning systems can be of particular interest.

Fig. 15
figure 15

The performance of the MLP and SBEL models by reducing the number of training epochs (all data)

Full size image

5 Conclusions

A reliable early flood forecasting and warning system (FFWS) is an essential part of non-structural integrated flood management strategies that can significantly reduce flood damages. To improve the performance of the FFWS, features such as prediction accuracy, fast learning, appropriate training even in the absence of sufficient data, reliable prediction of peak flows and accurate forecasts in rainy events are of essential importance. The cognitive model of brain emotional learning taken from the emotional brain has been developed as a center for receiving, processing and creating feelings in the human brain. SBEL has a simple structure and, due to the short paths in its structure, it can make quick responses to input impulses. Determining the number of hidden layers and the number of neurons in each hidden layer is challenging in the topology design and training of the MLP, which is not an issue in the SBEL due to the lack of the hidden layer in its structure.

In this paper, as the first application in hydrology, the SBEL neural network has been applied to the rainfall–runoff simulation of the Dez Dam watershed and has been compared with the MLP. The results show that the overall performance of the SBEL is superior to the MLP and improves the RMSE and MRE of MLP by 3.2% and 59.9%, respectively. Due to the importance of accurate peak flow prediction in flood forecasting systems, the estimation accuracy of these values has been investigated. The results of peak discharge estimation in each water year show that the SBEL model reduced the RMSE and MRE in MLP by 15.6% and 21%, respectively. Lack of sufficient recorded data to train data-driven models usually results in performance deterioration, especially in high flow predictions. To evaluate the robustness of models encountered with a limited training data, by reducing the number of training samples from 70% to 10% of total data and limiting them to a specific scenario, including placing reduced training data in dry, normal and wet periods, it has been observed that SBEL can generalize its knowledge with acceptable accuracy. In training scenarios located in the dry, normal and wet periods, SBEL improved the RMSE values of the MLP by 38.2%, 29.1% and 25.7%, respectively, and also improved the MRE values of the MLP by 68.2%, 68.7% and 76.6%, respectively. The prediction accuracy of both models is more desirable when training data are placed in the wet water years, than other scenarios. The river flow forecasting is more challenging in rainy events than days without precipitation records. Along with the precise performance of SBEL in predicting river flow in rainy days, this model can reduce the RMSE and MRE of MLP by 0.7% and 14.4%, respectively. On the other hand, fast learning is another essential feature needed in flood forecasting models. By reducing the number of training epochs, the results from networks performance indicated that SBEL could be trained faster with fewer training epochs, without significant changes in model performance. Also, compared to MLP, the SBEL generalization capability is reasonably maintained. For example, at very low iterations, i.e., 10 training epochs, the percentage of RMSE and MRE improvements of the SBEL compared to MLP were 46.6% and 59.4%, respectively.

Notable features of the SBEL neural network used in the present study are the simple structure, fast learning and considerable generalization capability. Also, due to some advantages presented in this case study, such as acceptable learning ability in case of insufficient recorded training data as well as high accuracy in predicting peak flows, the presented brain emotional learning-based neural network can be of particular interest for researchers to model hydrological processes in the future studies.