Hourly River Flow Forecasting: Application of Emotional Neural Network Versus Multiple Machine Learning Paradigms

Abstract

Monitoring hourly river flows is indispensable for flood forecasting and disaster risk management. The objective of the present study is to develop a suite of hourly river flow forecasting models for the Albert river, located in Queensland, Australia using various machine learning (ML) based models including a relatively new and novel artificial intelligent modeling technique known as emotional neural network (ENN). Hourly river flow data for the period 2011–2014 is employed for the development and evaluation of the predictive models. The performance of the ENN model in forecasting hourly stage river flow is compared with other well-established ML-based models using a number of statistical metrics and graphical evaluation methods. The ENN showed an outstanding performance in terms of their forecasting accuracies, in comparison with other ML models. In general, the results clearly advocate the ENN as a promising artificial intelligence technique for accurate forecasting of hourly river flow in the form of real-time.

1 Introduction

Innovative technological advances for short-term forecasting of river flow is very much essential for mitigation and management of high intensity floods triggered due to unprecedented weather hazards. The land use changes significantly affect the runoff volumes as well as its time distributions (Sun et al. 2017). Recently, there has been an increase in the overall imperviousness due to rapid infrastructural developments in urban watersheds along with the transformations of river morphology and drainage systems causing relatively rapid storm water runoff (Muñoz et al. 2018). A timely update of rainfall contributions to river flow is made available routinely through river flow-gauging program which serves for planning and management of river flow. The benefits of long-term to short-term river flow forecasting include, the reservoir water management, erosion and sedimentation estimation, environmental flow assessment, planning of safe recreation programs, flood defence scheme design and warnings systems that accommodate disaster management authorities to manage and mitigate them at their early-onset (Hester et al. 2006). Additionally, the forecasting of peak river flows for desired return period has a prominent role in the hydraulic design of engineering structures. Therefore, new forecast models, particularly at very short-term (i.e., near real-time horizons) are immensely attractive for future decision-makers, including water resource management experts, flood forecasters, hydrologists, environmental monitoring and management experts (Yaseen et al. 2018b).

In published literature, there exist several researches that aim to address river flow and flood forecasting problems using process-oriented, stochastic, deterministic and more recently, machine learning based approaches (Zhou et al. 2019). In the last decade, hydrological time series forecasting based on ML approaches that aim to automate the analytical model building through data analysis has progressed in a tremendous way due to the availability of quality checked historical data records from a wide range of scientific and technological agencies (Fahimi et al. 2017). The river flow forecast models based on ML techniques can provide significant advantages over empirical and process-based models in terms of their robustness, level of accuracy, handling multi-dimensional data and the regularization’s imposed on the model to avoid overfitting (Shortridge et al. 2016). The degree of uncertainty in process-oriented model outputs might also be higher because of a hurdle of model parameterization and explicitly stated assumptions (Chen et al. 2018). During the previous decades, considerable interest appears to be focused on the application of Artificial Neural Network (ANN) models of 15-min flow forecasts up to 6-h lead times (Dawson and Wilby 1998). Hourly flood forecasts of higher lead times (5-h) from ANNs were less accurate than 1-h forecasts owing to the basin characteristics and variations in the intensity of each flooding event. Several neural network variants evolved and for considerable period of time they were the only ones on board to provide accurate flood forecasts over all the lead times compared to other conceptual and linear stochastic models (Toth and Brath 2007). A detailed synthesis of literature related to river flow forecasting based on several ML models (published between the years 2000 to 2018) outlined in (Maier et al. 2010) and (Yaseen et al. 2018c) delivers insights on various kinds of techniques used, their advantages and, a comparative evaluation of individual model performances.

Hourly variations of river flow recorded from automated weather stations, that form the subject of this study, are very important as they can characterize hydrographs and flow duration curves, without having to interpret or estimate peaks (Hailegeorgis and Alfredsen 2017). The inflection point differentiating the storm recession from base flow can easily be identified via hourly estimates of river flow. Additional statistics can also be computed from hourly river flow values, such as flood peaks, low flows, and their temporal variability while calibrating the flow hydrograph. Short-range river flow forecast (i.e., on an hourly basis) is hence, imperative for prediction of flood magnitude and its duration. It also helps in determination of river flow on time scales from days to years and thus, decision making for water resources management. Using conceptual rainfall-runoff models, (Bennett et al. 2016), generated hourly hydrological simulations from simple disaggregation of daily rainfalls records to hourly data and then verified against hourly river flow data. However, the approach is not viable for catchments that are smaller and more prone to rapid river flow responses. In tandem with terrain information, (Merkuryeva et al. 2015) processed river water level time series with trend extraction to predict the hourly river water levels by means of a symbolic regression-based forecasting model. It’s worth noting that this approach requires heterogeneous data from both space and ground-based information sources. The ANN, Adaptive Neuro-fuzzy Inference System (ANFIS), Wavelet neural network (WNN) and, Wavelet ANFIS models were developed and applied by (Badrzadeh et al. 2015) for multiple hour lead-time flood forecasting at Casino station on Richmond River, Australia using hourly rainfall and runoff data. It’s worth mentioning that neither ANN nor ANFIS models provided reliable simulations of flood events. Li et al. (2017) developed an extended version of Error Reduction and Representation In Stages (ERRIS) model to forecast river flow at hourly time steps by quantifying model uncertainties that reduce forecast errors. This model, however, showed poor performance in the bias-correction with respect to the catchments having shorter series of data records. In the light of the reported literature, hourly river flow forecasting is an interesting topic to be studied comprehensively and the exploration of newly developed ML models is always the passionate of the hydrology researchers to provide and accurate and reliable forecasting modeling strategy.

Although several ML models have been applied for modeling river flow simulation, the interest of exploring more reliable and robust predictive models is still ongoing research motivation. Especially, for solving some associated problem in the existed models or discovering new models’ merits. Brian emotional learning is a recent discovered modeling strategy that is based on anatomical computation (Lotfi and Akbarzadeh-T 2014). The main merit of the ENN model is, there are two emotional responses during its learning including the anxiety and confidence. During the learning process, if the learning is momentous, then the confidence level is increased while the anxiety level is decreased (Lotfi and Akbarzadeh-T 2013). In addition, there are two additional emotional weights for the learning process which are not existed in the traditional ML models. The feasibility of the ENN model has been explored in diverse applications of water resources engineering (Sharghi et al. 2018, 2019; Nourani et al. 2019). However, for hourly scale river flow yet to be explored and investigated.

Considering the need for the hourly forecasts of river flow especially from a practical point of view, such as to provide near real-time forecasts of flood risk, the objective of the present research is to develop models for forecasting one-hour ahead hourly river flow using relatively a less explored ML tool known as Emotional Neural Network. To validate the utility of ENN compared to competing ML models, several well-established ML models were employed for validation including the Relevance Vector Machine (RVM), Minimax Probability Machine Regression (MPMR) and the Multivariate Adaptive Regression Splines (MARS). To the best of the authors’ knowledge, there exist no study to assess the competence of different ML models introduced in this study for short-range river flow forecasting. Statistically significant concurrent and correlated lagged data sets are used as the potential model inputs. The performance of the ML models in forecasting hourly river flow is comparatively evaluated using robust statistical score metrics and visual performance indicators.

2 Theoretical Overview

2.1 Emotional Neural Networks

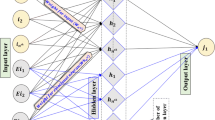
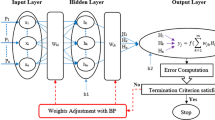
This research paper explores the application of Emotional Neural Networks (ENN) to model hourly river flow for the first time, sighting its suitability in some previous studies, yet in different contexts, related to hydrological modeling (Nourani 2017; Sharghi et al. 2018). ENN is popularly used as forecasting tool in different fields due to its simplicity and quick training time. This back propagation (BP) learning algorithm was introduced by (Rumelhart et al. 1986) utilizing generalized delta rules for training a layered neural network. Khashman (2008) modified BP algorithm with the addition of two emotional coefficients to construct the emotional back propagation model. ENN model is thus an improved version of a conventional ANN model that incorporates an emotional system emitting artificial hormones that modulate the operation of each neuron in a feedback loop. Its basic structure consists of three layers: the input layer followed by a hidden layer and lastly the output layer, with i, h and j neurons in their respective layers.

The data pre-processing and flow structure within the neural network from input layer to the output layer takes place in following phases. The neurons present in the input layer are non-processing and act as a carrier to pass the data, since its value and the output of each input-layer neuron is defined as follows:

$$ Y{I}_i=X{I}_i $$

(1)

where, XI_i and YI_i are the input and output values of neuron i in the input layer. The hidden neurons of ENN are represented as the processing neurons in the network where a sigmoidal function is usually used to activate each neuron for input feature extraction and subsequent modeling. Equation (2) gives the output of every hidden-layer neuron; which is usually a single layer however, this process will iterate even if there are more layers.

$$ Y{H}_h=\frac{1}{1+\exp \left(-X{H}_h\right)} $$

(2)

where, XH_h and YH_h are respectively, the input and output values of neurons in the h hidden layer.

In order to obtain the input XH_h to a hidden layer neuron, the following equation is used.

$$ X{H}_h=\sum \limits_{i=1}^r{W}_{hi}.Y{I}_i.{W}_{hb}.{X}_b+{W}_{hm}.{X}_m $$

(3)

where, W_hi is the weight provided by the hidden neuron h to the hidden layer i and YI_i is the output of the input neuron i and r is the maximum input-layer neurons. W_hbis the weight by hidden neuron h to the hidden layer bias neuron b and X_b is the input value to the bias neuron usually set to 1 X_b=1. W_hmis the weight given by hidden neuron h to the hidden layer emotional neuron m and X_m is input value to the emotional neuron representing the global input pattern average value Y_PAT. The applied transfer functions for ENN model were Tansing and Logsig with radial basis function kernel function.

2.2 Multivariate Adaptive Regression Splines

Multivariate adaptive regression splines (MARS) model introduced by (Friedman 1991) was also employed for hourly river flow prediction. MARS involves multivariate data to analyse the contributions from different predictors where interactive effects from explanatory data are used to forecast a target variable. It selects a regressor to implement with automatic smoothing (Krzyścin 2003) where inputs are split into subgroups and knots, located between different inputs and an interval to separate the subgroup (Friedman 1991; Sephton 2001). The MARS approach ensures adequate data in a subgroup, to avoid over-fitting by using shortest distance between neighbouring knots. Basis functions, BF_(x) are determined and projected on a target vector (Sharda et al. 2008). If X is the vector (x₁, x₂, … x_N), then:

$$ Y=f(x)+\xi $$

(4)

where, N is the number of training datum points, and xi is the distribution of error (Yaseen et al. 2018a). MARS model approximates the function f_(.) by applying basis functions BF_(x) having piece-wise function: max(0, x-c). The c represents the position of a knot, and max_(.) indicates the positive part of (.), otherwise it is zero, and is concordant with the following equation.

$$ \max \left(0,x-c\right)=\left\{\begin{array}{c}x-c\kern3.5em if\ c\ge t\\ {}0\kern4.25em otherwise\end{array}\right. $$

(5)

If (X) is constructed as a linear combination of BF(x).

$$ f(x)={\beta}_0+\sum \limits_{n=1}^{n=N}{\beta}_n BF(x) $$

(6)

where β is a constant estimated using least-squares and f(X) is a forward-backward stepwise method to identify the knots (Krzyścin 2003).

After the forward phase, an overlay elaborate model could result in, so a backward phase must be applied utilizing the Generalized Cross Validation (GCV). GCV estimates the mean square error (MSE) via the following equation (Zhang and Goh 2014).

$$ GCV=\frac{M\mathrm{S}E}{{\left(1-\frac{enp}{N}\right)}^2} $$

(7)

where, enp is the effective number of parameters, enp = k + c(k-1)/2; k is the number of basis functions in MARS model “equal to 10 in this study” (incl. Intercept term); c is a penalty (about 2 or 3); (k – 1)/2 is the number of hinge-function knots, which penalize the addition of knots.

2.3 Minimax Probability Machine Regression

MPMR model utilizes a linear discriminant and convex optimization, which are indeed an improved version of support vector machines (Strohmann and Grudic 2003). In MPMR, the data are analysed by shifting all regression data (+ε) along a dependent variable axis and the objective variable is analysed by shifting all regression data (−ε) along the dependent axis. The boundary is a regression surface where a model is trained to identify the bounds of probabilities for misclassifying a point without any assumption (Bertsimas and Sethuraman 2000). Consider a learning space (D-dimensional) from unknown regression function $f:{\mathfrak{R}}^D\mathfrak{\to}\mathfrak{R}$ an MPMR model is written as (Strohmann and Grudic 2003):

$$ y=f(X)+\rho $$

(8)

where, X$\in {\mathfrak{R}}^D$ is an input vector within a bounded distribution Ω, Y$\mathfrak{\in}\mathfrak{R}$ is an output vector and variance (ρ) =${\sigma}^2\mathfrak{\in}\mathfrak{R}$. MPMR aims to create an approximation $\hat{f\ }$ where for x_i generated from Ω, $\hat{y\ }$ is given by (Strohmann and Grudic 2003):

$$ \hat{y}=\hat{f}(x) $$

(9)

The model estimates the bounds on minimum probability ψ that $\hat{f\ }$ within ε of Y (Lanckriet et al. 2003):

$$ \psi =\mathit{\operatorname{inf}}\mathit{\Pr}\left\{\left|\hat{y}-y\right|\le \varepsilon \right\} $$

(10)

Equation (10) estimates a true regression by a bound on minimax probability and deduces ψ within of a true function. A final MPMR model based on kernel formulation is therefore written as (Strohmann and Grudic 2003):

$$ \hat{y}=\hat{f}(x)=\sum \limits_{i=1}^N{\beta}_iK\left({x}_i,{x}_j\right)+\rho $$

(11)

where, K_i.j=φ (x_i,x_j) is the kernel function satisfying mercer conditions and vector x_i is from the learned data and β_i and ρ are the output parameters. The MPMR model was developed with radial basis function width equal to 0.5 and error insensitive equal to 0.004.

2.4 Relevance Vector Machine

As a final benchmark model, Relevance Vector Machine (RVM) was applied. RVM proposed by (Tipping 2001) is an extension of support vector machine within a Bayesian context. A brief description of RVM framework is presented here but for greater details, the readers should refer (Tipping 2001). In this article, the RVM algorithm is considered a predictor for a set of inputs (x) according to:

$$ E=f\left(x,w\right)+{\varepsilon}_n $$

(12)

In Eq. (12), the error term ε_n = N(0, σ²) is a zero mean gaussian process and w = (w₀, ...,w_n)^T are the vectors of weights. The likelihood of the complete data can be represented as follows:

$$ p\left(\frac{E}{w},{\sigma}^2\right)={\left(2\pi {\sigma}^2\right)}^{-N/2}.\exp \left\{-\frac{1}{2{\sigma}^2}\ {\left\Vert E-\Phi w\right\Vert}^2\right\} $$

(13)

where, Φ(X_i) = [1, K(x_i, x₁), K(x_i, x₂), ......., K(x_i, x_N)]^T. Without imposing hyper-parameters on the weights, w, the maximum likelihood can suffer from over fitting. Following (Tipping 2001), a constraint, w is imposed by a complexity penalty to the likelihood or error function and an explicit zero mean gaussian prior probability distribution over the weights, w, with a diagonal covariance, α is adopted:

$$ p\left(w/\alpha \right)=\prod \limits_{i=0}^NN\left({w}_i/0,{\alpha}_i^{-1}\right) $$

(14)

where, α = vector of N + 1 hyper-parameters. The Bayes rule is applied to calculate the posterior over all unknowns given the defined non-informative prior distribution that follows:

$$ p\left(w,\alpha, {\sigma}^2/E\right)=\frac{p\left(E/w,\alpha, {\sigma}^2\right).p\left(w,\alpha, {\sigma}^2\right)}{f\ p\left(E/w,\alpha, {\sigma}^2\right).p\left(w,\alpha, {\sigma}^2\right)d\mathrm{w} d\alpha\ d{\sigma}^2} $$

(15)

It is important to note that the analytic solution is inexorable, so a decomposition of the posterior according to p(w, α, σ²/E) = (E/w, α, σ²). p(α, σ²/E) is used where the posterior distribution over the weights is written as:

$$ {\displaystyle \begin{array}{l}p\left(w/E,\alpha, {\sigma}^2\right)=\frac{p\left(E/w,{\sigma}^2\right).p\left(w/\alpha \right)}{p\left(E/\alpha, {\sigma}^2\right)}\\ {}={\left(2\pi \right)}^{-\left(N+1\right)/2}\ {\sum}^{-1/2}\exp \left\{-\frac{1}{2}{\left(w-\mu \right)}^T{\sum}^{-1}\left(w-\mu \right)\right\}\end{array}} $$

(16)

The posterior covariance and mean can be listed as:

$$ {\displaystyle \begin{array}{l}\sum ={\left({\sigma}^{-2}\ {\Phi}^T\Phi +A\right)}^{-1}\\ {}\mu ={\sigma}^{-2}\sum {\Phi}^TE\end{array}} $$

(17)

with A = diag(α₀, α₁, …, α_N). In the learning process, a search for hyper-parameters posterior is done by maximization of $p\left(\alpha, {\sigma}^2/E\right)\ \alpha\ p\left(\frac{E}{\alpha },{\sigma}^2\right)p\left({\alpha}^2\right)$ with respect to α and σ². For a uniform hyper-prior over α and σ², the term $p\left(\frac{E}{\alpha },{\sigma}^2\right)$ is minimized as:

$$ {\displaystyle \begin{array}{l}\rho \left(E/a,{\sigma}^2\right)=\int \rho \left(E/w,{\sigma}^2\right)\ \rho \left(w/a\right)\ dw\\ {}=\Big({\left(2\pi \right)}^{-\frac{N}{2}}/\sqrt{\mid {\sigma}^2+\Phi {A}^{-1}{\Phi}^T\mid}\times \exp \left\{-\frac{1}{2}{E}^T{\left({\sigma}^2+\varPhi {A}^{-1}{\varPhi}^T\right)}^{-1}E\right\}\end{array}} $$

(18)

The maximization of the quantity ρ(E/a, σ²) is known as the type II maximum likelihood method, also the evidence of hyper-parameter (Barto 1985). To attain an optimal RVM mode, an iterative formula is used to determine the hyper-parameters (Tipping 2001). RVM model was conducted with kernel radial basis function with width equal to 0.3.

3 Study Area and Model Data Set

The Albert River is a perennial river located in the South East region of Queensland, Australia with its headwaters in Lamington National Park McPherson Ranges (see Fig. 1). Its catchment lies within the Gold Coast, Logan City and Scenic Rim Region council’s boundaries and covers an area of 782 km². The Albert River is a large tributary of the Logan River which has a confluence with the Logan River some 25 km downstream of the boundary. The river starts near Hillview at an elevation of 184 m and ends at an elevation of 3.47 m merging with the Logan River near Beenleigh and the Logan then flows to southern Moreton Bay. It is a long narrow catchment in which the major streams flow from south to north dropping around 181 m over its 102 km length. The major soil type in the catchment is loam with varying texture profiles. Friable earths and cracking clays are also found in the area. The Albert catchment experiences very high average rainfall in the headwaters, with approximately 1600 mm per year at O’Reilly rain gauge station. This very high rainfall combined with good recharge of groundwater associated with the predominant basalt results in near-permanent flow. There are occasional landslips, which erode large areas of bank and increase sedimentation further downstream. It is estimated that during the 2008 flood event, approximately 70% of sediment in the Logan Estuary was derived from these Lamington Group rocks. The rest of the catchment experiences high to moderate average rainfall, with the slopes and coastal areas receive more rainfall than the low-lying mid reaches. These different rainfall levels combine to make up the rainfall of the Albert Catchment.

Fig. 1

The location of Albert river in the south region of Queensland, Australia

In this paper, a relatively lengthy dataset spanning hourly river flow values, from 1/01/2009 (5:00:00 AM) to 31/12/2014/ (00:00:00 AM) were used to develop ENN and MARS models. This comprises of 52,555 values that partitioned manually into training (60% “31,533 values”), validation (20% “10,511 values”) and testing (20% “10,511 values”) subsets. This dataset is significantly long to provide the input features of the predictive model. In accordance with PACF plot, a total of 3 statistically significant lagged inputs were used to model 1-h lead time river flow values.

4 Model Development and Performance Evaluation Measures

The performance of developed models depends on the dataset and design parameters. The design parameters are determined by trial and error approach. The normalized dataset (between 0 and 1) was employed for model development. The normalization process has been done to avoid the high magnitude variance in the actual data and simulate the data within an acceptable range (0–1) for the software modeling environment (Khosravi et al. 2018). The forecasting accuracy of the proposed predictive models were evaluated using various statistical formulations including Correlation coefficient (r), Normalized root mean square error (RMSE), Percent Bias (PBIAS), Nash-Sutcliffe Efficiency (NSE), Modified Index of Agreement (md), Persistence Index (cp), Relative index of agreement (rd), Kling-Gupta efficiency (KGE). Mathematically, the statistical formulations are expressed as follows:

$$ r=\frac{\sum_{i=1}^N\left({X}_o-\overline{X_o}\right)\left({X}_f-\overline{X_f}\right)}{\sqrt{\sum_{i=1}^N{\left({X}_o-\overline{X_o}\right)}^2}\sqrt{\sum_{i=1}^N{\left({X}_f-\overline{X_f}\right)}^2}} $$

(19)

$$ {\displaystyle \begin{array}{l} RMSE=\sqrt{\frac{1}{N}{\sum}_{i=1}^N{\left({X}_f-{X}_o\right)}^2}\\ {} MAE=\frac{1}{N}{\sum}_{i=1}^N\mid {X}_f-{X}_o\mid \end{array}} $$

(20)

$$ PBIAS=\frac{\sum_{i=1}^N\left({X}_o-{X}_f\right)}{\sum_{i=1}^N{X}_f} $$

(21)

$$ NSE=1-\left[\frac{\sum_{i=1}^N{\left({X}_o-{X}_o\right)}^2}{\sum_{i=1}^N{\left({X}_o-\overline{X_o}\right)}^2}\right] $$

(22)

$$ md=1-\frac{\sum_{i=1}^N{\left({X}_o-{X}_f\right)}^j}{\sum_{i=1}^N{\left(\left|{X}_f-\overline{X_o}\right|+\left|{X}_o-\overline{X_o}\right|\right)}^j} $$

(23)

$$ rd=1-\frac{\sum_{i=1}^N{\left(\frac{X_o-{X}_f}{X_o}\right)}^2}{\sum_{i=1}^N{\left(\frac{\left(\left|{X}_f-\overline{X_o}\right|+\left|{X}_o-\overline{X_o}\right|\right)}{\overline{X_o}}\right)}^2} $$

(24)

$$ KGE=1-\sqrt{{\left(r-1\right)}^2+{\left(\alpha -1\right)}^2+{\left(\beta -1\right)}^2} $$

(25)

where X_o and X_f are the actual and forecasted river flow, $\overline{X_o}$ and $\overline{X_f}$ are the mean values, r is the linear correlation between actual and forecasted, α is the variability $\alpha =\raisebox{1ex}{${\sigma}_f$}\!\left/ \!\raisebox{-1ex}{${\sigma}_o$}\right.$, β is the bias term $\beta =\raisebox{1ex}{${\mu}_f$}\!\left/ \!\raisebox{-1ex}{${\mu}_o$}\right.$. J is the exponent term. N is the number of observations. The physical explanation of the computed statistical formulations can be found in the following researches (Dawson et al. 2007; Chadalawada and Babovic 2019).

5 Results and Discussion

The input attributes of the models were constructed based on the partial auto-correlation function (PACF). PACF provides information about the correlation between two separate points on the time-series at different time lags and provides information about the repeating patterns in the time-series. PACF value ranges between 1 and − 1; the value near to 1 indicates near perfect correlation and the value near to −1 indicates complete anti-correlation. In this study, the PACF values equal to or more than 0.5 were considered for the selection of time-lag pattern. Figure 2 illustrates the PACF values for different time lags up to 12 h. It could be observed that the PACF values for the time-lags (t-1), (t-2) and (t-3) were more or less equal to 0.5 and therefore, Q(t-1), Q(t-2) and Q(t-3) were selected as inputs for forecasting one-hour ahead river flow using the predictive models.

Fig. 2

The partial auto-correlation function (PACF) of historical river flow data of Albert River

The performance of all the ML models in forecasting hourly river flow during model training and testing phases were evaluated using several statistical indices including r, R², RMSE, PBIAS, MAE, NSE, md, rd, and KGE. Table 1 shows that ENN, MARS and MPMR performed well in terms of r and R² during training phase. The results showed high degree of linearity between the simulated and the observed data with high predictive ability for all models. A positive linear relationship and higher coefficient value greater than 0.95 was obtained during training phase. Whereas, over the testing phase the r values were very satisfactory and indicated less error variance for each model. However, ENN and MARS models were observed to give the lowest level of scatter appearance (Fig. 3). Although r and R² have been widely used for model evaluation, it is oversensitive to high extreme values and insensitive to additive and proportional differences between model predictions and observed data (Legates and Jr 1999; Moriasi et al. 2007).

Table 1 The models performance based on correlation coefficient (r), coefficient of determination (R²), Root mean square errors (RMSE), Mean Absolute Error (MAE), Nash-Sutcliffe Efficiency (NSE), Modified Index of Agreement (md), relative Index of Agreement (rd) and Kling-Gupta efficiency (KGE) for hourly river flow simulation over the training and testing phases

Fig. 3

A scatter plot of hourly simulated and observed river flow during the testing period (Jan 2014 - Dec 2014) for ENN, MARS, MPMR and RVM models

MAE is considered in this study as its evaluation is less sensitive to extreme values in the forecast data than the RMSE (Fox 1981). ENN (5.32, 25.07) and MARS (4.39, 27.23) demonstrate the lowest deviation from the observed values compared to MPMR (4.39, 75.49) and RVM (213.46, 287.46) for the training and testing phase. Studies reported NSE is a normalized statistic that determines the relative magnitude of the residual variance compared to the measured data variance (Nash and Sutcliffe 1970). NSE values were found to be ideal (NSE = 1) for the training phase of ENN, MARS and MPMR models while for RVM model (NSE = 0.8). According to the guidelines of hydrological model performance evaluation proposed by (Moriasi et al. 2007), the performance of a hydrological model is very good if NSE is more than 0.75. Therefore, it can be remarked that all the models performed very good during the training phase. However, among these models, ENN and MARS models (NSE = 0.99) that is indicated better performance against MPMR (NSE = 0.88) and RVM (NSE = −0.59) over the testing phase. The modified index of agreement (md) developed by (Willmott 1981) as a standardized measure of the degree of model prediction error showed that ENN (0.98, 0.94) and MARS (0.99, 0.97) give the best model fit than MPMR (0.99, 0.48) and RVM (0.45, 0.12) for training and testing phases. Although md provides some improvement over R², it is still sensitive to extreme values due to the squared differences in the mean square error in the numerator (Legates and Jr 1999). In addition, the disadvantage of the results given by the previous R² and NSE arises from the fact that the differences of observed and predicted river flow use the squared values. Consequently, large errors in time series can be overestimated whereas small values can be neglected. To reduce the effect of absolute differences during peak flows and to improve the effect of absolute low flow differences, rd was subsequently applied to measure the differences between the observed and simulated values as relative deviations (Chadalawada and Babovic 2019). A perfect match (1.00) was obtained under rd for ENN and MARS compared with MPMR (1.00, 0.99) and RVM (0.97, 0.69) for the training and testing phases.

In this study, a refine version of KGE proposed by (Gupta 2011), was used to provide a diagnostically interesting decomposition of the NSE, which facilitates the analysis of the relative importance of its different components (correlation, bias and variability) in the context of hydrological modelling (Gupta et al. 2009). ENN (1.00, 0.92) and MARS (1.00, 0.97) give the best result with KGE compare to MPMR (1.00, 0.41) and RVM (0.46, 0.07) for the training and testing phases.

Percent bias (PBIAS) measures the average tendency of the simulated data to be either higher or lower compared to the observed data. According to (Moriasi et al. 2007), the PBIAS < ±10 indicates very good performance of river flow model. Based on this criterion, only ENN (0.0, −8.1) and MARS (0.0, −1.4) were found to perform very good during training and testing phases. However, there was observed a low degree of overestimation (negative value) for the testing phase of the forecast in capturing the extreme river flow. In terms of all these statistics, clearly ENN and MARS were found to perform much better compared to MPMR and RVM during training and testing phases. The performance of the ENN was found very close to MARS in terms of all statistics presented in Table 1.

The performance of the predictive models was also evaluated through visual inspection of graphical representations of the results. Scatter plots were useful to have better understanding of how well the models have estimated the observed data. The scatter plot over the testing phase shows that almost all the points were aligned along the diagonal line of the plots for both ENN and MARS (Fig. 3). However, the magnitude of the coefficient of determination was slightly better for the ENN model over the testing phase. ENN model was attained R² = 0.9881; whereas, MARS model was attained R² = 0.9863. On the other hand, a large deviation, particularly in forecasting higher river flow was noticed for MPMR and RVM.

Taylor diagram was used to show how the predicted river flow by different models are in proximity of observed river flow in terms of correlation, standard deviation and RMSE. Figure 4 shows that ENN and MARS were in the closest proximity to observed river flow during model training and testing. Moriasi et al. (2007) stated that a very good hydrological model should have a RMSE less than 50% of the standard deviation (SD) of the data. Taylor diagram shows that the ratio of RMSE and SD for both ENN and MARS simulated river flow was much less than 0.5 during training and testing phases. However, compared to MARS, the ENN was found much closer to observed point during model testing phase. The ENN predicted river flow was found to have almost same standard deviation of observed river flow during training and testing phases.

Fig. 4

Taylor diagram of the hourly river flow at Albert River, (a) training, (b) testing phases of ENN, MARS, MPMR and RVM models, showing their efficiency compared to observed river flow

All the models were capable to replicate the observed distribution of river flow during model training and testing phases. However, during models testing, the ENN and MARS were found to replicate the spread of data more accurately compared to MPMR and RVM. To summarize, it can be remarked that ENN and MARS were found to have higher capability to predict hourly river flow compared to MPMR and RVM. Between MPMR and RVM, the MPMR was found much better compared to RVM, which was found to perform worst during model testing in term of all statistics. The performance of ENN and MARS were found very close to each other in term of all statistics. However, visual inspection of scatter plots, Taylor diagrams and violin plots reveal marginally higher performance of ENN compared to MARS.

While this study has set a foundation to apply ENN for river flow forecasting over hourly scales, and the study strongly supports recent work that developed an hourly water monitoring index (Deo et al. 2018), further research on multiple lead times would also be useful. Such research would provide users of the model new information on how river flow and how it be predicted over longer-term horizons. While it is a useful subject, that sort of study was beyond the scope of the present work and can form a useful subject for further investigation in future where ENN model could be developed over hourly as well as other lead times. It is worth to mention, the application of the ML models in the stage of advancement and development. ML models are hyper-parameter models in which their modeling performance depend of on the modeling tuning (Chau 2019). However, ML models demonstrated an excellent performance in solving the stochastic problem in the hydrological engineering field.

6 Conclusions

In this study, a relatively less explored ML models, ENN was used for the forecasting of hourly river flow and its performance was compared with three recently developed ML models, namely MARS, MPMR and RVM which are considered competing models in the hydrological forecasting. The main aim of the current study was to develop a reliable intelligent model for hourly scale river flow forecasting and thus the application of ENN model for the first time in forecasting river flow. A case study of Albert River which is located in southeast Queensland, was examined. Flood is a challenging issue in the river basin and therefore, short-term river flow forecasting is an important task for water resource and flood risk management. The statistical assessment of the predictive models reveals superiority of the ENN and MARS models over the MPMR and RVM models. Both the ENN and the MARS models showed R² and an NSE values near to unity and relatively low errors during model testing, which indicate their excellent ability in forecasting hourly river flow. The scatter plots over the testing phase were evidenced the ability of both the ENN and MARS models to reproduce most of the values of the river flow including the extreme river flows with minimum error. However, the ENN model was found to perform marginally better than MARS when the model performance was assessed statistically. Similar to several other ML models, ENN model is associated with the hyper-parameter limitation and thus its internal parameters could be optimized using the advanced nature inspired optimization algorithms that can be investigated in future research. In addition, the capacity of the proposed ENN model can further studied through the investigation of different data division scenarios for the training and testing phases.