1 Introduction

Structural optimization has been a key research topic in engineering for several decades resulting to the development of various methodologies and formulations for dealing with such problems [2,3,4,5,6,7]. Applied structural optimization can also be considered as an added value to structural engineering design, since the advantages of performing structural optimization are rather significant in terms of performance, cost, performance-to-cost ratio and of course environmental responsibility [8]. Topology optimization (TO), a subfield of structural optimization, deals with the optimal distribution of specific volume percentage within the design domain while respecting performance criteria. The main approaches are proposed in modern literature for dealing with topology optimization problems with some of them being the solid isotropic material with penalization (SIMP) [9,10,11], level-set [12, 13], evolutionary (ESO) and bidirectional evolutionary structural optimization (BESO) [14,15,16].

Recent advances in the field have contributed significantly toward making the transition from the research domain to the productivity one. Some of the important challenges that need to be fully addressed in order for structural topology optimization (STO) to be incorporated into everyday procedures of engineering design are the computational demand required for dealing with STO problems since solution approaches are highly dependent on the finite element mesh discretization, the constructability of the optimized structures that are dependent on construction methods like 3D printing and the translation of optimized domains to CAD drawings with respect to curve reproduction, etc. In the current work, the focus is on assisting the computational efficiency of STO solution approaches via machine learning and model order upgrading. In up-to-date literature, several approaches can be found that deal with the above-mentioned computational demand issue with the use of either parallel programming [17,18,19,20,21,22] or reduced order models [23].

Several years have passed since the first time that soft computing methods have been introduced [24]. As the core of such methods relies on heuristics and not calculus, they were received with suspicions; however, they have proven their ability to solve efficiently among other NP hard problems [25]. Some of the most widely known soft computing methods that fall under the category of machine learning are neural networks and metaheuristic search algorithms. Although the use of such methods and especially neural networks was deprecated in the years until 2006, the achieved breakthrough of successfully training deeper architectures along with the ability to have access to massive amount of data led to a large increase in research interest in the field. Deeper architectures and big data have offered the ability to researchers to handle a large number of problems that were not solvable regardless of methods used. Such problems vary from computer vision [26] to natural language processing [27] or medical diagnosis [28] and several others.

With respect to structural optimization, a large number of applications of shallow neural networks [29,30,31] and other soft computing methods like kriging [32] can be found in modern literature. On the contrary, the exploitation of modern machine learning methodologies like deep learning has not been thoroughly examined. In detail, a work of applying deep convolutional neural networks in 2D STO problems can be found [33], while also, DLTOP, a method for reducing the computational load of STO problems with the use of deep belief networks can be found [1].

In this work, a new methodology labeled as DL-SCALE is presented, that aims to reduce the computational cost required for solving topology optimization problems with the use of deep learning combined with a reduced order modeling framework. Topology optimization procedures are quite computationally demanding as they require a large number of solutions of the finite element equilibrium equations. It is also worth noticing that the necessary computational load depends on the finite element mesh discretization used, especially when the discretization gets finer. The adoption of structural optimization procedures and their transformation from academic to real-life practice tools demand that the corresponding computational effort is significantly reduced; in this direction, DL-SCALE methodology is proposed in this work. Although several contributions have attempted to deal with the problem of the increased computational demands, e.g., implementation of parallel computing techniques for accelerating the topology optimization procedures, there are very few studies where the capabilities of machine learning are examined. Although suspicions still remain with respect to the effectiveness of machine learning methods in computationally demanding applications where accuracy in the calculations is also a requirement, in this work, a combination of machine learning methods is proposed to prove their efficiency in multiple benchmark test cases from the literature.

DL-SCALE relies on a pretrained deep belief network able to accelerate the application of the SIMP approach. More specifically, a topology optimization problem is translated into a series of lower order in terms of finite element mesh discretization but identically formulated TO problems, and DLTOP methodology is applied in a sequential manner along with a convolutional filter. As it was proven in a previous work by the authors [1], DLTOP depicts remarkable generality features with respect to its training and testing limits, the search algorithms used by SIMP, the type of loading, the filter used, the objective function adopted, etc., and therefore, all these features of DLTOP are inherited to the proposed DL-SCALE methodology.

The rest of this work is organized as follows: In the second section, named as “Deep Belief Networks,” a short description of deep belief networks adopted in this study is presented. In the third one, labeled as “Accelerated Structural Topology Optimization,” the topology optimization problem along with the SIMP approach and the DLTOP methodology are described. In the fourth section, the proposed DL-SCALE scheme is presented in detail, while in the fifth section, named as “Numerical Tests,” the performance of DL-SCALE is examined through its application to typical topology optimization problems taken from the literature.

2 Deep belief networks

Deep belief networks [34, 35] (DBNs) played a significant part in the breakthrough of deep learning practices around 2006 as they were the one of the first deep architectures that were successfully trained and managed to perform better than traditional machine learning algorithms in classification problems and better than principal component analysis (PCA) in order reduction problems [36]. DBNs can be considered as probabilistic generative models, which consist of a population of stochastic, latent variables that function as feature detectors. Feature detectors are trained to identify hidden higher-order correlations that exist in datasets.

From the networks architecture point of view, DBNs consist of a number of sequentially connected restricted Boltzmann machines (RBMs) [37]. In this network, the nodes of each layer are fully and symmetrically connected to all nodes of the next layer in a directed manner except for the last two layers which are connected in an undirected manner [38]. It is also worth mentioning that in the above architecture the hidden layer of \({\mathrm{RBM}}_{i-1}\) acts in the same as the visible layer of \({\mathrm{RBM}}_i\). A simple example of a DBN containing four RBMs can be viewed in Fig. 1, where RBM1 is defined by layers L1 and L2 and the rest RBMs are defined accordingly. Additionally, L2 acts as the hidden layer of RBM1, while it acts as well as the visual layer of RBM2.

Fig. 1
figure 1

A simple example of DBN

Full size image

In order to overcome the inability of training DBNs, a new training procedure was proposed, which follows a two-step procedure [36]. During the first step, each RBM existing in the DBN is separated from the rest and for each one unsupervised training is performed with by means of contrastive divergence algorithm. In this procedure, the weights of the connections of each RBM are updated as follows: [36, 39]:

$$\begin{aligned} \frac{\partial \log p(v;\theta )}{\partial w_{ij}}&= \left\langle {{v_i}{h_j}} \right\rangle _{{\mathrm{input}}} - \left\langle {{v_i}{h_j}} \right\rangle _{\mathrm{model}}\nonumber \\ w_{ij}^{new}&= w_{ij} + e\Delta w_{ij} \end{aligned}$$
(1)

where e is a parameter defining the desired range of weight change, known as weight learning rate. The DBN is reassembled by the pretrained RBMs and for the second step supervised training is performed for the DBN with the use of backpropagation [40] and the conjugate gradient algorithm [41] where the initialization values of the network parameters are the ones that were defined through the pretraining step.

3 Accelerated structural topology optimization

The goal of topology optimization is to distribute specific material volume inside the design domain in an optimal manner with respect to performance criteria (e.g., compliance) under given boundary and loading conditions [42]. The broad spectrum of topology optimization applications contains several productivity and construction sectors like aerospace design, implants manufacturing, architectural design, material design, fluid mechanics, structural design and more [43,44,45,46,47,48].

Ever since the presentation of the homogenization method [49], a number of other approaches have been proposed with the basic ones being [42]: (1) density method, (2) level-set method, (3) topological derivative method, (4) phase field method and (5) evolutionary method. Density method and its most well-known representative, solid isotropic material with penalization (SIMP), was firstly introduced around 1990 [9,10,11]; SIMP uses power law for simplifying the homogenization method, while the formulation of the TO problems can be summarized through the following expressions:

$$\begin{aligned} \begin{array}{ll} {\mathrm{Minimize}} \,F(x) &{}\\ {\text {with respect to}}:&{} \\ &{}K \times U=F \\ &{}g(x)\le 0 \\ &{}0 \le x \le 1 \end{array} \end{aligned}$$
(2)

where F(x) is the objective function, usually corresponding to the compliance of the system, x is the density variable vector, K is the global stiffness matrix, F and U are the loading and displacement vectors, respectively, and g(x) is the problem constraint.

3.1 Solid isotropic material with penalization approach

SIMP approach is one of the most established approaches in structural topology optimization (STO). The most commonly used performance indicator adopted by STO problem formulations is the compliance C of the structural system, and without loss of the generality, the proposed method is adopted in the current presentation. As the domain \(\Omega\) is discretized into n finite elements, the distribution of material is expressed by the density values \(x_i\) where \(i\;\in [1,\dots , n]\) and \(x_i\;\in (0,1]\) with \(x_i~=0\), indicating that no material is present on the \(i_{th}\) finite element and \(x_i=1\) indicating that the \(i_{th}\) finite element is fully filled with material. As a result of the above, Eq. 2 is transformed as follows:

$$\begin{aligned} \begin{aligned} {\text {Minimize}} \quad C(x) = F^T \times U(x) \qquad \qquad \qquad \\ \quad {\mathrm{with}} \quad {\mathrm{respect}} \quad {\mathrm{to}}: \qquad \qquad \qquad \qquad \\ K(x) \times U(x)=F \qquad \\ \frac{V(x)}{V_0} = V_t \qquad \qquad \; \;\\ 0 < x \le 1 \qquad \qquad \end{aligned} \end{aligned}$$
(3)

where C(x) is the system’s compliance for a given density vector x, K(x) is the global stiffness matrix, F and U(x) are the loading conditions vector and the global displacements vector, respectively, and \(V(x), V_0, V_t\) are the volumes corresponding to density vector x, the initial volume for \(x = x_0\) and the targeted volume of the optimized domain (\(x = T\)). In the SIMP approach, Young’s modulus E is correlated via power law to the density value of each finite element as follows:

$$\begin{aligned} \begin{aligned} E_x(x_i) = x_i^pE^0 \iff K_x(x_i) = x_i^pK^0 \end{aligned} \end{aligned}$$
(4)

where p is a penalization parameter usually setting \(p=3\). The above correlation is used for pushing SIMP toward generating density values \(x_i\) close to the lower or upper bound of x [50]. In Eq. 3, the compliance can be calculated as follows:

$$\begin{aligned} \begin{aligned} C(x)&= F^T \times U(x)\;\iff \\ C(x)&= U^T(x) \times K(x) \times U(x)\;\iff \\ C(x)&= \sum _{i=1}^{n} x_i^pU_i^TK_i^0U_i \end{aligned} \end{aligned}$$
(5)

Accordingly, Eq. 3 can be rewritten as follows:

$$\begin{aligned} \begin{aligned} {\text {Minimize}} \quad C(x) = \sum _{i=1}^{n} x_i^pU_i^TK_i^0U_i \qquad \qquad \qquad \\ \quad {\mathrm{with}} \quad {\mathrm{respect}} \quad {\mathrm{to}}: \qquad \qquad \qquad \qquad \\ K(x)*U(x)=F \qquad \\ \frac{V(x)}{V_0} = V_t \qquad \qquad \; \;\\ 0 < x \le 1 \qquad \qquad \; \; \end{aligned} \end{aligned}$$
(6)

In the literature, the optimization problem described in Eq. 6 is handled either by the moving asymptotes algorithm (MMA) or the optimality criteria (OC) one.

3.2 Deep learning-assisted topology optimization (DLTOP)

The capability of deep belief networks (DBNs) in discovering multiple representational levels of data nonlinearity in pattern recognition problems triggered the development of the methodology proposed by the authors recently [1], DLTOP, based on DBNs and SIMP. More specifically, a DBN is calibrated on transforming the input data containing density fluctuation pattern of the finite element (FE) discretization provided by a number of initial steps of the SIMP approach to a new higher-level representation. This representation corresponds to the final density value distribution over the domain as obtained by SIMP. DLTOP is a specially tailored methodology for accelerating SIMP approach in STO problems. For this reason, the DBN is used for predicting a close-to-optimal density value for each FE of the initial domain, according to initial densities produced in SIMP early iterations. In order for the prediction to be accurate, the DBN is trained once on a typical topology optimization problem before being applied to any STO problem regardless of differences in mesh and domain dimensions, mesh type, loading conditions, desired final density, filter value, etc.

Assuming, without loss of generality, that a structured FE mesh discretization of \(ne_x,ne_y,ne_z\) FEs per axis is implemented on a 3D rectangular domain, \(ne = ne_x \times ne_y \times ne_z\) is the number of finite elements used for the mesh discretization. In the initialization step of the SIMP approach, a density value \(d_i\) is assigned to each \(ne_i\) FE, while this density \(d_i\) of each element is updated in every iteration of SIMP until convergence is achieved. The fluctuation of density value \(d_i\) of the \(i_{th}\) FE with respect to the iteration step t can be expressed as follows:

$$\begin{aligned} d_i = F(t) \qquad \forall \; i \in [1,ne] \end{aligned}$$
(7)

Figure 2 presents several cases of the density fluctuation of a number of FEs with respect to SIMP iterations. It can be witnessed that there are several different patterns in density fluctuation of each FE. These different patterns can be explained due to different FE locations in the design domain, loading and support conditions, SIMP parameters, etc. Density fluctuation can be regarded as a discrete-time data history for each FE in the domain, which represents the optimization history of each element.

Fig. 2
figure 2

Fluctuation of density of various finite elements with respect to SIMP iterations

Full size image

DLTOP methodology can be described as a two-phase procedure. In the first step, SIMP performs a small number of initial iterations which are used as input data for DBN. Based on the input provided, DBN proposes an optimized domain at the end of the first phase. In the second phase, SIMP performs fine-tuning on the DBN-proposed optimized domain. A population of initial iterations (e.g., thirty-six [1]) of SIMP are executed for creating the necessary DBN input vectors of density per iteration per FE. The trained DBN evaluates the given input of initial density values of each FE and performs a discrete jump from the thirty-sixth iteration to a close-to-optimal density per FE. After that, SIMP is used in order to perform fine-tuning in the DBN proposed domain until convergence is achieved.

A flowchart of DLTOP methodology is presented in Fig. 3, while the application of the two-phase methodology in the case of a single finite element is shown in Fig. 4. The abscissa of Fig. 4 denotes the iterations performed by SIMP, while the ordinate corresponds to the density value of the single finite element.

Fig. 3
figure 3

Flowchart of DLTOP methodology

Full size image
Fig. 4
figure 4

Implementation of DLTOP methodology to a single FE

Full size image

The basic advantage of DLTOP methodology is its ability to generalize well. This means that it only needs to be trained once on a typical TO problem, and then, it can be applied to any TO problem formulated with different parameters without presenting a need for retraining. This advantage is owed to the fact that DLTOP does not need any information with respect to the geometrical position of each FE, the type of the mesh, the loading and support types and conditions, the filter used, etc. The only information needed by DLTOP is the density fluctuation in the initial iterations of SIMP.

Classification problems are a challenging area of predictive modeling. Contrary to regression predictive modeling, classification models require information also on the complexity of a sequence dependence among the input parameters. In the case of STO, the early density values represent the sequence dependence information that needs to be provided as inputs to the proposed classification methodology. The sequence of discrete-time data, i.e., the density value for every FE and the T iterations, are generated by SIMP approach and stored in matrix \(S_d\) presented below:

$$\begin{aligned} \begin{aligned} S_d = \left[ {\begin{array}{cccc} d_{1,1} &{} d_{1,2} &{} \dots &{} d_{1,T}\\ d_{2,1} &{} d_{2,2} &{} \dots &{} d_{2,T}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ d_{ne,1} &{} d_{ne,2} &{} \dots &{} d_{ne,T} \end{array}} \right] \end{aligned} \end{aligned}$$
(8)

where T denotes the maximum iterations needed by SIMP to achieve convergence. The above matrix is needed when setting-up the training data of a DBN for TO problems. A small part of the optimization procedure is equal to the first t iterations is transformed into time-series input data for training the DBN, while the vector of the density in the final iteration of SIMP approach corresponding to the \(T_{th}\) column of density matrix \(S_d\) is used as the target vector of DBN training. The training of the DBN focuses on discovering higher-order correlations between the training sample and the target as seen below:

$$\begin{aligned} \begin{aligned} \left[ {\begin{array}{c c c c | c c c | c} d_{1,1}&{}d_{1,2}&{} \dots &{} d_{1,t} &{} d_{1,t + 1}&{} \dots &{} d_{1,T - 1} &{} d_{1,T}\\ d_{2,1}&{} d_{2,2} &{} \dots &{} d_{2,t}&{} d_{2,t + 1}&{} \dots &{} d_{2,T - 1} &{} d_{2,T}\\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ d_{ne - 1,1}&{} d_{ne - 1,2} &{} \dots &{} d_{ne - 1,t} &{} d_{ne - 1,t + 1} &{} \dots &{} d_{ne - 1,T - 1} &{} d_{ne - 1,T}\\ d_{ne,1} &{} d_{ne,2}&{} \dots &{} d_{ne,t}&{} d_{ne,t + 1} &{} \dots &{} d_{ne,T - 1} &{} d_{ne,T} \end{array}} \right] \\ \begin{array}{c c c} Training \; Sample \qquad \quad \qquad \quad Not \; Used \qquad \qquad \quad Target \end{array} \end{aligned} \end{aligned}$$
(9)

4 The DL-SCALE methodology

The proposed DL-SCALE methodology aims to reduce the computational time required for solving structural topology optimization problems. DL-SCALE is based on a reduced order modeling scheme, introducing a new framework of combining SIMP and DBNs. In previous work by the authors [1], the combination of SIMP with DBNs labeled as DLTOP was found to perform remarkably well when applied to the full-scale order model both in terms of acceleration of the process, while its applicability was found to be very general. In this work, a new framework is presented, that is based on the exploitation of the fast results that can be derived from coarser discretized models for assisting the optimization of higher-order models. The new DL-SCALE methodology integrates DLTOP in a sequential “model-optimize-and-upgrade” framework that is presented in detail below.

Similar to any structural optimization problem, in structural topology optimization multiple finite element analyses are performed during the iterative solution process. As a result, the execution time is highly dependent on the size of the problem, i.e., the finite element mesh discretization adopted for the problem at hand. As the evolution of hardware capabilities is specific, research is focused on methods for reducing the computing time required for solving the structural topology optimization problem. Most efforts are focused on implementing parallel computing techniques either in CPU or in GPGPU [19, 21, 52, 53] or reduced order model methods [23]. The proposed DL-SCALE methodology suggests the transfer of knowledge from optimal topologies achieved when using lower-order models to higher-order ones.

DL-SCALE’s framework can be described as a multistage iterative applications of the DLTOP methodology. The idea is to use DLTOP for solving lower-order structural topology optimization problems and up-scale the knowledge obtained through the solution of the lower-order problems to higher-order ones before reapplying DLTOP. In DLTOP, a small number of iterations of SIMP are used as input for a trained DBN network which then predicts a close-to-optimal topology. The procedure terminates once this topology is fine-tuned by SIMP. The idea that generated DL-SCALE is based on combining low computational times required for solving coarse discretized domains in SIMP approach and the iterations reduction capabilities of DLTOP methodology. The goal of DL-SCALE is to achieve a significant reduction of computational times of fine-meshed domains. The performance of DL-SCALE is examined with the use of a number of typical test-examples taken from the literature that are presented in the following section.

4.1 The STO problem and FE mesh discretization

As it can be concluded from the description of the STO problem provided in the previous section, the definition of a topology optimization problem \({\mathrm{TOP}}_0\), where 0 refers to a reference STO problem, requires the following parameters to be provided:

  • Dimensions of the design domain \(L_{xyz}\)

  • Number of FEs in the mesh ne

  • Support conditions \(S_c\)

  • Loading conditions \(P_c\)

  • Target volume \(V_t\)

Therefore, complementary to the formulation of the STO given in Eq. 6, it can be said that the parameters of \({\mathrm{TOP}}_0\) can be summarized as: \([L_{xyz}^{(0)},\; ne^{(0)},\; S_c^{(0)},\; P_c^{(0)},\; V_t^{(0)}]\). In case that the computational time required for solving the optimization problem \({\mathrm{TOP}}_0\) is equal to \(t_0\), it can be stated that the execution time for solving \({\mathrm{TOP}}_1\) problem with parameters \([L_{xyz}^{(0)},\; ne^{(1)},\; S_c^{(0)},\; P_c^{(0)},\; V_t^{(0)}]\) with respect to \(t_0\) depends on the ratio: \(\frac{ne^{(0)}}{ne^{(1)}}\). In order for the two problems (i.e., \({\mathrm{TOP}}_0\) and \({\mathrm{TOP}}_1\) problems) to be comparable, they vary only with respect to the finite elements used for discretizing the design domain (i.e., \(ne^{(0)}\) and \(ne^{(1)}\), respectively). An indication for this statement can be seen from the results of Table 1 where the dependence of computational time per iteration and FE mesh discretization is presented for the case of the bridge 3D design domain [48] discretized with different number of finite elements, \(ne^{(0)}\;=\;406,456\) finite elements and \(ne^{(1)}\) vary from 4000 to 63,480. The specifications of the computing environment used for carrying out the optimization runs are an Intel Xeon E5-1620 at 3.70 GHz quad-core and 16 GB RAM, while the SIMP code used is the 3D version of the 88-line code [51]. As it can be seen in Table 1, the FE mesh discretization is critical for the execution time required for solving the STO problems, indicatively for one order of magnitude coarser mesh (i.e., \(ne^{(1)}\;=\;63,480\)) compared to the one used for solving \({\mathrm{TOP}}_0\) problem, and the computing time ratio is almost equal to 13. For underlining the importance of mesh discretization worth mentioning that even if the optimization runs for the \({\mathrm{TOP}}_1\) problems relying on the coarser discretizations where implemented sequentially, such a case would require computing time \(t_d\) that is equal to the sum of \(t_i^{(1)}\;\forall \;i\;\in \;[1,5]\) that refer to the computing time required for solving all the five \({\mathrm{TOP}}_1\) problems using coarser discretizations with \(ne_i^{(1)}\) FEs. The remarkable observation for this case is the value of the corresponding ratio: \(\frac{t^{(0)}}{t^{(d)}}\;=\;7.12\). Thus, performing several iterations using models with coarse mesh discretizations can be more economical in terms of computation time than performing even a single iteration of fine discretized domain, while coarser mesh discretizations might require less iterations than fine meshed ones.

Table 1 Mesh discretization and execution time ratio for SIMP
Full size table

4.2 Workflow of DL-SCALE methodology

The workflow of DL-SCALE can be summarized as follows: let us consider the case that a \({\mathrm{TOP}}_f\) problem is to be solved; the design domain of the problem is discretized with \(ne_f\) finite elements and its parameters are \([L_{xyz}^{(f)},\; ne^{(f)},\; S_c^{(f)},\; P_c^{(f)},\; V_t^{(f)}]\), where f stands for fine mesh discretization and denotes STO problem. In addition, a set of \(n_{\mathrm{probs}}\) auxiliary STO problems is defined as \({\mathrm{TOP}}_i^R\) where \(i\;\in \;[1,n_{\mathrm{probs}}]\) that rely on reduced order models compared to the \({\mathrm{TOP}}_f\) one. The \(n_{\mathrm{probs}}\) reduced order model-based optimization problems \({\mathrm{TOP}}_i\) are identical to the reference one \({\mathrm{TOP}}_f\) with respect to all parameters except for \(ne^{(i)}\). Thus, the ith reduced order model-based \({\mathrm{TOP}}_i^R\) problem can be described as \([L_{xyz}^{(f)},\; ne_i^{(R)},\; S_c^{(f)},\; P_c^{(f)},\; V_t^{(f)}]\), denoted with the notation (R), i.e., reduced. Regarding the FE mesh discretization adopted for defining the set of \(n_{probs}\) problems, it must be pointed out that very coarse meshes are used, compared to the \(ne^{(f)}\) FE mesh used for the formulation of the reference \({\mathrm{TOP}}_f\) problem:

$$\begin{aligned} \begin{aligned} ne_1^{(R)}< ne_2^{(R)}< ne_3^{(R)}< ne_4^{(R)}<\cdots< ne_{n_{\mathrm{probs}}}^{(R)}<< ne^{(f)} \end{aligned} \end{aligned}$$
(10)

It is worth pointing out that while all parameters for the \(n_{probs}\) \({\mathrm{TOP}}_i^{(R)}\) problems are defined, the initial material distribution over the design domain D for each \(TOP^{(R)}\) should be provided in order to implement SIMP approach. Only for \({\mathrm{TOP}}_1^{(R)}\) the material distribution is uniform, which is a common practice for STO problems; for the rest ones, it originates from the optimized topology achieved in the previous reduced order model-based \(TOP^{(R)}\) problem. The hierarchy of the \(n_{probs}\) STO problems starts with the one using the coarser mesh discretization to the finer one; therefore, the auxiliary problems are solved sequentially initiating from the one using the coarser mesh to the finer one. Once the definition of the five \(TOP^{(R)}\) problems is completed, the next step required by the proposed DL-SCALE methodology is the application of DLTOP on the first lower-order model, i.e., that adopted for the \({\mathrm{TOP}}_1^{(R)}\) problem. Hence, SIMP performs 36 iterations for the \({\mathrm{TOP}}_1^R\) problem, and then, the density values per iteration per FE are used by the trained DBN [1] for predicting a final density value for each FE of the mesh discretization of the design domain adopted for \({\mathrm{TOP}}_1^{(R)}\) problem. It must be pointed out that since the input and output used in DL-SCALE are identical with the ones used in DLTOP, in addition the procedure followed for creating a database, training and calibrating the DBN model is exactly the same, while the DBN architecture is also identical with the one used in DLTOP. Therefore, none of these operations need to be performed again; the trained DBN model is obtained ready to be used from the previous work by the authors [1].

4.2.1 The convolution step on the optimized domain

When the optimized domain by the \({\mathrm{TOP}}_1^{(R)}\) problem is obtained, a convolution step for the optimized domain is performed. The mathematical expression of the convolution step via filtering can be expressed as follows [38]:

$$\begin{aligned} D_c(i,j) = (D \times f)(i,j) \end{aligned}$$
(11)

This convolution step is performed according to Eq. 11, while the filter used is a Gaussian blur filter [54]. The dimensions \([a_f,b_f]\) of the filter f are chosen with respect to the elements per axis of the design domain D (i.e., \([ne_x,ne_y]\) for the case of 2D STO problems). An example of the filter f for a [7, 7] filter can be seen in Eq. 12:

$$\begin{aligned} \begin{aligned} f = \left[ {\begin{array}{c c c c c c c} 0 &{} 0 &{} 0 &{} 0.01961 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.01961 &{} 0.07059 &{} 0.12549 &{} 0.07059 &{} 0.01961 &{} 0\\ 0 &{} 0.07059 &{} 0.25098 &{} 0.39216 &{} 0.25098 &{} 0.07059 &{} 0\\ 0.01961 &{} 0.12549 &{} 0.39216 &{} 0.39216 &{} 0.39216 &{} 0.12549 &{} 0.01961\\ 0 &{} 0.07059 &{} 0.25098 &{} 0.39216 &{} 0.25098 &{} 0.07059 &{} 0\\ 0 &{} 0.01961 &{} 0.07059 &{} 0.12549 &{} 0.07059 &{} 0.01961 &{} 0\\ 0 &{} 0 &{} 0 &{} 0.01961 &{} 0 &{} 0 &{} 0\\ \end{array} } \right] \end{aligned} \end{aligned}$$
(12)

For implementing the convolution step, the size parameters of f are chosen accordingly in order for the convolved matrix \(D_c\) to be equal to the ones of the initial matrix D. Once convolution is performed, the convolved matrix \(D_c\) is normalized in the range of [0, 1]. It is worth mentioning that although above are referring to the case of 2D domains, the same procedure can be applied to 3D domains as well. The \(D_c\) matrix represents an optimized domain for the \({\mathrm{TOP}}_1^{(R)}\) problem. The DL-SCALE procedure continues with the translation of the result obtained for \({\mathrm{TOP}}_1^{(R)}\) problem to be the initial domain for the \({\mathrm{TOP}}_2^{(R)}\) one. This is achieved by reassigning the densities of each FE of the initial problem (i.e., \({\mathrm{TOP}}_1^{(R)}\)) to the FEs of the more densely meshed problem (i.e., \({\mathrm{TOP}}_2^{(R)}\)) as it can be seen in 5. As coordinates \(x_i^{(1:k)},\; y_i^{(1:k)}\) of the k edges of each \(i_{th}\) FE in \({\mathrm{TOP}}_1^{(R)}\) and \({\mathrm{TOP}}_2^{(R)}\) are known, the geometric center of each FE can be calculated according to:

$$\begin{aligned} \begin{aligned} x_i^c&=\frac{1}{k} \sum _{j=1}^{k} x_i^j\\ y_i^c&=\frac{1}{k} \sum _{j=1}^{k} y_i^j \end{aligned} \end{aligned}$$
(13)
Fig. 5
figure 5

Example of densities reassignment, transition from coarse to finer mesh discretization

Full size image

4.2.2 The DLTOP step

Before describing the next steps of DL-SCALE, it is worth mentioning that for the needs of this study the number \(n_{probs}\) of auxiliary STO problems was set equal to five. In the next step of DL-SCALE, DLTOP is applied again for the next \({\mathrm{TOP}}_2^{(R)}\) problem, i.e., \(t=36\) iterations of SIMP are performed for the \({\mathrm{TOP}}_2^{(R)}\) problem in order to generate the input for the second application of the trained DBN. The DBN proposes the optimized density distribution for each FE of mesh discretization of the design domain adopted for the \({\mathrm{TOP}}_2^{(R)}\) problem. Subsequently, similar to the procedure followed for the DBN-proposed optimized domain for the \({\mathrm{TOP}}_1^{(R)}\) problem, the one proposed by DBN for \({\mathrm{TOP}}_2^{(R)}\) is re-meshed according to the FE mesh discretization with \(ne_3^{(R)}\) elements of the \({\mathrm{TOP}}_3^{(R)}\) problem and is assigned to the elements of \({\mathrm{TOP}}_2^{(R)}\) based on proximity rules as previously described. The above-mentioned procedure is repeated for \({\mathrm{TOP}}_3^{(R)},\;{\mathrm{TOP}}_4^{(R)}\) and \({\mathrm{TOP}}_5^{(R)}\) in a sequential manner. At the final step of DL-SCALE, the DBN-proposed density distribution for the \({\mathrm{TOP}}_5\) problem is re-meshed according to the mesh discretization of \(ne_f\) FEs adopted for the reference \({\mathrm{TOP}}_f\) problem. Initial densities for each of the \(ne_f\) FEs are set equal to the density of the closer element of the mesh discretization adopted for the \({\mathrm{TOP}}_5^{(R)}\) problem as defined with respect to geometrical center distance. After applying convolution, as described previously, the produced output is used as SIMP initialization state for \({\mathrm{TOP}}_f\) and SIMP performs 36 needed iterations followed by a DBN-based prediction, as in DLTOP, of a close-to-optimal topology. The final output is produced after fine-tuning by SIMP performing the necessary iterations until convergence. A flowchart of DL-SCALE can be seen in Fig. 6.

4.2.3 From DLTOP to DL-SCALE

DL-SCALE methodology, as it can be seen in Fig.6, is initialized based on a rather low-order model (OM) (i.e., sparse FE mesh discretization); DLTOP is applied to this initial layout of the design domain where the aforementioned sparse FE mesh discretization is used and a DBN-proposed topology layout is acquired. The new layout is re-meshed using a denser FE mesh discretization, DLTOP is applied to the new layout and a newer DBN-proposed topology layout is achieved. This procedure represents the core of the DL-SCALE methodology, and it is repeated using incrementally denser FE mesh discretizations to the newer topology layouts achieved. At the last part of DL-SCALE methodology, DLTOP is applied to the final layout obtained, discretized using the finest FE mesh discretization chosen for the problem at hand and the optimized design is extracted.

The differences between DLTOP and DL-SCALE methodologies described previously are more evident when comparing the corresponding workflows where it can be seen that DLTOP represents a basic component of the DL-SCALE methodology. DLTOP relies on information extracted from the first iterations of the original SIMP approach applied to solve the STO problem; thus, no variation of layout information is neither introduced nor extracted. Only the fluctuation of the material density value of the finite elements observed during the first 36 iterations is needed. The deep network is trained once on several density fluctuation patterns and learns to recognize them with respect to the final density distribution proposed by SIMP. As a result, the application of the trained network to the same input will always conclude to the same output. On the contrary, DL-SCALE methodology incorporates DLTOP’s ability to accelerate the solution procedure of STO problems in conjunction with an OM upscaling scheme. Thus, DL-SCALE can take advantage of the layout information provided by a series of OMs contrary to DLTOP that uses only one. It is also worth pointing out that the selection of FE mesh discretizations used in the five different OMs used can differentiate the final topology obtained by the proposed methodology. Apart from the final topology differentiation ability, DL-SCALE methodology can be escalated to any FE mesh discretization with respect to the initial OMs chosen.

Fig. 6
figure 6

Flowchart of DL-SCALE methodology

Full size image

5 Numerical tests

The performance of DL-SCALE methodology is investigated against the conventional implementation of SIMP approach over a number of topology optimization benchmark problems. More specifically, SIMP is applied on five 2D test-examples that are chosen from literature until convergence. For each optimization run performed by SIMP, the executed iterations until convergence, the optimal objective function value (i.e., compliance value) and the necessary execution time are recorded. Once the conventional SIMP-based optimization runs are completed, DL-SCALE is applied on all test-examples as well. DL-SCALE methodology requires performing iterations on \(n_{\mathrm{probs}}=5\) reduced order models before performing the optimization run for the reference FE mesh discretization for the problem at hand. Due to the nature of DL-SCALE methodology, i.e., FE models of different order are involved in the optimization runs required, the comparison of SIMP is mainly based on the total execution time than the number of iterations; however, the iterations performed for the reference \({\mathrm{TOP}}_f\) problem that is based on the model having mesh discretization of \(ne_f\) FEs are recorded as well. The objective function value is recorded in order to validate the quality of the solution provided by DL-SCALE, while the number of iterations needed in both cases is recorded for validating the acceleration achieved by DL-SCALE. The recorded time starts from the definition of the \({\mathrm{TOP}}_1^{(R)}\) problem and terminates at the end of the final iteration of the optimization run performed for the \({\mathrm{TOP}}_f\) problem. The iterations recorded in DL-SCALE are the 36 iterations performed prior to DBN application along with the ones performed following DBN output until the convergence of the solution runs for the \({\mathrm{TOP}}_f\) problem. As previously stated, DL-SCALE requires the use of \(n_{\mathrm{probs}}=5\) different discretizations of the design domain with reduced number of FEs. For testing generality and that even very coarse FE models can be used efficiently, for this reason two different sets with the auxiliary STO problems \([{\mathrm{TOP}}_i^{R}]\) of are examined. In the first one, each of the \(ne_i^{(R)}\)’s for the coarse meshes is equal to \([1000,\;2000,\;3000,\;4000,\;5000]\) finite elements, respectively, while in the second case, each of the \(ne_i^{(R)}\)’s is equal to \([3000,\;4000,\;5000,\;7000,\;10,000]\) finite elements, respectively. Regarding the number of the FEs used to discretize the design domain for the reference STO problem of each test-example, four different discretizations for defining the reference optimization \({\mathrm{TOP}}_f\) problem are examined in order to evaluate the performance of DL-SCALE, specifically \(ne^{(f)}\) is equal to \([20,000,\; 50,000,\; 75,000,\; 100,000]\) finite elements. A detailed description of the five test-examples used in the comparison can be found below.

5.1 Test-example description

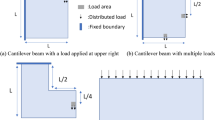
In test-example A, the support conditions refer to fully fixed boundary condition along the x-axis ending at the half of the x dimension and the loading condition refers to one concentrated force P along the y-axis and applied in the fourth of the y dimension. The ratio of \(ne_x\) to \(ne_y\) is equal to 0.5, while the volume fraction is equal to 35%. In test-example B, the support conditions refer to two fixed joints placed at both left and right lower-end corners of the domain and the loading conditions refer to one concentrated force P along the y-axis, applied in the middle of the y dimension at the base of the structure. The ratio of \(ne_x\) to \(ne_y\) is equal to 1/3, while the volume fraction is equal to 35%. In test-example C, the support conditions refer to two fixed joints placed at the two right corners of the domain and the loading conditions refer to two concentrated forces P along the x-axis and applied in the left and right middle of the span in the y dimension. The ratio of \(ne_x\) to \(ne_y\) is equal to 0.5, while the volume fraction is equal to 40%. In test-example D, the support conditions refer to fully fixed boundary conditions along the x-axis, starting at the 3:8ths of the x dimension and the loading conditions refer to four concentrated forces P along the y axis and applied at intermediate distances equal to 1:3 of the x dimension. The ratio of \(ne_x\) to \(ne_y\) is equal to 0.5, while the volume fraction is equal to 50%. In test-example E, the support conditions refer to two fixed joints placed at both left and right lower-end corners of the domain, and the loading conditions refer to one concentrated force P along the y, applied at the half of the y dimension at the top of the structure. The ratio of \(ne_x\) to \(ne_y\) is equal to 1/3, while the volume fraction is equal to 35%. It is worth pointing out that a sensitivity filter with a radius equal to 3 was chosen in all cases as SIMP filter. A schematic representation of all test-examples can be seen in Fig. 7.

Fig. 7
figure 7

Schematic representation of the test-examples

Full size image

5.2 Performance of the DL-SCALE methodology

DL-SCALE methodology performance is examined with reference to the total execution time required by the methodology until convergence. In addition, the reduction of the SIMP iterations needed, the improved objective function value and optimized domain achieved are also collected for every test-example considered. For the purposes of the current study, two sets of auxiliary \([{\mathrm{TOP}}_i^{R}]\) problems are examined: \(SET_1=[1000,\;2000,\;3000,\;4000,\;5000]\) and \(SET_2=[3000,\;4000,\;5000,\;7000,\;10,000]\). The performance of the DL-SCALE methodology is decomposed into two parts: in the first one the efficiency of the two sets of auxiliary STO problems is examined in two test-examples and then the chosen set is applied to three additional test-examples. Convolution over the optimized design achieved from the implementation of DLTOP for the auxiliary \([{\mathrm{TOP}}_i^{R}]\) problems is major important step of DL-SCALE methodology; for this reason, for the case of test-cases A and D the optimized domains generated by the DBN for each one of the five auxiliary \({\mathrm{TOP}}_i\) problems and the ones obtained through the convolution stage are shown.

5.2.1 Assessing the two sets of auxiliary STO problems

The data collected for all optimization runs performed for test-example A can be found in Table 2 for the case of \({\mathrm{SET}}_1\) and in Table 3 for the case of \({\mathrm{SET}}_2\). As it can be observed, for test-example A, the maximum reduction on the computational time achieved by DL-SCALE compared to the conventional implementation of SIMP is almost equal to \(82\%\). This reduction corresponds to the case that 100,000 finite elements were used for the discretization of the design domain for the reference \({\mathrm{TOP}}_f\) problem, while the objective function value was also improved achieving a better reduction of \(0.94\%\). The optimized domains achieved by the conventional implementation of SIMP for the case of \(ne_f = 20{,}000\) and \(ne_f = 100{,}000\) along with the ones obtained by DL-SCALE can be seen in Fig. 8. The optimized domains generated by the DBN for each one of the five auxiliary \({\mathrm{TOP}}_i\) problems for the case of \({\mathrm{SET}}_1\) and the ones obtained through the convolution stage can be seen in Fig. 9a, b, respectively, hierarchically starting from the coarser to the finer one.

Table 2 Acceleration achieved via DL-SCALE in test-example A for \(SET_1\)
Full size table
Table 3 Acceleration achieved via DL-SCALE in test-example A for \(SET_2\)
Full size table
Fig. 8
figure 8

Test-example A: optimized domains achieved by a SIMP and b DL-SCALE methodology for the case of \(ne_f = 20{,}000\) and \(ne_f = 100{,}000\) when \({\mathrm{SET}}_1\) is used

Full size image
Fig. 9
figure 9

Test-example A: optimized domains generated for each auxiliary \({\mathrm{TOP}}_i\) problem by: a DBN and b convolution step for the case of \({\mathrm{SET}}_1\)

Full size image

Similar to test-example A, the data collected for all optimization runs performed for test-example B can be found in Table 4 for the case of \({\mathrm{SET}}_1\) and in Table 5 for the case of \({\mathrm{SET}}_2\). As it can be observed, for test-example B, the maximum reduction on the computational time achieved by DL-SCALE compared to the conventional implementation of SIMP is almost equal to \(77\%\). This reduction corresponds to the case that 100,000 finite elements were used for the discretization of the design domain for the reference \({\mathrm{TOP}}_f\) problem, while the objective function value was also improved achieving a reduction of \(0.87\%\). The optimized domains achieved by the conventional implementation of SIMP for the case of \(ne_f\,=\,20{,}000\) and \(ne_f\,=\,100{,}000\) along with the ones obtained by DL-SCALE can be seen in Fig. 10.

For the two test-examples A and B when \({\mathrm{SET}}_1\) of auxiliary STO problems was used, the computational efficiency was improved compared to the one achieved for the case of \({\mathrm{SET}}_2\) auxiliary STO problems. In STO problems, the reduction of the material volume represents the most common criterion adopted in literature. For this reason, as slightly better optimization results in terms of objective function value were obtained by \({\mathrm{SET}}_2\), it was adopted instead of \({\mathrm{SET}}_1\) for performing the optimization runs presented in the next section.

Table 4 Acceleration achieved via DL-SCALE in test-example B for \(SET_1\)
Full size table
Table 5 Acceleration achieved via DL-SCALE in test-example B for \({\mathrm{SET}}_2\)
Full size table
Fig. 10
figure 10

Test-example B: optimized domains achieved by a SIMP and b DL-SCALE methodology for the case of \(ne_f=20{,}000\) and \(ne_f=100{,}000\) when \({\mathrm{SET}}_1\) is used

Full size image

5.2.2 Testing the chosen set of auxiliary STO problems

The data collected for all optimization runs performed for test-example C can be found in Table 6 for the case of \({\mathrm{SET}}_2\). As it can be observed, for test-example C, the maximum reduction on the computational time achieved by DL-SCALE compared to the conventional implementation of SIMP is almost equal to \(82\%\). This reduction corresponds to the case that 100,000 finite elements were used for the discretization of the design domain for the reference \({\mathrm{TOP}}_f\) problem, while the objective function value was also improved achieving reduction of \(0.40\%\). The optimized domains achieved by the conventional implementation of SIMP for the case of \(ne_f\,=\,20{,}000\) and \(ne_f\,=\,100{,}000\) along with the ones obtained by DL-SCALE can be seen in Fig. 11.

Table 6 Acceleration achieved via DL-SCALE in test-example C
Full size table
Fig. 11
figure 11

Test-example C: optimized domains achieved by a SIMP and b DL-SCALE methodology for the case of \(ne_f=20{,}000\) and \(ne_f=100{,}000\)

Full size image

Similar to the previous test-examples, the data collected for all optimization runs performed for test-example D can be found in Table 7 for the case of \({\mathrm{SET}}_2\). As it can be observed, also for test-example D, the maximum reduction on the computational time achieved by DL-SCALE compared to the conventional implementation of SIMP is almost equal to \(83\%\). This reduction corresponds to the case that 100,000 finite elements were used for the discretization of the design domain for the reference \({\mathrm{TOP}}_f\) problem, while the objective function value was also improved achieving a better reduction of \(1.65\%\). The optimized domains achieved by the conventional implementation of SIMP for the case of \(ne_f\) = 20,000 and \(ne_f\) = 100,000 along with the ones obtained by DL-SCALE can be seen in Fig. 12. The optimized domains generated by the DBN for each one of the five auxiliary \({\mathrm{TOP}}_i\) problems and the ones obtained through the convolution stage can be seen in Fig. 13a, b, respectively, hierarchically starting from the coarser to the finer one.

Table 7 Acceleration achieved via DL-SCALE in test-example D
Full size table
Fig. 12
figure 12

Test-example D: optimized domains achieved by a SIMP and b DL-SCALE methodology for the case of \(ne_f=20{,}000\) and \(ne_f=100{,}000\)

Full size image
Fig. 13
figure 13

Test-example D: optimized domains generated for each auxiliary \({\mathrm{TOP}}_i\) problem by: a DBN and b convolution step

Full size image

In accordance with the previous test-examples, the data collected for all optimization runs performed for test-example E can be found in Table 8 for the case of \({\mathrm{SET}}_2\). As it can be observed, for test-example E, the maximum reduction on the computational time achieved by DL-SCALE compared to the conventional implementation of SIMP is almost equal to \(78\%\). This reduction corresponds to the case that 100,000 finite elements were used for the discretization of the design domain for the reference \({\mathrm{TOP}}_f\) problem, while the objective function value was increased by \(2.14\%\). The optimized domains achieved by the conventional implementation of SIMP for the case of \(ne_f\) = 20,000 and \(ne_f\) = 100,000 along with the ones obtained by DL-SCALE can be seen in Fig. 14.

Table 8 Acceleration achieved via DL-SCALE in test-example E
Full size table
Fig. 14
figure 14

Test-example E: optimized domains achieved by a SIMP and b DL-SCALE methodology for the case of \(ne_f=20{,}000\) and \(ne_f=100{,}000\)

Full size image

6 Conclusions

In this work, the so-called DL-SCALE methodology for reducing the computational effort required for solving structural topology optimization (STO) problems is presented. The proposed methodology relies on the exploitation of knowledge gained from reduced order model-based optimal topologies together with the use of the DLTOP framework for accelerating the optimization procedure of a large-scale topology optimization problem. DLTOP is based on solid isotropic material with penalization (SIMP) approach in collaboration with deep belief networks (DBNs) and is used for making discrete jumps from the initial stage of the optimization procedure to the close-to-optimal stage. DL-SCALE is formulated by an iterative application of DLTOP on five auxiliary topology optimization problems formulated based on reduced order models; these models are generated as coarse mesh discretization of the original design domain. The hierarchy of the five STO problems starts with the one using the coarser mesh discretization to the finer one. The optimal topologies achieved by the five auxiliary STO problems with the reduced model are used as the initial topology of the next one until the reference STO problem that is using the fine discretized model is optimized.

The proposed methodology is compared with the conventional SIMP in five typical 2D benchmark test-examples obtained from the literature. All tests were performed on the same computer as the comparison is based on the total computational time required by SIMP and DL-SCALE from the problem definition to the final iteration performed. For comparing the quality of the solutions achieved, apart from the time required, the optimized topology along with the objective function value is also collected. By reviewing the results of DL-SCALE, as it was expected the acceleration achieved depends on the number of the finite elements of the mesh of the problem. As DL-SCALE methodology uses information gained from optimization runs performed over reduced order models, the denser the discretization of the domain is, the bigger the gain of DL-SCALE is. As it can be seen, for the test-examples considered, the acceleration achieved for the reference models discretized using 100,000 FEs is around 80%. It is also worth mentioning that the proposed methodology presents improvements with reference to the conventional implementation of SIMP in terms of objective function value as in almost all cases examined the value achieved by DL-SCALE is slightly lower than the one achieved by SIMP alone. The generality of the proposed methodology is also proved as in all test-examples presented, DL-SCALE performed remarkably well.

In the presented benchmark tests, it can be seen that DL-SCALE manages to reduce the computational time by at least one order of magnitude while this reduction increases as mesh density increases as well. The efficiency of the proposed methodology is also remarkable in terms of both objective function value and final layout achieved. It is worth underlying that the implementation of the DL-SCALE methodology to all test-examples requires no DBN retraining, and DBN was initially trained once over initial database. While DL-SCALE presents significant advantages on the reduction of the computational effort required for solving STO problems, there exist several ideas for future research. The first one focuses on the implementation of DL-SCALE to other topology optimization approaches apart from SIMP (i.e., BESO, level set, etc.). The second topic is related to the deep neural network used; although the training part is performed once, a more successfully trained network could assist even more in the reduction of the computational effort. For this reason, a state-of-the-art transfer function (SPOCU) [55] is going to be tested with respect to its performance.