Accelerated topology optimization by means of deep learning

Abstract

This study is focused on enhancing the computational efficiency of the solid isotropic material with penalization (SIMP) approach implemented for solving topology optimization problems. Solving such problems might become extremely time-consuming; in this direction, machine learning (ML) and specifically deep neural computing are integrated in order to accelerate the optimization procedure. The capability of ML-based computational models to extract multiple levels of representation of non-linear input data has been implemented successfully in various problems ranging from time series prediction to pattern recognition. The later one triggered the development of the methodology proposed in the current study that is based on deep belief networks (DBNs). More specifically, a DBN is calibrated on transforming the input data to a new higher-level representation. Input data contains the density fluctuation pattern of the finite element discretization provided by the initial steps of SIMP approach, and output data corresponds to the resulted density values distribution over the domain as obtained by SIMP. The representation capabilities and the computational advantages offered by the proposed DBN-based methodology coupled with the SIMP approach are investigated in several benchmark topology optimization test examples where it is observed more than one order of magnitude reduction on the iterations that were originally required by SIMP, while the advantages become more pronounced in case of large-scale problems.

1 Introduction

Since the 1970s, structural optimization has been the topic of intensive scientific development and several methods for achieving improved structural designs have been advocated (Moses 1974; Gallagher and Zienklewicz 1973; Haug and Arora 1974; Sheu and Prager 1968; Spunt 1971); structural optimization matured from simple academic problems to becoming the core of contemporary design in case of extremely complicated structural systems (Lagaros 2018). Topology optimization represents a material distribution numerical procedure for synthesizing structural layouts without any preconceived form. Many approaches have been proposed so far, specially tailored for solving the topology optimization problem, where the most widely used ones are the solid isotropic material with penalization (SIMP) approach introduced by Bendsøe (Bendsøe 1989; Zhou and Rozvany 1991; Mlejnek 1992), the level set one by Wang et al. (Wang et al. 2003) and Allaire et al. (Allaire et al. 2004) and the evolutionary structural optimization (ESO) one and its later version, labelled as bi-directional ESO (BESO) developed by Xie and Steven (Xie and Steven 1992; Xie and Steven 1993), in cooperation also with Querin (Querin et al. 1998), respectively. Despite the theoretical advancements in the field, similar to any type of structural optimization problem, serious computational obstacles arise especially when dealing with problems requiring finer finite element (FE) mesh discretization. In order to alleviate this drawback, so far, a number of parallel computing frameworks implemented successfully in CPU and/or GPU environments have been proposed (Papadrakakis et al. 2001; Mahdavi et al. 2006; Duarte et al. 2015; Aage et al. 2015; Martinez-Frutos and Herrero-Perez 2016; Wu et al. 2016).

Traditionally, computational mechanics relied on rigorous mathematical methods and on theoretical mechanics principles. However, a few decades ago, new families of computational procedures, labelled as soft computing (SC) methods, have been presented (Hajela et al. 1993). These methods rely on heuristic approaches rather than on rigorous mathematics. Although originally they were received with suspicion, in many problems, they have turned out to be surprisingly powerful, while their application is unceasingly growing. Neural networks (NNs) belonging to machine learning (ML) and genetic algorithms belonging to metaheuristics and fuzzy logic represent the foremost well-known SC approaches. Shallow NNs were the models used before 2006, as deep learning (DL) was incapable to train/test data due to the lack of computing power. Modern scientific breakthroughs in ML have offered scientists the ability to handle problems that were considered in the past computationally too demanding from the aspect of processor’s power or memory consumption, while completely new options of computer applications were proposed such as autonomous driving and many more. During the last decade, DL has attracted much interest due to fascinating results achieved in the fields of natural language processing (Collobert and Weston 2008), computer vision (Krizhevsky et al. 2012), big data management (Hinton and Salakhutdinov 2006), medical sciences (Greenspan et al. 2016) and many more. Many applications of shallow NNs on structural optimization problems can be found in modern literature. Adeli and Park (Adeli and Park 1995) together with Papadrakakis et al. (Papadrakakis et al. 1998) where the first ones that have integrated shallow NNs into the structural optimization procedure. Later, in the work by Papadrakakis and Lagaros (Papadrakakis and Lagaros 2002), a shallow NN model has also been used in reliability-based structural optimization. Since then, many studies have been published where various metamodels have been used into several formulations of structural optimization problems: indicatively, kriging approximations in structural optimization (Sakata et al. 2003), time history–based design optimization (Gholizadeh and Salajegheh 2009), performance-based design (Moller et al. 2009) and many more.

In this work, a generally applicable methodology is presented for dealing with the challenging concept to accelerate the SIMP-based solution part of topology optimization problems. In particular, deep belief networks (DBNs) are integrated into the SIMP approach aiming to reduce the computing requirements of the topology optimization procedure thus reducing drastically the necessary iterations of the SIMP approach. To the authors’ knowledge, there is only one study in the international literature presented by Sosnovik and Oseledets in a conference (Sosnovik and Oseledets 2017), where a convolutional neural network was applied to topology optimization where a metamodel is trained on 2D images in order to predict the final 2D image. On the other hand, the proposed DBN-based methodology has no limitations to 2D topology optimization problems while a different deep learning approach is also used. The main advantage of the methodology presented in this study is that although training is performed once over the patterns generated for a simple 2D test example corresponding to minimum compliance formulation, the trained DBN presents extremely good performance when implemented into any other test example with varying loading conditions, problem size/type (2D or 3D) and optimization constraints. In particular, in all test examples considered (2D or 3D), the number of iterations required is reduced by more than one order of magnitude, depicting also remarkable robustness converging to almost the same optimized objective function value. The major advantages of the proposed methodology originate from the generality of its application since it is not affected by the characteristics of the finite element mesh (structured or not), size type of the problem (2D or 3D formulation), the solution algorithm of the approach (optimality criteria (OC) method), method of moving asymptotes (MMA), etc.), the objective function, the loading type (gravity, thermal, acoustic, etc.) and filtering adopted. Worth mentioning as well a recent study by Yoo and Lee (Yoo and Lee 2017) which incorporates a dual-layer element and a variable grouping method for accelerating the topology optimization procedure in case of large 3D problems.

The rest of the paper is organized as follows: In the second section, a brief presentation of topology optimization problem and SIMP approach is presented while in the third one, restricted Boltzmann machines and deep belief networks are described. The proposed methodology is presented in detail in the fourth section along with the training procedure followed in this work. The fifth section is devoted to the assessment of the DBN parameters over a number of benchmark 2D test examples chosen from the literature. The performance of the proposed methodology is also underlined in this section in both 2D and 3D test examples. In the last section, the concluding remarks are noted.

2 Topology optimization

In order to present the framework of the proposed DBN-based acceleration methodology and make the paper more self-contained, a short description of the basic theoretical parts of topology optimization problem are provided in this section. The main objective of structural topology optimization is to define the proper arrangement of material into the design domain that transfers specific loading conditions to supports in the best possible way. It can be seen as the procedure of eliminating the material volume that is not of paramount importance, i.e. does not contribute to the domain’s structural resilience. Topology optimization could be utilized in order to derive the appropriate initial layout of the structural system that is then refined by means of shape optimization. Therefore, it can be used to assist the designer to outline the structural system that satisfies the operating conditions in the best way.

The general formulation of topology optimization problems is correlated to the optimizable domain Ω, the loading and boundary conditions as well as the volume fraction of optimized layout, whereas the form of the optimized layout depends on the objective function selected. Consequently, the question under investigation is how to distribute material volume into domain Ω so as to improve a certain criterion; compliance C is a commonly used one. The distribution of material into domain Ω is controlled by the density values x distributed over the domain. More specifically, it is controlled by design parameters that are associated to the densities x_e assigned to the FE discretization of domain Ω. The densities (x or x_e) take values in the range (0,1], where zero denotes no material in the specific finite element. The general mathematical formulation of the topology optimization problem can be expressed as follows:

$$ \left\{\begin{array}{c}\underset{x}{\min }C(x)={F}^T\overline{u}(x)\\ {}s.t.\left\{\begin{array}{c}\frac{V(x)}{V_0}=f\\ {}F=K(x)\overline{u}(x)\\ {}0<{x}_{\mathrm{min}}\le x\le 1\end{array}\right.\end{array}\right. $$

(1)

where C(x) represents the compliance of the structural system; F represents the loading conditions; $\overline{u}(x)$ is the corresponding global displacement vector; V(x), V₀ and f correspond to the current/initial volume of the domain Ω and desired volume fraction, respectively; K(x) is the stiffness matrix of the structural system for the current design x, 0 < x_min ≤ x ≤ 1 denotes the design set of the density value.

SIMP, BESO and level set are the most well-known approaches for solving the topology optimization problem; the proposed DBN-based acceleration methodology is integrated with SIMP since it is among the most popular ones and because those interested can easily familiarize with, by means of the 99 and 88 lines MATLAB codes written by Sigmund and colleagues (Sigmund 2001; Andreassen et al. 2011). According to the SIMP approach, the density values of the finite elements are correlated to their Young modulus value E as follows:

$$ {E}_e\left({x}_e\right)={x}_e^p{E}_e^0\iff {k}_e\left({x}_e\right)={x}_e^p{k}_e^0 $$

(2)

This power law approach was implemented by SIMP in order to achieve results with low representation of intermediate densities; parameter p varies for each problem; usually, its value is taken equal to 3. In the framework of SIMP approach, the problem can be solved using a number of gradient-based algorithms; the most common ones are the optimality criteria method and the method of moving asymptotes. For better understanding of both methods, the reader can refer to (Christensen and Klarbring 2009; Svanberg 1987; Bendsoe and Sigmund 2013). In order to avoid checkerboard patterns and other numerical instabilities that are described in (Sigmund and Petersson 1998), restrictions of filter type need to be implemented during the solution of the topology optimization problem. Many types of filters have been proposed so far; some of them are described in the works by Sigmund (Sigmund 2007; Sigmund 1994; Sigmund 1997); the sensitivity (Bourdin 2001) and density filtering (Bruns and Tortorelli 2001) are the most often used ones.

3 Deep belief networks

Deep belief networks (DBNs) are probabilistic generative models, which are created by combining several stochastic, latent variables. These variables, usually referred as feature detectors, are capable of understanding higher-order correlations in training datasets. Input data and feature detectors are grouped under a learning module like restricted Boltzmann machines (RBMs), and a DBN is created by sequentially combining several of such modules (Hinton 2009). The most important feature of DBNs is that they can be trained layer wise, targeting at defining the correlation between the effects the previous layer units have on the units of the next layer. Due to this feature, deeper networks are more precise and effective on various applications such as image recognition, natural language processing, time series prediction and many more.

3.1 Restricted Boltzmann machines

Boltzmann machines (BMs), similarly to Hopfield nets, are networks of fully and symmetrically connected units, which behave as neural nets activators with on/off signals and belong to the class of energy-based models (Bengio 2009). BMs were used in the past for locating hidden features in large training datasets but their architecture was responsible for low training speeds in networks with multiple layers of detectors (Hinton 2007).

Restricted Boltzmann machines (Smolensky 1986; Freund and Haussler 1992; Hinton 2002a) are probabilistic graphical models, which can also be inferred as stochastic neural networks (Fischer and Igel 2012). RBMs are actually energy-based two-layer networks where the first layer, called visible (v), consists of a set of nodes, which are fully and symmetrically connected to the stochastic nodes of the second layer, called hidden (h). It is worth noting that connections exist only between units belonging to different layers. A graphical representation of an RBM can be viewed in Fig. 1 where units v₁ to v₇ define the visible layer while units h₁ to h₄ belong to the hidden layer. The visible units represent the actual inputs of the network while the hidden units are the feature detectors. The energy of such a set of connections can be defined as seen in the following expression:

$$ E\left(v,h\right)=-\sum \limits_{i=1}^{i\max }{a}_i{v}_i-\sum \limits_{j=1}^{j\max }{b}_j{h}_j-\sum \limits_{i=1}^{i\max}\sum \limits_{j=1}^{j\max }{v}_i{h}_j{w}_{ij} $$

(3)

where v_i and b_i are the state and bias of the ith visible unit, h_j and b_j are the state and bias of the jth hidden unit and w_ij is the weight coefficient of the connection between these units. The energy function, similar to a cost function, is used to indicate the quality of the state of the two-layer network formed. Then, the state probability of the network regarding each existing pair of visible and hidden vectors is calculated. The state of the network with the lowest energy is the one with the highest probability. The energy is transformed into a probability distribution according to the following expression:

$$ p\left(v,h\right)=\frac{1}{Z}{e}^{-E\left(v,h\right)} $$

(4)

where Z is calculated according to (5) from the summation of all probabilities of existing pairs:

$$ Z=\sum \limits_{i=1}^{i\max}\sum \limits_{j=1}^{j\max }{e}^{-E\left(v,h\right)} $$

(5)

Fig. 1

RBM network representation

The probability p(v) for the visible vector is calculated from the summation of all probabilities of the hidden layer vector according to the following expression:

$$ p(v)=\frac{1}{Z}\sum \limits_{j=1}^{j\max }{e}^{-E\left(v,h\right)} $$

(6)

As mentioned before, RBMs opposite to BMs present no connections between units of the same layer (hidden or visible). Thus, the conditional probabilities can be calculated as seen below:

$$ p\left(v|h\right)=\prod \limits_{i=1}^{i\max }p\left({v}_i|h\right) $$

(7a)

$$ p\left(h|v\right)=\prod \limits_{j=1}^{j\max }p\left({h}_j|v\right) $$

(7b)

$$ p\left({v}_i=1|h\right)=\sigma \left(\sum \limits_{j=1}^{j\max }{w}_{ij}{h}_j+{b}_i\right) $$

(7c)

$$ p\left({h}_j=1|v\right)=\sigma \left(\sum \limits_{i=1}^{i\max }{w}_{ij}{v}_i+{b}_j\right) $$

(7d)

where σ(x) is the logistic function: σ(x) = 1/(1 + exp(−x)). Therefore, the derivative of the log probability of an input vector (visible layer) with respects to w_ij can be calculated:

$$ \frac{\partial \log p(v)}{\partial {w}_{ij}}={\left\langle {v}_i{h}_j\right\rangle}_{\mathrm{input}}-{\left\langle {v}_i{h}_j\right\rangle}_{\mathrm{model}} $$

(8)

where 〈v_ih_j〉_inputand 〈v_ih_j〉_model express the frequency in which v_i and h_j are on together in the training set and in the reconstructed model, respectively (Hinton 2012). More details on the training procedure of RBMs are given in the following subsection.

3.2 Training procedure of DBNs

As described earlier, a DBN is created by sequentially connecting multiple RBMs as it can be seen in Fig. 2 where a DBN formulation consisting of four RBMs is presented. The connections on a DBN are created based on the principal that the hidden layer of the RBM i − 1 is also the visible layer of the RBM i. For example, in Fig. 2, RBM1 is composed by layer L1 which is a visible layer and L2 which is the hidden one; accordingly for RBM2, L2 represents its visible layer and L3 is its hidden one.

Fig. 2

DBN network representation

Training such a network was not very successful in the past years until Hinton (Hinton et al. 2006) proposed a two-step approach for training DBNs. According to this approach, the first step is an unsupervised pre-training of each RBM separately while the second step is a supervised fine tuning of the network as a whole and not each RBM independently (Hinton 2012; Hinton et al. 2006). The pre-training procedure of the RBMs is performed by using the contrastive divergence algorithm (Hinton 2002b). The details of an RBM configuration can be seen in Fig. 3. The RBM in Fig. 3 consists of a visible layer v of size k and a hidden layer h of size l while the number of connections between all nodes is equal to k × l. For the case that i denotes a node of the visible layer and j a node of the hidden one, w_ij is the weight of connection between i and j while α_i and b_j are the biases of the nodes. These parameters can be represented as a set θ = {W, a, b}. Based on (3) and (4), the energy function and the joint probability distribution becomes

$$ E\left(v,h;\theta \right)=-\sum \limits_{i=1}^k{a}_i{v}_i-\sum \limits_{j=1}^l{b}_j{h}_j-\sum \limits_{i=1}^k\sum \limits_{j=1}^l{v}_i{h}_j{w}_{ij} $$

(9)

$$ p\left(v,h;\theta \right)=\frac{1}{Z}{e}^{-E\left(v,h;\theta \right)} $$

(10)

while according to (6), p(v;θ) is given by

$$ p\left(v;\theta \right)=\frac{1}{Z}\sum \limits_{j=1}^l{e}^{-E\left(v,h;\theta \right)} $$

(11)

and according to (8), the weight update is calculated by

$$ \frac{\partial \log p\left(v;\theta \right)}{\partial {w}_{ij}}={\left\langle {v}_i{h}_j\right\rangle}_{\mathrm{input}}-{\left\langle {v}_i{h}_j\right\rangle}_{\mathrm{model}} $$

(12)

$$ {w}_{ij}^{new}={w}_{ij}+e\cdot \varDelta {w}_{ij} $$

(13)

where e is the weight learning rate, defining the range of desired weight changes.

Fig. 3

RBM network details

The second part of the procedure represents the supervised training for the whole network with the use of the back-propagation algorithm (Rumelhart and McClelland 1986). Through this part, the weights that are proposed from the unsupervised pre-training are tuned working with the deep neural network as a whole. Back-propagation is an iterative procedure, which updates weight values according to the difference between a target output and the networks output for specific weights. Conjugate gradient (CG) method is usually used for adjusting the weights while steepest descent or others can also be used. For example, in the case of an RBM trained over m samples and with outputs of size n, the weight update is

$$ {W}_{all}^{new}={W}_{all}-c\cdot \frac{\partial E}{\partial W} $$

(14)

where

$$ E=\frac{1}{2}\sum \limits_{i=1}^m\sum \limits_{j=1}^n{\left({t}_j^i-{p}_j^i\right)}^2 $$

(15)

and t is the target output, p is the generated output and c is a weight learning rate factor.

Summarizing the above, worth mentioning that a DBN network is constructed as a series of stacked RBMs. Generally speaking, a DBN network can be used as a feature detector and has the ability to categorize a set of inputs according to the output classes, which are user-defined. Starting from an input vector, sequential RBMs are able to investigate for higher order features. Based on this characteristic, RBMs are capable to define the classification category of input vectors, according to features not visible in the initial input.

4 DLTOP methodology: deep learning–assisted topology optimization

In this section, the implementation characteristics of the proposed DBN-based acceleration methodology, specially tailored for dealing with topology optimization, are described in detail. The goal of the proposed methodology is to accelerate the topology optimization procedure. This is achieved by integrating a DBN into the topology optimization procedure that is used to predict a close-to-final density value for each finite element of the initial domain, in conjunction with the SIMP approach. The DBN is trained once on a typical topology optimization problem, and then, it can be successfully applied to any problem without taking under consideration dimensionality, problem size, loading conditions, target volume, etc. Before describing the key steps of the proposed DLTOP methodology, it should also be stated that both test examples considered and training data sets built rely on the assumption that the design domain is initialized with a uniform density value to all finite elements corresponding to the volume fraction value constraint. This assumption is based on the common initialization practice where the density value to all finite elements is initialized with the volume fraction value.

4.1 The outline of the DLTOP methodology

Assuming, without loss of generality, that a structured finite element mesh discretization is implemented and that the domain to be optimized is rectangular and is discretized into ne_x, ne_y, ne_z finite elements per axis, thus the total number of finite elements ne generated is equal to ne = ne_x × ne_y × ne_z. According to the topology optimization procedure, the density value for each of the ne finite elements is initialized and during the optimization procedure is updated in every iteration of SIMP approach. The fluctuation of density value d_i of the ith finite element with respect to the iteration step t can be expressed by a function with respect iteration t:

$$ {\displaystyle \begin{array}{l}{d}_i=F(t)\\ {}\forall i\in \left[1,s\right]\end{array}} $$

(16)

Samples of the graphical representation of this function can be seen in Fig. 4, where it can be observed that the evolution process varies drastically depending on the location of each finite element in the design domain. The density fluctuation of 10 different finite elements per SIMP iteration is presented where each finite element is represented with a different colour. The elements displayed are selected randomly from the domain presented in Fig. 6 b. The initial value of the density histories of Fig. 4 is equal to 0.4 for all elements since the target volume is 40% of the initial one, which is a common practice adopted when implementing SIMP (Yoo and Lee 2017; Sigmund 2001) to use uniform starting density value for all finite elements corresponding to the volume fraction value constraint; this is a basic assumption for the development and application of the proposed DLTOP methodology. Thus, every finite element is characterized by a different optimization history density value corresponding to a sequence of discrete time data similar to a time series. The large number of finite elements required by the domain discretization and the necessary computations of the SIMP approach can lead to severe computational demands for performing topology optimization studies even on rather simple 3D design domains. Indicatively, solving the topology optimization problem formulated for a simple 3D bridge test example discretized with 83,200 finite elements requires up to 25,200 s to carry out 200 SIMP iterations while by applying a GPGPU-based acceleration of the structural analysis procedure, the required time is reduced to 1 h (Kazakis et al. 2017), that still remains significant; in the test examples section, the acceleration capabilities achieved by the proposed DLTOP methodology are discussed, where the computing time is further reduced. Worth mentioning that significant improvements in terms of computing times have been achieved using GPGPU computing environment, indicatively the solution of a test example discretized with more than 27 millions of solid finite elements required 30,000 s to perform 1000 iterations (Aage et al. 2015).

Fig. 4

Evolution of the finite element density with respect to the SIMP iterations

The proposed methodology requires calibrating the DBN model that as it will be described in the following section is performed once. When a trained network is acquired, it can be implemented to assist any topology optimization problem. The proposed methodology represents a two-phase procedure: (i) the first one (denoted as phase I) refers to a specific number of initial iterations performed by SIMP and the use of the trained DBN based on these iterations. The elements’ densities recorded over these SIMP iterations are used as input arguments for the DBN which then derives the optimized elements’ density; (ii) the second one (denoted as phase II) concerns the SIMP refinement part, where the solution of the first phase resulted from the DBN are fine-tuned by SIMP. In phase I, 36 SIMP iterations are performed, and then, DBN is using them for predicting a close-to-final topology. Phase I can be described as a discrete jump from the initial 36 iterations of SIMP to a solution similar to the final one. In phase II, SIMP is used for fine tuning the DBN-proposed solution.

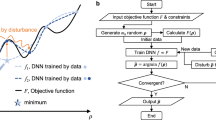
The flow chart of the proposed DLTOP methodology is presented in Fig. 5 a, while the application of the two-phase methodology in the case of a single finite element is shown in Fig. 5 b. The abscissa of Fig. 5b represents the iterations performed by SIMP while the ordinate corresponds to the density value of a single finite element, randomly selected from the example presented in Fig. 6 c. The scope of Fig. 5b is to schematically present the goal and functionality of DLTOP. The advantage of the proposed methodology is based on its feature that each finite element is handled separately regardless of its position in the domain, loading and boundary conditions of the domain, etc. Classification problems represent a challenging type of predictive models. Contrary to regression predictive modelling, classification models require information also on the complexity of a sequence dependence among the input parameters. In the case of topology optimization, the early density values represent the sequence dependence information that needs to be provided as inputs to the proposed (classification) methodology. The sequence of discrete time data, i.e. the density value for every finite element and the T iterations are generated by SIMP approach and stored in matrix D presented below:

Fig. 5

DLTOP methodology: a flow chart and b implementation for single finite element

Fig. 6

Training datasets generation, indicative FE discretization for a 1:2 and b 1:3 cantilever beam and c 1:2 and d 1:3 simply supported beam

$$ D=\left[\begin{array}{ccccc}{d}_{1,1}& {d}_{1,2}& .& .& {d}_{1,T}\\ {}{d}_{2,1}& {d}_{2,2}& .& .& {d}_{2,T}\\ {}.& .& .& .& .\\ {}.& .& .& .& .\\ {}{d}_{ne,1}& {d}_{ne,2}& .& .& {d}_{ne,T}\end{array}\right] $$

(17)

where T denotes the maximum iterations needed by SIMP to converge. Part of the optimization history corresponding to the first t iterations is used in order to construct the time series input data for training the DBN while the vector of the last iteration of SIMP approach corresponding to the Tth column of density matrix D is used as the target vector of DBN.

(18)

4.2 Construction of the training dataset used

ML-based mathematical models make data-driven classification decisions by using input data. These data that are used to build the final mathematical model is usually constructed based on multiple datasets. In general, the classification model is calibrated first on a series of data called training dataset; successively, the calibrated model (also called metamodel) is implemented in order to generate the responses for the measurements in the so called validation dataset; and finally, the test dataset is used to provide an unbiased assessment of the final model. In this section the construction of the training dataset for the problem at hand is described in detail.

The purpose of DBN-based classification is to recognize and combine with the final SIMP outcome, the pattern of the density value for all finite elements of the optimizable domain; thus, the training/validations/testing datasets are composed of sequences of the density values derived from the implementation of SIMP approach. In order to prove that the performance of the DLTOP methodology is independent of the test example used for developing the training dataset, two distinct training datasets are generated and compared with each other. The two datasets were constructed based on two benchmark rather simple 2D topology optimization test examples, the simply supported and cantilever beams, respectively. The two tests exampled considered for constructing the training datasets are shown in Fig. 6 (cantilever beam Fig. 6 a and b; simply supported beam Fig. 6 c and d).

In order to derive a well-constructed training dataset the following values are adopted for the two training datasets test examples: (i) two height to length ratios are implemented (i.e. 1:2 and 1:3) and (ii) eight different finite element mesh discretizations were adopted (it should be specified that the size of the unit finite element remains the same in all discretizations; thus, finer discretization results into larger domain sizes). Specifically, in order to build the datasets, the following discretizations were used D = [D_K D_3K D_6K D_10K D_20K D_40K D_60K D_100K]^T where D_K stands for the samples generated for a finite element mesh discretization of the order of 1000 finite elements while D_10K stands for the samples generated for the discretization of the order of 10,000 elements. Therefore, the samples used to derive the two training datasets are composed by the iteration histories of all the finite elements when solving by SIMP the following topology optimization problems:

$$ {\displaystyle \begin{array}{ccc}{D}_K\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=50\\ {}n{e}_y=25\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=60\\ {}n{e}_y=20\end{array}\right.\end{array}\right.& {D}_{10K}\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=145\\ {}n{e}_y=73\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=180\\ {}n{e}_y=60\end{array}\right.\end{array}\right.& {D}_{60K}\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=350\\ {}n{e}_y=175\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=425\\ {}n{e}_y=142\end{array}\right.\end{array}\right.\\ {}{D}_{3K}\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=80\\ {}n{e}_y=40\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=105\\ {}n{e}_y=35\end{array}\right.\end{array}\right.& {D}_{20K}\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=200\\ {}n{e}_y=100\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=245\\ {}n{e}_y=82\end{array}\right.\end{array}\right.& {D}_{100K}\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=450\\ {}n{e}_y=225\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=550\\ {}n{e}_y=184\end{array}\right.\end{array}\right.\\ {}{D}_{6K}\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=110\\ {}n{e}_y=55\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=135\\ {}n{e}_y=45\end{array}\right.\end{array}\right.& {D}_{40K}\left\{\begin{array}{c}1:2\left\{\begin{array}{c}n{e}_x=285\\ {}n{e}_y=143\end{array}\right.\\ {}1:3\left\{\begin{array}{c}n{e}_x=350\\ {}n{e}_y=117\end{array}\right.\end{array}\right.& \end{array}} $$

(19)

The loading conditions used can be seen in Fig. 6 for both test examples. The volume fraction value of the final domain is equal to 40% of the original one and the density filter is applied. In the first training test example, the radius chosen is equal to two elements for all discretizations and for the second one the radius ranges from three elements in the case of the 1000 elements discretization to 15 elements in the 10,000 elements one. The first dataset is formed by combining the observations out of the runs carried out for the simply supported beam cases while the same procedure was followed for the cantilever beam cases. By adding up the density time histories of each discretization, a population of 240,000 samples is acquired. By also adding the samples of the two different height-to-length ratios, a total of 480,000 samples is created for the cantilever beam example and another one of equal size for the simply supported beam example. Each of the two datasets consists of nearly 480,000 sequences and t = 36 corresponding to the 15% of the weighted sum of iterations with reference to the finite element discretization. Generally speaking, a favourable training dataset is composed by well-distributed representation of the patterns that are to be classified. In our case, although the values regarding the final density of finite elements range in (0, 1], comparing the two datasets it can be seen that they represent two completely different distributions of the density values in this range. The simply supported beam training dataset mainly consists of values equal to either zero or one while the cantilever beam training dataset consists of many varying values in the range of (0.1, 0.9]. This difference on the analogies of the classes explains the difference in terms of performance of the two datasets. In an effort to thoroughly examine the performance of the proposed methodology, it is important to assess both datasets as the outcome of the classification generated from each one is expected to have differences.

4.3 Calibration of DBN

Every ML model, DLTOP methodology included, is structured by means of the calibration and implementation phases. The calibration phase will be described first; the DBN part of the DLTOP methodology is used to recognize the pattern of the density values for each finite element relying on the initial iterations of the SIMP approach. These patterns are classified with reference to the final density value as obtained by SIMP approach for each finite element of the design domain. Before performing the training procedure, SIMP is implemented for generating the training samples, i.e. solve specific topology optimization problems as denoted in (19). Then, the training dataset is formed, composed by the inputs (i.e. ne vectors consisted of the finite elements’ densities for the first t iterations) and the target outputs (i.e. a vector of size ne elements corresponding to the densities achieved at the Tth final iteration). These training samples are then used for calibrating the DBN as described in the following expression:

(20)

Thus, during the calibration phase, DBN is adjusted for generating the non-linear transformations for each finite element from the pattern of the first iterations t densities to the final density ${d}_{i,T}^{DBN}$, i = 1, 2, …, ne. The DBN output values represent classification of the design domains’ finite elements with respect to the ${d}_{i,T}^{DBN}$ density values.

4.4 Implementation of DLTOP methodology

When the calibration phase is completed, that is performed once for each dataset, DBN metamodel can now be used in the implementation phase together with SIMP approach for accelerating the topology optimization procedure according to the following expression for every test example:

$$ DBN\left({\left[d\right]}_{1: ne,1:t}\right)\Rightarrow {\left[d\right]}_{1: ne,T}\kern1em \forall {\left[d\right]}_{1: ne,1:t}, ne,t,T $$

(21)

The implementation phase of the DLTOP methodology is composed by three steps: (i) in the first one, SIMP is used for generating the sequence of t samples for each finite element of the discretization used for the design domain; (ii) then, the trained DBN is applied for deriving the ${d}_{i,T}^{DBN}$ density value for each finite element of the domain. Worth mentioning that the computing requirements for applying DBN are small (in the order of 1.7E−04 s on an i7-3610QM processor), but in the case of million or even billion of finite elements it might become significant. However, the application of DBN metamodel is independent for each finite element and therefore can be performed in parallel without any interprocess communication. (iii) In the final part of the methodology, SIMP is fed with the ${d}_{i,T}^{DBN}$ density values of the finite elements of the design domain for correcting any defects of the DBN outcome. The structure and the implementation flow chart of the DLTOP methodology are presented in Fig. 5 a and the pseudocode in Fig. 7, respectively. According to the pseudocode of Fig. 7, lines #3 to #5 represent the SIMP approach of phase I, where the input data of the DBN model for each finite element are generated. These input date are used to feed the DBN and the optimized domain to be derived, this is denoted in lines #7 to #9. The density values of the optimized domain derived by the DBN are used as feedback for re-initializing the SIMP approach of phase II in order to fine tune the optimized domain (lines #11 to #13).

Fig. 7

Pseudocode of DLTOP methodology

The DBN used in this study consists of three RBMs and the framework was developed based on work by Hinton and Salakhutdinov (Hinton and Salakhutdinov 2006). The number of training samples is equal to the total number of finite elements generated by the domains of the topology optimization problems of (19), i.e. ne input density vectors is equal to 480,000 while the length t of each input vector was chosen equal to 36 recorded initial density calculations. The sizes of the three RBMs are equal to 30, 20 and 12. Two different classes are used, i.e. the output of the classification network is divided into 12 classes in the first one and in 3 classes in the second one as denoted below:

$$ {\displaystyle \begin{array}{l}C\mathrm{lassification}\ \mathrm{Case}\ \mathrm{I}\kern6.5em \mathrm{Classification}\ \mathrm{Case}\ \mathrm{I}\mathrm{I}\ \\ {}{d}_{i,T}=0\\ {}\begin{array}{l}{d}_{i,T}\in \left\{\begin{array}{c}\left(\mathrm{0,0.1}\right]\Rightarrow {d}_{i,T}=0.05\\ {}\left(\mathrm{0.1,0.2}\right]\Rightarrow {d}_{i,T}=0.15\\ {}\left(\mathrm{0.2,0.3}\right]\Rightarrow {d}_{i,T}=0.25\\ {}\left(\mathrm{0.3,0.4}\right]\Rightarrow {d}_{i,T}=0.35\\ {}\left(\mathrm{0.4,0.5}\right]\Rightarrow {d}_{i,T}=0.45\\ {}\left(\mathrm{0.5,0.6}\right]\Rightarrow {d}_{i,T}=0.55\\ {}\left(\mathrm{0.6,0.7}\right]\Rightarrow {d}_{i,T}=0.65\\ {}\left(\mathrm{0.7,0.8}\right]\Rightarrow {d}_{i,T}=0.75\\ {}\left(\mathrm{0.8,0.9}\right]\Rightarrow {d}_{i,T}=0.85\\ {}\left(\mathrm{0.9,1}\right)\Rightarrow {d}_{i,T}=0.95\end{array}\right.\kern0.5em {d}_{i,T}\in \left\{\begin{array}{c}\left[\mathrm{0,0.4}\right]\Rightarrow {d}_{i,T}=0\\ {}\left(\mathrm{0.4,0.7}\right)\Rightarrow {d}_{i,T}=0.50\\ {}\left[\mathrm{0.7,1}\right]\Rightarrow {d}_{i,T}=1\end{array}\right.\\ {}{d}_{i,T}=1\end{array}\end{array}} $$

(22)

A representation of the DBN used in the proposed methodology can be seen in Fig. 8.

Fig. 8

DBN network representation

5 Test examples

For the purposes of this study, three groups of test examples have been considered. The first one is composed by benchmark 2D test examples that have been adopted for performing the parametric investigation with respect to the two training datasets, RBM training parameters and different targets’ classification. The second and third groups contain three 2D and two 3D test examples where the efficiency of the DLTOP methodology is mainly assessed. As for the SIMP approach, without loss of generality, OC and MMA algorithms are chosen for solving the topology optimization problems at hand. The penalization factor is taken equal to 3 and is not changed for all test examples. Filtering is implemented by taking into consideration the weighted derivative of the adjacent elements for the calculation of each elements derivative in both 2D and 3D examples. Worth mentioning that no thresholding was used in any of the test examples examined below (i.e. no thresholding has been applied to any of the optimized domains presented in this work). The codes used for solving the topology optimization problem are based on the 88-line code, its 3D variant as well as the PolyTop (Talischi et al. 2012a). It should be underlined that the filter type and radius remain the same in the cases examined in each test example described below, i.e. both during the implementation of the proposed methodology and the conventional SIMP approach. Thus, it is confirmed that the compliance values per example are obtained under exactly the same parametric conditions.

Worth mentioning is that the proposed DLTOP methodology can easily be integrated with continuation of penalization techniques as described in (Xingjun et al. 2017; Labanda and Stolpe 2015; Li and Khandelwal 2015). According to the first category of techniques, penalization parameter p is taken equal to unity (1.0) and multiple topology optimization problems (TOPs) are solved through an iterative procedure. In every iteration, a TOP is solved, the optimized domain achieved in this step is used as the initial density distribution for the next one, while p value is increased until p becomes equal to the maximum value (p_max). The proposed DLTOP methodology can easily be applied in each TOP providing its optimized domain layout. In the second category of techniques, where p is changing values during the topology optimization problem (taking values from 1.0 to the maximum value p_max), DLTOP methodology can be applied to the topology optimization problem as it is applied in the examples presented in the present study. As DLTOP only deals with the volume time history of each element regardless its position, the abovementioned techniques can be applied in SIMP Phases of DLTOP without having to retrain the network.

5.1 Description of the five 2D benchmark test examples

Figure 9 a–e depict five 2D benchmark topology optimization test examples that are considered in order to present the computational efficiency of the DLTOP methodology and mainly to perform the parametric investigation part. The first one shown in Fig. 9 a is labelled as “short-beam (fine) test example”, the discretization along the x and y axes is equal to ne_x = 800 and ne_y = 150, respectively, the support conditions refer to four fixed joints placed at each corner of the domain (Fig. 9 a) and the single loading condition refers to two concentrated forces P along the y-axis and applied in the middle of the span of the x-dimension as depicted in Fig. 9 a. The term “fine” is used because subsequently the same test example is studied using coarser FE mesh discretization. The second one shown in Fig. 9 b is labelled as “antisymmetric test example”, the discretization along the x and y axes is equal to ne_x = 400 and ne_y = 400, respectively, the support conditions refer to two fixed joints placed at the two right corners of the domain (Fig. 9 b) and the loading condition refers to two concentrated forces P along the x-axis and applied in the middle of the span of the y-dimension (see Fig. 9b). The third one shown in Fig. 9 c is labelled as “column test example”, the discretization along the x and y axes are equal to ne_x = 300 and ne_y = 500, respectively, the support conditions refer to fully fixed boundary conditions along the x-axis and starts at the 3:8 of the x-dimension and the loading condition refers to four concentrated forces P along the y-axis and applied with distance equal to 1:3 of the x-dimension. The fourth test example shown in Fig. 9 d is labelled as “L-shaped test example”, the discretization along the x and y axes are equal to ne_x = 400 and ne_y = 400, respectively, the support conditions refer to fully fixed boundary conditions along the x-axis ending at the 1:2 of the x-dimension (Fig. 9d) and the loading condition refers to one concentrated force P along the y-axis and applied in the 1:4 of the y-dimension. Finally, the fifth test example shown in Fig. 9 e is labelled as “long-beam test example”, the discretization along the x and y axes are equal to ne_x = 400 and ne_y = 100, respectively, the boundary conditions refer to five simple supports applied along the x-axis with distance equal to 1:6 of the x-dimension between them and the loading conditions refer to distributed force q along the y-axis, applied on the top and bottom of the y-dimension.

Fig. 9

Two-dimensional test examples: a short-beam (fine), b antisymmetric, c column, d L-shaped and e long-beam

In these 2D test examples, the preference for final volume is equal to 40% of the original domain and the filter radius is equal to six elements for the short-beam (fine), antisymmetric, column and long-beam test examples and two elements for the L-shaped test example. The standard sensitivity filter is implemented to all five test examples, while it should be stated that the parametric conditions remain the same for the original topology optimization and the proposed methodology. It is worth pointing out that in the test examples shown in Fig. 9 a–c, the multiple loading vectors are applied according to section 5.2 of the “88-line code” article by Andreassen et al. (Andreassen et al. 2011) where it is suggested to apply each loading vector separately and then compute the compliance by summarizing each resulting response. For each experiment, a record is kept regarding the total iterations needed and the objective function value when only SIMP is used and when acceleration by means of DBN is used.

5.2 Evaluation of parameters, training datasets and classification types

In order to present a parametric investigation of the proposed DLTOP methodology with reference to factors that might influence its performance, the following factors are used for training and testing the DBN part of the DLTOP methodology: (i) the training dataset (two are examined), (ii) the RBM parameters (10 different sets are employed) and (iii) the classification types (two different groups of classes are implemented). Then, the efficiency of the above factors’ combinations is assessed on the five 2D benchmark topology optimization problems. As previously described, there are four parameters that define the learning behaviour of RBMs and in result the behaviour of DBNs. These parameters are the learning rates of the weights (e_w), the biases of the visible nodes $\left({e}_b^v\right)$, of the hidden nodes $\left({e}_b^h\right)$ and of the weight cost (w_c).

The parameter values used in the RBM pre-training procedure are presented on Table 1 along with all the training characteristics. The 10 different parameter sets (PS) defined in Table 1 are labelled as PS1 to PS10. In the back-propagation algorithm, 50 epochs were executed with 100 CG iterations. The selected values are in accordance with recommendations given by Hinton in (Hinton 2012). The results of the DLTOP methodology applied on the test examples can be witnessed in Figs. 10, 11, 12 and 13 and Tables 2, 3, 4 and 5 where SB3, SB12, CB3 and CB12 stand for the simply supported beam (SB) and cantilever beam (CB) datasets, respectively, with 3 and 12 classes. Specifically, Figs. 10 and 12 depict the function evaluations required for the DLTOP methodology to converge, the two databases and two classifications with respect to DBN training parameters are compared with those needed by SIMP alone (see the green line in Figs. 10 and 12). In these figures, for each of the two databases used, the total iterations needed for both phases of DLTOP (initial input generation phase and fine-tuning phase) methodology are compared against a typical SIMP implementation. Figures 11 and 13 illustrate the final objective function values achieved by DLTOP, i.e. with reference to the two databases, two classifications and DBN training parameters; their performances are compared with those achieved by SIMP alone (see the green line in Figs. 11 and 13). The results concerning average objective function value and COV, shown in Tables 2, 3, 4 and 5, were calculated using the 10 different sets of RBM training parameters (i.e. PS1 to PS10) as described previously.

Table 1 RBM pre-training parameter value sets

Fig. 10

Performance of classification 12—iterations: a short-beam (fine) test example, b antisymmetric test example, c column test example, d L-shaped test example and e long-beam test example

Fig. 11

Performance of classification 12—objective function value (compliance): a short-beam (fine) test example, b antisymmetric test example, c column test example, d L-shaped test example and e long-beam test example

Fig. 12

Performance of classification 3—iterations: a short-beam (fine) test example, b antisymmetric test example, c column test example, d L-shaped test example and e long-beam test example

Fig. 13

Performance of classification 3—objective function value (compliance): a short-beam (fine) test example, b antisymmetric test example, c column test example, d L-shaped test example and e long-beam test example

Table 2 Average and variance of classification 12 performance—SB dataset

Table 3 Average and variance of classification 12 performance—CB dataset

Table 4 Average and variance of classification 3 performance—SB dataset

Table 5 Average and variance of classification 3 performance—CB dataset

As it will be shown in the following investigation, comparing the acceleration efficiency derived from Figs. 10 and 12, it is clear that the use of three output classes provides significantly better and more stable results than 12 classes, regardless of the training parameters of the DBN network. It is also worth pointing out that the average computational efficiency performance of the SB database is better than that of the CB database. With respect to objective function value results as shown in Figs. 11 and 13, it is reported that both classes achieved a similar performance. As a general guide, it can be said that the simply supported beam represents the optimal choice for the database combined with three classes. In respect to results shown in Figs. 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 and 24, Panel (a) depicts the final outcome of conventional SIMP implementation; panel (b) shows the output of the DBN (end of phase I) while panel (c) represents the final output of DLTOP methodology after SIMP fine-tuning step (end of phase II).

Fig. 14

Optimized domain for the short-beam (fine) test example—classification 12: a original SIMP (objective function 85.99, iterations 372), b DLTOP phase I (objective function 86.43, iterations 36), c DLTOP phase II (objective function 85.86, iterations 43) and d density histories of selected finite elements located in the centre of the domain

Fig. 15

Optimized domain for the antisymmetric test example—classification 3: a original SIMP (objective function 22.64, iterations 599), b DLTOP phase I (objective function 22.95, iterations 36) and c DLTOP phase II (objective function 22.18, iterations 37)

Fig. 16

Optimized domain for the column test example—classification 3: a original SIMP (objective function 145.12, iterations 551), b DLTOP phase I (objective function 149.18, iterations 36) and c DLTOP phase II (objective function 140.90, iterations 15)

Fig. 17

Optimized domain for the L-shaped test example—classification 3: a original SIMP (objective function 73.06, iterations 186), b DLTOP phase I (objective function 71.92, iterations 36) and c DLTOP phase II (objective function 71.19, iterations 25)

Fig. 18

Optimized domain for the long-beam test example—classification 3: a original SIMP (objective function 576,936.84, iterations 775), b DLTOP phase I (objective function 479,880.00, iterations 36) and (c) DLTOP phase II (objective function 577,826.89, iterations 275)

Fig. 19

Optimized domain for the short-beam (coarse) test example—MMA: a original SIMP (objective function 30.34, iterations 91), b DLTOP phase I (objective function 29.77, iterations 36) and c DLTOP phase II (objective function 30.33, iterations 31)

Fig. 20

Optimized domain for the two-bar test example—classification 3: a original domain, b original SIMP (objective function 10.31, iterations 54), c DLTOP phase I (objective function 13.33, iterations 5), d DLTOP phase II (objective function 10.31, iterations 28), e original SIMP with threshold (objective function 25.16, iterations 5) and f difference between DLTOP and SIMP with threshold

Fig. 21

Optimized domain for the serpentine beam test example—classification 3: a original domain (Talischi et al. 2012b), b original SIMP (objective function 391.19, iterations 267), c DLTOP phase I (objective function 442.65, iterations 36) and d DLTOP phase II (objective function 394.46, iterations 30)

Fig. 22

Three-dimensional test examples: a L-shaped 3D, b bridge and c cantilever beam

Fig. 23

Optimized domain for the bridge test example—classification 3: a original SIMP (objective function to 1,632,305.73, iterations 509), b DLTOP phase I (objective function 1,612,500.00, iterations 36) and c DLTOP phase II (objective function 1,640,121.40, iterations 193)

Fig. 24

Optimized domain for the 3D L-shaped test example—classification 3: a original SIMP (objective function 15.33, iterations 660), b DLTOP phase I (objective function 13.36, iterations 36) and c DLTOP phase II (objective function 15.65, iterations 93)

5.2.1 DLTOP performance for 12 classes

Before discussing the performance of DLTOP methodology with reference to its parameters, the basis of the comparison needs to be described. Since the objective of the proposed methodology is the improvement of computational efficiency, the number of iterations required by the original SIMP for solving each problem represents the basis of comparison, while the iterations required by the DLTOP methodology are those required to feed the calibrated DBN (part of phase I) plus those needed by SIMP in phase II of the methodology. The comparison with reference to the computational performance between the original SIMP and DLTOP is presented in Fig. 10. Secondly, the original approaches versus the proposed one are also compared with respect to the objective function achieved; this is shown in Fig. 11, while Tables 2 and 3 also show the computational efficiency and robustness of DLTOP as the average number and variation of iterations required and objective function achieved.

Figures 10 and 11 along with Tables 2 and 3 present the computational performance and robustness of the proposed DLTOP methodology for the short-beam (fine) test example. As it can be observed from Table 2, SB training dataset on average achieved 83% reduction on the SIMP iterations; the iterations are reduced by almost one order of magnitude from 370 iterations originally required to only 64 iterations on average (the corresponding coefficient of variation (COV) is equal to 16%), while the maximum reduction of the iterations is equal to 87% (see Fig. 10 a). Accordingly, CB training dataset achieved on average 70% reduction of SIMP iterations, while the maximum reduction of SIMP iterations is equal to 77% and COV is equal to 38%. With respect to the objective function value achieved, as it can be seen from Table 2, with respect to the training parameter sets on average, 1.15% lower value was obtained compared with the one originally achieved by SIMP; correspondingly the objective function value obtained when CB dataset was used is practically equal to the original one. The optimized domain for the short-beam (fine) test example resulted originally by SIMP is shown in Fig. 14 a and those obtained from phases I and II of the proposed DLTOP methodology are depicted in Fig. 14 b and c, respectively. As it can be seen, the shapes obtained are very similar, while the corresponding objective function values achieved and iterations required are 85.99 and 372, 86.43 and 36, 85.86 and 43 for original SIMP, phases I and II of DLTOP, respectively. While the density histories of elements in the centre of the domain are shown in Fig. 14 d, where it can be seen the density values of elements’ history do not vary monotonously. In Fig. 14d, it can also be noticed that the proposed methodology is able to identify those elements whose density tends to be reduced when approaching the 36th iteration (i.e. purple and orange density lines) of SIMP and generate the hole in the centre of the domain of the DLTOP output.

Accordingly, the optimized domains for the antisymmetric, column, L-shaped and long-beam test example resulted originally by SIMP and those obtained from phases I and II of the proposed DLTOP methodology are depicted in Figs. 15, 16, 17 and18, respectively. The performance of DLTOP methodology for the rest of the test examples has a similar performance; more specifically, for the SB training dataset (see Table 2 and Figs. 10 and 11), on average the reduction of SIMP iterations varies from 24 to 73% while the maximum reduction achieved for all these test cases exceeds 80%, the corresponding objective function value achieved on average is slightly reduced. In the case of CB training dataset (see Table 3 and Figs. 10 and 11), on average, the reduction of SIMP iterations exceeds 15% while the maximum reduction achieved for all these test cases exceeds 60%, the corresponding objective function value achieved on average is also slightly reduced.

In general, it should be noted that DLTOP methodology resulted for all test cases examined to significant decrease of iterations and with the most proper selection of RBM training parameters the decrease exceeds 90%. It is also noticeable that the objective function value is unaffected by the training parameters values and achieving values similar to plain SIMP application. It was also observed that in the case of classification 12, CB training dataset is outperformed by the SB one both in terms of computational efficiency (reduction of SIMP iterations) and robustness.

5.2.2 DLTOP performance for three classes

Similar parametric study is performed for the case of three classes (see Figs. 12 and 13, Tables 4 and 5), where it is observed that in the short-beam (fine) test example (Figs. 12 a and 13 a), the SB training dataset achieved on average 85% reduction of SIMP iterations and the maximum one is equal to 87% (COV equal to 21%) while the objective function value achieved is on average 2.31% lower to that originally obtained by SIMP approach. The CB training dataset achieved on average 83% reduction of iterations with a maximum reduction equal to 86% (COV equal to 12%) while the objective function value is on average reduced by 3.48%.

Accordingly, the performance of DLTOP methodology for the rest of the test examples has a similar outcome; more specifically, for the SB training dataset (see Table 4 and Figs. 12 and 13), on average the reduction of SIMP iterations varies from 55 to 91% while the maximum reduction achieved for all these test cases exceeds 91%, the corresponding objective function value achieved on average is slightly increased. In the case of CB training dataset (see Table 3 and Figs. 10 and 11), on average the reduction of SIMP iterations varies from 72 to 84% while the maximum reduction achieved for all these test cases exceeds 85%; the corresponding objective function value achieved on average is also slightly increased. The optimized domain for the antisymmetric test example resulted originally by SIMP is shown in Fig. 15 a, and those obtained from phases I and II of the proposed DLTOP methodology are depicted in Fig. 15 b and c, respectively. As it can be seen, the forms obtained are almost identical, while the corresponding objective function values achieved and iterations required are equal to 22.64 and 599, 22.95 and 36, 22.18 and 37 for original SIMP, phases I and II of DLTOP, respectively.

Summarizing the results obtained for the case of classification 3, it becomes noticeable that DLTOP methodology for all test examples examined resulted to significant reduction of the iterations depicting also remarkable performance stability with reference to the training parameters values. It is also worth noticing that the objective function value is not influenced by these parameters. In classification 3, SB training dataset performed better compared with CB one in terms of iteration decrease but not in the case of objective function value and robustness where CB database performed better than the SB one. Comparing the classification 3 with the 12 one, it can be observed that the latter one is outperformed by the first one both in terms of computational efficiency (reduction of SIMP iterations) and robustness for both training datasets considered. In an attempt to explain this result, it must be pointed out that the classification three procedure is significantly less demanding in terms of DBN training while the classification 12 is not.

Additionally, it should be stated that, although it is not guaranteed that the DBN results satisfy the volume constraint, its violation is very limited and a single step of SIMP in phase II is adequate to correct the required volume fraction often leading to reduction of the objective function value (e.g. compliance) compared with the typical SIMP implementation. As a reference, it is noticeable that for a volume fraction equal to 40%, the predicted domain achieved for the short-beam (fine) test example is equal to 38.00%, for the antisymmetric one is equal to 39.42%, for the column one is equal to 38.70%, for the L-shaped one is equal to 39.74% and for the long-beam one is equal to 42.30%; the corresponding domains are those of Figs. 14b, 15b, 16b, 17b and 18b, respectively.

5.3 Performance of DLTOP methodology in 2D test examples

In order to assess the performance of the DLTOP methodology, three 2D test examples are tested using the parameters that were identified in the previous section. The first test example is presented to demonstrate the capabilities of the proposed methodology regarding different update schemes. In this example, the MMA update scheme is used. The example used is labelled as “short-beam (coarse) test example” described in the previous section (see Fig. 9 a) using coarser FE mesh discretization, the sensitivity filter radius changed to two elements and an additional density filter with radius of two elements as well. The new discretization along the x and y axes is equal to ne_x = 150 and ne_y = 50, respectively, whereas the results obtained are shown in Fig. 19. The next test example is inspired from the two-bar problem presented in (Sigmund and Maute 2013). The discretization along the x and y axes is equal to ne_x = 50 and ne_y = 20, respectively; the support conditions refer to fully fixed boundary conditions along the x-axis at the base (Fig. 20 a), and the single loading condition refers to one concentrated forces P along the x-axis and applied in the middle of the span of the x-dimension as depicted in Fig. 20 a. The preference for final volume is equal to 20% of the initial domain, and the filter applied is a density and sensitivity filter with radius equal to 1.5 elements; the results obtained are shown in Fig. 20 b–f. The last test example corresponds to the serpentine beam problem presented in the PolyTop (Talischi et al. 2012a). In particular, it corresponds to a non-regular design domain discretized with unstructured polygonal finite element mesh composed by 5000 elements; the discretization was generated using PolyMesher (Talischi et al. 2012b); the support conditions refer to fully fixed boundary conditions along the y-axis on the left side of the domain (see Fig. 21 a), and the single loading condition refers to one concentrated force P along the y-axis and applied in the pick of the span of the y-dimension as depicted in Fig. 21a. The preference for final volume is equal to 40% of the initial domain, and the filter applied is a density filter as described in (Talischi et al. 2012a) with radius equal to 0.25; the results obtained are shown in Fig. 21 b–d.

The results obtained when implementing DLTOP methodology for the above-described three test examples are presented in Table 6. In particular, regarding the short-beam (coarse) test example, DLTOP achieved reduction of more than 25% on the SIMP iterations required originally and the objective function value achieved is more or less equal to that obtained by SIMP approach. Accordingly, for the two-bar test example, DLTOP achieved almost 40% reduction on SIMP iterations and the objective function value achieved is equal to that originally obtained by the SIMP.

Table 6 Average and variance of performance in 2D and 3D test examples

Additionally, in the two-bar test example, a threshold was applied on the result of SIMP achieved after performing the same number of iterations with those used as input by DLTOP in order to witness the differences in these two applications. The result obtained by using a threshold is presented in Fig. 20 e; the result obtained by DLTOP phase I is presented in Fig. 20 c while the difference between these two results is shown in Fig. 20 f. In Fig. 20 f, black areas denote the elements present in the DLTOP phase I and not in the threshold and grey areas are the elements present in the threshold and not in the DLTOP phase I. According to DLTOP methodology material has been added in the outside areas of both “legs” while it has also removed plenty of material from the inner areas as well. This can be explained as DLTOP has identified the tendency of these density values to increase and decrease accordingly, leading to a result closer to the final one of just implementing SIMP (i.e. Fig. 20 b, 54 iterations).

It can be witnessed that in the serpentine beam test example, DLTOP achieved more than 75% reduction on the SIMP iterations required originally and the objective function value achieved is more or less equal to that obtained by SIMP approach. The optimized domains for the all three test example are shown in Figs. 19, 20 and 21 as well as the objective functions and compliance for the original topology optimization and phases I and II of the DLTOP.

5.4 Computational efficiency of DLTOP methodology in 3D test examples

Given the performance evaluation of the training parameter combination for the DBN part of the DLTOP methodology, its computational efficiency is also assessed over three 3D topology optimization test examples. The first one shown in Fig. 22 a is three-dimensional version of the L-shaped test example, where the discretization along the x, y and z axes is taken equal to 60, 60 and 20, resulting into 72,000 solid finite elements, respectively; the support conditions refer to fully fixed boundary conditions for the xz plane along the z-dimension, ending at the 1:3 of the x-dimension (Fig. 22 a), and the loading condition refers to a concentrated force P along the y-axis applied at the 1:4 of the y-dimension and middle of the span along the z-dimension. The second 3D test example also shown Fig. 22 b was taken from the example examined in (Kazakis et al. 2017). The discretization along the x, y and z axes is taken equal to 160, 40 and 13, respectively, resulting into 83,200 solid finite elements; the support conditions refer to fully fixed support at the xz plane spamming from the 1:3 to the 1.75:3 of the x-dimension and one element in each size from the centre of the z-dimension and the loading conditions refer to distributed loading q along that is applied on the top xz plane along the y-dimension (as shown in Fig. 22 b). The third 3D test example shown in Fig. 22 c refers a cantilever beam. The discretization along the x, y and z axes is taken equal to 120, 40 and 30, respectively, resulting into 144,000 solid finite elements. The support conditions refer to fully fixed boundary conditions on the zy plane at the left side of the beam, and the loading conditions refer to a concentrated load along the y-axis at the right side of the beam in the middle of the z-axis (as shown in Fig. 22 c).

In the first 3D test example, the preference for final volume is equal to 15% of the design domain and the filter radius is equal to 1.2 elements. In the second 3D test example, the preference for the final volume is equal to 40% of the design domain and the filter radius is equal to 1.5 elements, and in the third 3D test example, the final volume is equal to 20% of the design domain and the filter radius is equal to 1.5 elements. For all test examples, filtering was implemented using a combination of the standard sensitivity filtering with the density one.

The results obtained when implementing DLTOP methodology are presented in Table 6. In particular, regarding the L-shaped 3D test example, DLTOP achieved 81% reduction on the SIMP iterations required originally and the objective function value achieved is basically equal to that obtained by SIMP approach. Accordingly, for the bridge 3D test example, DLTOP achieved 62% reduction of SIMP iterations and the objective function value achieved is equal to that originally obtained by the SIMP and the cantilever beam achieved 52% reduction of SIMP iterations and the objective function value achieved is basically equal. The optimized domain for the bridge 3D test example resulted originally by SIMP is shown in Fig. 23 a, and those obtained from phases I and II of the proposed DLTOP methodology are depicted in Fig. 23 b and c, respectively. As it can be seen, the forms obtained are almost identical, while the corresponding objective function values achieved and iterations required are equal to 1,632,305.73 and 509, 1,612,500.00 and 36, 1,640,121.4 and 193 for original SIMP, phases I and II of DLTOP, respectively. In addition, the optimized domain of the L-shaped 3D example can be seen in Fig. 24 as well as the objective functions and compliance for the original topology optimization and phases I and II of the DLTOP and the optimized domain of the cantilever beam can be seen in Fig. 25 as well as the objective functions and compliance for the original topology optimization and phases I and II of the DLTOP.

Fig. 25

Optimized domain for the cantilever beam test example—classification 3: a original SIMP (objective function 9.16, iterations 305), b DLTOP phase I (objective function 7.80, iterations 36) and c DLTOP phase II (objective function 9.12, iterations 146)

The computer hardware platform that was used for the purposes of this work consists of an Intel Xeon E5-1620 at 3.70 GHz quad-core (with eight threads) with 16 GB RAM for the case of CPU-based computations and NVIDIA GeForce 640 with 384 cores and 2 GB RAM for the case of GPGPU-based computations, and the operating system was Windows 10 (64bit). For the bridge 3D test example, both sequential and parallel test runs are carried out, and as it can be seen, the computing time required for solving the topology optimization problem discretized with 83,200 solid finite elements SIMP requires up to 54,287 s to carry out 509 SIMP iterations while applying a GPGPU-based acceleration of the structural analysis procedure the required time is reduced to 8587 s (speedup factor of 6× for GPU when compared with CPU). The time required by the proposed DLTOP methodology is 20,910 s if the structural analysis part of the SIMP iterations is performed sequentially, while if a GPGPU-based acceleration of the structural analysis is performed the computing time is further reduced to 3256 s (speedup factor of 17× for DLTOP-GPU when compared with SIMP-CPU).

Worth mentioning is that the computational time required for training the network is not included in the time requirements described above as the network was not trained on the specific examples or on any of the test examples presented in the current study. Training of the network is performed only once based on a database derived using a single test example; the resulting metamodel through training is unique and is used for any 2D or 3D test examples without requiring additional training. For this reason, it would be misleading to add the training time required ones to the comparison between SIMP and DLTOP for every test example. Training is performed once, and the resulting metamodel can be applied to any topology optimization problems.

6 Conclusions

In this work, aiming to accelerate the topology optimization procedure, a novel two-phase methodology that relies on deep learning is proposed. In particular, DBNs are integrated into the SIMP approach in order to solve topology optimization problems. In detail, DBN is used for discovering higher order connections between the density values of each finite element of the domain along the first iterations of SIMP approach with its final outcome. DBN is trained over two training datasets that are constructed using two typical topology optimization test examples implementing several discretizations. The first one (i.e. simply supported beam test example) was found to deliver clearer but strict shapes that in some cases might require less iterations to be refined during phase II; however, it can derive shapes in phase I that cannot be handled in phase II. On the other hand, the second dataset (i.e. cantilever beam test example) is more likely to develop shapes that would be handled more effectively by phase II with a slight increase of the number of fine-tuning iterations in some cases. The trained network is then applied on various 2D and 3D topology optimization test examples where the performance and robustness of the proposed methodology are tested with regard to the training parameters, datasets considered and classification type.

Based on the tests performed for the needs of the study, it was observed that the proposed methodology succeeds in accelerating the SIMP method in all cases regardless of the parameters and datasets used for training and the classification type. More specifically, when the correct set of training parameters and dataset is used, the reduction of SIMP iterations achieved is greater than 90% (i.e. more than one order of magnitude reduction). It is also worth noticing that the proposed methodology is robust in terms of objective function value achieved as in all tests; the value of the objective function is almost equal to the one identified by the original SIMP. Furthermore, the new methodology is generally applicable in any shape of optimizable domain used to formulate the topology optimization problem, regardless of the domain type (2D or 3D), discretization (structures or unstructured), loading conditions and SIMP approach parameters like target volume fraction, filter size, etc. as well as methodologies like the continuation of penalization.