1 Introduction

Over the past two decades, multi-objective evolutionary algorithms (MOEAs) have been widely accepted as a major approach for solving multi-objective optimization problems (MOPs), which are able to approximate the whole Pareto front (PF) in a single run. According to the different selection mechanism adopted by the algorithm, the current MOEAs are roughly classified into three major categories, i.e., Pareto-based, decomposition-based and indicator-based algorithms.

Pareto dominance-based MOEAs generally adopt non-dominated sorting method to achieve convergence. The diversity maintenance strategy used in this type often serves as a secondary selection of solutions. Remarkable MOEAs based on Pareto dominance include PESA-II [11], NSGA-II [14] and SPEA2 [45]. In decomposition-based MOEAs, a set of decomposition vectors are either used for aggregating objectives or improving diversity and convergence. For example, the multi-objective evolutionary algorithm based on decomposition (MOEA/D) [42] decomposes a MOP into a number of scalar single-objective optimization subproblems by weight vectors. The indicator-based approaches adopt a certain metric of the performance indicator to guide the search process. The indicator values used in this type of MOEAs can evaluate the convergence and diversity performances of solutions, such as the fast hypervolume-based evolutionary algorithm (HypE) [2] and the enhanced inverted generational distance (IGD) indicator-based evolutionary algorithm [35].

The above-mentioned algorithms have achieved great success in handling the optimization problems with no more than three objectives. However, many real-world applications involve more than three objectives, such as land use management problems [9] and airfoil designing problem [38]. Generally, the MOPs with more than three objectives are regarded as many-objective optimization problems (MaOPs). Unfortunately, recent studies have suggested that the conventional Pareto-based MOEAs are faced with difficulties when tackling MaOPs [27]. They may encounter severe deterioration of selection pressure, because the number of non-dominated solutions increases exponentially with the number of objectives increasing. This phenomenon result in the efficiency of Pareto-based approaches decreasing significantly in tackling MaOPs. To overcome this challenge and enhance the performance of MOEAs to tackle MaOPs effectively, a variety of approaches have been proposed.

The most direct way is to relax the dominance relationship making solutions further distinguished form each other, so as to further enhance the selection pressure toward PFs, such as preference order ranking [15], \(\varepsilon\)-dominance [19] and L-optimality [46]. The second approach is indicator-based approaches, since they do not suffer from the selection pressure problem. However, this method is always time-consuming especially in high-dimensional objective space. Notably, decomposition-based methods have gained a lot of research and have been proved to be a promising method to deal with MaOPs.

Generally, a predefined set of uniformly distributed reference vectors (it is worth noting that reference vectors are also called weight vectors or direction vectors in some other literatures, such as [28, 36, 39, 42], and in this work, we use the term of reference vectors as a substitution to others for simplicity) is employed in decomposition-based MOEAs. However, it is difficult to ensure a uniform distribution of candidate solutions on the PF when solving MaOPs. As stated in [23], the shape of the PF has a huge impact on the performance of the decomposition-based MOEAs. If the PF is irregular, such as PFs with disparate scales, discontinuous segments or other complex shapes, the predefined fixed reference vectors may lead to poor performance of the decomposition algorithm. The reason for this phenomenon is that the distribution of the reference vectors is not suitable for the PF shape. In other words, fixed reference vectors may not be able to match the true PF and therefore cannot provide the correct direction of guidance.

In recent years, researchers have focused on adaptively adjusting reference vectors to make them more compliant with PF shape to improve the performance of the algorithm. In general, most adaptive adjustment of reference vector methods follows the add-and-delete procedure [1, 3, 8, 28, 31]. To some extent, this approach can increase the diversity of population. However, it is undoubted that computational complexity of the algorithm will increase because the algorithm frequently determines where to add or remove reference vectors. Different from the above methods, a hybrid weighting strategy is proposed in [24], which optimizes both random reference vectors and fixed reference vectors. However, randomly generated reference vectors increase the uncertainty of the search direction. Recently, Zhao [43] presented a method to adjust the reference vectors in-time, which always maintain a good approximation to the current PF. But what needs to be considered is whether the computational cost of the cumbersome steps in the strategy is worthwhile.

In addition to adaptively adjusting the reference vector, the selection mechanism is also a key component of the decomposition. In MOEAs, the selection is of great importance to the algorithm’s performance. In general, it is desirable to strike a balance between convergence and diversity to obtain a good approximation of the candidate solutions. Both MOPs and MaOPs demand a delicate balance between the convergence and diversity. Nevertheless, how to balance the two abilities is not an easy task, especially in the high-dimensional space.

Recently, some proposed MOEAs show competitive performance in maintaining a good balance between convergence and diversity. For instance, NSGA-III [13] adopts a reference point-based strategy as diversity maintenance operator instead of crowding distance based in NSGA-II to solve MaOPs effectively. Additionally, a two-layer weight vector generation method is introduced to generate a set of evenly distributed weight vectors in high-dimensional space. MaOEA_IT [34] addresses convergence and diversity in two independent and sequential stages. A non-dominated dynamic weight aggregation method is arranged to find the Pareto-optimal solutions, which is employed to learn the Pareto-optimal subspace for convergence. Then, the diversity is guaranteed by reference lines within the learned Pareto-optimal subspace. Luo et al. [30] proposed an indicator-based MOEA/D (IBMOEA/D), which is based on decomposition and preference information. A decomposition-based strategy is used to divide the search space, then a binary quality indicator-based selection is utilized for maintaining the external population, and the two strategies complement each other.

Some latest studies are devoted to balance convergence and diversity [4, 5, 29, 33, 41]. These algorithms can deal with the balance of convergence and diversity to a certain extent. However, the strategies of them to enhance convergence and diversity are separate, which may weaken the communication of the information. In other words, they always give priority to convergence and then consider diversity alone, or vice versa. Convergence and diversity are treated separately with different strategies, which makes it difficult to make full use of current population information to achieve a balance of them.

Aiming at dealing with the above problems, an enhanced reference vectors-based multi-objective evolutionary algorithm with neighborhood-based adaptive adjustment (MOEA-NAA) is presented. Different from existing approaches, decomposition in this paper does not depend on predefined fixed reference vectors. The contributions of this approach are summarized as follows:

  • A pioneer dynamic population strategy is introduced. In the initial stage of the algorithm, fewer individuals are used to search the solution space. When enough non-dominated solutions are found, the environment selection operation is performed. The purpose of the arrangement is to accelerate the convergence speed and improve the performance of the algorithm.

  • Multiple methods are adopted in the environmental selection mechanism to increase selection pressure. It refines the information of each generation and makes a proper combination of convergence methods and diversity methods. In other words, it combines the dominance-based method and the reference vectors-based method to achieve the balance of convergence and diversity.

  • A reference vector adaptive adjustment strategy based on neighborhood information is proposed. The large-scale adjustment of the reference vector may be excessive computation, and result in the increasement of computational complexity. So, the adjustment of the reference vector in MOEA-NAA is a small-scale reference vector adaptive fine-tuning strategy, which assigns computing resources to potential search areas. If the current search area is sparse or discrete, its computing resource is assigned to neighboring areas to enhance the adaptability to PF, especially for irregular PF.

The rest of this paper is organized as follows: Sect. 2 introduces related work in adaptive reference vector-based algorithms. The challenge of designing a new algorithm is also analyzed in Sect. 2. In Sect. 3, the details of the proposed algorithm MOEA-NAA are described and empirical results of MOEA-NAA compared with a number of existing MOEAs are presented in Sect. 4. Finally, conclusion and future work are discussed in Sect. 5.

2 Related work

In this section, several reference vector adaptive adjustment strategies of the existing reference vectors-based MOEAs and their limitations are detailed, which introduces the main motivation of this paper.

Reference vectors should be carefully specified based on the shape and the size of the PF [23]. Therefore, a proper adaptation mechanism is required in reference vectors-based MOEAs. To address MOPs or MaOPs with irregular PFs, several related works have already been proposed on reference vector adaptive adjustment strategies.

Qi et al. [31] recommended dynamically adjusting the reference points during the optimization (MOEA/D-AWA). Specifically, in the late stage of the algorithm, the periodic adaptive adjustment of the reference vectors is employed during the evolution process. An external population is maintained to estimate the density of solutions for each reference vector. The vicinity distance is adopted to determine the sparse region. Then, the reference vectors in the most crowded regions are removed, while new reference vectors are added in sparse regions. However, MOEA/D-AWA needs to perform the non-dominated sorting strategy and store the non-dominated solutions in an external archive. In addition, it is necessary to evaluate the sparsity and density of each solution in the population. Both of the above two operations are known to be computational expensive, especially in handling MaOPs.

In RVEA [8], there are two different reference vector adaptations to solve badly scaled PFs and irregular fronts. The reference vectors located in empty subspaces are deleted. Meanwhile, the minimum and maximum objective values are calculated from the current candidate solutions to construct a hyperspace. Then, the new reference vectors are randomly generated inside the hyperspace. The main feature of RVEA is that the new reference vectors are produced globally and randomly, which may increase the uncertainty of the algorithm search directions and result in the decline of the local solution density.

A MaOEA based on decomposition with two types of adjustments for the reference vectors (MaOEA/D-2ADV) is proposed in [3]. The number and the position of reference vectors are adjusted, respectively. First of all, M extreme vectors are used to find the boundary of PF. When the convergence rate of the population tends to be stable, that is, the convergence of the population is no longer significantly improved, and then, the number of reference vectors is adjusted. Then, the validity of the reference vector is detected by associating the current solutions with the reference vectors. Reference vectors associated with less than one solution are considered invalid. These ineffective reference vectors will be obsoleted, and new reference vectors will be inserted between two valid reference vectors. Unfortunately, if extreme reference vectors are associated with no solution, it may cause a missing of boundary solutions.

Similarly, Li et al. [28] proposed an algorithm (AdaW) to adapt the reference vectors during the evolutionary process. Reference vectors are updated periodically based on the information produced by the evolving population, and then, the adjusted vectors in turn guide population evolution. The undeveloped and promising search directions or areas are found out by contrasting the evolutionary population with the archive set, and then, reference vectors are added in these areas. Afterward, the existing unpromising reference vectors or the reference vectors associated with the crowded solutions in the population are removed. Similar to MOEA/D-AWA, AdaW also uses an external archive set to adjust the reference vectors.

The above adaptive reference vectors adjustment follows the add-and-delete procedure, which is the most commonly used adjustment strategy. In recent years, reference point design methods using inherent models have been proposed. Gu and Cheung [18] developed a reference point design method based on a self-organizing map (SOM) for decomposition-based MOEAs. It trains a SOM network periodically with N neurons by using the objective vectors of the recent population, and then, the weights of the neurons are employed as the reference vectors. Besides, the design of the weight vectors in MOEA-SOM has no constraints on the setting of the number of reference vectors. In [39], a learning-to-decompose (LTD) paradigm is developed to set reference vectors adaptively. Specifically, in the learning module, the current non-dominated solutions are considered as the training data, and Gaussian process (GP) regression is adopted to learn an analytical model. During the optimization module, the characteristics are extracted to adjust reference vectors. Similarly, a Gaussian process was utilized in [7]. Cheng et al. proposed a multi-objective evolutionary algorithm using Gaussian process-based inverse modeling (IM-MOEA), in which maps are built from candidate solutions in the objective space to the decision space during the optimization. However, this method is only suitable for MOPs with a continuous and uniform PF, thus an adaptive reference vector generation strategy for IM-MOEA to deal with a non-uniform or disconnected PF in [6]. One of the drawbacks is the expensive computational costs since the training of a model requires a large data set.

As the number of objectives increases, the distribution of reference vectors and their corresponding solutions in the objective space may become sparse, which is likely to cause insufficient search of the integral Pareto front. Thus, the idea of using two sets of reference vectors is developed. Sato et al. advocated to introduce supplemental reference vectors and solutions in the conventional MOEA/D algorithm framework [32] (abbreviated as MOEA/D-SW in this paper). The supplemental reference vectors and solutions are treated as additional variable information resource to enlarge the solution search. Experimental results prove the effectiveness of this method in dealing with many-objective knapsack problems, but this method may be difficult to solve irregular PFs. In order to improve the performance of irregular PFs, a “generalized” version of the decomposition-based evolutionary algorithm (g-DBEA) is proposed for periodic adaptation of the reference vectors [1]. With the evolution of the population, it records the information of the solutions and their preferred reference vectors to determine whether this reference vector is “active” or not. Based on the information, the inactive reference vectors are moved to the inactive set W rather than deleted altogether. Then, new reference vectors will be generated and added to the active set. Two reference vector sets simultaneously guide the search direction of the solution.

However, the method of two reference vector sets adds extra computation. In [37], Wang et al. proposed a preference-inspired co-evolutionary algorithm using weights (PICEA-w). The candidate solutions and the reference vectors are co-evolved simultaneously during the search process. The new reference vectors are generated randomly in each generation by the highest contributions to non-dominated solutions. In [36], the distribution of the reference points is adaptively adjusted, in terms of the contribution (IGD-NS) of candidate solutions into an external archive. In [20], it is unnecessary to pre-define extra reference vectors set, because the candidate solutions themselves are considered as reference vectors. These co-evolutionary methods are capable to guide candidate solutions toward the Pareto-optimal front effectively. Nevertheless, it can hardly maintain evenly distributed solutions toward the whole PF to a certain extent if there are sparse areas in the population.

Overall, the main limitations of the algorithms mentioned above are summarized to make a better readability, as shown in Table 1. Even though adaptive approaches have significant effect on obtaining a desirable distribution of solutions, they impose non-negligible cost, in terms of convergence [17]. Therefore, in the research of adaptive adjustment strategy, reducing computation and enhancing convergence are two major challenges.

Table 1 Summary of notable recent works in terms of reference vectors-based MOEAs
Full size table

3 The proposed algorithm

In this section, an enhanced reference vectors-based multi-objective evolutionary algorithm with neighborhood-based adaptive adjustment (i.e., MOEA-NAA) is presented. To be specific, the general framework of MOEA-NAA is outlined in Algorithm 1. Then, the details of the main steps are described step by step.

figure a

3.1 Framework of MOEA-NAA

The pseudo-code of the general framework of the proposed MOEA-NAA is provided in Algorithm 1, where the population size N, the number of objectives M, and the maximum fitness evaluation (FEmax) are entered. First of all, the initial population (POP) is randomly sampled with 0.2N individuals from the decision space, where 0.2N is attributed to the pioneer dynamic population strategy (refer to Sect. 3.2). N reference vectors are generated from a uniform distribution in objective space, and the nearest M neighbors vectors are determined by Euclidean distance for each reference vector.

As used in most algorithms, reference vectors are obtained by a systematic approach developed from Das and Dennis’s method [12]. Reference vectors are sampled from a unit simplex in this approach, and \(N=\)\(\begin{pmatrix} H+M-1\\ M-1 \end{pmatrix}\), where \(H>0\) is the number of divisions along each objective coordinate. But in high-dimensional objective space, there are a large number of reference vectors which obviously aggravate the computational burden of the algorithm. Therefore, a two-layer reference vectors generation method [13, 25, 26] is adopted when \(M\ge 7\). As depicted in Fig. 1, reference vectors consist of two different layers: boundary layer (denoted as \(B=\{b^1,b^2,\ldots ,b^{N_1}\}\)) and inside layer (denoted as \(I=\{i^1,i^2,\ldots ,i^{N_2}\}\)), where \(N_1+N_2=N\). In this work, reference vectors are initialized by using the generation method suggested in [25] when \(M\ge 7\). At first, reference vectors in boundary layer and inside layer are generated according to Das and Dennis’s method, with different H settings. Then, the reference vectors of the inside layer are shrunk by a coordinate transformation. For each reference vector \(i_r=(i^r_1,\ldots ,i^r_M)\), \(r \in \{1, 2,\ldots ,N_2\}\), its jth component is shrunken by the following formula:

$$\begin{aligned} i_j^r=\frac{\tau -1}{m}+\tau \times i_j^r \end{aligned}$$
(1)

where \(j \in {1,2,\ldots ,M}\), \(\tau\) is a shrinkage factor, generally set to 0.5.

Fig. 1
figure 1

Example of two-layer reference vector

Full size image

After the initialization is completed, the main while-loop updates the population in each iteration. In each generation G, a standard differential evolution operation is implemented to generate an offspring set Q. Each element \(y_k^i\) of ith offspring is generated as follows:

$$\begin{aligned} y_k^i=\left\{ \begin{array}{ll} x_{i}^{k}+F\times \left(x_{r_1}^{k}-x_{r_2}^{k}\right) \quad & \text {if} \ {\text{rand}}<{\text{CR}}\\ x_{i}^{k} & \text {otherwise.} \end{array}\right. \end{aligned}$$
(2)

where \(y\in Q\) and \(k=1,2,\ldots ,D\), CR and F are two control parameters. \(r_1\) and \(r_2\) are two indexes randomly selected from P:

$$\begin{aligned} P=\left\{ \begin{array}{ll} B(i), \quad & \text {if} \ {\text{rand}}<\xi \\ {1,2,\ldots ,N} & \text {otherwise.} \end{array}\right. \end{aligned}$$
(3)

Then, the polynomial mutation (PM) is performed on Q with probability \(p_{{\rm m}}\) in the following way:

$$\begin{aligned} q_k^i=\left\{ \begin{array}{ll} y_{i}^{k}+\sigma _k\times \left(b^{k}-a^{k}\right)\quad \quad & \text {if} \ {\text{rand}}<p_{{\rm m}}\\ y_{i}^{k} & \text {otherwise.} \end{array}\right. \end{aligned}$$
(4)

with

$$\begin{aligned} \sigma _k=\left\{ \begin{array}{ll} (2\times {\text{rand}})^{\frac{1}{\eta +1}}-1 \quad & \text {if} \ {\text{rand}}<0.5\\ 1-(2-2\times {\text{rand}})^{\frac{1}{\eta +1}} & \text {otherwise.} \end{array}\right. \end{aligned}$$
(5)

where \(a_k\) and \(b_k\) are the lower and upper bounds of the kth decision variable. The distribution index \(\eta\) and the mutation rate \(p_{{\rm m}}\) are two control parameters in PM.

Then, the ideal point is updated by the fitness values of Q. In the early stage of MOEA-NAA, the selection operation adheres to the criterion of convergence first. The non-dominated solutions in two consecutive generations of populations are chosen as the parent for the next generation. Subsequently, when the population size reaches N, the adaptive environmental selection is executed to select N solutions for the next generation (refer to Sect. 3.3). In this model, convergence and diversity are equally crucial and interdependent. At the end of a loop, a reference vector adaptive adjustment strategy is performed every \(T_{{\rm p}}\) generations (\(T_{{\rm p}}=60\)) for a more appropriate selection to improve the distribution over PF (refer to Sect. 3.4).

3.2 Pioneer dynamic population strategy

In [37], it has been demonstrated that adapting reference vectors during the search may affect the convergence performance of a MOEA, especially in high-dimensional objective space. Furthermore, only after the population has converged to a certain extent, reference vector adaptive adjustment will be activated [31]. To be specific, in the early stage of the algorithm, there are many dominant solutions in the population. If the diversity maintenance mechanism is introduced prematurely, it is likely to result in insufficient convergence of the population. As stated in [16], the number of non-dominated solutions reflects the degree of an algorithm to some extent. Thus, a pioneer dynamic population strategy is introduced in MOEA-NAA.

At the beginning, only 0.2N solutions are initialized to search the objective space. As the update of the population, the number of non-dominated solutions gradually increases. During this process, candidate solutions are selected only by using non-dominated sorting of the merged population, so that they can fast converge to approximate PF. The diversity maintenance mechanism is activated until the population size reaches N. Two benefits can be acquired from pioneer dynamic population strategy: Computing resources are economized and the convergence of the population is more adequate, attributed to the use of fewer excellent solutions to guide the algorithm process in the initial stage.

Two examples are given in Fig. 2, which represent two different situations. The IGD trend and HV trend of WFG7 and WFG8 are recorded, where IGDN and HVN represent the performance of MOEA-NAA without pioneer dynamic population strategy, while IGD and HV represent the performance of MOEA-NAA with pioneer dynamic population strategy. In the first case, there is no significant difference in the final performance of the two algorithms (IGD and IGDN, HV and HVN), i.e., Fig. 2a. It can be observed that the algorithm with the pioneer dynamic population strategy can converge quickly to a certain precision range. In another case, the difference in the final performance of the two algorithms is significant, i.e., Fig. 2b. Although the algorithm with the pioneer dynamic population strategy is more tortuous during the convergence process, compared to MOEA-NAA without the pioneer dynamic population strategy, it can obtain a better final performance. More discussion of the effectiveness of this strategy will be given in Sect. 4.3.4.

Fig. 2
figure 2

IGD and HV trend of WFG7 and WFG8, with parameters: \(N=100\), \(M=2\), \(\hbox {maximum iteration}=400\)

Full size image

Therefore, it can be determined that the introduction of the pioneer dynamic population strategy can accelerate the convergence speed of the algorithm or improve the performance of the algorithm.

3.3 Selection mechanism

In the proposed MOEA-NAA, environment selection operation is based on a fusion of reference vector-based and dominance-based methods to enhance the communication of information and make a balance of convergence and diversity. The detailed procedures of environment selection operation are presented in Algorithm 2 as follows:

figure b

  • Associated operation (lines 1–6 in Algorithm 2)

    First, calculate the angle between each solution and each reference vector according to Eq. (6).

    $$\begin{aligned} {\text{angle}}={\text{arccos}}<\frac{x\cdot \lambda }{|x|\cdot |\lambda |}>\end{aligned}$$
    (6)

    where x and \(\lambda\) are both vectors in the objective space. For an arbitrary solution (e.g., \(x_i\)) in the merged population, \(x_i\) is associated with \(\lambda _{{\rm R}}\) only when the angle between \(x_i\) and \(\lambda _{{\rm R}}\) is the smallest one compared to other reference vectors. \(\pi (k)\) records the number of solutions in the merged population which is associated with \(\lambda _k\).

  • Environmental selection 1 (lines 7–18 in Algorithm 2)

    For an arbitrary reference vector \(\lambda _i\), if there is only one solution \(x_k\) in the population associated with it, \(x_k\) directly survives. Otherwise, if more than one solution is associated with it, then the convergence measure is considered as the second criterion. The solution which is the closest one to the ideal point (\(z^*\)) is selected. It means that only one solution is retained among these solutions with regard to \(\lambda _i\). If a solution (e.g., \(X_L\)) is selected and it is associated with \(\lambda _i\), then flag(L) and age(i) plus one, respectively. Repeat the above steps until all reference vectors are traversed.

  • Environmental selection 2 (lines 19–22 in Algorithm 2)

    After the environment selection 1, environmental selection 2 is initiated to select (\(N-|S|\)) solutions in case if the number of population is less than N. Put unselected individuals from the merged population into selPOP. The filter operation is detailed in Algorithm 3. At first, non-dominated sorting is executed on selPOP, and then, the candidate solutions are preserved layer by layer according to the non-dominated level. Where the last layer of candidate solutions is found, a new round of selection mechanism needs to be enabled. On the last front, choose (\(N-S\)) solutions which have the greatest difference from the retained population S. Step 1: Calculate the angle between each solution in the last front and each solution in S. Step 2: Calculate the sum of the angle between each candidate solution and the solutions in S. Then, the candidate solution which possesses the largest difference (the largest angle) with S is selected and added in S. Meanwhile, it is removed from the last front. Step 3: Repeat step 1 and step 2 until the condition \(|S|=N\) is met.

    figure c

In MOEA-NAA, the environmental selection mechanism adopts multiple methods to increase selection pressure. It refines the information of each generation and makes a deep fusion of convergence methods and diversity methods. Therefore, this kind of environmental selection mechanism can achieve equilibrium between convergence and diversity.

3.4 Reference vector adaptive adjustment

Fixed reference vectors is poorly adaptable to different PFs, especially irregular PFs. On the other hand, large-scale adjustment of the reference vectors during the process of the algorithm may result in excessive computation and increasing unnecessary computational complexity. Hence, neighborhood-based reference vector adaptive adjustment is provided in MOEA-NAA, which is a small-scale reference vector adaptive fine-tuning strategy. The steps of neighborhood-based reference vector adaptive adjustment are shown in Algorithm 4.

figure d

Firstly, M extreme reference vectors (i.e., the reference vector located on each axis) are marked as consistent ones. The reason is that extreme reference vectors are special and important, which can be used to preserve the extreme solutions in the population during the optimization process. Afterward, the position of other reference vectors is adaptively adjusted based on neighbor information. For the reference vectors that have no solution associated with them in successive \(T_{{\rm p}}\) generations, find out the information of their M neighbors (the information here refers to the number of candidate solutions associated with the corresponding reference vector). For each reference vector to be adjusted \(\lambda _i\), two scenarios are considered in its neighbors. The first case is that only one neighbor vector possesses associated solution in the population. Then, the position of \(\lambda _i\) is moved to the location of this neighbor (lines 5–7 in Algorithm 4). Another situation is that more than one neighbor vector possesses associated solutions in the population. The position of \(\lambda _i\) is moved to the adjacent location of the neighbor who has the largest angle to \(\lambda _i\) (lines 8–10 in Algorithm 4). Notably, if no neighbor vector possesses an associated solution in the population for \(\lambda _i\), the position of \(\lambda _i\) is not adjusted.

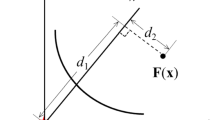
Figure 3 is depicted to better understand the reference vector adaptive adjustment procedure. In Fig. 3, \(\lambda _i\) is the reference vector which is prepared to adjust, and its neighbors are \(\lambda _{i-1}\) and \(\lambda _{i+1}\). In case 1, there are two solutions associated with \(\lambda _{i-1}\); the blue dot survived, while the red star one is removed in the environment selection operation. The area where the red star is located is a sparse area, so \(\lambda _i\) moves to \(\lambda _i'\) to strengthen search for sparse areas. Similarly, in case 2, \(\lambda _i\) moves to \(\lambda _i'\) to avoid over-searching for crowded areas.

Fig. 3
figure 3

Reference vector adaptive adjustment

Full size image

The main idea of this strategy is to assign computing resources to the objective space where optimal solutions may exist but not yet searched. If a reference vector has no associated solution during \(T_{{\rm p}}\) successive generations, a conclusion is made that this reference vector is invalid. This means that the search area is sparse or discrete; thus, its computing resource is assigned to neighboring areas to enhance the adaptability to PF. More details of the sensitivity of parameter of \(T_{{\rm p}}\) can be found in Sect. 4.3.3.

3.5 Computational complexity analysis

As introduced in Sect. 3.1, three main parts determine the computational complexity of MOEA-NAA in one generation, i.e., offspring reproduction (line 9 in Algorithm 1), environmental selection (lines 13–14, line 16 in Algorithm 1) and reference vector adaptive adjustment (lines 17–20 in Algorithm 1).

For the first part, the reproduction procedure requires O(DN) times, where D is the number of decision variables. The second part is environmental selection. When the population size is less than N, the time complexity is less than \(O(2N^2)\) to sort the non-dominated solutions (line 13 in Algorithm 1). When the population size is greater than N, the details of environmental selection are given in Algorithm 2 and Algorithm 3. First of all, it takes \(O(2N^2)\) to calculate the angle between each solution and each reference vector (line 1, Algorithm 2). Then, it costs O(N) to select one associated solution for each reference vector (lines 8–18, Algorithm 2). For those reference vectors that have no solution associated, the non-dominated sort process determines the computational complexity (line 21 in Algorithm 2, i.e., Algorithm 3), which requires a time complexity less than \(O(2N^2)\). The last part is reference vector adaptive adjustment (Algorithm 4). This program will trigger in case that a reference vector has no associated solution during 60 consecutive generations, so its time complexity is \(O(\frac{T_{\max}}{T_{{\rm p}}}*N)\), where \(T_{\max}\) is the maximum number of iterations.

Considering the above computational complexity analysis of all the procedures, the overall worst time complexity in one generation of MOEA-NAA is approximated to \(O(mN^2+\frac{T_{\max}}{T_{{\rm p}}}*N)=O(mN^2)\). The magnitude of the proposed algorithm is similar to most of the state-of-the-art many-objective algorithms, such as references [4, 40].

4 Experimental study

In order to examine the performance of the proposed MOEA-NAA algorithm in solving MOPs and MaOPs, a series of experiments are performed against peer competitors. First of all, NSGA-II [14] and MOEA/D [42] are selected on account of they are two basic and representative multi-objective optimization algorithms, so they are used as comparison when analyzing the performance on 2-, 3-objective test problems. Additionally, NSGA-III [13] is selected because it is typically used as a baseline in handling MaOPs. RVEA [8] is also chosen as a comparison algorithm due to it is a well-regarded algorithm when solving MaOPs. Furthermore, in order to demonstrate the effectiveness of the neighborhood-based reference vector adaptive adjustment strategy, MOEA-NAA0 is considered as a comparison algorithm, which is a variation of MOEA-NAA with fixed reference vectors. Above all, the benchmark test problems utilized in the comparisons and the parameter settings used in all the algorithms considered are enumerated in Sect. 4.1. Next, the chosen performance metrics are introduced in Sect. 4.2. Then, experimental results measured by the performance metric are presented and analyzed in Sect. 4.3.

4.1 Test problems and parameter settings

The well-known test suites Walking Fish Group (WFG1–WFG9) [22] are used in this study, in which attributes of convex or concave, separability or non-separability, unbiased or biased parameters, and unimodality or multimodality geometries are all covered. The detailed characteristics of PF shapes of all test suites are listed in Table 2. In this paper, the number of objectives (M) is set to 2, 3 and 4, 7, which tests the effectiveness of the algorithm in dealing with MOPs and MaOPs, respectively.

Table 2 Characteristics of PF shapes
Full size table

The standard toolkits are employed to implement the peer algorithms and follow the suggestions in their original study to set algorithmic parameters. The parameter settings of the comparison algorithm are presented in Table 3. In NSGA-II and NSGA-III, the simulated binary crossover (SBX) and the polynomial mutation are adopted to generate offspring solutions. The crossover probability \(p_{{\rm c}}\) and the mutation probability \(p_{{\rm m}}\) are set to 0.9 and 1 / D, respectively. The distribution index \(\eta _{{\rm c}}\) of SBX operator and the distribution index \(\eta _{{\rm m}}\) of mutation operator are set to 20 [13, 21, 42].

Table 3 Parameter settings of compared algorithms
Full size table

General parameter settings of all algorithms are enumerated in Table 4. The population size (N) is set to 100, 210, 286, 294 for 2-objective, 3-objective, 4-objective and 7-objective problems, respectively. For WFG test instances, according to [37], the number of position related variables \(k=18\) and the number of distance related variables \(l=14\), and the number of decision variables is set as \(D=k+l=32\). For each test instance, each algorithm will be run 30 times independently. The maximum number of generations is set to 1000, and the maximum number of function evaluations is \(N*1000\) for all the test instances.

Table 4 Parameter settings of all algorithms
Full size table

4.2 Performance metric

Two widely used performance metrics, i.e., inverted generational distance (IGD) [10] and hypervolume (HV) [44], are adopted to quantitatively evaluate the quality of the resulted solutions of all compared algorithms. They are able to concurrently measure the convergence and diversity of the tested algorithms.


Inverted generational distance (IGD) It measures the average distance from a set of evenly distributed points \(P^*\) on the PF to the approximation set P. It can be formulated as follows:

$$\begin{aligned} {\text{IGD}}(P,P^{*})=\frac{\sum\nolimits_{v\in P^{*}}d(v,P)}{\left| P^{*}\right| } \end{aligned}$$
(7)

where d(v, P) is the Euclidean distance from point \(v\in P^{*}\) to its nearest point in P, and \(|P^{*}|\) is the cardinality of \(P^{*}\). In this paper, the number of sampling points from the true PF is taken as 10,000 in the computational experiments. It can be analyzed that the smaller the IGD, the better the quality of P for approximating the whole PF.


Hypervolume (HV) Let \(R = (R_1,\ldots , R_M)^{{\rm T}}\) be a reference point in the objective space which is dominated by any point of Pareto-optimal solutions. The HV metric measures the size of the region that is dominated by the obtained non-dominated solutions S and dominates R. Pareto solution set with higher HV value indicates better convergence and diversity. Hypervolume metric is computed as follows:

$$\begin{aligned} {\text{HV}}(S)={\text{Leb}}\left( \cup _{x \in S}[f_1(x),R_1]\times \cdot \cdot \cdot \times [f_M(x),R_M]\right) \end{aligned}$$
(8)

where Leb(S) is the Lebesgue measure of S. The selection of the reference point is an important issue. In this experiment, R is set to \((3,5,\ldots ,2M+1)^{{\rm T}}\) for M-objective test instance, as recommended by [37].

4.3 Experimental results and analysis

To ensure clarity in the result comparisons, the results for WFG benchmark with 4 different dimensions are presented in Tables 5 and 6. The mean and standard deviation of HV and IGD metric value are recorded. The Wilcoxon rank sum test with a significance level of 0.05 is adopted to perform statistical analysis on the experimental results, and the symbols ‘+’ and ‘=’ in Tables 5 and 6 indicate that the result by MOEA-NAA is significantly better and statistically similar to that obtained by another MOEA, respectively.

Table 5 Comparison of the MOEAs on IGD value with means and standard deviations for WFG benchmark with four different dimensions
Full size table
Table 6 Comparison of the MOEAs on HV value with means and standard deviations for WFG benchmark with four different dimensions
Full size table

4.3.1 Performance comparisons on multi-objective test problems

In this experiment, WFG with 2- and 3-objective are adopted to verify the performance of algorithms in handling MOPs. For the 2-objective MOPs, as evidenced by statistical results of the IGD values summarized in Table 5, MOEA-NAA has shown the most competitive performance on WFG2, WFG3, WFG6, WFG8 and WFG9, while MOEA/D and NSGA-III have achieved the best performance on WFG7, WFG1 and WFG4, respectively. By contrast, the performance of NSGA-II on the WFG test functions is poor. The situation of the 3-objective is similar to that in bi-objective MOPs. In the following, some discussions on the experimental results will be presented.

WFG1 is designed with flat bias and a mixed structure of the PF containing both convex and concave segments. And it is used to assess whether MOEAs are capable of dealing with PF with complicated mixed geometries. As can be seen from Fig. 6, the obtained PF of MOEA-NAA on WFG1 is not smooth. Poor performance of MOEA-NAA on WFG1 indicates that MOEA-NAA may be not suitable for handling such complicated mixed geometries. But compared to MOEA/D, MOEA-NAA can search for more areas and get a more complete PF, which reflects the good search ability of MOEA-NAA. WFG2 is a test problem which has a disconnected PF. In Figs. 4 and 5, it can be observed that although the IGD and HV values obtained by each algorithm vary on this test problem, the overall performance is generally very good. The performance gradually improves as the number of iterations increases, which indicates the potential of MOEA-NAA in dealing with discrete problems. In addition, Figs. 4 and 5 present a tortuous process, which may be caused by the discreteness of PF. In the case of three objectives, MOEA-NAA gains worse IGD value in Fig. 7 but presents a good distribution compared to NSGA-II and MOEA/D on WFG2 in Fig. 9. WFG3 is a difficult problem where the PF is degenerate and the decision variables are non-separable. MOEA-NAA achieves comparable lower IGD values and higher HV values than other five algorithms on WFG3. In Figs. 4 and 5, IGD and HV values obtained by MOEA-NAA show a faster convergence and more accurate results. The obtained results of 2-objective PF are displayed in Fig. 6. It can be seen that MOEA-NAA receives more uniform distribution toward the whole PF on WFG3. Nevertheless, as depicted in Fig. 9, all compared algorithms have not reached the true degenerate PF.

Fig. 4
figure 4

Variation of IGD metric value on WFG2, WFG3, WFG5, WFG8 with 2-objective

Full size image
Fig. 5
figure 5

Variation of HV metric value on WFG2, WFG3, WFG5, WFG7 with 2-objective

Full size image
Fig. 6
figure 6

Pareto front on WFG1, WFG3 and WFG8 with 2-objective

Full size image
Fig. 7
figure 7

Variation of IGD metric value on WFG2, WFG3, WFG8, WFG9 with 3-objective

Full size image
Fig. 8
figure 8

Variation of HV metric value on WFG2, WFG3, WFG8, WFG9 with 3-objective

Full size image
Fig. 9
figure 9

Pareto front on WFG2, WFG3 and WFG9 with 3-objective

Full size image

WFG4–WFG9 are designed with different difficulties in the decision space, e.g., multimodality for WFG4, landscape deception for WFG5, non-separability for WFG6, WFG8, and WFG9, and biased for WFG7, but the true PFs of these problems are same convex structure. On 2-objective and 3-objective WFG4, MOEA-NAA is worse than NSGA-III and RVEA in terms of IGD values. On 2-objective WFG7, MOEA-NAA achieves comparable lower IGD values than RVEA and MOEA/D, but has been outperformed by the other four algorithms. On 3-objective WFG4, MOEA-NAA is worse than NSGA-III and RVEA in terms of HV values. In addition to the above mentioned, MOEA-NAA has reached the optimal value on other test functions of WGF4–WFG9. Figures 4, 5, 7 and 8 exhibit some of variation of metric value, and Figs. 6 and 9 depict the approximate front of the partial function. As can be seen from these figures, the convergence speed, the distribution and diversity of MOEA-NAA are significantly outperformed by other compared algorithms.

Notably, the algorithm with fixed reference vectors of MOEA-NAA, which recorded as MOEA-NAA0, is still significantly worse than MOEA-NAA even though they are similar in many test functions.

4.3.2 Performance comparisons on many-objective test problems

WFG test problems with 4-objective and 7-objective are also adopted to verify the performance of algorithms in handling MaOPs. As can be observed in Tables 5 and 6, MOEA-NAA shows the most competitive overall performance on these problems. More specifically, MOEA-NAA is significantly superior to NSGA-II, MOEA/D, while it has achieved the comparable performance to NSGA-III and RVEA in IGD and HV values. On the 4- and 7-objective WFG1, NSGA-III gains best performance just like that on 2- and 3-objective WFG1. For the 4-objective WFG2, WFG3, WFG5, WFG8 and WFG9, MOEA-NAA reaches the best HV values. For the 7-objective WFG4, WFG5 and WFG9, MOEA-NAA gains the best IGD values.

Figures 10, 11, 12, 13, 14 and 15 show the trend of IGD and HV values and the approximate front of some functions. The lines of different colors represent the different approximate solutions in Figs. 12 and 15. As the number of objectives increases, the difficulty of finding the true PF of WFG2 increases dramatically. The IGD metric value hardly converges, especially when dealing with 7-objective problems, so IGD value shows an increasing trend with the increase in the evaluations except for NSGA-II. This phenomenon reflects the weakness of reference vector-based or decomposition-based algorithms when handling discrete problems.

Fig. 10
figure 10

Variation of IGD metric value on WFG2, WFG3, WFG4, WFG8 with 4-objective

Full size image
Fig. 11
figure 11

Variation of HV metric value on WFG2, WFG3, WFG4, WFG8 with 4-objective

Full size image
Fig. 12
figure 12

Pareto front on WFG2, WFG3 and WFG8 with 4-objective

Full size image
Fig. 13
figure 13

Variation of IGD metric value on WFG2, WFG5, WFG7, WFG8 with 7-objective

Full size image
Fig. 14
figure 14

Variation of HV metric value on WFG2, WFG6, WFG7, WFG8 with 7-objective

Full size image
Fig. 15
figure 15

Pareto front on WFG6, WFG7 and WFG9 with 7-objective

Full size image

Besides, as can be observed from Figs. 12 and 15, MOEA-NAA gets a better distribution which means a good diversity is obtained.

4.3.3 Sensitivity of performance to the parameter \(T_{{\rm p}}\)

As described earlier, the parameter \(T_{{\rm p}}\) is an important factor for reference vector adaptive adjustment. In this part, the sensitivity of parameter \(T_{{\rm p}}\) is investigated to verify the performance of MOEA-NAA.

If \(T_{{\rm p}}\) is too large, the convergence gets affected for MOPs or MaOPs with irregular PF. If it is too small, it may undesirably make certain reference vectors invalid. Therefore, a suitable range is necessary for reference vector adaptive adjustment strategy to be effective for problems with different PF.

In order to study the sensitivity of performance the parameter \(T_{{\rm p}}\), different types of problems have be taken in account including mixed (WFG1), discontinuous (WFG2), degenerate (WFG3) and concave (WFG6). The experiment are executed with different \(T_{{\rm p}}\) values (i.e., \(T_{{\rm p}}\) = 20, 40, 60, 80, 100), and the mean IGD and HV of 20 independent runs are calculated. In order to intuitively observe the impact of \(T_{{\rm p}}\) on the performance of the algorithm, Fig. 16 shows the mean IGD obtained using different values of \(T_{{\rm p}}\) for WFG1–WFG3. Besides, Fig. 17 depicts the mean HV values for WFG1, WFG2 and WFG6.

Fig. 16
figure 16

Influence of the parameter \(T_{{\rm p}}\) with varying objectives 2, 3, 4 and 7 with respect to IGD values for a WFG1 (biased, mixed PF), b WFG2 (discontinuous PF) and c WFG3 (degenerate PF)

Full size image
Fig. 17
figure 17

Influence of the parameter \(T_{{\rm p}}\) with varying objectives 2, 3, 4 and 7 with respect to HV values for a WFG1 (biased, mixed PF), b WFG2 (discontinuous PF) and c WFG6 (concave PF)

Full size image

One phenomenon can be seen that \(T_{{\rm p}}\) has negligible effect for a problem having biased, mixed PF, i.e., WFG1 (Figs. 16a, 17a). For WFG2, there is a clear gap at \(T_{{\rm p}} = 60\) with regard to IGD value. As shown in Fig. 16b, the performance reaches the best IGD value at \(T_{{\rm p}} = 60\) when \(M = 2, 3, 7\). It seems very competitive when \(T_{{\rm p}} = 100\); nevertheless, there is a performance drop when \(M = 2\) both in IGD and HV value. For degenerate problem WFG3 (Fig. 16c), the performance is relatively stable when \(M = 2, 3, 4\), whereas there is a significant fluctuation when \(M = 7\). Ultimately, the optimal IGD value falls at \(T_{{\rm p}} = 60\). It can be observed from Fig. 17c that HV value tends to be stable at \(T_{{\rm p}} = 20, 40, 60, 100\) when \(M = 2, 3, 4, 7\), but the line of \(M = 7\) shows slight fluctuations. The optimal HV value of WFG6 is obtained at \(T_{{\rm p}} = 100\), while the suboptimal value is achieved at \(T_{{\rm p}} = 60\).

Based on our experiments, \(T_{{\rm p}}=60\) gives satisfactory results, regardless of the shape of the PF. In particular, for discontinuous fronts, more reasonable adaptive adjustment is required. Finally, a sufficient number of directional adjustments should be guaranteed to achieve the preferred distribution toward the PF, and the solution has sufficient generations to converge to the direction of the adjusted reference vector.

4.3.4 Effectiveness of the pioneer dynamic population strategy

As described earlier in Sect. 3.2, the pioneer dynamic population strategy can accelerate the convergence speed of the algorithm or improve the performance of the algorithm. In this subsection, the effectiveness of this strategy is assessed by implementing more detailed experimental analysis. Consistent with the experimental method used in Sect. 3.2, the effectiveness of the strategy is demonstrated by comparing the performance of the algorithm with the fixed population size N and the pioneer dynamic population strategy. Figures 18, 19, 20 and 21 record IGD and HV trend of several problems when \(M= 2, 3, 4\) and 7, respectively. It is worth noting that IGDN and HVN represent the performance of MOEA-NAA with fixed population size N, while IGD and HV represent the performance of MOEA-NAA with the pioneer dynamic population strategy in these figures.

Fig. 18
figure 18

IGD and HV trend of WFG1, WFG7 and WFG9, with parameters: \(N =100\), \(M = 2\), maximum iteration = 1000

Full size image
Fig. 19
figure 19

IGD and HV trend of WFG1, WFG6 and WFG9, with parameters: \(N =210\), \(M = 3\), maximum iteration = 1000

Full size image
Fig. 20
figure 20

IGD and HV trend of WFG3, WFG6 and WFG9, with parameters: \(N =286\), \(M = 4\), maximum iteration = 1000

Full size image
Fig. 21
figure 21

IGD and HV trend of WFG2, WFG5 and WFG9, with parameters: \(N =294\), \(M = 7\), maximum iteration = 1000

Full size image

From these figures, three observations can be gained. Firstly, the proposed pioneer dynamic population strategy performs much better than the compared method on accelerating the convergence speed in terms of IGD and HV trend. For example, in 2-objective WFG1 (Fig. 18a), 3-objective WFG1 (Fig. 19a), 4-objective WFG6 (Fig. 20b) and 7-objective WFG5 (Fig. 21b), the final indicator value is similar, whereas the convergence speed of the algorithm with the pioneer dynamic population strategy is faster than that of the algorithm with fixed population size. Secondly, the proposed strategy also shows competitive performance on improving the final performance of the algorithm. It can be observed from 2-objective WFG7 (Fig. 18b), 3-objective WFG6 (Fig. 19b), 4-objective WFG3 (Fig. 20a) and 7-objective WFG9 (Fig. 21c). For the two comparison algorithms, the algorithm with pioneer dynamic population strategy has no significant improvement in convergence in the early stage, but it is worth noting that the final performance of the algorithm has been significantly improved. Thirdly, as depicted in the figures, i.e., 2-objective WFG9 (Fig. 18c), 3-objective WFG9 (Fig. 19c), 4-objective WFG9 (Fig. 20c) and 7-objective WFG2 (Fig. 21a), the overall performance of the algorithm adopting this strategy is significantly better than the compared algorithm in both convergence speed and final performance.

On the basis of the empirical observations above, it can be conclude that the proposed pioneer dynamic population strategy performs well in convergence speed or final performance, regardless of the process of algorithm.

4.3.5 Overall performance analysis

As evidenced by Tables 5 and 6, MOEA-NAA shows the most competitive overall performance on WFG problems by achieving the best results on 16 of 36 instances IGD values, and 20 out of 36 instances of HV values. By contrast, NSGA-II shows high effectiveness on some 2-objective and 3-objective instances, and NSGA-III shows promising performance on most 7-objective instances.

In Table 7, the comparison summary of MOEA-NAA and five methods on the WFG test problems is exhibited. The first two lines in the table indicate that comparison algorithm is better than, similar to, and worse than MOEA-NAA during the overall test function. The data of the last two rows indicate the number of optimal values obtained by each algorithm. It can be concluded that the performance of MOEA-NAA is better than all comparison algorithms and the most optimal value is received. Therefore, MOEA-NAA has promising versatility in the optimization of MOPs and MaOPs with various Pareto fronts.

Table 7 The comparison summary of NAA and five methods on the WFG test problems
Full size table

5 Conclusions and future work

To handle MOPs and MaOPs with various types of Pareto fronts, an enhanced reference vectors-based multi-objective evolutionary algorithm with neighborhood-based adaptive adjustment is presented, termed MOEA-NAA. It contains three main improvements, i.e., pioneer dynamic population strategy, multi-criteria environment selection mechanism and reference vector adaptive adjustment strategy based on neighborhood information. Pioneer dynamic population strategy improves the convergence. In the proposed adaptation method, the reference points are adapted on the basis of a predefined reference point set to approximate more accurate PFs. Due to allocate computing resources in discrete areas to potential areas, the waste of computing resources is reduced as much as possible. Moreover, multi-criteria selection mechanism guarantees the effectiveness of the algorithm on MaOPs. MOEA-NAA is compared with four classical algorithms, i.e., two classical MOEAs and two MaOEAs. Empirical results have demonstrated that the proposed MOEA-NAA outperforms other representative MOEAs on overall 36 test problems. Therefore, MOEA-NAA is a promising and versatile algorithm which can obtain the good performance of convergence and diversity.

It is worthy mentioning that the proposed MOEA-NAA is a promising algorithm for solving MOPs and MaOPs. Nevertheless, it is a hindrance when dealing with PFs with complicated mixed geometries (e.g., WFG1). Future work will focus on dealing with problems with more complex PF shapes or more than seven objectives.