1 Introduction

The natural stones as one of the efficient but oldest recognized materials provide many possibilities in different civil and construction applications (e.g., building industry, road base, paving, concrete, and asphalt). However, due to heterogeneity of these materials plethora and quite variable engineering characteristics can be observed.

Strength properties, durability, attractiveness (appearance and color), cost, economy and quarrying susceptibility are the primary common criteria in selecting the appropriate building stones. In specific applications, some other properties such as hardness, toughness, specific gravity, porosity and water absorption, dressing, seasoning, workability, fire, and chemical resistance also may need to be considered. Using laboratory tests suitability of stones for building purposes can be evaluated. However, many scholars indicated that laboratory tests for determining uniaxial compressive strength (UCS) and elasticity modulus (E) as two of the most important rock mechanical characteristics is a challenging task (e.g., [2, 11, 42]). Thereby, in practice prediction of UCS and E using statistical regression of simple, inexpensive and non-destructive tests are preferred and notified (e.g., [1, 2, 36, 42, 43, 45, 53]). However, such correlations due to inconsistency of various rock types have shown different degrees of success. Furthermore, the regression analyses among the variables do not imply causality [50], and the strong relationship between variables can be the result of the influence of other unmeasured parameters [46]. Therefore, to interpret predictive statistical model different incompetence (e.g. assumptions, subjective judgment of unobserved data, effect of auxiliary factors, uncertainty of experimental tests, inaccurate prediction in wide expanded range of data) should be considered [2, 4, 27, 29].

The demerits of statistical techniques in producing more efficient and accurate predictive models can be covered using different subcategories of soft computing approaches. The literature reviews highlighted that soft computing techniques such as artificial neural networks (e.g. [5, 35, 36]), support vector machine [6], random forest [38], genetic programming [7, 14], ANFIS [53, 57], Gene expression programming [15] and hybrid systems [11, 31] are able to predict more promising results for the UCS and E than the conventional statistical methods.

The support vector regression (SVR) [24] is a developed novel kind of supervised-learning support vector machine (SVM) for both classification and regression purposes that can map the inputs to an n-dimensional feature space. This model using nonlinear kernel functions simultaneously can maximize predictive accuracy and avoids overfitting [58]. Similar to SVM, the main idea in SVR is always minimizing the error and individualizing the hyperplane which maximizes the margin. However, using small subset of training points in SVR gives enormous computational advantages than SVM which does not depend on the dimensionality of the input space and thus provides excellent generalization capability, with high prediction accuracy [13]. This implies that the possible poor performance of ANNs (e.g. few labeled data points, trapping into local minimal, overfitting) can be treated using SVR to achieve more precise results [49].

In the recent years, different metaheuristic algorithms have been used for possible enhancement in the performance and predictability level of intelligence models (e.g. [8, 11, 61, 65]). Designing supervised learning systems generally is a multi-objective optimization problem [55] which aims to find appropriate trade-offs between several objectives in complex models. However, in practice it is advised to make the number of function evaluations as few as possible in finding an optimal solution [65]. Moreover, the value of design variables (objectives) are obtained by real or computational experiments, where the form of objective functions is not given explicitly in terms of objectives [66]. However, the time dependent (dynamic) multi-objective optimization due to relying on different moments is a very difficult task [40]. Therefore, in the current paper a hybridized multi-objective support vector regression (MSVR) incorporated to firefly metaheuristic algorithm (FMA) for prediction of UCS and E was developed.

The population based stochastic FMA is a swarm intelligence method inspired by the flashing behavior of fireflies [61]. This trial and error procedure efficiently and simultaneously can be applied for solving the hardest optimization problems to find both global and local optima [64]. The performance of hybrid MSVR-FMA was examined by different error criteria and then compared with MSVR. The models were run using 222 datasets of different building stones including rock class, density (γ), porosity (n), P-wave velocity (Vp), water absorption (w) and point load index (Is) from almost all over quarry locations of Iran. It was demonstrated that by applying the FMA, the success of correct classification rate for UCS and E from 81.2% and 79.5% were progressed to 88.6% and 84.1%, respectively. The comparison of different error criteria showed that MSVR-FMA as an accurate enough model can efficiently be applied to estimate the UCS and E. The main effective factors on predicted values were then recognized using different sensitivity analyses.

2 Mathematical configuration of MSVR

In classification, SVR is characterized by the use of kernels, sparse solution and control of the margin, and the number of support vectors. Hence, the output of SVR is found from the mapped support vectors through feature space and calculated weights using Lagrange multipliers and assigned biases (Fig. 1). As the output of SVR is a real number, thus in regression purposes a tolerance margin (ε) known as ε-insensitive loss function is set in the approximation [58]. This provides a symmetrically flexible tube of minimal radius around the estimated function in which the absolute values of errors less than a certain threshold are ignored both above and below the estimate. Consequently, the points outside the tube are penalized, but those within the tube, either above or below the function receive no penalty.

Fig. 1
figure 1

Processing procedure in MSVR structure using support vector algorithm

Full size image

Considering to dimensionality of input and output spaces (d and Q), the output vector (yi ∈ RQ) subjected to a given set of training input data {(xi, yi)}i=1, 2,…n (xi ∈ Rd) is derived from minimizing of:

$$L_{{\text{P}}} \left( {{\varvec{W}},{\varvec{b}}} \right) = L_{{\text{P}}} \left( {\left[ {w_{1} , \ldots ,w_{Q} } \right],{ }\left[ {b_{1} , \ldots ,b_{Q} } \right]} \right) = \underbrace {{\frac{1}{2}\mathop \sum \limits_{j = 1}^{Q} w_{j}^{2} }}_{{\text{structural risk }}} + C\mathop \sum \limits_{i = 1}^{n} \underbrace {{\overbrace {{L_{\upsilon } \left( {y_{i} - (\phi \left( {x_{i} } \right)^{T} + w_{j} + b_{j} } \right)_{\varepsilon } }}^{{L\left( {u_{i} } \right)}}}}_{{\text{empirical risk}}}$$
(1)
$$u_{i} = \sqrt {e_{i}^{T} e_{i} } ;\quad e_{i}^{{\text{T}}} = y_{i}^{{\text{T}}} - \phi^{{\text{T}}} \left( {x_{i} } \right){\varvec{W}} - {\varvec{b}}^{{\text{T}}}$$
(2)

where; Lp(W, b) is the Lagrangian optimization function. wj (W ∈ RQ×d) represents an m × m weighted matrix corresponds the model parameter and thus each wi ∈ Rd is the predictor for yi. The bj (b ∈ RQ; j = {1,…, Q}) and ek ∈ R denote the bias matrix term and error variables. The w and b can be obtained using the iterative reweighted trial error least squares procedure (IRWLS) to lead a matrix for each component that to be estimated [47, 48]. The term structure risk (regularization term) is used to control the smoothness or complexity of the function. The user specified constant C > 0 determines the trade-off between the empirical error and the amount up to deviations larger than ε [16]. The parameter ε should be tuned and is equivalent to the approximation accuracy in the training process and shows that the datasets in the range of [+ ε, − ε] do not contribute to the empirical error [13]. ϕ(·) is the feature space factor to provide nonlinear transformation to a higher dimension. The term L(ui) as the loss function using Taylor expansion is defined as:

$$\left| {y_{i} - f\left( {x_{i} } \right)} \right|_{\varepsilon } = \left\{ {\begin{array}{*{20}l} 0 \hfill & { \left| {y_{i} - f\left( {x_{i} } \right)} \right| \le \varepsilon } \hfill \\ {\left| {y_{i} - f\left( {x_{i} } \right)} \right| - \varepsilon } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(3)

On kth iteration (Wk and bk), optimizing problem and constructing the quadratic approximation is expressed by:

$$L_{P}^{\prime } \left( {{\varvec{W}},{\varvec{b}}} \right) = \frac{1}{2}\mathop \sum \limits_{j = 1}^{Q} w_{j}^{2} + C\left( {\left[ {\mathop \sum \limits_{i = 1}^{n} L\left( {u_{i}^{k} } \right) + \frac{{{\text{d}}L\left( u \right)}}{{{\text{d}}u}}} \right]_{{u_{i}^{k} }} \frac{{\left( {e_{i}^{k} } \right)^{T} }}{{u_{k}^{i} }}\left[ {e_{i} - e_{i}^{k} } \right]} \right)$$
(4)
$$L_{P}^{\prime \prime } \left( {{\varvec{W}},{\varvec{b}}} \right) = \frac{1}{2}\mathop \sum \limits_{j = 1}^{Q} w_{j}^{2} + C\left( {\left[ {\mathop \sum \limits_{i = 1}^{n} L\left( {u_{i}^{k} } \right) + \frac{{{\text{d}}L\left( u \right)}}{{{\text{d}}u}}} \right]_{{u_{i}^{k} }} \frac{{u_{i}^{2} - \left( {u_{i}^{k} } \right)^{2} }}{{2u_{k}^{i} }}} \right) = \frac{1}{2}\mathop \sum \limits_{j = 1}^{Q} w_{j}^{2} + \frac{1}{2}\mathop \sum \limits_{i = 1}^{n} a_{i} u_{i}^{2} + C\tau$$
(5)

where \(C\tau\) as a sum of constant term is independent either on W or b. Applying W = Wk and b = bk, provide theame value and gradient for LP (W, b) and L′P (W, b). Thereby, \(\nabla L_{{\text{P}}}^{\prime } \left( {{\varvec{W}}^{k} ,{\varvec{b}}^{k} } \right) = \nabla L_{{\text{P}}} \left( {{\varvec{W}}^{k} , {\varvec{b}}^{k} } \right) \cdot L_{{\text{P}}}^{\prime } \left( {{\varvec{W}}^{k} ,{\varvec{b}}^{k} } \right)\) is a lower bound of LP (W, b) where LP (W, b) > L′P (W, b). The \(a_{i}\), \(u_{i}^{k}\) and \((e_{i}^{k} )^{T}\) then can be calculated using:

$$a_{i} = \left. {\frac{C}{{u_{i}^{k} }}\frac{{{\text{d}}L\left( u \right)}}{{{\text{d}}u}}} \right|u_{i}^{k} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {u_{i}^{k} < \varepsilon } \hfill \\ {\frac{{2c\left( {u_{i}^{k} - \varepsilon } \right)}}{{u_{i}^{k} }}} \hfill & {u_{i}^{k} \ge \varepsilon } \hfill \\ \end{array} } \right.$$
(6)
$$u_{i}^{k} = e_{i}^{k} = \sqrt {(e_{i}^{k} )^{{\text{T}}} e_{i}^{k} } ;\quad (e_{i}^{k} )^{{\text{T}}} = y_{i}^{{\text{T}}} - \emptyset \left( {x_{i} } \right)^{{\text{T}}} {\varvec{W}}^{k} - \left( {{\varvec{b}}^{k} } \right)^{{\text{T}}}$$
(7)

Linear combination of the training datasets can provide the best solution for optimizing the learning problem within the inner product of feature space kernel [56]:

$$w_{j} = \mathop \sum \limits_{i = 1}^{n} \phi (x_{i} )\beta_{j} = \phi^{{\text{T}}} \beta_{j} ,\quad 0 \le \beta \le C$$
(8)
$$\left[ {\begin{array}{*{20}l} {K + D_{\alpha }^{ - 1} } \hfill & 1 \hfill \\ {a^{{\text{T}}} K} \hfill & {1^{{\text{T}}} a} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\beta_{j} } \\ {b_{j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {y_{j} } \\ {a^{{\text{T}}} y_{j} } \\ \end{array} } \right]$$
(9)
$$K \left( {x_{i} ,x_{j} } \right) = \exp \left( { - \frac{{x_{i} - x_{j}^{2} }}{{2\sigma^{2} }}} \right) = \exp \left( { - \gamma \left\| {x_{i} - x_{j}^{2} } \right\|} \right.\;{\text{and}}\;\gamma > 0$$
(10)

Where 1 = [1, 1, …, 1]T is an n dimensional column vector and a = [a1,…, an]T shows an identity matrix. (K)ij = k (xi, xj) is the kernel matrix of two vectors xi and xj that can be easily evaluated [23]. The ||·|| correspond the Euclidean norm for vectors and γ denotes the variance of the radial basis function (RBF) kernel which controls the sensitivity of the kernel function. βj is the parameter which should be computed by searching algorithm and depends on Lagrange multipliers. Hereby, the training datasets via the kernel function are moved into a higher dimension space where various kernel functions may produce different support vectors (Fig. 1). Therefore, the jth output of each new incoming vector x can be expressed as:

$$y_{j} = \phi^{{\text{T}}} \left( x \right){\Phi }^{{\text{T}}} \beta_{j} ,\;{\Phi } = \left[ {\phi (x_{1} ), \ldots ,\phi (x_{n} )} \right] \to y_{j} = \mathop \sum \limits_{i = 1}^{n} K\left( {x,x_{i} } \right)\beta_{i}^{j} + b^{j}$$
(11)

where yj = [y1j, …, ynj]T is the outputs. Consequently, the final output (y) is computed by:

$$y = \phi^{{\text{T}}} \left( x \right){\Phi }^{{\text{T}}} \beta = K_{x} \beta ,\;k\left( {x_{i} ,x_{j} } \right) = \phi^{{\text{T}}} \left( {x_{i} } \right)\phi (x_{j} )$$
(12)

where ϕ (xi) and ϕ (xj) are the projection of the xi and xj in feature space. The number of support vectors and biases are noted by n and bj respectively. Kx is a vector that contains the kernel of the input vector x and the training datasets. RBF kernel (Eq. 10) has shown more promising results compared than other proposed kernels [33].

3 Firefly metaheuristic algorithm (FMA)

The FMA as a swarm intelligence population-based algorithm inspired by flashing behavior of fireflies [61] effectively can be applied to solve the hardest global and local optimization problems [64]. During the recent years the applicability of this algorithm has been modified. Gao et al. [25] improved this algorithm using particle filter and presented a powerful tool in solving visual tracking problems. Sayadi et al. [52] developed a powerful version of discrete FMA to deal with non-deterministic polynomial-time scheduling problems. An efficient binary coded FMA to investigate the network reliability was proposed by Chandrasekaran and Simon [17]. Coelho et al. [21] proposed a chaotic FMA that outperformed other algorithms [22]. The studies of Yang [62] on this version of FMA showed that under different ranges of parameter, an enhanced performance using tuning can be achieved. The Lagrangian FMA is another proposed variant [51] for solving the unit commitment problem for a power system. An interesting multi-objective discrete FMA version or the economic emission load dispatch problem was proposed by Apostolopoulos and Vlacho [9]. Meanwhile, Arsuaga-Rios and Vega-Rodriguez [10] independently proposed another multi-objective FMA tool for minimizing energy consumption in grid computing. This version further was developed to solve multi-objective production scheduling systems [34]. Furthermore, a discrete variant of FMA for the multi-objective hybrid problems [37], an extended FMA for converting the single objective to multi-objective optimization in continuous design problems [63], and an enhanced multi-objective FMA in complex networks [8] were also presented.

As presented in Fig. 2, the primary concept for a firefly's flash is based on signal system to attract other fireflies which can be figured out using brightness (I), attractiveness (β) of fireflies i and j in the adjacent distance (rij), absorption coefficient (γ) and tradeoff constant to determine the random behavior of movement (α). The fireflies in this system subjected to trial–error procedure tend to move towards the brighter one and aim to find a new solution using the updated distance between two considered fireflies.

Fig. 2
figure 2

The configuration of FMA and corresponding applied parameters

Full size image

The I of each firefly represents the solution, s, as a proportion of the objective function [I(s) ∝ f(s)]. The β is also proportional to the intensity of visible light for adjacent fireflies in each distance coordinate, I(r), as:

$$I\left( r \right) = I_{0} e^{{ - \gamma r^{2} }}$$
(13)
$$\beta = \beta_{0} e^{{ - \gamma r^{2} }}$$
(14)

The distance between any two si and sj or i and j fireflies in an n-dimensional problem is expressed as the Euclidean or the Cartesian distance by:

$$r_{ij} = s_{i} - s_{j} = \sqrt {\mathop \sum \limits_{k = 1}^{n} \left( {s_{ik} - s_{jk} } \right)^{2} }$$
(15)

where I0 denotes the light intensity of the source. γ is the absorption coefficient with a decisive impact on the convergence speed that can theoretically capture any value from interval γ ∈ [0, ∞) but in most optimizing problems typically varies within [0.1–10]. β0 is the attractiveness at rij = 0.

In each iteration of FMA, the fitness function (FT) of the optimal solution of each firefly will own its brightness. Therefore, searching for better FT corresponding to higher brightness level produces new solutions. This embedded iterative process will renew several times comparing to previous results, and only one new solution based on FT is kept. This iterative process can be expressed as:

$$s_{i}^{{{\text{new}}}} = s_{i}^{t} + \beta_{0} e^{{ - \gamma r_{ij}^{2} }} \left( {s_{j} - s_{i} } \right) + \alpha_{{\text{t}}} \left( {{\text{rand}} - 0.5} \right)$$
(16)

where αt denotes the tradeoff constant to determine the random behavior of movement and varies in [0, 1] interval. The rand function as a random number of solutions I and β0 at zero distance is normally set to 1. sj is a solution with lower FT than si and (sj − si) represents the updated step size.

Considering to variation of γ within [0, ∞) interval, when γ → 0 then β0 = β that express the standard particle swarm optimization (PSO). In the situation that γ → ∞, the second term falls out from Eq. (16) which not only indicate random walk movement but also is essentially a parallel version of simulated annealing. Consequently, the FMA generally is controlled by three parameters γ, β, and α where in β0 = 0, the movement is a simple random walk.

Depending on compared FT, the new solution (one or more than one or no new solution) between firefly i and other fireflies in the current population is described with:

$$s_{i}^{{{\text{new}}}} = \left\{ {\begin{array}{*{20}l} {s_{i} } \hfill & {s_{i} = s_{{{\text{best}}}} } \hfill \\ {s_{i}^{{{\text{new}}}} } \hfill & {s_{j} = s_{{{\text{best}}}} } \hfill \\ {s_{ij}^{{{\text{new}}}} {\text{ with FT}}_{{{\text{best}}}} } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(17)

Therefore, if the considered solution i is also the global best solution, no new solution will be generated. If the best global solution in the population (n) belongs to firefly j, then only one new solution \(s_{{\text{i}}}^{{{\text{new}}}}\) is achieved, else, at least two better solutions than si in n − 1 is available where the lowest FT (FTbest) is retained and others are discarded.

4 Acquired database

A database including 222 sets of rock class, density (γ), porosity (n), P-wave velocity (Vp), water absorption (w) and point load index (Is) from 49 different quarry locations in Iran was assembled (Tables 1 and 2). The statistically analyzed datasets as well as calculated 95% confidence intervals of mean and median of provided datasets are presented in Table 3 and Fig. 3. According to suggested classification by the International society of rock mechanics [30], the majority of compiled datasets fall in the medium to high strength categories (Table 4). The components of processed database due to different units were then normalized within the range of [0, 1] to produce dimensionless sets and improve the learning speed and model stability. These sets further were randomized into training (55%), testing (25%) and validation (20%). The rock classes including sedimentary, igneous, digenetic and metamorphic were coded from 1 to 4, respectively.

Table 1 Specification of acquired datasets
Full size table
Table 2 Sample of compiled datasets
Full size table
Table 3 Descriptive statistics of acquired datasets
Full size table
Fig. 3.
figure 3

95% confidence intervals of mean and median for the employed variables

Full size image
Table 4 Strength classification based on ISRM [30] for provided database
Full size table

5 Hybridized MSVR and system results

The structure of MSVR is developed through the input, intermediate and output layers subjected to a series of training experiments. As presented in Fig. 4, the MSVR was trained using iterative reweighted trial error least squares procedure (IRWLS) [47, 48]. Weighting is based on the output of the true objective function and thus the reweighting scheme is considered as a feedback control. The accuracy of MSVR output depends on the appropriate regularized C, ε as well as γ and σ (Min and Lee [39], but no unified procedure for estimating these parameters are accepted. To tune the optimum C and γ, numerous combinations of these parameters with step sizes of 20.2 and 20.1 over log2 using the LIBSVM code in Matlab (Chang and Lin [18] were examined. The FT of optimum parameters in the training process then was evaluated using separate validation datasets or cross-validation technique [19, 32] using:

$$f\left( m \right) = {\text{RMSE}}_{{\text{training data}}}^{{{\text{opimization}}}} + {\text{RMSE}}_{{\text{validation data}}}^{{{\text{optimization}}}}$$
(18)

where RMSE expresses the root mean square error.

Fig. 4
figure 4

Flowchart of model construction and assessing the optimized structure

Full size image

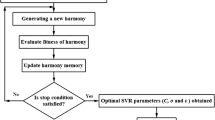
Due to ability of the FMA in control the parameters for effective balancing [20], it was applied to improve the quality of the initial population and optimizing the C and σ. Refer to Fig. 4, the main loop of FMA is controlled by the maximum number of generations (Max Gen). This loop using a gen-counter parameter (t), calculates the new values for the randomization parameter (α) through the functions Δ = 1–10−4/0.91/Max Gen and α(t+1) = 1 − Δ. α(t). Δ determines the step size of changing parameter α(t+1) and is descended with the increasing of t. Then, the new solution si(t) is evaluated based on a fitness function f(s(t)). With respect to the fitness function, f(si(t)) is ordered ascending the solutions si(t) for n populations, where si(t) = S(xi(t)) and thus the best solution s* = s0(t) is determined in the population P(t). The FMA parameters (n, α, β0, γ) were obtained considering variations in the weight results, meanwhile, one was tested the other one was fixed. The number of fireflies was obtained according to the convergence history of the iteration process. Tables 5 and 6 summarize the information about initial, final values and rate of variation in each parameter as well as a sample of series efforts in parametric analyzing. The number of iteration and corresponding fireflies were found through the convergence history of different populations (Fig. 5). The results showed that 1000, 30, 1, 0.2, 0.05, 0.2 and 0.5 corresponding to the number of iterations, number of fireflies, γ, β, Δ, α and β0 can be selected as the most appropriate tuned parameters in FMA.

Table 5 Adjusting the FMA parameters
Full size table
Table 6 A brief result of analyzing process to tune FMA parameters
Full size table
Fig. 5
figure 5

Convergence history subjected to different firefly populations

Full size image

In this study, for a stable learning process and reduce the computational effort the MSVR was managed using a quadratic loss function with the value of 0.1 and RBF kernel function subjected to tenfold cross-validation. In the cross-validation method (Fig. 6), the entire training dataset is randomly split into roughly equal subset folds. For K times, each of the folds can be chosen for test data and the remaining is used as training sets. The errors should be less than ε and any deviation larger than this is not accepted. As reflected in Table 7, the optimum values for C and γ were then selected from the lowest error and highest correlation coefficient (R2) in tenfold cross-validation. Accordingly, the performance of the hybridized MSVR-FMA using adjusted parameters comparing to measured values was checked and presented in Fig. 7.

Fig. 6
figure 6

K-fold cross-validation using split randomized dataset

Full size image
Table 7 Determining the optimal parameters of MSVR in tenfold cross-validation procedure
Full size table
Fig. 7
figure 7

Predictability level of optimum and hybridized MSVR in training stage for E (a, c) and UCS (b, d)

Full size image

6 Validation and discussion

The correct classification rate (CCR) is a leading assessment metric in discriminant analysis. This criterion can be extracted from the confusion matrix [54] as an unambiguous table layout method to present the predictability of machine learning classifier. Referring to conducted confusion matrix (Table 8), the calculated correct classification rate (CCR) showed 10.27% and 5.47% improvement in predictability of UCS and E using hybrid MSVR-FMA (Table 9). These results reflect the significant influence of incorporated FMA on the accuracy progress of prediction process.

Table 8 Confusion matrix of applied models using validation datasets
Full size table
Table 9 CCR of optimized models for validation and test datasets
Full size table

The area under the curve (AUC) of receiver operating characteristic (ROC) is one of the most important graphical metrics in performance and diagnostic ability of a classifier system. ROC is a probability curve that summarizes the trade-off between the true and false positive rates (TPR and FPR) for a predictive model at various threshold settings while AUC represents the degree of separability. Therefore, AUCROC expresses the capability and strength of the model in distinguishing classes (Fig. 8a). In machine learning, precision shows the capability of a classification model in identifying only the relevant data points, while recall monitors all the related cases within a dataset. An optimal combination of precision and recall can be interpreted using F1-score as:

$$F_{1} = 2 \times \frac{{{\text{precision}} \times {\text{recall}}}}{{{\text{precision}} + {\text{recall}}}}$$
(19)
Fig. 8
figure 8

Analyzed performance of MSVR and hybrid MSVR-FMA using AUCROC (a) and F1-score criteria (b)

Full size image

This criterion expresses a harmonic mean that can be used instead of a simple average. It avoids extreme values and thus is used in imbalanced classes when the false negatives and false positives are crucial [28]. High precision and low recall express extremely accurate model, but it misses a significant number of instances that are difficult to classify. In optimal recall and precision values, the F1-score of a balanced classification model tends to be maximize. This situation reflects veracity (correctly classified data) and robustness (not miss significant instances) of the classifier. In optimizing of the classifier to increase one and disfavor the other, the harmonic mean shows quick decreasing when both precision and recall are equal (Fig. 8b).

The performance of the presented models and forecasted outputs were also pursued using statistical error indices as reflected in Table 10. The formulation of these indices can widely be found in statistical textbooks. The MAPE is one of the most popular indexes for description of accuracy and size of the forecasting error. The MAD reflects the size of error in the same units as the data, and reveals that high predicted values cause higher error rates. The generic IA [60] indicates the compatibility of modeled and observations. The VAF as an intrinsically connected index between predicted and actual values is a representative of model performance. Therefore, higher values of VAF, IA and R2 as well as smaller values of MAPE, MAD and RMSE are interoperated as better model performance (Table 10).

Table 10 Comparison of statistical criteria to evaluate the MSVR and MVR models for all used datasets
Full size table

Sensitivity analyses cab express the influence of input parameters on predictability level and provide robust calibrated models in the presence of uncertainty [12]. This implies that removing the least effective inputs may lead to better results. The importance of input variables using the cosine amplitude (CAM) and partial derivative (PaD) [26] are calculated as:

$${\text{CAM}}_{ij} = \frac{{\mathop \sum \nolimits_{k = 1}^{m} \left( {x_{ik} \times x_{jk} } \right)}}{{\sqrt {\mathop \sum \nolimits_{k = 1}^{m} x_{ik}^{2} \mathop \sum \nolimits_{k = 1}^{m} x_{jk}^{2} } }};\quad {\text{PaD}}_{i} = \frac{{\mathop \sum \nolimits_{p} \left( {\frac{{\partial O_{p}^{k} }}{{\partial x_{i}^{p} }}} \right)^{2} }}{{\mathop \sum \nolimits_{i} \mathop \sum \nolimits_{p} \left( {\frac{{\partial O_{p}^{k} }}{{\partial x_{i}^{p} }}} \right)^{2} }}$$
(20)

where CAMij and PaDi express the importance (contribution) of ith variable. xi and xj denote elements of data pairs. Okp and xip are output and input values for pattern P, and SSDi is the sum of the squares of the partial derivatives respectively.

The results of CAM and PaD (Fig. 9) showed that Is, Vp and n are the main effective factors on predicted UCS and E, while the rock class and γ expressed the least influences.

Fig. 9
figure 9

Influence of input parameters on predicted UCS and E using different sensitivity analyses

Full size image

7 Conclusion

Due to the heterogeneity of rocks and dependency of strength parameters (UCS and E) to different physical and mechanical properties, conducting reliable and accurate predictive models is great of interest. In this paper, a new MSVR using 222 datasets of rock class, density (γ), porosity (n), P-wave velocity (Vp), water absorption (w) and point load index (Is) for a wide variety of quarried rocks in Iran was developed. To enhance the progress and improve the efficiency, the MSVR successfully was hybridized with FMA. The results showed that by applying the FMA, the characterized internal properties of MSVR were optimized. Hybridizing procedure revealed that the CCR for UCS from 81.2% was promoted to 88.6% in MSVR-FMA. Similarly, for E this criterion was updated from 79.5 to 84.1%. These values indicate for 8.35% and 5.47% improvement in predictability level of UCS and E in MSVR-FMA. Investigating the robustness of models using AUCROC, F1-score exhibited superior performance in MSVR-FMA (85.1%) than MSVR (82.9%). The figured out accuracy performance of both classifiers using statistical error indices represented higher reliability in MSVR-FMA. According to evaluated criteria, 21.35% and 16.36% improvements in RMSE for UCS and E subjected to hybrid model was observed. Correspondingly, progress of 3.1% (UCS) and 4.16% (E) in MSVR-FMA was raised. Calculated IA showed that the MSVR-FMA with 5.54% and 6.82% progress for UCS and E is more compatible than MSVR. The implemented sensitivity analyses showed that Is, Vp and n are the most effective factors on both UCS and E. This ranking can be interpreted with previous empirical correlations which mostly have been established by these three factors. The accuracy level of predicted outputs approved that the hybrid MSVR-FMA can efficiently utilizes a promising and superior alternative for the purpose of rock strength predictions in designing of construction projects.