1 Introduction

The rapid development of the mobile Internet of Things (IoT) has led to increased interest in mobile communication systems [1,2,3,4,5]. A novel mobile front haul architecture was proposed in [6] for passive optical mobile networks. In [7], a two-dimensional anti-jamming mobile communication scheme was proposed which employs reinforcement learning techniques.

As a promising technology for mobile IoT, cooperative diversity has gain popularity in recent years [8, 9]. [10] investigated the secrecy outage performance of a multiple-relay-assisted non-orthogonal multiple access (NOMA) network over Nakagami-m fading channels. Considering MIMO-NOMA systems, [11] proposed a max–min transmit antenna selection (TAS) strategy to improve the secrecy performance. Cooperative two-way cognitive relaying was used in [12] to reduce the influence of a passive eavesdropper. Full-duplex cooperative communications were considered to provide secure communications [13]. Cooperative device-to-device communications were proposed in [14] to reduce cellular resource consumption.

To date, the research on cooperative communications has been limited to Rayleigh, Rician, and Generalized-K fading channels. However, the fading in mobile cooperative communications systems is more complex and so cannot be accurately characterized by these channels [15,16,17,18]. In [19, 20], the secrecy performance of mobile cooperative networks was analyzed over 2-Rayleigh fading channels. Mobile cooperative systems over N-Rayleigh fading channels were examined in [21]. Vehicle-to-vehicle (V2V) communications over 2-Rayleigh fading channels was investigated in [22]. In [23], the secrecy outage probability (SOP) performance of wireless mobile sensor communication networks over 2-Nakagami fading channels was investigated.

In [24,25,26], N-Nakagami fading was considered to provide a realistic mobile channel model. N-Nakagami fading channels contain N-Rayleigh, 2-Rayleigh, Nakagami-m, and their mixtures as special cases. In particular, N-Nakagami fading is better suited to practical mobile communication environments than N-Rayleigh and 2-Rayleigh fading channels. Thus, N-Nakagami fading channels are considered here for the evaluation of mobile communication systems.

Due to the complexity of mobile IoT over N-Nakagami fading channels, secure communications is complicated. To ensure secure communications, performance changes in mobile IoT must be predicted accurately and timely. The average bit error probability (ABEP) is an important measure of mobile communication system performance, and it is important to predict the ABEP performance of mobile IoT. Because of good nonlinear prediction ability, back-propagation (BP) neural network models are very popular in engineering applications [27,28,29]. For complex environments such as mobile IoT, a BP neural network model is very suitable for performance prediction. To predict telecommunication customer churn, [30] used a particle classification method to optimize the BP network. Using BP neural network, [31] proposed a blind signal detection method. Weight splitting was used to improve the filtering performance of BP neural networks in [32].

However, with incremental amplify-and-forward (IAF) relaying, the ABEP performance of mobile cooperative communication systems has not previously been investigated. Further, ABEP performance prediction for mobile communication systems has not been considered. The main contributions of this paper are as follows.

  1. 1.

    The direct link signal-to-noise ratio (SNR) and end-to-end link SNR are derived. The probability density function (PDF) of these SNRs is derived, and the PDF is used to derive cumulative distribution function (CDF) expressions.

  2. 2.

    The PDF and CDF expressions are used to derive exact closed-form ABEP expressions. To verify the analysis, Monte-Carlo simulation results are compared with the theoretical ABEP. The impact of fading and other parameters on the ABEP is examined.

  3. 3.

    A BP neural network-based ABEP performance prediction algorithm is proposed. The ABEP theoretical results are used to generate training data. We test the extreme learning machine (ELM), linear regression (LR), support vector machines (SVM), and BP neural network methods. Compared to LR, SVM, and ELM methods, the experimental results verify that our method can consistently achieve higher ABEP performance prediction results.

This remainder of this paper is organized as follows. Section 2 presents the system model. The PDF and CDF for direct link SNR and end-to-end link SNR are obtained in Sects. 3 and 4, respectively. The ABEP is derived in Sect. 5. Based on a BP neural network, we propose a ABEP performance prediction algorithm in Sect. 6. The ABEP performance is evaluated and compared with the simulation results in Sect. 7 and Sect. 8 gives some concluding remarks.

2 System model

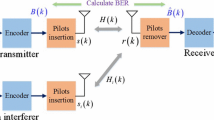
Figure 1 presents the mobile cooperative communication system model. This model includes a mobile source (MS) node and a mobile relay (MR) node that communicates with the mobile destination (MD) node. GSD = 1 is the relative gain of the MS → MD link, GSR is the relative gain of the MS → MR link, and GRD is the relative gain of the MR → MD link. The channel coefficient h = hg, g∈{SR,RD,SD}, follows an N-Nakagami distribution [24].

Fig. 1
figure 1

The system model

Full size image

The total energy in the system is denoted by E. In the first time slot, MS transmits a signal x, which has mean 0 and variance 1. MR and MD receive the signals

$$r_{\text{SD}} = \sqrt {KE} h_{\text{SD}} x + n_{\text{SD}} ,$$
(1)
$$r_{\text{SR}} = \sqrt {G_{\text{SR}} KE} h_{\text{SR}} x + n_{\text{SR}} ,$$
(2)

where nSD and nSR have mean 0 and variance N0/2 and K is the power allocation parameter, 0 < K ≤ 1.

The SNR of the MS → MD link is γSD. Whether MR forwards the signal to MD or not depends on the comparison between γSD and a threshold Rt. If γSD > Rt, the MR will not forward the signal to MD. In this case, the SNR at MD is

$$\gamma_{0} = \gamma_{\text{SD}} ,$$
(3)

where

$$\gamma_{\text{SD}} = \frac{{K\left| {h_{\text{SD}} } \right|^{2} E}}{{N_{0} }} = K\left| {h_{\text{SD}} } \right|^{2} \overline{\gamma } .$$
(4)

If γSD < Rt, the MR uses AF relaying. Then MD receives the signal

$$r_{\text{RD}} = \sqrt {cE} h_{\text{SR}} h_{\text{RD}} x + n_{\text{RD}}$$
(5)

where nRD has mean 0 and variance and N0/2 and c is given by [33]

$$c = \frac{{K(1 - K)G_{\text{SR}} G_{\text{RD}} E/N_{0} }}{{1 + KG_{\text{SR}} \left| {h_{\text{SR}} } \right|^{2} E/N_{0} + (1 - K)G_{\text{RD}} \left| {h_{\text{RD}} } \right|^{2} E/N_{0} }}.$$
(6)

The received SNR at MD is then

$$\gamma_{\text{SC}} = \hbox{max} (\gamma_{\text{SD}} ,\gamma_{\text{SRD}} ),$$
(7)

where the end-to-end link SNR is γSRD, which is given by

$$\gamma_{\text{SRD}} = \frac{{\gamma_{\text{SR}} \gamma_{\text{RD}} }}{{1 + \gamma_{\text{SR}} + \gamma_{\text{RD}} }},$$
(8)
$$\gamma_{\text{SR}} = \frac{{G_{\text{SR}} K\left| {h_{\text{SR}} } \right|^{2} E}}{{N_{0} }} = G_{\text{SR}} K\left| {h_{\text{SR}} } \right|^{2} \bar{\gamma },$$
(9)
$$\gamma_{\text{RD}} = \frac{{(1 - K)G_{\text{RD}} \left| {h_{\text{RD}} } \right|^{2} E}}{{N_{0} }} = (1 - K)G_{\text{RD}} \left| {h_{\text{RD}} } \right|^{2} \bar{\gamma }.$$
(10)

For an N-Nakagami distribution, h is given by [24]

$$h = \prod\limits_{{i = 1}}^{N} {a_{i} },$$
(11)

where ai is a Nakagami random variable with PDF

$$f(a) = \frac{{2m^{m} }}{{\Omega ^{m} \Gamma (m)}}a^{{2m - 1}} \exp \left( { - \frac{m}{\Omega }a^{2} } \right).$$
(12)

The PDF of h can be expressed as

$$f(h) = \frac{2}{{h\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{0,N}^{N,0} \left[ {h^{2} \prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {\overline{{m_{1} }} , \ldots ,m_{N} } \right.} \right].$$
(13)

Define y = |hg|2 which has CDF and PDF

$$F(y) = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{1,N + 1}^{N,1} \left[ {y\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right].$$
(14)
$$f(y) = \frac{1}{{y\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{0,N}^{N,0} \left[ {y\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {\overline{{m_{1} }} , \ldots ,m_{N} } \right.} \right].$$
(15)

3 PDF and CDF of the direct link SNR

The CDF of the direct link SNR γSD is

$$F_{{\gamma_{\text{SD}} }} (r) = \frac{1}{{\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right],$$
(16)

where

$$\overline{{\gamma_{\text{SD}} }} = K\overline{\gamma } ,$$
(17)

and the corresponding PDF is

$$f_{{\gamma_{\text{SD}} }} (r) = \frac{1}{{r\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} }}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right].$$
(18)

4 PDF and CDF of the end-to-end link SNR

From (8), the exact PDF and CDF of γSRD are intractable to obtain. Thus, the method in [18] is employed to approximate γSRD as

$$\gamma_{\text{e}} = \frac{{\gamma_{\text{SR}} \gamma_{\text{RD}} }}{{\gamma_{\text{SR}} + \gamma_{\text{RD}} }} = \frac{1}{2}\frac{2}{{\frac{1}{{\gamma_{\text{SR}} }} + \frac{1}{{\gamma_{\text{RD}} }}}}.$$
(19)

From [34], we obtain that

$$\gamma_{\text{e}} < \gamma_{\text{up}} = \hbox{min} (\gamma_{\text{SR}} ,\gamma_{\text{RD}} ),$$
(20)

so, the CDF is lower bounded as

$$F_{{\gamma_{\text{SRD}} }} (r) > F_{{\gamma_{\text{up}} }} (r).$$
(21)

The CDF of γup is

$$\begin{aligned} F_{{\gamma_{\text{up}} }} (r) & = 1 - \left( {1 - \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]} \right) \\ & \quad \times \left( {1 - \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]} \right) \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \\ & & \quad + \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \\ & & \quad - \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\limits_{tt = 1}^{N} {\varGamma (m_{tt} )} } }}G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \\ & & \quad \times G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \\ \end{aligned}$$
(22)

and the corresponding PDF is

$$\begin{aligned} f_{{\gamma_{\text{up}} }} (r) & = \frac{1}{{r\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right] \\ & \quad + \frac{1}{{r\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right] - \frac{1}{{r\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\limits_{tt = 1}^{N} {\varGamma (m_{tt} )} }} \\ & \quad \times \left( \begin{aligned} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \hfill \\ + G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}\left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} } \right]G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right] \hfill \\ \end{aligned} \right). \\ \end{aligned}$$
(23)

5 ABEP performance

The ABEP can be expressed as [35]

$$P({\text{e}}) = \Pr (\gamma_{\text{SD}} < R{\text{t}}) \times P_{\text{div}} ({\text{e}}) + \Pr (\gamma_{\text{SD}} \ge R{\text{t}}) \times P_{\text{direct}} ({\text{e}}),$$
(24)

where the error probability of MD is Pdiv(e), when MR forwards the signal to MD and Pdirect(e) is the corresponding error probability given that the MR does not forward the signal to MD. We have

$$\begin{aligned} \Pr (\gamma_{SD} < Rt) & = F_{{\gamma_{SD} }} (Rt) \\ & = \frac{1}{{\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{Rt}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}\left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} } \right], \\ \end{aligned}$$
(25)
$$\begin{aligned} \Pr (\gamma_{\text{SD}} \ge R{\text{t}}) & = 1 - \Pr (\gamma_{\text{SD}} < R{\text{t}}) \\ & = 1 - \frac{1}{{\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{{R{\text{t}}}}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right], \\ \end{aligned}$$
(26)

and

$$P_{\text{direct}} ({\text{e}}) = \int_{0}^{\infty } {P_{\text{direct}} ({\text{e}}\left| r \right.)} f_{{\gamma_{\text{SD}} }} (r\left| {\gamma_{\text{SD}} \ge R{\text{t}})dr} \right.,$$
(27)

where

$$P_{\text{direct}} ({\text{e}}\left| r \right.) = a \times {\text{erfc}}(\sqrt {br} ).$$
(28)

The type of modulation decides the constants a and b, e.g., a = 0.5 and b = 1 for BPSK, and a = 0.5 and b = 0.5 for QPSK. Further

$$\begin{aligned} f_{{\gamma_{\text{SD}} }} (r\left| {\gamma_{\text{SD}} \ge R{\text{t}})} \right. & = \left\{ {\begin{array}{*{20}l} {0,\begin{array}{*{20}l} {} & {r \le R{\text{t}}} \\ \end{array} } \\ {\frac{{\frac{1}{{r\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} }}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]}}{{1 - \frac{1}{{\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{{R{\text{t}}}}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]}}} \\ \end{array} ,\quad r > R{\text{t}}} \right. \\ & = \left\{ {\begin{array}{*{20}l} {0,\begin{array}{*{20}l} {} & {r \le R{\text{t}}} \\ \end{array} } \\ {\frac{{\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]}}{{\prod\limits_{i = 1}^{N} {\varGamma (m_{i} )} - G_{1,N + 1}^{N,1} \left[ {\frac{{R{\text{t}}}}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]}}} \\ \end{array} ,\quad r > R{\text{t}}} \right.. \\ \end{aligned}$$
(29)

Combining (28) and (29), we obtain

$$\begin{aligned} P_{\text{direct}} ({\text{e}}) & = \frac{a}{{\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} - G_{1,N + 1}^{N,1} \left[ {\frac{{R{\text{t}}}}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]}} \times \int_{Rt}^{\infty } {{\text{erfc}}(\sqrt {br} )} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{a}{{\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} - G_{1,N + 1}^{N,1} \left[ {\frac{{R{\text{t}}}}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]}} \times \left[ \begin{aligned} \int_{0}^{\infty } {{\text{erfc}}(\sqrt {br} )} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r - \hfill \\ \int_{0}^{Rt} {{\text{erfc}}(\sqrt {br} )} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \hfill \\ \end{aligned} \right] \\ & = \frac{a}{{\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} - G_{1,N + 1}^{N,1} \left[ {\frac{{R{\text{t}}}}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]}}\left[ {V_{1} - V_{2} } \right], \\ \end{aligned}$$
(30)

where

$$\begin{aligned} V_{1} & = \int_{0}^{\infty } {erfc(\sqrt {br} )} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{1}{\sqrt \pi }\int_{0}^{\infty } {r^{ - 1} G_{1,2}^{2,0} \left( {br\left| {_{{0,\frac{1}{2}}}^{1} } \right.} \right)} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r. \\ \end{aligned}$$
(31)

Using the results in [36], we obtain

$$V_{1} = \frac{1}{{\sqrt {\uppi } \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} }}G_{2,N + 1}^{N,2} \left[ {\frac{1}{{b\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{{1,\frac{1}{2}}} } \right.} \right].$$
(32)

Further, V2 is given by

$$\begin{aligned} v_{2} = \int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} {\text{d}}r \hfill \\ = \frac{1}{{\sqrt {\uppi } }}\int_{0}^{{R{\text{t}}}} {r^{ - 1} G_{1,2}^{2,0} \left( {br\left| {_{{0,\frac{1}{2}}}^{1} } \right.} \right)G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} {\text{d}}r. \hfill \\ \end{aligned}$$
(33)

A closed-form solution to (33) is difficult to obtain. Thus, using Meijer’s G-function [37]

$$\begin{aligned} G_{p,q}^{m,n} \left[ {z\left| {_{{b_{1} , \ldots ,b_{q} }}^{{a_{1, \ldots ,} a_{p} }} } \right.} \right] & = \sum\limits_{h = 1}^{m} {\frac{{\prod\nolimits_{i = 1}^{m} {\varGamma (b_{i} - b_{h} )\prod\nolimits_{i = 1}^{n} {\varGamma (1 + b_{h} - a_{i} )} } }}{{\prod\nolimits_{i = n + 1}^{p} {\varGamma (a_{i} - b_{h} )\prod\nolimits_{i = m + 1}^{q} {\varGamma (1 + b_{h} - b_{i} )} } }}z^{{b_{h} }} } \\ & \quad \times {}_{p}F_{q - 1} \left( {1 + b_{h} - a_{1} , \ldots ,1 + b_{h} - a_{p} ;1 + b_{h} - b_{1} , \ldots ,1 + b_{h} - b_{q} ;( - 1)^{p - m - n} z} \right). \\ \end{aligned}$$
(34)
$${}_{p}F_{q} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{p} ;\beta_{1} ,\beta_{2} , \ldots ,\beta_{q} ;z) = \sum\limits_{k = 0}^{\infty } {\frac{{(\alpha_{1} )_{k} (\alpha_{2} )_{k} \cdots (\alpha_{p} )_{k} }}{{(\beta_{1} )_{k} (\beta_{2} )_{k} \cdots (\beta_{q} )_{k} }}} \frac{{z^{k} }}{k!}.$$
(35)
$$(x)_{k} = \prod\limits_{t = 0}^{k - 1} {(x + t),} (x)_{0} = 1,$$
(36)

which gives

$$\begin{aligned} G_{1,2}^{2,0} \left[ {br\left| {_{{0,\frac{1}{2}}}^{1} } \right.} \right] & = \varGamma (1/2){}_{1}F_{1} \left( {0;1,\frac{1}{2}; - br} \right) \\ & + \frac{\varGamma ( - 1/2)}{\varGamma (1/2)}(br)^{{\frac{1}{2}}} {}_{1}F_{1} \left( {\frac{1}{2};\frac{3}{2},1; - br} \right) = \sqrt \pi \\ & + \frac{\varGamma ( - 1/2)}{\sqrt \pi }\sum\limits_{k = 0}^{\infty } {\frac{{(1/2)_{k} ( - 1)^{k} (b)^{{k + \frac{1}{2}}} }}{{(3/2)_{k} k!}}} r^{{k + \frac{1}{2}}} \\ \end{aligned}$$
(37)

so that

$$\begin{aligned} V_{2} & = \int_{0}^{{R{\text{t}}}} {r^{ - 1} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {\overline{{m_{1} }} , \ldots ,m_{N} } \right.} \right]} {\text{d}}r \\ & \quad + \frac{\varGamma ( - 1/2)}{{{\uppi }}}\sum\limits_{k = 0}^{\infty } {\frac{{(1/2)_{k} ( - 1)^{k} (b)^{{k + \frac{1}{2}}} }}{{(3/2)_{k} (k!)^{2} }}} \int_{0}^{{R{\text{t}}}} {r^{{k - \frac{1}{2}}} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {\overline{{m_{1} }} , \ldots ,m_{N} } \right.} \right]} {\text{d}}r \\ & = G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] + A\sum\limits_{k = 0}^{\infty } B G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - k - \frac{1}{2}}}^{{\frac{1}{2} - k}} } \right.} \right]. \\ \end{aligned}$$
(38)
$$A = \frac{\varGamma ( - 1/2)}{\pi },\quad B = \frac{{(1/2)_{k} ( - 1)^{k} (b)^{{k + \frac{1}{2}}} }}{{(3/2)_{k} (k!)^{2} }}.$$
(39)

We have

$$P_{\text{div}} (e) = a\int_{0}^{\infty } {{\text{erfc}}\left( {\sqrt {br} } \right)} f_{{\gamma_{\text{SC}} }} \left( {r|\gamma_{\text{SD}} < R{\text{t}}} \right){\text{d}}r,$$
(40)

where

$$f_{{\gamma_{\text{SC}} }} (r\left| {\gamma_{\text{SD}} < R{\text{t}}) = } \right.\left\{ {\begin{array}{ll} {\frac{1}{{F_{{\gamma_{\text{SD}} }} (R{\text{t}})}}\left( {f_{{\gamma_{\text{SD}} }} (r)F_{{\gamma_{\text{up}} }} (r) + F_{{\gamma_{\text{SD}} }} (r)f_{{\gamma_{\text{up}} }} (r)} \right),r \le R{\text{t}}} \\ {f_{{\gamma_{\text{up}} }} (r),\begin{array}{*{20}l} {} & {} \\ \end{array} r > R{\text{t}}} \\ \end{array} } \right..$$
(41)

Combining (32) and (33) gives

$$P_{\text{div}} ({\text{e}}) = a\left[ {\frac{1}{{F_{{\gamma_{\text{SD}} }} (R{\text{t}})}}\left( {V_{3} + \left. {V_{4} } \right)} \right. + V_{5} } \right],$$
(42)

where

$$\begin{aligned} V_{3} & = \int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{SD}} }} (r)F_{{\gamma_{\text{up}} }} (r){\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{SD}} }} (r)G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & \quad + \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{SD}} }} (r)G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots \infty ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & \quad - \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\limits_{tt = 1}^{N} {\varGamma (m_{tt} )} } }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{SD}} }} (r)G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \\ & \quad \times G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = {\text{VA}}_{1} + {\text{VA}}_{2} - {\text{VA}}_{3} . \\ \end{aligned}$$
(43)
$$\begin{aligned} V_{4} & = \int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)f_{{\gamma_{\text{up}} }} (r){\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots .m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & \quad + \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & \quad - \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\limits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & \quad - \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\limits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)\frac{1}{r}G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}\left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} } \right]G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = {\text{VB}}_{1} + {\text{VB}}_{2} - {\text{VB}}_{3} - {\text{VB}}_{4} . \\ \end{aligned}$$
(44)
$$\begin{aligned} V_{5} & = \int_{0}^{\infty } {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{up}} }} (r){\text{d}}r - \int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{up}} }} (r){\text{d}}r \\ & = {\text{VC}}_{1} - {\text{VC}}_{2} . \\ \end{aligned}$$
(45)

In (43)–(45), Meijer’s G-function gives

$$\begin{aligned} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] & = \sum\limits_{h = 1}^{N} {\frac{{\prod\nolimits_{j = 1}^{N} {\varGamma (m_{j} - m_{h} )\varGamma (m_{h} )} }}{{\varGamma (1 + m_{h} )}}} \left( {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} } \right)^{{m_{h} }} \\ & \quad \times {}_{1}F_{N} \left( {m_{h} ;1 + m_{h} - m_{1} , \ldots ,1 + m_{h} ;( - 1)^{ - N} \frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} } \right) \\ & = \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D (r)^{{k + m_{h} }} . \\ \end{aligned}$$
(46)
$$C = \frac{{\prod\nolimits_{j = 1}^{N} {\varGamma (m_{j} - m_{h} )\varGamma (m_{h} )} }}{{\varGamma (1 + m_{h} )}},\quad D = \frac{{( - 1)^{ - Nk} \left( {\frac{1}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} } \right)^{{k + m_{h} }} (m_{h} )_{k} }}{{(1 + m_{h} - m_{1} )_{k} (1 + m_{h} - m_{2} )_{k} \cdots (1 + m_{h} )_{k} k!}},$$
(47)

and for V3, V4, and V5

$$\begin{aligned} {\text{VA}}_{1} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }} \times \int_{0}^{Rt} {\frac{1}{\sqrt \pi }G_{1,2}^{2,0} \left[ {br\left| {_{{0,\frac{1}{2}}}^{1} } \right.} \right]} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{SD} }} }}\prod\nolimits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{SR} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\limits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\int_{0}^{Rt} {\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{SR} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \int_{0}^{Rt} {r^{{k - \frac{1}{2}}} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{SR} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D \int_{0}^{Rt} {r^{{k + m_{h} - 1}} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} {\text{d}}r \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D \int_{0}^{Rt} {r^{{2k + m_{h} - \frac{1}{2}}} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} {\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D (Rt)^{{k + m_{h} }} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{t} }}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} ,,m_{N} , - k - \frac{1}{2}}}^{{1 - k - m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D (Rt)^{{2k + m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{t} }}{{\overline{{\gamma_{SD} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(48)
$$\begin{aligned} {\text{VA}}_{2} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{SD}} }} (r)G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E (R{\text{t)}}^{{k + m_{h} }} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - k - \frac{1}{2}}}^{{1 - k - m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E (R{\text{t)}}^{{2k + m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(49)
$$E = \frac{{( - 1)^{ - Nk} \left( {\frac{1}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} } \right)^{{k + m_{h} }} (m_{h} )_{k} }}{{(1 + m_{h} - m_{1} )_{k} (1 + m_{h} - m_{2} )_{k} \cdots (1 + m_{h} )_{k} k!}}.$$
(50)
$$\begin{aligned} {\text{VA}}_{3} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\int_{0}^{{R{\text{t}}}} {\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \\ & \quad \times G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \\ & \quad \times \int_{0}^{{R{\text{t}}}} {r^{{k - \frac{1}{2}}} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D \int_{0}^{{R{\text{t}}}} {r^{{k + m_{h} - 1}} } G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D \int_{0}^{{R{\text{t}}}} {r^{{2k + m_{h} - \frac{1}{2}}} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - 2m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - 2m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E (R{\text{t)}}^{{3k + 2m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 3k - 2m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 3k - 2m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(51)
$$\begin{aligned} {\text{VB}}_{1} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F (R{\text{t)}}^{{k + m_{h} }} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - k - \frac{1}{2}}}^{{1 - k - m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F (R{\text{t)}}^{{2k + m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(52)
$$F = \frac{{( - 1)^{ - Nk} \left( {\frac{1}{{\overline{{\gamma_{\text{SD}} }} }}\prod\limits_{i = 1}^{N} {\frac{{m_{i} }}{{\varOmega_{i} }}} } \right)^{{k + m_{h} }} (m_{h} )_{k} }}{{(1 + m_{h} - m_{1} )_{k} (1 + m_{h} - m_{2} )_{k} \cdots (1 + m_{h} )_{k} k!}}.$$
(53)
$$\begin{aligned} {\text{VB}}_{2} & = \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F (R{\text{t)}}^{{k + m_{h} }} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - k - \frac{1}{2}}}^{{1 - k - m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )\prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F (R{\text{t)}}^{{2k + m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(54)
$$\begin{aligned} {\text{VB}}_{3} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E (R{\text{t)}}^{{2k + 2m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - 2m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - 2m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E (R{\text{t)}}^{{3k + 2m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 3k - 2m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 3k - 2m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(55)
$$\begin{aligned} {\text{VB}}_{4} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} F_{{\gamma_{\text{SD}} }} (r)G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}\left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} } \right]\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D (R{\text{t)}}^{{2k + 2m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - 2m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - 2m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} } }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } F \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D (R{\text{t)}}^{{3k + 2m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 3k - 2m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 3k - 2m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(56)
$$\begin{aligned} {\text{VC}}_{1} & = \int_{0}^{\infty } {{\text{erfc}}(\sqrt {br} )} f_{{\gamma_{\text{up}} }} (r){\text{d}}r \\ & = \frac{1}{{\sqrt {{\uppi }} \prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{2,N + 1}^{N,2} \left[ {\frac{1}{{b\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{{1,\frac{1}{2}}} } \right.} \right] \\ & \quad + \frac{1}{{\sqrt {{\uppi }} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}G_{2,N + 1}^{N,2} \left[ {\frac{1}{{b\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{{1,\frac{1}{2}}} } \right.} \right] - {\text{VD}} .\\ \end{aligned}$$
(57)
$$\begin{aligned} {\text{VC}}_{2} & = \int_{0}^{{R{\text{t}}}} {{\text{erfc}}\left( {\sqrt {br} } \right)} f_{{\gamma_{\text{up}} }} (r){\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}\left( {\sqrt {br} } \right)} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & \quad + \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}\left( {\sqrt {br} } \right)} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & \quad - \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}\left( {\sqrt {br} } \right)} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & \quad - \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}\left( {\sqrt {br} } \right)} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}\left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} } \right]\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & \quad = {\text{VE}}_{1} + {\text{VE}}_{2} - {\text{VE}}_{3} - {\text{VE}}_{4} . \\ \end{aligned}$$
(58)
$$\begin{aligned} {\text{VE}}_{1} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\sum\limits_{k = 0}^{\infty } B G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]. \\ \end{aligned}$$
(59)
$$\begin{aligned} {\text{VE}}_{2} & = \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}\left( {\sqrt {br} } \right)} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} }}\sum\limits_{k = 0}^{\infty } B G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]. \\ \end{aligned}$$
(60)
$$\begin{aligned} {\text{VE}}_{3} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} \frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E (R{\text{t)}}^{{k + m_{h} }} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - k - \frac{1}{2}}}^{{1 - k - m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } E (R{\text{t)}}^{{2k + m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(61)
$$\begin{aligned} {\text{VE}}_{4} & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{{R{\text{t}}}} {{\text{erfc}}(\sqrt {br} )} G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}\left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} } \right]\frac{1}{r}G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]{\text{d}}r \\ & = \frac{1}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D (R{\text{t)}}^{{k + m_{h} }} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - k - \frac{1}{2}}}^{{1 - k - m_{h} }} } \right.} \right] \\ & \quad + \frac{A}{{\prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\sum\limits_{k = 0}^{\infty } B \sum\limits_{h = 1}^{N} C \sum\limits_{k = 0}^{\infty } D (R{\text{t)}}^{{2k + m_{h} + \frac{1}{2}}} G_{1,N + 1}^{N,1} \left[ {\frac{{R_{\text{t}} }}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} , - 2k - m_{h} - \frac{1}{2}}}^{{\frac{1}{2} - 2k - m_{h} }} } \right.} \right]. \\ \end{aligned}$$
(62)
$$\begin{aligned} {\text{VD}} & = \frac{1}{{\sqrt {{\uppi }} \prod\nolimits_{t = 1}^{N} {\varGamma (m_{t} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }}\int_{0}^{\infty } {\frac{1}{r}G_{1,2}^{2,0} \left( {br\left| {_{{0,\frac{1}{2}}}^{1} } \right.} \right)} \times \left( \begin{aligned} G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right]G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} \right] \hfill \\ + G_{1,N + 1}^{N,1} \left[ {\frac{r}{{\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}\left| {_{{m_{1} , \ldots ,m_{N} ,0}}^{1} } \right.} } \right]G_{0,N}^{N,0} \left[ {\frac{r}{{\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} \left| {_{{m_{1} , \ldots ,m_{N} }}^{ - } } \right.} \right] \hfill \\ \end{aligned} \right){\text{d}}r \\ & = \frac{1}{{\sqrt \pi \prod\nolimits_{i = 1}^{N} {\varGamma (m_{i} )} \prod\nolimits_{tt = 1}^{N} {\varGamma (m_{tt} )} }} \times \left( {G_{2,1:0,N:1,N + 1}^{0,2:N,0:N,1} \left[ {\begin{array}{*{20}l} {1,\frac{1}{2}} \\ 0 \\ \end{array} } \right.\left| {\begin{array}{*{20}l} - \\ {m_{1} , \ldots ,m_{N} } \\ \end{array} } \right.\left| {\begin{array}{*{20}l} 1 \\ {m_{1} , \ldots ,m_{N} ,0} \\ \end{array} } \right.} \right.\left| {\frac{1}{{b\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} } \right.\left. {,\frac{1}{{b\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} } \right] \\ & \quad + G_{2,1:0,N:1,N + 1}^{0,2:N,0:N,1} \left[ {\begin{array}{*{20}l} {1,\frac{1}{2}} \\ 0 \\ \end{array} } \right.\left| {\begin{array}{*{20}l} - \\ {m_{1} , \ldots ,m_{N} } \\ \end{array} } \right.\left| {\begin{array}{*{20}l} 1 \\ {m_{1} , \ldots ,m_{N} ,0} \\ \end{array} } \right.\left. {\left| {\frac{1}{{b\overline{{\gamma_{\text{RD}} }} }}\prod\limits_{tt = 1}^{N} {\frac{{m_{tt} }}{{\varOmega_{tt} }}} } \right.\left. {,\frac{1}{{b\overline{{\gamma_{\text{SR}} }} }}\prod\limits_{t = 1}^{N} {\frac{{m_{t} }}{{\varOmega_{t} }}} } \right]} \right). \\ \end{aligned}$$
(63)

Equations (24)–(63) are used to obtain the analytical results.

6 ABEP performance prediction based on a BP neural network

6.1 Selection of input and output

The ABEP performance is affected significantly by m, N, V, and K. We therefore use 11 indicators as the input X, and the ABEP performance is output Y. The 11 indicators are mSR, mRD, mSD, GSR, GRD, NSR, NRD, NSD, K, Rt, \(\bar{\gamma }\) so X is

$$X = \left( {x_{1} ,x_{2} , \ldots ,x_{11} } \right).$$
(64)

6.2 BP neural network structure

The BP neural network is shown in Fig. 2. For the input layer, there are 11 neurons, for the hidden layer, there are q neurons and for the output layer, there is 1 neuron. For the input and hidden layers, wij is the weight coefficient and bj is the bias value. For the hidden and output layers, vj is the weight coefficient and θ is the bias value. The network steps are as follows.

Fig. 2
figure 2

The BP neural network structure

Full size image
  1. (1)

    For the hidden layer, the input is

$$s_{j} = \sum\limits_{i = 1}^{11} {w_{ij} x_{i} } + b_{j} ,\quad j = 1,2, \ldots ,q,$$
(65)

and the corresponding output is

$$c_{j} = f\left( {s_{j} } \right),$$
(66)

where f(x) is the activation function.

For the output layer, the input is

$$\beta = \sum\limits_{j = 1}^{q} {v_{j} c_{j} } + \theta .$$
(67)

and the corresponding output is

$$o = f\left( \beta \right).$$
(68)

P is the number of training data. For tth output neuron, ol is the output for the lth training data, and the error is given by

$$EE^{l} = \left( {d_{{}}^{l} - o_{{}}^{l} } \right)^{2} ,$$
(69)

where dl is the desired output.The overall output error E of P training data is

$$EE = \sum\limits_{l = 1}^{P} {\left( {d_{{}}^{l} - o_{{}}^{l} } \right)^{2} } .$$
(70)
  1. (2)

    For the different layers, the weights and biases are as follows.

The error of the output layer is

$$\delta = (d - o)(1 - o),$$
(71)

and the error of the hidden layer is

$$\sigma_{j} = \delta v_{j} (1 - y_{j} ).$$
(72)

The weights and thresholds are

$$v_{j} = v_{j} + \eta \delta y_{j} ,$$
(73)
$$\theta = \theta + \eta \delta ,$$
(74)
$$w_{ij} = w_{ij} + a\sigma_{j} x_{i} ,$$
(75)
$$b_{j} = b_{j} + a\sigma_{j} ,$$
(76)

where η is the weight adjustment parameter, 0 < η < 1, and a is the learning coefficient, 0 < a < 1.

6.3 ABEP performance prediction based on a BP neural network

Figure 3 shows the flowchart of the OP performance prediction algorithm. The algorithm steps are as follows.

Fig. 3
figure 3

The flowchart of the OP performance prediction algorithm

Full size image
  1. (1)

    Data collection and preparation. We use the derived closed-form expressions to generate 1000 groups of data. 950 groups are used for training, and 50 groups are used for testing. The groups of data are normalized.

  2. (2)

    Network initialization. To initialize the biases and weights, small random numbers are used. We also set the minimum error, maximum number of iterations, and the learning rate.

  3. (3)

    Network training. We provide input X and output Y which are randomly selected. During training, the network output of each layer and the training error are calculated, and the biases and weights of the layers are adjusted. When the learning converges or the error is less than the minimum, the training stops.

  4. (4)

    When model training is completed, the network structure is saved. Then, the testing data are used to detect whether it meets the accuracy requirements.

  5. (5)

    If the accuracy requirements are met, the network structure is used for ABEP performance prediction and the optimal weights and biases are obtained.

6.4 Metric

We use the mean squared error (MSE) to evaluate the performance. A higher prediction accuracy means a smaller MSE. The MSE is given by

$${\text{MSE}} = \frac{{\sum\limits_{l = 1}^{PP} {\left( {d_{{}}^{l} - o_{{}}^{l} } \right)^{2} } }}{PP},$$
(77)

where PP is the number of testing data.

7 Performance results

In this section, QPSK modulation is considered with E = 1 and μ = GSR/GRD. Figure 4 presents the ABEP performance comparison with the parameters given in Table 1. The ABEP performance of IAF is the best and the performance of direct communication is the worst. For SNR = 16 dB, the ABEP is 2 × 10−3 with IAF, 1.1 × 10−2 with end-to-end communication, and 2 × 10−2 with direct communication.

Fig. 4
figure 4

The ABEP performance comparison

Full size image
Table 1 The parameters for ABEP performance comparison
Full size table

Figure 5 presents the ABEP performance for μ = 0 dB, K = 0.5, and Rt = 4 dB with the combinations of N and m given in Table 2. These results show that the theoretical and simulation results are similar, which verifies the theoretical results. Further, the ABEP improves as the SNR increases.

Fig. 5
figure 5

The ABEP performance for two scenarios

Full size image
Table 2 The parameters for two scenarios
Full size table

The effect of Rt on the ABEP performance is presented in Fig. 6 for μ = 0 dB, K = 0.5, N = 2, m = 2, and Rt = −4 dB, 0 dB, and 4 dB. This shows that the ABEP improves as Rt is increased. This is because the probability that the MR cooperates increases with Rt. When SNR = 14 dB, the ABEP is 3 × 10−2 for Rt = −4 dB, 2 × 10−2 for Rt = 0 dB, and 9 × 10−3 for Rt = 4 dB. Further, the ABEP is better than that with direct transmission alone.

Fig. 6
figure 6

The effect of Rt on the ABEP performance

Full size image

The effect of N on the ABEP performance is given in Fig. 7 for N = 2, 3, 4, m = 2, μ = 0 dB, Rt = 2 dB, and K = 0.5. Figure 7 shows that the ABEP performance degrades as N increases. This is because a larger N results in more severe N-Nakagami fading channels.

Fig. 7
figure 7

The effect of N on the ABEP performance

Full size image

The effect of μ on the ABEP performance is given in Fig. 8 for μ = 15 dB, 0 dB, − 15 dB, Rt = 2 dB, N = 2, K = 0.5, and m = 2. As μ is reduced, this shows that the ABEP is improved. These results indicate that the MR should be located near the MD.

Fig. 8
figure 8

The effect of μ on the ABEP performance

Full size image

The effect of m on the ABEP performance is given in Fig. 9 for N = 2, m = 1, 2, 3, μ = 0 dB, Rt = 2 dB, and K = 0.5. These results indicate that increasing m improves the ABEP. When SNR = 15 dB, the ABEP is 2.8 × 10−2 for m = 1, 1 × 10−2 for m = 2, and 8 × 10−3 for m = 3.

Fig. 9
figure 9

The effect of m on the ABEP performance

Full size image

Figures 10, 11, 12, and 13 compare the performance of the BP neural network with the LR [38], SVM [39], and ELM [40] methods. The parameters for the four methods are given in Table 3. These results show that the MSE of the BP neural network is 0.00026, which is lower than that of the LR, SVM, and ELM methods, and indicate that the proposed method can consistently achieve higher ABEP performance prediction results.

Fig. 10
figure 10

Actual and predicted BP neural network outputs

Full size image
Fig. 11
figure 11

Actual and predicted ELM outputs

Full size image
Fig. 12
figure 12

Actual and predicted SVM outputs

Full size image
Fig. 13
figure 13

Actual and predicted LR outputs

Full size image
Table 3 The parameters for four methods
Full size table

Table 4 gives the running time and MSE for the four methods. This shows that, compared to ELM, BP has a longer running time, but the performance is better than with ELM. Also, compared to SVM and LR, BP has a shorter running time and smaller MSE. In conclusion, BP is the best forecasting model.

Table 4 The running time and MSE for four methods
Full size table

Figure 14 illustrates the validation performance. This shows that the MSE generally improves as the number of epochs increases. In our setup, if the validation error increases for 50 consecutive epochs, the training stops. In the figure, this occurs after 120 epochs while the best validation performance is 0.0019064 at epoch 70.

Fig. 14
figure 14

Validation performance of BP neural network

Full size image

In Fig. 15, we can obtain the training state. In training state, the BP uses gradient descent method. From Fig. 15, we can see how the gradient change as the number of epochs increases. From the 70 epoch, the validation error increases. After 50 consecutive increasing at the 120 epoch, the validation checks fail 50 times and the training state will stop.

Fig. 15
figure 15

Training state of the BP neural network

Full size image

The regression results are shown in Fig. 16. The relationship between the targets and outputs is indicated by the correlation coefficient R. A larger R means the BP neural network model has better prediction capability. In Fig. 16, R is 0.99214, which indicates that the proposed method has good prediction capability.

Fig. 16
figure 16

Regression results for the BP neural network

Full size image

Table 5 gives the effect of the number of neurons in the hidden layer on the MSE. This shows that when the number of neurons is small, the MSE performance is poor. The MSE performance improves as the number of neurons increases. However, with a sufficiently large number of neurons, the structure of the neural network is too complex and the MSE begins to decrease. In the proposed networks the best MSE performance is achieved when there are 10 neurons.

Table 5 The effect of the number of neurons in the hidden layer on the MSE
Full size table

The training function employed also affects the MSE performance. Table 6 shows the effect of six different training functions on the MSE. This indicates that the best training function is the Levenberg–Marquardt function with an MSE of 0.000260.

Table 6 The effect of different training functions on the MSE
Full size table

We also considered the effect of the number of hidden layers on the MSE performance. Figures 17, 18, 19, and 20, show the MSE performance, validation performance, training state, and regression for a network with two hidden layers.

Fig. 17
figure 17

Actual and predicted outputs of a network with two hidden-layers

Full size image
Fig. 18
figure 18

Validation performance of a network with two hidden layers

Full size image
Fig. 19
figure 19

Training state of a network with two hidden layers

Full size image
Fig. 20
figure 20

Regression results for a network with two hidden layers

Full size image

Table 7 shows the effect of different numbers of hidden layers on the MSE performance. The performance with two hidden layers is better than that with one hidden layer, but the running time with two hidden-layers is longer. Thus, increasing the number of layers can improve the MSE performance, but will also increases the running time.

Table 7 The effect of the number of hidden layers on the MSE
Full size table

8 Conclusion

Closed-form PDF and CDF expressions for the direct link SNR and end-to-end link SNR were derived for a mobile cooperative communication system. These results were used to derive an exact closed-form ABEP expression. A BP neural network-based ABEP performance prediction algorithm was proposed. To verify the analysis, theoretical results were compared with Monte-Carlo simulation results. In addition, these results indicated that m, N, μ, and K can significantly affect the ABEP performance. As m is increased and N and μ are reduced, the ABEP performance is improved. Compared to the LR, SVM, and ELM methods, the experimental results verify that the proposed method can consistently achieve higher ABEP performance prediction results.