Fading channel modelling using single-hidden layer feedforward neural networks

Abstract

Due to the complexity and extensive application of wireless systems, fading channel modeling is of great importance for designing a mobile network, especially for high speed environments. High mobility challenges the speed of channel estimation and model optimization. In this study, we propose a single-hidden layer feedforward neural network (SLFN) approach to modelling fading channels, including large-scale attenuation and small-scale variation. The arrangements of SLFN in path loss (PL) prediction and fading channel estimation are provided, and the information in both of them is trained with extreme learning machine (ELM) algorithm and a faster back-propagation (BP) algorithm called Levenberg-Marquardt algorithm. Computer simulations show that our proposed SLFN estimators could obtain PL prediction and the instantaneous channel transfer function of sufficient accuracy. Furthermore, compared with BP algorithm, the ability of ELM to provide millisecond-level learning makes it very suitable for fading channel modelling in high speed scenarios.

1 Introduction

High-speed railways (HSR) and highway networks have developed rapidly for nearly ten years to meet people’s travel needs. This explosive increase of high speed transportation raises higher requirements for wireless communication systems, including train ground communication (TGC) system (Shu et al. 2014), communication based train control (CBTC) system, vehicle ad hoc network (VAN) (Golestan et al. 2015), vehicle to vehicle (V2V) communication and so forth.

However, the speed of trains can reach 350 km/h and the speed of vehicles is up to 120 km/h, which make the users can not enjoy the smooth and high quality wireless services under low speed environment. In high mobility scenarios, large Doppler frequency shift, fast fading channel and fast handover issue seriously affect communication performances (Zhou and Ai 2014; Calle-Sanchez et al. 2013).

Wireless channel plays a key background role in transmission rate and the quality of mobile propagation. The modelling of radio wave propagation is essential for the planning of physical layer operations, such as the best modulation and coding interleaving scheme, equalizer design, antenna configuration and subcarrier allocation etc. Taking the continuous movements of the users into account, the profile of fading channel changes in real time and the parameters of the propagation process become random variables (Sotiroudis and Siakavara 2015). Fading channel is modelled in two ways, large-scale attenuation known as path loss (PL) prediction and small-scale variation known as channel transfer function estimation (Rappaport 2001). The former predicts the mean signal strength for an arbitrary large transmitter-receiver distance (several hundreds or thousands of meters; Phillips et al. 2013) while the latter characterizes the rapid fluctuations of received signal strength over very short distances (a few wavelengths) or short durations (on the order of seconds; Chang and Wu 2014).

PL prediction proposals in the literature can broadly be classified as (a) empirical and (b) measurement models. The models of type (a) (Friis 1946; Seidel and Rappaport 1991; ITU-R 2002; Herring et al. 2012) make use of available prior knowledge collected from a given environment, so that it is suitable in the situations impossible or difficult to obtain measurements. These empirical models are widely adopted into network simulators or served to derive a simplified version of more complex models since they are easy to implement, although they are questionably accurate. The models of type (b) (Lee 1985) define a sampling method and a means of PL predicting where PL could not be measured, based on the assumption that the burden of measurements and prediction is unavoidable and acceptable. The typical methods as explicit mapping (Hills 2001), partition-based models (Durgin 2009), iterative heuristic refinement (Robinson et al. 2008) and active learning and geostatistics (Marchant and Lark 2007) choose the measurements set to improve the accuracy of modelling.

Fading channel estimation is crucial for receiver design in coherent communication systems. Channel estimation models can be grouped into three categories: (a) estimation based on channel frequency response (Beek et al. 1995), (b) estimation with parametric model (Yang et al. 2001; Qing and Gang 2014) and (c) iterative channel estimation (Valenti and Woerner 2001; Kim and Hansen 2015). Approach (a) is a basic method with the minimal model complexity. It estimates the channel frequency response of pilot symbols first, and then obtains the responses of data symbols via interpolation. Approach (b) and (c) can provide better performance. For approach (b), a set of parameters are estimated in the reconstruction of channel response, which is suitable for sparse channels with 2–6 dominant paths (Chen et al. 1999). Approach (c) takes advantage of error-control coding techniques such as turbo code (Li et al. 2010) and LDPC code (Fang 2010) to estimate channel in an iterative manner.

Both PL prediction and fading channel estimation have two ways to model channels: blind and pilot channel modelling (Vieira et al. 2013; Larsen et al. 2009). Pilot model (Pun et al. 2011) is typically constructed by using pilot symbols strategically placed at the frame head or subcarrier. In blind modelling (Mielczarek and Svensson 2005), channel coefficients are predicted by using statistical features of received signals. Once a channel is estimated its time-frequency characteristics, relevant parameters are used to update the pre-set model. As in any estimation application, wireless channel estimation aims to quantify the best performance of wireless systems. However, due to the unlimited number of received signal, it is a challenge to extract optimal channel coefficients.

Feedforward neural networks (FNN) is extensively used to provide models for a natural or artificial phenomena that are difficult to handle using classical parametric techniques (Cao et al. 2012). A single-hidden layer FNN (SLFN) is found to be more computationally efficient for the work than 2- or 3-hidden layered forms (Sarma and Mitra 2013). Simsir and Taspinar (2015) and Seyman and Taspinar (2013) demonstrated that channel estimation based on neural network ensures better performance than conventional Least Squares (LS) algorithm without any requirements for channel statistics and noise. In the meantime, Sotiroudis and Siakavara (2015) and Cheng et al. (2015) also proved SLFNs can be used in channel estimation for various wireless environments. Most of the literatures (Sotiroudis and Siakavara 2015; Seyman and Taspinar 2013; Panda et al. 2015; Taspinar and Cicek 2013) proved that SLFNs are effective for static and slowly varying channels. Unfortunately, the learning speed of SLFNs has been a major bottleneck in many applications, and fast fading channel caused by high mobility makes this method unsuitable for channel modelling too. Unlike traditional SLFN implementations, a simple learning algorithm called extreme learning machine (ELM) with good generalization performance (Cao et al. 2012; Cao and Lin 2015, 2014) can learn thousands of times faster, which randomly chooses hidden nodes and analytically determined the output weights of SLFNs. The extremely fast learning speed of ELM makes the algorithm viable in fading channel modelling.

In this paper, we propose SLFN approaches based on ELM to modelling fading channel. Since the modelling has concentrate on large-scale attenuation and small-scale variation (Rappaport 2001), we choose path loss coefficient and channel transfer function to estimate. The performance of ELM estimator with SLFN architecture is compared to that of BP estimator. We use training and testing time, estimation error, bit error rate (BER) as the performance criteria.

The outline of the paper is as follows: Sect. 2 describes the basic considerations related to fading channel modelling using SLFNs. Sect. 3 proposes a PL prediction method based on ELM for large-scale attenuation and analyzes the simulation results. Sect. 4 develops an ELM estimator for channel transfer function and derives the results from the simulations. Conclusion is given in Sect. 5.

The performance of fading channel modelling based on ELM is in comparison with back-propagation (BP) algorithm (Tariq 1991) (Levenberg-Marquardt algorithm; Bogdan et al. 2010) which is a popular algorithm of SLFNs. All of the simulations are carried out in MATLAB 7.12.0. Levenberg-Marquardt algorithm is provided by MATLAB package, while ELM algorithm is from (Cao et al. 2015).

2 Fading channel and its modelling using SLFNs

In this section, fading channel model and its radio propagation expressions are developed. The SLFN architecture of ELM and BP algorithms are discussed in the arrangement for PL prediction and fading channel estimation.

2.1 Radio propagation

A linear fading channel in Fig. 1 is with output r and input s, where r can be expressed as $r = f\left( s \right)$. $f\left( \cdot \right)$ denotes a transform function at the receiver end, representing the propagation related variations due to fading, shadowing or phase shifting.

Fig. 1

Fading channel model with transmitter and receiver’s block diagrams

The input-output relationship is given by

$$\begin{aligned} r\left( k \right) = H\left( k \right) s\left( k \right) + w\left( k \right) \end{aligned}$$

(1)

where $s\left( k \right)$ is the transmit symbol at $k\hbox {th}$ time slot, $r\left( k \right)$ is the receive signal, $w\left( k \right)$ is an additive noise and $H\left( k \right)$ denotes channel transfer function, respectively. Considering the interference of co-channel, the relationship in (1) is written as

$$\begin{aligned} r\left( k \right) = H\left( k \right) s\left( k \right) + \sum \limits _{i = 1}^L {{H_i}\left( k \right) {s_i}\left( k \right) } + w\left( k \right) \end{aligned}$$

(2)

where L is the number of interferers, ${H_i}\left( k \right)$ is channel transfer function of the $i\hbox {th}$ interferer.

If the transmitter has transmit power ${P_{\mathrm{{t}}}}$ dBm and antenna gain ${G_{\mathrm{{t}}}}$ dBi, the total effective isotropic radiated power (EIRP) in the log domain is ${P_\mathrm{{t}}}+{G_\mathrm{{t}}}$. The entire channel in Eq. (1) in the form of power is expressed as

$$\begin{aligned} {P_\mathrm{{r}}} = {P_\mathrm{{t}}} + {G_\mathrm{{t}}} + {G_\mathrm{{r}}} - PL\left( k \right) - N_0 \end{aligned}$$

(3)

where ${P_\mathrm{{r}}}$ and ${G_\mathrm{{r}}}$ are receive power and antenna gain. PL encompasses all attenuation due to path loss and N is the power of thermal noise. Therefore, the signal to noise ratio (SNR) in log domain is $SNR = {P_\mathrm{{t}}} - N_0$. Considering interference in Fig. 1, the signal to interference and noise ratio (SINR) is defined as

$$\begin{aligned} SINR = {P_\mathrm{{t}}} - \left( {N_0 + \sum \limits _{i = 1}^L {{I_i}} } \right) \end{aligned}$$

(4)

where $I_i$ is the receive power from $i\hbox {th}$ interferer.

Commonly, fading channel modelling is aim to estimate the value of PL

$$\begin{aligned} PL\left( k \right) = {L_\mathrm{{p}}}\left( k \right) + {L_\mathrm{{s}}}\left( k \right) + {L_\mathrm{{f}}}\left( k \right) \end{aligned}$$

(5)

where ${L_\mathrm{{p}}}$ is free-space path loss, ${L_\mathrm{{s}}}$ is the loss due to shadowing (slow fading) from large obstacles. ${L_\mathrm{{p}}}\left( k \right) + {L_\mathrm{{s}}}\left( k \right)$ is the large-scale fading whereas ${L_\mathrm{{f}}}$ is the small-scale fading.

2.2 SLFN architecture and learning algorithms

The idea to employ SLFN algorithm for the solution of fading channel modelling is based on its learning ability to find out the relationship between channel parameters and the receive signals, even when the channel is complicated. SLFN basically consists of input, hidden and output layers where neurons connected to each other by parallel synaptic weights.

For N independent training samples $\left( {{\mathbf{{x}}_i},{\mathbf{{t}}_i}} \right)$ where ${\mathbf{{x}}_i} \in {\mathbf{{R}}^n},{\mathbf{{t}}_i} \in {\mathbf{{R}}^m},i = 1,2, \cdots ,N$, SLFNs with ${\tilde{N}}$ hidden nodes are modelled as

$$\begin{aligned} \sum \limits _{j = 1}^{\tilde{N}} {{\beta _j}{g_j}\left( {{x_i}} \right) } = \sum \limits _{j = 1}^{\tilde{N}} {{\beta _j}g\left( {{\mathbf{{w}}_j}\cdot {\mathbf{{x}}_i} + {\mathbf{{b}}_j}} \right) = {\mathbf{{o}}_i}} \end{aligned}$$

(6)

where ${{\mathbf{{w}}_j}}$ is the weight vector between the input node and $j\hbox {th}$ hidden node , ${\mathbf{{\beta }}_j}$ is the weight vector between $j\hbox {th}$ hidden node and the output nodes, and ${{\mathbf{{b}}_j}}$ is the threshold of $j\hbox {th}$ hidden nodes. The operational symbol ’$\cdot$’ represents inner product.

The objective function of SLFNs E that will be minimized is written as

$$\begin{aligned} E\left( {{\mathbf{{w}}_j},{\mathbf{{\beta }}_j},{\mathbf{{b}}_j}} \right) = \sum \limits _{i = 1}^N {\left\| {{\mathbf{{o}}_i} - {\mathbf{{t}}_i}} \right\| } \end{aligned}$$

(7)

where vector $\mathbf{{w}}$ is the set of weight $\left( {{\mathbf{{w}}_j},{\mathbf{{\beta }}_j}} \right)$ and biases $\left( {{\mathbf{{b}}_j}} \right)$ parameters .${{\mathbf{{o}}_i}}$ is $i\hbox {th}$ actual output and ${{\mathbf{{t}}_i}}$ is $i\hbox {th}$ desired output.

2.2.1 Levenberg-Marquardt algorithm

BP algorithm iteratively adjusts all of its parameters to minimize the objective function by using gradient-based algorithms (Bogdan et al. 2010). In the minimization procedure, vector $\mathbf{{w}}$ is iteratively adjusted as follows:

$$\begin{aligned} {\mathbf{{w}}_{l + 1}} = {\mathbf{{w}}_l} - \eta \frac{{\partial E\left( \mathbf{{w}} \right) }}{{\partial \mathbf{{w}}}} \end{aligned}$$

(8)

where $\mu$ is the learning speed.

The training steps of Levenberg-Marquardt algorithm are illustrated as:

• (1) Initialize the weight vector $\mathbf {w}$ and learning speed $\mu$.

• (2) Compute the objective function in terms of mean square error (MSE), i.e. $E = \frac{1}{N}{\sum \nolimits _{i = 1}^N {\left| {{\mathbf{{o}}_i} - {\mathbf{{t}}_i}} \right| } ^2}$.

• (3) Update weight vectors with formula $\varDelta \mathbf{{w}} = - {\left[ {{\mathbf{{J}}^\mathrm{{T}}}{} \mathbf{{J}} + \mu \mathbf{{I}}} \right] ^{ - 1}}{\mathbf{{J}}^\mathrm{{T}}}E$ where $\mathbf {J}$ is the Jacobian matrix.

• (4) Recompute the objective function with $\mathbf{{w}} + \varDelta \mathbf{{w}}$. $\alpha$ is a constant that regulates $\mu$ and $\alpha <1$. If error is smaller than the MSE value in step 2, reduce $\mu$ $\alpha$ times and go to step 3. If error is not reduced, increase $\mu$ $\alpha ^{-1}$ times and go to step 3.

• (5) Finish the training when error is less than its preset value or iteration epoches reach the maximum.

2.2.2 ELM algorithm

Although BP’s gradient can be computed efficiently, an inappropriate learning speed might raise several issues, such as slow convergence, divergence, or stopping at a local minima (Cao et al. 2015). ELM algorithm randomly assigns the hidden node learning parameters and analytically determines the network output weights without learning iterations. Therefore, this method is able to make learning extremely fast.

ELM algorithm steps are as follow:

• (1) Assign a training set $\aleph = \left\{ {\left. {\left( {{\mathbf{{x}}_i},{\mathbf{{t}}_i}} \right) } \right| i = 1,2, \cdots ,N} \right\}$, active function g(x) and the number of hidden neurons ${\tilde{N}}$,

• (2) Randomly assign input weight vector ${\mathbf{{w}}_j}$ and bias value ${b_j},j = 1,2, \cdots ,\tilde{N}$,

• (3) Calculate the hidden layer output matrix $\mathbf{{H}}$ and its $Moore-Penrose$ generalized inverse matrix ${\mathbf{{H}}^\dag }$,

• (4) Calculate the output weight $\hat{\beta } = {\mathbf{{H}}^\dag }{} \mathbf{{T}}$ with the least squares, where $\mathbf{{T}} = {\left[ {{\mathbf{{t}}_1},{\mathbf{{t}}_2}, \ldots ,{\mathbf{{t}}_N}} \right] ^\mathrm{{T}}}$.

For a linear system $\mathbf{{H}} \mathbf{{\beta }} = \mathbf{{T}}$, ELM algorithm finds a least-squares solution $\hat{\beta }$ rather than iterative adjustment (Cao and Xiong 2014). Seen from the steps, the learning time of ELM is mainly spent on calculating ${\mathbf{{H}}^\dag }$. Therefore, ELM saves a lot of time in most applications. The performance evaluation in Cao et al. (2012); Cao and Lin 2015) shows that ELM can produce good generalization performance in most cases and can learn more than hundreds of times faster than BP.

2.3 Configuring SLFN for fading channel modelling

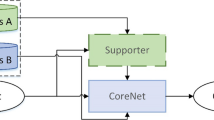
The application of SLFN for fading channel modelling is shown in Fig. 2. In our work, by adjusting the combination of training data, the corresponding training set is applied to the SLFN estimator with learning ability. The learning procedure is carried out with no parametric dependence.

Fig. 2

The application of SLFN for fading channel modelling

Figure 3 shows the arrangement of SLFN to perform PL prediction in subgraph (a) and (b) and fading channel estimation in subgraph (c) and (d). For PL prediction, the SLFN estimator is trained by receive signal $r\left( k \right) , k = 1,2, \cdots ,N$ or train data set $\left( {r\left( k \right) ,\tilde{\gamma } \left( k \right) } \right)$ where $\tilde{\gamma } \left( k \right)$ is the reference PL exponent obtained by pilot symbols. The output of SLFN estimator is ${\tilde{\gamma } \left( k \right) }$ at $k\hbox {th}$ time slot. Similarly, the SLFN estimator in fading channel estimation is trained by $r\left( k \right)$ or $\left( {r\left( k \right) ,\tilde{H}\left( k \right) } \right)$ and its output is channel transfer function $\hat{H}\left( k \right)$.

Fig. 3

Arrangement of SLFN in PL prediction and fading channel estimation

The performance of our proposed SLFN estimator for fading channels will be demonstrated by computer simulations. The performance of our proposed estimator is evaluated using MSE or BER versus SNR criterion. In addition, the mobility of terminals greatly limits the estimation speed, so we also consider the consuming time of the estimators. The parameters of fading channel we used in the simulations are shown in Table 1.

Table 1 Parameters used in fading channel modelling

3 PL prediction modelling

In this section, the structure of ELM estimator in the prediction of PL exponent is proposed and computer simulations show its performance compared with BP estimator.

3.1 Model analysis

PL exponent $\gamma$ indicates the rate at which PL increases with distance. The smaller $\gamma$ is, the less energy loss of wireless signal due to transceiver-receiver distance is. Typical value of $\gamma$ is determined by carrier frequency and propagation terrain. For example, in HSR environment, $\gamma$ is slightly larger than 2 in rural area (within 250–3200 m) with narrow band communication system while it is near to 4 in hilly terrain (within 800–2500 m) with broadband system.

In Friis (1946), a basic formula for free-space transmission loss with ideal isotropic antennas is simplified to

$$\begin{aligned} \frac{{{P_\mathrm{{t}}}}}{{{P_\mathrm{{r}}}}} = {\left( {\frac{\lambda }{{\pi d}}} \right) ^2} \end{aligned}$$

(9)

where $\lambda$ is the carrier’s wavelength and d is the transmitter-receiver distance in meters. Friis assumed that $\gamma =2$ so that signals degraded as a function of $d^2$ (Friis 1946). However, a common extension to non-line-of-sight (NLOS) environments is to use a larger $\gamma$. Both theoretical and measurement-based channel models (such as Egli model, two-ray model, Okumura model, Hata model etc) indicate that $\gamma$ is in the range 1–4 (Rappaport 2001). Considering shadowing effects component $\psi$ obeys a log-normal distribution, the statistical PL model (Erceg et al. 1999; Kastell 2011) is given by

$$\begin{aligned} {P_\mathrm{{r}}}={P_\mathrm{{t}}}+20\log _{10}\frac{\lambda }{4\pi }-10\gamma \log _{10} d-\psi \end{aligned}$$

(10)

where $\psi$ is a zero-mean Gaussian distributed random variable with standard deviation $\sigma _{\psi }$ (also in dBm).

PL exponent $\gamma$ could be obtained by fitting the minimum mean square error (MMSE) of measurements (Liu et al. 2012)

$$\begin{aligned} {\gamma }^*=F_{\mathrm{MMSE}}(\gamma )=\min \limits _{\gamma }\sum \limits _{i=1}^{N}\left[ M_{\mathrm{measured}}(d_i)-M_{\mathrm{model}}(d_i)\right] ^2 \end{aligned}$$

(11)

where $M={P_\mathrm{{t}}}/{P_\mathrm{{r}}}$, $M_{\mathrm{measured}}(d_i)$ is the measured values at distance $d_i$, and $M_{\mathrm{model}}(d_i)=20\log _{10}\left( {\lambda }/\left( {4\pi }\right) \right) -10\gamma \log _{10} d_i$. And the variance $\sigma _{\psi }^2$ is given by

$$\begin{aligned} \sigma _{\psi }^2=\left. \frac{1}{N}\sum \limits _{i=1}^{N}\left[ M_{\mathrm{measured}}(d_i)-M_{\mathrm{model}}(d_i)\right] ^2\right| _{{\gamma }^*} \end{aligned}$$

(12)

If the radius of the transmitter’s cell is 1 km and the vehicle’s velocity is 120 km/h, the receiver will carry out a handover procedure every 60 s, so that $\gamma$ needs to be calculated at the receiver at least once per minute. if the velocity is up to 350 km/h, $\gamma$ needs to be calculated every 20.6 s. According to Eqs. (11) and (12), the calculation of $\gamma$ requires hundreds or thousands of receive signal measurements, the introduction of learning algorithm into PL prediction would be effective in simplifying data processing.

3.2 PL prediction based on ELM

As Fig. 3a, our proposed ELM estimators’s structure at receiver end is shown in Fig. 4 and it periodically adjust PL prediction according to the latest received frame to trace the variation of large-scale propagation.

Fig. 4

The structure of ELM estimator in PL prediction

After the receiver receiving a frame, the procedure of ELM estimator is stated as follows:

• (1) Initialize the standard deviation $\hat{\sigma }_\psi ^2\left( 0 \right)$.

• (2) After receiving the $m\hbox {th}$ frame, assign a testing set $\left\{ {\left. \left( {{P_\mathrm{{r}}}_i,{\gamma _i}} \right) \right| i = 1,2, \cdots ,N} \right\}$ when N is the frame length.

• (3) Run ELM algorithm and obtain the prediction $\hat{\gamma }\left( m \right) = \overline{{{\hat{\gamma }}_i}}$ and $\hat{\sigma }_\psi ^2\left( m \right)$.

• (4) Update the value of the standard deviation for the next prediction.

Obviously, the whole procedure doesnt have any parameters to be tuned iteratively.

3.3 Simulation results

We use ELM and BP algorithms to predict PL exponent $\gamma$. The velocity is set at 120 km/h. A training set $\left( {{P_\mathrm{{r}}}_i,{\gamma _i}} \right)$ and testing set $\left( {{P_\mathrm{{r}}}_i,{\gamma _i}} \right)$ with 1000 data, respectively are created where ${{P_\mathrm{{r}}}_i}$ is uniformly randomly distributed on the interval $\left( { - 105, - 25} \right)$ dBm (Liu et al. 2012). Shadowing effect exponent $\psi$ has been added to all training samples while testing data are shadowing-free.

The number of hidden neurons of ELM is initially set at 20 and active function is sigmoidal. Simulation result is shown in Fig. 5. The train accuracy measured in terms of root mean square error (RMSE) is 0.27734 due to the shadowing effect, whereas the test accuracy is 0.012445. Figure 5 confirms that the prediction results of $\gamma$ are accurate, and there is a visible margin of error only when ${{P_\mathrm{{r}}}}>-30\hbox {dBm}$.

Fig. 5

The prediction of PL exponent $\gamma$ by ELM learning algorithm

Average 200 trails of simulation have been conducted for both ELM and BP algorithm, whose results are shown in Table 2. In BP, the input and output layers have log-sigmoidal and the hidden layer have tan-sigmoidal activation functions. When the number of hidden neurons is 20, ELM estimator spends 6.8 ms CPU time on training and 2.9 ms on testing. However, it takes 53.6 s for BP estimator on training and 67.1 ms on testing, which makes it unsuitable for high speed scenarios since the consuming time is larger than 20.6 s (for 350 km/s) or slightly lower than 60 s (for 120 km/h). ELM runs 7800 times faster than BP. Compared with 60 s and 20.6 s in Sect. 3.1, BP is too time-consuming to be used in PL prediction in a scenario with high mobility. Although ELM has a much higher testing error 0.0475 compared with 0.0031 in BP, this prediction error can be acceptable as shown in Fig. 5.

Table 2 Performance comparison for learning algorithms in PL prediction

In addition, considering network transmission rate is 1 Mbps, the reception of 1000 test data takes only 1 ms, so that ELM estimator can predict PL exponent $\gamma$ with RMSE less than 0.05 within a time interval less than 8 ms. If the velocity is 120 km/h, the vehicle has only moved 0.27 m during PL prediction interval. If the velocity is 350 km/h, the moving distance is less than 0.78 m. For large-scale fading, $\gamma$ and $\sigma _\psi ^2$ barely have a sharp change in the range, so that it is reasonable to use $\sigma _\psi ^2$ in the next prediction in Fig. 4.

Figure 6 shows the relationship between the generalization performance of ELM and the number of hidden neurons ${\tilde{N}}$ in PL prediction. Every ${\tilde{N}}$ simulates 50 times. Obviously, the generalization performance of ELM is stable when ${\tilde{N}}\ge 12$. Thus, the simulation result in Fig. 5 is reasonable when ${\tilde{N}}$ is set at 20.

Fig. 6

The generalization performance of ELM in PL prediction

Figure 7a shows the relationship between RMSE of ELM and the number of train/test data N when ${\tilde{N}}=20$, and Fig. 7b shows the impact of N on consuming time. Training RMSE is almost a constant (slightly less than 0.3) because ELM use Moore-Penrose inverse matrix calculation to solve the problem of finding the smallest norm least-squares output weight. Unlike it, testing RMSE decreases with an increase in the number of test data. The simulation confirms the conclusion in Cao et al. (2012) that ELM has no over-trained phenomenon. Both train and test consuming time increases with N, however, the increase of test time is less than that of train time. It should also be noted that, even N is up to $10^4$, the time consumed by ELM estimator is still acceptable, which is less than 70 ms.

Fig. 7

Number of train/test data of ELM in PL prediction

4 Fading channel estimation modelling

The channel transfer function $H\left( k \right)$ of fading channels in Eq. (1) is assumed to maintain a constant in a frame (Sarma and Mitra 2013), i.e. $H\left( k \right) = H$. A frame’s input-output relationship is

$$\begin{aligned} r\left( k \right) = Hs\left( k \right) + w\left( k \right) ,\mathrm{{ }}k = 1,2, \ldots ,N \end{aligned}$$

(13)

The actual H and w(k) is unknown to the receiver.

The Rayleigh multi-path fading channel assumes that the delay power profile and the Doppler spectrum of channel are separate. The channel with normalized power is given by

$$\begin{aligned} H\left( k \right) = \frac{1}{{\sqrt{2} }}\left[ {{n_\mathrm{{c}}}\left( k \right) + \mathrm{{j}}{n_\mathrm{{s}}}\left( k \right) } \right] \end{aligned}$$

(14)

where ${{n_\mathrm{{c}}}}$ and ${{n_\mathrm{{s}}}}$ are the phase and quadrature branches of the baseband signal in Gauss process.

Since BPSK modulation is employed in the model in Fig. 1, the transmit signal $s\left( k \right)$ is real. Rayleigh channel H is a complex variable so that the receive signal $r\left( k \right)$ is complex too. Considering the data sets in ELM and BP algorithms ${\mathbf{{x}}_i} \in {\mathbf{{R}}^n},{\mathbf{{t}}_i} \in {\mathbf{{R}}^m}$, the estimation of H should be divided into real and imaginary parts.

If we set up the data sets in SLFN as $\aleph 1 = \left\{ {\left. {\left( {r\left( k \right) ,{\mathop {\mathrm{Re}}\nolimits } \left( H \right) } \right) } \right| k = 1,2, \cdots ,N} \right\}$ and $\aleph 2 = \left\{ {\left. {\left( {r\left( k \right) ,{\mathop {\mathrm{Im}}\nolimits } \left( H \right) } \right) } \right| k = 1,2, \cdots ,N} \right\}$. As shown in Fig. 3c, the estimated channel transfer function is

$$\begin{aligned} \hat{H} = \frac{1}{N}\sum \limits _{k = 1}^N {\hat{H}\left( k \right) } = \frac{1}{N}\sum \limits _{k = 1}^N {\left[ {{\mathop {\mathrm{Re}}\nolimits } \left( {\hat{H}\left( k \right) } \right) + {\mathop {\mathrm{Im}}\nolimits } \left( {\hat{H}\left( k \right) } \right) } \right] } \end{aligned}$$

(15)

Figure 8 shows the ability of SLFN to capture the time-varying characteristic of fading channel. When Rayleigh pattern is applied, SLFN shows an inability to deal directly with the time-varying nature. The BER performance of ELM estimation is around 0.45, which is similar to random decision, whereas the BER performance of BP estimation is even worse. This is due to the receive signal ${r\left( k \right) }$ affected by three Gaussian random variables, ${{n_\mathrm{{c}}}\left( k \right) }$, ${{n_\mathrm{{s}}}\left( k \right) }$ and $w\left( k \right)$. Thus, we draw a conclusion that blind modelling is not suit for fading channel estimation base on SLFN architectures.

Fig. 8

The BER of Rayleigh fading channel with ${\hat{H}}$ estimated by ELM and BP algorithm

In order to narrow the estimation down, pilot signals are used in fading channel estimation to provide reference channel transfer function ${\tilde{H}}$, and it can be calculated by

$$\begin{aligned} \tilde{H} = \frac{1}{{{N_p}}}\sum \limits _{k = - {N_p}}^{ - 1} {r\left( k \right) s\left( k \right) } \end{aligned}$$

(16)

4.1 Fading channel estimation based on ELM

Our proposed ELM estimator’s structure at receiver end is shown in Fig. 9. As Fig. 3, the transmitter in fading channel inserts pilot symbols in frames’ headers to trace the time-varying characteristic of channel.

Fig. 9

The structure of ELM estimator in fading channel estimation

In Fig. 9, ELM estimator of channel transfer function H is divided into real and imaginary parts. The reference channel transfer function ${\tilde{H}}$ is used to estimate the error of channel transfer function ${\varDelta H}$, i.e. the data sets are $\aleph 1 = \left( {{\mathop {\mathrm{Re}}\nolimits } \left( {\tilde{H}} \right) ,{\mathop {\mathrm{Re}}\nolimits } \left( {\varDelta H} \right) } \right)$ and $\aleph 2 = \left( {{\mathop {\mathrm{Im}}\nolimits } \left( {\tilde{H}} \right) ,{\mathop {\mathrm{Im}}\nolimits } \left( {\varDelta H} \right) } \right)$. Thus, the estimation value is given by

$$\begin{aligned} \hat{H} = \tilde{H} + \varDelta H \end{aligned}$$

(17)

After the receiver receiving a frame, the procedure of ELM estimator is stated as follows:

• (1) Calculate the reference channel transfer function ${\tilde{H}}$ in Eq. (16).

• (2) Assign real testing set $\left\{ {\left. {\left( {{\mathop {\mathrm{Re}}\nolimits } \left( {\tilde{H}} \right) ,{\mathop {\mathrm{Re}}\nolimits } \left( {\varDelta {H_i}} \right) } \right) } \right| i = 1,2, \cdots ,N} \right\}$ and imaginary testing set $\left\{ {\left. {\left( {{\mathop {\mathrm{Im}}\nolimits } \left( {\tilde{H}} \right) ,{\mathop {\mathrm{Im}}\nolimits } \left( {\varDelta {H_i}} \right) } \right) } \right| i = 1,2, \cdots ,N} \right\}$.

• (3) Run ELM algorithm and obtain the estimation of channel transfer function $\hat{H} = \tilde{H} + \varDelta \overline{{H_i}}$.

• (4) Count BER and decide whether or not to adjust the number of pilot symbols.

4.2 Simulation results

We use ELM and BP algorithms to estimate channel transfer function H. The number of hidden neurons of SLFN is set at 10 and average 3000 packets have been conducted for two algorithm for comparison. The simulation results are shown in Table 3. ELM estimator spends less than 8 ms on training and 6 ms on testing. In contrast, BP estimator needs at least 42 s to complete the training process and 30 ms to perform the testing procedure. For the same reason in PL prediction, BP algorithm also could not be applied to fading channel estimation for high speed scenarios. In addition, both SNR and the number of pilot symbols determine estimation accuracy. ELM shows a higher accuracy than BP when SNR is 0 dBm. The result is quite opposite when SNR is 20 dBm. It implies that ELM estimator is more suitable for fading modelling with deteriorated channel condition.

Table 3 Performance comparison for learning algorithms in fading channel estimation

Figures 10 and 11 show the BER performance of estimators versus SNR, which is counted 3000 BPSK frames at every SNR value. Both figures indicate that the performance of ELM with SLFN architecture in Fig. 9 is as good as that of BP estimator, although their RMS is different in Table 3. In the range of SNR, the performance of SLFN estimators is better than pilot-based algorithm. The BER gap between ELM/BP algorithm and the known channel that the receiver uses ideal channel estimation decreases as the increase of the number of pilot symbols. In Fig. 10, the performance of BP estimator is even better than that of the known channel when SNR is larger than 15 dBm. As shown in Fig. 11, although the implementation of ELM estimator is quite than BP, the improvement of ELM performance is much stable.

Fig. 10

BER performance of estimators versus SNR with 1 pilot symbol

Fig. 11

BER performance of estimators versus SNR with 2 pilot symbols

Therefore, both ELM and BP estimators show the effectiveness of SLFN in fading channel modelling. Due to learning speed, ELM algorithm is more practical in the real scenarios with high mobility.

5 Conclusion

In this paper, fading channel modelling based on single-hidden layer feedforward neural networks is proposed for the scenarios with high mobility. In large-scale attenuation, the ELM estimator for the prediction of path loss exponent is developed, whose experimental results show that ELM run 8000 times fast than BP learning algorithm and its testing error is acceptable. In small-scale variation, the SLFN architecture based on ELM algorithm for the estimation of fading channel transfer function is provided, and simulation results shows ELM with fast learning speed has the same effectiveness as BP algorithm.