1 Introduction

Structural rock characteristics are important for geological studies, mining, petroleum engineering, and geotechnical surveys. Lithology and uniaxial compressive strength (UCS) are two variables used in the prediction of general rock failure. Therefore, measuring and estimating the UCS of rock materials is important for intact rock mass classification, foundation construction, tunneling, slope stability issues, and other rock failure criteria [1]. Accurate estimation of UCS, however, remains a challenging, yet important problem in a range of engineering disciplines.

The UCS of rocks can be measured in both the field and laboratory, through direct and indirect approaches. The International Society for Rock Mechanics (ISRM) has standardized the procedure for direct measurement, which involves producing high-quality rock core samples in engineering laboratories. The procedure requires destructive tests and is time-consuming and expensive [1]. Indirect determination of UCS can be carried out through various methods including the point load strength index test, block punch strength index test, and the Schmidt hammer test. These methods generally require many core samples, expensive devices, as well as significant time and funding [2]. Extraction of rock samples with the specific dimensions required for laboratory testing purposes is not always possible. In such cases, it is important to develop other methods to define the correlation of physio-mechanical features of materials, where one attribute can be predicted from another. In the preliminary stage of planning and design activities, understanding property interdependencies is useful [3]. Many studies have investigated the possibility of estimating UCS according to other material features, since the methods used to measure other features are relatively rapid, incur low costs, and are easy to execute in comparison with the ISRM UCS test.

The indirect estimation of UCS can be performed using conventional regression methods, which propose a functional relationship between underlying variables related to UCS. However, due to the evolution of computers, new techniques based on artificial intelligence (AI) that employ machine learning have been utilized to create predictive models that can estimate essential parameters [4,5,6,7]. Many studies have focused on the indirect estimation of rock UCS with AI. Table 1 lists the previous studies that have applied AI models to the prediction of UCS.

Table 1 Previous studies directed at UCS prediction using AI techniques
Full size table

Most of the above-mentioned AI models, however, are complex and computationally costly during the training processes. As such, tree-based machine learning models have become increasingly explored for regression problems because they are relatively simple, and have relatively lower computational costs [17, 18]. Although the aforementioned research studies confirmed that AI models showed significant advantages for UCS estimation, a comparative study among tree-based machine learning models (e.g., random forest (RF), M5 model tree, and multivariate adaptive regression splines (MARS)) has been not carried out. Moreover, developing an ensemble-based multi-model approach is useful as it integrates the advantages of different models. Thus, the current study developed an artificial neural network (ANN)-based committee ensemble model with three tree-based models. To the best of the authors’ knowledge, this study represents the first time such an ensemble model has been developed in this field.

In this study, data samples from travertine rocks were collected from different quarries in the Azarshahr area of northwest Iran, and the relationships between UCS (i.e., the target variable) and other rock properties (i.e., the predictor variables) were investigated. The goals of this research included: (1) development of single (or standalone) nonlinear tree-based machine learning models that utilized the RF, the M5 model tree, and MARS algorithms to model UCS, (2) comparison of the aforementioned models’ performances to select the best approach, and (3) integration of the advantages of the standalone tree-based machine learning models to construct and evaluate an ensemble committee-based model for USC prediction through application of an ANN algorithm. The purpose of this research was to propose a new ensemble-based model that could potentially lead to improved prediction accuracy, relative to standalone models, when applied to the prediction of UCS of travertine rock.

2 Materials and methods

2.1 Study area and data collection

Travertine, which is characterized by its high porosity, fine grain, and banded structure, is a particular form of carbonate deposit (also referred to as a type of limestone). It is deposited by hot spring water containing Ca2+ and CO32− and is mainly found in fault zones, karstic caves, and around spring cones. The travertine in the Azarshahr area is a fissure-ridge type, which extends to the eastern part of Urmia Lake in northwestern Iran [7].

A geological map of the study area and location of travertine formations is illustrated in Fig. 1. The active quaternary Sahand volcanic complex, near the travertine ridges, has had a significant impact on the Jurassic and Cretaceous carbonate solution, as well as the stained travertine layers [19]. Different colored travertine, aragonite, and onyx quarries exist in the area, which contain up to approximately 560 million m3 of travertine.

Fig. 1
figure 1

Geological features in the Azarshahr area

Full size image

Travertine samples, for modeling purposes, were obtained from ten quarries in four different provinces in the area. Overall, 30 travertine blocks were collected, each with the approximate dimension of 40 × 40 × 20 cm. Samples were then transferred to the Rock Mechanics Laboratory at Tarbiat Modarres University, where rock cores were prepared with a core-drilling machine. The ratio of the length to the diameter of core samples was found to be approximately two. The edges of the cores were subsequently cut parallel and smoothed. Rock mechanics tests were carried out on the 93 core samples prepared from the travertine rock blocks. Porosity (n%), P-wave velocity [Vp (Km/s)], Schmidt rebound hardness (Rn), Is (MPa), and UCS (MPa) were the primary physical and mechanical properties measured by the laboratory tests, in accordance with the methods recommended by the ISRM [20].

Histogram plots for each test are presented in Fig. 2. The UCS values ranged between 37.5 and 67.8 MPa (with a median value of 54.07 MPa). Based on the ISRM [20] UCS classification, the rock samples were categorized as medium (25–50 MPa) to high (50–100 MPa) strength rocks.

Fig. 2
figure 2

Histogram plots for the individual tests including Vp (km/s), Rn, n%, Is (MPa), and UCS (MPa)

Full size image

2.2 Multiple linear and nonlinear regression models

In order to identify the relationships between multiple independent or explanatory variables (Xi) and a dependent variable (Yi), multiple linear regression (MLR) was used, based on the assumption of linearity between Xi and Yi. The MLR equation is shown in Eq. (1) [21, 22].

$$Y = a + \beta_{1} X_{1} + \cdots + \beta_{k} X_{k}$$
(1)

where k denotes the number of observed values, \(a\) represents the intercept, and \(\beta\) is the slope or coefficient.

A multiple nonlinear regression (MNLR) model was also used. In contrast to MLR, MNLR assumes a nonlinear association between the dependent variable Yi and the explanatory variables Xi. The MNLR formula is shown in Eq. (2) [22, 23].

$$Y = a + \beta_{1} X_{i} + \beta_{2} X_{j} + \beta_{3} X_{i}^{2} + \beta_{4} X_{j}^{2} + \cdots + \beta_{k} X_{i} X_{j}$$
(2)

where \(a\) denotes the intercept, \(\beta\) represents the slope (also called the regression coefficient), and k is the number of observed values. For predictions, fitted multiple regression equations can be used to estimate the value of Y with new known values of X.

2.3 Objective model 1: Random Forest

The first objective algorithm used in this study was the random forest (RF), a model created by Ho [24]. An extension of the algorithm was later developed by Breiman [25]. The RF, known as an ensemble method, produces a set of repeated predictions of the same phenomenon by combining multiple decision tree algorithms. The RF includes a set of tree-structured classifiers {h(x, k), k = 1,…}, where {k} represents independent and identically distributed random vectors, in which each tree casts a unit vote for the most widespread class at input x [25].

Decision trees can be grouped into classification or regression types. For classification purposes, an RF considers a class vote from each tree and subsequently classifies the features that receive the majority of votes. In contrast, for regression purposes, the predicted values from each tree at a target point, x, are averaged [26]. A set of conditions form a regression tree (RT), which is organized from a root to a terminal node [27, 28]. An RT is introduced through recursive splitting and by performing multiple regressions on the model’s training dataset. For each internal node of a rule (of the tree), data partitioning is performed repeatedly until a previously-specified stop condition is reached. Each terminal node, or leaf, has a simple regression model attachment applied specifically to that node section. Upon completion of the tree’s induction process, pruning action is used to ameliorate the tree’s generalization capacity by minimizing its structural complexity. In each node, the number of cases can be considered as the pruning criteria [29].

According to Breiman et al. [27], the RT’s induction process needs to select the optimal splitting measurement vectors at an initial stage. Binary splits are created by dependent variables or the parent node (root), in which the child nodes are purer than the roots. Throughout this step, the RT explores all candidate splits to discover the best split, s, which maximizes the purity of the produced tree (as indicated by the largest reduction in the impurity). The RF model structure used for the prediction of UCS is shown in Fig. 3. The equation for the reduction in impurity that results from a given split is shown in Eq. (3).

$$\Delta i\left( {s,t} \right) = i\left( t \right) - p_{L} i\left( {t_{L} } \right) - p_{R} i\left( {t_{R} } \right)$$
(3)

where s represents a particular split at node t, in which node t is divided by s into two different child nodes; the left child node (tL) and the right child node (tR). The pL and pR are the proportion of data cases in t partitioned to the tL and tR, respectively. The impurity measure at node t is defined by i(t) and the impurity for the left and right child nodes are defined by (tR) and i(tL), respectively. Δi(s,t) is the difference between the impurity measure for node t and the impurity measures for the tR and tL.

Fig. 3
figure 3

An illustration of the RF model structure used for the prediction of UCS

Full size image

2.4 Objective model 2: M5 Model Tree

The second objective algorithm used in the current study, the M5 model tree, was first proposed by Quinlan [30]. This model, with linear regression functions at the terminal (leaf) nodes, has been used for continuous-class learning purposes and more recently for engineering problems [29,30,31]. The M5 model tree is a type of binary decision tree, which is generally applied to categorical datasets. Furthermore, the algorithm can be applied to quantitative data, which is an advantage in comparison with other tree-based regression models [30, 33].

The M5 model tree is developed in two steps [34, 35]. In the first step, the input-target data are divided into subcategories, and a decision tree is created. The division of the data is carried out based on two factors; first, the treatment of the standard deviation of the class values, and second, the calculation of the expected decrease in this error as a consequence of testing each attribute at that node [36]. The standard deviation reduction (SDR) is computed, as shown in Eq. (4) [37].

$${\text{SDR}} = {\text{sd}}\left( T \right) - \sum \frac{{\left| {T_{i} } \right|}}{T} {\text{sd}}\left( {T_{i} } \right)$$
(4)

where T expresses a set of examples that reach the node, Ti denotes the subset of examples that have the ith outcome of the potential set, and sd represents the standard deviation of the class values [34, 38].

As a result of the division process, the data in the child nodes have a smaller standard deviation than that of the parent nodes, and therefore, provide purer nodes. Next, the M5 model tree selects nodes with the highest expected error reduction after scanning all of the possible divisions in the resulting tree structure. As a result of this division, a large tree-like structure is frequently produced, which in turn, can cause over-fitting. The overgrown tree can be pruned by replacing sub-trees by linear regression functions in the second step of the modeling to avoid overfitting. By pruning, the accuracy of estimation can be significantly increased. Overall, the input space is divided into areas (i.e., the subspaces) and a linear regression model is created for each area [39]. The M5 model tree structure used for the prediction of UCS is provided in Fig. 4.

Fig. 4
figure 4

An illustration of the M5 model tree structure for prediction of UCS

Full size image

2.5 Objective model 3: Multivariate Adaptive Regression Splines

The third objective model used in this study, the multivariate adaptive regression splines (MARS) model, was initially proposed by Friedman [40]. MARS is a multivariate nonparametric technique used to predict continuous numeric results. MARS is a flexible technique for organizing relationships that contain interactions between a few variables; it can lead to a significant degree of accuracy in solving engineering problems (e.g., [31, 32]). Furthermore, the MARS model can estimate the basic practical relationship between input and output variables without any set assumptions [40, 41].

The MARS model aims to divide the solution space (i.e., the input-target matrix) into various intervals that indicate the feature space of the indicator variables. The individual splines are then fit to each interval [40]. Subsequently, for each data interval, a unique mathematical regression equation is determined. For each interval of the independent variable, a relationship to the output of the modeled system is developed according to the established mathematical equations. Every spline function is considered on a given interval, and the endpoints of the interval are called knots. This process can be carried out in two stepwise methods, forward and backward. A set of appropriate inputs are selected in the forward stepwise approach and consequently split, generating an over-fitted model with a high number of knots. In the backward procedure, which aims to improve prediction accuracy, the unnecessary variables are then removed from the previously selected set [42]. In order to uproot the repetitive knots, a pruning technique is used. The “basis function” (BF) is used to demonstrate each distinct interval of predictors, which are formed, as shown in Eqs. (5) and (6) [43].

$$Y = \hbox{max} \left( {0, X - c} \right)$$
(5)
$$Y = \hbox{max} \left( {0, c - X} \right)$$
(6)

where X is a predictor variable and c is a threshold value. In order to maintain the coherency of the BFs, two close splines are intersected at a knot. Accordingly, the function is connected to every input variable, which is used to characterize the location of the knots [42, 44]. The MARS model employs a two-sided truncated power function as the spline BFs, as shown in Eqs. (7) and (8) [45].

$$\left[ { - \left( {x - t} \right)} \right]_{ + }^{q} = \left\{ {\begin{array}{*{20}l} {\left( {t - x} \right)^{q} } \hfill & {{\text{if}}\;x < t} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(7)
$$\left[ { + \left( {x - t} \right)} \right]_{ + }^{q} = \left\{ {\begin{array}{*{20}l} {\left( {t - x} \right)^{q} } \hfill & {{\text{if}}\;x \ge t} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(8)

where \(q \left( { \ge 0} \right)\) represents the power to which the splines are raised, along with the degree of evenness of the resulting function. A schematic view of the MARS model structure for the prediction of UCS is shown in Fig. 5.

Fig. 5
figure 5

An illustration of the MARS structure for prediction of UCS

Full size image

2.6 Ensemble model: the ANN-committee-based model

Previous studies (e.g., [7, 43, 46]) that designed and evaluated ensemble-based models revealed their improved performances in comparison with individual (standalone) machine learning models in a number of engineering problems. To develop an ensemble model for UCS prediction in the present study, the ANN-committee-based model, which is a multi-model ensemble framework, was used. A feed-forward multilayer perceptron (MLP) was employed to construct the ANN-committee model. The MLP was organized into three layers, including an input, one or more hidden layers, and an output layer, as shown in Eq. (9) [7, 46, 47].

$$\hat{y}_{k} = f_{o} \left[ {\mathop \sum \limits_{i = 1}^{{M_{N} }} W_{kj} .f_{h} \left( {\mathop \sum \limits_{i = 1}^{{N_{N} }} W_{ji} X_{i} + W_{j0} } \right) + W_{k0} } \right]$$
(9)

where \(f_{\text{h}}\) is the activation function of the hidden neuron, \(f_{\text{o}}\) is the activation function of the output neuron, \(\hat{y}_{k}\) are the computed output variables, \(N_{N}\) is the number of neurons in the input layer, \(M_{N}\) is the number of neurons in the hidden layer, \(W_{ji}\) is a weight in the hidden layer connecting the \(i\) th neuron in the input layer and the jth neuron in the hidden layer, \(W_{j0}\) is the bias for the jth hidden neuron, \(W_{kj}\) is a weight in the output layer connecting the jth neuron in the hidden layer and the kth neuron in the output layer, \(W_{k0}\) is the bias for the kth output neuron, and \(X_{i}\) is the ith input variable for the input layer.

The structure of the developed ANN ensemble committee-based model utilizing the input, hidden layer, and output layer neurons, and used for the prediction of UCS, is shown in Fig. 6.

Fig. 6
figure 6

An illustration of the ANN ensemble committee-based model structure for the prediction of UCS

Full size image

2.7 Model design framework

In this study, three different machine learning regression models, including the M5 model tree, MARS, and RF, were explored for the prediction of travertine UCS, with data obtained from the Azarshahr area in northwestern Iran. The input matrix (x) defined by Vp, Rn, n%, and Is datasets represented the predictor variables, and the target variable (y), defined by UCS, were used in each tree-based model. Seventy percent of the original dataset was randomly selected for the training phase, and the remainder of the dataset was partitioned for the validation (15%) and testing (15%) phases. Before developing the machine learning models, all variables were normalized to a value between zero and one by a scaling factor to guarantee that all input-target variables received equal attention during the training phase.

All models were implemented using the MATLAB software on an Intel(R) core i7-4470CPU @ quad-core 3.74 GHz computer system. To develop the RF model, the initial number of weak learners (i.e., regression trees) was set to 800, and the initial number of leaves in each tree was set to five, the default of the Bagger algorithm [48]. Notably, no universal mathematical formula is used to set the optimum number of trees [49]. Generally, a larger number of trees generates more accurate results but increases computational cost.

The M5 model tree was constructed using a set of tuning parameters for model initialization. A minimum tree split value of five, a smoothing value of 15, and a split threshold value of 0.05 were selected, as suggested by Yaseen et al. [32] and Deo et al. [50, 51]. The model was pruned to prevent over-fitting of the model to the data, which has the dual purpose of implementing the “divide-and-conquer rule” in which the problem is broken down by splitting it into several smaller problems [34,35,36,37,38,39,40,41,42,43,44]. In order to improve prediction accuracy, the sharp discontinuities generated as a result of joining multiple piece-wise linear regression functions were eliminated during the smoothing process [38]. The model found the optimum number of decision trees (or ‘rules’) to be seven, as this value attained the smallest RMSE in the training step.

The MARS model was constructed using the ARESLab toolbox and followed the approach of earlier studies [31, 32, 43, 50, 51]. Generally, the MARS modeling process consisted of two stages: the forward and backward stages. In the forward stage, the reflected pair(s) of the BFs were added and the potential knots were identified to obtain the greatest decrease in the training error (RMSE). The approximate number of available knot locations, which are controlled using midspan and endspan, were found to be ten, eight, ten, and ten for x1 (Vp (km/s)), x2 (Rn), x3 (n%), and x4 (Is (MPa)) inputs, respectively. The number of BFs in the model after the forward stage was found to be 21. It is important to note that over-fitting of the modeled data is a risk when a large model is generated at the end of the forward phase. Therefore, by deleting a set of redundant BFs through a backward procedure, the MARS model was pruned to achieve a model that only included the intercept term [32]. The total effective number of parameters after the backward stage was found to be 23. The BFs and the optimal prediction functions of the developed MARS model are provided in Table 2.

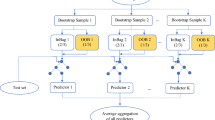
Table 2 Basis functions and optimal function for MARS-based UCS prediction
Full size table

Following the construction and evaluation of the standalone (i.e., MARS, RF, M5 tree) models, integration of the predicted UCS values from the three developed machine learning models was performed to improve the prediction accuracy of the UCS data, and for subsequent use in an ANN model. The predicted UCS values simulated from the standalone models were employed as the ANN-committee-based model’s inputs, and the measured UCS values were given as the target (output) of the ANN model. In accordance with earlier studies [43], the utilization of the output of each standalone model in the final predictive model (i.e., the ANN) was done to better assimilate data features present in the predictor variables, as some of these features may not have been fully identifiable by the individual standalone models. To develop an optimal ANN-committee-based model, the Levenberg–Marquardt (LM) training algorithm was used to design a three-layered feed-forward neural network model. The LM minimizes the mean square error (MSE) between the predicted and measured UCS values by applying a computationally efficient second-order training technique. The optimal number of hidden neurons was selected by considering a value set by log (N) and (2n + 1), where N and n are the numbers of training samples and input neurons, respectively, as recommended by Wanas et al. [52], Mishra and Desai [53], and Barzegar et al. [7, 46, 54]. In this case, the number of neurons in the hidden layer was set to four. The sigmoid and linear functions were selected as the hidden transfer and output functions between layer two and three, respectively, with a learning rate and a momentum factor of 0.1. Through an iterative modeling process, the best validation performance was attained at 10 epochs, based on an MSE of approximately 9.551 × 10−1 MPa. After training and validation of the ANN ensemble committee-based model, the testing phase, in which an independent test dataset was used to evaluate the final predictive model, was established.

2.8 Statistical performance evaluation

Statistical metrics were used to assess the performance of the models in this study. These metrics are comprised of the correlation coefficient (r), root mean square error (RMSE), mean absolute error (MAE), and their normalized equivalents expressed in percentages (RRMSE and RMAE). The basic equations of these metrics are shown in Eqs. (10) to (14).

$$r = \frac{{\mathop \sum \nolimits_{i = 1}^{i = N} \left[ {\left( {{\text{UCS}}_{i}^{\text{meas}} - \overline{\text{UCS}}^{\text{meas}} } \right).\left( {{\text{UCS}}_{i}^{\text{pred}} - \overline{\text{UCS}}^{\text{pred}} } \right)} \right]}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{i = N} \left( {{\text{UCS}}_{i}^{\text{meas}} - \overline{\text{UCS}}^{\text{meas}} } \right)^{2} .\sqrt {\mathop \sum \nolimits_{i = 1}^{i = N} \left( {{\text{UCS}}_{i}^{\text{pred}} - \overline{\text{UCS}}^{\text{pred}} } \right)} } }} \quad {\text{where}}, - 1 \le r \le 1$$
(10)
$${\text{RMSE}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{i = N} \left( {{\text{UCS}}_{i}^{\text{meas}} - {\text{UCS}}_{i}^{\text{pred}} } \right)^{2} }$$
(11)
$${\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{i = N} \left| {{\text{UCS}}_{i}^{\text{meas}} - {\text{UCS}}_{i}^{\text{pred}} } \right|$$
(12)
$${\text{RRMSE}} = 100\times\frac{\text{RMSE}}{{\overline{\text{UCS}}^{\text{meas}} }}$$
(13)
$${\text{RMAE}} = 100\times\frac{\text{MAE}}{{\overline{\text{UCS}}^{\text{meas}} }}$$
(14)

where N is the number of data points, \({\text{UCS}}_{i}^{\text{meas}}\) and \({\text{UCS}}_{i}^{\text{pred}}\) are the \(i\)th measured and predicted UCS values, respectively, and \(\overline{\text{UCS}}^{\text{meas}}\) and \(\overline{\text{UCS}}^{\text{pred}}\) are the mean of measured and predicted UCS values, respectively.

The covariance of the observed data, which is explained by the prediction model, was described by r. RMSE and MAE, which are represented in their absolute units, show the accuracy of the models as described by their goodness-of-fit. Moreover, RRMSE, which compares the percentage of deviation between the predicted and measured data, was used to evaluate the models’ precision. The RMAE was used to determine the average magnitude of total absolute bias error (in percent) between predicted and measured data.

The previously described statistical metrics demonstrate the linear agreement between the measured and predicted values in a modeling system. However, these metrics can be excessively sensitive to outliers in the measured data, while showing insensitivity to the additive or relative differences between predictions and measurements [32, 55, 56]. To overcome these challenges, two normalized performance indicators, the Willmott’s Index (WI) and Legates and McCabe Index (LMI), were used. The mathematical formulations associated with these metrics are given in Eqs. (15) and (16).

$${\text{WI}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{i = N} \left( {{\text{UCS}}_{i}^{\text{meas}} - {\text{UCS}}_{i}^{\text{pred}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{i = N} \left( {\left| {{\text{UCS}}_{i}^{\text{pred}} - \overline{\text{UCS}}^{\text{meas}} } \right| + \left| {{\text{UCS}}_{i}^{\text{meas}} - \overline{\text{UCS}}^{\text{meas}} } \right|} \right)^{2} }}} \right]$$
(15)
$${\text{LMI}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{i = N} \left| {{\text{UCS}}_{i}^{\text{meas}} - {\text{UCS}}_{i}^{\text{pred}} } \right|}}{{\mathop \sum \nolimits_{i = 1}^{i = N} \left| {{\text{UCS}}_{i}^{\text{meas}} - \overline{\text{UCS}}^{\text{meas}} } \right|}}} \right]$$
(16)

Note that the LMI has an advantage over WI when relatively high predicted values are expected, even for a poorly fitted model.

2.9 Results and discussion

Simple regression analysis was used to determine the relationships between the predicted (i.e., UCS) and predictor variables (i.e., Vp, Rn, n% and Is) (Table 3). The relationships between UCS and the predictor variables were analyzed using linear, exponential, power, and logarithmic functions. A meaningful relationship between UCS and Is (i.e., 0.7715 < r < 0.7726) was found, which was in accordance with several studies [53, 57, 58]. Conversely, weaker relationships were observed between UCS and the other input variables; Vp yielded a value of 0.4917 < r < 0.5078, Rn yielded a value of 0.5930 < r < 0.6093, and n% yielded a value of 0.5463 < r < 0.5842. These poor relationships may have been due to the use of different travertine rocks with diverse characteristics from the study area.

Table 3 Results of simple regression analyses for prediction of UCS
Full size table

In addition to the simple regression analysis, a correlation analysis was carried out between the predicted and predictor variables. In previous studies, it has been demonstrated that n% is the main control factor for the durability and strength of rock, and can thus influence Rn, Is, and UCS [59,60,61]. It has also been reported that increasing porosity was linked with decreasing UCS [61,62,63]. However, the results (Table 4) of the present study showed weak correlations between Vp and n% (r = − 0.003), and Rn and n% (r = − 0.162). Additionally, moderate correlations were found between Vp and Is (r = 0.458), Rn and Is (r = 0.511), and n% and Is (r = − 0.419), reinforcing the study’s objective to employ models based on multiple input parameters for the prediction of UCS, namely multiple regression and machine learning models.

Table 4 Correlation matrix of independent variables
Full size table

In the execution of multiple regression modeling, which included the MLR and MNLR procedures, the same datasets as the machine learning models were used. Implementation of the MLR and MNLR procedures yielded Eqs. (17) and (18), respectively, for the prediction of UCS. The MLR model obtained an r of 0.626, an RMSE of 7.527 MPa, and an MAE of 5.580 MPa. The MNLR yielded an r of 0.721, an RMSE of 6.172 MPa, and an MAE of 4.570 MPa, which highlighted the greater accuracy of nonlinear models, in comparison with linear models, for the prediction of UCS.

$$UCS = 2.96 + 0.43V_{p} + 0.46R_{n} - 0.78n + 6.90I_{s}$$
(17)
$${\text{UCS}} = 16.02 - 19.90V_{p} - 1.79R_{n} - 3.58n + 45.93I_{s} + 2.29V_{p}^{2} + 0.02R_{n}^{2} + 0.23n^{2} - 4.31I_{s}^{2}$$
(18)

Sensitivity analysis was used to evaluate the relative influence of input variables on the models’ output variable using the relative strength of effect (RSE) method. In this method, all data pairs were used to construct a data array X [64,65,66].

$$X = \left\{ {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{i} , \ldots ,x_{n} } \right\}$$

where the variable \(x_{i}\) in the array X is the vector of length m, shown as:

$$x_{i} = \left\{ {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{im} } \right\}$$

The RSE for the input unit “i” on the output unit “j”, between dataset \(X_{i}\) and \(X_{j}\) is calculated using Eq. (19).

$${\text{RSE}} = \frac{{\mathop \sum \nolimits_{k = 1}^{m} x_{ik} x_{jk} }}{{\sqrt {\mathop \sum \nolimits_{k = 1}^{m} x_{ik}^{2} \mathop \sum \nolimits_{k = 1}^{m} x_{jk}^{2} } }}$$
(19)

Figure 7 shows the calculated RSE values for the four input variables, with Is (MPa) (with an RSE of 0.993) having the highest impact on UCS prediction modeling. The variable n% had the lowest impact on UCS prediction modeling.

Fig. 7
figure 7

The relative impact of the input variables on the model output

Full size image

Table 5 shows a comparison of the statistical performances of the RF, M5 tree and MARS models, as well as the ANN-based ensemble model, in predicting UCS in travertine rocks. Statistical performance metrics (r, RMSE, and MAE) are provided for both the training and validation phases of each model. All standalone machine learning models that were trained and validated showed high values of r and low values of RMSE and MAE.

Table 5 Statistical metrics for each model’s performance evaluation in the training and validation phases
Full size table

Following the training and validation phases of the standalone machine learning models, the viability of the models for the prediction of UCS data was established through a testing phase. The statistical performance of the developed models, in terms of UCS prediction during the testing phase, is given in Table 6. Based on the calculated statistical indicators, the MARS model (r = 0.830, RMSE = 5.588 MPa, MAE = 4.461 MPa, WI = 0.997, and LMI = 0.359) obtained superior performance followed by the M5 tree (r = 0.572, RMSE = 8.147 Mpa, MAE = 5.745 MPa, WI = 0.993, and LMI = 0.175) and RF (r = 0.488, RMSE = 8.071 MPa, MAE = 6.436 MPa, WI = 0.600, and LMI = 0.076) models. The LMI has greater robustness than the WI and is thus always lower than the WI. In the current study, LMI was very low for the M5 tree and RF models, but relatively good for the MARS model. Additionally, the relative errors (i.e., RRMSE and RMAE) were low for all the single models (MARS = 11.24%, 8.99% vs. M5 tree = 16.68%, 12.38% and RF = 16.24%, 14.29%). It was also observed that the predicted values of UCS obtained using the MARS model were closer to the measured UCS values than in the M5 tree and RF models. The MARS model also showed the highest r-value, as well as fit by the linear regression equation (UCSpred = 1.032 UCSmeas + 0.013). This indicated, along with the other metrics used, that the MARS model outperformed the other standalone models. The superior performance of the MARS model may be the result of more effective feature identification resulting from the use of several cubic splines at different intervals in the input-target dataset.

Table 6 Statistical metrics of each model’s performance evaluation in the testing phase
Full size table

The ensemble model was then developed to integrate the advantages of each standalone machine learning model. After training and validation of the ANN-based committee model, the testing phase was executed. Based on the results given in Table 6, the ensemble model yielded an r of 0.890, an RMSE of 3.980 MPa, an MAE of 3.225 MPa, a WI of 0.931, and an LMI of 0.237, with a lower scatter than each of the standalone models, and a linear regression equation of UCSpred = 0.899 UCSmeas + 6.696.

Generally, results showed that the ensemble model improved the performance of the standalone machine learning models. Measured and predicted values of UCS by the RF, M5 tree, MARS, and ensemble models in the testing phase are compared in Fig. 8. It was observed that the ensemble model was the most efficient in predicting low and high USC values. The comparison between the simple multiple variable regression models and machine learning models for predicting UCS indicated that the performance of the RF and M5 tree models were relatively poor and that the MARS and ensemble models were superior. The improved performance of the AI models over the statistical approaches was confirmed, supporting the results of other studies [9, 11, 64, 67].

Fig. 8
figure 8

Measured and predicted UCS (MPa) values for travertine rocks by a RF, b M5 tree, c MARS, and d ensemble models in the testing phase

Full size image

2.10 Conclusions

In this study, 93 core samples were collected from travertine rocks in the Azarshahr area of northwestern Iran. Laboratory tests, including P-wave velocity (Vp (Km/s)), Schmidt Hammer (Rn), porosity (n%), point load index (Is (MPa)), and UCS (MPa), were carried out on the samples according to the ISRM. Simple regression analysis demonstrated a meaningful relationship between UCS and Is and a relatively weak relationship between USC and the other measured parameters, which may have been the result of the use of different travertine rocks with diverse characteristics from the study area. Furthermore, poor to moderate correlations existed between the input variables. Therefore, nonlinear machine learning models based on multi-input parameters were required to accurately predict UCS. In this case, the dataset used included Vp, Rn, n%, and Is as the input variables and UCS as the target variable for the tree-based machine learning models (e.g., MARS, RF, and M5 tree).

After training and validation, the MARS model (r = 0.830, RMSE = 5.588 MPa, MAE = 4.461 MPa, WI = 0.997, and LMI = 0.359) showed superior performance in the testing phase for prediction of UCS, followed by the M5 tree and RF models. An ensemble model based on an ANN-committee was implemented to integrate the advantages of each single machine learning model. The ensemble model yielded an r of 0.890, RMSE of 3.980 MPa, MAE of 3.225 MPa, WI of 0.931, and LMI of 0.237, which improved the prediction of UCS in comparison to the standalone models. In addition, the superiority of the machine learning models over the multiple linear and nonlinear models was confirmed. Sensitivity analysis was also applied to assess the relative influence of input variables on the models’ output variable using the relative strength of effect (RSE) method. The calculated RSE values showed that the Is, with an RSE of 0.993, and n%, with an RSE value of 0.8, had the highest and lowest impacts, respectively, on predicting UCS.

Future research should use the models proposed in the current study to predict the UCS of other rock types, such as sedimentary, volcanic, and metamorphic, in different parts of the world. Applying and comparing other ensemble techniques, for example, bagging, boosting, and voting, provides an additional opportunity for future research. Furthermore, other machine learning models (e.g., extreme learning machine and deep learning models) could be applied for modeling the UCS of different rock types.