Optimal design of fractional-order PID controller for five bar linkage robot using a new particle swarm optimization algorithm

Abstract

This paper introduces a new version of the particle swarm optimization (PSO) method. Two basic modifications for the conventional PSO algorithm are proposed to improve the performance of the algorithm. The first modification inserts adaptive accelerator parameters into the original velocity update formula of the PSO which speeds up the convergence rate of the algorithm. The ability of the algorithm in escaping from local optima is improved using the second modification. In this case, some particles of the swarm, which are named the superseding particles, are selected to be mutated with some probability. The proposed modified PSO (MPSO) is simple to be implemented, fast and reliable. To validate the efficiency and applicability of the MPSO, it is applied for designing optimal fractional-order PID (FOPID) controllers for some benchmark transfer functions. Then, the introduced MPSO is applied for tuning the parameters of FOPID controllers for a five bar linkage robot. Sensitivity analysis over the fractional order of the PID controller is also provided. Numerical simulations reveal that the MPSO can optimally tune the parameters of FOPID controllers.

1 Introduction

The main goal of an optimization algorithm is to seek values for a set of parameters that maximize/minimize objective functions subject to some constraints. Some of the optimization algorithms are traditional optimization techniques which use exact methods to find the best solution. If an optimization problem is solvable, then the traditional optimization algorithms can discover the global best solution. However, as the search space increases the computation and implementation costs of the exact algorithms are increased. Therefore, when the search space complexity increases, the exact algorithms are slow to find the global optimum. Linear and nonlinear programming, brute force or exhaustive search and divide and conquer methods are some of the exact-based optimization methods.

Calculus provides the tools for finding the optimum of many objective functions. Calculus-based methods can quickly find a single optimum but require a search scheme to find the global optimum. Continuous functions with analytical derivatives are necessary. If there are too many variables, then it is difficult to find all the optimum points. In such algorithms, the gradient of the objective function serves as the compass heading pointing to the steepest downhill path. It works well when the optimum is nearby, but cannot deal with cliffs or boundaries, where the gradient cannot be calculated.

Other optimization algorithms are heuristic algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), ant colony optimization (ACO), simulated annealing (SA), harmony search (HS), etc. Heuristic algorithms have several advantages compared to the other algorithms as follows (Wang et al. 2005):

• 1. Heuristic algorithms can be easily implemented.

• 2. They can be used efficiently in a multiprocessor environment.

• 3. They are able to deal with both continuous and discrete optimization problems.

One of the applied and well-known heuristic optimization methods is the particle swarm optimization. The PSO is a population-based searching technique proposed in 1995 (Kennedy and Eberhart 1995) as an alternative to the genetic algorithm. Its development is based on the observations of social behavior of animals such as bird flocking and fish schooling. Compared to GA, PSO has some attractive characteristics. First, PSO has memory which utilizes the knowledge of good solutions retained by all particles, whereas in GA, previous knowledge of the problem is destroyed once the population is updated. Second, PSO has constructive cooperation between particles and particles in the swarm share their information (Hung et al. 2008).

However, trapping in local optima and slow convergence rate are two main weaknesses of the original heuristic PSO. In order to improve the performance of the PSO and to overcome the above-mentioned weaknesses of the PSO, many studies have been performed in the literature. In Eberhart and Shi (2001), a random inertia weight PSO method (RPSO) has been proposed for tracking dynamic systems. Another new version of the PSO which modifies the velocity update formula of the original PSO, is the constriction factor approach PSO (CPSO) (Clerc and Kennedy 2002). In Ratnaweera et al. (2004), a simple PSO with time-varying acceleration coefficients has been proposed. The idea in Ratnaweera et al. (2004) is to have a high diversity for early iterations and a high convergence for late iterations. Meissner et al. (Van den Bergh and Engelbrecht 2002) have introduced a guaranteed convergence PSO which addresses the problem of stagnation and increases local convergence by using the global best particle to randomly search in an adaptively changing radius at every iteration. In Chen et al. (2010), a PSO-based intelligent decision algorithm has been constructed for VLSI floor planning problem. Forecasting of financial time series using a support vector machine optimized by PSO has been carried out in Zhiqiang et al. (2013). Tassopoulos and Beligiannis (2012) have proposed a PSO based parametric optimization method to solve effectively the school timetabling problem. However, since most of the above-mentioned works have been proposed some hybrid models for the improvement of the original PSO, they are either so complex to be implemented in real world situations or they are with high computational complexity.

Proportional–Integral–Derivative (PID) control is one of the earliest control strategies. It has been widely used in the industrial control field. Its widespread acceptability can be recognized by the familiarity with which it is perceived amongst researchers and practitioners within the control community, simple structure and effectiveness of algorithm, relative ease and high speed of adjustment with minimal down-time and wide range of applications where its reliability and robustness produce good control performances (Gaing 2004).

Fractional calculus, with more than 300 years old history, is a classical mathematical idea which allows to arbitrary (non-integer) order differentiation and integration. Although it has a long history, its applications to physics and engineering are only a recent subject of interest. It has been recognized that many systems in interdisciplinary fields can be elegantly described with the help of fractional-order differential equations. On the other hand, fractional order controllers may be employed to achieve feedback control objectives for such systems. Modeling and control topics using the concept of fractional order systems have recently attracted more attentions because of the introduction of useful applications (Podlubny 1999; Aghababa 2014a, b, c, 2015a, b, c, d).

Recently, fractional calculus has been used for designing fractional-order PID (FOPID) controllers. Various studies have demonstrated that the FOPID controllers improve the performance and robustness of the traditional PID controllers (Lee and Chang 2010). However, successful applications of FOPID controllers require the satisfactory tuning of five parameters: the proportional gain, the integrating gain, the derivative gain, the integrating order and the derivative order. Traditionally, these parameters have been determined by a trial and error approach. Manual tuning of FOPID controller is very tedious, time consuming and laborious to implement, especially where the performance of the controller mainly depends on the experiences of design engineers. Of late, some parameter tuning methods have been proposed to reduce the time consumption for determining the five controller parameters. The most well-known tuning method is the Ziegler–Nichols tuning formula (Valerio and Costa 2006), which determines suitable parameters by observing a gain and a frequency on which the plant becomes oscillatory.

More recently, artificial intelligence techniques such as electromagnetism-like algorithm (Lee and Chang 2010), fuzzy logic (Das et al. 2012), PSO and GA approaches (Bingul and Karahan 2012) and artificial bee colony (Rajasekhar et al. 2011) have been applied to improve the performance of the FOPID controllers. A set of tuning rules for standard (integer-order) PID and fractional-order PID controllers has been proposed in Padula and Visioli (2011). In the above-mentioned studies, it has been shown that the intelligent-based approaches provide good solutions in tuning the parameters of the FOPID controllers. However, there are several causes for developing improved techniques to design FOPID controllers. One of them is the important impact it may give because of the general use of the controllers. The other one is the enhancing operation of FOPID controllers that can be result from improved design techniques. Finally, an optimal tuned FOPID controller is more interested in real-world applications.

This paper proposes a modified new version of the standard PSO algorithm as an alternative numerical optimization algorithm. Two main modifications are proposed for improving the performance of the traditional PSO. The first modification inserts adaptive accelerator parameters into the original velocity update formula of the PSO to speed up the convergence rate of the algorithm. The second modification improves the ability of the original PSO algorithm in escaping from local optima trap. The idea is to introduce some mutated particles, which are named superseding particles, to the swarm to enhance the diversification property of the algorithm. The proposed modified PSO (MPSO) is applied for determining the optimal parameters’ values of the FOPID controllers. The problem of designing FOPID controller is first formulated as an optimization problem. Then, the objective function is defined as minimization of four performance indexes, namely the maximum overshoot, the settling time, the rise time and the integral absolute error of step response. Subsequently, an optimal FOPID controller is designed for a five bar linkage manipulator robot using the developed MPSO. The advantages of this methodology are its simplicity in theory and practice as well as its less computation burden, high-quality solution and speedy convergence.

The rest of this paper is organized as follows: In Sect. 2, preliminaries of the fractional derivatives are given. Section 3 deals with the introduction of the proposed modified PSO algorithm. The design procedure of the fractional PID controller for some typical benchmark transfer functions is presented in Sect. 4. In Sect. 5, the modified PSO method is applied for designing a fractional PID controller for a five-bar-linkage manipulator robot. At last, this paper ends with some concluding remarks in Sect. 6.

2 Preliminaries

In what follows, first some basic definitions of fractional calculus are given. Subsequently, the integer-order approximation of the fractional derivatives is presented.

2.1 Fractional calculus

The basic definitions of the fractional calculus are as follows (Podlubny 1999):

Definition 1

The $\alpha$th-order fractional integration of function f(t) is defined as below.

$$\begin{aligned} {}_{t_0 } D_{t}^{-\alpha } f(t)=\frac{1}{{\Gamma }(\alpha )}\mathop \int \limits _{t_0 }^t \frac{f(\tau )}{( {t-\tau })^{1-\alpha }}\mathrm{d}\tau , \end{aligned}$$

(1)

where $\Gamma (.)$ is the Gamma function.

Definition 2

The Riemann–Liouville fractional derivative of order $\alpha$ of function f(t) is defined as follows:

$$\begin{aligned} _{t_0 } D_t^\alpha f( t)=\frac{\mathrm{d}^\alpha f(t)}{\mathrm{d}t^\alpha }=\frac{1}{{\Gamma }(m-\alpha )}\frac{\mathrm{d}^m}{\mathrm{d}t^m}\mathop \int \limits _{t_0 }^t \frac{f(\tau )}{( {t-\tau })^{\alpha -m+1}}\mathrm{d}\tau , \end{aligned}$$

(2)

where $m-1<\alpha \le m$ and $m\in N$.

Definition 3

The Caputo fractional derivative of order $\alpha$ of a function f(t) is given by

$$\begin{aligned} _{t_0 } D_t^\alpha f( t)=\left\{ \begin{array}{*{20}l} {\frac{1}{{\Gamma }( {m-\alpha })}\mathop \int \limits _{t_0 }^{t}\frac{f^{(m)}( \tau )}{( {t-\tau })^{\alpha -m+1}}\mathrm{d}\tau ,\quad m-1<\alpha <m} \\ \frac{\mathrm{d}^m}{\mathrm{d}t^m}f(t),\quad \alpha =m, \\ \end{array} \right. \end{aligned}$$

(3)

where m is the smallest integer number larger than $\alpha$.

The Laplace transform of the Caputo fractional derivative becomes as follows (Podlubny 1999):

$$\begin{aligned} L\{ {_{t_0 } D_t^\alpha f( t)} \}=s^\alpha F( p)-\mathop \sum \limits _{k=1}^{m-1} s^{\alpha -k-1}f^{( k)}(0), \end{aligned}$$

(4)

where p is the Laplace operator.

Equation (4) means that, if zero initial conditions are assumed, systems with a dynamic behavior described by differential equations involving fractional derivatives give rise to transfer functions with fractional powers of s.

2.2 Integer-order approximation of fractional derivative

In both simulations and hardware implementations, the most common way of making use of transfer functions involving fractional powers of s is to approximate them with integer-order transfer functions with a similar behavior. So as to completely imitate a fractional transfer function, an integer transfer function would have to contain an infinite number of poles and zeroes. However, it is possible to obtain practical approximations with a finite number of zeroes and poles. One of the well-known approximations has been proposed in Oustaloup et al. (2000) and makes use of a recursive distribution of poles and zeroes. The approximating transfer function is given by

$$\begin{aligned} s^v\approx k\mathop \prod \limits _{n=1}^N \frac{1+( {s/\omega _{z,n} })}{1+( {s/\omega _{p,n} })},\quad v>0, \end{aligned}$$

(5)

where k is a gain and adjusted so that both sides of (5) shall have unit gain at 1 rad/s, and N is the number of poles and zeroes.

Remark 1

Approximation (5) is valid in the frequency range $[ {\omega _1 \omega _h } ]$.

Remark 2

The N is chosen beforehand, and the good performance of the approximation strongly depends thereon: low values not only result in simpler approximations, but also cause the appearance of a ripple in both gain and phase behaviors; such a ripple may be practically eliminated increasing N, but the approximation will be computationally heavier.

Frequencies of poles and zeroes in (5) are given by

$$\begin{aligned}&\omega _{z,1} =\omega _1 \sqrt{\eta },\\&\omega _{p,n} =\omega _{z,n} v, \quad n=1,\ldots ,N,\\&\omega _{z,n+1} =\omega _{p,n} \eta , \quad n=1,\ldots ,N-1,\\&\alpha =( {\omega _h /\omega _n })^{v/N}, \end{aligned}$$

$$\begin{aligned} \eta =( {\omega _h /\omega _1 })^{(1-v)/N} \end{aligned}$$

(6)

The case $v<0$ may be dealt with inverting (5). But if $| v |>1$ approximations become unsatisfactory; for that reason, it is usual to split fractional powers of s like this:

$$\begin{aligned} s^v=s^ns^\delta , \quad v=n+\delta , \quad n\in Z, \quad \delta \in [0,1] \end{aligned}$$

(7)

In this manner, only the latter term has to be approximated.

3 Proposed optimization method

3.1 Standard PSO algorithm

The PSO is a population-based stochastic optimization algorithm modeled based on the simulation of the social behavior of bird flocks. The PSO is a population-based search process where individuals initialized with a swarm of random solutions, referred to as particles. Each particle in the swarm represents a potential solution to the optimization problem, and if the solution is made up of a set of variables, the corresponding particle is a vector of variables. In a PSO system, each particle is flown through the multidimensional search space, adjusting its position in the search space according to its own experience and that of neighboring particles. The particle, therefore, makes use of the best position encountered by itself and that of its neighbors to place itself toward an optimal solution. The performance of each particle is evaluated using a predefined fitness function which encapsulates the characteristics of the optimization problem (Shi and Eberhart 1998).

The core operation of the PSO is the updating formulae of the particles, i.e. the equation of velocity updating and the equation of position updating. The global optimizing model proposed by Shi and Eberhart (1998) is as follows:

$$\begin{aligned} v_i (t+1)= & {} w\times v_i (t)+\mathrm{RAND}\times C_1 \times ( {P_{\mathrm{best}} (t)-x_i(t)}) \nonumber \\&+\,\mathrm{rand}\times C_2 \times ( {G_{\mathrm{best}} (t)-x_i (t)})\end{aligned}$$

(8)

$$\begin{aligned} x_i (t+1)= & {} x_i (t)+v_i (t+1), \end{aligned}$$

(9)

where w is the inertia weight factor, $v_i (t)$ is the velocity of particle i at iteration t, $x_i (t)$ is the particle position at iteration t, $C_1$ and $C_2$ are two positive constant parameters called acceleration coefficients, RAND and rand are the random functions in the range [0, 1], $P_{\mathrm{best}} (t)$ is the best position of the ith particle and $G_{\mathrm{best}} (t)$ is the best position among all particles in the swarm up to iteration t.

3.2 Modified PSO algorithm

In general, trapping in local optima and the slow convergence rate are two main weaknesses of the original PSO. In this paper, two modifications are proposed to overcome the aforementioned weaknesses of the original PSO.

The slow convergence rate of the standard PSO, which occurs before providing a precise solution, is closely related to the lack of any adaptive time varying accelerators in the velocity updating formula. In Eq. (8), the constants $C_1$ and $C_2$ determine the step size of the particle movements through the $P_{\mathrm{best}}$ and $G_{\mathrm{best}}$, respectively. Thus, in the original PSO, the algorithm step sizes are about constant and same for all the particles in the swarm. However, when optimizing complex multimodal functions, these constants are not able to meet the algorithm convergence requirements. Therefore, a mechanism which provides more precise acceleration to the algorithm movements is necessary. One mechanism is the use of time varying step sizes which introduces more sensitive and faster movements. To make this, the values of the cost functions in the iterations can be adopted, where in each iteration the value of the cost function can be interpreted as a criterion that gives the relative improvement of the present movement with respect to the previous movement. Moreover, when a new personal best position is found, it means that a better path (solution) in the search space is explored by a particle. Thus, an accelerated movement in the new found direction can quickly get the particle in the good path. Also, the introduction of a new global best position means that the swarm discoveries a better path (solution) in the whole search space. Therefore, more accelerated movements should be done in the new direction. So, the difference between the values of the cost function in the different iterations can be chosen as accelerators of the PSO. Accordingly, the insertion of two time varying multipliers to the original step sizes in Eq. (8) is proposed here. In this case, the time varying accelerators can provide more sensitive and adaptive movements. In this paper, the original velocity updating formulae is modified as follows:

$$\begin{aligned}&v_i (t+1)=w\times v_i (t)+\mathrm{RAND}\times C_1 \nonumber \\&\quad \times \frac{({f(P_{\mathrm{best}} (t))\!-\!f(x_i (t))})}{f(P_{\mathrm{best}} (t))}\! \times \! ({P_{\mathrm{best}} (t)\!-\!x_i(t)})+ \mathrm{rand} \!\times \! C_2 \nonumber \\&\quad \times \, \frac{( {f(G_{\mathrm{best}} (t))-f(x_i(t))})}{f(G_{\mathrm{best}} (t))}\times ( {G_{\mathrm{best}} (t)-x_i (t)}), \end{aligned}$$

(10)

where $f(P_{\mathrm{best}} (t))$ is the best fitness function found by ith particle at iteration t and $f(G_{\mathrm{best}} (t))$ is the best objective function found by the swarm up to iteration t. It is assumed that if $f(P_{\mathrm{best}} (t))$ and/or $f(G_{\mathrm{best}} (t))$ is equal to zero, then it is replaced by a small positive constant $\varepsilon$.

Remark 3

The terms $\frac{( {f(P_{\mathrm{best}} (t))-f(x_i (t))})}{f(P_{\mathrm{best}} (t))}$ and $\frac{( {f(G_{\mathrm{best}} (t))-f(x_i (t))})}{f(G_{\mathrm{best}} (t))}$ are named normalized local and global adaptive coefficients, respectively. In each iteration, the former term defines a normalized movement step size in the direction of best position which is found by ith particle and the latter term defines a normalized movement step size in the direction of the best optimum point which have been found by the swarm, yet. In other words, the time varying accelerators decrease or increase the movement step size relative to being close or far from the optimum point, respectively. By means of this method, velocity can be updated adaptively instead of being fixed or changed linearly.

The other weakness of the standard PSO occurs when strongly multi-modal problems are being optimized. In such cases, the PSO algorithm usually suffers from the premature suboptimal convergence (simply premature convergence or stagnation). Sticking in local optima happens when some poor particles attract the swarm prevent further exploration of the search space. According to Angeline (1998), although PSO finds good solutions faster than other evolutionary algorithms, it usually cannot improve the quality of the solutions as the number of iterations is increased. The rationale behind this problem is that the particles converge to a single point, which is on the line between the global best and personal best positions. This point is not guaranteed to be even a local optimum. Proofs can be found in Bergh and Engelbrecht (2002). Another reason for this problem is the fast rate of information flow between particles, resulting in the creation of similar particles (with a loss in diversity) which increases the possibility of being trapped in local minima (Riget and Vesterstrom 2002). This feature prevents the standard PSO from being really of practical interest for a lot of applications. Therefore, an alternative should increase the diversity property of the algorithm to prevent premature convergence and trapping local optimums. To do this, in this paper, the use of a new mutation procedure is proposed as follows: When new positions are determined for the particles of the swarm using Eqs. (9) and (10), $\gamma \,\%$ of the particles are randomly selected and are replaced by some other particles namely superseding particles with a probability. The superseding particles are generated using a random change in the current particle. If the new particle (i.e. the superseding particle) has a better cost function compared to the current particle’s cost function, it is accepted. Otherwise, the superseding particle is accepted with a probability of $\mathrm{e}^{-\frac{\Delta f(t)}{f(G_{\mathrm{best}} (t))}}$, where $\Delta f(t)$ is the difference of the cost functions of the superseding and current particles at iteration t. If the superseding particle is rejected, no replacement is done. This process is repeated in each iteration, for all particles.

Remark 4

To save the best solutions, the best particle in the swarm is exempted from the mutation.

Remark 5

In this paper, two main modifications are suggested for the original PSO. The first modification is to add some new accelerator coefficients to the terms into the available velocity formula. From a computational cost point of view and based on the proposed new velocity updating formula (10), it is clear that no extra computational cost is added to the algorithm via this modification (where the values of the accelerator coefficients are already computed in the original PSO, too). The second modification is to introduce the so-called superseding particles into the swarm. In this case, since the number of the superseding particles is small compared to the number of all the particles in the swarm ($\gamma \, \%$ of all particles maybe selected for mutation where $\gamma$ has a small value), this modification does not impose a great deal computational cost of to the MPSO algorithm compared to the original PSO.

The pseudo-code of the proposed MPSO algorithm is given in “Appendix”.

4 FOPID controller design

4.1 Objective function definition

The FOPID controller is used to improve the dynamic response and to reduce the steady-state error. The transfer function of a FOPID controller is described as

$$\begin{aligned} G( s)=K_\mathrm{P} +K_\mathrm{I} /s^\lambda +K_\mathrm{D} s^\mu , \end{aligned}$$

(11)

where $K_\mathrm{P}$, $K_\mathrm{I}$ and $K_\mathrm{D}$ are the proportional gain, integral and derivative time constants, respectively, and $\lambda$ and $\mu$ are fractional powers. For designing an optimal FOPID controller, a suitable objective function that represents system requirements should be defined based on some desired specifications. Some typical output specifications in the time domain are the overshoot ($M_\mathrm{p} )$, rise time ($T_\mathrm{r} )$, settling time ($T_{\mathrm{ss}} )$ and steady-state error ($E_{\mathrm{ss}} )$. In general, three kinds of the performance criteria, including the integrated absolute error (IAE), the integral of squared-error (ISE) and the integrated of time-weighted-squared-error (ITSE), are usually considered in the control design under step testing input. It is worth noticing that using different performance indices makes different solutions for the optimal FOPID controllers. The above-mentioned three integral performance criteria have some advantages and disadvantages. For example, a disadvantage of the IAE and ISE criteria is that their minimization can result in a response with relatively small overshoot but a long settling time. Although the ITSE performance criterion can overcome the disadvantage of the ISE criterion, the derivation processes of the analytical formula are complex and time-consuming (Gaing 2004). The IAE, ISE and ITSE performance criteria formulas are defined as follows:

$$\begin{aligned}&\mathrm{IAE}=\mathop \int \limits _0^\infty | {r( t)-y(t)} |\mathrm{d}t=\mathop \int \limits _0^\infty | {e(t)} |\mathrm{d}t\end{aligned}$$

(12)

$$\begin{aligned}&\mathrm{ISE}=\mathop \int \limits _0^\infty e^2(t)\mathrm{d}t\end{aligned}$$

(13)

$$\begin{aligned}&\mathrm{ITSE}=\mathop \int \limits _0^\infty te^2(t)\mathrm{d}t \end{aligned}$$

(14)

In this paper, another time domain performance criterion is defined by

$$\begin{aligned} J_\alpha ( K)=\frac{1}{1+\mathrm{e}^{-\alpha }}( {T_\mathrm{r} +T_\mathrm{s} })+\frac{\mathrm{e}^{-\alpha }}{1+\mathrm{e}^{-\alpha }}(M_\mathrm{p} +E_{\mathrm{ss}} ), \end{aligned}$$

(15)

where K is $[K_\mathrm{P} ,K_\mathrm{I} ,K_\mathrm{D} ,\lambda ,\mu ]$ is the parameter vector and $\alpha \in [-5,5]$ is the weighting factor. The optimum selection of $\alpha$ depends on the designer’s requirements and the characteristics of the plant under control. One can set $\alpha$ to be smaller than 0 to reduce the overshoot and steady-state error. On the other hand, if $\alpha$ is to be set larger than 0 the rise time and settling time are reduced. On the other hand, if $\alpha$ is set to 0, then all the performance criteria (i.e. the overshoot, rise time, settling time and steady-state error) will have the same worth.

4.2 MPSO-based FOPID controller

For designing an optimal FOPID controller, determination of the vector $K=[K_\mathrm{P} ,K_\mathrm{I} ,K_\mathrm{D} ,\lambda ,\mu ]$ with regard to the minimization of the performance index is the main issue. Here, the minimization process is performed using the proposed MPSO algorithm. For this purpose, step response of the plant is used for computing four performance criteria, including the overshoot ($M_\mathrm{p} )$, steady-state error ($E_{\mathrm{ss}} )$, rise time ($T_\mathrm{r} )$ and setting time ($T_\mathrm{s} )$. At first, the lower and upper bounds of the controller parameters are specified. Then, a swarm of the initial particles is randomly initialized in the specified range. Each particle represents a solution (i.e. controller parameters K) and the corresponding performance index of each particle is evaluated using the step response of the system. Afterward, the main procedure of the proposed heuristic MPSO algorithm starts to work as follows: First, all the parameters of Eq. (10) are determined. Subsequently, new positions of each particle are obtained using Eq. (9). Then, the superseding particles are created. The aforementioned process is repeated until a stopping criterion is satisfied. In this stage, the particle corresponding to the $G_{\mathrm{best}} (t)_{ }$ is designated as the optimal vector K. The flowchart of the design procedure of the MPSO-based FOPID controller is shown in Fig. 1.

Fig. 1

The design procedure of the MPSO-based FOPID controller

Table 1 Comparative results of the designed different FOPID controllers for the plant $G_1 (s)$

Table 2 Comparative results of the designed different FOPID controllers for the plant $G_2 ( s)$

Table 3 Comparative results of the designed different FOPID controllers for the plant $G_3 (s)$

4.3 Optimal FOPID controller for typical transfer functions

In order to verify the performance of the proposed MPSO-based  FOPID controller, comparative experiments are carried out for the following three typical control plants:

$$\begin{aligned}&G_1 ( s)=\frac{1}{s^3\!+\!6s^2\!+\!7s},\,\,\,G_2 (s)\!=\!\frac{s^2\!+\!2s}{s^4\!+\!2s^3\!+\!5s^2\!+\!s\!+\!0.1}, \nonumber \\&G_3 (s)=\frac{\mathrm{e}^{-0.1s}}{s^2+2s} \end{aligned}$$

(16)

It is assumed that the suitable ranges of the control parameters are as follows: $K_\mathrm{P} \in [ {0,25}],K_\mathrm{I} \in [ {0,10} ],K_\mathrm{D} \in [ {0,10} ],\lambda \in [0,1]$ and $\mu \in [0,1]$. A population of 20 particles is found to be suitable for providing good solutions. The maximum number of the iterations for all experiments is considered to be 100. Also, $\alpha$ in Eq. (15) is set to 0 (in this case, all the performance criteria have a same merit in the objective function). In order to design the optimal FOPID controller, the MPSO is run 10 times. The other parameters are selected as follows: $\gamma =15$ and $C_1 =C_2 =2$.

The performance of the proposed MPSO is compared to the standard PSO (SPSO) (Kennedy and Eberhart 1995), the constriction factor approach PSO (CPSO) (Clerc and Kennedy 2002) and random inertia weight PSO method (RPSO) (Eberhart and Shi 2001). The comparative results for the plants $G_1 ( s)$, $G_2 ( s)$ and $G_3 ( s)$ are summarized in Tables 1, 2 and 3, respectively. It is seen that the proposed MPSO-based FOPID controllers outperform those of the SPSO, RPSO and CPSO obtained controllers. In all tables, one can see that the proposed MPSO gives lesser overshoot compared to the three other methods. On the other hand, although the rise time of the proposed MPSO-based controller is somewhat greater than the rise time of the other methods, both the settling time and steady-state error criteria of the suggested controller are better than those of the other techniques. Nevertheless, one can set the parameter $\alpha$ to a larger value than 0 to result in a short rise time. Moreover, the last column in the three tables shows the computational effort (CE) of the different algorithms consumed to reach the final solution. The CE criterion is defined as the total number of function evaluation done by a method until reaching the optimal solution. This criterion is an indication of computational time and convergence speed of the algorithm. In this case, it can be seen that the number of function evaluation in the proposed MPSO method is lesser than those in the other methods. This means that the MPSO algorithm outperforms the SPSO, CPSO and RPSO methods from the computational effort point of view. The unit step responses of the case studies ${G}_1 ( {s})$, ${G}_2 ( {s})$ and ${G}_3 ( {s})$ are depicted in Figs. 2, 3 and 4, respectively. From the simulation results, it can be found that MPSO-based FOPID controllers produce the smooth curve for the output in conjunction with little fluctuation and small overshoot.

Fig. 2

Step response of $G_1 ( s)$ with FOPID controller designed by MPSO, SPSO, CPSO and RPSO

Fig. 3

Step response of $G_2 ( s)$ with FOPID controller designed by MPSO, SPSO, CPSO and RPSO

Fig. 4

Step response of $G_3 ( s)$ with FOPID controller designed by MPSO, SPSO, CPSO and RPSO

5 Design of MPSO-based FOPID controller for five-bar-linkage manipulator robot

5.1 Dynamics of five-bar-linkage manipulator robot

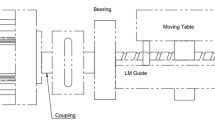
In recent years, there has been a growing interest in the design and control of lightweight robots. Several researchers have studied the modeling and control of a single link flexible beam. Figure 5 shows a typical five-bar-linkage manipulator, where Fig. 6 depicts the five-bar-linkage manipulator schematic where the links form a parallelogram. Let $q_i$, $T_i$ and $I_\mathrm{h}^i$ be the joint variable, torque and hub inertia of the ith motor, respectively. Also, let $I_i$, $l_i$, $l_{c_i }$ and $m_i$ be the inertia matrix, length, distance to the center of gravity and mass of the ith link, respectively.

Fig. 5

A typical five-bar-linkage manipulator

Fig. 6

Planar presentation of the manipulator robot (Badamchizadeh et al. 2010)

The dynamic equations of the manipulator are as follows: (Spong and Vidyasagar 2006).

$$\begin{aligned} T_{1}= & {} \left( {M_{{11}} + I_{h}^{1} } \right) \ddot{q}_{1} + M_{{12}} \ddot{q}_{2} + \frac{{\partial M_{{12}} }}{{\partial q_{2} }}\dot{q}_{2}^{2}\nonumber \\&+\, g\left( {m_{1} d_{{c_{1} }} + m_{3} l_{{c_{3} }} + m_{4} l_{1} } \right) \cos q_{1} \nonumber \\ T_{2}= & {} \left( {M_{{22}} + I_{h}^{2} } \right) \ddot{q}_{2} + M_{{21}} \ddot{q}_{1} + \frac{{\partial M_{{21}} }}{{\partial q_{1} }}\dot{q}_{1}^{2}\nonumber \\&+\, g\left( {m_{1} l_{{c_{2} }} + m_{3} l_{2} + m_{4} l_{{c_{4} }} } \right) \cos q_{2}, \end{aligned}$$

(17)

where g is the gravitational constant and $M_{11} =I_{11}^1 +I_{11}^3 + m_1 d_{c_1 }^2 + m_3 l_{c_3 }^2 + m_4 l_1^2$, $M_{22} =I_{11}^2 + I_{11}^4 + m_2 l_{c_2 }^2 + m_3 l_2^2 + m_4 l_{c_4 }^2$ and $M_{12} =M_{21} =( {m_3 l_{c_3 } -m_4 l_{c_4 } l_1 })\cos (q_1 -q_2 )$.

From the above-mentioned equations it is revealed that (Badamchizadeh et al. 2010)

$$\begin{aligned} m_3 l_{c_3 } l_2 =m_4 l_{c_4 } l_1 \end{aligned}$$

(18)

Thus, one has $M_{12} =M_{21} =0$, that is, the matrix of inertia is diagonal and constant. Hence the dynamic equations of this manipulator become

$$\begin{aligned}&T_1 =( {M_{11} +I_\mathrm{h}^1 })\ddot{q}_{1} + g\left( {m_{1} l_{{c_{1} }} + m_{3} l_{c_{3}} + m_{4} l_{1} } \right) \cos q_{1} \nonumber \\&T_2 =( {M_{22} +I_\mathrm{h}^2 })\ddot{q}_{2}+ g\left( {m_{1} l_{{c_{2} }} + m_{3} l_{2} + m_{4} l_{c_{4}}} \right) \cos q_{2} \end{aligned}$$

(19)

Notice that $T_1$ depends only on $q_1$ but not on $q_2.$ On the other hand $T_2$ depends only on $q_2$, but not on $q_1$. This discussion helps to explain the popularity of the parallelogram configuration in industrial robots. If the condition (18) is satisfied, then we can adjust the two rotations independently, without worrying about interactions between them.

Table 4 Five bar linkage robot parameters

Table 5 Summary of the simulation results of five-bar-linkage robot motor using different methods

5.2 MPSO-based FOPID controller for robot

Here, the main goal is to design an optimal MPSO-based FOPID controller for each of the motors of the robot to control their rotations with good performance. In what follows the results are given for one motor, where the same results are also valid for the second motor. Using Eq. (19), the five-bar-linkage manipulator robot is implemented in Matlab and Simulink environment. The manipulator specifications are given in Table 4.

The following process is done to determine the optimal values of the parameters of the proposed MPSO-based FOPID controller (i.e. the vector K). First, the MPSO algorithm is initialized, randomly. Each solution $K=[K_\mathrm{P} ,K_\mathrm{I} ,K_\mathrm{D} ,\lambda ,\mu ]$ is sent to the Simulink block and the values of four performance criteria in the time domain, i.e. $M_\mathrm{p}$, $E_{\mathrm{ss}}$, $T_\mathrm{r}$ and $T_\mathrm{s}$, are calculated. Afterwards, the objective function (15) is evaluated for each solution according to the obtained performance criteria. Then, the main procedure of the proposed MPSO algorithm is performed and new solutions are computed. At the end of any iteration, the program checks the stop criterion. When one termination condition is satisfied, the program stops and the latest global best solution is returned as the best solution of K. The Simulink diagram of the proposed procedure is illustrated in Fig. 7.

Fig. 7

Simulink diagram of the MPSO-based FOPID controller for robot

The parameter setting for the MPSO is as follows: The maximum iteration number is considered equal to 200. The parameter $\alpha$ is set to 0. The swarm is initialized with 30 particles. The other parameters are also selected as follows: $K_\mathrm{P} \in [ {0,30} ],K_\mathrm{I} \in [ {0,5}],K_\mathrm{D} \in [ {0,5} ],\lambda \in [0,1]$, $\mu \in [0,1]$, $\gamma =10$ and $C_1 =C_2 =2$.

Table 6 Results of sensitivity analysis for the parameter $\alpha$ in (15)

Figure 8 illustrates the state of the system with no control which is not a stable response. In other words, the system output is oscillatory and requires a suitable control. For comparison, the results of the PSO-based FOPID (Bingul and Karahan 2012), GA-based FOPID (Meng and Xue 2009) and ABC-based FOPID (Rajasekhar et al. 2011) controllers for the robot control are also obtained. The comparative results are summarized in Table 5. It is seen that the proposed MPSO-based FOPID controller outperforms those of the PSO-based FOPID, GA-based FOPID and ABC-based FOPID controllers. It is noted that the last column of Table 5 compares the controllers based on the control signal energy (CSE) where it is computed using $\mathop \int \nolimits _0^\infty | {u(t)} |\mathrm{d}t$. One can see that the MPSO-based FOPID controller needs less control energy compared to the other controllers, except the ABC method. However, the results of the ABC-based FOPID controller for the other criteria, such as the overshoot, the settling time, the steady-state error and the computational effort, are weaker than the corresponding results of the MPSO-based FOPID controller. This means that the controller obtained by the MPSO method is not only with a suitable transient and steady response, but also it is a cheap energy control scheme leading to a more practicable controller in real world applications. Figure 9 reveals the step response of the motor rotation for different FOPID controllers. It is obvious that the proposed MPSO-based FOPID controller produces a smooth and fast output compared to the other methods.

Fig. 8

Response of the robot motor without FOPID controller

Fig. 9

Step response of the robot motor rotation using MPSO method

Finally, sensitivity analysis is performed with different values for the parameter $\alpha$ in (15) to effects of the parameter $\alpha$ on the optimal results of the proposed MPSO-based FOPID controller for the robot. To do this, the parameter $\alpha$ is changed from $-5$ to 5 with a step size of 1. The obtained results are given in Table 6. It can be seen that when $\alpha <0$, the overshoot and steady-state error are reduced and the rise time and settling time are increased. In contrast, the case $\alpha >0$ results in small rise time and settling time and enlarges the overshoot and steady-state error. On the other hand, in the case of $\alpha =0$ all the performance criteria (i.e. the overshoot, rise time, settling time and steady-state error) are of the same worth. Moreover, the step responses of the robot with five typical values of $\alpha$ are shown in Fig. 10. Table 6 and Fig. 10 reveal that the value of the parameter $\alpha$ has little impact on the optimum value of the performance criterion $J_\alpha (K)$ in (15).

Fig. 10

The step responses of the robot with five typical values of $\alpha$

6 Conclusions

In this paper, a novel simple modified particle swarm optimization (MPSO) algorithm is proposed to overcome two main shortages of the traditional PSO method, namely slow convergence rate and trapping in local optima. Inserting accelerator parameters into the velocity updating formula and adding a new mutation process to the original PSO are the main proposed modifications. The introduced MPSO is applied for tuning the parameters of the fractional-order PID controllers for some typical transfer functions. Moreover, the proposed optimization method is implemented to design an optimal FOPID controller for a five-bar-linkage robot manipulator. Comparative simulation results reveal that the proposed MPSO can effectively tune the parameters of the FOPID controllers. From an application point of view, the introduced MPOS technique is simple and fast, has a suitable control energy and it can be easily implemented in real-world applications via a microcontroller chip.

Appendix: Pseudocode for MPSO algorithm

Begin;

• 1. Set initial values such as swarm size, random particles, random velocity vector, maximum number of iterations, etc;

• 2. For each particle calculate the objective value;

• 3. Update the global and local best particles and their corresponding objective values;

• 4. Find the new positions of each particle using Eqs. (9) and (10);

• 5. Replace up to $\gamma \, \%$ of the particles by superseding particles;

• 6. Check if termination condition is true then stop; otherwise, go to step 2;

End.