ELM-based driver torque demand prediction and real-time optimal energy management strategy for HEVs

Abstract

In hybrid electric vehicles, the energy economy depends on the coordination between the internal combustion engine and the electric machines under the constraint that the total propulsion power satisfies the driver demand power. To optimize this coordination, not only the current power demand but also the future one is needed for real-time distribution decision. This paper presents a prediction-based optimal energy management strategy. Extreme learning machine algorithm is exploited to provide the driver torque demand prediction for realizing the receding horizon optimization. With an industrial used traffic-in-the-loop powertrain simulation platform, an urban driving route scenario is built for the source data collection. Both of one-step-ahead and multi-step-ahead predictions are investigated. The prediction results show that for the three-step-ahead prediction, the 1st step can achieve unbiased estimation and the minimum root-mean-square error can achieve 100, 150 and 160 of the 1st, 2nd and 3rd steps, respectively. Furthermore, integrating with the learning-based prediction, a real-time energy management strategy is designed by solving the receding horizon optimization problem. Simulation results demonstrate the effect of the proposed scheme.

1 Introduction

The hybrid electric powertrain technology is recently spotlighted as a high efficient vehicular propulsion system. The advantage of the hybrid electric powertrain is to use the freedom in assigning the driver demand power into different power sources, mainly the internal combustion engine and electric machines, such that the energy consumption is much less than in conventional combustion engine-powered vehicles. In a hybrid powertrain, the power supplied by the different power sources effects not only the current vehicle states but also the future behaviors of the vehicle due to the mechanical inertia. In this case, not only the instantaneous energy efficiency but also the total energy consumption over a driving time interval or a targeted driving route can be optimized with efficient energy management strategies. In the past two decades, a lot of researches on hybrid electric vehicle (HEV) optimal energy management have been driven by this potential for saving energy [1, 2].

At early stage, focusing on the engine operating point, rule-based engine management strategies are proposed for improving instantaneous fuel efficiency [3]. This kind of solution requires low computing cost for the electronic control unite (ECU) of the vehicle powertrain system. However, instantaneously deciding the operating point according to the vehicle speed and the torque demand is generally not optimal if total energy consumption is evaluated along a route or a time interval. Targeting a given driving route, optimization of the global energy consumption is investigated by a lot of literatures [4,5,6,7]. These literatures present the solutions in such a way: first, define a cost function for evaluating total energy consumption along the route; then, calculate the demand power along the route based on the dynamic model of the vehicle and the battery state of charge (SoC); finally, the optimization result with respect to the cost function provides the power distribution of the demand power among the power sources and the operating point decision according to the topological structure of the powertrain. Dynamic programming (DP) is the typical tool to solve this optimization problem. For example, a DP-based solution is proposed in [5] where an attempt is made by using neural network to regulate the solution in real-time application, and stochastic DP is exploited to count the stochasticity in the demand power [6]. However, this kind of route-depended optimal energy management method is unfeasible in practice due to the requirement of fully previewed knowledge of future power demand. Hence, research attention has been focused on the real-time optimization, i.e., making decisions on power distribution and operating point of the power sources in real time without the exact information of the future trip. The cornerstone of real-time optimization is the prediction of the power demand or the vehicle behavior.

Real-time optimal energy management is usually conducted based on the models of the vehicle dynamics and/or the battery. Most proposed approaches formulate the real-time optimization of energy consumption as a finite-time optimal control problem and solve the problem numerically in the sense of discrete time. For example, a look-ahead optimization method is proposed to optimize the total fuel consumption of a future period in receding horizon policy [8]. Receding horizon optimization approaches are also proposed in [9, 10] where iterative algorithms based on GMRES (generalized minimum residual) method are presented to solve the Pontryagin condition approximately. Regarding these approaches, the energy management problem is solved along the model-based predicted trajectory of the future trip under the assumption that the torque demand over the horizon is a known constant [9] or a given approximate treatment, such as using the output of an exponentially decreasing model [11, 12]. To improve this unfeasible assumption, a lot of challenges are reported focusing the main attention on estimating the driver torque demand. In [13], auto-regressive models are exploited to predict the driver torque demand. Neural network method is proposed with the history vehicle velocity as inputs [12]. To take the stochastic factors into account, Gaussian process method is employed such that the prediction is achieved in the sense of mean value for convenience [14]. Meanwhile, Markov-chain based methods are proposed based on collected comprehensive data with respect to specific driving cycle route [6, 12].

Recently, the technical progress in connectivity motivates the research on HEV energy management with the driving environment information. Under the connected-vehicle (CV) environment, the information of vehicle-to-infrastructure (V2I), vehicle-to-vehicle (V2V) and vehicle-to-cloud (V2C) enables prediction for the future vehicle behaviors or the driver power demand [15, 16]. The paper [17] proposes a Bayesian network approach for short-term prediction of vehicle velocity. A neural network-based energy demand prediction approach is proposed for trip-oriented application [18]. A so-called radial basis function neural network is exploited to predict the driver power demand [19]. Considerable potential has been shown by these latest researches for developing prediction-based energy management strategies for HEVs under CV environment. On the other hand, it is noted that machine learning techniques have been widely applied as prediction method. Concerning time-serial signals, application of neural network-based learning or ELM predicts the future values based on the past and current data that have correlative relation with the predicted signal [20, 21]. In automotive control field, machine learning techniques have been used in different scenarios [22,23,24,25,26,27]. The ELM algorithm has shown significant advantages in time series prediction due to the following features [28]: the training cost of the ELM is computationally efficient, since the input weights and the feature mapping layer are chosen randomly and do not require adaptation; the ELM method has universal approximation and good generalization capabilities and can deal with global minima of convex optimization problem.

This paper proposes a novel prediction-based optimal energy management strategy where the ELM algorithm is exploited to provide the driver torque demand. With the predicted torque demand and the vehicle dynamic model, a real-time receding horizon optimal decision policy is constructed for torque demand distribution and the transmission gear operation. Regarding the prediction, both one-step-ahead and multi-step-ahead predictions with the ELM and a chained ELM (CELM) are investigated, respectively. Then, applying the ELM-based prediction in real time, the torque demand distribution and transmission gear ratio are decided by solving the optimization problem formulated with the cost function of the total energy consumption subject to the vehicle dynamics. Moreover, to evaluate the proposed optimization strategy, a traffic-in-the-loop (TILP) powertrain simulation platform is constructed. With the platform, a group of driver torque demand profiles with the V2V and V2I information are measured for training the ELM. Finally, the prediction performance and the effectiveness of the prediction-based energy management strategy are demonstrated with numerical simulations.

2 Problem formulation

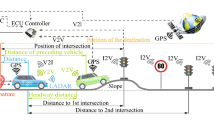
The energy management system for an HEV is sketched as Fig. 1. The vehicle is driven by the actual propulsion torque generated by the powertrain system, mainly the combustion engine and electric motor in HEVs. More exactly, the actual propulsion torque is determined by the power output of each power source, and the clutch and gear state according to the mechanical structure of the powertrain. For the parallel HEV, which is the targeted powertrain in this paper, the actual propulsion torque is determined by the engine torque, the motor torque and the gear ratio. The role of energy management strategy is to deliver the commands of the engine, motor and gear according to the driver torque demand since the driver requests the power for acceleration or deceleration with the accelerator or brake pedal operations. Generally, the main purpose of energy management is to minimize the energy consumption under the constraint that the actual propulsion torque satisfies the driver request torque.

Fig. 1

Framework of HEV driving system

The parallel HEV configuration is as shown in Fig. 2. The powertrain system consists of a combustion engine and an electric motor coupled by a mechanical coupling system. Since the engine can be cut off from the driveline by an equipped clutch, the powertrain can be switched between electric vehicle (EV) mode and HEV mode. Furthermore, consider that the powertrain system uses a constantly variable transmission (CVT) system. For this powertrain system, the vehicle speed v(t), the acceleration/deceleration of the vehicle $\dot{v}(t)$ and the actual propulsion torque $\tau _\mathrm{dr}(t)$ satisfy the following equation which can be easily deduced according to the physical energy conservation law,

$$\begin{aligned}&M \dot{v}(t) =\dfrac{\eta _f\tau_\mathrm{dr}(t)}{R_\mathrm{tire}} -F(v(t)), \nonumber \\&\mathrm{with}\quad F(v)= Mg(\mu _\mathrm{r}\cos \theta +\sin \theta ) + \dfrac{1}{2}\rho AC_\mathrm{d}v^2, \end{aligned}$$

(1)

where $\eta _f$, $R_\mathrm{tire}$, M, g, $\mu _\mathrm{r}$ and $\theta$ denote the differential efficiency, the wheel radius, the vehicle mass, the gravity acceleration, the coefficient of rolling resistance and the road slop, respectively, and $\rho$, A and $C_\mathrm{d}$ denote the air density, the frontal area of the vehicle and the drag coefficient, respectively. The actual propulsion torque is generated according to the engine torque $\tau _\mathrm{e}$, the motor torque $\tau _\mathrm{m}$ and the gear ratio $i_\mathrm{g}$ by the following relationship,

$$\begin{aligned} \tau _\mathrm{dr}= i_\mathrm{g}i_0\eta _f(\tau _\mathrm{e}+\tau _\mathrm{m}), \end{aligned}$$

(2)

where $i_0$ denotes the final differential gear ratio. Meanwhile, the mechanical coupling system determines that the speeds of the engine and motor are linked together and relate to the vehicle speed by

$$\begin{aligned} \omega _\mathrm{e} = \omega _\mathrm{m} = i_\mathrm{g}i_0\dfrac{1}{R_\mathrm{tire}}v, \end{aligned}$$

(3)

where $\omega _\mathrm{e}$ and $\omega _\mathrm{m}$ denote the speeds of the engine and motor, respectively.

Fig. 2

Configuration of a parallel HEV

It can be observed from the relation (2) that $\tau _\mathrm{e}$ and $\tau _\mathrm{m}$ are design variables to satisfy the driving demand. To achieve a torque demand $\tau _\mathrm{dr}$, there are various ways to distribute the engine torque $\tau _\mathrm{e}$ and the motor torque $\tau _\mathrm{m}$. Moreover, the speed relation (3) means that at a vehicle speed v, selection the gear ratio can shift the operating speeds of the engine and motor. These facts imply that under same driver torque demand and vehicle speed, different torque combinations of $\tau _\mathrm{e}$ and $\tau _\mathrm{m}$ and gear ratio selection produce different efficiencies of engine and motor as shown by the maps in Fig. 3, where in Fig. 3a, BSFC (break specific fuel consumption) denotes the fuel mass flow rate per unit power output of the engine and “isoPower” represents the isopotential curve of engine power. The curves of the engine map data show that the engine can generate same power by consuming distinct fuel; in other words, fuel economy can be achieved by regulating the engine operating point $(\tau _\mathrm{e}, \omega _\mathrm{e})$.

Fig. 3

Map data of the engine and motor: a maps of engine efficiency and maximum torque; b map of motor efficiency

The above specification explains the significant advantage of the HEV powertrain system and motivates the investigation for HEV energy management. The considered energy management problem in this work is to deal with the optimization design to distribute the driver torque demand between the engine and motor, and select a gear ratio such that the energy consumption can be minimized. The cost function can be represented by

$$\begin{aligned} J&= \int ^{t+T}_t \left( \dfrac{\gamma _\mathrm{f}}{\rho _\mathrm{f}} \dot{m}_\mathrm{f} (\tau _\mathrm{e}(\tau ), \omega _\mathrm{e}(\tau )) \right. \nonumber \\&\quad \left. +\, \gamma _\mathrm{e} \dot{m}_\mathrm{e} (\tau _\mathrm{m}(\tau ), \omega _\mathrm{m}(\tau )) \right) \mathrm{d}\tau , \end{aligned}$$

(4)

where T denotes a time horizon, $\dot{m}_\mathrm{f}$ (g/s) and $\dot{m}_\mathrm{e}$ (kWh) denote the fuel mass flow rate and the instantaneous electricity consumption, respectively, $\rho _\mathrm{f}$ (g/L) denotes the fuel density, and $\gamma _\mathrm{f}$ (¥/L) and $\gamma _\mathrm{e}$ (¥/kWh) denote the prices of the fuel and electricity, respectively. It is clear that the cost function relates to both of the engine operating point $(\tau _\mathrm{e}, \omega _\mathrm{e})$ and the motor operating point $(\tau _\mathrm{m}, \omega _\mathrm{m})$. Moreover, regarding the cost function (4), it should be noted that real-time optimization over a future time interval is the aim of the energy management strategy design.

Therefore, in order to achieve real-time optimization of the energy consumption, the torque commands $\tau _\mathrm{e}$ and $\tau _\mathrm{m}$ must be decided on-line according to the system trajectory. In other words, $\tau _\mathrm{e}$ and $\tau _\mathrm{m}$ must be provided by solving the optimization problem with the cost function (4) under the constraint of driver demand. To do this, estimation of the driver torque demand $\hat{\tau }_\mathrm{dr}(\tau )$, $\tau \in (t, t+T]$ is needed for predicting the trajectory of the system and using this as constraint of optimization. As shown in Fig. 1, the driver operates the accelerator/braking pedal mainly according to the traffic environment. However, the CV environment enables us to estimate the driver demand using the V2V and V2I information. In this work, an ELM algorithm is developed to estimate the driver demand. In order to training the ELM algorithm, the source data are collected by using a TILP powertrain simulation platform as shown in Fig. 4. This constructed co-simulation platform mainly consists of a high-fidelity traffic scenario simulator and enterprise-level powertrain model in MATLAB/Simulink. The V2V and V2I information, such as preceding vehicle speed and acceleration, and traffic light phase and timing can be real-timely detected and transferred to the ego vehicle. The traffic scenario is randomly generated by the real-word emulated traffic road simulation environment. Then, group data of torque demand are obtained under different driving environments.

Fig. 4

Traffic-in-the-loop powertrain simulation platform

As summary, the problem to be solved in this work is described as follows. For the HEV system modeled by Eqs. (1)–(3) under the system environment shown in Fig. 5, suppose that the driving route is not previously known, and the future driver torque demand is unknown. Develop a receding horizon optimization algorithm with the cost function (4) and control input $(\tau _\mathrm{e}, \tau _\mathrm{m}, i_\mathrm{g})$, and under the constraint that the actual driving torque satisfies the real-time driver torque demand. We solve this problem in the following two phases:

(i):

Find proper relevant V2V and V2I information for estimating the future driver torque demand and training the ELM to generate the real-time prediction of the torque demand $\hat{\tau }_\mathrm{dr}$ over a time interval $(t, t+T]$.

(ii):

Based on the powertrain models (1)–(3), find optimal torque commands $\tau _\mathrm{e}$ and $\tau _\mathrm{m}$, and gear command $i_\mathrm{g}$ that minimize the cost function J defined by Eq. (4) with the constraints that

$$\begin{aligned} \left\{ \begin{array}{l} \dot{v} (\tau ) = \dfrac{\eta _f\hat{\tau }_\mathrm{dr}(\tau )}{R_\mathrm{tire}} -F( v(\tau ))\\ i_\mathrm{g}(\tau ) i_0\eta _f(\tau _\mathrm{e}(\tau )+\tau _\mathrm{m}(\tau )) = \hat{\tau }_\mathrm{dr}(\tau ) \\ i_\mathrm{g}(\tau ) i_0 \dfrac{1}{R_\mathrm{tire}} v(\tau ) = \omega _\mathrm{e}(\tau ) =\omega _\mathrm{m}(\tau ) \end{array}, \quad \forall \tau \in (t, t+T]\right. \end{aligned}$$

(5)

and the following physical constraints

$$\begin{aligned}&\left\{ \tau _\mathrm{emin} \le \tau _\mathrm{e}\le \tau _\mathrm{emax}, ~~ \tau _\mathrm{mmin}\right. \nonumber \\&\quad \left. \le \tau _\mathrm{m}\le \tau _{\mathrm{mmax}}, ~~i_\mathrm{gmin}\le i_\mathrm{g} \le i_\mathrm{gmax} \right\} \end{aligned}$$

(6)

where the parameters with subscripts min and max denote the corresponding minimum and maximum values, respectively.

Fig. 5

Framework of the scheme for energy management

3 ELM-based driver torque demand prediction

The driver torque demand prediction during the considered future period based on the current states of ego vehicle and real-time V2V and V2I information is considered as a typical time series prediction problem. Machine learning methods are suited for handling such time series prediction problem. ELM is a state-of-the-art machine learning method and employed for one-step-ahead prediction in this research. Then a new algorithm is developed for performing multi-step-ahead prediction based on CELM. Details are given in the following subsections.

3.1 Basic ELM and chained ELM

Various machine learning methods are presented for prediction; however, many of them basically share the same general model structure, i.e., feedforward neural network, as shown in Fig. 6, which includes three layers: input layer, feature mapping layer, and output layer. Each input and each output are considered as a node or a unit. Machine learning process is to adjust the weights between nodes. In other words, what the model learns lies in these weights.

Fig. 6

A general model structure

ELM is an emerging learning paradigm proposed by Huang et al. [21], which is firstly proposed to improve the learning speed of feedforward neural networks. The basic idea of ELM is that the input weights $\varvec{a}_j\in R^{n_i\times 1}$ and feature mapping layer biases $\varvec{b}\in R^{n_h\times 1}$ need not be tuned but be randomly assigned instead and that the feature mapping layer can be represented by either random hidden nodes or kernels [29]. In such a setup, the model can be simply considered as a linear system and the output weights $\varvec{w}\in R^{n_h\times 1}$ of the model can be analytically determined through a simple generalized inverse operation of the feature mapping layer output matrices.

Consider the following data set for machine learning,

$$\begin{aligned} \varvec{D} = \{(\varvec{x}_1,y_1),(\varvec{x}_2,y_2), \ldots , (\varvec{x}_N,y_N)\}, \end{aligned}$$

(7)

where N denotes the number of training samples. Based on the training set $\varvec{D}$, ELM training becomes the following optimization problem,

$$\begin{aligned} \min _{\varvec{w}}||\varvec{Hw}-\varvec{Y}||^2, \end{aligned}$$

(8)

where $\varvec{H}=[\varvec{h}(\varvec{x}_1),\ldots ,\varvec{h}(\varvec{x}_N)]$, $\varvec{h}(\cdot ) = [h_1(\cdot ),\ldots ,h_j(\cdot ),\ldots ,h_{n_h}(\cdot )]^T$, and $\varvec{Y}=[y_1, \ldots , y_N]$. $h_j(\cdot )$ is the activation function (or the feature mapping function). Note that the sigmoidal function is chosen to give a nonlinear mapping in this research. Then the smallest norm least squares solution of $\varvec{w}^*$ to the above linear system can be expressed as follows,

$$\begin{aligned} \varvec{w}^*= \varvec{H}^\dag \varvec{Y}, \end{aligned}$$

(9)

where $\varvec{H}^\dag$ is the Moore–Penrose pseudoinverse of matrix $\varvec{H}$.

Till now, the basic ELM is introduced and it can be employed for one-step-ahead prediction. In this study, the multi-step-ahead prediction is also investigated for predicting the driver demand of future horizons.

Recursive of one-step-ahead predictions with an artificial neural network (ANN) is a classical method for multi-step-ahead prediction [30]. However, the accuracy of the ANN model may be seriously compromised when it is used recursively. In [30], the authors suggest that their proposed chained neural network (CNN) model performs better than the classical recursive method. By chaining a group of networks, the networks gradually take the prediction of their predecessors in the chain as an extra input. Along this line, a multiple neural network (MNN) model which includes a group of neural networks is proposed in [31]. All component neural networks work together, and each makes predictions at a different length of step ahead. The authors suggest that a MNN performs better than a single ANN for the multi-step-ahead prediction.

By making use of the chained structure, a CELM model that is composed of a series of ELM models is developed, as shown in Fig. 7. The CELM model for h-step-ahead prediction is composed of h one-step-ahead ELM prediction models: $\mathrm{ELM}_{\#1}$, $\mathrm{ELM}_{\#2},\ldots , \mathrm{ELM}_{\#h}$. The CELM starts with $\mathrm{ELM}_{\#1}$ which takes the time series of $\varvec{x}$ ($\varvec{x}_k$ means the kth step) as input and produces a one-step-ahead prediction, $\hat{y}_{k+1}$. The prediction $\hat{y}_{k+1}$ is then inserted into the next prediction model, $\mathrm{ELM}_{\#2}$, to perform the prediction of the subsequent step until one reaches the prediction horizon, h. The dimension of input of each sequential ELM gradually grows by adding the output of previous ELM model. When training the CELM model using a data set, h different ELM models should be trained successively. Each ELM model in the chain is trained in Eq. (9).

Fig. 7

Structure of a chained ELM for h-step-ahead prediction

3.2 One-step-ahead prediction

In this paper, one-step-ahead predictor for driver torque demand could be obtained with utilization of V2I and V2V information. This predictor is based on ELM learning algorithm, and the structure of one-step-ahead predictor is depicted in Fig. 8. There are four input vectors at the kth step, including constant variables $\mathbf {u}_{c,k}$, torque demand variables $\mathbf {u}_{\tau ,k}$, traffic light variables $\mathbf {u}_{l,k}$, and distance to intersection variables $\mathbf {u}_{s,k}$. Detail meanings of variables in each vector are given in Table 1. The output of the ELM-based predictor is driver torque demand at the $k+1$th step.

Fig. 8

Structure of one-step-ahead prediction of driver torque demand

Table 1 Meaning of inputs and output signals for one-step-ahead driver torque demand predictor

3.3 Multi-step-ahead prediction

For purpose of multi-step optimization problem, improved fuel economy would be obtained if a multi-step-ahead driver torque demand were from the $k+1$th step to the $k+N$th step. In this subsection, a multi-step-ahead torque predictor is developed. The predictor is composed of a series of one-step-ahead predictors proposed in Sect. 4.2. The structure of this multi-step-ahead torque predictor is shown in Fig. 9. In this chained structure predictor, constant variables in $\mathbf {u}_{c,k}$ are also used for the $k+2$th- and $k+3$th-step predictors. However, as can be seen in Fig. 10a, the elements of $\mathbf {u}_{\tau ,i}$ $(i = k+1, k+2)$ for the $k+2$th-step and the $k+3$th-step predictors increase with the addition of output of predictors in the $k+1$th step and the $k+2$th step, respectively. Solid balls in Fig. 10a represent elements of $\mathbf {u}_{\tau ,i}$ $(i = k-2, k-1, k, k+1, k+2)$, the black ones denote the obtained signals of ego vehicle, and the blue, green and yellow ones are the predicted signals. The detail of $\mathbf {u}_{\tau ,i}$ $(i = k+1,k+2)$ is expressed by

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf {u}_{\tau ,k+1}=[\tau _{\mathrm{dr}(k-2)},\ \tau _{\mathrm{dr}(k-1)},\ \tau _{\mathrm{dr}(k)},\ \hat{\tau }_{\mathrm{dr}(k+1)}]^\mathrm{T}\\ \mathbf {u}_{\tau ,k+2}=[\tau _{\mathrm{dr}(k-2)},\ \tau _{\mathrm{dr}(k-1)},\ \tau _{\mathrm{dr}(k)},\ \hat{\tau }_{\mathrm{dr}(k+1)},\ \hat{\tau }_{\mathrm{dr}(k+2)}]^\mathrm{T} \end{array} \right. \end{aligned}$$

(10)

Fig. 9

Structure of multi-step-ahead prediction of driver torque demand

Fig. 10

Illustration for multi-step-ahead prediction of driver torque demand

If the destination is given, a proper driving route of ego vehicle can be determined. Then, the future traffic light information at each intersection in this route consists of remaind timing and phase, can be pre-known and supplied to ego vehicle through V2I technology. Traffic light signals of phase $l_s$ and remaind timing $l_t$ are depicted in Fig. 10b. Thus, the elements in traffic light vector $\mathbf {u}_{l, i}$ $(i = k, k+1, k+2)$ are updated with credible values of traffic light information at the next intersection for sub-predictor in Fig. 9. Moreover, the elements in distance to intersection vector $\mathbf {u}_{s,i}$ $(i = k, k+1, k+2)$ are also updated since ego vehicle is nearer to intersection in the future steps as shown in Fig. 10c. To calculate the distance s to the next intersection of ego vehicle, vehicle speeds at the $k+1$th step and the $k+1$th step are assumed to be equal to that at the kth step. Then, the distances s can be obtained as follows,

$$\begin{aligned} s_{i+1} = s_{i}+v_{k}\times \varDelta t,\quad i = k, k+1, \end{aligned}$$

(11)

where $\varDelta t$ denotes the sampling period, and $v_{k}=v_{k+1}=v_{k+2}$.

4 Optimal energy management strategy

The optimization algorithms for solving the proposed optimal energy management problem that is formulated by Eqs. (4), (5) and (6) are introduced in this section.

First, for the cost function (4), an analytical expression for the fuel mass flow rate $\dot{m}_\mathrm{f}$ is obtained as polynomial with respect to the variables $\tau _\mathrm{e}$ and $\omega _\mathrm{e}$ by identification with the engine map data shown in Fig. 3a:

$$\begin{aligned} \dot{m}_\mathrm{f} = \mathscr {M}_f (\tau _\mathrm{e}, \omega _\mathrm{e}). \end{aligned}$$

(12)

Furthermore, the instantaneous electricity consumption can be calculated according to the battery SoC by

$$\begin{aligned}&\dot{m}_e= -U_\mathrm{o}Q_\mathrm{b}{\dot{\mathrm{SoC}}}, \nonumber \\&\mathrm{with }\ \dot{\mathrm{SoC}}=\dfrac{-U_\mathrm{o}+\sqrt{U^2_{o}-4R_\mathrm{b} (\tau _\mathrm{m}\omega _\mathrm{m}-P^\mathrm{loss}_\mathrm{m}(\tau _\mathrm{m}, \omega _\mathrm{m}))}}{2Q_\mathrm{b}R_\mathrm{b}}, \end{aligned}$$

(13)

where $U_\mathrm{o}$, $Q_\mathrm{b}$ and $R_\mathrm{b}$ denote the open circuit voltage, the maximum charge capacity and the internal resistance of the battery, respectively, and $P^\mathrm{loss}_\mathrm{m}$ denotes the operating point-dependent power losses of the motor, which is identified with the motor map data shown in Fig. 3b. Then, the following problem formulation with two specific cases is presented.

Furthermore, as mentioned in Sect. 2, the design variables for the energy optimization are the command values $(\tau _\mathrm{e}, \tau _\mathrm{m}, i_\mathrm{g})$. However, it can be observed that the condition (5) implies that dealing with the energy management problem can take the engine operating point $(\tau _\mathrm{e}, \omega _\mathrm{e})$ as the design variables equivalently. In this case, the optimal commands of $\tau _\mathrm{m}$ and $i_\mathrm{g}$ can be calculated according to the two relations and with the vehicle speed value as shown in Fig. 11.

Fig. 11

Block diagram of the optimization design problem

Consider that the road slop $\theta =0$, and the operating mode decision is according to the following switching condition,

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm{HEV\ mode}, &{}\quad P_{\mathrm{dr}}\left( = \dfrac{1}{R_\mathrm{tire}}\tau _{\mathrm{dr}}v \right) \ge P^0_{\mathrm{dr}} \\ \mathrm{EV\ mode}, &{}\quad \mathrm{others}, \end{array}\right. \end{aligned}$$

(14)

where $P^0_{\mathrm{dr}}$ is a constant. Then, during the HEV mode, the considered optimization problem characterized by Eqs. (4), (5) and (6) can be reformulated as the following constrained nonlinear optimWith the one-step-aheadization problem:

$$\begin{aligned} \left\{ \begin{array}{l} {\displaystyle \min \limits _{[\tau _\mathrm{e}, \omega _\mathrm{e}]^T} J = \int ^{t+T}_t \left[ \dfrac{\gamma _\mathrm{f}}{\rho _\mathrm{f}}\mathscr {M}_f(\tau _\mathrm{e}(\tau ), \omega _\mathrm{e}(\tau )) + \gamma _\mathrm{e} \dot{m}_\mathrm{e}(\hat{\tau }_{\mathrm{dr}}(\tau ), \omega _\mathrm{e}(\tau ), v(\tau ))\right] \mathrm{d}\tau }\\ \begin{array}{ll} \mathrm{subject\ to:\ } &{} M \dot{v}(\tau )=\dfrac{\eta _f \hat{\tau }_{\mathrm{dr}}(\tau )}{R_\mathrm{tire}} -F( v(\tau ))\\ &{} \tau _\mathrm{e}(\tau )\omega _\mathrm{e}(\tau ) \ge P^0_{\mathrm{dr}}\\ &{} \omega _\mathrm{emin}(v(\tau ))\le \omega _\mathrm{e}(\tau ) \le \omega _\mathrm{emax}(v(\tau )) \\ &{} \tau _{e}(\tau ) \le \tau _\mathrm{emax}(\omega _\mathrm{e}(\tau )) \end{array} \end{array}\right. \end{aligned}$$

(15)

where the variables with subscripts min and max denote the corresponding minimum and maximum, respectively. Here, the maximum engine torque $\tau _\mathrm{emax}$ is an identified polynomial function associated with the engine speed shown in Fig. 3, and for the motor, suppose that the maximum torque limitation is restricted outside the optimization block.

Finally, note that the formulation of the problem (15) is difficult to be solved and applied in real time directly. In order to facilitate solving the problem and combine the predicted $\hat{\tau }_{\mathrm{dr}(k)}$, the cost function of problem (15) is converted to the discrete type as

$$\begin{aligned}&\min \limits _{[\tau _\mathrm{e},\omega _\mathrm{e}]} \sum ^{N}_{l=1} \left[ \dfrac{\gamma _\mathrm{f}}{\rho _\mathrm{f}} \mathscr {M}_f(\tau _{\mathrm{e}(k+l)}, \omega _{\mathrm{e}(k+l)})\right. \nonumber \\&\quad \left. +\,\gamma _\mathrm{e} \dot{m}_\mathrm{e} (\hat{\tau }_{{\mathrm{dr}}(k+l)},\omega _{\mathrm{e}(k+l)},v_{k+l})\right] \varDelta t, \end{aligned}$$

(16)

where $N=T/\varDelta t$. Moreover, the powertrain dynamics (1) is discretized by approximating the vehicle acceleration with forward difference, then, obtain that

$$\begin{aligned} M\dfrac{v_{\tilde{k}+1}-v_{\tilde{k}}}{\delta t}=\dfrac{\eta _f \tau _{\mathrm{dr}(\tilde{k})}}{R_\mathrm{tire}}-F(v_{\tilde{k}}), \end{aligned}$$

(17)

where $\delta t=0.001$ is a selected constant. Furthermore, suppose that $\tau _{\mathrm{dr}(\tilde{k} +i)} = \tau _{\mathrm{dr}(k)}$ ($i=0,\ldots , n-1$), then, obtain that

$$\begin{aligned}&v_{k+1} = v_{k}+ \tilde{f}(\tau _{\mathrm{dr}(k)}, v_k),\nonumber \\&\mathrm{with }\quad \tilde{f}(\tau _{\mathrm{dr}(k)}, v_{k}) \nonumber \\&\quad = \sum \limits ^n_{i=1} \dfrac{\delta t}{M} \left( \dfrac{\eta _f}{R_\mathrm{tire}}\tau _{\mathrm{dr}(k)}-F(v_{\tilde{k}+i-1}) \right) ,\quad v_{\tilde{k}}=v_{k}, \end{aligned}$$

(18)

where $n=\varDelta t/ \delta t$.

4.1 One-step optimization

With the one-step-ahead torque demand prediction $\hat{\tau }_{\mathrm{dr}(k)}$ in Sect. 3.2, an instantaneous optimization design problem is solved first. The objective is that at the time instant k, decide the optimal operating point at the next time step, i.e., $(\tau _{\mathrm{e}(k+1)}, \omega _{\mathrm{e}(k+1)})$. In this case, take the discretized cost function (16) and the vehicle speed Eq. (18) into account, and let $U_{k+1}=[\tau _{\mathrm{e}(k+1)}, \omega _{\mathrm{e}(k+1)}]^T$, the formulation of problem (15) can be represented by the following one,

$$\begin{aligned} \left\{ \begin{array}{l} \min \limits _{U_{k+1}} J(U_{k+1})\\ \mathrm{subject\ to}: G(U_{k+1})\ge 0 \end{array}\right. \end{aligned}$$

(19)

with

$$\begin{aligned} J(U_{k+1}) &= \left[\dfrac{\gamma _\mathrm{f}}{\rho _\mathrm{f}}\mathscr {M}_f(\tau _{\mathrm{e}(k+1)}, \omega _{\mathrm{e}(k+1)})\right. \nonumber \\&\quad\left. +\, \gamma _\mathrm{e} \dot{m}_e (\hat{\tau }_{\mathrm{dr}(k+1)},\omega _{\mathrm{e}(k+1)},v_{k+1})\right] \varDelta t, \\ G(U_{k+1})&= \left[ \begin{array}{l} \tau _{\mathrm{e}(k+1)}\omega _{\mathrm{e}(k+1)} - P^0_{\mathrm{dr}}\\ \omega _{\mathrm{e}(k+1)}-\omega _\mathrm{emin}(v_{k+1})\\ -\,\omega _{\mathrm{e}(k+1)}+ \omega _\mathrm{emax}(v_{k+1})\\ -\,\tau _{{e}(k+1)} + \tau _\mathrm{emax}(\omega _{\mathrm{e}(k+1)}) \end{array}\right] . \end{aligned}$$

It can be found that for the above optimization problem (19), the required value $v_{k+1}$ can be obtained by Eq. (18), and the value $\hat{\tau }_{\mathrm{dr}(k+1)}$ can be generated by the ELM-based algorithm shown in Fig. 8. Then, the sequential quadratic programming (SQP) algorithm is applied to solve the instantaneous nonlinear optimization problem described by (19).

Let $\varDelta U_{k+1}= U^*_{k+1}-U_{k+1}$, then, the above problem (19) is solved by using the iterative method as the flowchart shown in Fig. 12, where $i_\mathrm{max}$ denotes the maximum iterative steps taken as the termination condition and $\nabla$ denotes the corresponding Jacobi matrix. At each time step $\varDelta t$, the driver torque demands $\hat{\tau }_{\mathrm{dr}(k+1)}$ and $v_{k+1}$ are calculated with the data $v_{k}$, $\tau _{\mathrm{dr}(k)}$ and $\hat{\tau }_{\mathrm{dr}(k)}$, and the SQP algorithm is repeated.

Fig. 12

Flowchart of SQP algorithm

4.2 Multi-step optimization

Note that the instantaneous optimization is limited by a really short preview for the driver demand. In this part, the above one-step-ahead optimization strategy is extended to the case of a multi-step-ahead optimization. The multi-step-ahead strategy actually provides a real-time receding horizon optimization procedure. Specifically, the aim is that at time step $\varDelta t$, determine the optimal solution $\mathscr {U}^*_{k+1} =[\tau _{\mathrm{e}(k+1)}, \omega _{\mathrm{e}(k+1)},\ldots , \tau _{\mathrm{e}(k+N)}, \omega _{\mathrm{e}(k+N)}]^T$ such that

$$\begin{aligned} \mathscr {U}^*_{k+1} &= \mathop {\arg \min }\limits _{\mathscr {U}_{k+1}} \sum \limits ^{N}_{l=1} \left[ \dfrac{\gamma _\mathrm{f}}{\rho _\mathrm{f}} \mathscr {M}_f(\tau _{\mathrm{e}(k+l)}, \omega _{\mathrm{e}(k+l)}) \right. \nonumber \\&\quad \left. +\,\gamma _\mathrm{e} \dot{m}_e (\hat{\tau }_{\mathrm{dr}(k+l)},\omega _{\mathrm{e}(k+l)},v_{k+l})\right] \varDelta t. \end{aligned}$$

(20)

Then only the first two values $(\tau _{\mathrm{e}(k+1)}, \omega _{\mathrm{e}(k+1)})$ of $\mathscr {U}^*_{k+1}$ are applied as the designed values.

The optimal series design variable $\mathscr {U}^*_{k+1}$ can be obtained by solving the following nonlinear optimization problem which is a direct extension of the instantaneous optimization problem (19) by using the multi-shooting technology, that is

$$\begin{aligned} \left\{ \begin{array}{l} \min \limits _{\mathscr {U}_{k+1}} J_M(\mathscr {U}_{k+1})\\ \mathrm{subject\ to}: G_M(\mathscr {U}_{k+1})\ge 0 \end{array}\right. \end{aligned}$$

(21)

with

$$\begin{aligned} J_M(\mathscr {U}_{k+1}) &= \sum \limits ^{N}_{l=1} \left[ \dfrac{\gamma _\mathrm{f}}{\rho _\mathrm{f}} \mathscr {M}_f(\tau _{\mathrm{e}(k+l)}, \omega _{\mathrm{e}(k+l)}) \right. \nonumber \\&\quad \left. +\,\gamma _\mathrm{e} \dot{m}_e (\hat{\tau }_{\mathrm{dr} (k+l)}, \omega _{\mathrm{e}(k+l)}, v_{k+l})\right] \varDelta t,\\ G_M(\mathscr {U}_{k+1})&= \left[ \begin{array}{l} \tau _{\mathrm{e}(k+1)}\omega _{\mathrm{e}(k+1)} - P^0_{\mathrm{dr}}\\ \omega _{\mathrm{e}(k+1)}-\omega _\mathrm{emin}(v_{k+1})\\ -\,\omega _{\mathrm{e}(k+1)}+ \omega _\mathrm{emax}(v_{k+1})\\ -\,\tau _{\mathrm{e}(k+1)} + \tau _\mathrm{emax}(\omega _{\mathrm{e}(k+1)})\\ \vdots \\ \tau _{\mathrm{e}(k+N)} \omega _{\mathrm{e}(k+N)} - P^0_{\mathrm{dr}}\\ \omega _{\mathrm{e}(k+N)}-\omega _\mathrm{emin}(v_{k+N})\\ -\,\omega _{\mathrm{e}(k+N)} + \omega _\mathrm{emax}(v_{k+N})\\ -\,\tau _{\mathrm{e}(k+N)} + \tau _\mathrm{emax}(\omega _{\mathrm{e}(k+N)}) \end{array}\right] . \end{aligned}$$

It is clear that the above problem can also be solved by applying the SQP algorithm shown in the flowchart of Fig. 12 directly. However, to obtain $\mathscr {U}^*_{k+1}$ over the prediction horizon, the $v_{k+l}$ and $\hat{\tau }_{\mathrm{dr}(k+l)}$, ($l=1,\dots ,N$) need to be known in advance. On the basis of the proposed CELM-based multi-step-ahead driver demand prediction in Sect. 3.3 and with the Eq. (18), the ahead values can be calculated by

$$\begin{aligned} v_{k+l} = v_{k+l-1} + \tilde{f}(\hat{\tau }_{\mathrm{dr}(k+l-1)}, v_{k+l-1}), \quad l=2,\ldots , N \end{aligned}$$

(22)

5 Simulation validation

5.1 Simulation setup

The evaluation of the driver torque demand prediction algorithms and the proposed energy management strategies are conducted by using the TILP powertrain simulation platform shown in Fig. 4. Figure 13 shows the graphical user interface (GUI) of the platform. In this simulation platform, there are powertrain models. Since it focuses on traffic flow and infrastructure emulation with simplified vehicle model, the structure amount and modeling accuracy are not enough for powertrain dynamic reflection and optimization strategy design. A solution to overcome this problem is to replace the existing powertrain system by a specific one built through mathematical modeling. The key of this solution is as shown in Fig. 14, where MCU and CCU denote the motor control unit and the clutch control unit, respectively. The powertrain structure of selected vehicle in traffic simulation platform is a traditional engine-propelling vehicle with a CVT.

Fig. 13

Graphical User Interface (GUI) of traffic powertrain simulation platform

Fig. 14

Main idea of replacement of powertrain model by specified HEV structure

It can be noted from Figs. 4 and 14 that the considered parallel HEV powertrain model is built with MATLAB/Simulink. Using signals from CarMaker, the torque commands of the engine and motor, and the clutch state and gear ratio, can be determined by the designed energy management strategy, and the output torque of parallel HEV powertrain is given back to CarMaker to propel the ego vehicle. Moreover, the V2V and V2I information can be transmitted into Simulink for the torque demand prediction. On the one hand, for the integration of co-simulation platforms, the different dimensions between vehicle model in traffic simulator and specify powertrain model should be managed, and the rotational inertias of different equipments should be considered during integration. More details on the integration process are referred to the work [32]. It should be noted that the powertrain performance will influence the ego vehicle dynamics and the surrounding vehicles will also be influenced by the ego vehicle sequently. Furthermore, reflection of the ego vehicle driver to real-time traffic scenario will affect the powertrain dynamics. Specially, the employed HEV powertrain model is based on automotive industry background structure and parameters for accurate simulation performance.

A real-world emulated traffic road situation is built in the simulation platform. The road map is as given in Fig. 15. The length of the simulation route is 4.1588 km. There are 6 traffic lights at the intersections. Traffic light time duration of green, yellow and red is set as 30 s, 3 s and 15 s, respectively. The locations of the departure, destination and intersections are also given in Fig. 15. Traffic densities of Link 1 (L1)–Link 6 (L6) are set as $30\%$, $25\%$, $25\%$, $20\%$, $10\%$ and $10\%$, respectively. Even with same traffic density in each link, the vehicle amounts are always not constant after different traffic scenarios generation. In this case, the speeds of ego vehicle and other traffic participants are also different. Therefore, different driving cases can be obtained for both of data training and simulation validation.

Fig. 15

Traffic scenario map

5.2 Driver torque demand prediction performance

With the above simulation setup, the current states of ego vehicle and real-time information of V2V and V2I listed in Table 1 are available in the co-simulation platform. A CELM is trained to predict the driver torque demand over a specific temporal horizon (one or several steps). Prediction results are presented as follows.

Over the route shown in Fig. 15, traffic lights, traffic speed, vehicle density as well as other parameters such as driving style and speed limit, etc. are set up. Then, 30 groups of vehicle speed scenarios simulated on the route are collected, where 20 groups are used to train the CELM prediction model and the remainders are used to validate the model. It should be noted that the sampling time of the collected data is $\varDelta t = 0.2$ s. To illustrate the sources of data collection, Fig. 16 shows a part of the ego vehicle speed and preceding vehicle speed that are six of the collected 30 group scenarios. It can be observed from Fig. 16 that due to the stochastic driving environment, the vehicle speed scenario is not deterministic even on the same urban route. The diversity of the collected scenarios is beneficial to the robustness of the CELM prediction model.

Fig. 16

A part of collected vehicle speed scenarios for training and validation: six of the 30 groups

A CELM model (see Fig. 9) is constructed for three-step-ahead prediction, i.e., prediction over 0.2 s, 0.4 s and 0.6 s horizons. The size of the hidden layer of each ELM model is set to 500. The inputs and outputs are described in Table 1. To show the accuracy of the CELM prediction model, driver torque demand prediction results over the 1st, 2nd, and 3rd steps for one test scenario are presented in Fig. 17. It can be observed that the predicted torque demand of the 1st step $\hat{\tau }_{\mathrm{dr}(k+1)}$ is closed to the real value $\tau _{\mathrm{dr}(k+1)}$; however, the prediction of the 3rd step $\hat{\tau }_{\mathrm{dr}(k+1)}$ has big difference to the real vale when the torque demand has fast changes. Figure 18 shows the difference of each predicted value to the counterpart real value of the three steps, respectively. From the data shown in Fig. 18, we can observe that the 1st step can achieve almost unbiased estimation, and the variance increases gradually as the step increases. Furthermore, to evaluate the prediction accuracy specifically, the root-mean-square error (RMSE) as formulated in Eq. (23) is calculated with respect to the 10 scenarios used for the validation of the CLEM prediction model, i.e.,

$$\begin{aligned} \mathrm{RMSE} = \sqrt{\frac{1}{I}\sum _{i=1}^I (\tau _{\mathrm{dr}(i)} - \hat{\tau }_{\mathrm{dr}(i)})^2}, \end{aligned}$$

(23)

where I is the number of samples. The RMSE for the 1st, 2nd, and 3rd steps of the 10 test scenarios is presented in Fig. 19. It can be seen that the RMSE increases along with more prediction steps, and the minimum RMSE can achieve 100, 150 and 160 for the three steps, respectively. However, although RMSE exists, the prediction can reflect the consistent pattern of stop, brake and acceleration.

Fig. 17

Three-step-ahead prediction for the driver torque demand of one scenario using CELM-time series

Fig. 18

Difference of each predicted value to the counterpart real value of one scenario

Fig. 19

Relationship between prediction step and prediction error of 10 different scenarios

5.3 Optimization performance

According to the optimization design, the potential of fuel economy and the cost efficiency (¥/MJ) of the energy generated by both of the fuel and electricity are the concerned evaluation indexes. In order to evaluate the performance of the ELM-based optimization strategies quantitatively, the proposed optimization algorithms are compared to two counterpart algorithms in which the torque demand is considered to be a constant over the prediction horizon, specifically, $\hat{\tau }_{\mathrm{dr}(k+1)}=\tau _{\mathrm{dr}(k)}$ in the one-step-ahead instantaneous optimization strategy and $\hat{\tau }_{\mathrm{dr}(k+i)} = \tau _{\mathrm{dr}(k)}$ $(i=1,2,3)$ in the three-step-ahead receding horizon optimization strategy, respectively.

The main parameters of the powertrain system are listed in Table 2. The parameters of the battery are $Q_\mathrm{b}=23.275$ (kWh), $U_\mathrm{o}=247$ (V) and $R_\mathrm{b}=0.13\,(\varOmega )$. $P^0_{\mathrm{dr}}=6$ (kW), and the limit engine speed is set as $\omega _{\mathrm{emin,max}}=i_{\mathrm{gmin,max}}i_0 v/ R_\mathrm{tire}$. The maximum iterative steps is set as $i_\mathrm{max}=3$ and validation tests demonstrate that the value for $i_\mathrm{max}$ is enough for real-time computation in solving the proposed two problems. On the other hand, it should be noted that the two parameters $\gamma _\mathrm{f}$ and $\gamma _\mathrm{e}$ which are actually weighting factors in the cost function (4) account for the solution of the proposed energy management problems. With a fixed $\gamma _\mathrm{f}$, a smaller $\gamma _\mathrm{e}$ means less electricity will be consumed while more fuel should be used. For the validation tests, three cases regarding the cost function are considered: no.1 ($\gamma _\mathrm{f}=150$, $\gamma _\mathrm{e}=38$); no.2 ($\gamma _\mathrm{f}=150$, $\gamma _\mathrm{e}=41$); no.3 ($\gamma _\mathrm{f}=150$, $\gamma _\mathrm{e}=45$).

Table 2 Main parameters of the HEV model

Figures 20 and 21 show the plots with respect to the one-step-ahead strategy and the three-step-ahead strategy, respectively, including the curves of the vehicle speed, the driver torque demand, the torques and speeds of the engine and motor, respectively, and the fuel mass flow rate and battery SoC. Note that as an illustration, only the plots of case no. 2 are shown. The curves of the engine $\tau _\mathrm{e}$ and $\omega _\mathrm{e}$ show that the real-time optimal solutions are obtained with that the inequality constraint conditions of the problem (15) are satisfied. Moreover, it can be observed from the torque and speed of the engine and motor that during the vehicle accelerations that require high demand torque, both of the engine and motor can operate at high effective zone to provide driving power. Besides the acceleration, it can be noted from the curves $\tau _\mathrm{e}$ versus $\tau _\mathrm{m}$ that when the vehicle operates at relatively constant speed higher than 60 km/h (such as the time period 57–70 s), the engine provides driving power while the motor works as generater to charge the battery as can be seen from the SoC curve. This result indicates the influence of the weighting factors $\gamma _\mathrm{f}$ and $\gamma _\mathrm{e}$ to the solution of the proposed optimization problems.

Table 3 provides the results in terms of the fuel cost, the electricity cost and the cost efficiency of the powertrain system with using the one-step-ahead prediction $\hat{\tau }_{\mathrm{dr}(k+1)}$ and without using the prediction. Table 4 provides the corresponding results of the case with using the three-step-ahead prediction. The results in the two tables indicate that the fuel cost increases while the electricity cost reduces as the parameter $\gamma _\mathrm{e}$ increases. Meanwhile, it can be observed that both of the two proposed strategies improve the fuel economy. Moreover, using multi-step-ahead torque demand prediction produces more fuel economy and clear cost efficiency improvement. However, it can be found that using one-step-ahead prediction, the cost efficiency has little improvement. These results imply that the cost efficiency can benefit from a longer prediction horizon for the driver torque demand and multi-step-ahead receding horizon optimization possesses advantage of taking more correlation V2V and V2I information data into the energy management.

Fig. 20

Simulation result with one-step-ahead prediction for torque demand: $\gamma _\mathrm{f}=150$, $\gamma _\mathrm{e}=41$

Fig. 21

Simulation result with three-step-ahead prediction for torque demand: $\gamma _\mathrm{f}=150$, $\gamma _\mathrm{e}=41$

Table 3 Result with one-step-ahead torque demand prediction

Table 4 Result with three-step-ahead torque demand prediction ($i=1, 2, 3$)

5.4 Discussion

The evaluation results on both of the ELM-based torque demand prediction and energy optimization algorithm imply the following significance of the proposed energy management strategies for HEVs. First, a novel torque demand prediction method is proposed in the sense of CV-based framework rather than the normal prediction with the history demand data of the ego vehicle [12, 13]. The essential feature of the proposed energy management strategy is that a receding horizon torque demand prediction method is constructed by using 16 input variables of instantaneous V2V and V2I information to deal with energy efficiency optimization during transient vehicle operations. This feature distinguishes our scheme from the trip-oriented predictions of vehicle velocity or energy demand for dealing with battery management [12, 18, 19]. Compared to the approaches based on Markov-chain and Neural network [6, 14, 15, 17], the proposed prediction with ELM algorithms has the advantage on generalization to adaptive real-world driving data. On the other hand, note that the proposed optimization strategy considers the driver behavior influence by taking both of the accelerator and brake pedal variations as inputs. Driver behavior influence is considerable to the energy efficiency optimization during the transient vehicle operations.

6 Conclusion

For HEVs, compared with route-dependent optimal energy management approaches, which are obtained by solving off-line optimization problem subject to the whole power demand or vehicle speed profile along the route, real-time optimization must be realized targeting the future driver power demand that cannot be known previously. A key to break through the challenging is the prediction of the unknown route or the non-occurred power demand. This paper focuses on investigating the issue of predictive optimal energy management problem in the HEV energy management design. As the first contribution, ELM-based and chained ELM algorithms for driver torque demand prediction are constructed, and for the algorithm, not only the past behavior of the driver is used to take the regressive effort into account but also the V2V and V2I information is taken as input. Under an automotive industry-used TILP powertrain simulation platform, demonstrated case studies show the prediction effort. The second contribution of this work is to propose a prediction-based optimal energy management strategy that combines with the ELM-based prediction. The optimization problem is formulated with the cost function concerning the total energy consumption for receding horizon minimization. Simulation results show that applying multi-step prediction receives better energy economy than using one-step-ahead prediction. Moreover, the potential of further energy saving is shown by the real-time receding horizon optimization integrated with the learning-based prediction. Most advantage of the proposed strategy is to deal with the optimization without any future trip knowledge. Finally, note that improving the prediction precision when the demand has fast variations needs further investigations by updating the proposed ELM-based algorithm. From the viewpoint of practice, the development of prediction-based energy management schemes that guarantee the co-optimization between transient energy efficiency and long-term energy management for HEVs is significant and is also the further investigation work.