1 Introduction

Air-ratio (also known as lambda) is an engine parameter indicating the amount of difference between the actual available air–fuel mixture and the stoichiometric ratio of the fuel being used [1]. The air-ratio plays an important role in engine performance control because it relates closely to engine emissions, power, and brake-specific fuel consumption. The rapid growth in the number of vehicles makes vehicular emissions become a major source of air pollution, which impacts on the public health and environment significantly, especially in urban areas. Studies [2–6] show that every year about hundred thousand of mortalities all over the world are related to vehicular emissions, resulting in billions of economic loss. To reduce the amount of toxic elements in vehicular emissions, the three-way catalytic converter is currently the most effective after-treatment device. When the air-ratio is stoichiometry (i.e., air-ratio = 1.0), the conversion efficiency of the three-way catalytic converter can reach as high as 98 %. However, the conversion efficiencies for carbon monoxide (CO), hydrocarbons (HC), and nitrogen oxides (NOX) drop more than 50 % when the air-ratio deviates more than 2 % from stoichiometry, causing more severe air pollution. Moreover, air-ratio can significantly affect brake-specific fuel consumption. Recent studies [7, 8] have showed that the air-ratio should be regulated to a value around 1.05 for achieving the best brake-specific fuel consumption. Furthermore, the maximum engine power can be achieved when the air-ratio is around 0.95. Therefore, optimal air-ratio control according to various operating conditions is significant and desired.

In the existing literature, there are a lot of control strategies on air–fuel ratio (AFR) rather than air-ratio. These strategies include sliding mode control [9], radial-basis-function neural network feedforward–feedback control [10], and model predictive control (MPC) using neural network-based models [11, 12]. Nevertheless, AFR control is ineffective for engine performance control because it does not consider the fuel variation. On the contrary, air-ratio is a fuel-independent index that can reflect the engine performance more effectively. Thus, this study focuses on air-ratio control rather than AFR. As air-ratio is associated with AFR, the control strategies developed for AFR can also be adopted to air-ratio. In the aforementioned researches, the latest and the most appropriate technique for AFR control is neural network-based MPC [11, 12], which is very robust and suitable for multivariable, time-varying, and delay systems, such as modern engine systems [13]. It is well known that a reliable engine performance prediction model is the core component of the MPC. However, the engine models developed in [10–12] were surrogate models. That is, the models were trained from the data generated by empirical equations rather than a real engine. In fact, many assumptions have been made in the empirical equations, and many coefficients in the equations are difficult to determine for a real engine [14]. Therefore, the neural network prediction models derived from the data generated by empirical equations cannot effectively reflect the actual performance of the controller in real engines. Moreover, the types of neural networks used in [11, 12] were radial-basis-function (RBF) neural network and diagonal recurrent neural network (DRNN). Both of these methods employ back-propagation (BP) algorithm that suffers from slow error convergence [15] and local minima [16]. Hence, the prediction models in these previous studies are not suitable for practical use.

To overcome the issues of BP, extreme learning machine (ELM) was proposed [17–20] that has a simple and effective modelling algorithm for training single hidden layer feedforward networks. In ELM, the training involves only the output weights; the parameters in the hidden nodes are generated randomly and unnecessary for adjustment. Many recent studies [16–18, 21–23] already showed that ELM can achieve better generalization and faster learning time than BP algorithms, and many variants of ELM have been introduced [15, 24–27]. However, classical ELM is only suitable for off-line batch training; it can only build the engine air-ratio model when all training data are ready. When a new datum arrives, the model cannot be updated dynamically, and a retraining from scratch is necessary. In practice, the air-ratio model in the MPC is required to be updated for any changes in engine performance due to engine aging or fair user modification on the engine. In other words, the training data for engine air-ratio performance will come sequentially in real time, so an online variant of ELM is necessary. Thankfully, online sequential extreme learning machine (OSELM) was developed in [15] for online learning of ELM. OSELM retains all the properties of ELM with advantages of efficient update and faster convergence speed. Moreover, its output weights can also be updated even when the data come one by one or chunk by chunk. This is a very favorable feature for real-time control applications. In order to develop a reliable prediction model for chaotic air-ratio behavior with online update ability, OSELM is therefore employed in this study.

In view of the deficiencies of the existing works, this paper proposes a nonlinear MPC algorithm for air-ratio control based on OSELM model, called online sequential extreme learning machine MPC (OEMPC). The OSELM air-ratio model can be updated continually to compensate for the air-ratio performance variation. This is a novel nontrivial application of OSELM. Based on the multiple-step-ahead prediction of the air-ratio, an optimal control signal is obtained to regulate the air-ratio to the desired values. The performance of the proposed OEMPC is compared with both the latest and conventional AFR control techniques, namely diagonal recurrent neural network MPC (DNMPC) [12] and proportional–integral–derivative (PID) controller in production cars, respectively. To the best knowledge of the authors, this paper is the first attempt at extending OSELM to the domain of automotive engine air-ratio modelling and control.

2 Online sequential extreme learning machine (OSELM)

OSELM is a simple and efficient online sequential modelling algorithm that can learn the training data one by one or chunk by chunk as well as discarding the data that are sequentially redundant. The OSELM modelling algorithm and update procedure are presented as below [15, 19]:

Given a chunk of initial training dataset D 0 of N 0 input vectors x n , n = 1 to N 0, along with N 0 corresponding scalar-valued output y n . The input vector x n  ∈ R m contains the previous measured engine parameters, including engine speed (ES), throttle position (TP), and air-ratio at a previous time instant. The corresponding air-ratio at that time is defined as the output y n  ∈ R. The OSELM air-ratio model with L hidden nodes and activation function g(x) can be mathematically expressed by:

$$ \hat{y}_{n} = f\left( {\varvec{x}_{n} } \right) = \sum\limits_{i = 1}^{L} {\beta_{i} g\left( {\varvec{a}_{i} ,b_{i} ,\varvec{x}_{n} } \right)} , $$
(1)

where ŷ n  = f(x n ) is the prediction of the true air-ratio, a i  = [a 0,…, a L ] and b i are the centers and variances of the ith RBF hidden node because RBF kernel is chosen in this study, and β i is the weight connecting the ith hidden node and the output node. Generally, the air-ratio model for predicting an unseen input datum x, which contains the recent measured engine parameters, can be expressed as

$$ \hat{y} = y_{p} = f(\varvec{x}) = \sum\limits_{i = 1}^{L} {\beta_{i} \exp \left( { - \frac{{\left\| {\varvec{a}_{i} - \varvec{x}} \right\|^{2} }}{{b_{i}^{2} }}} \right)} , $$
(2)

It has been theoretically shown that all weight vectors connecting the hidden nodes and the input nodes, a i and b i , can be randomly initialized and no update is needed. Only the weights connecting the hidden nodes and the output nodes, β i , are required to be optimized with Eq. (3) [15, 19].

$$ \varvec{\beta}^{(0)} = \varvec{K}_{0}^{ - 1} \varvec{G}_{0}^{T} \varvec{y}^{(0)} , $$
(3)

where β (0) = [β 1, β 2,…, β L ], y (0) = [y 1, y 2,…, y N0], G 0 is the hidden layer matrix that can be computed by Eq. (4), and K 0 is defined by Eq. (5):

$$ G_{0} = \left[ {\begin{array}{*{20}c} {\exp \left( { - \frac{{\left\| {\varvec{a}_{1} - \varvec{x}_{1} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} & \cdots & {\exp \left( { - \frac{{\left\| {\varvec{a}_{L} - \varvec{x}_{1} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} \\ \vdots & \ddots & \vdots \\ {\exp \left( { - \frac{{\left\| {\varvec{a}_{1} - \varvec{x}_{{N_{0} }} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} & \cdots & {\exp \left( { - \frac{{\left\| {\varvec{a}_{L} - \varvec{x}_{{N_{0} }} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} \\ \end{array} } \right], $$
(4)
$$ \varvec{K}_{0} = \varvec{G}_{0}^{T} \varvec{G}_{0} . $$
(5)

When there is a new chunk of dataset D 1 of N 1 input vectors x n , n = N 0 + 1 to N 0 + N 1, along with N 1 corresponding scalar-valued output y n , the air-ratio model is required to be updated to adapt the new scenario. As mentioned before, only the weights connecting the hidden nodes and the output nodes, β i , are required to be updated, which is accomplished by the following equation [15, 19]:

$$ \beta^{(1)} = \beta^{(0)} + \varvec{K}_{1}^{ - 1} \varvec{G}_{1}^{T} \left( {y^{(1)} - \varvec{G}_{1} \beta^{(0)} } \right), $$
(6)

where β (1) ∈ R L are the updated weights, y (1) = [y N0+1, y N0+2,…, y N0+N1], G 1 is another hidden layer matrix which can be computed by Eq. (7), and K 1 is defined by Eq. (8):

$$ \varvec{G}_{1} = \left[ {\begin{array}{*{20}c} {\exp \left( { - \frac{{\left\| {\varvec{a}_{1} - \varvec{x}_{{N_{0} + 1}} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} & \cdots & {\exp \left( { - \frac{{\left\| {\varvec{a}_{L} - \varvec{x}_{{N_{0} + 1}} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} \\ \vdots & \ddots & \vdots \\ {\exp \left( { - \frac{{\left\| {\varvec{a}_{1} - \varvec{x}_{{N_{0} + N_{1} }} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} & \cdots & {\exp \left( { - \frac{{\left\| {\varvec{a}_{L} - \varvec{x}_{{N_{0} + N_{1} }} } \right\|^{2} }}{{b_{i}^{2} }}} \right)} \\ \end{array} } \right], $$
(7)
$$ \varvec{K}_{1} = \varvec{K}_{0} + \varvec{G}_{1}^{T} \varvec{G}_{1} . $$
(8)

For the k + 1 chunk of dataset D k+1 of N k+1 input vectors x n , n = N k  + 1 to N k  + N k+1, along with N k+1 corresponding scalar-valued output y n , the optimal weights connecting the hidden node and the output nodes, β i , are given by [15, 19]:

$$ \varvec{\beta}^{(k + 1)} =\varvec{\beta}^{(k)} + \varvec{K}_{k + 1}^{ - 1} \varvec{G}_{k + 1}^{T} \left( {\varvec{y}^{(k + 1)} - \varvec{G}_{k + 1}\varvec{\beta}^{(k)} } \right), $$
(9)

where y (k+1) = [y Nk+1, y Nk+2,…, y Nk+Nk+1] and K k+1 is defined by Eq. (10):

$$ \varvec{K}_{k + 1} = \varvec{K}_{k} + \varvec{G}_{k + 1}^{T} \varvec{G}_{k + 1} . $$
(10)

In order to update β (k+1) from β (k) efficiently, K −1 k+1 is required to be computed efficiently, which could be derived using the Woodbury formula [28]:

$$ \begin{aligned} \varvec{K}_{k + 1}^{ - 1} & = \left( {\varvec{K}_{k} + \varvec{G}_{k + 1}^{T} \varvec{G}_{k + 1} } \right)^{ - 1} , \\ & = \varvec{K}_{k}^{ - 1} - \varvec{K}_{k}^{ - 1} \varvec{G}_{k + 1}^{T} \left( {\varvec{I} + \varvec{G}_{k + 1} \varvec{K}_{k}^{ - 1} \varvec{G}_{k + 1}^{T} } \right)^{ - 1} \times \varvec{G}_{k + 1} \varvec{K}_{k}^{ - 1} . \\ \end{aligned} $$
(11)

To avoid the term G T0 G 0 in Eq. (5) being singular, rank(G 0) must be equal to L. In order to make rank(G 0) = L, the OSELM must be initialized with a training dataset of N 0 data such that N 0 > L. The number of hidden nodes L in this study was chosen as 20 based on the model selection procedure presented in [15].

3 MPC with OSELM model

The structure of the proposed OEMPC is shown in Fig. 1. The controller consists of the OSELM air-ratio model and the optimizer based on Brent’s method [29]. The OSELM air-ratio model predicts the engine response over a specified time horizon. The predictions are used by the optimizer to determine the tentative fuel injection time u′, which minimizes the following performance criterion over the specified time horizon, and then the optimal fuel injection time signal u is sent to the engine.

$$ \hbox{min}\,J\left( {u^{\prime } } \right) = \sum\limits_{{j = N_{1} }}^{{N_{2} }} {\left( {y_{r} \left( {t + j} \right) - y_{p} \left( {t + j} \right)} \right)^{2} } + \rho \sum\limits_{j = 1}^{{N_{u} }} {\left( {u^{\prime } \left( {t + j - 1} \right) - u^{\prime } \left( {t + j - 2} \right)} \right)^{2} } , $$
(12)

where N 1 and N 2 define the prediction horizon. t and N u are the time step and the control horizon, respectively. ρ is a user-defined weight that penalizes excessive movement of the control signal (i.e., the fuel injection time). The variables u′(t + j − 1) and u′(t + j − 2) in the second part of Eq. (12) are the tentative fuel injection time at the time steps t + j − 1 and t + j − 2, respectively. The second part of Eq. (12) ensures the stability of the controller output. y r (t + j) is the target air-ratio at the time step t + j, and y p is the predicted air-ratio by the OSELM model which is computed from Eq. (2) at the time step t + j, from which the input vector x consists of three time series of engine parameters: engine speed ES(t + j − 1), ES(t + j − 2), etc.; throttle position TP(t + j − 1), TP(t + j − 2), etc; and previous measured air-ratio y(t + j − 1), y(t + j − 2), etc. In other words,

$$ y_{p} \left( {t + j} \right) = \sum\limits_{i = 1}^{L} {\beta_{i} \exp \left( { - \frac{{\left\| {\varvec{a}_{1} - \varvec{x}} \right\|^{2} }}{{b_{i}^{2} }}} \right)} . $$
(13)
Fig. 1
figure 1

Structure of OEMPC for engine air-ratio control

Full size image

3.1 Single-dimensional optimization approach

The original optimization problem involved in this paper is multidimensional and constrained with the tentative control signals, u′(t), u′(t + 1),…, u′(t + N u  − 1), over the control horizon N u , which can minimize the objective function J(u′) of Eq. (12). Then the predicted air-ratios, y p (t + N 1), y p (t + N 1 + 1),…, y p (t + N 2 ), can trace the target air-ratios, y r (t + N 1), y r (t + N 1 + 1),…, y r (t + N 2 ), by using the optimized fuel injection time series. Each fuel injection time is normally bounded within the range from 2 to 15 ms. However, the multidimensional optimization always requires heavy computation, especially when constraints exist. Real-time control applications often put emphasis on computational speed. The research of [11] showed that the one-dimensional approach is efficient for real-time AFR control and that the overall tracking error is similar to that using multidimensional optimization approach. Therefore, the optimization problem to be solved is reduced to one-dimensional. In this paper, the control signal u is assumed to remain constant over the control horizon. Therefore, the tentative control signal in the objective function is also constant over the control horizon, i.e., u′(t) = u′(t + 1),…, = u′(t + N u  − 1). In this way, only one parameter u′(t) is needed to be determined, and the final fuel injection time at each time step u is set to be the optimal value of u′(t).

3.2 Brent’s method

There are many optimization techniques available for MPC, and each technique has its pros and cons. A well-known technique—Brent’s method—was selected as the MPC optimizer in this study for illustrative purpose. Brent’s method is a robust and efficient optimization method. It combines the typical parabolic interpolation and golden-section search. The objective function in each iteration is approximated by interpolating a parabola through three existing points. The minimum point of the parabola is taken as a guess for the minimum point if certain criteria are met. Otherwise, golden-section search is carried out. The advantage of this method is that the high convergence rate of parabolic interpolation can be maintained without losing the robustness of golden-section search [29]. The general working principle of Brent’s method is shown in Fig. 2. The detailed optimization procedure of Brent’s method was presented in [29] and is not presented herein. There are three parameters of Brent’s method, which are the initial interval of the input variable, [a, b], that is the limit of the fuel injection time, the tolerance, tol, and the maximum iteration for stopping the optimization procedure. The three variables were set at [2, 15], 0.05, and 50, respectively, because the fuel injection time varies within 2–15 ms from 0 to 100 % throttle.

Fig. 2
figure 2

General working principle of Brent’s method

Full size image

4 Implementation and evaluation of OSELM air-ratio model

4.1 OSELM air-ratio model implementation

The objective of the OSELM air-ratio model is to predict the future air-ratio y p from the inputs of three time series of engine parameters: ES, TP, and previous measured air-ratio y. The structure of the OSELM model was chosen to be second order (i.e., 2 past time steps), which gives the minimum prediction error [11, 12], and the structure is shown in Fig. 3.

Fig. 3
figure 3

Structure of OSELM air-ratio model

Full size image

To obtain the engine data for building the air-ratio model, 5,800 data samples including air-ratio, ES, and TPs were collected. These 5,800 data samples were collected over a Honda DC5 Type-R test car with K20A i-VTEC engine connected to a MoTeC M800 programmable ECU with nonfactory calibration data. A dyno test was done for collecting the data samples. The first 3,000 data samples were used as initial training dataset D 0 to build the air-ratio model. The last 2,800 data samples were used as test dataset TEST. The first 2,700 data samples of TEST were also regarded as update dataset UPDATE for real-time updates. The air-ratio model was updated every 100 measured air-ratio data samples during prediction. In other words, UPDATE was divided into 27 datasets, D k , for k = 1–27. Each dataset D k was used as test data first to test the immediate model accuracy, and then D k was used again as update data for updating the model. The remaining 100 data samples of TEST were the last dataset for evaluating the accuracy of the air-ratio model after finishing the last update (i.e., updated by 2,601–2,700 data samples) in the test. With respect to the training dataset D 0, the test dataset TEST was the unseen case for testing the generalization of the built air-ratio model.

4.2 Evaluation of engine air-ratio model

To illustrate the accuracy, superiority, and online update ability of the proposed OSELM air-ratio model, its prediction result was compared with those obtained from the latest modelling algorithm for AFR control, DRNN [12]. For a fair comparison between the two modelling algorithms, both modelling algorithms were implemented using MATLAB 2011b and executed on a 3.4 GHz Intel Core i7 PC with eight GB RAM onboard.

After obtaining the air-ratio model EM(x) with OSELM through the modelling algorithm presented in Sect. 2 over D 0, EM(x) was then updated for 27 times with D k , for k = 1–27, 100 data samples each time, to build the updated OSELM air-ratio model EM*(x). Apart from the OSELM model, the DRNN modelling algorithm for model predictive AFR control presented in [12] was applied to build the air-ratio model, NN(x). The network was trained for 100 epochs. After that, NN(x) was updated with UPDATE but employing the dynamic BP with automatic differentiation technique presented in [12] to build the updated DRNN air-ratio model NN*(x).

After constructing EM*(x) and NN*(x), the performance of the two air-ratio models can be evaluated in terms of accuracy. Since the range of air-ratio for combustible mixture is very narrow, the prediction errors of the above two air-ratio models are presented by logarithmic mean absolute error (LMAE), and they were evaluated one by one against the test dataset, TEST, using Eq. (14):

$$ {\text{LMAE}} = - \log \left[ {\frac{1}{T}\sum\limits_{k = 1}^{T} {\left| {y_{k} - f*\left( {\varvec{x}_{k} } \right)} \right|} } \right] , $$
(14)

where f*(x k ) represents either EM*(x k ) or NN*(x k ), x k is the kth new input vector for air-ratio prediction, y k is the corresponding actual air-ratio of f*(x k ), and T is the total number of predictions. The value of T is equal to 2,800 in this case study. The larger the LMAE, the higher the model accuracy is. The prediction results between the predicted air-ratios and the corresponding actual air-ratios over TEST are shown in Fig. 4.

Fig. 4
figure 4

a Comparison between predicted air-ratios and the corresponding actual air-ratios; b in detail

Full size image

Apart from the model accuracy, computation speed is also an important factor in real-time control applications. Table 1 shows the LMAE, model training time, and model updating time of both OSELM and DRNN air-ratio models. According to the LMAE values in Table 1, the OSELM air-ratio model EM*(x) outperforms NN*(x) by approximately 22 %. The trends and tracking errors in Fig. 4 also imply that the accuracy of the OSELM air-ratio model will be well maintained if the model update is continually carried out to adapt to any changes in engine performance due to engine aging or fair user modification on the engine. In addition to model accuracy, OSELM can also reduce the time for training and updating the air-ratio model significantly. In Table 1, the air-ratio model training time, average model updating time, and cumulative model updating time of EM*(x) are 0.1783, 0.0060, and 0.1685 s, respectively. The average model updating time of EM*(x), 0.0060 s, is only about 128 of NN*(x). This achievement is accomplished by the effective online learning algorithm of OSELM. The total cumulative model updating time saved by OSELM from DRNN after 27 update iterations is 5.8654 s. However, if the air-ratio model is often updated, the cumulative model updating time saved by OSELM can be very significant. Obviously, OSELM is superior to DRNN algorithm. As a whole, the high accuracy and short updating time of the air-ratio model using OSELM make online model predictive air-ratio control more feasible. Hence, OSELM was confidently selected to implement the model predictive engine air-ratio controller in this research.

Table 1 Accuracy and computation time of different air-ratio models
Full size table

5 Implementation and evaluation of OEMPC

5.1 Experimental setup

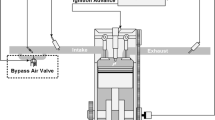
The proposed OEMPC algorithm was implemented and tested on a real car, Honda DC5 Type-R with K20A i-VTEC engine connected to a MoTeC M800 programmable electronic control unit (ECU) and National Instrument (NI) CompactDAQ chassis DAQ-9178. The MPC algorithm was implemented using MATLAB. MoTeC M800 is mainly used for engine control, whereas NI DAQ-9178 is used for sending control signal to the MoTeC ECU via a LabVIEW interface program according to the MATLAB MPC program embedded. In other words, NI DAQ-9178 serves as an interface between the MATLAB program and the MoTeC ECU. Apart from fuel injector control, the MoTeC ECU also contains many control maps, such as ignition map and valve timing map, to maintain the engine operation. The experimental setup and the signal flow between the test car and OEMPC are shown in Fig. 5.

Fig. 5
figure 5

Experimental setup and signal flow between test car and OEMPC

Full size image

The initial off-line training data for building the OSELM model were obtained using a wideband lambda sensor subject to random TPs and are discussed in Sect. 4. In this study, there are two pilot tests evaluating the tracking error and online update ability of the controllers.

5.2 Pilot test 1: tracking ability

In pilot test 1, the test cycle is shown in Fig. 6 where the TP gradually changes from 15 to 75 % throttle (the TP increases by 15 % every 5 s). Such test cycle is designed by referring to [12], which almost covers the whole operating condition. In this test, the air-ratio is required to track the target air-ratios from the stoichiometric value (1.00) for minimum emissions to a value for the best brake-specific fuel consumption (1.05) and then to a value for maximum engine power (0.95) as the TP is gradually changed from 15 to 75 % throttle. Such tracking of air-ratio changes is essential for automobiles to satisfy the emission, fuel consumption, and power requirements under different operating conditions [7, 8]. After choosing the sampling time to be 0.01 s, the tracking ability of the OEMPC can be examined. By testing many values around the parameters used in [11, 12], the parameters of the optimizer were chosen as N 1 = 1, N 2 = 8, ρ = 0.75, and N u  = 5. With the test cycle shown in Fig. 6 and the parameters chosen, the air-ratio control result and the corresponding fuel injection time of the OEMPC are shown in Fig. 7. To show the advantage of the OEMPC, its control result is compared with the latest model predictive controller, DRNN model predictive controller (DNMPC), as well as the PID controller used in the existing automotive ECU. The air-ratio model used in the DNMPC is the model mentioned in Sect. 4.2. The parameters of nonlinear optimization for the DNMPC were the same as those of OEMPC. The PID gains of the PID controller were obtained by the Ziegler–Nichols method. For a fair comparison, all the control algorithms were implemented using MATLAB 2011b and executed on a 3.4 GHz Intel Core i7 PC with eight GB RAM onboard. The air-ratio control results and the corresponding fuel injection time of the DNMPC and PID controller are shown in Figs. 8 and 9, respectively.

Fig. 6
figure 6

Test cycle: Throttle position versus time

Full size image
Fig. 7
figure 7

a Air-ratio control results and b corresponding fuel injection time of OEMPC in pilot test 1

Full size image
Fig. 8
figure 8

a Air-ratio control results and b corresponding fuel injection time of DNMPC in pilot test 1

Full size image
Fig. 9
figure 9

a Air-ratio control results and b corresponding fuel injection time of PID controller in pilot test 1

Full size image

Figure 7a shows that the OEMPC can regulate the air-ratio to follow the target air-ratios with the smallest deviation among all the controllers. As the range of air-ratio for combustible mixture is very narrow, logarithmic mean absolute error is chosen as the tracking index (TI) to evaluate the tracking ability of the controllers. The index is defined by

$$ {\text{TI}} = - \log \left[ {\frac{1}{{T_{s} }}\sum\limits_{t = 1}^{{T_{s} }} {\left| {y_{t} - y_{r} (t)} \right|} } \right] , $$
(15)

where t is time step, T s is the total number of time step in the test, y t is the actual air-ratio at each time step, and y r (t) is the corresponding target air-ratio at each time step. The target air-ratio varies according to the aforesaid practical operating conditions. In other words, when the TP is near 15 %, the target air-ratio is set to stoichiometry (1.00) to minimize the emissions, whereas the target air-ratio is set to a value of 1.05 to minimize the fuel consumption during partial throttle as the car is cursing. On the other hand, the target air-ratio is set to a value of 0.95 to maximize the engine power for 75 % throttle or above [7, 8].

The control performances of the three controllers are shown in Table 2, and the OEMPC outperforms the DNMPC and PID controller by approximately 2 and 4 %, respectively, in terms of TI. These results show the excellent tracking ability of the OEMPC. Apart from the superiority of TI, the maximum overshoot during transient state of the OEMPC also outperforms the DNMPC and PID controller by approximately 15 and 22 %, respectively.

Table 2 Control performance of pilot test 1 of different controllers
Full size table

5.3 Pilot test 2: online update ability

In the previous test, the “bypass air valve” of the test engine is 60 % opening. In order to test the update ability of the OEMPC, the “bypass air valve” was set from 60 to 30 % from 12 s to the end of the test. It is equivalent to the clogging of the engine intake filter as the engine is aging. Normally, the air-ratio must decrease under the same TP as lack of intake air. The testing procedure and the parameter setting are exactly the same as those in pilot test 1 except the sudden change of the “bypass air valve” position after 12 s. The air-ratio control result and the fuel injection time of the OEMPC are shown in Fig. 10. Similar to pilot test 1, the control result is compared with the DNMPC and typical PID controller. The control results and the corresponding fuel injection time of the DNMPC and PID controller are shown in Figs. 11 and 12, respectively. Figures 10a, 11a, and 12a depict that the air-ratios decrease after changing the position of the “bypass air valve” due to fuel rich. Figures 10a and 11a illustrate that the two controllers, OEMPC and DNMPC, can regulate air-ratios with obviously less deviation from the target air-ratios and overshoot than that of the PID controller because the air-ratio model can be self-updated for any changes in engine condition. The control performances of the three controllers are shown in Table 3, and the control performance of TI of the OEMPC outperforms the DNMPC and PID controller by approximately 6 and 14 %, respectively. Moreover, the maximum overshoot during transient state of the OEMPC outperforms the DNMPC and PID controller by approximately 9 and 15 %, respectively. This promising result indicates that the OEMPC can regulate air-ratio very well even though the engine ages and undergoes external disturbance simultaneously.

Fig. 10
figure 10

a Air-ratio control results and b corresponding fuel injection time of OEMPC in pilot test 2

Full size image
Fig. 11
figure 11

a Air-ratio control results and b corresponding fuel injection time of DNMPC in pilot test 2

Full size image
Fig. 12
figure 12

a Air-ratio control results and b corresponding fuel injection time of PID controller in pilot test 2

Full size image
Table 3 Control performance of pilot test 2 of different controllers
Full size table

5.4 Discussion of results

All experimental results show that the overall air-ratio control performance of the OEMPC is better than those of DNMPC and conventional PID controller. There are three important factors affecting the control performance of the model predictive controllers: air-ratio model accuracy, computational time, and adaptability. As presented in Table 1, the model accuracy and model updating time of the OSELM are better than those of DRNN. Moreover, the tracking errors from 12 to 25 s in Figs. 10a and 11a reveal that the model accuracy of the OSELM after update is obviously better than that of DRNN. This result shows that the online sequential learning algorithm of the OSELM is superior to the dynamic BP with automatic differentiation technique in DRNN. As a result, the overall control performance of the OSELM is better than the DNMPC. Furthermore, the PID controller cannot adapt to the changes of engine conditions, and no optimal PID gains can handle all situations. Therefore, PID controller is worse than both OEMPC and DNMPC in performance. In summary, the tracking and online update abilities of the OEMPC are the best among the three controllers. Hence, the OEMPC is the most suitable method for engine air-ratio control. Although Tables 2 and 3 show that the TI of the OEMPC has only been slightly improved, this small change in TI can practically result in a big change of engine performance because the air-ratio is a very delicate value. References [7, 8] stated clearly that if the air-ratio deviates 2 % from its stoichiometric ratio, CO, HC, and NOX emissions are significantly increased due to the degradation of conversion efficiency of the three-way catalytic converter. As a result, the actual improvement achieved by the OEMPC is very significant to this application.

6 Conclusions

This research is the first attempt at developing OEMPC for engine air-ratio control. The OEMPC for engine air-ratio control is trained and updated sequentially by real-time engine data so as to maintain the air-ratio model accuracy for any changes in engine performance, such as engine aging or fair user modification. The proposed OEMPC was successfully implemented and tested on a real automotive engine, whereas many previous researches were simulation tests only. Experimental results show that the air-ratio control performance of the OEMPC is significantly better than those of DNMPC and conventional PID controller. Tables 2 and 3 reveal that the OEMPC can effectively reduce the air-ratio deviation and maximum overshoot up to 5.75 and 15.23 %, and 14.02 and 22.23 % than those of DNMPC and conventional PID controller, respectively. Therefore, the OEMPC is a promising control scheme to replace conventional PID controller in the automotive ECU for engine air-ratio control. In the future, advanced optimization algorithms for the OEMPC and system stability will be studied.