1 Introduction

Markov jump linear systems (MJLSs), firstly proposed by Krasovskii and Lidskii [1] in 1961, can be considered as a kind of multi-model stochastic systems. In MJLSs, it contains two mechanisms, i.e., the modes and the states. The modes are jumping dynamics, modeled by finite-state Markov chains. The states are continuous or discrete, modeled by a set of differential or difference equations. With the development of control science and stochastic theory, MJLSs have been widely concerned and many research results are available, such as stochastic stability and stabilizability [2,3,4], controllability [5,6,7,8,9] and robust estimation and filtering [10,11,12].

In recent years, the adaptive optimal control problem has become a focused issue in controllers design and many related works have been published. For example, the authors in [13] studied the adaptive surface optimal control methods for strict-feedback systems. Then, the observer-based adaptive fuzzy control law was proposed for nonlinear nonstrict-feedback systems [14]. A general method to solve the optimal control problem related to the related algebraic Riccati equations (AREs) was studied in [15]. In [16], Kleinman considered an offline iterative technique to solve the AREs. In [17, 18], the iterative algorithm and the temporal difference method were, respectively, proposed to solve the discrete-time coupled AREs. To get the solutions of a set of coupled AREs for MJLSs, a Lyapunov iteration method [19] was derived. For more related researches, we can refer to [20,21,22,23,24]. However, all these algorithms are offline and have limitations to implement when the system dynamics are unknown.

Reinforcement learning (RL) and approximate/adaptive dynamic programming (ADP) algorithms are widely applied to solve the optimal control problems [25,26,27,28]. Moreover, we can use RL and ADP algorithm to obtain the optimal controller solutions through online learning. In [29], an online feedback control scheme is designed for linear systems by applying RL and ADP method. Then, it was developed to solve the zero-sum differential game [30]. In [31, 32], an adaptive policy iteration algorithm is considered for continuous-time and discrete-time nonlinear systems, respectively. Then, the reinforcement Q-learning for optimal tracking control problem was studied for linear discrete-time systems with unknown dynamics [33] and nonlinear discrete-time systems with unknown nonaffine dead-zone input [34]. Applying the H∞ state feedback scheme, an online policy update algorithm was proposed [35]. For more results on this studying, we refer readers to [36,37,38,39,40,41,42,43,44].

It is worth pointing out the relevant methods related to RL and ADP are mostly used to solve the optimal controller design problems for general linear/nonlinear dynamics. Due to the complexity of MJLSs which contain states and modes, the mode-based switching subsystems have coupling relationships. Obviously, the RL and ADP algorithms proposed above can not directly solve the adaptive optimal control problems of MJLSs. To study the online control problem for MJLSs, the authors in [45] considered an online adaptive optimal control scheme by applying a novel policy iteration algorithm. Then, the relevant results were developed to the Itô stochastic systems [46] and the H∞ optimal problem [47] of MJLSs. But in these results, we must partially know the system dynamics. Therefore, these published results can be considered as partial model-free ones.

In this paper, we propose a novel parallel RL algorithm to solve the optimal control problem of MJLSs with completely unknown dynamics. This algorithm is based on the subsystem transformation technique and the parallel RL algorithm. The subsystem transformation technique is used to obtain the N AREs. Then, we can parallelly solve the corresponding N AREs by collecting and learning the subsystems information of states and inputs. Comparing with the published results in [45, 46], we will not use the system dynamics in this paper and the exploration noise is added to describe the actual control input. Moreover, the solutions can be conducted directly in one step by repeated iteration and computation without using policy evaluation and improvement. It is clear that the iterative algorithm in this paper can be effective to study the online optimal control problems for MJLSs. The convergence has also been proved. In order to demonstrate the effectiveness of the designed method, two simulation examples are given at last.

The main contributions of this paper can be concluded as:

  1. 1.

    A novel parallel RL algorithm with completely unknown dynamic information is first proposed to solve the optimal control problem of MJLSs;

  2. 2.

    To deal with the jumping modes, we use the subsystem transformation technique to decompose the MJLSs.

  3. 3.

    Compared with the results in [19], we apply the online collecting and learning the subsystems information of states and inputs to obtain the dynamics information. Then, we optimize and update the iterative results to obtain the optimal control policy. The designed PI algorithm is online and does not require the dynamic information of the MJLSs.

This paper contains the following five sections. The problem formulation and preliminaries are introduced in Sect. 2. The novel parallel iteration algorithm is proposed in Sect. 3.1, and the online implementation of the algorithm is given in Sect. 3.2; Sect. 3.3 gives the convergence proof of the designed algorithm. Two simulation examples are shown in Sect. 4. A conclusion is given in Sect. 5.


Notations Throughout this paper, \( \Re^{n} \) is used to denote an n-dimensional real matrix; \( \lambda (A) \) denotes the eigenvalue of A; \( \text{rank}{\kern 1pt} (A) \) denotes the rank of A; \( Z_{ + } \) denotes a non-negative–positive integer set; \( {\mathbf{E}}{\text{\{ }} \cdot {\text{\} }} \) shows the mathematical expectation of stochastic processes or vectors; \( \left\| \cdot \right\| \) represents the Euclidean norm; \( \otimes \) is used to represent the Kronecker product which has the following properties: (1) \( (A \otimes B)^{\text{T}} = A^{\text{T}} \otimes B^{\text{T}} \), (2) \( x^{\text{T}} Px = (x^{\text{T}} \otimes x^{\text{T}} )\text{vec}{\kern 1pt} {\kern 1pt} (P) \). For a matrix \( A \in \Re^{n \times n} \), we denote \( \text{vec}{\kern 1pt} {\kern 1pt} (A) = [a_{1}^{\text{T}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2}^{\text{T}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{n}^{\text{T}} ]^{\text{T}} \), where \( a_{i} \in \Re^{n} \) is the ith column of \( A \).

2 Backgrounds and preliminaries

2.1 Problem description

Consider a class of continuous-time Markov jump linear systems (MJLSs) described by:

$$ \begin{aligned} \left\{ {\begin{array}{*{20}l} {\dot{x}(t) = A(r(t))x(t) + B(r(t))u(t)} \hfill \\ {x(0) = x_{0} ,{\kern 1pt} {\kern 1pt} r(0) = r_{0} ,t = 0} \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{aligned} $$
(1)

with the infinite horizon performance index:

$$ J\left( {x(t)} \right) = {\mathbf{E}}\left\{ {\int_{0}^{\infty } {\left. {\left[ {x^{\text{T}} (t)Q_{i} x(t) + u^{\text{T}} (t)R_{i} u(t)} \right]\text{d}t} \right|} t = 0,{\kern 1pt} {\kern 1pt} x_{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{0} } \right\} $$
(2)

where \( x(t) \in \Re^{n} \) is the system state with the initial value \( x_{0} \); \( u(t) \in \Re^{m} \) is the control input; \( A(r(t)) \), \( B(r(t)) \) are the coefficient matrices, \( Q(r(t)) \) and \( R(r(t)) \) are the weight matrices which are mode-dependent and positive-definite; the pair \( (A(r(t)),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Q^{1/2} (r(t))) \) is supposed to be observable; \( r(t) \) is a continuous-time and discrete-state right continuous Markov stochastic process which represents the system mode and takes on values in a discrete set \( M = \left\{ { 1,{\kern 1pt} {\kern 1pt} 2,{\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} N} \right\} \); \( r_{0} \) represents the initial mode. Here, MJLSs (1) is assumed to be stochastically stabilizable.

For MJLSs (1), the transition probabilities of each mode satisfy:

$$ P_{r} \left\{ {{\kern 1pt} r(t + \Delta t) = j\left| {r(t) = i} \right.} \right\} = \left\{ \begin{aligned} & \pi_{ij} \Delta t + o(\Delta t){\kern 1pt} \quad j \ne i \\ & 1 + \pi_{ii} \Delta t + o(\Delta t)\quad j = i \\ \end{aligned} \right.{\kern 1pt} $$
(3)

where \( i,{\kern 1pt} {\kern 1pt} j \in M \), \( \Delta t > 0{\kern 1pt} \) and \( {\kern 1pt} \mathop {{\kern 1pt} \lim }\nolimits_{\Delta t \to 0} \frac{o(\Delta t)}{\Delta t} = 0 \); \( \pi_{ij} \ge 0 \, (i \ne j) \) represents the transition rate from mode \( i \) to mode \( j \) at time \( t \to t + \Delta t \) and has \( \pi_{ii} = - \sum\nolimits_{i \ne j} {\pi_{ij} } \). For simplicity, when \( r(t) = i \), \( A(r(t)) \), \( B(r(t)) \), \( Q(r(t)) \), \( R(r(t)) \) can be labeled as \( A_{i} \), \( B_{i} \), \( Q_{i} \), \( R_{i} \), respectively.

For a given feedback control policy \( u(t) = - K_{i} x(t) \), we define the following cost function as:

$$ V(x(t)){\kern 1pt} = {\mathbf{E}}\left\{ {\int_{t}^{\infty } {\left. {\left[ {x^{\text{T}} (t)Q_{i} x(t) + u^{\text{T}} (t)R_{i} u(t)} \right]\text{d}t} \right|{\kern 1pt} {\kern 1pt} } t,x(t),r(t)} \right\} $$
(4)

The optimal control problem for MJLSs (1) is to find a mode-dependent admissible feedback control policy, which minimizes the performance index, i.e.

$$ \begin{aligned} V^{*} (x(t) & = \mathop {\hbox{min} }\limits_{u(t)} J\left( {x(t)} \right) \\ & {\kern 1pt} = \mathop {\hbox{min} }\limits_{u(t)} {\mathbf{E}}\left\{ {\int_{0}^{\infty } {\left. {\left[ {x^{\text{T}} (t)Q_{i} x(t) + u^{\text{T}} (t)R_{i} u(t)} \right]\text{d}t} \right|} {\kern 1pt} {\kern 1pt} {\kern 1pt} t = 0,{\kern 1pt} {\kern 1pt} x_{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{0} } \right\} \\ \end{aligned} $$
(5)

Then, the cost function (4) can be denoted as \( V(x(t)){\kern 1pt} = x_{{i,{\kern 1pt} {\kern 1pt} t}}^{\text{T}} P_{i} x_{{i,{\kern 1pt} {\kern 1pt} t}} \), where \( x_{{i,{\kern 1pt} {\kern 1pt} t}} \) is the state of the ith jump mode; \( P_{i} \) is a positive-definite and mode-dependent matrix which can be obtained through solving the following coupled algebraic Riccati equations (AREs):

$$ \hat{A}_{i}^{\text{T}} P_{i} + P_{i} \hat{A}_{i} + Q_{i} + \sum\limits_{j = 1,i \ne j}^{N} {\pi_{ij} P_{j} } - P_{i} B_{i} R_{i}^{ - 1} B_{i}^{\text{T}} P_{i} = 0 $$
(6)

where \( \hat{A}_{i} = A_{i} + \frac{{\pi_{ii} }}{2}I \). Then, the optimal feedback control policy can be determined by:

$$ u(t) = - K_{i} x(t) = - R_{i}^{ - 1} B_{i}^{\text{T}} P_{i} x(t) . $$
(7)

Definition 1

MJLSs (1) is stochastically stable (SS), if for any initial conditions \( x_{0} \) and \( r_{0} \), the following formula is satisfied:

$$ \mathop {\lim }\limits_{t \to \infty } {\mathbf{E}}{\kern 1pt} {\kern 1pt} \left\| {x(t)} \right\|^{2} = 0 . $$
(8)

Inspired by [48], according to the subsystem transformation technique, we can re-write MJLSs (1) as the following N re-constructed subsystems:

$$ \begin{aligned} \left\{ {\begin{array}{*{20}l} {\dot{x}_{{i,{\kern 1pt} {\kern 1pt} t}} = \hat{A}_{i} x_{{i,{\kern 1pt} {\kern 1pt} t}} + B_{i} u_{{i,{\kern 1pt} {\kern 1pt} t}} } \hfill \\ {x_{i} (0) = x_{{i,{\kern 1pt} 0}} ,{\kern 1pt} \quad {\kern 1pt} t_{0} = 0} \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{aligned} . $$
(9)

In order to guarantee the stabilizability of the N re-constructed subsystems in Eq. (9) by the optimal feedback control policy (7), the triples \( (A_{i} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} B_{i} ,{\kern 1pt} {\kern 1pt} \sqrt {Q_{i} } ) \) are assumed to be stabilizable-detectable [19].

2.2 An offline parallel policy iteration algorithm (OPPIA)

According to the assumptions mentioned above, the exact solution \( P_{i}^{*} \) of the positive-definite and mode-dependent matrix \( P_{i} \) can be obtained by solving AREs (6). Notice that AREs (6) is a set of nonlinear algebraic equations and it is difficult to be solved directly, especially for large dimensional matrices. To tackle this problem, some algorithms have been proposed by Kleinman [16] and Gajic and Borno [19]. For MJLSs (1), we give the following Lemma 1.

Lemma 1

[19] For each subsystems, we give an initial stabilizable value \( K_{i(0)} \). The solutions of the following decoupled algebraic Lyapunov equations are equivalent to the solutions of AREs (6).

$$ \begin{aligned} & (\hat{A}_{i} - B_{i} K_{i(k)} )^{\text{T}} P_{i(k + 1)} + P_{i(k + 1)} (\hat{A}_{i} - B_{i} K_{i(k)} ) \\ & {\kern 1pt} \quad = - Q_{i(k)} - P_{i(k)} B_{i} R_{i}^{ - 1} B_{i}^{\text{T}} P_{i(k)} \\ \end{aligned} $$
(10)

In order to solve the N parallel decoupled algebraic Lyapunov equations in (10), we give the following Algorithm 1.

figure a

Remark 1

Due to the fact that MJLSs (1) can be decomposed into N independent subsystems, the solutions can be obtained by parallel solving N decoupled algebraic Lyapunov linear equations. Thus, the solutions to the N parallel nonlinear AREs (6) are numerically approximated. By Algorithm 1, the exact solutions of \( P_{i}^{*} \) can be obtained while \( k \to \infty \). Notice that the method in Algorithm 1 is offline and the knowledge of the dynamics \( A_{i} \), \( B_{i} \) are all needed.

3 Main results

In this part, we will propose a parallel reinforcement learning (RL) algorithm to design the feedback control policy for MJLSs (1). This is a novel online learning strategy which will not require the knowledge of the coefficient matrices, i.e., \( A_{i} \) and \( B_{i} \). For each solution step, we can solve N parallel decoupled algebraic Lyapunov equations in (10). In the end, the convergence of this new algorithm is also proved.

3.1 A parallel RL algorithm with completely unknown dynamics

For the offline Algorithm 1, the N subsystems dynamics are required to solve the decoupled algebraic Lyapunov equations in (10). For practical applications, this algorithm will be difficult to achieve if we do not know the exact knowledge in advance. To overcome these weaknesses, a new online parallel RL algorithm is developed to study the optimal solutions of MJLSs with completely unknown dynamics. For the ith subsystem, the unique symmetric positive-definite solutions of \( P_{i(k)} \) and the state feedback gains \( {\kern 1pt} K_{i(k)} \) \( (\forall k \in Z_{ + } ) \) should satisfy Eqs. (10), (11).

Recalling to Eq. (9), we rewrite the system state equation as:

$$ \left\{ \begin{aligned} & \dot{x}_{{i,{\kern 1pt} t}} = \bar{A}_{i(k)} x_{i,t} + B_{i} (u_{i,t} + K_{i(k)} x_{i,t} ) \\ & x_{i} (0) = x_{{i,{\kern 1pt} 0}} ,\quad {\kern 1pt} {\kern 1pt} t_{0} = 0 \\ \end{aligned} \right. $$
(12)

where \( \bar{A}_{i} = \hat{A}_{i} - B_{i} K_{i(k)} \) and the pairs \( (\hat{A}_{i} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} B_{i} ) \) are stabilizable.

Then, the novel algorithm is given as follows:

figure b

Notice that the N subsystems in Eq. (9) are reconstructed into N new continuous-time subsystems in Eq. (12). Next, we will give an online implementation of the parallel RL algorithm to solve Eq. (13). In Eq. (12), \( A_{i} \) and \( \pi_{ii} \) are embedded in the reconstructed subsystem states; \( B_{i} \) is embedded in the reconstructed subsystem control inputs, which can be measured online. For real-time learning of the information of \( x_{{i,{\kern 1pt} {\kern 1pt} t}} {\kern 1pt} \) and \( u_{{i,{\kern 1pt} {\kern 1pt} t}} {\kern 1pt} \), we can choose \( u_{{i,{\kern 1pt} {\kern 1pt} t}} {\kern 1pt} = - K_{i(k)} x_{{i,{\kern 1pt} {\kern 1pt} t}} + e_{i} \) as a true control input, where \( e_{i} \) is an additional exploration noise.

Remark 2

Solving Eq. (13), we can get a series of solutions, where \( P_{i(k)} \), \( K_{i(k)} \) satisfy (10), (11), \( x_{{i,{\kern 1pt} {\kern 1pt} t}} \) is the solution of Eq. (12) with the arbitrary control input \( u_{{i,{\kern 1pt} {\kern 1pt} t}} \). This fact enables us to choose \( u_{{i,{\kern 1pt} {\kern 1pt} t}} {\kern 1pt} = - K_{i(k)} x_{{i,{\kern 1pt} {\kern 1pt} t}} + e_{i} \) as a real input signal for learning. Obviously, this operation will not affect the convergence of the learning process.

Remark 3

In Algorithm 2, we choose an exploration noise and assume that it is a nonzero measurable bounded signal. In fact, the choice of the exploration noise will not affect the algorithm. We add the exploration noise as an excitation signal to satisfy the persistence of the excitation conditions. For convenience, we always choose the exponentially decreasing probing noise and the sum of sinusoidal signals as the exploration noise.

Remark 4

In Eq. (13), the subsystems internal dynamics information is not needed, i.e., the dynamic matrices of \( A_{i} \), \( B_{i} \) are all not included. In order to solve Eq. (13) by the online RL algorithm, we should continuously sample the states and the inputs information online from the N subsystems at each iteration step. In fact, the dynamics information is already included in the sample information. Therefore, the online Algorithm 2 did not require the dynamics information, i.e., Algorithm 2 as a completely model-free algorithm.

3.2 Online implementation of the novel parallel RL algorithm

To find a set of pairs \( (P_{i(k)} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} K_{i(k + 1)} ) \) which satisfy Eqs. (10), (11), the novel online parallel RL implement approach is derived. It observes that the dynamics matrices \( A_{i} \), \( B_{i} \) and the transfer matrix element \( \pi_{ii} \) are not included in Algorithm 2. According to the Kronecker product representation, the left side of Eq. (13) can be rewritten as:

$$ \begin{aligned} & x_{{i,{\kern 1pt} t + T}}^{\text{T}} P_{i(k)} x_{{i,{\kern 1pt} t + T}} - x_{{i,{\kern 1pt} t}}^{\text{T}} P_{i(k)} x_{{i,{\kern 1pt} t}} \\ & \quad = \bar{P}_{i(k)}^{\text{T}} \left[ {x_{{i,{\kern 1pt} t + T}}^{\text{T}} \otimes x_{{i,{\kern 1pt} t + T}}^{\text{T}} - x_{{i,{\kern 1pt} t}}^{\text{T}} \otimes x_{{i,{\kern 1pt} t}}^{\text{T}} } \right]{\kern 1pt} {\kern 1pt} = \bar{P}_{i(k)}^{\text{T}} \delta_{ix} \\ \end{aligned} $$
(14)

where \( \bar{P}_{i(k)} \) is a set of positive-definite and mode-dependent matrices; \( \bar{P}_{i} \) is a column vector-valued matrix whose internal elements are produced by \( P_{i} \) and can be given as:

$$ \bar{P}_{i} = [p_{i11} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2p_{i12} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2p_{i1n} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} p_{i22} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2p_{i23} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} p_{inn} ]^{\text{T}} , $$
(15)
$$ x_{{_{i} }}^{\text{T}} \otimes x_{{_{i} }}^{\text{T}} = [x_{i1}^{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i1} x_{i2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i1} x_{in} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i2}^{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i2} x_{i3} ,{\kern 1pt} {\kern 1pt} \ldots x_{i2} x_{in} ,{\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x_{in}^{2} ]^{\text{T}} . $$
(16)

Using the similar method as Eq. (14), we have:

$$ x_{{i,{\kern 1pt} t}}^{\text{T}} {\kern 1pt} {\kern 1pt} \bar{Q}_{i(k)} {\kern 1pt} {\kern 1pt} x_{{i,{\kern 1pt} t}} = (x_{{i,{\kern 1pt} t}}^{\text{T}} \otimes x_{{i,{\kern 1pt} t}}^{\text{T}} ){\kern 1pt} {\kern 1pt} {\text{vec}}{\kern 1pt} {\kern 1pt} (\bar{Q}_{i(k)} ) $$
(17)

where \( \bar{Q}_{i(k)} = Q_{i(k)} + K_{i(k)}^{\text{T}} R_{i} K_{i(k)} \). Then, the right side of Eq. (13) can be rewritten as:

$$ \begin{aligned} & (u_{{i,{\kern 1pt} t}} + K_{i(k)} x_{{i,{\kern 1pt} t}} )^{\text{T}} R_{i} K_{i(k + 1)} x_{{i,{\kern 1pt} t}} \\ & {\kern 1pt} \quad {\kern 1pt} = [(x_{{i,{\kern 1pt} t}}^{\text{T}} \otimes x_{{i,{\kern 1pt} t}}^{\text{T}} )(I_{n} \otimes K_{i(k)}^{\text{T}} R_{i} ) + (x_{{i,{\kern 1pt} t}}^{\text{T}} \otimes u_{{i,{\kern 1pt} {\kern 1pt} {\kern 1pt} t}}^{\text{T}} )(I_{n} \otimes R_{i} )]{\kern 1pt} {\kern 1pt} {\text{vec}}(K_{i(k + 1)} ). \\ \end{aligned} $$
(18)

Meanwhile, we define the following operators:

$$ I_{ixx} = \left[ {\begin{array}{*{20}c} {\int_{{t_{0} }}^{{t_{1} }} {x_{{i,{\kern 1pt} \tau }}^{\text{T}} \otimes x_{{i,{\kern 1pt} \tau }}^{\text{T}} } \text{d}\tau } \\ {\int_{{t_{1} }}^{{t_{2} }} {x_{{i,{\kern 1pt} \tau }}^{\text{T}} \otimes x_{{i,{\kern 1pt} \tau }}^{\text{T}} } \text{d}\tau } \\ \vdots \\ {\int_{{t_{l - 1} }}^{{t_{l} }} {x_{{i,{\kern 1pt} \tau }}^{\text{T}} \otimes x_{{i,{\kern 1pt} \tau }}^{\text{T}} } \text{d}\tau } \\ \end{array} } \right] , $$
(19)
$$ I_{ixu} = \left[ {\begin{array}{*{20}c} {\int_{{t_{0} }}^{{t_{1} }} {x_{{i,{\kern 1pt} \tau }}^{\text{T}} \otimes u_{{i,{\kern 1pt} \tau }}^{\text{T}} } \text{d}\tau } \\ {\int_{{t_{1} }}^{{t_{2} }} {x_{{i,{\kern 1pt} \tau }}^{\text{T}} \otimes u_{{i,{\kern 1pt} \tau }}^{\text{T}} } \text{d}\tau } \\ \vdots \\ {\int_{{t_{l - 1} }}^{{t_{l} }} {x_{{i,{\kern 1pt} \tau }}^{\text{T}} \otimes u_{{i,{\kern 1pt} \tau }}^{\text{T}} } \text{d}\tau } \\ \end{array} } \right] . $$
(20)

Thus, Eq. (13) can be described as:

$$ \varTheta_{i(k)} \left[ {\begin{array}{*{20}c} {\bar{P}_{i(k)} } \\ {\text{vec}(K_{i(k + 1)} } \\ \end{array} } \right] = \varXi_{i(k)} $$
(21)

where \( \varTheta_{i(k)} \in \Re^{{l \times [\frac{1}{2}n(n + 1) + mn]}} \), \( \varXi_{i(k)} \in \Re^{l} \) and they can be described as:

$$ \varTheta_{i(k)} = \left[ {\begin{array}{*{20}c} {\delta_{ixx} } & { - 2{\kern 1pt} {\kern 1pt} {\kern 1pt} [I_{ixx} (I_{n} \otimes K_{i(k)}^{\text{T}} R_{i} ) + I_{ixu} (I_{n} \otimes R_{i} )]} \\ \end{array} } \right] , $$
(22)
$$ \varXi_{i(k)} = - I_{ixx} \text{vec}(\bar{Q}_{i(k)} ) . $$
(23)

For Eq. (21), if \( \varTheta_{i(k)} \) has full column rank, the least-squares solutions of Eq. (13) can be solved by:

$$ \left[ {\begin{array}{*{20}c} {\bar{P}_{i(k)} } \\ {\text{vec}(K_{i(k + 1)} } \\ \end{array} } \right] = (\varTheta_{i(k)}^{\text{T}} \varTheta_{i(k)} )^{ - 1} \varTheta_{i(k)}^{\text{T}} \varXi_{i(k)} $$
(24)

By formula (24), we can obtain \( P_{i(k)} \) and \( {\kern 1pt} K_{i(k + 1)} \). To compute the matrices of \( I_{ixx} \) and \( I_{ixu} \), we can use \( \frac{n(n + 1)}{2} + nm \) integrators to collect the information of the states and the control inputs of each subsystems. In order to guarantee that Algorithm 2 can be online implemented at each step, \( \varTheta_{i(k)} \) is required to have full column rank for all \( k \in Z_{ + } \), i.e., there is an integer \( l_{0} > 0 \), for \( \forall l > l_{0} \), the following condition holds:

$$ \text{rank}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{\kern 1pt} {\kern 1pt} \left[ {I_{ixx} ,{\kern 1pt} {\kern 1pt} I_{ixu} } \right]{\kern 1pt} {\kern 1pt} } \right) = \frac{n(n + 1)}{2} + nm . $$
(25)

3.3 The convergence proof

In order to prove the convergence of Algorithm 2, we establish the following Theorem 1.

Theorem 1

For the novel parallel RL Algorithm 2, we give a stabilizable value \( K_{i(0)} \), where \( \forall i \in M \) and assume that \( \varTheta_{i(k)} \) has the full column rank; then the solutions of Eq. (13) satisfy Eqs. (10), (11).

Proof

Give a stabilizable value \( K_{i(0)} \), i.e., \( A_{i} - {\kern 1pt} B_{i} K_{i(0)} \) is a Hurwitz. According to Algorithm 1, the exact solutions \( P_{i}^{*} = \mathop {\lim }\nolimits_{k \to \infty } P_{i(k)} \) can be obtained by the decoupled algebraic Lyapunov equations in (10), and the feedback gain \( K_{i}^{*} = \mathop {\lim }\nolimits_{k \to \infty } K_{i(k)} \) can be uniquely determined by Eq. (11). For \( \forall t > 0 \), we choose the cost function as \( V(x(t)){\kern 1pt} = x_{{i,{\kern 1pt} {\kern 1pt} t}}^{T} P_{i} x_{{i,{\kern 1pt} {\kern 1pt} t}} \). Then, for the new re-constructed ith N independent subsystems in Eq. (12) and along the solutions of (12) by (10) and (11), the following is satisfied:

$$ \begin{aligned} & x_{{i,{\kern 1pt} t + T}}^{\text{T}} P_{i(k)} x_{{i,{\kern 1pt} t + T}} - x_{{i,{\kern 1pt} t}}^{\text{T}} P_{i(k)} x_{{i,{\kern 1pt} t}} \\ & \quad = \int_{t}^{t + T} {\left[ {x_{{i,{\kern 1pt} \tau }}^{\text{T}} (\bar{A}_{i}^{\text{T}} P_{i(k)} + P_{i(k)} \bar{A}_{i} )x_{{i,{\kern 1pt} \tau }} } \right.} {\kern 1pt} \left. { + 2(u_{{i,{\kern 1pt} \tau }} + K_{i(k)} x_{{i,{\kern 1pt} \tau }} )^{\text{T}} B_{i}^{\text{T}} P_{i(k)} } \right]\text{d}\tau {\kern 1pt} \\ & {\kern 1pt} \quad = - \int_{t}^{t + T} {x_{{i,{\kern 1pt} \tau }}^{\text{T}} \bar{Q}_{i(k)} x_{{i,{\kern 1pt} \tau }} \text{d}\tau + } \int_{t}^{t + T} {2(u_{{i,{\kern 1pt} \tau }} + K_{i(k)} x_{{i,{\kern 1pt} \tau }} )^{\text{T}} R_{i} K_{i(k + 1)} x_{{i,{\kern 1pt} \tau }} \text{d}\tau } \\ \end{aligned} $$
(26)

Since \( \varTheta_{i(k)} \) has full column rank, the least-squares solutions in Eq. (24) is an online implement of Eq. (13). Therefore, the solutions of Eq. (13) are equivalent to the iteration solutions of Eqs. (10) and (11). The proof is completed.

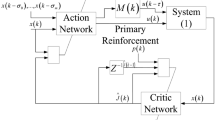
The flowchart of Algorithm 2 is given in Fig. 1.

Fig. 1
figure 1

The flowchart of Algorithm 2

Full size image

Remark 5

By the online implementation in Algorithm 2, we can see the differences between the offline Algorithm 1 and the online Algorithm 2. In Algorithm 1, we apply the offline iterative algorithm to solve the Riccati functions and equations directly, while in Algorithm 2, we use the online sampling and learning method. Moreover, Eqs. (10), (11) in Algorithm 1 depend on the dynamics information. But in Algorithm 2, we do not need any dynamics information by Eq. (13).

4 Simulation examples

Example 1

To show the applicability of Algorithm 2, we consider a fourth order jump linear model with two jump modes as:

$$ N = 2,\;\varPi = \left[ {\begin{array}{*{20}c} { - \;3} & 3 \\ {2.5} & { - \;2.5} \\ \end{array} } \right], $$
$$ A_{1} = \left[ {\begin{array}{*{20}c} { - \;2.2361} & { - \;1.1358} & 1 & {0.6324} \\ { - \;0.1024} & { - \;3} & {0.3835} & {0.85} \\ {0.7112} & {11.2346} & { - \;36.8199} & 4 \\ {1.0692} & {13.4230} & {20.1185} & { - \;12.1801} \\ \end{array} } \right], $$
$$ A_{2} = \left[ {\begin{array}{*{20}c} { - \;1.5326} & { - \;1.2436} & {0.5458} & {0.7136} \\ { - \;0.8} & { - \;2.9346} & {0.0920} & {0.42} \\ {11.1634} & {23} & { - \;26.4655} & { - \;1.8347} \\ {25} & {8.3132} & { - \;3.8714} & { - \;31.4631} \\ \end{array} } \right], $$
$$ B_{1} = B_{1} = \left[ {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ 1 \\ \end{array} } \right],\quad Q_{1} = Q_{2} = \left[ {\begin{array}{*{20}c} 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]. $$

In the simulation, we set \( R_{1} = R_{2} = 1 \), the error value \( \varepsilon \) as \( 10^{ - 15} \) and the initial stabilizing feedback gain as \( K_{i(0)} = 0 \). According to the OPPIA in Algorithm 1, AREs (6) can be directly solved. After the 14th iterations, the exactly solutions are obtained:

$$ P_{1}^{*} = \left[ {\begin{array}{*{20}c} {0.3505} & { - \;0.0320} & {0.0180} & {0.0191} \\ { - \;0.0320} & {0.5943} & {0.0572} & {0.0845} \\ {0.0180} & {0.0572} & {0.0268} & {0.0232} \\ {0.0191} & {0.0845} & {0.0232} & {0.0503} \\ \end{array} } \right], $$
$$ P_{2}^{*} = \left[ {\begin{array}{*{20}c} {0.5574} & { - 0.0483} & {0.0140} & {0.0227} \\ { - 0.0483} & {0.4057} & {0.0164} & {0.0111} \\ {0.0140} & {0.0164} & {0.0196} & { - 0.0003} \\ {0.0227} & {0.0111} & { - 0.0003} & {0.0178} \\ \end{array} } \right]. $$

The OPPIA in Algorithm 1 is offline and the subsystems dynamics matrices are all needed. To show the effectiveness and applicability of Algorithm 2, we use the same conditions mentioned above. For the two subsystems, we select the initial states as \( x_{10} = x_{20} = \left[ {\begin{array}{*{20}c} 0 & { - \;0.1} & {0.1} & 0 \\ \end{array} } \right]^{\text{T}} \) and the controller \( u_{i(k)} {\kern 1pt} = - K_{i(k)} x_{i} + e_{i} \) in the time interval \( \left[ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2} \right] \) with the exploration noises as \( e_{1} = e_{2} = 100\sum\nolimits_{n = 1}^{100} {\sin (\omega_{n} {\kern 1pt} t)} \), where \( \omega_{n} \) is a number and can be randomly selected in \( \left[ { - \;500,{\kern 1pt} \;{\kern 1pt} 500} \right] \). For the two subsystems, the information of the states and inputs is sampled every 0.01 s, and the optimal controller can be updated every 0.1 s. By the given iteration criterion, we can get the final calculation results of Algorithm 2 in step 4, after 7th iterations as:

$$ P_{1(7)} = \left[ {\begin{array}{*{20}c} {0.3505} & { - \;0.0320} & {0.0180} & {0.0191} \\ { - \;0.0320} & {0.5943} & {0.0572} & {0.0845} \\ {0.0180} & {0.0572} & {0.0268} & {0.0232} \\ {0.0191} & {0.0845} & {0.0232} & {0.0503} \\ \end{array} } \right], $$
$$ P_{2(7)} = \left[ {\begin{array}{*{20}c} {0.5574} & { - \;0.0483} & {0.0140} & {0.0227} \\ { - \;0.0483} & {0.4057} & {0.0164} & {0.0111} \\ {0.0140} & {0.0164} & {0.0196} & { - \;0.0003} \\ {0.0227} & {0.0111} & { - \;0.0003} & {0.0178} \\ \end{array} } \right]. $$

The optimal state feedback controller gains are:

$$ K_{1(7)} = \left[ {\begin{array}{*{20}c} {0.3557} & {0.7040} & {0.1253} & {0.1771} \\ \end{array} } \right], $$
$$ K_{2(7)} = \left[ {\begin{array}{*{20}c} {0.5458} & {0.3849} & {0.0497} & {0.0513} \\ \end{array} } \right]. $$

Then, we get the simulation results by using MATLAB. Figures 2, 3, 4 and 5 show the convergence of Algorithm 2. The convergence of \( P_{1} \) and \( P_{2} \) to the optimal values are shown in Figs. 2, 3. The elements of matrices \( P_{1} \) and \( P_{2} \) are updated which are shown in Figs. 4, 5.

Fig. 2
figure 2

The convergence of \( P_{1(k)} \) to the optimal value \( P_{1}^{*} \)

Full size image
Fig. 3
figure 3

The convergence of \( P_{2(k)} \) to the optimal value \( P_{2}^{*} \)

Full size image
Fig. 4
figure 4

The updated elements of \( P_{1(k)} \) at each step in Algorithm 2

Full size image
Fig. 5
figure 5

The updated elements of \( P_{2(k)} \) at each step in Algorithm 2

Full size image

Example 2

In order to further study the proposed approach, we give the following comparative results. Applying the parallel RL algorithm proposed in this paper and simulating the experiment with the same parameters as [45], we can get the final solutions after 7 iterations:

$$ P_{1(7)} = \left[ {\begin{array}{*{20}c} {0.2408} & {0.0705} & {0.0393} & {0.0182} \\ {0.0705} & {0.0308} & {0.0085} & {0.0064} \\ {0.0393} & {0.0085} & {0.0157} & {0.0025} \\ {0.0182} & {0.0064} & {0.0025} & {0.0016} \\ \end{array} } \right], $$
$$ P_{2(7)} = \left[ {\begin{array}{*{20}c} {0.5026} & {0.1343} & {0.0518} & {0.0097} \\ {0.1343} & {0.0485} & {0.0138} & {0.0026} \\ {0.0518} & {0.0138} & {0.0193} & {0.0002} \\ {0.0097} & {0.0026} & {0.0002} & {0.0003} \\ \end{array} } \right]. $$

Comparing with the online algorithms proposed in [45], the simulation errors between the calculated results proposed in this paper can nearly converge to zero. It shows that the parallel RL algorithm in this paper gives a more accurate solution. It is also seen from Figs. 6 and 7 that the convergence rate of the parallel RL algorithm is also faster than the results in [45].

Fig. 6
figure 6

The updated elements of \( P_{1(k)} \) using the parallel RL algorithm

Full size image
Fig. 7
figure 7

The updated elements of \( P_{2(k)} \) using the parallel RL algorithm

Full size image

Remark 6

In the two simulation examples, we solve the positive-definite solution \( P_{i(k)} \) by the online reinforcement learning method. First, we obtain N coupled Riccati equations by decomposing the subsystems. According to the online implementation process, we need to collect the states and the inputs of each subsystem, and satisfy the condition of the full rank of the least square equation. Then, we iteratively solve the least square formula, until the final optimal solution satisfying the limited precision requirement is obtained.

5 Conclusion

A novel online parallel RL algorithm is proposed with completely unknown dynamics. It can solve the AREs by collecting the information of the states and the inputs of each of the subsystems. Therefore, this novel parallel RL algorithm can parallelly compute the corresponding N coupled AREs with completely unknown dynamics. The convergence of the parallel RL algorithm is also proved. Two simulation results illustrate the applicability and effectiveness of the designed algorithm. In the future, the RL algorithm and the relevant optimal algorithm can be used in other aspects, such as artificial intelligence, industrial informatics, pattern processing and wireless automation devices.