1 Introduction

Adaptive dynamic programming (ADP), proposed by Werbos [33, 34], is an effective adaptive learning control approach to solve optimal control problems forward-in-time. There are several synonyms used for ADP, including "adaptive critic designs” [3, 4, 21], “adaptive dynamic programming” [20, 27], “approximate dynamic programming” [5, 34, 35], “neural dynamic programming” [9], "neuro-dynamic programming” [7], and “reinforcement learning” [22, 23]. In [21, 34, 35], ADP approaches were classified into several main schemes, which are heuristic dynamic programming (HDP), action-dependent HDP (ADHDP), also known as Q-learning [28], dual heuristic dynamic programming (DHP), action-dependent DHP (ADDHP), globalized DHP (GDHP), and ADGDHP. In recent years, iterative methods are also used in ADP to obtain the solution of Hamilton–Jacobi–Bellman (HJB) equation indirectly and have received lots of attention [1, 2, 10, 11, 12, 17, 20, 25, 27, 32, 35]. There are two main iterative ADP algorithms which are based on policy iteration and value iteration [14]. Policy iteration algorithms for optimal control of continuous-time systems with continuous state and action spaces were given in [1]. In 2011, Wang et al. [26] studied finite-horizon optimal control problems of discrete-time nonlinear systems with unspecified terminal time using policy iteration algorithms. Value iteration algorithms for optimal control of discrete-time nonlinear systems were given in [6]. In [5], a value iteration algorithm, which was referred to as greedy HDP iteration algorithm, was proposed for finding the optimal control law. The convergence property of the algorithm is also proved [5]. In [29], an iterative θ-ADP algorithm was established that permits the ADP algorithm to be implemented both on-line and off-line without the initial admissible control sequence.

Although iterative ADP algorithms attract a lot of attentions [3, 16, 19, 24, 37, 40, 41], for nearly all of the iterative algorithms, the iterative control of each iteration is required to be accurately obtained. These iterative ADP algorithms can be called "accurate iterative ADP algorithms”. For most real-world control systems, however, accurate control laws in the iterative ADP algorithms can hardly be obtained, no matter what kind of fuzzy and neural network structures are used [18, 31, 36, 38, 39]. In other words, we can say that the approximation errors are inherent in all real control systems. Hence, it is necessary to discuss the ADP optimal control scheme with approximation error. Unfortunately, discussions on the ADP algorithms with approximation error are very scarce. To the best of our knowledge, only in [30], the convergence property of the algorithm was proposed while the stability of the system cannot be guaranteed, which means the algorithm can only be implemented off-line. To overcome this difficulty, new methods must be developed. This motivates our research.

In this paper, inspired by [29, 30], a new stable iterative ADP algorithm based on iterative θ-ADP algorithm is established for discrete-time nonlinear systems. The theoretical contribution of this paper is that when the iterative control law and iterative performance index function in each iteration cannot be accurately obtained, using the present iterative ADP algorithm, it is proved that the performance index function will converge to a finite neighborhood of the optimal performance index function and the iterative control law can stabilize the system. First, it will show that the properties of the iterative ADP algorithms without approximation errors may be invalid after introducing the approximate errors. Second, we will show that the stability property of the algorithm in [30] cannot be guaranteed, when approximation errors exist. Third, the convergence properties of the iterative ADP algorithm with approximation errors are presented to guarantee that the iterative performance index function is convergent to a finite neighborhood of the optimal one. Next, it will show that the nonlinear system can be stabilized under the iterative control law which makes the developed iterative ADP algorithm feasible for implementations both on-line and off-line.

This paper is organized as follows. In Sect. 2, the problem statement is presented. In Sect. 3, the stable iterative ADP algorithm is derived. The convergence and stability properties are also analyzed in this section. In Sect. 4, the neural network implementation for the optimal control scheme is discussed. In Sect. 5, two simulation examples are given to demonstrate the effectiveness of the present algorithm. Finally, in Sect. 6, the conclusion is drawn.

2 Problem statement

In this paper, we will study the following discrete-time nonlinear systems

$$ x_{k+1}=F(x_k, u_k), \quad k=0, 1, 2,\ldots, $$
(1)

where \({x_k \in \mathbb{R}^n}\) is the n-dimensional state vector, and \({u_k \in \mathbb{R}^m }\) is the m-dimensional control vector. Let x 0 be the initial state.

Let \(\underline{u}_k=(u_k,u_{k+1},\ldots)\) be an arbitrary sequence of controls from k to \(\infty. \) The performance index function for state x 0 under the control sequence \(\underline{u}_0=(u_0,u_1,\ldots)\) is defined as

$$ J(x_0, \underline{u}_0)=\sum_{k=0}^{\infty}U(x_k,u_k), $$
(2)

where U(x k ,u k ) > 0, for ∀ x k , u k ≠ 0, is the utility function.

In this paper, the results are based on the following assumptions.

Assumption 1

The system (1) is controllable and the function F(x k , u k ) is Lipschitz continuous for ∀ x k , u k .

Assumption 2

The system state x k  = 0 is an equilibrium state of system (1) under the control u k  = 0, i.e., F(0,0) = 0.

Assumption 3

The feedback control u k  = u(x k ) is Lipschitz continuous function for ∀ x k and satisfies u k  = u(x k ) = 0 for x k  = 0.

Assumption 4

The utility function U(x k , u k ) is a continuous positive definite function of x k , u k .

Define the set of control sequences as \({\underline{\mathfrak{U}}_k=\big\{\underline {u}_k\colon \underline {u}_k=(u_k, u_{k+1}, \ldots), \forall u_{k+i}\in { \mathbb R}^m, \quad i=0,1,\ldots\big\}. }\) Then, for an arbitrary control sequence \({\underline {u}_k \in \underline {\mathfrak{U}}_k}\), the optimal performance index function can be defined as

$$ J^*(x_k)={\inf} \left\{ J(x_k,\underline {u}_k)\colon \underline {u}_k\in\underline {{\mathfrak{U}}}_{k}\right\}. $$

According to Bellman’s principle of optimality, J *(x k ) satisfies the discrete-time HJB equation

$$ J^*(x_k)=\inf_{u_k \in {\mathbb{R}}^m} \left\{ U(x_k,u_k)+J^*(F(x_k,u_k))\right\}. $$
(3)

Then, the law of optimal single control vector can be expressed as

$$ u^*(x_k)={{\hbox{arg}} \min_{u_k \in {\mathbb{R}}^m}} \left\{ U(x_k,u_k)+J^*(F(x_k,u_k))\right\}. $$

Hence, the HJB Eq. (3) can be written as

$$ J^*(x_k)=U(x_k,u ^*(x_k))+J^*(F(x_k,u ^*(x_k))). $$
(4)

Generally, J *(x k ) is impossible to obtain by solving the HJB Eq. (4) directly. In [29], an iterative θ-ADP algorithm was proposed to solve the performance index function and control law iteratively. The iterative θ-ADP algorithm can be expressed as in the following equations:

$$ {v_i}({x_k}) = {\hbox{arg}} \mathop{\min}\limits_{{u_k} \in {{\mathbb{R}}^m}} \left\{ {U({x_k},{u_k}) + {V_i}({x_{k + 1}})} \right\} $$
(5)

and

$$ \begin{aligned} {V_{i + 1}}({x_k}) =& \mathop{\min }\limits_{{u_k} \in {{\mathbb{R}}^m}} \left\{ {U({x_k},{u_k}) + {V_i}({x_{k + 1}})}\right\}\\ =& U({x_k},{v_i}({x_k})) + {V_i}(F({x_k},{v_i}({x_k}))) \end{aligned} $$
(6)

where \(V_0(x_k) =\theta \Uppsi(x_k), \Uppsi(x_k) \in \bar{\Uppsi}_{x_k}\), is the initial performance index function, and θ > 0 is a large finite positive constant. The set of positive definite functions \(\bar{\Uppsi}_{x_k}\) is defined as follows.

Definition 1

Let

$$ \begin{aligned} \bar{\Uppsi}_{x_k} &= \left\{ \Uppsi(x_k) \colon \Uppsi ({x_k}) > 0 \, {{{\it {\hbox{is}\,\hbox{positive} \,\hbox{definite}}}}}, \right.\\ &\quad \left.{\hbox{and}} \, \exists \nu ({x_k}) \in {\mathbb R}^m, \Uppsi (F({x_k},\nu ({x_k}))) < \Uppsi ({x_k}) \right\} \end{aligned} $$

be the set of initial positive definition functions.

In [29], it is proved that the iterative performance index function V i (x k ) converges to J *(x k ), as \(i\rightarrow\infty. \) It also shows that the iterative control law v i (x k ) is a stable control law for \(i=0,1,\ldots. \) For the iterative θ-ADP algorithm, the accurate iterative control law and accurate iterative performance index function must be obtained to guarantee the convergence of the iterative performance index function. To obtain the accurate control law, it also requires that the control space must be continuous with no constraints. In real-world implementations, however, for \(\forall i =0,1,\ldots\), the accurate iterative control law v i (x k ) and the iterative performance index function V i (x k ) are both generally impossible to obtain. For this situation, the iterative control law cannot guarantee the iterative performance index function to converge to the optimum. Furthermore, the stability property of the system cannot be proved under the iterative control law. These properties will be shown in the next section. To overcome this difficulty, a new ADP algorithm and analysis method must be developed.

3 Properties of the approximation error-based iterative ADP algorithm

In this section, based on the iterative θ-ADP algorithm, a new stable iterative ADP algorithm with approximation error is developed to obtain the nearly optimal controller for nonlinear systems (1). The goal of the present ADP algorithm is to construct an iterative controller, which moves an arbitrary initial state x 0 to the equilibrium, and simultaneously makes the iterative performance index function reach a finite neighborhood of the optimal performance index function. Convergence proofs will be presented to guarantee that the iterative performance index functions converge to the finite neighborhood of the optimal one. Stability proofs will be given to show the iterative controls stabilize the nonlinear system (1) which makes the algorithm feasible for implementation both on-line and off-line.

3.1 Derivation of the stable iterative ADP algorithm with approximation error

In the present iterative ADP algorithm, the performance index function and control law are updated by iterations, with the iteration index i increasing from 0 to infinity. For \({\forall x_k\in \mathbb{R}^n, }\) let the initial function \(\Uppsi(x_k) \) be an arbitrary function that satisfies \(\Uppsi(x_k)\in \bar{\Uppsi}_{x_k} \) where \(\bar{\Uppsi}_{x_k}\) is expressed in Definition 1. For \({\forall x_k\in \mathbb{R}^n, }\) let the initial performance index function \(\hat{V}_0(x_k) =\theta \Uppsi(x_k)\), where θ > 0 is a large finite positive constant. The iterative control law \(\hat{v}_0(x_k)\) can be computed as follows:

$$ \hat{v}_0 (x_k ) = \mathop{{\hbox{arg}}\min}\limits_{u_k \in {\mathbb{R}}^m} \left\{ {U(x_k,u_k ) + \hat{V}_0 (x_{k + 1})} \right\} +\rho_0(x_k) $$
(7)

where \(\hat{V}_0 (x_{k + 1} )= \theta\Uppsi(x_{k+1}),\) and the performance index function can be updated as

$$ \hat{V}_1 (x_k ) = U(x_k,\hat{v}_0 (x_k )) + \hat{V}_0 (F(x_k ,\hat{v}_0 (x_k )))+ \pi_0 (x_k), $$
(8)

where ρ 0(x k ) and π 0(x k ) are approximation error functions of the iterative control and iterative performance index function, respectively.

For \(i = 1, 2, \ldots\), the iterative ADP algorithm will iterate between

$$ \hat{v}_i (x_k ) =\mathop{{\hbox{arg}}\min }\limits_{u_k\in {\mathbb{R}}^m} \left\{ {U(x_k,u_k ) + \hat{V}_i (x_{k + 1} )} \right\}+\rho_i (x_k) $$
(9)

and performance index function

$$ \hat{V}_{i+1} (x_k )=U(x_k,\hat{v}_i (x_k )) + \hat{V}_i (F(x_k ,\hat{v}_i (x_k )))+\pi_i(x_k), $$
(10)

where ρ i (x k ) and π i (x k ) are finite approximation error functions of the iterative control and iterative performance index function, respectively.

Remark 1

From the iterative ADP algorithm (7)–(10), we can see that for \(i=0,1,\ldots\), the iterative performance index function V i (x k ) and iterative control law v i (x k ) in (5)–(6) are replaced by \(\hat{V}_i(x_k)\) and \(\hat{v}_i(x_k), \) respectively. As there exist approximation errors, generally, we have for \(\forall i \geq 0, \hat{v}_i(x_k) \neq {{v}}_i(x_k)\) and the iterative performance index function \(\hat{V}_{i+1} (x_k )\neq {V}_{i+1} (x_k ). \) This means there exists an error between \(\hat{V}_{i+1} (x_k )\) and V i+1 (x k ). It should be pointed out that the iterative approximation is not a constant. The fact is that as the iteration index \(i \rightarrow \infty\), the boundary of iterative approximation errors will also increase to infinity, although in the single iteration, the approximation error is finite. The following theorem will show this property.

Lemma 1

Let \({x_k \in \mathbb{R}^n}\) be an arbitrary controllable state and Assumptions 1–4 hold. For \(i=1,2,\ldots, \) define a new iterative performance index function as

$$ \Upgamma_{i}(x_k)=\mathop{\min}\limits_{{u_k\in {\mathbb{R}}^m}} \{ U({x_k},{u_k}) + {\hat{V}_{i-1}}({x_{k + 1}})\} $$
(11)

where \(\hat{V}_{i} (x_k)\) is defined in (10). If the initial iterative performance index function \(\hat{V}_0(x_k) ={\Upgamma}_0(x_k)= \theta \Uppsi({x_k})\) and \(i=1,2,\ldots, \) and there exists a finite constant \(\epsilon\) that makes

$$ \hat{V}_i(x_k) -\Upgamma_i(x_k)\leq \epsilon $$
(12)

hold uniformly, then we have

$$ \hat{V}_i(x_k)-V_i(x_k)\leq i\epsilon $$
(13)

where \(\epsilon\) is called uniform approximation error (approximation error in brief).

Proof

The theorem can be proved by mathematical induction. First, let i = 1. We have

$$ \begin{aligned} \Upgamma_1 (x_k) &= \mathop {\min }\limits_{{u_k \in {\mathbb{R}}^m}} \{ U({x_k},{u_k}) + {{\hat V}_{0}}({x_{k + 1}})\}\\ &= \mathop {\min }\limits_{{u_k \in {\mathbb{R}}^m}} \{ U({x_k},{u_k}) +{{V}_{0}}(F(x_{k},u_k))\} \\&=V_1(x_k). \end{aligned} $$

Then, according to (12), we can get

$$ \hat{V}_1(x_k) -V_1(x_k)\leq \epsilon. $$

Assume that (13) holds for \(i=l-1,\, l=2,3,\ldots. \) Then, for i = l, we have

$$ \begin{aligned} \Upgamma_l (x_k) =& \mathop {\min }\limits_{{u_k \in {\mathbb{R}}^m}} \{ U({x_k},{u_k}) + {{\hat V}_{l-1}}({x_{k + 1}})\}\\ \leq &\mathop {\min }\limits_{{u_k \in {\mathbb{R}}^m}} \{ U({x_k},{u_k}) + V_{l-1}(x_{k+1})+(l-1)\epsilon\}\\ =&{V}_l(x_k)+(l-1)\epsilon. \end{aligned} $$

Then, according to (12), we can get (13).

Remark 2

From Lemma 1, we can see that for the iterative θ-ADP algorithm (7)–(10), the error bound between V i (x k ) and \(\hat{V}_i(x_k)\) is increasing as i increases. This means that although the approximation error for each single step is finite and maybe small, as the iteration index \(i\rightarrow\infty\) increases, the approximation error between \(\hat{V}_i(x_k)\) and V i (x k ) may also increase to infinity. Hence, we can say that the original iterative θ-ADP algorithm may be invalid with the approximation error.

To overcome these difficulties, we must discuss the convergence and stability properties of the iterative ADP algorithm with finite approximation error.

3.2 Properties of the stable iterative ADP algorithm with finite approximation error

For convenience of analysis, we transform the expressions of the approximation error as follows. According to the definitions of \(\hat{V}_i(x_k)\) and \(\Upgamma_i(x_k)\) in (10) and (11), we have \(\Upgamma_i(x_k)\leq \hat{V}_i(x_k). \) Then, for \(\forall i =0,1,\ldots, \) there exists a σ ≥ 1 that makes

$$ \Upgamma_i(x_k)\leq \hat{V}_i(x_k)\leq\sigma\Upgamma_i(x_k) $$
(14)

hold uniformly. Hence, we can give the following theorem.

Theorem 1

Let \({x_k \in \mathbb{R}^n}\) be an arbitrary controllable state and Assumptions 1–4 hold. For \(\forall i=0,1,\ldots\) , let \(\Upgamma_i(x_k)\) be expressed as (11) and \(\hat{V}_i (x_k) \) be expressed as (10). Let \(\gamma < \infty\) and \(1 \leq \delta < \infty\) be constants that make

$$ J^*(F(x_k,u_k)) \leq \gamma U(x_k,u_k) $$

and

$$ J^*(x_k)\leq V_0(x_k) \leq \delta J^*(x_k) $$
(15)

hold uniformly. If there exists a σ, i.e., \(1\leq \sigma < \infty\) , that makes (14) hold uniformly, then we have

$$ \begin{aligned} J^*(x_k) \leq& \hat{V}_i(x_k)\\ \leq & \sigma \left( 1 + \sum\limits_{j = 1}^i {\frac{{{\gamma ^j}{\sigma ^{j - 1}}(\sigma - 1)}}{{{{(\gamma + 1)}^j}}}} + \frac{{{\gamma ^i}{\sigma ^i}(\delta - 1)}}{{{{(\gamma + 1)}^i}}} \right)\\ &\quad\times J^*(x_k) \end{aligned} $$
(16)

where we define \(\sum\nolimits_j^i {(\cdot) = 0} \) for ∀ j > i.

Proof

The theorem can be proved by mathematical induction. First, let i = 0. Then, (16) becomes

$$ J^*(x_k) \leq \hat{V}_0(x_k)\leq \sigma \delta J^*(x_k). $$
(17)

As J *(x k ) ≤ V 0(x k ) ≤ δJ *(x k ) and \(\hat{V}_0(x_k) ={V}_0(x_k)= \theta \Uppsi({x_k})\), we can obtain (17). Then, the conclusion holds for i = 0.

Assume that (16) holds for i = l − 1, \(l=1,2,\ldots. \) Then for i = l, we have

$$ \begin{aligned} {\Upgamma_l}({x_k})\leq & \mathop {\min }\limits_{{u_k}\in {\mathbb{R}}^m} \Bigg\{ \Bigg(1+\gamma \left.\sum\limits_{j = 1}^{l - 1} {\frac{{{\gamma ^{j - 1}}{\sigma ^{j - 1}}(\sigma - 1)}}{{{{(\gamma + 1)}^j}}}} \right.\\ &\quad\left.+ \frac{{{\gamma ^{l- 1}}{\sigma ^{l - 1}}(\sigma \delta - 1)}}{{{{(\gamma +1)}^l}}}\right)U(x_k,u_k)\\ &\quad+\Bigg[\sigma \Bigg( 1 + \sum\limits_{j = 1}^l {\frac{{{\gamma ^j}{\sigma ^{j - 1}}(\sigma -1)}}{{{{(\gamma + 1)}^j}}}} + \frac{{{\gamma ^l}{\sigma ^l}(\delta - 1)}}{{{{(\gamma + 1)}^l}}} \Bigg)\\ &\quad-\Bigg(\sum\limits_{j = 1}^{l - 1} {\frac{{{\gamma ^{j - 1}}{\sigma ^{j - 1}}(\sigma - 1)}}{{{{(\gamma + 1)}^j}}}} + \frac{{{\gamma ^{l - 1}}{\sigma ^{l - 1}}(\sigma \delta - 1)}}{{{{(\gamma + 1)}^l}}}\Bigg)\Bigg]\\ &\quad\times J^*(F(x_k,u_k))\Bigg\}\\ =&\left( {1 + \sum\limits_{j = 1}^l {\frac{{{\gamma ^j}{\sigma ^{j - 1}}(\sigma - 1)}}{{{{(\gamma + 1)}^j}}}} + \frac{{{\gamma ^l}{\sigma ^l}(\delta - 1)}}{{{{(\gamma + 1)}^l}}}} \right)J^*(x_k). \end{aligned} $$
(18)

Then, according to (14), we can obtain (16) which proves the conclusion for \(\forall i=0,1,\ldots\).

Lemma 2

Let \({x_k \in \mathbb{R}^n}\) be an arbitrary controllable state and Assumptions 1–4 hold. Suppose Theorem 1 holds for \({\forall x_k \in \mathbb{R}^n}\) . If for \(\gamma < \infty\) and σ ≥ 1, the inequality

$$ \sigma < \frac{{\gamma + 1}}{\gamma} $$
(19)

holds, and then as \(i\rightarrow \infty\) , the iterative performance index function \(\hat{V} _i({x_k})\) in the iterative ADP algorithm (7)–(10) is convergent to a finite neighborhood of the optimal performance index function J * (x k ), i.e.,

$$ \mathop{\lim }\limits_{i \to \infty } {\hat{V} _i}({x_k}) ={\hat{V}_\infty}({x_k}) \leq \sigma\left( {1 + \frac{{\gamma (\sigma - 1)}}{{1 - \gamma (\sigma - 1)}}} \right){J^*}({x_k}). $$
(20)

Proof

According to (18) in Theorem 1, we can see that for \(j=1,2,\ldots, \) the sequence \(\left\{\frac{{{\gamma ^j}{\sigma ^{j - 1}}(\sigma - 1)}}{{{{(\gamma + 1)}^j}}} \right\} \) is a geometrical series. Then, (18) can be written as

$$ \begin{aligned} {\Upgamma_i}({x_k}) \leq& \Bigg[ 1 + \frac{{\frac{{\gamma (\sigma - 1)}}{{\gamma + 1}}\left( {1 - {{\left( {\frac{{\gamma \sigma }}{{\gamma + 1}}} \right)}^i}} \right)}}{{1 - \frac{{\gamma \sigma }}{{\gamma + 1}}}}\\ &+ \frac{{{\gamma ^i}{\sigma ^i}\left( {\delta - 1} \right)}}{{{{\left( {\gamma + 1} \right)}^i}}} \Bigg]{J^*}({x_k}). \end{aligned} $$
(21)

As \(i\rightarrow \infty, \) if \(1 \leq \sigma < \frac{{\gamma + 1}}{\gamma }\), then (21) becomes

$$ \mathop{\lim}\limits_{i \to \infty } {\Upgamma _i}({x_k}) ={\Upgamma_\infty}({x_k}) \leq \left( {1 + \frac{{\gamma (\sigma - 1)}}{{1 - \gamma (\sigma - 1)}}} \right){J^*}({x_k}). $$
(22)

According to (14), let \(i\rightarrow\infty,\) and then we have

$$ \hat{V}_\infty(x_k)\leq\sigma\Upgamma_\infty(x_k). $$
(23)

According to (22) and (23), we can obtain (20).

Remark 3

We can see that if the approximation error σ satisfies \(\sigma < \frac{{\gamma + 1}}{\gamma }\), then the performance index function is convergent to the finite neighborhood of the optimal performance index function J *(x k ). However, the stability of the system under \(\hat{v}_i(x_k)\) cannot be guaranteed. The following theorem will show this property.

Theorem 2

Let \({x_k \in \mathbb{R}^n}\) be an arbitrary controllable state and Assumptions 1–4 hold. Let χ i be defined as

$$ \chi_i= \sigma \!\!\left( {1 + \sum\limits_{j = 1}^i {\frac{{{\gamma ^j}{\sigma ^{j - 1}}(\sigma - 1)}}{{{{(\gamma + 1)}^j}}}} + \frac{{{\gamma ^i}{\sigma ^i}(\delta - 1)}}{{{{(\gamma + 1)}^i}}}} \right). $$
(24)

Let the difference of the iterative performance index function be expressed as

$$ \Updelta \hat{V}_{i+1}(x_k)= \hat{V}_{i+1}(x_{k+1})- \hat{V}_{i+1}(x_k). $$
(25)

If Theorem 1 and Lemma 2 hold for \({\forall x_k \in \mathbb{R}^n, }\) then we have \(\Updelta \hat{V}_{i+1}(x_k)\) satisfies

$$ \begin{aligned} &-\frac{1}{{{\chi _i}}} U({x_k},{\hat v_i}({x_k})) - \frac{{({\chi _i} - 1){\chi _{i + 1}}}}{{{\chi _i}}}{J^*}({x_k})\\ &\le \Updelta {{\hat V}_{i + 1}}({x_k})\\ &\le - U({x_k},{{\hat v}_i}({x_k})) + ({\chi _{i+1}} - 1){J^*}(F(x_k,\hat{v}_i(x_k))). \end{aligned} $$
(26)

Proof

According to Theorem 1, we have the inequality (16) holds for \(\forall i=0,1,\ldots. \) Taking (16) to (10), we can get

$$ \begin{aligned} \hat{V}_{i+1}(x_k)&\leq U({x_k},{{\hat v}_i}({x_k})) + \chi_i J^*(x_{k+1}) \\ &\leq U({x_k},{{\hat v}_i}({x_k})) + \chi_i \hat{V}_{i+1}(x_{k+1}). \end{aligned} $$

Then, we have

$$ \begin{aligned} {\chi _i}({{\hat V}_{i + 1}}({x_{k + 1}}) - {{\hat V}_{i + 1}}({x_k})) \ge & - U({x_k},{{\hat v}_i}({x_k}))\\ &- ({\chi _i} - 1){{\hat V}_{i + 1}}({x_{k }}) \cr \ge & - U({x_k},{{\hat v}_i}({x_k}))\\ &- ({\chi _i} - 1){\chi _{i+1}}{J^*}({x_{k}}). \end{aligned} $$
(27)

Putting (25) into (27), we can obtain the left hand side of the inequality (26).

On the other hand, according to (10), we can also obtain

$$ \chi_{i+1} J^*(x_k)\geq \hat{V}_{i+1}(x_k)\geq U({x_k},{{\hat v}_i}({x_k}))+ J^*(x_{k+1}). $$

Then, we can get

$$ \begin{aligned} {{\hat V}_{i + 1}}({x_{k + 1}}) - {{\hat V}_{i + 1}}({x_k})\le& {\chi _{i+1}}{J^*}({x_{k + 1}}) - U({x_k},{{\hat v}_i}({x_k}))\\ &- {J^*}({x_{k + 1}})\\ =& - U({x_k},{{\hat v}_i}({x_k})) \\ &+({\chi _{i+1}} -1){J^*}({x_{k + 1}}). \end{aligned} $$
(28)

Putting (25) to (28), we can obtain the right hand side of the inequality (26).

According to Lemma 2, we have for \(\forall i=0,1,\ldots, \) χ i is finite. Furthermore, according to the definitions of σ and δ in (14) and (15), respectively, we know σ > 1 and δ > 1. Then, we have χ i  > 1 for ∀i = 0, 1,…. Hence, the inequality (26) is well defined for ∀i = 0, 1,…. The proof is completed.

From Theorem 2, we can see that for ∀i = 1, 2,…, \(\Updelta \hat{V}_{i}(x_k)\) in (25) is not necessarily negative definite. So, the function \(\hat{V}_{i}(x_k)\) is not sure to be a Lyapunov function and the system (1) may not be stable under the iterative control law \(\hat{v}_i(x_k)\). This means that the iterative θ-ADP algorithm (7)–(10) cannot be implemented on-line. To overcome this difficulty, in the following, we will establish new convergence criteria. It will be shown that if the new convergence conditions are satisfied, the stability of the system can be guaranteed, which makes the algorithm implementable both on-line and off-line.

Theorem 3

Let \({x_k \in \mathbb{R}^n}\) be an arbitrary controllable state and Assumptions 1–4 hold. Suppose Theorem 1 holds for \({\forall x_k \in \mathbb{R}^n}\) . If

$$ \sigma \le 1 + \frac{{\delta - 1}}{{\gamma \delta }}, $$
(29)

then the iterative performance index function \(\hat{V}_i(x_k)\) converges to a finite neighborhood of J * (x k ), as \(i\rightarrow\infty.\)

Proof

For \(i=0,1,\ldots\), let

$$ \bar{V}_i(x_k)=\chi_i J^*(x_k). $$
(30)

be the least upper bound of the iterative performance index function \(\hat{V}_i(x_k)\), where χ i is defined in (24). From (24), we can get

$$ \begin{aligned} \chi_{i+1}-\chi_i =& \frac{{{\gamma ^{i + 1}}{\sigma ^i}(\sigma - 1)}}{{{{\left( {\gamma + 1} \right)}^{i + 1}}}} + \frac{{{\gamma ^{i + 1}}{\sigma ^{i + 1}}(\delta - 1)}}{{{{\left( {\gamma + 1} \right)}^{i + 1}}}} \\ &- \frac{{{\gamma ^i}{\sigma ^i}(\delta - 1)}}{{{{\left( {\gamma + 1} \right)}^i}}}. \end{aligned} $$

Let χ i+1 − χ i  ≤ 0, and then we can obtain (29). On the other hand, we can see that

$$ \frac{{\gamma + 1}}{\gamma }= 1 + \frac{1}{\gamma } > 1 + \frac{{1 - \frac{1}{\delta }}}{\gamma }=1 + \frac{{\delta - 1}}{{\gamma \delta }}. $$

Hence, for \(\sigma \le 1 + \frac{{\delta - 1}}{{\gamma \delta }}\), according to Theorem 1, the least upper bound of the iterative performance index function \(\bar{V}_i(x_k)\) for the iterative ADP algorithm converges to a finite neighborhood of J *(x k ), as \(i\rightarrow\infty. \) As \(\bar{V}_i(x_k)\) is the least upper bound of the iterative performance index function, we have \(\hat{V}_i(x_k)\), which satisfies \(J^*(x_k)\leq \hat{V}_i(x_k) \leq \bar{V}_i(x_k)\)and also converges to a finite neighborhood of J *(x k ), as \(i\rightarrow\infty\).

Theorem 4

Let \({x_k \in \mathbb{R}^n}\) be an arbitrary controllable state and Assumptions 1–4 hold. For \(i=0,1,\ldots, \) the iterative performance index function \(\hat{V}_i(x_k)\) and the iterative control law \(\hat{v}_i(x_k)\) are obtained by (7)–(10) , respectively. If Theorem 1 holds for ∀ x k and σ satisfies (29), then we have for \(\forall i=0,1,\ldots\) , the iterative control law \(\hat{v}_i(x_k)\) is an asymptotically stable control law for system (1).

Proof

The theorem can be proved by three steps.

  1. (1)

    Show that for \(\forall i=0,1,\ldots, \hat{V}_{i}(x_k)\) is a positive definite function.

According to the iterative θ-ADP algorithm (7)–(10), for i = 0, we have

$$ \hat{V}_0 (x_k ) ={V}_0 (x_k ) = \theta \Uppsi(x_k). $$

As \(\Uppsi(0)=0, \) we have that \(\hat{V}_0 (x_k )=0\) at x k  = 0. According to Assumption 4 of this paper, we have that \(\hat{V}_0 (x_k)\) is a positive definite function.

Assume that for i, the iterative performance index function \(\hat{V}_i (x_k)\) is a positive definite function. Then, for i + 1, we have (10) holds. As U(0,0) = 0, then we have that \(\hat{V}_{i+1} (x_k )\) and \(\hat{v}_i(x_k)\) can be defined at x k  = 0. According to Assumptions 1–4, we can get

$$ \hat{V}_{i+1} (0) = U(0,\hat{v}_i (0)) + \hat{V}_i(F(0,\hat{v}_i(0))) =0 $$

for x k  = 0. As \(\hat{V}_i (x_k)\) is a positive definite function, we have \(\hat{V}_i (0)=0\). Then, we have \(\hat{V}_{i+1} (0)=0\). If x k  ≠ 0, according to Assumption 4, we have \(\hat{V}_{i+1} (x_k) > 0\). On the other hand, we let \(x_k \rightarrow \infty\). As U(x k , u k ) is a positive function for ∀ x k , u k , we have \(\hat{V}_{i+1} (x_k) \rightarrow \infty\). So, \(\hat{V}_{i+1} (x_k) \) is a positive definite function. The mathematical induction is completed.

  1. (2)

    Show that \(\hat{v}_i(x_k)\) is an asymptotically stable control law if \(\hat{V}_{i+1}(x_k)\) reaches its least upper bound.

Let \(\bar{V}_i(x_k)\) be defined as in (30). As \(\sigma \le 1 + \frac{{\delta - 1}}{{\gamma \delta }}\), according to Theorem 3, we have \(\bar{V}_{i+1}(x_k)\leq \bar{V}_i(x_k)\). Then, we can get

$$ \bar{V}_{i} (x_k)\geq \bar{V}_{i+1} (x_k) =U({x_k},{\bar{v}_i(x_k)}) + {{\bar V}_{i}}({x_{k + 1}}) $$

where

$$ \bar{v}_i (x_k ) = \mathop{{\hbox{arg}}\min }\limits_{u_k\in {\mathbb{R}}^m} \left\{ {U(x_k,u_k ) + \bar{V}_i (x_{k + 1} )} \right\}+\bar{\rho}_i(x_k). $$

So, we have \({{\bar V}_{i}}({x_{k + 1}})-\bar{V}_{i} (x_k)\leq - U({x_k},{\bar{v}_i(x_k)})\leq 0\). Hence, \(\bar V_i(x_k)\) is a Lyapunov function and \(\bar{v}_i(x_k)\) is an asymptotically stable control law for \(\forall i=0,1,\ldots.\)

  1. 3.

    Show that \(\hat{v}_i(x_k)\) is an asymptotically stable control law when \(\hat{V}_{i+1}(x_k)\) does not reach its least upper bound.

As \(\bar V_i(x_k)\) is a Lyapunov function, there exist two functions \(\alpha(\|x_k\|)\) and \(\beta(\|x_k\|)\) belong to class \(\mathcal{K}\) which satisfy \(\alpha(\|x_k\|)\geq \bar V_i(x_k) \geq \beta(\|x_k\|)\) (details can be seen in [15]). For \(\forall \varepsilon > 0, \) there exists \(\delta(\varepsilon) > 0 \) that makes \(\beta(\delta) \leq \alpha(\varepsilon)\). So for ∀k 0 and \( \left\|{x(k_0 )}\right\| < \delta (\varepsilon )\), there exists a \( k \in [k_0, \infty)\) that satisfies

$$ \alpha(\varepsilon) \geq \beta({\delta}) \geq \bar V_i (x_{k_0}) \geq \bar V_i (x_k) \geq \alpha (\|x_k\|). $$
(31)

As \(\bar V_i(x_k)\) is the least upper bound of \(\hat V_i(x_k)\) for \(\forall i=0,1,\ldots, \) we have

$$ \hat V_i(x_k)\leq \bar V_i(x_k). $$
(32)

For the Lyapunov function \(\bar V_i(x_k)\), if we let \(k\rightarrow \infty, \) then \(\bar V_i(x_k) \rightarrow 0\). So, according to (32), there exists a time instant k 1 that satisfies k 0 < k 1 < k and makes

$$ \bar V_i (x_{k_0}) \geq \bar V_i (x_{k_1}) \geq \hat V_i (x_{k_0}) \geq \bar V_i (x_{k}) $$

hold. Choose \(\varepsilon_1 >0\) that satisfies \(\hat V_i (x_{k_0}) \geq \alpha(\varepsilon_1) \geq \bar V_i (x_{k})\). Then, there exists \(\bar{\delta}_1(\varepsilon_1) > 0 \) that makes \(\alpha(\varepsilon_1) \geq \beta({\delta}_1) \geq \bar V_i (x_{k}) \) hold. Then, we can obtain

$$ \hat V_i (x_{k_0}) \geq \alpha(\varepsilon_1) \geq \beta(\delta_1) \geq \bar V_i (x_k) \geq \hat V_i (x_k) \geq \alpha(\|x_k\|). $$

According to (31), we have

$$ \begin{aligned} \alpha(\varepsilon) &\geq \beta({\delta}) \geq \hat V_i (x_{k_0}) \geq \alpha(\varepsilon_1) \geq \beta({\delta}_1) \geq \hat V_i (x_k)\\ &\geq \alpha(\|x_k\|). \end{aligned} $$

Since \(\alpha( \left\|x_k\right\| ) \) belongs to class \(\mathcal {K}\), we can obtain \(\left\|{x_k}\right\| \leq \varepsilon\). Therefore, we can conclude that \(\hat{v}_i(x_k)\) is an asymptotically stable control law for all \(\hat{V}_{i}(x_k)\).

Remark 4

According to the analysis of this subsection, we can see that the iterative performance index function \(\hat{V}_i(x_k)\) of the iterative ADP algorithm (7)–(10) possesses different convergence properties for different σ.

First, if σ = 1, then we say the iterative performance index function V i (x k ) and the iterative control law v i (x k ) can be accurately obtained. The stable iterative ADP algorithm (7)–(10) is reduced to the regular iterative θ-ADP algorithm (5)–(6). It has been proved in [29] that the iterative ADP algorithm \(\hat{V} _i({x_k})\) is nonincreasing convergent to J *(x k ) and the iterative ADP algorithm can be implemented both on-line and off-line.

Second, if σ satisfies (29), then the iterative performance index function V i (x k ) and the iterative control law v i (x k ) cannot be accurately obtained. In this situation, the iterative performance index function \(\hat{V}_i(x_k)\) will converge to a finite neighborhood of J *(x k ). In the iteration process, the iterative control law \(\hat{v}_i(x_k)\) is still stable which means the stable iterative ADP algorithm can also be implemented both on-line and off-line.

Third, when σ satisfies (19), the iterative performance index function \(\hat{V}_i(x_k)\) can also converge to a finite neighborhood of J *(x k ). But in the iteration process, the stability property of iterative control law \(\hat{v}_i(x_k)\) cannot be guaranteed, which means the iterative ADP algorithm can only be implemented off-line.

Finally, when σ does not satisfies (19), the convergence property of V i (x k ) cannot be guaranteed.

4 Implementation of the stable iterative ADP algorithm by neural networks

In this section, BP neural networks are introduced to approximate \(\hat{V}_i (x_k)\) and compute the control law v i (x k ). Assume that the number of hidden layer neurons is denoted by l, the weight matrix between the input layer and hidden layer is denoted by Y, and the weight matrix between the hidden layer and output layer is denoted by W, and then the output of the three-layer neural network is represented by:

$$ \hat{F}(X,Y,W) = W^T\sigma (Y^TX) $$

where \(\sigma (Y^TX) \in R^l,[\sigma (z)]_i = \frac{e^{z_{_i } } - e^{ - z_i }}{e^{z_{_i } } + e^{ - z_i }}, \quad i = 1,\ldots, l\), are the activation function.

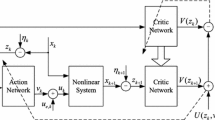
There are two networks, which are critic network and action network, respectively, to implement the stable iterative ADP algorithm. The whole structure diagram is shown in Fig. 1.

Fig. 1
figure 1

The structure diagram of the algorithm

Full size image

4.1 The critic network

The critic network is used to approximate the performance index function V i (x k ). The output of the critic network is denoted as

$$ \hat{V}_i (x_k) = W_{ci} ^T\sigma (Y_{ci} ^Tx_k). $$
(33)

The target function can be written as

$$ V_{i + 1} (x_k) = U(x_k, \hat{v}_i(x_k))+ \hat{V}_i (x_{k+1}). $$
(34)

Then, we define the error function for the critic network as

$$ e_{\hbox{ci}} (k) = \hat{V}_{i + 1} (x_k) - V_{i + 1} (x_k). $$
(35)

The objective function to be minimized in the critic network training is

$$ E_{\hbox{ci}} (k) = \frac{1}{2}e_{\hbox{ci}}^2 (k). $$
(36)

So, the gradient-based weight update rule [22] for the critic network is given by

$$ \begin{aligned} w_{c(i + 1)} (k) & =w_{\hbox{ci}} (k) + \Updelta w_{\hbox{ci}} (k),\\ &=w_{\hbox{ci}} (k) -\alpha _c \left[{\frac{\partial E_{\hbox{ci}} (k)}{\partial w_{\hbox{ci}}(k)}} \right],\\ &=w_{\hbox{ci}} (k) -\alpha _c\frac{\partial E_{\hbox{ci}} (k)}{\partial \hat {V}_i(x_k)}\frac{\partial \hat{V}_i (x_k)}{\partial w_{\hbox{ci}} (k)}, \end{aligned} $$
(37)

where α c  > 0 is the learning rate of critic network, and w c (k) is the weight vector in the critic network which can be replaced by W ci and Y ci. If we define

$$ {q_l}(k) = \sum\limits_{j = 1}^{{L_c}} {Y_{\hbox{ci}}^{{l_j}}(k){x_{jk}}}, \quad l = 1, 2, \ldots,{L_c} $$

and

$$ {p_l}(k) = \frac{{{e^{{q_l}(k)}} - {e^{ - {q_l}(k)}}}}{{{e^{{q_l}(k)}} + {e^{ - {q_l}(k)}}}},\qquad \quad l = 1,2, \ldots,{L_c}, $$

then we have

$$ {{\hat V}_{i + 1}}({x_k}) = \sum\limits_{l = 1}^{{L_c}} {W_{\hbox{ci}}^l(k){p_l}(k)}, $$

where L c is the total number of hidden nodes in the critic network. By applying the chain rule, the adaptation of the critic network is summarized as follows.

The hidden to output layer of the critic is updated as

$$ \begin{aligned} \Updelta W_{\hbox{ci}}^l(k) &= - {\alpha _c}\frac{{\partial {E_{\hbox{ci}}}(k)}}{{\partial {{\hat V}_{i + 1}}({x_k})}}\frac{{\partial {{\hat V}_{i + 1}}({x_k})}}{{\partial W_{\hbox{ci}}^l(k)}} \\ &= - {\alpha _c}{e_{\hbox{ci}}}(k){p_l}(k). \end{aligned} $$

The input to hidden layer of the critic is updated as

$$ \begin{aligned} \Updelta Y_{\hbox{ci}}^l(k) =& - {\alpha _c}\frac{{\partial {E_{\hbox{ci}}}(k)}}{{\partial {{\hat V}_{i + 1}}({x_k})}}\frac{{\partial {{\hat V}_{i + 1}}({x_k})}}{{\partial Y_{\hbox{ci}}^l(k)}} \\ =& - {\alpha _c}\frac{{\partial {E_{\hbox{ci}}}(k)}}{{\partial {{\hat V}_{i + 1}}({x_k})}}\frac{{\partial {{\hat V}_{i + 1}}({x_k})}}{{\partial {p_l}(k)}}\frac{{\partial {p_l}(k)}}{{\partial {q_l}(k)}}\frac{{\partial {q_l}(k)}}{{\partial Y_{\hbox{ci}}^l(k)}} \\ =& - {\alpha _c}{e_{\hbox{ci}}}(k)W_{\hbox{ci}}^l(k)\left[ {\frac{1}{2}\left( {1 - p_l^2(k)} \right)} \right]{x_{lk}}. \end{aligned} $$

4.2 The action network

In the action network, the state error x k is used as input to create the optimal control law as the output of the network. The output can be formulated as

$$ \hat{v}_i (x_k) = W_{\hbox{ai}}^T\sigma (Y_{\hbox{ai}} ^Tx_k). $$

The target of the output of the action network is given by (5). So, we can define the output error of the action network as

$$ e_{\hbox{ai}} (k) = \hat{v}_i (x_k) - v_i (x_k). $$

The weights in the action network are updated to minimize the following performance error measure:

$$ E_{\hbox{ai}} (k) = \frac{1}{2}e_{\hbox{ai}}^2 (k). $$

The weights updating algorithm is similar to the one for the critic network. By the gradient descent rule, we can obtain

$$ \begin{aligned} w_{a(i + 1)} (k) & =w_{\hbox{ai}} (k) + \Updelta w_{\hbox{ai}} (k), \\ &=w_{\hbox{ai}} (k)-\beta _a \left[ { \frac{\partial E_{\hbox{ai}} (k)}{\partial w_{\hbox{ai}} (k)}} \right] \\ &=w_{\hbox{ai}} (k)-\beta _a\frac{\partial E_{\hbox{ai}} (k)}{\partial e_{\hbox{ai}} (k)}\frac{\partial e_{\hbox{ai}} (k)}{\partial \hat{v}_i (k)}\frac{\partial \hat{v}_i (k)}{\partial w_{\hbox{ai}} (k)}, \end{aligned} $$
(38)

where β a  > 0 is the learning rate of action network.

If we define

$$ {g_l}(k) = \sum\limits_{j = 1}^{{L_a}} {Y_{\hbox{ai}}^{{l_j}}(k){x_{jk}}}, \quad l = 1,2, \ldots,{L_a} $$

and

$$ {h_l}(k) = \frac{{{e^{{g_l}(k)}} - {e^{ - {g_l}(k)}}}}{{{e^{{g_l}(k)}} + {e^{ - {g_l}(k)}}}},\qquad\quad l = 1,2, \ldots,{L_a}, $$

then we have

$$ {{\hat v}_{i}}({x_k}) = \sum\limits_{l = 1}^{{L_a}} {W_{\hbox{ai}}^l(k){h_l}(k)}, $$

where L a is the total number of hidden nodes in the action network. By applying the chain rule, the adaptation of the action network is summarized as follows.

The hidden to output layer of the action is updated as

$$ \begin{aligned} \Updelta W_{\hbox{ai}}^l(k) &= - {\beta _a}\frac{{\partial {E_{\hbox{ai}}}(k)}}{{\partial {{\hat v}_{i }}({x_k})}}\frac{{\partial {{\hat v}_{i }}({x_k})}}{{\partial W_{\hbox{ai}}^l(k)}} \\ &= - {\beta _a}{e_{\hbox{ai}}}(k){h_l}(k). \end{aligned} $$

The input to hidden layer of the action is updated as

$$ \begin{aligned} \Updelta Y_{\hbox{ai}}^l(k) &= - {\beta _a}\frac{{\partial {E_{\hbox{ai}}}(k)}}{{\partial {{\hat v}_{i}}({x_k})}}\frac{{\partial {{\hat v}_{i }}({x_k})}}{{\partial Y_{\hbox{ai}}^l(k)}} \\ &= - {\beta _a}\frac{{\partial {E_{\hbox{ai}}}(k)}}{{\partial {{\hat v}_{i}}({x_k})}}\frac{{\partial {{\hat v}_{i}}({x_k})}}{{\partial {h_l}(k)}}\frac{{\partial {h_l}(k)}}{{\partial {g_l}(k)}}\frac{{\partial {g_l}(k)}}{{\partial Y_{\hbox{ai}}^l(k)}} \\ &= - {\beta _a}{e_{\hbox{ai}}}(k)W_{\hbox{ai}}^l(k)\left[ {\frac{1}{2}\left( {1 - g_l^2(k)} \right)} \right]{x_{lk}}. \end{aligned} $$

The detailed neural training algorithm can also be seen in [22].

5 Simulation studies

Example 1

Our first example is chosen as the one in [8, 19, 37]. Consider the following discrete-time affine nonlinear system

$$ {x_{k + 1}} = f({x_k}) + g({x_k}){u_k}, $$
(39)

where \(f({x_k}) = \left[{\begin{array}{c} { - 0.8{x_{2k}}} \\ {\sin (0.8{x_{1k}} - {x_{2k}}) + 1.8{x_{2k}}} \\ \end{array}} \right]\) and \(g({x_k}) = \left[ {\begin{array}{c} 0 \\ { - {x_{2k}}} \\ \end{array}} \right]\). Let the initial state x 0 = [0.5, 0.5]T. Let the performance index function be a quadratic form which is expressed as

$$ J({x_0}, \underline {u}_0) = \sum\limits_{k = 0}^{\infty} {\left(x_k^TQ{x_k} + u_k^TR{u_k}\right)} $$

where the matrix Q = R = I, and I denotes the identity matrix with suitable dimensions. Neural networks are used to implement the stable iterative ADP algorithm. The critic network and the action network are chosen as three-layer BP neural networks with the structures of 2–8–1 and 1–8–1, respectively. Let θ = 7 and \(\Uppsi(x_k)=x^T_kQx_k\) to initialize the algorithm. We choose a random array of state variable in [−0.5, 0.5] to train the neural networks. For each iteration step, the critic network and the action network are trained for 800 steps under the learning rate α c  =  β a  = 0.01 so that the computation precision 10−6 is reached. The stable iterative ADP algorithm is implemented for 30 iteration steps to guarantee the convergence of the iterative performance index function. The admissible approximation error by (29) is shown in Fig. 2. From Fig. 2, we can see that the computation precision 10−6 satisfies (29). Hence, we say that the iterative performance index function is convergent. The trajectory of the iterative performance index function is shown in Fig. 3a.

Fig. 2
figure 2

The trajectories of the admissible approximation error

Full size image
Fig. 3
figure 3

The trajectories of the iterative performance index functions. a Iterative performance index function by stable iterative ADP algorithm. b Iterative performance index function by value iteration algorithm

Full size image

As value iteration algorithm is a most basic iterative ADP algorithm, in this paper, comparisons between stable iterative adaptive dynamic programming and value iteration algorithm in [19] will be displayed to show the effectiveness of the present algorithm. In [5, 19], it is proved that the iterative performance index function will nondecreasingly converge to the optimum. The trajectory of the iterative performance index function by value iteration is shown in Fig. 3b.

From Fig. 3a, b, we can see that the iterative performance index functions obtained by the stable iterative ADP algorithm and value iteration algorithm both converge, which shows the effectiveness of the present algorithm in this paper. By implementing the converged iterative control law by the stable iterative ADP algorithm to the control system (39) for T f  = 40 time steps, we get the optimal system states and optimal control trajectories. The trajectories of optimal system states by the stable iterative ADP algorithm are shown in Fig. 4a and the corresponding optimal control trajectory is shown in 4b. The trajectories of optimal system states obtained by value iteration algorithm are shown in Fig. 4c, and the corresponding optimal control trajectory is shown in 4d. From the simulation results, we can see that the present stable iterative ADP algorithm achieved effective results.

Fig. 4
figure 4

The trajectories of optimal states and controls. a Optimal states by stable iterative ADP algorithm. b Optimal control by stable iterative ADP algorithm. c Optimal states by value iteration algorithm. d Optimal control by value iteration algorithm

Full size image

For value iteration algorithm [37] and many other iterative ADP algorithms in [5, 40, 16, 24, 3, 37, 41], approximation errors were not considered. In the next example, we will analyze the convergence and stability properties considering different approximation errors.

Example 2

Our second example is chosen as the one in [13, 26, 30]. Consider the following discrete-time nonaffine nonlinear system

$$ {x_{k + 1}} = F(x_k,u_k)={x_k} + \sin (0.1x_k^2 + {u_k}) $$
(40)

with x 0 = 1. Let the performance index function be the same as in Example 1. Neural networks are used to implement the stable iterative ADP algorithm. The critic network and the action network are chosen as three-layer BP neural networks with the structures of 1–8–1 and 1–8–1, respectively. Let θ = 8 and \(\Uppsi(x_k)=x^T_kQx_k\) to initialize the algorithm. We choose a random array of state variable in [−0.5, 0.5] to train the neural networks. For the critic network and the action network, let the learning rate α c  = β a  = 0.01. The stable iterative ADP algorithm is implemented for 40 iteration steps. To show the effectiveness of the present stable iterative ADP algorithm, we choose four different approximation errors, which are \( \epsilon =10^{-6}, 10^{-4}, 10^{-3}, 10^{-1}, \) respectively. The trajectories of the iterative performance index functions under the four different approximation errors are shown in Fig. 5a–d, respectively.

Fig. 5
figure 5

The trajectories of the iterative performance index functions. a The approximation error \(\epsilon =10^{-6}\). b The approximation error \(\epsilon =10^{-4}\). c The approximation error \(\epsilon =10^{-3}\). d The approximation error \(\epsilon =10^{-1}\)

Full size image

In this paper, we have proved that if the approximation error satisfies (29), then iterative performance index function is convergent. As the approximation errors are different for different state x k , the admissible error trajectory obtained by (29) is shown in Fig. 6a. In [30], it shows that if the approximation error satisfies (19), then iterative performance index function is also convergent. The admissible error trajectory obtained by (19) is shown in Fig. 6b.

Fig. 6
figure 6

The trajectories of the admissible approximation error. a The trajectory of the admissible approximation error by (29). b The trajectory of the admissible approximation error by (19)

Full size image

From Figs. 5 and 6, we can see that for approximation errors \(\epsilon=10^{-6}\) and \(\epsilon=10^{-4}\), the performance index functions in Fig. 5a, b are both convergent. The trajectories of the control and state are displayed in Fig. 7a, b, respectively, where the implementation time is T f  = 15. For the approximation error \(\epsilon=10^{-3}\), we can see that the approximation error satisfies (19). From [30], we know that the iterative performance index function is also convergent, and the convergence trajectory of the iterative performance index function is shown in Fig. 5c. While in this case, the iterative performance index function is not convergent monotonically. The corresponding control and state trajectories are displayed in Fig. 7c. For the approximation error \(\epsilon=10^{-1}, \) we can see that the iterative performance index function is not convergent any more because of the large approximation error. The trajectories of the control and state are displayed in Fig. 7d.

Fig. 7
figure 7

The trajectories of states and controls under the approximation errors. a The approximation error \(\epsilon =10^{-6}\). b The approximation error \(\epsilon =10^{-4}\). c The approximation error \(\epsilon =10^{-3}\). d The approximation error \(\epsilon =10^{-1}\)

Full size image

According to Theorem 3, we know that if the approximation error \(\epsilon\) satisfies (29), then the iterative control is stable. To show the effectiveness of the present ADP algorithm, we display the state and control trajectories under the control law \(\hat{v}_0(x_k)\) with different approximation errors. The results can be seen in Fig. 8a–d, respectively. From Fig. 8a, b, we can see that the system is stable under the iterative control law \(\hat{v}_0(x_k)\) with approximation errors \(\epsilon =10^{-6}\) and \(\epsilon =10^{-4}\). In this paper, we have shown that the approximation error in [30] cannot guarantee the stability of the control system. From Fig. 8c, we can see that for the approximation error \(\epsilon =10^{-3}\), the system is not stable under the control law \(\hat{v}_0(x_k)\). From Fig. 8d, for \(\epsilon =10^{-1}\), as the iterative performance index function is not convergent, the stability of the system cannot be guaranteed.

Fig. 8
figure 8

The trajectories of states and controls under the control law \(\hat{v}_0(x_k)\) with different approximation errors. a The approximation error \(\epsilon =10^{-6}\). b The approximation error \(\epsilon =10^{-4}\). c The approximation error \(\epsilon =10^{-3}\). d The approximation error \(\epsilon =10^{-1}\)

Full size image

6 Conclusions

In this paper, an effective stable iterative ADP algorithm is developed to find the infinite horizon optimal control for discrete-time nonlinear systems. In the present stable iterative ADP algorithm, any of the iterative control is stable for the nonlinear system which makes the present algorithm feasible for implementations both on-line and off-line. Convergence analysis of the performance index function for the iterative ADP algorithm is proved and the stability proofs are also given. Neural networks are used to implement the present ADP algorithm. Finally, simulation results are given to illustrate the performance of the present algorithm.