Weighted Huber constrained sparse face recognition

Abstract

Recently sparse coding based on regression analysis has been widely used in face recognition research. Most existing regression methods add an extra constraint factor to the coding residual to make the fidelity term in the $l_{2}$ loss approach the Gaussian or Laplace distribution. But the essence of these methods is that only the fidelity term of $l_{1}$ loss or $l_{2}$ loss is used. In this paper, weighted Huber constrained sparse coding (WHCSC) is used to study the robustness of face recognition in occluded environments, and alternating direction method of multipliers is used to solve the problem of model minimization. In WHCSC, we propose a sparse coding with weight learning and use Huber loss to determine whether the fidelity is a $l_{2}$ loss or $l_{1}$ loss. For the WHCSC model, the two kinds of classification modes and the two kinds of weight coefficients are further studied for the intra-class difference and the inter-class difference in the face image classification. Through a large number of experiments on a public face database, WHCSC shows strong robustness in face occlusion, corrosion and illumination changes comparing to the state-of-the-art methods.

1 Introduction

In recent years, face recognition is still a hot research topic [1]. On the one hand, it is great potential for use; on the other hand, it reveals how machine learning can make feature selection and classification on complete images [2, 3]. The advantage of face recognition lies in its naturalness and the characteristics that are not perceived by the tested individual [4]. First, naturalness means that the recognition method is the same as the biological characteristics used by human (or even other organisms) for individual recognition. For example, in face recognition, humans beings also distinguish and confirm identity by observing face. Second, unobtrusive characteristics are also important for a method of identification, which makes it less objectionable and because it is not easy to attract people's attention, it is not easy to be deceived. Face recognition uses visible light to acquire face image information. This is different from fingerprint recognition or iris recognition, which requires the use of an electronic pressure sensor to capture fingerprints, or the use of infrared to acquire iris images. Fingerprint recognition or iris recognition is easily perceived and thus more likely deceived by camouflage.

Face recognition is considered as one of the most difficult research topics in the field of biometrics and even artificial intelligence. On the one hand, this difficulty comes from the characteristics of human biological characteristics. First, the similarity of the face: the structure and appearance of the faces between different individuals are very similar. This similarity is not conducive to the use of human face to distinguish between human beings. Second, the variability of the face: face shape is very unstable, human complex facial expression changes, but also in different angles of view, face the visual image is also very different. Finally, the difference in face: different genetic makeup makes each person’s face always different. On the other hand, the external noise changes. For example, expression changes, lighting conditions, true camouflage, continuous occlusion, pixel corrosion, etc., will reduce the valuable information of the face image and interfere with the recognition of the face [5].

Recently, the method based on regression analysis has attracted the widespread interest of researchers. The linear regression classifier (LRC) proposed by Naseem et al. [6] represents the query image by linear combination of dictionary atoms. Wright et al. [7] proposed a sparse coding classification algorithm (SRC) to identify the real camouflage and pixel erosion of human face images. The SRC uses a sparse linear combination of dictionary atoms to represent the query image. LRC and SRC cannot achieve the desired performance when the dictionary is not enough. Zhang et al. [8] considered that cooperative mechanisms are more important than sparse constraints. They proposed a collaborative representation classifier (CRC) based on $l_{2}$ norm constraints and further proposed its robust version (RCRC). Yang et al. [9] further proposed a matrix regression (NMR) classification framework based on kernel regularization of $l_{2}$ norm to obtain a better recognition rate in occlusion and lighting changes. Zhong et al. [10] considered that the balance between SRC and CRC can be adjusted through iteration and a classifier (LHC) of $l_{1/2}$ regularization and ITR iterative mechanism is proposed. Zheng et al. [11] attempted to obtain a more general classifier (IRGSC) through adaptive feature weight learning and adaptive distance-weighted learning. Lin et al. [12] propose a robust, discriminative and comprehensive dictionary learning (RDCDL) method, in which a robust dictionary is learned from comprehensive training sample diversities generated by extracting and generating facial variations.

Although these classifiers have made great progress, due to the complicated changes of occlusion, two types of changes of face image are still not well overcome. The first type of change is called inter-class difference. The inter-class difference should be amplified as a standard to distinguish between individuals. The second type of change is called intra-class difference. It should be eliminated because they can represent the same individual. For face images, intra-class difference interference is often greater than the inter-class difference, so it becomes very difficult to distinguish the individuals by the inter-class difference under the intra-class difference. Two types of changes are one of the biggest obstacles that face recognition technology is widely used and need to be solved urgently.

We propose a new scheme called weighted Huber constrained sparse coding (WHCSC) and establish a robust weighted regression model with sparse constraints. WHCSC seeks the problem with the maximum a posteriori (MAP) of sparse coding and is robust against noise values (such as occlusion, corrosion, illumination changes). The experiment uses a representative face database. The experimental results show that WHCSC has obvious advantages in dealing with facial occlusion, corrosion, and camouflage.

The main contributions of this article are summarized as follows:

• 1. Propose a more efficient taxonomy. On the one hand, the intra-class difference is reduced; on the other hand, the inter-class interference is effectively avoided when the coding coefficients of the query sample and the training sample are calculated.

• 2. The weighted method is adopted to reduce the influence of noise. At the same time, two kinds of exponential form of weight are researched to further expand the effect of weight vector, increase the inter-class difference and improve the recognition rate.

• 3. Utilize the robustness of Huber function to reduce outlier interference and solve the $l_{1}$ norm minimization problem by using alternating direction method of multipliers (ADMM) [13].

The rest of the paper is organized as follows: Sect. 2 introduces sparse robust coding. Section 3 introduces the WHCSC and its contributions. Section 4 analyzes the computational complexity of WHCSC. Section 5 analyzes the convergence of WHCSC. Section 6 tests WHCSC performance using a published face dataset. Finally, Sect. 7 summarizes WHCSC.

2 Sparse robust coding based on regression classifier

2.1 General classification framework based on regression analysis

In the general classification problem, the training samples are expressed as a dictionary matrix $X = \left[ {X_{1} \text{,}X_{2} , \ldots ,X_{c} } \right] \in {\mathbf{R}}^{m \times n}$, and c is the sample category. $X_{i} = \left[ {X_{i1} ,X_{i2} , \ldots ,X_{{in_{i} }} } \right] \in {\mathbf{R}}^{{m \times n_{i} }} \left( {i = 1,2, \ldots ,c} \right)$ is the sample subset of each category of the sample corpus $\varvec{X}$. $n_{i}$ is the number of training samples of class i, $n = \mathop \sum \nolimits_{i = 1}^{c} n_{i}$ is the total number of samples. In the regression, the training sample $X$ linearly represents the query sample

$$y = \varvec{X}_{1} \theta_{1} + \varvec{X}_{2} \theta_{2} + \cdots + \varvec{X}_{c} \theta_{c} = \varvec{X}_{11} \theta_{11} + \varvec{X}_{12} \theta_{12} + \cdots + \varvec{X}_{{cn_{c} }} \theta_{{cn_{c} }} = \varvec{X}\theta ,$$

(1)

where $\theta = [\theta_{11} ,\theta_{12} , \ldots ,\theta_{{cn_{c} }} ]^{\text{T}} \in {\mathbf{R}}^{n}$ is the coding coefficient of the query sample to be determined on the training sample.

The regression-based classification is to determine the class of the query sample $y \in {\mathbf{R}}^{m}$ in a given training sample. By computing the residuals $e_{i} = y - \varvec{X}_{i} \theta_{i}$ in the query sample and each category, the category of the smallest $e_{i}$ is regarded as the category of the query sample.

2.2 Sparse coding

Sparse coding is an artificial neural network method that simulates the simple cell receptivity field in the primary visual cortex V1 of the mammalian visual system and has been widely used in image processing and natural language [14, 15]. Some human visual studies suggest that many neurons in the visual pathway are selective for a variety of specific stimuli in lower- and intermediate-level human vision, such as color, texture, orientation, size. [16, 17]. Given the sparseness of the input image given by these neurons, it can be efficiently computed by convex optimization. Due to the difficulty in solving the $l_{0}$ norm minimization, the $l_{1}$ norm is usually used as the nearest solution to the $l_{0}$ norm minimization problem. In general, the problem of sparse coding can be expressed as

$$\mathop { \hbox{min} }\limits_{\theta } ||y - \varvec{X}\theta||_{2}^{2} + \lambda ||\alpha||_{1} \quad {\text{s}} . {\text{t}}.\,\alpha = \theta ,$$

(2)

where $\lambda$ is the penalty coefficient for the $l_{1}$ norm. The essence of formula (2) is the least squares estimation of sparse constraints when the residuals follow a Gaussian distribution. When the residuals follow the Laplace distribution, the sparse coding problem is

$$\mathop { \hbox{min} }\limits_{\theta } ||y - \varvec{X}\theta||_{1} + \lambda ||\alpha||_{1} \quad {\text{s}} . {\text{t}}.\,\alpha = \theta .$$

(3)

Sparse coding can capture high-order correlation structures in an image and represent the signal with as few atoms as possible in a given overcomplete dictionary [18]. However, there are mainly two problems with this model. The first one is whether the regularized $l_{1}$ norm constraint $\parallel\alpha\parallel_{1}$ is good enough to make the signal sufficiently sparse. The second one is whether the fidelity term ($\parallel y - \varvec{X}\theta\parallel_{2}^{2}$ or $\parallel y - \varvec{X}\theta\parallel_{1}$) is sufficiently effective to describe the fidelity of the signal, especially when the signal has noise or abnormal values.

Improve the first problem by modifying sparse constraints. For example, Liu et al. [19] added a nonnegative constraint on sparse coefficient α. Gao et al. [20] introduced Laplace coefficients in sparse coding. Wang et al. [21] used weighted $l_{2}$ norm for sparse constraints. In addition, Ramirez et al. [22] proposed a generic sparse modeling framework to design sparse regularization terms.

For the second problem, defining the fidelity terms using the $l_{2}$ or $l_{1}$ norm from the perspective of the maximum a posteriori probability (MAP) actually assumes that the encoded residuals follow a Gaussian or Laplace distribution. However, in practice, it may not be very good to follow a certain distribution of a single hypothetical residual, especially when occlusion, camouflage or corruption occurs in facial images. Therefore, a fidelity item that uses a single $l_{2}$ or $l_{1}$ norm in a sparse coding model may not be robust in these cases.

2.3 Sparse robust coding

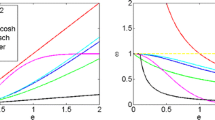
It can be observed from (c) in Fig. 1 that when the encoding residual approaches 0, the encoding residual of the $l_{2}$ norm is smaller, and when it is far from 0, the $l_{1}$ norm is smaller.

Fig. 1

a and b are two pictures of the same person. c is an $l_{2}$ loss and $l_{1}$ loss coded residual image of the coded residual of (a) and (b) when the residual threshold is 10

In practice, in a large number of training samples, it will naturally contain more or less some outliers. In linear coding, it is assumed that the sum of the residuals of the training samples and the query samples is $\mathop \sum \nolimits_{i = 1}^{m} e_{i}$, and the outliers have a great contribution to $\mathop \sum \nolimits_{i = 1}^{m} e_{i}$. Therefore, to some extent reduce the encoding residuals of outliers, will be greatly reduced $\mathop \sum \nolimits_{i = 1}^{m} e_{i}$. For example, in Fig. 1 (c), $l_{2}$ loss and $l_{1}$ loss show two different coding residuals. Therefore, in order to reduce the impact of outliers, it is important to query for different pixels using different fidelities ($||y - \varvec{X}\theta||_{2}^{2}$ or $||y - \varvec{X}\theta||_{1}$).

In the statistical learning perspective, the Huber loss function is a loss function of robust regression, which is insensitive to outliers compared to mean square error and is often used for classification problems. Huber loss function is expressed as

$$g\left( z \right) = \left\{ {\begin{array}{*{20}l} {|z|^{2} /2} \hfill & {\left| z \right| \le \eta } \hfill \\ {\eta \left| z \right| - \eta^{2} /2} \hfill & {\left| z \right| > \eta } \hfill \\ \end{array} } \right.,$$

(4)

where z is the residual and η is the Huber threshold.

$l_{2}$ loss and $l_{1}$ loss are mixed in the Huber loss (Fig. 2). If the absolute value of the residual $\left| z \right|$ is smaller than the threshold value $\eta$ (that is, the normal value), the fidelity of formula (4) uses $l_{2}$ loss. If the absolute value of the residual the value $\left| z \right|$ is greater than the threshold $\eta$, and the fidelity of formula (4) uses $l_{1}$ loss. For smooth connection with $l_{2}$ loss, the constant $\eta^{2} /2$ is subtracted from $l_{1}$ loss. The Huber loss balances the validity and robustness through the optimal combination of $l_{2}$ loss and $l_{1}$ loss.

Fig. 2

Huber loss function diagram

In order to improve the robustness and validity of sparse coding, a sparse Huber (SH) model is designed according to Huber loss mentioned above.

Byod explains in Sect. 6 of the article [13] that the Huber function corresponds to the standard form $\hbox{min} f\left( \theta \right) + g\left( z \right)$ of the ADMM model and can be expressed as:

$$\mathop {\hbox{min} }\limits_{\theta } g\left( z \right)\quad {\text{s}}.{\text{t}}.\,z = X\theta - y,$$

(5)

where $f\left( \theta \right) = 0$, $g\left( z \right) = \left\{ {\begin{array}{ll} { \frac{1}{2}||z||_{2}^{2} \left| z \right| \le \eta } \\ {\eta ||z||_{1} - \frac{1}{2}\eta^{2} \left| z \right| > \eta } \\ \end{array} } \right.$ and is constrained by $z = y - \varvec{X}\theta$.

SH can be expressed as

$$\mathop {\hbox{min} }\limits_{\theta } g\left( z \right) + \lambda \alpha_{1} \quad {\text{s}}.{\text{t}}.\,z = \varvec{X}\theta - y,\alpha = \theta ,$$

(6)

where $\lambda ||\alpha||_{1}$ is an $l_{1}$ norm penalty term with $\alpha = \theta$ constraints. In a certain range, the larger the value of $\lambda$, the more sparse $\theta$.

3 Weighted Huber constrained sparse coding

3.1 Weighted Huber constrained sparse coding model

To further reduce the effects of noise or outliers in the training samples, we design a weight for the training samples so that outliers are given a low weight value. In RSRC, an effective weight vector is proposed to convert the minimization problem into an iteratively reweighted sparse coding problem.

With reference to the weight vector in RSRC [23], combined with the above-mentioned sparse Huber model (SH), this paper proposes a weighted Huber constrained sparse coding model (WHCSC). The WHCSC model is essentially a maximum likelihood estimation (MLE) problem. The weight vector and the SH model are jointly used to reduce the noise interference, and ADMM is used to solve the $l_{1}$ norm minimization problem. A large number of experiments conducted in open face database show that WHCSC has good classification effect, especially when the facial image has complex changes such as occlusion, corrosion, light changes.

WHCSC can be expressed as

$$\mathop {\hbox{min} }\limits_{\theta } g\left( z \right) + \lambda ||\alpha||_{1} \quad {\text{s}}.{\text{t}}.\quad z = w \odot \left( {\varvec{X}\theta - y} \right),\alpha = \theta ,$$

(7)

where $f\left( \theta \right) = 0$, $g\left( z \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}||z||_{2}^{2} } \\ {\eta|| w \odot z||_{1} - \frac{1}{2}\eta^{2} w^{T} w} \\ \end{array} } \right. \begin{array}{*{20}c} {\left| {z_{k} } \right| \le \eta w_{k} } \\ {\left| {z_{k} } \right| > \eta w_{k} } \\ \end{array}$, $k = 1,2, \cdots m$, $w$ is the sample weight. $\eta$ is the residual threshold constant. There are different methods to determine the threshold of $\eta$ in many papers. In this paper, we propose a combined threshold of weight, that is $\eta w$, where $\eta$ is a constant. $\eta w$ makes the threshold value more in line with the distribution of training samples with weight $w$ constraint. $a \odot b$ represents the multiplication of the corresponding elements of a and b.

Weight $w = \left[ {w_{1} ,w_{2} , \cdots ,w_{m} } \right] \in {\mathbf{R}}^{m \times 1}$. $w_{m}$ is the weight of number m in training sample $\varvec{X} \in {\mathbf{R}}^{m \times n}$, ${\text{e}}_{\text{m}}$ is the residual with number m, $w_{m}$ is set to the following sigmoid function

$$w_{m} \left( {e_{m} } \right) = \frac{1}{{1 + { \exp }\left( { - q\left( {\frac{{\delta - e_{m}^{2} }}{\delta }} \right)} \right)}},$$

(8)

where $\delta$ is the residual threshold. $\delta - e_{m}^{2}$ represents the distance between the residual and the residual threshold, and $\frac{{\delta - e_{m}^{2} }}{\delta }$ unifies the dimension of this distance. q affects the penalty rate of weights and makes the distribution of weights smoother. The sigmoid function can constrain the weights value between [0,1]. Therefore, when the residual is greater than $\delta$, the weights is less than 0.5; when equal to $\delta$, the weights is equal to 0.5; when less than $\delta$, the weights is greater than 0.5.

Let $\varPsi = \left[ {e_{1}^{2} ,e_{2}^{2} , \cdots ,e_{m}^{2} } \right]$, and then ranking $\varPsi$ to get $\varPsi_{a}$. Let $k = \lfloor\tau m\rfloor$, where $\tau \in \left( {0,1} \right]$, $\lfloor\tau m\rfloor$ is an integer less than $\lfloor\tau m\rfloor$, then $\delta$ can be expressed as

$$\delta = \varPsi_{a} \left( k \right).$$

(9)

For ease of calculation, formula (8) is organized to get

$$w_{m} \left( {e_{m} } \right) = \frac{{{ \exp }\left( { - \mu e_{m}^{2} + \mu \delta } \right)}}{{1 + { \exp }\left( { - \mu e_{m}^{2} + \mu \delta } \right)}},$$

(10)

where the parameter $\mu = \frac{q}{\delta }$.

Compared with the model in formulas (6), (7) has the following advantages. Outliers (usual pixels with large residuals) are adaptively assigned a low weight to reduce their impact on regression estimates, which can greatly reduce the sensitivity to outliers. And formula (8) limits the weights between [0,1] using a sigmoid function and avoids the almost infinite weight value of pixels with very small residuals, which improves the stability of the encoding process. The important parameters $q$ and $\tau$ will be analyzed in conjunction with the experiment in Sect. 6.6.

3.2 WHCSC’s contribution

The purpose of the linear expression-based classification is to obtain the smallest encoding residual by linear expression with the optimal encoding coefficient θ, thereby distinguishing the category to which the test image belongs. Definition $y_{i} = F_{i} \left( \varvec{X} \right) = \left[ {\varvec{X}_{1} \theta_{1} + \varvec{X}_{2} \theta_{2} + \cdots + \varvec{X}_{i} \theta_{i} + \cdots + \varvec{X}_{c} \theta_{c} } \right]$, where $y_{i} = F_{i} \left( \varvec{X} \right)$ represents the linear expression of the sample set for the ith test sample. Due to the variability of the human face, two face images generated by the same person at different times do not appear to be identical, resulting in an intra-class difference, that is, $y_{i} - \varvec{X}_{i} \theta_{i} > 0$. Similarly, the inter-class difference is the difference between different people, that is, $y_{i} - \varvec{X}_{j} \theta_{j} > 0\left( {j \ne i} \right)$. Sparse coding has the function of feature selection. Its purpose is to select the training samples that are most similar to the test samples to be linearly combined into test samples [23]. First, we prefer to select samples belonging to the same class to linearly combine test samples and exclude interference from other classes of samples. This makes the coding coefficients $(\theta_{j})$ of samples of different categories small enough. Second, we also prefer to select the same type of training samples that have less interference with the test samples for the same type of samples. On the other hand, in actual tests, the linear expression of test samples in each category will be calculated. Therefore, we hope that the coding residuals of linear expressions in the same category will be small, while the coding residuals of different categories are large. Section 3.2.1 describes in detail the methods used to reduce intra-class difference and avoid inter-class interference. Section 3.2.2 describes in detail how to increase the inter-class difference.

3.2.1 Reduce the intra-class difference and remove inter-class interference

In Fig. 3, we assume that the query sample belongs to the category i. The residuals of the query samples and the training samples of each category are $e = \left[ {e_{i,1} ,e_{i,2} , \cdots ,e_{i,i} , \cdots ,e_{i,c} } \right] = \left[ {(\varvec{X}_{1} \theta_{1} - y_{i} } \right),(\varvec{X}_{2} \theta_{2} - y_{i} ), \cdots ,(\varvec{X}_{i} \theta_{i} - y_{i} ), \cdots ,(\varvec{X}_{c} \theta_{c}$$- y_{i} )]$, where $e_{i,i}$ represents the coding residuals of the query samples and training samples of the same class, that is, intra-class difference, and $e_{i,j}$ denotes the encoding residuals of the query samples and the training samples of different class, that is, inter-class difference.

Fig. 3

a is a classification mode I. The “different category” curve is the fitted image residual distribution of the query sample and different categories of training samples, and “Linear fitting (different category)” is the corresponding residual distribution fitting straight line. The “same category” curve is the fitted image residual distribution of the query sample and the same category of training samples, and “Linear fitting (same category)” is the corresponding residual distribution fitting straight line. b is a classification mode II. The “different category” curve is the fitted image residual distribution of the query sample and the different categories of training samples, and “Linear fitting (different category)” is the corresponding residual distribution fitting straight line. The “same category” curve is the fitted image residual distribution of the query sample and the same category of training samples, and “Linear fitting (same category)” is the corresponding residual distribution fitting straight line. c is a fitted image residual distribution of the query sample and the same category of training samples in the classification mode I and the classification mode II. The “Pattern one” curve and the “Linear fitting (Pattern one)” line respectively correspond to the residual distribution and the residual distribution fitting line in the classification mode I. The “Pattern two” curve and the “Linear fitting (Pattern two)” line respectively correspond to the residual distribution and the residual distribution fitting line in the classification mode II

In RSRC, the weight $w$ is defined based on the residual of the complete sample $X \in R^{m \times n}$ and the query sample. And all categories of samples use the same weight vector, i.e. $w \odot \left( {\varvec{X}\theta - y} \right) = \left[ {w \odot \left( {\varvec{X}_{1} \theta - y} \right),w \odot \left( {\varvec{X}_{2} \theta - y} \right), \ldots ,w \odot \left( {\varvec{X}_{c} \theta - y} \right)} \right]$. Here is defined as a classification model I, as shown in Fig. 3a, which shows the use of the complete works samples to define weights, the same type of coding residuals and the distribution of different types of coding residuals. However, in WHCSC, the weight $w$ is based on the residual definition of the sample subset $\varvec{X}_{i} \in {\mathbf{R}}^{{m \times n_{i} }}$ and the query sample, that is, $w \odot \left( {\varvec{X}\theta - y} \right) = \left[ {w_{1} \odot \left( {\varvec{X}_{1} \theta - y} \right),w_{2} \odot \left( {\varvec{X}_{2} \theta - y} \right), \ldots ,w_{c} \odot \left( {\varvec{X}_{c} \theta - y} \right)} \right]$. Here is defined as classification model II, as shown in Fig. 3b, which shows the distribution of the same class coded residual and the different class coded residuals when the weights defined by the sample subset are used.

Observing Fig. 3a–c, using the residuals of the sample subset and the query sample to define the weights can significantly reduce the coding residuals of the same class, although the different types of coding residuals also decrease, However, the same type and different types of residuals fit straight line is still a clear distinction.

Therefore, in classification model II, the weight of WHCSC can obtain the independent weights that are more suitable for the subset of samples in this category, and then the better coding coefficient $\theta_{i}$ under this weight is obtained, so as to reduce the intra-class difference.

3.2.2 Increase the inter-class difference

First, it is also assumed that $e = \left[ {e_{i,1} ,e_{i,2} , \cdots ,e_{i,i} , \cdots ,e_{i,c} } \right] = \left[ {(\varvec{X}_{1} \theta_{1} - y_{i} } \right),(\varvec{X}_{2} \theta_{2} - y_{i} ), \cdots ,(\varvec{X}_{i} \theta_{i} - y_{i} ), \cdots ,(\varvec{X}_{c} \theta_{c} - y_{i} )]$. The difference between the residuals in the different types of training samples and the residuals in the category i training samples, i.e. the relative differences between the inter-class difference and intra-class difference, is expressed as

$$\Delta e = \left[ {\frac{{e_{i,1} - e_{i,i} }}{{e_{i,i} }},\frac{{e_{i,2} - e_{i,i} }}{{e_{i,i} }}, \ldots ,\frac{{e_{i,i - 1} - e_{i,i} }}{{e_{i,i} }},\frac{{e_{i,i + 1} - e_{i,i} }}{{e_{i,i} }}, \ldots ,\frac{{e_{i,c} - e_{i,i} }}{{e_{i,i} }},} \right] \in {\mathbf{R}}^{c - 1} .$$

(11)

The larger the $\Delta e$ is, the larger inter-class difference is relative to the intra-class difference, the easier it is to distinguish between the query sample and other types of samples. Conversely, the smaller the $\Delta e$ is, the smaller inter-class difference is relative to the intra-class difference, the more difficult it is to distinguish between the query sample and other classes of samples.

In RSRC, the weighting effect on the residual is expressed as $w^{{\frac{1}{2}}} \odot \left( {\varvec{X}\theta - y} \right)$, and the definition of $w^{{\frac{1}{2}}}$ is 0.5 power exponent weights and the relative difference in residual is $\Delta e_{{W^{{\frac{1}{2}}} }}$. However in WHCSC, the weighting effect on the residual is expressed as $w \odot \left( {\varvec{X}\theta - y} \right)$, and the definition of $w$ is 1 power exponent weights, and the relative difference in residual is $\Delta e_{W}$. Figure 4 shows the experimental results of $w^{{\frac{1}{2}}}$ and $w$ in WHCSC. The ordinate is the distribution of $\Delta e_{{W^{{\frac{1}{2}}} }}$ and $\Delta e_{W}$, and the abscissa is the sample type.

Fig. 4

In two different weighting coefficients, the relative difference between the intra-class difference and the inter-class difference

It can be observed that the 1 power exponent weight makes the difference between $e_{i,j}$ and $e_{i,i}$ increase, that is to say, the inter-class difference is more different from the intra-class difference, that is, increase the inter-class difference.

3.3 The initial value of the weight

A good initial value will make the algorithm easier to get good performance. In order to initialize the weights, the coding residuals of the query samples should first be estimated. We can set the initial residual as $e = y - y_{{mn_{i} }}$. Because the weight of WHCSC is sub-category calculation, it is reasonable to set $y_{{mn_{i} }}$ as the average of the same pixels of the current training sample subset

$$\begin{aligned} y_{{mn_{i} }} & = \left[ {m\left( {y_{1} } \right),m\left( {y_{2} } \right), \ldots ,m\left( {y_{k} } \right)} \right] \\ & = \left[ {m\left( {\left[ {y_{11} ,y_{12} , \ldots ,y_{1j} } \right]} \right),m\left( {\left[ {y_{21} ,y_{22} , \ldots ,y_{2j} } \right]} \right), \ldots ,m\left( {\left[ {y_{k1} ,y_{k2} , \ldots ,y_{kj} } \right]} \right)} \right]k = \left[ {1,2, \ldots ,m} \right],j = \left[ {1,2, \ldots ,n_{i} } \right] \\ \end{aligned}$$

(12)

where m(x) represents the mean of x. For parameters $\tau$ and $q$, usually $\tau$ = 0.8 and $q$ = 1. In more complex environments, such as occlusion, camouflage, corrosion, you can set smaller $\tau$.

3.4 WHCSC iteration conditions

In each iteration, the formula (7) will gradually decrease, the lower bound is 0, and WHCSC will gradually converge. WHCSC converges and the iteration terminates when the difference in θ between adjacent iterations is small enough. The termination conditions are as follows

$$||\theta^{t} - \theta^{t - 1} \,||_{2}^{2} < \gamma$$

(13)

where $\gamma$ is a small enough positive number and $t$ is the number of iterations.

3.5 ADMM solves the sub-problem

$$\mathop {\hbox{min} }\limits_{\theta } g\left( z \right) + \lambda ||\alpha||_{1} \quad {\text{s}}.{\text{t}}.\,z = w \odot \left( {\varvec{X}\theta - y} \right),\alpha = \theta .$$

(14)

The Lagrange expression of a sub-problem is

$${\mathcal{L}}\left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right) = g\left( z \right) + \lambda ||\alpha||_{1} + \langle h_{z} ,w \odot \left( {\varvec{X}\theta - y} \right) - z\rangle + \langle h_{\alpha } ,\theta - \alpha\rangle$$

(15)

ADMM is an algorithm that aims to fuse the dual variable ascent method’s decomposability and the multiplier method’s upper bound convergence property. In order to increase the robustness of the dual variable ascent method and the strong convex constraint of the relaxation function, introducing the augmented Lagrangian formula

$${\mathcal{L}}_{{\rho_{1} ,\rho_{2} }} \left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right) = g\left( z \right) + \lambda ||\alpha||_{1} +\langle h_{z} ,w \odot \left( {\varvec{X}\theta - y} \right) - z\rangle + \frac{{\rho_{1} }}{2}||w \odot \left( {\varvec{X}\theta - y} \right) - z||_{2}^{2} +\langle h_{\alpha } ,\theta - \alpha\rangle + \frac{{\rho_{2} }}{2}||\theta - \alpha||_{2}^{2}$$

(16)

where $\rho_{1}$, $\rho_{2}$ is greater than zero. The ADMM iteration is made up of

$$\theta^{k + 1} : = \mathop {\arg \hbox{min} }\limits_{x} {\mathcal{L}}_{{\rho_{1} ,\rho_{2} }} \left( {\theta^{k} ,z^{k} ,\alpha^{k} ,h_{z}^{k} ,h_{\alpha }^{k} } \right)$$

(17)

$$z^{k + 1} : = \mathop {\arg \hbox{min} }\limits_{z} {\mathcal{L}}_{{\rho_{1} }} \left( {\theta^{k + 1} ,z^{k} ,h_{z}^{k} } \right)$$

(18)

$$\alpha^{k + 1} : = \mathop {\arg \hbox{min} }\limits_{\alpha } {\mathcal{L}}_{{\rho_{2} }} \left( {\theta^{k + 1} ,\alpha^{k} ,h_{\alpha }^{k} } \right)$$

(19)

$$h_{z}^{k + 1} : = h_{z}^{k} + \rho_{1} \left( {w \odot \left( {\varvec{X}\theta^{k + 1} - y} \right) - z^{k + 1} } \right)$$

(20)

$$h_{ \alpha }^{k + 1} : = h_{\alpha }^{k} + \rho_{2} \left( {\theta^{k + 1} - \alpha^{k + 1} } \right)$$

(21)

Formula (16) is brought into formula (17), (18), (19), (20) and (21), and the iterative step of ADMM is

$$\theta^{k + 1} : = \mathop {\arg \hbox{min} }\limits_{x} \left( {\frac{{\rho_{1} }}{2}||w \odot \left( {\varvec{X}\theta^{k} - y} \right) - z^{k} + u^{k} \;||_{2}^{2} + \frac{{\rho_{2} }}{2}||\theta^{k} - \alpha^{k} + u^{k} \;||_{2}^{2} } \right)$$

(22)

$$z^{k + 1} : = \mathop {\arg \hbox{min} }\limits_{z} \left( {g\left( {z^{k} } \right) + \frac{{\rho_{1} }}{2}||w \odot \left( {\varvec{X}\theta^{k + 1} - y} \right) - z^{k} + u^{k} \;||_{2}^{2} } \right)$$

(23)

$$\alpha^{k + 1} : = \mathop {\arg \hbox{min} }\limits_{z} \left( {\lambda ||\alpha^{k}||_{1} + \frac{{\rho_{2} }}{2}||\theta^{k + 1} - \alpha^{k} + u^{k} \;||_{2}^{2} } \right)$$

(24)

$$u_{z}^{k + 1} : = u_{z}^{k} + w \odot \left( {\varvec{X}\theta^{k + 1} - y} \right) - z^{k + 1}$$

(25)

$$u_{ \alpha }^{k + 1} : = u_{\alpha }^{k} + \theta^{k + 1} - \alpha^{k + 1}$$

(26)

where $u$ is an alternative variable for $u = \frac{h}{\rho }$. Solve the formula (22), (23), (24), (25) and (26) to get

$$\theta^{k + 1} = \left( {\rho_{1} \varvec{X}^{T} \varvec{W}^{T} \varvec{WX} + \rho_{2} } \right)^{ - 1} \left[ {\rho_{1} \varvec{X}^{T} \varvec{W}^{T} \left( {z^{k} - u^{k} + y} \right) + \rho_{2} \left( {\alpha^{k} - u^{k} } \right)} \right],$$

(27)

$$z^{k + 1} = \frac{{\rho_{1} }}{{1 + \rho_{1} }}\left[ {w \odot \left( {\varvec{X}\theta^{k + 1} - y} \right) + u^{k} \left] { + S_{{\frac{{\varvec{W}\eta }}{{\rho_{1} }}}} } \right[\frac{1}{{1 + \rho_{1} }}\left( {w \odot \left( {\varvec{X}\theta^{k + 1} - y} \right) + u^{k} } \right)} \right],$$

(28)

$$\alpha^{k + 1} = S_{{\frac{\lambda }{{\rho_{2} }}}} \left( {\theta^{k + 1} + u^{k} } \right),$$

(29)

$$u_{z}^{k + 1} = u_{z}^{k} + w \odot \left( {\varvec{X}\theta^{k + 1} - y} \right) - z^{k + 1} ,$$

(30)

$$u_{ \alpha }^{k + 1} = u_{\alpha }^{k} + \theta^{k + 1} - \alpha^{k + 1} ,$$

(31)

where $\varvec{W} = {\text{diag}}\left( w \right) = {\text{diag}}\left( {\left[ {w_{1} ,w_{2} , \ldots ,w_{m} } \right]} \right)$ and the S operator is defined as

$$S_{k} \left( a \right) = \left\{ {\begin{array}{*{20}l} {a - k,} \hfill & {a > k} \hfill \\ {0,} \hfill & {\left| a \right| \le k} \hfill \\ {a + k,} \hfill & {a < - k} \hfill \\ \end{array} .} \right.$$

(32)

3.6 Judgment query sample category

The residuals of the query sample in each category are calculated according to the categories $\theta_{i}$ obtained $e = \left[ {e_{1} ,e_{2} , \ldots ,e_{i} } \right]\text{,}i = 1,2, \ldots ,c$, where $e_{i} = y - \varvec{X}_{i} \theta_{i}$. The category of the smallest $e_{i}$ belongs to the category of the query sample.

4 Computational complexity analysis

The computational cost of the algorithm is mainly used to update the weight $w$ and the coding coefficient $\theta$. Given that there are $m$ face data sets of one category, and each image size is $n = p \times q$. The face data set has a total of c categories. The number of iterations of algorithm step 2 is denoted as $k_{1}$. The computational complexity of the weight $w \in R^{n \times 1}$ in step 4 is $O\left( n \right)$. WX and Wy can be calculated and cached in advance. The computational complexity of $\theta$ in formula (27) is $O\left( {nm^{2} } \right)$, $z$ in formula (28) is $O\left( {nm} \right)$ and $u_{z}$ in formula (30) is $O\left( {nm} \right)$. Therefore, the computational complexity of the coding coefficient $\theta$ in step 5 is $O\left( {k_{2} nm^{2} } \right)$, where ${\text{k}}_{2}$ is the number of iterations of the ADMM algorithm. In summary, the computational complexity of WHCSC is $O\left( {ck_{1} \left( {n + k_{2} nm^{2} } \right)} \right)$ [26, 27]. After many experiments, $k_{1}$ and $k_{2}$ are usually less than 10.

5 Convergence and convergence rate analysis

Before proofing of convergence, the standard form of the ADMM objective function is given by formula (7) as follows

$$\hbox{min} \,f\left( \theta \right) + g\left( z \right) + l\left( \alpha \right)\quad {\text{s}} . {\text{t}}. \,z = w \odot \left( {\varvec{X}\theta - y} \right),\alpha = \theta , ,$$

(33)

where $f\left( \theta \right) = 0$, $l\left( \alpha \right) = \lambda \alpha_{1}$, $g\left( z \right) = \left\{ {\begin{array}{ll} {\frac{1}{2}||z||_{2}^{2} } \\ {\eta ||w \odot z||_{1} - \frac{1}{2}\eta^{2} w^{T} w} \\ \end{array} } \right. \begin{array}{*{20}c} {\left| {z_{k} } \right| \le \eta w_{k} } \\ {\left| {z_{k} } \right| > \eta w_{k} } \\ \end{array}$, $k = 1,2, \cdots m$. The following are two theorems about the function $f\left( \theta \right), g\left( z \right), l\left( \alpha \right)$.

Theorem 1

The function of $f\left( \theta \right), g\left( z \right), l\left( \alpha \right)$ is closed, proper, and convex.

Proof

Obviously, $f\left( \theta \right) = 0$ must be a closed, proper, and convex function. Since $\lambda > 0$, the norm satisfies the triangle inequality; $l\left( \alpha \right)$ is a proper closed convex function. The epigraph of $g\left( z \right)$ can be expressed as the following form, i.e.

$$epi g = \left\{ {\left( {z,t_{z} } \right) \in {\mathbf{R}}^{m} \times {\mathbf{R}}|g\left( z \right) \le t_{z} } \right\}.$$

(34)

Obviously the epigraph of $g\left( z \right)$ is a non-empty closed convex set. According to the nature of the epigraph, $g\left( z \right)$ is a proper closed convex function when $epi g$ is a non-empty closed convex function. The iterative step of ADMM algorithm is to solve the optimal solution of each sub-problem. Obviously, the optimal solution of sub-problems $\theta^{k + 1} , z^{k + 1} , \alpha^{k + 1}$ is feasible. The problem of minimizing $\theta^{k + 1} ,z^{k + 1} ,\alpha^{k + 1}$ has solution (not necessarily unique). Therefore, $f\left( \theta \right),g\left( z \right),l\left( \alpha \right)$ are proper closed convex functions, and $f\left( \theta \right) + g\left( z \right) + l\left( \alpha \right)$ is also a proper closed convex function. Certificate completed.

Theorem 2

The unaugmented Lagrangian

$${\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right) = g\left( z \right) + l\left( \alpha \right) + \langle h_{z} ,w \odot \left( {\varvec{X}\theta - y} \right) - z\rangle +\langle h_{\alpha } ,\theta - \alpha\rangle$$

(35)

has a saddle point. Explicitly, there exist$\left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right)$, not necessarily unique, for which

$${\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z} ,h_{\alpha } } \right) \le {\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right) \le {\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z}^{*} ,h_{\alpha }^{*} } \right)$$

(36)

holds for all$\theta ,z,\alpha ,h_{z} ,h_{\alpha }$.

Proof

The primitive problem is $\mathop {\hbox{min} }\nolimits_{\theta ,z,\alpha } \mathop {\sup }\nolimits_{{h_{z} ,h_{\alpha } }} {\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right)$, represented by $P^{l}$. The dual problem is $\mathop {\hbox{max} }\nolimits_{{h_{z} ,h_{\alpha } }} \mathop {\inf }\nolimits_{\theta ,z,\alpha } {\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right)$, represented by $D^{l}$. For ${\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right)$, since $f\left( \theta \right) + g\left( z \right) + l\left( \alpha \right)$ is a proper closed convex function, $w \odot \left( {\varvec{X}\theta - y} \right) - z = 0$ and $\theta - \alpha = 0$ is an affine function, and the existence points $\left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right)$ satisfy the Karush–Kuhn–Tucker (KKT) condition, so according to the strong and weak duality and optimality conditions of the Lagrange multiplier method [24], the following conclusions can be obtained:

The primitive problem $P^{l}$ is equal to the optimal value of the dual problem $D^{l}$, that is, ${\text{val}}\left( {P^{l} } \right) = {\text{val}}\left( {D^{l} } \right)$. The duality gap between the original problem and the dual problem is zero, which means that satisfies the strong max–min property, and $P^{l}$ and $D^{l}$ have the same optimal solution. Where ${\text{val}}\left( {\text{x}} \right)$ represents the value of ${\text{x}}$.

Any point $\left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right)$ that satisfies the KKT condition in ${\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right)$ has

$$\mathop {\inf }\limits_{\theta ,z,\alpha } {\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z}^{*} ,h_{\alpha }^{*} } \right) \le {\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right) \le \mathop {\sup }\limits_{{h_{z} ,h_{\alpha } }} {\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z} ,h_{\alpha } } \right),$$

(37)

i.e.

$${\text{val}}\left( {D^{l} } \right) \le {\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right) \le {\text{val}}\left( {P^{l} } \right).$$

(38)

When the duality gap between the primitive problem and the dual problem is zero, i.e. ${\text{val}}\left( {P^{l} } \right) = {\text{val}}\left( {D^{l} } \right)$, we can get

$${\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right) = \mathop {\inf }\limits_{\theta ,z,\alpha } {\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z}^{*} ,h_{\alpha }^{*} } \right) \le {\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z}^{*} ,h_{\alpha }^{*} } \right),\quad \forall \theta ,z,\alpha \in R^{n} .$$

(39)

The same reason can get

$${\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right) = \mathop {\sup }\limits_{{h_{z} ,h_{\alpha } }} {\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z} ,h_{\alpha } } \right) \ge {\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z} ,h_{\alpha } } \right),\quad \forall h_{z} ,h_{\alpha } \in R^{n} .$$

(40)

In summary

$${\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z} ,h_{\alpha } } \right) \le {\mathcal{L}}_{0} \left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right) \le {\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z}^{*} ,h_{\alpha }^{*} } \right),$$

(41)

that is, ${\mathcal{L}}_{0} \left( {\theta ,z,\alpha ,h_{z} ,h_{\alpha } } \right)$ has a saddle point $\left( {\theta^{*} ,z^{*} ,\alpha^{*} ,h_{z}^{*} ,h_{\alpha }^{*} } \right)$, not necessarily unique. The standard Lagrangian function of Eq. (33) satisfies theorem 2 as evidence.

According to Theorem 1 and Theorem 2, the ADMM iteration satisfies the following conditions, and the convergence of proof Ref. [13] Appendix A:

Residual convergence. $r^{k} \to 0$ as $k \to \infty$, i.e., the iterates approach feasibility.

Objective convergence. $\left( {\theta^{k} } \right) + g\left( {z^{k} } \right) + l\left( {\alpha^{k} } \right) \to f\left( {\theta^{*} } \right) + g\left( {z^{*} } \right)$ + $l\left( {\alpha^{*} } \right)$ as $k \to \infty$, i.e., the objective function of the iterates approaches the optimal value.

Dual variable convergence.$h_{z}^{k} \to h_{z}^{*}$, $h_{\alpha }^{k} \to h_{\alpha }^{*}$ as $k \to \infty$, where $\left( {h_{z}^{*} , h_{\alpha }^{*} } \right)$ is a dual optimal point.

We know that the convergence rate is another important concept, which reflects the convergence speed of an iterative algorithm. The authors of [25, 26] have shown that ADMM can achieve $O\left( {1/k} \right)$ global convergence, where k is the number of iterations, under a strong convexity assumption. Without this strong convexity assumption, the author of [27] gives the most general result of ADMM convergence speed. Their results only require that both objective-function terms are convex (not necessarily smooth). Since here $f\left( \theta \right)$, $g\left( z \right)$ and $l\left( \alpha \right)$ are both convex, using ADMM to solve SMLR problems can achieve $O\left( {1/k} \right)$ convergence.

6 Experiment

In this section, experiments will be conducted on several public face databases to demonstrate WHCSC performance.

6.1 Experimental settings

WHCSC is compared to existing related methods, including NMR, RSRC, Sparse Huber (SH), RCRC, IRGSC. For RSRC, parameter $p$ defaults to 1, and $\tau$ takes the best of (0, 1). In SH, the parameter $\eta$ defaults to 10. For WHCSC, the parameter $p$ defaults to 1 and $\tau$ get the best between (0,1). The parameter p in IRGSC defaults to 1, and it should be noted that formula 21 in the IRGSC has errors and should be changed to

$$\begin{array}{*{20}c} {\mathop {\hbox{min} }\limits_{s} \mathop \sum \limits_{i = 1}^{m} \left\{ {s_{i} e_{i}^{2} + \gamma s_{i}^{2} } \right\} = \mathop {\hbox{min} }\limits_{s} s + \frac{E}{2\gamma }_{2}^{2} } \\ {{\text{s}} . {\text{t}}. \quad s^{T} I = 1,s_{i} \ge 0,i = 1 \sim m.} \\ \end{array} ,$$

(42)

where $E = \left[ {e_{1}^{2} ,e_{2}^{2} , \cdots ,e_{m}^{2} } \right]$, and the authors in [28] also have the same opinion. This article sets comparative experiments according to the original IRGSC article.

In Sect. 3, we described how to reduce intra-class changes (classification model I and classification model II) and increase the variation between classes (1 power exponent weights and 0.5 power exponent weights). In Sect. 6, we use WHCSC, RSRC, RCRC and its improved algorithm to experimentally test the two methods, other unspecified algorithms in accordance with the original essay method to help contrast. The 1 power exponent weights and 0.5 power exponent weights are tested for WHCSC, respectively, to prove the validity of the 3.2.1 and 3.2.2 theory, and the corresponding names are WHCSC_1 and WHCSC_0.5. RSRC tests the classification model I and classification model II, respectively, and the corresponding names are RSRC_1 and RSRC_2. The RCRC also tests the classification model I and classification model II, respectively, corresponding to RCRC_1 and RCRC_2. SH uses classification model II.

6.2 Face recognition without occlusion

The performance in WHCSC was first tested by illumination changes without occlusion. Datasets use ExYaleB database and PIE database.

• 1. FR with different samples size: This section tests the validity of WHCSC under changing the training sample size. The data set was randomly divided into two parts, one of which contained n images for each person for training and the other for testing, where n = 10, 20, 30, 40, 50. The already-divided data is saved to ensure that the different algorithm training sets and test sets are the same, and the average recognition rate of the 10 runs is counted. PIE database recognition rate as shown in Table 1, ExYaleB database recognition rate in Table 2. We can observe that WHCSC achieves the highest recognition rate in all other tests of ExYaleB database and PIE database except RSRC_1 and RSRC_2 at sample size 10. When the sample is larger than 30, WHCSC_1 is marginally higher than WHCSC_0.5. Second, the classification rates of RSRC_2, RCRC_2, SH and so on are higher than that of RSRC_1, RCRC_1, and NMR. In addition, RSRC is better than RCRC in most cases, reflecting the validity of its weight vector. Overall, the WHCSC proposed in this paper achieved the best results.

  Table 1 PIE database recognition rates for different sample sizes of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, NMR (Unit: percentage)

  Table 2 ExYaleB database recognition rates for different sample sizes of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, NMR (Unit: percentage)

• 2. FR with different feature dimension: This section tests WHCSC performance under different feature dimension. For databases (ExYaleB and PIE), 20 samples per subject were randomly selected for training, the rest of the samples were used for testing. Saving the divided data to ensure that when the parameters are changed, the test data sets of different algorithms are the same, and the average recognition rate of 10 runs is counted. PCA is a recognized projection technique used to reduce the dimensions of the original face image [3]. From Tables 3 and 4, not all WHCSCs achieve the best recognition rate in the different dimensional character tests. All recognition rates for WHCSC_1 are better than WHCSC_0.5. The results of RCRC_2 and RSRC_2 in different feature dimensions are better than RCRC_1 and RSRC_1, respectively. In the test of different characteristic dimensions, not all algorithms reduce the recognition rate as the feature dimension decreases. For example, the recognition rate in the 200-dimension is mostly higher than the 150-dimensional and 250-dimensional. This is because after the PCA reduces the dimension, the feature tries to obtain a more meaningful low-dimensional representation, but in fact may lose the original dictionary information contained in the high-dimensional feature.

  Table 3 PIE database recognition rates for different feature dimension of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, NMR (Unit: percentage)

  Table 4 ExYaleB database recognition rates for different feature dimension of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, NMR (Unit: percentage)

6.3 Face recognition with occlusion

One of the advantages of WHCSC is its robustness in terms of occlusion and noise damage. On the one hand, the parameter $W\eta$ is used to evaluate g (z) meets $l_{2}$ loss or $l_{1}$ loss, thus reducing the influence of noise or outliers. On the other hand, classification model II and 1 power exponent weight make it easier to distinguish between different categories of faces by lowering intra-class different and increasing inter-class difference. In this section, we will evaluate the robustness of WHCSC to different types of occlusions, such as Gaussian noise random pixel corruption, random block occlusion, masquerading, and so on. The WHCSCs are compared to existing related methods, including NMR, RSRC, Sparse Huber (SH), RCRC, IRGSC, and both the RSRC and RCRC will test both classification modes. The robustness of RSRC is achieved by repeatedly assigning weights to the training samples through a sigmoid function with variable parameters. The robustness of RCRC is achieved by sparse coding constrained coding coefficients. The robustness of SH is achieved by using $l_{2}$ loss and $l_{1}$ loss in combination with coding residuals. NMR is a recently proposed matrix-based regression classification method, which not only retains the structural information of face images but also has good robustness. The IRGSC achieves robustness by adaptive feature weights and distance-weighted learning. The WHCSC robustness was tested by real complex occlusion experiments.

• 1. FR with pixel corrosion: This section uses the ExYaleB database, which has a total of 64 face images for each theme and can be divided into 5 subsets depending on the lighting conditions and face angle. Sample images of each subset are shown in Fig. 5, wherein subset 1 and subset 2 have good lighting conditions, subset 3 has medium lighting conditions, subset 4 has most poor lighting conditions, and subset 5 has poor lighting conditions. A total of 22 face images of our fixed-sampling sub-sets 1, 2, 3 and 5 were used for training, and the rest of the 4 subsets were used for testing. All images are cropped to 32 $\times$ 28 pixel size. For each test image, a fixed proportion of noise is added using random grayscale and random locations, i.e., Gaussian noise. The original image shown in Fig. 6 is a face image of 192 $\times$ 168 pixels with different pixel noise.

  Fig. 5

  

  From left to right, Sample subset 1 through subset 5 sample images, respectively

  Fig. 6

  

  Different percentage pixels damaged face images (from 0 to 70%)

As can be observed in Fig. 7, the WHCSC test results are superior to other algorithms for pixel etches at different scales. Second, the recognition rate of the algorithm using classification model II is much higher than that of the algorithm using classification model I. The recognition rate of WHCSC_1 was 0.23%, 1.39%, 1.15% and 4.27% higher than that of WHCSC_0.5 when the signal to noise ratio was equal to 40%. In addition, the recognition rates of RSRC_1 and RSRC_2 are mostly higher than those of RCRC_1 and RCRC_2, respectively, and most of IRGSCs are better than RSRC_1. This indirectly verifies the validity of the IRGSC and RSRC algorithms. In summary, pixel-corrupted face recognition once again validates the robustness and validity of WHCSC for outliers. And on the other hand, it also validated the noise-based advantages of the classification model II and 1 power exponent weight.

Fig. 7

Different pixel corrosion face recognition

• 2. FR with Block Occlusion: In this section, we design two block occlusion experiments. In the first experiment, we replaced 10–50% of each test image with white or black blocks. Half of the face images of the fixed subset 1, 2 and 3 were acquired for training and the rest of the 3 subsets were used for testing. The position of the occlusion box is random. Figure 8 shows a partially occluded facial image of the ExYaleB database with different block blocking ratios. Figure 9 shows the recognition rates of RSRC, RCRC, IRGSC, SH, NMR and WHCSC in different block occlusions. We can observe that WHCSC has the obvious advantage of having the highest recognition rate at different occlusion percentages. At occlusion percentages above 20%, the RCRC, SH, and NMR discrimination rates dropped significantly. The recognition rate of WHCSC was 86.76% when the shielding ratio of black block reached 50%, which was 7.12% higher than that of RSRC_2 and 22.85% higher than that of IRGSC. However, RCRC, SH, and NMR had failed at this time. Meanwhile, WHCSC_1 is 6.12% higher than WHCSC_0.5, and RSRC_2 is 26.16% higher than RSRC_1. WHCSC_1 has a 92.72% recognition rate when the white block occlusion ratio reaches 50%, which is 2.16% higher than RSRC_2 and 3.98% higher than IRGSC. Meanwhile, RSRC_2 is 28.47% more than RSRC_1. However, RCRC, SH, NMR still failed. WHCSC_1 has the best occlusion ratio except 0.16% lower than WHCSC_0.5 at 50% occlusion percentage.

  Fig. 8

  

  a Face image of a black block occlusion, b face image of a white block occlusion

  Fig. 9

  

  a Face recognition rate of black block occlusion, and b face recognition rate of white block occlusion

In the second experiment, the classic Lena diagram was used as the occlusion element to replace 10–50% pixel of each test image. Figure 10 shows the test image samples. We can see that the pixels in the occlusion area are close to the original pixels relative to the first two experiments. Figure 11 shows the recognition rates of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH and NMR at 10–50% block occlusion. It can be observed that the overall recognition rate is increasing, and WHCSC still maintains the highest recognition rate. Surprisingly, RCRC_2 and SH showed a good recognition rate. On the one hand, it is easier to train a linear combination of images because of the occlusion area close to the original pixel. On the other hand, we further prove the good effect of WHCSC weight on image local optimization.

Fig. 10

The face image with Lina block occlusion

Fig. 11

The face recognition rate with Lina block occlusion

• 3. Real camouflage face recognition: The experiment in this section uses AR database, using the first three of each face subset 1 and subset 2, a total of six as a training image. Six pieces of camouflage images in Subset 1 and Subset 2 and 6 pieces of scarf camouflage images were taken as test images, respectively. The image is adjusted to $33 \times 24$ pixels. Table 5 shows the test results of several classifiers, WHCSC shows better results than RSRC, RCRC, IRGSC, SH, NMR. The performance of RCRC is unstable because of scarf camouflage masks effective pixels of more people, making RCRC vulnerable to interference when the image information is limited. IRGSC performs well and further reflects the effect of weight coefficient on local image optimization.

  Table 5 Recognition rate (unit: percentage) of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, NMR in sunglasses camouflage and scarf camouflage

6.4 Image reconstruction

Reconstructed block occlusion and real camouflage fitted images, and observe the reconstructed image of each algorithm. In this section, the training set uses a frontal, non-occluded image, and the test set uses an occlusion image. In algorithms with weights coefficients such as WHCSC, RSRC, IRGSC, the reconstructed image is represented as $w \odot X\theta$, and the corresponding test set image is represented as $w \odot y$. In algorithms without weights coefficients such as RCRC, SH, NMR, the reconstructed image is represented as $X\theta$, and the corresponding test set image is represented as $y$. The noise in the pixel-corroded image is randomly distributed, and the reconstructed image is not easy to observe, so no experiment is set.

Figure 12 is an image reconstruction of block occlusion. Looking at (f) and (g) of Fig. 12, because of a black occlusion block in the test set, these algorithms without weights coefficients in the reconstructed image, such as RCRC, SH and NMR, cannot generate an area similar to a black occlusion block. The reconstructed image of RSRC_1 has begun to corrode other normal image areas in a large amount when the black block has not been completely fitted. WHCSC_1, WHCSC_0.5, RSRC_2 and IRGSC can all fit the black occlusion block well. A closer look reveals that the forehead of the test image has subtle color differences due to different illumination angles. When the black occlusion block is completely fitted, RSRC_2 has obvious noise corrosion in the forehead area of the face. WHCSC_0.5 and IRGSC have slight noise corrosion, and WHCSC_1 is almost none. The (h) of Fig. 12 shows that as the parameter $\tau$ decreases, the residual threshold $\eta$ is smaller and the weights constraint is stronger. When τ is equal to 0.9, 0.8, 0.7 and 0.6, the reconstructed image does not completely fit the black block area; and when $\tau$ is 0.5, the $\eta$ that is too small causes the weight to over-constrain the residual, thus causing corrosion of the pixels outside the black block area. When τ is 0.58, the reconstructed image completely fits the black block area, and almost no other pixel points are corroded. In addition, $\tau = 0.58$ indicates that 42% of the pixels are considered to have larger residuals, slightly larger than the test set by 40%. Because the real image itself has noise generated by other factors, it is in line with theory and practice to reconstruct the image to obtain the optimal performance at $\tau = 0.58$ summary, in a complex noisy environment, the parameter q can make the weight coefficient smoother, and the value of the parameter $\tau$ can be easily determined by the actual number of residuals, which continues to show the superiority of the WHCSC.

Fig. 12

Reconstructed image of a 40% black block occluded face. From a–d are training sets. e Test sets. In f, reconstructed images of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, and NMR are shown from left to right. (g) shows a comparison of test sets of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, and NMR from left to right. h Reconstructed image of WHCSC_1 when the parameter τ is equal to 0.9, 0.8, 0.7, 0.6, 0.58, and 0.5, respectively

Figure 13 is the image reconstruction of the sunglasses camouflage. Looking at (h) and (i) of Fig. 13, since there is a sunglasses camouflage in the test sets, the algorithms with no weights cannot generate a region similar to the sunglasses in the reconstructed image, such as RCRC, SH and NMR. The reconstructed image of RSRC_1 has only a faint sunglasses frame, and the entire image is cluttered with noise. This indicates that in the noisy environment, the classification model I does not distinguish between noise and real images very well. Although IRGSC fits the sunglasses camouflage, its weights coefficient is not accurate enough for the boundary of the character’s outline and expression.

Fig. 13

Face reconstruction image with sunglasses camouflage. From a–f is a training sets for sunglasses camouflage. g Test sets for sunglasses camouflage. Reconstructed images of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH, and NMR are shown from left to right in h. In i, a comparison images of test sets of WHCSC_1, WHCSC_0.5, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH and NMR are shown from left to right

Compared with the corresponding test set comparison chart, the reconstructed images of WHCSC_1, WHCSC_0.5 and RSRC_2 have almost no difference, and they can reconstruct the characteristics of the test image very well. On the one hand, the reconstructed image fits the shape and gloss of the sunglasses. For the test set, the white area on the sunglasses belongs to the image point with large residuals, and its pixel value approaches zero under the weight coefficient, that is, it is black in the gray image. On the other hand, the reconstructed image weakens the facial expression influences brought about by (b) in Fig. 13.

6.5 Running time

Running time is one of the important reference indexes for judging classifier. Five robust classifiers, such as WHCSC, RSRC, RCRC, IRGSC, and SH, were run on the same computer with noise and real disguise. Algorithms involving $l_{1}$ norm minimization are all solved by ADMM. Table 6 lists the average run times for the 10 runs of the 5 classifiers. The IRGSC takes the longest time due to the additional computation of adaptive feature weights and adaptive distance weights, and its recognition rate is medium and stable; SH takes the least time, but the recognition rate is low; WHCSC_1 is less and the recognition rate is the highest and stable. Influenced by the experimental samples, the computational cost of classification model II has no obvious advantage. In summary, WHCSC sacrificed a small amount of computational cost and achieved the highest recognition rate.

Table 6 Run-time tests such as WHCSC_1, RSRC_1, RSRC_2, RCRC_1, RCRC_2, IRGSC, SH. Unit: second

6.6 The impact of parameters on the recognition rate

Parameter changes are another important reference indicator for judging classifiers. WHCSC has two important parameters, such as τ and q mentioned earlier. The position of the threshold residual in the residual sequence $\varPsi$ is determined by k = ⌊τm⌋; and the penalty rate of the weight is affected by q.

(a) and (c) of Fig. 14 show the fixed parameter τ, and the change in the recognition rate when the parameter q is changed. As q decreases, the recognition rate shows an upward trend overall. (b) and (d) of Fig. 14 show the change of the recognition rate when the parameter q is fixed and the parameter τ is changed. As τ increases, the recognition rate shows an upward trend overall. (e) and (f) of Fig. 14 show some of the characteristics of the sigmoid function. When the parameter x changes to $\frac{\text{x}}{2}$, the sigmoid function image is smoother. Therefore, when the parameter q becomes small, the degree of weights penalty can be reduced, so that the value of the weights change trend is smoother in the same iteration. (g) and (h) of Fig. 14 show residual distribution maps of face images of 896 size. It can be observed that only a small number of face images have large residuals. Therefore, when the parameter τ is increased, more image points can be obtained to obtain higher weights. In combination with the complex environment of the face image, when the noise is enhanced, the image points with large residuals will also increase, and the value of τ should be lowered. Conversely, the value of τ can be increased. The parameter q is usually small.

Fig. 14

a Recognition rate of the different parameters q in the case of 50% Gaussian noise. b Recognition rate of different parameters τ in the case of 50% Gaussian noise. c Recognition rate of the different parameters q in the case of 70% Gaussian noise. d Recognition rate of different parameters τ in the case of 70% Gaussian noise. e Schematic diagram of ${\text{sigmoid}} = \frac{1}{{1 + { \exp }\left( x \right)}}$. f Schematic diagram of ${\text{sigmoid}} = \frac{1}{{1 + { \exp }\left( {x/2} \right)}}$. g Residual distribution map of 50% Gaussian noise. h Residual distribution map of 70% Gaussian noise

7 Conclusion

In this paper, we propose a newly weighted Huber constrained sparse coding, and propose an effective optimization method to enhance the effect of weights. The benefits of WHCSC are reflected in the robustness and effectiveness of the occluded complex environment. On the one hand, the weight constraint can effectively find the noise pixels in the query sample and reduce the weight of the noise pixels at the time of regression, which achieves the local optimization. On the other hand, we use Huber’s estimation to choose different fidelity terms ($l_{1}$ or $l_{2}$ norm) to further accurately return the query samples. Secondly, the use of classification mode II can avoid the interference caused by other types of images when the current category is regressed. Finally, increasing the variability between classes through 1 power exponent weight makes it easier to classify. WHCSC is suitable for complex changes of PCA, illumination, corrosion, and occlusion. Experiments show that WHCSC is superior to IRGSC, RSRC, SRC, NMR and so on, and it is smoother and more accurate for noise processing. Its high robustness and strong effectiveness are the ideal choices in face recognition applications.