Robust Face Recognition Based on Supervised Sparse Representation

Abstract

Sparse representation-based classification (SRC) has become a popular methodology in face recognition in recent years. One widely used manner is to enforce minimum $l_{ 1}$-norm on coding coefficient vector, which requires high computational cost. On the other hand, supervised sparse representation-based method (SSR) realizes sparse representation classification with higher efficiency by representing a probe using multiple phases. Nevertheless, since previous SSR methods only deal with Gaussian noise, they cannot satisfy empirical robust face recognition application. In this paper, we propose a robust supervised sparse representation (RSSR) model, which uses a two-phase scheme of robust representation to compute a sparse coding vector. To solve the model of RSSR efficiently, an algorithm based on iterative reweighting is proposed. We compare the RSSR with other state-of-the-art methods and the experimental results demonstrate that RSSR obtains competitive performance.

1 Introduction

In recent years, face recognition (FR) has been studied for its broad application prospects, such as authentication and payment system. The primary task of FR consists of feature extraction and classification. Various changes including lighting, expression, pose, and occlusion can be seen in probes, which leads to that the computed feature becomes inefficient. Although facial images contain some redundant information, it is not easy to utilize the redundancy that retains discriminative information when the probe is interfered by variations. In this case, the key of a FR system is to develop a classifier making use of the most discriminative information in a probe even though containing variations and corruption.

To this end, methods based on linear regression (LR) are proposed recently, which show promising results in FR [1]. The basic assumption behind the methods is that a probe can be linearly represented by training samples from the same class of the probe. The decision of classification is in favor of the prediction which has minimum match residual. There are two typical approaches to achieve sparse representation of a probe. First, the unsupervised sparse representation(USR) incorporates collaborative representation and sparse representation together into a single optimization and the sparsity of the solution is guaranteed automatically. Inspired by theory of compressed sensing, USR formulizes sparse representation as the following optimization problem:

$$ {\mathbf{x}}^{*} = \arg \hbox{min} \,g({\mathbf{e}}) + \lambda \left\| {\mathbf{x}} \right\|_{1} $$

(1)

where ${\mathbf{e}} = {\mathbf{y}} - {\mathbf{Ax}} = [e_{1} ,e_{2} , \cdots ,e_{m} ]$ called the residual vector, and $g( \cdot )$ is an error function which uses the squared loss $\left\| \cdot \right\|_{2}$, and $\lambda$ is a small positive constant balancing between the loss function and the regularization term, which is called Lasso regression. The second approach is the SSR which uses collaborative representation itself to supervise the sparsity of representation vector with $l_{2}$-norm to regularize representation vector:

$$ {\mathbf{x}}^{*} = \arg \hbox{min} \left\| {\mathbf{e}} \right\|_{2} + \lambda \left\| {\mathbf{x}} \right\|_{ 2} $$

(2)

In this way, the solution can be computed with much lower time cost than $l_{1}$-norm based regression model, which uses a two-phase representation scheme to recognize a probe. A representative method of this kind is TPTSR [2].

In this paper, we propose a robust supervised sparse representation (RSSR) method for FR in which the Huber loss is used as fidelity term since it is superior to squared loss, when there are large outliers. To implement supervised sparse representation, the RSSR uses two-phase representation scheme. We solve the linear regression model of the RSSR by using the iteratively reweighted least squares minimization. The computational cost to recognize a probe is satisfactory.

In Sect. 2, we present the RSSR model and the classification algorithm. In Sect. 3, we validate and compare the RSSR with other related state-of-the-art methods on a public available face database.

2 Robust Coding Based Supervised Sparse Representation

2.1 Robust Regression Based on Huber Loss

In a practice, face recognition system has to deal with images contaminated with occlusion and corruption. Since a portion of pixels of the probe image is randomly distorted, the distribution of the residual ${\mathbf{e}}$ becomes heavy tailed. Commonly used loss functions which are less sensitive to outliers involve the absolute value function. Here we choose Huber loss which is defined as:

$$ \text{g} (e) = \left\{ {\begin{array}{*{20}c} {\tfrac{1}{2}e^{2} } & {{\text{if}} \;|e| \le k} \\ {k|e| - \tfrac{1}{2}k^{2} } & { {\text{if}}\; |e| > k} \\ \end{array} } \right. $$

(3)

where $k$ is a constant. As defined, Huber loss is a parabola in the vicinity of zero and increases linearly above a given level $|e| > k$. Therefore, in the paper we develop a linear representation-based FR method using Huber loss as the representation residual measure function $G({\mathbf{e}}) = \sum\nolimits_{\text{i}}^{{}} {\text{g} (e_{i} )}$ where $e_{i} = y_{i} - d_{i} {\mathbf{x}}$, $y_{i} \in {\mathbf{y}}$ and $d_{i}$ is the $i$ th row of matrix ${\mathbf{A}}$. Here, we denote the first order derivative function of the Huber loss as ${\psi (}p{) = }{{d\text{g} {(}p{)}} \mathord{\left/ {\vphantom {{d\text{g} {(}p{)}} {dp}}} \right. \kern-0pt} {dp}}$ called the influence function which describes the extent that how error affects the cost function. Next, we use the weight function $\upomega(p) = {{{\psi (}p{)}} \mathord{\left/ {\vphantom {{{\psi (}p{)}} p}} \right. \kern-0pt} p}$ which assigns a specific weight to a certain pixel. The weight function of Huber loss is piecewise function that $\upomega(e_{i} )\;{ = }\;1$ when $|e_{i} | \le k$ and $\upomega(e_{i} ) =$ ${1 \mathord{\left/ {\vphantom {1 {|e_{i} |}}} \right. \kern-0pt} {|e_{i} |}}$ when $|e_{i} |\; > \;k$. It is easy to see that if a pixel has a bigger value of residual (i.e. $|e_{i} |\; > \;k$) it will be assigned with a smaller weight (i.e. ${ 1\mathord{\left/ {\vphantom { 1{|e_{i} |}}} \right. \kern-0pt} {|e_{i} |}}$).

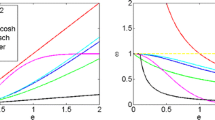
Although Huber loss and the $l_{1}$-norm fidelity employ a similar weighting function to lower the influence of outliers in a probe, their weighting functions still have large difference which is shown in Fig. 1. One can see that the assigned weight by the $l_{1}$-norm fidelity can be infinity when the residual approaches to zero, making the coding unstable. However, Huber loss views small residuals as thermal noises, and its weighting strategy is same as the $l_{2}$-norm fidelity, i.e. $\upomega(e_{i} ) = 1$.

Fig. 1.

Weight functions of the $l_{1}$-norm VS. Huber loss.

Huber loss is able to be transformed to the regression form of iterated reweighted-least-squares as:

$$ \hbox{min} \sum\nolimits_{\text{i}}^{{}} {w_{ii} e_{i}^{2} } $$

(4)

where $w_{ii}$ is the weight of the $i$ th pixel in ${\bar{\mathbf{y}}}$.

2.2 The Proposed Model

Our RSSR needs a two-phase representation of a probe. In the first phase, a probe is represented collaboratively and the corresponding coding vector is computed by solving the following problem:

$$ {\mathbf{x}} = \arg \mathop {\hbox{min} }\limits_{{\mathbf{x}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} G({\mathbf{y}} - {\mathbf{Ax}}) + {{\lambda \left\| {\mathbf{x}} \right\|_{2}^{2} } \mathord{\left/ {\vphantom {{\lambda \left\| {\mathbf{x}} \right\|_{2}^{2} } 2}} \right. \kern-0pt} 2} $$

(5)

where $\lambda$ is a balance parameter. Since the Huber loss is a piecewise function, we need to transform Eq. (5) so as to facilitate the computation. First of all, we define a sign vector ${\mathbf{s}} = [s_{1} ,s_{2} , \cdots ,s_{j} , \cdots ,s_{m} ]^{T}$ where $s_{j} = { - }1$ if $e_{j} < - k$, $s_{j} = 0$ if $|e_{j} | \le k$, and $s_{j} = { - }1$ if $e_{j} > k$ and define a diagonal matrix ${\mathbf{W}} \in {\mathbb{R}}^{m \times m}$ with diagonal elements $w_{jj} = 1 - s_{j}^{2}$. Now, by introducing ${\mathbf{W}}$ and ${\mathbf{s}}$, $G({\mathbf{e}})$ can be rewritten as

$$ G({\mathbf{e}},{\mathbf{s}},{\mathbf{W}}) = \tfrac{1}{2}\,{\mathbf{e}}^{\text{T} } {\mathbf{We}} + k{\mathbf{s}}^{\text{T} } ({\mathbf{e}} - \tfrac{1}{2}k{\mathbf{s}}) $$

(6)

If all residuals are smaller than $k$, the second term of the right side of Eq. (6) will disappear and the fidelity term degrades to quadratic function. Actually, in Eq. (6), the entries of ${\mathbf{s}}$ can be considered as the indicator for large residuals, and which divide the residuals into two groups, i.e., the small residuals and the large ones. By substituting the fidelity term of Eq. (5) with Eq. (6), the optimization function now is reformed as

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }} = \arg \mathop {\hbox{min} }\limits_{{\mathbf{x}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tfrac{1}{2}\,{\mathbf{e}}^{\text{T} } {\mathbf{We}} + k{\mathbf{s}}^{\text{T} } ({\mathbf{e}} - \tfrac{1}{2}k{\mathbf{s}}) + \tfrac{\lambda }{2}\left\| {\mathbf{x}} \right\|_{2}^{2} $$

(7)

where ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}$ is estimated coding vector. By selection scheme used in TPTSR, $M$ per cent training samples are retained in the next phase. In the second phase, the test sample is represented anew over the rest samples. Furthermore, since the second phase of representation involves less gallery samples, noises in the test sample are less likely to be compensated. It is beneficial for Huber loss to find polluted pixels. Moreover, the final Huber loss ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}^{'} \in {\mathbb{R}}^{M}$ of the coding vector can be obtained by Eq. (7) again.

2.3 Algorithm of RSSR

The Eq. (7) does not have a close form solution. Here, we present an iterative solution. First, we assume ${\mathbf{s}}$ and ${\mathbf{W}}$ are known and take a derivative with respective to ${\mathbf{x}}$:

$$ {\mathbf{A}}^{T} {\mathbf{WAx}} - {\mathbf{A}}^{T} {\mathbf{Wy}} + k{\mathbf{A}}^{T} {\mathbf{s}} + \lambda {\mathbf{x}} = 0 $$

(8)

The coding vector is obtained by:

$$ {\mathbf{x}} = ({\mathbf{A}}^{T} {\mathbf{WA}} + \lambda {\mathbf{I}})^{ - 1} ({\mathbf{A}}^{T} {\mathbf{Wy}} - k{\mathbf{A}}^{T} {\mathbf{s}}) $$

(9)

where ${\mathbf{I}}$ is an identity matrix. Then, we compute ${\mathbf{s}}$ and ${\mathbf{W}}$ respectively. And the formula of updating ${\mathbf{x}}$ in the $t$-th iteration is

$$ {\mathbf{x}}^{t} = {\mathbf{x}}^{t - 1} + u^{t} \text{h} ({\mathbf{W}}^{t} ,{\mathbf{s}}^{t} ) $$

(10)

where $h({\mathbf{W}}^{t} ,{\mathbf{s}}^{t} ) = ({\mathbf{A}}^{T} {\mathbf{W}}^{t} {\mathbf{A}} + \lambda {\mathbf{I}})^{ - 1} ({\mathbf{A}}^{T} {\mathbf{W}}^{t} {\mathbf{y}} - k{\mathbf{A}}^{T} {\mathbf{s}}^{t} ) - {\mathbf{x}}^{t - 1}$, and $0 < u^{t} \le 1$ which is a step size that makes the loss value of the $t$-th iteration lower than that of the last. In this paper, $u^{t}$ is determined via the golden section search if $t > 1$ ($u^{1} = 1$). Following the representation scheme of SSR, we will use the above algorithm twice.

After converge of computing the coding vector of a testing sample, we use a typical rule of collaborative representation to make the final decision:

$$ indentity({\mathbf{y}}) = { \arg }\mathop { \hbox{min} }\limits_{c} \,d_{c} $$

(11)

where $d_{c} = {{G({\mathbf{y}} - {\tilde{\mathbf{A}}}_{c} {\hat{\mathbf{x}}}_{c} ,{\hat{\mathbf{s}}},{\hat{\mathbf{W}}})} \mathord{\left/ {\vphantom {{G({\mathbf{y}} - {\tilde{\mathbf{A}}}_{c} {\hat{\mathbf{x}}}_{c} ,{\hat{\mathbf{s}}},{\hat{\mathbf{W}}})} {\left\| {{\hat{\mathbf{x}}}_{c} } \right\|}}} \right. \kern-0pt} {\left\| {{\hat{\mathbf{x}}}_{c} } \right\|}}_{2}$ (${\tilde{\mathbf{A}}}_{c}$ is a sub-dictionary that contains samples of class $c$, and ${\mathbf{x}}_{c}$ is the associated coding vector of class $c$).

3 Experiment Results

In this section, we compare RSSR with nine state-of-the-art methods, including ESRC [1, 3], CESR [4], RRC1, RRC2 [5], CRC [6], LRC [7], TPTSR (for TPTSR the candidate set is set to 10 percent of training set), NMR [8], and ProCRC [9]. In the following experiments, for the three parameters in RSSR, the value of $k$, $M$, and $\lambda$ are set to 0.001, 10%, and 0.001 respectively.

In the experiments, we verified the robustness of RSSR against to two typical facial image contaminations, namely random pixel corruption and random block occlusion.

FR with Pixel Corruption.

As in [5], we tested the performance of RSSR in FR with random pixel corruption on the Extended Yale B face database. We used only samples from subset 1 as training sample, and testing samples were from subset 3. On each testing image, a certain percentage of randomly selected pixels were replaced by corruption pixels whose values were uniformly chosen from 0 or twice as the biggest pixel value of the testing image.

In Fig. 2 the recognition rates versus different percentages of corrupted pixels are plotted. The performance of CESR under illumination conditions is the lowest when the corruption is not serious, but it drops very late, which shows its good robustness but poor accuracy. For our RSSR, the curve of recognition rate keeps straight at 100% correct rate and only starts to bend until 70% pixels are corrupted which indicates the best robustness of RSSR among all the compared methods.

Fig. 2.

The comparison of robustness of several algorithms against random pixel corruptions.

FR with Block Occlusion.

To compare RSSR with other methods, we plotted, in Fig. 3, the recognition rates versus sizes of the occlusion from 0% to 50%. With increase of size of the occlusion, the recognition rates of LRC, CRC and TPTSR decreased sharply, while the recognition rates of RRC1, RRC2, ESRC, and RSSR maintained 100% up to 20% occlusion. From 30% to 50%, occlusion the recognition rates of RSSR, RRC1, NMR and RRC2 preform more stable than ESRC.

Fig. 3.

Recognition rates under different sizes of block occlusion

4 Conclusions

A novel robust coding-based model, RSSR, is proposed for robust face recognition in this paper. RSSR uses a two-phase collaborative representation to implement supervised sparse representation. As to tolerate possible variations on probe images, we use Huber loss as fidelity term in cost function which reserves the more samples of correct class into the candidate set for the latter representation. Moreover, to solve the RSSR regression function we introduce two variables which can simplify the object function of RSSR in the process of optimization. As shown in experiments, we compare RSSR classification method with the other state-of-the-art methods under corruptions and occlusions. The performance of RSSR always ranks in the forefront of different comparisons and especially RSSR surpasses TPTSR, the original supervised sparse method, in all cases.