1 Introduction

Nowadays, with the development of computer science and technology, information era is coming. As the emergence of big data and cloud computing, it brought a large number of high-dimensional data [1]. For various reasons, it is sometimes difficult to obtain a lot of data, and you will also encounter the problem of dimensional disaster when processing data [2]. In order to alleviate these problems, the typical data preprocessing method-feature selection has received more and more attention. Preprocessing the data through feature selection can improve the data quality [3], reduce the data dimension, and make the data mining algorithm achieve better results. Therefore, it is very necessary for a large number of high-dimensional data to find a subset that can represent the original data features well [4,5,6].

Feature selection includes linear feature selection and nonlinear feature selection. Linear feature selection represents a linear relationship between data, and then finds a subset that represents the original features  [7]. In practical applications, data features may contain strong relationships [8, 9]. However, in low-dimensional space, these relationships are nonlinear and then lead to difficulties in mining, resulting in insufficient excavation. There are many previous feature selection algorithms [10,11,12], but they usually cannot represent the nonlinear relationship between data [13, 14]. For this reason, this paper first proposes a nonlinear feature selection with the kernel method. Specifically, this paper uses the kernel function to map each feature of the data to the high-dimensional space, so that the nonlinear relationship between them is linearly separable in the high-dimensional space. It considers the global information of the data (low-rank constraint) and the nonlinear relationship (through Gaussian kernel) for feature selection. A better feature selection algorithm is proposed, which is called the Unsupervised Nonlinear Feature Selection Algorithm via Kernel Function (KF_NFS).

Firstly, this paper processes the original data to obtain the kernel matrix by kernel function, which solves the limitation that can only perform linear feature selection. Secondly, in order to achieve the best feature selection model, we use original data itself to fit it. The kernel coefficient matrix is performed different sparsity of degree (using \({\ell _{2,p}}\)-norm) and low-rank constraint (removing noise samples). Finally, a \({l_1}\)-norm of vector is embedded to perform nonlinear feature selection. Because this algorithm considers the nonlinear relationship and global information of the data, it is better than the general linear feature selection method. The final result of the experiment shows that the feature selected by this algorithm can achieve better results in classification accuracy.

Our algorithm has the following advantages:

  • No matter whether it is high-dimensional data or low-dimensional data, the Gaussian kernel function [i.e., \(k({x_i},{x_j}) = \exp ( - \frac{{\left\| {{x_i} - {x_j}} \right\| _2^2}}{{2{\sigma ^2}}})\)] is suitable. By adjusting its width \(\sigma\), it can be found that it is usually better and more applicable than other kernel functions such as the linear kernel. At the same time, each feature of the data is mapped into a kernel matrix, so that the relationship between the features can be mined more thoroughly.

  • Because the algorithm has a low-rank constraint on the kernel coefficient matrix and a nonlinear relationship between the features in the high-dimensional space, the unimportant features and noise samples are effectively removed, and the algorithm accuracy is improved. At the same time, we add a \({\ell _{2,p}}\)-norm sparse regularization factor to the algorithm. By adjusting the value of p, we can remove unrelated features well.

  • The objective function of this paper is optimized by the method of accelerated proximal gradient descent. The optimization algorithm is an accelerated gradient descent algorithm, which is much lower in time complexity than the general gradient descent algorithm. Our algorithm can quickly converge through it. At the same time, it can ensure that the objective function gradually decreases during each iterative solution process. Finally it obtains the optimal solution.

2 Related work

The kernel function was introduced into the field of machine learning long ago. It has promoted the development of SVM to some extent [15]. It was initially proposed to avoid the computational obstacles in high-dimensional data. There are many commonly used kernel functions. Since the gaussian kernel can implement a nonlinear mapping, and it has less parameters than a polynomial kernel, we use the Gaussian kernel in this paper.

Unsupervised learning was proposed early. With the development of unsupervised learning, it was applied to various fields in machine learning. It is also widely used in feature selection algorithms. For example, Shao et al. [16] proposed that online unsupervised multi-view feature selection. It improves feature selection by combining feature of different views while using consistency and complementarity. Shi et al. [17] proposed a robust spectral learning for unsupervised feature selection. The feature selection algorithm is made more stable by constructing the Laplacian matrix of the graph with local learning. In addition, the method of retaining similar data points is better than different data points; Wei et al. [18] proposed a unsupervised feature selection by preserving stochastic neighbors.

Semi-supervised learning has also been applied to feature selection algorithms, such as Chang et al. [19] proposed a convex formulation for semi-supervised multi-label feature selection. This algorithm is different from the traditional semi-supervised algorithm. By limiting the training sample tags, the algorithm can select more representative features and reduce the computational complexity. Jian et al. [20] proposed multi-label informed feature selection; the algorithm uses the tag’s relevance to select partitioning features and guides feature selection by decomposing multiple tag information into a low-dimensional space. Feature selection based on global structure and local structure of data is a very novel method. For example, Liu et al. [21] proposed global and local structure preservation for feature selection. Another feature selection algorithm implements embedding learning and sparse regression at the same time, so that the effect is very obvious. For example, Hou et al. [22] proposed joint embedding learning and sparse regression—a framework for unsupervised feature selection. It combines embedded learning and sparse regression to work together.

In 1998, nonlinear feature selection had been proposed [23], which presents multiple techniques such as multidimensional scaling and Sammonia mapping in the same framework. But it does not use the kernel function for nonlinear learning, and the effect is not the best. Min et al. [24] proposed a deep nonlinear feature mapping for large-margin KNN classification. This method uses the nonlinear mapping to improve the traditional KNN algorithm and achieves good results. This explains the value of nonlinear research to a certain extent. Jawanpuria et al. [25] proposed on p-norm path following multiple kernel learning for nonlinear feature selection. This method uses the p-norm to reduce the cost of optimization, compared to other path-based algorithms, which reduces training time. We have also consulted a lot of literature, and we will not list them here. The study of nonlinear learning has been around for a while; its research and development have great significance.

3 Our method

In this section, we first introduce the symbols used in this article and then explain our proposed KF_NFS algorithm, in Sects. 3.1 and 3.2, respectively, and then elaborate the proposed optimization method in Sect. 3.3. Finally, we analyze the convergence of the objective function in Sect. 3.4.

3.1 Notations

For the data matrix \({\mathbf{X}} \in {\mathbb {R}^{n \times d}}\), the i-th row and the j-th column are denoted as \({\mathbf{X}^i}\) and \({{{\mathbf{X}}}_j}\) respectively, and the elements of the i-th row and the j-th column are denoted as \({x_{i,j}}\). The trace of the matrix \({\mathbf{X}}\) is denoted by \(tr({\mathbf{X}})\), \({\mathbf{X}^{\mathrm{T}}}\) denotes the transpose of the matrix \({\mathbf{X}}\), and \({\mathbf{X}^{ - 1}}\) represents the inverse of the matrix \({\mathbf{X}}\). We denote the \({l_{2,p}}\)-norm of a matrix \({\mathbf{X}}\) and \({l_1}\)-norm of a vector as \({\Vert {\mathbf{X}} \Vert _1} = \sum \nolimits _{j = 1}^d {| {x_j}|}\), \({\Vert {\mathbf {X}} \Vert _{2,p}} = {[ {\sum \nolimits _{i = 1}^n {{{({{\sum \nolimits _{j = 1}^d {| {{X_{ij}}} |} }^2})}^{p/2}}} }]^{1/p}}\).

3.2 KF_NFS algorithm

Assume a given sample data set \({\mathbf{X}} \in {\mathbb {R}^{n \times d}}\), where n and d represent the number of samples and the number of features, respectively. Here we divide the d-dimensional data matrix into d matrices, each of which is a matrix \({\mathbf{X}}_i \in {\mathbb {R}^{n \times 1}},i = 1,\ldots ,d\). Then each element of \({\mathbf{X}}_i\) is treated as an independent sample or feature \({x_{ij}} \in \mathbb {R},j = 1,\ldots ,n\). \({\mathbf{X}}_i\) is converted into the kernel matrix \({\mathbf{K}}^{(i)} \in {\mathbb {R}^{n \times n}}\) by projecting it into the heat kernel space:

$$\begin{aligned} {\mathbf{K}}^{(i)} = {\begin{array}{c} {k({x_{i1}},{x_{i1}})}{k({x_{i1}},{x_{i2}})} \ldots {k({x_{i1}},{x_{in}})}\\ {k({x_{i2}},{x_{i1}})}{k({x_{i2}},{x_{i2}})} \ldots {k({x_{i2}},{x_{in}})}\\ \ldots \ldots \ldots \ldots \\ {k({x_{in}},{x_{i1}})}{k({x_{in}},{x_{i2}})} \ldots {k({x_{in}},{x_{in}})} \end{array}} \end{aligned}$$
(1)

The unsupervised feature selection algorithm aims to mine more representative features in the data, thus paving the way for the next experiment. In the absence of the class label \({\mathbf{Y}}\), using the data matrix \({\mathbf{X}}\) as a response matrix can better preserve the internal structure of the data’s original features [26]. Since there is a linear relationship between features and features, there is also a nonlinear relationship. Therefore, the algorithm first converts the data matrix \({\mathbf{X}}\) into d kernel matrices \({\mathbf{K}}^{(i)},i = 1,\ldots ,d\) through a Gaussian kernel function. In order to fully exploit the nonlinear relationship between features, get the following formula:

$$\begin{aligned} {\mathbf{X}} = \sum \limits _{i = 1}^d {{\alpha _i}\mathbf{K}^{(i)}} {\mathbf{W}} \end{aligned}$$
(2)

where: \({{\mathbf{W}}} \in {\mathbb {R}^{n \times d}}\) denotes the kernel coefficient matrix, \({\varvec{\alpha }} \in {\mathbb {R}^{d \times 1}}\) is used to perform feature selection and is equivalent to the feature weight vector; \({\alpha _i}\) corresponds to an element of the vector \(\varvec{\alpha }\), \({{\mathbf{K}}^{\left( i \right) }} \in {\mathbb {R}^{n \times n}}\) is the kernel matrix. In order to make \({\mathbf{X}}\) get a better fitting effect, people usually use the \({l_F}\)-norm to detect residuals, and minimizing the residuals can better fit the data, that is:

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha } ,{\mathbf{W}}} \left\| {\mathbf{X} - \sum \limits _{i = 1}^d {{\alpha _i}{\mathbf{K}}^{(i)}}{\mathbf{W}}} \right\| _F^2 \end{aligned}$$
(3)

Simultaneously, in order to reduce the amount of calculation, and exclude noise samples, the following low-rank [27] constraint is applied to the kernel coefficient matrix \({{\mathbf{W}}}\):

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha } ,{\mathbf{W}}} \left\| {\mathbf{X} - \sum \limits _{i = 1}^d {\alpha _i{\mathbf{K}}^{(i)}} {\mathbf{W}}} \right\| _F^2 {{\hbox {s.t.\;rank}}}({\mathbf {W}}) \le \min (n,d) \end{aligned}$$
(4)

From formula (4), we can easily see that low rank reduces the amount of computation. And in real life, if the data is noisy or outliers, it will increase the rank of the matrix of kernel coefficients [28]. The low rank indicates a degree of redundancy. We use low-rank constraint to remove noise to a certain extent and filter out some outliers. Therefore, low-rank constraints are very useful. The kernel coefficient matrix can be expressed as the product of two matrices whose rank is not greater than r, ie:

$$\begin{aligned} {\mathbf{W}} = {\mathbf{A}}{\mathbf{B}} \end{aligned}$$
(5)

where: \({\mathbf{A}} \in {\mathbb {R}^{n \times r}}\), \({\mathbf{B}} \in {\mathbb {R}^{r \times d}}\). Substituting Eq. (5) into Eq. (4), we can get the general form of the low rank nonlinear feature selection model:

$$\begin{aligned} \mathop {\min }\limits _{{\mathbf{A}},\quad {\mathbf{B}},\varvec{\alpha }} \left\| {{\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i{\mathbf{K}}^{(i)}} \mathbf{A} \mathbf{B}} \right\| _F^2 \end{aligned}$$
(6)

At the same time, in order to improve the accuracy of nonlinear feature selection, we further optimize the above equation. That is, row sparse is performed by using \({l_{2,1}}\)-norm to substitute the \({l_F}\)-norm in the above formula to punish all the row coefficients of \(\left\| {{\mathbf{X}} - \sum \nolimits _{i = 1}^d {\alpha _i} {{\mathbf{K}}^{(i)}}{} \mathbf{A} \mathbf{B}} \right\| _F^2\). However, in practice, it is shown that the \({l_{2,p}}\)-norm can be adjusted to p to achieve better results [29], so we use the \({l_{2,p}}\)-norm to decompress the kernel coefficient matrix \(\mathbf{{AB}}\), that is:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{A},\mathbf{B},\varvec{\alpha } } {\left\| {{\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i{\mathbf{K}}^{(i)}} {\mathbf{A}} {\mathbf {B}} }\right\| _{2,p}} \end{aligned}$$
(7)

where \(0< p < 2\), when \(p=1\), it is the standard \({l_{2,1}}\)-norm. When we change the value of p, different sparse structures can be implemented for the matrix \({\mathbf{{AB}}}\). Since the objective function is a convex function, we make \({\mathbf{P}} = \sum \nolimits _{i = 1}^d {\alpha _i{\mathbf{K}}^{(i)}}\), and it is easy to know that the solution is: \({\mathbf{A}}{\mathbf{B}} = {\left( {{{\mathbf{P}}^{\mathrm{T}}}{} {\mathbf{P}}} \right) ^{ - 1}}{{\mathbf{P}}^{\mathrm{T}}}{} {\mathbf{X}}\). But, in reality, \({{\mathbf{P}}^{\mathrm{T}}}{} {\mathbf{P}}\) is not necessarily reversible, so we introduce a \({l_{2,p}}\)-norm regularization term to make it invertible, and reject the unimportant features in the data. In addition, we also do a orthogonal restrictions for \({\mathbf{B}}\), and achieve a better fitting effect. At the same time, we introduce a \({l_1}\)-norm of \(\varvec{\alpha }\) to select data features in the kernel space. In summary, the final objective function of this paper is:

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{{\mathbf{A}},{\mathbf{B}},\varvec{\alpha } } \left\| {{\mathbf{X}}} - \sum \limits _{i = 1}^d {\alpha _i} {{\mathbf{K}}^{(i)}}{\mathbf{AB}} \right\| _{2,p} + \lambda _1{\left\| {\mathbf{A}} \right\| _{2,p}} + \lambda _2{\left\| \varvec{\alpha } \right\| _1}\\ {{\hbox {s.t.}}}\;{\mathbf {BB}}^{\mathrm{T}} = {{{\mathbf {I}}}_r} \end{array} \end{aligned}$$
(8)

where \({\left\| {\mathbf{A}} \right\| _{2,p}} = {\left[ {\sum \nolimits _{i = 1}^n {{{({{\sum \nolimits _{j = 1}^r {\left| { A_{ij}} \right| } }^2})}^{p/2}}} } \right] ^{1/p}}\), \(\lambda _1\) and \(\lambda _2\) are nonnegative adjustment parameters. Orthogonal constraint conditions \({\mathbf{BB}}^{\mathrm{T}} = {{\mathbf{I}}_r} \in {{\mathbb{R}}^{r \times r}}\) ensure that the low rank can be studied by considering the relationship between the outputs [30], thus improving the classification accuracy. Different degrees of sparsity are applied to the coefficient matrix \({\mathbf{A}}\) by the \({l_{2,p}}\)-norm, it optimize the entire low-rank nonlinear feature selection model. The kernel matrix \({\mathbf{K}}\) is calculated based on the Gaussian kernel function. By mapping data features to high-dimensional kernel space, the nonlinear relationship between data features is represented in high-dimensional space. This can fully consider the nonlinear relationship between data features, so that the mining of data features more thorough. The last \({l_1}\)-norm of \(\varvec{\alpha }\) is sparse for \(\varvec{\alpha }\), and nonlinear feature selection is made at the same time. If the value of the corresponding element of the vector \(\varvec{\alpha }\) is zero, we won’t select the feature.

3.3 Optimization

Since the \({l_{2,p}}\)-norm and \({l_1}\)-norm are used in the objective function, the objective function cannot be closed-form solution. Therefore, this paper proposes an alternative iterative optimization method to solve this problem. Specifically divided into the following three steps.

3.3.1 Update \({\mathbf{A}}\) by fixing \(\varvec{\alpha }\) and \({\mathbf{B}}\)

When \(\varvec{\alpha }\) and \({\mathbf{B}}\) are fixed, the optimization (8) problem becomes:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{A}} {\left\| {{\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i} {\mathbf{K}}^{(i)} {\mathbf{A}} {\mathbf{B}}} \right\| _{2,p}} + \lambda _1\left\| {\mathbf{A}} \right\| _{2,p} \end{aligned}$$
(9)

We make \({\mathbf{P}}=\sum \nolimits _{i = 1}^d {\alpha _i{\mathbf{K}}^{(i)}}\), then the (9) formula can be transformed into: \(\mathop {\min }\nolimits _{\mathbf{A}} {\left\| {{\mathbf{X}} - {\mathbf{P}}{} {\mathbf{A}}{} {\mathbf{B}}} \right\| _{2,p}} + \lambda _1{\left\| {\mathbf{A}} \right\| _{2,p}}\), since matrix \({\mathbf{B}}\) has orthogonal constraint \({\mathbf{BB}}^{\mathrm{T}} = {\mathbf{I}}\) , we have the following formula:

$$\begin{aligned} {\left\| {{\mathbf{X}} - {\mathbf{P}}{} {\mathbf{A}}{} {\mathbf{B}}} \right\| _{2,p}}= & {} {\left\| {({\mathbf{X}} - {\mathbf{P}}{} {\mathbf{A}}{} {\mathbf{B}})({{\mathbf{B}}^{\mathrm{T}}},{\mathbf{B}^{''}})} \right\| _{2,p}}\nonumber \\= & {} {\left\| {\mathbf{X}{{\mathbf{B}}^{\mathrm{T}}} - {\mathbf{P}}{\mathbf{A}}} \right\| _{2,p}} + {\left\| {\mathbf{X}{\mathbf{B}^{''}}} \right\| _{2,p}} \end{aligned}$$
(10)

The matrix \(\mathbf{A}\) is not included in (10) \({\left\| \mathbf{X{\mathbf{B}^{''}}} \right\| _{2,p}}\), so when \(\varvec{\alpha }\) and \(\mathbf{B}\) are fixed, the optimization of the objective function (8) can be converted to:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{A}} {\left\| {\mathbf{X}{\mathbf{B}^{\mathrm{T}}} - \mathbf{P}{} \mathbf{A}} \right\| _{2,p}} + \lambda _1{\left\| \mathbf{A} \right\| _{2,p}} \end{aligned}$$
(11)

Further inference of the objective function (11) is available:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{A}} tr\left[ {\left( \mathbf{X}{\mathbf{B}^{\mathrm{T}}} - {\mathbf{P}} \mathbf{A}\right) ^{\mathrm{T}}}{\mathbf {Q}}\left( {\mathbf {X}}{{\mathbf {B}}^{\mathrm{T}}} - {\mathbf {P}}{\mathbf {A}}\right) \right] + \lambda _1tr\left( {\mathbf{A}^{\mathrm{T}}} {\mathbf{N}} \mathbf{A}\right) \end{aligned}$$
(12)

where \(\lambda _1\) is the tuning parameter, \({\mathbf {Q}} \in {\mathbb {R}^{n \times n}}\) and \({\mathbf {N}} \in {\mathbb {R}^{n \times n}}\) are both diagonal matrices and their main diagonal elements are: \({Q_{ii}} = \frac{1}{{\frac{2}{p}\left\| {{{(\mathbf{X}{\mathbf{B}^{\mathrm{T}}} - \mathbf{P}{} \mathbf{A})}_i}} \right\| _2^{2 - p}}}i = (1,2, \ldots ,n)\), \({ N_{jj}} = \frac{1}{{\frac{2}{p}\left\| {{\mathbf{A}}_j} \right\| _2^{2 - p}}}j = (1,2, \ldots ,n)\).

By setting the derivative of \(\mathbf{A}\) in (12) to zero, we obtain:

$$\begin{aligned} {\mathbf {A}} = {\left( {\mathbf{P}^{\mathrm{T}}}{\mathbf{Q}}{\mathbf{P}} + \lambda _1\mathbf N\right) ^{ - 1}}{\mathbf{P}^{\mathrm{T}}}{} \mathbf{Q}{} \mathbf{X}{\mathbf{B}^{\mathrm{T}}} \end{aligned}$$
(13)

3.3.2 Update \(\mathbf{B}\) by fixing \(\varvec{\alpha }\) and \(\mathbf{A}\)

By fixing \(\varvec{\alpha }\) and \(\mathbf{A}\), the objective function (8) can be simplified as follows:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{B}} {\left\| {\mathbf{X} - \hat{\mathbf{P}}{} \mathbf{B}} \right\| _{2,p}},\quad {\hbox {s.t.}}, {{\mathbf {B}} {{\mathbf {B}}^{\mathrm{T}}}} = {\mathbf{I}_r} \end{aligned}$$
(14)

where \(\hat{\mathbf{P}} = {\mathbf {P}}{\mathbf {A}} \in {\mathbb {R}^{n \times r}}\). It is easy to know that the objective function (14) is actually an orthogonal procrustes problem [31]. \({{\mathbf {X}}^{\mathrm{T}}}\hat{\mathbf{P}} = {\mathbf {U}} {\mathbf {S}}{{\mathbf {V}}^{\mathrm{T}}}\) is performed directly singular value decomposition. It can be seen that the optimal solution of subspace matrix \(\mathbf{B}\) is \({\mathbf {V}}{{\mathbf {U}}^{\mathrm{T}}}\), \({\mathbf {U}} \in {\mathbb {R}^{d \times r}}, \mathbf V \in {\mathbb {R}^{r \times r}}\).

3.3.3 Update \(\varvec{\alpha }\) by fixing \(\mathbf{A}\) and \(\mathbf{B}\)

After fixing \(\mathbf{A}\), \(\mathbf{B}\), the objective function (8) becomes:

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha }} {\left\| {{\mathbf{X}} - \sum \limits _{i = 1}^d \mathbf{\alpha }_i {{\mathbf{K}}^{(i)}}{} \mathbf{A}\mathbf{B}} \right\| _{2,p}} + \lambda _2{\left\| \varvec{\alpha } \right\| _1} \end{aligned}$$
(15)

Here’s a simple simplification:

$$\begin{aligned} &\mathop {\min }\limits _{\varvec{\alpha }} {\left\| {{\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i{{\mathbf{K}}^{(i)}}} \mathbf{A}{} \mathbf{B}} \right\| _{2,p}} = \mathop {\min }\limits _{\varvec{\alpha }} {\left\| {{\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i} {{\mathbf{Z}}^{(i)}}} \right\| _{2,p}}\\&\quad \Leftrightarrow \mathop {\min }\limits _{\varvec{\alpha }} \left[ \left( {\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i} {{\mathbf{Z}}^{(i)}}\right) ^{\mathrm{T}}{\mathbf{Q}}\left( {\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i} {{\mathbf{Z}}^{(i)}}\right) \right] \\&\quad \Leftrightarrow \mathop {\min }\limits _{\varvec{\alpha }} \sum \limits _{i = 1}^n tr\left[ \left( {\mathbf{X}}_i - \sum \limits _{i = 1}^d {\alpha _i} {\mathbf{Z}}_i^{(i)}\right) ^{\mathrm{T}}{Q_{ii}}\left( {\mathbf{X}}_i - \sum \limits _{i = 1}^d {\alpha _i} {\mathbf{Z}}_i^{(i)}\right) \right] \\&\quad \Leftrightarrow \mathop {\min }\limits _{\varvec{\alpha }} \sum \limits _{i = 1}^n {{Q_{ii}}tr} \left( {\mathbf{X}}_i - \sum \limits _{i = 1}^d {\alpha _i} {\mathbf{Z}}_i^{(i)}\right) ^{\mathrm{T}}\left( {\mathbf{X}}_i - \sum \limits _{i = 1}^d {\alpha _i} {\mathbf{Z}}_i^{(i)}\right) \\&\quad \Leftrightarrow \mathop {\min }\limits _{\varvec{\alpha }} \sum \limits _{i = 1}^n {{Q_{ii}}\left\| {{\mathbf{X}}_i - \left( \alpha _1\ Z_{i,.}^{^{(1)}} + \cdots + {\alpha }_d Z_{i,.}^{^{(d)}}\right) } \right\| _2^2} \end{aligned}$$
(16)

We make \({{\mathbf{S}}^{(i)}} = \left( {\begin{array}{lll} Z_{i,1}^{^{(1)}}& \ldots &{ Z_{i,d}^{^{(1)}}}\\ Z_{i,1}^{^{(d)}}& \ldots & Z_{i,d}^{^{(d)}} \end{array}} \right) \in {\mathbb {R}^{d \times d}}\), (16) formula is written the following form:

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha }} \sum \limits _{i = 1}^n {{Q_{ii}}\left\| {{\mathbf{X}}_i - {\varvec{\alpha }} ^{\mathrm{T}}\left( {{\mathbf{S}}^{(i)}}\right) } \right\| _2^2} \end{aligned}$$
(17)

After a series of simplifications, we can get (17) that is equivalent to the following formula:

$$\begin{aligned} &\mathop {\min }\limits _{\varvec{\alpha }} \sum \limits _{i = 1}^n {{Q_{ii}}{{\mathbf{X}}_i}{{\mathbf{X}}_i}^{\mathrm{T}}} - 2{{\varvec{\alpha }} ^{\mathrm{T}}}\sum \limits _{i = 1}^n {{Q_{ii}}{{\mathbf{S}}^{(i)}}{\mathbf{X}}_{_i}^{\mathrm{T}}}\\&\quad + {{\varvec{\alpha }} ^{\mathrm{T}}}\sum \limits _{i = 1}^n {{Q_{ii}}\left( \mathbf{S}^{(i)}{{\left( {\mathbf{S}}^{(i)}\right) }^{\mathrm{T}}}\right) } \varvec{\alpha } \end{aligned}$$
(18)

Since the objective function (15) is convex but not smooth, we design a new accelerated approximate gradient method to solve the function. We make:

$$\begin{aligned} f({\varvec{\alpha }} )&= {\left\| {{\mathbf{X}} - \sum \limits _{i = 1}^d {\alpha _i} {{\mathbf{K}}^{(i)}}{} \mathbf{A}{} \mathbf{B}} \right\| _{2,p}}\\ F({\varvec{\alpha }} )&= f({\varvec{\alpha }} ) + {\lambda _2}{\left\| {\varvec{\alpha }} \right\| _1} \end{aligned}$$
(19)

Notice \({\left\| {\varvec{\alpha }} \right\| _1}\) is convex but not smooth. So using the approximate gradient method, we can use the following rules to update iterations \(\varvec{\alpha }\).

$$\begin{aligned} {{\varvec{\alpha }} _{t + 1}} &=\arg \mathop {\min }\limits _{\varvec{\alpha }} {G_{\eta t}}({\varvec{\alpha }} ,{{\varvec{\alpha }} _t})\\ {G_{\eta t}}\left( {{\varvec{\alpha }} ,{{\varvec{\alpha }} _t}} \right) &=f\left( {{\varvec{\alpha }} _t} \right) + \langle \nabla f\left( {{\varvec{\alpha }} _t} \right) ,{\varvec{\alpha }} - {{\varvec{\alpha }} _t} \rangle \\&\quad + \frac{{{\eta _t}}}{2}{\left\| {{\varvec{\alpha }} - {\varvec{\alpha }} _t} \right\| ^2} + {\lambda _2}{\left\| \varvec{\alpha } \right\| _1} \end{aligned}$$
(20)

Here, \(\nabla f({\varvec{\alpha }} _t) = 2{\varvec{\alpha }} _t^{\mathrm{T}}\sum \nolimits _{i = 1}^n {{Q_{ii}}} ({{\mathbf{S}}^{(i)}}{({{\mathbf{S}}^{(i)}})^{\mathrm{T}}}) - 2\sum \nolimits _{i = 1}^n {{Q_{ii}}{\mathbf{X}}_i} {({\mathbf{S}}^{(i)})^{\mathrm{T}}}\) is calculated from (18), \(\eta _t\) is a tuning parameter, \({\varvec{\alpha }} _t\) is a value in the t-th iteration.

By ignoring the independent \(\varvec{\alpha }\) in formula (20), we can get:

$$\begin{aligned} {{\varvec{\alpha }} _{t + 1}} = {\pi _{\eta _t}}({\varvec{\alpha }} _t) = \arg \mathop {\min }\limits _{\varvec{\alpha }} \frac{1}{2}\left\| {\varvec{\alpha }} - {\mathbf{U}}_t \right\| _F^2 + \frac{\lambda _2}{\eta _t}{\left\| {\varvec{\alpha }} \right\| _1} \end{aligned}$$
(21)

where \({{\mathbf {U}}}_t = {\varvec{\alpha }} _t - \frac{1}{{\eta _t}}\nabla f({\varvec{\alpha }} _t)\), \({\pi _{\eta _t}}({\varvec{\alpha }} _t)\) is a Euclidean projection on a convex set \(\eta _t\), because \({\left\| {\varvec{\alpha }} \right\| _1}\) has a separable form, (21) can be written as follows:

$$\begin{aligned} \alpha _{t + 1}^i = \arg \mathop {\min }\limits _{\alpha ^i} \frac{1}{2}\left\| {\alpha ^i - U_t^i} \right\| _2^2 + \frac{{\lambda _2}}{{\eta _t}}\left| {\alpha ^i} \right| \end{aligned}$$
(22)

where \(\alpha ^i\) and \(\alpha _{t + 1}^i\) are respectively the i-th elements of \(\alpha\) and \({\alpha _{t + 1}}\), then according to formula (22), \(\alpha _{t + 1}^i\) can be obtained the following closed-form solution:

$$\begin{aligned} {\alpha ^{i*}} = \left\{ {\begin{array}{ll} {u_t^i - \frac{{{\lambda _2}}}{{{\eta _t}}} \times {\hbox {sign}}\left( u_t^i\right) ,}&{}\quad {\mathrm{{if}}\left\| {u_t^i} \right\| > \frac{{{\lambda _2}}}{{{\eta _t}}}}\\ {0,}&{}\quad {\mathrm{{otherwise}}.} \end{array}} \right. \end{aligned}$$
(23)

To speed up the approximate gradient algorithm in Eq. (20), we added an auxiliary variable:

$$\begin{aligned} {{\mathbf{V}}_{t+ 1}} = {{\varvec{\alpha }} _t} + \frac{{{\beta _t} - 1}}{{{\beta _{t + 1}}}}({\varvec{\alpha } _{t + 1}} - \varvec{\alpha } _t) \end{aligned}$$
(24)

where \({\beta _{t + 1}} = \frac{{1 + \sqrt{1 + 4\beta _t^2} }}{2}\).

3.4 Convergence analysis

We can prove that the value of the objective function (11) is monotonically decreasing in every iteration. The objective function is equivalent to:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{A}} tr\left[ {\left( {\mathbf{XB}}^{\mathrm{T}} - {\mathbf{P}}{\mathbf{A}}\right) ^{\mathrm{T}}}{\mathbf{Q}}\left( {\mathbf{XB}}^{\mathrm{T}} - {\mathbf{P}}{\mathbf{A}}\right) \right] + {\lambda _1}tr\left( {{\mathbf{A}}^{\mathrm{T}}}{\mathbf{N}}{\mathbf{A}}\right) \end{aligned}$$
(25)

So we have:

$$\begin{aligned} &tr\left[ {\left( {\mathbf{XB}}_{(t + 1)}^{\mathrm{T}} - {\mathbf{PA}}_{(t + 1)}\right) ^{\mathrm{T}}}{{\mathbf {Q}}_t}\left( {\mathbf{XB}}_{(t + 1)}^{\mathrm{T}} - {\mathbf{PA}}_{(t + 1)}\right) \right] \\&\quad + {\lambda _1}tr\left( {{\mathbf{A}}_{(t + 1)}}^{\mathrm{T}}{{\mathbf{N}}_t}{{\mathbf{A}}_{(t + 1)}}\right) \\&\quad \le tr\left[ {\left( {\mathbf{XB}}_t^{\mathrm{T}} - {\mathbf{PA}}_t\right) ^{\mathrm{T}}}{{\mathbf {Q}}_t}\left( {\mathbf{XB}}_t^{\mathrm{T}} - {\mathbf{PA}}_t\right) \right] \\&\qquad + {\lambda _1}tr\left( {\mathbf{A}}_t^{\mathrm{T}}{\mathbf{N}}_t{{\mathbf{A}}_t}\right) \\ \end{aligned}$$
(26)

According to the simple formula reasoning, we can get the following formula:

$$\begin{aligned} &\Rightarrow \sum \limits _{i = 1}^n \frac{{\Big \Vert {{{\mathbf {X}}^i}{{\mathbf{B}}_{(t + 1)}}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_{(t + 1)}}} \Big \Vert _2^{2(2 - p)}}}{{(2/p)\Big \Vert {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \Big \Vert _2^{2 - p}}} \\&\qquad + {\lambda _1}\sum \limits _{i = 1}^\mathrm{{n}} {\frac{{\Big \Vert {{a^i}_{(t + 1)}} \Big \Vert _2^{2(2 - p)}}}{{(2/p)\Big \Vert {{a^i}_t} \Big \Vert _2^{2 - p}}}} \\&\quad \le \sum \limits _{i = 1}^n {\frac{{\Big \Vert {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \Big \Vert _2^{2(2 - p)}}}{{(2/p)\Big \Vert {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \Big \Vert _2^{2 - p}}}} \\&\qquad + {\lambda _1}\sum \limits _{i = 1}^n {\frac{{\Big \Vert {{a^i}_t} \Big \Vert _2^{2(2 - p)}}}{{(2/p)\Big \Vert {{a^i}_t} \Big \Vert _2^{2 - p}}}} \\ \end{aligned}$$
(27)

The above can indicate that any nonzero vector in (10) has:

$$\begin{aligned} &\sum \limits _i {\left\| {{a^i}_{(t + 1)}} \right\| _2^{2(2 - p)}} - \sum \limits _i {\frac{{\left\| {{a^i}_{t + 1}} \right\| _2^{2(2 - p)}}}{{(2/p)\left\| {{a^i}_{t + 1}} \right\| _2^{2 - p}}}} \\&\quad \le \sum \limits _i {\left\| {{a^i}_t} \right\| _2^{2 - p}} - \sum \limits _i {\frac{{\left\| {{a^i}_t} \right\| _2^{2(2 - p)}}}{{(2/p)\left\| {{a^i}_t} \right\| _2^{2 - p}}}} \\&\sum \limits _{i = 1}^n {\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_{(t + 1)}}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_{(t + 1)}}} \right\| _2^{2 - p}} \\ &\qquad - \sum \limits _{i = 1}^n {\frac{{\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_{(t + 1)}}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_{(t + 1)}}} \right\| _2^{2(2 - p)}}}{{(2/p)\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \right\| _2^{2 - p}}}} \\&\quad \le \sum \limits _{i = 1}^n {\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \right\| _2^{2 - p}} \\&\qquad - \sum \limits _{i = 1}^n {\frac{{\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \right\| _2^{2(2 - p)}}}{{(2/p)\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \right\| _2^{2 - p}}}} \end{aligned}$$
(28)

To sum up, we can easily get:

$$\begin{aligned} &\sum \limits _{i = 1}^n {\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_{(t + 1)}}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_{(t + 1)}}} \right\| _2^{2 - p} + {\lambda _1}} \sum \limits _{i = 1}^n {\left\| {{a^i}_{t + 1}} \right\| _2^{2 - p}} \\&\quad \le \sum \limits _{i = 1}^n {\left\| {{{\mathbf {X}}^i}{{\mathbf{B}}_t}^{\mathrm{T}} - {{\mathbf {P}}^i}{{\mathbf{A}}_t}} \right\| _2^{2 - p} + {\lambda _1}} \sum \limits _{i = 1}^n {\left\| {{a^i}_t} \right\| _2^{2 - p}} \end{aligned}$$
(29)

Theorem 1 Let \({\varvec{\alpha } _t}\) be the sequence generated by Algorithm 1, then for \(\forall t \ge 1\), (29) holds:

$$\begin{aligned} F({\varvec{\alpha } _t}) - F({\varvec{\alpha } ^*}) \le \frac{{2\gamma L\left\| {{\varvec{\alpha } _1} - {\varvec{\alpha } ^*}} \right\| _F^2}}{{{{(t + 1)}^2}}} \end{aligned}$$
(30)
figure a

According to reference [32], \(\gamma\) is a constant defined in advance, L is the Lipschitz constant of the \(f(\varvec{\alpha } )\) gradient in Eq. (19) , and \({\varvec{\alpha } ^*} = \arg \mathop {\min }\limits _{\varvec{\alpha }} F(\varvec{\alpha } )\).

Through the above inequality and Theorem 1, we can easily see that our algorithm is convergent.

4 Experiments

In this section, we compare the KF_NFS algorithm with the comparison algorithms. The dimensionality is reduced by the feature selection algorithms, and then, the data after dimension reduction is conducted SVM classified. Finally, the performance of the algorithms is measured according to the classification accuracy.

4.1 Experiment settings

We tested our proposed nonlinear feature selection algorithm with five binary-class data sets and seven multi-class data sets. They are Glass, SPECTF, Sonar, Clean, Arrhythmia, Movements, Ecoli, Urban_land, Ionosphere, Yale, Colon, Lung_discrete, where the first nine are all from UCI Machine Learning RepositoryFootnote 1 and the last three are from feature selection data.Footnote 2 The details of the data set are shown in Table 1.

At the same time, we found eight comparison algorithms to compare with the KF_NFS algorithm. The information of the comparison algorithm is as follows:

RSR: It constrains the self-representation coefficient matrix by a \({l_{2,1}}\)-norm, so that the representative features are selected and the robustness of outliers are ensured [33].

SOGFS: It is an embedded unsupervised feature selection algorithm. It introduces local constraints on manifold structure learning by the reasonable constraints. It also performs feature selection and local structure learning simultaneously to select more valuable features [34].

EUFS: It is an unsupervised feature selection algorithm. It uses sparse learning to embed the feature selection algorithm into the clustering algorithm so as to achieve a better feature selection effect [35].

FSASL: It is also an unsupervised feature selection algorithm that combines feature learning with structural learning. Two learning methods are mutually promoted to achieve good results [36].

RFS: It is a supervised feature selection algorithm. It combines the \({l_{2,1}}\)-norm to limit the loss function and the regularization term, and achieves a very good robust effect [37].

LS: According to the distance of two data points, then they are likely to have many similar relationships. Calculating its Laplacian score to reflect the holding ability of the local structure. Finally achieve good feature selection effect [38].

NetFS: It is a robust unsupervised feature selection algorithm, which embeds potential representation learning into feature selection to mitigate the effects of noise and achieve good results [39].

RUFS: It is also a robust and unsupervised feature selection algorithm. It performs clustering and feature selection simultaneously, and reduces the time and space complexity of the algorithm [40].

In our proposed model, we set \(\{ \lambda _1,\lambda _2\} \in \{ 10^{ - 4},\ldots ,10^8\}\), the rank of the kernel coefficient matrix \(r \in \{ 1,\ldots ,\min (n,d)\}\), and the parameter of \({l_{2,p}}\)-norm \(p \in \{ 0.1,\ldots ,1.9\}\). The parameters \(c \in \{ {2^{ - 5}},\ldots ,{2^5}\}\) and \(g \in \{ {2^{ - 5}},\ldots ,{2^5}\}\) are used to select the best SVM for classification, and distinguish different types of samples. The experiment divides the data set randomly into a training set and a test set through a tenfold cross-validation. In order to maintain fairness, we carry out tenfold cross-validation of 10 times, and finally we take the average of the classification accuracy.

We use the classification accuracy and standard deviation as the evaluation criteria for our experiments. We define the classification accuracy as follows:

$$\begin{aligned} {{\hbox {acc}}} = {X_{{\mathrm{correct}}}}/X \end{aligned}$$
(31)

where X represents the total number of samples and \({X_{{\mathrm{correct}}}}\) represents the correct number of samples for classification. At the same time we define the standard deviation to measure the stability of our algorithm, as follows:

$$\begin{aligned} {\hbox {std}} = \sqrt{\frac{1}{N}\sum \limits _{i = 1}^N {{{({{\hbox {acc}}}_i - \mu )}^2}}} \end{aligned}$$
(32)

where N represents the number of experiments, \({{\hbox {acc}}}_i\) represents the classification accuracy of the i-th experiment, \(\mu\) represents the average classification accuracy, and the smaller the std, the more stable the representative algorithm.

Table 1 The information of the data sets
Full size table

4.2 Experiment results and analysis

In Fig. 1, the classification accuracy of 10 experiments for all algorithms is shown. To avoid the randomness of the training set and the test set, we use tenfold cross-validation to divide the data into training and test sets. At the same time, the average of 10 results is used to evaluate the accuracy of the algorithm. In this way, ten experiments were finally carried out. From Fig. 1, we can clearly see that our proposed algorithm has the highest classification accuracy in most cases. In Table 2, we show the results of all algorithms on 12 datasets. It can be seen that the KF_NFS algorithm has the highest classification accuracy compared with the other eight algorithms. Specifically, it is 6.58% higher than the EUFS algorithm on average, 14.49% higher than the LS algorithm on average, and 9.07% higher than the RFS algorithm on average. It shows that our algorithm is better than the general linear feature selection algorithm. Compared with the FSASL, NetFS, RUFS, RSR, and SOGFS algorithms, It increased by an average of 6.16%, 11.54%, 8.96%, 8.81%, and 5.42%, respectively.

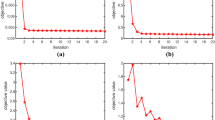
In Fig. 2, the value of each iteration of our objective function over 12 data sets is shown. We set the condition for our algorithm to converge on \(\frac{{\left| {{{\hbox {obj}}}(t + 1) - {{\hbox {obj}}}(t)} \right| }}{{{{\hbox {obj}}}(t)}} \le {10^{ - 5}}\). From Fig. 2, we can easily see that the value of the objective function gradually decreases as the number of iterations increases and finally converges to a certain value. Moreover, our objective function converges very quickly, and most converge before the fifth iteration.

In Table 3, we can see that the average standard deviation of accuracy rate of our algorithm is the smallest. On the one hand, it shows that our algorithm is more stable, and on the other hand, it shows that its overall performance is better.

The KF_NFS algorithm can achieve good results. It is mainly related to the following two points: (a) considering the nonlinear relationship between data; (b) Iteratively performing low-rank feature selection steps. At the same time, according to the standard deviation, we can easily find that our proposed algorithm is the most stable.

Fig. 1
figure 1

Average classification accuracy of all methods for all datasets

Full size image
Fig. 2
figure 2

Convergence rate of Algorithm 1 on all tested datasets

Full size image
Table 2 Average classification accuracy [acc (%)]
Full size table
Table 3 Standard deviation of classification accuracy [std (%)]
Full size table

5 Conclusion

This paper proposes a new unsupervised nonlinear feature selection algorithm through the nonlinear relationship between data features. That is, using the kernel function, applying the \({l_{2,p}}\)-norm to both the loss function and the regularization, and combining the low rank and the \({l_1}\)-norm sparse methods are used to further refine the proposed model; therefore, it achieves very good results. The algorithm has discovered the nonlinear relationship between the data features and has a more significant mining effect than the general feature selection algorithm. The experimental results show that the algorithm of this paper has greatly improved the classification accuracy and stability. In the future work, we will attempt to combine more advanced theoretical for improvement algorithms.