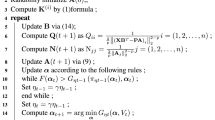1 Introduction

High-dimensional matrices are commonly used to store data [37, 38, 46] in image processing [35, 47, 54, 55] and data mining [8, 15, 42, 51]. On the one hand, high-dimensional matrices can store a large amount of information, on the other hand, they will bring feature redundancy [49, 50, 53, 56], taking up a lot of storage space. etc. In order to extract the valid information out of these data and improve the processing efficiency, we need to preprocess these data. Therefore, feature reduction has become an increasingly important area of research [52].Feature selection [43, 48] is a common feature reduction method. It mainly selects a subset of the original features that best represent the data from a variety of features according to a certain standard. Feature selection is widely used in pattern recognition, machine learning and other fields [9, 39].Most of the previous researches are based on the selection of features under linear conditions. However, the data in real life is often not exactly a linear relationship. Sometimes we need to consider more of the nonlinear relationships between data, so we can introduce kernel Functions to implement nonlinear property selection [44].

This paper first uses the kernel function to map each feature of the data to the kernel space. In the kernel space, these data are linearly separable. Then we perform the linear feature selection in the kernel space, which is equivalent to the nonlinear feature selection [30]. Secondly, the gained feature kernel matrix is used to do feature selection. At the same time, self-expression matrix is obtained through the self-representation of features and the deviation term to solve the problem of classless tags in unsupervised feature selection methods.

Then the low-rank feature selection is performed in the linear regression model framework, in which the low-rank feature selection uses sparsity (using the norm to remove redundant features) and low rank (assuming the matrix has a low rank to eliminate noise interference) methods.

Finally, a new optimization method is proposed, which is to implement the optimized solution algorithm of the low-rank feature selection and norm processing [10] to the objective function in order, and constantly alternate iterations make the result optimal, and finally obtain the global optimal solution. Since the kernel function is introduced in this paper to perform nonlinear feature selection, it has a better effect than the general linear feature selection learning method. Experimentally verified, this algorithm can achieve better results in classification accuracy.

2 Related work

Recent years, with the explosive growth of data, a large amount of feature selection algorithms came into our sight. Generally speaking, it can be introduced as three parts: unsupervised method, supervised method, and semi-supervised method.

In practical applications, due to the high cost of obtaining tags, a mass of unsupervised feature selection algorithms have been proposed. For instance, the maximum variance method [36] selects the highest ranked feature with the largest variance. The feature of the maximum variance method selection is the representation of data’s variance, but it cannot guarantee the differentiation of the classification [12]. The Laplacian score method [12] selects features to preserve the local manifold structure of the datasets, but does not consider sample redundancy. Multi-cluster feature selection (MCFS) [2] first uses the eigenvectors of the Laplacian operator for regression, and then uses the largest spectral regression coefficients to select features. Recently, Bhadra et al. proposed an unsupervised feature selection method using an improved version of differential evolution, but it always has a large computational complexity [17].

Supervised methods typically select features based on the availability of category tags and evaluate performance using known category tags. We have found that most monitoring methods can be formulated as a similar framework, and regularization terms are used for feature selection loss functions. For example, Wu et al. A method of least squares loss function was used to integrate a set of sparse regularization parameters for feature selection [33], and Ma et al. proposed feature selection through the mixed loss function and two sparse regularization functions [20]. Due to the presence of tag information, supervisory feature selection methods are often capable of outputting identifying features. For example, Feng et al. [7] proposed a supervisory feature selection method, using the tag information to establish a good dictionary learning discriminative framework.

The semi-supervised method trains with a limited number of marker samples and relatively large unlabeled samples. Zhao et al. applied spectral theory to unlabeled and labeled data to achieve semi-supervised feature selection [41]. Zhao et al. proposed to calculate the importance score of each feature on the Laplacian graph for labeled and unlabeled data in semi-supervised learning [40]. However, none of them can find a large number of features at the same time, ignoring the interdependence of features. In order to solve these problems, Ma et al. proposed a semi-supervised framework for automatic image annotation [21]. Recently, Han et al. proposed a semi-supervised feature selection method and spline regression method for video semantic recognition [11].

Nonlinear feature selection usually uses a kernel function to map the original dataset to a high dimensional space to achieve linear separability in high dimensional space. To deal with nonlinearities, Makoto Yamada et al. proposed HSIC Lasso [34]. In HSIC Lasso, the corresponding function is selected and then processed by lasso to find out the non-redundant features. Although the relevant experiment [34] confirmed that HSIC Lasso is superior to most existing feature selection methods, HSIC Lasso tends to be more expensive when the number of samples increases. Recently, some scholars have proposed some feature selection methods for wrapper types, including feature generating machine [29] and SVM-based methods [27]. These methods are more advanced feature selection methods for high dimensional and large scale data. However, for ultra-high dimensional and large-scale data sets, these methods are computationally expensive. The sparse additive model (SpAM) is very effective for high-dimensional feature selection problems [18, 25, 26, 28]. However, one potential weakness of SpAM is that it can only handle additive models and may not be suitable for non-additive models. Hierarchical multi-core learning (HMKL) [1, 13] is also a nonlinear feature selection method that cannot be complex functions such as non-additive functions. However, the computational cost of HMKL is quite expensive.

3 Our method

In this section, we will first give the symbolic representation and some detail work required in Section 3.1. Then a detailed introduction of the NSFS algorithm is given in Section 3.2 and the specific optimization of our algorithm in Section 3.3. In the end, the proof of the convergence of the optimization algorithm is given in Section 3.4.

3.1 Notations

In this article, bold letters are used to represent matrices and vectors. For a matrix X = [xij], its i-th row and j-th column are shown as Xi and Xj. The trace of the matrix X is expressed as tr(X). XT is representative of the transposition of the matrix. At the same time, Frobenius-norm and l2,p -norm of the matrix are expressed respecyively as: \(\|\mathbf {X}\|_{F} = \sqrt {{\sum }_{i}\|\mathbf {X}_{i}\|_{2}^{2}} = \sqrt {{\sum }_{j}\|\mathbf {X}^{j}{\|}_{2}^{2}}, {\|\mathbf {X}\|_{2,\mathrm {p}}}={\left [{\sum }_{i} {\left ({\sum }_{j}| x_{ij} |^{2}\right )}^{p/2}\right ]}^{1/p}\), where K(i)) is used to indicate that the i-th feature is mapped to the corresponding kernel matrix on the high-dimensional kernel space.

3.2 NSFS algorithm

In general, when feature selection is done, datasets are usually represented in the form of X ∈ Rn×d. In the case of supervised learning, our feature selection model is:

$$ \min\limits_{\mathbf{W}} \| {\mathbf{Y}-\mathbf{XW}\|_{F}^{2} + \alpha \|\mathbf{W}\|_{2,1}} + \beta \phi(\mathbf{W}),\mathbf{W} \in \mathbf{R}^{d \times c} $$
(1)

where ϕ(W) is the regularization factor for W. In most cases, the relationship between the data is not just a linear relationship, (1) can not usually show the nonlinear relationship between the data, so it is necessary to introduce a kernel function to improve the objective function.

Referring to the pattern recognition theory [22], it can be seen that linearly indivisible data in a low dimensional space can be linearly separable by mapping into a high dimensional space. However, if the low-dimensional data is directly mapped to high-dimensional space for machine learning related work, there will be ”dimension disasters” in the operation of high-dimensional space [31]. Therefore, we introduce the concept of a kernel function to reduce its computational complexity.

Assume x, z ∈ X, X ⊆Rn, the nonlinear function Φ achieves the mapping from the low-dimensional datasets to the high-dimensional space F ⊆ Rm, n << m. It can be obtained by the kernel method:

$$ {\mathrm{K}} (x,z{\mathrm{) = }}\langle {\Phi}(x),{\Phi} (z)\rangle $$
(2)

where 〈,〉 is the inner product, K(x, z) is a kernel function. The kernel function of (2) can be used to transform the inner product operation in the high-dimensional space into the calculation in the low-dimensional space, so the high computational complexity in the high-dimensional space can be avoided, so that we can achieve some high-dimensional problem in the area of machine learning. In this article, the Gaussian kernel function is mainly used.

Referring to the method in the GMKL algorithm [30] the objective function above can become:

$$ \begin{array}{l} \min\limits_{\mathbf{W},\alpha} \left\|\mathbf{Y}-\sum\limits_{i = 1}^{d} \alpha_{i} \mathbf{K}^{(i)} \mathbf{W} \right\|_{F}^{2} + {\lambda_{1}}\| \mathbf{W} \|_{F}^{2} + {\lambda_{2}}{\| {\boldsymbol{\alpha }} \|_{1}} \end{array} $$
(3)

where Y ∈ Rn×c, W ∈ Rn×c, α ∈ Rd×1 and K(i) ∈ Rn×n is a kernel matrix corresponding to the i-th feature.

In this way, W can not play a role in the selection of features, which is a coefficient matrix of the new data obtained by mapping the original data to the kernel space, so the sparse processing thereof cannot achieve the effect of selecting features on the original data set. Therefore, it is necessary to introduce a new feature selection coefficient vector α, so the l2-norm, which is easier to optimize , is used here instead of the l2,1-norm. For α, a sparse result is achieved with a l1-norm, α is obviously a vector with d elements. If α is 0 at a position, the corresponding feature in X is regarded as a redundant feature.

The model in (3) considers the similarity and selection characteristics of the data together. Although it is widely used in many feature selection methods, it is difficult to choose the appropriate response matrix. Due to the existence of self-representation properties of features, a regularized self-representation model for unsupervised feature selection is proposed in this section. The proposed model simply uses a matrix X as a response matrix, and each feature can be well represented by all features. For each feature fi of X, it is represented as a linear combination of other features:

$$ {\mathbf{f}_{i}}=\sum\limits_{j = 1}^{d} \mathbf{f}_{j} \mathrm{w}_{ji} +\mathbf{e}_{i} $$
(4)

Then according to the Representor theorem [14] of the kernel function, for all features there are:

$$ \mathbf{X} = \sum\limits_{i = 1}^{d} \boldsymbol{\alpha}_{i} \mathbf{K}^{(i)} \mathbf{W} + \mathbf{eb} $$
(5)

where W = [wij] ∈ Rn×d is the self-representation coefficient matrix, b ∈ R1×d is a deviation term that represents an all-one row vector, e ∈ Rn×1 is an all-one column vector. In order to adapt the right side of (5) to X as much as possible, the Frobenius-norm can be used to measure the deviation, i.e. \(\min \limits _{\textbf {W},\textbf {b}} \| \textbf {X} - \textbf {XW} - \textbf {eb} \|_{F}^{2}\). However, the Frobenius-norm is very sensitive to the outliers. Considering that the outlier sample is a row of data in the matrix, the use of the l2,p-norm to measure the deviation will play an important role. Next, objective function will use the l2,1-norm more.

By predicting each feature as a task, l2,p-norm regularization terms are used to constrain the sparsity between tasks. Then a new feature self-representation objective function is defined as follows:

$$ \min\limits_{\mathbf{W, b}, { \boldsymbol{\alpha}}} \left\| \mathbf{X} - \left( \sum\limits_{i = 1}^{d} \alpha_{i} \mathbf{K}^{(i)}\right) \mathbf{W}- \mathbf{eb} \right\|_{2,p}+\lambda_{1} \|\mathbf{W} \|_{2,p}+ {\lambda_{2}} \|\boldsymbol{\alpha} \|_{1} $$
(6)

Where λ1 and λ2 are the control parameters that affect the sparseness of the coefficient matrix W and the vector α, respectively. The l1-norm regularization term ∥α∥1 simultaneously punishes all the elements in α for the implementation of the sparsity of the feature selection vector α to make the choice of features and the decision not to choose. Where p(0 < p < 2) is an adjustable parameter that can control the degree of correlation between features.

In practical applications, it is often found that noise or anomalous data increases the rank of the self-mapping coefficient matrix [19]. Therefore, low-rank constraints are particularly reasonable when dealing with high-dimensional data. Low rank can reduce the impact of noise and reduce computational complexity. So we impose constraints on the rank of W[24]:

$$ \text{rank} (\mathbf{W}) = r,r \le \min(n,d) $$
(7)

In this way, the low-rank constraint for W can be naturally expressed as the product of the following two matrices:

$$ \mathbf{W}=\mathbf{AB} $$
(8)

where, A ∈ Rn×r, B ∈ Rr×d, then the final objective function becomes:

$$ \min\limits_{\mathbf{A B, b}, { \boldsymbol{\alpha}}} \left\| \mathbf{X} - \left( \sum\limits_{i = 1}^{d} {\alpha}_{i} \mathbf{K}^{(i)}\right) \mathbf{AB} - \mathbf{eb} \right\|_{2,p}+\lambda_{1}\| \mathbf{AB} \|_{2,p} + \lambda_{2} \| \boldsymbol{\alpha} \|_{1} $$
(9)

where X ∈ Rd×r, n and d are the number of samples and features, respectively, λ1, λ2 are adjustable parameters.

From the objective function (9), it can be inferred that W will be more row sparse when λ1 increased. λ1 only adjusts the line sparsity of W and prevents overfitting, so it’s necessary to find the best λ1 through experiment. When λ2 increased, α will be more sparse which represents fewer features will be selected. Therefore, when the noise feature and the irrelevant feature are just filtered out, the feature selection effect is the best. If λ2 continues to increase, the normal feature will be screened out, and the effect will be worse. As to the the parameter for the low-rank constraint, finding this most appropriate rank will take a lot of time, so the minimum value of n and d is used here to make low rank parameters.

3.3 Optimization

In this section, the optimization process of the objective function (9) will be given. Since l2,p-norm is used to remove outlier samples and l1-norm is used to implement feature selection, the objective function cannot find a closed solution. At the same time, for the four variables A, B, b,α, the objective function is not convex together. Therefore, with reference to the idea of the IRLS algorithm [5] with the advantages of fast convergence and close to the true value, we propose a new iterative optimization algorithm with A, B, b,α. In detail, we perform the following three steps iteratively until the predetermined conditions are met:

1)With α, A , B fixed update b

When α, A, B fixed, the last three terms in the objective function (9) can all be considered as constants, which is naturally zero with respect to the derivative b. We seek the derivative of b with the objective function (9) referred to \({\textbf {Z}} = \sum \limits _{i = {1}}^{d} {\alpha }_{i} \mathbf {K}^{(i)}\) to make it zero:

$$ 2\mathbf{e}^{T} \mathbf{eb}+ 2 \mathbf{e}^{T} \mathbf{ZAB} - 2 \mathbf{e}^{T}\mathbf{X}= 0 $$
(10)

After a simple calculation:

$$ {\mathbf{b}} = {{({{\mathbf{e}}^{T}}\mathbf{X} - {{\mathbf{e}}^{T}}{\mathbf{ZAB}})} {\left/ {\vphantom {{({{\mathbf{e}}^{T}}\mathbf{X} - {{\mathbf{e}}^{T}}{\mathbf{ZAB}})} n}} \right. \kern-\nulldelimiterspace} n} $$
(11)

2)With fixed α, b to update A, B

plug (11) to (9) and get:

$$ \min\limits_{\mathbf{A, B}} \left\| {\mathbf{X}-\mathbf{ZAB}} - \mathbf{e} ((\mathbf{e}^{T}\mathbf{X} - \mathbf{e}^{T} \mathbf{ZAB}) \left/\right. n)\right\|_{2,p} + \lambda_{1} \| \mathbf{AB}\|_{2,p} $$
(12)

To make H = In −eeT / n ∈ Rn×n, In ∈ Rn×n a unit matrix, (12) can be rewritten as:

$$ \min\limits_{\mathbf{A, B}} \left\| \mathbf{HX} - \mathbf{HZAB} \right\|_{2,p} + \lambda_{1} \| {{\mathbf{AB}}} \|_{2,p} $$
(13)
$$ \Leftrightarrow \min\limits_{\mathbf{A, B}} tr((\mathbf{HX} - \mathbf{HZAB})^{T} \mathbf{P}(\mathbf{HX}-\mathbf{HZAB} ))+ \lambda_{1}tr(\mathbf{B}^{T} \mathbf{A}^{T} \mathbf{QAB}) $$
(14)

where P ∈ Rn×n, Q ∈ Rd×d is the two diagonal matrix, among them:

$$ \mathbf{P}_{ii} = {p {\left/ {\vphantom {p {2\| {{{({\mathbf{HX}} - {\mathbf{HZAB}})}^{i}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {2\left\| {{{({\mathbf{HX}} - {\mathbf{HZAB}})}^{i}}} \right\|_{2}^{2 - p}}},i = 1, \cdot \cdot \cdot ,n,0 < p < 2 $$
(15)
$$ {{\mathbf{Q}}_{jj}} = {p {\left/ {\vphantom {p {2\| {(\mathbf{AB})}^{j} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {2\left\| {{{({\mathbf{AB}})}^{j}}} \right\|_{2}^{2 - p}}},j = 1, \cdot \cdot \cdot ,d,0 < p < 2 $$
(16)

To seek derivative for B, make it zero and obtain:

$$ {\mathbf{B}} = {({{\mathbf{A}}^{T}}({{\mathbf{Z}}^{T}}{{\mathbf{H}}^{T}}{\mathbf{PHZ}} + {\lambda_{1}}{\mathbf{Q}}){\mathbf{A}})^{- 1}}{{\mathbf{A}}^{T}}{{\mathbf{Z}}^{T}}{{\mathbf{H}}^{T}}{\mathbf{PHX}} $$
(17)

Substitute (17) into (14) and obtain:

$$ \begin{array}{l} \mathbf{A}^{*} = \arg\max\limits_{\mathbf{A}} tr{(\mathbf{A}^{T}({{\mathbf{Z}}^{T}}{{\mathbf{H}}^{T}}{\mathbf{PHZ}} + {\lambda_{1}}{\mathbf{Q}}){\mathbf{A}})^{- 1}}\\ \mathbf{A}^{T} \mathbf{Z}^{T} \mathbf{H}^{T} \mathbf{PHX} \mathbf{X}^{T} \mathbf{H}^{T} \mathbf{P}^{T} \mathbf{HZA} \end{array} $$
(18)

Through observation, we make:

$$ \mathbf{S}_{\mathbf{t}}= \mathbf{Z}^{\mathrm{T}} \mathbf{H}^{\mathrm{T}} \mathbf{PHZ}+\lambda_{1} \mathbf{Q} $$
(19)
$$ {{\mathbf{S}}_{\mathbf{b}}}={{\mathbf{Z}}^{\mathrm{T}}}{{\mathbf{H}}^{\mathrm{T}}}{\mathbf{PHX}}{\mathbf{X}^{\mathrm{T}}}{{\mathbf{H}}^{\mathrm{T}}}{{\mathbf{P}}^{\mathrm{T}}}{\mathbf{HZ}} $$
(20)

where St and Sb are the total class scatter matrix and the interclass scatter matrix defined in linear discriminante analysis (LDA), respectively. So the solution of (18) can be written as:

$$ {{\mathbf{A}}^{*}} = \arg\max\limits_{\mathbf{A}} tr\left[({{\mathbf{A}}^{T}}{{\mathbf{S}}_{\mathbf{t}}}{\mathbf{A}}{)^{- 1}}{{\mathbf{A}}^{T}}{{\mathbf{S}}_{\mathbf{b}}}{\mathbf{A}}\right] $$
(21)

This is obviously an LDA problem. The global optimal solution of (18) is the largest s eigenvector corresponding to the non-zero eigenvalue of St− 1Sb (if St is singular, St+ 1 indicating St pseudo-inverse in the eigenvector corresponding to the non-zero eigenvalue of St− 1Sb is calculated ).

3)With fixed A, B, b to update α

$$ \begin{array}{l} \min\limits_{\boldsymbol{\alpha}} \left\|\sum\limits_{i}^{d}{\alpha}_{i} \mathbf{K}^{(i)}\mathbf{W} - \mathbf{M}\right \|_{2,p} + \lambda_{2}\| {\boldsymbol{\alpha}} \|_{1}\\ = \min\limits_{\boldsymbol{\alpha}} \left\| \sum\limits_{i}^{d}{\alpha}_{i} \mathbf{Q}^{(i)} -\mathbf{M}\right \|_{2,p} +{\lambda_{2}}{\| \boldsymbol{\alpha}\|_{1}} \end{array} $$
(22)

where K(i)W = Q(i) ∈ Rn×d and M ∈ Rn×d represents X −eb.

Therefore, (22) can be rewrite as follow:

$$ \Leftrightarrow \min\limits_{\boldsymbol{\alpha}} tr\left( \left( \mathbf{M} - \sum\limits_{i = 1}^{d} \alpha_{i} \mathbf{Q}^{(i)}\right)^{T} \mathbf{P}\left( \mathbf{M} - \sum\limits_{i = 1}^{d} \alpha_{i} \mathbf{Q}^{(i)}\right)\right) + \lambda_{2} \|\boldsymbol{\alpha} \|_{1} $$
(23)
$$ \Leftrightarrow \min\limits_{\boldsymbol{\alpha}} \sum\limits_{i = 1}^{n}tr \left( \left( \mathbf{M}_{i} - \sum\limits_{j = 1}^{d} \alpha_{j} \mathbf{q}_{i,.}^{(j)} \right)^{T} \mathbf{P}_{ii} \left( \mathbf{M}_{i} - \sum\limits_{j = 1}^{d}\alpha_{j} \mathbf{q}_{i,.}^{(j)}\right)\right) + \lambda_{2} \|\boldsymbol{\alpha} \|_{1} $$
(24)

Here we can define: \(\mathbf {S}^{(i)} = \left ({\begin {array}{*{20}{c}} {\mathbf {q}_{i,1}^{(1)}}&{\mathbf {q}_{i,d}^{(1)}}\\ {\mathbf {q}_{i,1}^{(d)}}&{\mathbf {q}_{i,d}^{(d)}} \end {array}} \right ) \in {\mathbf {R}^{d \times d}}\)

Then (24) can be rewritten as follow:

$$ \Leftrightarrow \min\limits_{\boldsymbol{\alpha }} \sum\limits_{i = 1}^{n} tr({(\mathbf{m}_{i} - \boldsymbol{\alpha}^{T} \mathbf{S}^{(i)})}^{T} \mathbf{P}_{ii} ({{\mathbf{m}}_{i}} - {{\boldsymbol{\alpha }}^{T}}{{\mathbf{S}}^{(i)}}{\mathrm{))}} + {\lambda_{2}}{\| {\boldsymbol{\alpha }} \|_{1}} $$
(25)

By transforming, (25) can be converted to:

$$ \Leftrightarrow \min\limits_{\boldsymbol{\alpha }} \sum\limits_{i = 1}^{n} {{{\mathbf{P}}_{ii}}\| {{{\mathbf{m}}_{i}} - {{\boldsymbol{\alpha }}^{T}}{{\mathbf{S}}^{(i)}}} \|_{2}^{2}} + {\lambda_{2}}{\| {\boldsymbol{\alpha }} \|_{1}} $$
(26)

Expand (26) and we can get:

$$ \begin{array}{c} \Leftrightarrow \min\limits_{\boldsymbol{\alpha }} \sum\limits_{i = 1}^{n} \mathbf{P}_{ii} {\mathbf{m}}_{i}^{T} \mathbf{m}_{i} - 2{{\boldsymbol{\alpha }}^{T}}\sum\limits_{i = 1}^{n} {{{\mathbf{P}}_{ii}}{{\mathbf{S}}^{(i)}}{\mathbf{m}}_{i}^{T}} \\ + {{\boldsymbol{\alpha }}^{T}}\sum\limits_{i = 1}^{n} {{{\mathbf{P}}_{ii}}({{\mathbf{S}}^{(i)}}{{({{\mathbf{S}}^{(i)}})}^{T}}){\boldsymbol{\alpha }}} + {\lambda_{2}}{\| {\boldsymbol{\alpha }} \|_{1}} \end{array} $$
(27)

(27) can be written as:

$$ F({\boldsymbol{\alpha }}) = f({\boldsymbol{\alpha }}) + {\lambda_{2}}{\| {\boldsymbol{\alpha }} \|_{1}} $$
(28)

where \(\begin {array}{c} f({\boldsymbol {\alpha }}) = \left (\sum \limits _{i = 1}^{n} {{{\textbf {P}}_{ii}} {\textbf {m}}_{i}^{T}{{\textbf {m}}_{i}}-2{{\boldsymbol {\alpha }}^{T}}\sum \limits _{i = 1}^{n}{{{\textbf {P}}_{ii}} {{\textbf {S}}^{(i)}} {\mathbf {m}}_{i}^{T}} } \right .\\ \left .+ {{\boldsymbol {\alpha }}^{T}}\sum \limits _{i = 1}^{n} {{{\textbf {P}}_{ii}}({{\textbf {S}}^{(i)}}{{({{\textbf {S}}^{(i)}})}^{T}}){\boldsymbol {\alpha }}} \right ) \end {array}\).

The l1-norm of α can not be optimized by using the general method. Here the APGD algorithm [10] is used to optimize and solve the l1-norm of α, the specific process is as follows:

$$ {{\boldsymbol{\alpha }}^{t + 1}} = \arg\min\limits_{\boldsymbol{\alpha }} {G_{{\eta_{t}}}}({\boldsymbol{\alpha }},{{\boldsymbol{\alpha }}^{t}}) $$
(29)
$$ {G_{\eta_{t}}} ({\boldsymbol{\alpha}},{{\boldsymbol{\alpha }}^{t}}) = f({{\boldsymbol{\alpha }}^{t}}) + \left\langle {\nabla f({{\boldsymbol{\alpha }}^{t}}),{\boldsymbol{\alpha }} - {{\boldsymbol{\alpha }}^{t}}} \right\rangle + {{{\eta_{t}}{{\| {{\boldsymbol{\alpha }} - {{\boldsymbol{\alpha }}^{t}}} \|}^{2}}} {\left/ {\vphantom {{{\eta_{t}}{{\| {{\boldsymbol{\alpha }} - {{\boldsymbol{\alpha }}^{t}}} \|}^{2}}} 2}} \right. \kern-\nulldelimiterspace} 2} + {\lambda_{2}}{\| {\boldsymbol{\alpha }} \|_{1}} $$
(30)
$$ {{\boldsymbol{\alpha }}^{t + 1}} = \arg\min\limits_{\boldsymbol{\alpha }} \frac{1}{2}\left\| {{\boldsymbol{\alpha }} - {{({{\boldsymbol{\alpha }}^{t}} - \nabla f({{\boldsymbol{\alpha }}^{t}})} {\left/ {\vphantom {{({{\boldsymbol{\alpha }}^{t}} - \nabla f({{\boldsymbol{\alpha }}^{t}})} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}})}\right \|_{F}^{2} + {{{\lambda_{2}}{{\| {\boldsymbol{\alpha }} \|}_{1}}} {\left/ {\vphantom {{{\lambda_{2}}{{\| {\boldsymbol{\alpha }} \|}_{1}}} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}} $$
(31)

define Ut = αt −∇f(αt)/ ηt

$$ {{\boldsymbol{\alpha }}^{_{t + 1}}} = {\pi_{{\eta_{t}}}}({{\boldsymbol{\alpha }}^{t}}) = {\arg\min\limits_{\boldsymbol{\alpha}} \|\boldsymbol{\alpha}-{{\mathbf{U}}^{t}}} \|_{F}^{2} {\left/ {\vphantom {{\min\limits_{\boldsymbol{\alpha }} \| {{\boldsymbol{\alpha }} - {{\mathbf{U}}^{t}}} \|_{F}^{2}} 2}} \right. \kern-\nulldelimiterspace} 2 + {{{\lambda_{2}}{{\| {\boldsymbol{\alpha }} \|}_{1}}} {\left/ {\vphantom {{{\lambda_{2}}{{\| {\boldsymbol{\alpha }} \|}_{1}}} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}} $$
(32)

Make αi indicate the i-th component of α , expanding (31) according to components shows that there is no such αiαj(i ≠ j) term, so (31) has the following closed-form solution:

$$ {\boldsymbol{\alpha }}_{i}^{t + 1} = \left\{ {\begin{array}{*{20}{c}} {{\mathbf{U}}_{i}^{t} - {{{\lambda_{2}}} {\left/ {\vphantom {{{\lambda_{2}}} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}},{\mathrm{ }}{\mathbf{U}}_{i}^{t} > {{{\lambda_{2}}} {\left/ {\vphantom {{{\lambda_{2}}} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}}{\mathrm{; }}}\\ {0,{\mathrm{ }}\left| {{\mathbf{U}}_{i}^{t}} \right| \le {{{\lambda_{2}}} {\left/ {\vphantom {{{\lambda_{2}}} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}}{\mathrm{;}}}\\ {{\mathbf{U}}_{i}^{t} + {{{\lambda_{2}}} {\left/ {\vphantom {{{\lambda_{2}}} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}},{\mathrm{ }}{\mathbf{U}}_{i}^{t} < - {{{\lambda_{2}}} {\left/ {\vphantom {{{\lambda_{2}}} {{\eta_{t}}}}} \right. \kern-\nulldelimiterspace} {{\eta_{t}}}}{\mathrm{;}}} \end{array}} \right. $$
(33)

At the same time, in order to speed up the approximate gradient method in (29), this paper further introduces auxiliary variables, i.e.:

$$ {\mathbf{V}}(t{\mathrm{ + 1) = }}{\boldsymbol{\alpha }}(t{\mathrm{) + }}{{({\boldsymbol{\alpha }}(t + 1) - {\boldsymbol{\alpha }}(t{\mathrm{))(}}\beta (t) - 1)} {\left/ {\vphantom {{({\boldsymbol{\alpha }}(t + 1) - {\boldsymbol{\alpha }}(t{\mathrm{))(}}\beta (t) - 1)} {\beta (t + 1)}}} \right. \kern-\nulldelimiterspace} {\beta (t + 1)}} $$
(34)

where the coefficient is usually defined:

$$ \beta (t + 1) = {{(1 + \sqrt {1 + 4\beta {{(t)}^{2}}} )} {\left/ {\vphantom {{(1 + \sqrt {1 + 4\beta {{(t)}^{2}}} )} 2}} \right. \kern-\nulldelimiterspace} 2} $$
(35)

At this point, the optimization of the objective function (9) has been completed, and its concrete pseudo code can be given by the following Algorithm 1:

figure f

3.4 Convergence analysis

Next the convergence of the optimization of α is explained.

Theorem 1

Assume that {α(t)} isthe sequence generated by Algorithm 1, then for ∀ t ≥ 1, the following formula holds:

$$ L({\boldsymbol{\alpha }}(t{\mathrm{))}} - L({{\boldsymbol{\alpha }}^{*}}) \le {{2\gamma L\| {\mathbf{W}{\mathrm{(1) - }}{\mathbf{W}^{*}}} \|_{F}^{2}} {\left/ {\vphantom {{2\gamma L\| {\mathbf{W}{\mathrm{(1) - }}{\mathbf{W}^{*}}} \|_{F}^{2}} {{{(t + 1)}^{2}}}}} \right. \kern-\nulldelimiterspace} {{{(t + 1)}^{2}}}} $$
(36)

where γis a pre-defined constant, Lis the Lipschitz constant of the gradient in (28), \({{\boldsymbol {\alpha }}^{*}} = \arg \min \limits _{\boldsymbol {\alpha }} L({\boldsymbol {\alpha }})\) as well.

The proof of Theorem 1 is detailed in the literature [19]. Theorem 1 shows that the convergence rate of the accelerated approximate gradient algorithm proposed in this paper is \(O(\frac {1}{t^{2}})\), where t is the number of iterations in Algorithm 1.

Next we can prove that the value of the objective function in (13) monotonically decreases in each iteration. The objective function (13) is equivalent to:

$$ \min\limits_{\mathbf{A, B}} tr{\mathrm{((}}{\mathbf{HX}} - {\mathbf{HZAB}}{)^{T}}{\mathbf{P}}({\mathbf{HX}} - {\mathbf{HZAB}}{\mathrm{))}} + {\lambda_{1}}tr({{\mathbf{B}}^{T}}{{\mathbf{A}}^{T}}{\mathbf{QAB}}) $$
(37)

So we have

$$ \begin{array}{l} tr((\mathbf{HX} - \mathbf{HZ} \mathbf{A}^{(t + 1)} \mathbf{B}^{(t + 1)})^{T} \mathbf{P}^{(t)} (\mathbf{HX}- \mathbf{HZ} \mathbf{A}^{(t + 1)} \mathbf{B}^{(t + 1)}))\\ + {\lambda_{1}}tr(\mathbf{B}^{{(t + 1)}^{T}} \mathbf{A}^{{(t + 1)}^{T}} {\mathbf{Q}} \mathbf{A}^{(t + 1)} \mathbf{B}^{(t + 1)})\\ \le tr((\mathbf{HX} - \mathbf{HZ} \mathbf{A}^{(t + 1)} \mathbf{B}^{(t + 1)})^{T} \mathbf{P}^{(t)}(\mathbf{HX} - \mathbf{HZ} \mathbf{A}^{(t)} \mathbf{B}^{(t)}))\\ + {\lambda_{1}}tr({{\mathbf{B}}^{(t)}}^{T}{{\mathbf{A}}^{(t)}}^{T}{\mathbf{Q}}{{\mathbf{A}}^{(t)}}{{\mathrm{B}}^{(t)}}) \end{array} $$
(38)

Make Y = HX - HZAB, then we can go to:

$$\begin{array}{@{}rcl@{}} &&\Rightarrow \sum\limits_{i = 1}^{n} {{{\left\| {{{\mathbf{y}}^{i(t + 1)}}} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{y}}^{i(t + 1)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\| {{{\mathbf{y}}^{i(t)}}} \right\|_{2}^{2 - p}}}}\\ &&+ {\lambda_{1}}\sum\limits_{j = 1}^{d} {{{\left\| {{{\mathbf{w}}^{i(t + 1)}}} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{w}}^{i(t + 1)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\| {{{\mathbf{w}}^{i(t)}}} \right\|_{2}^{2 - p}}}}\\ && \le \sum\limits_{i = 1}^{n} {{{p\left\| \mathbf{y}^{i(t)} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{p\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\|\mathbf{y}^{i(t)} \right\|_{2}^{2 - p}}}}\\ &&+ {\lambda_{1}}\sum\limits_{j = 1}^{d} {{{p\left\| {{{\mathbf{w}}^{i(t)}}} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{p\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\| \mathbf{w}^{i(t)} \right\|_{2}^{2 - p}}}} \end{array} $$
(39)

For each i, we can get the following inequality:

$$ \begin{array}{l} \left\| \mathbf{y}^{i(t + 1)} \right\|_{2}^{2 - p} - {{\left\| {\mathbf{y}}^{i(t + 1)} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{y}}^{i(t + 1)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}\\ \le \| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p} - {{\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}} \end{array} $$
(40)

For each j, we can get the following inequality:

$$ \begin{array}{l} \lambda_{1}\left\| \mathbf{w}^{i(t + 1)} \right\|_{2}^{2 - p} - \lambda_{1} {{\left\| \mathbf{w}^{i(t + 1)} \right\|_{2}^{2(2 -p)}} {\left/ {\vphantom {{\| {{{\mathbf{w}}^{i(t + 1)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| \mathbf{w}^{i(t)} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2 - p}}}\\ \le {\lambda_{1}}\left\| {{{\mathbf{w}}^{i(t)}}} \right\|_{2}^{2 - p} - {\lambda_{1}}{{\left\| {\mathbf{w}}^{i(t)} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\| {{{\mathbf{w}}^{i(t)}}} \right\|_{2}^{2 - p}}} \end{array} $$
(41)

the following is available from (40) and (41):

$$\begin{array}{@{}rcl@{}} &&\sum\limits_{i = 1}^{n} {\left\| {{{\mathbf{y}}^{i(t + 1)}}} \right\|_{2}^{2 - p} - {{\left\| {{{\mathbf{y}}^{i(t + 1)}}} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{y}}^{i(t + 1)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\|\| {{{\mathbf{y}}^{i(t)}}} \right\|_{2}^{2 - p}}}}\\ &&+ {\lambda_{1}}\sum\limits_{j = 1}^{d} {\left\| {{{\mathbf{w}}^{i(t + 1)}}} \right\|_{2}^{2 - p} - {{\left\|\| {{{\mathbf{w}}^{i(t + 1)}}} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{w}}^{i(t + 1)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\| {{{\mathbf{w}}^{i(t)}}} \right\|_{2}^{2 - p}}}}\\ &&\le \sum\limits_{i = 1}^{n} {\left\| {{{\mathbf{y}}^{i(t)}}} \right\|_{2}^{2 - p} - {{\left\| {{{\mathbf{y}}^{i(t)}}} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}}}}\\ &&+ {\lambda_{1}}\sum\limits_{j = 1}^{d} {\left\| \mathbf{w}^{i(t)} \right\|_{2}^{2 - p} - {{\left\| {{{\mathbf{w}}^{i(t)}}} \right\|_{2}^{2(2 - p)}} {\left/ {\vphantom {{\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2(2 - p)}} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2 - p}}}} \right. \kern-\nulldelimiterspace} {({2 {\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p})\left\|\mathbf{w}^{i(t)} \right\|_{2}^{2 - p}}}} \end{array} $$
(42)

Then, combining (39) and (42) yields:

$$\begin{array}{@{}rcl@{}} \sum\limits_{i = 1}^{n} {\| {{{\mathbf{y}}^{i(t + 1)}}} \|_{2}^{2 - p}} &+& {\lambda_{1}}\sum\limits_{j = 1}^{d} {\| {{{\mathbf{w}}^{i(t + 1)}}} \|_{2}^{2 - p}} \\ &\le& \sum\limits_{i = 1}^{n} {\| {{{\mathbf{y}}^{i(t)}}} \|_{2}^{2 - p}} + {\lambda_{1}}\sum\limits_{j = 1}^{d} {\| {{{\mathbf{w}}^{i(t)}}} \|_{2}^{2 - p}} \end{array} $$
(43)

From the above analysis, it can be seen that the value of the objective function (9) is monotonically decreasing during each iteration, while the objective function (9) is a convex function respect to A, B, b, so it can be seen from (38) and Theorem 1, the objective function (9) will gradually converge to the global optimal solution.

4 Experiments

This section, some comparison algorithms are compared with NSFS Algorithm, and we use classification performance as evaluation index. Specifically, it is to first select features and then classify the datasets after dimension reduction.

4.1 Experiment settings

This paper tests the performance of the proposed feature selection algorithm on the bassis of twelve datasets,Footnote 1 Table 1 shows the details of Glass, Hill-Valley1 (with a lot of noise), Hill-valley2 (no noise), Yale, Yale, Colon, Arrhythmia , Clean, Sonar, Ionosphere, Lung_discrete, Urbanlandcover, Movements dataset.

Table 1 Dataset used in the experiment
Full size table

All experiments were run under the Win7 system and tested using MATLAB2014a software. This paper experimentally selects four comparison algorithms to compare with the NSFS algorithm:

  • LDA [6]: LDA is a global subspace learning method designed to minimize the distance between classes while maximizing the distance between classes when feature selection is performed.

  • SOGFS [23]: It gives an unsupervised feature selection algorithm for feature selection and maintaining local structure learning, while adaptively determining the similarity matrix, the restriction on the similarity matrix can retain more data structures information.

  • RLSR [4]: Propose a new semi-supervised feature selection method that can learn global and sparse solutions of projection matrix. This method uses a set of scale factors to re-adjust the regression coefficients in a least-squares regression. These scale factors are used to rank each feature to extend the least-squares regression model.

  • RSR [45]: Normalizes self-representation coefficient matrices by norm to select representative features and ensure robustness to outliers.

  • CSFS [3]: Convex Semi-supervised multi-label Feature Selection can conduct the feature selection via the norm regularization.

  • LS [12]: It evaluates the importance of a feature by the Laplacian Score, which considers the local manifold structure of the data set.

  • NetFS [16]: Propose a robust unsupervised feature selection framwork for data set, which embeds the latent representation learing into feature selection.

  • EUFS [32]: Propose a unsupervised feature selection methods by embedding feature selection into a clustering method.

4.2 Experiment results and analysis

This article uses the classification accuracy as an evaluation index, the higher the classification accuracy, the better the algorithm.And P_value is introduced to analyze the significant difference between the algorithms. In the experiment, the original datasets was divided into training set and test set by a 10-fold cross-validation method. The LIBSVM toolbox was used to classify the datasets after feature selection using each algorithm on the SVM, and the classification accuracy was obtained. For each algorithm, 10 experiments were performed on each datasets and the average of 10 experimental results was taken as the final classification accuracy, which can reduce the chance of accidents during the experiment. Take the results of 10 experiments and find the standard deviation to predict the stability of the model.

Accuracy refers to the classification accuracy rate of the original data processed by the feature selection algorithm, which can be expressed as:

$$ acc = \frac{m}{n} $$
(44)

where m represents the number of samples that are classified correctly and n represents the number of all samples.

The standard deviation represents the stability of the experimental results. Here, the paper finds the standard deviation of the classification accuracy results obtained from 10 times of 10-fold cross-validation. The smaller the standard deviation, the more stable the experimental results can be expressed as:

$$ std = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {{{({x_{i}} - \mu )}^{2}}} }}{N}} $$
(45)

where N represents the number of experiments, xi is the i-th experiment’s classification accuracy and μ is the average of the of N experiments’ classification accuracy.

The p-value is the probability that a statistical summary (such as the mean difference between two sets of samples) is the same as the actual observed data, or even larger, in a probability model. In other words, it is a test to assume that the null hypothesis is true or the performance is more serious. If the p-value is smaller than the selected significance level (0.05 or 0.01), the null hypothesis will be rejected and unacceptable.

It can be seen in Fig. 1 that the classification accuracy after the feature selection using the NSFS algorithm on each datasets is superior to the comparison algorithm in most cases. Because the Hill-Valley1 datasets contains a lot of noise, the classification accuracy of each algorithm fluctuates greatly, resulting in some of the experimental times the effect is slightly worse than the comparison algorithm, but the overall is still better than the comparison algorithm, this point in Table 2 Can be reflected.

Fig. 1
figure 1

Average classification accuracy of all methods for all datasets

Full size image
Table 2 Classification accuracy of different feature selection algorithms on different data sets (acc (%))
Full size table

From Table 2, it can be seen that our overall classification accuracy is 6.10% higher than that of the traditional LDA algorithm, 1.75% higher than the SOGFS algorithm, 1.42% higher than the RLSR algorithm, 2.26% higher than the RSR algorithm, 2.34% higher than the CSFS algorithm, 4.38% higher than the LS algorithm, 5.40% higher than the NetFS algorithm, and 5.41% higher than the EUFS algorithm. SOGFS, RLSR, CSFS and RSR algorithms are all extremely excellent algorithms in recent years. With the use of SVM with RBF kernels, our classification accuracy has been significantly improved. It can be seen that the NSFS algorithm has extremely excellent performance when performing feature selection. The datasets is not unrelated, and the relationship between them is not exactly linear. We introduce the kernel function to perform non-linear feature selection, taking full account of the non-linear relationship between the data, and therefore it has a good effect.

It can be seen from Table 3 that the standard deviation of the NSFS algorithm is relatively small compared to the comparison algorithm, so the NSFS algorithm has better robustness.

Table 3 Standard deviation of classification accuracy (std (%))
Full size table

As we can see in Table 4, the P_value between NSFS algorithm and other algorithms are all much more smaller than 0.01. Therefore, there are significant differences between the NSFS algorithm and the comparison algorithm.

Table 4 P_value between NSFS algorithm and other algorithms
Full size table

5 Conclusion

This paper introduces the kernel function based on the linear feature selection, considers the nonlinear relationship among data, and solves the problem that the data is linearly indivisible in the low-dimensional feature space, and improves the accuracy of feature selection. Low rank constraint, l2,p-norm, and lasso are all introduced to feature selection method to improve its performance. However, the computational complexity is increased when the kernel function is introduced. This is a problem that needs to be further solved. It can be seen from the experimental results in the previous section that the robustness of the NSFS algorithm needs to be improved. In the future work, we will expand the NSFS algorithm into a semi-supervised feature selection algorithm and gradually improve its computational complexity and robustness.