A possibilistic closed-loop supply chain: pricing, advertising and remanufacturing optimization

Abstract

This paper addresses pricing and reverse channel selection decisions in a closed-loop supply chain (CLSC) under fuzziness of demand function’s parameters. Despite numerous studies in which the demand is sensitive to selling price, in this paper demand function is considered as a function of both selling price and advertising level. Decisions are made in a CLSC consisting of a manufacturer, a retailer and a third party under centralized and decentralized decision making structures. In the decentralized structure, three different models are examined which differ on the member who collects used products from customers. Collection process is conducted by the manufacturer, the retailer or the third party. The problem is formulated as a Stackelberg game model in which the manufacturer acts as a leader. Moreover, various collection structures are deeply studied through a numerical analysis in which a real case study is provided and useful managerial insights are presented based on numerical results. The results show that the centralized structure outperforms the decentralized one in achieving the highest total expected profit, attaining highest demand by setting lowest selling price, and also by considering the environmental viewpoint and resource usage (achieving highest collection rate). Finally, sensitivity analysis on triangular fuzzy parameters is conducted to examine impact of triangular fuzzy parameters on model’s outputs.

1 Introduction

Environmental issues, importance of social responsibility and proper usage of materials, have increased the importance of recycling used products and induced firms to take the advantages of remanufacturing process. Closed-loop supply chain (CLSC) is a notion which arises in this area. A supply chain network is typically composed of suppliers, manufacturers, distributors and retailers [3]. CLSCs include both forward Logistics (supply, production and distribution) and Reverse Logistics (collecting and processing returned products) (Hajiaghaei-Keshteli & Fard). Remanufacturing process allows firms to produce products through collected used products from customers [33]. Usually, remanufacturing cost of a used product is less than the costs related to manufacturing a new product [12] which would stimulate firms to apply remanufacturing process and produce products through collecting used products. Therefore, remanufacturing process allows firms to increase their profit and undertake their social responsibility.

In this paper, we adopt the concepts of the fuzzy variable and possibility theory of fuzzy event defined by Liu [31]:

1.1 Possibility theory

In order to present the axiomatic definition of possibility, it is necessary to assign to each event A, a number $poss\left\{ A \right\}$ which indicates the possibility that A will occur. Let $\theta$ be a nonempty set representing the universe space, and $P\left\{ \theta \right\}$ the power set of $\theta$. In order to ensure that $poss\left\{ A \right\}$ has certain mathematical properties, we intuitively expect the possibility to have the following properties:

Axiom 1

$Pos\left\{ \theta \right\} = 1$.

Axiom 2

$Pos\left\{ \varTheta \right\} = 0$.

Axiom 3

$Pos\left\{ { \cup_{i} A_{i} } \right\} = \sup_{i} Pos\left\{ {A_{i} } \right\}$ for any collection $\left\{ {A_{i} } \right\}$ in $P\left\{ \theta \right\}$.

Axiom 4

Let $\theta_{i}$ be nonempty sets on which $Pos_{i} \left\{ \bullet \right\}$ satisfy the first three axioms, $i = 1,2, \ldots ,n$, respectively, and $\theta = \,\theta_{1} \times \theta_{2} \times \cdots \times \theta_{n}$. Then for each $A \in \,P(\theta )$, $Pos\left\{ A \right\} = \sup\nolimits_{{(\theta_{1} \times \theta_{2} \times \cdots \times \theta_{n} ) \in A}} Pos_{1} \left\{ {\theta_{1} } \right\} \wedge \,Pos_{2} \left\{ {\theta_{2} } \right\}\, \wedge \cdots \wedge \,Pos_{n} \left\{ {\theta_{n} } \right\}$. In this case $Pos = Pos_{1} \wedge \,Pos_{2} \, \wedge \cdots \wedge \,Pos_{n} .$.

The first three axioms were introduced to define a possibility measure and the fourth one was introduced to define the product possibility measure. Note that $Pos = Pos_{1} \wedge \,Pos_{2} \, \wedge \cdots \wedge \,Pos_{n}$ satisfies the first three axioms.

Definition 1

Let $\theta$ be a nonempty set and $P\left\{ \theta \right\}$ the power set of $\theta$. Then, $pos$ is called a possibility measure if it satisfies the first three axioms.

Definition 2

Let $\theta$ be a nonempty set, and $P\left\{ \theta \right\}$ the power set of $\theta$ and $Poss$, a possibility measure. Then the triplet $\left( {\theta ,P(\theta ),Poss} \right)$ is called possibility space.

Definition 3

A random fuzzy variable is a function from the possibility space $\left( {\theta ,P(\theta ),Poss} \right)$ to the set of random variables.

Definition 4

Consider two fuzzy variables as $\tilde{a}_{j} = \left( {a_{j1} ,a_{j2} ,a_{j3} } \right)$ and $\tilde{b}_{j} = \left( {b_{j1} ,b_{j2} ,b_{j3} } \right)$. Then, we will have:

$$\tilde{a}_{j} - \tilde{b}_{j} = \left( {a_{j1} - b_{j1} ,a_{j2} - b_{j2} ,a_{j3} - b_{j3} } \right)$$

$$\frac{1}{{\tilde{a}_{j} }} = \left( {\frac{1}{{a_{j3} }},\frac{1}{{a_{j2} }},\frac{1}{{a_{j1} }}} \right)$$

$$k\tilde{a}_{j} = \left\{ \begin{aligned} \left( {ka_{j1} \,\,,\,\,ka_{j2} \,\,,\,\,ka_{j3} } \right)\quad {\text{if}}\,\,\,k \in {\mathbb{R}}^{ + } \hfill \\ \left( {ka_{j3} \,\,,\,\,ka_{j2} \,\,,\,\,ka_{j1} } \right)\quad {\text{if}}\,\,\,k \in {\mathbb{R}}^{ - } \hfill \\ \end{aligned} \right.$$

$$\tilde{a}_{j} .\,\tilde{b}_{j} = \left\{ \begin{aligned} \left( {a_{j1} b_{j1} \,\,,\,\,a_{j2} b_{j2} \,\,,\,\,a_{j3} b_{j3} } \right)\quad {\text{if}}\,\,\,a_{i} > 0,\,\,\,b_{i} > 0 \hfill \\ \left( {a_{j3} b_{j3} \,\,,\,\,a_{j2} b_{j2} \,\,,\,\,b_{j1} a_{j1} } \right)\quad {\text{if}}\,\,\,a_{i} < 0,\,\,\,b_{i} < 0 \hfill \\ \left( {a_{j1} b_{j3} \,\,,\,\,a_{j2} b_{j2} \,\,,\,\,a_{j3} b_{j1} } \right)\quad {\text{if}}\,\,\,a_{i} < 0,\,\,\,b_{i} > 0 \hfill \\ \end{aligned} \right.$$

2 Literature review

The main decisions in a CLSC are pricing and products’ collecting policies. There is a vast body of research dealing with different aspects of remanufacturing process in a CLSC. Savaskan et al. [34] formulated a Stackelberg model for determining the products’ selling price and selecting a member who is in charge of collecting process among members of a CLSC (i.e., a manufacturer, a retailer or a third party). Product’s selling price and used product collection rate in the cellular telephone industry are determined by Guide et al. [20]. Debo et al. [10] presented a market model which determines the pricing decisions related to remanufactured products along with the technology to be selected for remanufacturing process.

In some studies, the member who is responsible for collecting used products is known a priori. Chang and Zhang [4] have studied the remanufacturing process in a CLSC, which consists of a manufacturer, a retailer and several customers, in which the retailer is in charge of collecting products, while Chung et al. [8] considered a third party to be responsible for collecting products in their article There are studies in which the member who is responsible for collecting used products has to be selected between potential members. Hong et al. [23] presented a model which aims to select the best reverse channel from the following alternatives: (1) both manufacturer and retailer undertake the responsibility of collecting used products, (2) the retailer and the third party undertake the responsibility of collecting used products and (3) both manufacturer and third party undertake the responsibility of collecting used products. Huang et al. [26] considered a CLSC in which customers buy the products through the retailer in the forward side of the supply chain, and in the reverse side, the retailer and a third party collect used products from customers in a competitive manner.

There are other studies which consider market competition between remanufactured and new products. Several studies have investigated pricing strategies for undifferentiated products in an unsegmented market. Ferrer and Swaminathan [17] have presented a multi-period model which considers competition between new products, which are manufactured from the first time period, and remanufactured products, which are produced from the beginning of the second time period. Their work is an extension to that of Majumder and Groenevelt [32] which considers the two-period model. The studies conducted by Atasu et al. [1], Heese et al. [22], Zhou and Yu [49] are other studies in this area. On the other hand, there are studies which investigate pricing strategies for differentiated products in a segmented market such as those presented by Chen and Chang [5], Ferguson and Toktay [16], Wu [42]. The study presented by Ferrer and Swaminathan [18] is another example in this field which determines optimal pricing and remanufacturing strategies for a producer who sells both new products and remanufactured products in different prices, in a monopoly environment.

Despite numerous studies on CLSCs, the majority of these studies are done under the certainty of data. Nevertheless, there are numerous cases for which considering certain data cannot reflect the real world’s conditions and it is essential to incorporate uncertainty in such cases. One way to deal with data uncertainty due to lack of knowledge in estimating the precise values of parameters is through fuzzy set theory which was introduced by Zadeh [46]. When there is lack of objective data, using fuzzy set theory allows decision makers to estimate the values of parameters based on subjective judgments of experts. There are few studies on CLSCs under fuzzy uncertainty. Wei et al. [41] investigated pricing decisions in a CLSC under fuzzy uncertainty. The optimal decisions are made in both centralized and decentralized decision making structures. In this study, parameters such as manufacturing and remanufacturing costs, market base and price elasticity are considered as fuzzy variables. Wei and Zhao [40] have determined the optimal decisions such as wholesale price and selling prices in a CLSC which is composed of a manufacturer and multiple retailers under retailers’ competition, where customers’ demand, products’ collection rate and remanufacturing costs are fuzzy variables. Zhao et al. [47] considered a CLSC which is composed of a manufacturer and two retailers. Decisions such as collection and pricing decisions are made in a fuzzy environment in which parameters such as customers’ demand, remanufacturing cost and manufacturing cost are considered as fuzzy variables. Ordering and pricing decisions in a CLSC under both centralized and decentralized decision making structures are investigated by Song et al. [36]. This study is conducted under fuzzy uncertainty, in which demand is a fuzzy variable.

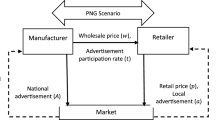
Advertising is one of the common measures to induce customers’ demand, which is highly invoked in the literature [38, 45]. Two prevalent manners of advertising are the manufacturer’s advertising and local advertising. Manufacturer’s advertising refers to a kind of advertising that the manufacturer pays for advertisement and the main target is to induce the long-term demand. Local advertising refers to a kind of advertising that the retailer pays for advertisement. Usually, local advertising is performed through the local media to induce short-term demand [25, 44]. Comparing the manufacturer’s advertising with local advertising, one can conclude that the former is more pervasive and it is done in a national level while the latter is done in a local level. Another common advertising in which the manufacturer and retailer jointly perform and pay for advertisement is the cooperative advertising. In the cooperative advertising, a portion or all of the advertisement budget for the manufacturer’s product which is done in a local level is paid by the manufacturer [2].

Many previous studies assume that demand is only affected by product’s price and therefore they considered the demand as a function of price. This assumption is highly invoked in the literature [30]. There are also studies which assume demand is only affected by advertising level. In the study conducted by Huang et al. [27], demand is only affected by advertisement (both local and national advertising efforts) and not by price. However, there are several other studies that assert that the amount of expenditure in marketing activities such as marketing research and product advertisement also affect customers’ demand. Xie and Wei [43] have taken into account both the selling price and advertisement effects on customers’ demand. In this study, demand is sensitive to price and both local and national advertisement. Esmaeili et al. [14] also considered the effects of marketing expenditure on customers’ demand where demand is affected by marketing expenditure along with the price charged by the buyer. In their study, several seller–buyer supply chain models under cooperative and noncooperative relationships are presented. Yue et al. [45] incorporated price effect on demand function presented by Huang et al. [27] and considered the effects of price and advertisement on customers’ demand and formulated demand as increasing function of local and national advertisement efforts and decreasing function of price. Esmaeili et al. [13] presented four separated CLSC models for which demand of customers are affected by both products’ selling price and marketing efforts. The models differ on products’ collection structure in which the manufacturer, retailer or both the manufacturer and retailer assume responsibility of collecting used products in models 1–3, respectively, and in model 4 no collection process is carried out. Hong et al. [24] presented four models in a CLSC that differ in a reverse channel structure and in each model a member carries out the used products collection process. They have considered demand to be affected by both selling price and advertising investment and investigated the optimal decisions in a deterministic environment where all parameters are assumed to be deterministic. Moreover, some related research can be found in the works of Zhu et al. [50], Koç [29], Khalilpourazari et al. [28], Hajiaghaei-Keshteli and Fard [21], Fallahpour et al. [15].

This study investigates the optimal pricing, used products’ collecting and advertising decisions in a CLSC which is composed of a manufacturer, a retailer and a third party under fuzzy uncertainty. Four models are developed by considering different reverse structures using game theory.

One of the models is formulated as a centralized decision making model, while the others are formulated as decentralized decision making models. Customers’ demand is considered as a linear function of both product’s selling price and advertising investment whose parameters are considered as fuzzy variables to capture their inherent epistemic uncertainty (i.e., lack of knowledge in estimating their precise values). Accordingly, the retailer can stipulate customers’ demand through setting the value of product’s price and the level of investment for advertising. Thus, pricing and advertising decisions have to be made in the presented models. It is also assumed that the retailer is responsible for advertising and decides about the amount of investment in advertising. In other words, the advertising type in this paper is the local advertising. The optimal values of selling price, collection rate of products and level of investment for advertising are derived so that the expected profit of each model is maximized. To examine the results, a numerical analysis on a real case study is conducted whose results are investigated in depth. Besides, a number of sensitivity analyses are conducted to show how different parameters can influence the models’ outputs. Finally, several managerial insights and implications are presented based on the numerical results.

The remainder of the paper is organized as follows. The problem description is presented in detail in Sect. 3. In Sect. 4, four mathematical models with different structures are formulated. It is worth noting that for the sake of readability and clarity, all proofs of propositions are given in appendices. Section 5 includes a numerical analysis on developed models from which useful managerial insights are derived. Finally, Sect. 6 presents the concluding remarks and some avenues for further research.

3 Problem description

In this paper, some optimal decisions are made in a CLSC under four different structures over a single-period setting. These CLSCs include a manufacturer, a retailer, and a third party. There are two types of channels, i.e., the forward and reverse channels in these CLSCs. The manufacturer produces products and sells them to customers through a retailer in the forward channel. One of the CLSC’s members collects the used products from customers and sends the collected products to the manufacturer in order to be used in remanufacturing process via the reverse channel. In this way, the manufacturer produces products using either new raw materials or the used products whose qualities are assumed to be equal.

Four different CLSC structures are investigated in this paper which mainly differ in their reverse channel structure (see Figs. 1, 2, 3 and 4). The first structure has a centralized decision making framework in which there is a single decision maker who makes all the decisions. In this case, the collection process is conducted by the integrated supply chain (Fig. 1). In the second structure, the collection process is directly conducted by the manufacturer (Fig. 2). In the third structure, the collection process is conducted by the retailer and collected products are transferred to the manufacturer to be utilized in remanufacturing process (Fig. 3). Finally, in the fourth structure, the collection process is outsourced and it is conducted by a third party by whom the collected products are transferred to the manufacturer (Fig. 4). As Figs. 1, 2, 3 and 4 show, the forward channel is common at these four structures.

Fig. 1

The CLSC structure under centralized model (Model 1)

Fig. 2

The CLSC structure under decentralized model-collection by the manufacturer (Model 2)

Fig. 3

The CLSC structure under decentralized model-collection by the retailer (Model 3)

Fig. 4

The CLSC structure under decentralized model-collection by a third party (Model 4)

A supply chain with these characteristics is usually common in different industrial sectors. For example, Apple’s retail stores and manufacturing sites are equipped with a reverse system for receiving old apple products (iPods) from the customers. Samsung collects some of its used products such as televisions from customers. Another similar examples are Canon, Kodak and Xerox [13, 34].

Following assumptions are considered in this study:

• The products which are produced through remanufacturing process are of the same quality as the products which are produced through the manufacturing process using new raw materials. So, they are sold at the same price at the same markets [7].

• Without losing generality, all of the collected products can be used in the remanufacturing process (i.e., there is no disposal) [7].

• This paper assumes a CLSC with symmetrical information where the information is known to all members and no member has any private information [34].

• Since customers’ total demand cannot be satisfied using remanufactured products, the manufacturer has to fulfill the total demand by producing products from new raw materials in addition to remanufacturing process [34].

Table 1 presents the notations used for mathematical formulation.

Table 1 Notations

Customers’ demand is considered as a linear function that is sensitive to the selling price ($p$) and the amount of investment in advertising for the products ($f$) [6, 11, 24, 39].

$$D(p,f) = \tilde{a} - \tilde{b}p + \tilde{c}\sqrt f \quad \quad \tilde{a},\tilde{b},\tilde{c} > 0,\,\,\,\tilde{a} > \tilde{b}s_{m}$$

(1)

where $\tilde{a},\;\tilde{b}$ and $\tilde{c}$ are presented as independent nonnegative triangular fuzzy variables to reflect their impreciseness due to the lack of required objective data. Accordingly, these parameters are mainly estimated based on experts’ subjective judgments and professional opinions.

The manufacturing cost of a product by the new raw material is labeled by $s_{m}$ and the production cost of a product produced through the remanufacturing process is labeled by $s_{r}$. We assume that $s_{m} \ge s_{r}$ which is commonly considered in the literature [34]. Xerox is a good example to approve this assumption. Producing products using remanufacturing process saves Xerox an approximate value of 45–60% in manufacturing costs. The expression $s = s_{m} - s_{r}$ expresses the money saved by producing a product through remanufacturing process.

The percentage of total products manufactured using collected products is shown by $\,u$. The cost of manufacturing a product from new raw materials is obtained by $(1 - u)s_{m}$ and the cost of producing a product from collected used products is obtained by $\,us_{r}$. Therefore, the average unit manufacturing cost of a product from both new raw materials and collected products is calculated as $(1 - u)s_{m} + us_{r}$ [34].

The collection process has a cost for the member who is responsible for collecting products. As it is commonly used in the literature, this cost is a function of remanufacturing effort and it is formulated as $Hu^{2}$ where $H$ is a scaling parameter. It can be easily proven that this function is convex with respect to $u$ [35].

4 Mathematical modeling

In this section, four mathematical models are developed considering centralized and decentralized decision making structures. The first model is adapted for a CLSC with a centralized structure in which the supply chain uses an integrated (i.e., central) decision making framework and all the members act as an integrated system. Models 2–4 are adapted for CLSCs with decentralized structures under different collection channels. The collection process in models 2, 3 and 4 is conducted by the manufacturer, the retailer and a third party, respectively.

4.1 The centralized structure—Model 1

The first model introduces a case in which the supply chain is considered as an integrated system and there is only one controller (i.e., decision maker) with the aim of optimizing the total system’s performance by means of maximizing the total system’s profit. To deal with fuzziness of demand function’s parameters, we have used expected value operator which is presented by Zhao et al. [48] as “Appendix 1.” The expected value of total profit is written as follows:

$$E\left[ {\pi_{total}^{1} (p,u,f)} \right] = E\left[ {(p - s_{m} + us)(\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f ) - Hu^{2} - f} \right]$$

(2)

Expected value (Total supply chain’s profit) = Expected value (gained revenue from selling products to customers − cost of manufacturing products from new raw materials + cost saving from remanufacturing process − investment in collecting used products − investment in advertising for products).

So the optimization problem is formulated as the following expected value model:

$$\left\{ \begin{aligned} Max_{p,u,f} E\left[ {\pi_{total}^{1} (p,u,f)} \right] \hfill \\ {\text{subject}}\,{\text{to}}: \hfill \\ \quad p - s_{m} + us \ge 0 \hfill \\ \quad Pos\left( {\left\{ {\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0} \right\}} \right) = 0 \hfill \\ \end{aligned} \right.$$

(3)

Since the customer’s demand is a nonnegative value, we set $Pos(\{ \tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0\} ) = 0$.

Proposition 1

• (a) The total supply chain’s expected profit,$E\left[ {\pi_{total}^{1} (p,u,f)} \right]$, is strictly jointly concave in$p$, $u$, concave in$f$, but not jointly concave in$p$, $u$and$f$.

  As a result from Proposition 1(a),$E\left[ {\pi_{total}^{1} (p,u,f)} \right]$has an optimal unique solution with respect to$p$and$u$, while the optimal value of decision variables$p$, $u$and$f$cannot be obtained only by taking the first-order partial derivatives of$E\left[ {\pi_{total}^{1} (p,u,f)} \right]$with respect to$p$, $u$and$f$. Thus, the two-stage optimization approach introduced by Dan et al. [9] is used in this case. Taking the first-order partial derivatives of total expected profit with respect to$p$and$u$, setting them equal to zero and solving them simultaneously, we can obtain the optimal values of$p$and$u$as functions of$f$. Then, two other steps are followed to obtain the optimal value of$f$. First, the optimal values of$p$and$u$are substituted in the total expected profit function. Second, the first-order partial derivative of total expected profit function with respect to$f$is taken and is set equal to zero.

• (b) The optimal values of selling price and collection rate for any given amount of investment in advertising ($f$) are given by:

  $$p^{*} (f) = \frac{{2HE(\tilde{a}) + 2H\sqrt f E(\tilde{c}) + 2Hs_{m} E(\tilde{b}) - s^{2} E(\tilde{a})E(\tilde{b}) - s^{2} \sqrt f E(\tilde{c})E(\tilde{b})}}{{E(\tilde{b})\left[ {4H - s^{2} E(\tilde{b})} \right]}}$$

  (4)
  $$u^{*} (f) = \frac{{sE(\tilde{a}) + s\sqrt f E(\tilde{c}) - sE(\tilde{b})s_{m} }}{{4H - s^{2} E(\tilde{b})}}$$

  (5)

• (c) The optimal value of investment in advertising is given by:

  $$f^{ * } = \left[ {\frac{{HE(\tilde{c})(E(\tilde{a}) - s_{m} E(\tilde{b}))}}{{E(\tilde{b})(4H - s^{2} E(\tilde{b})) - HE(\tilde{c})^{2} }}} \right]^{2}$$

  (6)

  If $Pos(\left\{ {\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0} \right\}) = 0$ holds.

  In order to get a solution in which$u^{*} \le 1$, we have$H > \frac{{sE(\tilde{b})(E(\tilde{a}) - s_{m} E(\tilde{b}) + sE(\tilde{b}))}}{{4E(\tilde{b}) - E(\tilde{c})^{2} }}$and$0 < E(\tilde{c}) < 2\sqrt {E(\tilde{b})}$. Substituting$f^{ * }$into Eqs. (4) and (5), the optimal values of selling price ($p^{*}$) and collection rate ($u^{*}$) are obtained. Substituting the optimal values of variables into Eq. (2), the total optimal expected profit is obtained.

Proof

See “Appendix 1.”

4.2 The decentralized structure (the manufacturer’s Stackelberg model)

In the decentralized structure, each member tries to maximize his own profit without considering other members. So, the Stackelberg game is used to model such decision making process. Using the Stackelberg game model, the manufacturer and the retailer are considered as the leader and the follower, respectively. In this condition, at first, the manufacturer announces his own decisions and then, after knowing the manufacturer’s decisions, the retailer makes his decisions.

In the decentralized structure, three cases are investigated. The main difference between these cases is on the member who is in charge of the collection process.

4.2.1 Model 2—Collection by the manufacturer

In this case, the collection process is carried out by the manufacturer. So the manufacturer is the member who makes decisions about the collection rate and the wholesale price. In the next layer, the retailer decides on the amount of investment in advertising and products’ selling price.

The expected values of the manufacturer’s and retailer’s profit are written as follows:

$$E\left[ {\pi_{man}^{2} (p,w,u,f)} \right] = E\left[ {(w - s_{m} + us)\tilde{D}(p,f) - Hu^{2} } \right]$$

(7)

$$E\left[ {\pi_{ret}^{2} (p,w,f)} \right] = E\left[ {(p - w)\tilde{D}(p,f) - f} \right]$$

(8)

The optimization problem is then formulated as follows:

$$\left\{ {\begin{array}{*{20}c} \begin{aligned} & Max_{w,u} \begin{array}{*{20}c} {E\left[ {\pi_{man}^{2} (p^{*} ,w,u,f^{*} )} \right]} \\ \end{array} \\ & {\text{subject}}\,{\text{to}}: \\ & \quad \quad \quad w - s_{m} + us \ge 0 \\ & \quad \quad \quad p^{*} ,f^{*} \,{\text{are derived from solving the following problem}} \\ & \quad \quad \quad \left\{ \begin{aligned} Max\,_{p,f} E\left[ {\pi_{ret}^{2} (p,w,f)} \right] \hfill \\ s.t: \hfill \\ p - w \ge 0 \hfill \\ Pos\left( {\left\{ {\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0} \right\}} \right) = 0 \hfill \\ \end{aligned} \right. \\ \end{aligned} \\ {} \\ \end{array} } \right.$$

(9)

Proposition 2

• (a) The retailer’s expected profit function is strictly concave in$p$but is not jointly concave in$p$and$f$.

• (b) The manufacturer’s expected profit function is strictly jointly concave in$u$and$w$.

• (c) The optimal values of collection rate, wholesale price and selling price for any given amount of investment in advertising are given by:

  $$u^{*} (f) = \frac{s}{{8H - s^{2} E(\tilde{b})}}(E(\tilde{a}) + \sqrt f E(\tilde{c}) - s_{m} E(\tilde{b}))$$

  (10)
  $$w^{*} (f) = \frac{{4HE(\tilde{a}) + 4H\sqrt f E(\tilde{c}) + 4Hs_{m} E(\tilde{b}) - s^{2} E(\tilde{a})E(\tilde{b}) - s^{2} \sqrt f E(\tilde{c})E(\tilde{b})}}{{E(\tilde{b})(8H - s^{2} E(\tilde{b}))}}$$

  (11)
  $$p^{*} (f) = \frac{{(6H - s^{2} E(\tilde{b}))(E(\tilde{a}) + \sqrt f E(\tilde{c})) + 2Hs_{m} E(\tilde{b})}}{{E(\tilde{b})(8H - s^{2} E(\tilde{b}))}}$$

  (12)

• (d) The optimal value of investment in advertising is given by:

  $$f^{*} = \left[ {\frac{{(4H^{2} E(\tilde{c}))(E(\tilde{a}) - s_{m} E(\tilde{b})}}{{E(\tilde{b})(8H - s^{2} E(\tilde{b}))^{2} - 4H^{2} E(\tilde{c})^{2} }}} \right]^{2}$$

  (13)

  If$w - s_{m} + us \ge 0$,$p - s_{m} + us \ge 0$and$Pos(\left\{ {\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0} \right\}) = 0$hold.

  Now, by substituting Eq. (13) into Eqs. (10–12), the optimal values of collection rate ($u^{*}$), wholesale price ($w^{*}$) and selling price ($p^{*}$), are obtained. Afterward, by substituting the optimal values of variables into Eqs. (7) and (8), the optimal values the members’ expected profits are obtained.

Proof

See “Appendix 2.”

4.2.2 Model 3—Collection by the retailer

In this case, the collection process is carried out by the retailer. Collected products are sent to the manufacturer to be used in remanufacturing process. The retailer is paid $k$ units of money by the manufacturer for each product he has collected (as the buy-back payment). So, the manufacturer is the member who makes decisions about both the buy-back payment and the wholesale price. In the next layer, the retailer decides about the amount of investment in advertising, selling price and collection rate.

The expected values of the members’ profit (i.e., the manufacturer and the retailer) are written as follows:

$$E\left[ {\pi_{man}^{3} (p,w,u,f,k)} \right] = E\left[ {(w - s_{m} + us - uk)\tilde{D}(p,f)} \right]$$

(14)

$$E\left[ {\pi_{ret}^{3} (p,w,u,f,k)} \right] = E\left[ {(p - w + ku)\tilde{D}(p,f) - Hu^{2} - f} \right]$$

(15)

The optimization problem is formulated as follows:

$$\left\{ \begin{aligned} & Max_{w,k} \begin{array}{*{20}c} {E\left[ {\pi_{man}^{3} (p^{*} ,w,u^{*} ,f^{*} ,k)} \right]} \\ \end{array} \\ & {\text{subject}}\,{\text{to}}: \\ & \quad \quad \quad w - s_{m} + us - uk \ge 0 \\ & \quad \quad \quad p^{*} ,u^{*} ,f^{*} \,{\text{are derived from solving the}}\,{\text{following problem:}} \\ & \quad \quad \quad \left\{ \begin{aligned} Max\,_{p,u,f} E\left[ {\pi_{ret}^{3} (p,w,u,f,k)} \right] \hfill \\ s.t: \hfill \\ p - w + ku \ge 0 \hfill \\ Pos(\left\{ {\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0} \right\}) = 0 \hfill \\ \end{aligned} \right. \\ \\ \end{aligned} \right.$$

(16)

Proposition 3

• (a) The retailer’s expected profit function is strictly jointly concave in$p$and$u$but it is not jointly concave in$p$, $u$and$f$.

• (b) The optimal values of wholesale price, collection rate and selling price for any given amount of investment in advertising and buy-back payment are given by:

  $$\begin{aligned} w^{*} (f,k) & = \frac{1}{{8HE(\tilde{b}) - 2ksE(\tilde{b})^{2} }}( - 2ksE(\tilde{a})E(\tilde{b}) - 2ks\sqrt f E(\tilde{b})E(\tilde{c}) + 4HE(\tilde{a}) \\ & \quad + \;4H\sqrt f E(\tilde{c}) + k^{2} \sqrt f E(\tilde{b})E(\tilde{c}) + 4Hs_{m} E(\tilde{b}) - k^{2} s_{m} E(\tilde{b})^{2} + k^{2} E(\tilde{a})E(\tilde{b})) \\ \end{aligned}$$

  (17)
  $$u^{*} (f,k) = \frac{{kE(\tilde{a}) + k\sqrt f E(\tilde{c}) + ks_{m} E(\tilde{b})}}{{2(4H - sE(\tilde{b}))}}$$

  (18)
  $$p^{*} (f,k) = \frac{{3HE(\tilde{a}) + 3H\sqrt f E(\tilde{c}) - ksE(\tilde{b})E(\tilde{a}) - ks\sqrt f E(\tilde{c})E(\tilde{b}) + Hs_{m} E(\tilde{b})}}{{(4H - ksE(\tilde{b}))E(\tilde{b})}}$$

  (19)

• (c) The optimal value of investment in advertising is given by:

  $$f^{*} (k) = \left[ {\frac{{HE(\tilde{c})(4H - k^{2} E(\tilde{b}))(E(\tilde{a}) - s_{m} E(\tilde{b}))}}{{(4H - ksE(\tilde{b}))^{2} 4E(\tilde{b}) - HE(\tilde{c})^{2} (4H - k^{2} E(\tilde{b}))}}} \right]^{2}$$

  (20)

  If$w - s_{m} + us - uk \ge 0$,$p - w + ku \ge 0$and$Pos(\left\{ {\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0} \right\}) = 0$hold.

  In this way, by substituting Eq. (20) into Eqs. (17) to (19), the optimal values of wholesale price ($w^{*}$), collection rate ($u^{*}$) and selling price ($p^{*}$) are obtained.

• (d) The optimal value of payment to retailer for each collected product is given by:

  $$k^{*} = s$$

  (21)

  Finally, by substituting the optimal values of variables into Eqs. (14) and (15), the optimal values of the members’ expected profits are obtained.

Proof

See “Appendix 3.”

4.2.3 Model 4—Collection by a third party

In this case, collection process is outsourced and carried out by a third party. The third party is then paid by the manufacturer for each collected product. In this case, the manufacturer as a leader is the member who makes decision about the payment for collected products. He also determines the value of wholesale price. In the next layer, decisions are made simultaneously by both the third party and the retailer based on Bertrand game model. In other words, the retailer makes decisions about selling price and amount of investment in advertising and the third party makes decision about the collection rate.

The expected value of the members’ profit for the manufacturer, the retailer and the third party are written, respectively, as follows:

$$E\left[ {\pi_{man}^{4} (p,w,u,f,k)} \right] = E\left[ {(w - s_{m} + us - uk)\tilde{D}(p,f)} \right]$$

(22)

$$E\left[ {\pi_{ret}^{4} (p,w,f)} \right] = E\left[ {(p - w)\tilde{D}(p,f) - f} \right]$$

(23)

$$E\left[ {\pi_{3par}^{4} (p,u,f,k)} \right] = E\left[ {(ku)\tilde{D}(p,f) - Hu^{2} } \right]$$

(24)

Accordingly, the optimization problem of this case is as follows:

$$\begin{aligned} & Max_{w,k} \begin{array}{*{20}c} {E\left[ {\pi_{man}^{4} (p^{*} ,w,u^{*} ,f^{*} ,k)} \right]} \\ \end{array} \\ & {\text{subject}}\,{\text{to}}: \\ & \quad \quad \quad w - s_{m} + us - uk \ge 0 \\ & \quad \quad \quad p^{*} ,f^{*} \,{\text{are derived from solving the following problem:}} \\ & \quad \quad \quad \left\{ \begin{aligned} Max\,_{p,f} E\left[ {\pi_{ret}^{4} (p,w,f)} \right] \hfill \\ s.t: \hfill \\ \,\,\,\,\,\,\,\,p - w \ge 0 \hfill \\ \,\,\,\,\,\,\,\,Pos(\left\{ {\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f < 0} \right\}) = 0 \hfill \\ \end{aligned} \right. \\ & \quad \quad \quad u^{*} \,{\text{is derived from solving the following problem:}} \\ & \quad \quad \quad \left\{ {Max\,_{u} E\left[ {\pi_{3par}^{4} (p,u,f,k)} \right]} \right. \\ \end{aligned}$$

(25)

Proposition 4

• (a) The retailer’s expected profit function is strictly concave in$p$and the third party’s expected profit function is strictly concave in$\,u$.

• (b) The optimal values of wholesale price, selling price and collection rate for any given amount of investment in advertising and buy-back payment are given by:

  $$\begin{aligned} w^{*} (f,k) & = \frac{1}{{8HE(\tilde{b}) - 2skE(\tilde{b})^{2} + 2k^{2} E(\tilde{b})^{2} }}(4HE(\tilde{a}) + 4H\sqrt f E(\tilde{c}) + 4Hs_{m} E(\tilde{b}) \\ & \quad - \;2ksE(\tilde{a})E(\tilde{b}) - 2ks\sqrt f E(\tilde{c})E(\tilde{b}) + 2k^{2} E(\tilde{a})E(\tilde{b}) + 2k^{2} \sqrt f E(\tilde{c})E(\tilde{b})) \\ \end{aligned}$$

  (26)
  $$p^{*} (f,k) = \frac{{(3H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))(E(\tilde{a}) + \sqrt f E(\tilde{c})) + Hs_{m} E(\tilde{b})}}{{E(\tilde{b})(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))}}$$

  (27)
  $$u^{*} (f,k) = \frac{{k(E(\tilde{a}) + \sqrt f E(\tilde{c}) + s_{m} E(\tilde{b}))}}{{2(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))}}$$

  (28)

• (c) The optimal value of investment in advertising is given by:

  $$f^{*} (k) = \left[ {\frac{{H^{2} E(\tilde{c})(E(\tilde{a}) - s_{m} E(\tilde{b}))}}{{E(\tilde{b})(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))^{2} - H^{2} E(\tilde{c})^{2} }}} \right]^{2}$$

  (29)

  Accordingly, by substituting Eq. (29) into Eqs. (26–28), the optimal values of wholesale price ($w^{*}$), selling price ($p^{*}$) and collection rate ($u^{*}$) are obtained.

• (d) The optimal value of payment to the third party for each collected product is given by:

  $$k^{*} = \frac{s}{2}$$

  (30)

  So, by substituting the optimal values of variables into Eqs. (22–24), the optimal values of the members’ expected profits are obtained.

Proof

See “Appendix 4.”

5 Computational and practical results

In this section, a numerical analysis on a real case study is conducted to show the applicability of developed models and to compare the results obtained in four different CLSC structures. As explained before, remanufacturing process is becoming noticeable and important for companies and companies tend to incorporate remanufacturing process into their production plan due to its benefits especially because of the cost saving it creates for them. In this section, one of the companies in Iran which has currently applied remanufacturing process is investigated and related data are gathered for our numerical analysis. This company produces printer cartridges for domestic customers. After several months of research and benchmarking of similar companies done by R & D department, the company concluded that remanufacturing process can be used as a means to reduce costs, satisfy customers’ demand and also optimize usage of natural resources. So, the company decided to incorporate the remanufacturing option into the production plan and it is currently equipped with a remanufacturing line. The company sells the products to customers indirectly where a retailer acts as an intermediate point between the manufacturer and customers. Gathering related data from the company, the values of deterministic parameters are as follows:$s_{m} = 40,\;\;s_{r} = 30,\;\;H = 2000$.

The primary demand ($\tilde{a}$), sensitivity of demand to selling price ($\tilde{b}$) and sensitivity of demand to investment in advertising ($\tilde{c}$) are assumed to be triangular fuzzy numbers (TFNs) due to lack of objective data and relying on subjective judgment of experts to estimate them. Table 2 shows the equivalent TFNs related to the different linguistic expressions. Here it is assumed that demand is very sensitive to both selling price and investment in advertising and the primary demand is small. Using Table 2 along with considering the following definition, the expected values of triangular fuzzy numbers can be calculated.

Table 2 The values of triangular fuzzy variables related to different linguistic expressions

Definition

The expected value of the TFN $\tilde{a} = (a_{1} ,a_{2} ,a_{3} )$ can be derived as follows [48]: $EV(\tilde{a}) = \frac{{a_{1} + 2a_{2} + a_{3} }}{4}$

Thus, for triangular fuzzy parameters, the expected values are obtained as follows:

$$\begin{aligned} EV(\tilde{a}) & = \frac{300 + 2*400 + 500}{4} = 400, \\ EV(\tilde{b}) & = \frac{1.6 + 2*1.8 + 2}{4} = 1.8, \\ EV(\tilde{c}) & = \frac{0.5 + 2*1 + 1.5}{4} = 1 \end{aligned}$$

The results of decision variables and expected profit functions for models 1, 2, 3 and 4 for the numerical case study are shown in Table 3.

Table 3 Results of expected profits and decision variables under four CLSC models

From Table 3, it is concluded that:

• The total expected profit of the supply chain for the centralized structure, where there is an integrated decision making framework, is the highest value among all other models because of double marginalization problem that causes channel inefficiency in the decentralized structures [19, 37].

• Comparing the total optimal demand of products in the centralized and decentralized structures, it is observed that the former is higher than the latter.

Regarding the decentralized structure, the following observations are concluded:

• The expected profit of the manufacturer reaches its highest value under model 3 in which the collection process is conducted by the retailer, while its lowest value is related to model 4 that the collection process is conducted by a third party.

• The retailer achieves his highest expected profit in model 3 in which the collection process is conducted by him and achieves his lowest expected profit in model 4 in which the collection process is conducted by a third party.

5.1 Managerial insights

Considering the results presented in Table 3, the following managerial implications could be inferred:

• The optimal selling price of the products under the centralized structure is lower than those of decentralized structures. Also, among the decentralized models, the optimal selling price achieves the lowest value under the decentralized model 3 in which the collection process is done by the retailer.

In model 4, a third party conducts collection process and is paid by manufacturer for each product he has collected. However, in model 2, the manufacturer is responsible for collection process and gains direct cost saving in manufacturing products from collected products. So he determines lower wholesale price to indirectly increase demand and save more money from remanufacturing process. While in model 4 third party is the member who benefits directly from investment in collection process and the investment has an indirect effect on manufacturer’s gain and his wholesale price. The selling price is affected by wholesale price and investment in collection process. Thus, considering model 2 in comparison with model 4, the lower wholesale price leads to the lower selling price and model 2 has lower optimal selling price than model 4. Comparing model 3 with these two models and by considering co-reaction between retailer and manufacturer decisions that exists in model 3, the retailer would set a lower selling price to increase his saving from product selling because he can directly affect costumer’s demand and his total saving.

• The optimal collection rate under centralized structure is higher than decentralized structures, and among decentralized models, model 3 has the highest collection rate.

In each decentralized model, a member of a supply chain is responsible for collection process. This member has to spend some money for collection process and gains some. The more the money gained from remanufacturing process, the more the tendency to collect used products. In model 2 the collection process is carried out by the manufacturer, and for each product he collects he gains $s$ units of money from remanufacturing cost saving. In model 3, the collection process is carried out by the retailer, and for each product he collects he gains $s$ units of money (as explained in properties 3(d)). In model 4 the collection process is outsourced and carried out by a third party, and for each product he collects he gains $s/2$ units of money (as explained in properties 4(d)).

Comparing decentralized models considering abovementioned statements, the collection rate in model 2 and 3 is higher than the collection rate in model 4. Comparing model 2 and 3, the collection rate under model 3 is higher than model 2. Collection rate is affected by customers’ demand. In model 2 the manufacturer can partially and indirectly increase demand through offering lower wholesale price while in model 3 the retailer is able to increase demand directly through offering lower selling price and achieves higher demand and collection rate in comparison with model 2.

• The optimal investment in advertising under centralized structure is higher than decentralized structures and among decentralized models; the optimal investment in advertising achieves its highest value under decentralized model 3.

From Eq. (1), it is concluded that selling price has an inverse effect on total demand. Besides, amount of money the retailer invests in advertising is affected by his gain. Comparing model 2 and 4, model 4 has the higher value of selling price, so lower demand and lower profitability. This condition makes the retailer decide to reduce his investment in advertising in model 4. Comparing model 2 and 3, model 3 has the lower value of selling price, so higher demand and higher profitability. This condition makes the retailer decide to increase his investment in advertising in model 3. Thus, model 3 has the highest optimal investment in advertising between decentralized models.

As it mentioned, centralized structure has an integrated decision making framework that aims to maximize the total system’s expected profit. This avoids double marginalization problem. In the other words, the supply chain can make all decisions simultaneously and coordinately. So the selling price of products is set at the lowest value (among all models), and as a result demand is the highest value. In this condition, the investment in advertising and collection rate takes their highest value. Considering Table 3, one can conclude that the centralized structure outperforms decentralized structures in:

• Collection rate: As used product Collection rate under centralized model is the highest rate among all models, the centralized model is the best model from the environmental viewpoint and resource usage.

• Customers’ demand: As centralized model has an integrated decision making framework that seeks optimality for the whole supply chain, it can attain highest demand by setting lowest selling price.

• Total expected profit of the supply chain: Again, as a result of the integrated decision making framework of the centralized structure, which seeks optimality for the whole supply chain not only for one member, avoiding double marginalization problem, the supply chain can attain highest total expected profit.

5.2 Sensitivity analyses

In this section sensitivity analyses are conducted and the effects of triangular fuzzy variables $\tilde{a}$, $\tilde{b}$ and $\tilde{c}$ on total expected profit, investment in advertising, collection rate and selling price are investigated. In Sects. 5.2.1–5.2.3, the effects of triangular fuzzy variables on decision variables are investigated. In each section, the value of one fuzzy variable is changed while the other parameters remain unchanged equal to their values in numerical example. In each figure, “C” and “D” refer to centralized and decentralized structures, respectively. Besides, “M1” to “M4” refer to model 1 to model 4 that are discussed in Sect. 4. In Sect. 5.2.4, the impact of fuzzy variables on total expected profit is investigated. In this section, each time the value of two fuzzy variable are changed and corresponding value of total expected profit is plotted. Plots of several models are not given in some figures for the sake of clarity.

5.2.1 Impact of primary demand ($\tilde{a}$)

The impact of primary demand ($\tilde{a}$) on investment in advertising, collection rate and selling price for centralized and decentralized structures are shown in Figs. 5, 6 and 7. From Figs. 5, 6 and 7, it is inferred that:

Fig. 5

Investment in advertising of centralized and decentralized CLSCs for different values of $\tilde{a}$

Fig. 6

Collection rate of centralized and decentralized CLSCs for different values of $\tilde{a}$

Fig. 7

Retail price of centralized and decentralized CLSCs for different values of $\tilde{a}$

• Investment in advertising increases as the primary demand increases. An amount of investment in advertising for centralized structure is more sensitive to primary demand compared to decentralized structures.

• Collection rate increases as the primary demand increases. Collection rate under centralized structure is higher than decentralized structures. So from the environmental viewpoint, centralized structure outperforms all three decentralized structures.

• Selling price increases as the primary demand increases. Figure 7 shows that the centralized structure has lower selling price in comparison with decentralized structures. Thus, from the costumer’s viewpoint, the centralized structure benefits him more. This remark is discussed in detail in Sect. 5.1.

5.2.2 Impact of selling price sensitivity of demand ($\tilde{b}$)

The impact of selling price sensitivity of demand ($\tilde{b}$) on investment in advertising, collection rate and selling price for centralized and decentralized structures is shown in Figs. 8, 9 and 10. From Figs. 8, 9 and 10, it is inferred that:

Fig. 8

Investment in advertising of centralized and decentralized CLSCs for different values of $\tilde{b}$

Fig. 9

Collection rate of centralized and decentralized CLSCs for different values of $\tilde{b}$

Fig. 10

Retail price of centralized and decentralized CLSCs for different values of $\tilde{b}$

• Investment in advertising decreases as $\tilde{b}$ increases. Amount of investment in advertising for centralized structure is more sensitive to $\tilde{b}$ compared to decentralized structures.

• Collection rate decreases as $\tilde{b}$ increases. Collection rate under centralized structure is higher than decentralized structures.

• Selling price decreases as $\tilde{b}$ increases. Figure 10 shows that the centralized structure has lower selling price in comparison with decentralized structures.

5.2.3 Impact of sensitivity of demand to investment in advertising ($\tilde{c}$)

The impact of sensitivity of demand to investment in advertising ($\tilde{c}$) on investment in advertising, collection rate and selling price for centralized and decentralized structures are shown in Figs. 11, 12 and 13. From Figs. 11, 12 and 13, it is inferred that:

Fig. 11

Investment in advertising of centralized and decentralized CLSCs for different values of $\tilde{c}$

Fig. 12

Collection rate of centralized and decentralized CLSCs for different values of $\tilde{c}$

Fig. 13

Retail price of centralized and decentralized CLSCs for different values of $\tilde{c}$

• Investment in advertising increases as $\tilde{c}$ increases. Amount of investment in advertising for centralized structure is more sensitive to $\tilde{c}$ compared to decentralized structures.

• Collection rate increases as $\tilde{c}$ increases. Collection rate of centralized structure is very sensitive to $\tilde{c}$ and changes significantly by changing $\tilde{c}$ while collection rate of decentralized structures change slightly by changing $\tilde{c}$.

• Selling price increases as $\tilde{c}$ increases. Figure 13 shows that the centralized structure has lower selling price in comparison with decentralized structures.

5.2.4 Impact of fuzzy variables on total expected profit

The impact of triangular fuzzy variables on optimal value of total expected profit for centralized and decentralized structures are shown in Figs. 14, 15 and 16.

Fig. 14

Total expected profit of centralized and decentralized CLSCs for different values of $\tilde{a}$ and $\tilde{b}$

Fig. 15

Total expected profit of centralized and decentralized CLSCs for different values of $\tilde{a}$ and $\tilde{c}$

Fig. 16

Total expected profit of centralized and decentralized CLSCs for different values of $\tilde{b}$ and $\tilde{c}$

From Figs. 14, 15 and 16, it is inferred that:

• Total expected profit for both centralized and decentralized structures increase as $\tilde{a}$ increases. When primary demand increases, the centralized structure makes more profit compared to decentralized structures.

• Total expected profit for both centralized and decentralized structures decrease as $\tilde{b}$ increases. When $\tilde{b}$ increases the centralized structure makes more profit compared to other decentralized structures.

• Total expected profit for both centralized and decentralized structures increase as $\tilde{c}$ increases.

6 Conclusion

This paper integrates the major decisions such as pricing, collection rate and investment in advertising in a CLSC in an uncertain triangular fuzzy environment. Demand function parameters are considered as triangular fuzzy numbers. 4 CLSC structures which are mainly different in collecting process and collector member are studied. The first structure is a centralized decision making framework in which all members act as an integrated whole. The other structures are considered in decentralized decision making framework where the manufacturer, the retailer and a third party conduct collection process, respectively. After conducting experiments on CLSCs with these features, it is concluded that the centralized structure outperforms decentralized structures from the customers’, environmental and whole system’s point of view. In other words, the centralized structure can achieve the highest total expected profit, the highest demand by setting lowest selling price, and also the highest collection rate in comparison with decentralized structures. However, where the centralized structure is not applicable, comparison of decentralized models led to the following implications: From the manufacturer’s perspective, giving the responsibility of collection process to retailer is more effective and profitable than outsourcing the collection process or collecting used products by himself. Also, the retailer prefers to collect the products by himself in order to achieve the highest profit. When collection process is done by the retailer, selling price of products is lower and as a result, market demand is higher than other collection models, so from the customers’ perspective collection by retailer is more preferred. Under third model where collection process is carried out by the retailer, higher quantities of used products are collected, so this structure is preferred from the environmental viewpoint. Finally, sensitivity analyses are conducted on fuzzy parameters to illustrate the impacts of triangular fuzzy parameters on optimal values of decision variables. There are several extensions to the proposed model and guidelines for future research based on our considered assumptions. First, the linear demand function which is considered in this paper can be modified and extended to include other forms of functions such as nonlinear functions. Second, in this research only the demand function parameters ($\tilde{a}$, $\tilde{b}$ and $\tilde{c}$) are considered as triangular fuzzy numbers. Future studies can incorporate fuzziness in other model’s parameters such as unit manufacturing and remanufacturing cost of products. Third, the single-period setting can be modified to a two-period or generally multi-period setting. Third, this paper assumes a CLSC with symmetric information where the information is known to all the members. Future studies can incorporate asymmetric information condition in proposed supply chain. The asymmetric information is a condition in which members have some private information. Moreover, considering dual channel and competition between the members would be of interest.

Appendices

Appendix 1: Proof of Proposition 1

(a) It follows from Eq. (2) together with lemmas 3–5 of Zhao et al. [48] that:

$$\begin{aligned} E\left[ {\pi_{\text{total}}^{1} (p,u,f)} \right] & = \frac{1}{2}\int\limits_{0}^{1} {\left( {\left[ {(p - s_{m} + us)(\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f ) - Hu^{2} - f} \right]} \right.}_{\alpha }^{U} \\ & \quad \left. { + \;\left[ {(p - s_{m} + us)(\tilde{a} - \tilde{b}p + \tilde{c}\sqrt f ) - Hu^{2} - f} \right]_{\alpha }^{L} } \right){\text{d}}\alpha \\ & = pE(\tilde{a}) - p^{2} E(\tilde{b}) + p\sqrt f E(\tilde{c}) - s_{m} E(\tilde{a}) + s_{m} pE(\tilde{b}) \\ & \quad - \;s_{m} \sqrt f E(\tilde{c}) + usE(\tilde{a}) - uspE(\tilde{b}) + us\sqrt f E(\tilde{c}) - Hu^{2} - f \\ \end{aligned}$$

(A-1)

The first- and second-order partial derivatives of $E\left[ {\pi_{\text{total}}^{1} (p,u,f)} \right]$ with respect to $p$, $u$ and $f$ are:

$$\left( {\frac{{\partial E(\pi_{\text{total}}^{1} )}}{\partial p}} \right) = E(\tilde{a}) - 2pE(\tilde{b}) + \sqrt f E(\tilde{c}) + s_{m} E(\tilde{b}) - usE(\tilde{b})$$

(A-2)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{{\partial p^{2} }}} \right) = - 2E(\tilde{b})$$

(A-3)

$$\left( {\frac{{\partial E(\pi_{\text{total}}^{1} )}}{\partial u}} \right) = sE(\tilde{a}) - spE(\tilde{b}) + s\sqrt f E(\tilde{c}) - 2Hu$$

(A-4)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{{\partial u^{2} }}} \right) = - 2H$$

(A-5)

$$\left( {\frac{{\partial E(\pi_{\text{total}}^{1} )}}{\partial f}} \right) = \frac{1}{2\sqrt f }(pE(\tilde{c}) - s_{m} E(\tilde{c}) + usE(\tilde{c})) - 1$$

(A-6)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{{\partial f^{2} }}} \right) = \frac{ - 1}{{4\sqrt {f^{3} } }}(pE(\tilde{c}) - s_{m} E(\tilde{c}) + usE(\tilde{c}))$$

(A-7)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial p\partial u}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial u\partial p}} \right) = - sE(\tilde{b})$$

(A-8)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial p\partial f}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial f\partial p}} \right) = \frac{{E(\tilde{c})}}{2\sqrt f }$$

(A-9)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial u\partial f}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial f\partial u}} \right) = \frac{{sE(\tilde{c})}}{2\sqrt f }$$

(A-10)

$$\left| \begin{aligned} \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{{\partial p^{2} }}} & {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial pu}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial up}} & {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{{\partial u^{2} }}} \\ \end{array} \hfill \\ \end{aligned} \right| = 4HE(\tilde{b}) - s^{2} E(\tilde{b})^{2} > 0$$

(A-11)

According to Eqs. (A-1), (A-5) and (A-11), it is concluded that $E\left[ {\pi_{\text{total}}^{1} (p,u,f)} \right]$ is strictly jointly concave in $p$ and $u$.

$$\left| \begin{aligned} \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{{\partial u^{2} }}} & {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial uf}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{\partial fu}} & {\frac{{\partial^{2} E(\pi_{\text{total}}^{1} )}}{{\partial f^{2} }}} \\ \end{array} \hfill \\ \end{aligned} \right| = \frac{H}{{2\sqrt {f^{3} } }}(pE(\tilde{c}) - s_{m} E(\tilde{c}) + usE(\tilde{c})) - \frac{{s^{2} E(\tilde{c})^{2} }}{4f}$$

(A-12)

Equation (A-12) may be negative for large enough values of $f$, so $E\left[ {\pi_{\text{total}}^{1} (p,u,f)} \right]$ is indefinite with respect to $u$ and $f$, and is not jointly concave in $p$, $u$ and $f$.

(b) As $E\left[ {\pi_{\text{total}}^{1} (p,u,f)} \right]$ is strictly jointly concave in $p$ and $u$. Setting Eqs. (A-2) and (A-4) equal to zero and solving them simultaneously, we obtain Eqs. (4) and (5).

(c) Substituting Eqs. (4) and (5) into Eq. (2), we have:

$$\begin{array}{*{20}c} {E\left[ {\pi_{\text{total}}^{1} (f)} \right]} \\ \end{array} = \frac{{H(E(\tilde{a}) + \sqrt f E(\tilde{c}) - s_{m} E(\tilde{b}))^{2} }}{{E(\tilde{b})(4H - s^{2} E(\tilde{b}))}} - f$$

(A-13)

Taking the first-order partial derivative of Eq. (A-13) with respect to $f$, and setting it equal to zero, the optimal value of $f$ is obtained as it is shown in Eq. (6).

Appendix 2: Proof of Proposition 2

(a) It follows from Eqs. (7) and (8) and lemmas 3–5 of Zhao et al. [48] that:

$$\begin{aligned} E\left[ {\pi_{\text{man}}^{2} (p,w,u,f)} \right] & = wE(\tilde{a}) - wpE(\tilde{b}) + w\sqrt f E(\tilde{c}) - s_{m} E(\tilde{a}) + s_{m} pE(\tilde{b}) \\ & \quad - \;s_{m} \sqrt f E(\tilde{c}) + \,usE(\tilde{a}) - uspE(\tilde{b}) + us\sqrt f E(\tilde{c}) - Hu^{2} \\ \end{aligned}$$

(B-1)

$$E\left[ {\pi_{\text{ret}}^{2} (p,w,f)} \right] = pE(\tilde{a}) - p^{2} E(\tilde{b}) + p\sqrt f E(\tilde{c}) - wE(\tilde{a}) + wpE(\tilde{b}) - w\sqrt f E(\tilde{c}) - f$$

(B-2)

The first- and second-order partial derivatives of retailer’s expected profit ($E\left[ {\pi_{\text{ret}}^{2} (p,w,f)} \right]$) with respect to $p$ and $f$ can be shown as:

$$\left( {\frac{{\partial E(\pi_{\text{ret}}^{2} )}}{\partial p}} \right) = E(\tilde{a}) - 2pE(\tilde{b}) + \sqrt f E(\tilde{c}) + wE(\tilde{b})$$

(B-3)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{{\partial p^{2} }}} \right) = - 2E(\tilde{b})$$

(B-4)

$$\left( {\frac{{\partial E(\pi_{\text{ret}}^{2} )}}{\partial f}} \right) = \frac{1}{2\sqrt f }(pE(\tilde{c}) - wE(\tilde{c}))$$

(B-5)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{{\partial f^{2} }}} \right) = \frac{1}{{4\sqrt {f^{3} } }}(wE(\tilde{c}) - pE(\tilde{c}))$$

(B-6)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{\partial p\partial f}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{\partial f\partial p}} \right) = \frac{{E(\tilde{c})}}{2\sqrt f }$$

(B-7)

$$\left| \begin{aligned} \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{{\partial p^{2} }}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{\partial pf}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{\partial fp}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{2} )}}{{\partial f^{2} }}} \\ \end{array} \hfill \\ \end{aligned} \right| = \frac{{E(\tilde{b})E(\tilde{c})(p - w)}}{{2\sqrt {f^{3} } }} - \frac{{E(\tilde{c})^{2} }}{4f}$$

(B-8)

It follows from Eq. (B-4) that the retailer’s expected profit is concave with respect to $p$ while Eq. (B-8) may be negative for large enough values of $f$. So $E\left[ {\pi_{\text{ret}}^{2} (p,w,f)} \right]$ is indefinite with respect to $p$ and $f$, and is not jointly concave in $p$ and $f$. As the retailer’s expected profit is concave with respect to $p$. Setting Eq. (B-3) equal to zero and solving it with respect to $p$, we obtain following result:

$$p^{*} (w,f) = \frac{1}{{2E(\tilde{b})}}(E(\tilde{a}) + \sqrt f E(\tilde{c}) + wE(\tilde{b}))$$

(B-9)

(b) Substituting Eq. (B-9) into Eq. (7), we have:

$$\begin{aligned} E\left[ {\pi_{\text{man}}^{2} (w,u,f)} \right] & = \left[ {(w - s_{m} + us)\left( {\frac{{E(\tilde{a}) - wE(\tilde{b}) + \sqrt f E(\tilde{c})}}{2}} \right) - Hu^{2} } \right] \\ & = \frac{1}{2}(wE(\tilde{a}) + w\sqrt f E(\tilde{c}) - w^{2} E(\tilde{b}) - s_{m} E(\tilde{a}) - s_{m} \sqrt f E(\tilde{c}) \\ & \quad + \;s_{m} wE(\tilde{b}) + usE(\tilde{a}) + us\sqrt f E(\tilde{c}) - uswE(\tilde{b})) - Hu^{2} \\ \end{aligned}$$

(B-10)

The first- and second-order partial derivatives of $E\left[ {\pi_{\text{man}}^{2} (w,u,f)} \right]$ with respect to $u$ and $w$ can be shown as:

$$\left( {\frac{{\partial E(\pi_{\text{man}}^{2} )}}{\partial w}} \right) = \frac{1}{2}(E(\tilde{a}) + \sqrt f E(\tilde{c}) - 2wE(\tilde{b}) + s_{m} E(\tilde{b}) - usE(\tilde{b}))$$

(B-11)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{{\partial w^{2} }}} \right) = - E(\tilde{b})$$

(B-12)

$$\left( {\frac{{\partial E(\pi_{\text{man}}^{2} )}}{\partial u}} \right) = \frac{s}{2}(E(\tilde{a}) + \sqrt f E(\tilde{c}) - wE(\tilde{b})) - 2Hu$$

(B-13)

$$\left| {\left( {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{{\partial u^{2} }}} \right)} \right| = - 2H$$

(B-14)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{\partial u\partial w}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{\partial w\partial u}} \right) = \frac{{ - sE(\tilde{b})}}{2}$$

(B-15)

$$\left| \begin{aligned} \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{{\partial w^{2} }}} & {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{\partial wu}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{\partial uw}} & {\frac{{\partial^{2} E(\pi_{\text{man}}^{2} )}}{{\partial u^{2} }}} \\ \end{array} \hfill \\ \end{aligned} \right| = 2HE(\tilde{b}) - \frac{{s^{2} E(\tilde{b})^{2} }}{4} > 0$$

(B-16)

It follows from Eqs. (B-12), (B-14) and (B-16) that $E\left[ {\pi_{\text{man}}^{2} (w,u,f)} \right]$ is jointly concave in $w$ and $u$.

(c) As $E\left[ {\pi_{\text{man}}^{2} (w,u,f)} \right]$ is jointly concave in $w$ and $\,u$. Setting Eqs. (B-11) and (B-13) equal to zero and solving them simultaneously, we obtain Eqs. (10) and (11).

Substituting Eq. (11) into Eq. (B-9), Eq. (12) can be obtained.

(d) Substituting Eqs. (11) and (12) into $E\left[ {\pi_{\text{ret}}^{2} (p,w,f)} \right]$, we have:

$$E\left[ {\pi_{\text{ret}}^{2} (f)} \right] = \frac{{(4H^{2} )(E(\tilde{a}) + \sqrt f E(\tilde{c}) - s_{m} E(\tilde{b}))^{2} }}{{E(\tilde{b})(8H - s^{2} E(\tilde{b}))^{2} }} - f$$

(B-17)

Taking the first-order partial derivative of Eq. (B-17) with respect to $f$, and setting it equal to zero the optimal value of $f$ is obtained as it is shown in Eq. (13).

Appendix 3: Proof of Proposition 3

(a) It follows from Eqs. (14) and (15) together with lemmas 3–5 of Zhao et al. [48] that:

$$\begin{aligned} E\left[ {\pi_{\text{man}}^{3} (p,w,u,f,k)} \right] & = wE(\tilde{a}) - wpE(\tilde{b}) + w\sqrt f E(\tilde{c}) - s_{m} E(\tilde{a}) + s_{m} pE(\tilde{b}) \\ & \quad - \;s_{m} \sqrt f E(\tilde{c}) + usE(\tilde{a}) - uspE(\tilde{b}) + us\sqrt f E(\tilde{c}) \\ & \quad - \;ukE(\tilde{a}) + ukpE(\tilde{b}) - uk\sqrt f E(\tilde{c}) \\ \end{aligned}$$

(C-1)

$$\begin{aligned} E\left[ {\pi_{\text{ret}}^{3} (p,w,u,f,k)} \right] & = pE(\tilde{a}) - p^{2} E(\tilde{b}) + p\sqrt f E(\tilde{c}) - wE(\tilde{a}) + wpE(\tilde{b}) - w\sqrt f E(\tilde{c}) \\ & \quad + \;kuE(\tilde{a}) - kupE(\tilde{b}) + ku\sqrt f E(\tilde{c}) - Hu^{2} - f \\ \end{aligned}$$

(C-2)

The first- and second-order partial derivatives of $E\left[ {\pi_{\text{ret}}^{2} (p,w,u,f,k)} \right]$ with respect to $p$, $u$ and $f$ can be shown as:

$$\left( {\frac{{\partial E(\pi_{\text{ret}}^{3} )}}{\partial p}} \right) = E(\tilde{a}) - 2pE(\tilde{b}) + \sqrt f E(\tilde{c}) + wE(\tilde{b}) - kuE(\tilde{b})$$

(C-3)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{{\partial p^{2} }}} \right) = - 2E(\tilde{b})$$

(C-4)

$$\left( {\frac{{\partial E(\pi_{\text{ret}}^{3} )}}{\partial u}} \right) = kE(\tilde{a}) - kpE(\tilde{b}) + k\sqrt f E(\tilde{c}) - 2Hu$$

(C-5)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{{\partial u^{2} }}} \right) = - 2H$$

(C-6)

$$\left( {\frac{{\partial E(\pi_{\text{ret}}^{3} )}}{\partial f}} \right) = \frac{{E(\tilde{c})}}{2\sqrt f }(p - w + ku) - 1$$

(C-7)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{{\partial f^{2} }}} \right) = \frac{{ - E(\tilde{c})}}{{4\sqrt {f^{3} } }}(p - w + ku)$$

(C-8)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial p\partial u}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial u\partial p}} \right) = - kE(\tilde{b})$$

(C-9)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial p\partial f}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial f\partial p}} \right) = \frac{{E(\tilde{c})}}{2\sqrt f }$$

(C-10)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial u\partial f}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial f\partial u}} \right) = \frac{{kE(\tilde{c})}}{2\sqrt f }$$

(C-11)

$$\left| \begin{aligned} \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{{\partial p^{2} }}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial pu}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial up}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{{\partial u^{2} }}} \\ \end{array} \hfill \\ \end{aligned} \right| = 4HE(\tilde{b}) - k^{2} E(\tilde{b})^{2} > 0$$

(C-12)

According to Eqs. (C-4), (C-6) and (C-12), $E\left[ {\pi_{\text{ret}}^{3} (p,w,u,f,k)} \right]$ is strictly jointly concave in $p$ and $u$.

$$\left| \begin{aligned} \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{{\partial u^{2} }}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial uf}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{\partial fu}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{3} )}}{{\partial f^{2} }}} \\ \end{array} \hfill \\ \end{aligned} \right| = \frac{{HE(\tilde{c})}}{{2\sqrt {f^{3} } }}(p - w + ku) - \frac{{k^{2} E(\tilde{c})^{2} }}{4f}$$

(C-13)

Equation (C-13) may be negative for large enough values of $f$, so $E\left[ {\pi_{\text{ret}}^{3} (p,w,u,f,k)} \right]$ is indefinite with respect to $u$ and $f$, and is not jointly concave in $u$ and $f$.

(b) As $E\left[ {\pi_{\text{ret}}^{3} (p,w,u,f,k)} \right]$ is strictly jointly concave in $p$ and $u$. Setting Eqs. (C-3) and (C-5) equal to zero and solving them simultaneously, we obtain Eqs. (C-14) and (C-15).

$$u^{*} (w,f,k) = \frac{{kE(\tilde{a}) + k\sqrt f E(\tilde{c}) - kwE(\tilde{b})}}{{4H - k^{2} E(\tilde{b})}}$$

(C-14)

$$p^{*} (w,f,k) = \frac{{2HE(\tilde{a}) + 2H\sqrt f E(\tilde{c}) + 2HwE(\tilde{b}) - k^{2} \sqrt f E(\tilde{c})E(\tilde{b}) - k^{2} E(\tilde{a})E(\tilde{b})}}{{(4H - k^{2} E(\tilde{b}))E(\tilde{b})}}$$

(C-15)

Substituting Eqs. (C-14) and (C-15) into Eq. (14) we have:

$$\begin{aligned} E\left[ {\pi_{\text{man}}^{3} (w,f,k)} \right] & = \frac{{(E(\tilde{a}) - wE(\tilde{b}) + \sqrt f E(\tilde{c}))}}{{(4H - k^{2} E(\tilde{b}))^{2} }} \\ & \quad *\;(8H^{2} w - 2HkswE(\tilde{b}) + 2Hks\sqrt f E(\tilde{c}) - 2Hk^{2} \sqrt f E(\tilde{c}) - 8H^{2} s_{m} \\ & \quad + \;2Hk^{2} s_{m} E(\tilde{b}) + 2HksE(\tilde{a}) - 2Hk^{2} E(\tilde{a}) \\ \end{aligned}$$

(C-16)

The first- and second-order partial derivatives of manufacturer’s expected profit, $E\left[ {\pi_{\text{man}}^{3} (w,f,k)} \right]$, with respect to $w$ can be shown as:

$$\begin{aligned} \left( {\frac{{\partial E(\pi_{\text{man}}^{3} )}}{\partial w}} \right) & = \frac{2H}{{(4H - k^{2} E(\tilde{b}))^{2} }}( - 2ksE(\tilde{a})E(\tilde{b}) - 2ks\sqrt f E(\tilde{b})E(\tilde{c}) + 4HE(\tilde{a}) - 8HwE(\tilde{b}) \\ & \quad + \;4H\sqrt f E(\tilde{c}) + 2kswE(\tilde{b})E(\tilde{b}) + k^{2} \sqrt f E(\tilde{b})E(\tilde{c}) + 4Hs_{m} E(\tilde{b}) \\ & \quad - \;k^{2} s_{m} E(\tilde{b})E(\tilde{b}) + k^{2} E(\tilde{a})E(\tilde{b})) \\ \end{aligned}$$

(C-17)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{man}}^{3} )}}{{\partial w^{2} }}} \right) = \frac{2H}{{(4H - k^{2} E(\tilde{b}))^{2} }}( - 8HE(\tilde{b}) + 2ksE(\tilde{b})^{2} )$$

(C-18)

According to Eq. (C-18), $E\left[ {\pi_{man}^{3} (w,f,k)} \right]$ is strictly concave in $w$.

As $E\left[ {\pi_{\text{man}}^{3} (w,f,k)} \right]$ is concave in $w$. Setting Eqs. (C-17) equal to zero and solving it with respect to $w$, we obtain Eq. (17). Substituting Eq. (17) into Eqs. (C-14) and (C-15), we obtain Eqs. (18) and (19).

(c) Substituting Eqs. (17)–(19) into Eq. (15) we have:

$$E\left[ {\pi_{\text{ret}}^{3} (f,k)} \right] = \frac{{H(E(\tilde{a}) + \sqrt f E(\tilde{c}) - s_{m} E(\tilde{b}))^{2} (4H - k^{2} E(\tilde{b}))}}{{(4H - ksE(\tilde{b}))^{2} 4E(\tilde{b})}} - f$$

(C-19)

Taking the first-order partial derivative of Eq. (C-19) with respect to $f$, and setting it equal to zero the optimal value of $f$ is obtained as it is shown in Eq. (20).

(d) Substituting the optimal values of variables into Eq. (14) we have:

$$E\left[ {\pi_{\text{man}}^{3} (k)} \right] = \frac{{8HE(\tilde{b})(4H - ksE(\tilde{b}))^{3} (E(\tilde{a}) - s_{m} E(\tilde{b}))^{2} }}{{\left[ {(4H - ksE(\tilde{b}))^{2} 4E(\tilde{b}) - HE(\tilde{c})^{2} (4H - k^{2} E(\tilde{b}))} \right]^{2} }}$$

(C-20)

The manufacturer decides about the amount of payment to the retailer for collection of used products. Taking first-order partial derivatives of $E\left[ {\pi_{\text{man}}^{3} (k)} \right]$ with respect to $k$, it is obvious that this value is always positive.

$$\left( {\frac{{\partial E(\pi_{\text{man}}^{3} )}}{\partial k}} \right) > 0$$

(C-21)

As said the optimal value of payment to retailer for each collected product which is decided and paid by the manufacturer is given by $k^{*} = s$. In other word, the manufacturer’s profit is maximized when $\,k = s$. Here, the reason is intuitively explained.

When the manufacturer increases the value of $k$ to be equal to $s$, the average unit cost of manufacturing decreases ($(1 - u)s_{m} + us_{r}$). This is because of that by increasing $k$, the retailer tends to increase level of investment in advertising to stimulate customers’ demand. As demand increases the collection process becomes more profitable for the retailer so he tends to increase investment in collection process and as a result the value of $\,u$ increases and cause more cost saving for the manufacturer.

Appendix 4: Proof of Proposition 4

(a) It follows from Eqs. (22)–(24) and lemmas 3–5 of Zhao et al. [48] that:

$$\begin{aligned} E\left[ {\pi_{\text{man}}^{4} (p,w,u,f,k)} \right] & = wE(\tilde{a}) - wpE(\tilde{b}) + w\sqrt f E(\tilde{c}) - s_{m} E(\tilde{a}) + s_{m} pE(\tilde{b}) - s_{m} \sqrt f E(\tilde{c}) \\ & \quad + \;usE(\tilde{a}) - uspE(\tilde{b}) + us\sqrt f E(\tilde{c}) - ukE(\tilde{a}) + ukpE(\tilde{b}) - uk\sqrt f E(\tilde{c}) \\ \end{aligned}$$

(D-1)

$$E\left[ {\pi_{\text{ret}}^{4} (p,w,f)} \right] = pE(\tilde{a}) - p^{2} E(\tilde{b}) + p\sqrt f E(\tilde{c}) - wE(\tilde{a}) + wpE(\tilde{b}) - w\sqrt f E(\tilde{c}) - f$$

(D-2)

$$E\left[ {\pi_{{ 3 {\text{par}}}}^{4} (p,u,f,k)} \right] = kuE(\tilde{a}) - kupE(\tilde{b}) + ku\sqrt f E(\tilde{c}) - Hu^{2}$$

(D-3)

The first- and second-order partial derivatives of $E\left[ {\pi_{\text{ret}}^{4} (p,w,f)} \right]$ with respect to $p$ and $f$ can be shown as:

$$\left( {\frac{{\partial E(\pi_{\text{ret}}^{4} )}}{\partial p}} \right) = E(\tilde{a}) - 2pE(\tilde{b}) + \sqrt f E(\tilde{c}) + wE(\tilde{b})$$

(D-4)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{{\partial p^{2} }}} \right) = - 2E(\tilde{b})$$

(D-5)

$$\left( {\frac{{\partial E(\pi_{\text{ret}}^{4} )}}{\partial f}} \right) = \frac{1}{2\sqrt f }(pE(\tilde{c}) - wE(\tilde{c}))$$

(D-6)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{{\partial f^{2} }}} \right) = \frac{1}{{4\sqrt {f^{3} } }}(wE(\tilde{c}) - pE(\tilde{c}))$$

(D-7)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{\partial p\partial f}} \right) = \left( {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{\partial f\partial p}} \right) = \frac{{E(\tilde{c})}}{2\sqrt f }$$

(D-8)

According to Eq. (D-5) $E\left[ {\pi_{\text{ret}}^{4} (p,w,f)} \right]$ is strictly concave in $p$.

$$\left| \begin{aligned} \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{{\partial p^{2} }}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{\partial pf}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{\partial fp}} & {\frac{{\partial^{2} E(\pi_{\text{ret}}^{4} )}}{{\partial f^{2} }}} \\ \end{array} \hfill \\ \end{aligned} \right| = \frac{{E(\tilde{b})E(\tilde{c})(p - w)}}{{2\sqrt {f^{3} } }} - \frac{{E(\tilde{c})^{2} }}{4f}$$

(D-9)

Equation (D-9) may be negative for large enough values of $f$, so $E\left[ {\pi_{\text{ret}}^{4} (p,w,f)} \right]$ is indefinite with respect to $p$ and $f$, and is not jointly concave in $p$ and $f$. As $E\left[ {\pi_{\text{ret}}^{4} (p,w,f)} \right]$ is concave in $p$, Setting Eq. (D-4) equal to zero and solving it with respect to $p$ we obtain Eq. (D-10).

$$p^{*} (w,f) = \frac{1}{{2E(\tilde{b})}}(E(\tilde{a}) + \sqrt f E(\tilde{c}) + wE(\tilde{b}))$$

(D-10)

The first- and second-order partial derivatives of $E\left[ {\pi_{{ 3 {\text{par}}}}^{4} (p,u,f,k)} \right]$ with respect to $u$ can be shown as:

$$\left( {\frac{{\partial E(\pi_{{ 3 {\text{par}}}}^{4} )}}{\partial u}} \right) = kE(\tilde{a}) - kpE(\tilde{b}) + k\sqrt f E(\tilde{c}) - 2Hu$$

(D-11)

$$\left( {\frac{{\partial^{2} E(\pi_{{ 3 {\text{par}}}}^{4} )}}{{\partial u^{2} }}} \right) = - 2H$$

(D-12)

According to Eq. (D-12) $E\left[ {\pi_{{ 3 {\text{par}}}}^{4} (p,u,f,k)} \right]$ is strictly concave in $\,u$. As $E\left[ {\pi_{{ 3 {\text{par}}}}^{4} (p,u,f,k)} \right]$ is concave in $\,u$, Setting Eq. (D-11) equal to zero and solving it with respect to $\,u$, we obtain Eq. (D-13).

$$u^{*} (p,f,k) = \frac{k}{2H}(E(\tilde{a}) - pE(\tilde{b}) + \sqrt f E(\tilde{c}))$$

(D-13)

(b) Substituting Eq. (D-10) into Eq. (D-13) we have:

$$u^{*} (w,f,k) = \frac{k}{4H}(E(\tilde{a}) - wE(\tilde{b}) + \sqrt f E(\tilde{c}))$$

(D-14)

Substituting Eqs. (D-10) and (D-14) into Eq. (22) we have:

$$\begin{aligned} E\left[ {(\pi_{\text{man}}^{4} (w,f,k)} \right] & = \frac{1}{8H}(E(\tilde{a}) - wE(\tilde{b}) + \sqrt f E(\tilde{c})) \\ & \quad *\;\left( {4Hw - 4Hs_{m} + skE(\tilde{a}) - skwE(\tilde{b}) + sk\sqrt f E(\tilde{c})} \right. \\ & \quad \left. { - \;k^{2} E(\tilde{a}) + k^{2} wE(\tilde{b}) - k^{2} \sqrt f E(\tilde{c})} \right) \\ \end{aligned}$$

(D-15)

The first- and second-order partial derivatives of $E\left[ {(\pi_{\text{man}}^{4} (w,f,k)} \right]$ with respect to $w$ can be shown as:

$$\begin{aligned} \left( {\frac{{\partial E(\pi_{\text{man}}^{4} )}}{\partial w}} \right) & = \frac{1}{8H}(4HE(\tilde{a}) + 4H\sqrt f E(\tilde{c}) - 8HwE(\tilde{b}) + 4Hs_{m} E(\tilde{b}) - 2ksE(\tilde{a})E(\tilde{b}) \\ & \quad - \;2ks\sqrt f E(\tilde{c})E(\tilde{b}) + 2skwE(\tilde{b})E(\tilde{b}) + 2k^{2} E(\tilde{a})E(\tilde{b}) + 2k^{2} \sqrt f E(\tilde{c})E(\tilde{b}) \\ & \quad - \;2k^{2} wE(\tilde{b})E(\tilde{b})) \\ \end{aligned}$$

(D-16)

$$\left( {\frac{{\partial^{2} E(\pi_{\text{man}}^{4} )}}{{\partial w^{2} }}} \right) = \frac{1}{8H}( - 8HE(\tilde{b}) + 2skE(\tilde{b})E(\tilde{b}) - 2k^{2} E(\tilde{b})E(\tilde{b}))$$

(D-17)

According to Eq. (D-17) $E\left[ {(\pi_{\text{man}}^{4} (w,f,k)} \right]$ is strictly concave in $w$.

As $E\left[ {(\pi_{\text{man}}^{4} (w,f,k)} \right]$ is concave in $w$, Setting Eq. (D-16) equal to zero and solving it with respect to $w$, we obtain Eq. (26). Substituting Eq. (26) into Eqs. (D-10) and (D-14) we obtain Eqs. (27) and (28).

(c) Substituting Eqs. (26–28) into Eq. (23) we have:

$$E\left[ {\pi_{\text{ret}}^{4} (f,k)} \right] = \frac{{H^{2} (E(\tilde{a}) + \sqrt f E(\tilde{c}) - s_{m} E(\tilde{b}))^{2} }}{{E(\tilde{b})(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))^{2} }} - f$$

(D-18)

Taking the first-order partial derivative of Eq. (D-18) with respect to $f$, and setting it equal to zero the optimal value of $f$ is obtained as it is shown in Eq. (29).

(d) Substituting the optimal value of variables into Eq. (22) we have:

$$E\left[ {\pi_{\text{man}}^{4} (k)} \right] = \frac{{HE(\tilde{b})(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))^{3} (E(\tilde{a}) - s_{m} E(\tilde{b}))^{2} }}{{2\left[ {E(\tilde{b})(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))^{2} - H^{2} E(\tilde{c})^{2} } \right]^{2} }}$$

(D-19)

The manufacturer decides about the amount of payment for used products to the third party. Taking the first-order partial derivative of manufacturer’s expected profit ($E\left[ {\pi_{\text{man}}^{4} (k)} \right]$) and setting it equal to zero, the optimal value of $k$ which maximizes the manufacturer’s expected profit is obtained.

$$\begin{aligned} \left( {\frac{{\partial E(\pi_{\text{man}}^{4} )}}{\partial k}} \right) & = \frac{{HE(\tilde{b})^{2} }}{{2(E(\tilde{b})(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))^{2} - H^{2} E(\tilde{c})^{2} )^{3} }}(E(\tilde{a}) - E(\tilde{b})s_{m} ) \\ & \quad *\;(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))^{2} (s - 2k)(3H^{2} E(\tilde{c})^{2} + E(\tilde{b})(4H - ksE(\tilde{b}) + k^{2} E(\tilde{b}))^{2} ) \\ \end{aligned}$$

(D-20)

As it is obvious for $k = \frac{s}{2}$ we have:

$$k = \frac{s}{2} \to \left( {\frac{{\partial E(\pi_{\text{man}}^{4} )}}{\partial k}} \right) = 0,\quad 0 < k < \frac{s}{2} \to \left( {\frac{{\partial E(\pi_{\text{man}}^{4} )}}{\partial k}} \right) > 0,\quad k > \frac{s}{2} \to \left( {\frac{{\partial E(\pi_{\text{man}}^{4} )}}{\partial k}} \right) < 0$$

So the optimal value of $k$ is achieved when $k = \frac{s}{2}$.