Optimal pricing decisions in a fuzzy dual-channel supply chain

Abstract

This paper analyzes the pricing decisions of a dual-channel supply chain including one retailer and one manufacturer who produces a product and sells it to the end customer through retailer or directly. Both the manufacturing cost and the customer demand are considered as fuzzy variables. Two pricing models, including centralized decision model and manufacturer-leader Stackelberg game, with consideration of different market power structures are adopted. Optimal decisions on wholesale price and retail prices are determined using game theoretical approach and fuzzy set theory for each model. Finally, a numerical example is solved to illustrate the effectiveness of models and provide some managerial insights from analysis.

1 Introduction

Nowadays, the issue of pricing decision is reshaped because the customer’s attitudes change and some of them prefer online shopping while the others like to go to the stores. In this situation, the manufacturers have to sell their product through a direct channel in addition to the retail channel. The pricing strategies are the critical factor in making profit for firms in a supply chain from operational and financial point of views as the manufacturers can manage the customer demand by handling pricing decisions.

Recently, a considerable amount of literature has been published on piecing decisions. Among these studies some of them are established in certain environment. For example, Zhang et al. (2012) investigated the effect of product substitutability and relative channel status on pricing decisions under different power structures of a dual exclusive channel system. Chen (2013) considered pricing policies in a supply chain with one manufacturer, who sells a product to an independent retailer and directly to consumers through an Internet channel. Wei et al. (2013) explored the pricing problems with regard to two complementary products in a supply chain with two manufacturers and one common retailer.

There are some uncertain parameters in real world that cannot be overlooked to make profitable decisions in supply chain. These uncertainties may be related to customer demand, product supply, manufacturing cost, etc. A number of studies have modeled these uncertainties using probability theory. Karakul and Chan (2010) defined the uncertainty of demand by probability distributions. Cao et al. (2012) considered a continuous time dynamic pricing problem for selling a given number of items that the demand is price sensitive and follows a non-homogeneous Poisson process.

However, it is impossible to find an appropriate probability distribution in some cases to consider these uncertainties since estimation of these parameters using traditional methods is not always possible. For example, there are many cases where no historical data are available to estimate the parameters such as the related costs because of the rapid changes in real-life situations (Xie et al. 2006), but we can get the useful information based on manager’s judgments, intuitions and experience so the fuzzy theory rather than the probability theory should be applied to model these kind of uncertainties (Zimmermann 2000).

There are some papers based on optimal pricing in fuzzy environments. For example, Zhao et al. (2012) studied the pricing problem of substitutable products in a supply chain with one manufacturer and two competitive retailers by fuzziness of consumer demand and manufacturing cost. The pricing problem of substitutable products in a fuzzy supply chain is analyzed by using game theory by Zhao et al. (2012). Wei and Zhao (2011) considered the optimal pricing decision problem of a fuzzy closed-loop supply chain with retail competition. Wei and Zhao (2012) explored the decisions of reverse channel choice in a fuzzy closed-loop supply chain. They investigated the implications of three different used-product collection modes on the decisions of the manufacturer, the retailer, and the third party, and on their own profits in the expected value model. Wei and Zhao (2013) considered the pricing decisions of substitutable products which are produced by duopolistic manufacturers, respectively, and then sold by one common retailer to the consumers by defining vertical and horizontal competition in fuzzy environments.

As far as we know, there is no study that explores the pricing decisions for a dual-channel supply chain in fuzzy environments. In this paper, we study a supply chain with one manufacturer and one retailer that the manufacturer has two channels for selling product: retailer channel and direct channel. The customer demand and manufacturing cost are considered as fuzzy variables and two structures are defined for power market including one centralized and one decentralized structures. We suppose that the manufacturer has more power in decentralized supply chain.

The reminder of this paper is organized as follows. Section 2 includes problem description and notations. Section 3 details the expected values of centralized decision model and decentralized decision model. A numerical example is presented to illustrate the effectiveness of each model in Sect. 4. In Sect. 5, conclusions of the article with some future research are stated.

2 Preliminaries

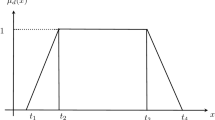
A possibility space is defined as a triplet $(\Theta , \mathcal {P}( \Theta ),\mathrm{pos})$, where $\Theta$ is a nonempty set, $\mathcal {P}( \Theta )$ the power set of $\mathcal {P}( \Theta )$, and Pos a possibility measure. Each element in $\mathcal {P}( \Theta )$ is called a fuzzy event. For each event $A$, $\mathrm{pos}(A)$ indicates the possibility that $A$ will occur. Nahmias (1978) and Liu (2002) gave the following four axioms.

• Axiom 1. $\mathrm{pos}(\Theta )=1$.

• Axiom 2. $\mathrm{pos}(\emptyset )=0$, where $\emptyset$ denotes the empty set.

• Axiom 3. $\mathrm{pos}( {\cup _{i=1}^m A_i })=sup_{1\le i\le m} \mathrm{pos}(A_i )$ for any collection of events $A_i$ in $\mathcal {P}(\Theta )$.

• Axiom 4. Let $\Theta _i$ be nonempty sets, on which $\mathrm{Pos}_i$ is possibility measure satisfying the first three axioms, $i=1,2,\ldots ,n,$ and $\Theta =\mathop \prod \nolimits _{i=1}^n \Theta _i$. Then

  

  For each $A\in \mathrm{pos}( \Theta )$. In that case we write $\mathrm{Pos}=\wedge _{i=1}^n \mathrm{Pos}_i$.

Lemma 1

(Liu 2002) Suppose that $(\Theta _i ,\mathcal {P}(\Theta )_i ,\mathrm{Pos}_i )$ is a possibility space, $i=1,2,\ldots ,n$. By Axiom 4, $(\mathop \prod \nolimits _{i=1}^n \Theta _i ,\mathcal {P}( {\mathop \prod \nolimits _{i=1}^n \Theta _i }),\wedge _{i=1}^n \mathrm{Pos}_i )$ is also a possibility space, which is called the product possibility space.

Definition 1

(Nahmias 1978) A fuzzy variable is defined as a function from the possibility space $(\Theta ,\mathcal {P}( \Theta ),\mathrm{pos})$ to the set of real numbers and its membership function is derived from the possibility by

$$\begin{aligned} \mu _\varepsilon ( x)=\mathrm{pos}( {\left\{ {\theta \in \Theta \vert \varepsilon ( \theta )=x} \right\} }), \quad \forall x\in R. \end{aligned}$$

Definition 2

(Liu 2002) A fuzzy variable $\varepsilon$ is said to be nonnegative (or positive) if $\mathrm{pos}( {\left\{ {\varepsilon <0} \right\} })=0$ (or $\mathrm{pos}( {\left\{ {\varepsilon \le 0} \right\} })=0)$.

Definition 3

(Liu 2002) Let $f{:}\;R^n\rightarrow R$ be a function, and $\varepsilon _i$ a fuzzy variable defined on the possibility space $(\Theta _i ,\mathcal {P}(\Theta )_i ,\mathrm{Pos}_i )$, $i=1,2,\ldots ,n$, respectively. Then $\varepsilon =f(\varepsilon _1 ,\varepsilon _2 ,\ldots ,\varepsilon _n )$ is a fuzzy variable defined on the product possibility space $( {\mathop \prod \nolimits _{i=1}^n \Theta _i ,\mathcal {P}({\mathop \prod \nolimits _{i=1}^n \Theta _i }),\wedge _{i=1}^n \mathrm{Pos}_i})$.

The independence of fuzzy variables was discussed by several researchers such as Liu (2002), Nahmias (1978) and Zadeh (1965).

Definition 4

(Liu 2002) The fuzzy variables $\varepsilon _1 ,\varepsilon _2 ,\ldots ,\varepsilon _n$ are independent if for any sets $B_1 ,B_2 ,\ldots ,B_n$ of $R$,

$$\begin{aligned} \mathrm{pos}( {\left\{ {\varepsilon _i \in B_i ,i=1,2,\ldots ,n} \right\} })=\mathop {\min }\limits _{1\le i\le n} \mathrm{pos}(\{\varepsilon _i \in B_i \}). \end{aligned}$$

Lemma 2

(Liu 2004) Let $\varepsilon _i$, $i=1,2,\ldots ,m$ be independent fuzzy variables, and $f_i :R^n\rightarrow R$ function. Then $f_1 ( {\varepsilon _1 }),f_2 ( {\varepsilon _2 }),\ldots ,f_n ( {\varepsilon _n })$ are independent fuzzy variables.

Definition 5

(Liu 2002) Let $\varepsilon$ be a fuzzy variable on the possibility space $(\Theta ,\mathcal {P}(\Theta ),\mathrm{pos})$, and $\alpha \in (0,1]$. Then,

$$\begin{aligned} \varepsilon _\alpha ^L&= \mathrm{inf} \left\{ {r \vert \mathrm{pos}(\left\{ {\varepsilon \le r} \right\} )\ge \alpha } \right\} \quad \hbox {and}\\ \varepsilon _\alpha ^U&= \mathrm{sup}\left\{ {r \vert \mathrm{pos}(\left\{ {\varepsilon \ge r} \right\} )\ge \alpha } \right\} \end{aligned}$$

are called the $\alpha$-pessimistic value and the $\alpha$ -optimistic value of $\varepsilon$, respectively.

Example 1

The triangular fuzzy variable $\varepsilon =(a_1 ,a_2 ,a_3 )$ has its $\alpha$-pessimistic value and $\alpha$-optimistic value

$$\begin{aligned} \varepsilon _\alpha ^L =a_2 \alpha +a_1 (1-\alpha ) \quad \hbox {and}\quad \varepsilon _\alpha ^U =a_2 \alpha +a_3 (1-\alpha ). \end{aligned}$$

Lemma 3

(Wang et al. 2007) Let $\varepsilon _i$, $i=1,2,\ldots ,n$ be independent fuzzy variables defined on the possibility spaces $( {\Theta _i ,\mathcal {P}( \Theta )_i ,\mathrm{Pos}_i })$ with continuous membership function, and $f{:}\;X\subset R^n\rightarrow R$ a measurable function. If $f(x_1 ,x_2 ,\ldots ,x_n )$ is monotonic with respect to $x_i$, respectively, then

• 1. $f_\alpha ^U (\varepsilon )=f(\varepsilon _{1\alpha }^\vee ,\varepsilon _{2\alpha }^\vee ,\ldots ,\varepsilon _{n\alpha }^\vee ),$ where $\varepsilon _{i\alpha }^\vee =\varepsilon _{i\alpha }^U$ if $f( {x_1 ,x_2 ,\ldots ,x_n })$ is non-decreasing with respect to $x_i$; $\varepsilon _{i\alpha }^\vee =\varepsilon _{i\alpha }^L$, otherwise,

• 2. $f_\alpha ^L (\varepsilon )=f(\varepsilon _{1\alpha }^{\bar{\vee }} ,\varepsilon _{2\alpha }^{\bar{\vee }} ,\ldots ,\varepsilon _{n\alpha }^{\bar{\vee }} ),$ where $\varepsilon _{i\alpha }^{\bar{\vee }} =\varepsilon _{i\alpha }^L$, if $f(x_1 ,x_2 ,\ldots ,x_n )$ is non-decreasing with respect to $x_i$; $\varepsilon _{i\alpha }^{\bar{\vee }} =\varepsilon _{i\alpha }^U$, otherwise,

where $f_\alpha ^U ( \varepsilon )$ and $f_\alpha ^L (\varepsilon )$ denote the $\alpha$-pessimistic value and the $\alpha$-optimistic value of the fuzzy variable $f(\varepsilon )$, respectively.

Definition 6

(Liu and Liu 2002) Let $(\Theta ,\mathcal {P}(\Theta ),\mathrm{pos})$ be a possibility space and $A$ is a set in $\mathcal {P}(\Theta )$. The credibility measure of $A$ is defined as

$$\begin{aligned} \mathrm{Cr}( A)=\frac{1}{2}( {1+\mathrm{pos}( A)-\mathrm{pos}( {A^c})}), \end{aligned}$$

where $A^c$ denotes the complement of $A$.

Definition 7

(Liu and Liu 2002) Let $\varepsilon$ be a fuzzy variable. The expected value of $\varepsilon$ is defined as

$$\begin{aligned} E\left[ \varepsilon \right] =\mathop \int \nolimits _0^{+\infty } \mathrm{Cr}( {\left\{ {\varepsilon \ge x} \right\} })\mathrm{d}x-\mathop \int \nolimits _{-\infty }^0 \mathrm{Cr}( {\left\{ {\varepsilon \le x} \right\} })\mathrm{d}x \end{aligned}$$

provided that at least one of the two integrals is finite.

Example 2

The triangular fuzzy variable $\varepsilon =(a_1 ,a_2 ,a_3 )$ has an expected value

$$\begin{aligned} E\left[ \varepsilon \right] =\frac{a_1 +2a_2 +a_3 }{4}. \end{aligned}$$

Definition 8

(Liu and Liu 2002) Let $f$ be a function on $R\rightarrow R$ and $\varepsilon$ be a fuzzy variable. Then the expected value $E\left[ {f( \varepsilon )} \right]$ is defined as

$$\begin{aligned} E\left[ {f(\varepsilon )} \right]&= \mathop \int \nolimits _0^{+\infty } \mathrm{Cr}( {\left\{ {f(\varepsilon )\ge x} \right\} })\mathrm{d}x\\&-\mathop \int \nolimits _{-\infty }^0 \mathrm{Cr}( {\left\{ {f(\varepsilon )\le x} \right\} })\mathrm{d}x \end{aligned}$$

provided that at least one of the two integrals is finite.

Lemma 4

(Liu and Liu 2003) Let $\varepsilon$ be a fuzzy variable with finite expected value. Then,

$$\begin{aligned} E\left[ \varepsilon \right] =\frac{1}{2}\mathop \int \nolimits _{0}^{1} \left( \varepsilon _\alpha ^{U} +\varepsilon _{\alpha }^{L}\right) \mathrm{d}x. \end{aligned}$$

Lemma 5

(Liu and Liu 2003) Let $\varepsilon$ and $\eta$ be independent fuzzy variables with finite expected values. Then for any numbers $a$ and $b$,

$$\begin{aligned} E\left[ {a\varepsilon +b\eta } \right] =aE\left[ \varepsilon \right] +bE\left[ \eta \right] . \end{aligned}$$

3 Problem description and notations

Consider a dual-channel supply chain with one manufacturer and one retailer. The manufacturer may sell the products through retailer or directly to the end customer. The manufacturer and the retailer make their pricing decisions to achieve their own maximal expected profits. The following notations are used to formulate the fuzzy supply chain models.

$p_r$ :

Unit retail price of product, which is the retailer’s decision variable

$p_d$ :

Unit direct sale price of product, which is the manufacturer’s decision variable

$w$ :

Unit wholesale price of product, which is the manufacturer’s variable

$\tilde{c}$ :

Unit manufacturing cost of product, which is a fuzzy variable

$\tilde{\beta }$ :

Cross-price sensitivity of a product’s demand to its own price, which is fuzzy variable

$\tilde{a}_1 , \tilde{a}_2$ :

Self-price sensitivities of a product’s demand to the price of other channel, which are fuzzy variables

$\rho$ :

The share of the demand goes to the direct channel

$\tilde{a}$ :

The primary demand for product, which is a fuzzy variable

$\tilde{D}_r ( {p_r ,p_d })$ :

The demand for product in the retail channel

$\tilde{D}_d ( {p_r ,p_d })$ :

The demand for product in the direct channel

Similar to McGuire and Staelin (1983), the consumer demand function is defined as a linear form of the retail price. The demand for retail channel can be expressed as follows:

$$\begin{aligned} \tilde{D}_r ( {p_r ,p_d })=( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d . \end{aligned}$$

(1)

The demand for direct channel is stated as follows:

$$\begin{aligned} \tilde{D}_d ( {p_r ,p_d })=\rho \tilde{a}- \tilde{a}_2 p_d +\tilde{\beta }p_r . \end{aligned}$$

(2)

We make some assumptions as follows:

• 1. All activities occurred in a single period.

• 2. The fuzzy parameters $\tilde{\beta }$, $\tilde{a}_1$, $\tilde{a}_2$, $\tilde{a}$, $\tilde{c}$ are mutually independent and nonnegative. The expected values of parameters $\tilde{a}_1$, $\tilde{a}_2$ are larger than the expected value of $\tilde{\beta }$, which means that the expected demand for a product should be more sensitive to changes in its price than to changes in the price of the product of the other channel.

• 3. The manufacturer and the retailer have perfect information of the demands and the cost structures of the other channel member.

• 4. The logistic cost components of the manufacturer and the retailer (i.e., transportation cost and inventory cost) are ignored for computational convenience.

The profits of the manufacturer, the retailer, and total system can be expressed as follows:

$$\begin{aligned} \pi _m ( {w,p_d })&= ( {w-\tilde{c}})[( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d ] \nonumber \\&+\,({p_d-\tilde{c}})[\rho \tilde{a}-\tilde{a}_2 p_d +\tilde{\beta }p_r ], \end{aligned}$$

(3)

$$\begin{aligned} \pi _r ( {p_\mathrm{r} })&= ( {p_\mathrm{r} -w})\left[ {( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d } \right] , \end{aligned}$$

(4)

$$\begin{aligned} \pi _c ( {p_r ,p_d })&= \pi _m ( {w,p_d })+\pi _r ( {p_\mathrm{r} })=( {p_r -\tilde{c}}) \nonumber \\&\times \,\left[ {( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d } \right] \nonumber \\&+\,( {p_d -\tilde{c}})[\rho \tilde{a}- \tilde{a}_2 p_d +\tilde{\beta }p_r ]. \end{aligned}$$

(5)

4 Analytical results

In this section, there are one centralized decision case and one decentralized decision case. We consider a Stackelberg structure for market power between manufacturer and the retailer. When one member has more market power than the other, he will have the advantage of the first move and can impose his decisions on the other.

The game-theoretical approach is applied to explore the pricing decision models for each case in the following.

4.1 Centralized decision model

We first examine the centralized decision case, in which, there is one central controller (manager) that aims to optimize the whole system performance. In this case, the wholesale price, $w$ becomes inner transfer price and can be ignored. So, the expected value of the profit can be determined by the retail price and direct sale price and formulated as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathop {\max }\limits _{(p_r ,p_d )} E\left[ {\pi _c ( {p_r ,p_d})}\right] ,}\\ \quad \mathrm{subject}\; \mathrm{to}\\ \quad {\mathrm{pos}\left( {\left\{ {( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d <0} \right\} }\right) =0,} \\ \quad \mathrm{pos}(\{\rho \tilde{a}-\tilde{a}_2 p_d +\tilde{\beta }p_r <0\})=0, \\ \quad \mathrm{pos}( {\left\{ {p_r -\tilde{c}<0} \right\} })=0, \\ \quad \mathrm{pos}( {\left\{ {p_d -\tilde{c}<0} \right\} })=0. \\ \end{array} \right. \end{aligned}$$

Proposition 1

The expected profit $E\left[ {\pi _c ( {p_r ,p_d })} \right]$ is jointly concave in $(p_r ,p_d )$.

Proof

Note that, the fuzzy parameters are all independent and nonnegative. By Eq. (5), Lemmas 3 and 4, the expected profit $E\left[ {\pi _c ( {p_r ,p_d })} \right]$ can be represented as follows:

$$\begin{aligned}&E\left[ {\pi _c ( {p_r ,p_d })} \right] =E\left[ ( {p_r -\tilde{c}})\left[ {( {1-\rho })\tilde{a}-\tilde{a}_{1} p_{r} +\tilde{\beta }p_d } \right] \right. \nonumber \\&\quad \left. +\,({p_d -\tilde{c}})[\rho \tilde{a}-\tilde{a}_2 p_d +\tilde{\beta }p_r ] \right] \nonumber \\&=\frac{1}{2}\mathop \int \nolimits _0^1 \{( ( {p_r -\tilde{c}})\left[ {( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d } \right] \nonumber \\&\quad +\,( {p_d -\tilde{c}})[\rho \tilde{a}-\tilde{a}_2 p_d +\tilde{\beta }p_r ])_\alpha ^{U} \nonumber \\&\quad +\,( ( {p_r -\tilde{c}})\left[ {( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d } \right] \nonumber \\&\quad +\,({p_d -\tilde{c}})[\rho \tilde{a}-\tilde{a}_2 p_d +\tilde{\beta }p_r ])_\alpha ^L \}\mathrm{d}\alpha =({1-\rho }) \nonumber \\&\quad \times E\left[ {\tilde{a}} \right] p_r -E\left[ {\tilde{a}_1 } \right] p_r ^2+2E\left[ {\tilde{\beta }} \right] p_r p_d +\rho E\left[ {\tilde{a}} \right] p_d \nonumber \\&\quad -\,E\left[ {\tilde{a}_2 } \right] p_d ^2 +\rho E\left[ {\tilde{c}\tilde{a}} \right] +E\left[ {\tilde{c}\tilde{a}_1 } \right] p_r \nonumber \\&\quad +\,E\left[ {\tilde{c}\tilde{a}_2}\right] p_d -\frac{({1-\rho })}{2}\mathop \int \nolimits _0^1 (\tilde{c}_\alpha ^L \tilde{a}_\alpha ^{U} +\tilde{c}_\alpha ^{U} \tilde{a}_\alpha ^L )\mathrm{d}\alpha \nonumber \\&\quad -\,\frac{( {p_d +p_r })}{2}\mathop \int \nolimits _0^1 (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L )\mathrm{d}\alpha . \end{aligned}$$

(6)

The first-order and second-order partial derivatives of $E\left[ {\pi _c ( {p_r ,p_d })} \right]$ with respect to $( {p_r ,p_d })$ can be given as

$$\begin{aligned} \frac{\partial E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_r }&= ( {1-\rho })E\left[ {\tilde{a}} \right] -2p_r E\left[ {\tilde{a}_1 }\right] \nonumber \\&+\,2E\left[ {\tilde{\beta }} \right] p_d \!+\!E\left[ {\tilde{c}\tilde{a}_1 } \right] \nonumber \\&-\,\frac{1}{2}\mathop \int \nolimits _0^1 (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L )\mathrm{d}\alpha , \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_d }&= \rho E\left[ {\tilde{a}} \right] -2E\left[ {\tilde{a}_2 } \right] p_d \nonumber \\&+\,2E\left[ {\tilde{\beta }} \right] p_r -E\left[ {\tilde{c}\tilde{a}_2 } \right] \nonumber \\&-\,\frac{1}{2}\mathop \int \nolimits _0^1 (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L )\mathrm{d}\alpha , \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_r ^2}&= -2E\left[ {\tilde{a}_1 } \right] \!, \end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_d ^2}&= -2E\left[ {\tilde{a}_2 } \right] \!, \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_r p_d }&= \frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_d p_r }=2E\left[ {\tilde{\beta }} \right] . \end{aligned}$$

(11)

By Eqs. (9), (10), and (11) the Hessian matrix

$$\begin{aligned} H_1&= \left[ \begin{array}{ll} {\frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_r^2}} &{} {\frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_r p_d }}\\ {\frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_d p_r}} &{} {\frac{\partial ^2E\left[ {\pi _c ( {p_r ,p_d })} \right] }{\partial p_d ^2}}\\ \end{array} \right] \nonumber \\&= \left[ \begin{array}{ll} {-2E\left[ {\tilde{a}_1 } \right] } &{} {2E\left[ {\tilde{\beta }} \right] }\\ {2E\left[ {\tilde{\beta }} \right] } &{} {-2E\left[ {\tilde{a}_2 } \right] }\\ \end{array} \right] . \end{aligned}$$

(12)

We can see that $H_1$ is negative definite according to abovementioned assumptions.

Let $\varepsilon _{0^+}^L =\mathop {\lim }\nolimits _{\alpha \rightarrow 0^+} \varepsilon _0^L ,\quad \varepsilon _{0^+}^U =\mathop {\lim }\nolimits _{\alpha \rightarrow 0^+} \varepsilon _0^U , \alpha \varepsilon \left( {0,1} \right] ,$ the notations will be used in the following propositions.

Proposition 2

The optimal prices are given as follows:

$$\begin{aligned}&p_r^*=\frac{E\left[ {\tilde{a}_2 } \right] A_1 + E\left[ {\tilde{\beta }} \right] A_2 }{2\left( E\left[ {\tilde{a}_1 } \right] E\left[ {\tilde{a}_2 } \right] -E^2\left[ {\tilde{\beta }} \right] \right) }, \end{aligned}$$

(13)

$$\begin{aligned}&p_d^*=\frac{E\left[ {\tilde{\beta }} \right] A_1 + E\left[ {\tilde{a}_1 } \right] A_2 }{2\left( E\left[ {\tilde{a}_1 } \right] E\left[ {\tilde{a}_2 } \right] -E^2\left[ {\tilde{\beta }} \right] \right) }. \end{aligned}$$

(14)

where

$$\begin{aligned} A_1&= ( {1-\rho })E\left[ {\tilde{a}} \right] +E\left[ {\tilde{c}\tilde{a}_1 } \right] -\frac{1}{2}\mathop \int \nolimits _0^1 \left( \tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L \right) \mathrm{d}\alpha \\ A_2&= \rho E\left[ \tilde{a} \right] +E\left[ {\tilde{c}\tilde{a}_2 } \right] -\frac{1}{2}\mathop \int \nolimits _0^1 \left( \tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L\right) \mathrm{d}\alpha \end{aligned}$$

Proof

By setting Eqs. (7) and (8) equal to zero and solving them with respect to $p_r$and $p_d$ concurrently, the results (13) and (14) can be gained. $\square$

4.2 Manufacturer-leader Stackelberg (MS) game

In this case, the retailer is smaller than the manufacturer. The manufacturer first determines optimal prices and the retailer makes her decision on retail price with respect to the wholesale price and direct sale price. The MS model is formulated as:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathop {\max }\limits _{(w,p_d )} E\left[ {\pi _m ( {w,p_d ,p_r^{*}(w,p_d )})} \right] ,\quad \mathrm{subject}\; \mathrm{to}} \\ \quad {\mathrm{pos}( {\left\{ {w-\tilde{c}<0} \right\} })=0, \mathrm{pos}( {\left\{ {p_d -\tilde{c}<0} \right\} })=0,} \\ \quad {\mathrm{pos}( {\left\{ {p_d -\tilde{c}<0} \right\} })=0, \mathrm{pos}\left( {\left\{ {\rho \tilde{a}- \tilde{a}_2 p_d +\tilde{\beta }p_r <0} \right\} }\right) =0} \\ \quad {p_r ^{*} (w,p_d )\; \text {are derived from solving the problem,}} \\ \quad \quad \left\{ \begin{array}{l} {\mathop {\max }\nolimits _{(p_r )} E\left[ {\pi _r ( {p_r })} \right] ,\quad \text {subject to}} \\ \quad {\mathrm{Pos}\left( {\left\{ {( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d <0} \right\} }\right) =0,} \\ \quad {p_r \ge w.} \\ \end{array}\right. \\ \end{array}\right. \end{aligned}$$

By considering $w$ and $p_d$, which are announced by the manufacturer, the retailer’s response function can be derived as follows:

Proposition 3

In the MS model, given decisions $w$ and $p_d$ made by the manufacturer, the retailer’s optimal retail price $p_r ^{*}( {w,p_d })$ is:

$$\begin{aligned} p_r ^{*}( {w,p_d })=\frac{w}{2}+\frac{E\left[ {\tilde{\beta }} \right] }{2E\left[ {\tilde{a}_1 } \right] }p_d + ( {1-\rho })\frac{E\left[ {\tilde{a}} \right] }{2E\left[ {\tilde{a}_1 } \right] }. \end{aligned}$$

(15)

Under the following condition that

$$\begin{aligned}&\left( {2E\left[ {\tilde{a}_1 } \right] +E\left[ {\tilde{\beta }} \right] p_d }\right) \tilde{a}_{0^+}^L +2E\left[ {\tilde{a}_1 } \right] p_d \tilde{\beta }_{0^+}^L +\rho E\left[ {\tilde{a}} \right] \tilde{a}_{10^+}^L \\&\quad >2\rho E\left[ {\tilde{a}_1 } \right] \tilde{a}_{0^+}^U +\left( E\left[ {\tilde{a}_1 } \right] w+E\left[ {\tilde{a}} \right] \right) \tilde{a}_{10^+}^U , \end{aligned}$$

Proof

By Eq. (4), Lemmas 3 and 4, the expected profit $E\left[ {\pi _r ( {p_r })} \right]$ can be expressed as follows:

$$\begin{aligned}&E\left[ {\pi _r ( {p_r })} \right] \nonumber \\&\quad =E\left[ {( {p_r -w})(( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d )} \right] \nonumber \\&\quad =\frac{1}{2}\mathop \int \nolimits _0^1 \left\{ \left( {( {p_r -w})(( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d )}\right) _\alpha ^U \right. \nonumber \\&\quad \quad \left. + \left( ( {p_r -w_i })(( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d )\right) _\alpha ^L \right\} \mathrm{d}\alpha \nonumber \\&\quad =( {1-\rho }) E\left[ {\tilde{a}} \right] p_r -E\left[ {\tilde{a}_1} \right] p_r ^2+E\left[ {\tilde{\beta }} \right] p_d p_r \nonumber \\&\quad \quad -( {1-\rho })E\left[ {\tilde{a}} \right] w +E\left[ {\tilde{a}_1 } \right] wp_r -E\left[ {\tilde{\beta }} \right] p_d w. \end{aligned}$$

(16)

The first-order and second-order partial derivatives of $E\left[ {\pi _r ( {p_r })} \right]$ with respect to $p_r$can be shown as:

$$\begin{aligned} \frac{\partial E\left[ {\pi _r ( {p_r })} \right] }{\partial p_r }&= ( {1-\rho })E\left[ {\tilde{a}} \right] -2E\left[ {\tilde{a}_1 }\right] p_r \nonumber \\&+E\left[ {\tilde{a}_1 } \right] w+E\left[ {\tilde{\beta }} \right] p_d , \end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial ^2E\left[ {\pi _r ( {p_r })} \right] }{\partial p_r ^2}&= -2E\left[ {\tilde{a}_1 } \right] . \end{aligned}$$

(18)

So, $E\left[ {\pi _r ( {p_r })} \right]$ is jointly concave with respect to $p_r$.

By setting Eq. (17) equal to zero and solving it with respect to $p_r$, the result (15) can be gained. By Definition 5, the following equation is equivalent to the abovementioned condition:

$$\begin{aligned} \mathrm{Pos}\left( {\left\{ {( {1-\rho })\tilde{a}-\tilde{a}_1 p_r +\tilde{\beta }p_d <0} \right\} }\right) =0. \end{aligned}$$

$\square$

Proposition 4

In this scenario, the manufacturer’ optimal wholesale price and direct sale price can be given as:

$$\begin{aligned}&w^{*}=\frac{2E[\tilde{a}_2 ]A_3 +E[\tilde{\beta }]A_4}{2E\left[ {\tilde{a}_1 } \right] E\left[ {\tilde{a}_2 } \right] -E^2[\tilde{\beta }]}, \end{aligned}$$

(19)

$$\begin{aligned}&p_d ^{*}=\frac{E[\tilde{\beta }]A_3 +E[\tilde{a}_1 ]A_4 }{2E\left[ {\tilde{a}_1 } \right] E\left[ {\tilde{a}_2 } \right] -E^2[\tilde{\beta }]}. \end{aligned}$$

(20)

where

$$\begin{aligned} A_3&= \frac{( {1-\rho })E\left[ {\tilde{a}} \right] }{2}+\frac{1}{2}E\left[ {\tilde{c}\tilde{a}_1 } \right] \!-\!\frac{1}{4}\mathop \int \nolimits _0^1 (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U \!+\!\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L )\mathrm{d}\alpha ,\\ A_4&= \frac{( {1-\rho })E\left[ {\tilde{a}} \right] E\left[ {\tilde{\beta }} \right] }{2E\left[ {\tilde{a}_1 } \right] }+\rho E\left[ {\tilde{a}} \right] +\frac{E^2\left[ {\tilde{\beta }} \right] }{E\left[ {\tilde{a}_1 } \right] }\\&-\frac{1}{2}\mathop \int \nolimits _0^1 \left( \tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L \right) \mathrm{d}\alpha , \end{aligned}$$

Proof

By Eqs. (7) and (8), Lemmas 3 and 4, the expected profit of the manufacturer, $E\left[ {\pi _m ( {w,p_d })} \right]$ can be represented as follows:

$$\begin{aligned}&E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] \nonumber \\&\quad =E\left[ ( {w-\tilde{c}})[( {1-\rho })\tilde{a}-\tilde{a}_1 p_r -\tilde{\beta }p_d ]+( {p_d -\tilde{c}}) \right. \nonumber \\&\quad \quad \times \left. [\rho \tilde{a}- \tilde{a}_2 p_d -\tilde{\beta }p_r ] \right] \nonumber \\&\quad =\frac{1}{2}\mathop \int \nolimits _0^1 \Bigg \{\left( ( {w-\tilde{c}})[( {1-\rho })\tilde{a}-\tilde{a}_1 p_r -\tilde{\beta }p_d ] \right. \nonumber \\&\quad \quad \left. +( {p_d -\tilde{c}})[\rho \tilde{a}-\tilde{a}_2 p_d -\tilde{\beta }p_r ]\right) _\alpha ^U \nonumber \\&\quad \quad + \left( ( {w-\tilde{c}})[( {1-\rho })\tilde{a}-\tilde{a}_1 p_r -\tilde{\beta }p_d ]+( {p_d -\tilde{c}}) \right. \nonumber \\&\quad \quad \times \left. [\rho \tilde{a}- \tilde{a}_2 p_d -\tilde{\beta }p_r ]\right) _\alpha ^L \Bigg \}\mathrm{d}\alpha \nonumber \\&\quad =( {1-\rho })E\left[ {\tilde{a}} \right] w-\frac{E\left[ {\tilde{a}_1 } \right] }{2}w^2-\frac{( {1-\rho })E\left[ {\tilde{a}} \right] }{2}w \nonumber \\&\quad \quad +E\left[ {\tilde{\beta }} \right] p_d w+\rho E\left[ {\tilde{a}} \right] p_d -E\left[ {\tilde{a}_2 } \right] p_d ^2 \nonumber \\&\quad \quad +\frac{( {1-\rho })E\left[ {\tilde{a}} \right] E\left[ {\tilde{\beta }} \right] }{2E\left[ {\tilde{a}_1 } \right] }p_d +\frac{E^2\left[ {\tilde{\beta }} \right] }{2E\left[ {\tilde{a}_1 } \right] }p_d ^2 \nonumber \\&\quad \quad -\frac{( {1-\rho })}{2}\mathop \int \nolimits _0^1 \Bigg (\tilde{c}_\alpha ^L \tilde{a}_\alpha ^U +\tilde{c}_\alpha ^U \tilde{a}_\alpha ^L \Bigg )\mathrm{d}\alpha +\rho E\left[ {\tilde{c}\tilde{a}} \right] \nonumber \\&\quad \quad +\frac{E\left[ {\tilde{c}\tilde{a}_1 } \right] }{2}w+\frac{( {1-\rho })E\left[ {\tilde{a}} \right] E\left[ {\tilde{c}\tilde{a}_1 } \right] }{2E\left[ {\tilde{a}_1 } \right] } \nonumber \\&\quad \quad -\frac{p_d }{2}\mathop \int \nolimits _0^1 \Bigg (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U+\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L \Bigg )\mathrm{d}\alpha +E\left[ {\tilde{c}\tilde{a}_2 } \right] \nonumber \\&\quad \quad -\frac{w}{4}\mathop \int \nolimits _0^1 \Bigg (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L\Bigg )\mathrm{d}\alpha \nonumber \\&\quad \quad -\frac{( {1-\rho })E\left[ {\tilde{a}} \right] }{4E\left[ {\tilde{a}_1 } \right] }\mathop \int \nolimits _0^1 \Bigg (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L \Bigg )\mathrm{d}\alpha \nonumber \\&\quad \quad -\frac{E\left[ {\tilde{\beta }} \right] }{4E\left[ {\tilde{a}_1 } \right] }\mathop \int \nolimits _0^1 \Bigg (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L \Bigg )\mathrm{d}\alpha . \end{aligned}$$

(21)

The first-order and second-order partial derivatives of $E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right]$ with respect to $w$ and $p_d$can be shown as:

$$\begin{aligned}&\frac{\partial E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial w}\nonumber \\&\quad =\frac{( {1-\rho })E\left[ {\tilde{a}} \right] }{2}-E\left[ {\tilde{a}_1 } \right] w \nonumber \\&\quad \quad +E\left[ {\tilde{\beta }} \right] p_d +\frac{1}{2}E\left[ {\tilde{c}\tilde{a}_1 } \right] \nonumber \\&\qquad -\frac{1}{4}\mathop \int \nolimits _0^1 (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L )\mathrm{d}\alpha , \end{aligned}$$

(22)

$$\begin{aligned}&\quad \quad \times \frac{\partial E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial p_d }\nonumber \\&\quad =\frac{( {1-\rho })E\left[ {\tilde{a}} \right] E\left[ {\tilde{\beta }} \right] }{2E\left[ {\tilde{a}_1 } \right] }+\rho E\left[ {\tilde{a}} \right] \nonumber \\&\quad \quad -2E\left[ {\tilde{a}_2 } \right] p_d +E\left[ {\tilde{\beta }} \right] w+\frac{E^2\left[ {\tilde{\beta }} \right] }{E\left[ {\tilde{a}_1 } \right] }p_d\nonumber \\&\qquad -\frac{1}{2}\mathop \int \nolimits _0^1 (\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L )\mathrm{d}\alpha , \end{aligned}$$

(23)

$$\begin{aligned}&\quad \quad \quad \frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial w^2}=-E\left[ {\tilde{a}_1 } \right] , \end{aligned}$$

(24)

$$\begin{aligned}&\quad \quad \quad \frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial p_d ^2}\nonumber \\&\quad =-2E\left[ {\tilde{a}_2 } \right] +\frac{E^2\left[ {\tilde{\beta }} \right] }{E\left[ {\tilde{a}_1 } \right] }, \end{aligned}$$

(25)

$$\begin{aligned}&\quad \quad \quad \frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial w\partial p_d } \nonumber \\&\quad =\frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial p_d \partial w}=E\left[ {\tilde{\beta }} \right] . \end{aligned}$$

(26)

By Eqs. (24), (25), and (26) the Hessian matrix

$$\begin{aligned} H_2&= \left[ \begin{array}{ll} {\frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial w^2}} &{} {\frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial w\partial p_d }} \\ {\frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial p_d \partial w}} &{} {\frac{\partial ^2E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right] }{\partial p_d ^2}} \\ \end{array} \right] \nonumber \\&= \left[ \begin{array}{ll} {-E\left[ {\tilde{a}_1 } \right] } &{} {E\left[ {\tilde{\beta }} \right] } \\ {E\left[ {\tilde{\beta }} \right] } &{} {-2E\left[ {\tilde{a}_2 } \right] +\frac{E^2\left[ {\tilde{\beta }} \right] }{E\left[ {\tilde{a}_1 } \right] }} \\ \end{array} \right] . \end{aligned}$$

(27)

We can see that $H_2$ is negative definite according to abovementioned assumptions, so $E\left[ {\pi _m ( {w,p_d ,p_r ^{*}(w,p_d )})} \right]$ is jointly concave with respect to $w$ and $p_d$.

By setting Eqs. (22) and (23) equal to zero and solving them with respect to $w$ and $p_d$ concurrently, the results (19) and (20) can be gained. $\square$

Proposition 5

The optimal retail price is shown as:

$$\begin{aligned} p_r ^{*}=\frac{w^{*}}{2}+\frac{E\left[ {\tilde{\beta }} \right] }{2E\left[ {\tilde{a}_1 } \right] }p_d ^{*}+(1-\rho )\frac{E\left[ {\tilde{a}} \right] }{2E\left[ {\tilde{a}_1 } \right] }. \end{aligned}$$

(28)

Proof

By substituting (19) in (15), the optimal retail price can be obtained. $\square$

5 Numerical example

In this section, we present a numerical example to show the effects of fuzzy parameters on optimal prices and the optimal expected profits for channel members by considering the centralized supply chain and MS game. We assume that the values of parameters are as follows:

$$\begin{aligned}&\tilde{a}=( {250,300,350}), \quad \rho =0.2, \quad \tilde{a}_1 =(12,15,18), \\&\tilde{a}_2 =(15,17,19), \quad \tilde{\beta }=(4,6,8), \quad \tilde{c}=(9,10,11) \end{aligned}$$

So, we would have

$$\begin{aligned}&E\left[ {\tilde{a}} \right] =\frac{250+2( {300})+350}{4}=300 \\&E\left[ {\tilde{a}_1 } \right] =\frac{12+2( {15})+18}{4}=15 \\&E\left[ {\tilde{a}_2 } \right] =\frac{15+2({17})+19}{4}=17 \\&E\left[ {\tilde{\beta }} \right] =\frac{4+2( 6)+8}{4}=6 \\&E\left[ {\tilde{c}} \right] =\frac{9+2( {10})+11}{4}=10. \end{aligned}$$

The $\alpha$-optimistic values and $\alpha$-pessimistic values of the parameters are:

$$\begin{aligned} \tilde{a}_\alpha ^U&= 350-50\alpha \quad \tilde{a}_\alpha ^L =250+50\alpha \\ \tilde{a}_{1\alpha }^U&= 18-3\alpha \quad \tilde{a}_{1\alpha }^L =12+3\alpha \\ \tilde{a}_{2x}^U&= 19-2\alpha \quad \tilde{a}_{2\alpha }^L =15+2\alpha \\ \tilde{\beta }_\alpha ^U&= 8-2\alpha \quad \tilde{\beta }_\alpha ^L =4+2\alpha \\ \tilde{c}_\alpha ^U&= 11-\alpha \quad \tilde{c}_\alpha ^L =9+\alpha . \end{aligned}$$

Using abovementioned values, we have

$$\begin{aligned}&E\left[ {\tilde{c}\tilde{a}} \right] =\frac{1}{2}\mathop \int \nolimits _0^1 \left( {\tilde{c}_\alpha ^L \tilde{a}_\alpha ^L +\tilde{c}_\alpha ^U \tilde{a}_\alpha ^U }\right) \mathrm{d}\alpha =\hbox {3,016.67} \\&E\left[ {\tilde{c}\tilde{a}_1 } \right] =\frac{1}{2}\mathop \int \nolimits _0^1 \left( {\tilde{c}_\alpha ^L \tilde{a}_{2_\alpha }^L +\tilde{c}_\alpha ^U \tilde{a}_{2_\alpha }^U }\right) \mathrm{d}\alpha =151 \\&E\left[ {\tilde{c}\tilde{a}_2 } \right] =\frac{1}{2}\mathop \int \nolimits _0^1 \left( {\tilde{c}_\alpha ^L \tilde{a}_{2_\alpha }^L +\tilde{c}_\alpha ^U \tilde{a}_{2_\alpha }^U }\right) \mathrm{d}\alpha =170.67 \\&\frac{1}{2}\mathop \int \nolimits _0^1 \left( {\tilde{c}_\alpha ^L \tilde{\beta }_\alpha ^U +\tilde{c}_\alpha ^U \tilde{\beta }_\alpha ^L }\right) \mathrm{d}\alpha =59.33 \\&\frac{1}{2}\mathop \int \nolimits _0^1 \left( {\tilde{c}_\alpha ^L \tilde{a}_\alpha ^U +\tilde{c}_\alpha ^U \tilde{a}_\alpha ^L }\right) \mathrm{d}\alpha =\hbox {2,983.33}. \end{aligned}$$

The optimal prices and the expected profits are given in Tables 1 and 2.

Table 1 Optimal expected profits of the channel members under different scenarios

Table 2 Optimal decisions of retail price, direct sale price and wholesale price under different scenarios

From the above tables, it can be found that the largest expected profit of the entire system can be gained in centralized supply chain structure and the expected profit of the manufacturer is more than the retailer’s expected profit in MS game.

We explore the effects of the fuzzy degrees of parameter $\tilde{\beta }$ on optimal values in MS game. The values of the other parameters are the same as before.

Tables 3 and 4 illustrate the optimal expected profits of the manufacturer and the entire channel degrade while the retailer’s optimal expected profit increases as the fuzzy degree of parameter $\tilde{\beta }$ decreases also the optimal prices are decreasing slightly up to down.

We study the effects of parameter $\tilde{a}_1$ on optimal values by reducing the fuzziness of this parameter. The values of the other parameters are considered as before.

Table 3 The changes of optimal expected profits in MS game with the fuzzy degree of parameter $\tilde{\beta }$

Table 4 The changes of optimal prices in MS game with the fuzzy degree of parameter $\tilde{\beta }$

By considering above Tables 5 and 6, it can be found that the optimal expected profits of the manufacturer and the entire channel increase while the retailer’s optimal expected profit decreases as the fuzzy degree of parameter $\tilde{a}_1$ decreases. The optimal prices decrease with decreasing the fuzzy degree of parameter $\tilde{a}_1$.

Table 5 The changes of optimal expected profits in MS game with the fuzzy degree of parameter $\tilde{a}_1$

Table 6 The changes of optimal prices in MS game with the fuzzy degree of parameter $\tilde{a}_1$

The effects of parameter $\tilde{a}_2$ on optimal values are considered by reducing the fuzziness of this parameter. The values of the other parameters are constant (Table 7).

Table 7 The changes of optimal expected profits in MS game with the fuzzy degree of parameter $\tilde{a}_2$

The optimal expected profits of the manufacturer and the entire supply chain decrease with falling the fuzzy degree of parameter $\tilde{a}_2$ while the retailer’s optimal expected profit and optimal prices are constant so these values are independent of this parameter (Table 8).

Table 8 The changes of optimal prices in MS game with the fuzzy degree of parameter $\tilde{a}_2$

6 Conclusion

In this paper, we study the pricing decisions for a dual-channel supply chain with one retailer and one manufacturer in fuzzy environments over two different structures for market power. This study makes several contributions to the current literatures. First, we consider demand and production cost as fuzzy variables rather than deterministic or stochastic ones and gain the optimization pricing problem under the uncertain environments. Second, using fuzzy theory and game-theoretical approach, the optimal prices and optimal expected profits for retailer and manufacturer are specified in two different scenarios. Third, we explore the effects of changing the fuzzy degrees of parameters on the behavior of firms in changing uncertain environments.

It is recommended that further research be undertaken in the following areas: different or more general forms of the demand function can be used to analyze the problem, the dual-channel supply chain with many manufacturers and many retailers can also be considered in the future. Moreover, we use the constant wholesale price contract in this paper. So, an extension would be to explore the other kinds of contracts between retailer and the manufacturer. We define a symmetric structure for demand or production cost information. It is also interesting to develop an asymmetric structure for information between channel members in uncertain environments.