A Novel Image Encryption Algorithm Based on the Two-Dimensional Logistic Map and the Latin Square Image Cipher

Abstract

In this paper, we introduce a new hybrid system consisting of a permutation-substitution network based on two different encryption techniques: chaotic systems and the Latin square. This homogeneity between the two systems allows us to provide the good properties of confusion and diffusion, robustness to the integration of noise in decryption. The security analysis shows that the system is secure enough to resist brute-force attack, differential attack, chosen-plaintext attack, known-plaintext attack and statistical attack. Therefore, this robustness is proven and justified.

Graphical Abstract

1 Introduction

The development of the IT field especially laptops, media supports and the Internet facilitated the diffusion and exchange of information. Many applications such as military databases, confidential video conferencing, medical imaging system, cable TVs, personal photo album online, etc., require reliable, fast and robust systems for secure transmission. The image encryption is different from text because of some intrinsic features of images, such as data redundancy and the strong correlation between adjacent pixels. Therefore, the traditional systems such as DES [1], AES [2], and Blowfish [3] are not suitable for images and videos encryption. To overcome this problem, many fast systems specially designed for digital images have been proposed in recent years, and their main purposes is to reduce the redundancy in image, to strengthen security and particularly to minimize the encryption time.

Among those existing approaches, Chaos-based scheme, with the desirable properties of pseudo randomness, ergodicity, high sensitivity to initial conditions and parameters, is recognized as great potential for multimedia encryption because such features are considered analogous to those of an ideal cryptosystem. The sequences generated by the chaotic maps are often pseudo-random sequences, and their structures are very complex and difficult to analyze [4–8]. Yue Wu et al. [9] proposed an image encryption using the two-dimensional logistic chaotic map, which has well-known weaknesses such as the key length which is insufficient, low security, and encryption time which is quite high. It completely loses its chaotic nature and becomes periodic when it is discretized [10] and the initial values can be estimated by a number of existing tools and methods [11, 12]. To overcome these drawbacks, we suggest a hybrid algorithm which consists of a substitution-permutation network of eight rounds based on the two-dimensional logistic map to take advantage of chaotic systems and Latin square [13], which would ensure a good diffusion, strengthen more safety and improve the encryption time considerably. With this homogeneity between the two systems, we can obtain a reliable, robust, and fast encryption algorithm.

The proposed algorithm is designed for medical imagery, because currently, most of Hospital Data Management Systems (HDMSs) and medical equipment’s are working in a computer network environment. Medical images are produced and stored in a digital form; moreover, they are exchanged through a computer network. These images are the most important entity in the healthcare diagnostic procedures because they are used to view features of patients such as anatomical cross-sections of internal organs and tissues, in addition they are used for physicians to evaluate the patient’s diagnosis and monitor the effects of the treatment. Therefore, protecting medical images from an unauthorized use is an essential requirement.

This article is organized as follows: In the second part, we give an overview of previous works, the third part presents a detailed description of the proposed algorithm, the fourth part contains the software implementation and experimental results (sensitivity towards the secret key, histogram analysis, correlation between adjacent pixels…), and ends with a general conclusion.

2 Previous Works

Due to the high sensitivity of chaotic systems to parameters and initial conditions as well as the availability of many circuit realizations [14, 15], chaos based algorithms are developed and studied as the core of encryption algorithms. Recently, many Chaos-based schemes are proposed: Telem ANK et al. [16] proposed A robust gray image encryption scheme using chaotic logistic map and artificial neural network (ANN), In the proposed method, an external secret key is used to derive the initial conditions for the logistic chaotic maps which are employed to generate weights and biases matrices of the multilayer perceptron (MLP). During the learning process with the back propagation algorithm, ANN determines the weight matrix of the connections. The plain image is divided into four sub images which are used for the first diffusion stage. The sub images obtained previously are divided into the square sub image blocks. In the next stage, different initial conditions are employed to generate a key stream which will be used for permutation and diffusion of the sub image blocks. Hegui Zhu et al. [17] proposed A novel image encryption–compression scheme using hyper-chaos and Chinese remainder theorem, Specifically, firstly they use 2D hyper-chaos discrete non linear dynamic system to shuffle the plain image, and then they apply Chinese remainder theorem (well known in number theory) to diffuse and compress the shuffled image. Hraoui et al. [18] proposed a mix of a compression technique called SPIHT (Set Partitioning in Hierarchical Trees) and chaotic encryption in order to elaborate a crypto-compressing scheme based on encrypting quantization by a modified logistic map. Kanso et al. [19] introduced a novel image encryption algorithm based on a 3D chaotic map, the proposed algorithm based on three phases: In phase I, the image pixels are shuffled according to a search rule based on the 3D chaotic map. In phases II and III, 3D chaotic maps are used to scramble shuffled pixels through mixing and masking rules.

On the other hand, non-chaotic methods have proved their existence and importance in implementing the confusion and diffusion stages. Such methods usually increase the algorithm complexity to protect against cryptanalysis: Yue Wu et al. [13] introduced a symmetric-key Latin square image cipher (LSIC) for grayscale and color image encryption.

Pareek et al. [20] divided the image into non-overlapping blocks and each block was scrambled using a zigzag-like algorithm. Furthermore, Al-Husainy [21] divided the image into a set of k-bit vectors, each of these vectors was substituted by XORing it with the previous vector and then permuted by circularly right rotating its bits. Pareek et al. [22] divided the image into non-overlapping blocks and for each encryption round the size of the block changed according to the round key. Within the same block, permutation was performed using a zigzag like algorithm.

The combination of both chaotic and non-chaotic algorithms showed some advantages in many cryptosystems. For example, Li et al. [23] used the 3D Arnold map and a Laplace-like equation to perform permutations and substitutions, respectively. Wang and Yang [24] used the water drop motion and a dynamic lookup table with the help of the logistic map to perform the diffusion and confusion processes. Furthermore, Fouda et al. [25] used a piecewise linear chaotic map to generate pseudo random numbers and these numbers were used in generating the coefficients of the Linear Diophantine Equation (LDE). By sorting the solutions of LDE, large permutations were created and used in scrambling the image pixels. Whereas Zhang et al. [26] used compressive sensing along with Arnold’s map in order to encrypt color images into grey images, Zhang et al. [27] used a coupled logistic map, self adaptive permutation, substitution boxes and combined global diffusion to perform the encryption. Finally, AbdEl Haleem et al. [28] used a chess-based algorithm to perform the permutation process and the Lorenz system to perform the substitution process. In summary, permutations and substitutions can be performed using chaotic systems, non-chaotic algorithms or a combination of both.

3 Proposed Method

The proposed algorithm uses two different encryption systems: the two-dimensional logistic map and the Latin square. This complementarity fatherly enhances the security and allows us to benefit from the advantages of each system.

3.1 Two-dimensional Logistic Map

The two-dimensional logistic map is known for its complex behavior of the evolution of basins and attractors [29]. It is more complex than the one-dimensional chaotic behavior.

The logistic map is defined by the system of Eqs. (1) below:

$$\left\{ {\begin{array}{l} {X_{i + 1} = r\left( {3Y_{i} + 1} \right)X_{i} (1 - X_{i} )} \\ {Y_{i + 1} = r\left( {3X_{i + 1} + 1} \right)Y_{i} (1 - Y_{i} )} \end{array}} \right.$$

(1)

where ‘r’ is the parameter of the system (with r ∈ [1.1, 1.19] it is the interval where the system is chaotic) and (X _i , Y _i ) is the point at the ith iteration. This card also depends on the initial conditions (x₀, y₀) to determine its trajectory.

3.2 Latin Square

A Latin square L of N order is a table of N × N elements filled with N distinct symbols, with each symbol appears exactly once in each row and each column. The name of the Latin square was introduced by the mathematician Leonhard Euler, who used Latin characters as symbols.

Mathematically, we can define a Latin Square of N order via the function F_L (l, c, i) according to Eq. (2):

$${\text{F}}_{\text{L}} \left( {{\text{l}}, {\text{c}}, {\text{i}}} \right) = \left\{ {\begin{array}{ll} &{{\text{l }} \quad {\text{si L}}\left( {{{l}}, {\text{c}}, {\text{i}}} \right) = {\text{S}}_{\text{i}} } \\ &{0 \quad {\text{Otherwise}}} \\ \end{array} } \right.$$

(2)

With l denotes the index of a line of an element of $L,\, l \in \mathbb{N} = {0,\, 1,\,\ldots,{\rm N}-1}$, c denotes the index of a column of an element of L c ∈ $\mathbb{N}$, i denotes the index of a symbol element in L and Si is ith symbol in the whole = {S₀, S₁,…, S_N−1}. This implies that each symbol appears exactly once in each row and each column of L. Figure 1 shows examples of Latin squares of different orders with different symbol sets.

Fig. 1

Examples of Latin squares

3.3 Detailed Algorithm

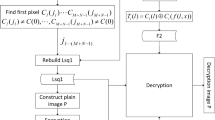
The proposed algorithm is of an SPN structure (substitution-permutation network) with eight rounds and an encryption key of 256 bits as shown in Fig. 2. It uses the two-dimensional logistic map and the Latin square. It consists of the integration of the probabilistic sound encryption LSB (least significant bit-plane) [30], and the SPN stage with five primitives of encryption: cyclic shift, Latin square substitution, Latin square permutation, permutation 2D and substitution 2D. The different steps will be defined in the following sections.

Fig. 2

Encryption images by the proposed algorithm

3.3.1 K. Key Generator

The encryption K. key is 256-bits long, and it is used in two different ways:

• Directly in the 2D permutation and 2D substitution, this is called: logistic map key.

• Transformed into Latin square when it is added to the cyclic shift, permutation and Latin square substitution. It will be named Latin square key.

3.3.1.1 Logistic Map Key

We cut the encrypting K. key into five parameters namely x₀, y₀, r, T and A₀···A₈ as shown in Fig. 3, with (x₀, y₀) and r as initial values of the two-dimensional logistic map expressed in Eq. 1. A and T are parameters of the generator of a linear congruence (see the detailed function in [31]).

Fig. 3

Logistic map Key

3.3.1.2 Latin Square Key

We transform the K. encryption key into eight Latin squares key which are 256 bits long, as follows:

• we divide the K. encryption key by using the SubKeyDiv function into eight subkeys of 32 bits: K = {K₀, K₁,…, K₇}

• We generate pairs of pseudo-random sequences: ($Q_{1}^{0} , Q_{2}^{0} ),\;(Q_{1}^{1} , Q_{2}^{1} ), \ldots ,(Q_{1}^{8} , Q_{2}^{8} )$, each pair is made of 2 × 256 elements by using PRNGs function (Pseudorandom number generator). These two steps are described in Algorithm 1.

Finally, we obtain Latin Square keys of 256 bits: L₀, L₁,…, L₈ of the 256 bits order by supplying these pseudo-random sequences in Algorithm 2: n {0, 1,…, 8}we have a Ln = GCL ($Q_{1}^{n} , Q_{2}^{n} )$.

Q1 and Q2 are two sequences produced by a pseudo-random number generator (PRNG), for example the generator of a linear congruence [32]. SortMap (Q) is a function that finds the cartographic index between a Q sequence and its filtered version Q* in the ascending order, and RowShift (Q, v) makes a cyclic shift of the Q sequence with v elements to the left [13].

3.3.2 Cyclic Shift

In the conventional SPN encryption by blocks [33, 34], the step of shifting normally mixes a clear P message with a key, for example, operation XOR.

We define the cyclic shift as an encryption by transposition [35] on the finite space GF(2⁸) for the image data, as shown in the following equation:

$${\text{y}} = [{\text{x}} + {\text{l}}]_{{2^{8} }}$$

(3)

where ‘x’ is a byte in the plain image, ‘l’ is the corresponding byte to the Latin key, and ‘y’ is the result of cyclic shift. [.]2⁸ denotes the computations over GF(2⁸). The shift Process above may easily be reversed by applying:

$${\text{x}} = [{\text{y}} + {\text{l}}]_{{2^{8} }}$$

(4)

In the image encryption, the plaintext of x byte is a pixel. It is located at the intersection of rth row and cth column hence x = P (r, c). Now, l = L (r, c) is a component located in the corresponding position of the Latin key square L and ‘y’ byte of cryptogram with y = C (r, c), then the equation is obtained at the pixel level (5):

$$\left\{ {\begin{array}{l} {{\text{C}}({\text{r}},{\text{c}}) = [ {\text{SR}}({\text{P}}({\text{r}},{\text{c}}),{\text{D}}) \oplus {\text{L}}({\text{r}},{\text{c}})]_{{2^{8} }} } \\ {{\text{P}}({\text{r}},{\text{c}}) = {\text{SR}}([{\text{C}}({\text{r}},{\text{c}}) \oplus {\text{L}}({\text{r}},{\text{c}})]_{{2^{8} }} , {\text{D}})} \\ \end{array} } \right.$$

(5)

D is the rotation parameter (D = L (0,0) mod 3), and SR denotes the function of spatial rotation (X, d) which retains an x image according to different values of the direction D as it is defined in the Eq. (6).

$$\left\{ {\begin{array}{ll} {\rm X};&{\rm if} \; {\rm d} = 0 \\ \text{Flip X up} \to {\rm down};& {\rm if}\; {\rm d} = 1 \\ \text{Flip X left} \to {\rm right};& {\rm si}\; {\rm d} = 2 \\ \end{array} } \right.$$

(6)

Equation 5 is applied to all pixels to obtain the cyclic shift denoted by:

$${\rm DC} = \left\{ {\begin{array}{l} {{\rm C} = {\text{Ecr}}_{\text{DC}} {\rm (L,P,D)}} \\ {{\rm P} = {\text{Dcr}}_{\text{DC}} {\rm (L,C,D)}} \\ \end{array} } \right.$$

(7)

3.3.3 Latin Square Substitution

An S-Box in Cryptography is a basic element to perform the substitution. The existence of the bijection FRM/MRI (Forward row mapping, inverse row mapping) and FCM/ICM (Forward column mapping, Inverse column mapping) [13] in a Latin square, we are able to perform the byte substitution in an encrypting image using bijections of rows and columns in a Latin square. The substitution according to a row in a Latin square is denoted by SLCL:

$${\rm SLCL} = \left\{ {\begin{array}{l} {{\rm C} = {\text{Ecr}}_{\text{s}}^{\text{ligne}} {\rm (L,P)}} \\ {{\rm P} = {\text{Dcr}}_{\text{s}}^{\text{ligne}} {\rm (L,C)}} \\ \end{array} } \right.$$

(8)

The functionsEcr ^ligne _s and Dcr ^ligne _s are obtained from Eqs. (9) and (10) below:

$${\text{Ecr}}_{\text{s}}^{\text{ligne}} = {\text{C}}\left({{\text{r}},{\text{c}}} \right) = \left\{\begin{array}{ll} {\rm FRM}\left( {{\text{L}},{\text{C}}\left( {{\text{r}} - 1,{\text{c}}}\right),{\text{P}}\left( {{\text{r}},{\text{c}}} \right)}\right);&\quad {\rm if} \;{\rm r} \ne 0 \\ {{\rm FRM}}\left({{\text{L}},0,{\text{P}}\left( {{\text{r}},{\text{c}}} \right)}\right);&\quad {\rm if}\; {\rm r} = 0 \\ \end{array} \right.$$

(9)

$${\text{Dcr}}_{\text{s}}^{\text{ligne}} = {\text{P}}\left({{\text{r}},{\text{c}}} \right) = \left\{ \begin{array}{ll} {\rm IRM}\left( {{\text{L}},{\text{C}}\left( {{\text{r}} - 1,{\text{c}}}\right),{\text{C}}\left( {{\text{r}},{\text{c}}} \right)}\right);&\quad{\rm if}\; {\rm r} \ne 0 \\ {\rm IRM}\left({{\text{L}},0,{\text{C}}\left( {{\text{r}},{\text{c}}} \right)}\right);&\quad{\rm if}\; {\rm r} = 0 \\ \end{array} \right.$$

(10)

Similarly, we use bijections of columns in a Latin square to make substitutions of bytes SCCL.

$${\rm SCCL} = \left\{ {\begin{array}{*{20}l} {{\rm C} = {\text{Ecr}}_{\text{s}}^{\text{colonne}} {\rm (L,P)}} \\ {{\rm P} = {\text{Dcr}}_{\text{s}}^{\text{colonne}} {\rm (L,C)}} \\ \end{array} } \right.$$

(11)

$${\text{Ecr}}_{\text{s}}^{\text{colonne}} = {\text{C}}\left({{\text{r}},{\text{c}}} \right) = \left\{ \begin{array}{ll} \rm{FCM}\left( {{\text{L}},{\text{P}}\left( {{\text{r}},{\text{c}}}\right),{\text{C}}\left( {{\text{r}},{\text{c}} - 1} \right)}\right);&\quad{\rm if} \; r \ne 0 \\ \rm {FCM}\left({{\text{L}},{\text{P}}\left( {{\text{r}},{\text{c}}} \right),0}\right);&\quad{\rm if} \; r = 0 \\ \end{array}\right.$$

(12)

$${\text{Dcr}}_{\text{s}}^{\text{colonne}} = {\text{P}}\left({{\text{r}},{\text{c}}} \right) = \left\{ \begin{array}{ll} {\rm ICM}\left( {{\text{L}},{\text{C}}\left( {{\text{r}},{\text{c}}}\right),{\text{C}}\left( {{\text{r}},{\text{c}} - 1} \right)}\right);&\quad{\rm if} \;{\rm r} \ne 0 \\ {\rm ICM}\left({{\text{L}},{\text{C}}\left( {{\text{r}},{\text{c}}} \right),0}\right);&\quad{\rm if} \;{\rm r} = 0 \\ \end{array} \right.$$

(13)

3.3.4 Latin Square Permutation

Unlike the byte substitution S-Box, the P-Box (permutation) performs a patch or a byte interference. Each P-Box can also be defined as a bijection [35]. If we consider both the input and output x and y in FRM and IRM as indices, an FRM then defines a mapping {0, 1, 2,…, 255} to {0, 1, 2,…, 255} and also an IRM defines the corresponding inverse mapping. We are therefore able to define the Latin square P-box row (PLCL) as follows:

$${\rm PLCL} = \left\{ {\begin{array}{l} {{\rm C}\left( {{\text{r}},c_{y} } \right) = {\rm P}({\rm r},{\rm FRM}({\rm L},{\rm r},c_{x} )} \\ {{\rm P}\left( {{\text{r}},c_{x} } \right) = {\rm C}({\rm r},{\rm IRM}({\rm L},{\rm r},{\text{c}}_{y} )} \\ \end{array} } \right.$$

(14)

In which c_x and c_y denotes column indices before and after the mapping. Similarly, we can also build the P-column Latin square box (PCCL) by the following equations:

$${\rm PCCL} = \left\{ {\begin{array}{l} {{\rm C}\left( {{\text{r}}_{\text{y}} ,{\text{c}}} \right) = {\rm P}({\rm r},{\rm FCM}\left( {{\text{L}},{\text{r}}_{\text{x}} ,{\text{c}}} \right),{\rm c})} \\ {{\rm P}\left( {{\text{r}}_{\text{x}} ,{\text{c}}} \right) = {\rm C}({\rm ICM}\left( {{\text{L}},{\text{r}}_{\text{y}} ,{\text{c}}} \right),{\rm c})} \\ \end{array} } \right.$$

(15)

In which r_x and r_y denote the row indices before and after the mapping.

To have the best performances, we build our Latin square permutation by cascading the row permutations PLCLs and the column permutations PCCL as follows:

$$\left\{ {\begin{array}{*{20}l} {{\rm C}{\rm (r,c)} = {\text{C}}^{ *} ({\rm FCM}{\rm (L,r,c)} ,{\rm c})} \\ {{\text{C}}^{ *} {\rm (r,c)} = {\rm P}({\rm r},{\rm FRM}{\rm (L,r,c)})} \\ \end{array} } \right.$$

(16)

In general, we write the function of the Latin square permutation as follows:

$$PCL = \left\{ {\begin{array}{*{20}l} {{\rm C} = {\text{Ecr}}_{\text{p}} {\rm (L,P)}} \\ {{\rm P} = {\text{Dcr}}_{\text{p}} {\rm (L,P)}} \\ \end{array} } \right.$$

(17)

3.3.5 2D Logistic Permutation

If we suppose that the size of the clear image P is M × N, then, the total number of pixels by P is M × N. If we Consider the initial value used in a round is (x₀, y₀), then a sequence of x and y of M × N length (excluding the initial value) can be generated by the 2D logistic map using Eq. (1). We notice that Xseq and Yseq, the sequences of x and y coordinates of the 2D logistic map sequences as the following Eq. (18) shows:

$$\left\{ {\begin{array}{*{20}l} {{\text{X}}_{\text{seq}} = \left\{ {{\text{x}}_{1} ,{\text{x}}_{2} , \ldots ,{\text{x}}_{\text{MN}} } \right\}} \\ {{\text{Y}}_{\text{seq}} = \left\{ {{\text{y}}_{1} ,{\text{y}}_{2} , \ldots ,{\text{y}}_{\text{MN}} } \right\}} \\ \end{array} } \right.$$

(18)

We rearrange the items of Xseq and Yseq whose number is M × N as matrices X and Y, then each row ‘r’ of X is sorted to build matrix X^sorted. There is a bijection between the matrix X and its sorted Version X^sorted which is named $e_{{\pi_{x} }}$ [35] as shown in Eq. (19). Similarly, there is also a bijection $e_{{\pi_{y} }}$ between the matrix Y and its sorted version according to the columns Y noted as Y^sorted.

$$\left\{ {\begin{array}{l} {{\text{X}}_{{{\text{r}},{\text{i}}}}^{\text{sorted}} = {\text{X}}_{{{\text{r}},{\text{e}}_{{{{\pi }}_{\text{x}} }} ({\text{i}})}} } \\ {{\text{Y}}_{{{\text{i}},{\text{c}}}}^{\text{sorted}} = {\text{Y}}_{{{\text{e}}_{{{{\pi }}_{\text{y}} }} \left( {\text{i}} \right),{\text{c}}}} } \\ \end{array} } \right.$$

(19)

Therefore, the matrix row of permutation U^x and the matrix column of permutation U^y can be obtained by the Eq. (20).

$$\left\{ {\begin{array}{*{20}l} {{\text{U}}^{\text{x}} = [ {\text{e}}_{{{\pi }_{\text{x}} }}^{{{\text{r}} = 1}} ; {\text{e}}_{{{\pi }_{\text{x}} }}^{{{\text{r}} = 2}} ; \ldots ; {\text{e}}_{{{\pi }_{\text{x}} }}^{{{\text{r}} = {\text{M}}}} ]^{\text{T}} } \\ {{\text{U}}^{\text{y}} = [ {\text{e}}_{{{\pi }_{\text{y}} }}^{{{\text{c}} = 1}} ; {\text{e}}_{{{\pi }_{\text{y}} }}^{{{\text{c}} = 2}} ; \ldots ; {\text{e}}_{{{\pi }_{\text{y}} }}^{{{\text{c}} = {\text{N}}}} ]} \\ \end{array} } \right.$$

(20)

Finally, the 2D logistic permutation is obtained by Algorithm 3 using row and column permutations of the Eq. (20).

We write the 2D permutation logistic function as follows:

$${\text{P}}_{{2{\text{D}}}} = \left\{ {\begin{array}{ll} & {C = {\text{Ecr}}_{{{\text{P}}_{{2{\text{D}}}} }} {\rm (P)}} \\ & {{\rm P} = {\text{Dcr}}_{{{\text{P}}_{{2{\text{D}}}} }} {\rm (L,P)}} \\ \end{array} } \right.$$

(21)

3.3.6 2D Logistic Substitution

In this phase, we change the pixels values while maintaining the reference matrix ‘I’ which depends on the sequences of the 2D logistic map and which will be calculated as follows:

X and Y are versions of Xseq and Yseq matrices, Z = X + Y, Each B block of 4 × 4 elements of Z will be converted with the following matrix:

$${\text{I}} = {\text{f}}\left( {\text{B}} \right) = \left( {\begin{array}{*{20}l} {\begin{array}{*{20}l} {{\text{g}}_{\text{N}} \left( {{\text{B}}_{1,1} } \right)} & {{\text{g}}_{\text{R}} \left( {{\text{B}}_{1,2} } \right) {\text{g}}_{\text{S}} \left( {{\text{B}}_{1,3} } \right){\text{g}}_{\text{D}} \left( {{\text{B}}_{1,4} } \right)} \\ {{\text{g}}_{\text{R}} \left( {{\text{B}}_{2,1} } \right)} & {{\text{g}}_{\text{S}} \left( {{\text{B}}_{2,2} } \right) {\text{g}}_{\text{D}} \left( {{\text{B}}_{2,3} } \right){\text{g}}_{\text{N}} \left( {{\text{B}}_{2,4} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}l} {{\text{g}}_{\text{S}} \left( {{\text{B}}_{3,1} } \right)} & {{\text{g}}_{\text{D}} \left( {{\text{B}}_{3,2} } \right) {\text{g}}_{\text{N}} \left( {{\text{B}}_{3,3} } \right){\text{g}}_{\text{R}} \left( {{\text{B}}_{3,4} } \right)} \\ {{\text{g}}_{\text{D}} \left( {{\text{B}}_{4,1} } \right)} & {{\text{g}}_{\text{N}} \left( {{\text{B}}_{4,2} } \right) {\text{g}}_{\text{R}} \left( {{\text{B}}_{4,3} } \right){\text{g}}_{\text{S}} \left( {{\text{B}}_{4,4} } \right)} \\ \end{array} } \\ \end{array} } \right)$$

(22)

With g_N(d) = T (d) mod F, g_R(d) = T($\sqrt {\text{d}}$) mod F, g_S(d) = T (d²) mod F andg_D(d) = T (2d) mod F,The function T (d)truncates a decimal d from the 9th digit to 16th digit to form an integer. For example, if b = 0.1234567890123456789 then T (b) = 90,123,456. Finally the encrypted image is defined by the equation:

$${\rm C} = \left( {{\rm P} + {\rm I}} \right) \, \bmod \, {\rm F}$$

(23)

where F is the number of allowed intensity scales of the plaintext image. For example, F = 256 for an 8-bit gray scale image.

We write the 2D logistic substitution function as follows:

$${\text{S}}_{{2{\text{D}}}} = \left\{ {\begin{array}{ll} &{{\rm C} = {\text{Ecr}}_{{{\text{S}}_{{2{\text{D}}}} }} {\rm (P)}} \\ &{{\rm P} = {\text{Dcr}}_{{{\text{S}}_{{2{\text{D}}}} }} {\rm (L,P)}} \\ \end{array} } \right.$$

(24)

4 Simulation Results and Security Analysis

Our simulation is performed in a Windows 7 environment, Core2, processor 2.6 and 2 GB of RAM. The images used can be downloaded from the database of the USC-SIPI (http://sipi.usc.edu/database 21/09/2013).

4.1 Key Space Analysis

The size of the key space characterizes the capability of resisting brute-force attack. A short key means that the best encryption algorithm can be broken by exhaustive search (also known as brute-force attack) in a reasonable amount of time, while the reverse is not true. In the proposed algorithm, the initial secret keys set K = 256 bit. Therefore, the key space is 2²⁵⁶ = 1.17 × 10⁷⁷, so the key space is large enough to resist all kinds of brute-force attacks.

4.2 Statistical Analysis

4.2.1 Histogram Analysis

An image histogram illustrates that how pixels in an image are distributed by plotting the number of pixels at each gray scale level. The distribution of cipher-text is of much importance. More specifically, it should hide the redundancy of plain-text and should not leak any information about the plain-text or the relationship between plain-text and cipher-text. Table 1 shows the histograms of plain-images and its ciphered images generated by the proposed scheme respectively. It’s clear from that the histograms of the cipher-images are fairly uniform and significantly different from that of the plain image and hence do not provide any clue to employ statistical attack.

Table 1 Resultant Encrypted Images and its histogram of proposed method

4.2.2 Information Entropy Analysis

In information theory, entropy is the most significant feature of disorder, or more precisely unpredictability. To calculate the entropy H(X) of a source x, we have:

$$H\left( X \right) = \mathop \sum \limits_{i = 1}^{n} P_{r} (x_{i} )\log_{2} \frac{1}{{P_{r} (x_{i} )}}$$

(25)

where X denotes the test image, x _i denotes the ith possible value in X, and $P_{r} \left( {x_{i} } \right)$ is the probability of X = x _i , that is, the probability of pulling a random pixel in $X$ and its value is x _i . For a truly random source emitting 2 N symbols, the entropy is H(X) = N. therefore, for a ciphered image with 256 gray levels, the entropy should ideally be H(X) = 8. If the output of a cipher emits symbols with entropy less than 8, there exists certain degree of predictability, which threatens its security. The entropies for plain image and ciphered images using various images are calculated in Table 2. Apparently, the proposed algorithm is much closer to the ideal situation. This means that information leakage in the encryption process is negligible and the cryptosystem is secure against entropy attack.

Table 2 Entropy

Table 3 shows the comparison of proposed algorithm with existing algorithm. As compared to entropy of encrypted images in Ref. [13, 36–39] resultant entropy of our proposed method is more nearer to entropy of random image.

Table 3 Encrypted image entropy of proposed algorithm with existing algorithms

4.2.3 Analysis of Correlation of Adjacent Pixels

There exists a high correlation between pixels of an image which is called intrinsic feature. Thus, a secure encryption scheme should remove it to improve resistance against statistical analysis. To test the correlation between two-adjacent pixels in plain-image and cipher image, we randomly select 1000 pairs of two-adjacent pixels (in vertical, horizontal, and diagonal direction) from plain-image and cipher-image, and calculate the coefficient of each pair by Eq. (26):

$$r_{xy} = \frac{cov(x,y)}{{\sqrt {D(x)} \sqrt {D(y)} }}$$

(26)

where

$$cov\left( {x,y} \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {x_{i} - E\left( x \right)} \right)\left( {y_{i} - E\left( y \right)} \right)$$

(27)

$$D\left( x \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {x_{i} - E\left( x \right)} \right)^{2}$$

(28)

$$E\left( x \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} x_{i}$$

(29)

where x and y are gray-scale values of two-adjacent pixels in the image.

Table 4 shows the correlation coefficients of two horizontally adjacent pixels, two vertically adjacent pixels and two diagonally adjacent pixels in the plain and the cipher-image. It is clear that the strong correlation between adjacent pixels in plain image is greatly reduced in the cipher image produced by the proposed scheme, which is a private high-level security.

Table 4 Correlation coefficients of two adjacent pixels in plain-image and ciphered-images of proposed method

Additionally, the correlation distribution of “Lena” and its ciphered image in each direction are plotted as shown in Fig. 4. Figure 4a–c shows the correlation distributions of the plain image, while Fig. 4d–f shows the correlation distributions of the ciphered image. The strong correlation between adjacent pixels of the plain image is evident as all the dots are congregated along the diagonal in Fig. 4a–c. However, in Fig. 4d–f, the dots are scattered over the entire plane, which indicates that the correlation is greatly reduced in the ciphered image. Table 5 shows the comparison with the schemes in Refs. [13, 36, 37, 39], the proposed scheme has smaller values in horizontal and diagonal directions.

Fig. 4

Correlations of two adjacent pixels for Lena image of size 512 × 512 a horizontal direction of the plain image, b horizontal direction of the cipher image, c vertical direction of the plain image, d vertical direction of the cipher image, e diagonal direction of the plain image, and f diagonal direction of the cipher image

Table 5 Comparison of the correlation coefficients of Lena

4.3 Sensitivity Analysis

A well-designed encryption algorithm should be highly sensitive to plain-image and keys, so a slight change in plain-image or keys will make the cipher-image quite different. If an encryption scheme contains no confusion or diffusion stage, it would easily be destroyed by differential attacks. In order to confirm whether the proposed encryption algorithm is sensitive to plain image and keys, this paper brings out two tests: Number of pixels change rate (NPCR) and Unified average changing intensity (UACI) [40]. The equation to calculate NPCR is Eq. (30):

$$NPCR = \frac{{\mathop \sum \nolimits_{i,j} D(i,j)}}{M \times N} \times 100\,\%$$

(30)

where, M stands for images width, N stands for images height, C ₁(i, j) means the gray-scale value of cipher-image in position (i, j), and C ₂(i, j) means the gray-scale value of the new cipher-image which is the encryption result of modified plain image that has just one different pixel to the original plain-image and where D(i, j) defined as follows:

$$D\left( {i,j} \right) = \left\{ \begin{array}{ll} 1 &\quad if \; C_{1} (i,j) \ne C_{2} (i,j) \\ 0 &\quad if \; C_{1} \left( {i,j} \right) = C_{2} (i,j) \\ \end{array} \right.$$

(31)

UACI can be calculated by the equation Eq. (32):

$$UACI = \frac{1}{M \times N}\mathop \sum \limits_{i,j} \frac{{\left| {C_{1} \left( {i,j} \right) - C_{2} (i,j)} \right|}}{255} \times 100\,\%$$

(32)

When one bit of a pixels gray-scale value in the plain image is changed, then a new plain image is generated from the original one. Encrypt the two images with the same secret keys, and then take cipher images into Eqs. (30) and (32) and results are shown in Table 6. From this results we can find that our algorithm is very sensitive to tiny changes in the plain image, even if there is only one bit difference between two plain images, the decrypted images will be completely different. Table 7 gives the comparison of performance of UACI and NPCR when encrypting the image of Lena with Ref. [13, 37–39].

Table 6 NPCR and UACI of proposed method

Table 7 Comparison results of the NPCR and UACI scores of the Lena image

4.3.1 Key Sensitivity Analysis

An ideal image encryption procedure should be sensitive to the secret key in both encryption and decryption processes. It means that a change in a single bit of the secret key should produce a completely different encrypted image. Simulation results with respect to encryption and decryption stages are shown in Figs. 5 and 6. The encryption keys in our simulations are listed below in the HEX format:

Fig. 5

Key sensitivity analysis at the encryption stage. a plaintext Lena, b Encrypted image by K1, c Encrypted image by K2, d Encrypted image by K3, e Ciphertext difference (C1–C2) and f ciphertext difference (C1–C3)

Fig. 6

Key sensitivity analysis at the decryption stage. a Decrypted image by K1, b Decrypted image by K2, c Decrypted image by K3

• K1 = D9218FA02ED9AD9E1ED4FA1288EB2DD3FFDCFDDB01D8F21FA2E4A79F2FE2E0F5

• K2 = D9218FA12ED9AD9E1ED4FA1288EB2DD3FFDCFDDB01D8F21FA2E4A79F2FE2E0F5

• K3 = D9218FA02ED9AD9E1ED4FA1288EB2DD3FFDCFDDB01D8F21FA2E4A79FAFE2E0F5

As can be seen, K1 differs K2 only for one bit, K2 differs K3 only for one bit, and K1 differs K3 only for two bits. Although the hamming distances between K1, K2 and K3 are very small, i.e. they are very similar to each other, their corresponding cipher text images C1, C2 and C3 have significant differences. These can be verified by the fact that their differences, i.e. |C1–C2|, |C1–C3|, are random-like images as shown in Fig. 5. The example shows the proposed algorithm is sensitive to the encryption keys in the encryption stage.

Similar results can also be obtained in the decryption stage as shown in Fig. 6. We decrypt the same cipher text image C1 using the encryption keys K1, K2 and K3, respectively. As can be seen, using the correct encryption key K1, decrypted image D1 perfectly reconstructs the original plaintext image. However, decrypted images D2 and D3 using key K2 and K3 are random-like ones which do not contain any information related to the original plaintext image.

4.3.2 Noise Robustness Analysis

A good cipher should also be able to tolerate a certain amount of noise, e.g. noise in a channel or decoding errors. The proposed Latin square image cipher adopts an asymmetric structure for encryption and decryption, and one noisy pixel in cipher image will only propagate in a factor of two in each round. As shown in Fig. 7 we find that in both cases, the decrypted image is still visible.

Fig. 7

shows the integration of noise in the encrypted image with a different degree. a Encrypted image with noise n1 and its decrypted image, b Encrypted image with noise n2 and its decrypted image

5 Conclusion

An appropriate image encryption system must be able to withstand all types of known attacks and cryptanalysis, and its performance must be independent whether from the encryption key or from the encrypted image itself. In addition, this system must have good properties of confusion and diffusion. Our system meets all of these criteria with the various stages that constitute it and has distinctive characteristics. The proposed algorithm is purely defined in integers, and thus it can be easily implemented in software and hardware without causing finite precision or discretization problems, the proposed algorithm constructs all encryption primitives based on one key generator, including cyclic shift, substitution and permutation, and thus the proposed method attains high sensitivities to any key change. The proposed algorithm arranges all encryption primitives in the framework of substitution–permutation network, and thus it attains good confusion and diffusion properties. The proposed method also integrates probabilistic encryption allowing to encrypt one plaintext image into different ciphertext images with one encryption key and the decryption stage is robust against a certain level of errors.

Security analysis including statistical attack analysis and differential attack analysis are performed numerically and visually. All the experimental results show that the proposed encryption scheme is secure thanks to its large key space, its high sensitivity to the cipher keys and plain-images. The results show that the proposed scheme leads to a higher security level in terms of NPCR, UACI and entropy of the cipher-images.