1 Introduction

Synchronization control ensures two or more systems to share a common dynamical behavior by coupling or external forcing. Since Pecora and Carroll [1] originally proposed the drive-response concept for achieving the synchronization of coupled chaotic systems in, a lot of alternative schemes to ensure the control and synchronization of such systems have been proposed in [1–7], and whose potential applications have been demonstrated in various fields such as chaos generator design, information science, secure communication, biological systems, etc.

Actually, there exist natural time delays in the operation of systems which are due to the finite information processing speed and the finite switching speed of amplifiers, and can cause undesirable dynamic behaviors such as oscillation and instability. Recently, it has been revealed that some types of delayed neural networks (DNNs) can exhibit some complicated dynamics and even chaotic behaviors if the parameters and time delays are appropriately chosen. Therefore, dynamic behaviors, especially the synchronization problems of (chaotic) DNNs, have been extensively considered [8–24]. So far, most studied models of synchronization problem are (chaotic) neural networks (NNs) with constant delays [8, 22, 25], time-varying and bounded delays [9, 11, 14, 15, 17–20], distributed delays [10, 12, 13, 16, 20], etc. Most the synchronization problems of (chaotic) DNNs are mainly based on such approaches as Lyapunov functional [11, 12, 14, 15, 22, 23, 25], Lyapunov-Krasovskii functional and Linear matrix inequality [13–15, 20], etc. In addition, delay-dependent stability criteria and synchronization control laws are related to the size of delay so that they can be used to design some better networks according to the allowed time delays of networks. Thus, it has both theoretical significance and practical value to establish the suitable delay-dependent synchronization control laws for the system with delays. Delay-dependent controllers and sufficient criteria have been derived for the error system to be stable, which ensure the response system to be synchronized with the drive system in [13, 15, 20, 22, 23].

As everyone knows that the proportional delay is one of many delay types and objectively existent. For example, in Web quality of service (QoS) routing decision, the proportional delay is usually required [26–31]. In recent years, a lot of the routing algorithms based on neural networks are obtained in [32, 33], and these routing algorithms have high parallelism, which have been proved to be able to get the exact solutions to the problem. If the QoS routing algorithms based on neural networks with proportional delays are proposed, they will be the most suitable algorithms corresponding with the actual situation. Then, the primary task to solve this problem is to study on dynamic behaviors of neural networks with proportional delays, such as stability and dissipativity. The proportional delay [34–38] is time-varying and unbounded, which is different from other types of delay, such as constant delay, bounded time-varying delay and distributed delay, etc. Since a neural network usually has a spatial nature due to the presence of an amount of parallel pathways of a variety of axon sizes and lengths, it is desired to model by introducing continuously proportional delay over a certain duration of time. That is to say, it is reasonable that the proportional delays are introduced in the neural networks according to the topology structure and parameters of neural networks. The proportional delay function \(\tau (t)=(1-q)t\) (\(0<q<1\)) is a monotonically increasing function about the time \(t\), then it will be convenient to control the network’s running time according to the time delays of network. It is important to design a synchronized drive-response system with proportional delays. Nowadays, a few results of dynamic behaviors of NNs with proportional delays have been reported in [34, 35, 39, 40]. Zhou [34, 39, 40] have discussed the global exponential stability and asymptotic stability of cellular neural networks (CNNs) with proportional delays, by employing matrix theory and constructing Lyapunov functional. Dissipativity of a class of CNNs with proportional delays has been investigated by using the inner product properties in [35]. To the best of the author’s knowledge, the synchronization problems of (chaotic) neural networks with proportional delays have not been investigated so far, which are still challenging and open.

Motivated by the discussion above, one will discuss the exponential synchronization problem of (chaotic) neural networks with multiple proportional delays in this paper. In Sect. 2, models and preliminaries are presented. A couple of neural networks with multiple proportional delays are introduced, then by using the nonlinear transformation \(v_{i}(t)=x_{i}(\hbox {e}^{t}), w_{i}(t)=z_{i}(\hbox {e}^{t})\), the systems are equivalently transformed into a couple of neural networks with multiple constant delays and time-varying coefficients. In Sect. 3, by using Lyapunov functional method and some inequality analysis technique, several delay-dependent decentralized feedback control inputs are derived to achieve the exponential synchronization. In Sect. 4, two numerical examples and their simulations are given to illustrate the effectiveness of the proposed method. Conclusions are presented in Sect. 5.

Notations \(\mathbb {R}^{n}\) denotes the \(n\)-dimensional Euclidean space. \(x^{T}\) denotes the transpose of a square matrix or a vector \(x\). For \(x\in \mathbb {R}^{n}\), let \(\Vert x\Vert =\sum \limits _{i=1}^{n}|x_{i}|\). \(\hbox {sgn}(y)\) is the sign function of \(y\), if \(y>0,\,\hbox {sgn}(y)=1\); if \(y=0,\,\hbox {sgn}(y)=0\); if \(y<0,\,\hbox {sgn}(y)=-1\).

2 System Description and Preliminaries

A class of recurrent neural networks with proportional delays in a general form can be described by the following equations:

$$\begin{aligned} \dot{x}_{i}(t)=-d_{i}(x_{i}(t))+\sum \limits _{j=1}^{n}a_{ij}f_{j}(x_{j}(t))+\sum \limits _{j=1}^{n}b_{ij}f_{j}(x_{j}(q_{ij}t))+I_{i}, \end{aligned}$$
(2.1)

for \(i=1,2,\ldots ,n,\,t\ge 1\). Where \(n\ge 2\) denotes the number of neurons in the network, \(x_{i}(t)\) is the state variable associated with the \(i\)th neuron; \(d_{i}(x_{i}(t))\) is an appropriately behaved function remaining the solution of drive neural networks (2.1) to be bounded. \(a_{ij}\) and \(b_{ij}\) are constants which denote the strengths of connectivity between the neurons \(j\) and \(i\) at time \(t\) and \(q_{ij}t\), respectively; \(q_{ij}, i,j=1,2,\ldots ,n\) are proportional delay factors and satisfy \(0<q_{ij}\le 1,\,q=\min \limits _{1\le i,j\le n}\{q_{ij}\}\) and \(q_{ij}t=t-(1-q_{ij})t\), in which \((1-q_{ij})t\) corresponds to the time delay required in processing and transmitting a signal from the \(j\)th neuron to the \(i\)th neuron, and \( (1-q_{ij})t\rightarrow +\infty ,\) as \(q\ne 1,t\rightarrow +\infty \); \(f_{i}(\cdot )\) denotes a non-linear activation function. \(I_{i}\) is an external constant input. Furthermore, the neural networks described in (2.1) possess initial conditions of \(x_{i}(t)=x_{i0}, t\in [q,1],\,x_{i0}, i=1,2,\ldots ,n\) are constants. Before proceeding, one makes the following assumptions for the functions \(d_{i}(x_{i}(t))\) and the activation functions \(f_{i}(x_{i}(t)), i=1,2,\ldots ,n\).

Assumption 1

Functions \(d_{i}(x_{i}(t))\) and \(d_{i}(x_{i}(t))^{-1}, i=1,2,\ldots ,n\), are global Lipschitz continuous. Moreover, \(d_{i}^{'}(x_{i})=\frac{\hbox {d}d(x_{i})}{\hbox {d}x_{i}}\ge \gamma _{i}>0\) for \(x_{i}\in \mathbb {R}\).

Assumption 2

Each function \(f_{i}\) satisfies that \(f_{i}:\mathbb {R}\rightarrow \mathbb {R},\,|f_{i}(u)-f_{i}(v)|\le L_{i}|u-v|\), for \(u,v\in \mathbb {R}\). Where \(L_{i}, i=1,2,\ldots ,n\) are positive constants.

Regarding model (2.1) as the drive system, the response system is given by

$$\begin{aligned} \dot{z}_{i}(t)=-d_{i}(z_{i}(t))+\sum \limits _{j=1}^{n}a_{ij}f_{j}(z_{j}(t))+\sum \limits _{j=1}^{n}b_{ij}f_{j}(z_{j}(q_{ij}t))+I_{i}+u_{i}(t), \end{aligned}$$
(2.2)

where \(u_{i}(t)\) is the unidirectionally coupled term, which is regarded as the control input and appropriately designed such that the specific control objective is achieved. The initial conditions of (2.2) are given by \(z_{i}(t)=z_{i0}, t\in [q,1],\,z_{i0}, i=1,2,\ldots ,n\) are constants.

Let \(v_{i}(t)=x_{i}(\hbox {e}^{t}), w_{i}(t)=z_{i}(\hbox {e}^{t})\) [34], then a couple of neural networks (2.1) and (2.2) are equivalently transformed into the following couple of neural networks with multiple constant delays and time-varying coefficients

$$\begin{aligned} \dot{v}_{i}(t)=\hbox {e}^{t}\Big \{-d_{i}(v_{i}(t))+\sum \limits _{j=1}^{n}a_{ij}f_{j}(v_{j}(t))+\sum \limits _{j=1}^{n}b_{ij}f_{j}(v_{j}(t-\tau _{ij}))+I_{i}\Big \}, \end{aligned}$$
(2.3)

and

$$\begin{aligned} \dot{w}_{i}(t)\!=\!\hbox {e}^{t}\Big \{-d_{i}(w_{i}(t))\!+\!\sum \limits _{j=1}^{n}a_{ij}f_{j}(w_{j}(t))\!+\!\sum \limits _{j=1}^{n}b_{ij}f_{j}(w_{j}(t\!-\!\tau _{ij}))\!+\!I_{i}+U_{i}(t)\Big \}\qquad \end{aligned}$$
(2.4)

for \(t\ge 0,\,i=1,2,\ldots ,n\). In which \(\tau _{ij}=-\log q_{ij}\ge 0,\,U_{i}(t)=u_{i}(\hbox {e}^{t})\).

The neural networks described in (2.3) and (2.4) possess initial conditions of \(v_{i}(t)=\varphi _{i}(t)\in C([-\tau ,0],\mathbb {R})\) and \(w_{i}(t)=\psi _{i}(t)\in C([-\tau ,0],\mathbb {R})\), in which \(\varphi _{i}(t)=x_{i0}, \psi _{i}(t)=z_{i0}, t\in [-\tau ,0],\,\tau =\max \limits _{1\le i,j\le n}\{\tau _{ij}\}\).

Definition 2.1

[16] Systems (2.3) and (2.4) are said to be exponentially synchronized if there exist constants \(M\ge 1\) and \(\lambda >0\) such that

$$\begin{aligned} \sum \limits _{i=1}^{n}|v_{i}(t)-w_{i}(t)|\le M\sum \limits _{i=1}^{n}\sup \limits _{-\tau \le s\le 0}|v_{i}(s)-w_{i}(s)|\mathrm{e}^{-\lambda t} \end{aligned}$$

for \(t\ge 0\). Moreover, the constant \(\lambda \) is defined as the exponential synchronization rate.

Thus, the goal in this paper is to design an appropriate controller \(u(t)=[u_{1}(t),u_{2}(t),\ldots , u_{n}(t)]^{T}\) such that the coupled neural networks (2.1) and (2.2) remain synchronized. By the equivalence, one only requires to design an appropriate controller \(U(t)=[U_{1}(t),U_{2}(t),\ldots ,U_{n}(t)]^{T}\) such that the coupled neural networks (2.3) and (2.4) remain synchronized. From (2.3) and (2.4), the following dynamic equations of synchronization error can be obtained

$$\begin{aligned} \dot{\tilde{y}}_{i}(t)=\hbox {e}^{t}\Big \{-c_{i}(\tilde{y}_{i}(t))+\sum \limits _{j=1}^{n}a_{ij}g_{j}(\tilde{y}_{j}(t))+\sum \limits _{j=1}^{n}b_{ij}g_{j}(\tilde{y}_{j}(t-\tau _{ij}))-U_{i}(t)\Big \}, \end{aligned}$$
(2.5)

for \(t\ge 0, i=1,2,\ldots ,n\). Where \(\tilde{y}_{i}(t)=v_{i}(t)-w_{i}(t),\,c_{i}(\tilde{y}_{i}(t))=d_{i}(v_{i}(t))-d_{i}(w_{i}(t)),\,g_{j}(\tilde{y}_{j}(t))=f_{j}(v_{j}(t))-f_{j}(w_{j}(t)),\,g_{j}(\tilde{y}_{j}(t-\tau _{ij}))=f_{j}(v_{j}(t-\tau _{ij}))-f_{j}(w_{j}(t-\tau _{ij})), ~i,j=1,2,\ldots ,n\).

Therefore, the problem of exponential synchronization of delayed neural networks given in (2.3) and (2.4) is transferred into an exponential stabilization problem of error dynamics (2.5).

3 Main Results

Theorem 3.1

Assume that Assumptions 1 and 2 hold. For the drive-response structure of neural networks given in (2.3) and (2.4), if the control input \(U_{i}(t)\) in (2.4) is suitably designed as

$$\begin{aligned} U_{i}(t)=\Big \{(\sigma -1)\hbox {e}^{-t}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\sigma \tau _{ji}})\Big \}\tilde{y}_{i}(t), \quad i=1,2,\ldots ,n, \end{aligned}$$
(3.1)

for \(t\ge 0\), where \(\sigma >1\) is a positive constant, then the exponential synchronization of systems (2.3) and (2.4) is obtained with a synchronization rate \(\alpha =\sigma -1>0\).

Proof

According to the definition of \(g_{j}(\tilde{y}_{j}(t))\) in (2.5) and Assumption 2 yields

$$\begin{aligned} |g_{j}(\tilde{y}_{j}(t))|\le L_{j}|\tilde{y}_{j}(t)|, |g_{j}(\tilde{y}_{j}(t-\tau _{ij}))|\le L_{j}|\tilde{y}_{j}(t-\tau _{ij})|, \quad i,j=1,2,\ldots ,n. \end{aligned}$$
(3.2)

Consider the following function

$$\begin{aligned} Y_{i}(t)=\hbox {e}^{\sigma t}|\tilde{y}_{i}(t)|,~ \sigma >1. \end{aligned}$$
(3.3)

From (2.5) and (3.3), one can conclude that

$$\begin{aligned} \dot{Y}_{i}(t)&= \sigma \hbox {e}^{\sigma t}|\tilde{y}_{i}(t)|+\hbox {e}^{\sigma t}\frac{\hbox {d}|\tilde{y}_{i}(t)|}{\hbox {d}t}\nonumber \\&= \sigma \hbox {e}^{\sigma t}|\tilde{y}_{i}(t)|+\hbox {e}^{\sigma t}\frac{\tilde{y}_{i}(t)\dot{\tilde{y}}_{i}(t)}{|\tilde{y}_{i}(t)|}\nonumber \\&= \sigma \hbox {e}^{\sigma t}|\tilde{y}_{i}(t)|+ \hbox {e}^{\sigma t} \nonumber \\&\quad \, \times \frac{\tilde{y}_{i}(t)\hbox {e}^{t}\Big \{-c_{i}(\tilde{y}_{i}(t))+\sum \limits _{j=1}^{n}a_{ij}g_{j}(\tilde{y}_{j}(t))+\sum \limits _{j=1}^{n}b_{ij}g_{j}(\tilde{y}_{j}(t-\tau _{ij}))-U_{i}(t)\Big \}}{|\tilde{y}_{i}(t)|}\nonumber \\&\le \sigma \hbox {e}^{\sigma t}|\tilde{y}_{i}(t)|+\hbox {e}^{\sigma t}\hbox {e}^{t}\Big \{-\gamma _{i}|\tilde{y}_{i}(t)|\nonumber \\&\quad +\,\sum \limits _{j=1}^{n}L_{j}|a_{ij}||\tilde{y}_{j}(t)|+\sum \limits _{j=1}^{n}L_{j}|b_{ij}||\tilde{y}_{j}(t-\tau _{ij})|-\frac{\tilde{y}_{i}(t)U_{i}(t)}{|\tilde{y}_{i}(t)|}\Big \}\nonumber \\&= \sigma Y_{i}(t)+\hbox {e}^{t}\Big \{-\gamma _{i}Y_{i}(t)\nonumber \\&\quad +\sum \limits _{j=1}^{n}L_{j}|a_{ij}|Y_{j}(t)+\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\hbox {e}^{\sigma \tau _{ij}}Y_{j}(t-\tau _{ij})-\hbox {e}^{\sigma t}\frac{\tilde{y}_{i}(t)U_{i}(t)}{|\tilde{y}_{i}(t)|}\Big \}. \end{aligned}$$
(3.4)

Now construct the following positive Lyapunov functional as

$$\begin{aligned} V(t)=\hbox {e}^{-t}\sum \limits _{i=1}^{n}Y_{i}(t)+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\hbox {e}^{\sigma \tau _{ij}}\int _{t-\tau _{ij}}^{t}Y_{j}(s)\hbox {d}s, \end{aligned}$$
(3.5)

for \(t\ge 0,\,\sigma >1\). Subsequently, the differential of \(V(t)\) along the trajectory of (3.4) is

$$\begin{aligned} \dot{V}(t)&= -\hbox {e}^{-t}\sum \limits _{i=1}^{n}Y_{i}(t)+\hbox {e}^{-t}\sum \limits _{i=1}^{n}\dot{Y}_{i}(t)+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\hbox {e}^{\sigma \tau _{ij}}(Y_{j}(t)-Y_{j}(t-\tau _{ij}))\nonumber \\&\le -\,\hbox {e}^{-t}\sum \limits _{i=1}^{n}Y_{i}(t)+\hbox {e}^{-t}\sum \limits _{i=1}^{n}\Big [\sigma Y_{i}(t)+\hbox {e}^{t}\Big \{-\gamma _{i}Y_{i}(t)\nonumber \\&\quad +\sum \limits _{j=1}^{n}L_{j}|a_{ij}|Y_{j}(t)+\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\hbox {e}^{\sigma \tau _{ij}}Y_{j}(t-\tau _{ij})-\hbox {e}^{\sigma t}\frac{\tilde{y}_{i}(t)U_{i}(t)}{|\tilde{y}_{i}(t)|}\Big \}\Big ]\nonumber \\&\quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\hbox {e}^{\sigma \tau _{ij}}(Y_{j}(t)-Y_{j}(t-\tau _{ij}))\nonumber \\&= \sum \limits _{i=1}^{n}\Big \{-\hbox {e}^{-t}Y_{i}(t)+\sigma \hbox {e}^{-t}Y_{i}(t)-\gamma _{i}Y_{i}(t)\nonumber \\&\quad +\sum \limits _{j=1}^{n}L_{i}|a_{ji}|Y_{i}(t)+\sum \limits _{j=1}^{n}L_{i}|b_{ji}|\hbox {e}^{\sigma \tau _{ji}}Y_{i}(t)-\hbox {e}^{\sigma t}\frac{\tilde{y}_{i}(t)U_{i}(t)}{|\tilde{y}_{i}(t)|}\Big \}\nonumber \\&\le \sum \limits _{i=1}^{n}\Big \{(\sigma -1)\hbox {e}^{-t}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}|a_{ji}|+\sum \limits _{j=1}^{n}L_{i}|b_{ji}|\hbox {e}^{\sigma \tau _{ji}}\Big \}Y_{i}(t)- \sum \limits _{i=1}^{n}\hbox {e}^{\sigma t}\frac{\tilde{y}_{i}(t)U_{i}(t)}{|\tilde{y}_{i}(t)|}\nonumber \\&= \sum \limits _{i=1}^{n}\hbox {e}^{\sigma t}\Big \{(\sigma -1)\hbox {e}^{-t}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}|a_{ji}|+\sum \limits _{j=1}^{n}L_{i}\hbox {e}^{\sigma \tau _{ji}}|b_{ji}|\Big \}|\tilde{y}_{i}(t)|\nonumber \\&\quad -\sum \limits _{i=1}^{n}\hbox {e}^{\sigma t}\frac{\tilde{y}_{i}(t)U_{i}(t)}{|\tilde{y}_{i}(t)|}. \end{aligned}$$
(3.6)

If the control input \(U_{i}(t)\) is suitably designed as

$$\begin{aligned} U_{i}(t)&= \Big \{(\sigma -1)\hbox {e}^{-t}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\sigma \tau _{ji}})\Big \}|\tilde{y}_{i}(t)|\hbox {sgn}(\tilde{y}_{i}(t))\nonumber \\&= \Big \{(\sigma -1)\hbox {e}^{-t}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\sigma \tau _{ji}})\Big \}\tilde{y}_{i}(t), \end{aligned}$$

then

$$\begin{aligned} \dot{V}(t)\le 0,~t\ge 0, \end{aligned}$$
(3.7)

which implies \(V(t)\le V(0)\) for \(t\ge 0\). Then, by (3.3) and (3.5), one has

$$\begin{aligned} \sum _{i=1}^{n}\hbox {e}^{-t}\hbox {e}^{\sigma t}|\tilde{y}_{i}(t)|\le V(t)\le V(0). \end{aligned}$$
(3.8)

And, it follows from (3.5) that

$$\begin{aligned} V(0)&= \sum \limits _{i=1}^{n}|y_{i}(0)|+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\hbox {e}^{\sigma \tau _{ij}}\int _{-\tau _{ij}}^{0}Y_{j}(s)\hbox {d}s\nonumber \\&\le \sum \limits _{i=1}^{n}(|y_{i}(0)|+\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\tau _{ij}\hbox {e}^{\sigma \tau _{ij}}\sup \limits _{-\tau _{ij}\le s\le 0}Y_{j}(s))\nonumber \\&\le \sum \limits _{i=1}^{n}|y_{i}(0)|+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{j}|b_{ij}|\tau \hbox {e}^{\sigma \tau }\sup \limits _{-\tau \le s\le 0}Y_{j}(s)\nonumber \\&= \sum \limits _{i=1}^{n}|y_{i}(0)|+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{i}|b_{ji}|\tau \hbox {e}^{\sigma \tau }\sup \limits _{-\tau \le s\le 0}Y_{i}(s)\nonumber \\&\le \max \limits _{1\le i\le n}\{1+L_{i}\tau \hbox {e}^{\sigma \tau }\sum \limits _{j=1}^{n}|b_{ji}|\}\sum \limits _{i=1}^{n}\sup \limits _{-\tau \le s\le 0}|\tilde{y}_{i}(s)|, \end{aligned}$$
(3.9)

where \(M=\max \limits _{1\le i\le n}\{1+L_{i}\tau \hbox {e}^{\sigma \tau }\sum \limits _{j=1}^{n}|b_{ji}|\}\ge 1\).

Substituting (3.8) into (3.9) yields

$$\begin{aligned} \sum \limits _{i=1}^{n}|v_{i}(t)-w_{i}(t)|\le M \sum \limits _{i=1}^{n}\sup \limits _{-\tau \le s\le 0}|v_{i}(s)-w_{i}(s)|\hbox {e}^{-\alpha t},\quad t\ge 0, \end{aligned}$$
(3.10)

where \(\alpha =\sigma -1>0\).

The proof is completed. \(\square \)

In terms of (3.10) and \(v_{i}(t)=x_{i}(\hbox {e}^{t}), w_{i}(t)=z_{i}(\hbox {e}^{t})\), one can conclude that

$$\begin{aligned}&\sum \limits _{i=1}^{n}|x_{i}(\hbox {e}^t)-z_{i}(\hbox {e}^t)|\le M\sum _{i=1}^{n}\sup _{-\tau \le s \le 0}|x_{i}(\hbox {e}^s)-z_{i}(\hbox {e}^s)|\hbox {e}^{-\alpha t},~ \hbox {e}^{t}\ge 1. \end{aligned}$$
(3.11)

Let \(\hbox {e}^{t}=\eta \), then \(\eta \ge 1\) and \(t=\log \eta \ge 0\); Let \(\hbox {e}^{s}=\xi \), then \(s=\log \xi \in [-\tau ,0]\) and \(\xi \in [q,1]\). Thus, it follows from (3.11) that

$$\begin{aligned}&\sum \limits _{i=1}^{n}|x_{i}(\eta )-z_{i}(\eta )|\le M\sum _{i=1}^{n}\sup _{q\le \xi \le 1}|x_{i}({\xi })-z_{i}(\xi )|\hbox {e}^{-\alpha \log \eta },~\eta \ge 1. \end{aligned}$$
(3.12)

Taking \(\eta =t\), the following inequality is obtained:

$$\begin{aligned} \sum \limits _{i=1}^{n}|x_{i}(t)-z_{i}(t)|\le M\sum _{i=1}^{n}\sup _{q\le \xi \le 1}|x_{i0}-z_{i0}|\hbox {e}^{-\alpha \log t},\quad t\ge 1. \end{aligned}$$
(3.13)

Thus, the drive-response systems (2.1) and (2.2) are said to be exponentially synchronized, and the exponential synchronization rate is less than \(\alpha \) for \(\log t<t\) as \(t\ge 1\).

By \(U_{i}(t)=u_{i}(\hbox {e}^{t})\), (3.1) can be written as

$$\begin{aligned} u_{i}(\hbox {e}^{t})=\Big \{(\sigma -1)\hbox {e}^{-t}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\sigma (-\log q_{ji})})\Big \}\tilde{y}_{i}(t), \quad t\ge 0, \end{aligned}$$

namely,

$$\begin{aligned} u_{i}(t)=\Big \{(\sigma -1)t^{-1}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\sigma (-\log q_{ji})})\Big \}\tilde{y}_{i}(\log t),\quad t\ge 1, \end{aligned}$$

in which \(\tilde{y}_{i}(\log t)=v_{i}(\log t)-w_{i}(\log t)=x_{i}(t)-z_{i}(t)\). Assume \(y_{i}(t)=x_{i}(t)-z_{i}(t)\), then

$$\begin{aligned} u_{i}(t)=\Big \{(\sigma -1)t^{-1}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\sigma (-\log q_{ji})})\Big \}y_{i}(t),\quad t\ge 1, \end{aligned}$$

Thus, the following theorem is derived.

Theorem 3.2

Assume that Assumptions 1 and 2 hold. For the drive-response structure of neural networks given in (2.1) and (2.2), if the control input \(u_{i}(t)\) in (2.2) is suitably designed as

$$\begin{aligned} u_{i}(t)=\Big \{(\sigma -1)t^{-1}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\sigma (-\log q_{ji})})\Big \}y_{i}(t), \end{aligned}$$
(3.14)

for \(i=1,2,\ldots ,n,\,t\ge 1\), where \(\sigma >1\) is a constant, \(y_{i}(t)=x_{i}(t)-z_{i}(t)\) denotes the resulting synchronization error, then the exponential synchronization of systems (2.1) and (2.2) is obtained with an exponential convergence rate which is less than \(\alpha =\sigma -1\).

In addition, let \(q_{ij}=1, i,j=1,2,\ldots ,n\) in (2.1) and (2.2), then systems (2.1) and (2.2) become the following drive-response structure of neural networks without delays,

$$\begin{aligned} \dot{x}_{i}(t)=-d_{i}(x_{i}(t))+\sum \limits _{j=1}^{n}m_{ij}f_{j}(x_{j}(t))+I_{i},\quad t\ge 0, \end{aligned}$$
(3.15)

and

$$\begin{aligned} \dot{z}_{i}(t)=-d_{i}(z_{i}(t))+\sum \limits _{j=1}^{n}m_{ij}f_{j}(z_{j}(t))+I_{i}+u_{i}(t),\quad t\ge 0. \end{aligned}$$
(3.16)

Corollary 3.3

Assume that Assumptions 1 and 2 hold. For the drive-response structure of neural networks given in (3.15) and (3.16), if the control input \(u_{i}(t)\) in (3.16) is suitably designed as

$$\begin{aligned} u_{i}(t)=\Big \{(\sigma -1)e^{-t}-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}|m_{ji}|\Big \}y_{i}(t),\quad t\ge 0 \end{aligned}$$
(3.17)

for \(i=1,2,\ldots ,n\), where \(\sigma >1\) is a constant, \(y_{i}(t)=x_{i}(t)-z_{i}(t)\) denotes the resulting synchronization error, then the exponential synchronization of systems (3.15) and (3.16) is obtained with an exponential convergence rate \(\alpha =\sigma -1\).

Remark 3.4

Systems (2.3) and (2.4) are asymptotically synchronized if the following conditions are satisfied: (i) the exponential synchronization rate is zero, i.e. \(\lambda =0\) and \(M>1\) such that \(\sum \limits _{i=n}^{n}|v_{i}(t)-w_{i}(t)|\le M\sum \limits _{i=n}^{n}\sup \limits _{-\tau \le s\le 0}|v_{i}(s)-w_{i}(s)|,~t\ge 0\); (ii) \(\lim \limits _{t\rightarrow \infty }\Vert \tilde{y}(t)\Vert =0\).

Remark 3.5

When \(\sigma =1\) in Theorems 3.1, 3.2 and Corollary 3.3, the exponential synchronization results reduce to the asymptotic synchronization results. Meanwhile, the control inputs (3.1), (3.14) and (3.17) are suitably designed as follows

$$\begin{aligned} U_{i}(t)&= \Big \{-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{\tau _{ji}})\Big \}\tilde{y}_{i}(t),\quad i=1,2,\ldots ,n,\quad t\ge 0, \\ u_{i}(t)&= \Big \{-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}(|a_{ji}|+|b_{ji}|\hbox {e}^{-\log q_{ji}})\Big \}y_{i}(t),\quad t\ge 1, \end{aligned}$$

and

$$\begin{aligned} u_{i}(t)&= \Big \{-\gamma _{i}+\sum \limits _{j=1}^{n}L_{i}|m_{ji}|\big \}y_{i}(t),\quad t\ge 0. \end{aligned}$$

4 Illustrative Examples

In this section, this paper presents two illustrative examples to demonstrate the effectiveness of the proposed synchronization scheme.

Example 4.1

Consider the following delayed Hopfield neural networks

$$\begin{aligned} \dot{x}_{i}(t)=-d_{i}(x_{i}(t))+\sum \limits _{j=1}^{2}a_{ij}f_{j}(x_{j}(t))+ \sum \limits _{j=1}^{2}b_{ij}f_{j}(x_{j}(t-\tau _{ij}(t)),\quad i=1,2, \end{aligned}$$
(4.1)

where \(d_{i}(x_{i}(t))=x_{i}(t),\,A=\begin{pmatrix}2.0 &{} -0.1\\ -5.0 &{} 3.0 \end{pmatrix},B=\begin{pmatrix}-1.5 &{} -0.1\\ -0.2&{} -2.5 \end{pmatrix}\) and \(f_{i}(x_{i})=\tanh (x_{i}),~i=1,2\). The system satisfies Assumptions 1 and 2 with \(\gamma _{i}=1, L_{i}=1, i=1,2\). The chaotic behavior of system (4.1) with the initial condition \([x_{1}(s),x_{2}(s)]^{T}=[0.4,0.6]^{T}\) for \(-1\le s\le 0\) has already been reported in the case of \(\tau _{ij}(t)=\tau _{j}(t)=1,i,j=1,2\) [11, 25](See Fig. 1).

The present example specifies the unbounded time-varying delays as \(\tau _{ij}(t)=(1-q_{ij})t\), in which \(q_{11}=q_{22}=0.5, q_{12}=q_{21}=0.8\). At the same time, the dynamic behavior of this system with \(\tau _{ij}(t)=(1-q_{ij})t\) can be seen in Fig. 2a. To achieve synchronization, the response system is designed as

$$\begin{aligned} \dot{z}_{i}(t)=-d_{i}(z_{i}(t))+\sum \limits _{j=1}^{2}a_{ij}f_{j}(z_{j}(t))+\sum \limits _{j=1}^{2}b_{ij}f_{j}(z_{j}(q_{ij}t))+u_{i}(t),~i=1,2. \end{aligned}$$
(4.2)
Fig. 1
figure 1

The chaotic HNNs with \(\tau _{1}=\tau _{2}=1\) in Example 4.1

Full size image
Fig. 2
figure 2

The trajectories of drive system and response system with \(\tau _{ij}(t)=(1-q_{ij})t\)

Full size image

From (3.14), the control input \(u_{i}(t),i=1,2\) are suitably chosen as

$$\begin{aligned} u_{1}(t)=\big \{(\sigma -1)t^{-1}-\gamma _{1}+\sum \limits _{j=1}^{2}L_{1}(|a_{j1}|+|b_{j1}|\hbox {e}^{\sigma (-\log q_{j1})})\big \}y_{1}(t), \end{aligned}$$

and

$$\begin{aligned} u_{2}(t)=\big \{(\sigma -1)t^{-1}-\gamma _{2}+\sum \limits _{j=1}^{2}L_{2}(|a_{j2}|+|b_{j2}|\hbox {e}^{\sigma (-\log q_{j2})})\big \}y_{2}(t), \end{aligned}$$

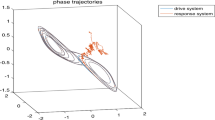
where \(y_{i}(t)=x_{i}(t)-z_{i}(t), i=1,2\). Taking \(\sigma =2\). In Fig. 2a and c show the dynamic behavior of drive system (4.1) and response system (4.2) in phase space with initial conditions \(x(t)=[0.4,0.6]^{T}\) and \(z(t)=[-1.0,2.0]^{T},\,t\in [0.5,1.0]\), respectively. Figure 2b shows the dynamic behavior of response system (4.2) in phase space without control input with initial condition \(z(t)=[-1.0,2.0]^{T},\,t\in [0.5,1.0]\). Figure 3 depicts the synchronization error of the state variables between drive system (4.1) and response system (4.2) with the initial conditions \(x(t) = [0.4, 0.6]^T\) and \(z(t) = [-1.0, 2.0]^T\) for \(t \in [0.5, 1.0]\), respectively. From the simulation result, it shows that the proposed controller guarantees global exponential synchronization of the couple networks.

Fig. 3
figure 3

The synchronization error between drive and response systems

Full size image

Example 4.2

Consider the following three-order CNNs with proportional delays

$$\begin{aligned} \dot{x}_{i}(t)=-\,d_{i}(x_{i}(t))+\sum \limits _{j=1}^{3}a_{ij}f_{j}(x_{j}(t))+\sum \limits _{j=1}^{3}b_{ij}f_{j}(x_{j}(q_{ij}(t)),\quad i=1,2,3 \end{aligned}$$
(4.3)

with

$$\begin{aligned} d_{i}(x_{i}(t))=x_{i}(t), \quad A=\begin{pmatrix}1.0 &{}\quad -1.0 &{}\quad 1.0\\ 1.8 &{}\quad -1.75&{}\quad -1.2\\ -2.5 &{}\quad -2.0&{}\quad 1.1 \end{pmatrix},\quad B=\begin{pmatrix}1.0 &{}\quad -0.2 &{}\quad -1.0\\ 0.2&{}\quad -3.5&{}\quad 2.4\\ 2.25&{}\quad 2.0 &{}\quad -2.0\end{pmatrix} \end{aligned}$$

and \(f_{i}(x_{i})=\frac{1}{2}(|x_{i}+1|-|x_{i}-1|),\,q_{ij}=0.5, i,j=1,2,3\). Clearly, the system satisfies Assumptions 1 and 2, with \(\gamma _{i}=1,L_{i}=1, i=1,2,3\).

It should be noted that the CNNs is actually a chaotic CNNs with proportional delays (see Fig. 4a) with initial values \(x(t)=[2.0,1.0,1.0]^{T}\) for \(t\in [0.5,1.0]\). To achieve synchronization, the response system is designed as

$$\begin{aligned} \dot{z}_{i}(t)=-d_{i}(z_{i}(t))+\sum \limits _{j=1}^{3}a_{ij}f_{j}(z_{j}(t))+\sum \limits _{j=1}^{3}b_{ij}f_{j}(z_{j}(q_{ij}t))+u_{i}(t),i=1,2,3. \end{aligned}$$
(4.4)

Furthermore, one designs the nonlinear controller for systems (4.3) and (4.4) by using Theorem 3.2. Let us define the control parameter \(\alpha =2\). From (3.14), the control inputs \(u_{i}(t),i=1,2,3\) are suitably chosen as

$$\begin{aligned}&u_{1}(t)=\big \{(\sigma -1)t^{-1}-\gamma _{1}+\sum \limits _{j=1}^{3}L_{1}(|a_{j1}|+|b_{j1}|\hbox {e}^{\sigma (-\log q_{j1})})\big \}y_{1}(t),\\&u_{2}(t)=\big \{(\sigma -1)t^{-1}-\gamma _{2}+\sum \limits _{j=1}^{3}L_{2}(|a_{j2}|+|b_{j2}|\hbox {e}^{\sigma (-\log q_{j2})})\big \}y_{2}(t), \end{aligned}$$

and

$$\begin{aligned} u_{3}(t)=\big \{(\sigma -1)t^{-1}-\gamma _{3}+\sum \limits _{j=1}^{3}L_{3}(|a_{j3}|+|b_{j3}|\hbox {e}^{\sigma (-\log q_{j3})})\big \}y_{3}(t). \end{aligned}$$

In Fig. 4a and c show the chaotic behavior of drive system (4.3) and response system (4.4) in phase space with initial conditions \(x(t)=[2.0,1.0,1.0]^{T}\) and \(z(t)=[1.0,2.0,3.0]^{T},\,t\in [0.5,1.0]\), respectively. Figure 4b shows the chaotic behavior of response system (4.4) in phase space without control input with initial condition \(z(t)=[1.0,2.0,3.0]^{T},\,t\in [0.5,1.0]\). Figure 5 depicts the synchronization error of the state variables between the drive system (4.3) and the response system (4.4) with the initial conditions \([x_{1},x_{2},x_{3}]^{T}=[2.0,1.0,1.0]^{T}\) and \([1.0,2.0,3.0]^{T}\), respectively. It can be seen that the state error between the drive system and the response system trends to zero, which implies that the drive system synchronizes with the response system.

Fig. 4
figure 4

The trajectories of drive system and response system with \(q_{ij}=0.5\)

Full size image
Fig. 5
figure 5

The synchronization error state trajectories of \(y_{i}(t)\) in Example 4.2

Full size image

5 Conclusions

In this paper, a drive-response synchronization control frame has been established. Different from the prior works, delays here are multiple proportional delays which are unbounded and time-varying. A model of synchronization control of recurrent neural networks with multiple proportional delays has been firstly proposed. And then, the exponential synchronization problem has been transformed to stabilize the addressed error system. By constructing the appropriate Lyapunov functional, several delay-dependent and decentralized control laws have been derived, which ensure the response system to be exponential synchronized with the drive system. Moreover, the synchronization degree can be easily estimated. Finally, two illustrative examples have been given to verify the theoretical results. Further, recurrent neural networks with proportional delays can be applied to QoS routing in computer networks to establish the QoS routing algorithm based on neural networks with proportional delays.