Dynamical regularized echo state network for time series prediction

Abstract

Echo state networks (ESNs) have been widely used in the field of time series prediction. However, it is difficult to automatically determine the structure of ESN for a given task. To solve this problem, the dynamical regularized ESN (DRESN) is proposed. Different from other growing ESNs whose existing architectures are fixed when new reservoir nodes are added, the current component of DRESN may be replaced by the newly generated network with more compact structure and better prediction performance. Moreover, the values of output weights in DRESN are updated by the error minimization-based method, and the norms of output weights are controlled by the regularization technique to prevent the ill-posed problem. Furthermore, the convergence analysis of the DRESN is given theoretically and experimentally. Simulation results demonstrate that the proposed approach can have few reservoir nodes and better prediction accuracy than other existing ESN models.

1 Introduction

Time series in nature are usually chaotic or nonlinear; thus, the prediction of time series is an issue of dynamic system modeling [1]. Recently, some neural network models and kernel-based techniques have been applied for time series prediction tasks, such as the recurrent neural network (RNN) [2, 3], fuzzy model [4], extended Kalman filter [5], extreme learning machine (ELM) [6], self-organizing map [7], echo state network (ESN) [8]. Among these methods, the ESN has attracted substantial interest. During the learning process of ESN, only the connection weights from the reservoir to readout need be adapted, while the input and internal weights remain fixed once determined [8]. Compared with the RNNs which utilize the gradient-based training algorithms, the ESNs have shown better prediction performance and faster running speed on time series prediction. Thus, the ESNs have been widely used in both industrial and academic fields, such as the temperature prediction [9], traffic series forecasting [10], image processing [11], rainfall series prediction [12].

In ESN, a large network structure is sometimes required due to the random process in initialization phase, and also the increased reservoir size (network complexity) could improve the learning performance [13]. However, the too large reservoir may face the overfitting problem which leads to lower generalization capability. Conversely, if the reservoir size is too small, the obtained ESN may not be able to solve the problem as expected [14]. Thus, how to determine the proper network architecture for a given task is an open question in ESN applications.

In original ESN [8], the reservoir is always designed with a fixed network size which can be determined by trial and error. This approach is straightforward, while the numerous trials and even luck are required for reservoir specification, and also the selected network size may not be optimal. Recently, some heuristic methods are developed to automatically determine the ESN, such as the evolutionary algorithms [11, 15, 16], the pruning methods [14, 17, 18], the growing technique [19].

The evolutionary algorithms are well known by global searching ability for complex problems [20]; thus, they are widely used to find the proper reservoir structure. For example, the pigeon-inspired optimization (PIO) approach is employed in [11] to optimize the reservoir size, the spectral radius, the sparse degree and other ESN parameters, and the optimized ESN could solve the image restoration problem successfully. By treating the ESN output weights connection optimization problem as a feature selection problem, the binary particle swarm optimization (BPSO) algorithm is introduced in [15] to determine the optimal readout connections. Moreover, the differential evolution (DE) algorithm is used to train the reservoir weight matrix in [16], and simulation results show that the optimized ESN could effectively predict the multiple superimposed oscillators. Although the evolutionary algorithms-based ESNs [11, 15, 16] could improve the prediction performance to some extent, they are easily trap into local optimal and always have slow convergence rate in the training process.

The pruning methods are widely used on static ESNs. In [17], a regularization technique-based pruning algorithm is firstly proposed to show how to delete the connections between the reservoir and readout, and the random deletion (RD), backward selection (BS) and the least angle regression (LAR) are used to rank and remove the output weights with the least significance. Furthermore, a sensitive iterative pruning algorithm [14] is designed, in which a sufficiently large reservoir is initialized and then the least sensitive reservoir neurons are pruned. Moreover, an online pruning method [18] is developed, in which the reservoir neurons are firstly measured and sorted according to the synapse significance, and then the nodes with the least significance are deleted one by one. Actually, the pruning methods are easily understood and operated [14, 17, 18], while the required initial network structure is always larger than necessary; thus, heavy computational burden is required especially when the size of training samples is huge.

On the other hand, it is proved that the growing methods could improve the performance of RNNs [21, 22]. These schemes always start with a small network and incrementally add hidden neurons during the network training process. Inspired by biological neural system, the information processing ability and competitiveness of neurons are used to add new hidden nodes into RNN [21]; then the adaptive second-order algorithm is employed to adjust the RNN parameters. Based on fuzzy theory, a self-evolving fuzzy neural network [22] is designed in which the fuzzy rules are learned via structure learning, and the network parameters are tuned by a rule-ordered Kalman filter. Compared with RNNs, since the echo state property (ESP) of ESN should be ensured during the network growing process [8], the incremental schemes [21, 22] could not be used on ESN directly. Fortunately, the singular value decomposition (SVD) method [23] provides an effective way to design the reservoir whose singular values are predefined and smaller than 1; thus, the ESP of the obtained ESN is guaranteed. Based on the SVD technique, the growing ESN (GESN) [19] is proposed which adds reservoir nodes group by group. Moreover, the output weights of GESN are incrementally updated which significantly reduces the computational complexity. The effectiveness of GESN is proved by simulation results in terms of network complexity and prediction performance. However, the GESN still faces some problems. Firstly, a large number of reservoir neurons will be obtained eventually if many algorithm iterations are done, while some reservoir nodes may have little contribution to network performance. Secondly, the output weights of GESN are estimated by the pseudo verse method during the network growing process, the estimated output weight matrix may be sensitive to the inputs noise or lager reservoir size, i.e., the ill-posed problem may exist.

Based on above discussion, in this paper, the dynamical regularized ESN (DRESN) is provided which could automatically determine the network structure for various applications. The essence of DRESN is to design a reservoir whose nodes can be added or deleted dynamically according to their significance to network performance, while the output weights are updated to minimize the sum of square error of the training data, and the regularization method is incorporated to avoid the ill-posed problem. Furthermore, the convergence analysis of DRESN is given to guarantee its successful application on time series prediction problems. The simulation results demonstrate that the proposed DRESN is better than other existing incremental or pruning algorithms in terms of network complexity and prediction accuracy.

The rest of this paper is organized as follows. A brief review of the original ESN and the regularized ESN is given in Sect. 2. The proposed DRESN and its convergence analysis are presented in Sect. 3. The performance of DRESN is evaluated in Sect. 4, followed by some conclusions in Sect. 5.

2 Preliminaries

In this section, the original ESN (OESN) [8] and the regularized ESN (RESN) [17] will be briefly described, respectively.

2.1 The original ESN

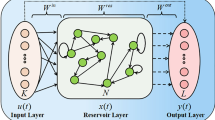
The OESN without output feedback connections can be subdivided into an input layer, a reservoir and a readout [8]. This is schematically illustrated in Fig. 1. It is assumed that the ESN has n input units, N reservoir neurons and m output nodes. For the given L arbitrary training samples $\{{\mathbf {u}}(k),{\mathbf {t}}(k)\}_{k=1}^L$, where ${\mathbf {u}}(k)=[ u_1(k), u_2(k), \ldots , u_n(k) ]^T\in {\mathbb {R}}^n$ denote the external stimulations and ${\mathbf {t}}(k)=[t_1(k), t_2(k), \ldots , t_m(k) ]^T\in {\mathbb {R}}^m$ are the corresponding target output, T stands for the Hermitian transpose, then the echo states ${\mathbf {x}}(k)= [ x_1(k), x_2(k), \ldots , x_N(k) ]^T \in {\mathbb {R}}^{N}$ of the reservoir can be updated by the following equation

$$\begin{aligned} {\mathbf {x}}(k)& = {\mathbf {f}}({\mathbf {W}}{\mathbf {x}}(k-1)+{\mathbf {W}}^{\rm in}{\mathbf {u}}(k)) \end{aligned}$$

(1)

where ${\mathbf {f}}(\cdot )=[f_1(\cdot ), \ldots , f_N(\cdot )]^T$ are activation functions of the reservoir units (typically sigmoid function); ${\mathbf {W}}^{\rm in}\in {\mathbb {{R}}} ^{N\times n}$ and ${\mathbf {W}}\in {\mathbb {R}}^{N\times N}$ are the input weight matrix and reservoir weight matrix, respectively. The prediction of ESN, ${\mathbf {y}}(k)=[ y_1(k), y_2(k), \ldots , y_m(k) ]^T\in {\mathbb {R}}^m$, is computed as below

$$\begin{aligned} {\mathbf {y}}(k)& = {} ({\mathbf {W}}^{\rm out})^T{\mathbf {X}}(k) \end{aligned}$$

(2)

where ${\mathbf {X}}(k)=[{\mathbf {x}}(k)^T, {\mathbf {u}}(k)^T]^T\in {\mathbb {R}}^{(N+n)}$ is the concatenation of reservoir states and input vectors, ${\mathbf {W}}^{\rm out}$ is the output weight matrix.

Fig. 1

The basic architecture of OESN. The black solid arrows stand for the reservoir weight connections, and the black dashed line arrows indicate the output connections

In the training process of an ESN, if we define the internal state matrix as ${\mathbf {H}}=[{\mathbf {X}}(1), {\mathbf {X}}(2), \ldots , {\mathbf {X}}(L)]^T$ and the corresponding target output matrix as ${\mathbf {T}}=[{\mathbf {t}}(1), {\mathbf {t}}(2), \ldots , {\mathbf {t}}(L)]^T$, then the following equation can be obtained

$$\begin{aligned} {\mathbf {H}}{\mathbf {W}}^{\rm out}&= {\mathbf {T}} \end{aligned}$$

(3)

The determination of ${\mathbf {W}}^{\rm out}$ is equivalent to finding the least square solution of the following linear formula

$$\begin{aligned} F({\mathbf {{W}}}^{\rm out})&= \arg \min \limits _{{\mathbf {{W}}}^{\rm out}}\Vert {\mathbf {H}}{\mathbf {W}}^{\rm out}-{\mathbf {T}} \Vert _2^2 \end{aligned}$$

(4)

where $\Vert \cdot \Vert _2$ denotes the $l_2$-norm. Then the solution of Eq. (4) can be calculated as below

$$\begin{aligned} {\mathbf {W}}^{\rm out}={\mathbf {H}}^{\dag } {\mathbf {T}}=({\mathbf {H}}^T{\mathbf {H}})^{-1}{\mathbf {H}}^T{\mathbf {T}} \end{aligned}$$

(5)

where ${\mathbf {H}}^{\dag }$ is the Moore–Penrose generalized inverse of the internal state matrix ${\mathbf {H}}$ [24].

For a given training data set $\{ ({\mathbf {u}}(k),{\mathbf {t}}(k)) \mid {\mathbf {u}}(k) \in {\mathbb {R}}^n, {\mathbf {t}}(k) \in {\mathbb {R}}^m, k=1,2,\ldots , L \}$, the number of reservoir nodes N and the activation functions ${\mathbf {f}}(\cdot )$, the main training steps of the OESN can be summarized as follows

• Step 1 Randomly generate a reservoir weight matrix ${\mathbf {W}}_0$ with predefined reservoir size N. Then scale ${\mathbf {W}}_0$ to ${\mathbf {W}}=(\alpha _{\mathbf {W}}/\rho ({\mathbf {W}}_0)){\mathbf {W}}_0$, where $\rho ({\mathbf {W}}_0)$ is the spectral radius of ${\mathbf {W}}_0$, $0<\alpha _{\mathbf {W}}<1$ is a scaling parameter; thus, ${\mathbf {W}}$ has the spectral radius of $\alpha _{\mathbf {W}}$.

• Step 2 Randomly generate the input weight matrix ${\mathbf {W}}^{\rm in}$ according to any continuous probability distribution, such as the uniform distribution.

• Step 3 Drive the reservoir by input signals as shown in Eq. (1); then collect the reservoir states to obtain the internal state matrix ${\mathbf {H}}$.

• Step 4 Calculate the output weight matrix ${\mathbf {W}}^{\rm out}$ by Eq. (5).

The training procedures of the OESN seem very simple. However, if the reservoir size becomes too large or the time series contain noise, the ill-posed problem may appear when the ${\mathbf {H}}^{\dag }$ is calculated [25]. As a result, ${\mathbf {W}}^{\rm out}$ in Eq. (5) is very sensitive to an arbitrary perturbation in ${\mathbf {H}}$ or ${\mathbf {T}}$, which may lead to bad numerical stability or unsatisfied prediction problem.

2.2 The regularized ESN

To obtain a stabilized solution of ${\mathbf {W}}^\mathrm{out}$, the regularization regression techniques have been widely used, such as the $l_1$ penalty (lasso method) [26] and the $l_2$ penalty method (also called Tikhonov regularization or ridge regression) [27]. The main advantage of lasso method is that it can achieve the sparse solution by forcing some parameters to zero; thus, it is always used to find the solution of ${\mathbf {W}}^\mathrm{out}$ whose most weights are zeros. However, the introduction of nondifferentiable $l_1$ form in the target function brings difficulty to find the appropriate value of the $l_1$ regularization parameter [26]. On the other hand, the use of Tikhonov regularization could achieve better prediction accuracy than the traditional least square methods by making a bias–variance trade-off. Moreover, the $l_2$ regularization parameter could be found by using the cross-validation or Bayesian approximation method [27].

Based on above discussion, in this paper, the Tikhonov regularization is used by introducing a $l_2$ penalty term into Eq. (4). Then, one obtains

$$\begin{aligned} F({\mathbf {{W}}}^\mathrm{out})&= \arg \min \limits _{{\mathbf {{W}}}^\mathrm{out}}\left( \Vert {\mathbf {H}}{\mathbf {W}}^\mathrm{out}-{\mathbf {T}} \Vert _2^2+C\Vert {\mathbf {W}}^\mathrm{out}\Vert _2^2\right) \end{aligned}$$

(6)

where $C>0$ is the $l_2$ penalty parameter. Differentiating with respect to ${\mathbf {W}}^{\rm out}$, one has

$$\begin{aligned} \frac{\partial F({\mathbf {{W}}}^\mathrm{out})}{\partial ({\mathbf {{W}}}^{\rm out})}=-2{\mathbf {H}}^T({\mathbf {T}}-{\mathbf {H}}{\mathbf {{W}}}^\mathrm{out})+2C{\mathbf {{W}}}^\mathrm{out} \end{aligned}$$

(7)

Let the derivative of function (7) be zero and we have

$$\begin{aligned} 2{\mathbf {H}}^T{\mathbf {H}}{\mathbf {{W}}}^\mathrm{out}-2{\mathbf {H}}^T{\mathbf {T}}+2C{\mathbf {{W}}}^\mathrm{out}=0 \end{aligned}$$

It is easy to get the following equation

$$\begin{aligned} (C{\mathbf {I}}+{\mathbf {H}}^T{\mathbf {H}}){\mathbf {{W}}}^\mathrm{out}={\mathbf {H}}^T{\mathbf {T}} \end{aligned}$$

(8)

where ${\mathbf {I}}$ is an unity matrix with the same row and column dimensions as the matrix ${\mathbf {H}}^T{\mathbf {H}}$. Since $C{\mathbf {I}}$ is positive definite, also matrix ${\mathbf {H}}^T{\mathbf {H}}$ is positive semidefinite; thus, matrix $C{\mathbf {I}}+{\mathbf {H}}^T{\mathbf {H}}$ is positive definite. Then, one obtains

$$\begin{aligned} {\mathbf {{W}}}^\mathrm{out}=(C{\mathbf {I}}+{\mathbf {H}}^T{\mathbf {H}})^{-1}{\mathbf {H}}^T{\mathbf {T}} \end{aligned}$$

(9)

It is obvious that the OESN is just the special case of RESN with $C=0$. In [17], some thorough demonstration about regularization techniques on ESNs has been given, other theories and applications are illustrated in [12, 28] to show the efficiency of the regularization methods. Thus, the $l_2$ penalty term will be used in this paper to calculate the output weight matrix ${\mathbf {{W}}}^\mathrm{out}$ of ESN.

3 The proposed dynamical regularized ESN

To guarantee an ESN work properly, the network echo state property (ESP) should be possessed, i.e., the reservoir states are uniquely defined by the history inputs. According to [29], the sufficient condition for ESP is that the largest singular value of the reservoir weight matrix ${\mathbf {W}}$ should be less than 1, while the necessary condition for ESP is that the spectral radius of ${\mathbf {W}}$ should be smaller than 1. In previous works [8, 17, 25], the initial ${\mathbf {W}}$ is always scaled to satisfy the necessary condition for ESP, while the sufficient condition is ignored which is more restrictive. To guarantee the sufficient condition for ESP without scaling of ${\mathbf {W}}$, the singular value decomposition (SVD) method is introduced by designing the reservoir whose singular values are less than 1 in [19]. To ensure the ESP of the proposed ESN, in this paper, the SVD-based reservoir design strategy will be used to construct reservoirs.

Compared with the OESN [8] and RESN [17] whose reservoir size is always fixed or predefined, the GESN [19] can add reservoir nodes group by group which is more flexible. However, some added reservoir nodes in GESN may play a minor role for network performance, and also the ill-posed problem may exist during the output weights calculation process. To obtain a more compact network architecture with better prediction accuracy, the dynamical regularized ESN (DRESN) will be proposed.

The DRESN starts with a randomly generated network. Then, in each subsequent iteration, several new ESNs with different reservoir sizes are generated; the one whose network size is the most compact among those having the best prediction performance is selected and compared with the current DRESN. If the performance of the current DRESN is good enough, it will be retained to the next iteration. Otherwise, it will be replaced by the newly generated network with better performance. Thus, the reservoir nodes of DRESN are dynamically changed according to their significance to network performance. After the network architecture of DRESN is modified, the output weights are updated by the error minimization-based algorithm which incorporates the regularization method to overcome the ill-posed problem. Hence, the output weights of DRESN are identified without gradients or generalized inverses.

To evaluate network performance, for a given ESN denoted as $\varPsi$, its residual error is defined as below

$$\begin{aligned} E(\varPsi )=\Vert {\mathbf {H}}{\mathbf {W}}^{\rm out}-{\mathbf {T}} \Vert _2^2+C\Vert {\mathbf {W}}^{\rm out}\Vert _2^2 \end{aligned}$$

(10)

where ${\mathbf {W}}^{\rm out}$ and ${\mathbf {H}}$ stand for the output weight matrix and internal state matrix of the network $\varPsi$, respectively. Smaller value of $E(\varPsi )$ means better training performance.

In the initialization phase of DRESN, a subreservoir $\varPsi _1$ with $N_1$ reservoir nodes is generated, where $N_1$ is a positive integer. Firstly, a diagonal matrix ${\mathbf {U}}_1=\text{ diag }\{\sigma _1, \sigma _2, \ldots , \sigma _{N_1}\}$ and two orthogonal matrices ${\mathbf {U}}_1=(u_{ij})_{N_1 \times N_1}$, $\mathbf {V}_1=(v_{ij})_{N_1 \times N_1}$ are randomly generated, where $0<\sigma _i<1\;(i=1,2,\ldots ,N_1)$, $u_{ij}$ and $v_{ij}, (i,j=1,2,\ldots ,N_1)$ are chosen from the range $(-\,1,1)$. By using the SVD method [23], the weight matrix ${\mathbf {W}}_1$ of the subreservoir $\varPsi _1$ is set as ${\mathbf {W}}_1={\mathbf {U}}_1{\mathbf {U}}_1\mathbf {V}_1$. Moreover, the input weight matrix ${\mathbf {W}}_1^{\rm in}$ of $\varPsi _1$ is randomly generated. Then, the echo states ${{\mathbf {x}}}_1$ and the internal state matrix ${\mathbf {H}}_1$ are collected, and the output weight matrix ${\mathbf {{W}}}^\mathrm{out}_{1}$ can be calculated according to Eq. (9). Based on ${\mathbf {H}}_1$ and ${\mathbf {{W}}}^\mathrm{out}_{1}$, the residual error $E(\varPsi _1)$ is obtained.

In the recursively updating process, a temporary network $\psi _{2}$ needs be built. Firstly, a homologous network $\psi _{21}$ with $N_{21}$ reservoir nodes is randomly generated. Secondly, the residual error $E(\psi _{21})$ of $\psi _{21}$ is compared with $E(\varPsi _{1})$ and the network with smaller residual error is retained. If the selected network is $\psi _{21}$, it will be set as the temporary network $\psi _{2}$. Otherwise, a network $\psi _{22}$ with $2N_{21}$ reservoir nodes is generated and compared with the network $\varPsi _{1}$. This procedure is continued until the reservoir size of the generated network is larger than $N_1$. Finally, a subreservoir $\varPhi _2$ with $N_{22}$ reservoir nodes is generated and added into $\psi _{2}$ to obtain the network $\varPsi _{2}$ at the current iteration.

To make the following analysis readable, we suppose that the temporary network $\psi _{2}$ has the reservoir weight matrix ${\bar{{\mathbf {W}}}}_2={\bar{{\mathbf {U}}}}_2{\bar{{\mathbf {U}}}}_2{\bar{\mathbf {V}}}_2$, internal states ${\bar{{\mathbf {x}}}}_2$, input weight matrix ${\bar{{\mathbf {W}}}}_2^{\rm in}$ and internal state matrix ${\bar{{\mathbf {H}}}}_2$. Then, the added subreservoir $\varPhi _{2}$ has the reservoir weight matrix ${{\tilde{{\mathbf {W}}}}}_2={{\tilde{{\mathbf {U}}}}}_2{{\tilde{{\mathbf {U}}}}}_2{{\tilde{\mathbf {V}}}}_2$, internal states ${{\tilde{{\mathbf {x}}}}}_2$, input weight matrix ${{\tilde{{\mathbf {W}}}}}_2^{\rm in}$ and internal state matrix ${{\tilde{ {\mathbf {H}}}}}_2$.

Now, the reservoir weight matrix ${\mathbf {W}}_2$ of the reservoir $\varPsi _2$ is constructed as ${\mathbf {W}}_2=\text{ diag }({\bar{{\mathbf {W}}}}_2, \tilde{{\mathbf {W}}}_2)$. Let ${\mathbf {U}}_2=\text{ diag }( {\bar{{\mathbf {U}}}}_2, \tilde{{\mathbf {U}}}_2)$, $\mathbf {V}_2=\text{ diag }({\bar{\mathbf {V}}}_2, \tilde{\mathbf {V}}_2)$, and ${\mathbf {U}}_2=\text{ diag }({\bar{{\mathbf {U}}}}_2, {\tilde{{\mathbf {U}}}}_2)$, then one has ${\mathbf {W}}_2={\mathbf {U}}_2{\mathbf {U}}_2\mathbf {V}_2$, where ${\mathbf {U}}_2$ and $\mathbf {V}_2$ are two orthogonal matrices. Obviously, ${\mathbf {W}}_2$ and ${\mathbf {U}}_2$ have the same singular values which are all smaller than 1. Hence, the sufficient condition for ESP of the DRESN is satisfied [19].

Then, for the network $\varPsi _2$, its internal states ${\mathbf {x}}_2$ and network outputs ${\mathbf {y}}_2$ can be updated as below

$$ \begin{array}{lllllllllll} {\mathbf {x}}_2(k)={\mathbf {f}}\left( \left[ \begin{array}{rr} {\bar{{\mathbf {W}}}}_2 &{} \quad \mathbf {0} \\ \mathbf {0} & \quad \tilde{{\mathbf {W}}}_2 \end{array} \right] \left[ \begin{array}{rr} {\bar{{\mathbf {x}}}}_2(k-1) \\ \tilde{{\mathbf {x}}}_2(k-1) \end{array} \right] +\left[ \begin{array}{rr} {\bar{{\mathbf {W}}}}_2^{\rm in} \\ \tilde{{\mathbf {W}}}^{\rm in}_2 \end{array} \right] {\mathbf {u}}(k) \right) \end{array} $$

(11)

$$\begin{aligned} {\mathbf {y}}_2(k)&= ({\mathbf {W}}^\mathrm{out}_2)^T {\mathbf {X}}_2(k) \end{aligned}$$

(12)

where ${\mathbf {X}}_2(k)=[{\mathbf {x}}_2(k)^T, {\mathbf {u}}(k)^T]^T$. By denoting ${\mathbf {H}}_2=[{\bar{{\mathbf {H}}}}_2, \tilde{{\mathbf {H}}}_2]$ as the internal state matrix of the reservoir $\varPsi _2$, its output weight matrix ${\mathbf {W}}^\mathrm{out}_2$ can be calculated by

$$ {\mathbf{W}}_{2}^{{{\text{out}}}} = (C{\mathbf{I}} + {\mathbf{H}}_{2}^{T} {\mathbf{H}}_{2} )^{{ - 1}} {\mathbf{H}}_{2}^{T} {\mathbf{T}} $$

(13)

with

$$\begin{aligned} (C{\mathbf {I}}+{\mathbf {H}}_{2}^T{\mathbf {H}}_{2})^{-1} & = \left( C{\mathbf {I}}+\left[ \begin{array}{rr} {\bar{{\mathbf {H}}}}_{2}^T \\ \tilde{{\mathbf {H}}}^T_2 \end{array} \right] \left[ \begin{array}{rr} {\bar{{\mathbf {H}}}}_{2} &{} \tilde{{\mathbf {H}}}_2 \end{array} \right] \right) ^{-1} \\ &= \left[ \begin{array}{rr} {\bar{{\mathbf {H}}}}^T_{2}{\bar{{\mathbf {H}}}}_{2}+C{\mathbf {I}} & \quad {\bar{{\mathbf {H}}}}^T_{2} \tilde{{\mathbf {H}}}_2\\ \tilde{{\mathbf {H}}}^T_2 {\bar{{\mathbf {H}}}}_{2} & \quad \tilde{{\mathbf {H}}}^T_2 \tilde{{\mathbf {H}}}_2+C{\mathbf {I}} \end{array} \right] ^{-1}\\ &\triangleq \left[ \begin{array}{rr} {\mathbf {A}}_1 & \quad {\mathbf {A}}_2\\ {\mathbf {A}}^T_2 & \quad {\mathbf {A}}_3 \end{array} \right] ^{-1} \end{aligned}$$

(14)

where

$$ \begin{aligned} {\mathbf{A}}_{1} & = \overline{{\mathbf{H}}} _{2}^{T} \overline{{\mathbf{H}}} _{2} + C{\mathbf{I}} \\ {\mathbf{A}}_{2} & = \overline{{\mathbf{H}}} _{2}^{T} \widetilde{{\mathbf{H}}}_{2} \\ {\mathbf{A}}_{3} & = \widetilde{{\mathbf{H}}}_{2}^{T} \widetilde{{\mathbf{H}}}_{2} + C{\mathbf{I}} \\ \end{aligned} $$

(15)

Because $C{\mathbf {I}}+{\mathbf {H}}_{2}^T{\mathbf {H}}_{2}$ is symmetric, its inverse matrix $(C{\mathbf {I}}+{\mathbf {H}}_{2}^T{\mathbf {H}}_{2})^{-1}$ is symmetric too. If one denotes that

$$ \begin{aligned} (C{\mathbf {I}}+{\mathbf {H}}_{2}^T{\mathbf {H}}_{2})^{-1}=\left[ \begin{array}{rr} {\mathbf {Q}}_1 &{} {\mathbf {Q}}_2\\ {\mathbf {Q}}^T_2 &{} {\mathbf {Q}}_3 \end{array} \right] \end{aligned}$$

(16)

Since

$$ \begin{aligned} {\mathbf{I}} & = \left[ {\begin{array}{*{20}r} \hfill {{\mathbf{A}}_{1} } & \hfill {{\mathbf{A}}_{2} } \\ \hfill {{\mathbf{A}}_{2}^{T} } & \hfill {{\mathbf{A}}_{3} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}r} \hfill {{\mathbf{Q}}_{1} } & \hfill {{\mathbf{Q}}_{2} } \\ \hfill {{\mathbf{Q}}_{2}^{T} } & \hfill {{\mathbf{Q}}_{3} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}r} \hfill {{\mathbf{A}}_{1} {\mathbf{Q}}_{1} + {\mathbf{A}}_{2} {\mathbf{Q}}_{2}^{T} } & \hfill {{\mathbf{A}}_{1} {\mathbf{Q}}_{2} + {\mathbf{A}}_{2} {\mathbf{Q}}_{3} } \\ \hfill {{\mathbf{A}}_{2}^{T} {\mathbf{Q}}_{1} + {\mathbf{A}}_{3} {\mathbf{Q}}_{2}^{T} } & \hfill {{\mathbf{A}}_{2}^{T} {\mathbf{Q}}_{2} + {\mathbf{A}}_{3} {\mathbf{Q}}_{3} } \\ \end{array} } \right] \\ \end{aligned} $$

(17)

Based on the inversion of $2\times 2$ block matrices [24], we have

$$ \begin{aligned} {\mathbf{Q}}_{1} & = {\mathbf{A}}_{1}^{{ - 1}} + {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} \left( {{\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} } \right)^{{ - 1}} \left( {{\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} } \right)^{T} \\ {\mathbf{Q}}_{2} & = - {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} ({\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{{ - 1}} \\ {\mathbf{Q}}_{3} & = {\mathbf{A}}_{1}^{{ - 1}} + {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} \left( {{\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} } \right)^{{ - 1}} \left( {{\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} } \right)^{T} \\ \end{aligned} $$

(18)

Then one has

$$ \begin{aligned} (C{\mathbf{I}} + {\mathbf{H}}_{2}^{T} {\mathbf{H}}_{2} )^{{ - 1}} {\mathbf{H}}_{2}^{T} & = \left[ {\begin{array}{*{20}r} \hfill {{\mathbf{Q}}_{1} } & \hfill {{\mathbf{Q}}_{2} } \\ \hfill {{\mathbf{Q}}_{2}^{T} } & \hfill {{\mathbf{Q}}_{3} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}r} \hfill {\overline{{\mathbf{H}}} _{2}^{T} } \\ \hfill {\widetilde{{\mathbf{H}}}_{2}^{T} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}r} \hfill {{\mathbf{Q}}_{1} \overline{{\mathbf{H}}} _{2}^{T} + {\mathbf{Q}}_{2} \widetilde{{\mathbf{H}}}_{2}^{T} } \\ \hfill {{\mathbf{Q}}_{2}^{T} \overline{{\mathbf{H}}} _{2}^{T} + {\mathbf{Q}}_{3} \widetilde{{\mathbf{H}}}_{2}^{T} } \\ \end{array} } \right] \\ & \triangleq \left[ {\begin{array}{*{20}r} \hfill {\mathbf{M}} \\ \hfill {\mathbf{P}} \\ \end{array} } \right] \\ \end{aligned} $$

(19)

If we denote

$$ {\mathbf{D}} = (C{\mathbf{I}} + \overline{{\mathbf{H}}} _{2}^{T} \overline{{\mathbf{H}}} _{2} )^{{ - 1}} \overline{{\mathbf{H}}} _{2}^{T} $$

(20)

By substituting Eqs. (15) and (18) to (11), one has

$$ \begin{aligned} {\mathbf{P}} & = - ({\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{{ - 1}} ({\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{T} \overline{{\mathbf{H}}} _{2}^{T} \\ & \quad + ({\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{{ - 1}} \widetilde{{\mathbf{H}}}_{2}^{T} \\ & = ({\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{{ - 1}} (\widetilde{{\mathbf{H}}}_{2}^{T} - (\overline{{\mathbf{H}}} _{2}^{T} \widetilde{{\mathbf{H}}}_{2} )^{T} \\ & \quad (\overline{{\mathbf{H}}} _{2}^{T} \overline{{\mathbf{H}}} _{2} + C{\mathbf{I}})^{{ - 1}} \overline{{\mathbf{H}}} _{2}^{T} ) \\ & = (C{\mathbf{I}} + \widetilde{{\mathbf{H}}}_{2}^{T} ({\mathbf{I}} - \overline{{\mathbf{H}}} _{2} {\mathbf{D}})\widetilde{{\mathbf{H}}}_{2} )^{{ - 1}} \widetilde{{\mathbf{H}}}_{2}^{T} ({\mathbf{I}} - \overline{{\mathbf{H}}} _{2} {\mathbf{D}}) \\ \end{aligned} $$

(21)

$$ \begin{aligned} {\mathbf{M}} & = {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} ({\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{{ - 1}} ({\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{T} \overline{{\mathbf{H}}} _{2}^{T} \\ & \quad + {\mathbf{A}}_{1}^{{ - 1}} \overline{{\mathbf{H}}} _{2}^{T} - {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} ({\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{{ - 1}} \widetilde{{\mathbf{H}}}_{2}^{T} \\ & = {\mathbf{D}} + {\mathbf{D}}\widetilde{{\mathbf{H}}}_{2} ({\mathbf{A}}_{3} - {\mathbf{A}}_{2}^{T} {\mathbf{A}}_{1}^{{ - 1}} {\mathbf{A}}_{2} )^{{ - 1}} \widetilde{{\mathbf{H}}}_{2}^{T} (\overline{{\mathbf{H}}} _{2} {\mathbf{D}} - {\mathbf{I}}) \\ & = {\mathbf{D}}({\mathbf{I}} - \widetilde{{\mathbf{H}}}_{2} {\mathbf{P}}) \\ \end{aligned} $$

(22)

It implies that the output weight matrix ${\mathbf {W}}^{\rm out}_2$ of the network ${\varPsi }_2$ can be calculated according to Eqs. (21) and (22).

3.1 The design procedures of DRESN

For a given training data set $\{ ({\mathbf {u}}(k),{\mathbf {t}}(k)) \mid {\mathbf {u}}(k) \in {\mathbb {R}}^n, {\mathbf {t}}(k) \in {\mathbb {R}}^m, k=1,2,\ldots , L \}$, the activation function ${\mathbf {f}}(\cdot )$ and the maximum algorithm iteration $g_{max}$, the main design steps of the DRESN are described as follows

• Step 1 Let $g=1$. Initialize a subreservoir ${\varPsi }_{1}$ with $N_{1}$ nodes, where $N_{1}$ is a predefined integer. Randomly design the diagonal matrix ${\mathbf {{S}}}_1=\text{ diag }\{\sigma _1, \sigma _2, \ldots , \sigma _{N_1}\}$ and two orthogonal matrices ${\mathbf {{U}}}_1=(u_{ij})_{N_1 \times N_1}$, ${\mathbf {{V}}}_1=(v_{ij})_{N_1 \times N_1}$, where $0<\sigma _i<1\;(i=1,2,\ldots ,N_1)$, $u_{ij}$ and $v_{ij}, (i,j=1,2,\ldots ,N_1)$ are chosen from the range $(-\,1,1)$. Set the reservoir weight matrix of the subreservoir ${\varPsi }_{1}$ as ${{\mathbf {{W}}}}_1=\mathbf {{U}}_1{\mathbf {{S}}}_1\mathbf {{V}}_1$. Then, randomly generate the input weight matrix ${{\mathbf {{W}}}}^{\rm in}_1$ according to any continuous probability distribution. Drive the subreservoir ${\varPsi }_{1}$ by the input signals as shown in Eq. (1) to obtain the echo states ${\mathbf {{x}}}_1$. By combining ${\mathbf {{X}}}_1(k)=[\mathbf {{x}}_1(k)^T, {\mathbf {u}}(k)^T]^T$ where $k=1,2,\ldots ,L$, one can collect the internal state matrix ${\mathbf {{H}}}_1=[{\mathbf {{X}}}_1(1), {\mathbf {{X}}}_1(2), \ldots , {\mathbf {{X}}}_1(L)]^T$. Furthermore, calculate the output weight ${\mathbf {{W}}}^{\rm out}_{1}=(C{\mathbf {I}}+{\mathbf {H}}^T_{1}{\mathbf {H}}_1)^{-1}{\mathbf {H}}^T_{1}{\mathbf {T}}$ and the residual error $E({{\varPsi }}_{1})=\Vert {\mathbf {H}}_{1}{\mathbf {W}}^{\rm out}_{1}-{\mathbf {T}} \Vert _2^2+C\Vert {\mathbf {W}}^{\rm out}_{1}\Vert _2^2$. Next, set $g=g+1$.

• Step 2 At the gth iteration, one needs generate a temporary network ${\psi }_g$ by performing the following procedures with a predefined integer $N_{g1}$. Now, initialize $p=1$. (I) If $p N_{g1}<N_{g-1}$, randomly generate an ESN ${{\varPsi }}_{gp}$ with $N_{gp}=p N_{g1}$ reservoir nodes. Set the reservoir weight matrix of ${{\psi }}_{gp}$ as ${\mathbf {{W}}}_{gp}={\mathbf {{U}}}_{gp}{\mathbf {{S}}}_{gp}{\mathbf {{V}}}_{gp}$, where ${\mathbf {{S}}}_{gp}=\text{ diag }\{\sigma _1, \sigma _2, \ldots , \sigma _{N_{gp}}\}$ is a diagonal matrix with $0<\sigma _i<1\;(i=1,2,\ldots ,N_{gp})$, ${\mathbf {{U}}}_{gp}=(u_{ij})_{N_{gp} \times N_{gp}}$ and ${\mathbf {{V}}}_{gp}=(v_{ij})_{N_{gp} \times N_{gp}}$ are orthogonal matrices in which $u_{ij}$ and $v_{ij}\; (i,j=1,2,\ldots ,N_{gp})$ are chosen from the range $(-\,1,1)$. Then, randomly generate the input weight matrix ${\mathbf {{W}}}^{\rm in}_{gp}$. Next, drive the network ${{\psi }}_{gp}$, collect the internal state matrix ${\mathbf {H}}_{gp}$, calculate the output weight matrix ${\mathbf {{W}}}^{\rm out}_{gp}$ as Eq. (9) and residual error $E({{\psi }}_{gp})$ as Eq. (10). (II) Compare $E({{\psi }}_{gp})$ and $E({{\varPsi }}_{g-1})$, if $E({\psi }_{gp})\le E(\varPsi _{g-1})$, set ${\psi }_{gp}$ as the temporary network ${\psi }_g$, turn to Step III; Otherwise, let $p=p+1$, go to Step I. (III) For the temporary network ${\psi }_g$, record its reservoir weight matrix ${\bar{{\mathbf {W}}}}_g$, internal states ${\bar{{\mathbf {x}}}}_g$, input weight matrix ${\bar{{\mathbf {W}}}}_g^{\rm in}$ and internal state matrix ${\bar{{\mathbf {H}}}}_g$.

• Step 3 Generate a subreservoir ${\varPhi }_{g}$ with $N_{g2}$ reservoir nodes by using the SVD method as shown in Step 1, and provide its reservoir weight matrix $\tilde{W}_{g}$ and input weight matrix $\tilde{W}^{\rm in}_{g}$. Then, drive the network to collect the internal state matrix $\tilde{{\mathbf {H}}}_g$ and calculate the output weight matrix ${{\tilde{{\mathbf {W}}}}}^{\rm out}_g$ as Eq. (9).

• Step 4 Add the subreservoir ${\varPhi }_{g}$ into $\psi _{g}$ to obtain the subreservoir ${\varPsi }_{g}$. Update the output weight matrix ${\mathbf {W}}^{\rm out}_{g}$ of ${\varPsi }_{g}$ as below

  $$ \begin{aligned} {\mathbf{D}}_{g} & = (C{\mathbf{I}} + \overline{{\mathbf{H}}} _{g}^{T} \overline{{\mathbf{H}}} _{g} )^{{ - 1}} \overline{{\mathbf{H}}} _{g}^{T} \\ {\mathbf{P}}_{g} & = (C{\mathbf{I}} + \widetilde{{\mathbf{H}}}_{g}^{T} ({\mathbf{I}} - \overline{{\mathbf{H}}} _{g} {\mathbf{D}}_{g} )\widetilde{{\mathbf{H}}}_{g} )^{{ - 1}} \widetilde{{\mathbf{H}}}_{g}^{T} ({\mathbf{I}} - \overline{{\mathbf{H}}} _{g} {\mathbf{D}}_{g} ) \\ {\mathbf{M}}_{g} & = {\mathbf{D}}_{g} ({\mathbf{I}} - \widetilde{{\mathbf{H}}}_{g} {\mathbf{P}}_{g} ) \\ {\mathbf{W}}_{g}^{{{\text{out}}}} & = \left[ {\begin{array}{*{20}r} \hfill {{\mathbf{M}}_{g} } \\ \hfill {{\mathbf{P}}_{g} } \\ \end{array} } \right] \\ \end{aligned} $$

  (23)

• Step 5 Update the weight matrices and internal state matrix of ${\varPsi }_{g}$ as follows

  $$ \begin{aligned} {\mathbf{W}}_{g}^{{{\text{in}}}} & = \left[ {\begin{array}{*{20}r} \hfill {\overline{{\mathbf{W}}} _{g}^{{{\text{in}}}} } \\ \hfill {\widetilde{{\mathbf{W}}}_{g}^{{{\text{in}}}} } \\ \end{array} } \right] \\ {\mathbf{W}}_{g} & = {\text{diag }}(\overline{{\mathbf{W}}} _{g} ,\widetilde{{\mathbf{W}}}_{g} ) \\ {\mathbf{H}}_{g} & = [\overline{{\mathbf{H}}} _{g} ,\widetilde{{\mathbf{H}}}_{g} ] \\ \end{aligned} $$

  (24)

• Step 6 Increase $g=g+1$. If g reaches to the maximum iteration $g_{max}$, the algorithm stops; otherwise, go to Step 2.

Remark 1

Compared with the ESNs whose reservoir nodes are recurrently added [19], or the ESNs whose existing reservoir nodes are recurrently deleted [14, 17, 18], the structure of DRESN will be either unchanged or replaced completely by a new network. At the gth ($g>1$) iteration of DRESN, the residual errors of all the possible candidates $\{{\psi }_{g1}, {\psi }_{g2}, \ldots , {\psi }_{gq}, \varPsi _{g-1} \}$ are compared, where $q=fix(N_{g-1}/ N_{g1})$¹. Then, among those networks with the smallest residual error, the one with the most compact structure is selected as the temporary network $\psi _{g}$. Specifically, if the network $\varPsi _{g-1}$ performs good enough, it will be retained to the next iteration; this means that no reservoir nodes are added or removed. Otherwise, $\varPsi _{g-1}$ will be replaced by the temporary network $\psi _{g}$, this operation implies that the existing structure of the network $\varPsi _{g-1}$ is completely replaced.

Remark 2

In DRESN, at the gth ($g>1$) iteration, if the temporary network $\psi _{g}$ is not generated, then the current network $\varPsi _{g}$ is obtained by adding the subreservoir $\varPhi _{g}$ into the existing network $\varPsi _{g-1}$. If the value of C in Eq. (23) is set as 0 simultaneously, the DRESN becomes the GESN model [19]. Thus, one can conclude that the GESN is just a special case of DRESN which only has the growing procedure without the replacing process; meanwhile, the value of C in Eq. (23) equals to 0.

3.2 The convergence analysis of DRESN

In this part, the convergence of the proposed DRESN is analyzed. Firstly, two lemmas are given for the proof of the convergence theorem.

Lemma 1

([19]) Given an ESN withNreservoir units, the sigmoidal activation function and a training sequence$\{ ({\mathbf {u}}(k), {\mathbf {t}}(k)) \mid {\mathbf {u}}(k) \in {\mathbb {R}}^n, {\mathbf {t}}(k) \in {\mathbb {R}}^m, k=1,2,\ldots , L \}$, if${\mathbf {W}}^{\rm in}\in {\mathbb {{R}}} ^{N\times n}$and${\mathbf {W}}\in {\mathbb {R}}^{N\times N}$are randomly generated according to any continuous probability distribution, then its internal state matrix${\mathbf {H}}$can be made column full rank with probability one.

Lemma 2

Given an ESN with$g_1$reservoir units, the sigmoidal activation function and a training sequence$\{ ({\mathbf {u}}(k), {\mathbf {t}}(k)) \mid {\mathbf {u}}(k) \in {\mathbb {R}}^n, {\mathbf {t}}(k) \in {\mathbb {R}}^m, k=1,2,\ldots , L \}$, denote${\bar{{\mathbf {H}}}}_g$as its corresponding internal state matrix. If a subreservoir with$g_2$nodes are added into the ESN, the new internal state matrix becomes${\mathbf {H}}_g=[{\bar{{\mathbf {H}}}}_g, \tilde{{\mathbf {H}}}_g]$, where$\tilde{{\mathbf {H}}}_g$is the internal state matrix of the added subreservoir. Define$E(\mathbf {\varPsi })=\Vert {\mathbf {H}}{\mathbf {W}}^{\rm out}-{\mathbf {T}} \Vert _2^2+C\Vert {\mathbf {W}}^{\rm out}\Vert _2^2$as the residual error function of the network$\varPsi$with${\mathbf {H}}$, then one has$E({\mathbf {H}}_g)\le E({\bar{{\mathbf {H}}}}_g)$.

Proof

Under the assumption that ${\mathbf {{W}}}^{\rm out}_g$ be the least square solution of $\min \nolimits _{{\mathbf {{W}}}^{\rm out}_g}(\Vert {\mathbf {H}}_g{\mathbf {W}}^{\rm out}_g-{\mathbf {T}} \Vert _2^2+C\Vert {\mathbf {W}}^{\rm out}_g\Vert _2^2)$, then one has

$$ \begin{aligned} E({\mathbf{H}}_{g} ) & = \left\| {{\mathbf{H}}_{g} {\mathbf{W}}_{g}^{{{\text{out}}}} - {\mathbf{T}}} \right\|_{2}^{2} + C\left\| {{\mathbf{W}}_{g}^{{{\text{out}}}} } \right\|_{2}^{2} \\ & = \left\| {[{\bar{{\mathbf {H}}}}_g ,\;{\tilde{\mathbf{H}}}_g ]{\mathbf{W}}_{g}^{{{\text{out}}}} - {\mathbf{T}}} \right\|_{2}^{2} + C\left\| {{\mathbf{W}}_{g}^{{{\text{out}}}} } \right\|_{2}^{2} \\ & \le \left\| {[{\bar{{\mathbf {H}}}}_g ,\;{\tilde{\mathbf{H}}}_g ][({\bar{\mathbf{W}}}_{g}^{{{\text{out}}}} )^{T} ,0]^{T} - {\mathbf{T}}} \right\|_{2}^{2} \\ & \quad + C\left\| {[({\bar{\mathbf{W}}}_{g}^{{{\text{out}}}} )^{T} ,0]^{T} } \right\|_{2}^{2} \\ & = \left\| {{\bar{{\mathbf{H}}}}_g {\bar{\mathbf{W}}}_{g}^{{{\text{out}}}} - {\mathbf{T}}} \right\|_{2}^{2} + C\left\| {{\bar{\mathbf{W}}}_{g}^{{{\text{out}}}} } \right\|_{2}^{2} \\ & = E({\bar{{\mathbf{H}}}}_g) \\ \end{aligned} $$

(25)

It means that the residual error decreases monotonously when some reservoir nodes are added into the existing ESN. Thus, the proof is completed. $\square$

Next, based on Lemmas 1 and 2, the convergence of the proposed DRESN will be theoretically analyzed.

Theorem 1

In DRESN, define$E(\varPsi _{g})=\Vert {\mathbf {H}}_g{\mathbf {W}}^{\rm out}_g-{\mathbf {T}} \Vert _2^2+C\Vert {\mathbf {W}}^{\rm out}_g\Vert _2^2$as the residual error function of the obtained$\varPsi _{g}$at thegth iteration, where${\mathbf {H}}_g$is the internal state matrix, then for a given training sequence$\{ ({\mathbf {u}}(k),{\mathbf {t}}(k)) \mid {\mathbf {u}}(k) \in {\mathbb {R}}^n, {\mathbf {t}}(k) \in {\mathbb {R}}^m, k=1,2,\ldots , L \}$and an arbitrary positive value$\epsilon >0$, there exists a positive integerKsuch that$E(\varPsi _{K})<\epsilon$.

Proof

To make the proof readable, $\{\psi _{g}\}$ and $\{\varPsi _{g}\}$ with $g>1$ are used to represent the temporary network sequence and the generated network sequence, respectively. Their corresponding residual error sequences are denoted as $\{E(\psi _{g})\}$ and $\{E(\varPsi _{g})\}$, respectively.

According to the design procedures of DRESN, at the gth iteration, the performance of the temporary network $\psi _{g}$ is always better or equals to that of $\varPsi _{g-1}$; thus, one has

$$\begin{aligned} E(\psi _g)\le E(\varPsi _{g-1}) \end{aligned}$$

(26)

On the other hand, since the network $\varPsi _{g}$ is obtained by adding some reservoir nodes into $\varPsi _g$, based on Lemma 2, we can have

$$\begin{aligned} E(\varPsi _{g})\le E(\psi _{g}) \end{aligned}$$

(27)

By combining Eqs. (26) and (27), one can obtain

$$\begin{aligned} E(\varPsi _g)\le \cdots \le E(\varPsi _2) \le E(\varPsi _1) \end{aligned}$$

(28)

According to Lemma 1, when $N_1+\sum _{i=2}^K N_{i2}=L$, ${\mathbf {H}}_K$ is invertible with probability one; thus, one has

$$\begin{aligned} E(\varPsi _K)=0 \end{aligned}$$

(29)

This means that there exists a positive integer K such that $N_1+\sum _{i=2}^K N_{i2}< L$ and $E(\psi _K)< \epsilon$. This completes the proof. $\square$

4 Simulation results and discussion

To demonstrate the effectiveness of the proposed DRESN, four time series prediction examples are discussed, including the Lorenz time series prediction [30], the Mackey–Glass time series prediction [29], the nonlinear autoregressive moving average (NARMA) system identification [31] and the NH$_4$–N concentration prediction in the wastewater treatment process (WWTP). The performance of DRESN is compared with some existing ESNs, including the original ESN (OESN) [8], the ridge regression-based ESN (RESN) [17], the growing ESN (GESN) [19], the ESN whose readout connections are pruned by the least angle regression algorithm (ESN-LAR) [17] and the ESN whose parameters are optimized by the differential evolutionary algorithm (ESN-DE) [16].

To be consistent with previous ESNs [19], the input weighs ${\mathbf {W}}^{\rm in}$ of all models are randomly generated from the range $[-\,0.1,0.1]$ without posterior scaling. For OESN, RESN and ESN-LAR, the original reservoir size, spectral radius and sparsity are optimized via the grid search as shown in Appendix A. For ESN-DE, the parameters of DE algorithm are given in Appendix A, they are same as the original paper [16]. For GESN and DRESN, the singular values of the subreservoir weight matrix are randomly chosen from the range [0.1, 0.99]. Moreover, the value of C in RESN, and values of C, $N_{g1}$, $N_{g2}$ in DRESN are tuned by the grid search strategy. A total of 11 values of $C\; (2^{-9}, 2^{-7}, \ldots , 2^7, 2^{9} )$, 5 values of $N_{g1}\;(5, 10, \ldots , 25)$ and 5 values of $N_{g2}\;(3, 5, \ldots , 11)$ are used during the grid search process. Furthermore, the sigmoid function $f(x)=1/(1+e^{-x})$ is employed as the activation function for reservoir nodes. It is noted that all the simulation results are carried out in MATLAB 2014 environment and the same PC with Intel Core i5 2.27 GHZ CPU and 4 GB RAM.

The training and testing performance of ESN is measured by the normalized root mean square error (NRMSE for short), which is defined as below [8]

$$\begin{aligned} \mathrm {NRMSE}&= \sqrt{\sum _{k=1}^{{L}} \frac{({\mathbf {t}}(k)-{{\mathbf {y}}}(k))^2}{{L}\cdot \theta ^2}} \end{aligned}$$

(30)

where ${\mathbf {y}}(k)$ and ${\mathbf {t}}(k)$ are the kth ESN output and the desired output, respectively; $\theta ^2$ denotes the variance of ${\mathbf {t}}(k)$. The smaller NRMSE value means better performance.

4.1 Lorenz time series prediction

As a chaotic dynamical time series, the Lorenz system is governed by the following equations [30]

$$ \begin{aligned} \frac{{{\text{d}}x}}{{{\text{d}}k}} & = a( - x + y) \\ \frac{{{\text{d}}y}}{{{\text{d}}k}} & = bx - y - xz \\ \frac{{{\text{d}}z}}{{{\text{d}}k}} & = xy - cz \\ \end{aligned} $$

(31)

where the parameters are set as $a=10$, $b=28$ and $c=8/3$. The Runge–Kutta method with step 0.01 is introduced to generate the Lorenz system; then the y-dimension samples are used for the time series prediction. 1200 samples with $k\in [1, 1200]$ are employed to train the ESN, and the first 200 sample are washed out to reduce the influence of reservoir initial state on solution of Eqs. (5) or (9). Subsequently, 1000 new samples with $k\in [1201, 2200]$ are generated to test the ESN model.

With the parameters as listed in Table 1, the training performance and network complexity of DRESN are analyzed and compared with GESN. In Fig. 2, the average training NRMSE values of 50 independent runs versus algorithm iterations are shown. It can be easily found that the training error of DRESN decreases monotonously when new reservoir nodes are added, which is in accord with Lemma 2 in Sect. 2.2. Moreover, the learning performance of DRESN is always better or comparable to GESN in each iteration, which is in accord with Remark 2 in Sect. 2.2. On the other hand, according to the updating progress of reservoir nodes number as shown in Fig. 3, the network architecture of DRESN is more compact than GESN. The reason is that the reservoir nodes of GESN are added group by group; thus, $100*5=500$ reservoir nodes are obtained eventually after 100 algorithm iterations, while the reservoir nodes number of DRESN is automatically determined through its internal growing and updating mechanism. According to Figs. 2 and 3, one can conclude that the proposed DRESN can obtain better learning performance and lower network complexity than GESN in solving the Lorenz system identification problem.

Fig. 2

The average training NRMES values of 50 independent runs versus iterations for DRESN and GESN

Fig. 3

The reservoir nodes number updating progress for DRESN and GESN

Table 1 Some parameters and simulation results of different ESNs for Lorenz time series prediction

To evaluate the testing performance, the prediction outputs and prediction errors obtained by OESN, GESN and DRESN are shown in Fig. 4, respectively. It is obvious that the proposed DRESN has the smallest prediction error range $[-\,0.033,0.01]$. This observation implies that the DRESN has better testing performance than OESN and GESN, which is also verified by the training NRMSE values as shown in Table 1 (the training NRMSE values of DRESN, OESN and GESN are $7.91\times 10^{-4}$, $9.65\times 10^{-3}$ and $3.28\times 10^{-3}$, respectively).

Fig. 4

The prediction and error curve produced by OESN, GESN and DRESN for Lorenz time series prediction. a The prediction curve versus time step k; b the prediction error versus time step k

The comparisons between DRESN and other existing ESNs are shown in Table 1, including the network complexity, the mean and standard deviation (std. for short) of training and testing NRMSE values, as well as the training time which contains the time to optimize network parameters. It is easily found that the OESN has the worst training and testing NRMSE values with too large reservoir size (800 reservoir nodes), while for the regularization technique-based ESNs, such as RESN and DRESN, the testing NRMSE values are always better than OESN, which demonstrates the validity of the $l_2$ penalty regression in the formula (6). In ESN-LAR model, even though some redundant output weights are delated, the prediction performance is only slightly improved than the OESN. Furthermore, it can be seen that the DRESN can obtain the best training and testing NRMSE values simultaneously; however, it needs longer training time than other ESNs except for the ESN-DE. This observation is reasonable, since the DRESN requires more time to seek for the most appropriate network architecture from all the possible candidates in each algorithm iteration.

Remark 3

For the Lorenz time series prediction problem, the training NRMSE decreasing trends and the reservoir nodes updating process versus algorithm iterations are given in Figs. 2 and 3, respectively. Since the similar curves could also be obtained for the rest three cases, including the Mackey–Glass system prediction, the NARMA system identification and the effluent NH$_4$–N concentration prediction in WWTP, their corresponding figures and analysis are not given due to page limitation.

4.2 Mackey–Glass system prediction

The Mackey–Glass time series is a standard benchmark model for time series prediction, on which the ESNs have shown good prediction performance [29]. It can be derived by the following differential equation

$$ \frac{{{\text{d}}x(k)}}{{{\text{d}}k}} = \frac{{ax(k - \tau )}}{{1 + x^{{10}} (k - \tau )}} + bx(k) $$

(32)

where $a=0.2$, $b=-\,0.1$ and $\tau =17$. In this experiment, 1200 data points with $k\in [1, 1200]$ are chosen as the training dataset and the first 200 samples are washed out, and then 1000 data points with $k\in [1201, 2200]$ are treated as the testing dataset.

For the Mackey–Glass time series, the predicted results produced by the OESN, GESN and DRESN are given in Fig. 5a, and the corresponding prediction errors are presented in Fig. 5b. Obviously, the DRESN shows more accurate prediction of the targets than OESN and GESN.

Fig. 5

The prediction and error curve produced by OESN, GESN and DRESN for Mackey–Glass system prediction. a The prediction curve versus time step k; b the prediction error versus time step k

In [29], Jaeger has proposed that the prediction and target outputs of the Mackey–Glass time series after 84 steps can be used to evaluate the performance of ESN; thus, the normalized root mean square error at the 84th time step (i.e., NRMSE$_{84}$) is described as below

$$\begin{aligned} \mathrm {NRMSE}_{84}&= \sqrt{\sum _{i=1}^{100} \frac{({\mathbf {y}}_i(84)-{{\mathbf {t}}}_i(84))^2}{100\cdot \sigma ^2}} \end{aligned}$$

(33)

where ${\mathbf {y}}_i(84)$ and ${{\mathbf {t}}}_i(84)$ are the predicted and desired output at the 84th time step of the ith independent run, respectively; $\sigma ^2$ is the variance of the Mackey–Glass signal. To compare the performance of the proposed DRESN and other ESNs, 50 independent simulations are conducted on the same sequence. The selected parameters and the detailed results of all ESNs are listed in Table 2. Compared with GESN, an approximation of 50% computational overhead is needed in DRESN since the subreservoir searching process is implemented. Furthermore, the mean and standard deviation of the testing NRMSE$_{84}$ values by the DRESN are the lowest; meanwhile, the reservoir size of DRESN is the smallest. These observations imply that the DRESN is a favorite model for Mackey–Glass time series prediction problem, since it presents more accurate prediction accuracy than other evaluated ESNs with relatively compact network topology.

Table 2 Some parameters and simulation results of different ESNs for Mackey–Glass system prediction

4.3 NARMA system identification

The NARMA system is difficult to be identified due to its nonlinearity and long memory. The 10-order NARMA system with time delay is given as below [31]

$$ \begin{aligned} x(k + 1) & = 0.3x(k) + 0.05x(k)\left( {\sum\limits_{{i = 1}}^{9} x (k - i)} \right) \\ & \quad + 1.5u(k - 9)u(k) + 0.1 \\ \end{aligned} $$

(34)

where u(k) is randomly chosen from the range [0, 1] and x(k) is initialized as 0 for $k=1,2,\ldots ,10$. This system is widely used to check the identification performance of neural networks [31]. In the training stage, 1200 samples with $k\in [1, 1200]$ are used and the first 200 samples are discarded to washout initial transient. In the testing process, 1000 samples with $k\in [1201, 2200]$ are employed.

The prediction result and error curve of x(k) produced by OESN, GESN and DRESN are presented in Fig. 6. It is noted that to see the figures more clearly, only the first 200 points of the testing sequence are shown in Fig. 6. The prediction errors of DRESN are limited between − 0.004 and 0.004 in most data points, while the prediction errors of GESN and OESN lie in the range $[-\,0.005, 0.008]$ and $[-\,0.008, 0.009]$, respectively. These observations mean that the proposed DRESN has better identification performance than OESN and GESN in this experiment.

Fig. 6

The prediction and error curve produced by OESN, GESN and DRESN for NARMA system prediction. a The prediction curve versus time step k; b the prediction error versus time step k

The parameter settings and simulation results of all the ESNs are listed in Table 3. Compared with OESN, it can be seen that the RESN and DRESN have much better testing performance, which demonstrates the validity of $l_2$ penalty term in Eq. (6). Obviously, among all the algorithms, the DRESN could obtain the most compact reservoir structure and the smallest testing NRMSE value. Furthermore, the standard deviations of testing NRMSE value of DRESN are the smallest, which illustrates the robustness of the proposed algorithm.

Table 3 Some parameters and simulation results of different ESNs for NARMA system prediction

4.4 Effluent NH$_4$–N concentration prediction in the WWTP

Recently, the water pollution has become a serious environmental problem due to the discharge of nutrients. Among all the effluent parameters, the NH$_4$–N concentration is an important parameter to evaluate the water quality of wastewater treatment process (WWTP). However, the WWTP is a typical nonlinear system with complex biochemical reaction; thus, the values of the effluent NH$_4$–N concentration is difficult to measure [32]. In this experiment, the ESNs are used to predict the effluent NH$_4$–N concentration of the WWTP. Some easily measured effluent parameters of WWTP are chosen as the input variables, including the temperature, oxidation reduction potential, dissolved oxygen, total soluble solid and pH values. Furthermore, the utilized data were obtained from January 2016 to October 2017 from a real WWTP in Beijing, China. After delating the abnormal data, 2464 samples were retained. 1400 data are treated as the training set in which the first 300 values are discarded to reduce the initial transient, and then the remaining 1064 values are used for testing.

The prediction outputs and error curve of the effluent NH$_4$–N obtained by OESN, GESN and DRESN are shown in Fig. 7a, b, respectively. The prediction errors of DRESN are limited into the range $[-\,0.6,0.7]$, while the prediction errors of OESN and GESN lie into the range $[-\,1.3,1.8]$ and $[-\,1,1.5]$, respectively. This fact means that both GESN and DRESN can predict the complicate dynamics of the effluent NH$_4$–N well except few data points, while the DRESN has better prediction performance.

Fig. 7

The prediction and error curve produced by OESN, GESN and DRESN for effluent NH$_4$–N concentration prediction. a The prediction curve versus time step k; b the prediction error versus time step k

For the effluent NH$_4$–N prediction, the parameters of all the ESNs and their corresponding simulation results are shown in Table 4. It is easily found that among all the evaluated ESNs, the DRESN obtains the best testing accuracy and the smallest network complexity when C takes the value $2^{-7}$. This observation implies that the proposed DRESN is a suitable tool to capture the complex dynamics of WWTP.

Table 4 Some parameters and simulation results of different ESNs for effluent NH$_4$–N concentration prediction

4.5 Discussion and future work

Based on above simulation results, it is easily concluded that the proposed DRESN outperforms other evaluated ESNs in terms of prediction accuracy and network complexity. Actually, the DRESN can be viewed as an improvement of the OESNs from the view of network architecture. Firstly, in DRESN, the subreservoirs are used rather than the single reservoir; thus, the coupling effects in a single reservoir are reduced to some extent. Secondly, the output weights of DRESN are updated by the error minimization-based method and regularization technique, which could overcome the ill-posed problem. Thirdly, the reservoir size of DRESN is automatically designed by the given task, which may avoid the overfitting problem. It should be noted that the proposed DRESN requires more training time than other evaluated ESNs except for the ESN-DE. This fact is reasonable since the DRESN needs more time to seek for the most appropriate network from all the possible candidates at each step, another reason is that the selection process of the $l_2$ penalty parameter C in Eq. (6) still spends some training time.

For DRESN and GESN, there are two common points. Firstly, a subreservoir is generated and added at each iteration during the network growth process. Secondly, the network output weights are updated by using the intermediate results. On the other hand, the main difference of DRESN and GESN is the changing trend of reservoir size. In GESN, the reservoir size is gradually increased when the algorithm iteration increases, while in DRESN, the reservoirs nodes are added or delated dynamically according to their significance to network performance, such architecture design method will lead to an appropriate network eventually.

In this paper, the $l_2$ penalty (ridge regression) technique is used to calculate the output weights of ESN. In the future, some other regularized regression methods, such as the $l_1$ penalty (lasso method) [26], the elastic net algorithm [33] which combines the $l_1$ and $l_2$ penalties together, will be tried to calculate the ESN output weight matrix to obtain better prediction performance.

5 Conclusions

How to determine the suitable network architecture is crucial for the successful application of ESNs. To solve this problem, the dynamical regularized ESN (DRESN) is proposed. Instead of adding subreservoirs group by group as done in the existing growing ESNs, the reservoir nodes of DRESN can be added or deleted dynamically according to their significance to network performance. Moreover, the output weights of DRESN are updated by the error minimization-based method, and the norms of the output weights are controlled by the regularized regression method to overcome the ill-posed problem. Furthermore, the convergence of DRESN is given to show its computational efficiency. The experimental results show that the proposed DRESN could have more compact network structure and better prediction performance than other existing ESN models.

Appendix 1: Parameters setting for OESN, RESN, ESN-LAR, ESN-DE and GESN

For OESN, RESN and ESN-LAR, the reservoir size varies from 100 to 1000 by the step 50, the sparsity varies from 0.005 to 0.5 by step of 0.005, the spectral radius varies from 0.5 to 0.95 by step of 0.05. In GESN, the size of the added subreservoir equals to 5, and the subreservoirs are added group by group until the predefined algorithm iteration is reached. For the ESN-DE, the parameters of DE algorithm are given as: the population size is 5, the maximum generation equals to 100, and the mutation rata and crossover probability are set as 0.2 and 0.4, respectively.