Memory augmented echo state network for time series prediction

Abstract

Echo state networks (ESNs), a special class of recurrent neural networks (RNNs), have attracted extensive attention in time series prediction problems. Nevertheless, the memory ability of ESNs is contradictory to nonlinear mapping, which limits the prediction performance of the network on complex time series. To balance the memory ability and the nonlinear mapping, an improved ESN model is proposed, named memory augmented echo state network (MA-ESN). When designing MA-ESN, both linear memory modules and nonlinear mapping modules are introduced into the reservoir in a new way of combination. The linear memory module improves the memory ability, while the nonlinear mapping module retains the nonlinear mapping of the network. Meanwhile, the echo state property of MA-ESN has been analyzed in theory. Finally, we have evaluated the memory ability and prediction performance of the proposed MA-ESN on benchmark time series data sets. The related experimental results demonstrate that the MA-ESN model outperforms some similar ESN models with a special memory mechanism.

1 Introduction

Time series prediction is the task of predicting future values based on historical data, which has attracted extensive attention in many fields in recent decades [1]. Due to the rich dynamics, recurrent neural networks (RNNs) become effective means for time series prediction problems [2]. However, due to gradient-based training algorithms for weights, the conventional RNNs suffer from some problems, such as high computational cost and slow convergence. Echo state networks (ESNs) are special RNNs, which only transform the optimization of output weights into a linear regression problem while the other weights do not need to be optimized after initialization. Hence, ESNs not only effectively overcome the above problems caused by gradient-based algorithms but also has rich dynamics [3]. The core component of ESNs is the random recurrent layer with a large number of sparsely connected neurons, named reservoir, which produces the richer dynamic representation for input signals. At present, ESNs have been widely used in scientific research and practical application fields, such as time series prediction [4], control [5], speech recognition [6], nonlinear signal processing [7], and system modeling [8].

Memory is a very important characteristic of ESNs and plays a crucial role in ESN-based time series prediction problems. Memory capacity (MC) was defined to measure the memory ability of ESNs, which is limited by the size of the reservoir [9]. A larger reservoir means a larger MC. But a larger reservoir would cause an overfitting problem. It is necessary to enhance the MC of ESNs with the limited size of the reservoir. Many efficient methods have been proposed by researchers to improve the MC of ESNs. In [10], a delay & sum readout is introduced to ESNs for obtaining larger MC, the main idea of which is adding trainable delays between the reservoir layer and the output layer. To improve the MC, Shuxian Lun et al. proposed a variable memory length echo state network (VML-ESN) whose memory length is automatically determined by the autocorrelation of input signals [11]. Qianli Ma et al. proposed an echo memory-augmented network (EMAN) by introducing an attention mechanism with sparse learnable weights to improve the long-term memory ability of ESNs [12]. To improve the MC of ESNs, leaky integrator units are used to design the reservoir [13]. In [14], long short-term echo state networks (LS-ESNs) were proposed to improve the memory ability of ESNs, where different skipping connections were introduced to different reservoirs. Although these methods mentioned above have improved the memory ability of ESNs, they inevitably added additional trainable parameters.

On the other hand, only increasing the MC of RNNs does not lead to better prediction performance on complex time series and it is necessary to maintain a certain nonlinear mapping ability [15]. There is a problem with the trade-off between memory and nonlinearity in the reservoir of ESNs [16]. To improve the ability of RNNs to learn long-term dependencies in sequential data, a linear memory network (LMN) was proposed by explicitly separating the recurrent layer into functional and memory components, which can be optimized by a standard backpropagation algorithm with a special initialization [17]. To effectively balance the memory-nonlinearity trade-off problem of ESNs, Butcher et al. proposed a novel architecture, named reservoir with random static projection ($R^{2} SP$) for time series prediction tasks, by combining a reservoir and two feedforward layers [18]. In [19], the memory-nonlinearity trade-off has been analyzed for reservoir computing in theory and improved the information processing ability by simultaneously introducing both linear and nonlinear activation functions into a mixed reservoir (mixture reservoir). The above literatures use the idea of nonlinear mapping and memory separation to solve the memory-nonlinearity trade-off problem.

Inspired by the above research, we propose an improved ESN model to balance the contradiction between the nonlinear mapping ability and memory capacity of ESNs, named memory augmented echo state network (MA-ESN). To better predict the complex time series, there are two interrelated tasks to be completed for prediction models, one is to nonlinear map an input sequence to a memory sequence which forms the outputs of the network, and the other is to remember the historical states which are used for nonlinear mapping. Based on the thought of the relative separation of nonlinear mapping and memory, MA-ESN introduces associated nonlinear mapping modules and linear memory modules, to simultaneously realize the nonlinear mapping and memory mechanisms in time series prediction. The linear memory module is mainly responsible for improving the memory capacity, while the nonlinear mapping module retains the nonlinear mapping of MA-ESNs. In addition, the stability of the network is analyzed in theory and a sufficient condition is developed. Finally, we have given a detailed experimental analysis to test the effectiveness of our method. The related experimental results demonstrate that the MA-ESN model outperforms the typical ESNs and some similar ESN variants on memory capacity and prediction performance.

The contributions of this paper mainly include the following aspects:

• 1) A special design method of reservoirs is proposed for ESNs to realize the memory-nonlinearity trade-off, which improves the memory capacity while retaining the nonlinear mapping ability.

• 2) The stability (ESP) of the proposed MA-ESN has been analyzed in theory, and a sufficient condition is given.

• 3) Compared with the typical ESNs and some ESN variants with special memory mechanisms, the MA-ESN model can obtain larger memory capacity and better prediction performance on some benchmark time series data sets.

The remainder of this article is organized in the following way. Section 2 has briefly reviewed the typical ESNs. In Sect. 3, the proposed MA-ESN has been described in detail, including the architecture, the training algorithm, the stability analysis in theory, as well as the computational complexity analysis. In Sect. 4, a detailed analysis of the experimental results on benchmark time series data sets has been given. Finally, Sect. 5 has concluded this article.

2 Echo state networks

In this section, we will briefly review the typical ESNs, including the basic architecture, the mathematical description, the echo state property, the reservoir parameters, and the memory capacity.

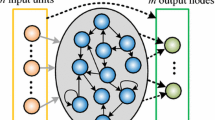
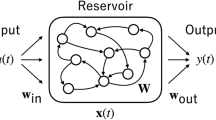
Figure 1 shows the basic architecture of typical ESNs. It can be seen from Fig. 1 that, similar to RNNs, the typical ESNs have three layers, including the input layer, the recurrent layer, and the output layer. Usually, the recurrent layer is named a reservoir layer, which consists of a larger number of neurons with sparse and random recurrent connections. Let K, N, and L denote the number of neurons in the input layer, the reservoir layer, and the output layer, respectively. $u(t) \in R^{K}$ represents the input signal at time step t, $x(t) \in R^{N}$ and $y(t) \in R^{L}$ respectively denote the corresponding reservoir state and output signal. $t = 1,2, \ldots ,T$, where T denotes the number of training samples. $W^{in} \in R^{N \times K}$, $W^{res} \in R^{N \times N}$, and $W^{out} \in R^{L \times (N + K)}$ represent the input weight matrix, reservoir weight matrix, and output weight matrix, respectively. $W^{{{\text{in}}}}$ and $W^{{{\text{res}}}}$ are fixed after random initialization with a certain degree of scaling, and $W^{out}$ needs to be trained for better performance. After feeding the input signal to the network, the computational model of the network can be described by the following mathematical formulas.

$$x(t) = f(W^{{{\text{in}}}} u(t) + W^{{{\text{res}}}} x(t - 1))$$

(1)

$$y(t) = W^{{{\text{out}}}} \left[ {u(t);x(t)} \right]$$

(2)

where f (usually tanh) denotes the activation function for reservoir neurons and $[u(t);x(t)]$ is the concatenation of $u(t)$ and $x(t)$.

Fig. 1

Architecture of typical ESNs

After a certain number of initial training steps (washout period), the influence of initial reservoir states gradually disappears, then the remainder of reservoir states $x(t)$ are stored in a matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}$. Let us store the desired output in a matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y}$, the optimal output weights can be computed by solving a regression problem as follows.

$$\min \left\| {W^{{{\text{out}}}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y} } \right\|_{2}^{2}$$

(3)

$$W^{{{\text{out}}}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}^{T} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}^{T} )^{ - 1}$$

(4)

However, overlarge reservoirs inevitably lead to the overfitting problem, which will weaken the generalization performance of the network. To solve this problem, a regularization term is usually needed to calculate the output weights $W^{{{\text{out}}}}$ as follows.

$$W^{{{\text{out}}}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}^{T} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}^{T} + \lambda I)^{ - 1}$$

(5)

where I is the identity matrix and $\lambda$ is a regularization coefficient.

Echo State Property (ESP) is a necessary feature for ESNs to work well, which ensures the dynamic stability of the reservoir. To hold the ESP, the reservoir weight matrix is usually initialized as follows.

$$W^{{{\text{res}}}} = SR \cdot \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W} }}{{\lambda _{{\max }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W} )}},\;0 < SR < 1$$

(6)

where SR is the spectral radius of $W^{res}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}$ is a sparse random matrix, and $\lambda_{\max } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W} )$ denotes its eigenvalue with the largest absolute value. Usually, the sparsity (SD) of the matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}$ is set to 2–5%. In addition, the input scale factor (IS) is another main parameter of ESNs, which is used to scale the input weight matrix $W^{{{\text{in}}}}$ for satisfying the specific activation range of reservoir units.

Memory is another important feature of ESNs, which plays a crucial role in ESN-based time series prediction problems. As a measure of memory ability, the memory capacity (MC), is proposed to evaluate the ability of ESNs to reconstruct a random input sequence, which is defined as follows.

$$MC_{k} = \frac{{\text{cov} ^{2} (u(t - k),y_{k} (t))}}{{\text{var} (u(t)) \cdot \text{var} (y_{k} (t))}}$$

(7)

$$MC = \sum\limits_{k = 1}^{\infty } {MC_{k} }$$

(8)

where $MC_{k}$ is named as the determination coefficient, u(t) is the input signal of ESNs at time t, $y_{k} (t)$ is the corresponding network output, k denotes the step size of delay, cov and var respectively represent the covariance and variance of the corresponding signals. It has been proved that, if the linear activation function is used for reservoir neurons, the MC of ESNs can reach its maximum under certain conditions. However, the memory ability of ESNs is contradictory to nonlinear mapping, which limits the prediction performance of the network on complex time series. Hence, it is a hot topic to solve the memory-nonlinearity trade-off problem for ESNs. Next, we will give our work in detail to balance the memory ability and the nonlinear mapping for ESNs, named memory augmented echo state network (MA-ESN).

3 Memory augmented echo state network

To solve the contradiction between the nonlinear mapping ability and memory capacity of ESNs, an ESN variant with a special memory mechanism was proposed by dividing the reservoir into nonlinear mapping modules and linear memory modules, where two types of modules interact with each other. We named it Memory Augmented Echo State Network (MA-ESN).

3.1 Architecture of memory augmented echo state network

It is known from Sect. 1 that, to solve the contradiction between the nonlinear mapping ability and memory capacity, ESNs need to perform two related assignments at the same time: one is to nonlinear map an input sequence to a memory sequence which forms the outputs of the network, and the other is to remember the historical states serving for the nonlinear mapping. Inspired by the thought of relatively separating the two associated assignments at the architectural level, we proposed a separation mechanism of memory-nonlinearity by designing two separate modules in the reservoir, including a nonlinear mapping module and a linear memory module. Figure 2 shows the proposed separation mechanism of memory-nonlinearity, where $V_{{{\text{Input}}}}$, $V_{{{\text{Hidden}}}}$, $V_{{{\text{Memory}}}}^{\prime }$, $V_{{{\text{Memory}}}}$, $V_{{{\text{Output}}}}$ respectively represent the input space, the hidden space, the memory space of the last moment, the memory space of the current moment, and the output space, the small black square in the connection between $V_{{{\text{Memory}}}}^{\prime }$ and $V_{{{\text{Memory}}}}$ denotes a time delay. As shown in Fig. 2, the two modules work independently and serve each other. The linear memory module M is used as an autoencoder to remember the output sequence of the nonlinear mapping module H, meanwhile, the nonlinear mapping module combines the input signals and the encoding outputs of the linear memory module to form the new features by a nonlinear activation function. The nonlinear mapping module works as a feedforward neural network with a nonlinear activation function to model the nonlinear characteristic of the input signals, and the linear memory module acts as a linear reservoir to learn the long-term dependence of the input sequence. The proposed separation mechanism combines the nonlinear feedforward network with a linear recurrent network in a special way. Hence, by explicitly separating the two modules, the reservoir can improve the memory capacity while keeping stronger nonlinear mapping ability. In the next, we will adopt the separation mechanism to balance the memory ability and the nonlinear mapping for ESNs.

Fig. 2

The separation mechanism of memory-nonlinearity

Based on the separation mechanism mentioned above, the proposed MA-ESN separates its reservoir into two parts, including a nonlinear mapping module and a linear memory module. As shown in Fig. 3, these two modules are relatively independent and communicate with each other, where the linear memory module and the nonlinear mapping module are respectively enclosed by blue dotted lines and red dotted lines, and the small black square in the edge represents a time delay.

Fig. 3

Architecture of memory augmented echo state network (MA-ESN)

The nonlinear mapping module is a feedforward neural network that generates new features from the input signals and the outputs of the linear memory module by a nonlinear activation function, meanwhile, the linear memory module is responsible for memorizing the output sequence of the nonlinear mapping module with a linear recurrent. Finally, only the outputs of the linear memory module are used to form the outputs of the network. Let $N_{x}$ and $N_{y}$ respectively denote the number of input and output neurons. The sizes of the nonlinear mapping module and linear memory module are defined as $N_{h}$ and $N_{m}$, respectively. $x^{t} \in R^{{N_{x} }}$, $h^{t} \in R^{{N_{h} }}$, $m^{t} \in R^{{N_{m} }}$, and $y^{t} \in R^{{N_{y} }}$ respectively denote the input signals of the input layer, the nonlinear mapping module, the linear memory module, and the output signals of the output layer, among which $h^{t}$, $m^{t}$ and $y^{t}$ are calculated by Eqs. (9), (10), and (11), respectively.

$$h^{t} = f(W^{xh} x^{t} + W^{mh} m^{t - 1} )$$

(9)

$$m^{t} = W^{hm} h^{t} + W^{mm} m^{t - 1}$$

(10)

$$y^{t} = W^{my} m^{t}$$

(11)

where f (usually tanh) is a nonlinear activation function of the neurons in the nonlinear mapping module, $W^{xh} \in R^{{N_{h} \times N_{x} }}$, $W^{mh} \in R^{{N_{h} \times N_{m} }}$, $W^{hm} \in R^{{N_{m} \times N_{h} }}$, $W^{mm} \in R^{{N_{m} \times N_{m} }}$, and $W^{my} \in R^{{N_{y} \times N_{m} }}$ respectively denote the input weights, the connection weights from the linear memory module to the nonlinear mapping module, the connection weights from the nonlinear mapping module to the linear memory module, the internal weights of the linear memory module, and the output weights of the network.

Algorithm 1

Memory Augmented Echo State Network

3.2 Training algorithm for MA-ESN

The whole training process of MA-ESN mainly includes three stages. The first stage is to randomly initialize the weights, including the input weights $W^{xh}$, the connection weights from the nonlinear mapping module to the linear memory module $W^{hm}$, and the connection weights from the linear memory module to the nonlinear mapping module $W^{mh}$, whose elements are randomly generated from [− 1,1] under the uniform distribution. The internal weights $W^{mm}$ in the linear memory module are obtained as done in (6). The second stage is to calculate the reservoir state. After the input signal and the random initial state of the linear memory module are fed into the nonlinear mapping module, the outputs of the nonlinear mapping module are calculated as done in (9) with a nonlinear mapping. Then, the state of the linear memory module is updated to remember the output sequence of the nonlinear mapping module as done in (10). Finally, the outputs of the linear memory module along with the input signals of the network are fed into the output layer for forming the predicted outputs. The third stage is to calculate the output weights $W^{my}$ as done in (5) after washing out a certain number of steps. The detailed training algorithm is listed in Algorithm 1.

3.3 Stability analysis

Echo State Property (ESP) is an important feature for the reservoir to work with the attenuation of the dynamic activity, which guarantees the dynamic stability of the network. To hold its dynamic stability, MA-ESN as an ESN-based variant must ensure the ESP. In the next, we will give a sufficient condition to ensure the ESP of MA-ESN. First, a definition of the Lipschitz condition is introduced for the activation function f as follows.

Definition 1.

Given an activation function f and a positive constant L, for all $y^{\prime},y^{\prime\prime} \in \Omega$, such that.

$$\left| {f(y^{\prime}) - f(y^{\prime\prime})} \right| \le L\left| {y^{\prime} - y^{\prime\prime}} \right|$$

(12)

Then, the activation function f satisfies the Lipschitz condition.

Let $m^{t}$ and $\tilde{m}^{t}$ be any two memory states of the linear memory module and define the distance between $m^{t}$ and $\tilde{m}^{t}$ as $\left\| {y^{t} } \right\| = \left\| {m^{t} - \tilde{m}^{t} } \right\|$. Then, the ESP of MA-ESN can be equivalently defined as the distance between the memory states of the linear memory module $m^{t}$ and $\tilde{m}^{t}$ satisfies the shrinkage property over time, that is $\left\| {y^{t} } \right\|_{2} \to 0$ when $t \to \infty$ for all right infinite input sequences $u^{ + \infty } \in U^{ + \infty }$. Based on the definition mentioned above, we will give the sufficient condition for the proposed MA-ESN to hold the ESP by the following Theorem 1.

Theorem 1.

Given the proposed MA-ESN model as shown in (9) and (10), define the maximum singular value for matrices $W^{hm}$, $W^{mh}$, and $W^{mm}$ as $\sigma_{\max } (W^{hm} )$, $\sigma_{\max } (W^{mh} )$ and $\sigma_{\max } (W^{mm} )$, respectively. If the following conditions are satisfied:

• 1. The activation function f satisfies the Lipschitz condition with the Lipschitz coefficient $L \le 1$;

• 2. $\sigma_{\max } (W^{hm} )\sigma_{\max } (W^{mh} ) + \sigma_{\max } (W^{mm} ) < 1$.

Then, the MA-ESN model holds the ESP, that is, $\mathop {\lim }\nolimits_{t \to \infty } \left\| {y^{t} } \right\|_{2} = 0$ for all right infinite input sequences $u^{ + \infty } \in U^{ + \infty }$.

Theorem 1 can be proved using a method similar to [3]. The detailed proof has been listed in Appendix A.

3.4 Computational complexity analysis

First, the computational complexity of the reservoir in the MA-ESN is calculated as follows.

$$C_{res} = C_{h} + C_{m} = O\,(TN_{x} N_{h} + 2TN_{h} N_{m} + SDTN_{m}^{2} )$$

(13)

where $T$, $N_{x}$, $N_{h}$, $N_{m}$ and $SD$ respectively represent the length of signals, the number of input neurons, the size of the nonlinear mapping module, the size of the linear memory module, and the sparsity. The size of the MA-ESN is $N_{m} + N_{x}$. Therefore, the computational complexity of output weights is calculated as follows.

$$C_{{{\text{reg}}}} = O\,(TN_{y} P + (T + P + N_{y} )P^{2} )$$

(14)

where $N_{y}$ represent the number of output neurons and $P = N_{m} + N_{x}$. Since the size of the linear memory module is usually larger than the number of input neurons, we can get $N_{m} \gg N_{x}$, so we have $P \approx N_{m}$. Moreover, the length of signals is usually larger than the number of output neurons, so we have $T \gg N_{y}$. Therefore, Eq. (14) can be rewritten as:

$$C_{{{\text{reg}}}} \approx O\,((T + P)P^{2} ) \approx O\,(TN_{m}^{2} + N_{m}^{3} )$$

(15)

In the MA-ESN, the size of the nonlinear mapping module is consistent with the size of the linear memory module. Therefore, the computational complexity of the MA-ESN is:

$$\begin{aligned} C_{{{\text{MA}} - {\text{ESN}}}} &= \;C_{{{\text{res}}}} + C_{{{\text{reg}}}} \\ \quad \quad \quad &=\; O\,(TN_{x} N_{h} + 2TN_{h} N_{m} + SDTN_{m}^{2} ) + O\,(TN_{m}^{2} + N_{m}^{3} ) \\ \quad \quad \quad &=\; O\,(TN_{x} N_{m} + 3TN_{m}^{2} + SDTN_{m}^{2} + N_{m}^{3} ) \\ \quad \quad \quad \; &\approx \;O\,(3TN_{m}^{2} + N_{m}^{3} ) \\ \end{aligned}$$

(16)

Moreover, the computational complexity of ESNs is:

$$C_{{{\text{ESNs}}}} = C_{{{\text{res}}}} + C_{{{\text{reg}}}} \approx O\,(TN_{m}^{2} + N_{m}^{3} )$$

(17)

Therefore, the relationship between $C_{MA - ESN}$ and $C_{ESNs}$ is:

$$\frac{{C_{{\text{MA - ESN}}} }}{{C_{{{\text{ESNs}}}} }} = \frac{{O\,(3TN_{m}^{2} + N_{m}^{3} )}}{{O\,(TN_{m}^{2} + N_{m}^{3} )}} < 3$$

(18)

Equation (18) shows that the computational complexity of the MA-ESN is less than 3 times that of ESNs.

4 Experiments results and analysis

In this section, the performance of the proposed MA-ESN model has been evaluated on benchmark time series data sets. First, the memory ability of MA-ESN is tested on a one-dimensional unstructured random sequence. Then, the prediction performance of MA-ESN is tested on some benchmark time series with different characteristic, including the 10-order NARMA system, the Lorenz system, the Sunspot time series, daily minimum temperatures [20, 20], and the NCAA2022 data set [21]. For further evaluation, the typical ESNs [3] and some ESN variants with special memory mechanisms are used to compare with the proposed MA-ESN, including R²SP [18], VML-ESN [11], LS-ESNs [14], mixture reservoir [19]. Meanwhile, as two state-of-the-art models, the long short-term memory (LSTM) [22] and the chain-structure echo state network (CESN) [23] are also used for comparisons. The MC is calculated as (7) and (8) to evaluate the memory ability of random series. Meanwhile, the root-mean-square error (RMSE) is used to test the prediction performance on benchmark time series, which is defined as:

$${\text{RMSE}} = \sqrt {\frac{1}{A}\sum\limits_{t = 1}^{A} {(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{t} - y_{t} )^{2} } }$$

(19)

where A is the total length of the training or testing sequence. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{t}$ and $y_{t}$ are the predicted output and desired output at time t, respectively. All simulations are carried out using MATLAB 2022a on a laptop with CPU @ 3.10GHz and RAM: 8.0GB.

4.1 Experiments on memory ability

The aim of the proposed MA-ESN is to improve the memory ability of ESNs while maintaining a certain nonlinear mapping properties by separating a reservoir into a nonlinear mapping module and a memory module. First, the memory ability of MA-ESN is evaluated. Unstructured sequences are usually used to test the memory ability of ESNs. Hence, to test the memory ability of MA-ESN, a one-dimensional random series with 6000 samples is generated from [− 0.8, 0.8] with uniform distribution, as shown in Fig. 4. Before calculating the output weights, the first 1000 samples are discarded. The number of output neurons of MA-ESN is twice the size of the linear memory module, where the kth output neuron is used to reconstruct the past inputs with a k-step delay. The ridge regression regularization is used for calculating the output weights of networks as done in (5).

Fig. 4

Random series

To investigate the role of nonlinear and memory modules in the memory capacity of the MA-ESN, we respectively fixed the size of the nonlinear modules as 50, 100, 150, 200, and gradually increased the size of the linear modules from 30 to 200 with the interval of 10. Figure 5 shows the effect of nonlinear and memory modules with different sizes on the memory capacity of MA-ESN. As shown in Fig. 5, the memory capacity of the proposed MA-ESN monotonically increases with the growth of nonlinear and memory modules. The maximum increment of MC caused by the growth of the linear memory module is 34, while the maximum increment of MC caused by the growth of the nonlinear mapping module is 17. It means that the linear memory module plays a larger role in improving the MC of MA-ESN than the nonlinear mapping module.

Fig. 5

The effect of nonlinear and memory modules on the memory capacity of MA-ESN

To further evaluate the memory ability of MA-ESN, the typical ESNs and several variants with special memory mechanisms are used for comparison. For the sake of fairness, all comparison models have the same reservoir parameters which are listed in Table 1, including the reservoir size (N), sparsity (SD), regularization coefficient (λ), spectral radius (SR), input scale factor (IS), and washout period (WP). It should be noted that the size of the reservoir of MA-ESN is defined as the size of the linear memory module. Meanwhile, linear memory modules and nonlinear mapping modules of MA-ESN have the same size. Figure 6 shows the k-delay MC ($MC_{k}$) for all models from k = 1 to k = 200, named forgetting curves, which measure the ability of the network to recover the delayed input signal. As shown in Fig. 6, the MA-ESN can recover the delayed input sequence close to 100% for delays up to 19, while the other three models only recover the delayed input sequence well with delays of less than 17. It means our method is effective in improving the memory ability of the network by separating reservoirs into nonlinear mapping modules and linear memory modules.

Table 1 Reservoir parameter settings for all models in the experiment on memory ability

Fig. 6

The forgetting curves of all comparison models

Table 2 lists the statistical comparison of the experiment results over 30 runs, including the mean (Mean) of MC, the standard deviation (Std) of MC, and the training time, where the winners are marked in bold. As shown in Table 2, compared with, the MC of the proposed MA-ESN has increased by 49.8%, 74.6%, 7.7%, 48.1%, 12.5%, 7.2%, and 23.0% than those of the typical ESNs, LSTM, $R^{2} SP$, VML-ESN, LS-ESNs, mixture reservoir, and CESN, respectively. It means that our method has greatly improved the memory capacity of the network by separating the reservoir into nonlinear mapping modules and linear memory modules. Meanwhile, the smallest standard deviation means the proposed MA-ESN has the best stability. On the other hand, the training time of MA-ESN is similar to that of ESNs, VML-ESN, and mixture reservoir models.

Table 2 Memory capacity for all comparison models

4.2 Experiments on prediction performance

Usually, complex time series shows strong nonlinearity and long-term dependency, which requires the nonlinear mapping and memory ability of prediction models. Hence, the prediction performance of the proposed MA-ESN is tested on some benchmark time series with strong nonlinearity and long-term dependency. Better prediction performance means strong nonlinearity and memory ability of prediction models. First, the benchmark time series data sets used in this experiment will be analyzed in detail, the main characteristics of which are listed in Fig. 7 and Table 3.

Fig. 7

Benchmark time series data sets

Table 3 Information from five benchmark time series data sets

4.2.1 Data sets

NARMA system: As shown in Eq. (20), the nonlinear auto-regressive moving average (NARMA) system is a discrete-time dynamical system with strong nonlinearity and long-term memory. Hence, the time series generated by the NARMA system is often used to test the prediction performance of ESN variants. The 10th-order NARMA system is given by

$$z(n + 1) = 0.3z(n) + 0.05z(n)\sum\limits_{j = 0}^{9} {z(n - j) + 1.5u(n)u(n - 9) + 0.1}$$

(20)

where the input sequence $u(n)$ is randomly generated from the interval [0,0.5] with uniform distribution, and the initial state $z(n)$ is set to 0 from $n = 0$ to $n = 9$. A sequence with 2400 points is generated with Eq. (20), the first 1800 of which are used to train the network and the remainder is used for testing.

Lorenz system: The Lorenz system is a multivariable chaotic dynamic system with strong nonlinearity, which is often used as a benchmark to evaluate the prediction performance of ESN variants on time series. Usually, the Lorenz system is defined by the following differential equation,

$$\left\{ {\begin{array}{*{20}l} {\frac{{dx}}{{dt}} = a( - x + y)} \\ {\frac{{dy}}{{dt}} = bx - y - xz} \\ {\frac{{dz}}{{dt}} = xy - cz} \\ \end{array} } \right.$$

(21)

where a, b, and c are usually set to 10, 28, and 8/3 for chaotic characteristics. After respectively setting the initial state $(x(0),\;y(0),\;z(0))$ and the step size to $(12,\;2,\;9)$ and 0.2, a time series with 2400 points is generated by the fourth-order Runge-Kutta method, the first 1800 points of which are used to train the network and the remainder are used as testing samples. It should be noted that the x-axis sequence of the system is used in this experiment after being normalized into [− 1, 1].

Sunspot data sets: The sunspot number series is the dynamic characteristics of the high-intensity magnetic field on the sun, which is usually used to measure the speckle activity of the sun and has an important impact on the earth. However, the potential solar activity has strong uncertainty and nonlinearity, which makes the sunspot number prediction very challenging. Hence, the sunspot number is usually used as a benchmark to evaluate the performance of ESN-based models on time series prediction. In this experiment, we use the smoothed monthly average number of sunspots to evaluate the performance of MA-ESN on time series prediction. 3198 samples from 1749 to 2020 from the WDC-SILSO are divided into two parts, the first 1800 of which are used to train the network and the remainder are used for testing. Before being input into the network, normalization is used on the total data set.

Daily minimum temperatures: Daily minimum temperatures exhibit long memory behavior and strong nonlinearity, the prediction of which is a challenging task. In this experiment, 3650 samples from January 1st, 1981 to December 31st, 1990 in Melbourne are used to test the performance of MA-ESN on time series prediction, the first 2500 of which are used as training samples and 2500 to 3500 are used for testing. The basic task is to directly predict the minimum temperature of the next day in Melbourne (one-step-ahead prediction). Before being input into the network, the data is smoothed with a 5-step moving window to reduce its nonlinearity and normalized to [− 1, 1].

NCAA2022 data set: NCAA2022 data set is comprehensive benchmark for fairly evaluating time series prediction models, which is designed by transforming four typical data sets with different characteristics into 16 prediction problems with different frequency characteristics [24]. In this paper, the stock index with low-pass, high-pass, band-pass, and band-stop frequency features is selected from NCAA2022 data set to evaluate the prediction performance of the proposed MA-ESN, i.e., the NCAA2022 data set I, NCAA2022 data set V, NCAA2022 data set IX, and NCAA2022 data set XIII. Each sequence includes 7500 data points, the first 5000 of which are used for training and the remainder are used for testing. It should be noted that the NCAA2022 data set is normalized into $[ - 1,1]$ before being fed into the network.

4.2.2 Parameter settings

The prediction models covered in this subsection involve the selection of several reservoir parameters which are listed in Table 4, including the reservoir size (N), sparsity (SD), regularization coefficient (λ), spectral radius (SR), input scale factor (IS), and washout period (WP). It is worth noting that the WP is 200 in the NARMA system, the Lorenz system, the sunspot time series, and the daily minimum temperatures, and 1000 in the NACC2022 data set. It should be noted that the size of the reservoir of MA-ESN is defined as the size of the linear memory module.

Table 4 Reservoir parameter settings for all models in the experiment on prediction performance

4.2.3 Analysis of experimental results

To investigate the role of nonlinear and memory modules in the prediction ability of the MA-ESN, we gradually increased the size of modules from 50 to 300 with the interval of 50. The testing RMSE of the MA-ESN with different sizes of nonlinear mapping modules and linear memory modules are shown in Figs. 8 and 9, respectively. Specifically, Fig. 8 corresponds to the model with a fixed size of linear memory modules and Fig. 9 corresponds to the model with a fixed size of nonlinear mapping modules. From the Figs. 8, we find that the testing RMSE monotonically decreases with the increase in the nonlinear mapping module over a range on most data sets, except for the NCAA2022 data set I, V and IX. From Fig. 9, we can see that the testing RMSE monotonically decreases with the increase in the linear memory module on the Lorenz system and NCAA2022 data sets. However, the testing RMSE on the other data sets descends firstly then ascends with the increase in the linear memory module, whose minimum value is located at $N_{m} = 100$. It means that both the nonlinear mapping module and linear memory module play a major role in time series predictions, and the MA-ESN can independently control the nonlinear mapping module and the memory module according to the characteristics of the given data.

Fig. 8

The effect of nonlinear mapping modules on the prediction performance of MA-ESN

Fig. 9

The effect of linear memory modules on the prediction performance of MA-ESN

The desired outputs vs the prediction outputs of the eight prediction models on all benchmark time series are shown in Fig. 10, and the corresponding prediction errors are listed in Fig. 11. As can be seen from Fig. 10 prediction outputs of MA-ESN are closer to the desired outputs compared to the prediction outputs of the other models. It can be seen from Fig. 11 that the MA-ESN model has a smaller error fluctuation compared to the remaining comparative models. Therefore, for all benchmark time series, the proposed MA-ESN model has outperformed the other seven models on prediction performance. This suggests that the memory mechanism of MA-ESN outperforms the remaining comparative models in prediction performance.

Fig. 10

The desired outputs vs the prediction outputs of the eight models on the five benchmark time series (The blue solid and the red dashed lines respectively denote the desired outputs and the prediction outputs of the prediction models)

Fig. 11

Prediction errors of the eight models on the five benchmark time series data sets (The red dashed line represents the prediction errors of MA-ESN)

For each model, we conduct 30 independent experiments on every time series, the statistical results of the experiments are shown in Tables 5, 6, 7, 8, 9, including training RMSE, testing RMSE, and training time, where the winners are marked in bold. It can be seen from Tables 5, 6, 7, 8, 9 that the MA-ESN has the smallest training RMSE on the given data sets except for the NCAA2022 data set I, V and IX, and has the smallest testing RMSE on the given data sets except for the NARMA system and NCAA2022 data set IX. This implies that the MA-ESN has improved the learning and prediction performance of ESNs by separating the reservoir into linear memory modules and nonlinear mapping modules. Although the training time of the MA-ESN is slightly longer than that of the typical ESNs, VML-ESN and mixture reservoir, it is much smaller than LSTM, LS-ESNs and CESN. This is because only the connection weights between the linear module and the output layer of the MA-ESN need to be calculated, which does not increase the computational burden too much. Meanwhile, the MA-ESN has the smallest standard deviation of the testing RMSE on most data sets except for NCAA2022 data sets I, IX and XIII, which means better stability. Overall, in most cases, it is effective to balance the memory and the nonlinear mapping ability by separating the reservoir into the relatively independent linear memory modules and nonlinear mapping modules.

Table 5 Experimental results on NARMA system

Table 6 Experimental results on Lorenz system

Table 7 Experimental results on sunspot time series

Table 8 Experimental results on daily minimum temperatures

Table 9 Experimental results on NCAA2022 data set

5 Conclusion

For the typical ESNs, the nonlinear mapping ability is contradictory to the memory capacity. To solve this problem, we propose a novel echo state network by separating the reservoir into nonlinear mapping modules and linear memory modules. The linear memory module improves the memory capacity, while the nonlinear mapping module retains the nonlinear mapping ability of the network. Meanwhile, the echo state property of MA-ESN has been analyzed in theory, and a sufficient condition has been provided. Compared with the typical ESNs, the LSTM, the $R^{2} SP$, the VML-ESN, the LS-ESNs, the mixture reservoir, and the CESN, the MA-ESN model has a larger memory capacity and better prediction performance on benchmark time series. In our further work, we will further improve the stability of the proposed MA-ESN and apply it to predict the key parameters in complex industrial processes.

Appendix A

Similar to [3], Theorem 1 can be proved as follows.

Recall that,

$$\left\| {f(z(n)) - f(z^{\prime}(n))} \right\| \le L\left\| {z(n) - z^{\prime}(n)} \right\|\;$$

and the activation function f satisfies the Lipschitz condition and the Lipschitz coefficient $L \le 1$.

So there are

$$\begin{gathered} \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} \left\| {f(W^{xh} x^{t + 1} + W^{mh} m^{t} ) - f(W^{xh} x^{t + 1} + W^{mh} \tilde{m}^{t} )} \right\|_{2} \hfill \\ \le \left\| {(W^{xh} x^{t + 1} + W^{mh} m^{t} ) - (W^{xh} x^{t + 1} + W^{mh} \tilde{m}^{t} )} \right\|_{2} \hfill \\ \end{gathered}$$

Thus there are

$$\begin{aligned} \left\| {y^{t + 1} } \right\|_{2} = & \left\| {m^{t + 1} - \tilde{m}^{t + 1} } \right\|_{2} = \left\| {(W^{hm} h^{t + 1} + W^{mm} m^{t} ) - (W^{hm} h^{t + 1} + W^{mm} \tilde{m}^{t} )} \right\|_{2} \\ \quad \quad \,\,\,\, = & \left\| {\left\{ {W^{hm} [f(W^{xh} x^{t + 1} + W^{mh} m^{t} )] + W^{mm} m^{t} } \right\} - \left\{ {W^{hm} [f(W^{xh} x^{t + 1} + W^{mh} \tilde{m}^{t} )] + W^{mm} \tilde{m}^{t} } \right\}} \right\|_{2} \\ \quad \quad \,\,\,\, = & \left\| {W^{hm} [f(W^{xh} x^{t + 1} + W^{mh} m^{t} )] - W^{hm} [f(W^{xh} x^{t + 1} + W^{mh} \tilde{m}^{t} )] + W^{mm} m^{t} - W^{mm} \tilde{m}^{t} } \right\|_{2} \\ \quad \quad \,\,\,\, \le & \left\| {W^{hm} \left\{ {[f(W^{xh} x^{t + 1} + W^{mh} m^{t} )] - [f(W^{xh} x^{t + 1} + W^{mh} \tilde{m}^{t} )]} \right\}} \right\|_{2} + \left\| {W^{mm} (m^{t} - \tilde{m}^{t} )} \right\|_{2} \\ \quad \quad \,\,\,\, = & \left\| {W^{hm} } \right\|_{2} \left\| {f(W^{xh} x^{t + 1} + W^{mh} m^{t} ) - f(W^{xh} x^{t + 1} + W^{mh} \tilde{m}^{t} )} \right\|_{2} + \left\| {W^{mm} } \right\|_{2} \left\| {m^{t} - \tilde{m}^{t} } \right\|_{2} \\ \quad \quad \;\,\, \le & \left\| {W^{hm} } \right\|_{2} \left\| {(W^{xh} x^{t + 1} + W^{mh} m^{t} ) - (W^{xh} x^{t + 1} + W^{mh} \tilde{m}^{t} )} \right\|_{2} + \left\| {W^{mm} } \right\|_{2} \left\| {m^{t} - \tilde{m}^{t} } \right\|_{2} \\ \quad \quad \;{\kern 1pt} \, = & \left\| {W^{hm} } \right\|_{2} \left\| {W^{mh} (m^{t} - \tilde{m}^{t} )} \right\|_{2} + \left\| {W^{mm} } \right\|_{2} \left\| {m^{t} - \tilde{m}^{t} } \right\|_{2} \\ \quad \quad \,\,\, = & \left\| {W^{hm} } \right\|_{2} \left\| {W^{mh} } \right\|_{2} \left\| {m^{t} - \tilde{m}^{t} } \right\|_{2} + \left\| {W^{mm} } \right\|_{2} \left\| {m^{t} - \tilde{m}^{t} } \right\|_{2} \\ \quad \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \, = & \left\| {W^{hm} } \right\|_{2} \left\| {W^{mh} } \right\|_{2} \left\| {y^{t} } \right\|_{2} + \left\| {W^{mm} } \right\|_{2} \left\| {y^{t} } \right\|_{2} \\ \quad \quad \,\,\, = & (\left\| {W^{hm} } \right\|_{2} \left\| {W^{mh} } \right\|_{2} + \left\| {W^{mm} } \right\|_{2} )\left\| {y^{t} } \right\|_{2} \\ \quad \quad \,\,\, = & (\sigma_{\max } (W^{hm} )\sigma_{\max } (W^{mh} ) + \sigma_{\max } (W^{mm} ))\left\| {y^{t} } \right\|_{2} \\ \end{aligned}$$

Therefore, if $\sigma_{\max } (W^{hm} )\sigma_{\max } (W^{mh} ) + \sigma_{\max } (W^{mm} ) < 1$ is true, then $\mathop {\lim }\nolimits_{t \to \infty } \left\| {y^{t} } \right\|_{2} = 0$ holds for all right infinite input sequences $u^{ + \infty } \in U^{ + \infty }$. That is, the MA-ESN model has the ESP.